2018届考前三个月高考数学(理科)总复习训练(江苏用) 解答题滚动练6 Word版含答案
全国通用2018版高考数学总复习考前三个月解答题滚动练6理.doc

解答题滚动练61.已知函数_f(x)=cos 2^r+2sin2^+2sin x.JI r JI JI (1)将函数广(2x)的图象向右平移;个单位长度得到函数g(x)的图象,若,—,求函0 J.乙乙数g(x)的值域;⑵已知a, b, c分别为△/此'中角』,B,。
的对边,且满足b=2,辰(0,成),f(A)=吏+1,胰a= 2力sin A,求ZX/H。
的面积.解f{x) =cos 2x+2sir?x+2sin x= cos 2x~\~ (1 —cos 2x) +2sin x=l + 2sin x.(1)平移可得g(x) =2sin(2x—耳]+1,r JI JI•12,'JI r JI 2 JI•Q y -- fZZ - -- -----3 6, 3 ,JI当入=正时,g(x)min=0;5 JI当X=~^时,&(才)max = 3 ,..•所求值域为[o, 3].⑵由已^n^3a=2Z?sin 4及正弦定理,得柬sin J=2sin ^sin A,..sin b=^~.JIJI二B=五,由f(W) =yj"^ +1,得sin A— %,由正弦定理,得加从而,=号~,•< _1 ,.厂1 2诉协+忠3+柘••S^ABC—Q abs 1 n C—X X 2 X —.Z L J O 7E O2.在等差数列{&}中,公差必0,勿=1,且切,血,禹成等比数列.(1)求数列{绥}的通项公式;⑵若上=令求数列{〃}的前刀项和Tn.解(1)由切,32, 35成等比数列知,总=3135,即(动+责』'(切+ 44),即d=2axd,又必0, 31 = 1,解得d=2,故&=2刀一1.9n—1 1 Q 4 ?n— 1(2)bn= 2〃,则几=云+瑚+瑚------ 2〃 , ①O O U U O1 / 1 1,3,5, . 2/7—1 —由①式两边><S,有云久=瑚+瑚+卒 ----- 史+i , ②O O O 0由①一②,刀+ 1 化简得1=1一千.3.如图,在四棱锥夕一/时中,底面/助为平行四边形,AP=AB=AC=a, AD=y]2a, PAL 底面ABCD.⑴求证:平面冏平面0G(2)在棱任?上是否存在一点E,使得二面角B-AE-D的平面角的余弦值为一碧?若存在, 求出4=争^值;若不存在,请说明理由.⑴证明在△/6Z?中,AC=a, CD=a, AD=吏a,由勾股定理得CD勾AC,\9PA1_底面0%,:.PAL CD,又也U平面用C,用u平面用乙PAHAC=A,:.CDL平面06:又•.・67XZ平面物,・.・平面皿_L平面PAC.⑵解由(1)知,ABLAC,又用上底面/及刀,・.・以刀为原点,AB, AC, #所在直线分别为x轴,y轴,z轴建立如图所示坐标系,则J(0, 0,0), B(a, 0, 0), C(0, a, 0), D( — a, a, 0), P(0, 0, a),CE 一一假设点E(&,Y E,勿)存在,且=—,则CE=入CP,即 3, Y E~ a., Z E)=人(0, ~a, a),・・ XE= 0, Y E= (1 — 4) a, ZE= 4 a.:.~AB= (a, 0, 0), AE= (0, (1一』)a, 』a), ~AD={~ a, a, 0).设平面冏拓的法向量为Z7i=(xi, yi, zi),平面/Z4E的法向量为4=(*2,巧,勿),则J[必=0,[(1——久)ayi+ az\ = 0,J一翊+a 乃=0,[(1— 4)砂+ 4 必=0..*./71=(0,久,久——1),刀2=(久,久,人——1),! \ Z21 , z?2 2 + ( _ I)2cos s’ m2.^p2+ A2+p_1)22 2— 2 4+1 寸2 J — 2 4+1由题意 | cos〈〃i, ni) I = 土-, o叩.2,「一2』+l 避月3—2 11— 3 '3 (2 2—2 4+1) =2 (3 人之一2 人+1),.•.棱密上存在一点反使得二面角B-AE-D的平面角的余弦值为一*,且此时4.对于函数/V)和g(x),若存在常数#, m,对于任意xER,不等式f(x) N奴+/Ng(x)都成立,则称直线y=kx+m是函数A A-) , g(x)的分界线.已知函数f3 =e'(<3x+l) (e为自然对数的底数,aER为常数).(1)讨论函数f(x)的单调性;⑵设日=1,试探究函数小(入)与函数g(x)=—x’ + 2x+l是否存在“分界线"?若存在,求出分界线方程;若不存在,请说明理由.(0) =0,当解⑴•.•/*(*) =/(宓+1), 「・尸(x) =e'(ax+a+l),.••当a=0时,f' (x) >0, f{x)在R 上单调递增.:・f3单调递减;在[一弓土 +8)上,尸(x)>o, .•.f(x)单调递增.当a<0时,在[—8,一之三]上,f (x)>0,.../■(x)单调递增;在[―弓」’+8)上,f' (x)<0, .♦./■(X )单调递减.(2)假设存在直线 y=kx+m,使不等式 e*(x+l) ^kx+m^~x+ 2x+1, 当 x=0 时,由于 1N 成Nl, m= 1,kx~\~ IN — x + 2x+1 恒成立,x + (k —2) xNO 恒成立.令力=(#—2)2<0,解得 #=2,...只需不等式e\x+l)》2x+1恒成立即可.设力(x) =e"(x+l) —2x —1,则 0 (x) =e 、(x+2) —2,令(H (x))‘ =e'(x+3)=0,得 x= —3,.••当xV —3时,h' (x)单调递减;当x>~3时,h' (x)单调递增,且力' 8时,H (x)—— 2,.••当 xVO 时,h' (x)V0,「.//(x)单调递减;当x>0时,h' (x)>0, .・M(x)单调递增..../(X )min =」(O )=0.h ( JT ) =e 、(x+l) —2x —1N0,.・.不等式e 、(x+l) N2x+1恒成立.综上所述,函数/'(x)与函数g(x)存在分界线,其分界线方程为y=2x+l.。
2018考前三个月高考数学理科江苏专用总复习考前回扣1 含答案 精品

考前回扣回扣1 函数的图象与性质1.函数的定义域和值域(1)求函数定义域的类型和相应方法①若已知函数的解析式,则函数的定义域是使解析式有意义的自变量的取值范围; ②若已知f (x )的定义域为[a ,b ],则f (g (x ))的定义域为不等式a ≤g (x )≤b 的解集;反之,已知f (g (x ))的定义域为[a ,b ],则f (x )的定义域为函数y =g (x )(x ∈[a ,b ])的值域. (2)常见函数的值域①一次函数y =kx +b (k ≠0)的值域为R ;②二次函数y =ax 2+bx +c (a ≠0):当a >0时,值域为⎣⎢⎡⎭⎪⎫4ac -b 24a ,+∞,当a <0时,值域为⎝ ⎛⎦⎥⎤-∞,4ac -b 24a ;③反比例函数y =kx(k ≠0)的值域为{y ∈R |y ≠0}. 2.函数的奇偶性、周期性(1)奇偶性是函数在其定义域上的整体性质,对于定义域内的任意x (定义域关于原点对称),都有f (-x )=-f (x )成立,则f (x )为奇函数(都有f (-x )=f (x )成立,则f (x )为偶函数). (2)周期性是函数在其定义域上的整体性质,一般地,对于函数f (x ),如果对于定义域内的任意一个x 的值,若f (x +T )=f (x )(T ≠0),则f (x )是周期函数,T 是它的一个周期. 3.关于函数周期性、对称性的结论 (1)函数的周期性①若函数f (x )满足f (x +a )=f (x -a ),则f (x )是周期函数,2a 是它的一个周期; ②设f (x )是R 上的偶函数,且图象关于直线x =a (a ≠0)对称,则f (x )是周期函数,2a 是它的一个周期;③设f (x )是R 上的奇函数,且图象关于直线x =a (a ≠0)对称,则f (x )是周期函数,4a 是它的一个周期. (2)函数图象的对称性①若函数y =f (x )满足f (a +x )=f (a -x ), 即f (x )=f (2a -x ),则f (x )的图象关于直线x =a 对称;②若函数y =f (x )满足f (a +x )=-f (a -x ), 即f (x )=-f (2a -x ),则f (x )的图象关于点(a,0)对称;③若函数y =f (x )满足f (a +x )=f (b -x ), 则函数f (x )的图象关于直线x =a +b2对称.4.函数的单调性函数的单调性是函数在其定义域上的局部性质. ①单调性的定义的等价形式:设x 1,x 2∈[a ,b ], 那么(x 1-x 2)[f (x 1)-f (x 2)]>0⇔f (x 1)-f (x 2)x 1-x 2>0⇔f (x )在[a ,b ]上是增函数;(x 1-x 2)[f (x 1)-f (x 2)]<0⇔f (x 1)-f (x 2)x 1-x 2<0⇔f (x )在[a ,b ]上是减函数.②若函数f (x )和g (x )都是减函数,则在公共定义域内,f (x )+g (x )是减函数;若函数f (x )和g (x )都是增函数,则在公共定义域内,f (x )+g (x )是增函数;根据同增异减判断复合函数y =f (g (x ))的单调性. 5.函数图象的基本变换 (1)平移变换y =f (x )――――→h >0,右移h <0,左移y =f (x -h ), y =f (x )――――→k >0,上移k <0,下移y =f (x )+k . (2)伸缩变换y =f (x )――――→0<ω<1,伸ω>1,缩y =f (ωx ), y =f (x )――――→0<A <1,缩A >1,伸y =Af (x ). (3)对称变换y =f (x )――→x 轴y =-f (x ), y =f (x )――→y 轴y =f (-x ), y =f (x )――→原点y =-f (-x ).6.准确记忆指数函数与对数函数的基本性质 (1)定点:y =a x(a >0,且a ≠1)恒过(0,1)点;y =log a x (a >0,且a ≠1)恒过(1,0)点.(2)单调性:当a >1时,y =a x在R 上单调递增;y =log a x 在(0,+∞)上单调递增;当0<a <1时,y =a x在R 上单调递减;y =log a x 在(0,+∞)上单调递减. 7.函数与方程(1)零点定义:x 0为函数f (x )的零点⇔f (x 0)=0⇔(x 0,0)为f (x )的图象与x 轴的交点. (2)确定函数零点的三种常用方法 ①解方程判定法:解方程f (x )=0;②零点定理法:根据连续函数y =f (x )满足f (a )f (b )<0,判断函数在区间(a ,b )内存在零点; ③数形结合法:尤其是方程两端对应的函数类型不同时多用此法求解.1.解决函数问题时要注意函数的定义域,要树立定义域优先原则. 2.解决分段函数问题时,要注意与解析式对应的自变量的取值范围.3.求函数单调区间时,多个单调区间之间不能用符号“∪”和“或”连接,可用“及”连接或用“,”隔开.单调区间必须是“区间”,而不能用集合或不等式代替.4.判断函数的奇偶性,要注意定义域必须关于原点对称,有时还要对函数式化简整理,但必须注意使定义域不受影响.5.准确理解基本初等函数的定义和性质.如函数y =a x(a >0,且a ≠1)的单调性容易忽视字母a 的取值讨论,忽视a x>0;对数函数y =log a x (a >0,且a ≠1)容易忽视真数与底数的限制条件.6.易混淆函数的零点和函数图象与x 轴的交点,不能把函数零点、方程的解、不等式解集的端点值进行准确互化.1.若函数f (x )=⎩⎪⎨⎪⎧2x +2,x ≤0,2x-4,x >0,则f (f (1))=________.答案 -2解析 f (f (1))=f (21-4)=f (-2)=2×(-2)+2=-2.2.函数f (x )=x 2-2ax +2在区间(-∞,1]上递减,则a 的取值范围是________. 答案 [1,+∞)解析 函数f (x )=x 2-2ax +2=x 2-2ax +a 2-a 2+2=(x -a )2-a 2+2, ∵二次函数图象开口向上,对称轴为直线x =a ,且在区间(-∞,1]上递减, ∴a 的取值范围是[1,+∞).3.(2017·江苏南通天星湖中学质检)若函数f (x )=⎩⎪⎨⎪⎧x (x -b ),x ≥0,ax (x +2),x <0(a ,b ∈R )为奇函数,则f (a +b )的值为________. 答案 -1解析 因为函数f (x )为奇函数,所以f (-1)=-f (1),f (-2)=-f (2),即⎩⎪⎨⎪⎧a (-1+2)=1(1-b ),2a (-2+2)=2(2-b ),解得a =-1,b =2.经验证a =-1,b =2满足题设条件, 所以f (a +b )=f (1)=-1.4.(2017·江苏如东中学质检)设函数f (x )=ax 2-2x +2,对于满足1<x <4的一切x 值都有f (x )>0,则实数a 的取值范围为________.答案 ⎝ ⎛⎭⎪⎫12,+∞解析 由题意得a >2x -2x2对1<x <4恒成立,又2x -2x 2=-2⎝ ⎛⎭⎪⎫1x -122+12,14<1x <1, ∴⎝ ⎛⎭⎪⎫2x -2x 2max =12,∴a >12.5.已知函数f (x )=||x +2||x ,且满足f (a -1)<f (2),则实数a 的取值范围是________. 答案 (-1,3)解析 因为f (-x )=f (x ),所以函数f (x )是偶函数,当x ≥0时,f (x )=x +2x是单调增函数,故由偶函数的性质及f (a -1)<f (2)可得|a -1|<2,即-2<a -1<2, 即-1<a <3.6.已知定义在R 上的奇函数f (x )满足f (x +2)=-f (x ),且f (-1)=2,则f (2017)=________. 答案 -2解析 由题意得f (x +4)=-f (x +2)=f (x ),所以函数是以4为周期的周期函数,所以f (2017)=f (1)=-f (-1)=-2.7.已知函数f (x )为奇函数,且在[0,2]上单调递增,若f (log 2m )<f (log 4(m +2))成立,则实数m 的取值范围是________________.答案 ⎣⎢⎡⎭⎪⎫14,2 解析 因为函数f (x )是奇函数,且在[0,2]上单调递增,所以函数f (x )在[-2,2]上单调递增.故由f (log 2m )<f (log 4(m +2)),可得⎩⎪⎨⎪⎧-2≤log 2m ≤2,-2≤log 4(m +2)≤2,log 2m <log 4(m +2),m >0,m +2>0,故有⎩⎪⎨⎪⎧14≤m ≤4,116≤m +2≤16,m 2<m +2,m >0,m +2>0,解得14≤m <2.综上可知,m 的取值范围是⎣⎢⎡⎭⎪⎫14,2. 8.定义在R 上的函数f (x )满足f (-x )=-f (x ),f (x -2)=f (x +2),且当x ∈(-1,0)时,f (x )=2x +15,则f (log 220)=__________.答案 -1解析 由f (x -2)=f (x +2)⇒f (x )=f (x +4), 因为4<log 220<5,所以0<log 220-4<1, -1<4-log 220<0.又因为f (-x )=-f (x ),所以f (log 220)=f (log 220-4)=-f (4-log 220)=-f ⎝ ⎛⎭⎪⎫log 245=-1.9.若函数f (x )=⎩⎪⎨⎪⎧(3-a )x -3,x ≤7,a x -6,x >7单调递增,则实数a 的取值范围是________.答案 ⎝ ⎛⎭⎪⎫94,3解析 因为函数f (x )=⎩⎪⎨⎪⎧(3-a )x -3,x ≤7,a x -6,x >7单调递增,所以1<a <3.又由题意得7(3-a )-3<a ,解得a >94,所以实数a 的取值范围是⎝ ⎛⎭⎪⎫94,3.10.已知函数f (x )=⎩⎪⎨⎪⎧2-|x |,x ≤2,(x -2)2,x >2,函数g (x )=3-f (2-x ),则函数y =f (x )-g (x )的零点个数为__________.答案 2解析 当x >2时,g (x )=x -1,f (x )=(x -2)2; 当0≤x ≤2时,g (x )=3-x ,f (x )=2-x ; 当x <0时,g (x )=3-x 2,f (x )=2+x .由于函数y =f (x )-g (x )的零点个数就是方程f (x )-g (x )=0的根的个数.当x >2时,方程f (x )-g (x )=0可化为x 2-5x +5=0,其根为x =5+52或x =5-52(舍去);当0≤x ≤2时,方程f (x )-g (x )=0可化为2-x =3-x ,无解;当x <0时,方程f (x )-g (x )=0可化为x 2+x -1=0,其根为x =-1-52或x =-1+52(舍去).所以函数y =f (x )-g (x )的零点个数为2.11.设函数f (x )=⎩⎪⎨⎪⎧x 2-6x +6,x ≥0,3x +4,x <0,若互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3),则x 1+x 2+x 3的取值范围是____________. 答案 ⎝⎛⎭⎪⎫113,6 解析 由题意可得函数f (x )的图象如图所示,若存在互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3)=k ,则k ∈(-3,4),不妨令x 1<x 2<x 3,则x 1∈⎝ ⎛⎭⎪⎫-73,0,x 2+x 3=6,故x 1+x 2+x 3∈⎝ ⎛⎭⎪⎫113,6.12.定义在R 上的函数f (x )满足f (x +2)=2f (x )-2,当x ∈(0,2]时,f (x )=⎩⎪⎨⎪⎧x 2-x ,x ∈(0,1),1x,x ∈[1,2],若当x ∈(0,4]时,t 2-7t 2≤f (x )≤3-t 恒成立,则实数t 的取值范围是______________. 答案 [1,2]解析 当x ∈(0,1)时,f (x )=x 2-x ,函数无最大值,最小值为-14;当x ∈[1,2]时,f (x )=1x ,函数最大值为1,最小值为12;当x ∈(2,3)时,f (x )=2f (x -2)-2=2x 2-10x +10,函数值满足-52≤f (x )<-2;当x ∈[3,4]时,f (x )=2f (x -2)-2=2x -2-2,函数值满足-1≤f (x )≤0.综上,当x ∈(0,4]时,函数f (x )的最小值为-52,最大值为1.由t 2-7t 2≤f (x )≤3-t 恒成立,得⎩⎪⎨⎪⎧t 2-7t 2≤-52,3-t ≥1,∴⎩⎪⎨⎪⎧1≤t ≤52,t ≤2,∴1≤t ≤2.。
2018考前三个月高考数学理科(江苏专用)总复习训练题(冲刺集合195页)

2018考前三个月高考数学理科(江苏专用)总复习训练题(冲刺集合195页)附加题高分练+解答题滚动练+小题满分练 +中档大题规范练+压轴大题突破练+考前回扣中档大题规范练 1.解三角形1.(2017·苏锡常镇调研)在△ABC 中,a ,b ,c 分别为角A ,B ,C 的对边.已知a cos B =3,b cos A =1,且A -B =π6.(1)求c 的长; (2)求B 的大小.解 (1)方法一 在△ABC 中,a cos B =3,由余弦定理,得a ·a 2+c 2-b 22ac=3,得a 2+c 2-b 2=6c ,①b cos A =1,则b ·b 2+c 2-a 22bc=1,得b 2+c 2-a 2=2c ,②①+②得2c 2=8c ,所以c =4.方法二 因为在△ABC 中,A +B +C =π, 则sin A cos B +sin B cos A =sin(A +B ) =sin(π-C )=sin C , 由asin A =b sin B =c sin C ,得sin A =a sin C c ,sin B =b sin C c,代入上式得 c =a cos B +b cos A =3+1=4.(2)由正弦定理得a cos Bb cos A =sin A cos B sin B cos A =tan Atan B=3. 又tan(A -B )=tan A -tan B 1+tan A tan B =2tan B 1+3tan 2B =33, 解得tan B =33.又B ∈(0,π),所以B =π6. 2.(2017·苏州暑假测试)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知b cos C +c cos B =2a cos A .(1)求角A 的大小;(2)若AB →·AC →=3,求△ABC 的面积.解 (1)方法一 在△ABC 中,由正弦定理及b cos C +c cos B =2a cos A , 得sin B cos C +sin C cos B =2sin A cos A , 即sin A =2sin A cos A .因为A ∈(0,π),则sin A ≠0,所以cos A =12,所以A =π3.方法二 在△ABC 中,由余弦定理及b cos C +c cos B =2a cos A ,得b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac =2a ·b 2+c 2-a 22bc ,所以a 2=b 2+c 2-bc ,所以cos A =b 2+c 2-a 22bc =12.因为A ∈(0,π),所以A =π3. (2)由AB →·AC →=bc cos A =3,得bc =23, 所以△ABC 的面积S =12bc sin A =12×23sin π3=32.3.(2017·南京、盐城一模)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b sin2C =c sin B .(1)求角C 的大小;(2)若sin ⎝⎛⎭⎪⎫B -π3=35,求sin A 的值.解 (1)由b sin2C =c sin B ,根据正弦定理得 2sin B sin C cos C =sin C sin B .因为sin B >0,sin C >0,所以cos C =12.又C ∈(0,π),所以C =π3.(2)因为C =π3,所以B ∈⎝ ⎛⎭⎪⎫0,2π3,所以B -π3∈⎝ ⎛⎭⎪⎫-π3,π3,又sin ⎝⎛⎭⎪⎫B -π3=35,又A +B =2π3,即A =2π3-B ,所以sin A =sin ⎝⎛⎭⎪⎫2π3-B =sin ⎣⎢⎡⎦⎥⎤π3-⎝ ⎛⎭⎪⎫B -π3 =sin π3cos ⎝ ⎛⎭⎪⎫B -π3-cos π3sin ⎝ ⎛⎭⎪⎫B -π3=32×45-12×35=43-310. 4.(2017·徐州、连云港、宿迁三检)如图,在△ABC 中,已知点D 在边AB 上,AD =3DB ,cos A =45,cos ∠ACB =513,BC =13.(1)求cos B 的值; (2)求CD 的长.解 (1)在△ABC 中,cos A =45,A ∈(0,π),所以sin A =1-cos 2A =1-⎝ ⎛⎭⎪⎫452=35. 同理可得,sin ∠ACB =1213.所以cos B =cos[π-(A +∠ACB )]=-cos(A +∠ACB ) =sin A sin ∠ACB -cos A cos ∠ACB =35×1213-45×513=1665.(2)在△ABC 中,由正弦定理,得AB =BCsin A sin ∠ACB =1335×1213=20.又AD =3DB ,所以BD =14AB =5.在△BCD 中,由余弦定理,得CD =BD 2+BC 2-2BD ·BC cos B=52+132-2×5×13×1665=9 2.3.空间平行与垂直1.(2017·南京学情调研)如图,在直三棱柱ABC-A1B1C1中,M,N分别为线段A1B,AC1的中点.(1)求证:MN∥平面BB1C1C;(2)若D在边BC上,AD⊥DC1,求证:MN⊥AD.证明(1)如图,连结A1C,在直三棱柱ABC-A1B1C1中,侧面AA1C1C为平行四边形,又因为N为线段AC1的中点,所以A1C与AC1相交于点N,即A1C经过点N,且N为线段A1C的中点.因为M为线段A1B的中点,所以MN∥BC.又MN⊄平面BB1C1C,BC⊂平面BB1C1C,所以MN∥平面BB1C1C.(2)在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,又AD⊂平面ABC,所以CC1⊥AD.因为AD⊥DC1,DC1⊂平面BB1C1C,CC1⊂平面BB1C1C,CC1∩DC1=C1,所以AD⊥平面BB1C1C. 又BC⊂平面BB1C1C,所以AD⊥BC.由(1)知MN∥BC,所以MN⊥AD.2.如图,在四棱锥P-ABCD中,底面ABCD是正方形,AC与BD交于点O,PC⊥底面ABCD,E为PB上一点,G为PO的中点.(1)若PD∥平面ACE,求证:E为PB的中点;(2)若AB=2PC,求证:CG⊥平面PBD.证明 (1)连结OE ,由四边形ABCD 是正方形知,O 为BD 的中点, 因为PD ∥平面ACE ,PD ⊂平面PBD ,平面PBD ∩平面ACE =OE , 所以PD ∥OE .因为O 为BD 的中点,所以E 为PB 的中点. (2)在四棱锥P -ABCD 中,AB =2PC , 因为四边形ABCD 是正方形,所以OC =22AB , 所以PC =OC .因为G 为PO 的中点,所以CG ⊥PO . 又因为PC ⊥底面ABCD ,BD ⊂底面ABCD , 所以PC ⊥BD .而四边形ABCD 是正方形,所以AC ⊥BD , 因为AC ,PC ⊂平面PAC ,AC ∩PC =C , 所以BD ⊥平面PAC ,因为CG ⊂平面PAC ,所以BD ⊥CG . 因为PO ,BD ⊂平面PBD ,PO ∩BD =O , 所以CG ⊥平面PBD .3.如图,已知平面PAC ⊥平面ABC ,AC ⊥BC ,PE ∥CB ,M 是AE 的中点. (1)若N 是PA 的中点,求证:平面CMN ⊥平面PAC ; (2)若MN ∥平面ABC ,求证:N 是PA 的中点.证明 (1)因为平面PAC ⊥平面ABC ,平面PAC ∩平面ABC =AC ,AC ⊥BC ,BC ⊂平面ABC , 所以BC ⊥平面PAC ,因为M ,N 分别为AE ,AP 的中点,所以MN ∥PE , 又因为PE ∥BC ,所以MN ∥BC , 即MN ⊥平面PAC ,又MN ⊂平面CMN , 所以平面CMN ⊥平面PAC .(2)因为PE ∥CB ,BC ⊂平面ABC ,PE ⊄平面ABC , 所以PE ∥平面ABC ,设平面PAE 与平面ABC 的交线为l ,则PE ∥l . 又MN ∥平面ABC ,MN ⊂平面PAE ,所以MN ∥l . 所以MN ∥PE ,因为M 是AE 的中点,所以N 为PA 的中点.4.如图,在直三棱柱ABC -A 1B 1C 1中,D 为棱BC 上一点. (1)若AB =AC ,D 为棱BC 的中点,求证:平面ADC 1⊥平面BCC 1B 1; (2)若A 1B ∥平面ADC 1,求BD DC的值.(1)证明 因为AB =AC ,点D 为BC 的中点, 所以AD ⊥BC .因为ABC -A 1B 1C 1是直三棱柱,所以BB 1⊥平面ABC . 因为AD ⊂平面ABC ,所以BB 1⊥AD .因为BC ∩BB 1=B ,BC ⊂平面BCC 1B 1,BB 1⊂平面BCC 1B 1, 所以AD ⊥平面BCC 1B 1.因为AD ⊂平面ADC 1,所以平面ADC 1⊥平面BCC 1B 1.(2)解 连结A 1C ,交AC 1于O ,连结OD ,所以O 为A 1C 的中点.因为A 1B ∥平面ADC 1,A 1B ⊂平面A 1BC ,平面ADC 1∩平面A 1BC =OD ,所以A 1B ∥OD . 因为O 为A 1C 的中点,所以D 为BC 的中点, 所以BD DC=1.4.应用题1.(2017·苏锡常镇调研)某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图).设计要求彩门的面积为S (单位:m 2),高为h (单位:m)(S ,h 为常数).彩门的下底BC 固定在广场底面上,上底和两腰由不锈钢支架组成,设腰和下底的夹底为α,不锈钢支架的长度之和记为l .(1)请将l 表示成关于α的函数l =f (α); (2)问:当α为何值时l 最小,并求最小值.解 (1)过D 作DH ⊥BC 于点H ,则∠DCB =α⎝ ⎛⎭⎪⎫0<α<π2,DH =h ,设AD =x .则DC =h sin α,CH =h tan α,BC =x +2htan α.因为S =12⎝ ⎛⎭⎪⎫x +x +2h tan α·h ,则x =S h -htan α, 则l =f (α)=2DC +AD =S h+h ⎝⎛⎭⎪⎫2sin α-1tan α⎝⎛⎭⎪⎫0<α<π2.(2)f ′(α)=h ·⎝⎛⎭⎪⎫-2cos αsin 2α--1sin 2α=h ·1-2cos αsin 2α, 令f ′(α)=h ·1-2cos αsin 2α=0,得α=π3. 当α变化时,f ′(α),f (α)的变化情况如下表:所以l min =f ⎝ ⎛⎭⎪⎫π3=3h +h .答 当α=π3时,l 有最小值,为3h +Sh(m).2.(2017·南京学情调研)如图,某城市有一块半径为40m 的半圆形绿化区域(以O 为圆心,AB 为直径),现计划对其进行改建,在AB 的延长线上取点D ,OD =80m ,在半圆上选定一点C ,改建后的绿化区域由扇形区域AOC 和三角形区域COD 组成,其面积为S m 2.设∠AOC =x rad.(1)写出S 关于x 的函数关系式S (x ),并指出x 的取值范围; (2)试问∠AOC 多大时,改建后的绿化区域面积S 取得最大值?解 (1)因为扇形AOC 的半径为40m ,∠AOC =x rad ,所以扇形AOC 的面积S 扇形AOC =x ·OA 22=800x,0<x <π.在△COD 中,OD =80,OC =40,∠COD =π-x , 所以△COD 的面积S △COD =12OC ·OD ·sin∠COD=1600sin(π-x )=1600sin x ,从而S =S △COD +S 扇形AOC =1600sin x +800x,0<x <π. (2)由(1)知,S (x )=1600sin x +800x,0<x <π, 则S ′(x )=1600cos x +800=1600⎝ ⎛⎭⎪⎫cos x +12, 由S ′(x )=0,解得x =2π3,从而当0<x <2π3时,S ′(x )>0;当2π3<x <π时,S ′(x )<0,因此S (x )在区间⎝ ⎛⎭⎪⎫0,2π3上单调递增,在区间⎝⎛⎭⎪⎫2π3,π上单调递减.所以当x =2π3时,S (x )取得最大值.答 当∠AOC =2π3时,改建后的绿化区域面积S 最大.3.某宾馆在装修时,为了美观,欲将客户的窗户设计成半径为1m 的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形ABCD 为中心在圆心的矩形,现计划将矩形ABCD 区域设计为可推拉的窗口.(1)若窗口ABCD 为正方形,且面积大于14m 2(木条宽度忽略不计),求四根木条总长的取值范围;(2)若四根木条总长为6m ,求窗口ABCD 面积的最大值.解 (1)设一根木条长为x m ,因为S 四边形ABCD >14,所以4-x 2>14,即x <152.又因为四根木条将圆分成9个区域,所以x >2, 所以42<4x <215.答 四根木条总长的取值范围为(42,215).(2)方法一 设AB 所在的木条长为a m ,则BC 所在的木条长为(3-a )m. 因为a ∈(0,2),3-a ∈(0,2),所以a ∈(1,2).S 矩形ABCD =41-a 24·1-(3-a )24=4-a 2·4-(3-a )2=a 4-6a 3+a 2+24a -20, 设f (a )=a 4-6a 3+a 2+24a -20,则f ′(a )=4a 3-18a 2+2a +24=2(a +1)(2a -3)(a -4), 令f ′(a )=0,得a =32或a =-1(舍去)或a =4(舍去).当a 变化时,f ′(a ),f (a )的变化情况如下表:所以当a =32时,f (a )max =f ⎝ ⎛⎭⎪⎫32=4916,即S max =74.答 窗口ABCD 面积的最大值为74m 2.方法二 设AB 所在的木条长为a m ,BC 所在的木条长为b m .由条件知,2a +2b =6,即a +b =3.因为a ,b ∈(0,2),所以b =3-a ∈(0,2),从而a ,b ∈(1,2). 由于AB =21-b 24,BC =21-a 24,S 矩形ABCD =41-b 241-a 24=4-b24-a 2,因为4-b24-a 2≤8-(a 2+b 2)2≤8-(a +b )222=74,当且仅当a =b =32∈(1,2)时,S 矩形ABCD =74为最大值.答 窗口ABCD 面积的最大值为74m 2.4.某隧道设计为双向四车道,车道总宽20m ,要求通行车辆限高4.5m ,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy . (1)若最大拱高h 为6m ,则隧道设计的拱宽l 是多少?(2)为了使施工的土方工程量最小,需隧道口截面面积最小.现隧道口的最大拱高h 不小于6m ,则应如何设计拱高h 和拱宽l ,使得隧道口截面面积最小?隧道口截面面积公式为S =23lh.解 (1)设抛物线的方程为y =-ax 2(a >0),则抛物线过点⎝⎛⎭⎪⎫10,-32,代入抛物线方程解得a =3200, 令y =-6,解得x =±20,则隧道设计的拱宽l 是40m.(2)抛物线最大拱高为h m ,h ≥6,抛物线过点⎝⎛⎭⎪⎫10,-h +92,代入抛物线方程得a =h -92100.令y =-h ,则-h -92100x 2=-h ,解得x 2=100hh -92,则⎝ ⎛⎭⎪⎫l 22=100h h -92,h =92l 2l 2-400.因为h ≥6,所以92l 2l 2-400≥6,即20<l ≤40.所以S =23lh =23l ·92l 2l 2-400=3l3l 2-400(20<l ≤40).所以S ′=9l 2(l 2-400)-3l 3·2l (l 2-400)2=3l 2(l 2-1200)(l 2-400)2=3l 2(l +203)(l -203)(l 2-400)2, 当20<l <203时,S ′<0;当203<l ≤40时,S ′>0,即S 在(20,203)上单调递减,在(203,40]上单调递增,所以S 在l =203时取得最小值,此时l =203,h =274.答 当拱高为274m ,拱宽为203m 时,使得隧道口截面面积最小.5.直线与圆1.已知圆心为C 的圆,满足下列条件:圆心C 位于x 轴正半轴上,与直线3x -4y +7=0相切,且被y 轴截得的弦长为23,圆C 的面积小于13. (1)求圆C 的标准方程;(2)设过点M (0,3)的直线与圆C 交于不同的两点A ,B ,以OA ,OB 为邻边作平行四边形OADB .是否存在这样的直线l ,使得直线OD 与MC 恰好平行?如果存在,求出l 的方程;若不存在,请说明理由.解 (1)设圆C :(x -a )2+y 2=r 2(a >0),由题意知⎩⎪⎨⎪⎧|3a +7|32+(-4)2=r ,a 2+3=r ,解得a =1或a =138,又S =πr 2<13,∴a =1,∴圆C 的标准方程为(x -1)2+y 2=4.(2)当斜率不存在时,直线l 为x =0,不满足题意.当斜率存在时,设直线l :y =kx +3,A (x 1,y 1),B (x 2,y 2),又l 与圆C 相交于不同的两点,联立得⎩⎪⎨⎪⎧y =kx +3,(x -1)2+y 2=4,消去y 得(1+k 2)x 2+(6k -2)x +6=0.∴Δ=(6k -2)2-24(1+k 2)=12k 2-24k -20>0, 解得k <1-263或k >1+263.x 1+x 2=-6k -21+k 2,y 1+y 2=k (x 1+x 2)+6=2k +61+k2, OD →=OA →+OB →=(x 1+x 2,y 1+y 2),MC →=(1,-3), 假设OD →∥MC →,则-3(x 1+x 2)=y 1+y 2,解得k =34∉⎝ ⎛⎭⎪⎫-∞,1-263∪⎝ ⎛⎭⎪⎫1+263,+∞,假设不成立,∴不存在这样的直线l .2.如图,在平面直角坐标系xOy 中,已知圆C :x 2+y 2-4x =0及点A (-1,0),B (1,2).(1)若直线l ∥AB ,与圆C 相交于M ,N 两点,MN =AB ,求直线l 的方程; (2)在圆C 上是否存在点P ,使得PA 2+PB 2=12?若存在,求点P 的个数;若不存在,请说明理由.解 (1)圆C 的标准方程为(x -2)2+y 2=4, 所以圆心C (2,0),半径为2.因为l ∥AB ,A (-1,0),B (1,2),所以直线l 的斜率为2-01-(-1)=1,设直线l 的方程为x -y +m =0,则圆心C 到直线l 的距离为d =|2-0+m |2=|2+m |2.因为MN =AB =22+22=22,而CM 2=d 2+⎝ ⎛⎭⎪⎫MN 22,所以4=(2+m )22+2,解得m =0或m =-4,故直线l 的方程为x -y =0或x -y -4=0.(2)假设圆C 上存在点P ,设P (x ,y ),则(x -2)2+y 2=4,PA 2+PB 2=(x +1)2+(y -0)2+(x -1)2+(y -2)2=12即x 2+y 2-2y -3=0,即x 2+(y -1)2=4.因为|2-2|<(2-0)2+(0-1)2<2+2,所以圆(x -2)2+y 2=4与圆x 2+(y -1)2=4相交, 所以点P 的个数为2.3.在平面直角坐标系xOy 中,已知椭圆C :x 24+y 23=1的左顶点为A ,右焦点为F ,P ,Q 为椭圆C 上两点,圆O :x 2+y 2=r 2(r >0).(1)若PF ⊥x 轴,且满足直线AP 与圆O 相切,求圆O 的方程;(2)若圆O 的半径为3,点P ,Q 满足k OP ·k OQ =-34,求直线PQ 被圆O 截得的弦长的最大值.解 (1)因为椭圆C 的方程为x 24+y 23=1,所以A (-2,0),F (1,0).如图,因为PF ⊥x 轴,所以P ⎝⎛⎭⎪⎫1,±32, 根据对称性,可取P ⎝ ⎛⎭⎪⎫1,32,则直线AP 的方程为y =12(x +2),即x -2y +2=0.由圆O 与直线AP 相切,得r =25,所以圆O 的方程为x 2+y 2=45.(2)易知,圆O 的方程为x 2+y 2=3. ①当PQ ⊥x 轴时,k OP ·k OQ =-k 2OP =-34,所以k OP=±32,不妨设OP :y =32x ,联立⎩⎪⎨⎪⎧y =32x ,x 24+y23=1,解得x =2,y =62,即P ⎝⎛⎭⎪⎫2,62, 此时得直线PQ 被圆O 截得的弦长为2. ②当PQ 与x 轴不垂直时,设直线PQ 的方程为y =kx +b ,P (x 1,y 1),Q (x 2,y 2)(x 1x 2≠0), 由k OP ·k OQ =-34,得3x 1x 2+4y 1y 2=0,即3x 1x 2+4(kx 1+b )(kx 2+b )=0,所以(3+4k 2)x 1x 2+4kb (x 1+x 2)+4b 2=0.(*)联立⎩⎪⎨⎪⎧y =kx +b ,x 24+y23=1消去y ,得(3+4k 2)x 2+8kbx +4b 2-12=0,将x 1+x 2=-8kb 3+4k 2,x 1x 2=4b 2-123+4k 2代入(*)式,得2b 2=4k 2+3.由于圆心O 到直线PQ 的距离为d =|b |k 2+1,所以直线PQ 被圆O 截得的弦长为l =23-d 2=4+2k 2+1,故当k =0时,l 有最大值 6. 综上,因为6>2,所以直线PQ 被圆O 截得的弦长的最大值为 6.4.如图,某市有一条东西走向的公路l ,现欲经过公路l 上的O 处铺设一条南北走向的公路m .在施工过程中发现在O 处的正北1百米的A 处有一汉代古迹.为了保护古迹,该市决定以A 为圆心,1百米为半径设立一个圆形保护区.为了连通公路l ,m ,欲再建一条公路PQ ,点P ,Q 分别在公路l ,m 上,且要求PQ 与圆A 相切.(1)当P 距O 处2百米时,求OQ 的长; (2)当公路PQ 长最短时,求OQ 的长.解 以O 为原点,直线l ,m 分别为x 轴,y 轴建立平面直角坐标系.设PQ 与圆A 相切于点B ,连结AB ,以1百米为单位长度,则圆A 的方程为x 2+(y -1)2=1.(1)由题意可设直线PQ 的方程为x 2+yq =1,即qx +2y -2q =0(q >2), ∵PQ 与圆A 相切, ∴|2-2q |q 2+22=1,解得q =83,故当P 距O 处2百米时,OQ 的长为83百米.(2)设直线PQ 的方程为x p +y q=1, 即qx +py -pq =0(p >1,q >2), ∵PQ 与圆A 相切,∴|p -pq |q 2+p 2=1,化简得p 2=q q -2, 则PQ 2=p 2+q 2=qq -2+q 2, 令f (q )=qq -2+q 2(q >2), ∴f ′(q )=2q -2(q -2)2=2(q -1)(q 2-3q +1)(q -2)2(q >2),当q >3+52时,f ′(q )>0,即f (q )在⎝ ⎛⎭⎪⎫3+52,+∞上单调递增,∴f (q )在q =3+52时取得最小值,故当公路PQ 长最短时,OQ 的长为3+52百米.6.圆锥曲线1.(2017·苏州期末)如图,已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,且过点P (2,-1).(1)求椭圆C 的方程;(2)设点Q 在椭圆C 上,且PQ 与x 轴平行,过点P 作两条直线分别交椭圆C 于A (x 1,y 1),B (x 2,y 2)两点,若直线PQ 平分∠APB ,求证:直线AB 的斜率是定值,并求出这个定值.解 (1)由e =ca =32,得a ∶b ∶c =2∶1∶3, 椭圆C 的方程为x 24b 2+y 2b2=1.把P (2,-1)代入,得b 2=2, 所以椭圆C 的方程是x 28+y 22=1.(2)由已知得PA ,PB 的斜率存在,且互为相反数. 设直线PA 的方程为y +1=k (x -2),其中k ≠0.由⎩⎪⎨⎪⎧y +1=k (x -2),x 2+4y 2=8消去y ,得x 2+4[kx -(2k +1)]2=8,即(1+4k 2)x 2-8k (2k +1)x +4(2k +1)2-8=0, 因为该方程的两根为2,x A ,所以2x A =4(2k +1)2-81+4k 2,即x A =8k 2+8k -21+4k 2, 从而y A =4k 2-4k -14k 2+1. 把k 换成-k ,得x B =8k 2-8k -21+4k 2,y B =4k 2+4k -14k 2+1. 故k AB =y B -y A x B -x A =8k -16k =-12,是定值. 2.(2017·常州期末)已知圆C :(x -t )2+y 2=20(t <0)与椭圆E :x 2a 2+y 2b2=1(a >b >0)的一个公共点为B (0,-2),F (c,0)为椭圆E 的右焦点,直线BF 与圆C 相切于点B . (1)求t 的值以及椭圆E 的方程;(2)过点F 任作与两坐标轴都不垂直的直线l 与椭圆交于M ,N 两点,在x 轴上是否存在一定点P ,使PF 恰为∠MPN 的平分线? 解 (1)由题意得b =2. 因为C (t,0),B (0,-2), 所以BC =t 2+4=20, 所以t =±4.因为t <0,所以t =-4.因为BC ⊥BF ,所以20+c 2+4=(c +4)2, 所以c =1,所以a 2=b 2+c 2=5. 所以椭圆E 的方程为x 25+y 24=1.(2)设M (x 1,y 1),N (x 2,y 2),设l :y =k (x -1)(k ≠0),代入x 25+y 24=1,化简得(4+5k 2)x 2-10k 2x +5k 2-20=0,所以⎩⎪⎨⎪⎧x 1+x 2=10k 24+5k2,x 1x 2=5k 2-204+5k2.若点P 存在,设P (m,0),由题意k PM +k PN =0, 所以y 1x 1-m +y 2x 2-m =k (x 1-1)x 1-m +k (x 2-1)x 2-m=0,所以(x 1-1)(x 2-m )+(x 2-1)(x 1-m )=0, 即2x 1x 2-(1+m )(x 1+x 2)+2m=2·5k 2-204+5k 2-(1+m )10k 24+5k 2+2m =0,所以8m -40=0,所以m =5.所以存在定点P (5,0),使PF 恰为∠MPN 的平分线.3.(2017·无锡期末)已知椭圆x 24+y 23=1,动直线l 与椭圆交于B ,C 两点(点B 在第一象限).(1)若点B 的坐标为⎝ ⎛⎭⎪⎫1,32,求△OBC 面积的最大值; (2)设B (x 1,y 1),C (x 2,y 2),且3y 1+y 2=0,求当△OBC 的面积最大时直线l 的方程. 解 (1)直线OB 方程为y =32x ,即3x -2y =0,设过点C 且平行于OB 的直线l ′方程为y =32x +b .则当l ′与椭圆只有一个公共点时,△OBC 的面积最大.由⎩⎪⎨⎪⎧x 24+y 23=1,y =32x +b消去y 整理得3x 2+3bx +b 2-3=0,此时Δ=9b 2-12(b 2-3),令Δ=0,解得b =±23, 当b =23时,C ⎝ ⎛⎭⎪⎫-3,32; 当b =-23时,C ⎝⎛⎭⎪⎫3,-32, 所以△OBC 面积的最大值为12×1+94×|33+3|13= 3. (2)显然,直线l 与y 轴不垂直,设直线l 的方程为x =my +n .由⎩⎪⎨⎪⎧x 24+y 23=1,x =my +n消去x 并整理得(3m 2+4)y 2+6mny +3n 2-12=0,所以⎩⎪⎨⎪⎧y 1+y 2=-6mn3m 2+4,y 1y 2=3n 2-123m 2+4.因为3y 1+y 2=0,所以⎩⎪⎨⎪⎧y 1=3mn3m 2+4,y 21=4-n23m 2+4,从而9n 2m 2(3m 2+4)2=4-n 23m 2+4, 即n 2=3m 2+43m 2+1,所以S △OBC =12|n |·|y 1-y 2|=2|n |·|y 1|=6|m |n 23m +4=6|m |3m +1.因为B 在第一象限,所以x 1=my 1+n =3m 2n3m 2+4+n >0,所以n >0.因为y 1>0,所以m >0, 所以S △OBC =6m 3m 2+1=63m +1m≤623=3,当且仅当3m =1m ,即m =33时取等号,此时n =102,4.(2017·南京、盐城二模)如图,在平面直角坐标系xOy 中,焦点在x 轴上的椭圆C :x 28+y 2b 2=1经过点(b,2e ),其中e 为椭圆C 的离心率.过点T (1,0)作斜率为k (k >0)的直线l 交椭圆C 于A ,B 两点(A 在x 轴下方). (1)求椭圆C 的标准方程;(2)过点O 且平行于l 的直线交椭圆C 于M ,N 两点,求AT ·BTMN 2的值; (3)记直线l 与y 轴的交点为P ,若AP →=25TB →,求直线l 的斜率k .解 (1)由点(b,2e )在椭圆C 上,得b 28+4e 2b =1.因为e 2=c 2a 2=8-b 28=1-b 28,所以b 28+4b 2=32.又b 2<a 2=8,解得b 2=4, 所以椭圆C 的标准方程是x 28+y 24=1.(2)设A (x 1,y 1),B (x 2,y 2),M (x 0,y 0), 由对称性知N (-x 0,-y 0),其中y 1<0. 因为MN ∥AB ,所以AT ·BT MN 2=-y 1y 24y 20. 直线AB 的方程为y =k (x -1),直线MN 的方程为y =kx ,其中k >0.由⎩⎪⎨⎪⎧ y =k (x -1),x 2+2y 2=8消去x ,得(1+2k 2)y 2+2ky -7k 2=0,所以y 1y 2=-7k21+2k2.由⎩⎪⎨⎪⎧y =kx ,x 2+2y 2=8消去x ,得(1+2k 2)y 2=8k 2,所以y 2=8k 21+2k ,从而得AT ·BT MN =732. (3)由AP →=25TB →,得-x 1=25(x 2-1).由⎩⎪⎨⎪⎧y =k (x -1),x 2+2y 2=8消去y ,得(1+2k 2)x 2-4k 2x +2k 2-8=0, 所以x 1+x 2=4k 21+2k 2,x 1x 2=2k 2-81+2k 2.又因为-x 1=25(x 2-1),所以x 1=-4k 2+23(1+2k 2),x 2=16k 2-23(1+2k 2),从而-4k 2+23(1+2k 2)·16k 2-23(1+2k 2)=2k 2-81+2k 2.整理得50k 4-83k 2-34=0, 解得k 2=2或k 2=-1750(舍).因为k >0,所以k = 2.压轴大题突破练 1.函数与导数1.设函数f (x )=x ln x +ax ,a ∈R .(1)当a =1时,求曲线y =f (x )在点(1,f (1))处的切线方程;(2)求函数y =f (x )在⎣⎢⎡⎦⎥⎤1e ,e 上的最小值; (3)若g (x )=f (x )+12ax 2-(2a +1)x ,求证:a ≥0是函数y =g (x )在x ∈(1,2)时单调递增的充分不必要条件.(1)解 由f (x )=x ln x +ax ,得f ′(x )=ln x +a +1. 当a =1时,f ′(x )=ln x +2,f (1)=1,f ′(1)=2, 求得切线方程为y =2x -1. (2)解 令f ′(x )=0,得x =e -(a +1).∴当e-(a +1)≤1e ,即a ≥0时,x ∈⎣⎢⎡⎦⎥⎤1e ,e 时f ′(x )≥0恒成立,f (x )单调递增, 此时f (x )min =f ⎝ ⎛⎭⎪⎫1e =a -1e .当e-(a +1)≥e ,即a ≤-2时,x ∈⎣⎢⎡⎦⎥⎤1e ,e 时f ′(x )≤0恒成立,f (x )单调递减,此时f (x )min=f (e)=a e +e.当1e <e -(a +1)<e ,即-2<a <0时,x ∈⎣⎢⎡⎭⎪⎫1e ,e -(a +1)时f ′(x )<0,f (x )单调递减;当x ∈(e -(a +1),e)时,f ′(x )>0,f (x )单调递增,此时f (x )min =f (e -(a +1))=-e-(a +1).(3)证明 g ′(x )=f ′(x )+ax -(2a +1) =ln x +ax -a =ln x +a (x -1),∴当a ≥0时,x ∈(1,2)时,ln x >0,a (x -1)≥0,g ′(x )>0恒成立,函数y =g (x )在x ∈(1,2)时单调递增,充分条件成立; 又当a =-12时,代入g ′(x )=ln x +a (x -1)=ln x -12x +12.设h (x )=g ′(x )=ln x -12x +12,x ∈(1,2),则h ′(x )=1x -12=2-x2x >0恒成立,∴当x ∈(1,2)时,h (x )单调递增.又h (1)=0,∴当x ∈(1,2)时,h (x )>0恒成立. 而h (x )=g ′(x ),∴当x ∈(1,2)时,g ′(x )>0恒成立, 函数y =g (x )单调递增, ∴必要条件不成立.综上,a ≥0是函数y =g (x )在x ∈(1,2)时单调递增的充分不必要条件. 2.设函数f (x )=e x-|x -a |,其中a 是实数. (1)若f (x )在R 上单调递增,求实数a 的取值范围;(2)若函数有极大值点x 2和极小值点x 1,且f (x 2)-f (x 1)≥k (x 2-x 1)恒成立,求实数k 的取值范围.解 (1)因为f (x )=e x-|x -a |=⎩⎪⎨⎪⎧e x-x +a ,x ≥a ,e x+x -a ,x <a ,则f ′(x )=⎩⎪⎨⎪⎧e x-1,x ≥a ,e x+1,x <a ,因为f (x )在R 上单调递增,所以f ′(x )≥0恒成立,当x <a 时,f ′(x )=e x+1≥1>0恒成立,当x ≥a 时,f ′(x )=e x-1≥0恒成立, 故应f ′(a )≥0,即a ≥0.(2)由(1)知当a ≥0时,f (x )在R 上单调递增,不符合题意,所以有a <0. 此时,当x <a 时,f ′(x )=e x+1≥1>0,f (x )单调递增, 当x ≥a 时,f ′(x )=e x-1,令f ′(x )=0,得x =0,所以f ′(x )<0在(a,0)上恒成立,f (x )在(a,0)上单调递减,f ′(x )>0在(0,+∞)上恒成立,f (x )在(0,+∞)上单调递增,所以f (x )极大=f (a )=e a,f (x )极小=f (0)=1+a ,即a <0符合题意.由f (x 2)-f (x 1)≥k (x 2-x 1)恒成立,可得e a-a -1≥ka 对任意a <0恒成立, 设g (a )=e a-(k +1)a -1,求导,得g ′(a )=e a-(k +1),①当k ≤-1时,g ′(a )>0恒成立,g (a )在(-∞,0)上单调递增,又因为g (-1)=1e +k <0,与g (a )>0矛盾;②当k ≥0时,g ′(a )<0在(-∞,0)上恒成立,g (a )在(-∞,0)上单调递减, 又因为g (0)=0,所以此时g (a )≥0恒成立,符合题意;③当-1<k <0时,g ′(a )>0在(-∞,0)上的解集为(ln(k +1),0),即g (a )在(ln(k +1),0)上单调递增,又因为g (0)=0,所以g (ln (k +1))<0不符合题意.综上,实数k 的取值范围为[0,+∞).3.(2017·江苏泰兴中学质检)已知函数f (x )=13x 3-mx 2-x +13m ,其中m ∈R .(1)求函数y =f (x )的单调区间;(2)若对任意的x 1,x 2∈[-1,1],都有|f ′(x 1)-f ′(x 2)|≤4,求实数m 的取值范围; (3)求函数f (x )的零点个数. 解 (1)f ′(x )=x 2-2mx -1,由f ′(x )≥0,得x ≤m -m 2+1或x ≥m +m 2+1;故函数f (x )的单调增区间为(-∞,m -m 2+1),(m +m 2+1,+∞), 由f ′(x )<0,得m -m 2-1<x <m +m 2+1,故函数f (x )的单调减区间为(m -m 2+1,m +m 2+1).(2)“对任意的x 1,x 2∈[-1,1],都有|f ′(x 1)-f ′(x 2)|≤4”等价于“函数y =f ′(x ),x ∈[-1,1]的最大值与最小值的差小于等于4”. 对于f ′(x )=x 2-2mx -1,对称轴x =m .①当m <-1时,f ′(x )的最大值为f ′(1),最小值为f ′(-1), 由f ′(1)-f ′(-1)≤4,即-4m ≤4,解得m ≥-1,舍去;②当-1≤m ≤1时,f ′(x )的最大值为f ′(1)或f ′(-1),最小值为f ′(m ),由⎩⎪⎨⎪⎧f ′(1)-f ′(m )≤4,f ′(-1)-f ′(m )≤4,即⎩⎪⎨⎪⎧m 2-2m -3≤0,m 2+2m -3≤0,解得-1≤m ≤1;③当m >1时,f ′(x )的最大值为f ′(-1),最小值为f ′(1), 由f ′(-1)-f ′(1)≤4,即4m ≤4,解得m ≤1,舍去. 综上,实数m 的取值范围是[-1,1]. (3)由f ′(x )=0,得x 2-2mx -1=0,因为Δ=4m 2+4>0,所以y =f (x )既有极大值也有极小值. 设f ′(x 0)=0,即x 20-2mx 0-1=0,x 20=2mx 0+1,则f (x 0)=13x 30-mx 20-x 0+13m =-13mx 20-23x 0+13m =-23x 0(m 2+1),所以极大值f (m -m 2+1)=-23(m -m 2+1)(m 2+1)>0,极小值f (m +m 2+1)=-23(m +m 2+1)(m 2+1)<0,故函数f (x )有三个零点.4.已知函数f (x )=x 3+ax 2-a 2x +2,a ∈R . (1)若a <0,试求函数y =f (x )的单调递减区间;(2)若a =0,且曲线y =f (x )在点A ,B (A ,B 不重合)处切线的交点位于直线x =2上,证明:A ,B 两点的横坐标之和小于4;(3)如果对于一切x 1,x 2,x 3∈[0,1],总存在以f (x 1),f (x 2),f (x 3)为三边长的三角形,试求正实数a 的取值范围.(1)解 函数f (x )的导函数f ′(x )=3x 2+2ax -a 2=3(x +a )⎝ ⎛⎭⎪⎫x -a 3.因为a <0,由f ′(x )<0,解得a3<x <-a .所以函数y =f (x )的单调递减区间为⎝ ⎛⎭⎪⎫a3,-a . (2)证明 当a =0时,f (x )=x 3+2.设在点A (x 1,x 31+2),B (x 2,x 32+2)处的切线交于直线x =2上一点P (2,t ). 因为y ′=3x 2,所以曲线y =f (x )在点A 处的切线斜率为k =3x 21, 所以在点A 处的切线方程为y -(x 31+2)=3x 21(x -x 1). 因为切线过点P ,所以t -(x 31+2)=3x 21(2-x 1), 即2x 31-6x 21+(t -2)=0. 同理可得2x 32-6x 22+(t -2)=0, 两式相减得2(x 31-x 32)-6(x 21-x 22)=0,即(x 1-x 2)(x 21+x 1x 2+x 22)-3(x 1-x 2)(x 1+x 2)=0, 因为x 1-x 2≠0,所以x 21+x 1x 2+x 22-3(x 1+x 2)=0, 即(x 1+x 2)2-x 1x 2-3(x 1+x 2)=0. 因为x 1x 2≤⎝ ⎛⎭⎪⎫x 1+x 222,且x 1≠x 2,所以x 1x 2<⎝⎛⎭⎪⎫x 1+x 222.从而上式可以化为(x 1+x 2)2-⎝⎛⎭⎪⎫x 1+x 222-3(x 1+x 2)<0,即(x 1+x 2)(x 1+x 2-4)<0.解得0<x 1+x 2<4,即A ,B 两点的横坐标之和小于4. (3)解 由题设知,f (0)<f (1)+f (1), 即2<2(-a 2+a +3),解得-1<a <2. 又因为a >0,所以0<a <2. 因为f ′(x )=3(x +a )⎝ ⎛⎭⎪⎫x -a 3,所以当x ∈⎝ ⎛⎭⎪⎫0,a 3时,f ′(x )<0,f (x )单调递减,当x ∈⎝ ⎛⎭⎪⎫a3,1时,f ′(x )>0,f (x )单调递增.所以当x =a 3时,f (x )有最小值f ⎝ ⎛⎭⎪⎫a 3=-527a 3+2. 从而条件转化为⎩⎪⎨⎪⎧f ⎝ ⎛⎭⎪⎫a 3=-527a 3+2>0, ①f (0)<2⎝ ⎛⎭⎪⎫-527a 3+2, ②f (1)<2⎝ ⎛⎭⎪⎫-527a 3+2. ③由①得a <33235;由②得a <335,再根据0<a <2,得0<a <335.不等式③化为1027a 3-a 2+a -1<0.令g (a )=1027a 3-a 2+a -1,则g ′(a )=109a 2-2a +1>0,所以g (a )为增函数.又g (2)=-127<0,所以当a ∈⎝ ⎛⎭⎪⎪⎫0,335时,g (a )<0恒成立,即③成立. 所以a 的取值范围为⎝⎛⎭⎪⎪⎫0,335.2.数 列1.已知数列{a n }中a 1=1,a n +1=⎩⎪⎨⎪⎧13a n +n ,n 为奇数,a n -3n ,n 为偶数.(1)是否存在实数λ,使得数列{a 2n -λ}是等比数列?若存在,求出λ的值;若不存在,请说明理由;(2)若S n 是数列{a n }的前n 项和,求满足S n >0的所有正整数n . 解 (1)由已知,得a 2(n +1)=13a 2n +1+(2n +1)=13[a 2n -3(2n )]+2n +1=13a 2n +1. 令a 2(n +1)-λ=13(a 2n -λ),得a 2(n +1)=13a 2n +23λ,所以λ=32.此时,a 2-λ=13+1-32=-16.所以存在λ=32,使得数列{a 2n -λ}是等比数列.(2)由(1)知,数列⎩⎨⎧⎭⎬⎫a 2n -32是首项为-16,公比为13的等比数列,所以a 2n -32=-16⎝ ⎛⎭⎪⎫13n -1=-12·13n ,即a 2n =12⎝ ⎛⎭⎪⎫3-13n .由a 2n =13a 2n -1+(2n -1),得a 2n -1=3a 2n -3(2n -1)=32⎝ ⎛⎭⎪⎫3-13n -6n +3,所以a 2n -1+a 2n =32⎝ ⎛⎭⎪⎫3-13n -6n +3+12⎝ ⎛⎭⎪⎫3-13n=-2⎝ ⎛⎭⎪⎫13n-6n +9,所以S 2n =(a 1+a 2)+(a 3+a 4)+…+(a 2n -1+a 2n )=-2⎣⎢⎡⎦⎥⎤13+⎝ ⎛⎭⎪⎫132+…+⎝ ⎛⎭⎪⎫13n -6(1+2+…+n )+9n =13n -3n 2+6n -1,从而S 2n -1=S 2n -a 2n =32×13n -3n 2+6n -52.因为13n 和-3n 2+6n =-3(n -1)2+3在n ∈N *时均单调递减,所以S 2n 和S 2n -1均各自单调递减.计算得S 1=1,S 2=73,S 3=-73,S 4=-89,所以满足S n >0的所有正整数n 的值为1和2.2.已知数列{a n }的前n 项和为S n ,设数列{b n }满足b n =2(S n +1-S n )S n -n (S n +1+S n )(n ∈N *). (1)若数列{a n }为等差数列,且b n =0,求数列{a n }的通项公式;(2)若a 1=1,a 2=3,且数列{a 2n -1},{a 2n }都是以2为公比的等比数列,求满足不等式b 2n <b 2n -1的所有正整数n 的集合.解 (1)设等差数列{a n }的公差为d , 所以a n +1=a 1+nd ,S n =na 1+n (n -1)2d .由b n =2(S n +1-S n )S n -n (S n +1+S n )(n ∈N *), 得b n =2a n +1S n -n (2S n +a n +1). 又由b n =0,得2(a 1+nd )⎣⎢⎡⎦⎥⎤na 1+n (n -1)2d -n [2na 1+n (n -1)d +a 1+nd ]=0对一切n ∈N *都成立,即(d 2-d )n 2+(3a 1d -d 2-2a 1)n +2a 21-a 1d -a 1=0对一切n ∈N *都成立. 令n =1,n =2,解得⎩⎪⎨⎪⎧d =0,a 1=0或⎩⎪⎨⎪⎧d =1,a 1=1,经检验,符合题意.所以数列{a n }的通项公式为a n =0或a n =n . (2)由题意得a 2n -1=2n -1,a 2n =3×2n -1,S 2n =2n -1+3(2n -1)=4×2n -4,S 2n -1=S 2n -a 2n =4×2n -4-3×2n -1=5×2n -1-4. b 2n =2a 2n +1S 2n -2n (2S 2n +a 2n +1)=2×2n×(4×2n-4)-2n (8×2n-8+2n) =2n +1(2n +2-9n -4)+16n .b 2n -1=2a 2n S 2n -1-(2n -1)(2S 2n -1+a 2n )=6×2n -1×(5×2n -1-4)-(2n -1)(10×2n -1-8+3×2n -1)=2n -1(30×2n -1-26n -11)+16n-8.所以b 2n -b 2n -1=2n +1(2n +2-9n -4)+16n -[2n -1(30×2n -1-26n -11)+16n -8]=2n⎝⎛⎭⎪⎫2n -1-5n -52+8=22n -1+8-2n ⎝⎛⎭⎪⎫5n +52. 记f (n )=22n -1+8-2n ⎝⎛⎭⎪⎫5n +52,即f (n )=2n ⎣⎢⎡⎦⎥⎤12×2n-⎝⎛⎭⎪⎫5n +52+8.记g (n )=12×2n-⎝⎛⎭⎪⎫5n +52,则g (n +1)-g (n )=12×2n +1-⎝⎛⎭⎪⎫5n +152-12×2n +5n +52=12×2n-5,当n =1,2,3时,g (n +1)-g (n )<0;当n ∈N *时,n ≥4,g (n +1)-g (n )=12×2n -5>0,因为当n =1时,g (1)=-132<0,所以g (4)<0,且g (6)=-12<0,g (7)=532>0.所以f (n )=2n ⎣⎢⎡⎦⎥⎤12×2n -⎝ ⎛⎭⎪⎫5n +52+8在n ≥7(n ∈N *)时也单调递增,当n =1时,f (1)=-5<0; 当n =2时,f (2)=-34<0; 当n =3时,f (3)=-100<0; 当n =4时,f (4)=-224<0; 当n =5时,f (5)=-360<0; 当n =6时,f (6)=-24<0; 当n =7时,f (7)=3400>0,所以满足条件的正整数n 的集合为{1,2,3,4,5,6}.3.已知等差数列{a n }的前n 项和为S n ,且2a 5-a 3=13,S 4=16. (1)求数列{a n }的前n 项和S n ;(2)设T n =∑ni =1(-1)i a i ,若对一切正整数n ,不等式λT n <[a n +1+(-1)n +1a n ]2n -1恒成立,求实数λ的取值范围;(3)是否存在正整数m ,n (n >m >2),使得S 2,S m -S 2,S n -S m 成等比数列?若存在,求出所有的m ,n ;若不存在,请说明理由. 解 (1)设数列{a n }的公差为d . 因为2a 5-a 3=13,S 4=16,所以⎩⎪⎨⎪⎧2(a 1+4d )-(a 1+2d )=13,4a 1+6d =16,解得⎩⎪⎨⎪⎧a 1=1,d =2,所以a n =2n -1,S n =n 2.(2)①当n 为偶数时,设n =2k ,k ∈N *,则T 2k =(a 2-a 1)+(a 4-a 3)+…+(a 2k -a 2k -1)=2k . 代入不等式λT n <[a n +1+(-1)n +1a n ]·2n -1,得λ·2k <4k,从而λ<4k2k.设f (k )=4k2k ,则f (k +1)-f (k )=4k +12(k +1)-4k2k =4k(3k -1)2k (k +1).因为k ∈N *,所以f (k +1)-f (k )>0,所以f (k )是递增的,所以f (k )min =2,所以λ<2. ②当n 为奇数时,设n =2k -1,k ∈N *, 则T 2k -1=T 2k -(-1)2ka 2k =2k -(4k -1)=1-2k . 代入不等式λT n <[a n +1+(-1)n +1a n ]2n -1,得λ(1-2k )<(2k -1)4k ,从而λ>-4k .因为k ∈N *,所以-4k的最大值为-4,所以λ>-4. 综上,λ的取值范围为(-4,2).(3)假设存在正整数m ,n (n >m >2),使得S 2,S m -S 2,S n -S m 成等比数列, 则(S m -S 2)2=S 2(S n -S m ),即(m 2-4)2=4(n 2-m 2), 所以4n 2=(m 2-2)2+12,即4n 2-(m 2-2)2=12, 即(2n -m 2+2)(2n +m 2-2)=12.因为n >m >2,所以n ≥4,m ≥3,所以2n +m 2-2≥15.因为2n -m 2+2是整数,所以等式(2n -m 2+2)(2n +m 2-2)=12不成立, 故不存在正整数m ,n (n >m >2),使得S 2,S m -S 2,S n -S m 成等比数列.4.若一个数列从第2项起,每一项与它前一项的差都大于2,则称这个数列为“A 型数列”. (1)若首项为1,公差为整数的等差数列{a n }为“A 型数列”,且其前n 项和为S n ,若对于任意n ∈N *,都有S n <32n 2+n ,求{a n }的通项公式;(2)已知等比数列{a n }的每一项均为正整数,且{a n }为“A 型数列”,b n =23a n ,c n =a n(n +1)·2n -5,当数列{b n }不是“A 型数列”时,试判断数列{c n }是否为“A 型数列”,并说明理由. 解 (1)设等差数列{a n }的公差为d ,则d >2, 由a 1=1,得S n =n +n (n -1)2d ,且S 1<52.由题意,得n +n (n -1)2d <32n 2+n 对n ∈N *均成立,即d <3nn -1对n ≥2均成立, ∵3n n -1=3+3n -1>3, ∴d ≤3,又d >2, ∴d =3,∴a n =3n -2.(2)设数列{a n }的公比为q ,则a n =a 1q n -1,∵{a n }的每一项均为正整数, 且a n +1-a n =a n q -a n =a n (q -1)>2>0, ∴a 1>0,且q >1,∵a n +1-a n =q (a n -a n -1)>a n -a n -1, 即在{a n -a n -1}中,a 2-a 1为最小项, 同理,在{b n -b n -1}中,b 2-b 1为最小项,由{a n }为“A 型数列”,可知只需a 2-a 1>2,即a 1(q -1)>2, 又∵{b n }不是“A 型数列”,且b 2-b 1为最小项, ∴b 2-b 1≤2,即a 1(q -1)≤3,由数列{a n }的每一项均为正整数,可得a 1(q -1)=3, ∴a 1=1,q =4或a 1=3,q =2. ①当a 1=1,q =4时,a n =4n -1,则c n =4n -1(n +1)·2n -5=2n +3n +1, 令d n =c n +1-c n (n ∈N *),则d n =2n +4n +2-2n +3n +1=2n +3·n (n +1)(n +2),令e n =d n +1-d n (n ∈N *),则e n =2n +4·n +1(n +2)(n +3)-2n +3·n (n +1)(n +2)=2n +3n +2·n 2+n +2(n +1)(n +3)>0,∴{d n }为递增数列, 即d n >d n -1>d n -2>…>d 1,即c n +1-c n >c n -c n -1>c n -1-c n -2>…>c 2-c 1, ∵c 2-c 1=323-8=83>2,∴对任意的n ∈N *都有c n +1-c n >2, 即数列{c n }为“A 型数列”. ②当a 1=3,q =2时,a n =3·2n -1,则c n =3·2n +1(n +1)·2n -5=48n +1, 显然,{c n }为递减数列,c 2-c 1<0≤2, 故数列{c n }不是“A 型数列”; 综上所述,当a n =4n -1时,数列{c n }为“A 型数列”,当a n =3·2n -1时,数列{c n }不是“A 型数列”.小题满分练小题满分练11.设全集U=R,A={x|x2-2x≤0},B={y|y=cos x,x∈R},则图中阴影部分表示的区间是________.答案(-∞,-1)∪(2,+∞)解析因为A={x|0≤x≤2}=[0,2],B={y|-1≤y≤1}=[-1,1],所以A∪B=[-1,2],所以∁R(A∪B)=(-∞,-1)∪(2,+∞).2.(2017·苏州暑假测试)命题“∃x>1,x2≥2”的否定是________.答案∀x>1,x2<2解析根据存在性命题的否定规则得“∃x>1,x2≥2”的否定是“∀x>1,x2<2”.3.若复数z满足z i=1+2i,则z的共轭复数是________.答案2+i解析∵z i=1+2i,∴z=1+2ii=2-i,∴z=2+i.4.(2017·徐州、连云港、宿迁三检)已知一组数据3,6,9,8,4,则该组数据的方差是________.答案265(或5.2)解析这组数据的平均数x=15(3+6+9+8+4)=6,方差s2=15(9+0+9+4+4)=265.5.若流程图如图所示,则该程序运行后输出的值是________.答案10000。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——中档大题规范练6 Word版含答案

a解 (1)由 e = =c 所以椭圆 C 的方程是 + =1.⎩y B -y A 8k 1故 k AB = x B -x A -16k 21+4k 2 1+4k 24k 2+1 1+4k 2 4k 2+16.圆锥曲线x 2 y 2 31.(2017·苏州期末 )如图,已知椭圆 C : 2+b 2=1(a >b >0)的离心率为 2,且过点 P (2,-1).(1)求椭圆 C 的方程;(2)设点 Q 在椭圆 C 上,且 PQ 与 x 轴平行,过点 P 作两条直线分别交椭圆 C 于 A (x 1,y 1),B (x 2,y 2)两点,若直线 PQ 平分∠APB ,求证:直线 AB 的斜率是定值,并求出这个定值.a 3 2,得 a ∶b ∶c =2∶1∶ 3,x 2 y 2椭圆 C 的方程为4b 2+b 2=1.把 P (2,-1)代入,得 b 2=2,x 2 y 28 2(2)由已知得 PA ,PB 的斜率存在,且互为相反数.设直线 PA 的方程为 y +1=k (x -2),其中 k ≠0.⎧⎪y +1=k (x -2), 由⎨⎪x 2+4y 2=8消去 y ,得 x 2+4[kx -(2k +1)]2=8,即(1+4k 2)x 2-8k (2k +1)x +4(2k +1)2-8=0,因为该方程的两根为 2,x A ,4(2k +1)2-8 8k 2+8k -2 所以 2x A = ,即 x A = ,4k 2-4k -1从而 y A = .8k 2-8k -2 4k 2+4k -1把 k 换成-k ,得 x B = ,y B = .= =- ,是定值.x 2 y 22.(2017·常州期末)已知圆 C :(x -t )2+y 2=20(t <0)与椭圆 E :a 2+b 2=1(a >b >0)的一个公共点为 B (0,-2),F (c,0)为椭圆 E 的右焦点,直线 BF 与圆 C 相切于点 B .所以椭圆 E 的方程为 + =1.设 l :y =k (x -1)(k ≠0),代入 + =1,⎧⎪10k x + 5k -20x x = .⎪⎩3.(2017·无锡期末)已知椭圆 + =1,动直线 l 与椭圆交于 B ,C 两点(点 B 在第一象限).(1)若点 B 的坐标为 1, ⎪,求△OBC 面积的最大值;解 (1)直线 OB 方程为 y = x ,即 3x -2y =0,所以⎨x 1-m x 2-m x 1-m x 2-m +k (x 1-1) k (x 2-1)y 1y =2· -(1+m ) +2m =0,⎛3⎫4+5k(1)求 t 的值以及椭圆 E 的方程;(2)过点 F 任作与两坐标轴都不垂直的直线 l 与椭圆交于 M ,N 两点,在 x 轴上是否存在一定点 P ,使 PF 恰为∠MPN 的平分线?解 (1)由题意得 b =2.因为 C (t,0),B (0,-2),所以 BC = t 2+4= 20,所以 t =±4.因为 t <0,所以 t =-4.因为 BC ⊥BF ,所以 20+c 2+4=(c +4)2,所以 c =1,所以 a 2=b 2+c 2=5.x 2 y 25 4(2)设 M (x 1,y 1),N (x 2,y 2),x 2 y 25 4化简得(4+5k 2)x 2-10k 2x +5k 2-20=0,21 2 4+5k 22 1 2 2若点 P 存在,设 P (m,0),由题意 k PM +k PN =0,所以 = + =0,所以(x 1-1)(x 2-m )+(x 2-1)(x 1-m )=0, 即 2x 1x 2-(1+m )(x 1+x 2)+2m5k 2-20 10k 24+5k 2 4+5k 2所以 8m -40=0,所以 m =5.所以存在定点 P (5,0),使 PF 恰为∠MPN 的平分线.x 2 y 24 3⎝ 2⎭(2)设 B (x 1,y 1),C (x 2,y 2),且 3y 1+y 2=△0,求当 OBC 的面积最大时直线 l 的方程.32设过点 C 且平行于 OB 的直线 l ′方程为 y = x +b .⎧⎪x +y =1, ⎪⎩y =3x +b⎛⎛所以△OBC 面积的最大值为 ×4 13所以⎨⎪⎩y y =3n -12.因为 3y +y =0,所以⎨⎪⎩y = 4-n , 3m +4 (3m 2+4)2 3m 2+4+ + +1 =+4 +1+432则当 △l ′与椭圆只有一个公共点时, OBC 的面积最大.2 2由⎨ 4 32消去 y 整理得 3x 2+3bx +b 2-3=0,此时 Δ =9b 2-12(b 2-3),令 Δ =0,解得 b =±2 3,当 b =2 3时,C - 3, ⎝3⎫ ⎪;2 ⎭当 b =-2 3时,C 3,- ⎝ 3⎫ ⎪,2 ⎭129 |3 3+ 3| 1+ × = 3.(2)显然,直线 l 与 y 轴不垂直,设直线 l 的方程为 x =my +n .⎧⎪x 2+y 2=1, 由⎨ 4 3消去 x 并整理得(3m 2+4)y 2+6mny +3n 2-12=0,⎪⎩x =my +n⎧⎪y 1+y 2=-3 6mn4,221 23m 2+4⎧⎪y 1=3 3mn4,2 1 2 22 129n 2m 2 4-n 2 从而 = ,3m 2+4即 n 2=3m 2 ,1 6|m |n2 6|m |所以 △S OBC 2|n |·|y 1-y 2|=2|n |·|y 1|=3m 2 =3m 2 .因为 B 在第一象限,3m 2n所以 x 1=my 1+n =3m 2 +n >0,所以 n >0.因为 y 1>0,所以 m >0,所以 △S OBC = 6m3m 2+1 1 2 3 m 3 2 3m +所以直线 l 的方程为 x = 3 y + ,即 y = 3x - .4.(2017·南京、盐城二模)如图,在平面直角坐标系 x Oy 中,焦点在 x 轴上的椭圆 C : +(2)过点 O 且平行于 l 的直线交椭圆 C 于 M ,N 两点,求AT ·BT的值;→ 2→ (3)记直线 l 与 y 轴的交点为 P ,若AP = TB ,求直线 l 的斜率 k . 所以椭圆 C 的标准方程是 +=1. AT ·BT -y 1y 2MN 24y 20=1- ,所以 +消去 x ,得(1+2k 2)y 2+2ky -7k 2=0,所以 y 1y 2= 1+2k 2⎧⎪6 6 1 3 10 = ≤ = 3,当且仅当 3m = ,即 m = 时取等号,此时 n = ,m10 303 2 2x 28y2b2=1 经过点(b,2e ),其中 e 为椭圆 C 的离心率.过点 T (1,0)作斜率为 k (k >0)的直线 l 交椭圆 C 于 A ,B 两点(A 在 x 轴下方).(1)求椭圆 C 的标准方程;MN 25b 2 4e 2解 (1)由点(b,2e )在椭圆 C 上,得 8 + b 2 =1. c 2 8-b 2 b 2 b 2 4 3因为 e 2=a 2= 8 8 8 b 2=2.又 b 2<a 2=8,解得 b 2=4,x 2 y 28 4(2)设 A (x 1,y 1),B (x 2,y 2),M (x 0,y 0),由对称性知 N (-x 0,-y 0),其中 y 1<0.因为 MN ∥AB ,所以= .直线 AB 的方程为 y =k (x -1),直线 MN 的方程为 y =kx ,其中 k >0. ⎧⎪y =k (x -1), 由⎨ ⎪⎩x 2+2y 2=8由⎨y =kx ,⎪⎩x 2+2y 2=8消去 x ,得(1+2k 2)y 2=8k 2,-7k 2 .所以 y 20= ,从而得 1+2k 2MN 2 32 (3)由AP= TB ,得-x 1= (x 2-1).5⎩,x 1x 2= 1+2k 2所以 x 1= ,x 2=3(1+2k 2) 3(1+2k 2)3(1+2k 2) 3(1+2k 2) 1+2k 2解得 k 2=2 或 k 2=- (舍).8k 2 AT ·BT 7= .→ 2→ 2 5⎧⎪y =k (x -1),由⎨⎪x 2+2y 2=8消去 y ,得(1+2k 2)x 2-4k 2x +2k 2-8=0,所以 x 1+x 2=1+2k 24k 2 2k 2-8 .2又因为-x 1=5(x 2-1),-4k 2+2 16k 2-2,-4k 2+2 16k 2-2 2k 2-8从而 · = .整理得 50k 4-83k 2-34=0,1750因为 k >0,所以 k = 2.。
2018版考前三个月高考数学理科全国通用总复习文档:解

解答题滚动练61.已知函数f (x )=cos 2x +2sin 2x +2sin x .(1)将函数f (2x )的图象向右平移π6个单位长度得到函数g (x )的图象,若x ∈⎣⎡⎦⎤π12,π2,求函数g (x )的值域;(2)已知a ,b ,c 分别为△ABC 中角A ,B ,C 的对边,且满足b =2,B ∈⎝⎛⎭⎫0,π2,f (A )=2+1,3a =2b sin A ,求△ABC 的面积.解 f (x )=cos 2x +2sin 2x +2sin x =cos 2x +(1-cos 2x )+2sin x =1+2sin x . (1)平移可得g (x )=2sin ⎝⎛⎭⎫2x -π3+1, ∵x ∈⎣⎡⎦⎤π12,π2, ∴2x -π3∈⎣⎡⎦⎤-π6,2π3, 当x =π12时,g (x )min =0;当x =5π12时,g (x )max =3,∴所求值域为[0,3].(2)由已知3a =2b sin A 及正弦定理,得3sin A =2sin B sin A , ∴sin B =32. ∵0<B <π2,∴B =π3,由f (A )=2+1,得sin A =22, 由正弦定理,得a =263<b ,从而A =π4,∴S △ABC =12ab sin C =12×263×2×6+24=3+33.2.在等差数列{a n }中,公差d ≠0,a 1=1,且a 1,a 2,a 5成等比数列. (1)求数列{a n }的通项公式;(2)若b n =a n3n ,求数列{b n }的前n 项和T n .解 (1)由a 1,a 2,a 5成等比数列知,a 22=a 1a 5,即(a 1+d )2=a 1(a 1+4d ),即d 2=2a 1d , 又d ≠0,a 1=1,解得d =2,故a n =2n -1. (2)b n =2n -13n ,则T n =13+332+533+…+2n -13n ,① 由①式两边×13,有13T n =132+333+534+…+2n -13n 1,②由①-②,得23T n =13+232+233+…+23n -2n -13n +1⇒23T n =13+232⎣⎡⎦⎤1-⎝⎛⎭⎫13n -11-13-2n -13n +1,化简得T n =1-n +13n .3.如图,在四棱锥P -ABCD 中,底面ABCD 为平行四边形,AP =AB =AC =a ,AD =2a ,P A ⊥底面ABCD.(1)求证:平面PCD ⊥平面P AC ;(2)在棱PC 上是否存在一点E ,使得二面角B -AE -D 的平面角的余弦值为-63?若存在,求出λ=CECP的值;若不存在,请说明理由.(1)证明 在△ACD 中,AC =a ,CD =a ,AD =2a , 由勾股定理得CD ⊥AC , ∵P A ⊥底面ABCD , ∴P A ⊥CD ,又AC ⊂平面P AC ,P A ⊂平面P AC ,P A ∩AC =A , ∴CD ⊥平面P AC . 又∵CD ⊂平面PCD , ∴平面PCD ⊥平面P AC .(2)解 由(1)知,AB ⊥AC ,又P A ⊥底面ABCD ,∴以A 为原点,AB ,AC ,AP 所在直线分别为x 轴,y 轴,z 轴建立如图所示坐标系,则A (0,0,0),B (a ,0,0),C (0,a ,0),D (-a ,a ,0),P (0,0,a ), 假设点E (x E ,y E ,z E )存在,且λ=CE CP ,则CE →=λCP →,即(x E ,y E -a ,z E )=λ(0,-a ,a ), ∴x E =0,y E =(1-λ)a ,z E =λa .∴AB →=(a ,0,0),AE →=(0,(1-λ)a ,λa ),AD →=(-a ,a ,0).设平面BAE 的法向量为n 1=(x 1,y 1,z 1),平面DAE 的法向量为n 2=(x 2,y 2,z 2),则⎩⎪⎨⎪⎧ax 1=0,(1-λ)ay 1+λaz 1=0, ⎩⎪⎨⎪⎧-ax 2+ay 2=0,(1-λ)ay 2+λaz 2=0.∴n 1=(0,λ,λ-1),n 2=(λ,λ,λ-1),cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=λ2+(λ-1)2λ2+(λ-1)2·λ2+λ2+(λ-1)2=2λ2-2λ+12λ2-2λ+1·3λ2-2λ+1=2λ2-2λ+13λ2-2λ+1,由题意|cos 〈n 1,n 2〉|=63, 即2λ2-2λ+13λ2-2λ+1=63,3(2λ2-2λ+1)=2(3λ2-2λ+1), ∴λ=12.∴棱PC 上存在一点E ,使得二面角B -AE -D 的平面角的余弦值为-63,且此时λ=12. 4.对于函数f (x )和g (x ),若存在常数k ,m ,对于任意x ∈R ,不等式f (x )≥kx +m ≥g (x )都成立,则称直线y =kx +m 是函数f (x ),g (x )的分界线.已知函数f (x )=e x (ax +1)(e 为自然对数的底数,a ∈R 为常数).(1)讨论函数f (x )的单调性;(2)设a =1,试探究函数f (x )与函数g (x )=-x 2+2x +1是否存在“分界线”?若存在,求出分界线方程;若不存在,请说明理由. 解 (1)∵f (x )=e x (ax +1), ∴f ′(x )=e x (ax +a +1),∴当a =0时,f ′(x )>0,∴f (x )在R 上单调递增. 当a ≠0时,f ′(x )=a e x ⎣⎡⎦⎤x -⎝⎛⎭⎫-a +1a ,当a >0时,在⎝⎛⎭⎫-∞,-a +1a 上,f ′(x )<0,∴f (x )单调递减;在⎝⎛⎭⎫-a +1a ,+∞上,f ′(x )>0,∴f (x )单调递增.当a <0时,在⎝⎛⎭⎫-∞,-a +1a 上,f ′(x )>0,∴f (x )单调递增;在⎝⎛⎭⎫-a +1a ,+∞上,f ′(x )<0,∴f (x )单调递减.(2)假设存在直线y =kx +m ,使不等式e x (x +1)≥kx +m ≥-x 2+2x +1, 当x =0时,由于1≥m ≥1,∴m =1, ∴kx +1≥-x 2+2x +1恒成立, ∴x 2+(k -2)x ≥0恒成立. 令Δ=(k -2)2≤0,解得k =2,∴只需不等式e x (x +1)≥2x +1恒成立即可. 设h (x )=e x (x +1)-2x -1,则h ′(x )=e x (x +2)-2, 令(h ′(x ))′=e x (x +3)=0,得x =-3,∴当x <-3时,h ′(x )单调递减;当x >-3时,h ′(x )单调递增,且h ′(0)=0,当x →-∞时,h ′(x )→-2,∴当x <0时,h ′(x )<0,∴h (x )单调递减; 当x >0时,h ′(x )>0,∴h (x )单调递增. ∴h (x )min =h (0)=0.∴h (x )=e x (x +1)-2x -1≥0, ∴不等式e x (x +1)≥2x +1恒成立.综上所述,函数f (x )与函数g (x )存在分界线,其分界线方程为y =2x +1.。
2018考前三个月高考数学理科(江苏专用)总复习——中档大题规范练2+Word版含答案

2.三角函数的图象、性质与三角变换1.已知α为锐角,cos ⎝ ⎛⎭⎪⎫α+π4=55. (1)求tan ⎝ ⎛⎭⎪⎫α+π4的值;(2)求sin ⎝⎛⎭⎪⎫2α+π3的值. 解 (1)因为α∈⎝ ⎛⎭⎪⎫0,π2,所以α+π4∈⎝ ⎛⎭⎪⎫π4,3π4,所以sin ⎝⎛⎭⎪⎫α+π4=1-cos 2⎝⎛⎭⎪⎫α+π4=255,所以tan ⎝ ⎛⎭⎪⎫α+π4=sin ⎝ ⎛⎭⎪⎫α+π4cos ⎝ ⎛⎭⎪⎫α+π4=2.(2)因为sin ⎝⎛⎭⎪⎫2α+π2=sin2⎝ ⎛⎭⎪⎫α+π4=2sin ⎝ ⎛⎭⎪⎫α+π4cos ⎝ ⎛⎭⎪⎫α+π4=45, cos ⎝ ⎛⎭⎪⎫2α+π2=cos2⎝ ⎛⎭⎪⎫α+π4=2cos 2⎝ ⎛⎭⎪⎫α+π4-1=-35, 所以sin ⎝ ⎛⎭⎪⎫2α+π3=sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫2α+π2-π6=sin ⎝ ⎛⎭⎪⎫2α+π2cos π6-cos ⎝⎛⎭⎪⎫2α+π2sin π6=43+310.2.(2017·南通、扬州、泰州、淮安三调)已知函数f (x )=A sin ⎝ ⎛⎭⎪⎫ωx +π3(A >0,ω>0)图象的相邻两条对称轴之间的距离为π,且经过点⎝ ⎛⎭⎪⎫π3,32.(1)求函数f (x )的解析式;(2)若角α满足f (α)+3f ⎝ ⎛⎭⎪⎫α-π2=1,α∈(0,π),求角α的值. 解 (1)由条件知周期T =2π,即2πω=2π,所以ω=1,即f (x )=A sin ⎝ ⎛⎭⎪⎫x +π3.因为f (x )的图象经过点⎝ ⎛⎭⎪⎫π3,32,所以A sin 2π3=32,所以A =1,所以f (x )=sin ⎝⎛⎭⎪⎫x +π3.(2)由f (α)+3f ⎝ ⎛⎭⎪⎫α-π2=1,得sin ⎝ ⎛⎭⎪⎫α+π3+3sin ⎝ ⎛⎭⎪⎫α+π3-π2=1,即sin ⎝ ⎛⎭⎪⎫α+π3-3cos ⎝ ⎛⎭⎪⎫α+π3=1, 所以2sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α+π3-π3=1,即sin α=12.因为α∈(0,π),所以α=π6或5π6.3.(2017·南京三模)已知向量a =(2cos α,sin 2α),b =(2sin α,t ),α∈⎝ ⎛⎭⎪⎫0,π2.(1)若a -b =⎝ ⎛⎭⎪⎫25,0,求t 的值;(2)若t =1,且a·b =1,求tan ⎝⎛⎭⎪⎫2α+π4的值. 解 (1)方法一 因为向量a =(2cos α,sin 2α),b =(2sin α,t ),且a -b =⎝ ⎛⎭⎪⎫25,0,所以cos α-sin α=15,t =sin 2α.由cos α-sin α=15,得(cos α-sin α)2=125,即1-2sin αcos α=125,从而2sin αcos α=2425.所以(cos α+sin α)2=1+2sin αcos α=4925.因为α∈⎝ ⎛⎭⎪⎫0,π2,所以cos α+sin α=75,所以sin α=(cos α+sin α)-(cos α-sin α)2=35,从而t =sin 2α=925.方法二 因为向量a =(2cos α,sin 2α),b =(2sin α,t ), 且a -b =⎝ ⎛⎭⎪⎫25,0,所以cos α-sin α=15,t =sin 2α.又sin 2α+cos 2α=1,所以sin 2α+⎝ ⎛⎭⎪⎫sin α+152=1,整理得50sin 2α+10sin α-24=0, 解得sin α=-45或sin α=35.因为α∈⎝ ⎛⎭⎪⎫0,π2,所以sin α>0,所以sin α=35, 从而t =sin 2α=925.(2)方法一 因为t =1,且a·b =1,所以4sin αcos α+sin 2α=1,即4sin αcos α=cos 2α. 因为α∈⎝ ⎛⎭⎪⎫0,π2,所以cos α≠0,从而tan α=14.所以tan2α=2tan α1-tan 2α=815. 从而tan ⎝⎛⎭⎪⎫2α+π4=tan2α+tanπ41-tan2α·tan π4=815+11-815=237.方法二 因为t =1,且a·b =1,所以4sin αcos α+sin 2α=1,即4sin αcos α=cos 2α. 所以2sin2α=1+cos2α2,即4sin2α-cos2α=1,又sin 22α+cos 22α=1,所以sin 22α+(4sin2α-1)2=1, 整理得17sin 22α-8sin2α=0, 解得sin2α=817或sin2α=0.因为α∈⎝⎛⎭⎪⎫0,π2,所以2α∈(0,π),所以sin2α>0,所以sin2α=817,代入4sin2α-cos2α=1,得cos2α=1517,因为tan2α=sin2αcos2α=815,从而tan ⎝⎛⎭⎪⎫2α+π4=tan2α+tanπ41-tan2α·tan π4=815+11-815=237.4.(2017·南通一调)如图,在平面直角坐标系xOy 中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A .以OA 为始边作锐角β,其终边与单位圆交于点B ,AB =255.(1)求cos β的值;(2)若点A 的横坐标为513,求点B 的坐标.解 (1)在△AOB 中,由余弦定理,得cos ∠AOB =OA 2+OB 2-AB 22OA ·OB=12+12-⎝ ⎛⎭⎪⎫25522×1×1=35,即cos β=35.(2)因为cos β=35,β∈⎝ ⎛⎭⎪⎫0,π2,所以sin β=1-cos 2β=1-⎝ ⎛⎭⎪⎫352=45. 因为点A 的横坐标为513,由三角函数定义可得cos α=513.因为α为锐角,所以sin α=1-cos 2α=1-⎝ ⎛⎭⎪⎫5132=1213.所以cos(α+β)=cos αcos β-sin αsin β=513×35-1213×45=-3365,sin(α+β)=sin αcos β+cos αsin β=1213×35+513×45=5665.所以点B 坐标为⎝ ⎛⎭⎪⎫-3365,5665.。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——考前回扣6 Word版含答案
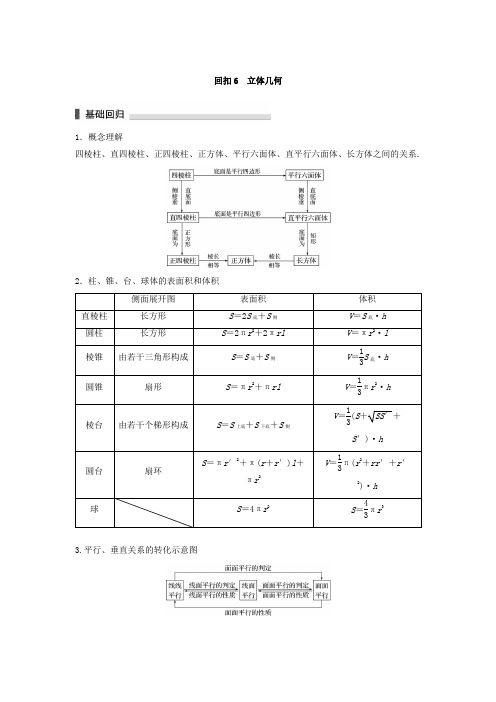
回扣6 立体几何1.概念理解四棱柱、直四棱柱、正四棱柱、正方体、平行六面体、直平行六面体、长方体之间的关系.2.柱、锥、台、球体的表面积和体积3.平行、垂直关系的转化示意图1.易混淆几何体的表面积与侧面积的区别,几何体的表面积是几何体的侧面积与所有底面面积之和,不能漏掉几何体的底面积;求锥体体积时,易漏掉体积公式中的系数13.2.不清楚空间线面平行与垂直关系中的判定定理和性质定理,忽视判定定理和性质定理中的条件,导致判断出错.如由α⊥β,α∩β=l ,m ⊥l ,易误得出m ⊥β的结论,就是因为忽视面面垂直的性质定理中m ⊂α的限制条件.3.注意图形的翻折与展开前后变与不变的量以及位置关系.对照前后图形,弄清楚变与不变的元素后,再立足于不变的元素的位置关系与数量关系去探求变化后的元素在空间中的位置与数量关系.1.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是________. 答案 2π解析 几何体的底面圆半径为1,高为1,则侧面积S =2πrh =2π×1×1=2π. 2.用平面α截球O 所得截面圆的半径为3,球心O 到平面α的距离为4,则此球的表面积为__________. 答案 100π解析 依题意,设球的半径为R ,满足R 2=32+42=25, ∴S 球=4πR 2=100π.3.(2017·南京高淳区质检)若正四棱锥的底面边长为22,体积为8,则其侧面积为__________. 答案 422解析 因为V =13×(22)2h =8,所以h =3,所以斜高h ′=32+(2)2=11.所以其侧面积为S 侧=4×⎝ ⎛⎭⎪⎫12×22×11=422. 4.设m ,n 是不同的直线,α,β,γ是不同的平面,有以下四个命题:①⎩⎪⎨⎪⎧ α∥β,α∥γ⇒β∥γ;②⎩⎪⎨⎪⎧α⊥β,m ∥α⇒m ⊥β;③⎩⎪⎨⎪⎧m ⊥α,m ∥β⇒α⊥β;④⎩⎪⎨⎪⎧m ∥n ,n ⊂α⇒m ∥α.其中正确的命题是________.(填序号) 答案 ①③解析 ①中平行于同一平面的两平面平行是正确的;②中m ,β可能平行,相交或直线在平面内;③中由面面垂直的判定定理可知结论正确;④中m ,α可能平行或线在面内. 5.在三棱锥S -ABC 中,底面ABC 是边长为3的等边三角形,SA ⊥SC ,SB ⊥SC ,SA =SB =2,则该三棱锥的体积为________. 答案354解析 如图,∵SA ⊥SC ,SB ⊥SC ,且SA ∩SB =S , ∴SC ⊥平面SAB ,在Rt △BSC 中,由SB =2,BC =3,得SC = 5.在△SAB 中,取AB 中点D ,连结SD ,则SD ⊥AB ,且BD =32,∴SD =22-⎝ ⎛⎭⎪⎫322=72,∴V =13×12×3×72×5=354.6.已知m ,n 为不同直线,α,β为不同平面,给出下列命题: ①若m ⊥α,m ⊥n ,则n ∥α; ②若m ⊥β,n ⊥β,则m ∥n ; ③若m ⊥α,m ⊥β,则α∥β; ④若m ⊂α,n ⊂β,α∥β,则n ∥m ;⑤若α⊥β,α∩β=m ,n ⊂α,m ⊥n ,则n ⊥β. 其中正确的命题是________.(填写所有正确命题的序号) 答案 ②③⑤解析 命题①,若m ⊥α,m ⊥n ,则n ∥α或n ⊂α,故不正确;命题②,若m ⊥β,n ⊥β,则m ∥n ,由线面垂直的性质定理易知正确;命题③,由线面垂直的性质定理易知正确;命题④,若m ⊂α,n ⊂β,α∥β,则n ∥m 或m ,n 异面,所以不正确;命题⑤是面面垂直的性质定理,所以是正确命题.故答案为②③⑤.7.如图,三棱锥A -BCD 的棱长全相等,点E 为AD 的中点,则直线CE 与BD 所成角的余弦值为__________.答案36解析 方法一 取AB 的中点G ,连结EG ,CG . ∵E 为AD 的中点,∴EG ∥BD .∴∠GEC 为CE 与BD 所成的角.设AB =1, 则EG =12BD =12,CE =CG =32,∴cos ∠GEC =EG 2+EC 2-GC 22×EG ×EC=⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫322-⎝ ⎛⎭⎪⎫3222×12×32=36. 方法二 设AB =1,则CE →·BD →=(AE →-AC →)·(AD →-AB →)=⎝ ⎛⎭⎪⎫12AD →-AC →·(AD →-AB →)=12AD →2-12AD →·AB →-AC →·AD →+AC →·AB →=12-12cos60°-cos60°+cos60°=14. ∴cos 〈CE→,BD →〉=CE →·BD →|CE →||BD →|=1432=36.8.如图所示,在边长为5+2的正方形ABCD 中,以A 为圆心画一个扇形,以O 为圆心画一个圆,M ,N ,K 为切点,以扇形为圆锥的侧面,以圆O 为圆锥底面,围成一个圆锥,则圆锥的全面积S =________. 答案 10π 解析设圆锥的母线长为l ,底面半径为r ,由已知条件得⎩⎪⎨⎪⎧l +r +2r =(5+2)×2,2πr l=π2,解得r =2,l =42,则S =πrl +πr 2=10π.9.如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,PD ⊥BC ,G 为PA 上一点. (1)求证:平面PCD ⊥平面ABCD ;(2)若PC ∥平面BDG ,求证:G 为PA 的中点.证明 (1)∵底面ABCD 为矩形,∴BC ⊥CD , 又∵PD ⊥BC ,PD ∩CD =D ,CD ,PD ⊂平面PCD , ∴BC ⊥平面PCD .又∵BC ⊂平面ABCD ,∴平面ABCD ⊥平面PCD .(2)连结AC 交BD 于点O ,连结GO ,∵PC ∥平面BDG , 平面PCA ∩平面BDG =GO , ∴PC ∥GO , ∴PG GA =COOA.∵底面ABCD 为矩形, ∴O 是AC 的中点,即CO =OA , ∴PG =GA ,∴G 为PA 的中点.10.在正四棱锥S -ABCD 中,底面边长为a ,侧棱长为2a ,P 为侧棱SD 上的一点. (1)当四面体ACPS 的体积为6a 318时,求SP PD的值;(2)在(1)的条件下,若E 是SC 的中点,求证:BE ∥平面APC .(1)解 设PD =x ,连结BD ,AC ,交点为O .过P 作PH ⊥BD 于点H ,∵平面SBD ⊥平面ABCD 且BD 为交线,则PH ⊥平面ABCD ,又SO ⊥平面ABCD , ∴PH ∥SO .在Rt △SOB 中,SO =SB 2-BO 2=62a , ∵PH SO =PD SD,∴PH =PD ·SOSD=x ·62a 2a=32x , ∴V SPAC =V S -ACD -V P -ACD=13×⎝ ⎛⎭⎪⎫12×a ×a ⎝ ⎛⎭⎪⎫62a -32x =618a 3, 解得x =23a , ∴SP PD =21=2.(2)证明 取SP 的中点Q ,连结QE ,BQ , 则EQ ∥PC ,EQ ⊄平面PAC ,PC ⊂平面PAC , ∴EQ ∥平面PAC .∵P 为QD 的中点,O 为BD 的中点, ∴BQ ∥PO ,又BQ ⊄平面PAC ,PO ⊂平面PAC , ∴BQ ∥平面PAC ,而EQ 与BQ 为平面BEQ 内的两条相交直线, ∴平面BEQ ∥平面PAC ,而BE ⊂平面BEQ ,∴BE ∥平面APC .。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——考前回扣3 含答案

;回扣3 三角函数与平面向量;;1.准确记忆六组诱导公式;; 对于“k π2±α,k ∈Z ”的三角函数值与α角的三角函数值的关系口诀:奇变偶不变,符号看象限.;2.三角函数恒等变换“四大策略”;;(1)常值代换:特别是“1”的代换,1=sin 2θ+cos 2θ=tan45°等. (2)降次与升次:正用二倍角公式升次,逆用二倍角公式降次. (3)弦、切互化:一般是切化弦.;;(4)灵活运用辅助角公式a sin α+b cos α=a 2+b 2sin(α+φ)⎝ ⎛⎭⎪⎫其中tan φ=b a .3.三种三角函数的性质;;4.函数y =A sin(ωx +φ)(ω>0,A >0)的图象 (1)“五点法”作图设z =ωx +φ,令z =0,π2,π,3π2,2π,求出相应的x 的值与y 的值,描点、连线可得.(2)由三角函数的图象确定解析式时,一般利用五点中的零点或最值点作为解题突破口. (3)图象变换y =sin x ―――――――――→向左(φ>0)或向右(φ<0)平移|φ|个单位长度y =sin(x +φ) ――――――――――――→横坐标变为原来的1ω(ω>0)倍纵坐标不变y =sin(ωx +φ) ―――――――――――→纵坐标变为原来的A (A >0)倍横坐标不变y =A sin(ωx +φ). 5.正弦定理及其变形asin A=b sin B =csin C=2R (2R 为△ABC 外接圆的直径).变形:a =2R sin A ,b =2R sin B ,c =2R sin C . sin A =a 2R ,sin B =b 2R ,sin C =c2R.a ∶b ∶c =sin A ∶sin B ∶sin C .6.余弦定理及其推论、变形a 2=b 2+c 2-2bc cos A ,b 2=a 2+c 2-2ac cos B , c 2=a 2+b 2-2ab cos C .推论:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.变形:b 2+c 2-a 2=2bc cos A ,a 2+c 2-b 2=2ac cos B ,a 2+b 2-c 2=2ab cos C .7.面积公式S △ABC =12bc sin A =12ac sin B =12ab sin C .8.平面向量的数量积(1)若a ,b 为非零向量,夹角为θ,则a·b =|a||b |cos θ. (2)设a =(x 1,y 1),b =(x 2,y 2),则a·b =x 1x 2+y 1y 2. 9.两个非零向量平行、垂直的充要条件 若a =(x 1,y 1),b =(x 2,y 2),则 (1)a ∥b ⇔a =λb (b ≠0)⇔x 1y 2-x 2y 1=0. (2)a ⊥b ⇔a·b =0⇔x 1x 2+y 1y 2=0. 10.利用数量积求长度(1)若a =(x ,y ),则|a |=a·a =x 2+y 2. (2)若A (x 1,y 1),B (x 2,y 2),则 |AB →|=(x 2-x 1)2+(y 2-y 1)2.11.利用数量积求夹角若a =(x 1,y 1),b =(x 2,y 2),θ为a 与b 的夹角, 则cos θ=a·b |a||b |=x 1x 2+y 1y 2x 21+y 21 x 22+y 22. 12.三角形“四心”向量形式的充要条件设O 为△ABC 所在平面上一点,角A ,B ,C 所对的边长分别为a ,b ,c ,则(1)O 为△ABC 的外心⇔|OA →|=|OB →|=|OC →|=a 2sin A.(2)O 为△ABC 的重心⇔OA →+OB →+OC →=0.(3)O 为△ABC 的垂心⇔OA →·OB →=OB →·OC →=OC →·OA →. (4)O 为△ABC 的内心⇔aOA →+bOB →+cOC →=0.1.利用同角三角函数的平方关系式求值时,不要忽视角的范围,要先判断函数值的符号. 2.在求三角函数的值域(或最值)时,不要忽略x 的取值范围.3.求函数f (x )=A sin(ωx +φ)的单调区间时,要注意A 与ω的符号,当ω<0时,需把ω的符号化为正值后求解.4.三角函数图象变换中,注意由y =sin ωx 的图象变换得y =sin(ωx +φ)时,平移量为⎪⎪⎪⎪⎪⎪φω,而不是φ. 5.在已知两边和其中一边的对角时,要注意检验解是否满足“大边对大角”,避免增解. 6.要特别注意零向量带来的问题:0的模是0,方向任意,并不是没有方向;0与任意非零向量平行.7.a·b >0是〈a ,b 〉为锐角的必要不充分条件;a·b <0是〈a ,b 〉为钝角的必要不充分条件.1.2sin45°cos15°-sin30°的值=________. 答案32解析 2sin45°cos15°-sin30°=2sin45°cos15°-sin(45°-15°)=2sin45°cos15°-(sin45°cos15°-cos45°sin15°)=sin45°cos15°+cos45°sin15°=sin60°=32. 2.(1+tan18°)(1+tan27°)的值是________. 答案 2解析 由题意得tan(18°+27°)=tan18°+tan27°1-tan18°tan27°,即tan18°+tan27°1-tan18°tan27°=1, 所以tan18°+tan27°=1-tan18°tan27°,所以(1+tan18°)(1+tan27°)=1+tan18°+tan27°+tan18°tan27°=2.3.(2017·江苏泰州中学期中)向量a =(cos10°,sin10°),b =(cos70°,sin70°),|a -2b |=________. 答案3解析 a ·b =cos70°cos10°+sin70°sin10°=cos60°=12,|a |=|b |=1,所以|a -2b |=a 2+4b 2-4a ·b =1+4-2= 3.4.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC 的面积是________. 答案332解析 c 2=(a -b )2+6,即c 2=a 2+b 2-2ab +6,① ∵C =π3,由余弦定理得c 2=a 2+b 2-ab ,②由①和②得ab =6,∴S △ABC =12ab sin C =12×6×32=332.5.已知两点A (1,0),B (1,1),O 为坐标原点,点C 在第二象限,且∠AOC =135°,设OC →=-OA →+λOB →(λ∈R ),则λ的值为__________. 答案 12解析 由∠AOC =135°知,点C 在射线y =-x (x <0)上,设点C 的坐标为(a ,-a ),a <0,则有(a ,-a )=(-1+λ,λ),得a =-1+λ,-a =λ,消去a 得λ=12.6.已知a ,b 为同一平面内的两个向量,且a =(1,2),|b |=12|a |,若a +2b 与2a -b 垂直,则a 与b 的夹角为________. 答案 π解析 |b |=12|a |=52,而(a +2b )·(2a -b )=0,即2a 2-2b 2+3a·b =0,所以a·b =-52,从而cos 〈a ,b 〉=a·b|a||b |=-1,所以〈a ,b 〉=π.7.已知函数f (x )=3sin ⎝⎛⎭⎪⎫ωx -π6(ω>0)和g (x )=3cos(2x +φ)的图象的对称中心完全相同,若x ∈⎣⎢⎡⎦⎥⎤0,π2,则f (x )的取值范围是________.答案 ⎣⎢⎡⎦⎥⎤-32,3解析 由两个三角函数图象的对称中心完全相同可知,两函数的周期相同,故ω=2, 所以f (x )=3sin ⎝⎛⎭⎪⎫2x -π6, 那么当x ∈⎣⎢⎡⎦⎥⎤0,π2时,-π6≤2x -π6≤5π6, 所以-12≤sin ⎝ ⎛⎭⎪⎫2x -π6≤1,故f (x )∈⎣⎢⎡⎦⎥⎤-32,3.8.在等腰梯形ABCD 中,已知AB ∥DC ,AB =2,BC =1,∠ABC =60°,动点E 和F 分别在线段BC 和DC 上,且BE →=λBC →,DF →=19λDC →,则AE →·AF →的最小值为__________.答案2918解析 方法一 在梯形ABCD 中,AB =2,BC =1,∠ABC =60°,可得DC =1,AE →=AB →+λBC →,AF →=AD →+19λDC →(λ>0),∴AE →·AF →=(AB →+λBC →)·⎝ ⎛⎭⎪⎫AD →+19λDC →=AB →·AD →+AB →·19λDC→+λBC →·AD →+λBC →·19λDC →=2×1×cos60°+2×1×19λ+λ×1×1×cos60°+λ×19λ×1×1×cos120°=29λ+λ2+1718≥229λ·λ2+1718=2918,当且仅当29λ=λ2,即λ=23时,取得最小值为2918. 方法二 以点A 为坐标原点,AB 所在的直线为x 轴建立平面直角坐标系,则B (2,0),C ⎝ ⎛⎭⎪⎫32,32,D ⎝ ⎛⎭⎪⎫12,32.又BE →=λBC →,DF →=19λDC →,则E ⎝ ⎛⎭⎪⎫2-12λ,32λ,F ⎝ ⎛⎭⎪⎫12+19λ,32,λ>0,∴AE →·AF →=⎝ ⎛⎭⎪⎫2-12λ⎝ ⎛⎭⎪⎫12+19λ+34λ=1718+29λ+12λ≥1718+229λ·12λ=2918,λ>0,当且仅当29λ=12λ,即λ=23时取等号,故AE →·AF →的最小值为2918.9.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3-3sin ⎝ ⎛⎭⎪⎫2x -π6. (1)求函数f (x )的最小正周期和单调增区间;(2)当x ∈⎣⎢⎡⎦⎥⎤-π6,π3时,试求f (x )的最值,并写出取得最值时自变量x 的值.解 (1)由题意知,f (x )=-sin2x +3cos2x =2sin ⎝⎛⎭⎪⎫2x +2π3, 所以f (x )的最小正周期为T =2π2=π.当-π2+2k π≤2x +2π3≤π2+2k π(k ∈Z )时,f (x )单调递增,解得x ∈⎣⎢⎡⎦⎥⎤-7π12+k π,-π12+k π(k ∈Z ), 所以f (x )的单调增区间为⎣⎢⎡⎦⎥⎤-7π12+k π,-π12+k π(k ∈Z ). (2)因为x ∈⎣⎢⎡⎦⎥⎤-π6,π3,所以π3≤2x +2π3≤4π3,当2x +2π3=π2,即x =-π12时,f (x )取得最大值2,当2x +2π3=4π3,即x =π3时,f (x )取得最小值- 3.10.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知cos C +(cos A -3sin A )cos B =0.(1)求角B 的大小;(2)若a =2,b =7,求△ABC 的面积. 解 (1)由已知得-cos(A +B )+cos A cos B -3sin A cos B =0, 即sin A sin B -3sin A cos B =0, 因为sin A ≠0, 所以sin B -3cos B =0,又cos B ≠0,所以tan B =3, 又0<B <π,所以B =π3.(2)因为sin B =32,cos B =12, 所以a sin A =b sin B =732=2213,又a =2, 所以sin A =321=217, 因为a <b , 所以cos A =277.所以sin C =sin(A +B )=sin A cos B +cos A sin B =32114,所以S =12ab sin C =332.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解答题滚动练6
1.在△ABC 中,三个内角分别为A ,B ,C ,已知sin ⎝
⎛⎭⎪⎫A +π6=2cos A . (1)若cos C =63
,求证:2a -3c =0; (2)若B ∈⎝
⎛⎭⎪⎫0,π3,且cos(A -B )=45,求sin B . (1)证明 因为sin ⎝
⎛⎭⎪⎫A +π6=2cos A ,得32sin A +12cos A =2cos A , 即sin A =3cos A ,因为A ∈(0,π),且cos A ≠0,
所以tan A =3,所以A =π3
. 因为sin 2C +cos 2C =1,cos C =
63,C ∈(0,π), 所以sin C =33
, 由正弦定理知a sin A =c sin C ,即a c =sin A sin C =3233
=32
, 即2a -3c =0.
(2)解 因为B ∈⎝ ⎛⎭⎪⎫0,π3,所以A -B =π3-B ∈⎝ ⎛⎭⎪⎫0,π3, 因为sin 2(A -B )+cos 2(A -B )=1, 所以sin(A -B )=35
, 所以sin B =sin(A -(A -B ))=sin A cos(A -B )-cos A ·sin(A -B )=43-310
. 2.已知函数f (x )=ax 3-2x -ln x ,a ∈R .
(1)若曲线y =f (x )在x =1处的切线方程为y =b ,求a +b 的值;
(2)在(1)的条件下,求函数f (x )零点的个数.
解 (1)f ′(x )=3ax 2-2-1x
, 由题意,f ′(1)=0,f (1)=b ,解得,a =1,b =-1,
所以a +b =0.
(2)由(1)知,f (x )=x 3
-2x -ln x ,
f ′(x )=3x 2-2-1x =3x 3
-2x -1x
=(x -1)(3x 2
+3x +1)x
, 令f ′(x )=0,得x =1,
且当0<x <1时,f ′(x )<0;当x >1时,f ′(x )>0,
所以函数f (x )在(0,1)上单调递减,在(1,+∞)上单调递增.
因为f (1)=-1<0,f ⎝ ⎛⎭⎪⎫1e =1e 3-2e +1>0,f (e)=e 3-2e -1>0,函数f (x )在区间⎣⎢⎡⎦
⎥⎤1e ,1和[1,e]上的图象是一条不间断的曲线,由零点存在性定理,知函数f (x )有两个零点.
3.已知圆M :x 2+(y -4)2
=4,点P 是直线l :x -2y =0上的一动点,过点P 作圆M 的切线PA ,PB ,切点为A ,B .
(1)当切线PA 的长度为23时,求点P 的坐标;
(2)若△PAM 的外接圆为圆N ,试问:当P 运动时,圆N 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
(3)求线段AB 长度的最小值.
解 (1)由题意可知,圆M 的半径r =2,设P (2b ,b ),
因为PA 是圆M 的一条切线,A 为切点,
所以∠MAP =90°,
所以MP =(0-2b )2+(4-b )2=AM 2+AP 2=4,
解得b =0或b =85
, 所以P (0,0)或P ⎝ ⎛⎭
⎪⎫165,85. (2)设P (2b ,b ),因为∠MAP =90°,所以经过A ,P ,M 三点的圆N 以MP 为直径, 其方程为(x -b )2
+⎝ ⎛⎭⎪⎫y -b +422=4b 2+(b -4)24, 即(2x +y -4)b -(x 2+y 2-4y )=0.
由⎩⎪⎨⎪⎧ 2x +y -4=0,x 2+y 2-4y =0,
解得⎩⎨⎧ x =0,
y =4,或⎩⎪⎨⎪⎧ x =85,y =45,
所以圆过定点(0,4),⎝ ⎛⎭⎪⎫85,45. (3)因为圆N 方程为(x -b )2+⎝ ⎛⎭
⎪⎫y -b +422=4b 2+(b -4)24,
即x 2+y 2-2bx -(b +4)y +4b =0.①
圆M :x 2+(y -4)2=4,即x 2+y 2-8y +12=0.②
②-①得圆M 与圆N 的相交弦AB 所在直线方程为
2bx +(b -4)y +12-4b =0,
点M 到直线AB 的距离d =45b 2-8b +16
, 相交弦长AB =24-d 2=4
1-45b 2-8b +16 =41-
45⎝ ⎛⎭⎪⎫b -452+645. 当b =45
时,AB 有最小值11. 4.如图是一“T ”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m ,东西向渠宽2m(从拐角处,即图中A ,B 处开始).假定渠内的水面始终保持水平位置(即无高度差).
(1)在水平面内,过点A 的一条直线与水渠的内壁交于P ,Q 两点,且与水渠的一边的夹角为
θ⎝
⎛⎭⎪⎫0<θ<π2,将线段PQ
的长度l 表示为θ的函数; (2)若从南面漂来一根长为7m 的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?请说明理由.
解 (1)由题意,PA =2sin θ,QA =4cos θ,所以l =PA +QA =2sin θ+4cos θ
⎝
⎛⎭⎪⎫0<θ<π2. (2)设f (θ)=2sin θ+4cos θ,θ∈⎝
⎛⎭⎪⎫0,π2. 由f ′(θ)=-2cos θsin 2θ+4sin θcos 2θ=2(22sin 3θ-cos 3θ)sin 2θcos 2θ
, 令f ′(θ)=0,得tan θ0=22. 且当θ∈(0,θ0),f ′(θ)<0;当θ∈⎝
⎛⎭⎪⎫θ0,π2,f ′(θ)>0,所以f (θ)在(0,θ0)上单调递减,在⎝
⎛⎭⎪⎫θ0,π2上单调递增,
所以当θ=θ0时,f(θ)取得极小值,即为最小值.
当tanθ0=
2
2
时,sinθ0=
1
3
,cosθ0=
2
3
,所以f(θ)的最小值为36,
即这根竹竿能通过拐角处的长度的最大值为36m.因为36>7,所以这根竹竿能从拐角处一直漂向东西向的水渠.。
