(完整)初一下相交线与平行线题型复习(重难点+难题突破)

合集下载

(完整版)初一相交线与平行线所有知识点总结和常考题提高难题压轴题练习(含答案解析)(20210212

初一相交线与平行线所有知识点总结和常考题提高难题压轴题练习（含答案解析）知识点：1、两条直线相交所成的四个角中，相邻的两个角叫做邻补角，特点是两个角共用一条边，另一条边互为反向延长线，性质是邻补角互补;相对的两个角叫做对顶角，特点是它们的两条边互为反向延长线。

性质是对顶角相等.2、三线八角：对顶角（相等），邻补角（互补），冋位角，内错角，同旁内角。

3、两条直线被第三条直线所截：同位角F （在两条直线的同一旁，第三条直线的同一侧）内错角Z （在两条直线内部，位于第三条直线两侧）同旁内角U （在两条直线内部，位于第三条直线同侧）4、两条直线相交所成的四个角中，如果有一个角为90度，则称这两条直线互相垂直。

其中一条宜线叫做另外一条直线的垂线•他们的交点称为垂足。

5、垂直三要素：垂直关系，垂直记号，垂足6、垂直公理：过一点有且只有一条直线与已知直线垂直。

7、垂线段最短。

8、点到直线的距离：直线外一点到这条直线的垂线段的长度。

9、平行公理：经过直线外一点，有且只有一条直线与这条直线平行。

推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

如果b//a,c//a,那么b//c10、平行线的判定：①同位角相等，两直线平行。

②内错角相等，两直线平行。

③同旁内角互补，两直线平行。

11、推论：在同一平面内，如果两条直线都垂直干同一条直线，那么这两条直线平行。

12、平行线的性质：①两直线平行，同位角相等：②两直线平行，内错角相等：③两直线平行，同旁内角互补。

13、___________________________________________ 平而上不相重合的两条直线之间的位置关系为_________________________________ 或 _______14、平移：①平移前后的两个图形形状大小不变，位置改变。

②对应点的线段平行且相等。

平移:在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移平移变换•简称平移。

人教七年级数学下《相交线与平行线》复习指导.doc

初中数学试卷马鸣风萧萧《相交线与平行线》复习指导知识要点1. 相交线所成的角及其基本结论.2. 垂线、垂线段的概念及性质，点到直线的距离.3. 三线八角（同位角、内错角、同旁内角），两直线平行的判定s.4. 平行线的性质及一些结论.5. 平移的特征.重点、难点易错、易混点6. 重点：垂线的概念，直线平行的条件和平行线的性质，学好这些重点知识的关键是掌握相交线与平行线的有关的角的知识.7. 难点：两直线平行的判定与平行线的性质，图形的平移及应用，说理的思路、步骤、格式的掌握，是本章的三个难点.8. 对顶角、邻补角的位置关系，它们的名称反映了它们的本质特征.9. 两条直线的位置关系中，垂直只是两条直线相交的一种特殊情况.10. 同位角、内错角、同旁内角的区分与判别. 11. 两直线平行的判定与平行线的性质的区别与运用.例析一、考查相交线例1 当光线从空气射入水中，光的传播方向发生了改变，这就是折射现象（如图），图中∠1与∠2是对顶角吗？例2 如图1，直线AB 、CD 、EF 都经过点O ，图中有几对对顶角。

例3 如图，直线AB 、CD 相交于点O ，若∠1︰∠2=1︰4，则 ∠1=__________________，∠3=____________________.例4 如图，已知AB CD 、相交于点O ，OE AB ⊥，28EOC ∠=，则AOD ∠=__________．二、两直线平行的判定和平行线的性质例5 如图，直线a 、b 都与直线c 相交，给出下列条件：①∠1=∠2；②∠3=∠6；③∠4＋∠7=180°；④∠5＋∠8=180°.其中能判断a ∥b 的是（）. 12 ≈≈≈ ≈≈≈≈≈≈≈（A ）①③ （B ）②④ （C ）①③④ （D ）①②③④例6 如图，直线a 、b 与直线c 相交，形成∠1、∠2、… 、∠8共八个角，请填上你认为适当的一个条件：______，使a//b.例7 如图4，若AB CD ∥，EF 与AB CD ，分别相交于点E F EP EF EFD ∠，，，⊥的平分线与EP 相交于点P ，且40BEP ∠=，则EPF ∠= 度．例8如图2，AB ∥CD ，P 为AB 、CD 之间的一点，已知∠1=∠2=250，求∠BPC 的度数？例9 如图5，CD ⊥AB 于D ，E 是BC 上一点，EF ⊥AB 于F ，∠l=∠2．试说明：∠AGD=∠ACB ．三、平移的性质及应用例10 下列A 、B 、C 、D 四幅图案中，能通过平移图案（1）得到的是（）例11 如图，直角ABC △沿直角边BC 所在的直线向右平移得到DEF △，下列结论中错误的是（）A ．EF DE BC AB ∙=∙2121 B ．90DEF ∠=C ．AC DF =D ．EC CF =例12 在5×5的方格纸中将图①中的图形N 平移后的位置如图②所示，那么下面平移中正确的是（）（A ）先向下移动1格，再向左移动1格（B ）先向下移动1格，再向左移动2格（C ）先向下移动2格，再向左移动1格（D ）先向下移动2格，再向左移动2格例13 1010⨯的正方形如图，在个小正方形的边长均为1个单位，将ABC △向下平移4网格中，每到A B C '''△，请你画出A B C '''△（不要求写画法）．个单位，得AB C A专题训练相交线一、选择题1.如图所示,∠1和∠2是对顶角的图形有( )12121221A.1个B.2个C.3个D.4个2.如图所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )A.150°B.180°C.210°D.120°3.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A.1个B.2个C.3个D.4个4.如图所示,直线AB 和CD 相交于点O,若∠AOD 与∠BOC 的和为236°,则∠AOC•的度数为( )A.62°B.118°C.72°D.59°二、填空题1.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.2.如图5所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.3.如图6所示,已知直线AB,CD 相交于O,OA 平分∠EOC,∠EOC=70°,则∠BOD=•______.4.对顶角的性质是______________________.5.如图7所示,直线AB,CD相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.6.如图8所示,直线AB,CD 相交于点O,OE 平分∠AOC,若∠AOD-∠DOB=50°,•则∠EOB=______________.7.如图9所示,直线AB,CD 相交于点O,已知∠AOC=70°,OE 把∠BOD 分成两部分,• 且∠BOE:∠EOD=2:3,则∠EOD=________. 三、训练平台1. 如图所示,AB,CD,EF 交于点O,∠1=20°,∠BOC=80°,求∠2的度数.2. 如图所示,L 1,L 2,L 3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.四、提高训练1. 如图所示,AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE•的度数.2. 如图所示,直线AB 与CD 相交于点O,∠AOC:∠AOD=2:3,求∠BOD 的度数.3. 如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.OF EDCBA 1234l 3l 2l 112OF ED C BA O DCBA专题训练垂线一、选择题1.如图1所示,下列说法不正确的是( )A.点B到AC的垂线段是线段AB;B.点C到AB的垂线段是线段ACC.线段AD是点D到BC的垂线段;D.线段BD是点B到AD的垂线段D CB ADCBAO DCBA(1) (2) (3)2.如图1所示,能表示点到直线(线段)的距离的线段有( )A.2条B.3条C.4条D.5条3.下列说法正确的有( )①在平面内,过直线上一点有且只有一条直线垂直于已知直线;②在平面内,过直线外一点有且只有一条直线垂直于已知直线;③在平面内,过一点可以任意画一条直线垂直于已知直线;④在平面内,有且只有一条直线垂直于已知直线.A.1个B.2个C.3个D.4个4.如图2所示,AD⊥BD,BC⊥CD,AB=acm,BC=bcm,则BD的范围是( )A.大于acmB.小于bcmC.大于acm或小于bcmD.大于bcm且小于acm5.到直线L的距离等于2cm的点有( )A.0个B.1个;C.无数个D.无法确定6.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )A.4cmB.2cm;C.小于2cmD.不大于2cm二、填空题1.如图3所示,直线AB与直线CD的位置关系是_______,记作_______,此时,•∠AOD=∠_______=∠_______=∠_______=90°.2.过一点有且只有________直线与已知直线垂直.3.画一条线段或射线的垂线,就是画它们________的垂线.4.直线外一点到这条直线的_________,叫做点到直线的距离.三、训练平台:(共15分)如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,•求∠DOG的度数.四、提高训练:(共15分)如图所示,村庄A要从河流l引水入庄,需修筑一水渠,请你画出修筑水渠的路线图.五、探索发现:(共20分)lAGOFED CB A如图6所示,O 为直线AB 上一点,∠AOC=13∠BOC,OC 是∠AOD 的平分线. (1)求∠COD 的度数;(2)判断OD 与AB 的位置关系,并说明理由. 六、中考题与竞赛题如图7所示,一辆汽车在直线形的公路AB 上由A 向B 行驶,M,N•分别是位于公路AB 两侧的村庄,设汽车行驶到P 点位置时,离村庄M 最近,行驶到Q 点位置时,•离村庄N 最近,请你在AB 上分别画出P,Q 两点的位置.专题训练平行线一、选择题1.在同一平面内,两条不重合直线的位置关系可能是( )A.平行或相交B.垂直或相交;C.垂直或平行D.平行、垂直或相交 2.下列说法正确的是( )A.经过一点有一条直线与已知直线平行B.经过一点有无数条直线与已知直线平行C.经过一点有且只有一条直线与已知直线平行D.经过直线外一点有且只有一条直线与已知直线平行3.在同一平面内有三条直线,若其中有两条且只有两条直线平行,则它们交点的个数为( ) A.0个 B.1个 C.2个 D.3个4.下列说法正确的有( )①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种; ③若线段AB 与CD 没有交点,则AB ∥CD;④若a ∥b,b ∥c,则a 与c 不相交. A.1个 B.2个 C.3个 D.4个 5.过一点画已知直线的平行线,则( )A.有且只有一条B.有两条;C.不存在D.不存在或只有一条二、填空题1.在同一平面内,____________________________________叫做平行线.2.若AB ∥CD,AB ∥EF,则_____∥______,理由是__________________.3.在同一平面内,若两条直线相交,则公共点的个数是________;•若两条直线平行,则公共点的个数是_________.4.同一平面内的三条直线,其交点的个数可能为________.5.直线L 同侧有A,B,C 三点,若过A,B 的直线L 1和过B,C 的直线L 2都与L 平行,则A,•B,C 三点________,理论根据是___________________________. 三、训练平台1. 已知直线a ∥b,b ∥c,c ∥d,则a 与d 的关系是什么?为什么?2.如图所示,梯形ABCD 中,AD ∥BC,P 是AB 的中点,过P 点作AD 的平行线交DC 于Q 点. (1)PQ 与BC 平行吗?为什么?(2)测量PQ 与CQ 的长,DQ 与CQ 是否相等? 四、提高训练1. 如图所示,a ∥b,a 与c 相交,那么b 与c 相交吗?为什么?2.根据下列要求画图.(1)如图(1)所示,过点A 画MN ∥BC;(2)如图(2)所示,过点P 画PE ∥OA,交OB 于点E,过点P 画PH ∥OB,交OA 于点H;(3)如图(3)所示,过点C 画CE ∥DA,与AB 交于点E,过点C 画CF ∥DB,与AB•的延长线交于点F.Q P DCBA c ba NM BAC BAP O B AD CBA(1) (2) (3)专题训练平行线的判定一、选择题1.如图1所示,下列条件中,能判断AB ∥CD 的是( )A.∠BAD=∠BCDB.∠1=∠2;C.∠3=∠ 4D.∠BAC=∠ACD2.如图2所示,如果∠D=∠EFC,那么( )A.AD ∥BCB.EF ∥BCC.AB ∥DCD.AD ∥EF 3.如图3所示,能判断AB ∥CE 的条件是( )A.∠A=∠ACEB.∠A=∠ECDC.∠B=∠BCAD.∠B=∠ACE 4.下列说法错误的是( )A.同位角不一定相等B.内错角都相等C.同旁内角可能相等D.同旁内角互补,两直线平行5.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( ) A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交二、填空题1.在同一平面内,直线a,b 相交于P,若a ∥c,则b 与c 的位置关系是______.2.在同一平面内,若直线a,b,c 满足a ⊥b,a ⊥c,则b 与c 的位置关系是______.3.如图所示,BE 是AB 的延长线,量得∠CBE=∠A=∠C.(1)由∠CBE=∠A 可以判断______∥______,根据是_________.(2)由∠CBE=∠C 可以判断______∥______,根据是_________. 三、训练平台1. 如图所示,已知∠1=∠2,AB 平分∠DAB,试说明DC ∥AB.2. 如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=•30°,试说明AB ∥CD.DCBA21GH KFEDCB A四、提高训练如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a 与c 平行吗?•为什么?ED CB A如图所示,请写出能够得到直线AB ∥CD 的所有直接条件.d ecb a 3412876534DCBA 12六、中考题与竞赛题如图所示,直线a,b 被直线c 所截,现给出下列四个条件:•①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a ∥b 的条件序号为( ) A.①② B.①③ C.①④ D.③④专题训练平行线性质1.如图1所示,AB ∥CD,则与∠1相等的角(∠1除外)共有( )A.5个B.4个C.3个D.2个DCBA 1EDCBAOF E D C BAFE DCBAG FED C BA 1FE DCB A(1) (2) (3) (4) (5) (6) 2.如图2所示,已知DE ∥BC,CD 是∠ACB 的平分线,∠B=72°,∠ACB=40°,•那么∠BDC 等于( ) A.78° B.90° C.88° D.92°3.下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;•③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( ) A.① B.②和③ C.④ D.①和④4.如图3所示,CD ∥AB,OE 平分∠AOD,OF ⊥OE,∠D=50°,则∠BOF 为( ) A.35° B.30° C.25° D.20°5.如图4所示,AB ∥CD,则∠A+∠E+∠F+∠C 等于( )A.180°B.360°C.540°D.720°6.如图5所示,AB ∥EF ∥CD,EG ∥BD,则图中与∠1相等的角(∠1除外)共有( )• A.6个 B.5个 C.4个 D.3个二、填空题1.如图6所示,如果DE ∥AB,那么∠A+______=180°,或∠B+_____=180°,根据是______;如果∠CED=∠FDE,那么________∥_________.根据是________.2.如图7所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、•后的两条路平行,若第一次拐角是150°,则第二次拐角为________.D CBADCBA12D C B A EDC BAba3412(7) (8) (9) (10) (11) (12) 3.如图8所示,AB ∥CD,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=_______,∠ACD=•_______. 三、训练平台1. 如图9所示,AD ∥BC,∠1=78°,∠2=40°,求∠ADC 的度数.2. 如图10所示,AB ∥CD,AD ∥BC,∠A 的2倍与∠C 的3倍互补,求∠A 和∠D 的度数.•8765cba34123. 如图11所示,已知AB ∥CD,∠ABE=130°,∠CDE=152°,求∠BED 的度数.4. 如图12所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数. 四、提高训练1. 如图所示,已知直线MN 的同侧有三个点A,B,C,且AB ∥MN,BC ∥MN,试说明A,•B,C 三点在同一直线上.2. 如图所示,把一张长方形纸片ABCD 沿EF 折叠,若∠EFG=50°,求∠DEG 的度数. 五、探索发现如图所示,已知AB ∥CD,分别探索下列四个图形中∠P 与∠A,∠C 的关系,•请你从所得的四个关系中任选一个加以说明.专题训练平移一、选择题1.如图所示,△FDE 经过怎样的平移可得到△ABC.( )A.沿射线EC 的方向移动DB 长;B.沿射线EC 的方向移动CD 长C.沿射线BD 的方向移动BD 长;D.沿射线BD 的方向移动DC 长2.如图所示,△DEF 经过平移可以得到△ABC,那么∠C 的对应角和ED 的对应边分别是( ) A.∠F,AC B.∠BOD,BA; C.∠F,BA D.∠BOD,AC3.如图所示,右边的两个图形中,经过平移能得到左边的图形的是( ) 4.在平移过程中,对应线段( )A.互相平行且相等; B.互相垂直且相等 C.互相平行(或在同一条直线上)且相等二、填空题1.在平移过程中,平移后的图形与原来的图形________和_________都相同,•因此对应线段和对应角都________.2.如图所示,平移△ABC 可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=•____度,∠EDF=_______度,∠F=______度,∠DOB=_______度.3.如图所示,长方体中,平移后能得到棱AA 1的棱有________.4.小明的一本书一共有104页,在这104页的页码中有两个数码的,并且这两个数码经过平移其中一个能得到另一个,则这样的页共有________页. 三、训练平台1.如右图所示,请将图中的“蘑菇”向左平移6个格,再向下平移2个格.E CBAD CBADCB A(2) (3) (4) (5)2.如图2所示,将△ABC 平移,可以得到△DEF,点B 的对应点为点E,请画出点A 的对应点D 、点C 的对应点F 的位置.3.如图3所示,画出平行四边形ABCD 向上平移1厘米后的图形. 四、提高训练1.如图4所示的是某商品包装盒上图案的一部分,•请分析这个图案的基本图形和形成过程.2.如图5所示,四边形ABCD 中,AD ∥BC,AB=DC=AD,将DC 向左平移AD 长,•平移后你得到的两个图形是什么样的? 五、能力提高1.如图所示,四边形ABCD 中,AD ∥BC,AB=DC,∠B=80°,求∠A,∠D,∠C 的度数.2.如图所示,大圆O 内有一小圆O 1,小圆O 1从现在的位置沿O 1O 的方向平移4•个单位后,得到小圆O 2,已知小圆半径为1.(1)求大圆的面积;(2)求小圆在平移过程中扫过的面积.OF ECB A D OFECB ADD 1C 1B 1A 1CBADNMC B A NMG F EDC BA PDC B APDC BAP DCB A PDCB A DCBA3. 两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB=10，DH=4，平移距离为6，求阴影部分的面积。

初一下相交线与平行线题型复习(重难点+难题突破)

初一下相交线与平行线题型复习(重难点+难题突破)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN相交线及平行线复习1. 如图所示, ∠1和∠2是对顶角的图形有( )12121221A.1个B.2个C.3个D.4个2. 如图所示,已知直线AB , CD 相交于O , OA 平分∠EOC ,∠EOC =70°, 则∠BOD =•______.3. 如图所示, 直线AB ,CD 相交于点O , 已知∠AOC =70°, OE 把∠BOD 分成两部分,• 且∠BOE :∠EOD =2:3, 则∠EOD =________.4.如图所示, 直线a ,b ,c 两两相交, ∠1=2∠3, ∠2=65°, 求∠4的度数。

5. 如图所示，∠AOB =∠COD =90°，则下列叙述中正确的是（）A.∠AOC =∠AODB.∠AOD =∠BODC.∠AOC =∠BODD.以上【练习】1、下列语句正确的是（）.A 、相等的角是对顶角B 、相等的两个角是邻补角C 、对顶角相等D 、邻补角不一定互补，但可能相等 2、下列语句错误的有（）个.（1）两个角的两边分别在同一条直线上，这两个角互为对顶角（2）有公共顶点并且相等的两个角是对顶角OE D CBA OE DCBAcba3412（3）如果两个角相等，那么这两个角互补（4）如果两个角不相等，那么这两个角不是对顶角A 、1B 、2C 、3D 、4 3、如果两个角的平分线相交成90°的角，那么这两个角一定是（）.A 、对顶角B 、互补的两个角C 、互为邻补角D 、以上答案都不对 4、已知∠1与∠2是邻补角，∠2是∠3的邻补角，那么∠1与∠3的关系是（）.A 、对顶角B 、相等但不是对顶角C 、邻补角D 、互补但不是邻补角 5、下列说法正确的是（）.A 、有公共顶点的两个角是对顶角B 、两条直线相交所成的两个角是对顶角C 、有公共顶点且有一条公共边的两个角是邻补角D 、两条直线相交所成的无公共边的两个角是对顶角6、如图1所示,下列说法不正确的是( )A.点B 到AC 的垂线段是线段AB;B.点C 到AB 的垂线段是线段ACC.线段AD 是点D 到BC 的垂线段;D.线段BD 是点B 到AD 的垂线段 7、下列说法正确的有( )①在平面内,过直线上一点有且只有一条直线垂直于已知直线; ②在平面内,过直线外一点有且只有一条直线垂直于已知直线; ③在平面内,过一点可以任意画一条直线垂直于已知直线; ④在平面内,有且只有一条直线垂直于已知直线.A.1个B.2个C.3个D.4个8、点P 为直线m 外一点,点A,B,C 为直线m 上三点,PA=4cm,PB=5cm,PC=2cm,则点P 到直线m 的距离为( )A.4cmB.2cmC.小于2cmD.不大于2cm9.则下列结论：垂足为如图，,,,90D BC AD BAC ⊥︒=∠ （1）点C 到AB 的垂线段是线段AB ；（2）点A 到BC 的距离是线段AD; （3）线段AB 的长度是点B 到AC 的距离；（4）线段BC 的长度是点B 到AC 的距离。

(完整)初一数学七下相交线与平行线所有知识点总结和常考题型练习题,推荐文档

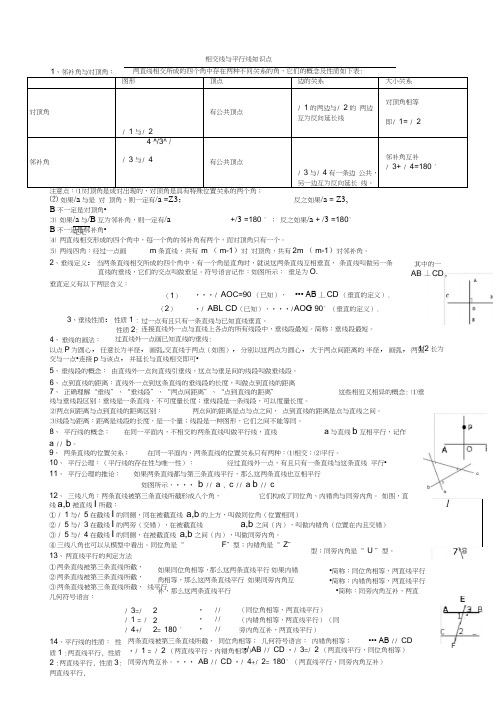
相交线与平行线知识点⑵ 如果/a 与是对顶角，则一定有/a =Z3；反之如果/a = Z3,B 不一定是对顶角•⑶ 如果/a 与/B 互为邻补角，则一定有/a+/3 =180 ° ；反之如果/a + /3 =180°B 不一定是邻补角• ⑷ 两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个。

⑸ 两线四角：经过一点画m 条直线，共有 m （ m-1）对对顶角，共有2m （ m-1）对邻补角。

2、垂线定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，条直线叫做另一条直线的垂线，它们的交点叫做垂足。

符号语言记作：如图所示：垂足为O.垂直定义有以下两层含义：心曰疋疋•••/ AO C=90 （已知），••• AB 丄CD （垂直的定义）.•/ ABL CD （已知），•••/AO G 90° （垂直的定义）.3、垂线性质：性质1 : 性质2: （1）（2）过一点有且只有一条直线与已知直线垂直。

连接直线外一点与直线上各点的所有线段中，垂线段最短。

简称：垂线段最短。

其中的一4、垂线的画法：以点P 为圆心，任意长为半径，画弧,交直线于两点（如图），分别以这两点为圆心，大于两点间距离的半径，画弧，两弧交与一点•连接p 与该点，并延长与直线相交即可• 5、垂线段的概念：由直线外一点向直线引垂线，这点与垂足间的线段叫做垂线段。

6、点到直线的距离：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离7、正确理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近又相异的概念: ⑴垂线与垂线段区别：垂线是一条直线，不可度量长度；垂线段是一条线段，可以度量长度。

⑵两点间距离与点到直线的距离区别：两点间的距离是点与点之间，点到直线的距离是点与直线之间。

⑶线段与距离：距离是线段的长度，是一个量；线段是一种图形，它们之间不能等同。

人教版七年级数学下册期末复习：相交线与平行线(附练习答案).doc

期末复习(一) 相交线与平行线01各个击破命题点1命题【例1】已知下列命题：①若a＞0，b＞0，则a＋b＞0；②若a≠b，则a2≠b2；③两点之间，线段最短；④同位角相等，两直线平行．其中真命题的个数是()A．1个B．2个C．3个D．4个【思路点拨】命题①、③、④显然成立，对于命题②，当a＝2、b＝－2时，虽然有a≠b，但a2＝b2，所以②是假命题．【方法归纳】要判断一个命题是假命题，只需要举出一个反例即可．和命题有关的试题，多以选择题的形式出现，以判断命题真假为主要题型．1．下列语句不是命题的是()A．两直线平行，同位角相等B．锐角都相等C．画直线AB平行于CDD．所有质数都是奇数2．(兴化三模)说明命题“x＞－4，则x2＞16”是假命题的一个反例可以是x＝________．3．(日照期中)命题“同旁内角互补”的题设是_____________________，结论是____________，这是一个________命题(填“真”或“假”)．命题点2相交线中的角【例2】如图所示，直线AB，CD相交于点O，作∠DOE＝∠BOD，OF平分∠AOE.(1)判断OF与OD的位置关系；(2)若∠AOC∶∠AOD＝1∶5，求∠EOF的度数．【思路点拨】(1)根据∠DOE＝∠BOD，OF平分∠AOE，求得∠FOD＝90°，从而判断OF与OD的位置关系．(2)根据∠AOC，∠AOD的度数比以及邻补角性质，求得∠AOC.然后利用对顶角性质得∠BOD的度数，从而得∠EOD的度数．最后利用∠FOD＝90°，求得∠EOF的度数．【解答】【方法归纳】求角的度数问题时，要善于从图形中挖掘隐含条件，如：邻补角、对顶角，然后结合条件给出的角的和、差、倍、分等关系进行计算．4．(滕州校级模拟)如图，两条直线AB ，CD 交于点O ，射线OM 是∠AOC 的平分线，若∠BOD ＝80°，则∠BOM 等于( )A ．40°B ．120°C ．140°D ．100°5．如图，直线AB ，CD 相交于点O ，已知：∠AOC ＝70°，OE 把∠BOD 分成两部分，且∠BOE ∶∠EOD ＝2∶3，求∠AOE 的度数．6．如图所示，O 是直线AB 上一点，∠AOC ＝13∠BOC ，OC 是∠AOD 的平分线．(1)求∠COD 的度数；(2)判断OD 与AB 的位置关系，并说出理由．命题点3平行线的性质与判定【例3】已知：如图，四边形ABCD中，∠A＝106°－α，∠ABC＝74°＋α，BD⊥DC 于点D，EF⊥DC于点F.求证：∠1＝∠2.【思路点拨】由条件得∠A＋∠ABC＝180°，得AD∥BC，从而∠1＝∠DBC.由BD⊥DC，EF⊥DC，可得BD∥EF，从而∠2＝∠DBC，所以∠1＝∠2，结论得证．【解答】【方法归纳】本题既考查了平行线的性质又考查了平行线的判定．题目的证明用到了“平行线迁移等角”．7．(燕山区一模)如图，∠1＝∠B，∠2＝25°，则∠D＝()A．25°B．45°C．50°D．65°8．(山亭区期末)如图所示是一条街道的路线图，若AB∥CD，且∠ABC＝130°，那么当∠CDE等于________时，BC∥DE.()A．40°B．50°C．70°D．130°9．已知，如图，∠1＝132°，∠ACB＝48°，∠2＝∠3，FH⊥AB于H，问AB与CD是否垂直？并说明理由．命题点4平移【例4】(晋江中考)如图，在方格纸中(小正方形的边长为1)，三角形ABC的三个顶点均为格点，将三角形ABC沿x轴向左平移5个单位长度，根据所给的直角坐标系(O是坐标原点)，解答下列问题：(1)画出平移后的三角形A′B′C′，并直接写出点A′、B′、C′的坐标；(2)求出在整个平移过程中，三角形ABC扫过的面积．【思路点拨】(1)根据网格结构找出点A′、B′、C′的位置，然后顺次连接即可，再根据平面直角坐标系写出坐标即可；(2)观察图形可得三角形ABC扫过的面积为四边形AA′B′B的面积与三角形ABC的面积的和，然后列式进行计算即可．【解答】【方法归纳】熟练掌握网格结构，准确找出对应点的位置是解题的关键．10．(宁德中考)如图，将直线l1沿着AB的方向平移得到直线l2，若∠1＝50°，则∠2的度数是()A．40°B．50°C．90°D．130°11．如图，在直角三角形ABC中，∠C＝90°，AC＝4，将三角形ABC沿CB方向向右平移得到三角形DEF，若平移距离为2，则四边形ABED的面积等于________．12．如图，在长方形草地内修建了宽为2米的道路，则草地面积为________米2.02整合集训一、选择题(每小题3分，共30分)1．图中，∠1、∠2是对顶角的为()2．如图，直线AB、CD被直线EF所截，则∠3的同旁内角是()A．∠1 B．∠2 C．∠4 D．∠5 3．如图，已知AB⊥CD，垂足为点O，图中∠1与∠2的关系是()A．∠1＋∠2＝180°B．∠1＋∠2＝90°C．∠1＝∠2 D．无法确定4．如图，梯子的各条横档互相平行，若∠1＝80°，则∠2的度数是() A．80°B．100°C．110°D．120°5．如图，“龟兔赛跑”的故事图案的形成过程叙述不正确的是()A．它可以看作是一个龟兔图案作为“基本图案”经过平移得到的B．它可以看作是上面三个龟兔图案作为“基本图案”经过平移得到的C．它可以看作是相邻两个龟兔图案作为“基本图案”经过平移得到的D．它可以看作是左侧两个龟兔图案作为“基本图案”经过平移得到的6．命题：①对顶角相等；②过一点有且只有一条直线与已知直线平行；③相等的角是对顶角；④同位角相等．其中假命题有()A．1个B．2个C．3个D．4个7．以下关于距离的几种说法中，正确的有()①连接两点间的线段长度叫做这两点的距离；②连接直线外的点和直线上的点的线段叫做点到直线的距离；③从直线外一点所引的这条直线的垂线叫做点到直线的距离；④直线外一点到这条直线的垂线段叫做这点到直线的距离．A．1个B．2个C．3个D．4个8．下列图形中，由AB∥CD，能得到∠1＝∠2的是()9．如图，点E在CD的延长线上，下列条件中不能判定AB∥CD的是()A．∠1＝∠2 B．∠3＝∠4C．∠5＝∠B D．∠B＋∠BDC＝180°10．如图，l∥m，∠1＝115°，∠2＝95°，则∠3＝()A．120°B．130°C．140°D．150°二、填空题(每小题4分，共20分)11．将命题“两直线平行，同位角相等”写成“如果……那么……”的形式是_______________________________．12．将线段AB平移1 cm，得到线段A′B′，则点A到点A′的距离是________．13．(1)如图1，村庄A到公路BC最短的距离是AD，根据是________________；(2)如图2，建筑工人常在一根细绳上拴上一个重物，做成一个“铅锤”，挂铅锤的线总垂直于地面内的任何直线，当这条线贴近墙壁时，说明墙与地面垂直，请说出它的根据是________________________________________．图1图214．如图，BC⊥AE，垂足为点C，过C作CD∥AB.若∠ECD＝48°，则∠B＝________．15．(温州中考)如图，直线AB，CD被BC所截，若AB∥CD，∠1＝45°，∠2＝35°，则∠3＝________度．三、解答题(共50分)16．(7分)如图，∠1＝60°，∠2＝60°，∠3＝85°，求∠4的度数．解：∵∠1＝60°，∠2＝60°，∴∠1＝∠2.∴a∥________(________________)．∴∠4＝∠________(________________)．∵∠3＝85°，∴∠4＝________．17．(9分)如图，直线AB、CD相交于点O，P是CD上一点．(1)过点P画AB的垂线段PE，垂足为E；(2)过点P画CD的垂线，与AB相交于F点；(3)说明线段PE、PO、FO三者的大小关系，其依据是什么？18．(10分)如图，O是直线AB上一点，OD平分∠AOC.(1)若∠AOC＝60°，请求出∠AOD和∠BOC的度数；(2)若∠AOD 和∠DOE 互余，且∠AOD ＝13∠AOE ，请求出∠AOD 和∠COE 的度数．19．(12分)如图，∠1＋∠2＝180°，∠A ＝∠C ，DA 平分∠BDF.(1)AE 与FC 平行吗？说明理由；(2)AD 与BC 的位置关系如何？为什么？(3)BC 平分∠DBE 吗？为什么？20．(12分)探究题：(1)如图1，若AB ∥CD ，则∠B ＋∠D ＝∠E ，你能说明理由吗？(2)反之，若∠B＋∠D＝∠E，直线AB与CD有什么位置关系？(3)若将点E移至图2的位置，此时∠B，∠D，∠E之间有什么关系？(4)若将点E移至图3的位置，此时∠B，∠D，∠E之间的关系又如何？(5)在图4中，AB∥CD，∠E＋∠G与∠B＋∠F＋∠D之间有何关系？图1图2图3图4参考答案各个击破例1 C例2 (1)∵OF 平分∠AOE ，∴∠AOF ＝∠EOF ＝12∠AOE. 又∵∠DOE ＝∠BOD ＝12∠BOE ， ∴∠DOE ＋∠EOF ＝12(∠BOE ＋∠AOE)＝12×180°＝90°，即∠FOD ＝90°.∴OF ⊥OD. (2)设∠AOC ＝x °，∵∠AOC ∶∠AOD ＝1∶5，∴∠AOD ＝5x °.∵∠AOC ＋∠AOD ＝180°，∴x ＋5x ＝180，解得x ＝30.∴∠DOE ＝∠BOD ＝∠AOC ＝30°.又∵∠FOD ＝90°，∴∠EOF ＝90°－30°＝60°.例3 证明：∵∠A ＝106°－α，∠ABC ＝74°＋α，∴∠A ＋∠ABC ＝180°.∴AD ∥BC.∴∠1＝∠DBC.∵BD ⊥DC ，EF ⊥DC ，∴∠BDF ＝∠EFC ＝90°.∴BD ∥EF.∴∠2＝∠DBC.∴∠1＝∠2.例4 (1)平移后的三角形A′B′C′如图所示；点A′、B′、C′的坐标分别为(－1，5)、(－4，0)、(－1，0)．(2)由平移的性质可知，四边形AA′B′B 是平行四边形，∴S ＝S 四边形AA′B′B ＋S 三角形ABC ＝B′B·AC ＋12BC ·AC ＝5×5＋12×3×5＝652. 题组训练1．C 2.－3 3.两个角是两条直线被第三条直线所截得到的同旁内角这两个角互补假4.C5.解：∵∠AOC ＝70°，∴∠BOD ＝∠AOC ＝70°.∵∠BOE ∶∠EOD ＝2∶3，∴∠BOE ＝22＋3×70°＝28°. ∴∠AOE ＝180°－28°＝152°.6.解：(1)∵∠AOC ＋∠BOC ＝180°，∠AOC ＝ 13∠BOC ， ∴13∠BOC ＋∠BOC ＝180°.∴∠BOC ＝135°.∴∠AOC ＝45°. ∵OC 平分∠AOD ，∴∠COD ＝∠AOC ＝45°.(2)OD ⊥AB.理由如下：∵∠COD ＝∠AOC ＝45°，∴∠AOD ＝∠COD ＋∠AOC ＝90°.∴OD ⊥AB.7.A 8.B9.解：AB ⊥CD.理由：∵∠1＝132°，∠ACB ＝48°，∴∠1＋∠ACB ＝180°.∴DE ∥BC.∴∠2＝∠DCF.又∵∠2＝∠3，∴∠3＝∠DCF.∴FH ∥CD.∴∠BHF ＝∠BDC.又∵FH ⊥AB ，∴∠BHF ＝90°.∴∠BDC ＝90°.∴AB ⊥CD.10.B 11.8 12.144整合集训1．C 2.B 3.B 4.B 5.C 6.C 7.A 8.B 9.A 10.D11.如果两直线平行，那么同位角相等12.1 cm13.(1)垂线段最短 (2)过一点有且只有一条直线与已知直线垂直14.42°15.8016.b 同位角相等，两直线平行 3 两直线平行，同位角相等 85°17.解：(1)、(2)如图．(3)PE<PO<FO ，依据是垂线段最短．18.解：(1)∵OD 平分∠AOC ，∠AOC ＝60°，∴∠AOD ＝12×∠AOC ＝30°，∠BOC ＝180°－∠AOC ＝120°.(2)∵∠AOD 和∠DOE 互余，∴∠AOE ＝∠AOD ＋∠DOE ＝90°.∵∠AOD ＝13∠AOE ，∴∠AOD ＝13×90°＝30°. ∴∠AOC ＝2∠AOD ＝60°.∴∠COE ＝90°－∠AOC ＝30°.19.解：(1)AE ∥FC.理由：∵∠1＋∠2＝180°，∠2＋∠CDB ＝180°，∴∠1＝∠CDB.∴AE ∥FC.(2)AD ∥BC.理由：∵AE ∥CF ，∴∠C ＝∠CBE.又∠A ＝∠C ，∴∠A ＝∠CBE.∴AD ∥BC.(3)BC 平分∠DBE.理由：∵DA 平分∠BDF ，∴∠FDA ＝∠ADB.∵AE ∥CF ，AD ∥BC ，∴∠FDA ＝∠A ＝∠CBE ，∠ADB ＝∠CBD.∴∠CBE ＝∠CBD. ∴BC 平分∠DBE.20.解：(1)理由：过点E 作EF ∥AB ，∴∠B ＝∠BEF.∵CD ∥AB ，∴CD ∥EF.∴∠D ＝∠DEF.∴∠B ＋∠D ＝∠BEF ＋∠DEF ＝∠BED.(2)AB ∥CD.(3)∠B ＋∠D ＋∠E ＝360°.(4)∠B ＝∠D ＋∠E.(5)∠E ＋∠G ＝∠B ＋∠F ＋∠D.。

人教版七年级数学下册第五章相交线与平行线全章知识点归纳及典型题目练习含复习资料

相交线与平行线全章知识点归纳及典型题目练习1.两直线相交所成的四个角中，有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为_____________.2.两直线相交所成的四个角中，有一个公共顶点，并且一个角的两边分别是另一个角两边的反向延长线，具有这种关系的两个角，互为__________.对顶角的性质：______ _________.3.两直线相交所成的四个角中，如果有一个角是直角，那么就称这两条直线相互_______.垂线的性质：⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中，_______________.4.直线外一点到这条直线的垂线段的长度，叫做________________________.5.两条直线被第三条直线所截，构成八个角，在那些没有公共顶点的角中，⑴如果两个角分别在两条直线的同一方，并且都在第三条直线的同侧，具有这种关系的一对角叫做___________ ；⑵如果两个角都在两直线之间，并且分别在第三条直线的两侧，具有这种关系的一对角叫做____________ ；⑶如果两个角都在两直线之间，但它们在第三条直线的同一旁，具有这种关系的一对角叫做_______________.6.在同一平面内，不相交的两条直线互相___________.同一平面内的两条直线的位置关系只有________与_________两种.7.平行公理：经过直线外一点，有且只有一条直线与这条直线______.推论：如果两条直线都与第三条直线平行，那么_____________________.8.平行线的判定：⑴两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简单说成：_____________________________________.⑵两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.简单说成：___________________________.⑶两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.简单说成：________________________________________.9.在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线_______ .10.平行线的性质：⑴两条平行直线被第三条直线所截，同位角相等.简单说成：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.⑵两条平行直线被第三条直线所截，内错角相等.简单说成：__________________________________.⑶两条平行直线被第三条直线所截，同旁内角互补.简单说成：____________________________________ .11. 判断一件事情的语句，叫做_______.命题由________和_________两部分组成.题设是已知事项，结论是______________________.命题常可以写成“如果……那么……”的形式，这时“如果”后接的部分是＿＿＿＿＿，“那么”后接的部分是_________.如果题设成立，那么结论一定成立.像这样的命题叫做___________.如果题设成立时，不能保证结论一定成立，像这样的命题叫做___________.定理都是真命题.12. 把一个图形整体沿某一方向移动，会得到一个新图形，图形的这种移动，叫做平移变换，简称_______.图形平移的方向不一定是水平的.平移的性质：⑴把一个图形整体平移得到的新图形与原图形的形状与大小完全______. ⑵新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点.连接各组对应点的线段_________________.熟悉以下各题：13. 如图，,8,6,10,BC AC CB cm AC cm AB cm ⊥===那么点A 到BC 的距离是_____，点B 到AC 的距离是_______，点A 、B 两点的距离是_____，点C 到AB 的距离是________．14. 设a 、b 、c 为平面上三条不同直线，a) 若//,//a b b c ，则a 与c 的位置关系是_________；b) 若,a b b c ⊥⊥，则a 与c 的位置关系是_________；c) 若//a b ，b c ⊥，则a 与c 的位置关系是________．15. 如图，已知AB 、CD 、EF 相交于点O ，AB ⊥CD ，OG 平分∠AOE ，∠FOD ＝28°，求∠CO E 、∠AOE 、∠AOG 的度数．16. 如图，AOC ∠与BOC ∠是邻补角，OD 、OE 分别是AOC ∠与BOC ∠的平分线，试判断OD 与OE 的位置关系，并说明理由．17. 如图，AB ∥DE ，试问∠B 、∠E 、∠BCE 有什么关系．解：∠B ＋∠E ＝∠BCE过点C 作CF ∥AB ，则B ∠=∠____（）又∵AB ∥DE ，AB ∥CF ，∴____________（）∴∠E ＝∠____（）∴∠B ＋∠E ＝∠1＋∠2即∠B ＋∠E ＝∠BCE ．18. ⑴如图，已知∠1＝∠2 求证：a ∥b ．⑵直线//a b ，求证：12∠=∠．19. 阅读理解并在括号内填注理由：如图，已知AB ∥CD ，∠1＝∠2，试说明EP ∥FQ ．证明：∵AB ∥CD ，∴∠MEB ＝∠MFD （）又∵∠1＝∠2，∴∠MEB －∠1＝∠MFD －∠2，即 ∠MEP ＝∠______∴EP ∥_____．（）20. 已知DB ∥FG ∥EC ，A 是FG 上一点，∠ABD ＝60°，∠ACE ＝36°，AP 平分∠BAC ，求：⑴∠BAC 的大小；⑵∠P AG 的大小.21. 如图，已知ABC ∆，AD BC ⊥于D ，E 为AB 上一点，EF BC ⊥于F ，//DG BA∠=∠.交CA于G.求证1222.已知：如图∠1=∠2，∠C=∠D，问∠A与∠F相等吗？试说明理由．参考答案1.邻补角2. 对顶角，对顶角相等3.垂直有且只有垂线段最短4.点到直线的距离5.同位角内错角同旁内角6.平行相交平行7.平行这两直线互相平行8.同位角相等两直线平行；内错角相等两直线平行；同旁内角互补两直线平行.9.平行 10.两直线平行同位角相等；两直线平行内错角相等；两直线平行同旁内角互补.11.命题题设结论由已知事项推出的事项题设结论真命题假命题 12.平移相同平行且相等 13.6cm 8cm 10cm 4.8cm. 14.平行平行垂直 15. 28° 118° 59° 16. OD ⊥OE 理由略 17. 1（两直线平行，内错角相等）DE ∥CF （平行于同一直线的两条直线平行） 2 （两直线平行，内错角相等）. 18.⑴∵∠1＝∠2 ，又∵∠2＝∠3（对顶角相等），∴∠1＝∠3∴a ∥b （同位角相等两直线平行） ⑵∵a ∥b ∴∠1＝∠3(两直线平行，同位角相等)又∵∠2＝∠3（对顶角相等） ∴∠1＝∠2. 19. 两直线平行，同位角相等 MFQ FQ 同位角相等两直线平行 20. 96°，12°.21.,AD BC FE BC ⊥⊥Q 90EFB ADB ∴∠=∠=o//EF AD ∴23∴∠=∠ //,31DG BA ∴∠=∠Q 1 2.∴∠=∠ 22. ∠A ＝∠F .∵∠1＝∠DGF （对顶角相等）又∠1＝∠2 ∴∠DGF ＝∠2 ∴DB ∥EC （同位角相等，两直线平行） ∴∠DBA ＝∠C （两直线平行，同位角相等）又∵∠C ＝∠D ∴∠DBA ＝∠D ∴DF ∥AC （内错角相等，两直线平行）∴∠A ＝∠F (两直线平行,内错角相等).。

人教版七年级数学下册第五章相交线与平行线知识整理复习（含答案）

⼈教版七年级数学下册第五章相交线与平⾏线知识整理复习（含答案）七年级数学下册第五章知识整理知识梳理1.两个⾓有⼀条公共边，它们的另⼀条边互为反向延长线，具有这样位置关系的两个⾓，互为___________.2.两个⾓有⼀个公共顶点，并且⼀个⾓的两边分别是另⼀个⾓两边的反向延长线，具有这种位置关系的⾓，互为___________.对顶⾓的性质:___________.3.垂直是相交的⼀种特殊情形，两条直线互相垂直，其中的⼀条直线叫做另⼀条直线的___________，它们的交点叫做___________。

4.在同⼀平⾯内，过⼀点有且只有___________直线与已知直线垂直。

5.连接直线外⼀点与直线上各点的所有线段中，___________最短，简单说成：___________。

6.直线外⼀点到这条直线的垂线段的长度，叫做___________。

7.如图，∠1和∠4，这两个⾓分别在直线AB，CD的同⼀⽅(上⽅)，并且都在直线EF的同侧(右侧)，具有这种位置关系的⼀对⾓叫做_______;∠2和∠4，这两个⾓都在直线AB，CD之间，并且分别在直线EF两侧，具有这种位置关系的⼀对⾓叫做_______;∠2和∠3也都在直线AB，CD之间，但它们在直线EF的同⼀旁，具有这种位置关系的⼀对⾓叫做_______;8.在同⼀平⾯内不相交的两条直线(a与b)互相_______,记作_______.9.平⾏线的基本事实(平⾏公理):经过直线外⼀点，有且只有_______直线与这条直线平⾏.10.如果两条直线都与第三条直线平⾏，那么这两条直线也_______.11.平⾏线的判定⽅法:(1)_______相等，两直线平⾏;(2)_______相等，两直线平⾏;(3)_______互补，两直线平⾏。

12.平⾏线的性质:(1)两直线平⾏，同位⾓_______;(2)两直线平⾏，内错⾓_______;(3)两直线平⾏，同旁内⾓_______.13.判断⼀件事情的语句，叫做_______.经过推理证实的真命题叫做_______.14.在很多情况下，⼀个命题的正确性需要经过推理才能作出判断，这个推理过程叫做_______.15.平移得到的新图形与原图形的形状和⼤⼩_______.知识反馈★知识点1;邻补⾓与对顶⾓1.下列说法正确的是( )A.和为180°的⾓为邻补⾓B和为180°的两个⾓为邻补⾓C，有公共顶点，和为90°的⾓为邻补⾓D.有公共顶点和⼀条公共边，它们的另⼀边互为反向廷长线的两个⾓为邻补⾓2.如图，∠1和∠2是对顶⾓的是( )3.如图，直线AB、CD相交于点O，若∠AOC＝(3x+10°),∠BOC＝(2x-10°)，求∠AOD的度数.★知识点2:垂线与垂线段4.过直线AB外⼀点P画直线AB的垂线，则( )A.能画⽆数条B只能画2条 C.只能画1条 D.不能画成5.在数学课上，同学们在练习过点B作线段AC所在直线的垂线段时，有⼀部分同学画出下列四种图形，请你数⼀数，错误的个数为( )A.1个B.2个C.3个D.4个6.如图，在体育测试中，裁判员测量某同学的跳远成绩，在直线l上的A、B、C三点中，点________到沙坑中脚印点P的距离为该同学的成绩.7.如图，在三⾓形ABC中，∠BCA＝90°，CD⊥AB，垂⾜为点D.线段AB，BC，CD的⼤⼩关系如何?并说明理由.★知识点3:同位⾓、内错⾓、同旁内⾓8.如图，下⾯说法中正确的是( )A.∠2和∠3是同位⾓B.∠3和∠4是同旁内⾓C，∠1和∠2是内错⾓ D.∠1和∠3是同旁内⾓9.如图所⽰，直线DE、BC被直线AB所截，∠1与∠4是_________,∠2与∠4是_________，∠1与∠2是_________，∠3与∠4是_________.★知识点4:平⾏线的定义及画法10.下列⽣活中的线是平⾏线的有( )①铁路上并排的两条铁轨;②上体育课时，双杠的两个横杠;③滑雪时两只雪撬滑动轨迹;④操场上的升旗杆与教室屋梁。

七年级下册第二章相交线与平行线复习总结(全)

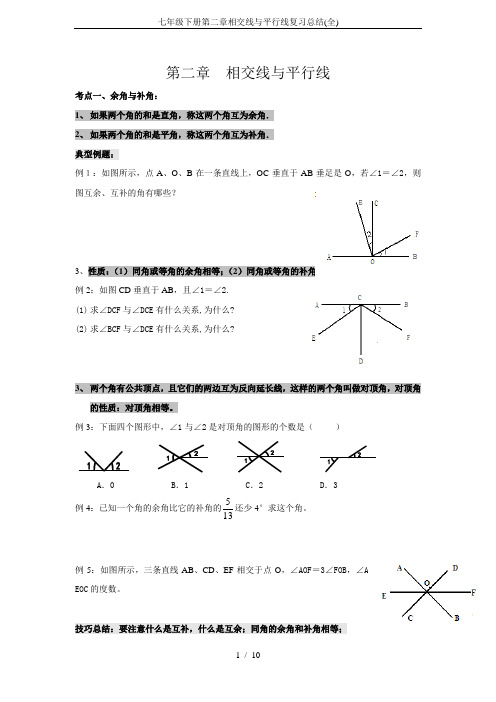
第二章相交线与平行线考点一、余角与补角：1、如果两个角的和是直角，称这两个角互为余角．2、如果两个角的和是平角，称这两个角互为补角．典型例题：例１：如图所示，点A 、O 、B 在一条直线上，OC 垂直于AB 垂足是O ，若∠1＝∠2，则图互余、互补的角有哪些？3、性质：（1）同角或等角的余角相等；（2）同角或等角的补角相等。

例2：如图CD 垂直于AB ，且∠1＝∠2. (1) 求∠DCF 与∠DCE 有什么关系,为什么? (2) 求∠BCF 与∠DCE 有什么关系,为什么?3、两个角有公共顶点，且它们的两边互为反向延长线，这样的两个角叫做对顶角，对顶角的性质：对顶角相等。

例3：下面四个图形中，∠1与∠2是对顶角的图形的个数是（）12121212A ．0B ．1C ．2D ．3 例4：已知一个角的余角比它的补角的135还少4°求这个角。

例5：如图所示，三条直线AB 、CD 、EF 相交于点O ，∠AOF ＝3∠FOB ，∠AOC=90°,求∠EOC 的度数。

技巧总结：要注意什么是互补，什么是互余；同角的余角和补角相等；对应的课堂练习：一、填空题1.如图1，直线l1与l2相交，∠1=50°，则∠2=_________，∠3=_________.图1 图22.如图2，直线AB与CD相交于O点，且∠AOD=90°，则∠AOC=_________=_________ =_________=_________.3.如图3，若AO⊥CO，BO⊥DO，∠BOC=150°，则∠DOC=________，∠AOD=________.图3 图44.如图4，直线AB与CD相交于O，∠EOD=90°，正确填写下列两角关系的名称.∠1与∠2:______________________________________________________∠2与∠3:______________________________________________________∠2与∠4:______________________________________________________∠1与∠4:______________________________________________________三、选择题1.两条直线相交于一点，则共有对顶角的对数为（）A.1对B.2对C.3对D.4对2.下面说法正确的个数为（）①对顶角相等②相等的角是对顶角③若两个角不相等，则这两个角一定不是对顶角④若两个角不是对顶角，则这两个角不相等A.1个B.2个C.3个D.4个3.若∠1和∠2互余，∠2与∠3互余，∠1=40°，则∠3等于（） A.40°B.130°C.50°D.140°4.如图，∠1和∠2是对顶角的图形有（）A.（1）（3）B.（2）（3）C.（3）D.（3）（4）一、判断题1.若∠1+∠2=90°，则∠1与∠2互余.（）2.若∠A 与∠B 互补，则∠A +∠B =180°.（）3.若∠1与∠2互补，∠2与∠3互补，则∠1与∠3互补.（）4.若∠AOB +∠BOC =180°，则点A 、O 、C 必在同一直线上.（）5.若∠α+∠β+∠γ=90°，则∠α、∠β、∠γ互余.（）四、解答题1.如图，AO ⊥BO ，直线CD 经过点O ，∠AOC =30°，求∠BOD 的度数.考点二、探索直线平行的条件同位角的特征：（１）在被截两直线的同旁；（２）在截线的两旁内错角的特征：（１）在被截两直线之间；（２）在截线的两旁同旁内角的特征：（１）在被截两直线之间；（２）在截线的同旁例1：如图，写出图中的同位角、内错角和同旁内角。

七年级数学下册第五章相交线与平行线题型总结及解题方法(带答案)

七年级数学下册第五章相交线与平行线题型总结及解题方法单选题1、如图，四边形ABCO是矩形，点D是BC边上的动点（点D与点B、点C不重合），则∠BAD+∠DOC∠ADO的值为（）A．1B．12C．2D．无法确定答案：A分析：过点D作DE//AB交AO于点E，由平行的性质可知∠BAD=∠ADE,∠DOC=∠ODE，等量代换可得∠BAD+∠DOC∠ADO的值.解：如图，过点D作DE//AB交AO于点E，∵四边形ABCO是矩形∴AB//OC∵DE//AB∴AB//DE,DE//OC∴∠BAD=∠ADE,∠DOC=∠ODE∴∠BAD+∠DOC∠ADO=∠BAD+∠DOC∠ADE+∠ODE=∠BAD+∠DOC∠BAD+∠DOC=1故选：A.小提示：本题主要考查了平行线的性质，灵活的添加辅助线是解题的关键.2、如图，直线a、b被直线c所截，a∥b，∠2=35°，则∠1的度数是（）A．135°B．140°C．145°D．150°答案：C分析：根据邻补角的含义先求解∠3=145°,再利用平行线可得∠1=∠3=145°即可．解：如图，∵∠2=35°,∴∠3=180°−35°=145°,∵a∥b，∴∠1=∠3=145°,故选：C.小提示：本题考查的是邻补角的含义，平行线的性质，利用平行线的性质证明∠1=∠3是解本题的关键．3、如图，直线AB、CD相交于点O．若∠1+∠2=100°，则∠BOC的大小为（）A．50°B．100°C．130°D．150°答案：C分析：根据对顶角相等，以及∠1+∠2=100°，求得∠1=50°，根据邻补角即可求解．解：∵∠1+∠2=100°，∠1=∠2，∴∠1=50°，∴∠BOC=180°-∠1=180°-50°=130°，故选C．小提示：本题考查了对顶角相等，邻补角，掌握以上知识是解题的关键．4、如图，从位置P到直线公路MN共有四条小道，若用相同的速度行走，能最快到达公路MN的小道是( )．A．PA B．PB C．PC D．PD答案：B根据垂线段最短得，能最快到达公路MN的小道是PB，故选：B.5、如图，直线AB、CD相交于点O，EO⊥CD，下列说法错误的是（）A．∠AOD＝∠BOC B．∠AOE＋∠BOD＝90°C．∠AOC＝∠AOE D．∠AOD＋∠BOD＝180°答案：C分析：根据对顶角性质、邻补角定义及垂线的定义逐一判断可得．A、∠AOD与∠BOC是对顶角，所以∠AOD=∠BOC，此选项不符合题意；B、由EO⊥CD知∠DOE=90°，所以∠AOE+∠BOD=90°，此选项不符合题意；C、∠AOC与∠BOD是对顶角，所以∠AOC=∠BOD，此选项符合题意；D、∠AOD与∠BOD是邻补角，所以∠AOD+∠BOD=180°，此选项不符合题意；故选C．小提示：本题主要考查垂线、对顶角与邻补角，解题的关键是掌握对顶角性质、邻补角定义及垂线的定义．6、下列命题中，是真命题的有（）①两条直线被第三条直线所截，同位角的平分线平行；②垂直于同一条直线的两条直线互相平行；③过一点有且只有一条直线与已知直线平行；④对顶角相等，邻补角互补．A．1个B．2个C．3个D．4个答案：A分析：根据平行线的性质及基本事实，对顶角及邻补角的性质进行判断．两条平行线被第三条直线所截，同位角的平分线平行，故①是假命题；在同一平面内，垂直于同一条直线的两条直线互相平行，故②是假命题；过直线外一点有且只有一条直线与已知直线平行，故③是假命题；对顶角相等，邻补角互补，故④是真命题．故选A．小提示：本题考查命题的真假判断，熟练掌握平行线的性质，对顶角及邻补角的性质是解题的关键．7、如图，将△ABC沿BC方向平移1cm得到对应的△A′B′C′．若B′C=2cm，则BC′的长是（）A．2cmB．3cmC．4cmD．5cm答案：C分析：据平移的性质可得BB′=CC′=1，列式计算即可得解．解：∵△ABC沿BC方向平移1cm得到△A′B′C′，∴BB′=CC′=1cm，∵B′C=2cm，∴BC′=BB′+B′C+CC′=1+2+1=4（cm）．故选：C．小提示：本题考查了平移的性质，熟记性质得到相等的线段是解题的关键．8、下列命题是假命题的( )A．在同一平面内，若a∥b，b∥c，则a∥cB．在同一平面内，若a⊥b，b∥c，则a⊥cC．在同一平面内，若a⊥b，b⊥c，则a⊥cD．在同一平面内，若a⊥b，b⊥c，则a∥c答案：C分析：根据平行的判定方法对A、C、D进行判断；根据平行的性质和垂直的定义对B进行判断．A．在同一平面内，若a∥b，b∥c，则a∥c，所以A选项为真命题；B．在同一平面内，若a⊥b，b∥c，则a⊥c，所以B选项为真命题；C．在同一平面内，若a⊥b，b⊥c，则a∥c，所以C选项为假命题；D．在同一平面内，若a⊥b，b⊥c，则a∥c，所以D选项为真命题．故选:C．小提示：本题考查了平行公理及平行线的判定定理，熟练掌握平行线的判定定理是解决本题的关键.9、如图，小明从A处出发沿北偏东40°方向行走至B处，又从B处沿南偏东70°方向行走至C处，则∠ABC等于（）A．130°B．120°C．110°D．100°答案：C分析：根据方位角和平行线性质求出∠ABE，再求出∠EBC即可得出答案．解：如图：∵小明从A处沿北偏东40°方向行走至点B处，又从点B处沿南偏东70°方向行走至点C处，∴∠DAB=40°，∠CBE=70°，∵向北方向线是平行的，即AD∥BE，∴∠ABE=∠DAB=40°，∴∠ABC=∠ABE+∠EBC=40°+70°=110°，故选：C．小提示：本题考查了方向角及平行线的性质，熟练掌握平行线的性质：两直线平行，内错角相等是解题的关键．10、对于命题“若a2＞b2，则a＞b”，下面四组关于a，b的值中，能说明这个命题是假命题的是（）A．a=3，b=2B．a=－3，b=2C．a=3，b=－1D．a=－1，b=3答案：B试题解析：在A中，a2=9，b2=4，且3＞2，满足“若a2＞b2，则a＞b”，故A选项中a、b的值不能说明命题为假命题；在B中，a2=9，b2=4，且－3＜2，此时虽然满足a2＞b2，但a＞b不成立，故B选项中a、b的值可以说明命题为假命题；在C中，a2=9，b2=1，且3＞－1，满足“若a2＞b2，则a＞b”，故C选项中a、b的值不能说明命题为假命题；在D中，a2=1，b2=9，且－1＜3，此时满足a2＜b2，得出a＜b，即意味着命题“若a2＞b2，则a＞b”成立，故D 选项中a、b的值不能说明命题为假命题；故选B．考点：命题与定理．填空题11、如图，直线a∥b，AB⊥BC，如果∠1=48°，那么∠2=_______度．答案：42．∵AB⊥BC，∴∠ABC=90°，即∠1+∠3=90°，∵∠1=48°，∴∠3=42°，∵a∥b，∴∠2=∠3=42°.故答案为42.点睛：本题关键利用平行线的性质解题.12、如图，若AB⊥BC，BC⊥CD，则直线AB与CD的位置关系是______．答案：AB∥CD∵AB⊥BC，BC⊥CD，∴∠ABC=∠BCD=90°，∴AB∥CD，故答案为AB∥CD.13、如图，AB∠CD，若GE平分∠DGH，HE平分∠GHB，GF平分∠CGH，若∠CGH=70°，则∠EHB的度数是______，图中与∠DGE互余的角共有______个．答案： 35°##35度 5分析：由平行线的性质可得，∠CGH=∠GHB=70°，∠GFH=∠CGF，利用邻角的补角可得∠DGH=∠GHA= 110°，利用角平分线的性质可得∠EHB=∠GHE=35°，∠CGF=∠GFH=∠HGF=35°，∠DGE=∠HGE= 55°，进而可求得答案．解：∵AB//CD，∴∠CGH=∠GHB=70°，∠DGH=∠GHA，∠GFH=∠CGF∴∠DGH=∠GHA=180°−70°=110°，又∵HE平分∠GHB，∵GE平分∠DGH，HE平分∠GHB，GF平分∠CGH，∴∠EHB=∠GHE=12∠GHB=35°，∠CGF=∠GFH=∠HGF=12∠CGH=35°，∠DGE=∠HGE=12∠DGH=55°，∴∠DGE+∠BHE=90°，∠DGE+∠GHE=90°，∠DGE+∠CGF=90°，∠DGE+∠HGF=90°，∠DGE+∠GFH=90°，∴与∠DGE互余的角共有5个，所以答案是：35°，5．小提示：本题考查了平行线的性质、角平分线的性质以及互余的定义，熟练掌握角平分线的性质及互余的定义是解题的关键．14、如图，将△ABC沿BC方向平移至△DEF处．若EC＝2BE＝2，则CF的长为_____．答案：1分析：利用平移的性质得到BE＝CF，再用EC＝2BE＝2得到BE的长，从而得到CF的长．解：∵△ABC沿BC方向平移至△DEF处．∴BE＝CF，∵EC＝2BE＝2，∴BE＝1，∴CF＝1．故答案为1．小提示：本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．15、命题“如果a+b=0，那么a，b互为相反数”的逆命题为____________________________.答案：如果a，b互为相反数，那么a+b=0分析：交换原命题的题设与结论即可得到其逆命题.解：逆命题为：如果a，b互为相反数，那么a+b=0.所以答案是：如果a，b互为相反数，那么a+b=0.小提示：本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．也考查了逆命题．解答题16、如图，已知AB∥DE，那么∠A+∠C+∠D的和是多少度？为什么？答案：∠A+∠C+∠D的和是360度，理由见解析．分析：如图（见解析），过点C作CF//AB，则CF//DE，先根据平行四边形的性质（两直线平行，同旁内角互补）得出∠A+∠FCA=180°,∠D+∠DCF=180°，再根据角的和差即可得．如图，过点C作CF//AB，则所求的问题变为∠A+∠ACD+∠D的和是多少度∴∠A+∠FCA=180°∵AB//DE∴CF//DE∴∠D+∠DCF=180°∴∠A+∠FCA+∠D+∠DCF=180°+180°=360°即∠A+∠ACD+∠D=360°．小提示：本题考查了平行线的性质、角的和差，熟记平行线的性质是解题关键．17、如图，钱塘江入海口某处河道两岸所在直线（PQ，MN）夹角为20°，在河道两岸安装探照灯B和A，若灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BQ逆时针旋转至BP便立即回转，两灯不停交叉照射巡视．设灯A转动的速度是a度/秒，灯B转动的速度是b度/秒．已知∠BAN＝50°．（1）当b＝2时，问灯B转动几秒后，射出的光束第一次经过灯A？（2）当a＝3，b＝6时，若两灯同时转动，在1分钟内（包括1分钟），问A灯转动几秒，两灯的光束互相平行？（3）若A、B两灯同时转动（a＞b），在45秒与90秒时，两灯的光束各平行一次，求a，b的值．答案：（1）15秒；（2）1609秒；（3）269，23．分析：（1）根据B 灯转动30度时第一次经过灯A ，列出方程即可得解；（2）根据内错角相等，两灯的光线平行，构建方程求解可得结果；（3）分两种情形，根据平行线的判定，构建方程解决问题即可．解：（1）设灯B 转动t 秒后，射出的光束第一次经过灯A ．由题意得：2t ＝30，解得：t ＝15，答：灯B 转动15秒后，射出的光束第一次经过灯A ．（2）设A 灯转动x 秒，两灯的光束互相平行．根据题意得：180﹣50﹣3x ＝6x ﹣30时，两灯的光束互相平行，解得：x ＝1609，答：A 灯转动1609秒，两灯的光束互相平行．（3）在45秒与90秒时，两灯的光束各平行一次45秒时第一次平行，由题意得：45a ﹣130＝30﹣45b ，90秒时第二次平行，由题意得：90a ﹣180﹣50＝90b ﹣30，解得：a ＝269，b ＝23 答：a ，b 的值分别为269，23．小提示：本题主要考查了平行线的判定以及角的和差关系的运用，解决问题的关键是运用分类思想进行求解，解题时注意：内错角相等，两直线平行．18、完成下面的证明：如图，BE 平分∠ABD ，DE 平分∠BDC ，且∠α+∠β＝90°，求证：AB ∠CD ．证明：∵BE平分∠ABD（已知），∴∠ABD＝2∠α（）∵DE平分∠BDC（已知），∴∠BDC＝（）．∴∠ABD+∠BDC＝2∠α+2∠β＝2（∠α+∠β）（）∵∠α+∠β＝90°．（已知），∴∠ABD+∠BDC＝（）．∴AB∠CD（）答案：角平分线的定义；2∠β；角平分线的定义；等量代换；180°；等量代换，同旁内角互补两直线平行分析：首先根据角平分线的定义可得∠ABD=2∠α，∠BDC=2∠β，根据等量代换可得∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)，进而得到∠ABD+∠BDC=180°，然后再根据同旁内角互补两直线平行可得答案．证明：∵BE平分∠ABD（已知），∴∠ABD＝2∠α（角平分线的定义）∵DE平分∠BDC（已知），∴∠BDC＝2∠β(角平分线的定义)．∴∠ABD+∠BDC＝2∠α+2∠β＝2（∠α+∠β）（等量代换）∵∠α+∠β＝90°．（已知），∴∠ABD+∠BDC＝180°（等量代换），∴AB∠CD（同旁内角互补两直线平行）．所以答案是：角平分线的定义；2∠β；角平分线的定义；等量代换；180°；等量代换，同旁内角互补两直线平行．小提示：此题主要考查了角平分线的定义，平行线的判定，解题的关键是掌握角平分线定义和平行线的判定方法．。

专题01 相交线与平行线全章复习攻略(考点清单)解析版-2024学年7下数学期末考点大串讲(人教版)

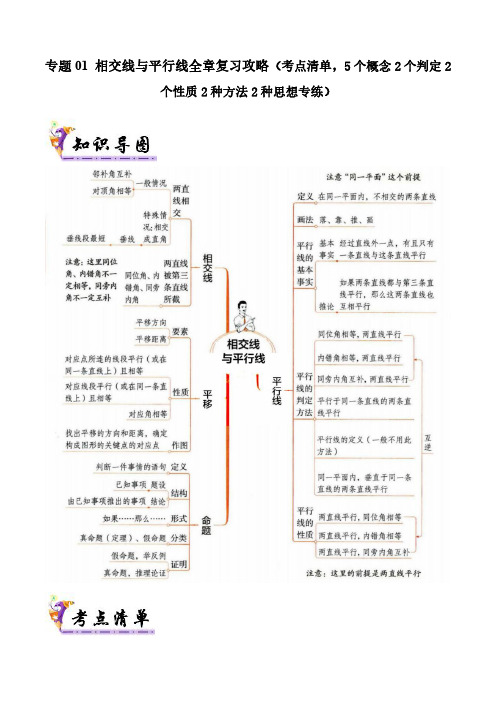
专题01相交线与平行线全章复习攻略（考点清单，5个概念2个判定2个性质2种方法2种思想专练）5个概念【考点题型一】相交线（1）相交线的定义两条直线交于一点，我们称这两条直线相交．相对的，我们称这两条直线为相交线．（2）两条相交线在形成的角中有特殊的数量关系和位置关系的有对顶角和邻补角两类．（3）在同一平面内，两条直线的位置关系有两种：平行和相交（重合除外）．【例1】（2023春•澄迈县期末）平面上画三条直线，交点的个数最多有()A．3个B．2个C．1个D．0个【分析】根据相交线的性质可得答案．【解答】解：平面内，三条直线两两相交，最多有3个交点，故选：A．【点评】本题考查相交线，理解平面内两条直线相交只有一个交点，三条直线两两相交最多有3个交点是正确判断的前提．l与直线2l相交，点M在直线1l上，直线2l不经过点M．”【变式1-1】（2023秋•路北区期末）根据语句“直线1画出的图形是()A．B．C．D．l与直线2l相交，点M在直线1l上，直线2l不经过点M进行判断，即可得出结论．【分析】根据直线1l不经过点M，故本选项不合题意；【解答】解：A．直线2B．点M在直线l上，故本选项不合题意；1C．点M在直线l上，故本选项不合题意；1D．直线l与直线2l相交，点M在直线1l上，直线2l不经过点M，故本选项符合题意；1故选：D．【点评】本题主要考查了相交线以及点与直线的位置关系，两条直线交于一点，我们称这两条直线为相交线．【变式1-2】（2023春•攸县期末）同一平面内不重合的三条直线，其交点的个数可能为()A．0个或1个B．1个或2个C ．2个或3个D ．0个或1个或2个或3个【分析】分三条直线互相平行、有两条平行和三条直线都不平行三种情况讨论．【解答】解：因为三条直线位置不明确，所以分情况讨论：①三条直线互相平行，有0个交点；②一条直线与两平行线相交，有2个交点；③三条直线都不平行，有1个或3个交点；所以交点的个数可能为0个或1个或2个或3个．故选：D ．【点评】考查了相交线，本题要注意列举出所有可能的情况．【变式1-3】（2023春•秦都区期末）如图，直线CD 与EF 交于点O ，OC 平分AOF ∠，若40AOE ∠=︒，求DOE ∠的度数．【分析】先根据平角定义可得140AOF ∠=︒，从而利用角平分线的定义可得1702COF AOF ∠=∠=︒，然后利用对顶角相等可得70DOE COF ∠=∠=︒，即可解答．【解答】解：40AOE ∠=︒ ，180140AOF AOE ∴∠=︒-∠=︒，OC 平分AOF ∠，1702COF AOF ∴∠=∠=︒，70DOE COF ∴∠=∠=︒，DOE ∴∠的度数为70︒．【点评】本题考查了对顶角、邻补角，角平分线的定义，根据题目的已知条件并结合图形进行分析是解题的关键．【考点题型二】“三线八角”（1）同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．（2）内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．（3）同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．（4）三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．【例2】（2023春•黄石港区期末）如图，图中1∠是同位角的是()∠与2A．（2）（3）B．（2）（3）（4）C．（1）（2）（4）D．（3）（4）【分析】根据同位角的定义作答．【解答】解：（1）（2）（4）中，1∠不是同位角，因为这两个角的边∠与2∠是同位角；图（3）中，1∠与2所在的直线没有一条公共边．故选：C．【点评】两条直线被第三条直线所截，在截线的同侧，在两条被截直线的同旁的两个角是同位角．如果两个角是同位角，那么它们一定有一条边在同一条直线上．【变式2-1】．（2023秋•同安区期末）如图，1∠的位置关系是()∠和4A．对顶角B．同位角C．内错角D．同旁内角【分析】两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角，由此即可判断．【解答】解：1∠和4∠的位置关系是同位角．故选：B．【点评】本题考查同位角，关键是掌握同位角的定义．【变式2-2】（2023秋•思明区校级期末）如图所示，B∠与3∠是一对()A．同位角B．内错角C．同旁内角D．对顶角【分析】根据“同位角、内错角、同旁内角”的意义进行判断即可．【解答】解：B∠与3∠是直线DE和直线BC被直线AB所截得到的同旁内角，故选：C．【点评】本题考查“同位角、内错角、同旁内角”的意义，理解和掌握“同位角、内错角、同旁内角”的特征是正确判断的前提．【变式2-3】（2023春•清远期末）如图，已知直线a，b被直线c所截，下列属于同旁内角是()A．1∠和4∠B．3∠和5∠C．2∠和3∠D．1∠和3∠【分析】根据对顶角、邻补角，同位角、内错角、同旁内角的意义，逐一判断即可解答．【解答】解：A、1∠属于同位角，故A不符合题意；∠与4B、3∠与5∠属于对顶角，故B不符合题意；C、2∠与3∠属于内错角，故C不符合题意；D、1∠与3∠属于同旁内角，故D符合题意；故选：D．【点评】本题考查了对顶角、邻补角，同位角、内错角、同旁内角，熟练掌握这些数学概念是解题的关键．【考点题型三】平行线在同一平面内，两条直线的位置关系有两种：平行和相交（重合除外）．（1）平行线的定义：在同一平面内，不相交的两条直线叫平行线．记作：a∥b；读作：直线a平行于直线b．（2）同一平面内，两条直线的位置关系：平行或相交，对于这一知识的理解过程中要注意：①前提是在同一平面内；②对于线段或射线来说，指的是它们所在的直线．【例3】（2023春•敦化市期末）在同一平面内，不重合的两条直线只有相交和两种位置关系．【分析】根据两直线的位置关系解答即可．【解答】解：在同一平面内，不重合的两条直线的位置关系是平行和相交，故答案为：平行．【点评】此题主要考查了平行线，关键是掌握在同一平面内，两条直线的位置关系有两种：平行和相交（重合除外）．【变式3-1】（2023春•青龙县期末）在同一平面内，不重合的两条直线的位置关系是()A．平行B．相交C．平行或相交D．以上都不对【分析】根据直线的位置关系解答．【解答】解：在同一平面内，不重合的两条直线只有两种位置关系，是平行或相交，所以在同一平面内，不重合的两条直线的位置关系是：平行或相交．故选：C．【点评】本题考查了两直线的位置关系，需要特别注意，垂直是相交特殊形式，在同一平面内，不重合的两条直线只有平行或相交两种位置关系．【变式3-2】（2023春•东昌府区校级月考）下列语句正确的有()个①任意两条直线的位置关系不是相交就是平行②过一点有且只有一条直线和已知直线平行③过两条直线a，b外一点P，画直线c，使//c bc a，且//④若直线//c a．b c，则//a b，//A．4B．3C．2D．1【分析】根据同一平面内，任意两条直线的位置关系是相交、平行；过直线外一点有且只有一条直线和已知直线平行；如果两条直线都与第三条直线平行，那么这两条直线也互相平行进行分析即可．【解答】解：①任意两条直线的位置关系不是相交就是平行，说法错误，应为根据同一平面内，任意两条直线的位置关系不是相交就是平行；②过一点有且只有一条直线和已知直线平行，说法错误，应为过直线外一点有且只有一条直线和已知直线平行；③过两条直线a，b外一点P，画直线c，使//a b时才能画出，故说法错误；c b，只有//c a，且//④若直线//c a，说法正确；a b，//b c，则//故选：D．【点评】此题主要考查了平行线，关键是掌握平行公理：过直线外一点有且只有一条直线和已知直线平行；推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．【变式3-3】（2023春•双牌县期末）下列说法正确的有（填序号）:．①同位角相等；②一条直线有无数条平行线；③在同一平面内，两条不相交的线段是平行线；④在同一平面内，如果//a c；a b，//b c，则//⑤过一点有且只有一条直线与已知直线平行．【分析】根据平行线的性质，平行公理以及平行线与线段的区别对各小题分析判断后利用排除法求解．【解答】解：①应是两直线平行，同位角相等，故本小题错误；②一条直线有无数条平行线，正确；③因为线段有端点，所以有长短，不相交也不一定平行，故在同一平面内，两条不相交的线段不一定是平行线，故本小题错误；④在同一平面内，如果//a c，符合平行公理，正确；b c，则//a b，//⑤应为过直线外一点可以而且只可以画一条直线与已知直线平行，故本小题错误，故答案为：②④．【点评】本题主要考查了平行线的性质及平行公理，都是基础知识，需要熟练记忆．【考点题型四】平移概念：把一个图形整体沿某一直线方向移动,会得到一个新的图形图形的这种移动,叫做平移要素：一是平移的方向,二是平移的距离性质：平移后的新图形与原图形的形状和大小完全相同对应边平行(或在同一条直线上)且相等,对应角相等连接各组对应点的线段平行(或在同一条直线上)相等注意：“连接各组对应点的线段”与“对应线段”的区别:前者是由原图形上的点与平移后图形上的对应点连接而成的;而后者本身就存在于原来的图形与平移后的图形之中，是图形的一条边【例4】．（2023春•南山区期末）如图，将直角ABC∆的位置，连结BE，若∆沿边AC的方向平移到DEF6CD =，14AF =，则BE 的长为()A ．4B ．6C ．8D ．12【分析】根据平移的性质得到BE AD =，DF AC =，结合图形计算，得到答案．【解答】解：由平移的性质可知，BE AD =，DF AC =，则DF DC AC DC -=-，即CF AD =，11()(146)422AD AF CD ∴=-=-=，4BE ∴=，故选：A ．【点评】本题考查的是平移的性质，经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．【变式4-1】．（2023春•鼎城区期末）如图，在三角形ABC 中，90ABC ∠=︒，将三角形ABC 沿BC 方向平移得到三角形DEF ，其中7AB =，3BE =，2DM =，则阴影部分的面积是()A ．15B ．18C ．21D ．不确定【分析】根据平移的性质得出3AD BE CF ===，再根据ADM ACFD S S S ∆=-阴影部分平行四边形进行计算即可．【解答】解：如图，连接AD ，由平移的性质可知，3AD BE CF ===，ADMACFD S S S ∆∴=-阴影部分平行四边形137232=⨯-⨯⨯18=，故选：B ．【点评】本题考查平移的性质，掌握平移前后对应线段平行且相等是正确解答的前提．【变式4-2】．（2022秋•临淄区期末）如图，4AB cm =，5BC cm =，2AC cm =，将ABC ∆沿BC 方向平移a (05)cm a <<，得到DEF ∆，连接AD ，则阴影部分的周长为cm ．【分析】根据平移的性质得到4DE AB cm ==，AD BE a ==cm ，根据周长公式计算，得到答案．【解答】解：由平移的性质可知：4DE AB cm ==，AD BE a ==cm ，(5)EC a cm ∴=-，∴阴影部分的周长(5)2411()AD EC AC DE a a cm =+++=+-++=，故答案为：11．【点评】本题考查的是平移的性质，平移不改变图形的形状和大小、经过平移，对应点所连的线段平行且相等，对应线段平行且相等．【变式4-3】．（2023春•重庆期末）如图，在平面直角坐标系xOy 中，三角形ABC 三个顶点的坐标分别是(4,2)A ，(1,0)B ，(5,3)C -，三角形ABC 中任意一点0(P x ，0)y ，经平移后对应点为0(6P x '-，02)y +，将三角形ABC 作同样的平移得到三角形A B C '''，点A ，B ，C 的对应点分别为A '，B '，C '．（1）点A '的坐标为，点B '的坐标为；（2）①画出三角形A B C '''；②写出三角形A B C '''的面积；（3）过点A '作//A D y '轴，交B C ''于点D ，则点D 的坐标为．【分析】（1）由点P 的对应点P '坐标知，需将三角形向左平移6个单位、向上平移2个单位，据此可得；（2）①根据平移规律求出C '点的坐标，根据A '，B '，C '点的坐标即可画出三角形A B C '''；②利用割补法求解可得答案；（3）设(2,)D m -，利用面积法求解．【解答】解：（1）点A '的坐标为(46,22)-+，点B '的坐标为(16,02)-+，即(2,4)A -，(5,2)B -；故答案为：(2,4)-，(5,2)-；（2）①如图，△A B C '''即为所求；②△A B C '''的面积11117545123342222=⨯-⨯⨯-⨯⨯-⨯⨯=；（3）设(2,)D m -，则有171(4)422m =⨯-⨯，解得14m =-，1(2,4D ∴--，故答案为：1(2,)4--．【点评】此题主要考查了平移作图，关键是正确确定组成图形的关键点平移后的位置．【考点题型五】命题1、判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．2、有些命题的正确性是用推理证实的，这样的真命题叫做定理．3、定理是真命题，但真命题不一定是定理．4、命题写成“如果…，那么…”的形式，这时，“如果”后面接的部分是题设，“那么”后面解的部分是结论．5、命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．【例5】（2023春•大竹县校级期末）下列说法正确的是()A．同位角相等B．对顶角相等C．两条直线被第三条直线所截，内错角相等D．两条平行直线被第三条直线所截，同旁内角相等【分析】根据平行线的性质对A、C、D进行判断；根据对顶角的性质对B进行判断．【解答】解：A、两直线平行，同位角相等，所以A选项错误；B、对顶角相等，所以B选项正确；C、两条平行直线被第三条直线所截，内错角相等，所以C选项错误；D、两条平行直线被第三条直线所截，同旁内角互补，所以D选项错误．故选：B．【点评】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果⋯那么⋯”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．【变式5-1】（2023春•汝南县期末）发现：如图，AOBPC OB交OA于点C，画∠内有一点P：过点P画//∠的数量关系；∠与CPD//PD OA交OB于点D；根据所画图形试说明：O验证：完善下面的解答过程，并填写理由或数学式：PC OB//∴∠=ACP()OPD OA//∴∠=∠∴∠=O CPDCPD探究：某数学兴趣小组通过以上练习发现了命题“两边分别平行的两个角相等”，甲同学认为该命题是真命题并画了图1进行验证，乙同学对甲同学的判断提出质疑，认为该命题不一定成立，是假命题，并作图如图2所示，题设与甲同学相同，得到B D∠与D∠的数量关系，∠≠∠，根据乙同学的作图，试判断此时B并说明理由．归纳：综合甲乙两同学的证明得到结论：两边分别平行的两个角．【分析】验证：利用平行线的性质和等量代换进行填空即可；探究：结合图1和图2，利用平行线的性质解答即可．【解答】解：验证：如图，，PC OB//∴∠=∠（两直线平行，同位角相等），O ACP，PD OA//∴∠=∠（两直线平行，内错角相等），CPD ACP∴∠=∠．O CPD故答案为：ACP∠；∠；两直线平行，同位角相等；ACP探究：两边分别平行的两个角相等或互补，理由：如图1，，DF BC//∴∠=∠．D CGE，DE BA//∴∠=∠，B CGE∴∠=∠．D B∴两边分别平行的两个角相等；如图2，DF BC，//∴∠=∠．D DGB，//DE BA∴∠+∠=︒，B DGB180∴∠+∠=︒．D B180∴两边分别平行的两个角互补，综上，两边分别平行的两个角相等或互补．故答案为：相等或互补．【点评】本题主要考查了平行线的性质，对顶角相等，分类讨论是思想方法，等量代换，熟练掌握平行线的性质是解题的关键．【变式5-2】．（2023春•盐山县期末）图形的世界丰富且充满变化，用数学的眼光观察它们，奇妙无比．（1）如图，//∠=∠，EF CD，数学课上，老师请同学们根据图形特征添加一个关于角的条件，使得BEF CDG并给出证明过程．小丽添加的条件：180∠+∠=︒．B BDG请你帮小丽将下面的证明过程补充完整．证明：//（已知）EF CDBEF∴∠=BCD∠()∠+∠=︒（已知）B BDG180∴()BC//∴∠=()CDG∴∠=∠（等量代换）BEF CDG（2）拓展：如图，请你从三个选项①//∠，③B BCD∠=∠中任选出两个作为条DG BC，②DG平分ADC件，另一个作为结论，组成一个真命题，并加以证明．①条件：，结论：（填序号）．②证明：．【分析】（1）根据平行线的判定定理和性质定理解答；（2）根据真命题的概念写出命题的条件和结论，根据平行线的判定定理和性质定理、角平分线的定义解答．【解答】（1）证明：//EF CD （已知），BEF BCD ∴∠=∠（两直线平行，同位角相等），180B BDG ∠+∠=︒ （已知），//BC DG ∴（同旁内角互补，两直线平行），CDG BCD ∴∠=∠（两直线平行，内错角相等），BEF CDG ∴∠=∠（等量代换）；（2）①条件：//DG BC ，B BCD ∠=∠（答案不唯一），结论：DG 平分ADC ∠，②证明：//DG BC ，ADG B ∴∠=∠，CDG BCD ∠=∠，B BCD ∠=∠ ，ADG CDG ∴∠=∠，即DG 平分ADC ∠．故答案为：（1）BCD ∠；两直线平行，同位角相等；DG ；同旁内角互补，两直线平行；BCD ∠；两直线平行，内错角相等；（2）①、①③；②，//DG BC ，ADG B ∴∠=∠，CDG BCD ∠=∠，B BCD ∠=∠ ，ADG CDG ∴∠=∠，即DG 平分ADC ∠．【点评】本题考查的是命题的真假判断、平行线的判定和性质，掌握平行线的判定定理和性质定理是解题的关键．【变式5-3】．（2023春•清江浦区期末）探究问题：已知ABC ∠，画一个角DEF ∠，使//DE AB ，//EF BC ，且DE 交BC 于点P ．ABC ∠与DEF ∠有怎样的数量关系？（1）我们发现ABC ∠与DEF ∠有两种位置关系：如图1与图2所示．①图1中ABC ∠与DEF ∠数量关系为；图2中ABC ∠与DEF ∠数量关系为；请选择其中一种情况说明理由．②由①得出一个真命题（用文字叙述）:．（2）应用②中的真命题，解决以下问题：若两个角的两边互相平行，且一个角比另一个角的2倍少30︒，请直接写出这两个角的度数．【分析】（1）①利用平行线的性质即可判断；②根据平行线的性质解决问题即可．（2）设两个角分别为x 和230x -︒，由题意230x x =-︒或230180x x +-︒=︒，解方程即可解决问题．【解答】解：（1）①如图1中，180ABC DEF ∠+∠=︒．如图2中，ABC DEF ∠=∠，故答案为：180ABC DEF ∠+∠=︒，ABC DEF ∠=∠．理由：如图1中，//BC EF ，DPB DEF ∴∠=∠，//AB DE ，180ABC DPB ∴∠+∠=︒，180ABC DEF ∴∠+∠=︒．如图2中，//BC EF ，DPC DEF ∴∠=∠，//AB DE ，ABC DPC ∴∠=∠，ABC DEF ∴∠=∠．②结论：如果两个角的两边互相平行，那么这两个角相等或互补．故答案为：如果两个角的两边互相平行，那么这两个角相等或互补．（2）设两个角分别为x和230x-︒，由题意230+-︒=︒，x xx x=-︒或230180解得30x=︒或70x=︒，∴这两个角的度数为30︒，30︒或70︒和110︒．【点评】本题考查平行线的判定和性质，一元一次方程的应用等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．2个判定【考查题型六】垂线（1）垂线的定义当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足．（2）垂线的性质在平面内，过一点有且只有一条直线与已知直线垂直．注意：“有且只有”中，“有”指“存在”，“只有”指“唯一”“过一点”的点在直线上或直线外都可以．【例6】（2023春•澄迈县期末）过点C向AB边作垂线段，下列画法中正确的是()A．B．C．D．【分析】根据垂线段的定义及题意逐个图进行判断即可得出正确结论．【解答】解：A．此选项是过点A作BC边的垂线段，故错误；B．此选项是过点B作AB边的垂线段，故错误；C．此选项是过点C作AB边的垂线段，故此项正确；D．此选项是过点B作CA边的垂线段，故错误．故选：C．【点评】本题考查了垂线段的定义及作法，是一道基础题，解题时要善于观察，准确理解垂线段的定义是解题的关键．【变式6-1】（2023春•孟村县期末）已知，如图所示，AB CD ⊥，垂足为O ，EF 为过O 点的一条直线，则α∠与β∠的关系一定成立的是()A ．相等B ．互余C ．互补D ．互为对顶角【分析】根据图形可看出，β∠的对顶角COE ∠与α∠互余，那么α∠与β∠就互余．【解答】解：图中，COE β∠=∠（对顶角相等），又AB CD ⊥ ，90COE α∴∠+∠=︒，90αβ∴∠+∠=︒，∴两角互余．故选：B ．【点评】本题考查了余角和垂线的定义以及对顶角相等的性质．【变式6-2】．（2022秋•太仓市期末）如图，直线AB 与CD 相交于点O ，OE AB ⊥，OF CD ⊥．（1）如图中与COE ∠互补的角是；（把符合条件的角都写出来）（2）若15AOD EOF ∠=∠，求AOD ∠的度数．【分析】（1）根据互补的两个角的和等于180︒，结合图形找出与COE ∠的和等于180︒的角即可；（2）设AOd x ∠=，可以得到5EOF x ∠=，然后列式求解即可．【解答】解：（1）180COE EOD ∠+∠=︒ ，EOD ∴∠与COE ∠互补；90COE BOC ∠+∠=︒ ，90BOC BOF ∠+∠=︒，COE BOF ∴∠=∠，180BOF AOF ∠+∠=︒ ，180COE AOF ∴∠+∠=︒，AOF ∴∠与COE ∠互补；综上：EOD ∠和AOF ∠与COE ∠互补．故答案为：EOD ∠，AOF ∠．（2）设AOD x ∠=，则5EOF x ∠=，90EOC x ∠=︒-，AOD BOC ∠=∠ （对顶角相等），90905EOF EOC COF x x ∴∠=∠+∠=︒+︒-=，即6180x =︒，解得：30x =︒．30AOD ∴∠=︒．【点评】本题考查了补角的和等于180︒的性质，以及对顶角相等，周角等于360︒的性质，结合图形找出各角的关系是解题的关键．【变式6-3】．（2023春•红山区期末）如图，直线AB 与CD 相交于点O ，EO CD ⊥于点O ，OF 平分AOD ∠，且50BOE ∠=︒，求COF ∠的度数．【分析】依据垂线以及邻补角，即可得到AOC ∠的度数，再根据角平分线即可得出AOF ∠的度数，进而得出COF ∠的度数．【解答】解：EO CD ⊥ ，50BOE ∠=︒，90DOE ∴∠=︒．180905040AOC ∴∠=︒-︒-︒=︒，140AOD BOC ∠=∠=︒．又OF 平分AOD ∠，1702AOF AOD ∴∠=∠=︒．4070110COF AOC AOF ∴∠=∠+∠=︒+︒=︒．【点评】本题考查角平分线的定义、角的和差关系的运用，解题的关键是灵活运用所学知识解决问题．【考查题型七】平行线判定（1）平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．（2）应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．【例7】（2023春•西乡塘区期末）如图，下列条件中，能判断//AB CD的是()A．12∠=∠B．34∠=∠C．180∠=∠DAB ABC∠+∠=︒D．B D【分析】结合图形分析两角的位置关系，根据平行线的判定方法逐项进行判断即可得到结论．【解答】解：12，∠=∠∴，AB CD//故①选项符合题意；，34∠=∠∴，//AD BC故②选项不符合题意；，180∠+∠=︒DAB ABC∴，AD BC//故③选项不符合题意；∠=∠，不能判定//B DAB CD，故④选项不符合题意；故选：A．【点评】本题主要考查了平行线的判定，能根据图形准确找出同位角、内错角和同旁内角是解决问题的关键．【变式7-1】．（2023春•高新区校级期末）如图，ABC ADC ∠=∠，BF ，DE 分别是ABC ∠，ADC ∠的角平分线，12∠=∠，求证：//DC AB ．【分析】先利用角平分线定义得到132ADC ∠=∠，122ABC ∠=∠，而ABC ADC ∠=∠，则32∠=∠，加上12∠=∠，则13∠=∠，于是可根据平行线的判定得到//DC AB ．【解答】证明：BF ，DE 分别是ABC ∠，ADC ∠的角平分线，132ADC ∴∠=∠，122ABC ∠=∠，ABC ADC ∠=∠ ，32∴∠=∠，12∠=∠ ，13∴∠=∠，//DC AB ∴．【点评】本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．【变式7-2】．（2023春•武胜县校级期末）完成下面的证明如图，BE 平分ABD ∠，DE 平分BDC ∠，且90αβ∠+∠=︒，求证：//AB CD ．完成推理过程BE 平分ABD ∠（已知），2(ABD α∴∠=∠)．DE 平分BDC ∠（已知），2BDC β∴∠=∠()222()ABD BDC αβαβ∴∠+∠=∠+∠=∠+∠()90αβ∠+∠=︒ （已知），180(ABD BDC ∴∠+∠=︒)．//(AB CD ∴)．【分析】首先根据角平分线的定义可得2ABD α∠=∠，2BDC β∠=∠，根据等量代换可得222()ABD BDC αβαβ∠+∠=∠+∠=∠+∠，进而得到180ABD BDC ∠+∠=︒，然后再根据同旁内角互补两直线平行可得答案．【解答】证明：BE 平分ABD ∠（已知），2ABD α∴∠=∠（角平分线的定义）．DE 平分BDC ∠（已知），2BDC β∴∠=∠（角平分线的定义）222()ABD BDC αβαβ∴∠+∠=∠+∠=∠+∠（等量代换）90αβ∠+∠=︒ （已知），180ABD BDC ∴∠+∠=︒（等量代换）．//AB CD ∴（同旁内角互补两直线平行）．故答案为：角平分线的定义，角平分线的定义，等量代换，等量代换，同旁内角互补两直线平行．【点评】此题主要考查了平行线的判定，关键是掌握角平分线定义和平行线的判定方法．【变式7-3】．（2023春•岳池县校级期末）如图，已知点E 、F 在直线AB 上，点G 在线段CD 上，ED 与FG 交于点H ，C EFG ∠=∠，CED GHD ∠=∠．（1）求证：//CE GF ；（2）试判断AED ∠与D ∠之间的数量关系，并说明理由；（3）若100EHF ∠=︒，30D ∠=︒，求AEM ∠的度数．【分析】（1）根据同位角相等两直线平行，可证//CE GF ；（2）根据平行线的性质可得C FGD ∠=∠，根据等量关系可得FGD EFG ∠=∠，根据内错角相等，两直线平行可得//AB CD ，再根据平行线的性质可得AED ∠与D ∠之间的数量关系；（3）根据对顶角相等可求DHG ∠，根据三角形外角的性质可求CGF ∠，根据平行线的性质可得C ∠，AEC ∠，再根据平角的定义可求AEM ∠的度数．【解答】（1）证明：CED GHD ∠=∠ ，//CE GF ∴；（2）解：//CE GF ，C FGD ∴∠=∠，C EFG ∠=∠ ，FGD EFG ∴∠=∠，//AB CD ∴，180AED D ∴∠+∠=︒；（3）100DHG EHF ∠=∠=︒ ，30D ∠=︒，10030130CGF ∴∠=︒+︒=︒，//CE GF ，18013050C ∴∠=︒-︒=︒，//AB CD ，50AEC ∴∠=︒，18050130AEM ∴∠=︒-︒=︒．【点评】考查了平行线的判定和性质，三角形外角的性质，平角的定义，平行线的性质有：同位角相等两直线平行；内错角相等两直线平行；同旁内角互补两直线平行；平行线的性质有：两直线平行同位角相等；两直线平行内错角相等；两直线平行同旁内角互补．2个性质【考查题型八】垂线段的性质（1）垂线段：从直线外一点引一条直线的垂线，这点和垂足之间的线段叫做垂线段．（2）垂线段的性质：垂线段最短．正确理解此性质，垂线段最短，指的是从直线外一点到这条直线所作的垂线段最短．它是相对于这点与直线上其他各点的连线而言．（3）实际问题中涉及线路最短问题时，其理论依据应从“两点之间，线段最短”和“垂线段最短”这两个中去选择．【例8】（2023秋•婺城区期末）如图，某污水处理厂要从A 处把处理过的水引入排水渠PQ ，为了节约用料，铺设垂直于排水渠的管道AB ．这种铺设方法蕴含的数学原理是()。

人教版七年级数学-下册-第五章相交线与平行线-复习课件-(共32张PPT)

且DOE 5COE。求AOD的度数。
CE
┓
AO
B
D 此题需要正确地
应用、对顶角、
邻补角、垂直的
概念和性质。
解 :由邻补角的定义知: COE+DOE=1800，又由DOE 5COE COE 5COE 1800 COE 300 又 OE AB BOE 900 BOC BOE COE 1200 由对顶角相等得: AOD=BOC=1200
x=30°
∴∠AOC=∠DOB=60°
• 7、如图，在长方形ABCD中，∠ADB＝20°，
• 现将这一长方形纸片沿AF折叠，若使AB’ ∥BD，
• 则折痕AF与AB的夹角∠BAF应为多少度？
B' A
解：长方形ABCD中， ∠BAD=90° D ∵AB'//BD, ∠ADB=20°
∴∠B'AD=∠ADB=20°
第5章相交线与平行线复习课
一、学习目标
1、进一步巩固邻补角、对顶角的概念和性质 2、理解垂线、垂线段的概念和性质 3、掌握两条直线平行的判定和性质 4、通过平移，理解图形平移变换的性质 5、能区分命题的题设和结论以及命题的真假
二、重点和难点
重点：垂线的性质和平行线的判定和性质。
难点：平行线的判定和性质。
例3. 2.已知OA OC，OB OD，AOB : BOC 32 :13，
求COD的度数。
CB
解.由OA OC知 : AOC 900 即AOB BOC 900
D O
由AOB : BOC 32 :13，
A 设AOB 32x，则BOC=13x 列方程:32x+13x=900
由垂直先找到 900 的
C
E

七年级数学下册第五章相交线与平行线重难点归纳(带答案)

七年级数学下册第五章相交线与平行线重难点归纳单选题1、下列说法不正确的是（）A．对顶角相等B．两点确定一条直线C．两点之间线段最短D．一个角的补角一定大于这个角答案：D分析：根据对顶角的性质，直线的性质，两点之间线段最短，补角的定义，依次判断即可得到答案．解：A、对顶角相等，故该项不符合题意；B、两点确定一条直线，故该项不符合题意；C、两点之间线段最短，故该项不符合题意；D、一个角的补角不一定大于这个角，说法错误，故该项符合题意；故选：D．小提示：此题考查对顶角的性质，直线的性质，两点之间线段最短，补角的定义，正确理解各性质及定义是解题的关键．2、如图，将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上，若∠α=135°，则∠β等于（）A．45°B．60°C．75°D．85°答案：C分析：直接利用平行线的性质以及三角形的性质进而得出答案．由题意可得：∵∠α=135°，∴∠1=45°，∴∠β=180°−45°−60°=75°．故选C．小提示：此题主要考查了平行线的性质，正确得出∠1的度数是解题关键．3、如图，两只蚂蚁以相同的速度沿两条不同的路径，同时从A出发爬到B，则( )A．乙比甲先到B．甲和乙同时到C．甲比乙先到D．无法确定答案：B分析：根据平移可得出两蚂蚁行程相同，结合二者速度相同即可得出结论．如图：根据平移可得两只蚂蚁的行程相同，∵甲、乙两只蚂蚁的行程相同，且两只蚂蚁的速度相同，∴两只蚂蚁同时到达．故选B.小提示：本题考查了生活中的平移现象，结合图形找出甲、乙两只蚂蚁的行程相等是解题的关键．4、如图，AB和CD相交于点O，则下列结论正确的是（）A．∠1＝∠2B．∠2＝∠3C．∠3＝∠4D．∠1＝∠5答案：A分析：根据平行线的性质和对顶角的性质进行判断．解：A、∵∠1与∠2是对顶角，∴∠1＝∠2，本选项说法正确；B、∵AD与AB不平行，∴∠2≠∠3，本选项说法错误；C、∵AD与CB不一定平行，∴∠3≠∠4，本选项说法错误；D、∵CD与CB不平行，∴∠1≠∠5，本选项说法错误；故选：A．小提示：本题考查平行线的应用，熟练掌握平行线的性质和对顶角的意义与性质是解题关键．5、如图，已知a//b，∠1=120°，∠2=90°，则∠3的度数是( )A．120°B．130°C．140°D．150°答案：D分析：延长∠1的边与直线b相交，然后根据两直线平行，同旁内角互补求出∠4，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．如图，延长∠1的边与直线b相交，∵a//b，∴∠4=180°−∠1=180°−120°=60°，由三角形的外角性质可得，∠3=90°+∠4=90°+60°=150°．故选：D．小提示：本题考查了平行线的性质，以及三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质并作出辅助线是解题的关键．6、如图，点P是直线a外的一点，点A、B、C在直线a上，且PB⊥a，垂足是B，PA⊥PC，则下列不正确的语句是（）A．线段PB的长是点P到直线a的距离B．PA、PB、PC三条线段中，PB最短C．线段AC的长是点A到直线PC的距离D．线段PC的长是点C到直线PA的距离答案：C分析：根据点到直线的距离等于垂线段的长度，垂线段最短逐项分析判断即可．解：A. 线段PB的长是点P到直线a的距离，故该选项正确，不符合题意；B.PA、PB、PC三条线段中，PB最短，故该选项正确，不符合题意；C. 线段AP的长是点A到直线PC的距离,故该选项不正确，符合题意；D. 线段PC的长是点C到直线PA的距离，故该选项正确，不符合题意；故选C小提示：本题考查了点到直线的距离等于垂线段的长度，垂线段最短，掌握垂线段的定义是解题的关键．7、如图，OB⊥CD于点O，∠1＝∠2，则∠2与∠3的关系是( )A．∠2＝∠3B．∠2与∠3互补C．∠2与∠3互余D．不能确定答案：C分析：根据垂线定义可得∠1+∠3=90°，再根据等量代换可得∠2+∠3=90°．解：∵OB⊥CD，∴∠1+∠3=90°，∵∠1=∠2，∴∠2+∠3=90°，∴∠2与∠3互余，故选：C．小提示：本题考查了垂线和余角，解题的关键是掌握垂线的定义，当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线．8、如图，下列说法错误的是（）A．∠1与∠2是对顶角B．∠1与∠3是同位角C．∠1与∠4是内错角D．∠B与∠D是同旁内角答案：C分析：分别根据对顶角、同位角、内错角以及同旁内角的定义判断即可．解：A、∠1与∠2是对顶角，正确，故该选项不合题意；B、∠1与∠3是同位角，正确，故该选项不合题意；C、∠1与∠4是内错角，错误，故该选项符合题意；D、∠B与∠D是同旁内角，正确，故该选项不合题意；故选：C．小提示：本题主要考查了对顶角、同位角、内错角以及同旁内角的定义，熟记定义是解答本题的关键．9、如图所示，直线a∥b，∠1=35°，∠2=90°，则∠3的度数为（）A．125°B．135°C．145°D．155°答案：A分析：如图求出∠5即可解决问题．详解：∵a∥b，∴∠1=∠4=35°，∵∠2=90°，∴∠4+∠5=90°，∴∠5=55°，∴∠3=180°-∠5=125°，故选A．点睛：本题考查平行线的性质、三角形内角和定理，邻补角的性质等知识，解题的关键是灵活运用所学知识解决问题．10、如图，直线a，b被直线c所截，a//b，∠1=60°，则∠2的度数是（）A．120°B．60°C．45°D．30°答案：B分析：根据平行线的性质可得解.详解：∵a//b∴∠1=∠2又∵∠1=60°，∴∠2=60°故选B.点睛：两条平行线被第三条直线所截，同位角相等.填空题11、如图a∥b,∠1＋∠2=75°，则∠3+∠4＝______________.答案：105°分析：根据平行线的性质和等量代换可以求得∠3+∠4=∠5+∠4，所以根据三角形内角和是180°进行解答即可．如图，∵a∥b，∴∠3=∠5，又∠1+∠2=75°，∠1+∠2+∠4+∠5=180°，∴∠5+∠4=105°，∴∠3+∠4=∠5+∠4=105°，故答案是：105°．小提示：本题考查了平行线的性质和三角形内角和定理．解题的技巧性在于把求（∠3+∠4）的值转化为求同一三角形内的（∠5+∠4）的值．12、如图，将三角尺与两边平行的直尺（EF∥HG）贴在一起（∠ACB＝90°）在直尺的一边上．若∠2＝47°，则∠1的大小为 _____度．答案：43分析：先根据平行线的性质求出∠2的度数，再由∠1与∠3互余即可得出结论．解：如图所示：∵EF//HG，∠2=47°，∴∠2=∠3=47°又∵∠ACB＝90°，∠1+∠3=∠ACB＝90°，∴∠1=∠ACB−∠3＝90°−47°=43°，∴∠1=43°．所以答案是：43．小提示：本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．13、如图，添加一个你认为合适的条件______使AD//BC．答案：∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°（答案不唯一，写一个正确的即可）分析：根据平行线的判定方法即可求解．第一种情况，同位角相等，两直线平行，即∠ADF=∠C时，AD//BC；第二种情况，内错角相等，两直线平行，即∠A=∠ABE时，AD//BC；第三种情况，同旁内角互补，两直线平行，即∠A+∠ABC=180°或∠C+∠ADC=180°时，AD//BC；故答案为∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°．小提示：本题考查了平行线的判定方法，同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．14、如图，将△ABE向右平移2cm得到△DCF，如果△ABE的周长是16cm，那么四边形ABFD的周长是_____．答案：20cm分析：根据平移的性质可得DF＝AE，然后判断出四边形ABFD的周长＝△ABE的周长+AD+EF，然后代入数据计算即可得解．解：∵△ABE向右平移2cm得到△DCF，∴DF＝AE，∴四边形ABFD的周长＝AB+BE+DF+AD+EF，＝AB+BE+AE+AD+EF，＝△ABE的周长+AD+EF，∵平移距离为2cm，∴AD＝EF＝2cm，∵△ABE的周长是16cm，∴四边形ABFD的周长＝16+2+2＝20cm．所以答案是：20cm．小提示：本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．15、如图，已知直角三角形ABC，∠A=90∘，AB＝4cm，BC＝5cm．将△ABC沿AC方向平移1.5cm得到△A′B′C′，求四边形BCC′B′的面积为________cm2．答案：6分析：根据题意，再结合平移的性质，可得AB=A′B′，AA′=BB′=CC′=1.5cm，BB′∥CC′，S△ABC=S△A′B′C′，然后再根据等量代换，得出S四边形AA′OB =S四边形OCC′B′，然后再根据等量代换，得出S四边形BCC′B′=S四边形AA′B′B，然后再根据长方形的特征，得出四边形AA′B′B是长方形，然后再根据长方形的面积公式，算出长方形AA′B′B的面积，即可得出四边形BCC′B′的面积．解：如图，∵△ABC沿AC方向平移1.5cm得到△A′B′C′，∴A的对应点为点A′，点B的对应点为点B′，点C的对应点为点C′，∴由平移的性质，可得：AB=A′B′=4cm，AA′=BB′=CC′=1.5cm，BB′∥CC′，又∵△ABC沿AC方向平移1.5cm得到△A′B′C′，∴S△ABC=S△A′B′C′，又∵S△ABC=S四边形AA′OB+S△A′OC，S△A′B′C′=S四边形OCC′B′+S A′OC，∴S四边形AA′OB =S四边形OCC′B′，∵S四边形BCC′B′=S四边形OCC′B′+S△BOB′，S四边形AA′B′B =S四边形AA′OB+S△BOB′，∴S四边形BCC′B′=S四边形AA′B′B，∵AB=A′B′，AA′=BB′，∠A=90∘，∴根据长方形的特征，可得：四边形AA′B′B是长方形，∴S长方形AA′B′B=AB⋅AA′=4×1.5=6cm2，∴S四边形BCC′B′=S四边形AA′B′B=6cm2所以答案是：6小提示：本题考查了平移的性质，等量代换，根据长方形的特征判定长方形，长方形的面积公式，解本题的关键在熟练掌握平移的性质．平移的性质：1、形状大小不变；2、对应点的连线平行（或在同一直线上）且相等；3、对应线段平行（或在同一直线上）且相等，对应角相等．解答题16、已知：如图，∠1=∠2．求证：AB//CD．分析：如图，欲证AB//CD，只要证∠1=______．证明：∵∠1=∠2，（已知）又∠3=∠2，（）∴∠1=__________．（）∴AB//CD．（__________，____________）答案：∠3；对顶角相等；∠3；等量代换；同位角相等，两直线平行．分析：根据等量代换和同位角相等，两直线平行即可得出结果．分析：如图，欲证AB//CD，只要证∠1=∠3．证明：∵∠1=∠2，（已知）又∠3=∠2，（对顶角相等）∴∠1=∠3．（等量代换）∴AB//CD．（同位角相等，两直线平行）小提示：本题主要考查平行线的判定，属于基础题，掌握平行线的判定定理是解题的关键．17、如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE．(1)若∠AOC=76°，求∠BOF的度数；(2)若∠BOF=36°，求∠AOC的度数；答案：(1)∠BOF=33°(2)∠AOC=72°分析：（1）先根据对顶角相等求出∠BOD=76°，再由角平分线定义得∠DOE=∠BOE=38°，由邻补角得∠COE=142°，再根据角平分线定义得∠EOF=71°，从而可得结论．（2）利用角平分的定义得出∠BOE=∠EOD，∠COF=∠FOE，进而表示出各角求出答案．（1）∵∠AOC、∠BOD是对顶角，∴∠BOD=∠AOC=76°，∵OE平分∠BOD，∠BOD=38°∴∠DOE=∠BOE=12∴∠COE=142°，∵OF平分∠COE．∠COE=71°，∴∠EOF=12又∠BOE+∠BOF=∠EOF，∴∠BOF=∠EOF−∠BOE=71°−38°=33°，（2）∵OE平分∠BOD，OF平分∠COE，∴∠BOE=∠EOD，∠COF=∠FOE，∴设∠BOE=x，则∠EOD=x，故∠COA=2x，∠EOF=∠COF=x+36°，则∠AOC+∠COF+∠BOF=2x+x+36°+36°=180°，解得x=36°，故∠AOC=72°．小提示：本题考查了角平分线的定义和对顶角的性质，解决本题的关键是掌握对顶角的定义（从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线）．18、完成下面的证明如图．已知：AD∥EF，∠1＝∠2，求证：AD平分∠BAC．证明：∵AD∥EF（），∴∠2＝（），∠1＝（）．∵∠1＝∠2（已知），∴∠BAD＝∠CAD（）．即AD平分∠BAC．答案：已知；∠CAD，两直线平行，同位角相等；∠BAD，两直线平行，内错角相等；等量代换．分析：根据平行线的性质进行推理即可解答．解：∵AD∥EF（已知），∴∠2＝∠CAD（两直线平行，同位角相等），∠1＝∠BAD（两直线平行，内错角相等），∵∠1＝∠2（已知），∴∠CAD＝∠BAD(等量代换），即AD平分∠BAC（角平分线的定义）．小提示：本题主要考查了平行线的性质，掌握两直线平行、内错角相等，两直线平行、同位角相等成为解答本题的关键．。

难点突破“相交线与平行线(提高)”压轴题50道(含详细解析)

难点突破“相交线与平行线(提高)”压轴题50道(含详细解析)1．如图，//AD BC ，D ABC ∠=∠，点E 是边DC 上一点，连接AE 交BC 的延长线于点H ．点F 是边AB 上一点．使得FBE FEB ∠=∠，作FEH ∠的角平分线EG 交BH 于点G ，若100DEH ∠=︒，则BEG ∠的度数为( )A ．30︒B ．40︒C ．50︒D ．60︒2．如图，已知//AB CD ，CE 、BE 的交点为E ，现作如下操作：第一次操作，分别作ABE ∠和DCE ∠的平分线，交点为1E ，第二次操作，分别作1ABE ∠和1DCE ∠的平分线，交点为2E ，第三次操作，分别作2ABE ∠和2DCE ∠的平分线，交点为3E ，⋯，第n 次操作，分别作1n ABE -∠和1n DCE -∠的平分线，交点为n E ．若1n E ∠=度，那BEC ∠等于度3．如图，//AB CD ，CF 平分DCG ∠，GE 平分CGB ∠交FC 的延长线于点E ，若34E ∠=︒，则B ∠的度数为．4．如图，直线//a b ，A 是直线a 上一点，D 、E 分别是直线b 上的点，C 是AE 上一点，80ACD ∠=︒，//EG CD 交AD 于G ，F 是GE 上一点使FGC FCG ∠=∠，作CB 平分ACF ∠，则BCG ∠= ．5．如图，已知//AB CD ，直线EF 分别交AB 、CD 于点A 、C ，CH 平分ACD ∠，点G 为CD 上一点，连接HA 、HG ，HC 平分AHG ∠，若42AHG ∠=︒，180HGD EAB ∠+∠=︒，则ACD ∠的度数是 ︒．6．如图，直线//MN PQ ，点A 在直线MN 与PQ 之间，点B 在直线MN 上，连结AB ．ABM ∠的平分线BC 交PQ 于点C ，连结AC ，过点A 作AD PQ ⊥交PQ 于点D ，作A F A B⊥交PQ于点F ，AE 平分DAF ∠交PQ 于点E ，若45CAE ∠=︒，52ACB DAE ∠=∠，则ACD ∠的度数是．7．探究：如图①，////AB CD EF ，试说明BCF B F ∠=∠+∠．下面给出了这道题的解题过程，请在下列解答中，填上适当的理由．解：//AB CD ，（已知） 1B ∴∠=∠．( )同理可证，2F ∠=∠．12BCF ∠=∠+∠， BCF B F ∴∠=∠+∠．( )应用：如图②，//AB CD ，点F 在AB 、CD 之间，FE 与AB 交于点M ，FG 与CD 交于点N ．若115EFG ∠=︒，55EMB ∠=︒，则DNG ∠的大小为度．拓展：如图③，直线CD 在直线AB 、EF 之间，且////AB CD EF ，点G 、H 分别在直线AB 、EF 上，点Q 是直线CD 上的一个动点，且不在直线GH 上，连结QG 、QH ．若70GQH ∠=︒，则AGQ EHQ ∠+∠= 度．8．综合与探究如图，已知//AM BN ，60A ∠=︒，点P 是射线AM 上一动点（与点A 不重合）．BC ，BD 别平分ABP ∠和PBN ∠，分别交射线AM 于点C ，D ．（1）求ABN ∠、CBD ∠的度数；根据下列求解过程填空．解：//AM BN ，180ABN A ∴∠+∠=︒60A ∠=︒， ABN ∴∠= ， 120ABP PBN ∴∠+∠=︒，BC 平分ABP ∠，BD 平分PBN ∠， 2ABP CBP ∴∠=∠、PBN ∠= ，( )22120CBP DBP ∴∠+∠=︒， CBD CBP DBP ∴∠=∠+∠= ．（2）当点P 运动时，APB ∠与ADB ∠之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．（3）当点P 运动到使ACB ABD ∠=∠时，直接写出ABC ∠的度数．9．已知直线12//l l ，直线3l 与1l 、2l 分别交于C 、D 两点，点P 是直线3l 上的一动点，如图①，若动点P 在线段CD 之间运动（不与C 、D 两点重合），问在点P 的运动过程中是否始终具有312∠+∠=∠这一相等关系？试说明理由；如图②，当动点P 在线段CD 之外且在CD 的上方运动（不与C 、D 两点重合），则上述结论是否仍成立？若不成立，试写出新的结论，并说明理由．10．课上教师呈现一个问题：已知：如图1，//AB CD ，EF AB ⊥于点O ，FG 交CD 于点P ，当130∠=︒时，求EFG ∠的度数．甲、乙、丙三位同学用不同的方法添加辅助线解决问题，如图：甲同学辅助线的做法和分析思路如下：辅助线：过点F 作//MN CD ．分析思路：①欲求EFG ∠的度数，由图可知只需转化为求2∠和3∠的度数之和； ②由辅助线作图可知，21∠=∠，从而由已知1∠的度数可得2∠的度数； ③由//AB CD ，//MN CD 推出//AB MN ，由此可推出34∠=∠； ④由已知EF AB ⊥，可得490∠=︒，所以可得3∠的度数； ⑤从而可求EFG ∠的度数．（1）请你根据乙同学所画的图形，描述辅助线的做法，并写出相应的分析思路．辅助线：分析思路：（2）请你根据丙同学所画的图形，求EFG ∠的度数． 11．已知，//AB CD ，点E 为射线FG 上一点．（1）如图1，若30EAF ∠=︒，40EDG ∠=︒，则AED ∠= ︒；（2）如图2，当点E 在FG 延长线上时，此时CD 与AE 交于点H ，则AED ∠、EAF ∠、EDG ∠之间满足怎样的关系，请说明你的结论；（3）如图3，DI 平分EDC ∠，交AE 于点K ，交AI 于点I ，且:1:2EAI BAI ∠∠=，22AED ∠=︒，20I ∠=︒，求EKD ∠的度数．12．已知，直线//AB DC ，点P 为平面上一点，连接AP 与CP ．（1）如图1，点P 在直线AB 、CD 之间，当60BAP ∠=︒，20DCP ∠=︒时，求APC ∠．（2）如图2，点P 在直线AB 、CD 之间，BAP ∠与DCP ∠的角平分线相交于点K ，写出AKC ∠与APC ∠之间的数量关系，并说明理由．（3）如图3，点P 落在CD 外，BAP ∠与DCP ∠的角平分线相交于点K ，AKC ∠与APC ∠有何数量关系？并说明理由．13．如图，已知：EF AC ⊥，垂足为点F ，DM AC ⊥，垂足为点M ，DM 的延长线交AB 于点B ，且1C ∠=∠，点N 在AD 上，且23∠=∠，试说明//AB MN ．14．（1）如图①，90CEF ∠=︒，点B 在射线EF 上，//AB CD ，若130ABE ∠=︒，求C ∠的度数；（2）如图②，把“90CEF ∠=︒”改为“120CEF ∠=︒”，点B 在射线EF 上，//AB CD ．猜想ABE ∠与C ∠的数量关系，并说明理由．15．如图1，已知//AB CD ，30B ∠=︒，120D ∠=︒；（1）若60E ∠=︒，则F ∠= ；（2）请探索E ∠与F ∠之间满足的数量关系？说明理由；（3）如图2，已知EP 平分BEF ∠，FG 平分EFD ∠，反向延长FG 交EP 于点P ，求P ∠的度数．16．已知直线12//l l ，直线3l 和直线1l 、2l 交于点C 和D ，点P 是直线3l 上一动点（1）如图1，当点P 在线段CD 上运动时，PAC ∠，APB ∠，PBD ∠之间存在什么数量关系？请你猜想结论并说明理由．（2）当点P 在C 、D 两点的外侧运动时(P 点与点C 、D 不重合，如图2和图3)，上述（1）中的结论是否还成立？若不成立，请直接写出PAC ∠，APB ∠，PBD ∠之间的数量关系，不必写理由．17．（1）如图（1），已知任意三角形ABC ，过点C 作//DE AB ，求证：DCA A ∠=∠；（2）如图（1），求证：三角形ABC 的三个内角（即A ∠、B ∠、)ACB ∠之和等于180︒；（3）如图（2），求证：AGF AEF F ∠=∠+∠；（4）如图（3），//AB CD ，119CDE ∠=︒，GF 交DEB ∠的平分线EF 于点F ，150AGF ∠=︒，求F ∠．18．如图，已知直线12//l l ，且3l 和1l ，2l 分别交于A ，B 两点，4l 和1l ，2l 相交于C ，D 两点，点P 在直线AB 上，（1）当点P 在A ，B 两点间运动时，问1∠，2∠，3∠之间的关系是否发生变化？并说明理由；（2）如果点P 在A ，B 两点外侧运动时，试探究ACP ∠，BDP ∠，CPD ∠之间的关系，并说明理由．19．已知直线//AB CD ，（1）如图1，点E 在直线BD 上的左侧，直接写出ABE ∠，CDE ∠和BED ∠之间的数量关系是．（2）如图2，点E 在直线BD 的左侧，BF ，DF 分别平分ABE ∠，CDE ∠，直接写出BFD ∠和BED ∠的数量关系是．（3）如图3，点E 在直线BD 的右侧BF ，DF 仍平分ABE ∠，CDE ∠，那么BFD ∠和BED ∠有怎样的数量关系？请说明理由．20．（1）如图1，//a b ，则12∠+∠=（2）如图2，//AB CD ，则123∠+∠+∠= ，并说明理由（3）如图3，//a b ，则1234∠+∠+∠+∠=（4）如图4，//a b ，根据以上结论，试探究1234n ∠+∠+∠+∠+⋯+∠= （直接写出你的结论，无需说明理由）21．问题情境：（1）如图1，//AB CD ，130PAB ∠=︒，120PCD ∠=︒．求APC ∠度数．小颖同学的解题思路是：如图2，过点P 作//PE AB ，请你接着完成解答问题迁移：（2）如图3，//AD BC ，点P 在射线OM 上运动，当点P 在A 、B 两点之间运动时，ADP α∠=∠，BCP β∠=∠．试判断CPD ∠、α∠、β∠之间有何数量关系？（提示：过点P 作//)PE AD ，请说明理由；（3）在（2）的条件下，如果点P 在A 、B 两点外侧运动时（点P 与点A 、B 、O 三点不重合），请你猜想CPD ∠、α∠、β∠之间的数量关系．22．如图，AD 是ABC ∆的角平分线，点E 在BC 上．点G 在CA 的延长线上，EG 交AB 于点F ，AFG G ∠=∠，求证：//GE AD ．23．如图1，//AB CD ，直线EF 交AB 于点E ，交CD 于点F ，点G 在CD 上，点P 在直线EF 左侧、且在直线AB 和CD 之间，连接PE 、PG ．（1）求证：EPG AEP PGC ∠=∠+∠；（2）连接EG ，若EG 平分PEF ∠，110AEP PGE ∠+∠=︒，12PGC EFC ∠=∠，求AEP ∠的度数；（3）如图2，若EF 平分PEB ∠，PGC ∠的平分线所在的直线与EF 相交于点H ，则EPG ∠与EHG ∠之间的数量关系为．24．已知E 、D 分别在AOB ∠的边OA 、OB 上，C 为平面内一点，DE 、DF 分别是CDO ∠、CDB ∠的平分线．（1）如图1，若点C 在OA 上，且//FD AO ，求证：DE AO ⊥；（2）如图2，若点C 在AOB ∠的内部，且DEO DEC ∠=∠，请猜想DCE ∠、AEC ∠、CDB ∠之间的数量关系，并证明；（3）若点C 在AOB ∠的外部，且DEO DEC ∠=∠，请根据图3、图4分别写出DCE ∠、AEC ∠、CDB ∠之间的数量关系（不需证明）．25．如图 1 ，//MN PQ ，直线AD 与MN 、PQ 分别交于点A 、D ，点B 在直线PQ 上，过点B 作BG AD ⊥，垂足为点G ．（1）求证：90MAG PBG ∠+∠=︒；（2）若点C 在线段AD 上（不与A 、D 、G 重合），连接BC ，MAG ∠和PBC ∠的平分线交于点H ，请在图 2 中补全图形，猜想并证明CBG ∠与AHB ∠的数量关系；（3）若直线AD 的位置如图 3 所示，（2）中的结论是否成立？若成立，请证明；若不成立，请直接写出CBG ∠与AHB ∠的数量关系．26．已知：如图，点C 在AOB ∠的一边OA 上，过点C 的直线//DE OB ，CF 平分ACD ∠，CG CF ⊥于点C ．（1）若40O ∠=︒，求ECF ∠的度数；（2）求证：CG 平分OCD ∠．27．完成下面的证明．已知：如图，//BC DE ，BE 、DF 分别是ABC ∠、ADE ∠的平分线．求证：12∠=∠．证明：//BC DE ，(ABC ADE ∴∠=∠ )．BE 、DF 分别是ABC ∠、ADE ∠的平分线．132ABC ∴∠=∠，142ADE ∠=∠．34∴∠=∠．∴ // ( )．12(∴∠=∠ )．28．将一副三角板中的两根直角顶点C 叠放在一起（如图①)，其中30A ∠=︒，60B ∠=︒，45D E ∠=∠=︒．（1）若150BCD ∠=︒，求ACE ∠的度数；（2）试猜想BCD ∠与ACE ∠的数量关系，请说明理由；（3）若按住三角板ABC 不动，绕顶点C 转动三角板DCE ，试探究BCD ∠等于多少度时，//CD AB ，并简要说明理由．29．如图，已知AD BC ⊥，EF BC ⊥，12∠=∠．求证：//DG BA ．30．如图，已知12180∠+∠=︒，3B ∠=∠，试判断AED ∠与ACB ∠的大小关系，并说明理由．31．如图，已知//AB CD ，点E 在AC 的右侧，BAE ∠，DCE ∠的平分线相交于点F ．探索AEC ∠与AFC ∠之间的等量关系，并证明你的结论．32．已知：如图，12∠=∠，34∠=∠，56∠=∠．求证：//ED FB ．33．操作探究：如图，对折长方形纸片ABCD ，使AD 与BC 重合，得到折痕EF ，把纸片展开：再一次折叠纸片，使点A 落在EF 上（设落地为)N ，并使折痕经过点B ，得到折痕BM ，连接BN 、MN ，请你猜想MBN ∠的度数是多少，并证明你的结论．34．长江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图，灯A 射线自AM 顺时针旋转至AN 便立即回转，灯B 射线自BP 顺时针旋转至BQ 便立即回转，两灯不停交叉照射巡视．若灯A 转动的速度是/a ︒秒，灯B 转动的速度是/b ︒秒，且a 、b 满足2|3|(4)0a b a b -++-=．假定这一带长江两岸河堤是平行的，即//PQ MN ，且45BAN ∠=︒（1）求a 、b 的值；（2）若灯B 射线先转动20秒，灯A 射线才开始转动，在灯B 射线到达BQ 之前，A 灯转动几秒，两灯的光束互相平行？（3）如图，两灯同时转动，在灯A 射线到达AN 之前．若射出的光束交于点C ，过C 作CD AC ⊥交PQ 于点D ，则在转动过程中，BAC ∠与BCD ∠的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请求出其取值范围．35．已知：射线//OP AE（1）如图1，AOP ∠的角平分线交射线AE 与点B ，若58BOP ∠=︒，求A ∠的度数．（2）如图2，若点C 在射线AE 上，OB 平分AOC ∠交AE 于点B ，OD 平分COP ∠交AE 于点D ，39ADO ∠=︒，求ABO AOB ∠-∠的度数．（3）如图3，若A m ∠=，依次作出AOP ∠的角平分线OB ，BOP ∠的角平分线1OB ，1B OP∠的角平分线2OB ，1n B OP -∠的角平分线n OB ，其中点B ，1B ，2B ，⋯，1n B -，n B 都在射线AE 上，试求n AB O ∠的度数．36．请把下列证明过程补充完整．已知：如图，B ，C ，E 三点在同一直线上，A ，F ，E 三点在同一直线上，12E ∠=∠=∠，34∠=∠．求证：//AB CD证明：2E ∠=∠（已知）∴ //(BC )3∴∠=∠ ( )34∠=∠（已知）4∴∠=∠ ( )12∠=∠（已知）12CAF CAF ∴∠+∠=∠+∠即BAF ∠=∠4∴∠=∠ （等量代换）∴ ( )37．如图所示，已知//AB CD ，分别探索下列四个图形中P ∠与A ∠，C ∠的关系．要求：（1）、（3）直接写出结论，（2）、（4）写出结论并说明理由．结论：（1）；（2）；（3）；（4）．证明：（2）（4）38．如图，已知直线12//l l ，直线3l 和直线1l 、2l 交于点C 和D 、A 、B 两点分别在1l 和2l 上，直线3l 上有一动点P（1）如果P 点在C 、D 之间运动时，猜测PAC ∠，APB ∠，PBD ∠之间有什么关系，证明你的结论（2）若点P 在DC 的延长线上运动时，PAC ∠，APB ∠，PBD ∠之间的关系为（3）在（2）的条件下，PAC ∠和PBD ∠的角平分线相交于点Q ，探索APB ∠和AQB ∠的关系，并证明．39．已知如图，90COD ∠=︒，直线AB 与OC 交于点B ，与OD 交于点A ，射线OE 与射线AF 交于点G ．（1）若OE 平分BOA ∠，AF 平分BAD ∠，42OBA ∠=︒，则OGA ∠= ；（2）若13GOA BOA ∠=∠，13GAD BAD ∠=∠，42OBA ∠=︒，则OGA ∠= ；（3）将（2）中的“42OBA ∠=︒”改为“OBA α∠=”，其它条件不变，求OGA ∠的度数．（用含α的代数式表示）（4）若OE 将BOA ∠分成1:2两部分，AF 平分BAD ∠，(3090)ABO αα∠=︒<<︒，求OGA ∠的度数．（用含α的代数式表示）40．“一带一路”让中国和世界更紧密，“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯．如图1所示，灯A射线从AM开始顺时针旋转至AN便立即回转，灯B射线从BP开始顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是每秒2度，灯B转动的速度是每秒1度．假定主道路是平行的，即//PQ MN，且∠∠=．BAM BAN:2:1（1）填空：BAN∠=︒；（2）若灯B射线先转动30秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？（3）如图2，若两灯同时转动，在灯A射线到达AN之前．若射出的光束交于点C，过C作∠与BCD∠=︒，则在转动过程中，请探究BAC∠的数量∠交PQ于点D，且120ACDACD关系是否发生变化？若不变，请求出其数量关系；若改变，请说明理由．41．如图，BG平分CBDCBD∠=︒，EF BG交AC于点F，100∠，E为BC的延长线上一点，//∠=︒，求EFC∠的度数．A2542．如图①，将一副直角三角板放在同一条直线AB上，其中30∠=OCD∠=︒，45ONM（1）将图①中的三角板OMN绕点O按逆时针方向旋转，使30∠=︒，如图②，MN与BON∠的度数；CD相交于点E，求CEN（2）将图①中的三角尺OMN 绕点O 按每秒15︒的速度沿逆时针方向旋转一周，在旋转的过程中，在第秒时，边MN 恰好与边CD 平行；在第秒时，直线MN 恰好与直线CD 垂直．（直接写出结果） 43．我们知道同一平面内的两条直线有相交和平行两种位置关系．（1）观察与思考：如图1，若//AB CD ，点P 在AB 、CD 内部，BPD ∠、B ∠、D ∠之间的数量关系为，不必说明理由；（2）猜想与证明：如图2，将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ，利用（1）中的结论（可以直接套用）求BPD ∠、B ∠、D ∠、BQD ∠之间有何数量关系？并证明你的结论；（3）拓展与应用：如图3，设BF 交AC 于点M ，AE 交DF 于点N ，已知140AMB ∠=︒，105ANF ∠=︒．利用（2）中的结论直接写出B E F ∠+∠+∠的度数为度，A ∠比F ∠大度．44．已知：直线//a b ，点A ，B 分别是a ，b 上的点，APB 是a ，b 之间的一条折弦，且90APB ∠<︒，Q 是a ，b 之间且在折线APB 左侧的一点，如图．（1）若133∠=︒，74APB ∠=︒，则2∠= 度．（2）若Q ∠的一边与PA 平行，另一边与PB 平行，请探究Q ∠，1∠，2间满足的数量关系并说明理由．（3）若Q ∠的一边与PA 垂直，另一边与PB 平行，请直接写出Q ∠，1∠，2之间满足的数量关系．45．直线MN 与直线PQ 相交于O ，点A 在射线OP 上运动，点B 在射线OM 上运动．（1）如图1，若80AOB ∠=︒，已知AE 、BE 分别是BAO ∠和ABO ∠的角平分线，点A 、B 在运动的过程中，AEB ∠的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出AEB ∠的大小．（2）如图2，若80AOB ∠=︒，已知AB 不平行CD ，AD 、BC 分别是BAP ∠和ABM ∠的角平分线，AD 、BC 的延长线交于点F ，点A 、B 在运动的过程中，F ∠= ；DE 、CE 又分别是ADC ∠和BCD ∠的角平分线，点A 、B 在运动的过程中，CED ∠的大小也不发生变化，其大小为：CED ∠= ．（3）如图3，若90AOB ∠=︒，延长BA 至G ，已知BAO ∠、OAG ∠的角平分线与BOQ ∠的角平分线及其延长线相交于E 、F ，则EAF ∠= ；（4）如图3，若AF ，AE 分别是GAO ∠，BAO ∠的角平分线，90AOB ∠=︒，在AEF ∆中，如果有一个角是另一个角的4倍，则ABO ∠的度数= ．46．在学习“相交线与平行线”一章时，课本中有一道关于潜望镜的拓广探索题，老师倡议班上同学分组开展相关的实践活动．小钰所在组上网查阅资料，制作了相关PPT 介绍给同学（图1、图2)；小宁所在组制作了如图所示的潜望镜模型并且观察成功（图3)．大家结合实践活动更好地理解了潜望镜的工作原理．（1）图4中，AB，CD代表镜子摆放的位置，动手制作模型时，应该保证AB与CD平行，入射光线与反射光线满足12∠=∠，34∠=∠，这样离开潜望镜的光线MN就与进入潜望镜的光线EF平行，即//MN EF．请完成对此结论的以下填空及后续证明过程（后续证明无需标注理由）．//AB CD（已知），2∴∠=∠()．12∠=∠，34∠=∠（已知），1234(∴∠=∠=∠=∠)．（2）在之后的实践活动总结中，老师进一步布置了一个任务：利用图5中的原理可以制作一个新的装置进行观察，那么在图5中方框位置观察到的物体“影像”的示意图为．A．B．C．D．47．已知，////AB CD EF，且CB平分ABF∠，CF平分BEF∠，请说明BC CF⊥的理由．解：//AB E（已知）∴∠+∠=．CB平分ABF∠（已知）1 12ABF∴∠=∠同理，142BEF ∠=∠114()2ABF BEF ∴∠+∠=∠+∠= ．又//AB CD （已知）12∴∠=∠同理，34∠=∠1423∴∠+∠=∠+∠2390∴∠+∠=︒（等量代换）即90BCF ∠=︒BC CF ∴⊥ ．48．如图，已知40ABC ∠=︒，射线DE 与AB 相交于点O ，且//DE BC ．解答以下问题：（注EDF ∠为小于180︒的角）（1）画EDF ∠，使DF ∠的另一边//DF AB ．请在如图①和图②中画出符合题意的图形，并求EDF ∠的度数．（2）如果EDF ∠的顶点D 在ABC ∠的内部，边//DE BC ，另一边//DF AB ．请在如图③和图④中画出相应的图形，并使用量角器分别测量出ABC ∠与EDF ∠的度数后，直接写出ABC ∠与EDF ∠的关系，不必说明理由．（3）如果EDF ∠的顶点D 在ABC ∠的内部，边DF BC ⊥，请在如图⑤中画出相应的图形，并使用量角器分别测量出ABC ∠与EDF ∠的度数后，直接写出ABC ∠与EDF ∠的关系，不必说明理由．49．如图（1），四边形ABCD 中，//AD BC ，点E 是线段CD 上一点，（1）说明：AEB DAE CBE ∠=∠+∠；（2）如图（2），当AE 平分DAC ∠，ABC BAC ∠=∠． ①说明：90ABE AEB ∠+∠=︒；②如图（3）若ACD ∠的平分线与BA 的延长线交于点F ，且60F ∠=︒，求BCD ∠．50．如图，已知射线//CD AB ，110C ABD ∠=∠=︒，E ，F 在CD 上，且满足EAD EDA ∠=∠，AF 平分CAE ∠．（1）求FAD ∠的度数；（2）若向右平行移动BD ，其它条件不变，那么:ADC AEC ∠∠的值是否发生变化？若变化，找出其中规律；若不变，求出这个比值；（3）在向右平行移动BD 的过程中，是否存在某种情况，使AFC ADB ∠=∠？若存在，请求出ADB ∠度数；若不存在，说明理由．难点突破“相交线与平行线(提高)”压轴题50道(含详细解析)参考答案与试题解析一．选择题（共1小题）1．如图，//AD BC ，D ABC ∠=∠，点E 是边DC 上一点，连接AE 交BC 的延长线于点H ．点F 是边AB 上一点．使得FBE FEB ∠=∠，作FEH ∠的角平分线EG 交BH 于点G ，若100DEH ∠=︒，则BEG ∠的度数为( )A ．30︒B ．40︒C ．50︒D ．60︒【解答】解：设FBE FEB α=∠=，则2AFE α∠=，FEH ∠的角平分线为EG ，设GEH GEF β∠=∠=， //AD BC ，180ABC BAD ∴∠+∠=︒，而D ABC ∠=∠，180D BAD ∴∠+∠=︒，//AB CD ∴，100DEH ∠=︒，则100CEG FAE ∠=∠=︒，1801802AEF AED BEG β∠=︒-∠-∠=︒-，在AEF ∆中，10021802180αβ︒++︒-=︒，故40βα-=︒，而40BEG FEG FEB βα∠=∠-∠=-=︒，故选：B ．二．填空题（共5小题）2．如图，已知//AB CD ，CE 、BE 的交点为E ，现作如下操作：第一次操作，分别作ABE ∠和DCE ∠的平分线，交点为1E ，第二次操作，分别作1ABE ∠和1DCE ∠的平分线，交点为2E ，第三次操作，分别作2ABE ∠和2DCE ∠的平分线，交点为3E ，⋯，第n 次操作，分别作1n ABE -∠和1n DCE -∠的平分线，交点为n E ．若1n E ∠=度，那BEC ∠等于 2n 度【解答】解：如图①，过E 作//EF AB ，//AB CD ， ////AB EF CD ∴，1B ∴∠=∠，2C ∠=∠， 12BEC ∠=∠+∠， BEC ABE DCE ∴∠=∠+∠；如图②，ABE ∠和DCE ∠的平分线交点为1E ，111111222CE B ABE DCE ABE DCE BEC ∴∠=∠+∠=∠+∠=∠．1ABE ∠和1DCE ∠的平分线交点为2E ，22211111112224BE C ABE DCE ABE DCE CE B BEC ∴∠=∠+∠=∠+∠=∠=∠；如图②，2ABE ∠和2DCE ∠的平分线，交点为3E ，33322211112228BE C ABE DCE ABE DCE CE B BEC ∴∠=∠+∠=∠+∠=∠=∠；⋯以此类推，12n nE BEC ∠=∠． ∴当1n E ∠=度时，BEC ∠等于2n 度．故答案为：2n ．3．如图，//AB CD ，CF 平分DCG ∠，GE 平分CGB ∠交FC 的延长线于点E ，若34E ∠=︒，则B ∠的度数为 68︒ ．【解答】解：如图，延长DC 交BG 于M ．由题意可以假设CDF GCF x ∠=∠=，CGE MGE y ∠=∠=．则有22x y GMC x y E =+∠⎧⎨=+∠⎩①②，①-②2⨯可得：2GMC E ∠=∠，34E ∠=︒， 68GMC ∴∠=︒， //AB CD ， 68GMC B ∴∠=∠=︒，故答案为68︒．4．如图，直线//a b ，A 是直线a 上一点，D 、E 分别是直线b 上的点，C 是AE 上一点，80ACD ∠=︒，//EG CD 交AD 于G ，F 是GE 上一点使FGC FCG ∠=∠，作CB 平分ACF ∠，则BCG ∠= 40︒ ．【解答】解：设BCD y ∠=，FGC FCG x ∠=∠=，//CD EG ，DCG FGC x ∴∠=∠=， CB 平分ACF ∠， ACB BCF ∴∠=∠，80y x y x ∴︒-=++， 2280x y ∴+=︒， 40x y ∴+=︒， 40BCG x y ∴∠=+=︒，故答案为40︒5．如图，已知//AB CD ，直线EF 分别交AB 、CD 于点A 、C ，CH 平分ACD ∠，点G 为CD 上一点，连接HA 、HG ，HC 平分AHG ∠，若42AHG ∠=︒，180HGD EAB ∠+∠=︒，则ACD ∠的度数是 106 ︒．【解答】解：HC 平分AHG ∠，且42AHG ∠=︒，21CHG ∴∠=︒， HC 平分ACG ∠，12HCG ACG ∴∠=∠，180CAB EAB ∠+∠=︒，180HGD EAB ∠+∠=︒， BAC HGD ∴∠=∠，//AB CD ，180BAC ACD ∴∠+∠=︒，设ACD α∠=，则1122MCG ACD α∠==，180BAC HGD α∠=∠=︒-， HGD ∠是CHG ∆的外角，HGD CHG HCG ∴∠=∠+∠，即1180212αα︒-=︒+，解得106α=︒，106ACD ∴∠=︒．故答案为：106︒．6．如图，直线//MN PQ ，点A 在直线MN 与PQ 之间，点B 在直线MN 上，连结AB ．ABM ∠的平分线BC 交PQ 于点C ，连结AC ，过点A 作AD PQ ⊥交PQ 于点D ，作A F A B⊥交PQ于点F ，AE 平分DAF ∠交PQ 于点E ，若45CAE ∠=︒，52ACB DAE ∠=∠，则ACD ∠的度数是 27︒ ．【解答】解：设DAE α∠=，则EAF α∠=，52ACB α∠=，AD PQ ⊥，AF AB ⊥，90BAF ADE ∴∠=∠=︒，90BAE BAF EAF α∴∠=∠+∠=︒+，90CEA ADE DAE α∠=∠+∠=︒+， BAE CEA ∴∠=∠，//MN PQ ，BC 平分ABM ∠，BCE CBM CBA ∴∠=∠=∠，又360ABC BCE CEA BAE ∠+∠+∠+∠=︒，180BCE CEA ∴∠+∠=︒， //AE BC ∴，ACB CAE ∴∠=∠，即5452α=︒，18α∴=︒， 18DAE ∴∠=︒，Rt ACD ∴∆中，9090(4518)27ACD CAD ∠=︒-∠=︒-︒+︒=︒，故答案为：27︒．三．解答题（共44小题）7．探究：如图①，////AB CD EF ，试说明BCF B F ∠=∠+∠．下面给出了这道题的解题过程，请在下列解答中，填上适当的理由．解：//AB CD ，（已知） 1B ∴∠=∠．( 两直线平行内错角相等 )同理可证，2F ∠=∠．12BCF ∠=∠+∠， BCF B F ∴∠=∠+∠．( )应用：如图②，//AB CD ，点F 在AB 、CD 之间，FE 与AB 交于点M ，FG 与CD 交于点N ．若115EFG ∠=︒，55EMB ∠=︒，则DNG ∠的大小为度．拓展：如图③，直线CD 在直线AB 、EF 之间，且////AB CD EF ，点G 、H 分别在直线AB 、EF 上，点Q 是直线CD 上的一个动点，且不在直线GH 上，连结QG 、QH ．若70GQH ∠=︒，则AGQ EHQ ∠+∠= 度．【解答】解：探究：：//AB CD，∴∠=∠．（两直线平行内错角相等）B1同理可证，2∠=∠．F∠=∠+∠，BCF12∴∠=∠+∠．（等量代换）BCF B F故答案为：两直线平行，内错角相等，等量代换．应用：由探究可知：MFN AMF CNF∠=∠+∠，1155560∴∠=∠=︒-︒=︒．CNF DNG故答案为60．拓展：如图③中，当的Q在直线GH的右侧时，36070290∠+∠=︒-︒=︒，AGQ EHQ当点Q'在直线GH的左侧时，70∠'+∠'=∠'=︒．AGQ EHQ GQ H故答案为70或290．8．综合与探究如图，已知//∠=︒，点P是射线AM上一动点（与点A不重合）．BC，BDAAM BN，60别平分ABP∠，分别交射线AM于点C，D．∠和PBN（1）求ABN∠的度数；根据下列求解过程填空．∠、CBD解：//AM BN，∴∠+∠=︒180ABN A∠=︒，60AABN ∴∠= 120︒ ， 120ABP PBN ∴∠+∠=︒，BC 平分ABP ∠，BD 平分PBN ∠， 2ABP CBP ∴∠=∠、PBN ∠= ，( )22120CBP DBP ∴∠+∠=︒， CBD CBP DBP ∴∠=∠+∠= ．（2）当点P 运动时，APB ∠与ADB ∠之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．（3）当点P 运动到使ACB ABD ∠=∠时，直接写出ABC ∠的度数．【解答】解：（1）//AM BN ，180ABN A ∴∠+∠=︒， 60A ∠=︒， 120ABN ∴∠=︒120ABP PBN ∴∠+∠=︒，BC 平分ABP ∠，BD 平分PBN ∠，2ABP CBP ∴∠=∠、2PBN PBD ∠=∠，（角平分线的定义）， 22120CBP DBP ∴∠+∠=︒， 60CBD CBP DBP ∴∠=∠+∠=︒．故答案为120︒，2PBD ∠，角平分线的定义，60︒．（2）APB ∠与ADB ∠之间数量关系是：2APB ADB ∠=∠．不随点P 运动变化．理由是：//AM BN ，APB PBN ∴∠=∠，ADB DBN ∠=∠（两直线平行内错角相等）， BD 平分PBN ∠（已知）， 2PBN DBN ∴∠=∠（角平分线的定义）， 22APB PBN DBN ADB ∴∠=∠==∠=∠（等量代换），即2APB ADB ∠=∠．（3）结论：30ABC ∠=︒．理由：//AM BN ，ACB CBN ∴∠=∠，当ACB ABD ∠=∠时，则有CBN ABD ∠=∠，ABC CBD CBD DBN ∴∠+∠=∠+∠，ABC DBN ∴∠=∠，由（1）可知120ABN ∠=︒，60CBD ∠=︒，60ABC DBN ∴∠+∠=︒， 30ABC ∴∠=︒9．已知直线12//l l ，直线3l 与1l 、2l 分别交于C 、D 两点，点P 是直线3l 上的一动点，如图①，若动点P 在线段CD 之间运动（不与C 、D 两点重合），问在点P 的运动过程中是否始终具有312∠+∠=∠这一相等关系？试说明理由；如图②，当动点P 在线段CD 之外且在CD 的上方运动（不与C 、D 两点重合），则上述结论是否仍成立？若不成立，试写出新的结论，并说明理由．【解答】解：（1）312∠+∠=∠成立，理由如下：如图①，过点P 作1//PE l ，1AEP ∴∠=∠，12//l l ， 2//PE l ∴，3BPE ∴∠=∠，2BPE APE ∠+∠=∠， 312∴∠+∠=∠；（2）312∠+∠=∠不成立，新的结论为312∠-∠=∠，理由为：如图②，过P 作1//PE l ，1APE ∴∠=∠，12//l l ，2//PE l ∴，3BPE ∴∠=∠，2BPE APE ∠-∠=∠，312∴∠-∠=∠．10．课上教师呈现一个问题：已知：如图1，//AB CD ，EF AB ⊥于点O ，FG 交CD 于点P ，当130∠=︒时，求EFG∠的度数．甲、乙、丙三位同学用不同的方法添加辅助线解决问题，如图：甲同学辅助线的做法和分析思路如下：辅助线：过点F 作//MN CD ．分析思路：①欲求EFG ∠的度数，由图可知只需转化为求2∠和3∠的度数之和；②由辅助线作图可知，21∠=∠，从而由已知1∠的度数可得2∠的度数； ③由//AB CD ，//MN CD 推出//AB MN ，由此可推出34∠=∠；④由已知EF AB ⊥，可得490∠=︒，所以可得3∠的度数；⑤从而可求EFG ∠的度数．（1）请你根据乙同学所画的图形，描述辅助线的做法，并写出相应的分析思路．辅助线：过点P 作//PN EF 交AB 于点N分析思路：（2）请你根据丙同学所画的图形，求EFG ∠的度数．【解答】解：（1）辅助线：过点P 作//PN EF 交AB 于点N ．分析思路：①欲求EFG ∠的度数，由辅助线作图可知，EFG NPG ∠=∠，因此，只需转化为求NPG ∠的度数；②欲求NPG ∠的度数，由图可知只需转化为求1∠和2∠的度数和；③又已知1∠的度数，所以只需求出2∠的度数；④由已知EF AB ⊥，可得490∠=︒；⑤由//PN EF ，可推出34∠=∠；//AB CD 可推出23∠=∠，由此可推24∠=∠，所以可得2∠的度数；⑥从而可以求出EFG ∠的度数．（2）如图，过点O 作//ON FG ，//ON FG ，130EFG EON ONC ∴∠=∠∠=∠=︒，//AB CD ，30ONC BON ∴∠=∠=︒，EF AB ⊥，90EOB ∴∠=︒，9030120EFG EON EOB BON ∴∠=∠=∠+∠=︒+︒=︒．11．已知，//AB CD ，点E 为射线FG 上一点．（1）如图1，若30EAF ∠=︒，40EDG ∠=︒，则AED ∠= 70 ︒；（2）如图2，当点E 在FG 延长线上时，此时CD 与AE 交于点H ，则AED ∠、EAF ∠、EDG ∠之间满足怎样的关系，请说明你的结论；（3）如图3，DI 平分EDC ∠，交AE 于点K ，交AI 于点I ，且:1:2EAI BAI ∠∠=，22AED ∠=︒，20I ∠=︒，求EKD ∠的度数．【解答】解：（1）如图，延长DE 交AB 于H ，//AB CD ，40D AHE ∴∠=∠=︒，AED ∠是AEH ∆的外角，304070AED A AHE ∴∠=∠+∠=︒+︒=︒，故答案为：70；（2）EAF AED EDG ∠=∠+∠．理由：//AB CD ，EAF EHC ∴∠=∠，EHC ∠是DEH ∆的外角，EHG AED EDG ∴∠=∠+∠，EAF AED EDG ∴∠=∠+∠；（3）:1:2EAI BAI ∠∠=，∴设EAI α∠=，则3BAE α∠=，22AED ∠=︒，20I ∠=︒，DKE AKI ∠=∠，又180EDK DKE DEK ∠+∠+∠=︒，180KAI KIA AKI ∠+∠+∠=︒， 2EDK α∴∠=-︒， DI 平分EDC ∠，224CDE EDK α∴∠=∠=-︒，//AB CD ，EHC EAF AED EDG ∴∠=∠=∠+∠，即32224αα=︒+-︒，解得18α=︒，16EDK ∴∠=︒，∴在DKE ∆中，1801622142EKD ∠=︒-︒-︒=︒．12．已知，直线//AB DC ，点P 为平面上一点，连接AP 与CP ．（1）如图1，点P 在直线AB 、CD 之间，当60BAP ∠=︒，20DCP ∠=︒时，求APC ∠．（2）如图2，点P 在直线AB 、CD 之间，BAP ∠与DCP ∠的角平分线相交于点K ，写出AKC ∠与APC ∠之间的数量关系，并说明理由．（3）如图3，点P 落在CD 外，BAP ∠与DCP ∠的角平分线相交于点K ，AKC ∠与APC ∠有何数量关系？并说明理由．【解答】解：（1）如图1，过P 作//PE AB ，//AB CD ，////PE AB CD ∴，APE BAP ∴∠=∠，CPE DCP ∠=∠，602080APC APE CPE BAP DCP ∴∠=∠+∠=∠+∠=︒+︒=︒；（2）12AKC APC ∠=∠．理由：如图2，过K 作//KE AB ，//AB CD ，////KE AB CD ∴，AKE BAK ∴∠=∠，CKE DCK ∠=∠，AKC AKE CKE BAK DCK ∴∠=∠+∠=∠+∠，过P 作//PF AB ，同理可得，APC BAP DCP ∠=∠+∠，BAP ∠与DCP ∠的角平分线相交于点K ，1111()2222BAK DCK BAP DCP BAP DCP APC ∴∠+∠=∠+∠=∠+∠=∠， 12AKC APC ∴∠=∠；（3）12AKC APC ∠=∠．理由：如图3，过K 作//KE AB ，//AB CD ，////KE AB CD ∴，BAK AKE ∴∠=∠，DCK CKE ∠=∠，AKC AKE CKE BAK DCK ∴∠=∠-∠=∠-∠，过P 作//PF AB ，同理可得，APC BAP DCP ∠=∠-∠，BAP ∠与DCP ∠的角平分线相交于点K ，1111()2222BAK DCK BAP DCP BAP DCP APC ∴∠-∠=∠-∠=∠-∠=∠， 12AKC APC ∴∠=∠．13．如图，已知：EF AC ⊥，垂足为点F ，DM AC ⊥，垂足为点M ，DM 的延长线交AB于点B ，且1C ∠=∠，点N 在AD 上，且23∠=∠，试说明//AB MN ．【解答】证明：EF AC ⊥，DM AC ⊥，90CFE CMD ∴∠=∠=︒（垂直定义）， //EF DM ∴（同位角相等，两直线平行）， 3CDM ∴∠=∠（两直线平行，同位角相等）， 32∠=∠（已知）， 2CDM ∴∠=∠（等量代换）， //MN CD ∴（内错角相等，两直线平行）， AMN C ∴∠=∠（两直线平行，同位角相等）， 1C ∠=∠（已知）， 1AMN ∴∠=∠（等量代换）， //AB MN ∴（内错角相等，两直线平行）．14．（1）如图①，90CEF ∠=︒，点B 在射线EF 上，//AB CD ，若130ABE ∠=︒，求C ∠的度数；（2）如图②，把“90CEF ∠=︒”改为“120CEF ∠=︒”，点B 在射线EF 上，//AB CD ．猜想ABE ∠与C ∠的数量关系，并说明理由．【解答】解：（1）如图①，过E 作//EK AB ，则1180ABE ∠+∠=︒， 118050ABE ∴∠=︒-∠=︒，90CEF ∠=︒，290140∴∠=︒-∠=︒，//AB CD ，//EK AB ，//EK CD ∴，240C ∴∠=∠=︒；（2）60ABE C ∠-∠=︒，理由：如图②，过E 作//EK AB ，则1180ABE ∠+∠=︒， 1180ABE ∴∠=︒-∠，//AB CD ，//EK AB ，//EK CD ∴，2C ∴∠=∠，12120CEF ∠=∠+∠=︒，即180120ABE C ︒-∠+∠=︒， 18012060ABE C ∴∠-∠=︒-︒=︒．15．如图1，已知//AB CD ，30B ∠=︒，120D ∠=︒；（1）若60E ∠=︒，则F ∠= 90︒ ；（2）请探索E ∠与F ∠之间满足的数量关系？说明理由；（3）如图2，已知EP 平分BEF ∠，FG 平分EFD ∠，反向延长FG 交EP 于点P ，求P ∠的度数．【解答】解：（1）如图1，分别过点E ，F 作//EM AB ，//FN AB ， ////EM AB FN ∴，30B BEM ∴∠=∠=︒，MEF EFN ∠=∠，又//AB CD ，//AB FN ，//CD FN ∴，180D DFN ∴∠+∠=︒，又120D ∠=︒，60DFN ∴∠=︒，30BEF MEF ∴∠=∠+︒，60EFD EFN ∠=∠+︒， 60EFD MEF ∴∠=∠+︒3090EFD BEF ∴∠=∠+︒=︒；故答案为：90︒；（2）如图1，分别过点E ，F 作//EM AB ，//FN AB ， ////EM AB FN ∴，30B BEM ∴∠=∠=︒，MEF EFN ∠=∠，又//AB CD ，//AB FN ，//CD FN ∴，180D DFN ∴∠+∠=︒，又120D ∠=︒，60DFN ∴∠=︒，30BEF MEF ∴∠=∠+︒，60EFD EFN ∠=∠+︒， 60EFD MEF ∴∠=∠+︒，30EFD BEF ∴∠=∠+︒；（3）如图2，过点F 作//FH EP ，由（2）知，30EFD BEF ∠=∠+︒，设2BEF x ∠=︒，则(230)EFD x ∠=+︒， EP 平分BEF ∠，GF 平分EFD ∠，12PEF BEF x ∴∠=∠=︒，1(15)2EFG EFD x ∠=∠=+︒， //FH EP ，PEF EFH x ∴∠=∠=︒，P HFG ∠=∠，15HFG EFG EFH ∠=∠-∠=︒，15P ∴∠=︒．16．已知直线12//l l ，直线3l 和直线1l 、2l 交于点C 和D ，点P 是直线3l 上一动点（1）如图1，当点P 在线段CD 上运动时，PAC ∠，APB ∠，PBD ∠之间存在什么数量关系？请你猜想结论并说明理由．（2）当点P 在C 、D 两点的外侧运动时(P 点与点C 、D 不重合，如图2和图3)，上述（1）中的结论是否还成立？若不成立，请直接写出PAC ∠，APB ∠，PBD ∠之间的数量关系，不必写理由．【解答】解：（1）APB PAC PBD ∠=∠+∠，如图1，过点P 作1//PE l ，APE PAC ∴∠=∠，12//l l ，2//PE l ∴，BPE PBD ∴∠=∠，APE BPE PAC PBD ∴∠+∠=∠+∠， APB PAC PBD ∴∠=∠+∠；（2）不成立，如图2:PAC APB PBD ∠=∠+∠，理由：过点P 作1//PE l ，APE PAC ∴∠=∠，12//l l ，2//PE l ∴，BPE PBD ∴∠=∠，APB APE BPE PAC PBD ∠=∠-∠=∠-∠，PAC APB PBD ∴∠=∠+∠；如图3:PBD PAC APB ∠=∠+∠，理由：过点P 作1//PE l ，APE PAC ∴∠=∠，12//l l ，2//PE l ∴，BPE PBD ∴∠=∠，APB BPE APE PBD PAC =∠-∠=∠-∠，PBD PAC APB ∴∠=∠+∠．17．（1）如图（1），已知任意三角形ABC ，过点C 作//DE AB ，求证：DCA A ∠=∠；（2）如图（1），求证：三角形ABC 的三个内角（即A ∠、B ∠、)ACB ∠之和等于180︒；（3）如图（2），求证：AGF AEF F ∠=∠+∠；（4）如图（3），//AB CD ，119CDE ∠=︒，GF 交DEB ∠的平分线EF 于点F ，150AGF ∠=︒，求F ∠．【解答】证明：（1）//DE BC ，DCA A ∴∠=∠；（2）如图1所示，在ABC ∆中，//DE BC ，1B ∴∠=∠，2C ∠=∠（内错角相等）． 12180BCA ∠+∠+∠=︒，180A B C ∴∠+∠+∠=︒．即三角形的内角和为180︒；（3）180AGF FGE ∠+∠=︒，由（2）知，180GEF EG FGE ∠+∠+∠=︒，AGF AEF F ∴∠=∠+∠；（4）//AB CD ，119CDE ∠=︒，119DEB ∴∠=︒，61AED ∠=︒， GF 交DEB ∠的平分线EF 于点F ，59.5DEF ∴∠=︒，120.5AEF ∴∠=︒，150AGF ∠=︒，AGF AEF F ∠=∠+∠，150120.529.5F ∴∠=︒-︒=︒．18．如图，已知直线12//l l ，且3l 和1l ，2l 分别交于A ，B 两点，4l 和1l ，2l 相交于C ，D 两点，点P 在直线AB 上，（1）当点P 在A ，B 两点间运动时，问1∠，2∠，3∠之间的关系是否发生变化？并说明理由；（2）如果点P 在A ，B 两点外侧运动时，试探究ACP ∠，BDP ∠，CPD ∠之间的关系，并说明理由．【解答】证明：（1）如图1，过点P 作1//PQ l ，1//PQ l ，14∴∠=∠（两直线平行，内错角相等）， 1//PQ l ，12//l l （已知），2//PQ l ∴（平行于同一条直线的两直线平行），52∴∠=∠（两直线平行，内错角相等）， 345∠=∠+∠，312∴∠=∠+∠（等量代换）；（2）如图2，过P 点作//PF BD 交CD 于F 点，//AC BD ，//PF AC ∴，ACP CPF ∴∠=∠，BDP DPF ∠=∠，CPD DPF CPF BDP ACP ∴∠=∠-∠=∠-∠；同理，如图③，CPD ACP BDP ∠=∠-∠；。