机械原理大作业一
机械原理大作业——牛头刨床

机械原理大作业——牛头刨床大作业,一,平面连杆机构的运动分析题号: 6班级 : 姓名 : 学号 : 同组者 :成绩 :完成时间 :目录题目、原始数据及要求 ..................................................................... .......................1 一平面连杆机构运动分析方程 ..................................................................... . (1)1.1速度计算公式 ..................................................................... .. (2)1.2加速度计算公式 ..................................................................... ..............2 二程序 ..................................................................... (3)2.1计算程序框图 ..................................................................... (3)2.2计算源程序 ..................................................................... .........................4 三 3.1 (一组数据 Lab =200mm)计算结果 (9)3.2运动线图 ..................................................................... . (10)3.3 体会 ..................................................................... .................................... 12 四 4.1(第二组数据 Lab =150mm)计算结果 . (12)4.2 运动线图 ..................................................................... .. (13)4.3 体会 ..................................................................... .................................... 15 五 5.1(第三组数据 Lab =220mm)计算结果 . (16)5.2 运动线图 ..................................................................... (17)5.3 体会 ..................................................................... ...................................... 21 六参考资料 ..................................................................... (21)题目、原始数据及要求:图所示为一牛头刨床(?级机构)。
机械原理大作业1
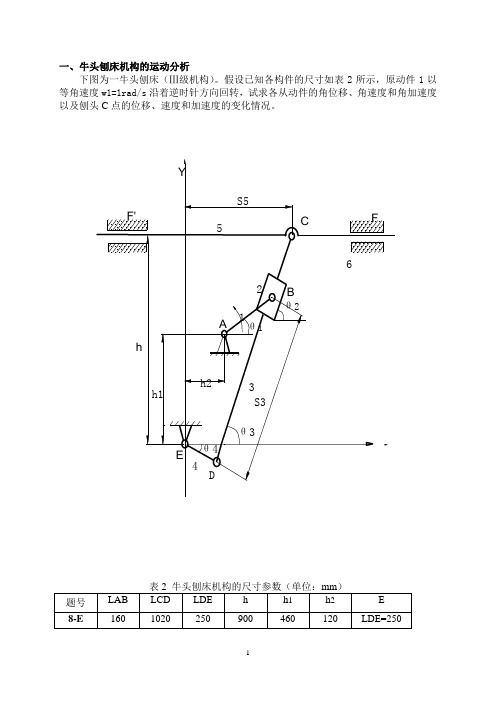
一、牛头刨床机构的运动分析下图为一牛头刨床(Ⅲ级机构)。
假设已知各构件的尺寸如表2所示,原动件1以等角速度w1=1rad/s沿着逆时针方向回转,试求各从动件的角位移、角速度和角加速度以及刨头C点的位移、速度和加速度的变化情况。
二、牛头刨床机构的运动分析方程 1)位置分析建立封闭矢量多边形建立一直角坐标系,并标出各杆矢量及其方位角,其中共有4个未知量3θ(θ2=3θ)、4θ、3S 、5S 。
利用两个封闭图形ABDEFA 和EDCGE ,建立两个封闭矢量方程,由此可得:3125DE AB DE CD l s h h l l l h s →→→→→→→→→⎧+=++⎪⎨⎪+=+⎩(1)把(1)写成投影方程得:433214331143543cos *cos *cos *sin *sin *sin *cos *cos 0*sin *sin DE AB DE AB DE CD DE CD l s h l l s h l l l s l l h θθθθθθθθθθ*+=+⎫⎪+=+⎪⎬+-=⎪⎪+=⎭(2) 由以上各式用型转化法可求得4335s s θθ、、、,滑块2的方位角23θθ=2111*cos *sin b AB b AB x h l y h l θθ=+⎧⎨=+⎩ 44*cos *sin d DE d DE x l y l θθ=⎧⎨=⎩3s =3)*sin *()/*cos *(/c d CD d CD b d c d CD d CD b d s x x l x l x x s y y l y l y y s αα=+=+-⎧⎪⎨=+=+-⎪⎩ 3tan c dc dy y x x θ-=- 5c s x =()ae AE =44()tan *cos d c DE y h y l θθ+-=高斯消去法求解 2)速度分析对(2)求一次导数得:44333331144333331144334433*sin *s '*cos *sin **sin **cos *'*sin *cos **cos **sin **sin *0*cos **cos *0DE AB DE AB DE CD c DE CD l s l l s s l l l v l l θωθθωθωθωθθωθωθωθωθωθω-+-=-⎫⎪++=⎪⎬---=⎪⎪+=⎭(3)矩阵式:3334313334313443cos *sin *sin 0'*sin sin *cos *cos 0*cos 0*sin *sin 100*cos *cos 00DE AB DE AB CD DE CD DE c s l s l s l l l l l l v θθθθθθθθθθωθθ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥ω⎢⎥⎢⎥⎢⎥=ω1⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (4)采用高斯消去法可求解(4)可解得角速度ω2,ω3; 3)加速度分析把(4)对时间求导数得:333433334334434cos *sin *sin 0''sin *cos *cos 00*sin *sin 10*cos *cos 0DE DE CD DE CD DE c s l s s l l l l l a θθθθθθθθαθθ--⎡⎤⎡⎤⎢⎥⎢⎥α⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦33333444433333343443334443344*sin '*sin **cos **cos 0'*cos '*cos **sin **sin 00**cos **cos 00**sin **sin 0DE DE CD DE CD DE c s s l s s s l l l l l v ωθθωθωθωθθωθωθωθωθωωθωθ----⎡⎤⎡⎤⎢⎥⎢⎥--ω⎢⎥⎢⎥=-⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦⎣⎦1111**cos **sin 00AB AB l l ωθωθ-⎡⎤⎢⎥-⎢⎥+ω1⎢⎥⎢⎥⎣⎦(5)采用高斯消去法可求解(5)可解得角加速度α2,α3,α5,α6三、程序流程图四、计算源程序#include<stdio.h>#include<stdlib.h>#include<math.h>/* 定义变量*/const double PI = 3.14159265358979;const int N = 4;const double EPSILON = 0.0001;const int T = 1000;/* 代入已知量*/double Lab=160,Lcd=1020,Lde=250,h=900,h1=460,h2=120,Omega1=1;/* 声明子函数*/void AngleDisplacement(double[12],double);/* 角位移函数*/void AngleVelocity(double[N][N],double[N],double[12],double);/* 角速度函数*/void AngleAcceleration(double[N][N],double[N][N],double[N],double [12]);/* 角加速度函数*/void GaussE(double [N][N],double [N],double [N]);/* 高斯消去法函数*/void ModulusMatrixA(double [12],double [N][N]);/* 矩阵A函数*/void ModulusMatrixB(double [12],double ,double [N]);/* 矩阵B函数*/void MatrixDA(double [12],double [N][N]);/* 矩阵DA函数*/void MatrixDB(double [12],double ,double [N]);/* 矩阵DB函数*//* 主函数*/void main(){int i,j;FILE *fp;double data[36][12];double value[12],a[N][N],da[N][N],b[N],db[N],Phi1;char flag;/* 打开文件*/if((fp = fopen("Data","w")) == NULL){printf("文件打开错误!\n");exit(0);}fprintf(fp,"Lab =%lf \n",Lab);fprintf(fp,"s3\tPhi3\tPhi4\ts5\t");fprintf(fp,"s3'\tOmega3\tOmega4\ts5'\t");fprintf(fp,"s3''\tEpsilon3\tEpsilon4\ts5''");printf("\n\n 牛头刨床机构运动分析程序\n\n\n");printf("\n");printf(" 是否开始计算(Y/N):");scanf("%c",&flag);if(flag =='Y'){/*计算并写入文件*/value[0] = 480;value[1] = 65 * PI / 180;value[2] = 10 * PI / 180;value[3] = 500;for(i = 0;i < 36; i++){Phi1 = i * PI / 18;AngleDisplacement(value,Phi1);ModulusMatrixB(value,Phi1,b);ModulusMatrixA(value,a);AngleVelocity(a,b,value,Phi1);MatrixDA(value,da);MatrixDB(value,Phi1,db);AngleAcceleration(a,da,db,value);for(j = 1;j < 3; j++)value[j] = value[j] * 180 / PI;for(j = 0;j < 12; j++)data[i][j] = value[j];fprintf(fp,"\n");for(j = 0;j < 12; j++)fprintf(fp,"%12.3f\t",data[i][j]);}fclose(fp);/* 输出数据*/printf("\n\n\n计算结果如下:\n");for(i = 0;i < 36; i++){Phi1=i * PI / 18;printf("\n输出Phi1=%d时的求解\n",i*10);printf(" S3 Phi3 Phi5 S5\n");for(j = 0;j < 4; j++)printf("%lf\t",data[i][j]);printf("\n");printf(" S3' Omega3 Omega5S5'\n");for(j = 4;j < 8; j++)printf("%lf\t",data[i][j]);printf("\n");printf(" S3'' Epsilon3 Epsilon5 S5''\n");for(j = 8;j < 12; j++)printf("%lf\t",data[i][j]);printf("\n");}printf("\n程序运行结束,计算结果已写入Date文件中,请打开查看。
机械原理大作业

function [ v_Nx,v_Ny ] =v_crank(s,v_Ax,v_Ay,omiga,theta,phi) v_Nx=v_Ax-s*omiga.*sin(theta+phi); v_Ny=v_Ay+s*omiga.*cos(theta+phi); end
3>加速度计算
function [ a_Nx,a_Ny ]=a_crank(s,a_Ax,a_Ay,alph,omiga,theta,phi) a_Nx=a_Ax-alph.*s.*sin(theta+phi)-omiga.^2.*s.*cos(theta+phi);
。
1) 位置分析
将已知 P1P2 两点的坐标差表示为:
u=x2-x1,v=y2-y1
(1)
杆 l1 及 l2 投影方程式为:
l1cosθ1-l2cosθ2=u
l1sinθ1-l2sinθ2=v
(2)
消去θ1 得:vsinθ2+ucosθ2+c=0
(3)
其中: 解式(3)可得:
t(4) 式中+号和-号分别对应图 2 中 m=+1 和 m=-1 两位置。
由式(2)可得:
(5) 2) 速度分析
对 式 (2) 求 导 一 次 得 :
(6)
其中:
解式(6)可得:
(7)
其中: 3) 加速度分析
对式(6)求导一次得:
(8)
其中:
'.
解式(8)可得:
由上述式子可设计出 RRR 杆组运动分析子程序:
1>位置分析:
function[cx,cy,phi2,phi3]=s_RRR(bx,by,dx,dy,l2,l3,m,phi) d=sqrt((dx-bx).^2+(dy-by).^2); if(d>(l2+l3))|(d<abs(l2-l3))
机械原理课程大作业

机械原理课程大作业基于MATLAB平面连杆机构运动学和动力学分析指导老师:王玉丹目录作业一:平面连杆机构运动学分析第2页作业二:平面连杆机构动力学分析第15页作业一L(AE)=70mm,L(AB)=40mm,L(EF)=60mm,L(DE)=35mm,L(CD)=75m m,L(BC)=50mm,原动件以等角速度W1=10rad/s回转。
试以图解法求在θ1=50°时C点的速度和加速度.对机构进行运动分析,写出C点的位置、速度及加速度方程。
解题过程:令AB=r1, BC=r2, CD=r3, DE=r4,AE=r6,EF=r8, AF=r7,角EAF=θ1。
分析:对机构进行位置分析由封闭形ABCDEA可得:r1+r2=r6+r3+r4 (1)由封闭图形AEFA可得:r7=r6+r8 (2)将(1)(2)两式整理可得:r2-r3-r4=-r1+r6-r8+r7=r6【一】(1)位置方程:【二】速度方程:【三】加速度方程:【四】根据位置方程式编制如下函数:【五】进行数据输入,运行程序进行运算。
根据上面分析的θ1 的极限位置取θ1 的范围为40°-55°并均分成15个元素:输出的P、矩阵的第二列到第四列分别是θ2 、θ3 、4θ4 的值,第一列是AF杆的长度r1’。
【六】第二步根据速度方程式编写如下函数:根据第一步得到的数据进行数据输入,运行程序计算各速度值。
程序如下:程序运行得到q矩阵,第一行到第三行分别是a2、a3、a4 的值,第四行是杆AF上滑块运动的速度,即F点的速度。
【七】第三步编写加速度计算函数:【八】根据第一步和第二步输入数据,运行程序得到各加速度的值:【1】计算C点在θ1 =55°,w1 =10rad/s时的速度,加速度:总结数据绘出各构件的位置、速度和加速度的表格如下:【2】输出图像1)角位置程序及输出的图像:2)F点速度程序及输出的图像:3)角加速度程序及输出的图像:4)F点的加速度程序及输出图像:作业二在图示的正弦机构中,已知:L(AB)=100mm,h1=120mm,h2=80mm, W1=10rad/s(常数),滑块2和构件3的重量分别为,G2 =40 N 和G3 =100 N,质心S2 和S3 的位置如图所示,加于构件3上的生产阻力Fr=400 N,构件1的重力和惯性力略去不计。
哈工大机械原理大作业一连杆运动分析(02)

哈⼯⼤机械原理⼤作业⼀连杆运动分析(02)⼀.设计题⽬⼆. 结构分析与基本杆组划分1.机构的结构分析机构各构件都在同⼀平⾯内运动,活动构件数n=3 P L=4 P H=0则机构的⾃由度为: F = 3n -2P L –P H = 3×3-2×4 = 12.基本杆组划分(1)去除虚约束和局部⾃由度本机构中⽆虚约束或局部⾃由度,此步骤跳过。
(2)拆杆组。
从远离原动件(即杆1)进⾏拆分,就可以得到由杆2,3组成的RRRⅡ级杆组和Ⅰ级机构杆1。
如下图:(3)确定机构的级别由(2)知,机构为Ⅱ级机构。
三. 运动分析数学模型以A为原点建⽴坐标系,如图:原动件AB的转⾓:φ1=0--2π运动副A的位置坐标:x A=0 y A=0 运动副D的位置坐标:x D=d y D=0 则运动副B的位置坐标:x B = acosφ1 y B = asinφ1其中:t=0:0.001:2*pi;a=60;b=90;c=120;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd)曲柄a=50,55,60,65红蓝绿黄b=90,c=120,d=100 t=0:0.001:2*pi; a=50;b=90;c=120;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'r'); hold on;grid on;t=0:0.001:2*pi;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'b'); hold on;t=0:0.001:2*pi;a=60;b=90;c=120;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'g'); hold on;t=0:0.001:2*pi;a=65;b=90;c=120;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'y');a=50,55,60,65红蓝绿黄2.摇杆c=105,115,125,135红蓝绿黄a=50,b=90,d=100 t=0:0.001:2*pi; a=50;b=90;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'r'); hold on;grid on;t=0:0.001:2*pi;a=50;b=90;c=115;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'b');t=0:0.001:2*pi;a=50;b=90;c=125;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'g'); hold on;t=0:0.001:2*pi;a=50;b=90;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'y');c=105,115,125,135红蓝绿黄3.连杆b=80,90,100,110红蓝绿黄a=50,c=120,d=100 t=0:0.001:2*pi; a=50;b=80;c=120;d=100;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'r'); hold on;grid on;t=0:0.001:2*pi;a=50;b=90;c=120;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'b'); hold on;t=0:0.001:2*pi;a=50;b=100;c=120;d=100;xa=0;ya=0;xd=d;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'g'); hold on;t=0:0.001:2*pi;a=50;b=110;c=120;d=100;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'y');b=80,90,100,110红蓝绿黄4.机架d=85,95,105,115 红蓝绿黄a=50,b=90,c=120 t=0:0.001:2*pi; a=50;b=90;c=120;d=85;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'r'); hold on;grid on;t=0:0.001:2*pi;a=50;b=90;c=120;d=95;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'b'); hold on;t=0:0.001:2*pi;d=105;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'g'); hold on;t=0:0.001:2*pi;a=50;b=90;c=120;d=115;xa=0;ya=0;xd=d;yd=0;xb=a.*cos(t);yb=a.*sin(t);m=xd-xb;n=yd-yb;lbd=(m.^2+n.^2).^(1/2);a0=2*b.*(xd-xb);b0=2*b.*(yd-yb);c0=b.^2+lbd.^2-c.^2;dd=2*atan((b0+(a0.^2+b0.^2-c0.^2).^(1/2))./(a0+c0)); plot(dd,'y');d=85,95,105,115 红蓝绿黄。
机械原理大作业-连杆机构

设计内容
结论
1. 机构结构分析 1)计算机构自由度,确定机构是否有确定运动。
机构自度 F=1
本机构中,n= 5 , pL= 7
,pH = 0
则有:F=3n-2PL –PH= 3*5-2*7=1
是否有确定
机构确定运动判断: 因 F= 1 ,原动件个数= 1 ,可知: 自由度等于原动件数,机构有确定 的运动。
➢ 求解速度 vB 、角速度 2 : 矢量方程:
大小 ? √ ? 方向 ⊥BD ⊥OA ⊥AB
逆时针方向 ➢ 求解速度 vC 、2 杆质心 S2 的速度 vs2 :
vB =1.57m/s 2 =0.36rad/s, 逆时针方向
vC =1.56m/s vs2 =1.53m/s
-3-
➢ 求解速度 vE 、角速度 4 : 矢量方程:
动态静力学参数:m2=20 kg , JS2 = 1.1 kg m2 ,m5=50 kg
表 2 阻抗力参数表
班级序号 1
2
3
4
5
6
7
8
9
10
Fr /N
500 600 700
800
900
1000 1100 1200 1300 1400
-1-
机械原理模块训练一
二、 训练要求
通过对干草压缩机六杆机构进行结构分析、运动分析和力分析,对该设备的运动性能做出 定量的计算,为新设备的设计与评价提供依据。 机构结构分析:了解机构组成,学会对机构工作原理简图表达,判断机构的结构组成是否可行。 机构运动分析:已知原动件运动参数情况下,学会求解机构输出端和机构中关键点的运动参数。 机构动态静力分析:当已知工作阻力时,需要给机器配置动力,通过平衡力求解可以获得;当 机器安装时需要知道支座的反力,可通过动态静力分析获得。
机械原理大作业1(六杆机构)
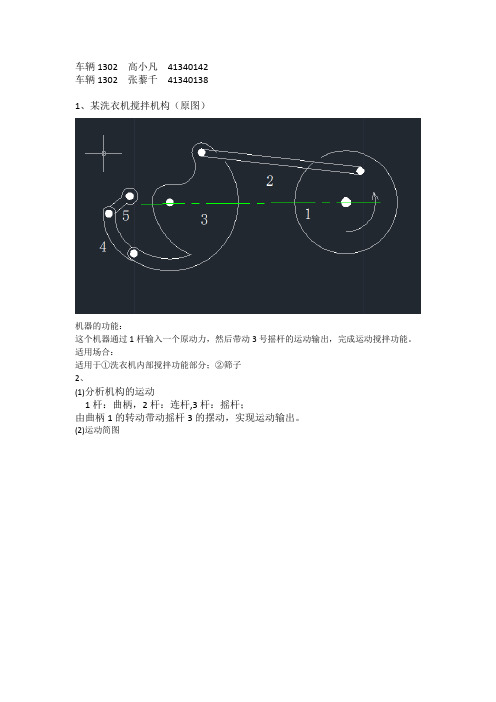
车辆1302 高小凡41340142车辆1302 张藜千413401381、某洗衣机搅拌机构(原图)机器的功能:这个机器通过1杆输入一个原动力,然后带动3号摇杆的运动输出,完成运动搅拌功能。
适用场合:适用于①洗衣机内部搅拌功能部分;②筛子2、(1)分析机构的运动1杆:曲柄,2杆:连杆,3杆:摇杆;由曲柄1的转动带动摇杆3的摆动,实现运动输出。
(2)运动简图(3)如图,该六杆机构只有一个原动件----1杆(4)自由度F=3(n-1)-2P5=3*5-2*7=1上述六杆机构的运动形式可简化为如图四杆机构的运动形式,4,5杆的运动作为摇杆3的输出机构。
3、大致测绘出构件尺寸4、确定机构所含杆组的数目和级别(拆杆组),并判断机构的级别;依次拆下4-5/2-3两个II级杆组及原动件1(II级杆组),所以该机构为II级杆组5、用图解法求出最小传动角值:由下图可知,在极限位置2时,压力角最大为70°,则最小传动角为42°6、分析该机构有无急回特性和死点位置;有急回,无死点;180+1809k 1.11180-1809θθ+===>-7、用瞬心法对机构进行运动分析上图中标出了该机构的简化四杆机构的所有瞬心P 12 P 13 P 16 P 23 P 26 P 36其中,绝对瞬心有:P 16 P 36 P 26 相对瞬心有:P 12P 13 P 23速度分析:若1的角速度为w1,则V(P12)=l1*w1V(P23)= [V(P12)/|P12P13|]*|P13P23 | w3= V(P23)/l3w6= V(P23)/| P23P26 |(1)角速度比mv=w6/w2=l1sinv/l3sinuv=0, mv=0,w6=0,此时构件1、2共线,机构处于极限位置;(2)mv=w6/w2=OP13/CP13 (瞬心P13能够用来确定速度比)上图为该机构(六杆机构)全部瞬心(15个)绝对瞬心:P16, P26,P36,P46,P56相对瞬心:P15,P25,P35,P45P14,P24,P34,P13,P23P12中间密集部分的的放大图如下图:8、用杆组法(或其他解析法)对机构进行运动分析(写出数学模型和程序框图);已知该机构的尺寸为:两个固定铰链点a,d,g的坐标分别为(0,0)(420,0)(-80,-35),曲柄原动件|ab|=100mm,连杆2长为300mm,摇杆3长150mm,杆4长100mm,杆5长50mm.经分析,该机构由一个曲柄原动件和两个RRR二级杆组组成的二级机构用杆组法搭建该机构的步奏如下:1)添加曲柄原动件ab;2)添加RRR二级杆组(2-3),杆组的两个动铰链点分别为已有铰链点b和固定铰链点d; 3)在连杆cd上添加铰链点e;4)添加RRR二级杆组(4-5),杆组的两个动铰链点分别为已有铰链点e和固定铰链点g; 5)该机构搭建完成,利用该程序可自动求出任意给定铰链点或构件的位置、速度、和加速度。
机械原理大作业一 33题

机械原理大作业(一)作业名称:机械原理设计题目:连杆机构运动分析院系:机电工程学院班级: xxxxxx设计者: xxx学号: xxxxxx指导教师: xxxxx设计时间: 6.25---7.1哈尔滨工业大学机械设计一,运动分析题目二,建立以点G为原点的固定平面直角坐标系G-x,y三,对机构进行结构分析该机构由原动件AB(Ι级组),EFG(RRRⅡ级杆组),EHK(RRRⅡ级杆组),ECD(RRRⅡ级杆组)组成。
四,各基本杆组的运动运动分析数学模型(1)原动件AB(Ⅰ级组)已知原动件AB的转角ψ1=0~2π原动件AB的角速度ω1=10rad/s原动件AB的角加速度α1=0运动副A的位置坐标 XA=0 YA=0A点与机架相连,即该点速度和加速度均为0。
运动副A的速度 VxA=0 VyA=0运动副A的加速度 aXA=0 aYA=0原动件AB长度 lAB=200mm可求出运动副B的位置坐标 XA=XA+lABcosψ1 YB=YA+lABsinψ1 运动副B的速度 vXB=vXA-ω1lABsinψ1 vYB=vYA+ω1lABcosψ1运动副B的加速度aXB=aXA-ω12lABcosψ1-α1lABsinψ1aYB=aYA-ω12lABsinψ1+α1lABcosψ1(2)ECD (RRR Ⅱ级杆组)由(1)知B 点位置坐标、速度、加速度运动副D 点位置坐标 XD=XA+lADcos ψ2 YD=YA+lADsin ψ2D 点与机架相连,即该点速度和加速度均为0。
运动副D 的速度 v X D=0 v Y D=0运动副D 的加速度 a X D=0 a Y D=0杆BC 长 lBC=800mm杆CD 长 lCD=448mm可求得BC 杆相对于X 轴正方向转角Ψ3=2arctan ()00/()0202020(C A C B A B +-++)CD 杆相对于x 轴正方向转角Ψ4=arctan ((YC-YD )/(XC-XD ))其中,A0=2lBC(XD-XB)B0=2lBC(YD-YB)C0=l 2BC+l 2BD-l 2CDl 2BD=(XD-XB)2+(YD-YB)2求导可得BC 杆ω3、α3和CD 杆ω4、α4最后求导得vXC 、vYC 以及aXC 、aYCC 的轨迹即是E 的轨迹(3)EFG (RRR Ⅱ级杆组)运动副G点位置坐标 X G=XA+lAGcosψ5 YG=YA+lAGsinψ5G点与机架相连,即该点速度和加速度均为0。
机械原理大作业1.

Harbin Institute of Technology机械原理大作业一课程名称:机械原理设计题目:连杆机构运动分析院系:机电工程学院班级:1108101设计者:张舜晨学号:1110810117指导教师:陈明设计时间:2013年7月哈尔滨工业大学一、运动分析题目如图1-21 所示机构,已知机构各构件的尺寸为AB=120mm,h=70mm,BC=170mm,CD=350mm,CF=300mm,BE=400mm,FG=340mm,xD=348mm,yD=138mm,构件1 的角速度为ω1=10rad/s,试求构件5 上点E 及构件7 上点G 的位移、速度和加速度,并对计算结果进行分析。
二、机构的结构分析及基本杆组划分1.机构的结构分析机构各构件都在同一平面内运动,活动构件数n=7,=10,=0则机构的自由度为:F=3×n-2×-1×=3×7-2×10-0=12.基本杆组划分(1)去除虚约束和局部自由度本机构中无虚约束或局部自由度,此步骤跳过。
(2)拆杆组。
从远离原动件(即杆1)进行拆分,就可以得到由杆2,3 组成的RRRⅡ级杆组,4,5 组成的RRPⅡ级杆组,以及6,7 组成的RRPⅡ级杆组,最后剩下Ⅰ级机构杆1。
(3)确定机构的级别由(2)知,机构为Ⅱ级机构三、各基本杆组的运动分析数学模型为了程序的简便,以下分别对所涉及的杆组的一般形式进行分析,以方便建立函数。
①RRR Ⅱ级杆组的运动分析如下图所示,当已知RRR杆组中两杆长、和两外副B、D的位置和运动时,求内副C的位置及运动以及两杆的角位置、角运动。
1) 位置方程其中φi:式中,为保证机构的正确装配,必须同时满足l BD≤l i+l j和l BD≥|l i-l j|。
表达式中的“+”表示运动副B、C、D为顺时针排列(如图中实线位置);“-”表示B、C、D为逆时针排列(如图中虚线位置)。
以上两组式子联立,求得(xc,yc)后,可求得φj:2) 速度方程将式(3-16)对时间求导,可得两杆角速度方程为式中,内运动副C的速度方程为3) 加速度方程两杆角加速度为式中,内副C的加速度为②RRP Ⅱ级杆组运动分析RRP Ⅱ级杆组是由两个构件和两个回转副及一个外移动副组成的。
机械原理大作业1

2 2 2
2al
l (1 M d d
0
)
tan M [co t
0
a sin
]
凸轮与 杆转动同向时式中 取 ,反之,则取 ,将 取绝对值 后代入压力角计算公式。由上式计算压力角,有时为正, 有时为负,正值表示轮廓接触点法线 位于此时摆杆速 度方向线的顺 一侧,否则为逆 一侧。
通过查阅相关资料后,得出结论:摆杆从动盘形凸 轮压力角 与 是非独立的关系,增大基圆半径 不一定 能减小压力角 ,有可能反而增大。所以在确定基圆 半径 ,中心距 时,先拟定摆杆 长某一定值1。基圆 r a * * r 0 半径系数 ,中心距系数a 。 l l * * 所以在此取 r 0 .7 , a 1 .4 ,由上式得 0 2 8 .0 9 8 。以 f ( ) tan ( )为函数作出凸轮转过一个周期函数 图像,如图;容易得出凸轮角位移在 处分别取得最大值。
推送机工作要求
方案一
凸轮机构:如图4-所示的凸轮机构,其结构简单,易于设计与制造,凸轮 以等角速度回转,它的轮廓驱使从动件,可使推杆实现任意的运动规律, 但行程较小。
方案二
凸轮-齿条机构:图4-2所示的凸轮-齿条机构可以将摆 动从动件的摆动转化为齿轮齿条机的往复运动。当 扇形齿轮的分度圆半径大于摆杆长度时,可以加大 齿条的位移量。对于因齿轮具有良好的耐磨性和稳 定性,因而用此方案进行物品推送可以得到较好的 效果。但是此机构的缺点是中间的扇形齿比较难加 工。
m ax 1 0 .3 9 9 5 7 tan [3 5 ], m ax 2 0 .5 7 3 8 9 7 tan [7 0 ]
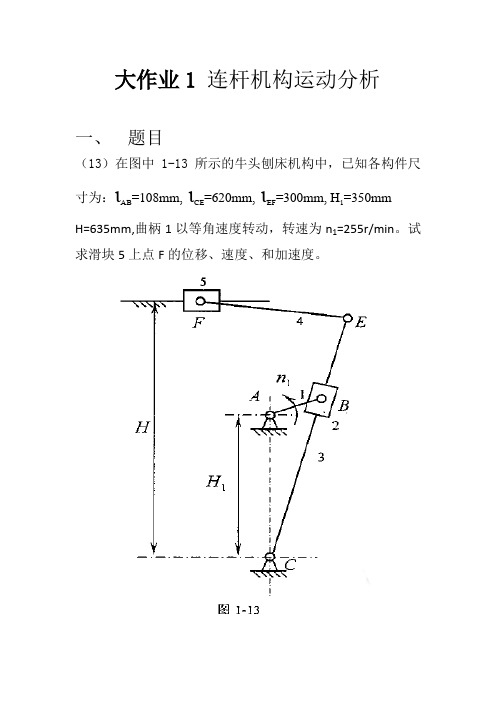
机械原理大作业1连杆机构27题
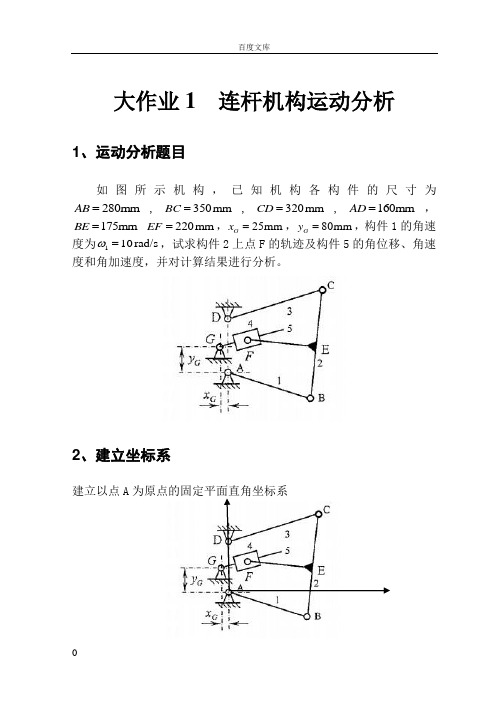
大作业1 连杆机构运动分析1、运动分析题目如图所示机构,已知机构各构件的尺寸为280mm AB =,350mm BC =,320mm CD =,160mm AD =,175mm BE = 220mm EF =,25mm G x =,80mm G y =,构件1的角速度为110rad/s ω=,试求构件2上点F 的轨迹及构件5的角位移、角速度和角加速度,并对计算结果进行分析。
2、建立坐标系建立以点A 为原点的固定平面直角坐标系图13、对机构进行结构分析该机构由I级杆组RR(原动件1)、II级杆组RRR(杆2、杆3)和II级杆组RPR(滑块4及杆5)组成。
I级杆组RR,如图2所示;II级杆组RRR,如图3所示;II级杆组RPR,如图4所示。
图2图 3图 44、各基本杆组运动分析的数学模型(1)同一构件上点的运动分析:图 5如图5所示的构件AB,,已知杆AB 的角速度=10/rad s ω,AB 杆长i l =280mm,可求得B 点的位置B x 、B y ,速度xB v 、yB v ,加速度xB a 、yB a 。
=cos =280cos B i x l ϕϕ;=sin =280sin B i y l ϕϕ;==-sin =-BxB i B dx v l y dt ωϕω; ==cos =;B yB i B dyv l x dt ωϕω222B 2==-cos =-BxB i d x a l x dt ωϕω;2222==-sin =-ByB i B d y a l y dtωϕω。
(2)RRRII 级杆组的运动分析:图 6如图6所示是由三个回转副和两个构件组成的II 级组。
已知两杆的杆长2l 、3l 和两个外运动副B 、D 的位置(B x 、B y 、D x 、D y )、速度(xB yB xD yD v v v v 、、、)和加速度(xB yB xD yD a a a a 、、、)。
求内运动副C 的位置(C C x 、y )、速度(xC yC v 、v )、加速度(xC yC a 、a )以及两杆的角位置(23ϕϕ、)、角速度(23ϕϕ、)和角加速度(23ϕϕ、)。
机械原理大作业1-连杆机构运动分析-30题

机械原理作业设计说明书课程名称:机械原理设计题目:连杆机构运动分析院系:班级:设计者:学号:设计时间:连杆机构运动分析题目:如图1-1所示机构,已知机构各构件的尺寸为AB=100mm ,BC=2.73AB ,CD=1.36AB ,CG=2.32AB ,BG=4.9AB ,AF=2.36AB ,AD=2.87AB ,DF=2AB ,GE=1.45AB ,EF=2.82AB ,GM=1.36AB ,MK=1.91AB ,KD=0.54AB ,KF=2.18AB ,HF=3.1AB ,DH=3.63AB ,o 135=β,构件1的角速度为s /rad 101=ω。
试求构件2上G 点的轨迹及构件4、构件6和构件8的角位移、角速度和角加速度,并对计算结果进行分析。
HGMECFKDBAXY图1 解:1、建立坐标系建立以点H 为原点的固定平面直角坐标系D-x ,y ,如图1所示。
1.对机构进行结构分析该机构由I级杆组RR(原动件AB)、II级杆组RRR(杆2、9)、II级杆组RRR(杆5、6)、II级杆组RRR(杆7、8)和II级杆组RPR (杆4、滑块3)组成。
I级杆组RR(原动件AB)如图2所示,II 级杆组RRR(杆2、9)如图3所示,II级杆组RRR(杆5、6)如图5所示,II级杆组RRR(杆7、8)如图6所示,II级杆组RPR(杆4、滑块3)如图7所示。
图2 I级杆组RR 图3 II级杆组RRR图5 II级杆组RRR 图6 II级杆组RRR图7 II 级杆组RPR2.各基本杆组运动分析1. I 级杆组RR (原动件AB )如图2所示,已知原动件杆1的转角 ︒︒=360-0ϕ pi =δ角速度 s rad /101==ωϕ角加速度 0==εϕ运动副A 的位置坐标为 mm y mm x A A 5.41,3.542==速度为 0,0==A A y x加速度为 0,0==A A y x原动件杆1的长度 mm l AB 100=所以,运动副B 的位置、速度和加速度分子如下: 1 位置分析)cos(δϕ++=i AB A B l x x )sin(δϕ++=i AB A B l y y2 速度分析)sin(δϕ+⨯⨯-=i AB xA xB l w v v )sin(δϕ+⨯⨯+=i AB yA yB l w v v 3 加速度分析)sin()cos(2δϕδϕ+-+-=i AB i AB xA xB el l w a a )()sin(2δϕδϕ+++-=i AB i AB yA yB coa el l w a a 求出运动副B 的yB xB yB xB B B a a v v y x ,,,,,各个运动参数。
机械原理大作业一
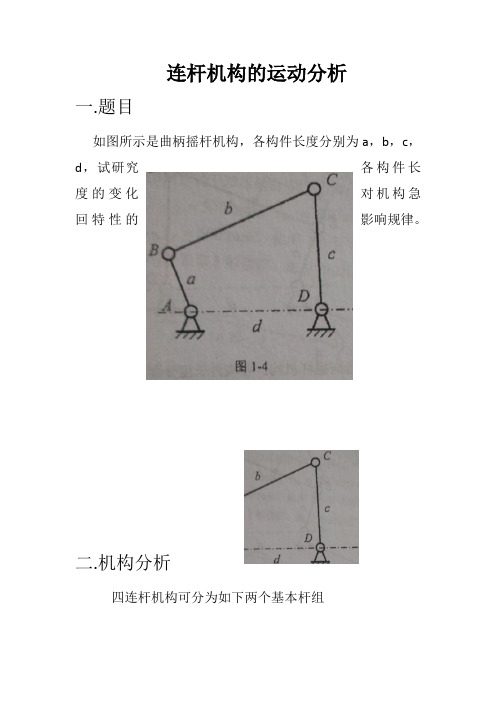
连杆机构的运动分析一.题目如图所示是曲柄摇杆机构,各构件长度分别为a,b,c,d,试研究各构件长度的变化对机构急回特性的影响规律。
二.机构分析四连杆机构可分为如下两个基本杆组Ⅰ级杆组RRRⅡ级杆组AB为曲柄,做周转运动;CD为摇杆,做摆动运动;BC为连杆;AB,CD均为连架杆,AB为主动件。
三.建立数学模型θ为极位夹角,φ为最大摆角必须满足条件为:1.a≤b,a≤c,a≤d(a为最短杆);2.L min+L max≤其他两杆之和。
下面分析杆长和极位夹角的关系:在△AC2B中,=;在△AC1B中,=。
θ=-K=最后分以下四种情况讨论:1.机架长度d变化令a=5,b=30,c=29d由6开始变化至54,步长为1输出杆长a,b,c,d和K。
2.连杆长度b变化令a=5,b=29,d=30b由6开始变化至54,步长为1 输出杆长a,b,c,d和K。
3.摇杆长度c变化令a=5,b=29,d=30c由6开始变化至54,步长为1 输出杆长a,b,c,d和K。
4.曲柄长度a变化令b=29,c=28,d=30a由5开始变化至27,步长为1 输出杆长a,b,c,d和K。
四.MATLAB计算编程a=5;b=30;c=29;d=6:1:54;m=(d.^2-216)./(50.*d);n=(384+d.^2)./(70.*d);p=acos(m);q=acos(n);w=p-q;o=(w.*180)/3.14;K=(180+o)./(180-o);fprintf('%.6f\n',K);plot(d,K,'b')xlabel('机架长度d变化时');ylabel('极位夹角/度');tilte('极位夹角变化图');———————————————————————————————————————a=5;d=30;c=29;b=6:1:54;m=((b-5).^2+59)./(60.*(b-5));n=(59+(b+5).^2)./(60.*(b+5));p=acos(m);q=acos(n);w=p-q;o=(w.*180)/3.14;K=(180+o)./(180-o);fprintf('%.6f\n',K);plot(b,K,'b')xlabel('连杆长度b变化时');ylabel('极位夹角/度');tilte('极位夹角变化图');———————————————————————————————————————a=5;d=30;b=29;c=6:1:54;m=(1476-c.^2)./(1440);n=(2056-c.^2)./(2040);p=acos(m);q=acos(n);w=p-q;o=(w.*180)/3.14;K=(180+o)./(180-o);fprintf('%.6f\n',K);plot(c,K,'b')xlabel('摇杆长度c变化时');ylabel('极位夹角/度');tilte('极位夹角变化图');c=28;d=30;b=29;a=5:1:27;m=(116+(29-a).^2)./(60*(29-a) );n=(116+(29+a).^2)./(60*(29+a) );p=acos(m);q=acos(n);w=p-q;o=(w.*180)/3.14;K=(180+o)./(180-o);fprintf('%.6f\n',K);plot(a,K,'b')xlabel('曲柄长度a变化时');ylabel('极位夹角/度');tilte('极位夹角变化图');五.计算结果机架长度变化连杆长度变化摇杆长度变化曲柄长度变化六.计算结果分析1.当机架d增大,其余三杆不变时,K一直减小,减小速度先快后慢。
哈工大机械原理大作业1

1、运动分析题目
如图所示的六杆机构的位移,速度和加速度。
2、建立坐标系
建立以点 A 为原点的固定平面直角系
3、对机构进行结构分析
哈尔滨工业大学机械原理课程设计
该机构由 I 级杆组 RR(原动件 1)、II 级杆组 RRR(杆 2、杆 3)和 II 级杆组 PRP(滑块 4 及滑块 5)组成。I 级杆组 RR,如图 2 所示;II 级杆组 RRR,如图 2 所示;II 级杆组 PRP,如图 3 所示。
}
哈尔滨工业大学机械原理课程设计
//C 点坐标值函数 void Ccorner(double *a,double *b,double c)//&Xc,&Yc,o {
double i,j,x,y,z;//中间参数
i=(pow(Lcd,2)-pow(Lbc,2)+pow(Lab*sin(c),2)-pow(Yd,2)+pow(Lab*cos(c),2)-pow((Xd+Xf), 2))/(2*(Lab*cos(c)-Xd-Xf)); j=(Lab*sin(c)-Yd)/(Lab*cos(c)-Xf-Xd); x=pow(j,2)+1; y=2*(Xf+Xd)*j-2*i*j-2*Yd; z=pow(i,2)-2*(Xf+Xd)*i+pow((Xf+Xd),2)+pow(Yd,2)-pow(Lcd,2); *b=(-y+sqrt(pow(y,2)-4*x*z))/(2*x); *a=i-j*(*b); }
21
21.537112 11.635926
22
23.572877 11.689145
23
机械原理大作业-齿轮

机械原理大作业-齿轮三、齿轮传动设计一、设计题目如图所示一个机械传动系统,运动由电动机1输入,经过机械传动系统变速后由圆锥齿轮16输出三种不同的转速。
根据表中的传动系统原始参数设计该传动系统。
1.机构运动简图1.电动机 2,4.皮带轮 3.皮带 5,6,7,8,9,10,11,12,13,14.圆柱齿轮15,16.圆锥齿轮2.机械传动系统原始参数二、传动比的分配计算电动机的转速1450/min n r ,输出转速1n =50r/min ,2n =45r/min ,3n =40r/min,带传动的最大传动比max2.5p i ,滑移齿轮的传动的最大传动比max4v i ,定轴齿轮传动的最大传动比max4d i 。
根据系统的原始参数,系统的总传动比为1i =1n n=1450/50=29.00 2i =2n n =1450/45=32.222 3i =3n n=1450/40=36.25 传动系统的总传动比由带传动、滑移齿轮传动和定轴齿轮传动三部分实现。
设带传动的传动比为max2.5p i ,滑移齿轮的传动比为1v i 、2v i 和3v i ,定轴齿轮传动的传动比为f i 则总传动比为 1max 1p v f i i i i 2max 2p v f i i i i 3max 3p v f i i i i令3max4v v i i则可得定轴齿轮传动部分的传动比为f i =maxmax 3*v p i i i =4*5.225.36=3.625 滑移齿轮传动的传动比为1v i =fp i i i *max 1=9.2*5.229=42v i =fp i i i *max 2=9.2*5.222.32=4.444定轴齿轮传动由3对齿轮传动组成,则每对齿轮的传动比为d i =3f i =3625.3=1.536三、齿轮齿数的确定根据滑移齿轮变速传动系统中对齿轮齿数的要求,可大致选择齿轮5、6、7、8、9和10、为角度变位齿轮,其齿数:52,19,41,17,50,231098765======z z z z z z 它们的齿顶高系数1ah ,顶隙系数0.25c ,分度圆压力角=20,实际中心距取mm a 73=。
哈工大机械原理大作业(连杆机构)
建立坐标系:以C为原点,水平方向为X轴,CA所在直线为Y轴建立直角坐标系(如图4)。
取曲柄1水平且位于A点右侧为初始时刻,设曲柄1角速度为w,由题意知w= =8.5π rad/s………………(1)
设曲柄1转角为θ,则B点坐标:
xB=ιABcosθ=ιABcoswt
yB=H1+ιABsinθ=H1+ιABsinwt………………(2)
form=1:length(t)-1
ddxF(m)=(dxF(m+1)-dxF(m))/0.0001;
end
ddxF(length(t))=ddxF(length(t)-1);
figure
plot(t,ddxF)
title('¼ÓËÙ¶ÈͼÏñ');
xlabel('t /s'),ylabel('v /(m/s^2)');
输出图像:
xE(m)=yE(m)/k(m);
xF(m)=xE(m)-(-H^2+lEF^2-yE(m)^2+2*yE(m)*H)^(1/2)+0.1142;
end
form=1:length(t)-1
dxF(m)=(xF(m+1)-xF(m))/0.0001;
end
dxF(length(t))=dxF(length(t)-1);
∵ιEF+ιCE>H且ιCE<H
∴E点始终在F点的右下方
∴xF<xE,所以x2舍去,只取xF=x1……………(8)
∴点F坐标为(xF,H)
当t=0时,可得F点初始位置坐标,不妨设为(xo,H)。
则F点位移(通过计算,t=0时,得xo=-0.1142)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连杆机构的运动分析
一.题目
如图所示是曲柄摇杆机构,各构件长度分别为a,b,c,d,试研究各构件长度的变化对机构急回特性的影响规律。
二.机构分析
四连杆机构可分为如下两个基本杆组
Ⅰ级杆组RRRⅡ级杆组
AB为曲柄,做周转运动;CD为摇杆,做摆动运动;
BC为连杆;AB,CD均为连架杆,AB为主动件。
三.建立数学模型
θ为极位夹角,φ为最大摆角
必须满足条件为:≤b,a≤c,a≤d(a为最短杆);
+L max≤其他两杆之和。
下面分析杆长和极位夹角的关系:
在△AC2B中,=;
在△AC1B中,=。
θ=-
K=
最后分以下四种情况讨论:
1.机架长度d变化
令a=5,b=30,c=29
d由6开始变化至54,步长为1 输出杆长a,b,c,d和K。
2.连杆长度b变化
令a=5,b=29,d=30
b由6开始变化至54,步长为1 输出杆长a,b,c,d和K。
3.摇杆长度c变化
令a=5,b=29,d=30
c由6开始变化至54,步长为1 输出杆长a,b,c,d和K。
4.曲柄长度a变化
令b=29,c=28,d=30
a由5开始变化至27,步长为1 输出杆长a,b,c,d和K。
四.MATLAB计算编程
a=5;b=30;c=29;
d=6:1:54;
m=(d.^2-216)./(50.*d);
n=(384+d.^2)./(70.*d);
p=acos(m);
q=acos(n);
w=p-q;
o=(w.*180)/;
K=(180+o)./(180-o);
fprintf('%.6f\n',K);
plot(d,K,'b')
xlabel('机架长度d变化时');
ylabel('极位夹角/度');
tilte('极位夹角变化图');
———————————————————————————————————————a=5;d=30;c=29;
b=6:1:54;
m=((b-5).^2+59)./(60.*(b-5));
n=(59+(b+5).^2)./(60.*(b+5));
p=acos(m);
q=acos(n);
w=p-q;
o=(w.*180)/;
K=(180+o)./(180-o);
fprintf('%.6f\n',K);
plot(b,K,'b')
xlabel('连杆长度b变化时');
ylabel('极位夹角/度');
tilte('极位夹角变化图');
———————————————————————————————————————a=5;d=30;b=29;
c=6:1:54;
m=(1476-c.^2)./(1440);
n=(2056-c.^2)./(2040);
p=acos(m);
q=acos(n);
w=p-q;
o=(w.*180)/;
K=(180+o)./(180-o);
fprintf('%.6f\n',K);
plot(c,K,'b')
xlabel('摇杆长度c变化时');
ylabel('极位夹角/度');
tilte('极位夹角变化图');
c=28;d=30;b=29;
a=5:1:27;
m=(116+(29-a).^2)./(60*(29-a)
);
n=(116+(29+a).^2)./(60*(29+a)
);
p=acos(m);
q=acos(n);
w=p-q;
o=(w.*180)/;
K=(180+o)./(180-o);
fprintf('%.6f\n',K);
plot(a,K,'b')
xlabel('曲柄长度a变化时');
ylabel('极位夹角/度');
tilte('极位夹角变化图');
五.计算结果
机架长度变化
a b c d K
5 30 29 6
5 30 29 7
5 30 29 8
5 30 29 9
5 30 29 10
5 30 29 11
5 30 29 12
连杆长度变化
摇杆长度变化
曲柄长度变化
六.计算结果分析
1.当机架d增大,其余三杆不变时,K一直减小,减小速度先快后慢。
说明机架距离越大,摇杆急回运动越不明显,但机架过长时,K减小不明显,但仍然减小。
2.当连杆b增大,其余三杆不变时,K一直增大,增大速度先快后慢再快。
说明连杆越长,摇杆急回运动越明显,连杆长度达到一定程度时,K增大不明显,趋于不变,再增长时,急回增大速度加快。
3.当摇杆c增大,其余三杆不变时,K一直增大,增大速度先慢后快。
说明摇杆越长,摇杆急回运动越明显,摇杆过长时,K增大速度骤增。
4.当曲柄a增大,其余三杆不变时,K减小,变化速度是先快后慢。
说明摇杆越长,摇杆急回运动速度开始增加,当曲柄长度超过某个值后,急回运动速度骤减。
