机械原理大作业凸轮机构设计
机械原理大作业凸轮设计

机械原理大作业凸轮设计本文档旨在介绍《机械原理大作业凸轮设计》的背景和目的。
凸轮设计在机械工程中具有重要性和挑战,因此本文档将探讨凸轮设计的原理和方法,并提供相应的示例和解释。
本文档包括以下内容:凸轮设计的背景和意义凸轮设计的原理和方法凸轮设计的实例和案例分析结论和建议每一部分将详细阐述相关的知识和技术,旨在帮助读者理解和应用凸轮设计的原理及方法。
请继续阅读以下各章节,以便全面了解凸轮设计的重要性和实践应用。
凸轮的定义和作用凸轮是一种机械元件,具有特殊形状的轮缘。
它主要用于传递运动和改变运动方向。
凸轮通常与其他机械部件,如凸轮轴和凸轮销,一起使用,以实现特定的工作任务。
凸轮的重要性和应用凸轮在机械原理中具有重要的作用。
它被广泛应用于不同的机械系统中。
首先,凸轮在传输运动方面非常重要。
通过凸轮的特殊形状,它可以转换来自动力源的旋转运动为直线或曲线的机械运动。
这使得凸轮能够将动力传递给其他部件,实现机械装置的工作。
其次,凸轮还能够改变运动方向。
通过将凸轮与其他机械部件连接,如齿轮或连杆,可以改变运动的方向和速度。
这使得凸轮在不同机械系统中能够实现不同的功能,例如提供机械装置的正向和反向运动。
最后,凸轮还可以用于执行特定的运动模式。
通过调整凸轮的形状和轮缘的位置,可以实现不同的运动曲线和运动模式。
这为机械系统的设计师提供了更大的灵活性,以满足特定的工作要求。
总之,凸轮在机械原理中起着关键的作用。
它通过传输运动和改变运动方向,为不同机械系统的功能实现提供支持。
凸轮的设计和应用需要充分考虑机械装置的工作需求和运动特性,以确保凸轮的有效性和可靠性。
本文介绍凸轮设计的基本原则,包括凸轮外形的选择和凸轮参数的确定。
我们将讨论凸轮的轮廓曲线以及与其相关的几何特征。
此外,我们还将介绍凸轮的运动学和动力学分析,以及对凸轮进行性能评估和优化的方法。
本文以一个具体案例为例,详细介绍凸轮设计的过程。
通过该案例研究,读者可以了解凸轮设计的步骤和方法,以及可能遇到的问题和解决方案。
机械原理大作业二凸轮(完整版) 20

Harbin Institute of Technology机械原理大作业二作业名称:凸轮机构设计设计题目: 20 院系:机电工程学院班级:设计者:学号:指导教师:**设计时间: 2014年5月哈尔滨工业大学一、设计题目如图1所示直动从动件盘形凸轮机构,其原始参数见表1。
表1 凸轮机构参数升程/h mm 升程运动角 0/ϕ 升程运动规律 升程许用压力角[]/α 回程运动角 0/ϕ'回程运动规律 回城许用压力角[]/α'远休止角/s ϕ 近休止角/s ϕ' 110 120 正弦加速度 3590 正弦加速度 65 50 100二、运动方程式及运动线图本实验假设凸轮逆时针旋转。
1.确定凸轮机构推杆升程、回程运动方程(ϕ为凸轮转角,ω为凸轮角速度)。
推程(余弦加速度)(203ϕπ≤≤): 图1远休止段:当21738πϕπ≤≤时,110s h==,0v=,0a=回程(正弦加速度)(171389πϕπ≤≤):近休止段:当1329πϕπ≤≤时,0s=,0v=,0a=2.绘制推杆位移、速度、加速度线图图2三、绘制凸轮机构的ds s d ϕ-线图,并由此确定凸轮的基圆半径和偏距图3图4如图3、图4所示,在ds d ϕ轴正侧(对应于推程),以tan(90[])α-为斜率做ds s d ϕ-曲线的切线1L ,在ds d ϕ轴负侧(对应于回程),以tan(90[])α'+为斜率做ds s d ϕ-曲线的切线2L ,再过点(0,0)O 做斜率为tan(90[])α+的直线3L ,则直线1L 、2L 、3L 与s 轴的夹角分别为[]α、[]α'、[]α。
显然,1L 、2L 、3L 三条直线下方的公共部分即为满足推程压力角不超过[]α和回程压力角不超过[]α'时,凸轮回转中心的可取区域。
记直线1L 与2L 的交点为12P ,直线1L 与3L 的交点为13P ,则最小基圆半径013r OP ==45.79mm ,对应的偏距e =26.27mm (点13P 到s 轴的距离),2200s r e =-=37.51mm 。
机械原理大作业凸轮结构设计

机械原理大作业(二) 作业名称:机械原理设计题目:凸轮机构设计院系: 机电工程学院班级:设计者:学号:指导教师:丁刚陈明设计时间:哈尔滨工业大学机械设计1、设计题目如图所示直动从动件盘形凸轮机构,根据其原始参数设计该凸轮。
表一:凸轮机构原始参数序号升程(mm) 升程运动角(º)升程运动规律升程许用压力角(º)回程运动角(º)回程运动规律回程许用压力角(º)远休止角(º)近休止角(º)12 80 150正弦加速度30 100 正弦加速度60 60 502、凸轮推杆运动规律(1)推杆升程运动方程S=h[φ/Φ0-sin(2πφ/Φ0)]V=hω1/Φ0[1-cos(2πφ/Φ0)]a=2πhω12sin(2πφ/Φ0)/Φ02式中:h=150,Φ0=5π/6,0<=φ<=Φ0,ω1=1(为方便计算)(2)推杆回程运动方程S=h[1-T/Φ1+sin(2πT/Φ1)/2π]V= -hω1/Φ1[1-cos(2πT/Φ1)]a=-2πhω12sin(2πT/Φ1)/Φ12式中:h=150,Φ1=5π/9,7π/6<=φ<=31π/18,T=φ-7π/63、运动线图及凸轮线图运动线图:用Matlab编程所得源程序如下:t=0:pi/500:2*pi;w1=1;h=150;leng=length(t);for m=1:leng;if t(m)<=5*pi/6S(m) = h*(t(m)/(5*pi/6)-sin(2*pi*t(m)/(5*pi/6))/(2*pi));v(m)=h*w1*(1-cos(2*pi*t(m)/(5*pi/6)))/(5*pi/6);a(m)=2*h*w1*w1*sin(2*pi*t(m)/(5*pi/6))/((5*pi/6)*(5*pi/6));% 求退程位移,速度,加速度elseift(m)<=7*pi/6S(m)=h;v(m)=0;a(m)=0;% 求远休止位移,速度,加速度elseif t(m)<=31*pi/18T(m)=t(m)-21*pi/18;S(m)=h*(1-T(m)/(5*pi/9)+sin(2*pi*T(m)/(5*pi/9))/(2*pi));v(m)=-h/(5*pi/9)*(1-cos(2*pi*T(m)/(5*pi/9)));a(m)=-2*pi*h/(5*pi/9)^2*sin(2*pi*T(m)/(5*pi/9));%求回程位移,速度,加速度elseS(m)=0;v(m)=0;a(m)=0;% 求近休止位移,速度,加速度endend推杆位移图推杆速度图推杆加速度图4、确定凸轮基圆半径与偏距在凸轮机构得ds/dφ-s线图里再作斜直线Dt dt与升程得[ds/dφ-s(φ)]曲线相切并使与纵坐标夹角为升程许用压力角[α],则D t d t线得右下方为选择凸轮轴心得许用区。
机械原理大作业 凸轮设计(1)(1)

目录一、题目及原始数据 (2)二、推杆运动规律及凸轮廓线方程 (4)三、计算程序 (5)四、计算结果及分析 (12)五、凸轮机构图 (12)六、体会及建议 (15)七、参考书 (15)一、题目及原始数据试用计算机辅助设计完成偏置直动滚子推杆盘形凸轮机构的设计表1 凸轮结构的推杆运动规律直动推杆组题号推程运动规律回程运动规律10-A 等加速等减速运动五次多项式运动表2 凸轮结构的推杆在近休、推程、远休及回程段的凸轮转角题号近休凸轮转角推程凸轮转角远休凸轮转角回程凸轮转角10-A 0°~60°60°~180°180°~270°270°~360°表3 偏置直动滚子推杆盘形凸轮机构的已知参数题号初选的基圆半径r0/mm 偏距e/mm滚子半径R r/mm推杆行程h/mm许用压力角许用最小曲率半径[ρamin][α1] [α2]10-A 15 +5 10 28 30 70 0.3r r(1)打印出原始数据;(2)打印出理论轮廓和实际轮廓的坐标值;(3)打印出推程和回程的最大压力角,以及出现最大压力角时凸轮的相应转角;(4)打印出凸轮实际轮廓曲线的最小曲率半径,以及相应的凸轮转角;(5)打印最后所确定的凸轮的基圆半径。
计算点数:100πδ0δ二、推杆运动规律及凸轮廓线方程1、推杆运动规律(1)近休阶段:0°≤δ< 60°=s0/=δd ds 0/22=δd s d(2)推程阶段:60°≤δ< 180° 等加速段运动方程 s=2h(3)远休阶段:210°≤δ< 280°30==h s 0/=δd ds/22=δd s d(4)回程阶段:280°≤δ< 360° 2、凸轮廓线方程(1)理论廓线方程2200er s -=δδcos sin )(0e s s x ++= δδsin cos )(0e s s y -+=(2)工作廓线方程 x′=θcos rrx -y′=θsin rry -三、计算程序#include<stdio.h> #include<math.h> void main(){//freopen("xxx.txt","w",stdout); doubler0,dr,rr,h,e,q1,q2,q3,q4,a,a11,a22,Q,pi,pa,paa,QQ,A1,A2,B1,B2,C1,C2; /*定义变量*/double xz[90],yz[90],sz[90],x1z[90],y1z[90],Q1,Q2;doubles0,s,x,y,y1,x1,dx,dxx,dy,dyy,ds,dss,sino,coso,p;int N,i,j;r0=22;e=14;h=35;rr=18;q1=30;q2=180;q3=70;q4=80;a11=35 ;a22=65;dr=1;pi=3.141592653;pa=6.3; /*给已知量赋值*/ N=90;A1=0;B1=0;C1=1000;for(; ;){Q=0;C1=1000;QQ=180/pi;r0=r0+dr;s0=sqrt(r0*r0-e*e);for(i=1,j=0;i<=N;i++,j++){if(Q<30){ /*近休阶段*/s=0;ds=0;dss=0;a=atan(e/sqrt(r0*r0-e*e)); /*求压力角*/if(a>a11/QQ){break;}else{if(a>A1)A1=a;A2=Q;}}elseif(Q>=30&&Q<210){ /*推程阶段*/ Q1=Q-30;s=h*(1-cos(pi*Q1/q2))/2;ds=pi*h*sin(pi*Q1/q2)/(2*q2);dss=pi*pi*h*cos(pi*Q1/q2)/(2*q2*q2);a=atan(fabs(ds-e)/(sqrt(r0*r0-e*e)+s));if(a>a11/QQ){break;}else{ /*远休阶段*/if(a>A1)A1=a;A2=Q;}}else if(Q>=210&&Q<280){s=35;ds=0;dss=0;a=atan(fabs(ds-e)/(sqrt(r0*r0-e*e)+s));if(a>a22/QQ){break;}else{if(a>B1)B1=a;B2=Q;}}elseif(Q>=280&&Q<360){ /*回程阶段*/Q2=Q-280;s=h*(1-(Q2/q4)+sin(2*pi*Q2/q4)/(2*pi));ds=h*(cos(2*pi*Q2/q4)-1)/q4; dss=-2*pi*h*sin(2*pi*Q2/q4)/(q4*q4);a=atan(fabs(ds-e)/(sqrt(r0*r0-e*e)+s));if(a>a22/QQ){break;}else{if(a>B1)B1=a;B2=Q;}}dx=(ds-e)*sin(Q/QQ)+(s0+s)*cos(Q/QQ);dy=(ds-e)*cos(Q/QQ)-(s0+s)*sin(Q/QQ);dxx=dss*sin(Q/QQ)+(ds-e)*cos(Q/QQ)+ds*cos(Q/QQ)-(s0+s)* sin(Q/QQ);dyy=dss*cos(Q/QQ)-(ds-e)*sin(Q/QQ)-ds*sin(Q/QQ)-(s0+s)* cos(Q/QQ);sino=dx/(sqrt(dx*dx+dy*dy));coso=-dy/(sqrt(dx*dx+dy*dy));x=(s0+s)*sin(Q/QQ)+e*cos(Q/QQ);y=(s0+s)*cos(Q/QQ)-e*sin(Q/QQ);x1=x-rr*coso;y1=y-rr*sino;sz[j]=s;yz[j]=y;xz[j]=x;x1z[j]=x1;y1z[j]=y1;p=pow(dx*dx+dy*dy,1.5)/(dx*dyy-dy*dxx); /*求理论轮廓曲率半径*/if(p<0){paa=(fabs(p)-rr);if(paa<pa){break;}else{if(paa<C1)C1=paa;C2=Q;}}Q=Q+4;}if(i==91){break;}}for(j=0;j<90;j++){printf("第%d组数据 ",j+1); /*输出数据*/printf("s=%f ",sz[j]);printf("x=%f ,y=%f ;",xz[j],yz[j]);printf("x1=%f ,y1=%f\n",x1z[j],y1z[j]);}printf("r0=%f\n",r0);printf("推程最大压力角(弧度)=%f,相应凸轮转角=%f\n",A1,A2-4);printf("回程最大压力角(弧度)=%f,相应凸轮转角=%f\n",B1,B2-4);printf("最小曲率半径=%f,相应凸轮转角=%f\n",C1,C2-4);}四、计算结果及分析五、凸轮机构图Matlab绘图x=[14.000000 15.410715 16.746350 18.000399 19.166752 20.239726 21.214094 22.085109 22.854177 23.556980 24.209136 24.819841 25.396590 25.944936 26.468300 26.967836 27.442352 27.888294 28.299787 28.668732 28.984970 29.236490 29.409692 29.489697 29.460687 29.306288 29.009969 28.555457 27.927166 27.110613 26.092836 24.862782 23.411678 21.733355 19.824539 17.685091 15.318189 12.730454 9.932014 6.936504 3.760995 0.425869-3.045381 -6.626403 -10.288302 -14.000000 -17.728645 -21.440063-25.099229 -28.670776 -32.119500 -35.410884 -38.511609 -41.395702-44.073115 -46.535808 -48.771783 -50.770147 -52.521164 -54.016303-55.248280 -56.211093 -56.900051 -57.311798 -57.444328 -57.296994-56.870516 -56.166970 -55.189784 -53.943719 -52.434845 -50.642721-48.444586 -45.721768 -42.406762 -38.494686 -34.046072 -29.180734-24.063677 -18.885153 -13.837781 -9.093986 -4.786983 -0.997898 2.249248 4.984188 7.279382 9.233165 10.949732 14.000000];y=[20.712315 19.685270 18.562321 17.348938 16.051032 14.674928 13.227328 11.715287 10.155210 8.605179 7.071191 5.547906 4.028334 2.5041510.966043 -0.595920 -2.191898 -3.831884 -5.525313 -7.280673 -9.105140 -11.004237 -12.981525 -15.038337 -17.173559 -19.383462 -21.661588-23.998702 -26.382794 -28.799157 -31.230513 -33.657210 -36.057462-38.407658 -40.682702 -42.856404 -44.901901 -46.792104 -48.500165-49.999950 -51.266511 -52.276556 -53.008891 -53.444842 -53.568639-53.367760 -52.833222 -51.959822 -50.746310 -49.195504 -47.314339-45.113841 -42.609040 -39.827853 -36.843216 -33.679083 -30.350869-26.874788 -23.267776 -19.547405 -15.731802 -11.839555 -7.889627-3.901261 0.106111 4.112966 8.099784 12.047140 15.935803 19.746829 23.461650 27.055239 30.461071 33.572280 36.259587 38.390725 39.851417 40.564743 40.505890 39.709940 38.271358 36.335020 34.079893 31.697536 29.368412 27.239317 25.405150 23.897652 22.682758 20.712315];x1=[3.920000 4.315000 4.688978 5.040112 5.366690 5.667123 5.939946 6.183831 6.407565 6.656245 6.939957 7.262933 7.627623 8.034738 8.483268 8.970511 9.492073 10.041892 10.612251 11.193822 11.775737 12.345689 12.890081 13.394214 13.842522 14.218843 14.506733 14.689800 14.752070 14.678354 14.454625 14.068384 13.509012 12.768088 11.839684 10.720610 9.410609 7.912503 6.232279 4.379110 2.365319 0.206274 -2.079773-4.471913 -6.946854 -9.479256 -12.042104 -14.607122 -17.145218-19.626947 -22.022998 -24.304672 -26.444369 -28.424511 -30.262966-31.953983 -33.489324 -34.861508 -36.063850 -37.090493 -37.936434-38.597553 -39.070629 -39.353357 -39.444359 -39.343192 -39.050348-38.567256 -37.896268 -37.040653 -36.004579 -34.769401 -33.220147-31.245851 -28.787411 -25.848578 -22.498389 -18.864538 -15.118342-11.453008 -8.057698 -5.090569 -2.654686 -0.781762 0.570733 1.505255 2.154694 2.647497 3.079986 3.920000];y1=[5.799448 5.511876 5.197450 4.857703 4.494289 4.108980 3.703652 3.280280 2.840231 2.411219 1.994237 1.578653 1.153648 0.708380 0.232122 -0.285610 -0.854923 -1.485412 -2.185991 -2.964711 -3.828560 -4.783237 -5.832928 -6.980083 -8.225211 -9.566690 -11.000625 -12.520742 -14.118339 -15.782286 -17.499088 -19.253010 -21.026255 -22.799200 -24.550682-26.258332 -27.898945 -29.448882 -30.884491 -32.182550 -33.320701-34.277896 -35.034810 -35.574247 -35.881505 -35.944704 -35.755071-35.307167 -34.599059 -33.632433 -32.412639 -30.948670 -29.253078-27.347942 -25.298530 -23.125866 -20.840535 -18.453672 -15.976904-13.422298 -10.802300 -8.129674 -5.417441 -2.678815 0.072862 2.824184 5.561746 8.272213 10.942378 13.559233 16.110028 18.567736 20.858131 22.874250 24.490421 25.581511 26.043773 25.814282 24.885999 23.315941 21.224639 18.785871 16.206636 13.698834 11.446845 9.578710 8.150077 7.145668 6.494271 5.799448];plot(x,y,x1,y1,'r')六、体会及建议这次作业让我们收获良多,尽管编出程序后的不断调试henkun难,消耗了大量时间来纠正错误。
机械原理大作业凸轮机构设计
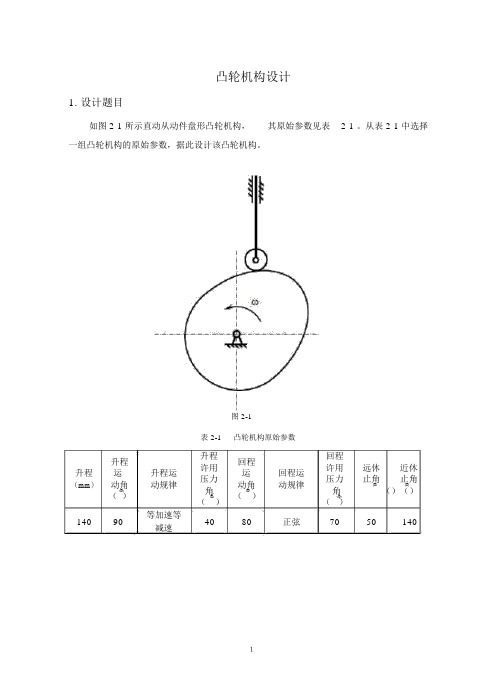
凸轮机构设计1.设计题目如图 2-1 所示直动从动件盘形凸轮机构,其原始参数见表2-1 。
从表 2-1 中选择一组凸轮机构的原始参数,据此设计该凸轮机构。
图 2-1表 2-1凸轮机构原始参数升程升程回程回程许用许用远休近休升程运升程运运回程运压力压力止角止角(mm)动角动规律动角动规律角角()()()()()()14090等加速等4080正弦7050140减速2.凸轮机构的设计要求(1)确定凸轮推杆升程、回程运动方程,并绘制推杆位移、速度、加速度线图;【1】确定推杆的升程回程运动方程对于不同运动规律的凸轮结构,其上升与下降的方式不一,但遵循同样的运动顺序:上升、远休止点恒定、下降、近休止点恒定。
因此设计它仅需确定这四个阶段的角度与位置即可。
推程阶段:1120s22回程阶段:v22401222402a1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2s1120(2)21402v2240 1 (2)222402a1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2(97)sin(97)s140[1422]23151[1cos(97)]v22(0)4()422835 12 sin(97)711a222⋯⋯⋯⋯⋯ ()99【 2】绘制推杆位移、速度、加速度线图①位移图像程序:i1=(0:0.01:(1/4)*pi);s1=280.*(((2/pi).*i1).^2);i2=((1/4)*pi:0.01:(1/2)*pi);s2=140-1120.*(((pi/2)-i2).^2)/((pi).^2);i3=((1/2)*pi:0.01:(7/9)*pi);s3=140;i4=((7/9)*pi:0.01:(11/9)*pi);s4=140.*(1-((9.*i4-7*pi)/(4*pi))+sin(((9.*i4)-(7*pi))./2)/(2*pi)); i5=((11/9)*pi:0.01:2*pi);s5=0;plot(i1,s1,'b',i2,s2,'b',i3,s3,'b',i4,s4,'b',i5,s5,'b')位移图像②速度图像程序令1 1 则可以得到速度图像的程序i1=(0:0.01:(1/4)*pi);v1=(2240.*i1)/((pi).^2);i2=((1/4)*pi:0.01:(1/2)*pi);v2=(2240.*((pi/2)-i2))/((pi).^2);i3=((1/2)*pi:0.01:(7/9)*pi);v3=0;i4=((7/9)*pi:0.01:(11/9)*pi);v4=-315.*(1-cos(((9.*i4)-(7*pi))./2))/(pi);i5=((11/9)*pi:0.01:2*pi);v5=0;plot(i1,v1,'b',i2,v2,'b',i3,v3,'b',i4,v4,'b',i5,v5,'b')速度图像③加速度程序及其图像a1=2240/((pi).^2);i2=((1/4)*pi:0.01:(1/2)*pi);a2=-2240/((pi).^2);i3=((1/2)*pi:0.01:(7/9)*pi);a3=0;i4=((7/9)*pi:0.01:(11/9)*pi);a4=-2835.*sin(((9*i4)-(7*pi))/2)/(2*pi);i5=((11/9)*pi:0.01:2*pi);a5=0;plot(i1,a1,'b',i2,a2,'b',i3,a3,'b',i4,a4,'b',i5,a5,'b')加速度图像【3】绘制凸轮机构的dss 线图 di1=(0:0.01:(1/4)*pi);s1=(1120.*(i1.^2))/(pi.^2);i2=((1/4)*pi:0.01:(1/2)*pi);ds2=1120/pi-(2240.*i2)/(pi.^2);s2=140-1120.*(((pi/2)-i2).^2)/((pi).^2);i3=((1/2)*pi:0.01:(7/9)*pi);ds3=i3-i3;s3=140+i3-i3;i4=((7/9)*pi:0.01:(11/9)*pi);ds4=(315/pi).*(-1+cos(((9.*i4)-(7.*pi))/2));s4=140.*(1-((9.*i4-7*pi)/(4*pi))+sin(((9.*i4)-(7*pi))./2)/(2*pi)); i5=((11/9)*pi:0.01:2*pi);s5=i5-i5;ds5=i5-i5;plot(ds1,s1,ds2,s2,ds3,s3,ds4,s4,ds5,s5,)凸轮机构的【4】确定凸轮基圆半径和偏距d ssd线图由图像可知道凸轮的轴心应该在公共区以下凸轮偏心距取 e 3mm ,s0200mm【 5】凸轮的理论轮廓i1=(0:0.01:(1/4)*pi);x1=(200+280.*(((2/pi).*i1).^2)).*cos(i1)-3.*sin(i1);y1=(200+280.*(((2/pi).*i1).^2)).*sin(i1)+3.*cos(i1);i2=((1/4)*pi:0.01:(1/2)*pi);x2=(200+140-1120.*(((pi/2)-i2).^2)/((pi).^2)).*cos(i2)-3.*sin(i2); y2=(200+140-1120.*(((pi/2)-i2).^2)/((pi).^2)).*sin(i2)+3.*cos(i2); i3=((1/2)*pi:0.01:(7/9)*pi);x3=340.*cos(i3)-3.*sin(i3);y3=340.*sin(i3)+3.*cos(i3);i4=((7/9)*pi:0.01:(11/9)*pi);x4=(200+140.*(1-((9.*i4-7*pi)/(4*pi))+sin(((9.*i4)-(7*pi))./2)/(2*pi))). *cos(i4)-3.*sin(i4);y4=(200+140.*(1-((9.*i4-7*pi)/(4*pi))+sin(((9.*i4)-(7*pi))./2)/(2*pi))). *sin(i4)+3.*cos(i4);i5=((11/9)*pi:0.01:2*pi);x5=200.*cos(i5)-3.*sin(i5);y5=200.*sin(i5)+3.*cos(i5);plot(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5)凸轮的理论轮廓【 6】确定滚子半径的程序v=[];syms i1 i2 i3 i4 i5s0 = 200;e = 20;s1=280*(((2/pi)*i1).^2);t1 = (s1 + s0)*cos(i1)-e*sin(i1);y1 = (s0 + s1)*sin(i1) - e*cos(i1);ti1=diff(t1,i1);tii1=diff(t1,i1,2);yi1=diff(y1,i1);yii1=diff(y1,i1,2);for ii1=(0:0.01:(1/4)*pi);k1=subs(abs((ti1*yii1-tii1*yi1)/(ti1^2+yi1^2)^1.5),{i1},{ii1});v=[v,1/k1];ends2=140-1120.*(((pi/2)-i2).^2)/((pi).^2);t2= (s2 + s0)*cos(i2)-e*sin(i2);y2 = (s0 + s2)*sin(i2) - e*cos(i2);ti2=diff(t2,i2);tii2=diff(t2,i2,2);yi2=diff(y2,i2);yii2=diff(y2,i2,2);for ii2=((1/4)*pi:0.01:(1/2)*pi);k2=subs(abs((ti2*yii2-tii2*yi2)/(ti2^2+yi2^2)^1.5),{i2},{ii2});v=[v,1/k2];ends3=140;t3 = (s3 + s0)*cos(i3)-e*sin(i3);y3 = (s0 + s3)*sin(i3) - e*cos(i3);ti3=diff(t3,i3);tii3=diff(t3,i3,2);yi3=diff(y3,i3);yii3=diff(y3,i3,2);for ii3=((1/2)*pi:0.01:(7/9)*pi);k3=subs(abs((ti3*yii3-tii3*yi3)/(ti3^2+yi3^2)^1.5),{i3},{ii3});v=[v,1/k3];ends4=140.*(1-((9.*i4-7*pi)/(4*pi))+sin(((9.*i4)-(7*pi))./2)/(2*pi)); t4 = (s4 + s0)*cos(i4)-e*sin(i4);y4 = (s0 + s4)*sin(i4) - e*cos(i4);ti4=diff(t4,i4);tii4=diff(t4,i4,2);yi4=diff(y4,i4);yii4=diff(y4,i4,2);for ii4=((7/9)*pi:0.01:(11/9)*pi);k4=subs(abs((ti4*yii4-tii4*yi4)/(ti4^2+yi4^2)^1.5),{i4},{ii4});v=[v,1/k4];Ends5=0;t5 = (s5 + s0)*cos(i5)-e*sin(i5);y4 = (s0 + s5)*sin(i5) - e*cos(i5);ti5=diff(t5,i5);tii5=diff(t5,i5,2);yi5=diff(y5,i5);yii5=diff(y5,i5,2);for ii5=((11/9)*pi:0.01:2*pi);k5=subs(abs((ti5*yii5-tii5*yi5)/(ti5^2+yi5^2)^1.5),{i5},{ii5});v=[v,1/k5];endmin(v)确定之后发现滚子半径是r 2mm【 7】确定凸轮的实际轮廓凸轮的实际轮廓x1=(200+280.*(((2/pi).*i1).^2)).*cos(i1)-3.*sin(i1);y1=(200+280.*(((2/pi).*i1).^2)).*sin(i1)+3.*cos(i1);i2=((1/4)*pi:0.01:(1/2)*pi);x2=(200+140-1120.*(((pi/2)-i2).^2)/((pi).^2)).*cos(i2)-3.*sin(i2); y2=(200+140-1120.*(((pi/2)-i2).^2)/((pi).^2)).*sin(i2)+3.*cos(i2);i3=((1/2)*pi:0.01:(7/9)*pi);x3=340.*cos(i3)-3.*sin(i3);y3=340.*sin(i3)+3.*cos(i3);i4=((7/9)*pi:0.01:(11/9)*pi);x4=(200+140.*(1-((9.*i4-7*pi)/(4*pi))+sin(((9.*i4)-(7*pi))./2)/(2*pi))).*cos(i4)-3.*sin(i4);y4=(200+140.*(1-((9.*i4-7*pi)/(4*pi))+sin(((9.*i4)-(7*pi))./2)/(2*pi))).*sin(i4)+3.*cos(i4);i5=((11/9)*pi:0.01:2*pi);x5=200.*cos(i5)-3.*sin(i5);y5=200.*sin(i5)+3.*cos(i5);dx1=(2240.*i1.*cos(i1))/((pi).^2)+(200+1120.*((i1).^2)/((pi).^2)).*sin(i 1)-3.*cos(i1);dy1=(2240.*i1.*sin(i1))-(200+1120.*((i1).^2)/((pi).^2)).*cos(i1)-3.*sin( i1);dx2=(-(1120.*(2.*i2-pi).*cos(i2)/((pi).^2)))-(340-1120.*((2.*i2-pi).^2)) .*sin(i2)-3.*cos(i2);dy2=-(1120.*(2.*i2-pi).*sin(i2)/((pi).^2))+(340-1120.*((2.*i2-pi).^2)).* cos(i2)-3.*sin(i2);dx3=-340.*sin(i3)-3.*cos(i3);dy3=340.*cos(i3)-3.*sin(i3);dx4=((-315/pi)+630.*cos((9.*i4-7.*pi)/2)).*cos(i4)-(200+140.*(1-((9.*i4-7*pi)/(4*pi))+sin(((9.*i4)-(7*pi))./2)/(2*pi))).*sin(i4)-3.*cos(i4);dy4=((-315/pi)+630.*cos((9.*i4-7.*pi)/2)).*sin(i4)+(200+140.*(1-((9.*i4-7*pi)/(4*pi))+sin(((9.*i4)-(7*pi))./2)/(2*pi))).*cos(i4)-3.*sin(i4);dx5=-200.*sin(i5)-3.*cos(i5);dy5=200.*cos(i5)-3.*sin(i5);X1=x1+3.*dy1/sqrt(dy1.^2+dx1.^2);Y1=y1-3.*dx1/sqrt(dy1.^2+dx1.^2);X2=x2+3.*dy2/sqrt(dy2.^2+dx2.^2);Y2=y2-3.*dx2/sqrt(dy2.^2+dx2.^2);X3=x3+3.*dy3/sqrt(dy3.^2+dx3.^2);Y3=y3-3.*dx3/sqrt(dy3.^2+dx3.^2);X4=x4+3.*dy4/sqrt(dy4.^2+dx4.^2);Y4=y4-3.*dx4/sqrt(dy4.^2+dx4.^2);X5=x5+3.*dy5/sqrt(dy5.^2+dx5.^2);Y5=y5-3.*dx5/sqrt(dy5.^2+dx5.^2);plot(X1,Y1,X2,Y2,X3,Y3,X4,Y4,X5,Y5)。
机械原理凸轮大作业程序、图与设计说明说

一、 设计题目:27题如图所示直动从动件盘形凸轮机构,其原始参数见下表,据此设计该凸轮机构。
二、 凸轮推杆升程、回程运动方程和位移、速度、加速度线图对于不同运动规律的凸轮结构,其上升与下降的方式不一,但遵循同样的运动顺序:上升、远休止点恒定、下降、近休止点恒定。
因此设计它仅需确定这四个阶段的角度与位置即可。
1、对于凸轮的升程的运动方程如下所示:12[sin()]2s h ϕπϕφπφ=-12[1cos()]h v ωπϕφφ=- 21222sin()h a πωπϕφφ=升程 (mm ) 升程运动角(°) 升程运动规律 升程许用压力角(°) 回程运动角(°) 回程运动规律 回程许用压力角(°) 远休止角(°) 近休止角(°) 130 150正弦加速度30100余弦加速度6030802、对于凸轮的回程运动方程如下所示:01{1cos[()]}2s h s πϕφφφ=+-+1011sin[()]s h v πωπϕφφφφ=--+2210121cos[()]2s h a πωπϕφφφφ=--+3、推杆位移线图(横坐标凸轮转过角度,单位:°;纵坐标推杆位移,单位:mm )4、推杆速度线图(横坐标图轮转过角度,单位°;纵坐标为推杆速度,单位mm/s)5、推杆加速度线图(横坐标为凸轮转过角度,单位:°;纵坐标为推杆加速度,单位:mm/s^2)三、 凸轮机构的ds sd ϕ-线图,凸轮的基圆半径和偏距1、根据ds s d ϕ-线图得无偏心距时最小基圆半径0116r =。
具体作图过程见下页。
2、查阅相关文献,知直动从动件盘形凸轮最小基圆半径求解公式为:00022(arctan)tan tan h r πππφαφα=-经计算得:0116.7835r =四、 滚子半径的确定及凸轮理论廓线和实际廓线的绘制查阅有关文献,得知在有偏置机构的凸轮最小基圆半径求解公式为 最小基圆半径:02cos p r r α=其对应的偏心距:0tan 2r e α=计算得:67.55p r =;33.78e =。
机械原理第9章凸轮机构及其设计

第二十一页,编辑于星期日:十四点 分。
②等减速推程段:
当δ =δ0/2 时,s = h /2,h/2 = C0+C1δ0/2+C2δ02/4 当δ = δ0 时,s = h ,v = 0,h = C0+C1δ0+C2δ02
0 = ωC1+2ωC2δ ,C1=-2 C2δ0 C0=-h,C1= 4h/δ0, C2=-2h/δ02
如图所示,选取Oxy坐标系,B0 点为凸轮廓线起始点。当凸轮转过δ 角度时,推杆位移为s。此时滚子中 心B点的坐标为
x (s0 s) sin e cos
y
(s0
s) cos
A7
C8 A6 C7
w
A8
-w
A9
C9 B8 B9 B7 r0
C10
B12100 ° B0
O
B1 a B2
C1 L C2φ1φ0
A10 A0
φ
Φ
o
2
1
2 3 456
180º
7 8 9 10
60º 120º
δ
(1)作出角位移线图;
(2)作初始位置;
A5
C6
B6 B1580°B4
C4
C5
φ3
φC23
A1
↓对心直动平底推杆盘形凸 轮机构
↑偏置直动尖端推杆盘形凸轮机 构
第十一页,编辑于星期日:十四点 分。
↑尖端摆动凸轮机构
↓平底摆动凸轮机构
↑滚子摆动凸轮机构
第十二页,编辑于星期日:十四点 分。
(4)按凸轮与从动件保持接触的方式分
力封闭型凸轮机构
利用推杆的重力、弹簧力或其他外力使推杆与凸轮保持接
触的
此外,还要考虑机构的冲击性能。
机械原理大作业2_凸轮机构设计

机械原理⼤作业2_凸轮机构设计1. 设计题⽬第32题:升程/mm 升程运动⾓/。
升程运动规律升程许⽤压⼒⾓/。
回程运动⾓/。
回程运动规律回城许⽤压⼒⾓/。
远休⽌⾓/。
近休⽌⾓/。
150120余弦加速度 35 90 正弦加速度65 55 952.运动⽅程式及运动线图本实验假设凸轮逆时针旋转。
(1)确定凸轮机构推杆升程、回程运动⽅程,并绘制推杆位移、速度、加速度线图。
(设定⾓速度为ω= 2π/3.)升程:( 0 <φ< 2π/3)由公式:;v =πh ω/(2)sin(); a = /(2) cos().由此得:s = 75*(1 - cos(1.5*φ));v=0.225/2 * ω * sin(1.5 *φ); a = 0.675/4 *φ^2 .* cos(1.5*φ);回程:( 35*π/36 <φ< 53*π/36)由公式 s = h[1 – T/ + 1/2πsin(2πT/)];v = - h ω/[1 –cos(2πT/)];a = -2πh sin(2πT/) ; T = φ–()得到s= 0.150*(53/18 - 2*φ/π + 1/(2*π)*sin (4*φ- 35* π/9)); v = -0.300/π * ω* (1 - cos(4*φ- 35*π/9)); a = -1.200 *φ^2/π*sin(4*φ- 35*π/9);由上述公式通过编程得到位移、速度、加速度曲线如下:(编程见附录)1. 凸轮机构的sd ds-?线图及基圆半径和偏距的确定2.凸轮机构的s d ds-?线图如下图所⽰(代码详见附录):确定凸轮基圆半径与偏距:见下页:基圆半径为r 0 = 142mm ,偏距e = 20mm 。
3. 滚⼦半径的确定及凸轮理论廓线和实际廓线的绘制得到的理论轮廓曲线为:求其最⼩曲率半径 = 90.0051= 10mm。
这⾥取半径为 rr程序代码见附录3.凸轮轮廓绘制得到的外包络轮廓,得到图线为:得到的内包络线图为:这⾥取内包络线图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理大作业凸轮机构设计
一、凸轮机构概述
凸轮机构是一种常见的传动机构,它通过凸轮的旋转运动,带动相应
零件做直线或曲线运动。
凸轮机构具有结构简单、运动平稳、传递力
矩大等优点,在各种机械设备中得到广泛应用。
二、凸轮基本结构
1. 凸轮
凸轮是凸起的圆柱体,通常安装在主轴上。
其表面通常为圆弧形或其
他曲线形状,以便实现所需的运动规律。
2. 跟随件
跟随件是与凸轮配合的零件,它们通过接触面与凸轮相互作用,并沿
着规定的路径做直线或曲线运动。
跟随件可以是滑块、滚子、摇臂等。
3. 连杆
连杆连接跟随件和被驱动部件,将跟随件的运动转化为被驱动部件所
需的运动。
连杆可以是直杆、摇杆等。
三、凸轮机构设计要点
1. 几何参数设计
设计时需要确定凸轮半径、角度和曲率半径等参数,这些参数的选择
将直接影响凸轮机构的运动规律和性能。
2. 运动规律设计
根据被驱动部件的运动要求,选择合适的凸轮曲线形状,以实现所需的运动规律。
3. 稳定性设计
在设计凸轮机构时,需要考虑其稳定性。
例如,在高速旋转时,可能会发生跟随件脱离凸轮或者产生振动等问题,因此需要采取相应措施提高稳定性。
4. 材料和制造工艺设计
在材料和制造工艺方面,需要考虑凸轮机构所承受的载荷和工作环境等因素,选择合适的材料和制造工艺。
四、几种常见凸轮机构及其应用
1. 摇臂式凸轮机构
摇臂式凸轮机构由摇臂、连杆和被驱动部件组成。
它通常用于实现直线运动或旋转运动,并且具有结构简单、运动平稳等优点。
摇臂式凸轮机构广泛应用于各种机械设备中,如发动机气门控制系统、纺织设备等。
2. 滑块式凸轮机构
滑块式凸轮机构由凸轮、滑块、连杆和被驱动部件组成。
它通常用于实现直线运动,并且具有结构简单、运动平稳等优点。
滑块式凸轮机构广泛应用于各种机械设备中,如冲压设备、印刷设备等。
3. 滚子式凸轮机构
滚子式凸轮机构由凸轮、滚子、连杆和被驱动部件组成。
它通常用于
实现圆弧形运动,并且具有运动平稳、传递力矩大等优点。
滚子式凸
轮机构广泛应用于各种机械设备中,如汽车发动机气门控制系统等。
五、结论
综上所述,凸轮机构是一种重要的传动机构,在各种机械设备中得到
广泛应用。
在设计凸轮机构时,需要考虑其结构参数、运动规律、稳
定性以及材料和制造工艺等因素,以实现所需的运动规律和性能要求。
不同类型的凸轮机构具有不同的优点和适用范围,在实际应用中需要
根据具体情况进行选择和设计。
