§10—2齿轮的齿廓曲线
合集下载
渐开线齿轮的完整齿廓曲线方程及精确建模
渐开线齿轮的完整齿廓曲线方程及精确建模一、引言在机械设计领域中，渐开线齿轮被广泛应用于传动装置中。
它具有传动平稳、传动比准确、噪音小等优点，因此备受青睐。
为了更深入地了解渐开线齿轮，我们需要探索其完整齿廓曲线方程及精确建模。
二、了解渐开线齿轮1.渐开线齿轮的概念渐开线齿轮是一种特殊的齿轮，其齿廓曲线定义为齿廓曲线上任意一点到齿轮轴线的距离，均等于该点切线方向与齿轮轴线之间的夹角的正切值乘以该点到轴线的距离。
这种设计使得渐开线齿轮在传动过程中具有更加稳定的性能。
2.渐开线齿轮的应用渐开线齿轮被广泛应用于各种机械传动装置中，如汽车变速箱、工业机械设备等。
其传动平稳、传动比准确的特点，使其在高速、大扭矩传动系统中具有重要的地位。
对其完整齿廓曲线方程及精确建模的研究具有重要意义。
三、渐开线齿轮的完整齿廓曲线方程1.齿廓曲线方程的推导渐开线齿轮的完整齿廓曲线是由渐开线和圆弧段组成的，因此其完整齿廓曲线方程可以分段推导。
在渐开线段上，齿廓曲线可以表示为直线段，而在圆弧段上，齿廓曲线可以表示为圆弧段。
将两者组合起来，即可得到渐开线齿轮的完整齿廓曲线方程。
2.完整齿廓曲线方程的数学表达根据上述推导过程，我们可以得到渐开线齿轮的完整齿廓曲线方程，该方程包含了渐开线段和圆弧段的数学表达式。
这个方程的推导过程相对复杂，但是对于深入理解渐开线齿轮的齿廓曲线具有重要意义。
四、渐开线齿轮的精确建模1.建立渐开线齿轮的三维模型在实际应用中，我们需要对渐开线齿轮进行精确建模。
建立渐开线齿轮的三维模型是一个复杂而重要的工作，需要结合完整齿廓曲线方程，使用CAD软件进行精确建模。
2.精确建模的意义精确建模能够帮助工程师更全面、准确地了解渐开线齿轮的结构和性能特点，有助于优化设计，提高传动效率和可靠性。
五、个人观点和理解对于渐开线齿轮的研究，我深刻地认识到它在机械设计中的重要性。
作为传动装置的核心部件，渐开线齿轮的完整齿廓曲线方程及精确建模对于提高机械传动系统的性能至关重要。
机械原理第10章齿轮机构及其设计
2、具有标准顶隙：c = c *m
2.1.2 标准中心距
a=ra1+c+rf2 =r1+h*am+c*m+r2-( h*am+c*m)
=r1+r2=m(z1+z2) / 2
两轮的中心距a应等于两轮分度 圆半径之和，我们把这种中心距称为 标准中心距a
实际中心距a’
2.1.3 啮合角
啮合角α’——两轮传动时其节点P的圆周速度方向与啮合线 N1N2之间所夹的锐角，其值等于节圆压力角。 压力角α和啮合角α’的区别
2、对于按标准中心距安装的标准齿轮传动，当两轮的 齿数趋于无穷大时的极限重合度εαmax=1.981。
3、重合度εα还随啮合角α’的减小和齿顶高系数ha*的增 大而增大。
4、重合度是衡量齿轮传动质量的指标。 重合度承载能力传动平稳性
[例] 已知 z1=19、z2=52、=20、m =5mm、ha*=1。求 。
rb1+rb2=(r1+r2)cosα=(r1’+r2’)cos α’
齿轮的中心距与啮合角的关系为： a’cos α’=acos α
r1 =r1
O1
ω1 rb1 N1
=
r1 r1
O1
ω1 rb1 N1
N2
P
rb2 r2 =r2
P
N2 a
rb2
r2
r2
a
ω2
ω2
O2
O2
2.2 齿轮与齿条啮合传动 齿轮与齿条标准安装：齿轮的分度圆和齿条的分度线相切。
2．齿轮传动的中心距和啮合角
2.1 外啮合传动
2.1.1 齿轮正确安装的条件： 1、齿侧间隙为零：
即 s'1 e'2 及s'2 e'1
机械原理_齿轮传动
齿轮机构及其设计 渐开线直齿圆柱齿轮的啮合传动 一对轮齿的啮合过程及连续传动条件
1 [ Z1(tg a1 tg ) Z 2 (tg a 2 tg )] 外啮合 2 1 [ Z1 (tg a1 tg ) Z 2 (tg a 2 tg )] 内啮合 2 2ha Z1 (tg a1 tg ) 齿轮齿条 2 sin 2 与m无关，随Z增大而增大，当Z 也增大到无
齿轮机构及其设计 渐开线标准齿轮的基本参数和几何尺寸 标准齿条的特点
1) 各同侧齿廓均为相互平行的直线，且齿廓上各 点压力角α相等，均等于齿形角 2) 不同线上的齿距相等，均为pi=p =πm，但 只有分度线上e=s
ha 、 h f 、h 、e 、s 、p 、c 等 仍用表10—2中有关公式计算
齿轮机构及其设计 渐开线直齿圆柱齿轮的啮合传动 渐开线直齿圆柱齿轮传动的 啮合过程 N1N2—理论上可能 的最长啮合线段， 特称为理论啮合线 N1、N2为啮合极限点 B1B2—实际啮合线
齿轮机构及其设计 渐开线直齿圆柱齿轮的啮合传动 一对轮齿的啮合过程及连续传动条件 齿轮齿条啮合传动
PB1不变， ha 2 ha m PB2 且 sin sin 2 h 1 a [ Z1 (tg a1 tg ) ] 2 sin cos 2ha Z1 (tg a1 tg ) 2 sin 2
m1 m2 m 正确啮合条件 1 2
齿轮机构及其设计 渐开线直齿圆柱齿轮的啮合传动 齿轮传动的中心距与啮合角
1 a (d 1 d 2 ) 2 m ( Z1 Z 2 ) 2
c
c c m
标准安装
1 d2 ) a (d 1 2
机械原理课后答案第十章作业
解： db = d cosα= m z′cosα df = d -2 hf=(z′-2ha*-2 c*)m
由df ≥db ，有： z′≥2(ha*+2 c*) / (1 - cosα) =41.45（不能圆整）
∴ 当齿根圆与基圆重合时，z′=41.45； 当 z ≥ 42时，齿根圆大于基圆。
10-5 已知一对渐开线标准外啮合圆柱齿轮传动，其模数 m=10mm，
解：1）确定传动类型
a = m ( z1+z2 ) /2 = 10 ( 12+12 ) /2 =120 < a′= 130mm 故此传动应为 正 传动。
2）确定两轮变位系数 α′ = arccos(a cosα/ a′) = arccos(120 cos20°/ 130) = 29.83° x1 + x2 = (z1+z2) (invα′-invα) / (2tanα)
10-2 设有一渐开线标准齿轮 z=20，m=8mm，α=20°，ha* =1，试
求：1)其齿廓曲线在分度圆及齿顶圆上的曲率半径ρ、ρa 及齿顶圆压
力角αa ；2)齿顶圆齿厚 s a 及基圆齿厚 s b ；3）若齿顶变尖( s a =0)时，
齿顶圆半径 ra′又应为多少？并完成图示各尺寸的标注。 解：1）求ρ、αa 、ρa d = m z =8×20=160(mm) da= d +2 ha=(z+2ha*)m=(20+2×1)×8= 176(mm) db= d cosα= 160cos20°= 160×0.9397= 150.35(mm) ρ= rb tanα= 75.175 tan20°= 75.175×0.3640= 27.36(mm) αa =arccos( rb/ra )= arccos( 75.175/88 ) = arccos0.8543=31.32° ρa = rb tanαa =75.175tan31.32°= 75.175×0.6085=45.74(mm) 2）求s a 及s b sa=s(ra/r)-2ra(invαa-invα)= 8π/2×88/80-176×(inv31.32°-inv20°)
由df ≥db ，有： z′≥2(ha*+2 c*) / (1 - cosα) =41.45（不能圆整）
∴ 当齿根圆与基圆重合时，z′=41.45； 当 z ≥ 42时，齿根圆大于基圆。
10-5 已知一对渐开线标准外啮合圆柱齿轮传动，其模数 m=10mm，
解：1）确定传动类型
a = m ( z1+z2 ) /2 = 10 ( 12+12 ) /2 =120 < a′= 130mm 故此传动应为 正 传动。
2）确定两轮变位系数 α′ = arccos(a cosα/ a′) = arccos(120 cos20°/ 130) = 29.83° x1 + x2 = (z1+z2) (invα′-invα) / (2tanα)
10-2 设有一渐开线标准齿轮 z=20，m=8mm，α=20°，ha* =1，试
求：1)其齿廓曲线在分度圆及齿顶圆上的曲率半径ρ、ρa 及齿顶圆压
力角αa ；2)齿顶圆齿厚 s a 及基圆齿厚 s b ；3）若齿顶变尖( s a =0)时，
齿顶圆半径 ra′又应为多少？并完成图示各尺寸的标注。 解：1）求ρ、αa 、ρa d = m z =8×20=160(mm) da= d +2 ha=(z+2ha*)m=(20+2×1)×8= 176(mm) db= d cosα= 160cos20°= 160×0.9397= 150.35(mm) ρ= rb tanα= 75.175 tan20°= 75.175×0.3640= 27.36(mm) αa =arccos( rb/ra )= arccos( 75.175/88 ) = arccos0.8543=31.32° ρa = rb tanαa =75.175tan31.32°= 75.175×0.6085=45.74(mm) 2）求s a 及s b sa=s(ra/r)-2ra(invαa-invα)= 8π/2×88/80-176×(inv31.32°-inv20°)
§10—2齿轮的齿廓曲线
圆盘1上的已知曲线C1就会走出一 1 C 系列的轨迹，作这些轨迹的包络 线，则得到所求的齿廓曲线C2。
三、齿廓曲线的选择 理论上，只要给出一齿廓C1 ，就可以求出另一条满足 定传动比的共轭齿廓C2。但生产实际上，选择齿廓曲线时， 不仅要满足传动比要求，还必须从设计、制造、安装和使 用等方面予以考虑。 目前对定传动比传动的齿轮来说，最常用的齿廓是渐 开线(Involute) ，其次是摆线(Cycloid) 和变态摆线，近年 来出现了圆弧(Arc) 、抛物线(Parabola) 等。 由于渐开线齿廓具有良好的传动性能，便于制造、安 装、测量和互换性好等优点，所有目前绝大部分齿轮都采 用渐开线齿廓。 本章只讨论渐开线齿轮。
一、齿廓啮合的基本定律
(Basic Law of Tooth Profile Meshing)
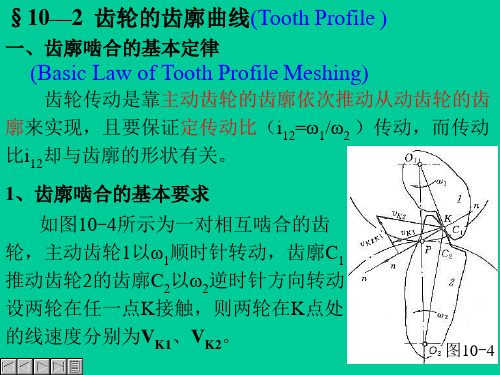
齿轮传动是靠主动齿轮的齿廓依次推动从动齿轮的齿 廓来实现，且要保证定传动比（i12=ω1/ω2 ）传动，而传动 比i12却与齿廓的形状有关。 1、齿廓啮合的基本要求 、 如图10-4所示为一对相互啮合的齿 轮，主动齿轮1以ω1顺时针转动，齿廓C1 推动齿轮2的齿廓C2以ω2逆时针方向转动。 设两轮在任一点K接触，则两轮在K点处 的线速度分别为VK1、VK2。
目前对定传动比传动的齿轮来说最常用的齿廓是渐开线involute其次是摆线cycloid和变态摆线近年来出现了圆弧arc抛物线parabola由于渐开线齿廓具有良好的传动性能便于制造安装测量和互换性好等优点所有目前绝大部分齿轮都采用渐开线齿廓
齿轮的齿廓曲线(Tooth Profile ) §10—2 齿轮的齿廓曲线
4、节点(pitch point) 和节圆(pitch circle) 、 1）节点 节点P——过齿廓啮合点的公法线与连心线的交点。 节点 2）节圆 节圆 如要求定比传动即i12=C，则应 使O2P/ O1P= C。由于O1、O2为定点， 所以欲使 O2P/ O1P= C，则节点P在 O1O2上必须是定点。 ∴ 定比传动齿轮的齿廓啮合基本定律 可以表述为：要使两齿轮作定传动 比传动，则不论两齿廓在何处接触， 过接触点所作的公法线必须与连心 线交于一定点。
机械原理(PDF)孙桓复习笔记chapter10
齿顶高 ha：分圆到顶圆的经向距离。 齿根高 hf： 根圆到分圆的经向距离。
全齿高 h： 根圆到顶圆的经向距离。即 h = h a + hf 任意圆 ri： 以任意半径所作的圆；其齿厚、齿槽宽、齿距分别以
注： 单个齿轮无节圆。
si、ei、pi表示
基 节 pb： 相邻两齿同侧齿廓沿基圆的弧长。
pb = pcos α
2 ．刀具标准位置： 齿条型刀具的分度线与被切齿轮的分度圆相切并纯滚。
注： 因刀具在分度线上的齿厚等于齿槽宽，所以被加工齿轮的分度圆的
齿厚也等于齿槽宽，即切制成的齿轮为标准齿轮。
三．渐开线齿郭的根切现象和标准齿轮不发生根切的最少齿数
1．根切现象： 用范成法加工齿轮时，轮齿根部的部分渐开线齿廓
被切去的现象。（图 8-12 ）
α
P
se
p
1
ha hf α
才能使齿顶部分的齿廓均为渐开线）
63
《机械原理》 （第七版）孙桓主编
§10—5 渐开线直 齿圆柱齿轮的 啮合传动 一．一对渐开线齿轮正确啮合的条件
由于渐开线齿轮副的接触点都在线
1 2上
所以各齿对要在 1 2上同时啮合，两轮的法节应相等：
pn1=p b1=πｍc1os α =K1 K′=πｍ cos2α =p b22=p n2
5 ）基圆内与渐开线（∵ nn 总与基圆相切）
二．渐开线方程方 方 程 程 式 式 及 及 渐 渐 开 开 线 线 函 函 数 数 当齿轮绕轴心 O 转动时，渐开线齿廓 AK 上 K 点的速度 vk⊥rk，又该齿廓与另一 轮的齿廓在 K 接触时，所受法向力 F n必沿 nn。
60
《机械原理》 （第七版）孙桓主编
*
机械原理第十章
齿槽：相邻两轮齿之间的空间
齿槽一宽个：齿在槽任两意侧半齿径廓rK圆间周弧上长，。eK
齿距：在任意半径rK圆周上，相
邻两齿同侧齿廓间弧长。pK
在同一圆周上：pK sK eK
法向齿距：相邻两齿同侧齿 廓间法线长度，pn=pb
分度圆：为了计算齿轮的各部分尺寸， 在齿顶圆和齿根圆之间人为规定了 一个直径为d，半径为r，用作计算 基准的圆。 分度圆上齿距、齿厚、齿槽宽分别 用p、s、e表示。 p=s+e
已知传动比、中心距、 齿轮1的齿廓曲线K1，用 包络线法求与齿廓K1共 轭的齿廓曲线K2。
3.齿廓曲线的选择 理论上，满足齿廓啮合定律的曲线有无穷多，但考
虑到便于制造和检测等因素，工程上只有极少数几种 曲线可作为齿廓曲线，如渐开线、其中应用最广的是 渐开线，其次是摆线(仅用于钟表)和变态摆线 (摆线针 轮减速器)，近年来提出了圆弧和抛物线。
o1
点P 称为两轮的啮合节点(简称节点）。 r’1 节圆：
ω1
节圆
n
两个圆分别为轮1和轮2的节圆
k
两节圆相切于P点，且两轮节点处速 度相同，故两节圆作纯滚动。
P n
ω 2 r’2
o2
根据这一定律， 可求得齿廓曲线与齿廓传动比的关系；
也可按给定的传动比来求得两轮齿廓的共轭曲线。
2.共轭齿廓
所谓共轭齿廓是指两轮相互连续接触并能实现预 定传动比规律的一对齿廓。
rK
k
=
rb/ cosK inv K = tan K
K
三、 渐开线齿廓的啮合特性
O1
ω1
1.渐开线齿廓满足定传动比要求
N1
两齿廓在任意点K啮合时，过K作两 齿廓的法线N1N2，是基圆的切线，为 N2
齿槽一宽个：齿在槽任两意侧半齿径廓rK圆间周弧上长，。eK
齿距：在任意半径rK圆周上，相
邻两齿同侧齿廓间弧长。pK
在同一圆周上：pK sK eK
法向齿距：相邻两齿同侧齿 廓间法线长度，pn=pb
分度圆：为了计算齿轮的各部分尺寸， 在齿顶圆和齿根圆之间人为规定了 一个直径为d，半径为r，用作计算 基准的圆。 分度圆上齿距、齿厚、齿槽宽分别 用p、s、e表示。 p=s+e
已知传动比、中心距、 齿轮1的齿廓曲线K1，用 包络线法求与齿廓K1共 轭的齿廓曲线K2。
3.齿廓曲线的选择 理论上，满足齿廓啮合定律的曲线有无穷多，但考
虑到便于制造和检测等因素，工程上只有极少数几种 曲线可作为齿廓曲线，如渐开线、其中应用最广的是 渐开线，其次是摆线(仅用于钟表)和变态摆线 (摆线针 轮减速器)，近年来提出了圆弧和抛物线。
o1
点P 称为两轮的啮合节点(简称节点）。 r’1 节圆：
ω1
节圆
n
两个圆分别为轮1和轮2的节圆
k
两节圆相切于P点，且两轮节点处速 度相同，故两节圆作纯滚动。
P n
ω 2 r’2
o2
根据这一定律， 可求得齿廓曲线与齿廓传动比的关系；
也可按给定的传动比来求得两轮齿廓的共轭曲线。
2.共轭齿廓
所谓共轭齿廓是指两轮相互连续接触并能实现预 定传动比规律的一对齿廓。
rK
k
=
rb/ cosK inv K = tan K
K
三、 渐开线齿廓的啮合特性
O1
ω1
1.渐开线齿廓满足定传动比要求
N1
两齿廓在任意点K啮合时，过K作两 齿廓的法线N1N2，是基圆的切线，为 N2
齿轮的齿廓曲线--ppt课件(2024版)
∴ pb1= pb2
将pb=πmcosα代入得： m1cosα1=m2cosα2
因m和α都取标准值，使上式成立 的条件为：
m1=m2，α1=α2
pb2
pb1
由前述可知，一对渐开线齿廓能保证定传动比传动，但这不等于说任意两个渐开线齿轮都能搭配起来正确传动，比如说一个齿轮的齿距很小，另一个齿轮的齿距很大，显然两个齿轮是无法搭配传动的。
§10－5 渐开线直齿圆柱齿轮的啮合传动
*
ppt课件
B1B2——实际啮合线
N1N2： 理论上可能的最长啮合线段——
由于基圆内无渐开线，故B1、B2两点不能超出N1、N2两点，因此N1、N2两点称为啮合极限点。
理论啮合线段
一对轮齿啮合传动的区间是有限的。要使齿轮能连续转动，则在前一对轮齿脱离啮合之前，后一对轮齿必须及时地进入啮合。
基节pb=法节pn
*
ppt课件
rb
O
pn
齿距 (周节)—— pk= sk +ek 同侧齿廓弧长
齿宽(face-width)—— B
ha
hf
h
B
p
ra
法向齿距(法节) —— pn
s
e
sk
ek
= pb(基节)
pb
rf
r
pk
轮齿介于分度圆与齿顶圆之间的部分称为齿顶，其径向高度称为齿顶高，
同一圆上
*
ppt课件
A
K
渐开线
B
发生线
渐开线AK 的展角
O
基圆
rb
(1)渐开线的形成
定直线
*
ppt课件
*
ppt课件
N
发生线
渐开线k0k 的展角
将pb=πmcosα代入得： m1cosα1=m2cosα2
因m和α都取标准值，使上式成立 的条件为：
m1=m2，α1=α2
pb2
pb1
由前述可知，一对渐开线齿廓能保证定传动比传动，但这不等于说任意两个渐开线齿轮都能搭配起来正确传动，比如说一个齿轮的齿距很小，另一个齿轮的齿距很大，显然两个齿轮是无法搭配传动的。
§10－5 渐开线直齿圆柱齿轮的啮合传动
*
ppt课件
B1B2——实际啮合线
N1N2： 理论上可能的最长啮合线段——
由于基圆内无渐开线，故B1、B2两点不能超出N1、N2两点，因此N1、N2两点称为啮合极限点。
理论啮合线段
一对轮齿啮合传动的区间是有限的。要使齿轮能连续转动，则在前一对轮齿脱离啮合之前，后一对轮齿必须及时地进入啮合。
基节pb=法节pn
*
ppt课件
rb
O
pn
齿距 (周节)—— pk= sk +ek 同侧齿廓弧长
齿宽(face-width)—— B
ha
hf
h
B
p
ra
法向齿距(法节) —— pn
s
e
sk
ek
= pb(基节)
pb
rf
r
pk
轮齿介于分度圆与齿顶圆之间的部分称为齿顶，其径向高度称为齿顶高，
同一圆上
*
ppt课件
A
K
渐开线
B
发生线
渐开线AK 的展角
O
基圆
rb
(1)渐开线的形成
定直线
*
ppt课件
*
ppt课件
N
发生线
渐开线k0k 的展角
《机械设计原理》齿轮的齿廓曲线
节线为椭圆的非圆齿轮机构图
§6-2 齿轮的齿廓曲线
2. 齿廓曲线的选择
共轭：按一定的规律相配的一对。
共轭齿廓：能按预
轭
定传动比规律相互啮
合传动的一对齿廓。
给定预定的传动比和 一条齿廓曲线，可根据 齿廓啮合基本定律求得 另一条齿廓曲线。
§6-2 齿轮的齿廓曲线
能满足一定传动比规律的共轭齿廓曲线有很多。
➢ 瞬时传动比为多少？
2
O2
根据速度瞬心可知，瞬时传动比：
i12 1 / 2 O2P / O1P
§6-2 齿轮的齿廓曲线
O1
1
n K
n
P C2 C1
此式表明：相互啮合传动的一对 齿轮，在任意位置时的传动比，都 与其连心线O1O2被其啮合齿廓在接 触点处的公法线所分成的两线段长 成反比。
这个规律称为齿廓啮合基本定律。
第6章 齿轮机构
§6-2 齿轮的齿廓曲线
主要内容： ➢ 齿廓啮合基本定律 ➢ 齿廓曲线的选择
平均传动比：
i12 n1 / n2 z2 / z1
§6-2 齿轮的齿廓曲线
O1
1. 齿廓啮合基本定律
1
➢ 怎样才能使一对齿廓连续接触而传
n 动？
vc1 vc2
K
n
P C2 C1
两齿廓沿接触点的公法线方向的 速度应相等；相对速度只能沿接触 点处的公切线方向。
比传动。
r2 P 点在轮1或2的运动平面上的轨迹为
一个圆，称为节圆（pitch circle）。
2
O2
传动过程中，两齿轮的节圆作纯滚 动。
§6-2 齿轮的齿廓曲线
变传动比传动：两齿廓的节点P 按其传动比
的变化规律在其连心线上移动。
§6-2 齿轮的齿廓曲线
2. 齿廓曲线的选择
共轭：按一定的规律相配的一对。
共轭齿廓：能按预
轭
定传动比规律相互啮
合传动的一对齿廓。
给定预定的传动比和 一条齿廓曲线，可根据 齿廓啮合基本定律求得 另一条齿廓曲线。
§6-2 齿轮的齿廓曲线
能满足一定传动比规律的共轭齿廓曲线有很多。
➢ 瞬时传动比为多少？
2
O2
根据速度瞬心可知，瞬时传动比：
i12 1 / 2 O2P / O1P
§6-2 齿轮的齿廓曲线
O1
1
n K
n
P C2 C1
此式表明：相互啮合传动的一对 齿轮，在任意位置时的传动比，都 与其连心线O1O2被其啮合齿廓在接 触点处的公法线所分成的两线段长 成反比。
这个规律称为齿廓啮合基本定律。
第6章 齿轮机构
§6-2 齿轮的齿廓曲线
主要内容： ➢ 齿廓啮合基本定律 ➢ 齿廓曲线的选择
平均传动比：
i12 n1 / n2 z2 / z1
§6-2 齿轮的齿廓曲线
O1
1. 齿廓啮合基本定律
1
➢ 怎样才能使一对齿廓连续接触而传
n 动？
vc1 vc2
K
n
P C2 C1
两齿廓沿接触点的公法线方向的 速度应相等；相对速度只能沿接触 点处的公切线方向。
比传动。
r2 P 点在轮1或2的运动平面上的轨迹为
一个圆，称为节圆（pitch circle）。
2
O2
传动过程中，两齿轮的节圆作纯滚 动。
§6-2 齿轮的齿廓曲线
变传动比传动：两齿廓的节点P 按其传动比
的变化规律在其连心线上移动。
第十章齿轮机构
齿根圆直径
周 齿 节 厚
df
p s pb a
基圆周节 中心距
Pb= p m cosa
a=m(z1 ±z2)/2
注：上面符号用于外齿轮或外啮合传动，下面符号用于内齿轮或内啮合传动。
§10-5 渐开线直齿圆柱齿轮的啮合传动
一、一对渐开线齿轮正确啮合的条件：
O1 ω1 r2 rb1 (avi)
pb1
N1 N2 P
二、根切现象及其避免方法
1. 根切现象及产生原因
根切现象：因某种原因，轮齿根部 的渐开线被切削掉的现象。 用范成法加工渐开线齿轮过程中， 有时刀具齿顶会把被加工齿轮根部的渐 开线齿廓切去一部分，这种现象称为根 切。 根切的危害： 根切将削弱齿根强度，甚至可能降 低传动的重合度，影响传动质量。 根切现象
内啮合齿轮传动 用于平行轴间传 动的齿轮机构 齿 轮 机 构 分 类 外啮合齿轮传动 齿轮齿条传动 用于相交轴间传 圆锥齿轮传动 —— 动的齿轮机构 人字齿轮传动 螺旋齿轮传动 蜗轮蜗杆传动 直齿轮传动 斜齿轮传动 人字齿轮传动 直齿 斜齿 曲齿 用于交错轴间传 动的齿轮机构
1. 用于平行轴之间传递的齿轮机构
（1）交错轴斜齿圆柱齿轮机构 特点： 两螺旋角数值不 等的斜齿轮啮合时， 可组成两轴线任意 交错传动，两轮齿 为点接触，且滑动 速度较大，主要用 于传递运动或轻载 传动。
（2）蜗杆蜗轮传动
特点：蜗杆蜗轮传动多用于两轴交错角为90的传动，其 传动比大，传动平稳，具有自锁性，但效率较低。
4. 齿轮机构的机构运动简图
§10-3 渐开线齿廓及其啮合特点
一、渐开线的形成及其特性:
1、渐开线的形成
2、 渐开线的性质
1) 发生线在基圆上滚过的线段长 度等于基圆上被滚过的圆弧长度。 2) 渐开线上任一点的法线恒与基圆
机械原理复习资料6
渐开线直齿圆柱齿轮的啮合传动(3/6) 渐开线直齿圆柱齿轮的啮合传动
（2）啮合角 渐开线齿轮传动的啮合角α′就等于其节圆压力角。 当两轮按标准中心距安装时，则 a′= a； 当两轮实际中心距 a′与标准中心距 a 不同时，则： 若 a′＞a 时， r1′＞r1，r2′＞r2； c′＞0，c＞c*m；α′＞α。 若 a′＜a 时，两轮将无法安装。 （3）齿轮传动的中心距与啮合角的关系 a′cosα′= a cosα
§10-8 斜齿圆柱齿轮传动
1、螺旋角β 2、 端面参数—— 来计算 法面参数 ——标准值
斜齿圆柱齿轮传动(3/5) 斜齿圆柱齿轮传动
3、斜齿轮的正确啮合的条件 mn1=mn2= m αn1= αn2 = α β1=-β2 (外啮合) β1=β2 (内啮合)
4、斜齿轮传动的标准中心距为 a = (d1+d2)/2 = mt(z1+z2)/2 = mn(z1+z2)/(2 cosβ ) 斜齿轮的中心距与 m Z β 有关
Hale Waihona Puke §10-9 圆锥齿轮传动圆锥齿轮传动是用来传递两相交轴之间的运动和动力的，一般 。 Σ = 90 。通常取圆锥齿轮大端的参数为标准值，
渐开线直齿圆柱齿轮的啮合传动(4/6) 渐开线直齿圆柱齿轮的啮合传动
3．连续传动条件 重合度 εα = B1B2 /pb ≥1 重合度εα 的计算 εα= [z1(tanαa1 － tanα′) +z2(tanαa2 － tanα′)]/(2π) 结论 重合度εα 与模数m无关，而随着齿数z的增多而增大， 还随啮合角α′减少和齿顶高系数ha*的增大而加大，
§10-5 渐开线直齿圆柱齿轮的啮合传动
1．齿轮正确啮合的条件 m1 = m2 = m α1 = α2 = α
(完整版)齿轮的齿廓曲线
k K
Fn rk
NB rb k k KA0
力方向与速度方向所夹锐角
O
为渐开线上该点之压力角
αk(pressure angle)。
基圆
rb＝rk cosαk
离中心越远，渐开线上的压力角
越大。基圆上的压力角为0。
(4)渐开线形状取决于基圆 基圆越大，渐开线越平直，
当rb→∞，变成直线。
Σ3 Σ1
Σ2
互相啮合的一对齿轮在任一位置时的传动比，
都与连心线O1O2被其啮合齿廓的在接触处的公法线 所分成的两段成反比。
如果要求传动比为常数，则应使O2P/O1P为常数。
由于O2 、O1为定点，故P必为一个定点，称为节点
(the pitch point) 。
o1
节圆(the pitch circle)：
r’1
发生线
K
当直线沿一圆周作相切纯滚 动时，直线上任一点的轨迹 AK，称为该圆的渐开线。
B
rb
定直线
基圆
A
k
O
二、渐开线的性质
发生线
(1)BK = A B
(2) BK为渐开线在K点的法 线，又因发生线恒切于基 圆，故知渐开线上任意点 的法线切于基圆。
(3)渐开线上点Ｋ的压力角 定义：啮合时K点正压
Vk
(5)基圆内无渐开线。
B2
B1
rb1
思考：10-20
K
KO2
o2 KO1 o1
三、渐开线方程式及渐开线函数
αk
k
rk是渐开线在任意点K的向径。当渐开线与 vk
r r cos 其共轭齿廓在K点啮合时，在三角形BOK
中
A
θk
b
K
Fn rk
NB rb k k KA0
力方向与速度方向所夹锐角
O
为渐开线上该点之压力角
αk(pressure angle)。
基圆
rb＝rk cosαk
离中心越远，渐开线上的压力角
越大。基圆上的压力角为0。
(4)渐开线形状取决于基圆 基圆越大，渐开线越平直，
当rb→∞，变成直线。
Σ3 Σ1
Σ2
互相啮合的一对齿轮在任一位置时的传动比，
都与连心线O1O2被其啮合齿廓的在接触处的公法线 所分成的两段成反比。
如果要求传动比为常数，则应使O2P/O1P为常数。
由于O2 、O1为定点，故P必为一个定点，称为节点
(the pitch point) 。
o1
节圆(the pitch circle)：
r’1
发生线
K
当直线沿一圆周作相切纯滚 动时，直线上任一点的轨迹 AK，称为该圆的渐开线。
B
rb
定直线
基圆
A
k
O
二、渐开线的性质
发生线
(1)BK = A B
(2) BK为渐开线在K点的法 线，又因发生线恒切于基 圆，故知渐开线上任意点 的法线切于基圆。
(3)渐开线上点Ｋ的压力角 定义：啮合时K点正压
Vk
(5)基圆内无渐开线。
B2
B1
rb1
思考：10-20
K
KO2
o2 KO1 o1
三、渐开线方程式及渐开线函数
αk
k
rk是渐开线在任意点K的向径。当渐开线与 vk
r r cos 其共轭齿廓在K点啮合时，在三角形BOK
中
A
θk
b
K
机械原理(第七版)优秀课件—第十章 齿轮机构及其设计
第十章 齿轮机构及其设计
Gears and its Design
• 10.1 齿轮机构的特点及分类
• 10.1.1 概述 • 1.什么是齿轮？
• 2.特点：适应范围广（v、p、r)；效率
高（0.99)；速比稳定、传动精度高；工 作可靠；可实现任意轴间的传动。制造 和安装精度要求高，成本较高；不适于 远距离传动。
• 刀具不标准
2.变位齿轮问题的提出
1）z＜zmin时又要不根切； 2）a’≠a；
3）ρ小＜ρ大, σ小＞σ大， u小＞u大,
• 3.刀具的变位 1）正变位 2）负变位 • 4. 变位传动
1）零变位齿轮传动：∑x=0，α’=α, a’=a • x1=x2=0 标准齿轮传动 x1=-x2 等移距变位齿轮传动 • 2）非零变位齿轮传动：∑x≠0，α’≠α, a’≠a
曲齿
交错轴斜齿轮传动
• 3.按齿廓曲线分：渐开线、摆线、圆弧 • 4.按工作条件分： • 1）开式：2）闭式：
• 5.按运动速度分：
• 低速：＜1m/s
• 中速：1～25
• 高速：＞25m/s • 超高：＞100m/s
• 10.1.3 对齿轮传动的基本要求
– 1.传动准确平稳
i 1 d1
2 d 2
α
r
α N1
xm ha m
p
Q
• 2. 变位齿轮的几何计算
• m、a由强度计算确定，α、z、d、db不变化 • h高a和、齿h厚f 、的d变a化、 df、s 、e 、α’都将变化，而关键是齿
• 1）齿顶高、齿根高
hai (ha* xi y)m
hfi (ha* c* xi)m
x的选择:无侧隙、不根
2
c os '
Gears and its Design
• 10.1 齿轮机构的特点及分类
• 10.1.1 概述 • 1.什么是齿轮？
• 2.特点：适应范围广（v、p、r)；效率
高（0.99)；速比稳定、传动精度高；工 作可靠；可实现任意轴间的传动。制造 和安装精度要求高，成本较高；不适于 远距离传动。
• 刀具不标准
2.变位齿轮问题的提出
1）z＜zmin时又要不根切； 2）a’≠a；
3）ρ小＜ρ大, σ小＞σ大， u小＞u大,
• 3.刀具的变位 1）正变位 2）负变位 • 4. 变位传动
1）零变位齿轮传动：∑x=0，α’=α, a’=a • x1=x2=0 标准齿轮传动 x1=-x2 等移距变位齿轮传动 • 2）非零变位齿轮传动：∑x≠0，α’≠α, a’≠a
曲齿
交错轴斜齿轮传动
• 3.按齿廓曲线分：渐开线、摆线、圆弧 • 4.按工作条件分： • 1）开式：2）闭式：
• 5.按运动速度分：
• 低速：＜1m/s
• 中速：1～25
• 高速：＞25m/s • 超高：＞100m/s
• 10.1.3 对齿轮传动的基本要求
– 1.传动准确平稳
i 1 d1
2 d 2
α
r
α N1
xm ha m
p
Q
• 2. 变位齿轮的几何计算
• m、a由强度计算确定，α、z、d、db不变化 • h高a和、齿h厚f 、的d变a化、 df、s 、e 、α’都将变化，而关键是齿
• 1）齿顶高、齿根高
hai (ha* xi y)m
hfi (ha* c* xi)m
x的选择:无侧隙、不根
2
c os '
1、齿轮传动的基本知识(2024版)
二、斜齿轮的基本参数
计算斜齿轮端面参数与尺寸：
1.齿距：Pt mt Pn mn
在△DFE中 Pn Pt cos
见图11-22
2.模数 ： mn mt cos
二、斜齿轮的基本参数
3.压力角 ：
tgat
AB BB'
,
tga
n
AC CC'
AC AB cos
∵BB’=CC’
tga n
AC CC'
二、正确啮合的条件
保证前后两对轮齿有可能同时在啮
合线上相切接触。一对齿轮连续顺ຫໍສະໝຸດ 利地传动，需要各对轮齿依次正确
啮合而互不干扰。如图所示，B1B2
是啮合线的实际长度，若每对齿轮
的基圆齿距都不相等，则必会出现
齿廓的局部重叠或过大间隙，即发
生卡死（pb1<pb2）或冲击（ pb1 >
pb2 ）的现象。因此，为保证齿轮的
=
—co—sa— cosa'
a'
r2'
② ∵ rb1 + rb2 = r1cosa + r2cosa
r1'cosa' + r2'cosa'
∴ a'cosa' = a cosa
r O1 b1 a'
P
rb2
O2
分度圆、节圆、 压力角、啮合角
5.齿轮与齿条啮合传动
分度圆与节线相切
特点 啮合线切于齿轮基圆并垂直于齿条齿廓 标准安装或非标准安装 d = d a = a
高级制齿工
齿轮技术基础
齿轮传动的基本知识（部分）
概述
• 齿轮是大家都十分熟悉的一个名词，对于齿 轮的形状，我们大家并不陌生，同时也知道 几乎所有的机器上都有齿轮的应用。但是， 对于各种各样的齿轮各有什么特点，为什么 应用的这么广泛，我们如何才能对其进行科 学的分类等等，我们也许不太清楚，或者说 不能用科学的语言对其进行描述。那么这一 节中我们就要来了解这些内容，这些内容也 是我们对齿轮进行进一步讨论所必须的。
齿轮的齿廓曲线
b1
o1 r
n N1N2—啮合点的轨迹线
∴传力方向不变。 传力方向不变。
3、渐开线齿廓传动具有中心距可分性 ω1 n Q O N P ~ O N P ∵
or 1
b1
1
n
N2
rb 2
P
o2
N1
∴ i12
ω1 O2P = = ω2 O1P
1
2
2
ω2
O2N 2 rb 2 = = rb 1 O1N 1
可分性： 传动比虽然不变，啮合 可分性：当实际中心距与设计中心距 注： 传动比虽然不变， 略有变化， 略有变化，也不会影响两轮的传动比 参数将发生变化。 参数将发生变化。 这一特性称为渐开线齿轮的可分性. ,1
N1 kP k o2
n
ω2
1.两齿廓在K K 1.两齿廓在K点 点 为定点。 则当两齿廓在 P为定点。 2.当两齿廓在 当两齿廓在K 2.两齿廓在 啮合时, 啮合时 b1 啮合时, , r 啮合时, rP，b2不变 ω O 常数） ∴i = = = C(常数） 常数 N1ω 2—两齿廓的 N —仍为两齿 两齿廓的 仍为两齿 OP 结论： 共法线 结论：廓的共法线 渐开线齿廓能满 NNNN与OOOO的交点 1 1 2 2与 1 1 2 2的交 足定传动比传动。 足定传动比传动。 点为P. 点为 仍为P. 仍为P.P.
o1
n
K(K1,K2 )
ω1 O2 P i12 = = ω2 OP 1
P— 称为啮合节点， 称为啮合节点， 简称节点。 简称节点。 1.若 为定点， 1.若P为定点，i12=C 点的轨迹称为节圆。 P点的轨迹称为节圆。
VP
P n o2
ω2
2.若 为动点， =C， 2.若P为动点，i12=C，P点的轨迹称为 节线。 节线。
o1 r
n N1N2—啮合点的轨迹线
∴传力方向不变。 传力方向不变。
3、渐开线齿廓传动具有中心距可分性 ω1 n Q O N P ~ O N P ∵
or 1
b1
1
n
N2
rb 2
P
o2
N1
∴ i12
ω1 O2P = = ω2 O1P
1
2
2
ω2
O2N 2 rb 2 = = rb 1 O1N 1
可分性： 传动比虽然不变，啮合 可分性：当实际中心距与设计中心距 注： 传动比虽然不变， 略有变化， 略有变化，也不会影响两轮的传动比 参数将发生变化。 参数将发生变化。 这一特性称为渐开线齿轮的可分性. ,1
N1 kP k o2
n
ω2
1.两齿廓在K K 1.两齿廓在K点 点 为定点。 则当两齿廓在 P为定点。 2.当两齿廓在 当两齿廓在K 2.两齿廓在 啮合时, 啮合时 b1 啮合时, , r 啮合时, rP，b2不变 ω O 常数） ∴i = = = C(常数） 常数 N1ω 2—两齿廓的 N —仍为两齿 两齿廓的 仍为两齿 OP 结论： 共法线 结论：廓的共法线 渐开线齿廓能满 NNNN与OOOO的交点 1 1 2 2与 1 1 2 2的交 足定传动比传动。 足定传动比传动。 点为P. 点为 仍为P. 仍为P.P.
o1
n
K(K1,K2 )
ω1 O2 P i12 = = ω2 OP 1
P— 称为啮合节点， 称为啮合节点， 简称节点。 简称节点。 1.若 为定点， 1.若P为定点，i12=C 点的轨迹称为节圆。 P点的轨迹称为节圆。
VP
P n o2
ω2
2.若 为动点， =C， 2.若P为动点，i12=C，P点的轨迹称为 节线。 节线。
《机械设计手册》之直齿轮
'
B1
用重合度 来衡量：
B1B2 pb
1
连续传动条件
P317 表10-3
实际应用中： [ ]
结束
§ 10-5 渐开线直齿圆柱齿轮的啮合传动
三、一对齿轮的啮合过程及连续传动条件
3、重合度的计算
B1B2 pb
PB1 PB2
p cos
z1(tana1 tan ') z2 (tana2 tan ') 2
K
展开法
纯滚动法
不论哪一种方法，只要基圆的半径rb相同, 渐开线形状也一定相同。 结束
§10－3 渐开线齿廓曲线的啮合特点
一、渐开线的形成及其特性
2、渐开线性质
K点的 压力角 cosαk=rb/RK
（1）KN = AN
（2）KB K点的法线；
发生线L
渐开线基上圆任的意切线一点的法 线恒切瞬于时基速圆度中心；
一、正确啮合条件
法向齿距 pN 基圆上的齿距
pN = pb
啮pb合点在N1N2 线上 N1 N2 — 理论啮合线
正确啮合→(BK)1= (BK)2
→否则嵌入或出现间隙
→ pN1 = pN2 （pb1 = Pb2）
db=d cos → db= d cos pb z=p z cos →pb = p cos = m cos → m1 cos 1 = m2 cos 2
节圆处的压力角→ ´
Fn —— 沿N1N2 始终不变 →轴、轴承受力稳定→传动平稳
结束
§10－3 渐开线齿廓曲线的啮合特点
三、渐开线齿廓的啮合特点
3、渐开线齿廓传动具有可分性
i 1 2
r2' r1'
rb2 rb1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆盘1上的已知曲线C1就会走出一 1 C 系列的轨迹，作这些轨迹的包络 线，则得到所求的齿廓曲线C2。
三、齿廓曲线的选择 理论上，只要给出一齿廓C1 ，就可以求出另一条满足 定传动比的共轭齿廓C2。但生产实际上，选择齿廓曲线时， 不仅要满足传动比要求，还必须从设计、制造、安装和使 用等方面予以考虑。 目前对定传动比传动的齿轮来说，最常用的齿廓是渐 开线(Involute) ，其次是摆线(Cycloid) 和变态摆线，近年 来出现了圆弧(Arc) 、抛物线(Parabola) 等。 由于渐开线齿廓具有良好的传动性能，便于制造、安 装、测量和互换性好等优点，所有目前绝大部分齿轮都采 用渐开线齿廓。 本章只讨论渐开线齿轮。
齿轮的齿廓曲线(Tooth Profile ) §10—2 齿轮的齿廓曲线
一、齿廓啮合的基本定律
(Basic Law of Tooth Profile Meshing)
齿轮传动是靠主动齿轮的齿廓依次推动从动齿轮的齿 廓来实现，且要保证定传动比（i12=ω1/ω2 ）传动，而传动 比i12却与齿廓的形状有关。 1、齿廓啮合的基本要求 、 如图10-4所示为一对相互啮合的齿 轮，主动齿轮1以ω1顺时针转动，齿廓C1 推动齿轮2的齿廓C2以ω2逆时针方向转动。 设两轮在任一点K接触，则两轮在K点处 的线速度分别为VK1、VK2。
2、传动比 (Transmission Ratio) ： 、 两轮的瞬时角速度（或转速）之比，即i12=ω1/ω2=n1/n2 由瞬心知识（三心定理）知：两啮合齿廓接触点处的 公法线nn与两轮连心线的交点P，即为两齿轮的相对速度 瞬心。则 V1P=V2P → ω1·O1P=ω2·O2P ∴ i12=ω1 /ω2= O2P/ O1P 3、齿廓啮合基本定律 、 互相啮合的一对齿轮，其传动比 等于其连心线O1O2被啮合齿廓接触点 处的公法线所分成的两段线段的反比。
下面简要介绍一下包络线法——齿轮加工时所采用的方法： 已知：i12=ω1 /ω2=C，中心距a ′ ，一个齿轮的齿廓曲 线C1；求另一齿轮上与之共轭的齿廓曲线C2。 i12、a ′
i12= r2′/ r1′ r1′+r2′=a ′
r1′、r2′
画出
两个齿轮的节圆
两节圆相切纯滚动，相当 于两圆盘相切纯滚动时
二、共轭齿廓曲线(Conjugate Profiles) 共轭齿廓是指能满足啮合基本定律（即能实现预定传 共轭齿廓 动比传动）的一对齿廓。共轭齿廓在啮合时，两齿廓接触 点（啮合点）的公法线通过节点P。 理论上，只要给定一齿轮的齿廓曲线C1，并给定中心 距O1O2和传动比i12，就可以求出与之共轭的另一齿轮的齿 廓曲线C2。这一点对于齿轮的加工是很有意义的，齿轮加 工的刀具→已知的齿廓曲线，待加工齿廓的齿轮→未知曲 线。 共轭齿廓曲线的求法，有：包络线法、鲁罗图解法、 共轭齿廓曲线的求法 齿廓法线法等。
以O1为圆心，O1P为半径作圆；以O2为圆心，O2P为 半径作圆。这两个圆分别称为齿轮 、2的节圆 齿轮1、 的节圆 的节圆，节圆半径 齿轮 用r1′、r2′（节圆上的参数用带′的字母）来表示。 节圆特征： 节圆特征 ① r1′+r2′=a′：说明一对齿轮传动时， 两节圆必相切； ② 两节圆作纯滚动，因为节点是速度 瞬心，此点具有相同的。 ③ i12=ω1 /ω2= O2P/ O1P= r2′/ r1′，传动比 等于两节圆半径的反比。
4、节点(pitch point) 和节圆(pitch circle) 、 1）节点 节点P——过齿廓啮合点的公法线与连心线的交点。 节点 2）节圆 节圆 如要求定比传动即i12=C，则应 使O2P/ O1P= C。由于O1、O2为定点， 所以欲使 O2P/ O1P= C，则节点P在 O1O2上必须是定点。 ∴ 定比传动齿轮的齿廓啮合基本定律 可以表述为：要使两齿轮作定传动 比传动，则不论两齿廓在何处接触， 过接触点所作的公法线必须与连心 线交于一定点。
图10-4
过K点作两齿廓C1、C2的公法线 nn。两齿轮在公法线nn上的分速度分 别VK1n、V K2 n。则： 1）若VK1n>V K2 n ——两齿廓互相嵌入 （齿廓干涉）； 2）若VK1n<V K2 n ——两齿廓互相分离 （传动中断）； 3）若VK1n=V K2 n ——能连续接触传动。 ∴ 齿廓啮合的基本要求 齿廓啮合的基本要求为：在齿廓接触点K的公法线nn上， 两齿廓间不能有相对运动，即两齿廓在接触点的公法线 上的分速度要相等。 VK1n =V K2 n ——齿廓啮合的基本方程式 齿廓啮合的基本方程式。 齿廓啮合的基本方程式