中考数学经典题型
中考数学十大必考题型

中考数学十大必考题型有许多,这里列举一些常见的题型:
1. 方程问题:这是中考必考题型,主要考察方程的解法、方程组的解法以及应用题等。
2. 函数图像问题:主要考察函数图像的画法、图像的变化以及根据图像求函数解析式等。
3. 圆的相关问题:中考数学中,圆是必考内容之一,包括圆的性质、圆的有关定理、定理的应用等。
4. 三角形的问题:中考数学中,三角形也是一个重要的考点,包括三角形的内角和、三角形的分类讨论、直角三角形、等腰三角形、等边三角形的性质和定理等。
5. 最值问题:中考数学中,常常会涉及到一些最值问题,如一元二次方程的最值、三角函数的最值、几何图形的最值等。
6. 统计与概率问题:中考数学中,统计与概率也是一个重要的考点,包括数据的收集、数据的整理、数据的分析、概率的求法等。
7. 开放性试题:这类试题可以考查学生的发散性思维和创新能力,是中考数学的一个热点。
8. 跨学科问题:如与物理、化学、生物等结合在一起的应用题,考查综合运用数学知识解决实际问题的能力。
9. 阅读理解题:中考数学也常涉及到一些阅读理解题,需要学生认真阅读题目并理解题目的意思。
10. 方案设计题:这类题目需要学生设计出符合题意的方案,需要学生有一定的创新能力。
需要注意的是,中考数学试题千变万化,除了以上十大必考题型外,还有许多其他类型的题目,例如难题、新题等。
考生需要掌握好基础知识,并多做练习,才能应对各种不同类型的题目。
以上是中考数学十大必考题型的简要介绍,希望能对您有所帮助。
总之,考生在备考中考数学时,需要注重基础知识的学习和练习,同时要注意培养自己的思维能力和创新能力。
数学中考常见题型选择题汇总

数学中考常见题型选择题汇总1. 选择题:已知等差数列{an}的通项公式为an=2n-1,求该数列的前n项和Sn。
2. 选择题:一个圆的半径为5cm,求该圆的面积和周长。
3. 选择题:解方程:2x^2-5x+3=0。
4. 选择题:已知a、b、c是三角形ABC的三边,且满足a^2+b^2-c^2=2ab,求三角形ABC的类型。
5. 选择题:计算下列代数式的值:2^3×4^2÷3^2。
6. 选择题:已知函数f(x)=x^2-2x+1,求函数的值域。
7. 选择题:一个正方体的边长为4cm,求该正方体的对角线长度。
8. 选择题:已知函数g(x)=x^3-3x^2+3x,求函数的导数。
9. 选择题:解不等式:3x^2-6x+2>0。
10. 选择题:已知等比数列{bn}的通项公式为bn=2^n,求该数列的前n项和Sn。
11. 选择题:计算下列代数式的值:(-3)^4÷(-2)^2。
12. 选择题:解方程:x^2-4x+3=0。
13. 选择题:已知a、b、c是三角形ABC的三边,且满足a^2+b^2-c^2=2ab,求三角形ABC的类型。
14. 选择题:一个圆的半径为5cm,求该圆的面积和周长。
15. 选择题:已知函数f(x)=x^2-2x+1,求函数的值域。
16. 选择题:一个正方体的边长为4cm,求该正方体的对角线长度。
17. 选择题:已知函数g(x)=x^3-3x^2+3x,求函数的导数。
18. 选择题:解不等式:3x^2-6x+2>0。
19. 选择题:已知等比数列{bn}的通项公式为bn=2^n,求该数列的前n项和Sn。
20. 选择题:计算下列代数式的值:(-3)^4÷(-2)^2。
21. 选择题:解方程:x^2-4x+3=0。
22. 选择题:已知a、b、c是三角形ABC的三边,且满足a^2+b^2-c^2=2ab,求三角形ABC的类型。
23. 选择题:一个圆的半径为5cm,求该圆的面积和周长。
初三数学经典总结题型

初三数学经典总结题型包括但不限于以下几种:
1. 线段、角的计算与证明:包括线段长度的计算、角的度数计算、线段与角的综合问题等。
2. 函数问题:包括一次函数、二次函数等,涉及到函数的性质、图像、最值等问题。
3. 方程与不等式问题:包括一元一次方程、一元二次方程、不等式的解法及实际应用等。
4. 三角形问题:包括三角形的性质、全等三角形、相似三角形等,涉及到三角形的边长、角度、面积等问题。
5. 四边形问题:包括平行四边形、矩形、菱形、正方形等,涉及到四边形的性质、判定条件及面积计算等。
6. 圆的问题:包括圆的性质、圆与直线的位置关系、圆与圆的位置关系等,涉及到圆的半径、直径、周长、面积等问题。
7. 统计与概率问题:包括数据的收集与整理、概率初步知识与事件的概率等,涉及到数据的分析、预测及概率的计算等。
8. 综合题:包括多个知识点的综合应用,如函数与三角形、四边形、圆的综合应用等,需要学生综合运用所学知识进行分析和解答。
中考数学大题题型归纳

中考数学大题题型归纳一、函数与方程类大题中考数学里,函数与方程类的大题可不少呢。
比如说二次函数的综合题,它可能会让你求函数的解析式,这时候你就得根据已知条件来设函数表达式啦,像一般式、顶点式或者交点式。
要是给了你几个点的坐标,那把点代入相应的表达式就能求出系数了。
还有那种函数图像与坐标轴交点的问题,求交点就是让y = 0或者x = 0去计算。
另外,方程与函数结合的题目也很常见,像是根据函数值的关系列出方程然后求解。
二、几何证明与计算类大题1. 三角形相关在三角形的证明中,全等三角形和相似三角形是重点。
证明全等的时候,要牢记那几个判定条件,像SSS、SAS、ASA、AAS还有HL(直角三角形特有的哦)。
相似三角形的判定也类似,什么三边对应成比例啦,两角相等啦。
在计算三角形的边长或者角度的时候,可能会用到三角函数,像sin、cos、tan这些,要把特殊角的三角函数值背得滚瓜烂熟才行。
等腰三角形和直角三角形也有很多出题点。
等腰三角形的两腰相等,两底角相等,要是知道其中一个条件,就能推出其他的。
直角三角形除了勾股定理a² + b² = c²之外,还有直角三角形斜边上的中线等于斜边的一半这样的性质。
2. 四边形相关四边形里平行四边形是基础,对边平行且相等,对角线互相平分这些性质要牢记。
矩形、菱形和正方形都是特殊的平行四边形,矩形的四个角是直角,菱形的四条边相等,正方形就更特殊啦,既是矩形又是菱形。
在做四边形的证明和计算大题时,要善于利用这些图形的性质和判定条件来解题。
三、统计与概率类大题1. 统计统计类大题可能会让你计算平均数、中位数、众数。
平均数就是所有数据的总和除以数据的个数;中位数呢,要先把数据从小到大或者从大到小排列,如果数据个数是奇数,中间那个数就是中位数,如果是偶数,中间两个数的平均数是中位数;众数就是数据中出现次数最多的那个数。
还有方差的计算,方差能反映数据的波动大小。
中招数学经典例题

中招数学经典例题中考数学经典例题在中考数学考试中占据重要地位,考生们应该掌握这些例题,才能够顺利应对中考数学考试。
下面我们来介绍一些经典例题。
一、平面向量1. 有两个平面向量 $\vec{a}=3\vec{i}-\vec{j}$,$\vec{b}=2\vec{i}+\vec{j}$,求它们的数量积。
2. 已知两个平面向量 $\vec{a}=2\vec{i}-\vec{j}+3\vec{k}$,$\vec{b}=-\vec{i}+5\vec{j}+2\vec{k}$,求它们的叉积。
3. 已知两个平面向量 $\vec{a}=3\vec{i}+4\vec{j}$,$\vec{b}=2\vec{i}-\vec{j}$,试求它们的夹角 $cos\alpha$。
二、三角函数1. 求证:$cos\frac{\pi}{6}=\frac{\sqrt{3}}{2}$。
2. 已知 $\frac{sinx}{cosx}+tanx=1$,求 $x$ 的值。
3. 已知正弦函数 $y=a\sin\omega x$,求 $y$ 的最大值和最小值。
三、平面几何1. 已知四边形 $ABCD$,$E$、$F$ 分别为 $AB$、$BC$ 上的点,$EF$ 与 $AD$、$CD$ 的延长线交于 $P$、$Q$,试证明:四边形$APBQ$ 与 $EPFQ$ 的面积相等。
2. 在 $\triangle ABC$ 中,点 $E$、$F$ 分别在 $AC$、$AB$ 上,$BE$ 与 $CF$ 交于点 $O$,若 $\frac{AE}{EC}=\frac{BF}{FA}$,则证明 $AO$ 是 $\triangle ABC$ 中的角平分线。
3. 已知圆 $O$ 的半径为 $r$,圆上分别取两点 $A$、$B$,则弦$AB$ 的中垂线长为多少?四、解析几何1. 已知点 $A$、$B$ 的坐标分别为 $A(-2,-1)$,$B(4,3)$,求点 $M$ 到$AB$ 的距离。
初中数学题经典题型

初中数学题经典题型一、代数式求值代数式求值是初中数学的基本题型之一,也是中考数学必考题型。
这类题主要考察学生的运算能力和对基本公式的掌握程度。
以下是一些典型的代数式求值题目:1. 求代数式(2x+3)/(x+1)的值,其中x=4。
2. 求代数式(2x+1)/(x+3)的值,其中x=2。
3. 求代数式(x^2-1)/(x+1)的值,其中x=3。
二、方程求解方程求解是初中数学中非常重要的一个知识点,也是中考数学必考题型。
这类题主要考察学生的运算能力和对方程的掌握程度。
以下是一些典型的方程求解题目:1. 求方程2x+3=7的解。
2. 求方程3x-2=5的解。
3. 求方程4x+2=7的解。
三、不等式求解不等式求解是初中数学中的一个重要知识点,也是中考数学必考题型。
这类题主要考察学生的运算能力和对不等式的掌握程度。
以下是一些典型的不等式求解题目:1. 求不等式5x+3>7的解集。
2. 求不等式2x-1<9的解集。
3. 求不等式4x-5>=0的解集。
四、函数与图像函数与图像是初中数学中的一个难点和重点,也是中考数学必考题型。
这类题主要考察学生的数形结合能力和对函数的掌握程度。
以下是一些典型的函数与图像题目:1. 已知函数y=2x-1,求当x=3时y的值。
2. 已知函数y=-x+4,求当y=3时x的值。
3. 已知函数y=x^2,求当y=4时x的值。
五、三角形与四边形三角形与四边形是初中数学中非常重要的一个知识点,也是中考数学必考题型。
这类题主要考察学生的空间思维能力和对几何图形的掌握程度。
以下是一些典型的三角形与四边形题目:1. 求等边三角形的边长为10厘米时,其面积和周长分别是多少?2. 一个矩形长为6厘米,宽为4厘米,求其对角线的长度是多少?。
初中数学中考必考题型

初中数学中考必考题型
题型一
运用同三角函数关系、诱导公式、和、差、倍、半等公式进行化简求
值类。
题型二
运用三角函数性质解题,通常考查正弦、余弦函数的单调性、周期性、最值、对称轴及对称中心。
题型三
解三角函数问题、判断三角形形状、正余弦定理的应用。
题型四
数列的通向公式得求法。
题型五
数列的前n项求和的求法。
题型六
利用导数研究函数的极值、最值。
题型七
利用导数几何意义求切线方程。
题型八
利用导数研究函数的单调性,极值、最值
题型九
利用导数研究函数的图像。
题型十
求参数取值范围、恒成立及存在性问题。
题型十一
数形结合确定直线和圆锥曲线的位置关系。
题型十二
焦点三角函数、焦半径、焦点弦问题。
题型十三
动点轨迹方程问题。
中考数学必背题型归纳总结

中考数学必背题型归纳总结在中考数学中,各种题型繁多,但是在备考过程中,有一些题型是必须要掌握的,因为它们经常出现。
本文将对中考数学中的必背题型进行归纳总结,并提供相应的解题思路和方法。
一、选择题选择题在中考数学中占据重要的比重,因此必须要熟练掌握解题技巧。
以下是几种常见的选择题题型及解题思路:1. 增减百分数题增减百分数题是一种常见的选择题题型,要求计算某个数值的增加或减少百分之多少。
解题时,根据题目给出的百分数,将要计算的数值乘以相应的百分数即可。
例如,计算120的60%是多少,可以直接将120乘以0.6得到72,因此答案为72。
2. 几何图形题几何图形题在中考数学中也经常出现,解题时需要根据题目给出的条件进行分析。
常见的几何图形题有平行四边形的性质、三角形的性质等。
解题时可以根据题目条件绘制几何图形,并运用相应的几何定理进行推理。
3. 坐标题坐标题是中考数学中的基础题型,要求对平面上的点进行坐标定位。
解题时需要根据题目给出的条件,确定点的坐标,并进行相应的计算。
在解答坐标题时,可以通过绘制坐标图、运用距离公式等方法进行求解。
二、填空题填空题在中考数学中也是常见的题型之一,考查学生对基础知识的掌握程度。
以下是几种常见的填空题题型及解题思路:1. 算式填空题算式填空题要求填写适当的数值,使得等式成立。
解题时需要分析等式中各个数值的关系,并利用已知的条件来求解。
例如,对于等式5 + □ = 10,可以通过计算得到□的数值为5。
2. 几何图形填空题几何图形填空题主要考查学生对几何图形性质的理解。
解题时可以根据已知条件对图形进行推理,并根据已有的线段长度、角度等信息填空。
在解答几何图形填空题时,需要灵活运用几何定理和计算方法。
三、解答题解答题是中考数学中较为复杂的题型,要求学生进行详细的计算和推理。
以下是几种常见的解答题题型及解题思路:1. 单方程解答题单方程解答题要求求解方程中的未知数。
解答此类题目时,需要运用一些解方程的方法,如等式相加减、等式相乘除等,将方程转换为较简单的形式,并求解出方程中的未知数。
数学中考常见题型选择题汇总

数学中考常见题型选择题汇总1. 选择题:已知一个等差数列的前三项分别是a、b、c,且a+b+c=9,a+b=11,a+c=8,求a、b、c的值。
2. 选择题:如果一个三角形的两个内角分别是120度和30度,那么第三个内角的度数是多少?3. 选择题:一个长方形的长是8厘米,宽是3厘米,求这个长方形的周长和面积。
4. 选择题:一个正方体的棱长是4厘米,求这个正方体的表面积和体积。
5. 选择题:一个圆的半径是5厘米,求这个圆的周长和面积。
6. 选择题:已知两个正方体的体积分别是16立方厘米和8立方厘米,求这两个正方体的棱长。
7. 选择题:一个长方体的长是8厘米,宽是3厘米,高是2厘米,求这个长方体的对角线长度。
8. 选择题:一个等差数列的前两项分别是3和7,公差是2,求这个等差数列的第10项。
9. 选择题:一个圆锥的底面半径是3厘米,高是4厘米,求这个圆锥的体积和表面积。
10. 选择题:已知一个三角形的两个内角分别是60度和90度,求第三个内角的度数。
11. 选择题:一个长方体的长是6厘米,宽是4厘米,高是2厘米,求这个长方体的对角线长度。
12. 选择题:一个正方体的棱长是6厘米,求这个正方体的表面积和体积。
13. 选择题:一个圆的半径是8厘米,求这个圆的周长和面积。
14. 选择题:已知一个等差数列的前两项分别是1和4,公差是3,求这个等差数列的第10项。
15. 选择题:一个圆锥的底面半径是4厘米,高是6厘米,求这个圆锥的体积和表面积。
16. 选择题:已知一个三角形的两个内角分别是45度和45度,求第三个内角的度数。
17. 选择题:一个长方体的长是5厘米,宽是3厘米,高是2厘米,求这个长方体的对角线长度。
18. 选择题:一个正方体的棱长是5厘米,求这个正方体的表面积和体积。
19. 选择题:一个圆的半径是10厘米,求这个圆的周长和面积。
20. 选择题:已知一个等差数列的前两项分别是2和7,公差是3,求这个等差数列的第10项。
中考数学经典难题集锦

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、Ptolemy (托勒密)定理:设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD . (初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:1≤L <中考数学经典难题集锦2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC=∠ACB =800,D 、E 分别是AB 、AC 上的点,∠EBA =200,求∠BED 的度数.。
南充市数学中考24题常见题型

南充市数学中考24题常见题型
南充市数学中考24题常见题型有:
1. 几何证明:主要涉及三角形、四边形、圆等图形的性质和定理,需要进行严密的逻辑推理和证明。
2. 函数与方程:主要考查一次函数、二次函数、反比例函数等函数的性质和图象,以及一元二次方程的解法。
3. 代数运算:主要涉及整式、分式、根式的化简和求值,以及实数的运算和不等式的求解。
4. 概率与统计:主要考查概率的基本概念、统计图表、平均数、中位数、众数、方差等统计量及其计算方法。
5. 坐标系与图形变换:主要考查平面直角坐标系、函数的图象与性质,以及图形的平移、对称、相似等变换。
6. 开放性问题:主要涉及条件开放、策略开放、结论开放等问题,需要学生灵活运用所学知识进行探究和推理。
7. 应用性问题:主要涉及生活中的实际问题,如行程问题、工程问题、利润问题等,需要学生建立数学模型进行解决。
以上是南充市数学中考24题常见题型的一些总结,希望对你有所帮助。
中考高等数学常见题型及解题思路

中考高等数学常见题型及解题思路中考数学常见题型及解题思路中考数学对于每一位初中生来说都是一项重要的挑战。
要在中考数学中取得好成绩,不仅需要扎实的基础知识,还需要熟练掌握各种题型的解题思路。
以下是中考数学中常见的题型及对应的解题思路。
一、选择题选择题是中考数学中最常见的题型之一,通常占据了较大的分值。
1、直接法直接从题设条件出发,通过准确的运算、严谨的推理,得出正确的结论,然后对照选项做出判断。
2、排除法根据题目所给的条件,对选项进行逐一分析,排除不符合条件的选项,从而得出正确答案。
3、特殊值法通过选取符合条件的特殊值代入题目进行计算和判断,往往能快速得到答案。
4、图像法对于一些与函数、几何图形相关的选择题,可以通过画出图像来直观地分析问题,从而做出选择。
例如:若关于 x 的一元二次方程$x^2 2x + m = 0$有两个不相等的实数根,则 m 的取值范围是()A $m < 1$B $m > 1$C $m\leqslant 1$D $m\geqslant 1$解题思路:对于一元二次方程$ax^2 + bx + c = 0$($a≠0$),其判别式为$\Delta = b^2 4ac$。
当$\Delta > 0$时,方程有两个不相等的实数根。
在方程$x^2 2x + m = 0$中,$a = 1$,$b =-2$,$c = m$,所以$\Delta =(-2)^2 4×1×m > 0$,解得$m < 1$,故选 A。
二、填空题填空题要求考生直接填写答案,注重考查对基础知识的掌握和简单的计算能力。
1、概念性填空题这类题目主要考查数学中的基本概念、定理、公式等,需要考生对相关知识有清晰的理解和记忆。
2、计算性填空题需要进行一定的计算才能得出答案,要注意计算的准确性和规范性。
3、推理填空题通过对题目所给条件的分析和推理,得出结论。
例如:因式分解:$x^3 4x =$________。
中考数学专题练习 十种题型试题

币仍仅州斤爪反市希望学校十种题型类型一:实数混合运算1.计算:()001260cos 2214π-+-⎪⎭⎫ ⎝⎛+-. 2.计算:20245sin 18)12013(-︒+-.3.计算:13160cos 216-⎪⎭⎫⎝⎛--- 。
4.()22171382-⎪⎭⎫ ⎝⎛---+--• 类型二:化简求值 1.先化简,再求值:()()()()b a a b a b a b a +--++-22 其中31-=x ,6-=y2.先化简,再求值 ()xx x x x 224422+÷+++ ,其中 x =2 .3.化简: 1211112-÷⎪⎭⎫⎝⎛--+x x x 类型三:方程〔组〕不等式〔组〕1.解方程组:⎩⎨⎧=+=-1634y x y x 2.解方程:0322=--x x3.关于x 的一元二次方程022=+-m x x 有两个不相等的实数根21,x x〔1〕求m 的取值范围。
〔2〕如果82121=•-+x x x x ,求m 的值。
4.解不等式组:⎩⎨⎧-≤-->+128,312x x x ,并把解集在数轴上表示出来.类型四:列方程组解应用题1.某城规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的局部按每千米另收费.甲说:“我乘这种出租车走了11千米,付了17元〞;乙说:“我乘这种出租车走了23千米,付了35元〞.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?2.某商场方案购进A ,B 两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:类型 价格 进价〔元/盏〕 售价〔元/盏〕 A 型 30 45 B 型5070〔1〕假设商场预计进货款为3500元,那么这两种台灯各购进多少盏?〔2〕假设商场规定B 型台灯的进货数量不超过A 型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元? 类型五:函数题1.某出租车计费方法如下列图,x 〔km 〕表示行驶里程,y 〔元〕表示车费, 请根据图象答复下面的问题:〔1〕出租车的起步价是多少元?当x >3时,求y 关于x 的函数关系式. 〔2〕假设某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.2.“五一节“期间,申老师一家自驾游去了离家170千米的某地,下面是 他们离家的距离y (千米)与汽车行驶时间x 〔小时〕之间的函数图象。
中考数学10道经典题型分析
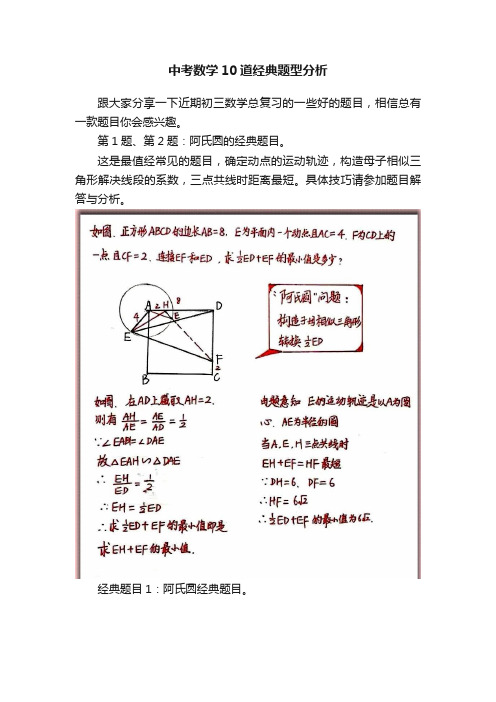
中考数学10道经典题型分析跟大家分享一下近期初三数学总复习的一些好的题目,相信总有一款题目你会感兴趣。
第1题、第2题:阿氏圆的经典题目。
这是最值经常见的题目,确定动点的运动轨迹,构造母子相似三角形解决线段的系数,三点共线时距离最短。
具体技巧请参加题目解答与分析。
经典题目1:阿氏圆经典题目。
经典题目2:阿氏圆问题。
第3题:费马点问题。
费马点问题也是最值问题最常见的题型,三线线段之和最短,通过旋转构造全等三角形,实现线段的转换(移到同一直线上),四点共圆时,线段之和最短。
经典题目3:胡不归问题。
第4题:胡不归问题。
胡不归问题同样的线段最值常见问题,AB+kCD的最值问题,首先要解决其中一条线段的K值,阿氏圆通常采用构造母子相似三角形来解决这个问题,而胡不归通常采用三角函数来解决这个问题。
这道综合题还是很不错的,值得练一练。
经典题目4:胡不归问题。
第5,6题:二次函数中的a,b,c问题。
在选择题中,这也算是比较有点难度的问题了,而且考试的频率往往非常高,需要熟练掌握。
基本的技巧我已经在下面列出了。
经典题目5:二次函数多结论问题。
经典题目7:二次函数多结论问题。
第7题:相似三角形综合题目。
这是一次模拟测验的倒数第2题,三角形综合题。
这道题比较好,是因为它不只一种解法,尤其是在第3问中,有不同的作辅助线的方法,有点意思。
经典题目7:三角形综合题。
第8题:中考压轴题模拟题。
这是深圳南山区联考模拟卷的压轴题,最后一问其实并不难,根据题意不难理解,动点的运动轨迹是某个圆的一段弧,在同一个圆中,同弧(弦)所对的圆周角相等,从而可以确定动点的运动轨迹,三点共线时,由距离最短。
具本思路和过程可参照下面答案。
经典题目8:中考压轴题目。
第9题:平行四边形的存在性问题。
这道题目真的很不错,弄懂这道题目,平行四边形的存在性问题就基本弄懂了。
我在参考答案中列举了三种常见的方法,其中包括点的坐标平移法,中点坐标(平行四边形对角顶点坐标之间的关系要熟练掌握)等。
中考数学经典习题(50题)

中考数学经典大题1.已知在△ABC中,∠ABC=90°,AB=6,BC=8.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.(1)当点P在线段AB上时,求证:△APQ~△ACB;(2)当△PQB是等腰三角形时,求AP的长.2.如图,对称轴为x=−1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(-3,0).(1)求点B的坐标;(2)已知a=1,C为抛物线与y轴的交点.①若点P是抛物线上第三象限内的点,是否存在点P,使得S△POC=4S△BOC,若存在,求点P的坐标;若不存在,请说明理由.②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.③若M是x轴上方抛物线上的点,过点M作MN⊥x轴于点N,若△MNO与△OBC相似,求M点的坐标.3.如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径.4. 如图,已知函数y =−x 2+2x +3与坐标轴分别交于A 、D 、B 三点,顶点为C.(1)求△BAD 的面积;(2)点P 是抛物线上一动点,是否存在点P ,使S △ABP =12S △ABC ?若存在,求出点P 的坐标;若不存在,请说明理由;(3)在轴上是否存在一点Q ,使得△DOQ 与△ABC 相似,如果存在,求出点P 的坐标,如果不存在,请说明理由.5. 如图,在平面直角坐标系中,四边形ABCD 是以AB 为直径的⊙M 的内接四边形,点A 、B在x 轴上,△MBC 是边长为2的等边三角形。
过点M 作直线ι与x 轴垂直,交⊙M 于点E ,垂足为点M ,且点D 平分AĈ. (1)求过A 、B 、E 三点的抛物线的解析式;(2)求证:四边形AMCD 是菱形;(3)请问在抛物线上是否存在一点P ,使得△ABP 的面积等于定值5?若存在,请求出所有的点P 的坐标;若不存在,请说明理由.6. 如图1,直角△ABC 中,∠ABC=90°,AB 是⊙O 的直径,⊙O 交AC 于点D ,取CB 的中点E ,DE 的延长线与AB 的延长线交于点P .(1)求证:PD 是⊙O 的切线;(2)若OB=BP ,AD=6,求BC 的长;(3)如图2,连接OD ,AE 相交于点F ,若tan ∠C =2,求AF FE 的值.7. 已知抛物线y =ax 2+bx +c 经过点A (3,2),B (0,1)和点C (-1,−23).(1)求抛物线的解析式;(2)如图,若抛物线的顶点为P ,点A 关于对称轴的对称点为M ,过M 的直线交抛物线于另一点N (N 在对称轴右边),交对称轴于F ,若S △PFN =4S △PFM ,求点F 的坐标;(3)在(2)的条件下,在轴上是否存在点G ,使△BMA 与△MBG 相似?若存在,求点G 的坐标;若不存在,请说明理由.8. 如图,PB 切⊙O 于B 点,直线PO 交⊙O 于点E 、F ,过点B 作PO 的垂线BA ,垂足为点D ,交⊙O 于点A ,延长AO 交⊙O 于点C ,连结BC ,AF.(1)直线PA 是否为⊙O 的切线,并证明你的结论;(2)若BC=16,⊙O 的半径的长为17,求tan ∠AFD 的值;(3)若OD :DP=1:3,且OA=3,则图中阴影部分的面积为?9. 将抛物线C 1:y =x 2平移后的抛物线C 2与x 轴交于A 、B 两点(点A 在点B 的左边)与y 轴负半轴交于C 点,已知A (-1,0),tan ∠CAB =3.(1)求抛物线C 2的解析式;(2)若点P 是抛物线C 2上的一点,连接PB ,PC.求S △BPC =34S △CAB 时点P 的坐标; (3)D 为抛物线C 2的顶点,Q 是线段BD 上一动点,连接CQ ,点B ,D 到直线CQ 的距离记为d 1,d 2,试求出d 1+d 2的最大值,并求出此时Q 点坐标.10. 如图1,AB 为⊙O 的直径,TA 为⊙O 的切线,BT 交⊙O 于点D ,TO 交⊙O 于点C 、E.(1)若BD=TD ,求证:AB=AT ;(2)在(1)的条件下,求tan ∠BDE 的值;(3)如图2,若BD TD =43,且⊙O 的半径r=√7,则图中阴影部分的面积为?11. 如图,过A (1,0),B (3,0)作x 轴的垂线,分别交直线y =4−x 于C 、D 两点.抛物线y =ax 2+bx +c 经过O 、C 、D 三点.(1)求抛物线的表达式;(2)点M 为直线OD 上的一个动点,过M 作x 轴的垂线交抛物线于点N ,问是否存在这样的点M ,使得以A 、C 、M 、N 为顶点的四边形为平行四边形?若存在,求此时点M 的横坐标;若不存在,请说明理由;(3)若点P 为抛物线上的一点,连接PD ,PC. 求S △PCD =13S △CDB 时点P 的坐标.(4)若△AOC 沿CD 方向平移(点C 在线段CD 上,且不与点D 重合),在平移的过程中 △AOC 与△OBD 重叠部分的面积记为S ,试求S 的最大值.12. 如图,点C 在以AB 为直径的⊙O 上,AD 与过点C 的切线垂直,垂足为点D ,AD 交⊙O 于点E.(1)求证:AC 平分∠DAB ;(2)连接BE 交AC 于点F ,若cos ∠CAD =45,求AF FC 的值.13. 如图,在矩形ABCD 中,E 是AB 边的中点,沿EC 对折矩形ABCD ,使B 点落在点P 处,折痕为EC ,连结AP 并延长交CD 于F 点.(1)求证:四边形AECF 为平行四边形;(2)若△AEP 是等边三角形,连结BP ,求证:△APB ≅△EPC ;(3)若矩形ABCD 的边AB=6,BC=4,求△CPF 的面积.14. 如图,在平面直角坐标系xoy 中,抛物线y =ax 2−2ax −3a (a <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),经过点A 的直线l :y =kx +b 与y 轴负半轴交于点C ,与抛物线的另一个交点为D ,且CD=4AC.(1)直接写出点A 的坐标,并求出直线l 的函数表达式(其中k 、b 用含a 的式子表示);(2)点E 是直线l 上方的抛物线上的动点,若△ACE 的面积的最大值为54,求a 的值; (3)设P 是抛物线的对称轴上的一点,点Q 在抛物线上,以点A 、D 、P 、Q 为顶点的四边形能否成为矩形?若能,求出点P 的坐标;若不能,请说明理由.15. 如图,已知AB 为⊙O 的直径,PA 与⊙O 相切于点A ,线段OP 与弦AC 垂直并相交于点D ,OP 与弧AC 相交于点E ,连接BC.(1)求证:PA ·BC=AB ·CD.(2)若PA=10,sin P =35,求PE 的长.16. 已知:点P 是平行四边形ABCD 对角线AC 所在直线上的一个动点(点P 不与点A 、C 重合),分别过点A 、C 向直线BP 作垂线,垂足分别为点E 、F ,点O 为AC 的中点.(1)当点P 与点O 重合时如图1,求证:OE=OF ;(2)直线BP 绕点B 逆时针方向旋转,当∠OFE=30°时.①若转到如图2的位置,线段CF 、AE 、OE 之间有一个不变的相等关系式,请写出这个关系式.(不用证明)②若转到图3的位置,猜想线段CF 、AE 、OE 之间有怎样的数量关系?请予以证明.17. 已知如图,在平面直角坐标系xoy 中,点A 、B 、C 分别为坐标轴上的三个点,且OA=1,OB=2,OC=4.(1)求经过A 、B 、C 三点的抛物线的解析式;(2)在平面直角坐标系xoy 中是否存在一点P ,使得以点A 、B 、C 、P 为顶点的四边形为菱形?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)若点M 为该抛物线上一动点,在(2)的条件下,请求出当|PM -AM|为最大值时,点M 的坐标,并直接写出|PM -AM|的最大值.18. 如图,在Rt △ABC 中,∠C=90°,BD 平分∠ABC ,DE ⊥BD 交AB 于E ,⊙O 是△BDE 的外接圆,交BC 于点F.(1)求证:AC 是⊙O 的切线;(2)连接EF ,若BC=9,CA=12,求EF AC 的值.19. 如图,在正方形ABCD 中,AB=5,P 是BC 边上任意一点,E 是BC 延长线上一点,连接AP ,作PF ⊥AP ,使PF=PA ,连接CF 、AF ,AF 交CD 边于点G ,连接PG.(1)求证:∠GCF=∠FCE ;(2)判断线段PG ,PB 与DG 之间的数量关系,并证明你的结论;(3)若BP=2,在直线AB 上是否存在一点M ,使四边形DMPF 是平行四边形,若存在,求出BM 的长度,若不存在,请说明理由.20. 已知抛物线y =−12x 2+bx +c 与y 轴交于点C ,与x 轴的两个交点分别为A (-4,0),B (1,0). (1)求抛物线的解析式;(2)已知点P 在抛物线上,连接PC ,PB ,若△PBC 是以BC 为直角边的直角三角形,求点P 的坐标;(3)已知点E 在x 轴上,点F 在抛物线上,是否存在以A ,C ,E ,F 为顶点的四边形是平行四边形?若存在,请直接写出点E 的坐标;若不存在,请说明理由.21. 如图1,直角△ABC 中,∠ABC=90°,AB 是⊙O 的直径,⊙O 交AC 于点D ,取CB 的中点E ,DE 的延长线与AB 的延长线交于点P.(1)求证:PD 是⊙O 的切线;(2)如图2,连接OD ,AE 相交于点F ,若tan ∠C =2,求AF FE 的值.22.已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.23.如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(-3,0)和点B(1,0).与y轴交于点C,顶点为D.(1)求顶点D的坐标(用含a的代数式表示);(2)若△ACD的面积为3.①求抛物线的解析式;②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.24.如图1,△ABC中,AB=AC,AE平分∠BAC,BM平分∠ABC交AE于点M,经过点B,M两点的⊙O交BC于点G,交AB于点F,FB恰好为⊙O的直径.(1)求证:AE是⊙O的切线;(2)若AC=6,CE=4,EN⊥AB于点N,求BN的长;(3)如图2,若CBAB =23,求tan∠MBA的值.25. 如图,抛物线y =−12x 2+bx +c 与x 轴分别相交于点A (-2,0)、B (4,0),与y 轴交于点C ,顶点为点P.(1)求抛物线的解析式;(2)动点M 、N 从点O 同时出发,都以每秒1个单位长度的速度分别在线段OB 、OC 上向点B 、C 方向运动,过点M 作x 轴的垂线交BC 于点F ,交抛物线于点H.①当四边形OMHN 为矩形时,求点H 的坐标;②是否存在这样的点F ,使△PFB 为直角三角形?若存在,求出点F 的坐标;若不存在,请说明理由.26. 已知:如图,⊙O 的直径AB 垂直于弦CD ,过点C 的切线与直径AB 的延长线相交于点P ,连结PD.(1)求证:PD 是⊙O 的切线;(2)求证:PD 2=PB ·PA ;(3)若PD=4,tan ∠CDB =12,求直径AB 的长.27. 已知抛物线y =a (x +3)(x −1)(a ≠0),与x 轴从左至右依次相交于A 、B 两点,与y 轴相交于点C ,经过点A 的直线y =−√3x +b 与抛物线的另一个交点为D.(1)若点D 的横坐标为2,求抛物线的解析式;(2)若在第三象限内的抛物线上有点P ,是以A 、B 、P 为顶点的三角形与△ABC 相似,求点P 的坐标;(3)在(1)的条件下,设点E 是线段AD 上的一点(不含端点),连接BE.一动点Q 从点B 出发,沿线段BE 以每秒1个单位的速度运动到点E ,再沿线段ED 以每秒2√33个单位的速度运动到点D 后停止,问当点E 的坐标是多少时,点Q 在整个运动过程中所用时间最少?28.如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.x+2与x轴、y轴分别交于B、C两点,经过B、C 29.如图,在平面直角坐标系中,直线y=−23两点的抛物线与x轴的另一交点为A(-1,0).(1)求B、C两点的坐标及该抛物线的解析式;(2)P是线段BC上的一个动点(不与B、C重合),过点P作直线L//y轴,交抛物线于点E,交x轴于点F,设P点的横坐标是m,△BCE的面积为S.①求S与m的函数关系式,并写出自变量m的取值范围;②在①的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并判断△OBE的形状;若不存在,请说明理由;③Q是线段AC上的一个动点(不与点A、C重合),且PQ//x轴,试问在x轴上是否存在点R,使△PQR为等腰直角三角形?若存在,求出R的坐标;若不存在,请说明理由.30.我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状(不必证明).31. 如图,已知抛物线y =ax 2+bx +c 与x 轴交于A (-1,0)、B 两点(点A 在点B 左侧),其顶点为M (1,4),MA 交y 轴于点N ,连接OM.(1)求此抛物线的函数表达式;(2)若P 为(1)中抛物线上一点,当S △OAM =S △PAM 时,求P 点的坐标;(3)将(1)中的抛物线沿y 轴折叠,使点A 落在点D 处,连接MD ,Q 为(1)中的抛物线上的一点,直线NQ 交x 轴于点G ,当Q 点在抛物线上运动时,是否存在点Q ,使△ANG 与△ADM 相似?若存在,求出符合条件的Q 点的坐标;若不存在,请说明理由.32. 如图1,△ABC 内接于⊙O ,∠BAC 的平分线交⊙O 于点D ,交BC 于点E (BE >EC ),且BD=2√3.求过点D 作DF//BC ,交AB 的延长线于点F.(1)求证:DF 为⊙O 的切线;(2)若∠BAC=60°,DE=√7,求图中阴影部分的面积;(3)若AB AC =43,DF+BF=8,如图2,求BF 的长.33. 如图,在平面直角坐标系中,已知抛物线y =x 2+bx +c 过A 、B 、C 三点,点A 的坐标是(3,0),点C 的坐标是(0,-3),动点P 在抛物线上.(1)求b ,c 的值,B 的坐标;(直接写出结果)(2)是否存在点P ,使得△ACP 是以AC 为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,说明理由;(3)过动点P 作PE ⊥y 轴于点E ,交直线AC 于点D ,过点D 作x 轴的垂线.垂足为F ,连接EF ,当线段EF 的长度最短时,求出点P 的坐标.34.如图,经过的三个顶点A、C、D作⊙O,交BC边于点H,AB切⊙O于点A,延长半径AO交CD于E,交⊙O于F,P是射线AF上一点,且∠PCD=2∠DAF(1)求证:AB=AH;(2)求证:PC是⊙O的切线;(3)若AB=2,AD=√17,求⊙O的半径.35.如图,抛物线y=ax2+bx+c的图象经过点A(-1,0)、B(3,0)、C(0,3),D为抛物线的顶点.(1)求抛物线的解析式及点D的坐标;(2)点C关于抛物线对称轴的对称点为点E,连接BC,BE,求tan∠CBE的值;(3)点M是抛物线对称轴上一动点,若△DMB与△BCE相似,求点M的坐标.36.如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.(1)求证:DF是⊙O的切线;(2)求证:OC2=OE·OP;(3)求线段EG的长.37.如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3).(1)求抛物线的解析式;(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积;(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.38.在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB、BC(或它们的延长线)于点M,N.(1)观察图1,直接写出∠AEM与∠BNE的关系为:▲▲▲;(不用证明)(2)如图1,当M、N都分别在AB、BC上时,可探究出BN与AM的关系为:▲▲▲;(不用证明)(3)如图2,当M、N都分别在AB、BC的延长线上时,(2)中BN与AM的关系式是否仍然成立?若成立,请说明理由;若不成立,写出你认为成立的结论,并说明理由.x+c经过B、C 39.如图,直线y=−x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+12两点,点E是直线BC上方抛物线上的一动点.(1)求抛物线的解析式;,请求出点E和点M (2)过点E作y轴的平行线交直线BC于点M,交x轴于点F,当S△BEC=32的坐标;(3)在(2)的条件下,当E点的横坐标为1时,在EM上是否存在点N,使得△CMN和△CBE 相似?如果存在,请直接写出点N的坐标;如果不存在,请说明理由.40.如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.(1)求证:CE是⊙O的切线;(2)若AE=1,CE=2,求⊙O的半径.41.在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.(1)观察猜想:如图1,当点D在线段BC上时,①BC与CF的位置关系为:②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)(2)数学思考:如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请予以证明;若不成立,请你写出正确结论再给予证明;(3)拓展延伸:如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.已知AB=2√2,CD=1BC,请求出CF的长.442.如图,在平面直角坐标系中,已知抛物线y=ax2+bx−8与x轴交于点A、B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A、D的坐标分别为(-2,0),(6,-8).(1)求抛物线的解析式,并分别求出点B和点E的坐标;(2)探究抛物线上是否存在点F使得△FOE≅△FCE?若存在,请直接写出点F的坐标,若不存在,请说明理由;(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究,当M为何值时,△OPQ为等腰三角形.43.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点G,过点D作EF⊥AC于点E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)当AB=5,BC=6时,求tan∠BAC的值.44.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF.(1)如图1,当点D在线段BC上时,求证:CF+CD=BC;(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变:①请直接写出CF,BC,CD三条线段之间的关系;②若正方形ADEF的边长为2√2,对角线AE,DF相交于点O,连接OC.求OC的长度.x2+bx+c与x轴分别相交于点A(-2,0),B(4,0),与y轴交于点45.如图,抛物线y=−12C,顶点为点P.(1)求抛物线的解析式;(2)动点M、N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.①当四边形OMHN为矩形时,求点H的坐标;②是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.46.如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.(1)求证:∠1=∠BAD;(2)求证:BE是⊙O的切线.47.我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”.(1)概念理解:请你根据上述定义举一个等邻角四边形的例子:▲▲▲;(2)问题探究:如图1,在等邻角四边形ABCD中,∠DAB=∠ABC,AD,BC的中垂线恰好交于AB边上一点P,连结AC,BD,试探究AC与BD的数量关系,并说明理由;(3)应用拓展:如图2,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,BC=BD=3,AB=5,将Rt △ABD绕着点A顺时针旋转α(0°<∠α<∠BAC)得到Rt△AB,D,(如图3),当凸四边形AD,BC为等邻角四边形时,求出它的面积.48.如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-3,0),B(5,0),C(0,5)三点,O为坐标原点.(1)求此抛物线的解析式;个单位长度,再向右平移n(n>0)(2)若把抛物线y=ax2+bx+c(a≠0)向下平移133个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.49. 如图1,在正方形ABCD 中,P 是对角线BD 上的一点,点E 在AD 的延长线上,且PA=PE.(1)判断△PCE 的形状;(不必说明理由)(2)如图2,若点P 是BD 延长线上一点,其他条件不变,则(1)的结论是否仍然成立,请说明理由;(3)如图3,把“正方形ABCD ”改成“菱形ABCD ”,其他条件不变,当∠ABC=120°时,连接CE ,试探究线段AP 与线段CE 的数量关系,并说明理由.50. 如图,在△ABC 中,∠ABC=∠ACB ,以AC 为直径的⊙O 分别交AB ,BC 于点M ,N ,点P 在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP 是⊙O 的切线;(2)若BC=2√5,sin ∠BCP =√55,求点B 到AC 的距离;(3)在(2)的条件下,求△ACP 的周长.51. 如图,抛物线y =−x 2+bx +c 与直线y =12x +2交于C ,D 两点,其中点C 在y 轴上,点D 的坐标为(3,72),点P 是y 轴右侧的抛物线上一动点,过点P 作PE ⊥x 轴于点E ,交CD 于点F.(1)求抛物线的解析式;(2)若点P 的横坐标为m ,当m 为何值时,以O ,C ,P ,F 为顶点的四边形是平行四边形?请说明理由;(3)若存在点P ,使∠PCF=45°,请直接写出相似的点P 的坐标.。
中考数学复习题三种典型题

中考数学复习题三种典型题中考数学复习题三种典型题数学作为一门重要的学科,对于中学生来说是必修的科目之一。
中考数学试卷中,常常会出现一些典型的题型,这些题型在考试中占有一定的比重。
在复习阶段,了解并掌握这些典型题型,对于提高数学成绩是非常有帮助的。
本文将介绍中考数学复习中的三种典型题型。
第一种典型题是选择题。
选择题是中考数学试卷中最常见的题型之一。
它的特点是给出几个选项,考生需要选择其中一个作为答案。
在复习过程中,我们需要掌握一些解题技巧。
首先,要仔细阅读题目,理解题目的意思。
其次,要对选项进行分析,排除一些明显不符合题意的选项。
最后,要根据题目的要求进行计算或推理,选择正确的选项。
选择题的答案通常是唯一的,因此要仔细思考,避免粗心错误。
第二种典型题是填空题。
填空题在中考数学试卷中也是比较常见的题型。
它的特点是给出一些空格,考生需要根据题目的要求填写相应的数字或符号。
在复习过程中,我们需要注意一些填空题的解题技巧。
首先,要仔细阅读题目,理解题目的要求。
其次,要根据已知条件进行计算或推理,找到填空的答案。
填空题的答案通常是唯一的,因此要仔细计算,避免出现计算错误。
第三种典型题是解答题。
解答题在中考数学试卷中也是比较重要的题型之一。
它的特点是给出一个问题,考生需要通过计算、推理或证明等方法来解答问题。
在复习过程中,我们需要掌握一些解答题的解题技巧。
首先,要仔细阅读问题,理解问题的意思。
其次,要根据已知条件进行计算、推理或证明,找到问题的答案。
解答题的答案通常不是唯一的,因此要灵活运用所学的知识,避免陷入固定的思维模式。
除了掌握这三种典型题型的解题技巧,我们还需要在复习过程中多做一些相关的练习题。
通过做题可以加深对知识的理解和记忆,提高解题的能力。
在做题过程中,我们要注意题目的要求,避免粗心错误。
如果遇到不会做的题目,可以先尝试一下,如果还是无法解答,可以向老师或同学请教。
在复习过程中,我们还可以参考一些数学辅导书籍或网上的学习资源,扩大自己的数学知识面。
中考数学20道经典几何题

中考数学20道经典几何题1.已知三角形ABC,AB=AC,∠A=36°,求BC与AB的比值。
2.直角三角形ABC中,∠C=90°,AC=3,BC=4,求斜边AB上的高。
3.四边形ABCD是平行四边形,对角线AC、BD相交于点O,若AB=5,AC=8,BD=6,求平行四边形ABCD的面积。
4.三角形ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且DE⊥DF,求证:BE²+CF²=EF²。
5.圆O的半径为5,弦AB=8,求圆心O到弦AB的距离。
6.等腰梯形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=3,BC=7,求梯形ABCD的周长。
7.三角形ABC中,∠C=90°,∠A=30°,BC=3,求三角形ABC的外接圆半径。
8.正方形ABCD的边长为4,E是BC中点,F是CD上一点,且CF=1,求∠AEF的度数。
9.三角形ABC是等边三角形,D是AC中点,E在BC延长线上,CE=CD,求证:BD=DE。
10.矩形ABCD中,AB=6,BC=8,点P在AD上,且AP=2,求点P到对角线BD的距离。
11.三角形ABC中,AB=AC,D是BC中点,DE⊥AB于E,DF⊥AC于F,若AB=5,DE=3,求DF的值。
12.菱形ABCD的对角线AC=6,BD=8,求菱形ABCD的边长。
13.三角形ABC中,∠B=90°,AB=3,BC=4,以BC为直径作圆O,交AC于D,求AD的长。
14.等腰三角形ABC中,AB=AC,∠A=120°,AB=4,求三角形ABC的面积。
15.三角形ABC中,∠C=90°,AC=4,BC=3,以AC为一边向三角形外作等腰直角三角形ACD,∠ACD=90°,求BD的长。
16.圆O的直径AB=10,弦AC=6,∠BAC的平分线交圆O于D,求CD的长。
中考数学常见题型解析

中考数学常见题型解析数学作为中考必考科目之一,对于学生来说是一项不可忽视的重要考试内容。
而在数学中,各种题型也是我们必须熟练掌握的。
本文将对中考数学中常见的题型进行解析,帮助同学们更好地备考。
一、选择题选择题是中考数学中最常见的题型之一。
它的特点是给出若干个选项,只有一个选项是正确的,考生需要根据题目的要求选择正确答案。
下面以常见的三种选择题为例进行解析。
1. 单项选择题单项选择题是中考数学中最基础的题型,也是最容易的题型之一。
在这类题目中,通常有一个问题和四个选项。
【例题】若函数y=ax²+bx+c的图象与x轴交于两个点,且交点的横坐标之和等于3,纵坐标之和等于2,则a+b+c=?A. -2B. -1C. 0D. 1解析:由题意可知,函数图象与x轴交点的纵坐标之和等于零。
根据函数的定义可知,纵坐标为0时,横坐标为3。
因此,该函数的一个根为x=3。
另一个根为x=0。
根据二次函数性质可知,两根之和为-x₁/x₂。
所以,x₁+x₂=-3。
因此,a+b+c=0。
所以答案为C。
2. 判断题判断题是中考数学中常见的题型之一。
它的特点是给出一个命题,考生需要判断该命题的正确性。
【例题】对于任意的实数a,有a^2≥0。
解析:根据平方的性质可知,任意实数的平方都大于等于零,因此该命题为真。
3. 完形填空完形填空是一种较为复杂的选择题类型。
它通常给出一篇文章,文章中有若干个空格,考生需要根据上下文的意思选择正确的答案来填充空格。
【例题】阅读下面的短文,从每题所给的A、B、C、D四个选项中选出可以填入空白处的最佳选项。
Life is like a marathon. We may start at the ____1____ time, but we have to run our own race on our own course. We can't go too fast, or we may die before reaching __2__ finish. We can't go too slow, or everyone may__3__ us and make fun of us.Along the way, we will make many friends. Some will __4__ with us for a while, and some will stay with us for the long run. Friends are like running shoes----they help ________ (5) the journey much better. They may ____6__ us or encourage us when we're feeling ____7__. The most important thing is they __8__ us for who we are.Along the way, there will be a lot of _______ (9). We may lose the race, feel pain and want to give up. But we __10__ give up. We have to keeprunning. After all, life is not about __11__, it's about how __12__ we can get up and keep ____13____.【例题】1. A. same B. different C. right D. wrong 解析:根据上下文可知,该句意为"人生就像一场马拉松,我们可能在不同时间开始,但必须按照自己的路线去跑",因此填入不同。
(完整版)中考数学必考经典题型

中考数学必考经典题型题型一 先化简再求值命题趋势由河南近几年的中考题型可知,分式的化简求值是每年的考查重点,几乎都以解答题的形式出现,其中以除法和减法形式为主,要求对分式化简的运算法则及分式有意义的条件熟练掌握。
例:先化简,再求值:,12)1111(22+--÷-++x x xx x x 其中.12-=x 分析:原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,将x 的值带入计算即可求值。
题型二 阴影部分面积的相关计算命题趋势近年来的中考有关阴影面积的题目几乎每年都会考查到,而且不断翻新,精彩纷呈.这类问题往往与变换、函数、相似等知识结合,涉及到转化、整体等数学思想方法,具有很强的综合性。
例 如图17,记抛物线y =-x 2+1的图象与x 正半轴的交点为A ,将线段OA 分成n 等份.设分点分别为P 1,P 2,…,P n -1,过每个分点作x 轴的垂线,分别与抛物线交于点Q 1,Q 2,…,Q n -1,再记直角三角形OP 1Q 1,P 1P 2Q 2,…的面积分别为S 1,S 2,…,这样就有S 1=2312n n -,S 2=2342n n-…;记W=S 1+S 2+…+S n -1,当n 越来越大时,你猜想W 最接近的常数是( )(A)23(B)12(C)13 (D )14分析 如图17,抛物线y =-x 2+1的图象与x 正半轴的交点为A(1,0),与y轴的交点为8(0,1).设抛物线与y轴及x正半轴所围成的面积为S,M(x,y)在图示抛物线上,则222OM x y=+()21y y=-+=21324y⎛⎫-+⎪⎝⎭.由0≤y≤1,得34≤OM2≤1.这段图象在图示半径为32、1的两个14圆所夹的圆环内,所以S在图示两个圆14面积之间,即从而316π<S<14π.显然,当n的值越大时,W的值就越来越接近抛物线与y轴和x正半轴所围成的面积的一半,所以3 32π<W<18π.与其最接近的值是,故本题应选C.题型三解直角三角形的实际应用命题趋势解直角三角形的应用是中考的必考内容之一,它通常以实际生活为背景,考查学生运用直角三角形知识建立数学模型的能力,解答这类问题的方法是运用“遇斜化直”的数学思想,即通过作辅助线(斜三角形的高线)把它转化为直角三角形问题,然后根据已知条件与未知元素之间的关系,利用解直角三角形的知识,列出方程来求解。
中考数学经典习题(50题)

中考数学经典习题(50题)1. 已知一边长为6cm的正三角形ABC,点D、E分别位于线段AB、AC上,使得AD = DE = EC,求三角形ADE的面积。
2. 在正方形ABCD中,点E、F、G、H分别位于线段AB、BC、CD、DA上,使得AE = BF = CG = DH = 4cm,求四边形EFGH的面积。
3. 已知直边三角形ABC,点D、E分别分别位于BC、AC 上,使得BD = DE = EC,连接CF,若$ \angleACF=45^{\circ} $,求$ \angle ABD $ 的度数。
4. 已知正方形ABCD,点E、F分别位于线段AB、CD上,且AE = CF = 4cm,求三角形DEF的面积。
5. 已知等腰梯形ABCD中,AD = BC = 4cm,AB = 8cm,点E、F分别位于线段AB、DC上,且$ \angle AED=45^{\circ} $,求$ \angle CFB $ 的度数。
6. 已知正方形ABCD,点E、F、G分别位于线段AB、BC、AC上,且AE = BF = CG = 3cm,连接DE、EF、FG,求四边形DEFG的面积。
7. 在正方形ABCD中,点E、F、G分别位于线段AB、BC、CD上,且AE = BF = CG = 2cm,求三角形EFG的面积。
8. 已知等腰梯形ABCD中,AD = BC = 6cm,AB = 14cm,点E、F分别位于线段AB、CD上,使得EF平行于AB,且$ \angle ADE=60^{\circ} $,求三角形DEF的面积。
9. 已知正方形ABCD的边长为10cm,点E、F分别位于线段AB、CD上,使得AE = DF = 4cm,连接CE、EB、AF,求四边形CEFB的面积。
10. 在正方形ABCD中,点E、F、G分别位于线段AB、BC、CD上,使得AE = BF = CG,连接AG、BF,若$ \angleAGB=90^{\circ} $,求AE的长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8. 如图,矩形纸片ABCD 中,BC=4,AB=3,点P 是BC 边上的动点(点P 不与点B 、CC .D .8.如图所示是张老师晚上出门散步时离家的距离y 与时间x 之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是A .B .C .D .8. 如图,在矩形ABCD 中,AB=2,BC=1,动点P 从点B 出发, 沿路线B C D →→作匀速运动,那么△ABP 的面积S 与点P 运动的路程x 之间的函数图象大致是A .B .C .D .D C P BAFEDCBA8.如图,已知⊙O 是以数轴的原点O 为圆心,半径为1的圆,45AOB ∠=︒,点P 在数轴上运动,若过点P 且与OA 平行的直 线与⊙O 有公共点, 设x OP =,则x 的取值范围是A .-1≤x ≤1 B.x ≤2 C .0≤x ≤2 D .x >2 8.下面是按一定规律排列的一列数:第1个数:11122-⎛⎫-+ ⎪⎝⎭; 第2个数:2311(1)(1)1113234⎛⎫⎛⎫---⎛⎫-+++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭; 第3个数:234511(1)(1)(1)(1)11111423456⎛⎫⎛⎫⎛⎫⎛⎫-----⎛⎫-+++++ ⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭; ……第n 个数:232111(1)(1)(1)111112342n n n -⎛⎫⎛⎫⎛⎫----⎛⎫-++++ ⎪⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭.那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是A .第10个数B .第11个数C .第12个数D .第13个数8.如图,平面直角坐标系中,在边长为1的菱形ABCD 的边上有一动点P 从点A 出发沿A B C D A →→→→匀速运动一周,则点P 的纵坐标y 与点P 走过的路程S 之间的函数关系用图象表示大致是AB C D8.在正方形ABCD 中,点E 为BC 边的中点,点F 在对角线AC 上,连接FB 、FE .当点F 在AC 上运动时,设AF=x ,△BEF 的周长 为y ,下列图象中,能表示y 与x 的函数关系的图象大致是第8题第8题图8.如图,在矩形ABCD 中,2AB =,1BC =,动点P 从点B出发,沿路线B C D →→作匀速运动,那么ABP △的面积S 与点P 运动的路程x 之间的函数图象大致是8.小明将一张正方形包装纸,剪成图1所示形状,用它包在一个棱长为10的正方体的表面(不考虑接缝),如图2所示.小明所用正方形包装纸的边长至少为A . 40B . 2230+C . 220D . 21010+8.函数y=x 2-2x-2的图象如右图所示,根据其中提供的信息,可求得使y ≥1成立的x 的取值范围是A .31≤≤-xB .31<<-xC .31>-<x x 或D .31≥-≤x x 或8.如图,如果从半径为9cm 的圆形纸片剪去13圆周的一个扇形,将留下的扇形围成一个圆锥(接缝 处不重叠),那么这个圆锥的高为( ) A .6cm B.C .8cmD. (第8题图).A .B .C .D .D C P BA 8题图图2图110.若将代数式中的任意两个字母互相替换,代数式不变,则称这个代数式为完全对称式.如在代数式a +b +c 中,把a 和b 互相替换,得b +a +c ;把a 和c 互相替换,得c +b +a ;把b 和c……;a +b +c 就是完全对称式.下列三个代数式:①(a -b)2;② ab +bc +ca ;③ a 2b +b 2c +c 2a .其中为完全对称式的是 A .① ② B .② ③ C .① ③ D .① ② ③8. 如图2,点A 、B 、C 、D 为圆O 的四等分点,动点P 从圆心O 出发,沿O-C-D-O 的路线作匀速运动.设运动时间为t 秒, ∠APB 的度数为y 度,则下列图象中表示y 与t 之间函数关系最恰当的是( )(图2 )12.一组按规律排列的式子:2581114916,,,,...(0)a a a a a --≠,其中第8个式子是 ,第n 个式子是 (n 为正整数).12.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A 1B 1C 1D 1,A 2B 2C 2D 2,A 3B 3C 3D 3……每个正方形四条边上的整点的个数.按此规律推算出正方形A 10B 10C 10D 10四条边上的整点共有 个.12. 如图,以等腰三角形AOB 的斜边为直角边向外作第2个等腰直角三角形ABA 1,再以等腰直角三角形ABA 1的斜边为直角边向外作第3个等腰直角三角形A 1BB 1,……,如此作下去,若OA =OB =1,则第n 个等腰直角三角形的面积S n =________(n 为正整数).12.如图,45AOB ∠=,过OA 上到点O 的距离分别为1357911 ,,,,,,的点作OA 的垂线与OB 相交,得到并标出一组黑色梯形,它们的面积分别为1234S S S S ,,,,. 则第一个黑色梯形的面积=1S ;观察图中的规律, 第n(n 为正整数)个黑色梯形的面积=n S .12.已知正六边形的边长为1cm ,分别以它的三个不相邻的顶点为圆心, 1cm 长为半径画弧(如图),则所得到的三条弧的长度之和 为 cm (结果保留π).B 1B 2A 1A OB第12题12题图A BCDEFM N12.已知:如图,直角△ABC 中,︒=∠90ACB ,1==BC AC ,的圆心为A ,如果图中两个阴影部分的面积相等,那么AD 的长是 (结果不取近似值).12.在平面直角坐标系中,点A 的坐标为(4),0,点B 的坐标为(410),,点C 在y 轴上,且ABC △是直角三角形,则满足条件的C 点的坐标为 .12.如图,将正方形纸片ABCD 折叠,使点B 落在CD 边上 一点E (不与点C ,D 重合),压平后得到折痕MN .设2AB =, 当21=CD CE 时,则=BNAM. 若n CD CE 1=(n 为整数),则=BNAM. (用含n 的式子表示)12. 51 ; 1)1(22+-n n12.在平面直角坐标系中,我们称边长为1、且顶点的横、纵坐标均为整数的正方形为单位格点正方形.如图,在菱形ABCD 中,四个顶点坐标分别是(-8,0),(0,4),(8,0),(0,-4),则菱形ABCD 能覆盖的单位格点正方形的个数是 个;若菱形A n B n C n D n 的四个顶点坐标分别为(-2n ,0),(0, n ),(2n ,0),(0,-n )(n 为正整数),则菱形A n B n C n D n 能覆盖的单位格点正方形的个数为(用含有n 的式子表示).12.如图,在梯形ABCD 中,AB ∥CD ,AB =a ,CD =b ,E 为边AD 上的任意一点,EF ∥AB ,且EF 交BC 于点F .若E 为边AD 上的中点,则EF = (用含有a ,b 的式子表示);若E 为边AD 上距点A 最近的n 等分点(2n ≥,且n 为整数),则EF = (用含有n ,a ,b 的式子表示).BAx12.某些植物发芽有这样一种规律:当年所发新芽第二年不发芽,老芽在以后每年都发芽.发芽规律见下表(设第一年前的新芽数为a )照这样下去,第8年老芽数与总芽数的比值为 .16.如图所示,等边△ABC 中,D 、E 分别是AB 、AC 上的点,将△ADE 沿直线DE 翻折后,点A 落在 点A '处,且点A '在△ABC 的外部,若原等边 三角形的边长为a ,则图中阴影部分的 周长为 .12.如图4所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n 个图形需要黑色棋子的个数是 .1.去掉有一个交点在PC 边上,求m 的取值范围。
2. 定义{},,a b c 为函数2y ax bx c =++的 “特征数”.如:函数223y x x =-+的“特征数”是{}1,2,3-,函数23y x =+的“特征数”是{}0,2,3,函数y x =-的“特征数”是{}0,1,0-(1)将“特征数”是⎪⎭⎪⎬⎫⎩⎨⎧1,33,0的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是 ;(2)在(1)中,平移前后的两个函数分别与y 轴交于A 、B 两点,与直线3=x 分别交于D 、C两点,判断以A 、B 、C 、D 四点为顶点的四边形形状,请说明理由并计算其周长. (3)若(2)中的四边形与“特征数”是211,2,2b b ⎧⎫-+⎨⎬⎩⎭的函数图象的有交点,求满足条件的实数b 的取值范围?第1个图形 第2个图形 第3个图形 第4个图形(图4)1点B、C、E在同一直线上,点A、D在直线CE的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F。
(1)如图①,若∠BAC=60°,则∠AFB=_________;如图②,若∠BAC=90°,则∠AFB=_________;(2)如图③,若∠BAC=α,则∠AFB=_________(用含α的式子表示);(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合),得图④或图⑤。
在图④中,∠AFB与∠α的数量关系是________________;在图⑤中,∠AFB与∠α的数量关系是________________。
请你任选其中一个结论证明。
