第13章全等三角形复习题

合集下载

2024—2025学年华东师大版数学八年级上册第13章《全等三角形》基础复习

第13章基础复习知识点1命题、定理与证明1.一般地，判断某一件事情的语句叫做命题.命题一般由条件和结构两部分组成，可以写成“如果……,那么……”的形式.2.基本事实是在继续学习过程中用来判断其他命题真假的原始依据.3.定理：有些命题可以从基本事实或其他真命题出发，用逻辑推理的方法判断它们是正确的，并且可以作为进一步判断其他命题真假的依据，这样的真命题叫做定理.4.根据条件、定义以及基本事实、定理等，经过演绎推理，来判断一个命题是否正确，这样的推理过程叫做证明.1.下列命题中，是真命题的是()A.无限小数是无理数B.从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离C.平行于同一条直线的两条直线平行D.过一点有且只有一条直线与已知直线垂直2.判断命题“如果n<1，那么W−1<0”是假命题，只需举出一个反例.反例中的n可以为()A.-2u−12 C.0D123.把命题“对顶角相等”改写成“如果⋯⋯，那么⋯⋯”的形式：.4.填写下列证明过程中的推理根据：已知:如图所示,AC、BD相交于点O,DF平分∠CDO与AC相交于点F,BE平分∠ABO与AC相交于点E,∠A=∠C.求证:∠1=∠2.证明:∵∠A=∠C(),∴AB∥CD(),∴∠ABO=∠CDO(),又∵DF平分∠CDO,BE平分∠ABO,∴∠1=12∠Cs∠2=12∠B(),∴∠1=∠2().知识点2三角形全等的判定1.能够完全重合的两个三角形是全等三角形，相互重合的顶点是对应顶点，相互重合的边是对应边，相互重合的角是对应角，全等三角形的对应边相等，对应角相等.2.全等三角形的判定条件：①两边及其夹角分别相等的两个三角形全等.简写为S. A.S.(或边角边).②两角及其夹边分别相等的两个三角形全等.简写为A.S. A.(或角边角).③两角分别相等且其中一组等角的对边相等的两个三角形全等.简写为A. A.S.(或角角边).④三边分别相等的两个三角形全等.简写为S.S.S.(或边边边).⑤斜边和一条直角边分别相等的两个直角三角形全等.简写为H.L.(或“斜边直角边”).5.如图,AB=AD,CB=CD,∠B=32°,∠BAD=72°,则∠ACD的度数是()A.102°B.112°C.114°D.1226.如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是()A.∠A=∠DB.AC=DFC.AB=EDD.BF=EC7.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是()A.0.5B.1C.1.5D.28.图中的小正方形边长都相等，若△MNP≌△MFQ，则点Q可能是图中的()A.点DB.点CC.点BD.点A9.下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC一定全等的是()A.甲和乙B.乙和丙C.甲和丙D.只有丙10.如图所示,在Rt△ACD和Rt△BCE中,若AD=BE,DC=EC,则不正确的结论是()A.Rt△ACD≌Rt△BCEB.OA=OBC.E是AC的中点D.AE=BD11.如图,点D在线段BC上,若BC=DE,AC=DC,AB=EC,且∠ACE=180°-∠ABC-2x°,则下列角中，大小为x°的角是()A.∠EFCB.∠ABCC.∠FDCD.∠DFC12.如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且C B=14,点E、F在线段AD上，满足∠BED=∠CFD=∠BAC,若△B=20,则.△B+△C=()A.18B.15C.12D.913.如图,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有()A.1个B.2个C.3个D.4个14.如图,AC=DC,BC=EC,请你添加一个适当的条件:,使得△ABC≌△DEC.15.如图,∠1=∠2,∠3=∠4,,则全等三角形有对.16.如图,已知△ABC中,F是高AD和BE的交点,且AD=BD,CD=4,则线段DF的长度为.17.(南通中考)如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B.连结AC并延长到点D，使CD=CA.连结BC并延长到点E，使CE= CB.连结DE，那么量出DE的长就是A、B的距离.为什么?18.如图,在△ABC中,AC=5,中线AD=7,求边AB的取值范围.19.如图,点O是线段AB的中点,OD∥BC且OD=BC.(1)求证:△AOD≌△OBC.(2)若∠ADO=35°,求∠DOC的度数.20.王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板(AC=BC，∠ACB=90°)，点C在DE上，点A和B分别与木墙的顶端重合.(1)求证:△ADC≌△CEB.(2)求两堵木墙之间的距离.21.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE.(2)求∠FAE的度数.(3)求证:CD=2BF+DE.。

第13章全等三角形华东师大版八年级数学上册单元测试(含答案)

第13章　全等三角形(90分钟　100分)一、选择题(每小题3分,共24分)1.△ABC中,AB=AC=2,∠B=60°,则BC=( )A.2B.3C.4D.52.(2024·泉州期末)下列命题的逆命题是真命题的是( )A.全等三角形的对应角相等B.对顶角相等C.若x>y,则x-y>0D.若C是线段AB的中点,则AC=BC3.(2024·南通质检)如图,已知△ABC≌△DEC,∠ACB=100°,∠D=35°,则∠E=( )A.35°B.45°C.55°D.无法计算4.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )5.(2023·台州中考)如图,锐角三角形ABC中,AB=AC,点D,E分别在边AB,AC上,连结BE,CD.下列命题中,假命题是( )A.若CD=BE,则∠DCB=∠EBCB.若∠DCB=∠EBC,则CD=BEC.若BD=CE,则∠DCB=∠EBCD.若∠DCB=∠EBC,则BD=CE6.如图,在Rt△ABC中,∠C=90°,AC=12 cm,BC=6 cm,线段PQ=AB,P,Q两点分别在线段AC和AC的垂线AX上移动,若以A,B,C为顶点的三角形与以A,P,Q为顶点的三角形全等,则AP的值为( )A.8 cmB.12 cmC.12 cm或6 cmD.12 cm或8 cm7.如图,OE是∠AOB的平分线,BD⊥OA,AC⊥OB,垂足分别为D,C,BD,AC都经过点E,则图中全等的三角形共有对( )A.3B.4C.5D.68.(2024·天津期中)如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④连结OC,OC平分∠AOE;⑤∠AOB=60°.恒成立的结论有( )A.①⑤B.①②⑤C.①②③⑤D.①②③④⑤二、填空题(每小题4分,共24分)9.定理“直角三角形的两个锐角互余”的逆定理是.10.检测房梁是否水平,可以采用下面的方法:在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端拴一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的顶点,则可以判断房梁是水平的.这样做的根据是:.11.如图,D在BC边上,△ABC≌△ADE,∠EAC=44°,则∠B的度数为.12.如图,在△ABC中,∠B=30°,∠C=50°,通过观察尺规作图的痕迹,∠DEA的度数是.13.(2023·重庆中考A卷)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC上一点,连结AD.过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F.若BE=4,CF=1,则EF的长度为.14.如图,∠BOC=60°,A是BO的延长线上一点,OA=10 cm,动点P从点A出发,沿AB 以3 cm/s的速度移动,动点Q从点O出发沿OC以2 cm/s的速度移动,若点P,Q 同时出发,当△OPQ是等腰三角形时,移动的时间是.三、解答题(共52分)15.(6分)(2023·云南中考)如图,C是BD的中点,AB=ED,AC=EC.求证:△ABC≌△EDC.16.(8分)(2024·北京期中)下面是“过直线上一点作已知直线的垂线”的尺规作图过程:已知:如图,点P在直线l上.求作:直线PQ,使PQ⊥l.作法:①以点P为圆心,任意长为半径画弧,交直线l于A,B两点,AB长为半径画弧,两弧在直线l上方交于点Q,②分别以A,B为圆心,大于12③作直线PQ.直线PQ即为所求的垂线.(1)使用直尺和圆规,补全图形(保留作图痕迹);(2)完成下面的证明.证明:连结AQ,BQ,∵根据作法,有AQ=BQ,AP=BP,∴PQ⊥AB,即PQ⊥l.()(填推理的依据)17.(8分)如图,在长方形纸片ABCD中,点P在BC边上,将△CDP沿DP折叠,点C 落在点E处,PE,DE分别交AB于点G,F,且GF=GP.(1)求证:△GEF≌△GBP;(2)若PC=2,求BF的长.18.(8分)(2023·苏州中考)如图,在△ABC中,AB=AC,AD为△ABC的角平分线.以点A 为圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连结DE,DF.(1)求证:△ADE≌△ADF;(2)若∠BAC=80°,求∠BDE的度数.19.(10分)已知,如图,AD为△ABC的角平分线,且AD=AC,E为AD延长线上的一点,AE=AB.(1)求证:△ABD≌△AEC;(2)求证:BE=EC.20.(12分)如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.(1)若点D是AC的中点,如图1,则线段AD与CE的数量关系是;(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论;(提示:过点D作DF∥BC,交AB于点F)(3)若点D在线段AC的延长线上,(2)中的结论是否仍成立?如果成立,请给予证明;如果不成立,请说明理由.【附加题】(10分)(1)已知△ABC中,∠BAC=60°,以AB和BC为边向外作等边△ABD和△BCE.①连结AE,CD,如图1,求证:∠BCD=∠AEB;②若AB⊥BC,延长AB交DE于点M,求证:点M为DE的中点;(2)如图3,HE⊥CE于点E,∠BEH=30°,点G在EH上运动,以BG为边作等边△BGF,当BF的长最小时,求∠FBE的度数.第13章　全等三角形(90分钟　100分)一、选择题(每小题3分,共24分)1.△ABC中,AB=AC=2,∠B=60°,则BC=(A)A.2B.3C.4D.52.(2024·泉州期末)下列命题的逆命题是真命题的是(C)A.全等三角形的对应角相等B.对顶角相等C.若x>y,则x-y>0D.若C是线段AB的中点,则AC=BC3.(2024·南通质检)如图,已知△ABC≌△DEC,∠ACB=100°,∠D=35°,则∠E=(B)A.35°B.45°C.55°D.无法计算4.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是(B)5.(2023·台州中考)如图,锐角三角形ABC中,AB=AC,点D,E分别在边AB,AC上,连结BE,CD.下列命题中,假命题是(A)A.若CD=BE,则∠DCB=∠EBCB.若∠DCB=∠EBC,则CD=BEC.若BD=CE,则∠DCB=∠EBCD.若∠DCB=∠EBC,则BD=CE6.如图,在Rt△ABC中,∠C=90°,AC=12 cm,BC=6 cm,线段PQ=AB,P,Q两点分别在线段AC和AC的垂线AX上移动,若以A,B,C为顶点的三角形与以A,P,Q为顶点的三角形全等,则AP的值为(C)A.8 cmB.12 cmC.12 cm或6 cmD.12 cm或8 cm7.如图,OE是∠AOB的平分线,BD⊥OA,AC⊥OB,垂足分别为D,C,BD,AC都经过点E,则图中全等的三角形共有对(B)A.3B.4C.5D.68.(2024·天津期中)如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④连结OC,OC平分∠AOE;⑤∠AOB=60°.恒成立的结论有(D)A.①⑤B.①②⑤C.①②③⑤D.①②③④⑤二、填空题(每小题4分,共24分)9.定理“直角三角形的两个锐角互余”的逆定理是　有两个角互余的三角形是直角三角形　.10.检测房梁是否水平,可以采用下面的方法:在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端拴一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的顶点,则可以判断房梁是水平的.这样做的根据是:　等腰三角形的底边上的中线、底边上的高重合　.11.如图,D在BC边上,△ABC≌△ADE,∠EAC=44°,则∠B的度数为　68°　.12.如图,在△ABC中,∠B=30°,∠C=50°,通过观察尺规作图的痕迹,∠DEA的度数是　85°　.13.(2023·重庆中考A卷)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC上一点,连结AD.过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F.若BE =4,CF =1,则EF 的长度为　3　.14.如图,∠BOC =60°,A 是BO 的延长线上一点,OA =10 cm,动点P 从点A 出发,沿AB 以3 cm/s 的速度移动,动点Q 从点O 出发沿OC 以2 cm/s 的速度移动,若点P ,Q 同时出发,当△OPQ 是等腰三角形时,移动的时间是　2 s 或10 s .三、解答题(共52分)15.(6分)(2023·云南中考)如图,C 是BD 的中点,AB =ED ,AC =EC.求证:△ABC ≌△EDC.【解析】∵C 是BD 的中点,∴BC =DC ,在△ABC 和△EDC 中,AB =ED AC =EC BC =DC,∴△ABC ≌△EDC (S.S.S.).16.(8分)(2024·北京期中)下面是“过直线上一点作已知直线的垂线”的尺规作图过程:已知:如图,点P 在直线l 上.求作:直线PQ ,使PQ ⊥l.作法:①以点P 为圆心,任意长为半径画弧,交直线l 于A ,B 两点,②分别以A ,B 为圆心,大于12AB 长为半径画弧,两弧在直线l 上方交于点Q ,③作直线PQ.直线PQ即为所求的垂线.(1)使用直尺和圆规,补全图形(保留作图痕迹);(2)完成下面的证明.证明:连结AQ,BQ,∵根据作法,有AQ=BQ,AP=BP,∴PQ⊥AB,即PQ⊥l.(等腰三角形底边上的中线与底边上的高重合)(填推理的依据)【解析】(1)补全的图形如图所示:【解析】(2)连结AQ,BQ,∵根据作法,有AQ=BQ,AP=BP,∴PQ⊥AB,即PQ⊥l.(等腰三角形底边上的中线与底边上的高重合)17.(8分)如图,在长方形纸片ABCD中,点P在BC边上,将△CDP沿DP折叠,点C 落在点E处,PE,DE分别交AB于点G,F,且GF=GP.(1)求证:△GEF≌△GBP;【解析】(1)∵纸片ABCD为长方形,∴∠B=∠C=90°,由折叠的性质得,∠E=∠C,∴∠E=∠B,在△GEF 和△GBP 中,∠E =∠B ∠EGF =∠BGP GF =GP,∴△GEF ≌△GBP (A.A.S.);(2)若PC =2,求BF 的长.【解析】(2)由△GEF ≌△GBP 得GE =GB ,∵GF =GP ,∴BF =GB +GF =GE +GP =PE ,由折叠的性质得,PE =PC =2,∴BF =2.18.(8分)(2023·苏州中考)如图,在△ABC 中,AB =AC ,AD 为△ABC 的角平分线.以点A 为圆心,AD 长为半径画弧,与AB ,AC 分别交于点E ,F ,连结DE ,DF.(1)求证:△ADE ≌△ADF ;【解析】(1)∵AD 是△ABC 的角平分线,∴∠BAD =∠CAD.由作图知:AE =AF.在△ADE 和△ADF 中,AE =AF ∠BAD =∠CAD AD =AD,∴△ADE ≌△ADF (S.A.S.);(2)若∠BAC =80°,求∠BDE 的度数.【解析】(2)∵∠BAC =80°,AD 为△ABC 的角平分线,∴∠EAD =12∠BAC =40°,由作图知:AE =AD ,∴∠AED =∠ADE ,∴∠ADE =12×(180°-40°)=70°,∵AB =AC ,AD 为△ABC 的角平分线,∴AD ⊥BC ,∴∠BDE =90°-∠ADE =20°.19.(10分)已知,如图,AD 为△ABC 的角平分线,且AD =AC ,E 为AD 延长线上的一点,AE =AB.(1)求证:△ABD≌△AEC;【证明】(1)∵AD平分∠BAC,∴∠BAD=∠DAC,在△ABD与△AEC中,AB=AE∠BAD=∠EAC AD=AC,∴△ABD≌△AEC(S.A.S.); (2)求证:BE=EC.【证明】(2)∵AD=AC,AE=AB,∴∠ACD=∠ADC=180°-∠DAC2,∠ABE=∠AEB=180°-∠BAD2,∴∠ACD=∠ADC=∠ABE=∠AEB,∵∠BDE=∠ADC,∴∠BDE=∠BED,∴BD=BE,∵△ABD≌△AEC,∴BD=EC,∴BE=EC.20.(12分)如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.(1)若点D是AC的中点,如图1,则线段AD与CE的数量关系是AD=CE;【解析】(1)AD=CE,理由如下:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC=BC.∵点D为AC的中点,∴∠DBC=30°,AD=DC,∵BD=DE,∴∠E=∠DBC=30°,∵∠ACB=∠E+∠CDE,∴∠CDE=∠E=30°,∴CD=CE,又∵AD=DC,∴AD=CE.(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论;(提示:过点D作DF∥BC,交AB于点F)【解析】(2)AD=CE,理由如下:如图,过点D作DF∥BC,交AB于点F,则∠ADF=∠ACB=60°,∵∠A=60°,∴△AFD是等边三角形,∴AD=DF=AF,∠AFD=60°,∴∠BFD=∠DCE=180°-60°=120°,∵DF∥BC,∴∠FDB=∠DBE=∠E,在△BFD和△DCE中,∠FDB=∠E∠BFD=∠DCE BD=DE,∴△BFD≌△DCE(A.A.S.),∴DF=EC,又∵AD=DF,∴AD=CE;(3)若点D在线段AC的延长线上,(2)中的结论是否仍成立?如果成立,请给予证明;如果不成立,请说明理由.【解析】(3)结论仍成立,理由如下:如图,过点D作DP∥BC,交AB的延长线于点P,则∠ABC=∠APD=60°,∠ACB=∠ADP=60°,∵∠A=60°,∴△APD是等边三角形,∴AP=PD=AD,∴∠DCE=∠ACB=∠P,∵DP∥BC,∴∠PDB=∠CBD,∵DB=DE,∴∠DBC=∠DEC,∴∠PDB=∠DEC,在△BPD和△DCE中,∠PDB=∠CED ∠P=∠DCE BD=DE,∴△BPD≌△DCE(A.A.S.),∴PD=CE,又∵AD=PD,∴AD=CE.【附加题】(10分)(1)已知△ABC中,∠BAC=60°,以AB和BC为边向外作等边△ABD和△BCE.①连结AE,CD,如图1,求证:∠BCD=∠AEB;②若AB⊥BC,延长AB交DE于点M,求证:点M为DE的中点;【解析】(1)①∵△ABD和△BCE是等边三角形,∴BD=BA,BC=BE,∠DBA=∠EBC=60°,∴∠DBA+∠ABC=∠EBC+∠ABC,即∠DBC=∠ABE,在△DBC和△ABE中,BD=BA∠DBC=∠ABE BC=BE,∴△DBC≌△ABE(S.A.S.),∴∠BCD=∠AEB;②如图,过点E作AD的平行线,交AM的延长线于点F,∵AD∥EF,∴∠DAM=∠AFE=60°,∵AB⊥BC,∴∠EBF=180°-∠ABC-∠CBE=30°,∴∠BEF=90°,在△ABC与△FEB中,∠BAC=∠EFB ∠ABC=∠FEB BC=EB,∴△ABC≌△FEB(A.A.S.),∴AB=EF=AD,在△MAD与△MFE中,∠AMD=∠FME ∠DAM=∠EFM AD=FE,∴△MAD≌△MFE(A.A.S.),∴DM=EM,即点M为DE的中点;(2)如图3,HE⊥CE于点E,∠BEH=30°,点G在EH上运动,以BG为边作等边△BGF,当BF的长最小时,求∠FBE的度数.【解析】(2)当BF的长最小时,即BG最小,则BG⊥HE,当以BG为边在BG左侧作等边△BGF时,如图所示:可得∠GBE=180°-∠BEH-∠BGE=60°,∵△FBG为等边三角形,∴∠FBG=60°,∴∠FBE=∠FBG+∠GBE=120°;当以BG为边在BG右侧作等边△BGF时,如图所示:此时点F在BE上,∴∠FBE=0°,综上所述,∠FBE=0°或120°.。

冀教版八年级上册数学第十三章全等三角形单元复习试题

第十三章全等三角形一、选择题1.下列定理中，没有逆定题的是（）①内错角相等，两直线平行②等腰三角形两底角相等③对顶角相等④直角三角形的两个锐角互余．A. 1个B. 2个C. 3个D. 4个2.下列语句是命题的是（）A. 作直线AB的垂线B. 在线段AB上取点CC. 同旁内角互补D. 垂线段最短吗？3.如图，△ABC中，AB=AC ，EB=EC ，则由“SSS”可以判定（）A. △ABD≌△ACDB. △ABE≌△ACEC. △BDE≌△CDED. 以上答案都不对4.如图：AB=AD，AE平分∠BAD，则图中有（）对全等三角形。

A. 2B. 3C. 4D. 55.下列语句：①相等的角是对顶角；②如果两条直线被第三条直线所截，那么同位角相等；③过直线外一点有且只有一条直线与已知直线平行；④平行线间的距离处处相等．其中正确的命题是（）A. ①②B. ②③C. ③④D. ①④6.如图，△AOC≌△BOD，∠A和∠B，∠C和∠D是对应角，下列几组边中是对应边的是（）A. AC与BDB. AO与ODC. OC与OBD. OC与BD7.下列命题是假命题的是（）A. 若x<y，则x+2021<y+2021B. 单项式-的系数是-4C. 若|x-1|+（y-3）2=0则x=1,y=3D. 平移不改变图形的形状和大小8.如图，△ABC≌△DEF，点A与D，B与E分别是对应顶点，且测得BC=5cm，则EF的长为（）A. 2cmB. 3cmC. 4cmD. 5cm9.下列关于几何画图的语句正确的是（）A. 延长射线AB到点C ，使BC=2ABB. 点P在线段AB上，点Q在直线AB的反向延长线上C. 将射线OA绕点O旋转180°，终边OB与始边OA的夹角为一个平角D. 已知线段a ，b满足2a＞b＞0，在同一直线上作线段AB=2a ，BC=b ，那么线段AC=2a-b10.甲、乙、丙、丁四个小朋友正在教室里玩耍，忽听“砰”的一声，讲台上的花盆被打破了．甲说：“是乙不小心闯的祸．”乙说：“是丙闯的祸．”丙说：“乙说的不是实话．”丁说：“反正不是我闯的祸．”如果刚才四个小朋友中只有一个人说了实话，那么这个小朋友是（）A. 甲B. 乙C. 丙D. 丁二、填空题11.请把命题“对顶角相等。

冀教版八年级上册数学第13章全等三角形复习

第13章全等三角形复习一、教学目标复习总结全等三角形整章内容。

二、知识点梳理证明两个三角形全等的基本思路：⎪⎩⎪⎨⎧）找是否有直角（）找夹角（）找第三边（）已知两边（HL SAS SSS 1⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧）（已知角是直角，找一边）找一角（已知一边和它的对角）找这边的对角（）找这个角的另一个边（）找这边的另一个邻角（已知一边和它的邻角）已知一边一角（HL AAS AAS SAS ASA 2 ()()⎩⎨⎧AAS ASA 3找夹边外的任意边找两角的夹边）已知两角（三、典型例题讲解考点一三角形全等的判定例1 如下图，在△ABC 与△DCB 中，AC 与BD 交于点E ，且∠A=∠D ，AB=DC 。

（1）求证：△ABE ≌△DCE ；（2）当∠AEB=50°时，求∠EBC 的度数。

考点二运用全等三角形证明线段相等例2 如下图，∠AOB=90°，OA=OB，直线l经过点O，分别过A，B两点作AC⊥l于点C，BD⊥l交l于点D。

求证：AC=OD。

考点三结论开放题例3 如下图，已知∠C=∠D，∠ABC=∠BAD，AC与BD相交于点O，请写出图中一组相等的线段__________。

例3 例4考点四条件开放题例 4 如图，已知BC=EC，∠BCE=∠ACD，要使△ABC≌△DEC，则应添加的一个条件为__________。

（答案不唯一，只需填一个）例5 已知命题：如下图，点A，D，B，E在同一条直线上，且AD=BE，∠A=∠FDE，则△ABC≌△DEF。

判断这个命题是真命题还是假命题，如果是真命题，请给出证明：如果是假命题，请添加一个适当条件使它成为真命题，并加以证明。

四、课堂练习1、下面结论中错误的是（）A、全等三角形对应边上的角平分线相等B、全等三角形对应边上的中线相等C、两个锐角对应相等的两个直角三角形全等D、全等三角形的周长相等2、如图1，∠ABC=∠DCB=70°，∠ABD=40°，AB=DC，则∠BAC等于（）A、70°B、80°C、100°D、90°3、两个三角形如果具有下列条件：①三条边分别相等；②两条边和夹角分别相等；③两条边和其中一边的对角分别相等；④两个角和一条边分别相等；⑤三个角分别相等。

八年级数学上册第13章全等三角形复习

△DCE和△DBE能全等吗？你能证明它们全等吗？请你写出证明过程.
第四页，共十一页。
观察图形复习 (túxíng) 知识
你能把下面给的图形所涉及到的知识都说出来吗：
边的
已知，AB=AC,D是BC
DE⊥AB,DF⊥AC
中点，
E,F,为垂足.
图形变(biànhuàn)演示课件的副本.gsp图形变换动画.gsp
出条件，最后写出两个三角形全等； 6.SSS;
7.全等形； 8.叫做全等三角形；
9.如果两个三角形全等，那么对应边相等，对应角相等；
10.假命题。
第二页，共十一页。
请看下面的选 (xiàmian)
择题 1.如果(rúguǒ)等腰三角形的一个底角为
，则一定有（）；
° . （A) 不大于45° （B)0°＜＜90°（C) = 90° (D) 90° ＜＜180
• 2.如图，在△ABC中，AB=AC,DB=DC, • AD的延长线交BC于点E. • 求证：∠BAE=∠CAE.
第十页，共十一页。
内容(nèiróng)总结
全等三角形知识(zhī shi)的回顾。图形变换演示课件的副本.gsp图形变换动画.gsp。（2）角的平分线的判定。（2）线段的垂直平分线的判定。1.已知，∠AOB,求作：∠AOB的平分线OC.。3. 已知，∠AOB和∠AOB内的两点P和Q.
第十一页，共十一页。
（1）线段的垂直平分线的性质；（2）线段的垂直平分线的判定。 5.命题，定理，逆命题逆定理。
同学们，这些知识(zhī shi)你都说出来了吗？
第六页，共十一页。
请看下面的作 (xiàmian) • 1.已知图，问∠A题OB,求作：∠AOB的平分线OC.

第13章 13.2 1.全等三角形+2.全等三角形的判定条件

(1)证明：∵△BAD≌△ACE，∴BD＝AE，CE＝AD，∵AE＝AD＋DE，∴ BD＝DE＋CE； (2)解：∵△BAD≌△ACE，∴∠ADB＝∠AEC，∵BD∥CE，∴∠BDE＝∠ AEC，∴∠ADB＝∠BDE，∵∠ADB＋∠BDE＝180°，∴∠ADB＝90°，即 △ABD 中，∠ADB＝90°时，BD∥CE.
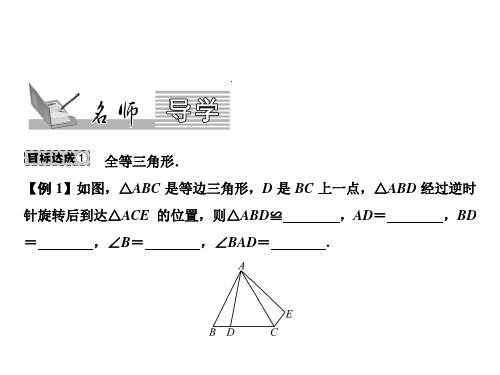
全等三角形的性质．
【例 2】如图所示，△ABE 和△ADC 是△ABC 分别沿着 AB、AC 边翻折 180° 形成的，若∠1∶∠2∶∠3＝28∶5∶3，则∠α＝ 80° .
【思路分析】据∠1∶∠2∶∠3＝28∶5∶3，可求出∠2＝25°，∠3＝15°， △ABC 沿 AB 翻折得到△ABE，∴△ABC≌△ABE，△ABC 沿 AC 翻折得到△ACD，∴△ABC≌△ADC，然后根据全等性质计算．
【方法归纳】经过平移、旋转、翻折得到图形与原图形全等，以获取边和角对应相等的关系．
知识点一：全等三角形能够完全重合的两个三角形是全等三角形，相互重合的顶点是对应顶点，相互重合的边是对应边，相互重合的角是对应角，全等三角形的对应边相等，对应角相等． 1．下列命题中正确的是( D ) A．全等三角形是指形状相同的两个三角形 B．全等三角形是指面积相等的两个三角形 C．两个等边三角形是全等三角形 D．全等三角形是指能够完全重合的两个三角形
到的三角形与原三角形是全等三角形．其中正确的命题是( B )
A．1 个
B．2 个
C．3 个
D．4 个
4．如图，△ABC 在一条直线上运动到△A′B′C′的位置，延长 AC、A′B′ 相交于 D 点．
(1)试说明∠A＝∠D； (2)试说明 BB′＝CC′； (3)你还能发现哪些信息？

2021-2022学年华师大版八年级数学上册《第13章全等三角形》期末复习解答题专题训练(附答案)

2021-2022学年华师大版八年级数学上册《第13章全等三角形》期末复习解答题专题训练（附答案）1．如图，点E，C，F，B在同一条直线上，EC＝BF，AC∥DF，∠A＝∠D．求证：AB＝DE．2．已知，如图，AB＝AD，∠B＝∠D，∠1＝∠2＝60°．（1）求证：△ADE≌△ABC；（2）求证：AE＝CE．3．已知：如图，B、C、E三点在同一条直线上，AC∥DE，AC＝CE，∠ACD＝∠B．求证：△ABC≌△CDE．4．如图，四边形ABCD中，对角线AC、BD交于点O，AB＝AC，点E是BD上一点，且∠ABD＝∠ACD，∠EAD＝∠BAC．（1）求证：AE＝AD；（2）若∠ACB＝65°，求∠BDC的度数．5．已知：如图，A、F、C、D四点在一直线上，AF＝CD，AB∥DE，且AB＝DE．求证：（1）△ABC≌△DEF；（2）BC∥EF．6．如图，点A，D，B，E在一条直线上，AD＝BE，AC＝DF，AC∥DF．求证：BC＝EF．7．如图，BE⊥AE，CF⊥AE，垂足分别为E、F，D是EF的中点，CF＝AF．（1）请说明CD＝BD；（2）若BE＝6，DE＝3，请直接写出△ACD的面积．8．如图，在△ABC中，∠ACB＝90°，AC＝BC，点E是∠ACB内部一点，连接CE，作AD⊥CE，BE⊥CE，垂足分别为点D，E．（1）求证：△BCE≌△CAD；（2）若BE＝5，DE＝7，求△ACD的周长．9．如图，在△ABC中，BD⊥AC于点D，CE⊥AB于点E，BD、CE相交于点G，BD＝DC，DF∥BC交AB于点F，连接FG．求证：（1）△DAB≌△DGC；（2）CG＝FB+FG．10．如图，在△ABC中，∠A＝60°，BE，CD是△ABC的角平分线，BE与CD相交于点P．（1）求∠BPC的度数；（2）求证：BC＝BD+CE．11．如图，在△ABC中，∠ACB＝90°，AC＝BC，BE⊥CE于E，AD⊥CE于D．（1）求证：△ADC≌△CEB．（2）AD＝5cm，DE＝3cm，求BE的长度．12．如图，BD为△ABC的角平分线，且BD＝BC，E在BD的延长线上，连接AE，∠BAE ＝∠BEA，连接CE．求证：（1）△ABD≌△EBC；（2）∠BCE+∠BCD＝180°．13．如图，已知点A，B，C，D在同一条直线上，AB＝DC，AF＝DE，CF＝BE．求证：AF ∥DE．14．如图，∠A＝∠D＝90°，AB＝DC，点E，F在BC上且BE＝CF．（1）求证：AF＝DE；（2）若OM平分∠EOF，求证：OM⊥EF．15．如图，在四边形ABCD中，∠B＝∠D＝90°，点E，F分别在AB，AD上，AE＝AF，CE＝CF，求证：CB＝CD．16．如图，在△ABC中，∠C＝90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB 于点E．（1）求证：△ACD≌△AED；（2）若∠B＝30°，CD＝1，求BD的长．17．如图，BD是∠ABC的平分线，AB＝BC，点E在BD上，连接AE、CE，过点D作DF ⊥AE，DG⊥CE，垂足分别是F、G．（1）求证：△ABE≌△CBE；（2）求证：DF＝DG．18．如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD＝CD．（1）求证：△ABD≌△CFD；（2）已知BC＝7，AD＝5，求AF的长．19．如图，在△ABE中，AB＝AE，AD＝AC，∠BAD＝∠EAC，BC、DE交于点O．求证：（1）△ABC≌△AED；（2）OB＝OE．20．如图，△AOC和△BOD中，OA＝OC，OB＝OD，∠AOC＝∠BOD＝α（0＜α＜90°），AD与BC交于点P．（1）求证：△AOD≌△COB；（2）求∠APC（用含α的式子表示）；（3）过点O分别作OM⊥AD，ON⊥BC，垂足分别为点M、N，请直接写出OM和ON 的数量关系．参考答案1．证明：∵EC＝BF，∴EC+CF＝BF+CF，即EF＝BC，∵AC∥DF，∴∠ACB＝∠DFE，在△ABC和△DEF中，，∴△ABC≌△DEF（AAS），∴AB＝DE．2．（1）证明：∵∠1＝∠2，∴∠1+∠BAE＝∠2+∠BAE，即∠DAE＝∠BAC，在△ABC和△ADE中，，∴△ABC≌△ADE（ASA）；（2）证明：由（1）得△ABC≌△ADE，∴AE＝AC，∵∠2＝60°，∴△ACE是等边三角形，∴AE＝CE．3．证明：∵AC∥DE，∴∠ACB＝∠E，∠ACD＝∠D，∵∠ACD＝∠B，∴∠D＝∠B，在△ABC和△EDC中，∴△ABC≌△CDE（AAS）．4．证明：（1）∵∠BAC＝∠EAD∴∠BAC﹣∠EAC＝∠EAD﹣∠EAC即：∠BAE＝∠CAD在△ABE和△ACD中，∴△ABE≌△ACD（ASA），∴AE＝AD；（2）解：∵∠ACB＝65°，AB＝AC，∴∠ABC＝∠ACB＝65°，∴∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣65°﹣65°＝50°，∵∠ABD＝∠ACD，∠AOB＝∠COD，∴∠BDC＝∠BAC＝50°．5．证明：（1）∵AF＝CD，∴AF+FC＝CD+FC即AC＝DF．∵AB∥DE，∴∠A＝∠D．∵AB＝DE，∴在△ABC和△DEF中．∴△ABC≌△DEF（SAS）．（2）∵△ABC≌△DEF（已证），∴∠ACB＝∠DFE．∴EF∥BC．6．证明：∵AD＝BE，∴AD+BD＝BE+BD，即AB＝DE，∵AC∥DF，∴∠A＝∠EDF，在△ABC与△DEF中，，∴△ABC≌△DEF（SAS），∴BC＝EF．7．解：（1）∵BE⊥AE，CF⊥AE，∴∠BED＝∠CFD，∵D是EF的中点，∴ED＝FD，在△BED与△CFD中，，∴△BED≌△CFD（ASA），∴CD＝BD；（2）由（1）得：CF＝EB＝6，∵AF＝CF，∴AF＝6，∵D是EF的中点，∴DF＝DE＝3，∴AD＝9，∴△ACD的面积：AD•CF＝×9×6＝27．8．（1）证明：∵BE⊥CE，AD⊥CE，∴∠E＝∠ADC＝90°，∴∠EBC+∠BCE＝90°．∵∠BCE+∠ACD＝90°，∴∠EBC＝∠DCA．在△BCE和△CAD中，，∴△BCE≌△CAD（AAS）；（2）解：∵：△BCE≌△CAD，BE＝5，DE＝7，∴BE＝DC＝5，CE＝AD＝CD+DE＝5+7＝12．∴由勾股定理得：AC＝13，∴△ACD的周长为：5+12+13＝30，故答案为：30．9．证明：（1）∵BD⊥AC，CE⊥AB，∴∠ABD+∠A＝90°，∠ACE+∠A＝90°，∴∠ABD＝∠ACE，在△DAB和△DGC中，，∴△DAB≌△DGC（ASA）；（2）∵△DAB≌△DGC，∴AB＝CG，DA＝DG，∵BD＝CD．∠BDC＝90°，∴∠DBC＝∠DCB＝45°，∵DF∥BC，∴∠FDA＝∠FDG＝45°，在△DF A和△DFG中，，∴△DF A≌△DFG（SAS），∴F A＝FG．∴CG＝AB＝FB+F A＝FB+FG．10．解：（1）∵BE，CD是△ABC的角平分线，∴∠PBC＝∠ABC，∠PCB＝∠ACB，∵∠A＝60°，∴∠BPC＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣60°）＝120°；（2）证明：在BC上取点G使得CG＝CE，∵∠BPC＝120°，∴∠BPD＝∠CPE＝60°，在△CPE和△CPG中，，∴△CPE≌△CPG（SAS），∴∠CPG＝∠CPE＝60°，∴∠BPG＝120°﹣60°＝60°＝∠BPD，在△BPD和△BPG中，，∴△BPD≌△BPG（ASA），∴BD＝BG，∴BD+CE＝BG+CG＝BC．11．（1）证明：∵AD⊥CE，∠ACB＝90°，∴∠ADC＝∠ACB＝90°，∴∠BCE＝∠CAD（同角的余角相等），在△ADC与△CEB中∴△ADC≌△CEB（AAS）；（2）解：由（1）知，△ADC≌△CEB，则AD＝CE＝5cm，CD＝BE．∵CD＝CE﹣DE，∴BE＝AD﹣DE＝5﹣3＝2（cm），即BE的长度是2cm．12．证明：（1）∵∠BAE＝∠BEA，∴BA＝BE，∵BD为△ABC的角平分线，∴∠ABD＝∠EBC，在△ABD和△EBC中，，∴△ABD≌△EBC（SAS）；（2）由（1）得：△ABD≌△EBC，∴∠ADB＝∠BCE，∵BD＝BC，∴∠BDC＝∠BCD，又∵∠ADB+∠BDC＝180°，∴∠BCE+∠BCD＝180°．13．证明：∵AB＝CD，∴AB+BC＝CD+BC，即AC＝BD，在△ACF和△DBE中，，∴△ACF≌△DBE（SSS），∴∠A＝∠D，∴AF∥DE．14．证明：（1）∵BE＝CF，∴BE+EF＝CF+EF，即BF＝CE，∵∠A＝∠D＝90°，∴△ABF与△DCE都为直角三角形，在Rt△ABF和Rt△DCE中，，∴Rt△ABF≌Rt△DCE（HL），∴AF＝DE；（2）由（1）得：Rt△ABF≌Rt△DCE，∴∠AFB＝∠DEC，∴OE＝OF，∵OM平分∠EOF∴OM⊥EF．15．证明：连接AC，在△AEC与△AFC中，∴△AEC≌△AFC（SSS），∴∠CAE＝∠CAF，∵∠B＝∠D＝90°，∴CB＝CD．16．（1）证明：∵AD平分∠CAB，DE⊥AB，∠C＝90°，∴CD＝ED，∠DEA＝∠C＝90°，∵在Rt△ACD和Rt△AED中，∴Rt△ACD≌Rt△AED（HL）；（2）∵DC＝DE＝1，DE⊥AB，∴∠DEB＝90°，∵∠B＝30°，∴BD＝2DE＝217．证明：（1）∵BD是∠ABC的平分线，∴∠ABE＝∠CBE，在△ABE和△CBE中，∴△ABE≌△CBE（SAS）；（2）∵△ABE≌△CBE，∴∠AEB＝∠CEB，∴∠AED＝∠CED，∵DF⊥AE，DG⊥CE，∴FD＝DG．18．（1）证明：∵AD⊥BC，CE⊥AB，∴∠ADB＝∠CDF＝∠CEB＝90°，∴∠BAD+∠B＝∠FCD+∠B＝90°，∴∠BAD＝∠FCD，在△ABD和CFD中，，∴△ABD≌△CFD（ASA），（2）解：∵△ABD≌△CFD，∴BD＝DF，∵BC＝7，AD＝DC＝5，∴BD＝BC﹣CD＝2，∴AF＝AD﹣DF＝5﹣2＝3．19．证明：（1）∵∠BAD＝∠EAC，∴∠BAD+∠DAC＝∠EAC+∠DAC，即∠BAC＝∠EAD，在△BAC和△EAD中，，∴△BAC和≌EAD；（2）∵△BAC≌△EAD，∴∠ABC＝∠AED，∵AB＝AE，∴∠ABE＝∠AEB，∴∠OBE＝∠OEB，∴OB＝OE．20．解：（1）∵∠AOC＝∠BOD，∴∠AOC+∠COD＝∠BOD+∠COD，∴∠AOD＝∠COB，在△AOD和△COB中，，∴△AOD≌△COB（SAS）；（2）由（1）可知△AOD≌△COB，∴∠OAD＝∠OCB，令AD与OC交于点E，则∠AEC＝∠OAD+∠AOC＝∠OCB+∠APC，∴∠AOC＝∠APC，∵∠AOC＝α，∴∠APC＝α；（3）∵△AOD≌△COB，∴∠P AO＝∠BCO，即∠MAO＝∠NCO，∵OM⊥AD，ON⊥BC，∴∠AMO＝∠CNO＝90°，在△AOM和△CON中，，∴△AOM≌△CON（AAS），∴OM＝ON．。

第13章全等三角形(13.1) 华东师大版八年级数学上册同步练习(含答案)

命题　定理与证明【A层基础夯实】知识点1　命题是分式;③过点P作直线l 1.(2024·保定期中)下列句子:①负数没有相反数;②2x3x+5的平行线;④两个单项式的和一定是多项式.其中是命题的有( )A.1个B.2个C.3个D.4个2.(易错警示题·概念不清)下列命题中是假命题的是( )A.对顶角相等B.两直线平行,同旁内角互补C.同位角相等D.三角形的内角和是180°3.(2024·宁波期中)能说明“三角形的高线一定在三角形的内部(含边界)”是假命题的反例是( )4.指出下列命题的条件和结论,并判断它们是真命题还是假命题,如果是假命题,举出一个反例.(1)两个角的和等于平角时,这两个角互为补角;(2)内错角相等;(3)两条平行线被第三条直线所截,同旁内角互补.知识点2　定理与证明5.“同角或等角的补角相等”是( )A.定义B.基本事实C.定理D.假命题6.下列能作为证明依据的是( )A.已知条件B.定义和基本事实C.定理和推论D.以上三项都可以7.请举出一个关于角相等的定理:.8.推理填空:如图,已知∠B=∠CGF,∠BGC=∠F.求证:∠B+∠F=180°,∠F+∠BGD=180°.证明:∵∠B=∠CGF(已知),∴AB∥CD().∵∠BGC=∠F(已知),∴CD∥EF(),∴AB∥EF(),∴∠B+∠F=180°().又∵∠BGC+∠BGD=180°(),∠BGC=∠F(已知),∴∠F+∠BGD=180°().【B层能力进阶】9.下列命题:①各边相等的多边形是正多边形;②正多边形是轴对称图形;③正六边形的每个外角均为60°;④正n边形有(n-3)条对角线.其中是真命题的个数为( )A.4B.3C.2D.110.下列命题是定理的是( )A.内错角相等B.同位角相等,两直线平行C.一个角的余角不等于它本身D.在同一平面内,有且只有一条直线与已知直线垂直11.(2024·上海期中)把命题“关于某个点中心对称的两个三角形全等”改写成“如果……,那么……”的形式是.12.说明命题“若a>b,则ac>bc”是假命题的一个反例的c的值可以是.13.(2024·漳州期中)(1)如图,“若∠1=∠2,则AB∥CD”,该命题是(填“真命题”或“假命题”).(2)若上述命题为真命题,请说明理由;若上述命题为假命题,请你再添加一条件,使该命题成为真命题,并说明理由.【C层创新挑战(选做)】14.(推理能力)【阅读】在证明命题“如果a>b>0,c<0,那么a2+bc>ab+ac”时,小明的证明过程如下:证明:∵a>b>0,∴a2>,∴a2+bc>.∵a>b,c<0,∴bc>,∴ab+bc>,∴a2+bc>ab+ac.【问题解决】(1)请将上面的证明过程填写完整;(2)有以下几个条件①a>b,②a<b,③a<0,④b<0.请从中选择两个作为已知条件,得出结论|a|>|b|.你选择的条件序号是,并给出证明过程.　命题　定理与证明【A层基础夯实】知识点1　命题是分式;③过点P作直线l 1.(2024·保定期中)下列句子:①负数没有相反数;②2x3x+5的平行线;④两个单项式的和一定是多项式.其中是命题的有(C)A.1个B.2个C.3个D.4个2.(易错警示题·概念不清)下列命题中是假命题的是(C)A.对顶角相等B.两直线平行,同旁内角互补C.同位角相等D.三角形的内角和是180°3.(2024·宁波期中)能说明“三角形的高线一定在三角形的内部(含边界)”是假命题的反例是(C)4.指出下列命题的条件和结论,并判断它们是真命题还是假命题,如果是假命题,举出一个反例.(1)两个角的和等于平角时,这两个角互为补角;【解析】(1)条件:两个角的和等于平角,结论:这两个角互为补角,是真命题. (2)内错角相等;【解析】(2)条件:两个角是内错角,结论:这两个角相等,是假命题.如图,∠1与∠2是内错角,∠2>∠1.(3)两条平行线被第三条直线所截,同旁内角互补.【解析】(3)条件:两条平行线被第三条直线所截,结论:同旁内角互补,是真命题.知识点2　定理与证明5.“同角或等角的补角相等”是(C)A.定义B.基本事实C.定理D.假命题6.下列能作为证明依据的是(D)A.已知条件B.定义和基本事实C.定理和推论D.以上三项都可以7.请举出一个关于角相等的定理:　两直线平行,同位角相等(答案不唯一)　.8.推理填空:如图,已知∠B=∠CGF,∠BGC=∠F.求证:∠B+∠F=180°,∠F+∠BGD=180°.证明:∵∠B=∠CGF(已知),∴AB∥CD(　同位角相等,两直线平行　).∵∠BGC=∠F(已知),∴CD∥EF(　同位角相等,两直线平行　),∴AB∥EF(　平行公理的推论　),∴∠B+∠F=180°(　两直线平行,同旁内角互补　).又∵∠BGC+∠BGD=180°(　平角的定义　),∠BGC=∠F(已知),∴∠F+∠BGD=180°(　等量代换　).【B层能力进阶】9.下列命题:①各边相等的多边形是正多边形;②正多边形是轴对称图形;③正六边形的每个外角均为60°;④正n边形有(n-3)条对角线.其中是真命题的个数为(C)A.4B.3C.2D.110.下列命题是定理的是(B)A.内错角相等B.同位角相等,两直线平行C.一个角的余角不等于它本身D.在同一平面内,有且只有一条直线与已知直线垂直11.(2024·上海期中)把命题“关于某个点中心对称的两个三角形全等”改写成“如果……,那么……”的形式是　如果两个三角形关于某个点中心对称,那么这两个三角形全等　.12.说明命题“若a>b,则ac>bc”是假命题的一个反例的c的值可以是　0(答案不唯一)　.13.(2024·漳州期中)(1)如图,“若∠1=∠2,则AB∥CD”,该命题是假命题(填“真命题”或“假命题”).【解析】(1)由题中图形可知,∠1,∠2既不是同位角也不是内错角,即使∠1=∠2也不能得到AB∥CD,故该命题为假命题;(2)若上述命题为真命题,请说明理由;若上述命题为假命题,请你再添加一条件,使该命题成为真命题,并说明理由.【解析】(2)添加BE∥DF(答案不唯一).理由如下:∵BE∥DF,∴∠EBD=∠FDN.又∵∠1=∠2,∴∠EBD-∠1=∠FDN-∠2,即∠ABD=∠CDN,∴AB∥CD.【C层创新挑战(选做)】14.(推理能力)【阅读】在证明命题“如果a>b>0,c<0,那么a2+bc>ab+ac”时,小明的证明过程如下:证明:∵a>b>0,∴a2> ,∴a2+bc> .∵a>b,c<0,∴bc> ,∴ab+bc> ,∴a2+bc>ab+ac.【问题解决】(1)请将上面的证明过程填写完整;(2)有以下几个条件①a>b,②a<b,③a<0,④b<0.请从中选择两个作为已知条件,得出结论|a|>|b|.你选择的条件序号是 ,并给出证明过程.【解析】(1)∵a>b>0,∴a2> ab,∴a2+bc> ab+bc.∵a>b,c<0,∴bc>ac,∴ab+bc> ab+ac,∴a2+bc>ab+ac.(2)选择②④.证明如下: ∵a<b,b<0,∴a<0,∴|a|=-a,|b|=-b.∵a < b,∴-a>-b,∴|a|>|b|.。