零基础学数据结构---- 队列
数据结构-栈与队列

栈 1.6栈的应用
运算符的优先级关系表在运算过程中非常重要,它是判定进栈、出栈的重要依据。
θ1
θ2
+
-
+
>
>
-
>
>
*
>
>
/
>
>
(
<
<
)
>
>
#
<
<
*
/
(
)
#
<
<
<
>
>
<
<
<
>
>
>
>
<
>
>
>
>
<
>
>
<
<
<
=
>
>
>
>
<
<
<
=
栈
1.6栈的应用
下面以分析表达式 4+2*3-12/(7-5)为例来说明求解过程,从而总结出表达式求值的算 法。求解中设置两个栈:操作数栈和运算符栈。从左至右扫描表达式:# 4+2*3-12/(7-5) #, 最左边是开始符,最右边是结束符。表达式求值的过程如下表所示:
1.4栈的顺序存储结构
设计进栈算法——Push 函数。首先,判断栈是否已满,如果栈已满,就运用 realloc 函 数重新开辟更大的栈空间。如果 realloc 函数返回值为空,提示溢出,则更新栈的地址以及栈 的当前空间大小。最终,新元素入栈,栈顶标识 top 加 1。
数据结构-队列基本运算的实现及其应用

数据结构-队列基本运算的实现及其应用篇一数据结构-队列基本运算的实现及其应用一、队列的基本概念队列是一种特殊的数据结构,它遵循先进先出(FIFO)的原则,即先进入队列的元素先出队列。
在队列中,新元素被添加到队列的末尾,而删除操作总是发生在队列的开头。
队列常用于解决各种问题,如处理事件、任务调度、缓冲处理等。
二、队列的基本操作队列的基本操作包括入队(enqueue)、出队(dequeue)、查看队首元素(peek)和判断队列是否为空。
入队操作:向队列的末尾添加一个新元素。
这个操作的时间复杂度通常为O(1),可以通过在队列的末尾添加元素来实现。
出队操作:删除队列开头的元素并返回它。
这个操作的时间复杂度通常为O(1),可以通过移除队列开头的元素来实现。
查看队首元素:返回队列开头的元素但不删除它。
这个操作的时间复杂度通常为O(1),可以通过返回队列开头的元素来实现。
判断队列是否为空:检查队列是否包含任何元素。
这个操作的时间复杂度通常为O(1),可以通过比较队列的长度和0来实现。
三、队列的实现队列可以通过不同的数据结构来实现,如数组、链表和循环列表等。
在这里,我们将介绍使用数组和链表来实现队列的基本操作。
使用数组实现队列使用数组实现队列时,我们需要保留一个空间来跟踪队列的开头和结尾。
通常,我们使用两个指针,一个指向队列的开头,另一个指向队列的结尾。
当我们在队列中添加一个新元素时,我们将它添加到结尾指针所指向的位置,并将结尾指针向后移动一位。
当我们要删除一个元素时,我们只需将开头指针向后移动一位并返回该位置的元素即可。
使用链表实现队列使用链表实现队列时,我们通常使用一个头指针指向队首元素,一个尾指针指向队尾元素的下一个位置。
入队操作时,我们在尾指针的位置创建一个新节点,并将尾指针移动到下一个位置。
出队操作时,我们只需删除头指针指向的节点,并将头指针移动到下一个位置。
四、队列的应用队列在计算机科学中有着广泛的应用,下面列举几个常见的例子:事件处理:在多线程编程中,队列经常用于事件驱动的系统来传递事件或消息。
数据结构--栈和队列基础知识

数据结构--栈和队列基础知识⼀概述栈和队列,严格意义上来说,也属于线性表,因为它们也都⽤于存储逻辑关系为 "⼀对⼀" 的数据,但由于它们⽐较特殊,因此将其单独作为⼀篇⽂章,做重点讲解。
既然栈和队列都属于线性表,根据线性表分为顺序表和链表的特点,栈也可分为顺序栈和链表,队列也分为顺序队列和链队列,这些内容都会在本章做详细讲解。
使⽤栈结构存储数据,讲究“先进后出”,即最先进栈的数据,最后出栈;使⽤队列存储数据,讲究 "先进先出",即最先进队列的数据,也最先出队列。
⼆栈2.1 栈的基本概念同顺序表和链表⼀样,栈也是⽤来存储逻辑关系为 "⼀对⼀" 数据的线性存储结构,如下图所⽰。
从上图我们看到,栈存储结构与之前所了解的线性存储结构有所差异,这缘于栈对数据 "存" 和 "取" 的过程有特殊的要求:1. 栈只能从表的⼀端存取数据,另⼀端是封闭的;2. 在栈中,⽆论是存数据还是取数据,都必须遵循"先进后出"的原则,即最先进栈的元素最后出栈。
拿图 1 的栈来说,从图中数据的存储状态可判断出,元素 1 是最先进的栈。
因此,当需要从栈中取出元素 1 时,根据"先进后出"的原则,需提前将元素 3 和元素 2 从栈中取出,然后才能成功取出元素 1。
因此,我们可以给栈下⼀个定义,即栈是⼀种只能从表的⼀端存取数据且遵循 "先进后出" 原则的线性存储结构。
通常,栈的开⼝端被称为栈顶;相应地,封⼝端被称为栈底。
因此,栈顶元素指的就是距离栈顶最近的元素,拿下图中的栈顶元素为元素 4;同理,栈底元素指的是位于栈最底部的元素,下中的栈底元素为元素 1。
2.2 进栈和出栈基于栈结构的特点,在实际应⽤中,通常只会对栈执⾏以下两种操作:向栈中添加元素,此过程被称为"进栈"(⼊栈或压栈);从栈中提取出指定元素,此过程被称为"出栈"(或弹栈);2.3 栈的具体实现栈是⼀种 "特殊" 的线性存储结构,因此栈的具体实现有以下两种⽅式:1. 顺序栈:采⽤顺序存储结构可以模拟栈存储数据的特点,从⽽实现栈存储结构。
基本的数据结构

基本的数据结构数据结构是计算机科学中的基础概念,用于组织和存储数据,以便有效地进行检索和操作。
在编程和算法中,数据结构是不可或缺的。
在本文中,我们将介绍几种基本的数据结构,并说明它们各自的特点和用途。
1. 数组(Array)数组是一种线性数据结构,用于存储相同类型的元素。
它的特点是固定大小和连续的存储空间。
数组的访问是通过索引进行的,可以快速访问元素。
但是,数组的大小是固定的,无法动态调整,且插入和删除操作较慢。
2. 链表(Linked List)链表也是一种线性数据结构,但与数组不同,它的元素在内存中是分散存储的。
每个元素包含指向下一个元素的指针,这样就能够把它们连接起来。
链表的大小可以动态增减,插入和删除操作比数组快。
然而,链表的访问比数组慢,需要遍历整个链表才能找到特定元素。
3. 栈(Stack)栈是一种后进先出(Last-In-First-Out,LIFO)的数据结构。
它有两个主要操作:压入(Push)和弹出(Pop)。
在栈中,元素只能从顶部进行插入和删除。
栈常用于实现递归算法、表达式求值和后缀表达式转换等场景。
4. 队列(Queue)队列是一种先进先出(First-In-First-Out,FIFO)的数据结构。
它有两个主要操作:入队(Enqueue)和出队(Dequeue)。
在队列中,元素从队尾插入,从队头删除。
队列常用于模拟等待队列、任务调度和广度优先搜索等情况。
5. 树(Tree)树是一种非线性数据结构,它由节点和边组成。
每个节点可以有零个或多个子节点,其中一个节点被称为根节点。
树具有层次结构,可以用于表示层级关系。
常见的树结构包括二叉树、二叉搜索树、平衡二叉树和堆。
6. 图(Graph)图是一种非线性数据结构,它由节点和边组成。
图中的节点可以以任意方式连接,并且可以有多个连接点。
图可以表示各种实际问题,如社交网络、路线规划和网络拓扑等。
根据边的方向性,图可以分为有向图和无向图。
结构体类型的队列

结构体类型的队列1. 介绍队列是一种常见的数据结构,它遵循先进先出(FIFO)的原则,即最先进入队列的元素最先被取出。
在编程中,我们经常需要使用队列来处理一系列按顺序排列的数据。
在C语言中,可以使用结构体类型来实现队列。
结构体是一种用户自定义的数据类型,它可以包含多个不同类型的成员变量。
通过定义一个结构体类型,并使用该类型创建变量,我们可以将多个相关联的数据组织在一起。
本文将介绍如何使用结构体类型实现一个简单的队列,并提供相应的代码示例和解释。
2. 队列结构体定义首先,我们需要定义一个结构体来表示队列。
该结构体应该包含两个成员变量:一个用于存储队列元素的数组和两个指针分别指向队头和队尾。
#define MAX_SIZE 100typedef struct {int elements[MAX_SIZE];int front;int rear;} Queue;上述代码中,elements数组用于存储队列中的元素,front指针指向队头元素所在位置,rear指针指向下一个可插入元素的位置。
3. 队列操作函数接下来,我们需要实现一些操作函数来对队列进行操作。
以下是一些常用的队列操作函数:3.1 初始化队列在使用队列之前,我们需要先初始化它。
初始化操作包括将front和rear指针都设置为-1,表示队列为空。
void initQueue(Queue *queue) {queue->front = -1;queue->rear = -1;}3.2 判断队列是否为空我们可以通过判断front和rear指针是否相等来确定队列是否为空。
如果它们相等且不为-1,则表示队列为空。
int isEmpty(Queue *queue) {return (queue->front == queue->rear && queue->front == -1);}3.3 判断队列是否已满当插入元素到达数组的末尾时,我们认为队列已满。
班队列动作七个内容

班队列动作引言队列是一种常见的数据结构,它按照先进先出(FIFO)的原则进行操作。
在班级中,队列可以用来管理学生的进出顺序,帮助老师和学生保持有序。
本文将探讨班队列的动作,包括创建队列、入队、出队、队列长度、查看队首元素、查看队尾元素以及清空队列。
创建队列在使用队列之前,我们需要先创建一个空队列。
创建队列的步骤如下:1.定义一个队列变量,用来存储队列的元素。
2.初始化队列变量为空。
下面是创建队列的示例代码:queue = []入队学生进入班级时,我们需要将其加入队列,保持进入班级的顺序。
入队操作即将元素添加到队列的末尾。
入队的步骤如下:1.检查队列是否已满(如果有队列大小限制)。
2.将新元素添加到队列的末尾。
下面是入队的示例代码:def enqueue(queue, element):if len(queue) == MAX_SIZE:print("队列已满,无法入队")else:queue.append(element)出队学生离开班级时,我们需要将其从队列中移除,保持离开班级的顺序。
出队操作即移除队列的第一个元素。
出队的步骤如下:1.检查队列是否为空。
2.移除队列的第一个元素。
下面是出队的示例代码:def dequeue(queue):if len(queue) == 0:print("队列为空,无法出队")else:return queue.pop(0)队列长度队列长度即队列中元素的个数。
可以通过计算队列的长度来获取当前队列中元素的个数。
队列长度的步骤如下:1.返回队列的长度。
下面是计算队列长度的示例代码:def get_length(queue):return len(queue)查看队首元素队首元素即队列中的第一个元素。
通过查看队首元素,我们可以了解下一个将要离开班级的学生是谁。
查看队首元素的步骤如下:1.检查队列是否为空。
2.返回队列的第一个元素。
c语言队列数据结构

c语言队列数据结构队列是一种常见的数据结构,它遵循先进先出(FIFO)的原则。
在C语言中,我们可以使用数组或链表来实现队列数据结构。
本文将介绍C语言中队列的实现方法及其应用。
一、数组实现队列数组是一种简单且常用的数据结构,可以用来实现队列。
在C语言中,我们可以使用数组来创建一个固定大小的队列。
下面是一个使用数组实现队列的示例代码:```c#include <stdio.h>#define MAX_SIZE 100int queue[MAX_SIZE];int front = -1;int rear = -1;void enqueue(int data) {if (rear == MAX_SIZE - 1) {printf("队列已满,无法插入元素。
\n");return;}if (front == -1) {front = 0;}rear++;queue[rear] = data;}void dequeue() {if (front == -1 || front > rear) {printf("队列为空,无法删除元素。
\n"); return;}front++;}int getFront() {if (front == -1 || front > rear) {printf("队列为空。
\n");return -1;}return queue[front];}int isEmpty() {if (front == -1 || front > rear) {return 1;}return 0;}int main() {enqueue(1);enqueue(2);enqueue(3);printf("队列的第一个元素:%d\n", getFront());dequeue();printf("队列的第一个元素:%d\n", getFront());return 0;}```在上述代码中,我们使用了一个数组`queue`来存储队列的元素。
数据结构基础栈和队列

栈的应用 十进制数N和其它d进制数的转换是实现计算的基本问题,
解决方法很多,下面给出一种算法原理: N=(N / d)×d+N % d (其中 / 为整除运算,%为求余运算)。
例如:(1348)10=(2504)8运算过程如下:
default:x=0; while (s[i]!=' ') x=x*10+s[i++]-'0'; stack[++top]=x;
break;
}
i++;
}
//while
return stack[top];
}
main() {
printf("input a string(@_over):"); gets(s); printf("result=%d",comp(s)); return 0; }
cout<<"Please enter a number(N) base 10:"; cin>>n; cout<<"please enter a number(d):"; cin>>d; do{
a[++i]=n%d; n=n/d; }while(n!=0); for (j=i;j>=1;j--)cout<<a[j]; return 0; }
集合
• 数据元素的物理结构有两种:顺序存储结构和链 式存储结构
• 顺序存储结构:用数据元素在存储器中的相对位 置来表示数据元素之间的逻辑关系。
数据结构(一)——线性表、栈和队列

数据结构(⼀)——线性表、栈和队列数据结构是编程的起点,理解数据结构可以从三⽅⾯⼊⼿:1. 逻辑结构。
逻辑结构是指数据元素之间的逻辑关系,可分为线性结构和⾮线性结构,线性表是典型的线性结构,⾮线性结构包括集合、树和图。
2. 存储结构。
存储结构是指数据在计算机中的物理表⽰,可分为顺序存储、链式存储、索引存储和散列存储。
数组是典型的顺序存储结构;链表采⽤链式存储;索引存储的优点是检索速度快,但需要增加附加的索引表,会占⽤较多的存储空间;散列存储使得检索、增加和删除结点的操作都很快,缺点是解决散列冲突会增加时间和空间开销。
3. 数据运算。
施加在数据上的运算包括运算的定义和实现。
运算的定义是针对逻辑结构的,指出运算的功能;运算的实现是针对存储结构的,指出运算的具体操作步骤。
因此,本章将以逻辑结构(线性表、树、散列、优先队列和图)为纵轴,以存储结构和运算为横轴,分析常见数据结构的定义和实现。
在Java中谈到数据结构时,⾸先想到的便是下⾯这张Java集合框架图:从图中可以看出,Java集合类⼤致可分为List、Set、Queue和Map四种体系,其中:List代表有序、重复的集合;Set代表⽆序、不可重复的集合;Queue代表⼀种队列集合实现;Map代表具有映射关系的集合。
在实现上,List、Set和Queue均继承⾃Collection,因此,Java集合框架主要由Collection和Map两个根接⼝及其⼦接⼝、实现类组成。
本⽂将重点探讨线性表的定义和实现,⾸先梳理Collection接⼝及其⼦接⼝的关系,其次从存储结构(顺序表和链表)维度分析线性表的实现,最后通过线性表结构导出栈、队列的模型与实现原理。
主要内容如下:1. Iterator、Collection及List接⼝2. ArrayList / LinkedList实现原理3. Stack / Queue模型与实现⼀、Iterator、Collection及List接⼝Collection接⼝是List、Set和Queue的根接⼝,抽象了集合类所能提供的公共⽅法,包含size()、isEmpty()、add(E e)、remove(Object o)、contains(Object o)等,iterator()返回集合类迭代器。
队列
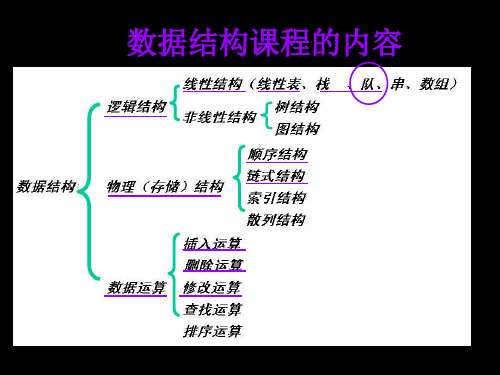
例1: 一循环队列如下图所示,若先删除4个元素,接着再 插入4个元素,请问队头和队尾指针分别指向哪个位置? front front 1
2
J2
J3 J4 J5
front
J8
J9
front
0
J1
3
front
J7 J6 J5
rear
rear 解:由图可知,队头和队尾指针的初态分别为front=0 和rear=5。maxsize=6 删除4个元素后front=4;再插入4个元素后,r=(5+4)%6=3
16
链队列示意图
rear Q front p
a1 (队首) a2
a3 ^
(队尾)
讨论:
① 空队列的特征? front=rear
front
rear
^
② 队列会满吗?一般不会,因为删除时有free动作。除非内存不足! ③ 怎样实现入队和出队操作? 入队(尾部插入):rear->next=S; rear=S; 出队(头部删除):front->next=p->next;
2
1. 定
义
只能在表的一端进行插入运算,在表的另 一端进行删除运算的线性表 (头删尾插)
与同线性表相同,仍为一对一关系。 顺序队或链队,以循环顺序队更常见。
2. 逻辑结构 3. 存储结构
4. 运算规则
只能在队首和队尾运算,且访问结点时依 照先进先出(FIFO)的原则。
5. 实现方式 关键是掌握入队和出队操作,具体实现依顺序
14
5
4
front
例2 :数组Q[n]用来表示一个循环队列,f 为当前队列头元
素的前一位置,r 为队尾元素的位置。假定队列中元素的个 数小于n,计算队列中元素的公式为: (A) r-f (B)(n+f-r)% n (C)n+r-f (D) (n+r-f)% n
数据结构课件队列备课讲稿

链队列示意图
*q q.front
null
q.rear
非空队列
*q
q.front
null
q.rear
空队列
和顺序队列类似,我们也是将这两个指针封 装在一起,将链队列的类型LinkQueue定义为 一个结构类型:
typedef struct queuenode{
ElemType data;
struct queuenode *next;
第二个例子就是主机与外部设备之间速度不匹配的问 题。以主机和打印机为例来说明,主机输出数据给打 印机打印,主机输出数据的速度比打印机打印的速度 要快得多,若直接把输出的数据送给打印机打印,由 于速度不匹配,显然是不行的。所以解决的方法是设 置一个打印数据缓冲区,主机把要打印输出的数据依 此写如到这个缓冲区中,写满后就暂停输出,继而去 做其它的事情,打印机就从缓冲区中按照先进先出的 原则依次取出数据并打印,打印完后再向主机发出请 求,主机接到请求后再向缓冲区写入打印数据,这样 利用队列既保证了打印数据的正确,又使主机提高了 效率。
Q.rear=p; }
4、出队操作:
*q q.front q.rear
p null x null
存储池
Status DeQueue(LinkQueue &Q,ElenType &e)
{
QueueNode *p; if(QueueEmpty(Q))
return ERROR; p=Q.front->next; e=p–>data;
队列的抽象数据定义见书P59
3.4.2 非循环队列和循环队列
分配一块连续的存储区域来存放队列里的元素。由 于队列的队头和队尾的位置是变化的,因而要设两个 指针和分别指示队头和队尾元素在队列中的位置。
第3章数据结构基本类型3.3操作受限的线性表——队列-高中教学同步《信息技术-数据与数据结构》(教案
编程实践:请实现一个循环队列,包含入队(enqueue)、出队(dequeue)、判断队列是否为空(is_empty)等基本操作。你可以使用Python语言进行编程,并编写相应的测试用例来验证你的实现。
理论思考:
思考并解释为什么队列的“先进先出”特性在现实生活中有广泛的应用。
假设你是一家大型超市的经理,你需要设计一个顾客结账排队系统。请说明你会如何利用队列的原理来设计一个既高效又公平的排队系统。
队列的应用:
结合日常生活中的排队场景,解释队列原理的实际应用,如银行取号系统、医院挂号系统等。
强调队列在处理具有“先来先服务”特性问题时的有效性,以及如何通过队列来优化服务流程。
教学难点
循环队列的实现与理解:
理解循环队列如何通过循环使用数组空间来避免“假溢出”现象。
掌握如何根据队列的头部和尾部指针判断队列的空和满状态。
完成后与同学交流并分享自己的解题思路和经验。
通过编程练习巩固所学知识,提高学生的编程能力和解决实际问题的能力。
鼓励学生互相交流和讨论,培养学生的团队协作能力和沟通能力。
课堂小结
作业布置
课堂小结
本节课我们深入学习了数据结构中的队列(Queue)这一重要概念。首先,通过日常生活中排队的例子,我们直观地理解了队列的基本特点——先进先出(FIFO),即新加入的元素总是排在队尾,而需要处理的元素总是从队头开始。
准备课后作业:设计一些与队列相关的课后作业,如编写顺序队列和链式队列的实现代码、分析队列在实际问题中的应用等,以巩固学生的学习效果。
教学媒体
教材或讲义:
提供了队列的基本概念、特征、实现方式以及应用实例的文字描述。
包含了队列的抽象数据类型定义、队列的存储结构(顺序队列、循环队列、链队列)等核心知识点的详细解释。
1队列

第一讲队列前言什么是数据结构128313245678站队家谱城市交通什么是数据结构数据结构是计算机存储数据、组织数据的方式。
数据结构是指相互之间存在一种或多种关系的数据元素的集合以及该集合中数据元素之间的关系。
记为:Data_Struct=(D,R)D是数据元素的集合;R是数据元素之间的关系的有限集合。
如:家谱D={1,2,3,4,5,6,7,8}R={<1,2>,<1,3>,<2,4>,<2,5>,<2,6>,<3,7>,<3,8>}什么是数据结构数据结构分为逻辑结构和物理结构逻辑结构:反映数据元素之间的逻辑关系(先后关系),与在计算机中的存储位置无关。
包括:集合,线性结构,树形结构,图形结构。
通常所说的数据结构指的是逻辑结构什么是数据结构①集合结构:元素之间没有关系。
②线性结构:元素是一对一的关系。
③树形结构:元素存在着一对多的关系。
④图形结构:元素是多对多的关系。
12341 2341235461234图1图2图3图4什么是数据结构物理结构:数据的逻辑结构在计算机存储空间中的存放形式:顺序结构和链式结构。
顺序存储结构:是把数据元素放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的。
链式存储结构:把数据元素放在任意的存储单元了,这组存储单元可以是连续的,也可以是不连续的。
物理结构:顺序存储结构物理结构:链式存储结构第一部分线性结构—队列线性结构(线性表)是最基本、最简单、最常用的数据结构。
所有元素排成一排。
除了第一个元素都有“前一个元素”,除了最后一个都有“后一个元素”。
常用的线性表:栈,队列,链表2020/1/13《数据结构与算法》11赵宗昌队列(queue )队列是一种运算受限的线性表:在一端删除(队首head ),另一端插入(队尾tail )操作原则:先进先出FIFO队列的两个操作:出队与入队队首:head (习惯指向队首元素)队尾:tail (指向队尾元素的后一个空位置)head tailq[i]16102130下标i012345678int q[100001];headq[i]16102130下标i012345678tail出队列(注意顺序):t=q[head];head=head+1;或:t=q[head++]入队列(注意顺序):q[tail]=x;tail++;或:q[tail++]=x队列非空:Head<tail【例1】卡片游戏桌上有一叠牌,从第一张牌(即位于顶面的牌)开始从上往下依次编号为1~n;当至少还剩两张牌时进行以下操作:把第一张牌扔掉,然后把新的第一张放到整叠牌的最后。
【数据结构】队列实现的5种方式及时间复杂度对比分析

【数据结构】队列实现的5种⽅式及时间复杂度对⽐分析1. 使⽤数组实现⼀个简单的队列/*** ===========================* 队列⾸部 00000000000000000000000000 队列尾部* ===========================*/public class ArrayQueue<Element> implements Queue<Element>{// 通过内部的array来实现private Array<Element> array;// 构造函数public ArrayQueue(int capacity){this.array = new Array<>(capacity);}// 默认的构造函数public ArrayQueue(){this.array = new Array<>();}@Overridepublic int getSize() {return this.array.getSize();}@Overridepublic boolean isEmpty() {return this.array.isEmpty();}public int getCapacity(){return this.array.getCapacity();}@Overridepublic void enqueue(Element element) {// 进⼊队列(数组的末尾来添加元素)this.array.addLast(element);}@Overridepublic Element dequeue() {// 出队列(删除最后⼀个元素),数组的第⼀个元素return this.array.removeFirst();}@Overridepublic Element getFront() {// 获取第⼀个元素(对⾸部的第⼀个元素)return this.array.getFirst();}@Overridepublic String toString(){StringBuilder stringBuilder = new StringBuilder();// 使⽤⾃定义的⽅式实现数组的输出stringBuilder.append("Queue:");// 开始实现数组元素的查询stringBuilder.append("front [");for (int i = 0; i < this.array.getSize(); i++) {stringBuilder.append(this.array.get(i));// 开始实现数组元素的回显(只要下表不是最后⼀个元素的话,就直接输出这个元素)if (i != this.array.getSize()-1)stringBuilder.append(", ");}stringBuilder.append("] tail");// 实现数组元素的输出return stringBuilder.toString();}}2. 使⽤数组实现⼀个循环队列(维护⼀个size变量)/*** 循环队列的⼏个要点:* 1. tail = head 说明队列就是满的* 2. 循环队列需要空出来⼀个位置*/public class LoopQueue<E> implements Queue {private E[] data;private int head; // ⾸部指针private int tail; // 尾部指针private int size; // 可以通过head以及tail的位置情况去计算size的⼤⼩【注意是不能直接使⽤getCapacity的】// 实现循环队列public LoopQueue() {// 设置⼀个队列的默认的⼤⼩this(10);}// 循环队列的实现public LoopQueue(int capacity) {this.data = (E[]) new Object[capacity + 1];// 需要多出来⼀个this.head = 0;this.tail = 0;this.size = 0;}@Overridepublic int getSize() {// 计算容量⼤⼩return this.size;}// capacity表⽰的这个队列中最⼤可以容纳的元素个数【这是⼀个固定值】@Overridepublic int getCapacity() {// 由于队列默认占了⼀个空的位置,因此sizt = this.length-1return this.data.length - 1;}// 当head和tail的值相同的时候队列满了public boolean isEmpty() {return head == tail;}@Overridepublic void enqueue(Object value) {// 1. 开始判断队列有没有充满, 因为数组的下表是不会改变的,所以这⾥需要以数组的下标为⼀个参考点,⽽不是this.data.length-14if ((tail + 1) % this.data.length == head) {// 2. 开始进⾏扩容, 原来的⼆倍, 由于默认的时候已经⽩⽩浪费了⼀个空间,因此这⾥就直接扩容为原来的⼆倍即可resize(2 * getCapacity());}// 2. 如果没有满的话,就开始添加元素this.data[tail] = (E) value;// 3. 添加完毕之后(tail是⼀个循环的位置,不可以直接相加)// this.tail = 2;this.tail = (this.tail+1) % data.length; // data.length对于数组的下标// int i = (this.tail + 1) % data.length;// 4. 队⾥的长度this.size++;}/*** 开始resize数组元素** @param capacity*/private void resize(int capacity) {// 开始进⾏数组的扩容// 1. 创建⼀个新的容器(默认多⼀个位置)E[] newData = (E[]) new Object[capacity + 1];// 2. 开始转移元素到新的容器for (int i = 0; i < size; i++) {int index = (head + i) % data.length;newData[i] = data[index];}// 添加完毕之后,开始回收之前的data,data⾥⾯的数据⼀直是最新的数据this.data = newData; // jvm的垃圾回收机制会⾃动回收内存data// 3. 添加完毕this.head = 0;// 4. 指向尾部this.tail = size;}@Overridepublic Object dequeue() {// 1. 先来看下队列中有没有元素数据if (this.size == 0)throw new IllegalArgumentException("Empty queue cannot dequeue!");// 2. 开始看⼀下内存的⼤⼩Object ret = this.data[head];// 3. 开始删除数据this.data[head] = null;// TODO 注意点:直接使⽤+1⽽不是使⽤++// 4. 开始向后移动,为了防⽌出错,尽量使⽤ this.head+1来进⾏操作,⽽不是使⽤ this.haad++, 否则可能会出现死循环的情况【特别注意】 this.head = (this.head+1) % data.length;// 5. 计算新的容量⼤⼩this.size--;// 6. 开始进⾏缩容操作, d当容量为1, size为0的时候,就不需要缩⼩容量、、if (this.size == this.getCapacity() / 4)// 缩⼩为原来的⼀半⼤⼩的容量resize(this.getCapacity() / 2);// 获取出队列的元素return ret;}@Overridepublic Object getFront() {// 由于front的位置⼀直是队列的第⼀个元素,直接返回即可if (this.size == 0)throw new IllegalArgumentException("Empty queue cannot get element!");return this.data[head];}@Overridepublic String toString() {StringBuilder stringBuilder = new StringBuilder();stringBuilder.append(String.format("Array : size=%d, capacity=%d; ", size, getCapacity()));stringBuilder.append("LoopQueue head [");// 第⼀个元素在head的位置,最后⼀个元素在tail-1的位置// 注意循环队列的遍历⽅式,是⼀个循环for (int i = this.head; i != tail; i = (i+1) % data.length) {stringBuilder.append(data[i]);// 只要不是最后⼀个元素的话, 由于循环条件中已经规定了i!=tail, 因此这⾥是不能直接这样来判断的if ((i+1)%data.length == this.tail) {// 此时就是最后⼀个元素} else {stringBuilder.append(", ");}}stringBuilder.append("] tail");return stringBuilder.toString();}}3.使⽤数组实现⼀个循环队列(不维护size变量)/*** 使⽤数组实现⼀个循环队列的数据结构*/public class WithoutSizeLoopQueue<E> implements Queue<E> {private E[] data;private int head;private int tail;public WithoutSizeLoopQueue(int capacity) {// 泛型不能直接被实例化,由于循环队列默认会空出来⼀个位置,这⾥需要注意this.data = (E[]) new Object[capacity + 1];this.head = 0;this.tail = 0;}public WithoutSizeLoopQueue() {this(10);}@Overridepublic int getSize() {// 计算数组的元素个数if (tail >= head) {return tail - head;} else {int offSet = head - tail;return this.data.length - offSet;}}@Overridepublic int getCapacity() {return data.length - 1;}@Overridepublic void enqueue(E value) {// 开始进⼊队列// 1. 先来看下队列有没有满if ((tail + 1) % data.length == head)// 开始扩⼤容量resize(2 * getCapacity());// 2. 开始进⼊队列data[tail] = value;// 3. 开始移动下标tail++;// 4. 开始更新容量【没必要】}public void resize(int newCapacity) {// 1. 更新为新的容量E[] newData = (E[]) new Object[newCapacity + 1];// 2. 开始转移数据到新的数组中去for (int i = 0; i < getSize(); i++) {newData[i] = data[(i + head) % data.length];}// 3. 销毁原来的数据信息data = newData;// 【错误警告】bug:移动到新的这个数组⾥⾯之后,需要重新改变head和tail的位置【bug】tail = getSize(); // 尾部节点始终指向最后⼀个元素的后⾯⼀个位置,此时如果直接使⽤getSize实际上获取到的是上⼀次的元素的个数,⽽不是最新的元素的个数信息(需要放在前⾯,否在获取到的size就不是同⼀个了,特别重要) head = 0; // 头节点指向的是第⼀个元素// 4. 直接销毁newData = null;}@Overridepublic E dequeue() {// 1.先来看下队列是否为空if (getSize() == 0)throw new IllegalArgumentException("Empty queue cannot dequeue!");// 2.开始出head位置的元素E value = data[head];// 3. 删除元素data[head] = null;// 4. 移动headhead = (head+1) % data.length;// 此时需要进⾏⼀次判断if (getSize() == getCapacity() / 4 && getCapacity() / 2 != 0)resize(getCapacity() / 2);// 如果数组缩⼩容量之后,这⾥的return value;}@Overridepublic E getFront() {return dequeue();}@Overridepublic String toString(){// 开始遍历输出队列的元素StringBuilder stringBuilder = new StringBuilder();stringBuilder.append(String.format("LoopQueue: size = %d, capacity = %d\n", getSize(), getCapacity())); stringBuilder.append("front ");// 从head位置开始遍历for (int i = head; i != tail ; i = (i+1) % data.length) {stringBuilder.append(data[i]);if ((i + 1) % data.length != tail)stringBuilder.append(", ");}return stringBuilder.append(" tail").toString();}}4. 使⽤链表实现⼀个队列/*** 使⽤链表实现的队列*/public class LinkedListQueue<E> implements Queue<E>{// 这是⼀个内部类,只能在这个类的内部可以访问(⽤户不需要了解底层是如何实现的)private class Node {// ⽤于存储元素public E e;// ⽤于存储下⼀个节点public Node next;public Node(E e, Node next) {this.e = e;this.next = next;}public Node(E e) {this(e, null);}public Node() {this(null, null);}@Overridepublic String toString() {return e.toString();}}// 定义队列需要的参数private Node head, tail;private int size;public LinkedListQueue(){this.head = null;this.tail = null;this.size = 0;}@Overridepublic int getSize() {return this.size;}public boolean isEmpty(){return this.size == 0;}@Overridepublic int getCapacity() {return 0;}/*** ⼊队* @param value*/@Overridepublic void enqueue(E value) {// ⼊队从尾部开始if (tail == null){// 1. 如果此时没有元素的话tail = new Node(value);head = tail;}else {// 2. 如果已经存在了元素,那么队列尾部肯定是不为空的,⽽是指向了⼀个空节点tail.next = new Node(value);// 移动尾节点tail = tail.next;}size++;}/*** 出队* @return*/@Overridepublic E dequeue() {if (isEmpty())throw new IllegalArgumentException("Empty queue cannot dequeue!");// 1. 存储出队的元素Node retNode = head;// 2.head节点下移动head = head.next;// 3.删除原来的头节点retNode.next = null; // 实际上删除的是这个节点的数据域// 如果删除了最后⼀个元素之后if (head == null)tail = null;size--;return retNode.e;}@Overridepublic E getFront() {if (isEmpty())throw new IllegalArgumentException("Empty queue cannot dequeue!");return head.e;}@Overridepublic String toString(){StringBuilder stringBuilder = new StringBuilder();Node cur = head;stringBuilder.append("head:");// 1. 第⼀种循环遍历的⽅式, 注意这⾥判断的是每⼀次的cur是否为空,⽽不是判断cur.next,否则第⼀个元素是不能打印输出的 while (cur != null) {stringBuilder.append(cur + "->");// 继续向后移动节点cur = cur.next;}stringBuilder.append("NULL tail");return stringBuilder.toString();}}5. 使⽤⼀个带有虚拟头结点的链表实现⼀个队列/*** 带有虚拟头结点的链表实现的队列*/public class DummyHeadLinkedListQueue<E> implements Queue<E> {// 这是⼀个内部类,只能在这个类的内部可以访问(⽤户不需要了解底层是如何实现的)private class Node {// ⽤于存储元素public E e;// ⽤于存储下⼀个节点public Node next;public Node(E e, Node next) {this.e = e;this.next = next;}public Node(E e) {this(e, null);}public Node() {this(null, null);}@Overridepublic String toString() {return e.toString();}}// 定义⼀个虚拟头结点private Node dummyHead, tail;private int size;public DummyHeadLinkedListQueue(){this.dummyHead = new Node(null, null);this.tail = null;this.size = 0;}@Overridepublic int getSize() {return this.size;}public Boolean isEmpty(){return this.size == 0;}@Overridepublic int getCapacity() {throw new IllegalArgumentException("LinkedList cannot getCapacity!");}@Overridepublic void enqueue(E value) {// 开始⼊队列(从队列的尾部进⾏⼊队列)// 1. 构造插⼊的节点Node node = new Node(value);// 2. 尾部插⼊节点 //bug : 由于默认的时候 tail为null,此时如果直接访问tail.next 是错误的if (tail == null) {dummyHead.next = node;// 说明此时队列为空的tail = node;} else {tail.next = node;// 3. 尾部节点向后移动tail = tail.next;}// 4. 队列长度增加size++;}@Overridepublic E dequeue() {// 元素出队列从链表的头部出去// 1. 获取头结点的位置Node head = dummyHead.next;// 缓存出队的元素Node retNode = head;// 2. 移动节点dummyHead.next = head.next;// 4. 更新容量size--;head = null;if (isEmpty())tail = null; // bug修复return (E) retNode;}@Overridepublic E getFront() {return null;}@Overridepublic String toString(){StringBuilder stringBuilder = new StringBuilder();stringBuilder.append("Queue head:");Node cur = dummyHead.next;while (cur != null){stringBuilder.append(cur + "->");cur = cur.next;}return stringBuilder.append("null tail").toString();}}以上就是创建队列实现的5中⽅式,每种⽅式都有各⾃的特点,就做个简单总结吧! 队列的时间复杂度分析:+ 队列Queue[数组队列]void enqueue(E) O(1) 均摊复杂度E dequeue() O(n) 移出队列⾸部的元素,需要其他元素向前补齐E getFront() O(1)void dequeue() O(1)Int getSize() O(1)bool isEmpty() O(1)+ 循环队列void enqueue(E) O(1) 均摊复杂度E dequeue() O(1)E getFront() O(1)void dequeue() O(1)Int getSize() O(1)bool isEmpty() O(1)以上就是对于队列实现的⼏种⽅式的总结了。
数据结构(牛小飞)6队列PPT课件

循环队列的应用
循环队列是一种利用固定长度的数组实现的队列,通过 循环利用数组的空间来达到动态扩展的效果。
循环队列在实现上需要处理队列为空和队列满的情况, 以保证数据的正确性。
循环队列在处理大量数据时具有较高的效率,能够避免 频繁的内存分配和释放操作。
代码的复杂性。
04
出队操作:删除循环队列头部的元素,并将头部指针 向前移动一位。如果头部指针已经达到数组的最后一 个位置,则将其重置为数组的第一个位置。
04
队列的运算性能分析
队列的插入性能分析
总结词
队列的插入操作通常具有较好的 性能,时间复杂度为O(1)。
详细描述
在队列中,插入操作通常在队尾进 行,因为队列是一种先进先出 (FIFO)的数据结构,所以插入操 作可以在常数时间内完成。
消息中间件
使用队列可以实现异步的消息传递, 提高系统的解耦性和扩展性。
02
队列的基本操作
入队操作
总结词
在队列的尾部添加元素
详细描述
入队操作是指将一个元素添加到队列的尾部。在队列中,新元素总是被放置在 队尾,等待被处理。入队操作的时间复杂度通常为O(1),即常数时间复杂度。
出队操作
总结词
从队列的头部移除元素
详细描述
出队操作是指从队列的头部移除一个元素。在队列中,最先进入的元素最先被处理, 因此出队操作总是从队头开始。出队操作的时间复杂度通常为O(1),即常数时间复 杂度。
队列的初始化与销毁
总结词
创建和释放队列所占用的资源
详细描述
队列的初始化操作是创建一个空队列,并分配必要的存储空间。销毁队列的操作则是释放队列所占用的存储空间, 并解除与队列相关的所有资源。初始化与销毁操作的时间复杂度通常为O(1)。
数据结构14:队列(Queue),“先进先出”的数据结构

数据结构14:队列(Queue),“先进先出”的数据结构队列是线性表的⼀种,在操作数据元素时,和栈⼀样,有⾃⼰的规则:使⽤队列存取数据元素时,数据元素只能从表的⼀端进⼊队列,另⼀端出队列,如图1。
图1 队列⽰意图称进⼊队列的⼀端为“队尾”;出队列的⼀端为“队头”。
数据元素全部由队尾陆续进队列,由队头陆续出队列。
队列的先进先出原则队列从⼀端存⼊数据,另⼀端调取数据的原则称为“先进先出”原则。
(first in first out,简称“FIFO”)图1中,根据队列的先进先出原则,(a1,a2,a3,…,a n)中,由于 a1 最先从队尾进⼊队列,所以可以最先从队头出队列,对于 a2来说,只有a1出队之后,a2才能出队。
类似于⽇常⽣活中排队买票,先排队(⼊队列),等⾃⼰前⾯的⼈逐个买完票,逐个出队列之后,才轮到你买票。
买完之后,你也出队列。
先进⼊队列的⼈先买票并先出队列(不存在插队)。
队列的实现⽅式队列的实现同样有两种⽅式:顺序存储和链式存储。
两者的区别同样在于数据元素在物理存储结构上的不同。
队列的顺序表⽰和实现使⽤顺序存储结构表⽰队列时,⾸先申请⾜够⼤的内存空间建⽴⼀个数组,除此之外,为了满⾜队列从队尾存⼊数据元素,从队头删除数据元素,还需要定义两个指针分别作为头指针和尾指针。
当有数据元素进⼊队列时,将数据元素存放到队尾指针指向的位置,然后队尾指针增加 1;当删除对头元素(即使想删除的是队列中的元素,也必须从队头开始⼀个个的删除)时,只需要移动头指针的位置就可以了。
顺序表⽰是在数组中操作数据元素,由于数组本⾝有下标,所以队列的头指针和尾指针可以⽤数组下标来代替,既实现了⽬的,⼜简化了程序。
例如,将队列(1,2,3,4)依次⼊队,然后依次出队并输出。
代码实现:#include <stdio.h>int enQueue(int *a, int rear, int data){a[rear] = data;rear++;return rear;}void deQueue(int *a, int front, int rear){//如果 front==rear,表⽰队列为空while (front != rear) {printf("%d", a[front]);front++;}}int main(){int a[100];int front, rear;//设置队头指针和队尾指针,当队列中没有元素时,队头和队尾指向同⼀块地址front = rear = 0;rear = enQueue(a, rear, 1);rear = enQueue(a, rear, 2);rear = enQueue(a, rear, 3);rear = enQueue(a, rear, 4);//出队deQueue(a, front, rear);return0;}顺序存储存在的问题当使⽤线性表的顺序表⽰实现队列时,由于按照先进先出的原则,队列的队尾⼀直不断的添加数据元素,队头不断的删除数据元素。
3.3.1《队列》-教学设计-粤教版(2019)高中信息技术-数据与数据结构选修1

2. 教学手段:
- 多媒体设备:利用PPT、动画等形式展示队列的操作过程,使抽象概念形象化,便于学生理解。
- 教学软件:运用编程软件或模拟工具,让学生实时观察队列操作的结果,提高学习效果。
- 网络资源:提供在线教程和案例,引导学生课后自主学习,拓展知识面。
- 教学方法/手段/资源:
讲授法:通过讲解,帮助学生理解队列的理论知识。
实践活动法:通过编程实践,让学生亲身体验队列的操作。
合作学习法:通过小组合作,培养学生的团队协作能力。
- 作用与目的:
加深学生对队列知识点的理解,掌握队列操作技能。
通过实践活动,提高学生的问题解决能力和动手能力。
3. 课后拓展应用
信息技术手段:利用在线平台和微信,实现资源共享和互动。
- 作用与目的:
让学生提前接触队列知识,为课堂学习打下基础。
培养学生自主学习能力和问题意识。
2. 课中强化技能
- 教师活动:
导入新课:通过一个实际生活中的排队场景视频,引出队列的概念。
讲解知识点:详细讲解队列的先进先出特性、插入和删除操作的实现。
- 针对应用题,评价学生分析的合理性,给出改进建议,帮助学生深入理解队列的应用。
- 对思考题的答案进行评阅,指出学生分析中的不足,并给出优化建议,引导学生深入思考队列的存储结构。
- 反馈方式:通过在线学习平台或书面形式,及时将作业批改结果反馈给学生,同时提供个别指导,帮助学生改进不足。
课后拓展
- 队列在操作系统中的应用,如进程调度、线程同步等。
- 队列与栈的比较:学生需理解队列与栈这两种常见数据结构的异同,以及它们适用的不同场景。
软件技术--队列

lq[rear]=x; } }
(3)出队列
出队列成功,返回x;否则给出相应信息。
datatype delloopque(datatype lq[]) {datatype x; if (front= =rear) {printf("队列为空!下溢!\n"); return(0); } else {front=(front+1)%N;
(4)取队头元素 取队头数据使用,不删除该数据元 素;
(5)队列空判断 判断队列是否为空,是出队列和 取队头元素时常用的操作;
(6)队列满判断 判断队列是否已满,是进队时首 先进行的操作。
※顺序队列
队列的顺序存储是指用一组连续的存储单元依次存放队列中的元素。在 C语言中用一维数组来存放队列中的元素。因为队列的队头和队尾的位置是 变化的,所以还需附设两个指针front和rear,front指针指向队列头元素的 位置,rear指针指向队列尾元素的位置。约定当队列为空时,令 front=rear=-1。每当插入新的队尾元素时,尾指针rear增加1;每当删除队 头元素时,头指针front增加1。
front= =( rear+1)%N; 成立时,认定队列为满。当判断队列为空时,条件是:front= = rear;
※循环队列的基本算法
这里以第二种方法区别循环队列的空、满状态。 循环队列的类型定义: #define N 100 datatype lq[N];
int front,rear;
(1)构造空队列
如下图(a)所示循环队列中,队列头元素是A,尾元素是C。当元素A、B、 C从图4-15(a)所示的队列中删除后,则队列变成空的状态,如图(b)所示。 反之,在图(a)的队列中,若元素D、E、F相继插入,则队列空间被占满,如图 (c)所示。不管队列为空还是为满,均出现front= =rear的情况。因此仅凭 front= = rear不能判定队列是空还是满。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
顺序队列的定义为一个结构体类型,该类型变量有 3 个数据域:queue,front,rear。其中,queue 为存储队列中的一维数组,front 和 rear 分别表示队列中的队头指针和队尾指针,通过整型变量表示,取 值范围为 0~ QueueSize。 在队列中,队满指的是元素占据了队列中的所有存储空间,没有空闲的存储空间可以插入元素。队 空指的是队列中没有一个元素,也叫空队列。假设 Q 是一个队列,若不考虑队满,则入队操作语句为 Q.queue[rear++]=x;若不考虑队空,则出队操作语句为 x=Q.queue[front++]。 下面是顺序队列的实现算法。以下顺序队列的实现算法存放在 SeqQueue.h 文件中。 (1)队列的初始化操作。队列的初始化就是要把队列初始化为空队列,只需要把队头指针和队尾 指针同时置为 0 即可。队列的初始化实现代码如下。
5.1.2
队列的抽象数据类型
队列的抽象数据类型包括数据对象集合和基本操作集合。其中,数据对象集合定义了队列的数据元 素及元素之间的关系,基本操作集合定义了在该数据对象上的一些基本操作。 1.数据对象集合 队列的数据对象集合为{a1,a2,…,an},每个元素的类型均为 DataType。队列与栈一样,也是一 种线性表,具有线性表的特点:除了第一个元素 a1 外,每一个元素有且只有一个直接前驱元素,除了最
(4)出队操作。出队操作就是将队列中的队首元素即队头指针指向的元素删除。在删除队首元素 时,应首先通过队头指针和队尾指针是否相等判断队列是否已空。若队列非空,则删除队头元素,然后 将队头指针向后移动,使其指向下一个元素。出队操作的实现代码如下。
int DeleteQueue(SeqQueue *SQ,DataType *e) /*删除顺序队列中的队头元素,并将该元素赋值给 e,删除成功返回 1,否则返回 0*/ { if(SQ->front==SQ->rear) return 0; else { *e=SQ->queue[SQ->front]; /*将要删除的元素赋值给 e*/ SQ->front=SQ->front+1; /*将队头指针向后移动一个位置,指向新的队头*/ return 1; } } /*在删除元素之前,判断队列是否为空*/
pdfMachine Is a pdf writer that produces quality PDF files with ease! Produce quality PDF files in seconds and preserve the integrity of your original documents. Compatible across nearly all Windows platforms, if you can print from a windows application you can use pdfMachine. Get yours now!
(3)入队操作。入队操作就是要将元素插入到队列。在将元素插入到队列之前首先要判断队列是 否已经已满,因为队尾指针的最大值是 QueueSize,所以通过检查队尾指针 rear 是否等于 QueueSize 来 判断队列是否已满。如果队列未满,则执行插入运算,然后队尾指针加 1 把队尾指针向后移动。入队操 作的实现代码如下。
队列也是一种限定性线性表,允许在表的一端进行插入操作,在表的另一端进行删除操作。本节主 要介绍队列的定义和队列的抽象数据类型。
5.1.1
队列的定义
队列是一种特殊的线性表,它包含一个队头(front)和一个队尾(rear)。其中,队头只允许删除 元素,队尾只允许插入元素。队列的特点是先进入队列的元素先出来,即先进先出(FIFO)。假设队列 为 q=(a1,a2,…,ai,…,an),那么 a1 就是队头元素,an 则是队尾元素。进入队列时,是按照 a1, a2,…,an 进入的,退出队列时也是按照这个顺序退出的。出队列时,只有当前面的元素都退出之后, 后面的元素才能退出。因此,只有当 a1,a2,…,an-1 都退出队列以后,an 才能退出队列。队列操作的示 意图如图 5.1 所示。
图 5.2
顺序队列示意图
为了方便用 C 语言描述,我们约定:初始化建立空队列时,front=rear=0,队头指针 front 和队尾指 针 rear 都指向队列的第一个位置,如图 5.3 所示。插入新的元素时,队尾指针 rear 增 1,空队列中插入 3 个元素 a,b,c 之后队头和队尾指针状态如图 5.4 所示。删除元素时,队头指针 front 增 1,在删除 2 个元素 a,b.之后队头和队尾指针状态如图 5.5 所示。队列为非空时,队头指针 front 指向队头元素的位 置,队尾指针 rear 指向队尾元素所在位置的下一个位置。
·217· 后一个元素 an 外,每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。 2.基本操作集合 队列的基本操作主要有下面 6 种: (1)InitQueue(&Q):初始化操作,建立一个空队列 Q。这就像日常生活中,火车站售票处新增加了 一个售票窗口,这样就可以新增一队用来排队买票。 (2)QueueEmpty(Q):若 Q 为空队列,返回 1,否则返回 0。这就像日常生活中,火车窗口前是否 还有人排队买票。 (3)EnterQueue(&Q,x):插入元素 x 到队列 Q 的队尾。这就像日常生活中,新来买票的人要在队列 的最后一样。 (4)DeleteQueue(&Q,&e):删除 Q 的队首元素,并用 e 返回其值。这就像买过票的排在队头的人离 开队列。 (5)Gethead(Q,&e):用 e 返回 Q 的队首元素。这就像询问排队买票的人是谁。 (6)ClearQueue(&Q):将队列 Q 清空。这就像排队买票的人全部买完了票,离开队列。
pdfMachine Is a pdf writer that produces quality PDF files with ease! Produce quality PDF files in seconds and preserve the integrity of your original documents. Compatible across nearly all Windows platforms, if you can print from a windows application you can use pdfMachineaType queue[QueueSize]; int front,rear; /*队头指针和队尾指针*/ }SeqQueue; #include”SeqQueue.h” /*包含顺序队列的实现算法文件*/
void main() { SeqQueue Q; char str[]="ABCDEFGH"; /*定义将要插入队列的字符串*/ int i,length=8; /*定义队列的元素个数*/ char x; InitQueue(&Q); /*初始化顺序队列*/
图 5.1
队列操作的示意图
在日常生活中,人们排队买票排的队就是一个队列。新来买票的人到队尾排队,形成新的队尾,即 入队,在队首的人买完票离开,即出队。在程序设计中也经常会遇到排队等待服务的问题。一个典型的 例子就是操作系统中的多任务处理。在计算机系统中,同时有几个任务等待输出,那么就要按照请求输 出的先后顺序进行输出。
例 5_1 编程实现顺序队列的入队操作和出队操作,并将出队结果输出。 分析:主要考察队列基本操作的使用。具体实现代码如下。
#define QueueSize 50 typedef char DataType; #include<stdio.h> typedef struct Squeue{ /*定义队列的最大容量*/ /*定义队列元素的类型为字符类型*/ /*包含头文件,主要包含输入输出函数*/ /*顺序队列类型定义*/
for(i=0;i<length;i++) { EnterQueue(&Q,str[i]);
/*将字符依次插入到顺序队列中*/
} DeleteQueue(&Q,&x); /*将队头元素出队列*/ printf("出队列的元素为:%c\n",x); /*显示输出出队列的元素*/ printf("顺序队列中的元素为:"); if(!QueueEmpty(Q)) /*判断队列是否为空队列*/
5.2 队列的顺序存储及实现
队列有两种存储表示:顺序存储和链式存储。采用顺序存储结构的队列被称之为顺序队列,采用链 式存储结构的队列被称之为链式队列。
5.2.1
顺序队列的表示
顺序队列通常采用一维数组进行存储。其中,连续的存储单元依次存放队列中的元素。同时,使用 两个指针分别表示数组中存放的第一个元素和最后一个元素的位置。其中,指向第一个元素的指针被称 为队头指针 front,指向最后一个元素的位置的指针被称为队尾指针 rear。队列的表示如图 5.2 所示。 在图 5.2 中,队列中的元素存放在数组中,用队头指针 front 指向第一个元素 a,队尾指针指向最后 一个元素 h。
pdfMachine Is a pdf writer that produces quality PDF files with ease! Produce quality PDF files in seconds and preserve the integrity of your original documents. Compatible across nearly all Windows platforms, if you can print from a windows application you can use pdfMachine. Get yours now!
