湖北省黄冈中学2013届高三11月月考数学理试题(解析版)

合集下载

2013届11月份湖北黄冈试题部分解析

湖北黄冈部分解析
21. demonstrate vt.证明，证实；论证；显示，展示；演示，说明 vi.示威游行 dominate vt.& vi.控制；在……中占首要地位；在……中具有最重要（或明显）的特色；在……中拥有最重要的位置 vt.耸立于，俯临；支配；施加 proceed vi.进行；前进；（沿特定路线）行进；（尤指打断后）继续说 n.收入，获利 promote vt.促进，推进；提升，助长；促销；使（学生）升级 They discussed how to promote cooperation between the two countries. 他们讨论如何促进两国间的合作。 He has been promoted to general manager. 他已被提升为总经理。
bend vt.（使）弯曲，屈身；拉弯；使成形，强行；集中全力于 vi.偏向；使变曲，成角度；弯身，弯腰；专心 n.弯曲（处）；（尤指道路或河流的）拐弯；弯道；（潜水员过快浮出水面造成的）减压病现在分词：bending；过去式：bent；bended； The branch bent but didn't break when the boy climbed along it. 那男孩爬上树枝时，树枝弯曲了，但是没有折断。 The stream takes a sudden bend to the east. 小溪突然转向东流。 bend常与介词to连用,表示河流、道路等弯曲的方向; 与above, on, round等介词连用,常用于引申义。
41.
I usually go into action at midnight. 我通常半夜开始工作。 Our factory was bombed out at that time, but we soon managed to go into production again. 那时我们的工厂被炸停工，但我们很快恢复了生产。

湖北省黄冈中学2013届高三第二次模拟考试(理科)数学及其答案

请在各题的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
20．（12 分）
21．（13 分）
22．（14 分）
二、填空题（请将答案填在对应题号的位置上，一题两空的题，其答案先后次序填写）
11． 13． 14． 15．
三、解答题 17．（12 分）
12．
16．
请在各题的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题的答题区域内作答，超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效第 1 页共 2 页
请在各题的答题区域内作答，超出黑色矩形边框限定区域的答案无效请在各题的答题区域内作答，超出黑色矩形边框限定区域的答案无效请在各题的答题区域内作答，超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效第 2 页共 2 页
贴条形码区
请在各题的答题区域内作答，超出黑色矩形边框限定区域的答案无效
18．（12 分）
一.选择题 1 2 3 4 5 6 7 8 9 10
请在各题的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
湖北省黄冈中学 2013 届高三第二次模拟考试数学答题卡（理科）

湖北省黄冈中学2013届高三10月月考数学试题

湖北省黄冈中学2013届高三10月月考数学试题(理学生一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的1.复数1i i-的共轭复数为( A .1122i -+ B .1122i + C .1122i -- D .1122i - 2.已知:p “,,a b c 成等比数列”,:q “ac b =”,那么p 成立是q 成立的( A .充分不必要条件 B .必要不充分条件 C .充要条件 D. 既不充分又非必要条件3.等差数列{}n a 的前n 项和为n S ,若3915170a a a a +++=,则21S 的值是(A.1B. 1-C. 0D.不能确定4.如图,已知正六边形P 1P 2P 3P 4P 5P 6,下列向量的数量积中最大的是(A .1213PP PP ⋅ B .1214PP PP ⋅C .5121P P P P ⋅D .1216PP PP ⋅5.某几何体的正视图和侧视图均为如图1所示,则在图2的四个图中可以作为该几何体的俯视图的是(A .(1,(3B .(1,(4C .(2,(4D .(1,(2,(3,(4A. 0B. ln 2C. 21e +D.1ln 2+ 7.ABC ∆中,3π=A ,BC =3,则ABC ∆的周长为(A .33sin 34+⎪⎭⎫⎝⎛+πB B .36sin 34+⎪⎭⎫⎝⎛+πB C .33sin 6+⎪⎭⎫⎝⎛+πB D .36sin 6+⎪⎭⎫⎝⎛+πB 8.已知实数,a b 满足等式23a b =,下列五个关系式:①0;b a <<②0;a b<<③0;a b << ④0;b a <<⑤.a b =其中可能成立的关系式有(A .①②③B .①②⑤C .①③⑤D .③④⑤9.函数(x f y =为定义在R 上的减函数,1(-=x f y 的图像关于点(1,0对称,实数,x y 满足不等式02(2(22≤-+-y y f x x f ,若(1,2,(,M N x y ,O 为坐标原点,则当41≤≤x 时,OM ON ⋅的取值范围为(A .[]12,+∞ B. []0,3 C. []3,12 D.[]0,1210.已知函数31,0(3,0x x f x xx x ⎧+>⎪=⎨⎪+≤⎩,则方程2(2f x x a +=(2a >的根的个数不可能为( A .3 B. 4 C.5 D. 6二、填空题:(本大题共5小题,每小题5分,共25分.把答案填在答题卡中相应的横线上11.如图,下图为幂函数n y x =在第一象限的图像,则1c 、2c 、3c 、4c 的大小关系为 .第11题图第12题图12.函数(sin((0,0f x A x A ωϕω=+>>的图象如图所示,则(((123f f f +++ (2012f += .13.已知△ABC 中,点D 是BC 的中点,过点D 的直线分别交直线AB 、AC 于E 、F 两点,若AB AE λ= (0λ>,(0AC AF μμ=> ,则14λμ+的最小值是 . 14.设:p x ∃∈5(1,2使函数22(log (22g x tx x =+-有意义,若p ⌝为假命题,则t 的取值范围为 .15.对于各项均为整数的数列{}n a ,如果i a i +(i =1,2,3,…为完全平方数,则称数列{}n a 具有“P 性质”.不论数列{}n a 是否具有“P 性质”,如果存在与{}n a 不是同一数列的{}n b ,且{}n b 同时满足下面两个条件:①123,,,...,n b b b b 是123,,,...,n a a a a 的一个排列;②数列{}n b 具有“P 性质”,则称数列{}n a 具有“变换P 性质”.下面三个数列:①数列{}n a 的前n 项和2(13n n S n =-;②数列1,2,3,4,5;③1,2,3,…,11.具有“P 性质”的为 ;具有“变换P 性质”的为 .三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分已知集合}01(7(2(4(|{<+-+-=x x x x x M ,集合}032|{<->=a x a ax x N ,,求集合.}|{∅≠=N M a T 17.(本小题满分12分已知6π=x 是函数21cos cos sin ((-+=x x x a x f 图象的一条对称轴. (Ⅰ求a 的值;(Ⅱ作出函数(x f 在],0[π∈x 上的图象简图(不要求书写作图过程.18.(本小题满分12分已知数列{}n a 满足11=a ,132-=a ,62212-=+-++n a a a n n n(Ⅰ设1,n n n b a a +=-求数列{}n b 的通项公式;(Ⅱ求n 为何值时,n a 最小(不需要求n a 的最小值.19.(本小题满分12分某工厂去年的某产品的年销售量为100万只,每只产品的销售价为10元,每只产品固定成本为8元.今年,工厂第一次投入100万元(科技成本,并计划以后每年比上一年多投入100万元(科技成本,预计销售量从今年开始每年比上一年增加10万只,第n 次投入后,每只产品的固定成本为1(+=n k n g (k >0,k 为常数,Z ∈n 且n ≥0,若产品销售价保持不变,第n 次投入后的年利润为(n f 万元.(Ⅰ求k 的值,并求出(n f 的表达式;(Ⅱ若今年是第1年,问第几年年利润最高?最高利润为多少万元?20.(本小题满分13分已知函数((2211x f x x R x x -=∈++. (Ⅰ求函数(f x 的极大值;(Ⅱ若(2220t t t e x e x e +++-≥对满足1x ≤的任意实数x 恒成立,求实数t 的取值范围(这里e 是自然对数的底数; (Ⅲ求证:对任意正数a 、b 、λ、μ,恒有 2222a b a b a b f f λμλμλμλμλμλμ⎡⎤⎛⎫⎛⎫⎛⎫+++-⎢⎥⎪⎪⎪+++⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦≥22a b λμλμ+-+.21.(本小题满分14分已知数列{}n a ,122a a ==,112(2n n n a a a n +-=+≥(Ⅰ求数列{}n a 的通项公式n a ;(Ⅱ当2n ≥时,求证:12111...3na a a +++<; (Ⅲ若函数(f x 满足:2*1(1,(1((.(f a f n f n f n n N =+=+∈求证:111.(12n k f k =<+∑。

湖北省黄冈中学2013届高三11月月考数学理试题(解析版)

湖北省黄冈中学2013届高三上学期11月月考数学（理）试题(2012-11-3)一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．sin(1920)-的值为（）A ．32-B ．12-C ．32D ．12解析：sin(1920)sin(2406360)sin(18060)-=-⨯=+，即原式sin60=-，故选A ．答案：A2．命题“x ∀∈R ，20x >”的否定是（）A ．x ∀∈R ，20x ≤B ．x ∃∈R ，20x >C ．x ∃∈R ，20x <D ．x ∃∈R ，20x ≤解析：全称命题的否定是特称命题，易知应选D ．答案：D3．已知集合{P =正奇数}和集合{|M x x ==,,}a b a P b P ⊕∈∈，若M P ⊆，则M 中的运算“⊕”是（）A ．加法B ．除法C ．乘法D ．减法解析：由已知集合M 是集合P 的子集，设*21,21(,)a m b n m n =-=-∈N ，∵(21)(21)a b m n ⋅=--42()12[2()1]1mn m n mn m n P =-++=-++-∈，∴M P ⊆，而其它运算均不使结果属于集合P ，故选C ．答案：C 4．已知某几何体的侧视图与其正视图相同，相关的尺寸如下图所示，则这个几何体的体积是（）A . 8πB . 7πC . 2π`D .74π 解析：依题意该几何体为一空心圆柱，故其体积2237[2()]124V ππ=-⨯=，选D ．答案：D5．已知A 、B 两点分别在两条互相垂直的直线20x y -=和0x ay +=上，且AB 线段的中点为俯视图正视图侧视图3 41P 10(0,)a，则线段AB 的长为（） A ．8B ．9C ．10D ．11解析：由已知两直线互相垂直得2a =，∴线段AB 中点为P (0,5)，且AB 为直角三角形AOB 的斜边，由直角三角形的性质得||2||10AB PO ==，选C ．答案：C6．已知各项为正的等比数列{}n a 中，4a 与14a 的等比中项为22，则7112a a +的最小值为（） A ．16B ．8C ．22D ．4解析：由已知2414(22)8a a ==，再由等比数列的性质有4147118a a a a ==，又70a >，110a >，7117112228a a a a +≥=，故选B ．7．设函数2,0(),01x x bx c f x x ≥⎧++=⎨<⎩，若(4)(0)f f =，(2)2f =，则函数()()g x f x x =-的零点的个数是（）A ．0B ．1C ．2D ．3解析：已知即164422b c c b c ++=⎧⎨++=⎩，∴46b c =-⎧⎨=⎩，若0x ≥，则246x x x -+=，∴2x =，或3x =；若0x <，则1x =舍去，故选C ．答案：C8．给出下列的四个式子：①1a b -，②1a b +，③1b a +，④1ba-；已知其中至少有两个式子的值与tan θ的值相等，则（）A ．cos 2,sin 2a b θθ==B ．sin 2,cos 2a b θθ==C ．sin,cos22a b θθ==D ．cos,sin22a b θθ==解析：sin sin 21cos2tan ,cos2,sin 2cos 1cos2sin 2a b θθθθθθθθθ-===∴==+时，式子①③与tan θ的值相等，故选A ．答案：A9．设集合(){}(){},|||||1,,()()0A x y x y B x y y x y x =+≤=-+≤，M AB =，若动点(,)P x y M ∈，则22(1)x y +-的取值范围是（）A ．15[,]22B ．25[,]22C ．110[,]22D ．210[,]22解析：在同一直角坐标系中画出集合A 、B 所在区域，取交集后如图，故M 所表示的图象如图中阴影部分所示，而22(1)d x y =+-表示的是M 中的点到(0,1)的距离，从而易知所求范围是15[,]22，选A ． 10．已知O 为平面上的一个定点，A 、B 、C 是该平面上不共线的三个动点，点P 满足条件2OB OC OP +=(),(0,)||cos ||cos AB ACAB B AC Cλλ++∈+∞，则动点P 的轨迹一定通过ABC ∆的（）A ．重心B ．垂心C ．外心D ．内心解析：设线段BC 的中点为D ，则2OB OCOD +=，∴2OB OC OP +=()||cos ||cos AB AC AB B AC C λ++()||cos ||cos AB ACOD AB B AC Cλ=++，∴()||cos ||cos AB ACOP OD DP AB B AC Cλ-=+=，∴()()||cos ||cos ||cos ||cos AB AC AB BC AC BCDP BC BC AB B AC C AB B AC Cλλ⋅⋅⋅=+⋅=+||||cos()||||cos ()(||||)0||cos ||cos AB BC B AC BC CBC BC AB B AC Cπλλ-=+=-+=，∴DP BC ⊥，即点P 一定在线段BC 的垂直平分线上，即动点P 的轨迹一定通过ABC ∆的外心，选C ．答案：C二．填空题：本大题共5小题，每小题5分，共25分，把答案直接填在题中横线上． 11．1220x e dx =⎰______________．解析：1122220011|(1)22xx e dx e e ==-⎰．答案：1(1)2e - 12．定义运算a c ad bcb d =-，复数z 满足11z ii i =+，则复数z 的模为_______________．解析：由11z i i i=+得1212izi i i zi i +-=+⇒==-，∴222(1)5z =+-=．答案：513．已知方程22220x y kx y k ++++=所表示的圆有最大的面积，则直线(1)2y k x =-+的倾斜角α=_______________．解析：2214412r k k =+-≤，当有最大半径时有最大面积，此时0k =，1r =，∴直线方程为2y x =-+，设倾斜角为α，则由tan 1α=-且[0,)απ∈得34πα=．答案：34π14．已知函数2()m f x x -=是定义在区间2[3,]m m m ---上的奇函数，则()f m =_______．解析：由已知必有23m m m -=+，即2230m m --=，∴3m =，或1m =-；当3m =时，函数即1()f x x -=，而[6,6]x ∈-，∴()f x 在0x =处无意义，故舍去；当1m =-时，函数即3()f x x =，此时[2,2]x ∈-，∴3()(1)(1)1f m f =-=-=-．答案：1-15．在工程技术中，常用到双曲正弦函数2x xe e shx --=和双曲余弦函数2x x e e chx -+=，双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质，请类比正、余弦函数的和角或差角公式，写出关于双曲正弦、双曲余弦函数的一个正确的类似公式．解析：由右边2222x x y y x x y ye e e e e e e e ----++--=⋅-⋅1()4x yx y x y x y x y x y x y x y e e e e e e e e +--+--+--+--=+++-++-()()1(22)()42x y x y x y x y e e e e ch x y ------+=+==-=左边，故知．答案：填入()c c c s s h x y hx hy hx hy -=-，()c c c s s h x y hx hy hx hy +=+，()c s sh x y shx hy chx hy -=-，()c s sh x y shx hy chx hy +=+四个之一即可．三．解答题：本大题共6小题，共75分，请给出各题详细的解答过程．16．（本小题满分12分）已知数列{}n a 的前n 项和为n S ，且*41()n n S a n =+∈N ．（1）求1a ，2a ；（2）设3log ||n n b a =，求数列{}n b 的通项公式．解答：（1）由已知1141S a =+，即1141a a =+，∴=1a 13，……………………2分又2241S a =+，即1224()1a a a +=+，∴219a =-； ……………………5分（2）当1n >时，1111(1)(1)44n n n n n a S S a a --=-=+-+，即13n n a a -=-，易证数列各项不为零（注：可不证），故有113n n a a -=-对2n ≥恒成立，∴{}n a 是首项为13，公比为13-的等比数列，∴1111()(1)333n n n n a ---=-=-， ……………………10分∴33log ||log 3n n n b a n -===-． ……………………12分17．（本小题满分12分）已知 1:(),3xp f x -=且|()|2f a <； q ：集合2{|(2)10,}A x x a x x =+++=∈R ，且A ≠∅．若p ∨q 为真命题，p ∧q 为假命题，求实数a 的取值范围. 解答：若1|()|||23af a -=<成立，则616a -<-<，即当57a -<<时p 是真命题； ……………………4分若A ≠∅，则方程2(2)10x a x +++=有实数根，由2(2)40a ∆=+-≥，解得4a ≤-，或0a ≥，即当4a ≤-，或0a ≥时q 是真命题； ……………………8分由于p ∨q 为真命题，p ∧q 为假命题，∴p 与q 一真一假，故知所求a 的取值范围是(,5](4,0)[7,)-∞--+∞． ……………………12分（注：结果中在端点处错一处扣1分，错两处扣2分，最多扣2分）18．（本小题满分12分）已知ABC ∆的两边长分别为25AB =，39AC =，且O 为ABC ∆外接圆的圆心．（注：39313=⨯，65513=⨯）（1）若外接圆O 的半径为652，且角B 为钝角，求BC 边的长；（2）求AO BC ⋅的值．解答：（1）由正弦定理有2sin sin AB ACR C B==，∴253965sin sin C B ==，∴3sin 5B =，5sin 13C =， ……………………3分且B 为钝角，∴12cos 13C =，4cos 5B =-， ∴3125416sin()sin cos sin cos ()51313565B C B C C B +=+=⨯+⨯-=，又2sin BCR A=，∴2sin 65sin()16BC R A B C ==+=； ……………………6分（2）由已知AO OC AC +=，∴22()AO OC AC +=，即2222||2||||39AO AO OC OC AC +⋅+== ……………………8分同理AO OB AB +=，∴2222||2||||25AO AO OB OB AB +⋅+==， …………10分两式相减得22(3925)(3925)896AO OC AO OB ⋅-⋅=-+=，即2896AO BC ⋅=，∴448AO BC ⋅=． ……………………12分19．（本小题满分12分）在如图所示的多面体ABCDE中，AB ⊥平面ACD ，DE ⊥平面ACD ，AC=AD=CD=DE=2，AB=1，G 为AD 中点．（1）请在线段CE 上找到点F 的位置，使得恰有直线BF ∥平面ACD ，并证明这一事实；（2）求平面BCE 与平面ACD 所成锐二面角的大小；（3）求点G 到平面BCE 的距离．解法一：以D 点为原点建立如图所示的空间直角坐标系，使得x 轴和z 轴的正半轴分别经过点A 和点E ，则各点的坐标为(0,0,0)D ，(2,0,0)A ， (0,0,2)E ，(2,0,1)B ，(1,3,0)C ，（1）点F 应是线段CE 的中点，下面证明：设F 是线段CE 的中点，则点F 的坐标为13(,,1)22F ，∴33(,,0)22BF =-，显然BF 与平面xOy 平行，此即证得BF ∥平面ACD ； ……………………4分（2）设平面BCE 的法向量为(,,)n x y z =，则n CB ⊥，且n CE ⊥，由(1,3,1)CB =-，(1,3,2)CE =--，BA DCG EBADCG FEzx y∴30320x y z x y z ⎧-+=⎪⎨--+=⎪⎩，不妨设3y =，则12x z =⎧⎨=⎩，即(1,3,2)n =，∴所求角θ满足(0,0,1)2cos 2||n n θ⋅==，∴4πθ=； ……………………8分（3）由已知G 点坐标为（1，0，0），∴(1,0,1)BG =--，由（2）平面BCE 的法向量为(1,3,2)n =， ∴所求距离3||24||BG n d n ⋅==． ……………………12分解法二：（1）由已知AB ⊥平面ACD ，DE ⊥平面ACD ，∴AB//ED ，设F 为线段CE 的中点，H 是线段CD 的中点，连接FH ，则//FH =12ED ，∴//FH =AB ， …………………2分∴四边形ABFH 是平行四边形，∴//BF AH ，由BF ⊄平面ACD 内，AH ⊂平面ACD ，//BF ∴平面ACD ； ……………4分（2）由已知条件可知ACD ∆即为BCE ∆在平面ACD 上的射影，设所求的二面角的大小为θ，则cos ACDBCES S θ∆∆=， ……………………6分易求得BC=BE 5=，CE 22=，∴221||()622BCE CES CE BE ∆=⨯-=，而23||34ACD S AC ∆==，∴2cos 2ACD BCE S S θ∆∆==，而02πθ<<， ∴4πθ=；………………8分（3）连结BG 、CG 、EG ，得三棱锥C —BGE ，由ED ⊥平面ACD ，∴平面ABED ⊥平面ACD ，又CG AD ⊥，∴CG ⊥平面ABED ，设G 点到平面BCE 的距离为h ，则C BGE G BCE V V --=即1133BGE BCE S GC S h ∆∆⨯=⨯，由32BGE S ∆=，6BCE S ∆=，3CG =， BA DCGE∴3332246BGE BCE S GC h S ∆∆⨯===即为点G 到平面BCE 的距离．………………12分 20．（本小题满分13分）已知椭圆22221y x a b +=(0)a b >>的一个顶点为B (0,4)，离心率e =55，直线l 交椭圆于M 、N 两点．（1）若直线l 的方程为4y x =-，求弦MN 的长；（2）如果ΔBMN 的重心恰好为椭圆的右焦点F ，求直线l 方程的一般式．解答：（1）由已知4b =，且55c a =，即2215c a=，∴22215a b a -=，解得220a =，∴椭圆方程为2212016y x +=； ……………………3分由224580x y +=与4y x =-联立，消去y 得29400x x -=，∴10x =，2409x =， ∴所求弦长221402||11||9MN x x =+-=； ……………………6分（2）椭圆右焦点F 的坐标为(2,0)，设线段MN 的中点为Q 00(,)x y ，由三角形重心的性质知2BF FQ =，又(0,4)B ， ∴00(2.4)2(2,)x y -=-，故得003,2x y ==-，求得Q 的坐标为(3,2)-； ……………………9分设1122(,),(,)M x y N x y ，则12126,4x x y y +=+=-，且222211221,120162016x y x y +=+=， ……………………11分以上两式相减得12121212()()()()02016x x x x y y y y +-+-+=，1212121244665545MN y y x x k x x y y -+==-=-=-+-∴，故直线MN 的方程为62(3)5y x +=-，即65280x y --=． ……………………13分（注：直线方程没用一般式给出但结果正确的扣1分） 21．（本小题满分14分）已知函数[)1()ln 1,sin g x x x θ=++∞⋅在上为增函数，且(0,)θπ∈，12()ln m ef x mx x x-+=--，m ∈R ．（1）求θ的值；（2）当0m =时，求函数()f x 的单调区间和极值；（3）若在[1,]e 上至少存在一个0x ，使得00()()f x g x >成立，求m 的取值范围．解答：（1）由已知/211()0sin g x xx θ=-+≥⋅在[1,)+∞上恒成立，即2sin 10sin x xθθ⋅-≥⋅，∵(0,)θπ∈，∴sin 0θ>，故sin 10x θ⋅-≥在[1,)+∞上恒成立，只需sin 110θ⋅-≥，即sin 1θ≥，∴只有sin 1θ=，由(0,)θπ∈知2πθ=； ……………………4分（2）∵0m =，∴12()ln ef x x x-+=--，(0,)x ∈+∞， ∴/2221121()e e x f x x x x---=-=，令/()0f x =，则21x e =-(0,)∈+∞，∴x ，/()f x 和()f x 的变化情况如下表：x (0,21)e -21e -(21,)e -+∞/()f x+0 -()f x极大值(21)1ln(21)f e e -=---即函数的单调递增区间是(0,21)e -，递减区间为(21,)e -+∞，有极大值(21)1ln(21)f e e -=---； ……………………9分（3）令2()()()2ln m eF x f x g x mx x x +=-=--，当0m ≤时，由[1,]x e ∈有0m mx x -≤，且22ln 0e x x--<，∴此时不存在0[1,]x e ∈使得00()()f x g x >成立；当0m >时，2/222222()m e mx x m eF x m x x x +-++=+-=， ∵[1,]x e ∈，∴220e x -≥，又20mx m +>，∴/()0F x >在[1,]e 上恒成立，故()F x 在[1,]e 上单调递增，∴max ()()4mF x F e me e==--，令40m me e -->，则241e m e >-，故所求m 的取值范围为24(,)1ee +∞-． ……………………14分。

【VIP专享】湖北省黄冈中学2013年秋季高三数学(理科)函数、平面向量、数列、不等式、复数、立体几何、解析

2014 届高三上数学测试题（13）（理科）
考查范围：函数、平面向量、数列、不等式、复数、立体几何、解析几何命题人：张智
一．选择题：本大题共 10 小题，每小题 5 分，共 50 分，在每小题给出的四个选项中，只有一项是符合题目要求的
1．集合 A 0,2, a, B 1, a 2 ,若 A B 0,1,2,4,16,则 a 的值为 (B )
A． 1
2
1
B．
2 2
4.【答案】D.法一:【解析】∵| a b || c | ∴| a b || c || a | ，∴解得：
2a b ∴ cos
2 b
a, b
|b |2 a b
a b
| a || b | | b |2 2
1
∴
sin
5. 已知点 M (a, b)(a 0, b 0) 是圆 C : x2 y2 1 内任意一点，点 P(x, y) 是圆上任意一
，解得
D． 0
2
，把点
6 2 62
6
(
6
A
）
,1) 的坐标代入，
2013 f ( n ) f (2011) f (2012) f (2013) f (1) f (2) f (3) 1 。
i 1
7．已知函数
6
f
(
x)
实数 k 的取值范围是 D
A． k 2
kx 2, x lnx, x 0
C． 3 3 2
9【答案】 B(教材选修 4-5 P10 页第 14 题改编）【解析】设该三棱柱的底面边长为 a ，高为
h ，则底面正三角形的外接圆半径是
a2
即
9 12
h2
1，1
a2

湖北省武汉市2013届高三11月调研测试数学(理科)-含答案

武汉市2013届高三11月调研测试数学（理科）2012.11.16一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若复数z 满足i ·z ＝1－2i ，则z ＝A ．2＋iB ．－2＋iC ．－2－iD ．2－i 2．“m ＜1”是“函数f (x )＝x 2＋2x ＋m 有零点”的A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件3．(x ＋12x)8的展开式中常数项为A ．3516B ．358C ．354 D ．1054．若tan θ＋1tan θ＝4，则sin2θ＝A ．15B ．14C ．13D ．125．执行如图所示的程序框图，若输入n 的值为8，则输出s 的值为 A ．16 B ．8 C ．4 D ．26．如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为A ．14B ．15C ．16D ．177．某汽车销售公司在A ，B 两地销售同一种品牌车，在A 地的销售利润（单位：万元）为y 1＝4.1x －0.1x 2，在B 地的销售利润（单位：万元）为y 2＝2x ，其中x 为销售量（单位：辆）．若该公司在这两地共销售16辆这种品牌车，则能获得的最大利润是 A ．10.5万元 B ．11万元 C ．43万元 D ．43.025万元8．已知椭圆x 2m ＋y 2＝1（m ＞1）和双曲线x 2n －y 2＝1（n ＞0）有相同的焦点F 1、F 2，P 是它们的一个交点，则ΔF 1PF 2的形状是A ．锐角三角形B ．直角三角形C ．钝角三角形D ．随m ，n 变化而变化 9．如图，在棱长为a 的正方体ABCD-A 1B 1C 1D 1中，P 是A 1D 1的中点，Q 是A 1B 1上的任意一点，E 、F 是CD 上的任意两点，且EF 的长为定值．现有如下结论： ①异面直线PQ 与EF 所成的角是定值；②点P 到平面QEF 的距离是定值；③直线PQ 与平面PEF 所成的角是定值； ④三棱锥P-QEF 的体积是定值； ⑤二面角P-EF-Q 的大小是定值．其中正确结论的个数是A ．0B ．1C ．2D ．310．设函数f (x )＝1x，g (x )＝ax 2＋bx （a ，b ∈R ，a ≠0），若y ＝f (x )的图象与y ＝g (x )的图象有且仅有两个不同的公共点A (x 1，y 1)，B (x 2，y 2)，则下列判断正确的是 A ．当a ＜0时，x 1＋x 2＜0，y 1＋y 2＜0 B ．当a ＜0时，x 1＋x 2＞0，y 1＋y 2＞0 C ．当a ＞0时，x 1＋x 2＞0，y 1＋y 2＜0 D ．当a ＞0时，x 1＋x 2＜0，y 1＋y 2＞0二、填空题：本大题共5小题，每小题5分，共25分．请将答案填在答题卡对应题号．．．．．．．的位置上．答错位置，书写不清，模棱两可均不得分． 11．在△ABC 中，若∠A ＝60°，∠B ＝45°，BC ＝32，则AC ＝． 12．某几何体的三视图如图所示，则该几何体的表面积是．13．已知正方形ABCD 的边长为1，点E 是AB 边上的动点，则（Ⅰ）→DE ·→CB 的值为；（Ⅱ）→DE ·→DC 的最大值为． 14．已知不等式组⎩⎪⎨⎪⎧x ≤1，x ＋y ＋2≥0，kx －y ≥0．表示的平面区域为Ω，其中k ≥0，则当Ω的面积取得最小值时的k 的值为．15．在如图所示的数表中，第i 行第j 列的数记为a i ，j ，且满足a 1，j＝2j －1，a i ，1＝i ，a i ＋1，j ＋1＝a i ，j ＋a i ＋1，j （i ，j ∈N *）；又记第3行的数3，5，8，13，22，39，…为数列{b n }．则（Ⅰ）此数表中的第6行第3列的数为；（Ⅱ）数列{b n }的通项公式为．三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤． 16．（本小题满分12分）函数f (x )＝A sin(ωx －π6)＋1（A ＞0，ω＞0）的最大值为3，其图象相邻两条对称轴之间的距离为π2．（Ⅰ）求函数f (x )的解析式；（Ⅱ）设α∈(0，2π)，f (α2)＝2，求α的值．17．（本小题满分12分）在等差数列{a n }中，a 1＝3，其前n 项和为S n ，等比数列{b n }的各项均为正数，b 1＝1，公比为q ，且b 2＋S 2＝12，q ＝S 2b 2．（Ⅰ）求{a n }与{b n }的通项公式；（Ⅱ）证明：13≤1S 1＋1S 2＋…＋1S n ＜23．18．（本小题满分12分）某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50)，[50，60)，[60，70)，[70，80)，[80，90)，[90，100]．（Ⅰ）求图中x 的值；（Ⅱ）从成绩不低于80分的学生中随机选取2人，该2人中成绩在90分以上（含90分）的人数记为ξ，求ξ的数学期望．19．（本小题满分12分）如图，直三棱柱ABC-A ′B ′C ′，∠BAC ＝90°，AB ＝AC ＝λAA ′，点M ，N 分别为A ′B 和B ′C ′的中点．（Ⅰ）证明：MN ∥平面A ′ACC ′；（Ⅱ）若二面角A ′-MN-C 为直二面角，求λ的值．20．（本小题满分13分）已知椭圆E ：x 2a 2＋y 2b 2＝1（a ＞b ＞0）的离心率为32，其长轴长与短轴长的和等于6．（Ⅰ）求椭圆E 的方程；（Ⅱ）如图，设椭圆E 的上、下顶点分别为A 1、A 2，P 是椭圆上异于A 1、A 2的任意一点，直线PA 1、PA 2分别交x 轴于点N 、M ，若直线OT 与过点M 、N 的圆G 相切，切点为T ．证明：线段OT 的长为定值．21．（本小题满分14分）已知函数f (x )＝(a ＋1a )ln x ＋1x－x （a ＞1）．（Ⅰ）讨论f (x )在区间(0，1)上的单调性；（Ⅱ）当a ≥3时，曲线y ＝f (x )上总存在相异两点P (x 1，f (x 1))，Q (x 2，f (x 2))，使得曲线y ＝f (x )在点P ，Q 处的切线互相平行，求证：x 1＋x 2＞65．武汉市2013届高三11月调研测试数学（理科）试题参考答案及评分标准一、选择题1．C 2．A 3．B 4．D 5．B 6．C 7．C 8．B 9．D 10．D 二、填空题11．2 3 12．92 13．（Ⅰ）1；（Ⅱ）114．1 15．（Ⅰ）20；（Ⅱ）b n ＝2n －1＋n ＋1 三、解答题16．（本小题满分12分）解：（Ⅰ）∵函数f (x )的最大值为3，∴A ＋1＝3，即A ＝2，∵函数图象的相邻两条对称轴之间的距离为π2，∴最小正周期T ＝π，∴ω＝2．故函数f (x )的解析式为f (x )＝2sin(2x －π6)＋1．……………………………………6分（Ⅱ）f (α2)＝2sin(α－π6)＋1＝2，即sin(α－π6)＝12．∵0＜α＜2π，∴－π6＜α－π6＜11π6，∴α－π6＝π6，或α－π6＝5π6，故α＝π3，或α＝π．………………………………………………………………12分17．（本小题满分12分）解：（Ⅰ）设{a n }的公差为d ，则⎩⎪⎨⎪⎧q ＋6＋d ＝12，q ＝6＋dq ．消去d ，得q 2＋q －12＝0，解得q ＝－4（舍去），或q ＝3，从而可得d ＝3．∴a n ＝3＋(n －1)×3＝3n ，b n ＝3n －1．……………………………………………4分（Ⅱ）由（Ⅰ），得S n ＝n (3＋3n )2＝3n (n ＋1)2，∴1S n ＝23n (n ＋1)＝23(1n －1n ＋1)．∴1S 1＋1S 2＋…＋1S n ＝23[(1－12)＋(12－13)＋…＋(1n －1n ＋1)]＝23(1－1n ＋1)． ∵n ≥1，∴0＜1n ＋1≤12，∴12≤1－1n ＋1＜1，∴13≤23(1－1n ＋1)＜23．故13≤1S 1＋1S 2＋…＋1S n ＜23．………………………………………………………12分18．（本小题满分12分）解：（Ⅰ）由频率分布直方图，知3×0.006×10＋0.01×10＋0.054×10＋10x ＝1，解得x ＝0.018．………………4分（Ⅱ）成绩不低于80分的学生有(0.018＋0.006)×10×50＝12人，成绩在90分以上（含90分）的学生有0.006×10×50＝3人． ∴ξ的可能取值为0，1，2．P (ξ＝0)＝C 29C 212＝611，P (ξ＝1)＝C 13C 19C 212＝922，P (ξ＝2)＝C 23C 212＝122．∴ξ的分布列为：ξ 0 1 2 P611922122∴E (ξ)＝0×611＋1×922＋2×122＝12．……………………………………………12分19．（本小题满分12分）解：（Ⅰ）法（一）：如图，连结AB ′，AC ′．由已知∠BAC ＝90°，AB ＝AC ，三棱柱ABC-A ′B ′C ′为直三棱柱， ∴M 为AB ′的中点．又∵N 为B ′C ′的中点， ∴MN ∥AC ′；又MN ⊄平面A ′ACC ′，AC ′⊂平面A ′ACC ′， ∴MN ∥平面A ′ACC ′．……………………6分法（二）：取A ′B ′的中点P ，连结MP ，NP ． ∵M ，N 分别为AB ′和B ′C ′的中点， ∴MP ∥AA ′，PN ∥A ′C ′，∴MP ∥平面A ′ACC ′，PN ∥平面A ′ACC ′．又MP ∩NP ＝P ，∴平面MPN ∥平面A ′ACC ′．而MN ⊂平面MPN ，∴MN ∥平面A ′ACC ′．……………………………………………………………6分（Ⅱ）以A 为坐标原点，分别以直线AB ，AC ，AA ′为x 轴，y 轴，z 轴建立直角坐标系O -xyz ，如图所示．设AA ′＝1，则AB ＝AC ＝λ，∴A (0，0，0)，B (λ，0，0)，C (0，λ，0)，A ′(0，0，1)，B ′(λ，0，1)，C ′(0，λ，1)， ∴M (λ2，0，12)，N (λ2，λ2，1)．设m ＝(x 1，y 1，z 1)是平面A ′MN 的法向量，由⎩⎪⎨⎪⎧m ·→A ′M ＝0，m ·→MN ＝0．得⎩⎨⎧λ2x 1－12z 1＝0，λ2y 1＋12z 1＝0．可取m ＝(1，－1，λ)．设n ＝(x 2，y 2，z 2)是平面MNC 的法向量，由⎩⎪⎨⎪⎧n ·→NC ＝0，n ·→MN ＝0．得⎩⎨⎧－λ2x 2＋λ2y 2－z 2＝0，λ2y 2＋12z 2＝0．可取n ＝(－3，－1，λ)．∵A ′-MN-C 为直二面角，∴m ·n ＝0．即－3＋(－1)×(－1)＋λ2＝0，解得λ＝2．……………………………………12分20．（本小题满分13分）解：（Ⅰ）由e ＝c a ＝a 2－b 2a ＝32，得a ＝2b ． ①又2a ＋2b ＝6，即a ＋b ＝3． ②解①②，得a ＝2，b ＝1．故椭圆E 的方程为x 24＋y 2＝1．……………………………………………………4分（Ⅱ）由（Ⅰ），知A 1(0，1)，A 2(0，－1)，设P (x 0，y 0)，则直线PA 1的方程为y －1＝y 0－1x 0x ，令y ＝0，得x N ＝－x 0y 0－1；直线PA 2的方程为y ＋1＝y 0＋1x 0x ，令y ＝0，得x M ＝x 0y 0＋1．设G (12(x 0y 0＋1－x 0y 0－1)，h ），则r 2＝[12(x 0y 0＋1－x 0y 0－1)－x 0y 0＋1]2＋h 2＝14(x 0y 0＋1＋x 0y 0－1)2＋h 2，|OG |2＝14(x 0y 0＋1－x 0y 0－1)2＋h 2，∴|OT |2＝|OG |2－r 2＝14(x 0y 0＋1－x 0y 0－1)2＋h 2－14(x 0y 0＋1＋x 0y 0－1)2－h 2＝x 201－y 20．∵x 204＋y 20＝1，即x 20＝4(1－y 20)， ∴|OT |2＝4(1－y 20)1－y 20＝4，∴|OT |＝2．即线段OT 的长为定值2．……………13分 21．（本小题满分14分）解：（Ⅰ）f (x )的定义域为(0，＋∞)．求导数，得f ′(x )＝a ＋1a x －1x 2－1＝－x 2－(a ＋1a )x ＋1x 2＝－(x －a )(x －1a)x 2，令f ′(x )＝0，解得x ＝a ，或x ＝1a ．∵a ＞1，∴0＜1a＜1，∴当0＜x ＜1a 时，f ′(x )＜0；当1a＜x ＜1时，f ′(x )＞0．故f (x )在(0，1a )上单调递减，在(1a ，1)上单调递增．……………………………6分（Ⅱ）由题意得，当a ≥3时，f ′(x 1)＝f ′(x 2)（x 1，x 2＞0，且x 1≠x 2），即a ＋1a x 1－1x 21－1＝a ＋1a x 2－1x 22－1，∴a ＋1a ＝1x 1＋1x 2＝x 1＋x 2x 1x 2．∵x 1，x 2＞0，且x 1≠x 2，∴x 1x 2＜(x 1＋x 22)2恒成立，∴1x 1x 2＞4(x 1＋x 2)2，又x 1＋x 2＞0， ∴a ＋1a ＝x 1＋x 2x 1x 2＞4x 1＋x 2，整理，得x 1＋x 2＞4a ＋1a ．令g (a )＝4a ＋1a＝4aa 2＋1，则g ′(a )＝4(1－a 2)(a 2＋1)2＜0，∴g (a )在[3，＋∞)上单调递减，∴g (a )在[3，＋∞)上的最大值为g (3)＝65，∴x 1＋x 2＞65．………………………………………………………………………14分。

湖北省黄冈中学2013届高三第一次模拟考试数学理试题 Word版含答案

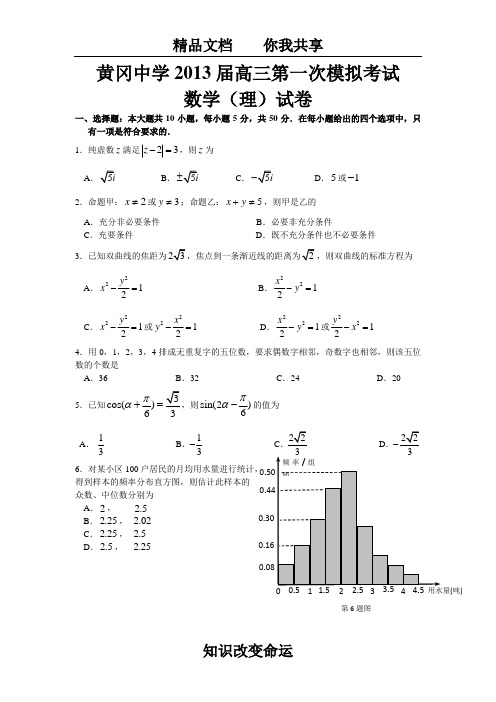
(吨)0.0.0.0.0.第6题图黄冈中学2013届高三第一次模拟考试数学（理）试卷一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合要求的．1．纯虚数z 满足23z -=，则z 为 AB． C ． D ．5或1-2．命题甲：2≠x 或3≠y ；命题乙：5≠+y x ，则甲是乙的A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既不充分条件也不必要条件3．已知双曲线的焦距为A ．2212y x -= B ．2212x y -= C ．2212y x -=或2212x y -= D ．2212x y -=或2212y x -= 4．用0，1，2，3，4排成无重复字的五位数，要求偶数字相邻，奇数字也相邻，则该五位数的个数是 A ．36 B ．32C ．24D ．20 5．已知cos(63πα+=，则sin(26πα-的值为 A ．13 B ．13-C ．D ．- 6．对某小区100户居民的月均用水量进行统计，得到样本的频率分布直方图，则估计此样本的众数、中位数分别为 A ．2， 2.5B ．2.25， 2.02C ．2.25， 2.5D ．2.5， 2.25第9题图侧视图俯视图正视图第8题图第127．在游乐场，有一种游戏是向一个画满均匀方格的桌面上投硬币，若硬币恰落在任何一个方格内不与方格线重叠，即可获奖．已知硬币的直径为2，若游客获奖的概率不超过19，则方格边长最长为(单位：cm )A ．3B ．4C ．5D ．6 8．某几何体的三视图如图示，则此几何体的体积是 A ．20π3B ．6πC ．10π3D ．16π9．如图，AB 是圆O 的直径，C D 、是圆O 上的点，60CBA ∠=，45ABD ∠=， CD xOA yBC =+，则xy +的值为A ．B ．13-C ．23D ． 10．已知定义在(0,)+∞上的单调函数()f x ，对(0,)x ∀∈+∞，都有2[()log ]3f f x x -=，则方程()'()2f x f x -=的解所在的区间是 A ．（0，12） B ．（1,12） C ．（1，2） D ．（2，3）二、填空题：本大题共6小题，考生共需作答5小题，每小题5分，共25分．请将答案填在答题卡对应题号的位置上，书写不清楚，模拟两可均不得分．（一）必考题（11 — 14题）11．1012x x ⎛⎫- ⎪⎝⎭的展开式中,含4x 项的系数为． 12．执行如图所示的程序框图，输出的k 值是．M第16题图13．已知(0,)x y z ∈+∞、、，且2221ln ln ln 3x y z ++=，则2x yz的最大值为． 14．对于实数x ，将满足“01y ≤<且x y -为整数”的实数y 称为实数x 的小数部分，用符号x 〈〉表示．已知无穷数列{}n a 满足如下条件：①1a a =〈〉；②11(0)0(0)n nn n a a a a +⎧〈〉≠⎪=⎨⎪=⎩．（Ⅰ）若a ={}n a 通项公式为；（Ⅱ）当13a >时，对任意*n N ∈都有n a a =，则a 的值为．（二）选考题（请考生在第15、16两题中任选一题作答，请先在答题卡指定位置将你所选的题目序号后的方框用2B 铅笔涂黑．如果全选，则按第15题作答结果给分．） 15．（极坐标与参数方程）已知抛物线C 的极坐标方程为2sin 8cos 0ρθθ-=，若斜率为1的直线经过抛物线C 的焦点，与圆()2224(0)x y r r -+=>相切，则r= ．16．（几何证明选讲）如图，过半径为4的O 上的一点A 引半径为3的O '的切线，切点为B ，若O 与O '内切于点M ，连结AM 与O '交于C 点，则ABAM= ．三、解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）已知ABC ∆中，角A B C 、、的对边分别为a b c 、、，a =(1,1)m =-，(cos cos ,sin sin )2n B C B C =-，且m n ⊥．（Ⅰ）求A 的大小；（Ⅱ）当7sin cos()12B C π+-取得最大值时，求角B 的大小和ABC ∆的面积．ACMPQ D第19题图18．（本小题满分12分）某象棋比赛规则如下：两名选手比赛时，每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时结束.假设选手甲与选手乙比赛时，甲、乙每局获胜的概率分别为23和13，且各局比赛胜负互不影响. （Ⅰ）求比赛进行4局结束，且乙比甲多得2分的概率；（Ⅱ）设ξ表示比赛停止时已比赛的局数，求随机变量ξ的分布列和数学期望．19．（本小题满分12分）如图，在四棱锥P ABCD -中，底面ABCD 为菱形，60BAD ︒∠=，Q 为AD 的中点，2PA PD AD ===．（Ⅰ）点M 在线段PC 上，PM tPC =，试确定t 的值，使//PA 平面MQB ；（Ⅱ）在（I ）的条件下，若平面PAD ⊥平面ABCD ，求二面角M BQ C --的大小．20．（本小题满分12分）数列{}n a 中，已知11a =，2n ≥时，11122333n n n a a --=+-．数列{}n b 满足：1*3(1)()n n n b a n N -=+∈．（Ⅰ）证明：{}n b 为等差数列，并求{}n b 的通项公式；（Ⅱ）记数列1n a n +⎧⎫⎨⎬⎩⎭的前n 项和为n S ，是否存在正整数,m n ，使得1331m n m n S m S m +-<-+ 成立？若存在，求出所有符合条件的有序实数对(,)m n ；若不存在，说明理由．21．（本小题满分13分）我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．如图，“盾圆C ”是由椭圆22221(0)x y a b a b+=>>与抛物线24y x =中两段曲线弧合成，第21题图12F F 、为椭圆的左、右焦点，2(1,0)F ．A 为椭圆与抛物线的一个公共点，252AF =．（Ⅰ）求椭圆的方程；（Ⅱ）求定积分时，可以使用下面的换元法公式：函数()y f x =中，令()x t ϕ=，则[][]2211()()()()()bt t a t t f x dx f t d t f t t dt ϕϕϕϕ'==⎰⎰⎰（其中12()()a tb t ϕϕ==、）．如22221cos2(sin )cos (sin )cos 2tt t t dt tdt dt πππ+'====⎰⎰⎰⎰．阅读上述文字，求“盾圆C ”的面积．（Ⅲ）过2F 作一条与x 轴不垂直的直线，与“盾圆C ”依次交于M N G H 、、、四点，P 和P '分别为NG MH 、的中点，问22MH PF NG P F ⋅'是否为定值？若是，求出该定值；若不是，说明理由．22．（本小题满分14分）设函数()ln ()ln()f x x x a x a x =+--(0)a >．（Ⅰ）当1a =时，求函数()f x 的最小值；（Ⅱ）证明：对12,(0,)x x ∀∈+∞，都有[]11221212ln ln ()ln()ln2x x x x x x x x +≥++-；（Ⅲ）若211nii x==∑，证明：21ln ln 2nn i i i x x =≥-∑ *(,)i n ∈N ．数学（理）试卷答案BBCD ABAC AC11答案：15- 12答案：5 13答案：14答案：（1）1n a =；（21-或1215 16答案：121答案：B解析：设()z bi b R =∈9b =∴=z =．2答案：B解析：甲⇒/乙，例如，1,4x y ==；乙⇒甲，“若5≠+y x ，则2≠x 或3≠y ”的逆否命题为“若2x =且3y =，则5x y +=”此逆否命题为真命题，所以原命题为真命题． 3答案：C解析：由题易知2c b ==1a =，这样的双曲线标准方程有两个．4答案：D解析：排除法．偶数字相邻，奇数字也相邻有32232224A A A =，然后减去0在首位的情况，有22224A A =，故322223222220A A A A A -=．5答案：A解析：由cos()63πα+=得，1cos(2)33πα+=-，所以1sin(2)sin(2)cos(2)63233ππππααα-=+-=-+=． 6答案：B解析：样本的众数为最高矩形底边中点对应的横坐标，为2 2.52.252+= 中位数是频率为0.5时，对应的样本数据，由于(0.080.160.300.44)0.50.49+++⨯=，故中位数为0.0120.5 2.020.25+⨯=． 7答案：A解析：设方格边长为x ，则221()39x x x -≤⇒≤．8答案：C解析：此几何体为半个圆锥与半个圆柱的组合体，体积1110[4241]233V πππ=⨯+⨯=．9答案：A解析：()()CD xOA yBC xOA y OC OB x y OA yOC =+=+-=++设1OA =，建立如图所示坐标系，则1(,12CD =-(1,0)OA =-，1(,22OC =-，故3x y +=10答案：C解析：由题2()log f x x C -=（C 为常数），则()f x 故22[()log ]()log 3f f x x f C C C -==+=，得2C =，故2()log 2f x x =+，记21()()()2log ln 2g x f x f x x x '=--=-在(0,)+∞上为增函数且112ln 21(1)0,(2)10ln 22ln 22ln 2g g -=-<=-=>, 故方程()'()2f x f x -=的解所在的区间是（1，2）． 11答案：15-12答案：5解析：由题意，得：5,016,18,2n k n k n k ==⇒==⇒==4,32,41,5n k n k n k ⇒==⇒==⇒==⇒终止当2n =时，执行最后一次循环；当1n =时，循环终止，这是关键，输出5k =． 13答案：解析：2222222(ln ln ln )[2(1)(1)](2ln ln ln )x y z x y z +++-+-≥-- 14答案：（1）1na =-；（21或12- 解析：（Ⅰ）若a 时，11a ==-,则21a ===．（Ⅱ）当13a >时，由n a a =知，1a <，所以1a a a =〈〉=，21a a =〈〉，且1(1,3)a ∈．①当1(1,2)a ∈时，211a a a 1=〈〉=-，故1112a a a -=⇒=（12a =舍去） ②当1[2,3)a ∈时，212a a a 1=〈〉=-，故21a a a1-=⇒=（1a =舍去）综上，1a =-或1215解析：将2sin 8cos 0ρθθ-=化为普通方程即28y x =，得(2,0)F 16答案：12解析：作两圆的公切线MDE ，连结AO ，CO '，则2AB AC AM =所以222AB AM AC ACAM AM AM == 由弦切角定理知2AOM EMA ∠=∠，2CO M EMA '∠=∠，则AOM CO M '∠=∠,AO CO ',所以434AC OO AM AO '-==，即12AB AM ==. 17答案：（1）因为m n ⊥，所以cos cos sin sin 02B C B C -+-= 即()cos 2B C +=-，因为A B C π++=，所以cos()cos B C A +=- 所以c o s,4A A π==． 4分（2）由3,44A CB ππ==-，故73sin cos()sin cos()sin )12626B C B B B B B πππ+-=+-==+ 由3(0,)4B π∈cos()4B C π-+最大值时，3B π=． 8分由正弦定理，2sin sin a bA B==，得b =故1sin sin()243ab C ππ=+=． 12分ME18答案：（Ⅰ）比赛进行4局结束，且乙比甲多得2分即头两局乙胜一局，3,4局连胜，则所求概率为1212114333381P C =⋅⋅⋅=. 4分（Ⅱ）由题意知，ξ的取值为2,4,6. 则22215(2)()()339P ξ==+=，12122212212120(4)()()33333381P C C ξ==+=1221216(6)()3381P C ξ=== 故ξ的分布列为10分则520162662469818181E ξ=⨯+⨯+⨯=12分 19解：（I ）当13t =时，//PA 平面MQB证明：连AC 交BQ 于N ，连MN ．由//AQ BC 可得，ANQ BNC ∆∆∽，12AQ AN BC NC ∴==，所以13AN AC =．若13t =，即13PM ANPC AC==， //PA MN ∴由MN ⊂平面PAC ，故//PA 平面MQB ． 4分（II ）由PA=PD=AD=2， Q 为AD 的中点，则PQ ⊥AD 又平面PAD ⊥平面ABCD ，所以PQ ⊥平面ABCD ，连BD ，∵四边形ABCD 为菱形，∴AD=AB ，由 ∠BAD=60°得△ABD 为正三角形，又∵Q 为AD 中点， ∴AD ⊥BQ8分以Q 为坐标原点，分别以QA 、QB 、QP 所在的直线为,,x y z 轴，建立如图所示的坐标系，则各点坐标为A （1，0，0），B （），Q （0，0，0），P （0，0设平面MQB 的法向量为()z y x n ,,=，可得00,//,00n QB n QB PA MN n MN n PA ⎧⎧⋅=⋅=⎪⎪∴⎨⎨⋅=⋅=⎪⎪⎩⎩，⎪⎩⎪⎨⎧=-=0303z x y 令z=1，解得(3,0,1)n = 取平面ABCD 的法向量()3,0,0=，设所求二面角为θ，则21cos ==θ 故二面角M BQ C --的大小为60°． 12分 20解答： (Ⅰ)方法1：由2n ≥时，11122333n n n a a --=+-得，11121(1)33n n n a a --+=++ 两边同时乘以13n -得，1213(1)3(1)2n n n n a a ---+=++，即2n ≥时，12n n b b -=+故{}n b 是公差为2的等差数列．又01322b =⨯=，所以22(1)2n b n n =+-=． 6分方法2：2n ≥时，12113(1)3(1)n n n n n n b b a a -----=+-+，代入11122333n n n a a --=+- 整理得12n 11111213()3(1)2333n n n n n n b b a a -------=++-+=，故{}n b 是公差为2的等差数列． (Ⅱ)由(Ⅰ)得，13(1)2n n n b a n -=+=，故1123n n a n -+=，所以12(1)133(1)1313n n n S -==-- 8分则111111323331111(3)313333n n n n nn n n m S m S m m m m --+----==-=-------- 因为13113131m n m mn S m S m +-<=--++，得21(3)3131n m m >--+ *(3)310,1,2n m m N m -->∈∴=当1m =时，2112314n n >⇒=⋅-；当2m =时，211,23110nn >⇒=- 综上，存在符合条件的所有有序实数对(,)m n 为：(1,1),(2,1),(2,2)． 12分21解答：（Ⅰ）由24y x =的准线为1x =-，2512A AF x ∴=+=，故记3(2A 又1(1,0)F -，所以12752622a AF AF =+=+=，故椭圆为22198x y +=． 3分（Ⅱ）由22198x y +=知，y =3sin ()26x t t ππ=-≤≤1S ==62(3sin )t ππ-=⎰262cos tdt ππ-=62(1cos2)t dt ππ-+621sin 2)|2x x ππ-=+=3322204()|3S x ===根据对称性， “盾圆C ”的面积为122()S S -=． 7分（Ⅲ）设过2F 的直线为1(0)x my m =+≠，(,)(,)(,)(,)M M N N G G H H M x y N x y G x y H x y 、、、联立221198x my x y=+⎧⎪⎨+=⎪⎩，得22(89)16640m y my ++-=，则2216896489M H M H m y y m y y m -⎧+=⎪⎪+⎨-⎪=⎪+⎩联立214x my y x=+⎧⎨=⎩，得2440y my --=，则44N G N G y y my y +=⎧⎨=-⎩由M N G H P P '、、、、、共线，所以2222N GM H M HN G y y MH PF y y y y NG P F y y +-⋅=⋅+'-代入韦达定理整理得，222431689MH PF mm NG P F m ⋅=='+故22MH PF NG P F ⋅'为定值3． 13分 22答案：（Ⅰ）1a =时，()ln (1)ln(1)f x x x x x =+--，(01x <<)，则()ln ln(1)ln1xf x x x x'=--=-．令()0f x '=，得12x =．当102x <<时，()0f x '<，()f x 在1(0,)2是减函数，当112x <<时，()0f x '>，()f x 在1(,1)2是增函数，所以 ()f x 在12x =时取得最小值，即11()ln 22f =．（4分）（Ⅱ）因为 ()ln ()ln()f x x x a x a x =+--，所以 ()ln ln()ln xf x x a x a x'=--=-．所以当2ax =时，函数()f x 有最小值．∀x 1，x 2∈R +，不妨设12x x a +=，则121211221111ln ln ln ()ln()2ln()22x x x xx x x x x x a x a x +++=+--≥⋅[]1212()ln()ln 2x x x x =++-．（8分）（Ⅲ）（证法一）数学归纳法ⅰ)当1n =时，由（Ⅱ）知命题成立． ⅱ）假设当n k =( k ∈N *)时命题成立，即若1221k x x x +++=，则112222ln ln ln ln2k k k x x x x x x +++≥-．当1n k =+时，1x ，2x ，…，121k x +-，12k x +满足 11122121k k x x x x ++-++++=．设11111122212122()ln ln ln ln k k k k F x x x x x x x x x ++++--=++++，由（Ⅱ）得11111212212212()()l n [()l n2]()l n [()l n2]k k k k F x x x x x xx xx ++++--≥++-++++-=111111212122122122()ln()()ln()(...)ln 2k k k k k x x x x x x x x x x x +++++--++++++-+++ =11111212212212()ln()()ln()ln 2k k k k x x x x x x x x ++++--++++++-．由假设可得 1()ln 2ln 2ln 2kk F x +≥--=-，命题成立．所以当 1n k =+时命题成立．由ⅰ)，ⅱ）可知，对一切正整数n ∈N *，命题都成立，所以若211nii x==∑，则21ln ln 2nniii x x =≥-∑ *(,)i n ∈N ．（13分）（证法二）若1221n x x x +++=，那么由（Ⅱ）可得112222ln ln ln n n x x x x x x +++1212212212()ln[()ln 2]()ln[()ln 2]n n n n x x x x x x x x --≥++-++++-1212122122122()ln()()ln()(...)ln 2n n n n n x x x x x x x x x x x --=++++++-+++ 1212212212()ln()()ln()ln 2n n n n x x x x x x x x --=++++++-12341234212212()ln()()ln()2ln 2n n n n x x x x x x x x x x x x --≥+++++++++-121222(...)ln[()ln 2](1)ln 2n n x x x x x x n ≥≥++++++---ln 2n =-．（14分）薄雾浓云愁永昼，瑞脑消金兽。

湖北省黄冈中学2013年秋季高三数学(理)期末考试

湖北省黄冈中学2013年秋季高三数学（理）期末考试考试时间：2014年1月20日下午14：30—16：30本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页。

全卷满分150分，考试时间120分钟．★★★ 祝考试顺利 ★★★第Ⅰ卷（选择题，共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.复数20132(12a i i i i+⋅-是虚数单位）为纯虚数，则实数a 的值为（） A ． B ．1- C ．14 D ．14-2．已知,b c 是平面α内的两条直线，则“直线a α⊥”是“直线a b ⊥且直线a c ⊥”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 3．某空间组合体的三视图如图所示，则该组合体的体积为（） A ．48 B ．56 C ．64 D ．724.设ABC ∆的内角,,A B C 所对的边分别为,,a b c ，若cos cos sin b C c B a A +=，则ABC ∆的形状为（） A ．直角三角形 B ．锐角三角形 C ．钝角三角形 D ．等腰三角形 5．如果若干个函数的图像经过平移后能够重合，则称这些函数为“同簇函数”．给出下列函数： ①()sin cos f x x x =；②()2sin()4f x x π=+；③()sin f x x x =+；④()21f x x =+．其中“同簇函数”的是（）A ．①②B ．①④C ．②③D ．③④6．已知()f x 是定义在R 上以2为周期的偶函数，且当01x ≤≤时，12()log (1)f x x =-，则2011()4f -=（） A ．2- B ．12C ．D ．2 7.双曲线221x y a-=的一条渐近线与圆()2222x y -+=相交于,M N 两点，且2MN=，则此双曲线的离心率第3题图为（）AB．3 8．已知(2,1)A ，(1,2)B -，31,55C ⎛⎫- ⎪⎝⎭，动点(,)P a b 满足02OP OA ≤⋅≤ 且02OP OB ≤⋅≤ ，则点P 到点C的距离大于14的概率为（） A ．5164π- B ．564π C ．116π- D ．16π9．已知数列{}n a 的通项222cos sin 33n n n a n ππ⎛⎫=- ⎪⎝⎭，其前n 项和为n S ，则60S =（） A ．1840 B ．1880 C ．1960 D ．198010．已知函数()()()212ln f x a x x =---，1()xg x xe -=(a R ∈,e 为自然对数的底数)，若对任意给定的(]00,x e ∈，在(]0,e 上总存在两个不同的i x （1,2i =），使得()()0i f x g x =成立，则a 的取值范围是（）A ．25-1e e -⎛⎤∞ ⎥-⎝⎦，B ．22,e e -⎛⎫-∞ ⎪⎝⎭C ．222e e -⎛⎫ ⎪⎝⎭，D ． 2522,1e e e e --⎡⎫⎪⎢-⎣⎭ 第Ⅱ卷（非选择题，共100分）二、填空题：本大题共5小题，每小题5分，共25分．（一）必考题（11—14题）11．已知集合{}2|560A x x x =--<，{}|2B x x =<，则()R A C B ⋂=___________．12．由直线12x =，2x =，曲线1y x =及x 轴所围图形的面积为___________．则a 与b的夹角的取13．已知20a b =≠ ，且关于x 的方程20x a x a b ++⋅= 有实根，值范围是___________．14.如图，有一个形如六边形的点阵，它的中心是一个点（算第．．1．层．），第2层每边有两个点，第3层每边有三个点，依次类推．（1）试问第n 层()2n N n *∈≥且的点数为___________个；（2）如果一个六边形点阵共有169个点，那么它一共有___________层．（二）选考题（请考生在15、16两题中任选一题作答．如果全选，则按第15题作答结果计分） 15．（选修4—1：几何证明选讲）如图所示，,EB EC 是圆O 的两条切线，,B C 是切点，,A D 是圆O 上两点，如果第14题图46E ︒∠=，32DCF ︒∠=，则A ∠的度数是___________．16. （选修4—4：坐标系与参数方程）在极坐标系中，过点18,2P π⎛⎫⎪⎝⎭引圆10sin ρθ=的两条切线,PA PB ，切点分别为,A B ，则线段AB 的长为___________．三、解答题：本大题共6小题，共75分解答应写出文字说明、证明过程或演算步骤．17．已知函数()f x m n =⋅，其中()sin cos m x x x ωωω=+ ，()cos sin ,2sin n x x x ωωω=- ，0ω>，()f x 的相邻两条对称轴间的距离大于等于2π．（1）求ω的取值范围；（2）在ABC ∆中，角,,A B C 所对的边依次为,,a b c，3a b c =+=，当ω的值最大时，()1f A =，求ABC ∆的面积．18.如图所示，为处理含有某种杂质的污水，要制造一底宽为2米的无盖．．长方体沉淀高度为b 米．已知箱，污水从A 孔流入，经沉淀后从B 孔流出，设箱体的长度为a 米，流出的水中该杂质的质量分数与,a b 的乘积ab 成反比，现有制箱材料60平方米．（注：制箱材料必须用完）（1）求出,a b 满足的关系式；（2）问当,a b 各为多少米时，经沉淀后流出的水中该杂质的质量分数最小（A 、B 孔的面积忽略不计）？19. 如图所示，四边形PDCE 为矩形，四边形ABCD 为梯形，平面PDCE ⊥平面ABCD ，90BAD ADC ︒∠=∠=，1,2AB AD CD a PD ====．（1）若M 为PA 中点，求证：//AC 平面MDE ；（2）求平面PAD 与平面PBC 所成锐二面角的大小．第15题图第18题图20．设数列{}n a 的首项112a =，且11(214nn n a n a a n +⎧⎪⎪=⎨⎪+⎪⎩为偶数）（为奇数），记211()4n n b a n N *-=-∈．（1）求23,a a ；（2）证明：{}n b 是等比数列；（3）求数列31n n b ⎧⎫+⎨⎬⎩⎭的前n 项和n T ．21．如图，椭圆22122:1(0)x y C a b a b +=>>，x 轴被曲线22:C y x b =-截得的线段长等于1C 的长半轴长.（1）求1C ，2C 的方程；（2）设2C 与y 轴的交点为M ，过坐标原点O 的直线与2C 相交于点A,B,直线MA,MB 分别与1C 相交与D,E. （i ）证明：MA MB ⊥；(ii)记△MAB,△MDE 的面积分别是12,S S .问：是否存在直线,使得21S S =3217?请说明理由．22．已知函数1ln ()xf x x +=．（1）若函数在区间1,2a a ⎛⎫+ ⎪⎝⎭（其中0a >）上存在极值，求实数a 的取值范围；（2）如果当1x ≥时，不等式()1kf x x ≥+恒成立，求实数k 的取值范围；（3）求证：()()()221!1n n n e n N -*+>+⋅∈⎡⎤⎣⎦．湖北省黄冈中学2013年秋季高三数学（理）期末考试参考答案（附评分细则）一、选择题二、填空题11．[)2,6 12．2ln 2 13．,3ππ⎡⎤⎢⎥⎣⎦14．(1)()61n - (2)15．99︒16．120138．动点(,)P a b 满足的不等式组为022022a b a b ≤+≤⎧⎨≤-≤⎩，画出可行域可知P 的运动区域为以31,55C ⎛⎫- ⎪⎝⎭为中心且边的正方形，而点P 到点C 的距离小于或等于14的区域是以31,55C ⎛⎫- ⎪⎝⎭为圆心且半径为14的圆以及圆的内部，所以22145164P ππ⎛⎫-==- 9．222cos sin 33n n n a n ππ⎛⎫=- ⎪⎝⎭22cos 3n n π=，所以()()()22232313115323139222k k k a a a k k k k --++=----+=-，其中k N *∈ 所以60S =()5912202018905018402++⋅⋅⋅+-⨯=-=10．易得函数()g x 在(]0,e 上的值域为(]0,1()(]'2222()2,0,a x a f x a x e x x⎛⎫-- ⎪-⎝⎭=--=∈当22x a =-时，'()0f x =，()f x 在22x a=-处取得最小值222ln 22f a a a ⎛⎫=- ⎪--⎝⎭由题意知，()f x 在(]0,e 上不单调，所以202e a <<-，解得22e a e-<所以对任意给定的(]00,x e ∈，在(]0,e 上总存在两个不同的i x （1,2i =），使得()()0i f x g x =成立，当且仅当a 满足条件202f a ⎛⎫≤ ⎪-⎝⎭且()1f e ≥因为(1)0f =，所以202f a ⎛⎫≤⎪-⎝⎭恒成立，由()1f e ≥解得251e a e -≤- 综上所述，a 的取值范围是25,1e e -⎛⎤-∞ ⎥-⎝⎦14. 观察图形，可以看出，第一层是1个点，其余各层的点数都是6的倍数且倍数比层数少1，所以：（1）第n层的点数为()61(2)n n -≥；（2）n 层六边形点阵的总点数为()16121n +⨯++⋅⋅⋅+-=()131n n +-令()131169n n +-=解得7n =-（舍去）或8n = 所以8n = 三、解答题17．解：（1）22()cos sin sin f x m n x x x x ωωωω=⋅=-+=cos 22x x ωω=2sin 26x πω⎛⎫+ ⎪⎝⎭----------------------------3分因为0ω>，所以函数()f x 的周期22T ππωω== 由题意可知22T π≥，即T π≥，ππω≥----------------------------5分解得01ω<≤-----------------------------6分（2）由（1）可知ω的最大值为1，所以()2sin 26f x x π⎛⎫=+⎪⎝⎭因为()1f A =，所以1sin 262A π⎛⎫+= ⎪⎝⎭----------------------------7分而132,666A πππ⎛⎫+∈ ⎪⎝⎭，所以5266A ππ+=，所以3A π=-------------------------9分而2222cos b c bc A a +-=，所以223b c bc +-= ① 而()22229b c b c bc +=++= ②联立①②解得：2bc =-------------------------11分所以1sin 2ABC S bc A ∆==-------------------------12分 18．解：（1）由题意可得242600,0a b ab a b ++=⎧⎨>>⎩，即2300,0a b ab a b ++=⎧⎨>>⎩------------------------6分注：若没写0,0a b >>，扣两分，少写一个扣1分（2）因为该杂质的质量分数与,a b 的乘积ab 成反比，所以当ab 最大时，该杂质的质量分数最小由均值不等式得2a b +≥（当且仅当2a b =时取等号）所以2a b ab ab ++≥+，即30ab +≤（当且仅当2a b =时取等号）-----------------------8分即0+-≤，0>≤18ab ≤-----------------------10分所以当且仅当218a b ab =⎧⎨=⎩即()()63a m b m =⎧⎪⎨=⎪⎩时，ab 取得最大值18，此时该杂质的质量分数最小 -------------------12分19．20．解：（1）21321313,4428a a a a =+=== ------------------2分（2）证明：因为2114n n b a -=-，所以121221211111111142424424n n n n n b a a a a ++--⎛⎫⎛⎫=-=-=+-=- ⎪ ⎪⎝⎭⎝⎭------------------5分即112n n b b +=，------------------6分而1111044b a =-=≠，所以{}n b 是以14为首项，公比为12的等比数列-----------7分注：若没写10b ≠，扣一分（3）1111122n n n b b -+⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭，所以31nn b +=()1312n n ++ 所以()()()23131123212312n n T n +=⨯++⨯++⋅⋅⋅++()()()()3412231123212322312n n n T n n ++=⨯++⨯++⋅⋅⋅+-++--------8分两式相减得：()()2341312322216n n n T n ++=+-++⋅⋅⋅+---------10分即()23228n n T n +=-+ --------12分21．解：（1）由题意知c e a ==2a b =，又a =，解得2,1a b ==。

湖北省黄冈中学2013年秋季高三数学(理科)函数、平面向量、数列、不等式、复数、立体几何、解析几何测试卷

2014届高三上数学测试题（13）（理科）考查范围：函数、平面向量、数列、不等式、复数、立体几何、解析几何命题人：张智一．选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的1．集合{}a A ,2,0=,{}2,1a B =,若{}16,4,2,1,0=B A ,则a 的值为 (B ) A.2 B.4 C.-2 D.-4 2.复数 ,1i z -=则=+z z1D A.i 2321+B.i 2321- C.i 2323- D.i 2123- 3．“,2παπ⎛⎫∈ ⎪⎝⎭”是“方程22cos 1x y α+=表示焦点在x 轴上的双曲线”的（ A ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 3.[答案]A （教材选修2-1 80P 页第4题改编）4.设非零向量a b c 、、，满足||||||a b c ==，||||a b c +=，则sin ,a b <>= ( ) A ． 12-B ．12 C． D4.【答案】D.法一:【解析】∵||||a b c +=∴||||||a b c a +==，∴解得：222||a b b b ∙=-=- ∴21cos ,2||||||a b a b a b a b b ∙∙<>===-∴3sin ,a b <>=法二:利用向量几何意义画图求解.5. 已知点(,)(0,0)M a b a b >>是圆22:1C x y +=内任意一点，点(,)P x y 是圆上任意一点，则实数1ax by +- ( A ) A ．一定是负数 B ．一定等于0 C ．一定是正数 D ．可能为正数也可能为负数6.已知函数()sin()(0,)2f x x πωϕωϕ=+><的部分图像如图，则20131()6n n f π==∑（） A ．1- B ． 12C ．1D ．0 6.【答案】C 【解析】根据图像1254126πππω⨯=-，解得2ω=，把点(,1)6π的坐标代入，得1sin(2)6πϕ=⨯+，结合2πϕ<得6πϕ=，故()sin(2)6f x x π=+，213145161()1,(),(),()1,(),()6626266262f f f f f f ππππππ===-=-=-=，函数的最小正周期是π，在一个周期内的各个函数值之和为0，201363353=⨯+， 20131()(2011)(2012)(2013)(1)(2)(3)16i n f f f f f f f π==++=++=∑。

黄冈中学2013届高三11月月考数学(理)

黄冈中学2013届11月月考数学试题（理）一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．sin(1920)- 的值为（）A．2- B ．12- C．2D ．12解析：sin(1920)sin(2406360)sin(18060)-=-⨯=+ ，即原式sin 60=- ，故选A ．答案：A2．命题“x ∀∈R ，20x >”的否定是（）A ．x ∀∈R ，20x ≤B ．x ∃∈R ，20x >C ．x ∃∈R ，20x <D ．x ∃∈R ，20x ≤解析：全称命题的否定是特称命题，易知应选D ．答案：D3．已知集合{P =正奇数}和集合{|M x x ==,,}a b a P b P ⊕∈∈，若M P ⊆，则M 中的运算“⊕”是（） A ．加法 B ．除法C ．乘法D ．减法解析：由已知集合M 是集合P 的子集，设*21,21(,)a m b n m n =-=-∈N ，∵(21)(21)a b m n ⋅=--42()12[2()1]1mn m n mn m n P =-++=-++-∈，∴M P ⊆，而其它运算均不使结果属于集合P ，故选C ．答案：C4．已知某几何体的侧视图与其正视图相同，相关的尺寸如下图所示，则这个几何体的体积是（）A . 8πB . 7πC . 2π`D .74π解析：依题意该几何体为一空心圆柱，故其体积2237[2()]124V ππ=-⨯=，选D ．答案：D5．已知A 、B 两点分别在两条互相垂直的直线20x y -=和0x ay +=上，且AB 线段的俯视图正视图侧视图中点为P 10(0,)a，则线段AB 的长为（）A ．8B ．9C ．10D ．11解析：由已知两直线互相垂直得2a =，∴线段AB 中点为P (0,5)，且AB 为直角三角形AO B 的斜边，由直角三角形的性质得||2||10AB PO ==，选C ．答案：C6．已知各项为正的等比数列{}n a 中，4a 与14a 的等比中项为，则7112a a +的最小值为（）A ．16B ．8C ．D ．4解析：由已知24148a a ==，再由等比数列的性质有4147118a a a a ==，又70a >，110a >，71128a a +≥=，故选B ．7．设函数2,0(),01x x bx c f x x ≥⎧++=⎨<⎩，若(4)(0)f f =，(2)2f =，则函数()()g x f x x=-的零点的个数是（） A ．0B ．1C ．2D ．3解析：已知即164422b c c b c ++=⎧⎨++=⎩，∴46b c =-⎧⎨=⎩，若0x ≥，则246x x x -+=，∴2x =，或3x =；若0x <，则1x =舍去，故选C ．答案：C8．给出下列的四个式子：①1a b-，②1a b+，③1b a+，④1b a-；已知其中至少有两个式子的值与tan θ的值相等，则（） A ．cos 2,sin 2a b θθ== B ．sin 2,cos 2a b θθ== C ．sin,cos22a b θθ==D ．cos,sin22a b θθ==解析：sin sin 21cos 2tan ,cos 2,sin 2cos 1cos 2sin 2a b θθθθθθθθθ-===∴==+ 时，式子①③与tan θ的值相等，故选A ．答案：A9．设集合(){}(){},|||||1,,()()0A x y x y B x y y x y x =+≤=-+≤，M A B = ，若动点(,)P x y M ∈，则22(1)x y +-的取值范围是（）A ．15[,]22B ．5]22C ．1[,22D ．[22解析：在同一直角坐标系中画出集合A 、B 所在区域，取交集后如图，故M所表示的图象如图中阴影部分所示，而d =表示的是M 中的点到(0,1)的距离，从而易知所求范围是15[,]22，选A ．10．已知O 为平面上的一个定点，A 、B 、C 是该平面上不共线的三个动点，点P 满足条件2O B O C O P += (),(0,)||cos ||cos AB ACAB B AC C λλ++∈+∞ ，则动点P 的轨迹一定通过A B C ∆的（）A ．重心B ．垂心C ．外心D ．内心解析：设线段BC 的中点为D ，则2O B O CO D += ，∴2O B O C O P += ()||cos ||cos AB ACAB B AC Cλ++ ()||cos ||cos AB ACO D AB B AC Cλ=++，∴()||cos ||cos AB ACO P O D D P AB B AC Cλ-=+=，∴()()||cos ||cos ||cos ||cos AB AC AB BC AC BCD P BC BC AB B AC C AB B AC C λλ⋅⋅⋅=+⋅=+||||cos()||||cos ()(||||)0||cos ||cos AB BC B AC BC CBC BC AB B AC Cπλλ-=+=-+=， ∴D P BC ⊥，即点P 一定在线段B C 的垂直平分线上，即动点P 的轨迹一定通过A B C ∆的外心，选C ．答案：C二．填空题：本大题共5小题，每小题5分，共25分，把答案直接填在题中横线上．11．1220xe dx =⎰______________．解析：1122220011|(1)22xxe dx ee ==-⎰．答案：1(1)2e -12．定义运算a c ad bc bd=-，复数z 满足11z i i i=+，则复数z 的模为_______________．解析：由11z i i i=+得1212i zi i i z i i+-=+⇒==-，∴z ==．13．已知方程22220x y kx y k ++++=所表示的圆有最大的面积，则直线(1)2y k x =-+的倾斜角α=_______________．解析：1r =≤，当有最大半径时有最大面积，此时0k =，1r =，∴直线方程为2y x =-+，设倾斜角为α，则由tan 1α=-且[0,)απ∈得34πα=．答案：34π14．已知函数2()m f x x -=是定义在区间2[3,]m m m ---上的奇函数，则()f m =_______．解析：由已知必有23m m m -=+，即2230m m --=，∴3m =，或1m =-；当3m =时，函数即1()f x x -=，而[6,6]x ∈-，∴()f x 在0x =处无意义，故舍去；当1m =-时，函数即3()f x x =，此时[2,2]x ∈-，∴3()(1)(1)1f m f =-=-=-．答案：1-15．在工程技术中，常用到双曲正弦函数2xxe e shx --=和双曲余弦函数2x xe echx -+=，双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质，请类比正、余弦函数的和角或差角公式，写出关于双曲正弦、双曲余弦函数的一个正确的类似公式．解析：由右边2222x xy yx xy ye ee ee ee e----++--=⋅-⋅1()4x yx yx yx yx y x yx yx ye eee eee e +--+--+--+--=+++-++-()()1(22)()42x yx y x yx y ee eech x y ------+=+==-=左边，故知．答案：填入()c c c s s h x y hx hy hx hy -=-，()c c c s s h x y hx hy hx hy +=+，()c s sh x y shx hy chx hy -=-，()c s sh x y shx hy chx hy +=+四个之一即可．三．解答题：本大题共6小题，共75分，请给出各题详细的解答过程．16．（本小题满分12分）已知数列{}n a 的前n 项和为n S ，且*41()n n S a n =+∈N ．（1）求1a ，2a ；（2）设3log ||n n b a =，求数列{}n b 的通项公式．解答：（1）由已知1141S a =+，即1141a a =+，∴=1a 13，……………………2分又2241S a =+，即1224()1a a a +=+，∴219a =-； ……………………5分（2）当1n >时，1111(1)(1)44n n n n n a S S a a--=-=+-+，即13n n a a -=-，易证数列各项不为零（注：可不证），故有113n n a a -=-对2n ≥恒成立，∴{}n a 是首项为13，公比为13-的等比数列，∴1111()(1)333n n nn a ---=-=-， ……………………10分∴33log ||log 3nn n b a n -===-． ……………………12分17．（本小题满分12分）已知 1:(),3x p f x -=且|()|2f a <；q ：集合2{|(2)10,}A x x a x x =+++=∈R ，且A ≠∅．若p ∨q 为真命题，p ∧q 为假命题，求实数a 的取值范围. 解答：若1|()|||23a f a -=<成立，则616a -<-<，即当57a -<<时p 是真命题； ……………………4分若A ≠∅，则方程2(2)10x a x +++=有实数根，由2(2)40a ∆=+-≥，解得4a ≤-，或0a ≥，即当4a ≤-，或0a ≥时q 是真命题； ……………………8分由于p ∨q 为真命题，p ∧q 为假命题，∴p 与q 一真一假，故知所求a 的取值范围是(,5](4,0)[7,)-∞--+∞ ． ……………………12分（注：结果中在端点处错一处扣1分，错两处扣2分，最多扣2分） 18．（本小题满分12分）已知A B C ∆的两边长分别为25A B =，39AC =，且O 为A B C∆外接圆的圆心．（注：39313=⨯，65513=⨯）（1）若外接圆O 的半径为652，且角B 为钝角，求BC 边的长；（2）求AO BC ⋅的值．解答：（1）由正弦定理有2sin sin A B A C R CB ==，∴253965sin sin CB==，∴3sin 5B =，5sin 13C =， ……………………3分且B 为钝角，∴12cos 13C =，4cos 5B =-，∴3125416sin()sin cos sin cos ()51313565B C B C C B +=+=⨯+⨯-=，又2sin B C R A=，∴2sin 65sin()16BC R A B C ==+=； ……………………6分（2）由已知AO OC AC += ，∴22()AO OC AC += ，即2222||2||||39AO AO O C O C AC +⋅+==……………………8分同理AO OB AB += ，∴2222||2||||25A O A O O B O B A B +⋅+==， …………10分两式相减得22(3925)(3925)896AO O C AO O B ⋅-⋅=-+=，即2896AO BC ⋅= ，∴448AO BC ⋅=． ……………………12分19．（本小题满分12分）在如图所示的多面体ABCDE中，AB ⊥平面ACD ，DE ⊥平面ACD ，AC=AD=CD=DE=2，AB=1，G 为AD 中点．（1）请在线段CE 上找到点F 的位置，使得恰有直线BF ∥平面ACD ，并证明这一事实；（2）求平面BCE 与平面ACD 所成锐二面角的大小；（3）求点G 到平面BCE 的距离．解法一：以D 点为原点建立如图所示的空间直角坐标系，使得x 轴和z 轴的正半轴分别经过点A 和点E ，则各点的坐标为(0,0,0)D ，(2,0,0)A ，(0,0,2)E ，(2,0,1)B，(1,0)C ，（1）点F 应是线段CE 的中点，下面证明：设F 是线段CE 的中点，则点F的坐标为1(,1)22F，∴3(,0)22B F =- ，显然BF与平面xOy 平行，此即证得BF ∥平面ACD ； ……………………4分（2）设平面BCE 的法向量为(,,)n x y z =，则n CB ⊥ ，且n CE ⊥ ，由(1,C B =，(1,2)C E =-，∴020x z x z ⎧-+=⎪⎨--+=⎪⎩，不妨设y =12x z =⎧⎨=⎩，即2)n = ，∴所求角θ满足(0,0,1)cos 2||n n θ⋅==，∴4πθ=； ……………………8分（3）由已知G 点坐标为（1，0，0），∴(1,0,1)BG =--，由（2）平面BCE的法向量为(1,2)n =，∴所求距离||||BG n d n ⋅==……………………12分解法二：（1）由已知AB ⊥平面ACD ，DE ⊥平面ACD ，∴AB//ED ，设F 为线段CE 的中点，H 是线段CD 的中点，连接FH ，则//FH =12ED ，∴//FH =AB ，…………………2分∴四边形ABFH 是平行四边形，∴//BF AH ，由B F ⊄平面ACD 内，AH ⊂平面ACD ，//B F ∴平面ACD ； ……………4分（2）由已知条件可知A C D ∆即为B C E ∆在平面ACD 上的射影，设所求的二面角的大小为θ，则cos AC D BC ES S θ∆∆=， ……………………6分易求得BC=BE =CE =∴1||2BC E S C E ∆==而2||4AC D S AC ∆==∴cos 2AC D BC ES S θ∆∆==，而02πθ<<，∴4πθ=； ………………8分（3）连结BG 、CG 、EG ，得三棱锥C —BGE ，由ED ⊥平面ACD ，∴平面ABED ⊥平面ACD ，又C G A D ⊥，∴C G ⊥平面ABED ，设G 点到平面BCE 的距离为h ，则C BG E G BC E V V --=即1133BG E BC E S G C S h ∆∆⨯=⨯，E由32B G E S ∆=，BCE S ∆=C G =∴B G E B C ES G C h S ∆∆⨯===G 到平面BCE 的距离．………………12分20．（本小题满分13分）已知椭圆22221y x ab+=(0)a b >>的一个顶点为B (0,4)，离心率e=5，直线l 交椭圆于M 、N 两点．（1）若直线l 的方程为4y x =-，求弦MN 的长；（2）如果ΔBMN 的重心恰好为椭圆的右焦点F ，求直线l 方程的一般式．解答：（1）由已知4b =，且5c a =，即2215c a=，∴22215a b a-=，解得220a =，∴椭圆方程为2212016yx+=； ……………………3分由224580x y +=与4y x =-联立，消去y 得29400x x -=，∴10x =，2409x =，∴所求弦长21||||9M N x x =-=； ……………………6分（2）椭圆右焦点F 的坐标为(2,0)，设线段MN 的中点为Q 00(,)x y ，由三角形重心的性质知2B F F Q =，又(0,4)B ，∴00(2.4)2(2,)x y -=-，故得003,2x y ==-，求得Q 的坐标为(3,2)-； ……………………9分设1122(,),(,)M x y N x y ，则12126,4x x y y +=+=-，且222211221,120162016x y x y +=+=， ……………………11分以上两式相减得12121212()()()()02016x x x x y y y y +-+-+=，1212121244665545M N y y x x k x x y y -+==-=-=-+- ∴，故直线MN 的方程为62(3)5y x +=-，即65280x y --=． ……………………13分（注：直线方程没用一般式给出但结果正确的扣1分） 21．（本小题满分14分）已知函数[)1()ln 1,sin g x x x θ=++∞⋅在上为增函数，且(0,)θπ∈，12()ln m ef x m x x x-+=--，m ∈R ．（1）求θ的值；（2）当0m =时，求函数()f x 的单调区间和极值；（3）若在[1,]e 上至少存在一个0x ，使得00()()f x g x >成立，求m 的取值范围．解答：（1）由已知/211()0sin g x xxθ=-+≥⋅在[1,)+∞上恒成立，即2sin 10sin x xθθ⋅-≥⋅，∵(0,)θπ∈，∴sin 0θ>，故sin 10x θ⋅-≥在[1,)+∞上恒成立，只需sin 110θ⋅-≥，即sin 1θ≥，∴只有sin 1θ=，由(0,)θπ∈知2πθ=； ……………………4分（2）∵0m =，∴12()ln e f x x x-+=--，(0,)x ∈+∞，∴/2221121()e e xf x xxx---=-=，令/()0f x =，则21x e =-(0,)∈+∞，∴x ，/()f x 和()f x 的变化情况如下表：即函数的单调递增区间是(0,21)e -，递减区间为(21,)e -+∞，有极大值(21)1ln(21)f e e -=---； ……………………9分（3）令2()()()2ln m e F x f x g x m x x x+=-=--，当0m ≤时，由[1,]x e ∈有0m m x x-≤，且22ln 0e x x --<，∴此时不存在0[1,]x e ∈使得00()()f x g x >成立；当0m >时，2/222222()m e mx x m eF x m xxx+-++=+-=，∵[1,]x e ∈，∴220e x -≥，又20mx m +>，∴/()0F x >在[1,]e 上恒成立，故()F x 在[1,]e 上单调递增，∴m ax ()()4m F x F e m e e==--，令40m m e e-->，则241e m e >-，故所求m 的取值范围为24(,)1e e +∞-． ……………………14分。

2013-2014年湖北省黄冈中学高三上学期数学期末试卷(理科)与解析

2．（5 分）已知 b，c 是平面 α 内的两条直线，则“直线 a⊥α”是“直线 a⊥b 且直线 a⊥c”的（） B．必要不充分条件 D．既不充分也不必要条件
A．充分不必要条件 C．充要条件
3．（5 分）某空间组合体的三视图如图所示，则该组合体的体积为（
A．48
B．56
C．64
D．72
4．（5 分）设△ABC 的内角 A， B， C 所对的边分别为 a， b， c，若 bcosC+ccosB=asinA，则△ABC 的形状为（ A．直角三角形） C．钝角三角形 D．不确定
） C．②③ D．③④
B．①④
6．（5 分）已知 f（x）是定义在 R 上以 2 为周期的偶函数，且当 0≤x≤1 时，f （x）=log A．﹣2 7．（5 分）双曲线（1﹣x），则 f（﹣ B．）=（ C．1 ）
D．2
﹣y2=1 的一条渐近线与圆（x﹣2）2+y2=2 相交于 M，N 两点，） C． D．3
，且关于 x 的方程．
第 2 页（共 25 页）
有实根，则与
14．（5 分）如图，有一个形如六边形的点阵，它的中心是一个点（算第 1 层），第 2 层每边有两个点，第 3 层每边有三个点，依此类推．（1）试问第 n 层（n∈N*且 n≥2）的点数为个；层．
（2）如果一个六边形点阵共有 169 个点，那么它一共有
第 3 页（共 25 页）
，b+c=3，当 ω 最
大时，f（A）=1，求△ABC 的面积． 18．（12 分）如图所示，为处理含有某种杂质的污水，要制造一底宽为 2 米的无盖长方体沉淀箱，污水从 A 孔流入，经沉淀后从 B 孔流出，设箱体的长度为 a 米，高度为 b 米．已知流出的水中该杂质的质量分数与 a，b 的乘积 ab 成反比，现有制箱材料 60 平方米．（注：制箱材料必须用完）（1）求出 a，b 满足的关系式；（2）问当 a，b 各为多少米时，经沉淀后流出的水中该杂质的质量分数最小（A、 B 孔的面积忽略不计）？

湖北省黄冈中学届高三年级十一月月考数学理

湖北省黄冈中学2007届高三年级十一月月考数学试题（理）命题：霍祝华审稿：王宪生校对：胡华川第Ⅰ卷（选择题，共50分）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设全集I =R ，{|()0},{|()0}P x f x Q x g x =<=>，且满足∅ P Q R ，则集合{|()0()0}M x f x g x =且≥≤等于（）A ．1P ðB ．1Q ðC ．∅D ．11PQ 痧2．若1tan22x =，则cos x 值为（） A ．45 B ．35 C ．45-D ．35-3．设221:200,:0||2x p x x q x ---><-，则p 是q 的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件4．已知函数()log (1)xa f x a x =++在区间[0, 1]上的最大值和最小值之和为a ，则a 的值为（） A ．14B ．12C ．2D ．45．等差数列{a n }中，a 1>0，公差d <0, S n 为其前n 项和，对任意自然数n ，若点（n, S n ）在以下4条曲线中的某一条上，则这条曲线应是（）6．非零向量,,OA OB ==b a 若点B 关于OA 所在直线的对称点为B 1，则向量1OB 为（） A ．22()||-b b a aa B ．2-b a C ．22()||-b b a a a D ．2()||-b ba a a 7．已知函数sin()y x ωϕ=+与直线12y =的交点中，距离最近的两点间距离为3π，那么此函数的周期是（） A ．3πB ．πC ．2πD ．4π8．若某等差数列{a n }中，2616a a a ++为一个确定的常数，则下列各个和中也为确定的常数的是（） A ．S 17B ．S 10C ．S 8D ．S 159．平面向量22(,),(,),(1,1),(2,2)x y x y ====b d a c ，若1==b d ac ，则这样的向量a 有（）A ．1个B ．2个C ．多于2个D ．不存在10．设函数3()2()f x x x x =+∈R ，若当02πθ≤≤时，(cos )(1)0f m f m θ+->恒成立，则实数m 的取值范围是（）≠ ≠ ≠A ．（0，1）B ．（－∞，0）C ．（－∞，1）D ．（－∞，12）第Ⅱ卷（非选择题，共100分）二、填空题：本大题共5小题，每小题5分，共25分. 把答案填在答题卡的相应位置上.11．已知点P 是圆C ：22450x y x ay +++-=上任意一点，P 点关于直线210x y +-=的对称点也在圆C 上，则实数a =_________________.12x则不等式1(|1|)0fx --<的解集为_______________.13．已知数列{a n }中，1111,3(2),lim n n n n n n a a a a a n na --→+∞==-=则≥_____________.14．定义运算x *y 为x *y =,x x y yx y⎧≥⎪⎨<⎪⎩求()(sin )(cos )f x x x =*的值域为_________.15．设函数f (x )的定义域为D ，如果对于任意的1x D ∈，存在唯一的2x D ∈，使12()()2f x f x C +=（C为常数）成立，则称函数()f x 在D 上均值为C . 下列5个函数：①4sin y x =； ②3y x =； ③lg y x =； ④2x y =； ⑤2 1.y x =-则满足在其定义域上均值为2的所有函数的序号是_______________.三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤. 16．（本小题满分12分）在△ABC 中，a 、b 、c 分别是角A 、B 、C 对边的长，且满足cos .cos 2B bC a c=-+（1）求角B 的值；（2）若5b a c =+=，求a 、c 的值. 17．（本小题满分12分）某公司准备进行两种组合投资，稳健型组合投资是由每份金融投资20万元，房地产投资30万元组成；进取型组合投资是由每份金融投资40万元，房地产投资30万元组成. 已知每份稳健型组合投资每年可获利10万元，每份进取型投资每年可获利15万元. 若可作投资用的资金额，金融投资不超过160万元，房地产投资不超过180万元，那么这两种组合投资应各注入多少份，能使一年获利总额最多？设(1cos ,sin ),(1cos ,sin ),(1,0),(0,),(,2)ααββαπβππ=+=-=∈∈b a c ， a 与c 的夹角为1,θb 与c 的夹角为212,6πθθθ-=，求sin8αβ-的值.19．（本小题满分12分）（1）已知直线l 1：0x y +=，将l 1按向量11,22⎛⎫=-- ⎪⎝⎭a 平移到l 2，求l 2的方程；（2）以11,22⎛⎫=-- ⎪⎝⎭a 为一个方向向量的动直线l 分别交（1）中的l 1、l 2于点Q 、P . 又已知两定点A （－1，2），B （2，1），问是否存在一个适当的l 的位置，使||||||AP PQ QB ++最小？若存在，求出此时点Q 、P 的坐标及此时直线AP 、PQ 、QB 的方程；若不存在，说明理由.设a 、b 为常数，{()|()cos sin }M f x f x a x b x ==+，映射F 把点（a, b ）对应到函数cos sin .a x b x +（1）证明：不存在两个不同点对应于同一个函数；（2）证明：当0()f x M ∈时，10()()f x f x t M =+∈，这里t 为常数；（3）对于属于M 的一个函数0()f x ，得10{()|}M f x t t =+∈R ，在映射F 的作用下，M 1作为象集，求其原象集，并说明它是什么图象？已知函数*()()n f x n ∈N 具有下列性质：（1）当n 一定，记1()kn a k f n =，求k a 的表达式（k =0, 1, …，n ）；（2）对*n ∈N ，证明11(1)43n f <≤.。

湖北黄冈中学2013高三第一次模拟考试--数学理

(吨)0.0.0.0.0.第6题图黄冈中学2013届高三第一次模拟考试数学（理）试卷一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合要求的．1．纯虚数z 满足23z -=，则z 为AB． C ． D ．5或1-2．命题甲：2≠x 或3≠y ；命题乙：5≠+y x ，则甲是乙的A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既不充分条件也不必要条件3．已知双曲线的焦距为，则双曲线的标准方程为 A ．2212y x -= B ．2212x y -= C ．2212y x -=或2212x y -= D ．2212x y -=或2212y x -= 4．用0，1，2，3，4排成无重复字的五位数，要求偶数字相邻，奇数字也相邻，则该五位数的个数是 A ．36 B ．32C ．24D ．20 5．已知cos()63πα+=，则sin(2)6πα-的值为 A ． 13B ．13-C ．D ．-6．对某小区100户居民的月均用水量进行统计，得到样本的频率分布直方图，则估计此样本的众数、中位数分别为 A ．2， 2.5 B ．2.25， 2.02 C ．2.25， 2.5 D ．2.5， 2.25第9题图侧视图俯视图正视图第8题图第127．在游乐场，有一种游戏是向一个画满均匀方格的桌面上投硬币，若硬币恰落在任何一个方格内不与方格线重叠，即可获奖．已知硬币的直径为2，若游客获奖的概率不超过19，则方格边长最长为(单位：cm )A ．3B ．4C ．5D ．6 8．某几何体的三视图如图示，则此几何体的体积是 A ．20π3B ．6πC ．10π3D ．9．如图，AB 是圆O 的直径，C D 、是圆O 上的点，60CBA ∠=o ，45ABD ∠=o ，CD xOA yBC=+u u u r u u u r u u u r ，则x y +的值为 A ．3-B ．13-C ．23D ．10．已知定义在(0,)+∞上的单调函数()f x ，对(0,)x ∀∈+∞，都有2[()log ]3f f x x -=，则方程()'()2f x f x -=的解所在的区间是A ．（0，12）B ．（1,12） C ．（1，2） D ．（2，3）二、填空题：本大题共6小题，考生共需作答5小题，每小题5分，共25分．请将答案填在答题卡对应题号的位置上，书写不清楚，模拟两可均不得分．（一）必考题（11 — 14题） 11．1012x x ⎛⎫- ⎪⎝⎭的展开式中,含4x 项的系数为．12．执行如图所示的程序框图，输出的k 值是． 13．已知(0,)x y z ∈+∞、、，且2221ln ln ln 3x y z ++=，则2x yz的最大值为．14．对于实数x ，将满足“01y ≤<且x y -为整数”的实数y 称为实数x 的小数部分，用符号x 〈〉表示．已知无穷数列{}na 满足如下条件：①1aa =〈〉；②11(0)0(0)n nn n a a a a +⎧〈〉≠⎪=⎨⎪=⎩．（Ⅰ）若a ={}n a 通项公式为；（Ⅱ）当13a >时，对任意*n N ∈都有n a a =，则a 的值为．（二）选考题（请考生在第15、16两题中任选一题作答，请先在答题卡指定位置将你所选的题目序号后的方框用2B 铅笔涂黑．如果全选，则按第15题作答结果给分．） 15．（极坐标与参数方程）已知抛物线C 的极坐标方程为2sin 8cos 0ρθθ-=，若斜率为1的直线经过抛物线C 的焦点，与圆()2224(0)x y r r -+=>相切，则r = ．16．（几何证明选讲）如图，过半径为4的O e 上的一点A 引半径为3的O 'e 的切线，切点为B ，若O e 与O 'eACM P Q D第19题图三、解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）已知ABC ∆中，角A B C 、、的对边分别为a b c 、、，a =(1,1)m =-u r，(cos cos ,sin sin 2n B C B C =-r ，且m n ⊥u r r ．（Ⅰ）求A 的大小；（Ⅱ）当7sin cos()12B C π+-取得最大值时，求角B 的大小和ABC ∆的面积． 18．（本小题满分12分）某象棋比赛规则如下：两名选手比赛时，每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时结束.假设选手甲与选手乙比赛时，甲、乙每局获胜的概率分别为23和13，且各局比赛胜负互不影响.（Ⅰ）求比赛进行4局结束，且乙比甲多得2分的概率；（Ⅱ）设ξ表示比赛停止时已比赛的局数，求随机变量ξ的分布列和数学期望．19．（本小题满分12分）如图，在四棱锥P ABCD -中，底面ABCD 为菱形，60BAD ︒∠=，Q 为AD 的中点，2PA PD AD ===．（Ⅰ）点M 在线段PC 上，PM tPC =，试确定t 的值，使//PA 平面MQB ；（Ⅱ）在（I ）的条件下，若平面PAD ⊥平面ABCD ，求二面角M BQ C --的大小．20．（本小题满分12分）数列{}n a 中，已知11a =，2n ≥时，11122333n n n a a --=+-．数列{}n b 满足：1*3(1)()n n n b a n N -=+∈．（Ⅰ）证明：{}n b 为等差数列，并求{}n b 的通项公式；（Ⅱ）记数列1n a n +⎧⎫⎨⎬⎩⎭的前n 项和为nS ，是否存在正整数,m n ，使得1331m n m n S m S m +-<-+ 成立？若存在，求出所有符合条件的有序实数对(,)m n ；若不存在，说明理由．21．（本小题满分13分）我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．如图，“盾圆C ”是由椭圆22221(0)x y a b ab+=>>与抛物线24y x =中两段曲线弧合成，12F F 、为椭圆的左、右焦点，2(1,0)F ．A 为椭圆与抛物线的一个公共点，252AF =．（Ⅰ）求椭圆的方程；（Ⅱ）求定积分时，可以使用下面的换元法公式：函数()y f x =中，令()x t ϕ=，则[][]2211()()()()()bt t at t f x dx f t d t f t t dtϕϕϕϕ'==⎰⎰⎰（其中12()()a t b t ϕϕ==、）．如222201cos 2(sin )cos (sin )cos 2t t t t dt tdt dt πππ+'====⎰⎰⎰⎰．阅读上述文字，求“盾圆C ”的面积．（Ⅲ）过2F 作一条与x 轴不垂直的直线，与“盾圆C ”依次交于M NGH 、、、四点，P 和P '22．（本小题满分14分）设函数()ln ()ln()f x x x a x a x =+--(0)a >．（Ⅰ）当1a =时，求函数()f x 的最小值；（Ⅱ）证明：对12,(0,)x x ∀∈+∞，都有[]11221212ln ln ()ln()ln 2x x x x x x x x +≥++-；（Ⅲ）若211nii x==∑，证明：21ln ln 2nni ii x x=≥-∑*(,)i n ∈N ．数学（理）试卷答案BBCD ABAC AC11答案：15- 12答案：5 13答案：14答案：（1）1n a =；（21-或12- 15 16答案：121答案：B 解析：设()z bi b R =∈9b =∴=，则z =．2答案：B解析：甲⇒/乙，例如，1,4x y ==；乙⇒甲，“若5≠+y x ，则2≠x 或3≠y ”的逆否命题为“若2x =且3y =，则5x y +=” 此逆否命题为真命题，所以原命题为真命题．3答案：C 解析：由题易知2c b ==1a =，这样的双曲线标准方程有两个．4答案：D解析：排除法．偶数字相邻，奇数字也相邻有32232224A A A =，然后减去0在首位的情况，有22224A A =，故322223222220A A A A A -=．5答案：A 解析：由cos()63πα+=得，1cos(2)33πα+=-，所以1sin(2)sin(2)cos(2)63233ππππααα-=+-=-+=．6答案：B解析：样本的众数为最高矩形底边中点对应的横坐标，为2 2.52.252+=中位数是频率为0.5时，对应的样本数据，由于(0.080.160.300.44)0.50.49+++⨯=，故中位数为0.0120.5 2.020.25+⨯=． 7答案：A解析：设方格边长为x ，则221()39x x x -≤⇒≤．8答案：C解析：此几何体为半个圆锥与半个圆柱的组合体，体积1110[4241]233V πππ=⨯+⨯=．9答案：A解析：()()CD xOA yBC xOA y OC OB x y OA yOC=+=+-=++u u ur u u u r u u u r u u u r u u u r u u u r u u u r u u u r设1OA =，建立如图所示坐标系，则1(,12CD =-+u u u r(1,0)OA =-u u u r，1(,22OC =-u u ur ，故3x y +=10答案：C解析：由题2()log f x x C -=（C 为常数），则()f x 故22[()log ]()log 3f f x x f C C C -==+=，得2C =，故2()log 2f x x =+，记21()()()2log ln 2g x f x f x x x '=--=-在(0,)+∞上为增函数且112ln 21(1)0,(2)10ln 22ln 22ln 2g g -=-<=-=>, 故方程()'()2f x f x -=的解所在的区间是（1，2）． 11答案：15- 12答案：5 解析：由题意，得：5,016,18,2n k n k n k ==⇒==⇒==4,32,41,5n k n k n k ⇒==⇒==⇒==⇒终止当2n =时，执行最后一次循环；当1n =时，循环终止，这是关键，输出5k =． 13答案：解析：2222222(ln ln ln )[2(1)(1)](2ln ln ln )x y z x y z +++-+-≥-- 14答案：（1）1n a =-；（21-解析：（Ⅰ）若a=时，11a ==-,则21a ===．（Ⅱ）当13a >时，由n a a =知，1a <，所以1a a a =〈〉=，21a a =〈〉，且1(1,3)a ∈． ①当1(1,2)a∈时，211a a a 1=〈〉=-，故1112a a a -=⇒=（a =舍去）②当1[2,3)a∈时，212a a a 1=〈〉=-，故21a a a1-=⇒=（1a =舍去）综上，1a =-或1215解析：将2sin 8cos 0ρθθ-=化为普通方程即28y x =，得(2,0)F 16答案：12解析：作两圆的公切线MDE ，连结AO ，CO '，则2AB AC AM =g 所以222AB AM AC AC AM AM AM==g 由弦切角定理知2AOM EMA ∠=∠，2CO M EMA '∠=∠，则AOM CO M '∠=∠,AO CO 'P , 所以434ACOO AM AO '-==，即12AB AM ==.17答案：（1）因为m n ⊥u r r，所以cos cos sin sin 02B C B C -+-=即()cos B C +=A B C π++=，所以cos()cos B C A +=-所以cos 24A A π==． 4分（2）由3,44A C Bππ==-，E故73sin cos()sin cos()sin )126226B C B B B B B πππ+-=+-=+=+由3(0,)4B π∈cos()4B C π-+最大值时，3B π=． 8分由正弦定理，2sin sin a b A B==，得b =故1sin sin()243ab C ππ=+= 12分18答案：（Ⅰ）比赛进行4局结束，且乙比甲多得2分即头两局乙胜一局，3,4局连胜，则所求概率为1212114333381P C =⋅⋅⋅=. 4分（Ⅱ）由题意知，ξ的取值为2,4,6. 则22215(2)()()339P ξ==+=，12122212212120(4)()()33333381P C C ξ==+=1221216(6)()3381P C ξ===故ξ的分布列为 10分则520162662469818181E ξ=⨯+⨯+⨯=12分19解：（I ）当13t =时，//PA 平面MQB 证明：连AC 交BQ 于N ，连MN ．由//AQ BC 可得，ANQ BNC ∆∆∽，12AQ AN BC NC ∴==，所以13AN AC =．若13t =，即13PM AN PC AC==， //PA MN ∴由MN ⊂平面PAC ，故//PA 平面MQB ． 4分（II ）由PA=PD=AD=2， Q 为AD 的中点，则PQ ⊥AD 又平面PAD ⊥平面ABCD ，所以PQ ⊥平面ABCD ，连BD ，∵四边形ABCD 为菱形，∴AD=AB ，由 ∠BAD=60°得△ABD 为正三角形，又∵Q 为AD 中点， ∴AD ⊥BQ 8分以Q 为坐标原点，分别以QA 、QB 、QP 所在的直线为,,x y z 轴，建立如图所示的坐标系，则各点坐标为A （1，0，0），B （3,0），Q （0，0，0），P （0，03）设平面MQB 的法向量为()z y x ,,=，可得00,//,00n QB n QB PA MN n MN n PA ⎧⎧⋅=⋅=⎪⎪∴⎨⎨⋅=⋅=⎪⎪⎩⎩r u u u r r u u u r Q r u u u u r r u u u r ，⎪⎩⎪⎨⎧=-=0303z x y 令z=1，解得(3,0,1)n =r 取平面ABCD 的法向量()3,0,0=，设所求二面角为θ，则21cos ==θ 故二面角M BQ C --的大小为60°． 12分20解答： (Ⅰ)方法1：由2n ≥时，11122333n n n a a --=+-得，11121(1)33n n n a a --+=++两边同时乘以13n -得，1213(1)3(1)2n n n n a a ---+=++，即2n ≥时，12n n b b -=+故{}n b 是公差为2的等差数列．又01322b =⨯=，所以22(1)2n b n n =+-=． 6分方法2：2n ≥时，12113(1)3(1)n n n n n n b b a a -----=+-+，代入11122333n n n a a --=+-整理得12n 11111213()3(1)2333n n n n n n b b a a -------=++-+=，故{}nb 是公差为2的等差数列． (Ⅱ)由(Ⅰ)得，13(1)2n n n b a n -=+=，故1123n n a n -+=，所以12(1)133(1)1313n n n S -==-- 8分则111111323331111(3)313333n n nn nn n nm S m S m m m m --+----==-=--------因为13113131m n m mn S m S m +-<=--++，得21(3)3131n m m >--+*(3)310,1,2n m m N m -->∈∴=Q当1m =时，2112314n n >⇒=⋅-；当2m =时，211,23110n n >⇒=- 综上，存在符合条件的所有有序实数对(,)m n 为：(1,1),(2,1),(2,2)． 12分 21解答：（Ⅰ）由24y x =的准线为1x =-，2512A AF x ∴=+=，故记3(2A 又1(1,0)F -，所以12752622a AF AF =+=+=，故椭圆为22198x y +=． 3分（Ⅱ）由22198x y +=知，y =3sin ()26x t t ππ=-≤≤1S ==62(3sin )t ππ-=⎰262cos tdt ππ-=62(1cos2)t dtππ-+621sin 2)|24x x ππ-=+=+；3322204()|3S x ===根据对称性， “盾圆C”的面积为122()2S S -=-． 7分（Ⅲ）设过2F 的直线为1(0)x my m =+≠，(,)(,)(,)(,)M M N N G G H H M x y N x y G x y H x y 、、、联立221198x my x y =+⎧⎪⎨+=⎪⎩，得22(89)16640m y my ++-=，则2216896489M H M H m y y m y y m -⎧+=⎪⎪+⎨-⎪=⎪+⎩联立214x my y x=+⎧⎨=⎩，得2440y my --=，则44N G N G y y m y y +=⎧⎨=-⎩由M N G H P P '、、、、、共线，所以2222N G M H M HN G y y MH PF y y y y NG P F y y +-⋅=⋅+'-代入韦达定理整理得，222431689MH PF mm NG P F m ⋅=='+故22MH PF NG P F ⋅'为定值3． 13分22答案：（Ⅰ）1a =时，()ln (1)ln(1)f x x x x x =+--，(01x <<)，则()ln ln(1)ln 1x f x x x x '=--=-．令()0f x '=，得12x =．当102x <<时，()0f x '<，()f x 在1(0,)2是减函数，当112x <<时，()0f x '>，()f x 在1(,1)2是增函数，所以 ()f x 在12x =时取得最小值，即11()ln22f =．（4分）（Ⅱ）因为 ()ln ()ln()f x x x a x a x =+--，所以()ln ln()lnx f x x a x a x'=--=-．所以当2a x =时，函数()f x 有最小值．∀x 1，x 2∈R +，不妨设12x x a +=，则 121211221111ln ln ln ()ln()2ln()22x x x x x x x x x x a x a x +++=+--≥⋅[]1212()ln()ln 2x x x x =++-．（8分）（Ⅲ）（证法一）数学归纳法ⅰ)当1n =时，由（Ⅱ）知命题成立． ⅱ）假设当n k =( k ∈N *)时命题成立，即若1221k x x x +++=L ，则112222ln ln ln ln 2k k k x x x x x x +++≥-L ．当1n k =+时，1x ，2x ，…，121k x +-，12k x +满足 11122121k k x x x x ++-++++=L ．设11111122212122()ln ln ln ln k k k k F x x x x x x x x x ++++--=++++L ，由（Ⅱ）得11111212212212()()ln[()ln 2]()ln[()ln 2]k k k k F x x x x x x x x x ++++--≥++-++++-L=111111212122122122()ln()()ln()(...)ln 2k k k k k x x x x x x x x x x x +++++--++++++-+++L =11111212212212()ln()()ln()ln 2k k k k x x x x x x x x ++++--++++++-L ．由假设可得 1()ln 2ln 2ln 2k k F x +≥--=-，命题成立．所以当 1n k =+时命题成立．由ⅰ)，ⅱ）可知，对一切正整数n ∈N *，命题都成立，所以若211nii x==∑，则21ln ln 2nni ii x x=≥-∑ *(,)i n ∈N ．（13分）（证法二）若1221n x x x +++=L ，那么由（Ⅱ）可得112222ln ln ln n n x x x x x x +++L1212212212()ln[()ln 2]()ln[()ln 2]n n n n x x x x x x x x --≥++-++++-L 1212122122122()ln()()ln()(...)ln 2n n n n n x x x x x x x x x x x --=++++++-+++L 1212212212()ln()()ln()ln 2n n n n x x x x x x x x --=++++++-L12341234212212()ln()()ln()2ln 2n n n n x x x x x x x x x x x x --≥+++++++++-L121222(...)ln[()ln 2](1)ln 2n n x x x x x x n ≥≥++++++---L L ln 2n =-．（14分）。

湖北省黄冈中学高三数学11月月考试题(理)

湖北省黄冈中学2009届高三11月月考数学试题（理）命题人：陈晓洁★请将答案填写在答题卡的相应位置上★一、选择题：本次题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．函数sin 2y x =的一个增区间是（） A ．,22ππ⎡⎤-⎢⎥⎣⎦ B ．,44ππ⎡⎤-⎢⎥⎣⎦ C ．0,2π⎡⎤⎢⎥⎣⎦ D ．,02π⎡⎤-⎢⎥⎣⎦2．已知向量(2,3)=a ，(1,2)=-b ，若m n +a b 与2-a b 共线，则nm等于（） A ．2-；B ．2C ．21-D ．213．已知(3,1),(2,1)AB =-=n ，且7AC ⋅=n ，则BC ⋅=n （） A ．2- B ．0 C ．2-或2 D ． 2 4．设1tan10,1tan10a b +==- （）A ．222a b a b +<<B ．222a b b a +<<C ．222a b a b +<<D ．222a b b a +<< 5．已知120a a >>，则使得2(1)1i a x -<(1,2)i =都成立的x 取值范围是（） A ．11(0,)a B ．12(0,)a C ．21(0,)a D. 22(0,)a6．由下列条件解ABC ∆，其中有两解的是（） A ．20,45,80b A C === B ．30,28,60a c B === C ．14,16,45a c A === D ．12,15,120a c A ===7．若向量,,a b c 两两的夹角相等，且满足1,2,4===a b c ，则=a +b+c （） A ．7 B ．7CD ．78．已知两不共线向量(cos ,sin )αα=a ，(cos ,sin )ββ=b ，则下列说法不正确．．．的是（） A ．()()+⊥-a b a b B ．a 与b 的夹角等于αβ- C ．2++->a b a bD ．a 与b 在+a b 方向上的投影相等9．已知()g x 是定义在R 上的二次函数，2,1(),1x x f x x x ⎧≥⎪=⎨<⎪⎩，若[]()f g x 的值域是[)0,+∞，则()g x 的值域是（） A ．(][),11,-∞-+∞ B ．(][),10,-∞-+∞C ．[)0,+∞D ．[)1,+∞10．关于x 的不等式22cos lg(9)cos lg(9)x x x x +-<+-的解集为（）A．(3,(22,3)-- B．()(,22)22ππ--C．(- D ．(3,3)-二、填空题：本大题共5小题，每小题5分，共25分． 11x >的解集为____________． 12．函数11()sin()cos 633f x x x π=-+图象的相邻的两个对称中心的距离是__________． 13．等差数列{}n a 中，351024a a a ++=，则此数列的前13项的和等于___________． 14．如图，半圆的直径6AB =，O 为圆心，C 为半圆上不同于A B 、的任意一点，若P 为半径OC 上的动点，则()PA PB PC +⋅的最小值是__________． 15．若对任意的[]0,1x ∈1kx ≤-总成立，则实数k 的取值范围是______．P CBA第14题图三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤.16．（本小题满分12分）已知R A B ∈,，且22sin 2cos 2cos22y A B A B =+-+．（1）若A B C ,,为ABC ∆的三内角，当y 取得最小值时，求C ；（2）当2A B π+=时，将函数22sin 2cos 2cos22y A B A B =+-+的图象按向量p 平移后得到函数2cos2y A =的图象，求出所有满足条件的向量p ．17．（本小题满分12分）数列{}n a 的前n 项和为1,1n S a =且*121()N n n a S n +=+∈．（1）求数列{}n a 的通项公式；（2）等差数列{}n b 的各项均为正数，其前n 项和为n T ，315T =，又112233,,a b a b a b +++ 成等比数列，求n T ．18．（本小题满分12分）（1）设x 是正实数，求证：233(1)(1)(1)8x x x x +++≥；（2）若R x ∈，不等式233(1)(1)(1)8x x x x +++≥是否仍然成立？如果成立，请给出证明；如果不成立，请举出一个使它不成立的x 的值．19．（本小题满分12分）定义12,,,n x x x 的“倒平均数”为*12()N nn n x x x ∈+++，已知数列{}n a 前n 项的“倒平均数”为124n +．（1）记*()1N nna c n n =∈+，试比较n c 与1n c +的大小；（2）是否存在实数λ，使得当x λ≤时，2()401na f x x x n =-+-≤+对任意n N *∈恒成立？若存在,求出最大的实数λ；若不存在，说明理由．20．（本小题满分13分）甲、乙两公司同时开发同一种新产品，经测算，对于函数(),()f x g x ，当甲公司投入x 万元作宣传时，若乙公司投入的宣传费小于()f x 万元，则乙公司对这一新产品的开发有失败的风险，否则没有失败的风险；当乙公司投入x 万元作宣传时，若甲公司投入的宣传费小于()g x 万元，则甲公司对这一新产品的开发有失败的风险，否则没有失败的风险．（1）若(0)10f =，(0)20g =，试解释它们的实际意义；（2）设()104xf x =+，()20g x =，甲、乙公司为了避免恶性竞争，经过协商，同意在双方均无失败风险的情况下尽可能少地投入宣传费用，问甲、乙两公司应投入多少宣传费？21．（本小题满分14分）已知定义在[]0,1的函数()f x 同时满足以下三条：①对任意的[]0,1x ∈，总有()0f x ≥；②(1)1f =；③当12120,0,1x x x x ≥≥+≤时，总有1212()()()f x x f x f x +≥+成立．（1）函数()21x g x =-在区间[]0,1上是否同时适合①②③？并说明理由；（2）假设存在[]0,1a ∈，使得[]()0,1f a ∈且[]()f f a a =，求证：()f a a =．答案1 ～ 5 BCDAB 6 ～ 10 CDBCB11答案：(,0)-∞ 12答案：3π 13答案：1314答案： 92- 15答案：⎛-∞ ⎝⎦16解答：（1）221(sin 2(cos2)122y A B =-+-+由题，sin 2,1cos 22A B ⎧=⎪⎪⎨⎪=⎪⎩6A π=或3π，6B π=或56π，又A B π+<，故2C π=或23π．（2）当2A B π+=时，22,cos2cos2A B B A π+==-，cos 2232cos(2)33y A A A π∴=+=++按向量p 平移后得到函数2cos2y A =的图象，故(,3)()6Z k k ππ=+-∈p ．17解答：（1）当2n ≥时，11(21)(21)n n n n a a S S +--=+-+，即有13n n a a += 又21121213a S a =+=+=，{}n a ∴是公比为3的等比数列，且11a =，故13n n a -=．（2）由（1），1231,3,9a a a ===，又312313215,210T b b b b b b =++=∴+==，依题112233,,a b a b a b +++成等比数列，有131164(1)(9)(1)(19)b b b b =++=+-，解得13b =或15，因{}n b 的各项均为正数，13,2b d ∴==，故23(1)2n T n n n n n =+-=+． 18解答：（1）证明：x是正数，由重要不等式知，2312,1x x x x +≥+≥+≥故233(1)(1)(1)28x x x x x +++≥⋅（当1x =时等号成立）．（2）若R x ∈，不等式233(1)(1)(1)8x x x x +++≥仍然成立．证明：由（1）知，当0x >时，不等式成立；当0x ≤时，380x ≤，而2322222213(1)(1)(1)(1)(1)(1)(1)(1)()024x x x x x x x x x x ⎡⎤+++=++-+=++-+≥⎢⎥⎣⎦此时不等式仍然成立．19解：（1）记数列{}n a 的前n 项和为n S ，则依题有124n n S n =+ 2(24)24n S n n n n ∴=+=+，故116(1)42(2)n n n S n a S S n n -==⎧=⎨-=+≥⎩ 故数列的通项为42n a n =+．故422411n n c n n +==-++，易知，1n n c c +<．（2）假设存在实数λ，使得当x λ≤时，2()401na f x x x n =-+-≤+对任意N n *∈恒成立，则241n a xx n -+≤+对任意N n *∈都成立，，24x x -+≤1min ()3111n a a n ==++，得2430x x -+≥，有1x ≤或3x ≥．故存在最大的实数1λ=符合题意．20解答：（1）(0)10f =表示当甲公司不投入宣传费时，乙公司要避免新产品的开发有失败风险，至少要投入10万元宣传费；(0)20g =表示当乙公司不投入宣传费时，甲公司要避免新产品的开发有失败的风险，至少要投入20万元宣传费.（2）设甲公司投入宣传费x 万元，乙公司投入宣传费y 万元，若双方均无失败的风险，依题意，当且仅当1()104()20y f x x x g y ⎧≥=+⎪⎨⎪≥=⎩成立．故120)104y ≥+，则4600,15)0y ≥∴≥4故16,2024y x ≥≥≥即在双方均无失败风险的情况下尽可能少地投入宣传费用，甲公司应投入24万元宣传费，乙公司应投入16万元的宣传费用．21解答：（1）显然()21xg x =-，在[0，1]满足①()0g x ≥；满足②(1)1g =；对于③，若12120,0,1x x x x ≥≥+≤，则[]121212121212()()()2121212221x x x x x x x x g x x g x g x ++⎡⎤+-+=----+=--+⎣⎦ 21(21)(21)0x x =--≥ ．故()g x 适合①②③．（2）由③知，任给[]0,1m n ∈、时，当m n >时，()()()f m f n f m n -=-由于(]01,0,1n m m n ≤<≤∴-∈，()()()0f m f n f m n -=-≥所以()()f m f n ≥ 若()a f a <，则()[()]f a f f a a ≤= 前后矛盾若()a f a >，则()[()]f a f f a a ≥= 前后矛盾故()a f a =得证．。

湖北省黄冈中学等八所著名高中2013届高三第一次联考理科数学试题以及答案详解

湖北省鄂南高中、荆州中学、华师一附中、孝感高中、黄冈中学、襄阳四中、黄石二中、襄阳五中八所校2013届高三第一次联考数学试题（理）考试时间：2012年12月21日下午15:00——17:00 试卷满分：150分一、选择题：本大题共10小题，每题5分，共50分.在每小题给出的四个选项中，只有一个符合一目要求的.1.集合A={}1610-2-+=x x y x ，集合B ={}A x x y y ∈=,log 2，则=⋂B C A R ( )A .[]32，B .(]21，C .[]83， D.(]83， 2.若命题p:[]012,3,3-0200≤++∈∃x x x ，则对命题p 的否定是（）A []012,3,3-0200>++∈∀x x xB ()()012,,33-,-0200>+++∞∞∈∀x x xC . ()()012,,33-,-0200≤+++∞∞∈∃x x x D. []012,3,3-0200<++∈∃x x x 3.某实心机器零件的三视图如图所示，该机器零件的体积为（）A .π236+B .π436+C .π836+D .π1036+4.等比数列{}n a 各项为正，453-,,a a a 成等差数列.n S 为{}n a 的前n 项和，则36S S =（） A .2 B .87 C .89 D .45 5.如图MN 是半圆O 的直径，MN=2，等边三角形OAB 的顶点A 、B 在半圆弧上，且AB//MN ，点P 半圆弧上的动点，则PB PA ⋅的取值范围是（）A .⎥⎦⎤⎢⎣⎡+32323，B .⎥⎦⎤⎢⎣⎡233-23，C .⎥⎦⎤⎢⎣⎡+3233-23，D .⎥⎦⎤⎢⎣⎡2323-3， 6.若双曲线1222=+m y x 的一条渐近线的倾斜角⎪⎭⎫ ⎝⎛∈30πα，，则m 的取值范围是（） A .()0,3- B .()0,3- C .()3,0 D .）（0,33- 7.在ABC ∆中，,3,23sin )(sin AC BC C B A ==+-则=∠B （）A .3πB .6πC .36ππ或 D.2π 8.已知R c b a ∈,,，则1632222=++c b a 是[]1,1-∈++c b a 的（）A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件9.若实数y x ,满足：⎩⎨⎧-≤≥-2502x y x y ，则y x 2+的最大值是（）A .3B .52C .5D 5510.已知函数⎩⎨⎧<≥=)0()-(log )0(3)(3x x x x f x ，函数)()()()(2R t t x f x f x g ∈++=.关于)(x g 的零点，下列判断不正确．．．的是（） A .若)(,41x g t =有一个零点 B .若)(,412-x g t <<有两个零点 C .若)(,2-x g t =有三个零点 D .若)(,2-x g t <有四个零点二、填空题：本大题共5小题，每小题5分，共25分.（一）必做题（11-14题）11.已知复数i i i z ),43()21(-÷+=为虚数单位，则z 的共轭复数是 .12.函数x x x f ln )(=，)41(),31(),2(f c f b f a ===，则c b a ,,从小到大的排列是 .13.阅读如图所示程序框图，运行相应程序，输出结果n = .14.如图把函数 ,6)(,)(321x x x f x x f -==,50401206)(,1206)(7534533x x x x x f x x x x f -+-=+-=36288050401206)(97535x x x x x x f +-+-=，依次称为x x f sin )(=在[]π，0上的第1项、2项、3项、4项、5项多项式逼近函数.以此类推，请将x x f sin )(=的n 项多项式逼近函数)(x f n 在横线上补充完整：∑-==121)(n k n x f ( ) ）（+∈N k n ,. （二）选做题（请考生在15、16两题中任选一题作答.如果全选，则按第15题作答结果计分）15.（选修4-1：几何证明选讲）如图过点A 作圆O 的一条切线AB ，切点为B ，OA 交圆O 于点C .若1,==BC CA OC ,则=AB .16.(选修4-4：坐标系与参数方程）曲线C 的极坐标方程为：θθρsin cos -=，化成普通方程为 .三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.A ．（本小题满分12分）函数1)sin()(-+=ϕwx A x f ,00>>w A ，（ϕ)2π<的最大值为2，其图像相邻两个对称中心之间的距离为2π，且经过点)121,12-π（. (1)求函数)(x f 的单调递增区间；(2)若57)(=αf ，且∈α⎥⎦⎤⎢⎣⎡412ππ，，求)62(πα+f 的值.18.（本小题满分12分）已知数列}{n a 满足：，32-1=a 4332-1+-=+n n n a a a ）（+∈N n . （1）证明数列}11{+n a 是等差数列，并求{}n a 的通项公式；第一次八校联考数学（理）试题第3页（共5页）（2）数列}{n b 满足：13+=n nn a b ）（+∈N n ，求}{n b 的前n 项和n S .19.（本小题满分12分）如图I ，平面四边形ABCD 中，，，，421506000====∠=∠BC AD AB ABC A 把ABD ∆沿直线BD 折起，使得平面⊥ABD平面BCD ，连接AC 得到如图II 所示四面。

湖北省黄冈市2013届高三年级数学调研理科试题

湖北省黄冈市2013届高三年级数学调研理科试题注意事项：1．答第一卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试卷上。

3．考试结束后，考生将本试卷和答题卡一并交第Ⅰ卷一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设,a R ∈b ，已知命题:p a b =；命题222:22a b a bq ++⎛⎫≤⎪⎝⎭，则p 是q 成立的（）A ．必要不充分条件B ．充分不必要条件C ．充分必要条件D ．既不充分也不必要条件2．集合1{|0}1x A x x -=<+、{|B x x b a =-<，若"1"a =是""A B ⋂≠∅的充分条件，则b 的取值范围可以是（） A ．20b -≤< B ．02b <≤ C ．31b -<<- D ．12b -≤<3．如果b a >>0且0>+b a ，那么以下不等式正确的个数是 ①ba 11< ②ba 11> ③33ab b a < ④23ab a < ⑤32b b a <A ．2B ．3C ．4D ．54．已知a 1＞a 2＞a 3＞0，则使得2(1)1(123)i a x i -<=，，都成立的x 取值范围是（）A ．110a ⎛⎫⎪⎝⎭，B ．120a ⎛⎫ ⎪⎝⎭，C ．310a ⎛⎫ ⎪⎝⎭，D ．320a ⎛⎫ ⎪⎝⎭，5．函数f (x（）A ．25B ．2C ．12D ．1 6．函数()f x =（）A ．[)+∞-,3log 22B ．()3,-∞-C ．[)3,3log 22-D ．[)3,3log 22--7．若,,0a b c >且222412a ab ac bc +++=，则a b c ++的最小值是（）A ．B ．3C ．2D 8． 1 0() 1 0x f x x ≥⎧=⎨-<⎩ 则不等式x ＋(x ＋2)f (x ＋2)≤5 的解集是（）A ．RB ．32,2⎡⎤-⎢⎥⎣⎦C ．(],1-∞D ．3,2⎛⎤-∞ ⎥⎝⎦9．已知不等式1()()9ax y x y++≥对任意正实数,x y 恒成立，则正实数a 的最小值为（）A ．8B ．6C ．4D ．210．在R 上定义运算(1)x y x y ⊗=-，若不等式()()1x a x a -⊗+<对任意实数x 成立，则（）A ．11a -<<B ．02a <<C ．1322a -<< D ．3122a -<< 第Ⅱ卷二、填空题：本大题共5小题，每小题4分，共20分．把答案填在横线上．11．某公司一年购买某种货物400吨，每次都购买x 吨，运费为4万元/次，一年的总存储费用为4x 万元，要使一年的总运费与总存储费用之和最小，则x = __吨． 12．不等式112x x ->+的解集是__________． 13． 2*,,,230,y x y z R x y z xz∈-+=的最小值为．14．设a,b 是两个实数,给出下列条件:①a+b >1； ②a+b=2；③a+b >2；④a 2+b 2>2；⑤ab >1，其中能推出:“a 、b 中至少有一个实数大于1”的条件是___________ 15．不等式224122x x +-≤的解集为．三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．16．（本小题满分12）设2()32.0f x ax bx c a b c =++++=若,(0)0,(1)0f f >>，求证：（1）a ＞0且21ba-<<-；（2）方程()0f x =在（0，1）内有两个实根 17．（本小题满分12分）（08年江苏选修）设a ，b ，c 为正实数，求证：333111a b c +++abc ≥18．（本小题满分14分）已知()()21,,,a x b x xx ==+- ，解关于x 的不等式221a b m a b ⎛⎫∙+>+ ⎪∙⎝⎭（其中m 是满足2m ≤-的常数）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。