考研高数基本初等函数图像与性质
最新(考研高数)基本初等函数图像与性质
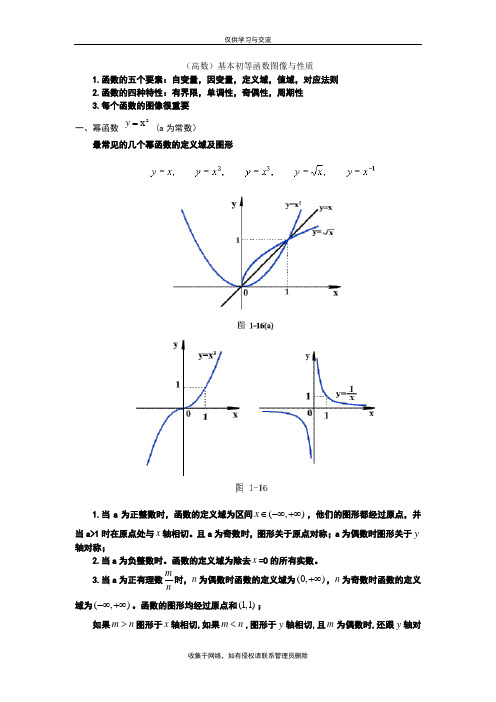
(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数 a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n均为奇数时,跟原点对称。
4.当a为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数。
二、指数函数xay=(a是常数且01a a>≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数xyalog=(a是常数且01a a>≠,),(0,)x∈+∞;四、三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y , 反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数xy arctan=,),(+∞-∞∈x,)2,2(ππ-∈y,反余切函数xy cotarc=,),(+∞-∞∈x,),0(π∈y.Αα:阿尔法 Alpha Ββ:贝塔 BetaΓγ:伽玛 Gamma Δδ:德尔塔 DelteΕε:艾普西龙 Epsilon ζ :捷塔Zeta Ζη:依塔 Eta Θθ:西塔 Theta Ιι:艾欧塔 IotaΚκ:喀帕 Kappa ∧λ:拉姆达 LambdaΜμ:缪 Mu Νν:拗 NuΞξ:克西 Xi Οο:欧麦克轮 Omicron∏π:派 Pi Ρρ:柔 Rho∑σ:西格玛 Sigma Ττ:套 TauΥυ:宇普西龙 Upsilon Φφ:fai PhiΧχ:器 Chi Ψψ:普赛 PsiΩω:欧米伽 Omega七年级下册道德与法治第一次月考试卷班级姓名一.单选题(共18小题,每小题2分,共36分)1.欣赏漫画《宅童》,你最想对“宅童”说的是()①封闭自己,脱离现实世界,会使自己陷入孤立②这种把自己“宅”起来的做法,会使自己的人际关系萎缩③应该保持积极开放的态度,接触更多的人④在虚拟世界中获得成就感也能形成良好的性格,人生才更精彩。
六大基本初等函数图像及其性质
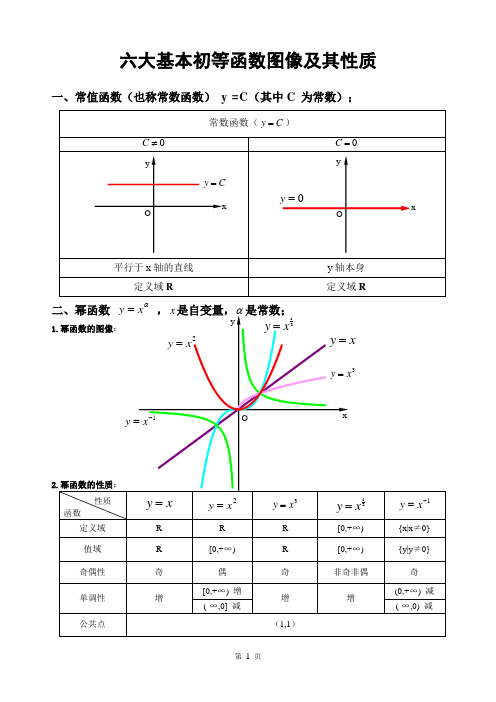
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2xy =3x y =21xy =1-=x y定义域 R RR [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=x y 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性 在),(∞+∞-是增函数在),(∞+∞-是减函数1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像及其性质(总12页)

六大基本初等函数图像及其性质(总12页)抛物线函数 y = x^2- 图像为开口朝上的抛物线,顶点在原点(0,0)- 奇函数,即f(-x) = -f(x)- 定义域为全体实数,值域为[0, +∞)- 极值点为顶点(0,0),不存在最大值和最小值- 函数单调递增且无拐点反比例函数 y = 1/x-tu.grid正比例函数 y = x- 图像为平面直线,通过原点(0,0)- 定义域为全体实数,值域为全体实数- 函数单调递增,无拐点- 斜率代表变化率,斜率越大表示变化速度越快,斜率为正则表示函数单调增加,斜率为负则表示函数单调减少指数函数 y = a^x (a>0且a≠1)- 图像为上凸曲线,通过点(0,1)- 定义域为全体实数,值域为(0,+∞)- 当a>1时,函数单调递增;当0<a<1时,函数单调递减- 随着自变量x的增大,函数值加速增大或减小对数函数y = logₐ(x) (a>0且a≠1)- 反指数函数,图像和指数函数的图像呈镜像关系- 定义域为(0,+∞),值域为全体实数- 当a>1时,函数单调递增;当0<a<1时,函数单调递减- 随着自变量x的增大,函数值增长速度逐渐变慢三角函数 y = sin(x), y = cos(x), y = tan(x)- 正弦函数图像为周期性上下波动的连续曲线,取值范围[-1, 1] - 余弦函数图像为周期性波动的连续曲线,取值范围[-1, 1]- 正弦函数、余弦函数的定义域为全体实数,值域为[-1, 1]- 正弦函数、余弦函数是周期性函数,周期为2π- 正切函数图像为周期性波动的连续曲线,定义域为实数集合-{(2n + 1)π/2 | n∈Z},值域为全体实数这些基本初等函数的图像和性质对数学的学习和应用有着重要的作用,掌握这些函数的图像及其性质,有助于理解数学问题的规律,并能够在实际问题中进行分析和求解。
高数总结:基本初等函数图像及其性质
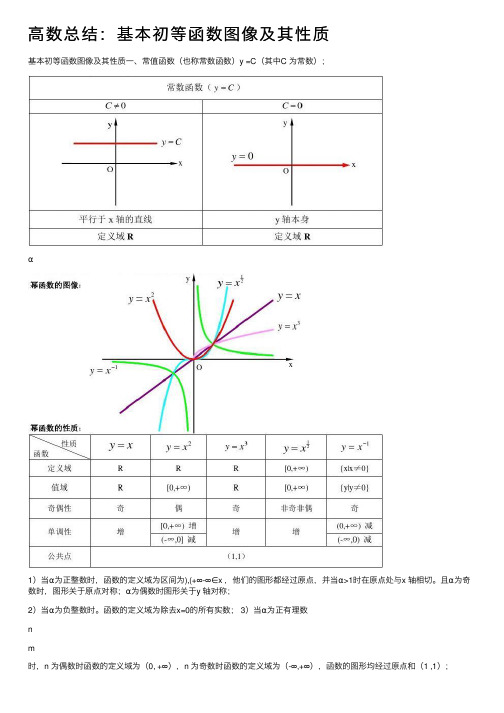
⾼数总结:基本初等函数图像及其性质基本初等函数图像及其性质⼀、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数n4)如果m>n 图形于x 轴相切,如果m5)当α为负有理数时,n 为偶数时,函数的定义域为⼤于零的⼀切实数;n 为奇数时,定义域为去除x=0以外的⼀切实数。
三、指数函数xa y =(x 是⾃变量,a 是常数且0>a ,1≠a ),定义域是R ;[⽆界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上⽅; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的⼤⼩⽐较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ?=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越⼤,xa y =的图像越靠近y 轴;b.2.当10<的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=?m n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m n m(2))1,,,0(11*>∈>==-n Z n m a a amnm nm yxf x xxx g ?=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [⽆界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式⼦N a log 叫做对数式。
2020年(考研高数)基本初等函数图像与性质
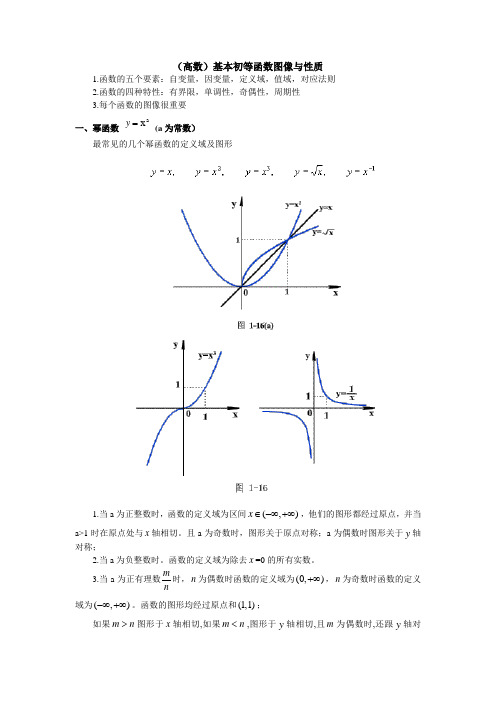
(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数 a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n 时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n均为奇数时,跟原点对称。
4.当a为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数。
二、指数函数xay=(a是常数且01a a>≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数xyalog=(a是常数且01a a>≠,),(0,)x∈+∞;四、三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y , 余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数 反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y , 反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数xy arctan=,),(+∞-∞∈x,)2,2(ππ-∈y,反余切函数xy cotarc=,),(+∞-∞∈x,),0(π∈y.Αα:阿尔法Alpha Ββ:贝塔BetaΓγ:伽玛Gamma Δδ:德尔塔DelteΕε:艾普西龙Epsilon ζ :捷塔Zeta Ζη:依塔Eta Θθ:西塔Theta Ιι:艾欧塔IotaΚκ:喀帕Kappa ∧λ:拉姆达LambdaΜμ:缪Mu Νν:拗NuΞξ:克西Xi Οο:欧麦克轮Omicron ∏π:派Pi Ρρ:柔Rho∑σ:西格玛Sigma Ττ:套TauΥυ:宇普西龙Upsilon Φφ:fai PhiΧχ:器Chi Ψψ:普赛PsiΩω:欧米伽Omega。
6类基本初等函数以及三角函数(考研数学基础)
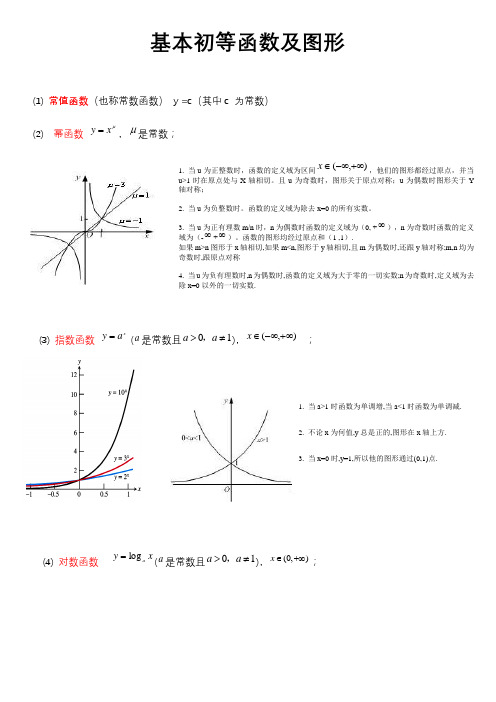
基本初等函数及图形(1) 常值函数(也称常数函数) y =c (其中c 为常数)(2) 幂函数 μx y =,μ是常数;(3) 指数函数 xa y = (a 是常数且01a a >≠,),),(+∞-∞∈x ;(4) 对数函数x y a log =(a是常数且01a a >≠,),(0,)x ∈+∞;1. 当u 为正整数时,函数的定义域为区间),(+∞-∞∈x ,他们的图形都经过原点,并当u>1时在原点处与X 轴相切。
且u 为奇数时,图形关于原点对称;u 为偶数时图形关于Y 轴对称;2. 当u 为负整数时。
函数的定义域为除去x=0的所有实数。
3. 当u 为正有理数m/n 时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞+∞)。
函数的图形均经过原点和(1 ,1).如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n 均为奇数时,跟原点对称4. 当u 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数.1. 当a>1时函数为单调增,当a<1时函数为单调减.2. 不论x 为何值,y 总是正的,图形在x 轴上方.3. 当x=0时,y=1,所以他的图形通过(0,1)点.(5) 三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;1. 他的图形为于y 轴的右方.并通过点(1,0)2. 当a>1时在区间(0,1),y 的值为负.图形位于x 的下方,在区间(1, +∞),y 值为正,图形位于x 轴上方.在定义域是单调增函数. a<1在实用中很少用到/(6)反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数 x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数 x y cot arc =,),(+∞-∞∈x ,),0(π∈y .小结:(a 为任意实数)(正弦函数)正弦函数是奇函数且三角公式汇总一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦:r y =αsin 余弦:r x=αcos 正切:xy=αtan 余切:y x =αcot正割:xr=αsec 余割:y r =αcsc注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如图,与单位圆有关的有向..线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线。
考研数学必备函数图像大全

函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释 (1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$ $cos(pi/2+a)=-sin(a)$ $sin(pi-a)=sin(a)$ $cos(pi-a)=-cos(a)$ $sin(pi+a)=-sin(a)$ $cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$ $tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$ $sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$ $cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$ $cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式 (上面公式反过来就得到了)$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的)$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$$1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:正弦函数余弦函数正切函数余切函数正割函数余割函数直角坐标系中的定义。
六大基本初等函数图像及其性质
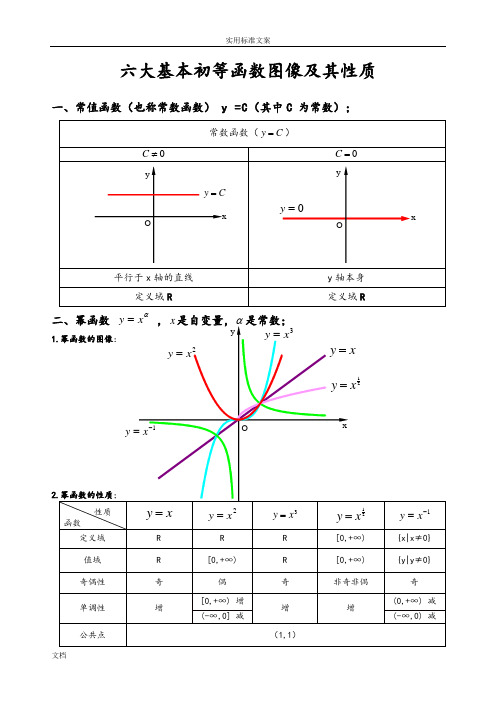
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
基本初等函数图像及性质
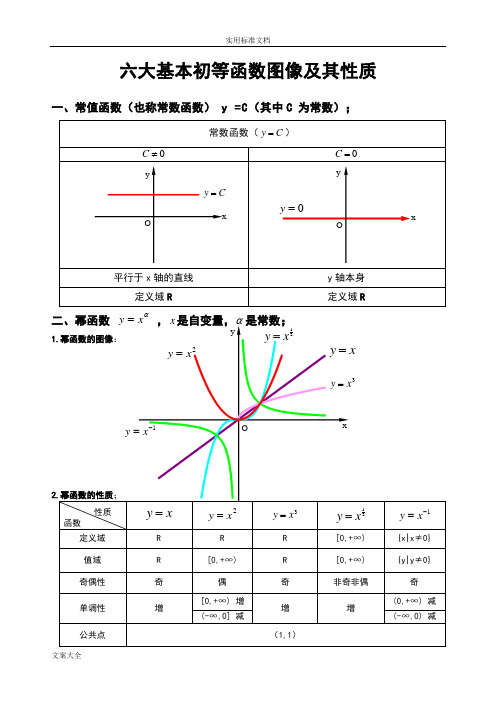
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像及其性质

六大基本初等函数图像及其性质六大基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数。
1. 常数函数:y = c,其中c是一个常数。
常数函数的图像是一条平行于x轴的直线,与y轴相距c个单位。
它没有自变量的限制,函数值始终为常数。
2. 幂函数:y = x^n,其中n是任意实数。
幂函数的图像依赖于指数n的符号及大小。
当n为正数时,随着x的增大,函数值也增大;当n为负数时,随着x的增大,函数值减小。
若n为奇数,图像穿过原点;若n为偶数,图像在原点有一个极小值或极大值。
3. 指数函数:y = a^x,其中a是一个正数且不等于1。
指数函数的图像是递增或递减的曲线。
如果a大于1,函数图像是递增的,如果a在0和1之间,函数图像是递减的。
指数函数没有定义域的限制,但其值范围从0到正无穷大。
4. 对数函数:y = log_a(x),其中a是一个正数且不等于1。
对数函数的图像与指数函数的图像是关于直线y = x对称的。
当x在0到正无穷大之间变化时,函数值从负无穷大逐渐增大到正无穷大。
对数函数的定义域为正实数,值域为负无穷大到正无穷大。
5. 三角函数:包括正弦函数y = sin(x),余弦函数y = cos(x),正切函数y = tan(x),割函数y = sec(x),余割函数y = csc(x),和余切函数y = cot(x)。
三角函数的图像是周期性的波形,沿x 轴变化。
例如,正弦函数和余弦函数的图像是在[-π, π]范围上的曲线。
正弦函数的值域在[-1, 1]之间,余弦函数的值域也在[-1, 1]之间。
6. 反三角函数:包括反正弦函数y = arcsin(x),反余弦函数y = arccos(x),反正切函数y = arctan(x),反割函数y = arcsec(x),反余割函数y = arccsc(x),和反余切函数y = arccot(x)。
反三角函数的图像是由对应的三角函数的图像上截取而来的。
五大基本初等函数性质及其图像

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。
如,,,都是幂函数。
没有统一的定义域,定义域由值确定。
如,。
但在内总是有定义的,且都经过(1,1)点。
当时,函数在上是单调增加的,当时,函数在内是单调减少的。
下面给出几个常用的幂函数:的图形,如图1-1-2、图1-1-3。
图1-1-2图1-1-32.指数函数函数称为指数函数,定义域,值域;当时函数为单调增加的;当时为单调减少的,曲线过点。
高等数学中常用的指数函数是时,即。
以与为例绘出图形,如图1-1-4。
图1-1-43.对数函数函数称为对数函数,其定义域,值域。
当时单调增加,当时单调减少,曲线过(1,0)点,都在右半平面内。
与互为反函数。
当时的对数函数称为自然对数,当时,称为常用对数。
以为例绘出图形,如图1-1-5。
图1-1-54.三角函数有,它们都是周期函数。
对三角函数作简要的叙述:(1)正弦函数与余弦函数:与定义域都是,值域都是。
它们都是有界函数,周期都是,为奇函数,为偶函数。
图形为图1-1-6、图1-1-7。
图1-1-6 正弦函数图形图1-1-7 余弦函数图形(2)正切函数,定义域,值域为。
周期,在其定义域内单调增加的奇函数,图形为图1-1-8图1-1-8(3)余切函数,定义域,值域为,周期。
在定义域内是单调减少的奇函数,图形如图1-1-9。
图1-1-9(4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1-1-10。
图1-1-10(5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11。
图1-1-115.反三角函数反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1-1-12;图1-1-12,为有界函数,在其定义域内为单调减少的非奇非偶函数,图形如图1-1-13;图1-1-13反正切函数,定义域,值域为,为有界函数,在定义域内是单调增加的奇函数,图形如图1-1-14;图1-1-14为有界函数,在其定义域内单调减少的非奇非偶函数。
六大基本初等函数图像及性质
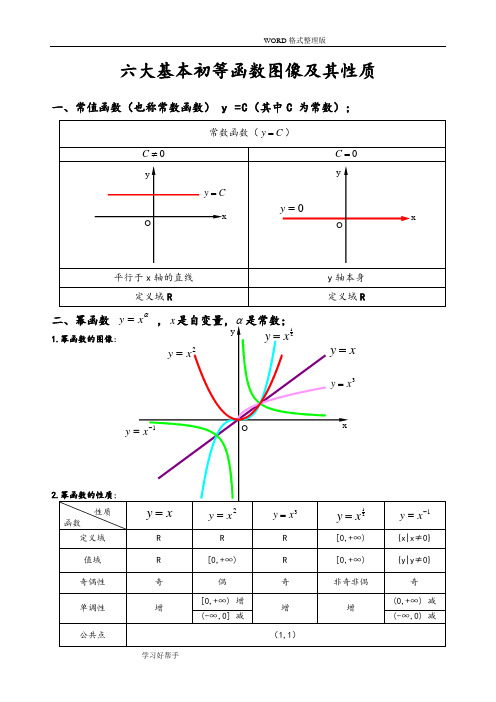
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
函数、基本初等函数的图象与性质

()
A.-1
B.1
C.-2
D.2
解析:∵f(x+5)=f(x)且 f(-x)=-f(x),
∴f(3)=f(3-5)=f(-2)=-f(2)=-2,
f(4)=f(-1)=-f(1)=-1,
故 f(3)-f(4)=(-2)-(-1)=-1.
答案:A
题型三 函数的图象及应用
【例 3】 设函数 f(x)=2x2+xb>x+0,c x≤0, 若 f(-4)= f(0),f(-2)=-2,求关于 x 的方程 f(x)=x 的解的个数. 解:方法一:由 f(-4)=f(0),f(-2)=-2,
∵f(a)=f(b)=f(c),
由图象可知 0<a<1,1<b<10,10<c<12.
∵f(a)=f(b),∴|lg a|=|lg b|,
∴lg a=-lg b,即 lg a=lg1b⇒a=1b,
∴ab=1,10<abc=c<12,故选 C.
答案:C
题型二 函数的性质及应用
【例 2】 (2010·南京市高三调研阅试)设 f(x)是定义在 R 上的奇函数, 且满足 f(x+2)=-f(x),又当 0≤x≤1 时,f(x)=12x,则{x|f(x)= -12}=________. 解析:由已知条件,f(x+4)=-f(x+2)=f(x),则 f(x)是以 4 为周期 的周期函数. 当-1≤x≤0 时,0≤-x≤1,f(x)=-f(-x)=12x, 当 1≤x <3 时,-1≤x-2<1,f(x)=-f(x-2)=-12(x-2).
论
并且有 f (a) f (b) 0,那么,函数 y f (x)在区间a,b内有零点,
即存在c a,b ,使得 f (c) 0,这个c 也就是方程 f (x) 0的根。
4、基本初等函数图像及其性质

基本初等函数图像以及性质一、指数函数的图象及性质函数y =a x (a >0,且a ≠1)图象0<a <1a >1图象特征在x 轴上方,过定点(0,1)当x 逐渐增大时,图象逐渐下降当x 逐渐增大时,图象逐渐上升性质定义域 R 值域(0,+∞)单调性 减增 函数值 变化 规律当x =0时,y =1当x <0时,y >1; 当x >0时,0<y <1当x <0时,0<y <1; 当x >0时,y >1在同一平面直角坐标系中,分别作出指数函数y =a x ,y =b x ,y =c x ,y =d x (a >1,b >1,0<c <1,0<d <1)的图象,如图所示.作出直线x =1,分别与四个图象自上而下交于点A (1,a ),B (1,b ),C (1,c ),D (1,d ),得到底数的大小关系是:a >b >1>c >d >0.根据y 轴右侧的图象,也可以利用口诀:“底大图高”来记忆.考点一 指数函数的图像例1、如果函数在R 上是减函数,那么实数a 的取值范围是( ) A .|a |> B .<|a |< C .|a |> D .|a |<3x a x f )2()(2-=22331、已知指数函数(0,1)x y a a a =>≠在[]1,2上的最大值比最小值大2a,则a =例2、函数y =a x -a -1(a >0且a ≠1)的图象可能是( )A BC D1、函数f (x )=21-x 的大致图象为( )2、函数y=xa x|x|(a>1)的图象大致是()例3、若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是________.1、若方程|3x-1|=k有一解,则k的取值范围为________.2、若函数y=21-x+m的图象不经过第一象限,则m的取值范围为________.考点二指数函数单调性的应用例4、设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系是() A.a<b<c B.a<c<bC.b<a<c D.b<c<a1、已知函数f(x)=a x+b(a>0,a≠1)的定义域和值域都是[-1,0],则a+b=________.2、如果函数y=a2x+2a x-1(a>0,a≠1)在区间[-1,1]上的最大值是14,则a 的值为()A.13B.1C.3 D.13或33、(2017·合肥模拟)若2x+5y≤2-y+5-x,则有() A.x+y≥0 B.x+y≤0C.x-y≤0 D.x-y≥0 对数函数的图象与性质定义域:(0,+∞)在同一平面直角坐标系中,分别作出对数函数y=log a x,y=log b x,y=log c x,y=log d x(a>1,b>1,0<c<1,0<d<1)的图象,如图所示.作出直线y=1,分别与四个图象自左向右交于点A(c,1),B(d,1),C(a,1),D(b,1),得到底数的大小关系是:b>a>1>d>c>0.根据直线x=1右侧的图象,单调性相同时也可以利用口诀:“底大图低”来记忆.考点三对数的图像例5、函数y=2log4(1-x)的图象大致是()1、【2019年高考浙江】在同一直角坐标系中,函数1xya=,1(2log)ay x=+(a>0,且a≠1)的图象可能是2、已知函数y=log a(x+c)(a,c为常数,其中a>0,a≠1)的图象如图所示,则下列结论成立的是()A.a>1,c>1B.a>1,0<c<1C.0<a<1,c>1D.0<a<1,0<c<13、(2018·张家界三模)在同一直角坐标系中,函数f(x)=2-ax,g(x)=log a(x+2)(a>0,且a≠1)的图象大致为()A BC D例6、函数y =log a (x +4)-1(a >0,a ≠1)的图象恒过定点A ,若点A 在直线x m +yn =-1上,且m >0,n >0,则3m +n 的最小值为( )A .13B .16C .11+6 2D .281、(2017·河北五校质监)函数y =log a (x +3)-1(a >0,且a ≠1)的图象恒过定点A ,若点A 在直线mx +n y +2=0上,其中m >0,n>0,则2m +1n 的最小值为 ( )A .2 2B .4 C.52 D.92 考点六 解不等式以及定义域 例7、求不等式的解集 (1)()113log 3<+x (2) 0log )12(21≥-x1、已知集合=⋂>-=<=N M x x N x M x x 则},0)1(log |{},33|{21322A .)23,0(B .)2,23(C .)23,1(D .(0,1)2、设函数f (x )=⎩⎨⎧21-x ,x ≤1,1-log 2x ,x >1,则满足f (x )≤2的x 的取值范围是( )A .[-1,2]B .[0,2]C .[1,+∞)D .[0,+∞)例8、求下列函数的定义域 (1))1(log 121-=x y (2)y =1、【2018年江苏卷】函数f (x )=log 13(4x -5)的定义域为( )A.⎝ ⎛⎭⎪⎫54,+∞ B.⎝ ⎛⎭⎪⎫-∞,54 C.⎝ ⎛⎦⎥⎤54,32 D.⎝ ⎛⎭⎪⎫54,32 2、(2016年全国II 卷高考)下列函数中,其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是( )(A )y =x (B )y =lg x (C )y =2x (D)y =考点七 复合函数的定义域 例9、求下列函数的单调区间(1) xx y 2221-⎪⎭⎫⎝⎛= (2)20.2()log (45)f x x x =-++1、【2017课标II ,文8】函数2()ln(28)f x x x =-- 的单调递增区间是 A.(,2)-∞- B. (,1)-∞- C. (1,)+∞ D. (4,)+∞2、【2014江苏高考】若f (x )=lg(x 2-2ax +1+a )在区间(-∞,1]上递减,则a 的取值范围为( )A .[1,2)B .[1,2]C .[1,+∞)D .[2,+∞)3、(2016·青海平安一中月考)已知函数f (x )=log 12(x 2-ax +a )在区间(2,+∞)上是减函数,则实数a 的取值范围是________.考点八 比较大小例10、(2017·天津一模)已知a =log 25,b =log 5(log 25),c =⎝ ⎛⎭⎪⎫12-0.52,则a ,b ,c的大小关系为( )A .a <b <cB .b <c <aC .c <b <aD .b <a <c1、【2019年高考全国Ⅰ卷理数】已知0.20.32log 0.220.2a b c ===,,,则 A .a b c << B .a c b << C .c a b <<D .b c a <<2、【2019年高考天津理数】已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b << B .a b c << C .b c a <<D .c a b <<3、已知奇函数f (x )在R 上是增函数.若a =-f (log 215),b =f (log 24.1),c =f (20.8),则a ,b ,c 的大小关系为( )A .a <b <cB .b <a <cC .c <b <aD .c <a <b考点九 数形结合例11、已知函数f (x )=log a (2x -a )(a >0且a ≠1)在区间[12,23]上恒有f (x )>0,则实数a 的取值范围是( )A .(13,1) B .[13,1) C .(23,1) D .[23,1)1、(2017·合肥月考)当0<x ≤12时,4x <log a x ,则a 的取值范围是( )A.⎝ ⎛⎭⎪⎫0,22 B.⎝ ⎛⎭⎪⎫22,1C .(1,2)D .(2,2)2、(2016·南京师大附中等四校联考)若函数 f (x )=⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫12x -3,x ≤2,log a x ,x >2(a >0且a ≠1)的值域是[2, +∞),则实数a 的取值范围是________.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(高数)基本初等函数图像与性质
1.函数的五个要素:自变量,因变量,定义域,值域,对应法则
2.函数的四种特性:有界限,单调性,奇偶性,周期性
3.每个函数的图像很重要
一、幂函数 a x =y (a 为常数)
最常见的几个幂函数的定义域及图形
1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;
2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n
时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);
如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称。
4.当a 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x =0以外的一切实数。
二、指数函数 x a y =(a 是常数且01a a >≠,),),(+∞-∞∈x
图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后
用的较多。
三、对数函数
x y a log =(a 是常数且01a a >≠,),(0,)x ∈+∞; 四、三角函数
正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,
余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,
正切函数 x y tan =,2π
π+≠k x ,k Z ∈,),(+∞-∞∈y ,
余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;
五、反三角函数
反正弦函数 x y arcsin =, ]1,1[-∈x ,
]2,2[ππ-∈y , 反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,
反正切函数
x y arctan =,),(+∞-∞∈x ,)2,2(π
π-∈y , 反余切函数x y cot arc =,),(+∞-∞∈x ,),0(π∈y .
Αα:阿尔法 Alpha
Ββ:贝塔 Beta Γγ:伽玛 Gamma
Δδ:德尔塔 Delte Εε:艾普西龙 Epsilon
ζ :捷塔 Zeta Ζ η:依塔 Eta
Θθ:西塔Theta Ιι:艾欧塔Iota
Κκ:喀帕Kappa ∧λ:拉姆达Lambda Μμ:缪Mu Νν:拗Nu
Ξξ:克西Xi Οο:欧麦克轮Omicron ∏π:派Pi Ρρ:柔Rho
∑σ:西格玛Sigma Ττ:套Tau
Υυ:宇普西龙Upsilon Φφ:fai Phi
Χχ:器Chi Ψψ:普赛Psi
Ωω:欧米伽Omega。
