7.图
【人教版地理(2024)七年级上册同步练习】2.1 地图的阅读(含答案)
【人教版地理(2024)七年级上册同步练习】第一节地图的阅读一、单选题1.下列比例尺中最大的是()A.千分之一B.万分之一C.十万分之一D.百万分之一2.下图为某地区中学校园示意图,读图回答下列问题。
(1)图中学校大门的朝向是()方向A.正北B.正南C.正西D.正东(2)该学校的比例尺最可能为()A.1:100B.1:1000C.1:10000D.1:100000 3.在野外考察时不能用来辨别方向的是()A.树干年轮B.北极星C.流星D.指南针4.地图三要素包括()A.方向、颜色、图例B.图例、指向标、符号C.比例尺、符号、图形D.比例尺、方向、图例和注记5.在比例尺为1:500000的地图上,图上4厘米代表实地距离是()A.200千米B.20千米C.2千米D.0.2千米6.下图中缺少了地图三要素中的()A.经纬线B.指向标C.比例尺D.图例二、判断题7.如果在北极点盖一间房,房的四周都是朝南的。
8.任何地图上判定方向都遵循“上北下南、左西右东”的原则。
9.在有指向标的地图上,指向标箭头一般指向南方。
10.比例尺越小,表示的内容越详细。
()11.在有指向标的地图上,指向标指的方向是正南。
12.甲在乙的正西方向。
三、填空题13.地图的三要素:。
14.图幅相等的地图,比例尺越大,表示的实际范围越,图的内容就越。
15.比例尺的三种表示方法是:、、。
16.读“某村平面图”,并回答问题:(1)此图可用来辨别方向,图中A村在B村的方向。
(2)图中公路实地长度为3000米,在图上量得其长度是6厘米,则该图比例尺为(任写一种形式即可)。
17.如果小明站在南极点上,他的正前方是方。
18.地图的基本要素是、、图例和注记。
四、综合题19.把下列比例尺用其他两种形式表示出来。
文字式线段式数字式A图上一厘米代表实地距离5千米B千米C1:1500000 20.学地理,用地理。
在认识地图的时候,老师让同学们在一张A4纸(约20×30厘米)上画出学校平面图,已知校园的长、宽均大约是1000米,据此回答下列问题。
期末卷(冲刺高分卷)2024-2025学年七年级地理上册单元考点梳理分层卷(中图·北京版)(原卷版)

2024-2025学年七年级地理上册单元考点梳理分层卷(中图·北京版)期末卷(冲刺高分卷)(考试时间:60分钟试卷满分:100分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.测试范围:中图·北京版七年级上册5.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本大题共25小题,每小题2分,共50分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)2020年11月24日,“嫦娥五号”探测器从我国海南文昌发射基地出发,计划取回约2千克月球土壤。
这是自1976年苏联“月球24号”任务后,人类第一次从月球采集样品。
图中左图为世界部分卫星发射中心分布图,右图为台风“木恩”移动路径图,据此完成下列1-3小题。
1.海南文昌航天发射基地的经纬度位置是()A.(20°N,110°W)B.(20°S,110°W)C.(20°N,110°E)D.(20°S,110°E)2.关于海南文昌发射中心的描述,正确的是()A.位于西半球、中纬度B.一年有1次太阳直射C.位于北温带,四季分明D.位于热带,终年炎热3.台风“木恩”于2020年7月3日在海南省沿海登陆,成为今年登陆我国的首个台风。
读“木恩”移动路径图,判断其前进方向是()A.自东南向西北B.自东北向西南C.自西南向东北D.自西北向东南我国某镇利用当地主产的粮食制作粮画,打造粮画小镇。
左图是M学校设计的小镇地理位置指示牌,右图是该校学生设计的四条“行走的思政课”精华路线示意图。
读图,完成下面4-5小题。
第三天——画好七张图 卖好平安福

图3-买保险就是买平安
解决客户不信任的疑问,产生信任,做出决定
公司 1.世界500强128位 2.总资产突破3.8万亿 3.代理人队伍超过60万 自己(业务员) 提供专业的 服务 客户 乐享平安 优质服务
பைடு நூலகம்
1. 讲客户:乐享平安优质服务 2. 讲自己:为客户提供为客户提供专业的服务”,若有天风险不幸降临在自己身 上,还有非常有实力的公司守护客户 3. 讲公司:平安的实力守护客户终身
(仅供内部培训使用)
新客户
7
图2-平安福夫妻百年好合
我们不仅爱自己,更爱家人,用保单守护爱情,体现爱的真谛
1.意外医疗 男,30岁 豁免B\C 女,30岁 爱家人 契约 爱自己
6853.64
2.住院医疗 3.重疾保障 4.住院日额补贴 5.意外伤残 1.一方发生合同约定的重疾双方保费豁免 2.一方身故或1-3类合同约定的伤残,高额 身故赔付并豁免对方保费
序号 1 图 社保商保对比T形图 逻辑 解决客户不了解的疑问 我有社保,我干嘛买保险? 解决客户不认可的疑问 不买保险亲人互为包袱,促成、转介绍
2
包袱图
3 4
买保险就是买平安 保险到底保不保险
解决客户不信任的疑问 产生信任,做出决定
让客户了解保险责任的分类,懂得买全险的重 要性
(仅供内部培训使用)
9
图1-有社保情况下有无商保对比T形图
解决客户不了解的疑问,我有社保,我干嘛买保险?
有新农合无平安福 有新农合有平安福
30年,年交6853元 1.重疾15万 2.住院费用3份 3.住院日额 20份
案例 张三,重疾手术花费10万, 住院90天 1.新农合:10万*70%=7万
7-7 元素电势图及其应用,实用化学电源

第 7 讲 电化学基础知行合一、经世致用7.7 元素电势图及其应用,实用化学电源7.7 Element potential diagram and its application,Practical chemical power supply本次课主要内容:元素电势图及其应用实用化学电源元素电势图:把同一元素的不同氧化态物质,按照其氧化数由高到低的顺序从左至右排列成图,并在两种氧化态之间的连线上标出 25℃时相应电对的标准电极电势值而得到的图。
-有注明了E A Ө 、E B Ө 的酸性介质和碱性介质中的元素电势图之分。
-如 Cu 在酸性介质中的元素电势图:Cu 2+ Cu + Cu0.16070.5180E A Ө / V 0.3394-主要用于求未知电对的标准电极电势和判断歧化反应能否发生元素电势图的应用1. 求未知电对的标准电极电势z 1z 2z 3A B z x E xE 1C E 2DE 3图中,z 为任意一电对不同氧化态之间元素氧化数的差值。
(1)A + z1e-⇌ B E1Ө ∆r G m1Ө = –z1FE1Ө(2)B + z1e-⇌ C E2Ө ∆r G m2Ө = –z2FE2Ө(3)C + z3e-⇌ D E3Ө ∆r G m3Ө = –z3FE3Ө +)(4)A + z x e-⇌ D E xӨ ∆r G m xӨ = –z x FE xӨ根据盖斯定律,由于电极反应(4)=(1)+(2)+(3) 则: ∆r G m xӨ = ∆r G m1Ө + ∆r G m2Ө + ∆r G m3Ө且:z x = z1 + z2 + z3再根据: r G mӨ = – z FEӨ则有: -z x FE xӨ = - z1FE1Ө - z2FE2Ө - z3FE3Өz x E xӨ = z1E1Ө + z2E2Ө + z3E3Ө故:E xӨ =z1E1Ө + z2E2Ө + z3E3Өz x已知 25 ℃ 时,在酸性溶液中 E 1Ө(Cu 2+/Cu +) = 0.1607V , E 2Ө(Cu 2+/Cu) = 0.3394 V ,试求 E x Ө(Cu +/Cu)。
第7章状态机图

7 第章状态图
7.6 并发状态
7.6.1 并发状态的含义 7.6.2 同步状态
7.6.1 并发状态的含义
并发状态:在一个状态机或一个复合状态中,如果同时存 在相互可以独立的几组状态,则称这几组状态是并发状态 (concurrent state)。
例如:
7.6.2 同步状态
同步状态:指多个并发区间中的状态在转换过程彼此存在 同步关系,一个区间中的一个转换需要等到另一个区间中的 某个转换发生后才能进行。 例如:
• 初始状态表示一个状态机从此结点开始,但事物不会此状态 停留,会立即转换到初始状态所连接的第下一个状态。
• 初始状态只有输出,没有输入。
7.7.2 分叉与汇合
• 分叉 (fork) :指将一个转换分成两个或多个转换,用来描述 需要并发的状态。
• 汇合 (join) :指将从并发状态来的转换合并形成一个转换, 用来描述多个并发状态的控制同步。
7.8.5 状态机与其他的图比较
1)状态机图用于事物状态及其变换的建模;活动图用于过 程流程建模 。 2)状态结点表示事物一个状态,活动结点表示一个过程中 的一个动作。 3)交互图用于多个对象为完成一个任务的交互关系,状态 机图表示一个事物所处的状态,及其变换。 4)可以用状态机描述一个交互过程中所处的状态及其转换, 用活动图描述一个交互执行的流程。
3 交互状态建模:一个交互描述为完成某项功能,系统中 若干个对象相互交互消息的过程。一个交互过程也会存在 多种状态,及其状态的转换,可以用状态机图来描述交互 状态的转换。
订货交互的状态机:
7.8.2 状态机的用途
4 构件状态建模:构件封装了多个类,构件在其生命周期 中也会存在不同状态,可以用状态机对构件的状态及其转 换进行建模。
7施工总平面图

施工总平面图第1节. 施工现场总平面布置一、施工现场总平面布置原则1、根据本工程栋的特点, 本施工总平面设计依据业主提供的《建筑总平面图》及施工场地的情况及各阶段的施工重点分阶段进行布置。
2、本工程施工场地内设置现场办公室、电工房、钢筋加工房、钢筋堆场、保卫房、周转材料、木工加工房、及配套的生活设施。
3、施工总平面布置合理与否, 将直接关系到施工进度的快慢与安全文明施工管理水平的高低, 为保证现场施工顺利进行, 确定具体的施工平面布置原则为:(1) 总平面布置合理, 场内做到硬化、绿化、亮化;(2) 在总平面布置上, 实行明确施工区域的划分;(3) 科学规划现场施工道路与出入口, 以利于车辆、机械设备的进出场与物资材料的运输, 并尽可能的减少对周边环境的影响。
(4) 满足施工需要与文明施工的前提下, 尽可能减少临时建设投资;(5) 在保证场内交通畅通与满足施工对材料要求的前提下, 最大限度地减少场内运输, 特别就是减少场内二次搬运;(6) 在施工现场总平面利用上, 要尽量减少各工种间相互干扰;(7) 符合施工现场卫生及安全技术要求与防火规范。
(8) 做好对总平面的统一分配与管理, 协调各专业与各分包单位对总平面的使用。
二、施工现场围墙、大门、临时道路设置1、进入施工现场后我们将根据业主的要求, 在业主指定的红线范围按照国家与对施工现场安全与文明施工的要求, 保证施工现场的临时围墙在使用周期内结构安全与使用功能。
(1) 大门、围墙根据现场的实际情况与业主提供的施工区域范围,现场设置一个宽6m 的大门, 供施工机械与材料运输车辆进出, 在红线范围内砌筑 2.2 米高的围墙。
(2) 现场临时道路:土方开挖与回填时, 安排专人轮班在工地出入口冲洗土方运输车辆的轮胎,并设置洗车槽, 避免运输车辆轮胎的淤泥污染路面三、办公区临时设施的布置办公区主要分为业主办公室、监理办公室、施工单位办公室。
设置一幢两层办公楼, 采用彩钢板活动房。
市政工程识图与构造第七章给水排水工程图

1 : 25 ~ 1 : 200 ,视构筑物的大小及复杂程度 而定。
对于初步设计可取较小比例;施工图设计则宜
取较大比例。
22:24:40
《工程制图》
58
(2)图线
绘制净水构筑物的图线,一般有池体的 内外轮廓线、附属设备的外形线、管道 的外径线及中心线、长度起迄的尺寸线、 建筑材料的图例线等。 由于图样中所画的内容有主次之分,因 此图线的线型及宽度要有所区分,不宜 一样粗细。
单法兰直 管 弯折管
闸阀井 总压水管
图7-20 取水泵房平面图
22:24:40 《工程制图》 40
图7-21 取水泵房剖面图
22:24:40 《工程制图》 41
7.7 净水构筑物工艺图 7.7.1 快滤池的工艺构造和流程
7.7.2 工艺图的比例和图线
7.7.3 工艺图的尺寸标注
7.7.4 详图
22:24:40 《工程制图》 36
7.6 水泵房设备图
22:24:40
《工程制图》
37
图7-20 取水泵房平面图
22:24:40 《工程制图》 38
双法兰三 单法兰偏 双法兰异 直管 吸水管 防水套管 单法兰直管 闸阀 通管 水泵和电机 心异径管 径管 Βιβλιοθήκη 阀图7-20 取水泵房平面图
22:24:40 《工程制图》 39
22:24:40
《工程制图》
59
(2)图线
1 )双线画的大直径管道,单线画的小直径管道, 其图线宽度为中粗线。
2 )构筑物的附属设备及构件的轮廓线,池体的 内外轮廓线及剖面轮廓线等,其图线宽度为中 线。 3 )视图及剖面图中的中心线、尺寸线、图例线、 引出线等,其图线宽度为细线。
第7章-图练习题及标准答案

第七章 图一、单选题( C )1. 在一个图中,所有顶点的度数之和等于图的边数的 倍。
A .1/2 B. 1 C. 2 D. 42. 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的( B )倍。
A .1/2 B. 1 C. 2 D. 4 (B )3. 有8个结点的无向图最多有 条边。
A .14 B. 28 C. 56 D. 112 ( A )一个n 个顶点的连通无向图,其边的个数至少为( )。
A .n-1B .nC .n+1D .nlogn ; ( C )5. 有8个结点的有向完全图有 条边。
A .14 B. 28 C. 56 D. 112 (B )6. 用邻接表表示图进行广度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列 C. 树 D. 图 ( A )7. 用邻接表表示图进行深度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列 C. 树 D. 图8. 下面关于求关键路径的说法不正确的是( C )。
A .求关键路径是以拓扑排序为基础的B .一个事件的最早开始时间同以该事件为尾的弧的活动最早开始时间相同C .一个事件的最迟开始时间为以该事件为尾的弧的活动最迟开始时间与该活动的持续时间的差D .关键活动一定位于关键路径上9. 已知图的邻接矩阵如下,根据算法思想,则从顶点0出发,按深度优先遍历的结点序列是( D )A . 0 2 4 3 1 5 6 B. 0 1 3 5 6 4 2 C. 0 4 2 3 1 6 5 D. 0 ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡01000111011000010110101100110010001100100110111101 3 42 5 610、设数据结构A=(D,R),其中D={1,2,3,4},R={r},r={<1,2>,<2,3>,<3,4>,<4,1>,<4,2>},则数据结构A是(C )。
7图的基本概念

18
7.2通路、回路、图的连通性
Graphs/图论
有向图的连通性 (1)弱连通:
若G=(V,E)对应的无向图是连通图,则称 G为弱连通。 (2)强连通:
若G=(V,E)中任两点间都有路,即对a与 b,a到b可达,b到a可达,称G为强连通。
(3)单侧连通
有向图 G 中,任何一对结点间,至少从一个结点到另一个
的始点
j
0,vi与e
不关联
j
-1,vi为e
的终点
j
则称 (mij )nm 为D的关联矩阵, 记为M(D)
v1
e2
v4
e1 e3 e4
v2
e5
v3
1 1 0 0 0
M
(G)
1 0
0 0
1 0
1
1
0 1
0 1 1 1 0
1/3/2020 9:03 PM
当V0=Vk时,该通路称为回路。
1/3/2020 9:03 PM
13
7.2通路、回路、图的连通性
Graphs/图论
简单通路 一条通路中没有两条边是相同的,称此通路为
简单通路(迹)。当其是回路时,称为简单回路。
初级通路 一条通路中,除了起点和终点可以相同,没有
其他相同顶点出现,称此通路为初级通路(基本通 路或路径)。当其是回路时,称为初级回路(基本 回路或圈)。
vi 与边 e j的关联次数,则称矩阵 (mij )nm为G的关联矩阵,记为
M(G) .
显然, mij 的可能取值为0( vi 与 e j不关联),1( vi与 e j 关联1次), 2( vi与e j 关联2次)即 e j 的以 vi 为端点的环.
图论讲义第7章-平面图

第七章 平面图§7.1 平面图的概念定义7.1.1 如果图G 能画在曲面S 上,使得任意两边互不交叉,则称G 可嵌入曲面S 。
若图G 可嵌入平面,则称G 是可平面图或平面图,画出的无交叉边的图形称为图G 的平面嵌入。
例如,下面是三个平面图及其平面嵌入。
根据定义,下列定理是显然的。
定理7.1.1 若图G 是平面图,则G 的任何子图都是平面图。
定理7.1.2 若图G 是非平面图,则G 的任何母图都是非平面图。
定理7.1.3 若图G 是平面图, 则在G 中添加重边或环边后所得之图仍是平面图。
注:由以上定理知(1) K n ( n ≤4 ) 和 K 1,n (n ≥ 1)及其所有子图都是平面图。
(2) 环边和重边不影响图的平面性。
故以下讨论平面性时总假定图G 是简单图。
定义7.1.2 设图G 是平面图 (已平面嵌入),G 的边将平面划分出的若干区域都称为图G 的面。
其中面积无限的面称为无限面或外部面,面积有限的面称为有限面或内部面。
包围一个面的所有边称为该面的边界。
一个面边界上的边数称为该面的次数 (割边按两次计),面R 的次数记为deg (R )。
定理7.1.4 平面图G 中所有面的次数之和等于G 的边数的两倍,即其中R 1, R 2, … , R r 是G 的所有面。
证明: 对G 的任何一条边e ,若e 是两个面 R i 和 R j 的公共边界,则在计算R i 和 R j 的次数时,e 各提供了1;若e 只是某一个面的边界,则在计算该面的次数时,e 提供了2。
可见每条边在计算总次数时,都提供2。
因而结论成立。
1deg()2().r ii R G ε==∑定义7.1.3设G为简单平面图,若在G的任意不相邻的顶点u, v之间加边uv 后,所得之图成为非平面图,则称G是极大平面图。
易见K1, K2, K3, K4, K5– e 都是极大平面图。
定义7.1.4 若非平面图G任意删除一条边后,所得之图都是平面图,则称G为极小非平面图。
〖地 理〗地形图的判读—分层设色地形图课件 2024-2025学年七年级地理上学期(人教版2024)

顶的爬升高度约( )
A.100米 B.400米
C.700米 D.1000米
6.“纯光伏基站”项目选址在水源山的主
要原因是( ) A.落整较大,水能丰富
B.海拔较高,光照充足
C.风电充足,供电稳定
D.人烟稀少,空气洁净
五、课堂练习
联合国世界旅游组织大会于10月19日公布了2023年“最佳旅游乡村”名单,我国江 西篁岭村成功入选。江西篁岭古村,地无二里平,人们房前屋后及自家窗台、屋顶 用竹篾盘架晒或挂晒农作物,演变成一种传统农俗现象——晒秋。下图是篁岭古村 周边地形图、篁岭晒秋图,据此,完成下面小题。
地名+地形类型。
青藏高原
三、分层设色地形图的判读 2.陆地地形
高原
山地
盆地
平原
丘陵
雪线 5000 3000 2000 1000 500 200 0
海拔/米
思考:这些基本地形在地形图上怎么识别?有什么特点?
三、分层设色地形图的判读 (1)陆地地形——高原
➢ 海拔在500米以上, 面积较大,外围较陡、 内部起伏较为和缓。
宽广平坦
较高(在500米以上) 较高(在500米以上) 较低(在500米以下)
外围较陡、内部起伏较 为和缓(外陡内缓) 有耸立的山峰、陡峭的 山坡 坡度较小,相对高度在 200米以下,较山地小
地面起伏小 地面崎岖不平
盆地 四周多被山地或高原环绕,中部相对低平(四周高,中间低)
课本P36活动:绘制并判读分层设色地形图。
第7章专题图制作

7.3.1 饼图制作方法
以全国各省人口专题图制作为例,说明饼 图的制作方法。
① 打开全国政区图。 ② 选择“地图”→“创建专题地图”菜单项。 如 图7-1所示。 ③ 在 “ 创 建 专 题 图 - 步 骤 1/3” 对 话 框 中 选 择 “饼 图”,模板选择“缺省饼图”。如图7-28所示。 ④ 单击“下一步”,在“创建专题图-步骤 2/3”
7.3.2 饼图高级制作
图7-32 自定义饼图样式
1. 字段列表 2. 图表类型 3. 饼图尺度 4. 方位 5. 饼图属性 6. 大小分级
推荐使用平方根比例,因为饼图面积按 半径的平方变化。
7.4 等级符号专题图
等级符号图对表中每个记录显示一 个符号,其大小与数据数值成比例。等级 符号图用指定的数值来显示数据点。它在 说明数量信息如从高到低的顺序时很有用。 例如,使用等级符号图来显示不同区域的 年销售额,MapInfo将根据销售额字段中的 值改变每个区域内符号的大小。
图7-28 饼图制作步骤1/3
图7-29 饼图制作步骤2/3
⑤ 单击“下一步”,在“创建专题图步骤
3/3”对话框中单击“确定”。如图7-30所示。 ⑥ 显示专题图图例。选择“选
项”→“显 示专题图例”,如图7-5所示。
⑦ 专题图制作完毕,如图7-31所示。
图7-30 饼图制作步骤3/3
图7-31 饼图
框。 如图7-62所示。
图7-62 格网设置
7.8 习题
一、 思考题 1. 常用的专题图制作的方法有哪些? 2. 比较这些方法的异同。 3. 如何针对不同变量选择合适的专题图类型?
二、 上机练习 1. 选择一个表,对其中某个变量制作专题图。 2. 修改所制作的专题图的样式、图例,并将其
7.MAOINFO建立LAC、TAC专题地图-泰森图(voronoi图)
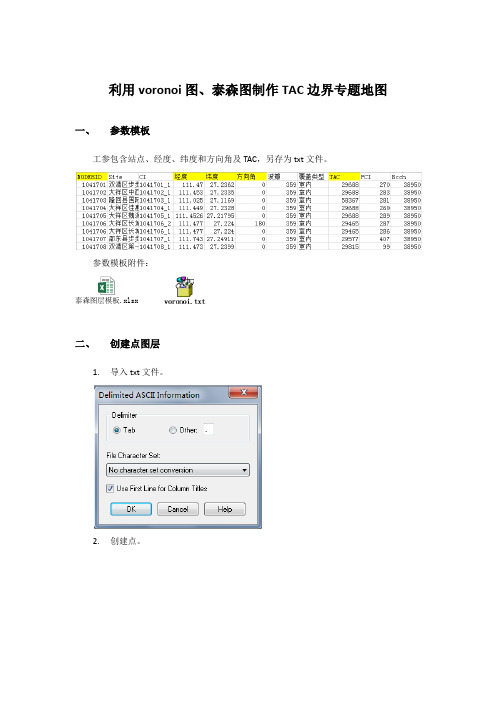
利用voronoi图、泰森图制作TAC边界专题地图一、参数模板
工参包含站点、经度、纬度和方向角及TAC,另存为txt文件。
参数模板附件:
泰森图层模板.xlsx
二、创建点图层
1.导入txt文件。
2.创建点。
3.点图如下。
三、创建表结构
这步LAC的表结构要与后面新建的表结构保持一致。
四、制作voronoi多边形泰森图
1.选择table-voronoi。
2.选择做好的点图层,结果选择存储新表。
3.根据需要选择是否新建new mapper,选择新建表结构。
4.创建的表结构与之前voronoi图层的保持一致,选择创建。
5.图层自动保存。
6.选择对应的值,否则图层没有值,做不成专题地图(很重要的一步)。
7.等待图层创建。
8.创建泰森图完成,打开刚生成的TAC图层,内容为选中状态,空白处点击取消选中
即可。
五、创建TAC专题地图
1.map-创建专题地图。
2.选择需要创建的专题模板。
3.选择需要的表和对应项。
4.这步不做修改。
5.结果如下。
六、制作合并同小区后的TAC的边界专题地图table-合并对象。
选择需要合并的图层。
新建图层,这里使用TAC图的表结构。
创建表结构,默认不修改。
另存为TAC边界。
聚合方式选择value数值。
打开保存的TAC边界图层。
创建专题地图,不再重复,结果如图,可方便核查是否存在插花站点。
中考生物重点题型突破:题型一 识图题(七) 动植物类群、生殖及发育

(七)动植物类群、生殖及发育知识要点:常见动植物实物图、植物营养繁殖图、鸟卵结构图、昆虫发育过程图、鱼结构图。
1. (济宁A卷)下列植物按照从高等到低等的顺序排列正确的( )第1题图A. ①②③④B. ①②④③C. ④③②①D. ③④②①2. (贺州)如图分别为玉米、向日葵、葫芦藓、肾蕨、油松、水绵六种植物。
将它们分类,正确的选项是()第2题图A. ③⑤⑥为苔藓植物B. ①③④为蕨类植物C. ③④⑥为藻类植物D. ①②⑤为种子植物3. (遵义)如图所示。
阴影部分表示藻类植物、苔藓植物和蕨类植物的共同特征,这一特征不包括()第3题图A. 由细胞组成B. 能进行光合作用和呼吸作用C. 不能用种子繁殖后代D. 有根、茎、叶的分化4. (保定)如图表示各种概念之间的关系。
下列选项与图示相符的是()第4题图甲乙丙丁戊A 动物脊椎动物无脊椎动物软体动物爬行动物B 动物无脊椎动物脊椎动物鱼类节肢动物C 植物种子植物孢子植物藻类单子叶植物D 植物孢子植物种子植物裸子植物被子植物5. (宜宾)如图表示的是植物两种繁殖方法的有关过程,下列描述正确的是()第5题图A. 该图表示扦插的两种方法过程B. 图中所示均为有性生殖过程C. ②为①提供生长发育所需营养D. ①以后所结果实性状由②决定6. (宜宾)对植物进行分类必须仔细观察植物形态结构方面的特征。
据图分析下列不正确的一项是()第6题图A. 图中①、②和③是无种子植物B. 图中④与⑤是不同的植物物种C. 图中④、⑤和⑥是有种子植物D. 图中②与③是同一类群的植物7. (郴州)如图为鸡卵结构示意图。
请据图回答:第7题图(1)[⑧]________能为鸡胚胎发育提供主要的营养物质,[]气室能为鸡胚胎发育提供氧气。
卵中央的小白点⑤名称是________。
鸡卵外层有[①]________和卵壳膜的保护,能减少水分的散失,这些都有利于鸡在陆地上繁殖后代。
(2)鸡卵产出后,自然环境下母鸡会________(填一种繁殖行为),卵内胚胎才能继续发育。
北师大版七年级上册数学第三章整式及其加减——图形找规律专项练习60题(含答案)

图形找规律专项练习60题(有答案)1.按如下方式摆放餐桌和椅子:填表中缺少可坐人数_________ ;_________ .2.观察表中三角形个数的变化规律:图形0 1 2 …n横截线条数6 ??…?三角形个数若三角形的横截线有0条,则三角形的个数是6;若三角形的横截线有n条,则三角形的个数是_________ (用含n的代数式表示).3.如图,在线段AB上,画1个点,可得3条线段;画2个不同点,可得6条线段;画3个不同点,可得10条线段;…照此规律,画10个不同点,可得线段_________ 条.4.如图是由数字组成的三角形,除最顶端的1以外,以下出现的数字都按一定的规律排列.根据它的规律,则最下排数字中x的值是_________ ,y的值是_________ .5.下列图形都是由相同大小的单位正方形构成,依照图中规律,第六个图形中有_________ 个单位正方形.6.如图,用相同的火柴棒拼三角形,依此拼图规律,第7个图形中共有_________ 根火柴棒.7.图1是一个正方形,分别连接这个正方形的对边中点,得到图2;分别连接图2中右下角的小正方形对边中点,得到图3;再分别连接图3中右下角的小正方形对边中点,得到图4;按此方法继续下去,第n个图的所有正方形个数是_________ 个.8.观察下列图案:它们是按照一定规律排列的,依照此规律,第6个图案中共有_________ 个三角形.9.如图,依次连接一个边长为1的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第二个正方形的面积是_________ ;第六个正方形的面积是_________ .10.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形有1个小正方形,第2个图形有3个小正方形,第3个图形有6个小正方形,第4个图形有10个小正方形…,按照这样的规律,则第10个图形有_________ 个小正方形.11.如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为_________ .12.为庆祝“六一”儿童节,幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,则摆n条“金鱼”需用火柴棒的根数为_________ .13.如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有_________ 个交点,二十条直线相交最多有_________ 个交点.14.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:图形编号(1)(2)(3)…n火柴根数从左到右依次为_________ _________ _________ _________ .15.图(1)是一个黑色的正三角形,顺次连接三边中点,得到如图(2)所示的第2个图形(它的中间为一个白色的正三角形);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形.如此继续作下去,则在得到的第5个图形中,白色的正三角形的个数是_________ .16.如图,一块圆形烙饼切一刀可以切成2块,若切两刀最多可以切成4块,切三刀最多可以切成7块…通过观察、计算填下表(其中S表示切n刀最多可以切成的块数)后,可探究一圆形烙饼切n刀最多能切成_________ 块(结果用n的代数式表示).n 0 1 2 3 4 5 …n17.如图,是用相同的等腰梯形拼成的等腰梯形图案.第(1)个图案只有1个等腰梯形,其两腰之和为4,上下底之和为3,周长为7;第(2)个图案由3个等腰梯形拼成,其周长为13;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为_________ .(用正整数n表示)18.下列各图均是用有一定规律的点组成的图案,用S表示第n个图案中点的总数,则S= _________ (用含n 的式子表示).19.如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有n(n≥3)盆花,每个图案中花盆总数为S,按照图中的规律可以推断S与n(n≥3)的关系是_________ .20.用火柴棍象如图这样搭图形,搭第n个图形需要_________ 根火柴棍.21.现有黑色三角形“”和白色三角形“”共有2011个,按照一定的规律排列如下:则黑色三角形有_________ 个.22.假设有足够多的黑白围棋子,按照一定的规律排成一行:○●●○○●○●●○○●○●●○○●○●●○○●…请问第2011个棋子是黑的还是白的?答:_________ .23.观察下列由等腰梯形组成的图形和所给表中数据的规律后填空:1 2 3 4 5 …梯形的个数图形的周5 8 11 14 17 …长当梯形个数为2007个时,这时图形的周长为_________24.如图,下面是一些小正方形组成的图案,第4个图案有_________ 个小正方形组成;第n个图案有_________个小正方形组成.25.如图所示是由火柴棒按一定规律拼出的一系列图形:依照此规律,第7个图形中火柴棒的根数是_________ .26.图中的每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,每个图案的棋子总数为s,按图的排列规律推断,s与n之间的关系可用式子_________ 表示.27.观察下列图形,它是按一定规律排列的,那么第_________ 个图形中,十字星与五角星的个数和为27个.28.2条直线最多只有1个交点;3条直线最多只有3个交点;4条直线最多只有6个交点;2000条直线最多只有_________ 个交点.29.以下各图分别由一些边长为1的小正方形组成,请填写图2、图3中的周长,并以此推断出图10的周长为_________ .30.如图所示,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么设第n个图案中有白色地面砖m块,则m与n的函数关系式是_________ .31.用同样大小的黑色棋子按如图所示的规律摆放:(1)分别写出第6、7两个图形各有多少颗黑色棋子?(2)写出第n个图形黑色棋子的颗数?(3)是否存在某个图形有2012颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.32.如图,给出四个点阵,s表示每个点阵中点的个数,按照图形中的点的个数变化规律,(1)猜想第n个点阵中的点的个数s= _________ .(2)若已知点阵中点的个数为37,问这个点阵是第几个?33.用棋子摆出下列一组图形:(1)填写下表:图形编号 1 2 3 4 5 6图中棋子数 5 8 11 14 17 20(2)照这样的方式摆下去,写出摆第n个图形所需棋子的枚数;(3)其中某一图形可能共有2011枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形.34.观察图中四个顶点的数字规律:(1)数字“30”在_________ 个正方形的_________ ;(2)请你用含有n(n≥1的整数)的式子表示正方形四个顶点的数字规律;(3)数字“2011”应标在什么位置.35.如图,各图表示若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案中花盆的总数为S.问:①当每条边有2盆花时,花盆的总数S是多少?②当每条边有3盆花时,花盆的总数S是多少?③当每条边有4盆花时,花盆的总数S是多少?④当每条边有10盆花时,花盆的总数S是多少?⑤按此规律推断,当每条边有n盆花时,花盆的总数S是多少?36.如下图是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第④、第⑤个“上”字分别需用_________ 和_________ 枚棋子;(2)第n个“上”字需用_________ 枚棋子;(3)七(3)班有50名同学,把每一位同学当做一枚棋子,能否让这50枚“棋子”按照以上规律恰好站成一个“上”字?若能,请计算最下一“横”的学生数;若不能,请说明理由.37.下列表格是一张对同一线段上的个数变化及线段总条数的探究统计.线段上点的个数线段的总条数11+2=31+2+3=6……(1)请你完成探究,并把探究结果填在相应的表格里;(2)若在同一线段上有10个点,则线段的总条数为_________ ;若在同一线段上有n个点,则有_________ 条线段(用含n 的式子表示)(3)若你所在的班级有60名学生,20年后参加同学聚会,见面时每两个同学之间握一次手,共握手_________ 次.38.如图是用棋子摆成的“H”字.(1)摆成第一个“H”字需要_________ 个棋子;摆第x个“H”字需要的棋子数可用含x的代数式表示为_________ ;(2)问第几个“H”字棋子数量正好是2012个棋子?39.我们知道,两条直线相交只有一个交点.请你探究:(1)三条直线两两相交,最多有_________ 个交点;(2)四条直线两两相交,最多有_________ 个交点;(3)n条直线两两相交,最多有_________ 个交点(n为正整数,且n≥2).40.如图所示,小王玩游戏:一张纸片,第一次将其撕成四小片,手中共有4张纸片,以后每次都将其中一片撕成更小的四片.如此进行下去,当小王撕到第n次时,手张共有S张纸片.根据上述情况:(1)用含n的代数式表示S;(2)当小王撕到第几次时,他手中共有70张小纸片?41.如图①是一张长方形餐桌,四周可坐6人,2张这样的桌子按图②方式拼接,四周可坐10人.现将若干张这样的餐桌按图③方式拼接起来:(1)三张餐桌按题中的拼接方式,四周可坐_________ 人;(2)n张餐桌按上面的方式拼接,四周可坐_________ 人(用含n的代数式表示).若用餐人数为26人,则这样的餐桌需要_________ 张.42.用棋子摆出下列一组图形:(1)填写下表:图形编号 1 2 3 4 5 6图形中的棋子(2)照这样的方式摆下去,写出摆第n个图形棋子的枚数;(用含n的代数式表示)(3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?43.如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,(1)第5个“广”字中的棋子个数是_________ .(2)第n个“广”字需要多少枚棋子?44.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察图形并解答有关问题:(1)在第n个图中共有_________ 块黑瓷砖,_________ 块白瓷砖;(2)是否存在黑瓷砖与白瓷砖块数相等的情形?你能通过计算说明吗?45.用火柴棒按如图的方式搭三角形.(1)搭4个这样的三角形要用_________ 根火柴棒;13根火柴棒可以搭_________ 个这样的三角形;(2)搭n个这样的三角形要用_________ 根火柴棒(用含n的代数式表示).46.观察图中的棋子:(1)按照这样的规律摆下去,第4个图形中的棋子个数是多少?(2)用含n的代数式表示第n个图形的棋子个数;(3)求第20个图形需棋子多少个?47.如图,用正方体石墩垒石梯,下图分别表示垒到一、二、三阶梯时的情况.那么照这样垒下去,请你观察规律,并完成下列问题.(1)填出下表中未填的两个空格:阶梯级数一级二级三级四级石墩块数 3 9(2)当垒到第n级阶梯时,共用正方体石墩多少块(用含n的代数式表示)?并求当n=100时,共用正方体石墩多少块?48.有一张厚度为0.05毫米的纸,将它对折1次后,厚度为2×0.05毫米.(1)对折3次后,厚度为多少毫米?(2)对折n次后,厚度为多少毫米?(3)对折n次后,可以得到多少条折痕?49.如图所示,用同样规格正方形瓷砖铺设矩形地面,请观察下图:按此规律,第n个图形,每一横行有_________ 块瓷砖,每一竖列有_________ 块瓷砖(用含n的代数式表示)按此规律,铺设了一矩形地面,共用瓷砖506块,请问这一矩形的每一横行有多少块瓷砖,每一竖列有多少瓷砖?50.找规律:观察下面的星阵图和相应的等式,探究其中的规律.(1)在④、⑤和⑥后面的横线上分别写出相应的等式:①1=12②1+3=22③1+3+5=32④_________ ;⑤_________ ;⑥_________ ;(2)通过猜想,写出第n个星阵图相对应的等式.51.将一张正方形纸片剪成四个大小一样的小正方形,然后将其中的一个正方形再剪成四个小正方形,如此循环下去,如图所示:(1)完成下表:所剪次数n 1 2 3 4 5正方形个数Sn 4(2)剪n次共有S n个正方形,请用含n的代数式表示S n= _________ ;(3)若原正方形的边长为1,则第n次所剪得的正方形边长是_________ (用含n的代数式表示).52.如图是用五角星摆成的三角形图案,每条边上有n(n>1)个点(即五角星),每个图案的总点数(即五角星总数)用S表示.(1)观察图案,当n=6时,S= _________ ;(2)分析上面的一些特例,你能得出怎样的规律?(用n表示S)(3)当n=2008时,求S.53.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点.观察图中每一个正方形(实线)四条边上的格点的个数,请回答下列问题:(1)由里向外第1个正方形(实线)四条边上的格点个数共有_________ 个;由里向外第2个正方形(实线)四条边上的格点个数共有_________ 个;由里向外第3个正方形(实线)四条边上的格点个数共有_________ 个;(2)由里向外第10个正方形(实线)四条边上的格点个数共有_________ 个;(3)由里向外第n个正方形(实线)四条边上的格点个数共有_________ 个.54.下列各图是由若干花盆组成的形如正方形的图案,每条边(包括两个顶点)有n(n>1)个花盆,每个图案花盆总数是S.(1)按要求填表:n 2 3 4 5 …S 4 8 12 …(2)写出当n=10时,S= _________ .(3)写出S与n的关系式:S= _________ .(4)用42个花盆能摆出类似的图案吗?55.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并解答下列问题.(1)在第1个图中,共有白色瓷砖_________ 块.(2)在第2个图中,共有白色瓷砖_________ 块.(3)在第3个图中,共有白色瓷砖_________ 块.(4)在第10个图中,共有白色瓷砖_________ 块.(5)在第n个图中,共有白色瓷砖_________ 块.56.淮北市为创建文明城市,各种颜色的菊花摆成如下三角形的图案,每条边(包括两个顶点)上有n(n>1)盆花,每个图案花盆的总数为S,当n=2时,S=3;n=3时,S=6;n=4时,S=10.(1)当n=6时,S= _________ ;n=100时,S= _________ .(2)你能得出怎样的规律?用n表示S.57.下面是按照一定规律画出的一系列“树枝”经观察,图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出4个“树枝”,图(4)比图(3)多出8个“树枝”,按此规律:图(5)比图(4)多出_________ 个树枝;图(6)比图(5)多出_________ 个树枝;图(8)比图(7)多出_________ 个树枝;…图(n+1)比图(n)多出_________ 个树枝.58.如图是用棋子成的“T”字图案.从图案中可以出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”图案需要11枚棋子.(1)照此规律,摆成第八个图案需要几枚棋子?(2)摆成第n个图案需要几枚棋子?(3)摆成第2010个图案需要几枚棋子?59.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:(1)当黑砖n=1时,白砖有_________ 块,当黑砖n=2时,白砖有_________ 块,当黑砖n=3时,白砖有_________ 块.(2)第n个图案中,白色地砖共_________ 块.60.下列图案是晋商大院窗格的一部分.其中,“o”代表窗纸上所贴的剪纸.探索并回答下列问题:(1)第6个图案中所贴剪纸“o”的个数是_________ ;(2)第n个图案中所贴剪纸“o”的个数是_________ ;(3)是否存在一个图案,其上所贴剪纸“o”的个数为2012个?若存在,指出是第几个;若不存在,请说明理由.图形找规律60题参考答案:1.结合图形和表格,不难发现:1张桌子座6人,多一张桌子多2人.4张桌子可以座10+2=12.即n张桌子时,共座6+2(n﹣1)=2n+4.2.当横截线有n条时,在6个的基础上多了n个6,即三角形的个数共有6+6n=6(n+1)个.故应填6(n+1)或6n+63.∵画1个点,可得3条线段,2+1=3;画2个点,可得6条线段,3+2+1=6;画3个点,可得10条线段,4+3+2+1=10;…;画n个点,则可得(1+2+3+…+n+n+1)=条线段.所以画10个点,可得=66条线段;4.根据图形可以发现,第七排的第一个数和第二数与第八排的第二个数相等,而第八排的第二个数就是x,所以x=61.另外,由图形可知,x右边的数是2×61=122,y左边的数是2×61+56=178,所以y=178+46=2245.根据题意分析可得:第1个图案中正方形的个数2个,第2个图案中正方形的个数比第1个图案中正方形的个数多4个,第3个图案中正方形的个数比第2个图案中正方形的个数多6个…,依照图中规律,第六个图形中有2+4+6+8+10+12=42个单位正方形6.图形从上到下可以分成几行,第n行中,斜放的火柴有2n根,下面横放的有n根,因而图形中有n排三角形时,火柴的根数是:斜放的是2+4+…+2n=2(1+2+…+n)横放的是:1+2+3+…+n,则每排放n根时总计有火柴数是:3(1+2+…+n)=21)nn3(把n=7代入就可以求出.故第7个图形中共有=84根火柴棒7.图1中,是1个正方形;图2中,是1+4=5个正方形;图3中,是1+4×2=9个正方形;依此类推,第n个图的所有正方形个数是1+4(n﹣1)=4n﹣3.8.∵第1个图案中有2×2+2×1=6个三角形;第2个图案中有2×3+2×2=10个三角形;第3个图案中有2×4+2×3=14个三角形;…∴第6个图案中有2×7+2×6=26个三角形.故答案为269.∵正方形的边长是1,所以它的斜边长是:=,所以第二个正方形的面积是:×=,第三个正方形的面积为=()2,以此类推,第n个正方形的面积为()n﹣1,所以第六个正方形的面积是()6﹣1=;故答案为:,.10.∵第一个有1个小正方形,第二个有1+2个,第三个有1+2+3个,第四个有1+2+3+4,第五个有1+2+3+4+5,∴则第10个图形有1+2+3+4+5+6+7+8+9+10=55个.故答案为:5511.依题意得:(1)摆第1个“小屋子”需要5个点;摆第2个“小屋子”需要11个点;摆第3个“小屋子”需要17个点.当n=n时,需要的点数为(6n﹣1)个.故答案为6n﹣112.由图形可知:第一个金鱼需用火柴棒的根数为:2+6=8;第二个金鱼需用火柴棒的根数为:2+2×6=14;第三个金鱼需用火柴棒的根数为:2+3×6=20;…;第n个金鱼需用火柴棒的根数为:2+n×6=2+6n.故答案为2+6n13.6条直线两两相交,最多有n(n﹣1)=×6×5=15,20条直线两两相交,最多有n(n﹣1)=×20×19=190.故答案为:15,190.14.如表格所示:(1)(2)(3)…n图形编号7 12 17 …5n+2火柴根数15.设白三角形x个,黑三角形y个,则:n=1时,x=0,y=1;n=2时,x=0+1=1,y=3;n=3时,x=3+1=4,y=9;n=4时,x=4+9=13,y=27;当n=5时,x=13+27=40,所以白的正三角形个数为:40,故答案为:4016.n=1时,S=1+1=2,n=2时,S=1+1+2=4,n=3时,S=1+1+2+3=7,n=4时,S=1+1+2+3+4=11,…所以当切n刀时,S=1+1+2+3+4+…+n=1+n(n+1)=n2+n+1.故答案为n2+n+117.根据题意得:第(1)个图案只有1个等腰梯形,周长为3×1+4=7;第(2)个图案由3个等腰梯形拼成,其周长为3×3+4=13;第(3)个图案由5个等腰梯形拼成,其周长为3×5+4=19;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为3(2n﹣1)+4=6n+1;故答案为:6n+118.观察发现:第1个图形有S=9×1+1=10个点,第2个图形有S=9×2+1=19个点,第3个图形有S=9×3+1=28个点,…第n个图形有S=9n+1个点.故答案为:9n+119.n=3时,S=6=3×3﹣3=3,n=4时,S=12=4×4﹣4,n=5时,S=20=5×5﹣5,…,依此类推,边数为n数,S=n•n﹣n=n(n﹣1).故答案为:n(n﹣1).20.结合图形,发现:搭第n个三角形,需要3+2(n﹣1)=2n+1(根).故答案为2n+121.因为2011÷6=335…1.余下的1个根据顺序应是黑色三角形,所以共有1+335×3=1006.故答案为:100622.从所给的图中可以看出,每六个棋子为一个循环,∵2011÷6=335…1,∴第2011个棋子是白的.故答案为:白23.依题意可求出梯形个数与图形周长的关系为3n+2=周长,当梯形个数为2007个时,这时图形的周长为3×2007+2=6023.故答案为:6023.24.观察图形知:第一个图形有1=12个小正方形;第二个图形有1+3=4=22个小正方形;第三个图形有1+3+5=9=32个小正方形;…第n个图形共有1+2+3+…+(2n﹣1)=n2个小正方形,当n=4时,有n2=42=16个小正方形.故答案为:16,n225.根据已知图形可以发现:第2个图形中,火柴棒的根数是7;第3个图形中,火柴棒的根数是10;第4个图形中,火柴棒的根数是13;∵每增加一个正方形火柴棒数增加3,∴第n个图形中应有的火柴棒数为:4+3(n﹣1)=3n+1.当n=7时,4+3(n﹣1)=4+3×6=22,故答案为:2226.观察图形发现:当n=2时,s=4,当n=3时,s=9,当n=4时,s=16,当n=5时,s=25,…当n=n时,s=n2,故答案为:s=n227.∵第1个图形中,十字星与五角星的个数和为3×2=6,第2个图形中,十字星与五角星的个数和为3×3=9,第3个图形中,十字星与五角星的个数和为3×4=12,…而27=3×9,∴第8个图形中,十字星与五角星的个数和=3×9=27.故答案为:828.2条直线最多的交点个数为1,3条直线最多的交点个数为1+2=3,4条直线最多的交点个数为1+2+3=6,5条直线最多的交点个数为1+2+3+4=10,…所以2000条直线最多的交点个数为1+2+3+4+…+1999==1999000.故答案为199900029.∵小正方形的边长是1,∴图1的周长是:1×4=4,图2的周长是:2×4=8,图3的周长是3×4=12,…第n个图的周长是4n,∴图10的周长是10×4=40;故答案为:8,12,4030.首先发现:第一个图案中,有白色的是6个,后边是依次多4个.所以第n个图案中,是6+4(n﹣1)=4n+2.∴m与n的函数关系式是m=4n+2.故答案为:4n+2.31.第一个图需棋子6,第二个图需棋子9,第三个图需棋子12,第四个图需棋子15,第五个图需棋子18,…第n个图需棋子3(n+1)枚.(1)当n=6时,3×(6+1)=21;当n=7时,3×(7+1)=24;(2)第n个图需棋子3(n+1)枚.(3)设第n个图形有2012颗黑色棋子,根据(1)得3(n+1)=2012解得n=,所以不存在某个图形有2012颗黑色棋子32.(1)由点阵图形可得它们的点的个数分别为:1,5,9,13,…,并得出以下规律:第一个点数:1=1+4×(1﹣1)第二个点数:5=1+4×(2﹣1)第三个点数:9=1+4×(3﹣1)第四个点数:13=1+4×(4﹣1)…因此可得:第n个点数:1+4×(n﹣1)=4n﹣3.故答案为:4n﹣3;(2)设这个点阵是x个,根据(1)得:1+4×(x﹣1)=37解得:x=10.答:这个点阵是10个33.(1)观察图形,得出枚数分别是,5,8,11,…,每个比前一个多3个,所以图形编号为5,6的棋字子数分别为17,20.故答案为:17和20.(2)由(1)得,图中棋子数是首项为5,公差为3的等差数列,所以摆第n个图形所需棋子的枚数为:5+3(n﹣1)=3n+2.(3)不可能由3n+2=2010,解得:n=669,∵n为整数,∴n=669不合题意故其中某一图形不可能共有2011枚棋子34.(1)由图可知,每个正方形标4个数字,∵30÷4=7…2,∴数字30在第8个正方形的第2个位置,即右上角;故答案为:8,右上角;(2)左下角是4的倍数,按照逆时针顺序依次减1,即正方形左下角顶点数字:4n,正方形左上角顶点数字:4n﹣1,正方形右上角顶点数字:4n﹣2,正方形右下角顶点数字:4n﹣3;(3)2011÷4=502…3,所以,数字“2011”应标第503个正方形的左上角顶点处35.依题意得:①n=2,S=3=3×2﹣3.②n=3,S=6=3×3﹣3.③n=4,S=9=3×4﹣3④n=10,S=27=3×10﹣3.…⑤按此规律推断,当每条边有n盆花时,S=3n﹣336.(1)第①个图形中有6个棋子;第②个图形中有6+4=10个棋子;第③个图形中有6+2×4=14个棋子;∴第⑤个图形中有6+3×4=18个棋子;第⑥个图形中有6+4×4=22个棋子.故答案为18、22;(3分)(2)第n个图形中有6+(n﹣1)×4=4n+2.故答案为4n+2.(3分)(3)4n+2=50,解得n=12.最下一横人数为2n+1=25.(4分)37.(1)5个点时,线段的条数:1+2+3+4=10,6个点时,线段的条数:1+2+3+4+5=15;(2)10个点时,线段的条数:1+2+3+4+5+6+7+8+9=45,n个点时,线段的条数:1+2+3+…+(n﹣1)=;(3)60人握手次数==1770.故答案为:(2)45,;(3)1770.38.(1)摆成第一个“H”字需要7个棋子,第二个“H”字需要棋子12个;第三个“H”字需要棋子17个;…第x个图中,有7+5(x﹣1)=5x+2(个).(2)当5x+2=2012时,解得:x=402,故第402个“H”字棋子数量正好是2012个棋子39.(1)如图(1),可得三条直线两两相交,最多有3个交点;(2)如图(2),可得三条直线两两相交,最多有6个交点;(3)由(1)得,=3,由(2)得,=6;∴可得,n 条直线两两相交,最多有个交点(n为正整数,且n≥2).故答案为3;6;.40.(1)由题目中的“每次都将其中﹣片撕成更小的四片”,可知:小王每撕一次,比上一次多增加3张小纸片.∴s=4+3(n﹣1)=3n+1;(2)当s=70时,有3n+1=70,n=23.即小王撕纸23次41.(1)结合图形,发现:每个图中,两端都是坐2人,剩下的两边则是每一张桌子是4人.则三张餐桌按题中的拼接方式,四周可坐3×4+2=14(人);(2)n张餐桌按上面的方式拼接,四周可坐(4n+2)人;若用餐人数为26人,则4n+2=26,解得n=6.故答案为:14;(4n+2),642.(1)如图所示:图形编号1 2 3 4 5 6图形中的棋子6 912 15 18 21(2)依题意可得当摆到第n个图形时棋子的枚数应为:6+3(n﹣1)=6+3n﹣3=3n+3;(3)由上题可知此时3n+3=99,∴n=32.答:第32个图形共有99枚棋子13.由题目得:第1个“广”字中的棋子个数是7;第2个“广”字中的棋子个数是7+(2﹣1)×2=9;第3个“广”字中的棋子个数是7+(3﹣1)×2=11;第4个“广”字中的棋子个数是7+(4﹣1)×2=13;发现第5个“广”字中的棋子个数是7+(5﹣1)×2=15…进一步发现规律:第n个“广”字中的棋子个数是7+(n﹣1)×2=2n+5.故答案为:1544.(1)在第n个图形中,需用黑瓷砖4n+6块,白瓷砖n(n+1)块;(2)根据题意得n(n+1)=4n+6,n2﹣3n﹣6=0,此时没有整数解,所以不存在.故答案为:4n+6;n(n+1)45.(1)结合图形,发现:后边每多一个三角形,则需要多2根火柴.则搭4个这样的三角形要用3+2×3=9根火柴棒;13根火柴棒可以搭(13﹣3)÷2+1=6个这样的三角形;(2)根据(1)中的规律,得搭n个这样的三角形要用3+2(n﹣1)=2n+1根火柴棒.故答案为9;6;2n+146.(1)第4个图形中的棋子个数是13;(2)第n个图形的棋子个数是3n+1;(3)当n=20时,3n+1=3×20+1=61∴第20个图形需棋子61个47.(1)第一级台阶中正方体石墩的块数为:=3;第一级台阶中正方体石墩的块数为:=9;第一级台阶中正方体石墩的块数为:;…依此类推,可以发现:第几级台阶中正方体石墩的块数为:3与几的乘积乘以几加1,然后除以2.阶梯级一级二级三级四级数3 9 18 30石墩块数(2)按照(1)中总结的规律可得:当垒到第n级阶梯时,共用正方体石墩块;当n=100时,∴当n=100时,共用正方体石墩15150块.答:当垒到第n级阶梯时,共用正方体石墩块;当n=100时,共用正方体石墩15150块48.由题意可知:第一次对折后,纸的厚度为2×0.05;可以得到折痕为1条;第二次对折后,纸的厚度为2×2×0.05=22×0.05;可以得到折痕为3=22﹣1条;第三次对折后,纸的厚度为2×2×2×0.05=23×0.05;可以得到折痕为7=23﹣1条;…;第n次对折后,纸的厚度为2×2×2×2×…×2×0.05=2n×0.05.可以得到折痕为2n﹣1条.故:(1)对折3次后,厚度为0.4毫米;(2)对折n次后,厚度为2n×0.05毫米;(3)对折n次后,可以得到2n﹣1条折痕49.由图形我们不难看出横行砖数量为n+3,竖行砖数量为n+2,总数量为n2+5n+6;若用瓷砖506块,可以求n2+5n+6=506;所以答案为:(1)n+3,n+2;(2)每一行有23块,每一列有22块50.等号左边是从1开始,连续奇数相加,等号右边是奇数个数也就是n的平方.(1)①1+3+5+7=42;②1+3+5+7+9=52;③1+3+5+7+9+11=62.(2)1+3+5+…+(2n﹣1)=n2(n≥1的正整数)51.(1)依题意得:所剪次数n 1 2 3 4 54 7 10 13 16正方形个数Sn(2)可知剪n次时,S n=3n+1.(3)n=1时,边长=;n=2时,边长=;n=3时,边长=;…;剪n次时,边长=.52.(1)S=15(2)∵n=2时,S=3×(2﹣1)=3;n=3时,S=3×(3﹣1)=6;n=4时,S=3×(4﹣1)=9;…∴S=3×(n﹣1)=3n﹣3.(3)当n=2008时,S=3×2008﹣3=6021.53.第1个正方形四条边上的格点共有4个第2个正方形四条边上的格点个数共有(4+4×1)个第3个正方形四条边上的格点个数共有(4+4×2)个…第10个正方形四条边上的格点个数共有(4+4×9)=40个第n个正方形四条边上的格点个数共有[4+4×(n﹣1)]=4n个54.由图可知,每个图形为边长是n的正方形,因此四条边的花盆数为4n,再减去重复的四个角的花盆数,即S=4n﹣4;(1)将n=5代入S=4n﹣4,得S=16;(2)将n=10入S=4n﹣4,得S=36;(3)S=4n﹣4;(4)将S=42代入S=4n﹣4得,4n﹣4=42解得n=11.5所以用42个花盆不能摆出类似的图案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
那么从一个顶点出来的边至少有3条边是同色的,不妨设为红色
那么对于这三条边的另的三个顶点之间,如果有一条是红色的,得证
否则都是蓝色的,得证,
13.若无向图G中恰有两个奇数顶点,证明这两个奇数顶点必然相通
证明:解题思路:反证法,如果不相通,那么这两个奇数顶点位于不同的连通分支中
1, 证明对于n≥6,任何一种随意的涂法,总存在红色的K3或蓝色的K3
证明:这道题和图的第12题类似
2.用1)的结论证明任何6个人中,或者有3个人彼此认识,或有3个人彼此不认识
证明:把本题转化为图的模型,然后利用第一题的结论即可
把6个人看作是6个顶点,两个人认识就着红边,两个人不认识就着蓝边,
11.设G为n阶自补图,证明 n=4k或者n=4k+1其中 k为正整数。
证明 设n阶自补图中边数为 m, 所以度数为 2m
显然n(n-1)=2*2m=4m =>n=4k,或者n=4k+1
12.设G是6阶简单无向图,证明G或者G的补图存在3个顶点彼此相邻
证明;通过着色问题可以解决,
证明:建一个图的模型:每个选手相当于图的顶点,选手下的盘数相当于顶点得度数,两
个选手的对局相当于两个顶点的边,已知 顶点的度数是 1----n-1, 选手有n个,根据鸽
巢原理
可知,比存在两个顶点的度数相同,也就是总能找到两名选手,他们下过的盘数是相同的
。
5.设n阶无向简单图G为3次图(3-正则图),边数m和n满足以下关系2n-3=m
如果对于任意(u,v),(v,w) ∈E(G),而(u,w) ∈E(G)
那么<u1,u2>,<u2,u3>,….<un-1,un)=> <u1,u3,>,<u1,u4>,….<u1,un>,…..<u2,u3,>,
<u2,u4>……<u2,un>,………………..<un-1,un>
得出G为完全图,矛盾,所以得证
那么 m1+m2+…+mn= D mi为奇数,n奇数,所以D为奇数
但对于上式来说,每条棱都记了两次,那么 D=2*(总棱数) 为偶数 矛盾
所以空间不可能存在奇数个面而且每个面均有奇数条棱的多面体
4.在一次象旗比赛中,任意两个选手之间至多只下一盘棋,又每个人至少下一盘,证明总
能找到两名选手,他们下过的盘数是相同的
1) d=(1,2,2,4,4,5) 可图化
2) d=(1,1,2,2,3,3,5) 不可图化
非同构的图,赫赫在BBS上没法画!
7.判断下列三个整数列中哪些是可以简单图化的?对于可简单图化的试给出两个非同构的
图.
1)(6,6,5,5,3,3,2)
(6,6,5,5,3,3,2)<=>(5,4,4,2,2,1)<=><3,3,1,1,0)<=>,<2,0,0,0> 显然不可以简单图化
15.设G是无向简单图,δ(G) ≥2,证明G中存在长度大于等于δ(G)+1的圈
证明: 用极大路径法证明,易
16.设G是无向简单图,δ(G)≥3 证明G中各圈长度的最大公约数为1或者2。
证明:用极大路径法构造一个长度为m的一个圈 d1,d2,….dm
因为δ(G)≥3,所以 dj(1<j<m)(d1和 d2,dm相邻,dm 和d1和
dm-1相邻)除了与 d(j-1) 和d(j+1)相邻还与圈中的另一点相邻, 任取这样的两点(dk, d
w) 连接,那么就能构成了两个圈n1,n2,而且 |n1|+|n2|=m+2
如果各圈长度存在最大公约数Q≥3,那么|n1|+|n2|和m也有最大公约数Q,这与|n1|+|n2
|=m+2矛盾,所以G中各圈长度的最大公约数为1或者2
G) ≠2
得证
21,设n阶无向图G中有m 条边,已知m≥n,证明G中必含圈
证明:假如δ(G) ≥2 ,显然得证
如果存在 d(G)=1,0,那么去掉改顶点 ,那么m-m’ ≥n-n’,直到保证δ(G) ≥2,
当m-m’=3≥n-n’ 时 显然该图有圈。(有点象归纳法)
22.设n(n≥2)阶无向简单连通图G中不含有偶圈,证明G中的块或为K2或为奇圈
在与圈中的点连接,否则存在比围长小的圈)
取该圈中2个相邻的顶点v1,v2,显然v1所连接的k-2个点和v2所连接的k-2个点没有交集
(否则围长为3),此时G至少有(k-2) + (k-2) + 4个顶点,即G至少有2k个顶点。
2)假设有2个图G1和G2,它们都是围长为4的K-正则图,且正好有2k个顶点。
1.设G有16条边,有三个四度顶点,四个三度顶点,其余顶点的度数都小于3,问G中至少
有几个顶点?
答:总度数=16*2=32
3*4+4*3=24
(32-24)/2=4 至少有 3+4+4=11
至少有11个顶点
2.设9阶无向图G中,每个顶点的度数不是5就是6,证明G中至少有5个六度定点或者至少
即与v1_1和v1_3连接的k-2个点中任意一点都与所有与v1_2和v1_4连接的k-2个点相连,
与v1_2和v1_4连接的k-2个点中任意一点也都与所有与v1_1和v1_3连接的k-2个点相连。
这样就得到G1中所有的边了。
将与v1_1和v1_3连接的k-2个点任意标记为 v1_5, ..., v1_k+2,将与v1_2和v1_4连接
=>当去掉任意 n-3个点时,剩下的三个顶点 dn1,dn2,dn3≥1 , 那么d1,dn2,dn3 构成的
图至少存在2条边,且G为n阶无向图,所以 任去掉n-3个点,d1,dn2,dn3仍然是连通的。
=>当去掉任意 n-r(n>r>3)个点,身下 r个顶点 ,dn1,dn2,…dnr≥r-2,至少存在 一个r-
在与v1_1和v1_3连接的k-2个点中任取一点v,显然v不能与v1_2或v1_4相连,否则根据
19.(1),围长为3;v也不能与与v1_1和v1_3连接的k-2个点中除v外任意一点相连,否则
围长为3。
v的度数为k,除与v1_1和v1_3连接外,只能与所有与v1_2和v1_4连接的k-2个点相连。
2)(5,3,3,2,2,1)<=>(2,2,1,1,0)<=>(1,0,1,0) 显然可以简单图化(赫赫,图在
BBS没法画)
3)(3,3,2,2,2,2)<=>(2,1,1,2,2)(不符合定理的条件,可先调整顶点次序)
<=>(2,2,2,1,1)(根据课本例题)
证明:分类讨论
1.G中不含奇圈,因为题设给出G中不含偶圈,所以G中不含圈,所以任意条边都是桥,也就
是
任意个点都是割点,所以G中的块为K2,
2.G中含有奇圈,讨论奇圈中的相对位置。
可以证明两奇圈如果有边重合的话 必可以从中找到一个偶圈,方法如下:
若重合的边是一段连续的边,那么两奇圈剩余的边可以构成一偶圈
1)当δ(G) ≥n/2时,G为连通图;2)当δ(G) ≥1/2(n&#简单图的最大度≤n-1
用反证法,假设G至少有两个连通分支,设G1,G2为其中的两个,并设G1,G2的阶数分别为
n1,和n2,则n1+n2≤n,且min{n1,n2}≤n/2(或者n/2-1)。于是,对于任意的v∈V(G1)
问G有几种非同构的情况?并证明你的结论
解:3n=2m 2n-3=m => n=6 m=9
所以G是6阶 3正则图.设G1,G2均为无向简单图,G1同构于 G2 等价于 G1的补图同构
于G2的补图。所以可知 有两种同构的情况
6.下面给出的两个整数列,哪个是可图化的,对于可图化的请至少给出三个非同构的图
若G1,G2重合的边是不连续的,G1被划分为若干段,设其中一段L1=a1e1a2e2...am为其中
一段 若L1为奇数阶 则可和(a1, am)构成偶圈 否则L1(偶数) ∪ {G2-(a1, am)(偶数)}构
成偶圈
23,这个图很容易画出来!!
24.将无向完全图Kn的边涂上红色或者蓝色,
<=>(1,1,1,1)显然(1,1,1,1)是可简单图化的
8.9题(略)大家一定要画呀,挺好的一道题呀!!!
10,现有5个4阶的无向简单图,他们均有3条边,证明这5个图中至少有两个是同构的
证明:可以得知,这样的非同构的图有3个,所以得证
(图省略)
有6个5度顶点
证明,因为: 4*6+5*5=24+25=49不可能,
所以当n6<4 时, n5>=6 满足条件
当 n6>=5时,满足条件
得证
3.空间不可能存在奇数个面而且每个面均有奇数条棱的多面体
答: 假如有 奇数个面 n 每个面都有奇数个棱mi(I=1,2,…n),
(谢谢riveria同学!!!!!!!!!!!!!)
17.设G为n阶无向简单图,δ(G) ≥n-2 证明k(G)= δ(G)
证明 因为 δ(G) ≤n-1,所以δ(G)只有两种取值可能
1)当δ(G)=n-1,那么G为完全图,所以G的点连通度为n-1,得k(G)= δ(G)
2) δ(G)=n-2,
的k-2个点任意标记为 v1_k+3, ..., v1_2k。
