应用回归分析课后习题参考答案 全部版 何晓群,刘文卿
应用回归分析第三版·何晓群-第三章所有习题答案

应用回归分析第三章习题 3.1y x =β基本假定:(1) 诸1234n x ,x x ,x x ……非随机变量,rank (x )=p+1,X 为满秩矩阵(2) 误差项()()200i i j E ,i j cov ,,i j⎧ε=⎪⎧δ=⎨εε=⎨⎪≠⎩⎩(3)()20i i j ~N ,,⎧εδ⎪⎨εε⎪⎩诸相互独立3.2()10111ˆX X X X |rank(X X )p rank(X )p n p -'β'≠'=+≥+≥+存在,必须使存在。
即|则必有故3.3()()()()()22111221222211111111n nn i i ii i i i nii i ni i E e D e h n h n p ˆE E e n p n p n p =====⎛⎫==-δ ⎪⎝⎭⎛⎫=-δ=--δ ⎪⎝⎭⎛⎫∴δ==--δ=δ ⎪----⎝⎭∑∑∑∑∑3.4并不能这样武断地下结论。
2R 与回归方程中的自变量数目以及样本量n 有关,当样本量n 与自变量个数接近时,2R 易接近1,其中隐含着一些虚假成分。
因此,并不能仅凭很大的2R 就模型的优劣程度。
3.5首先,对回归方程的显著性进行整体上的检验——F 检验001230p H :β=β=β=β==β=……接受原假设:在显著水平α下,表示随机变量y 与诸x 之间的关系由线性模型表示不合适 拒绝原假设:认为在显著性水平α下,y 与诸x 之间有显著的线性关系第二,对单个自变量的回归系数进行显著性检验。
00i H :β=接受原假设:认为i β=0,自变量i x 对y 的线性效果并不显著3.6原始数据由于自变量的单位往往不同,会给分析带来一定的困难;又由于设计的数据量较大,可能会以为舍入误差而使得计算结果并不理想。
中心化和标准化回归系数有利于消除由于量纲不同、数量级不同带来的影响,避免不必要的误差。
3.71122011122201122ppp p p p p ˆˆˆˆˆy x x x ˆˆˆˆˆˆy y (x x )(x x )(x x )ˆˆˆˆy x x )x x )x x )y =β+β+β++β-=β+β-+β-++β--ββ=-+-++-=对最小二乘法求得一般回归方程:……对方程进行如下运算:…………*jjˆ+β=……即3.812132123313221231221233131231123233213231313*********111r r r r r r r r rr r r r r r r r r r r r ⎛⎫ ⎪= ⎪ ⎪⎝⎭∆==-∆==-∆==-即证3.9()()()()()1211121121211111j jj j j p j j j p yj j j p SSR /SSE F SSE /n p SSE /n p SSE x ,x ,,x ,x x SSE x ,x ,,x ,x ,x x r SSE x ,x ,,x ,x x -+-+-+∆∆==-----=……,?………,?…而……,?…由上两式可知,其考虑的都是通过j SSE ∆在总体中所占比例来衡量第j 个因素的重要程度,因而j F 与2yj r 是等价的。
《应用回归分析》课后习题部分答案-何晓群版

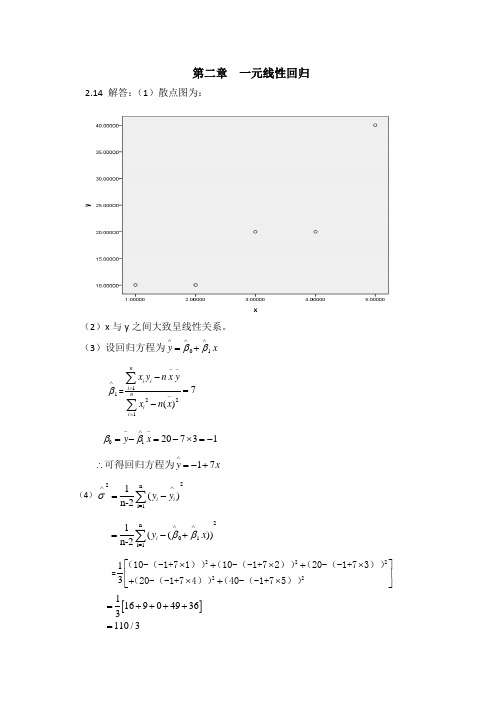
第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=(5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2||(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()ni i nii y y r y y ∧-=-=-==≈-∑∑(7)由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
《应用回归分析》课后题答案解析

《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
《应用回归分析》课后题答案

、《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x 与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
《应用回归分析》课后题标准答案

3
(5)由于 1
N
(1,
2 Lxx
)
t
1 1 2 / Lxx
(1
)
Lxx
服从自由度为 n-2 的 t 分布。因而
P
|
(
1
)
Lxx
|
t
/
2
(n
2)
1
也即: p(1 t /2
Lxx
1 1 t /2
) =1 Lxx
可得
ቤተ መጻሕፍቲ ባይዱ
1
的置信度为95%的置信区间为(7-2.353
1 3
33,7+2.353 1 3
1
第二章 一元线性回归
2.14 解答:(1)散点图为:
(2)x 与 y 之间大致呈线性关系。
(3)设回归方程为 y 0 1 x
n
xi yi n x y
1=
i 1 n
7
xi2 n(x)2
i 1
0 y 1 x 20 7 3 1
可得回归方程为 y 1 7x
2
(4)
1 n-2
1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题? 答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判 断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。应注意 的问题有:在选择变量时要注意与一些专门领域的专家合作,不要认为一个回归 模型所涉及的变量越多越好,回归变量的确定工作并不能一次完成,需要反复试 算,最终找出最合适的一些变量。
t /2
0
0
1 n
( x)2 Lxx
t
/
2
)
1
可得 1的置信度为95%的置信区间为( 7.77,5.77)
应用回归分析_第2章课后习题参考答案

2.1 一元线性回归模型有哪些基本假定?答:1. 解释变量 1x , ,2x ,p x 是非随机变量,观测值,1i x ,,2 i x ip x 是常数。
2. 等方差及不相关的假定条件为⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧≠=====j i n j i j i n i E j i i ,0),,2,1,(,),cov(,,2,1,0)(2 σεεε 这个条件称为高斯-马尔柯夫(Gauss-Markov)条件,简称G-M 条件。
在此条件下,便可以得到关于回归系数的最小二乘估计及误差项方差2σ估计的一些重要性质,如回归系数的最小二乘估计是回归系数的最小方差线性无偏估计等。
3. 正态分布的假定条件为⎩⎨⎧=相互独立n i n i N εεεσε,,,,,2,1),,0(~212 在此条件下便可得到关于回归系数的最小二乘估计及2σ估计的进一步结果,如它们分别是回归系数的最及2σ的最小方差无偏估计等,并且可以作回归的显著性检验及区间估计。
4. 通常为了便于数学上的处理,还要求,p n >及样本容量的个数要多于解释变量的个数。
在整个回归分析中,线性回归的统计模型最为重要。
一方面是因为线性回归的应用最广泛;另一方面是只有在回归模型为线性的假设下,才能的到比较深入和一般的结果;再就是有许多非线性的回归模型可以通过适当的转化变为线性回归问题进行处理。
因此,线性回归模型的理论和应用是本书研究的重点。
1. 如何根据样本),,2,1)(;,,,(21n i y x x x i ip i i =求出p ββββ,,,,210 及方差2σ的估计;2. 对回归方程及回归系数的种种假设进行检验;3. 如何根据回归方程进行预测和控制,以及如何进行实际问题的结构分析。
2.2 考虑过原点的线性回归模型 n i x y i i i ,,2,1,1 =+=εβ误差n εεε,,,21 仍满足基本假定。
求1β的最小二乘估计。
答:∑∑==-=-=ni ni i i i x y y E y Q 1121121)())(()(ββ∑∑∑===+-=--=∂∂n i n i ni i i i i i i x y x x x y Q111211122)(2βββ 令,01=∂∂βQ即∑∑===-n i ni i i i x y x 11210β 解得,ˆ1211∑∑===ni ini i i xyx β即1ˆβ的最小二乘估计为.ˆ1211∑∑===ni ini ii xyx β2.3 证明: Q (β,β1)= ∑(y i-β0-β1x i)2因为Q (∧β0,∧β1)=min Q (β0,β1 )而Q (β0,β1) 非负且在R 2上可导,当Q 取得最小值时,有即-2∑(y i -∧β0-∧β1x i )=0 -2∑(y i-∧β0-∧β1x i ) x i=0又∵e i =yi -( ∧β0+∧β1x i )= yi -∧β0-∧β1x i ∴∑e i =0,∑e i x i =0(即残差的期望为0,残差以变量x 的加权平均值为零)2.4 解:参数β0,β1的最小二乘估计与最大似然估计在εi~N(0, 2 ) i=1,2,……n 的条件下等价。
应用回归分析人大前四章课后习题答案详解Word版

3.10验证决定系数 与F值之间的关系式: 38
3.11研究货运总量y(万吨)与工业总产值38
1)计算出y, x1 ,x2, x3的相关系数矩阵39
2)求y关于x1, x2, x3的三元线性回归方程40
3)对所求的的方程作拟合优度检验41
③不论是时间序列数据还是横截面数据的手机,样本容量的多少一般要与设置的解释变量数目相配套。
4)统计数据的整理中不仅要把一些变量数据进行折算,差分,甚至把数据对数化,标准化等,有时还须注意剔除个别特别大或特别小的“野值”,有时需要利用差值的方法把空缺的数据补齐。
1.7构造回归理论模型的基本根据是什么?
1)绘制y对x的散点图,可以用直线回归描述两者之间的关系吗?31
2)建立y对x的线性回归;32
3)用线性回归的Plots功能绘制标准残差的直方图和正态概率图,检验误差项的正态性假设。32
3多元线性回归34
3.1写出多元线性回归模型的矩阵表示形式,并给出多元线性回归模型的基本假设。34
3.2讨论样本容量n与自变量个数p的关系,它们对模型的参数估计有何影响?35
由于许多经济变量的前后期之间总是有关联的,因此时间序列数据容易产生模型中随机误差项的序列相关。对于具有随机误差项序列相关的情况,就要通过对数据的某种计算整理来消除序列相关性,最常用的处理方法是差分法。
②横截面数据是在同一时间截面上的统计数据。由于一个回归模型往往涉及众多解释变量,如果其中某一因素或一些因素随着解释变量观测值的变化而对被解释变量产生不同影响,就产生异方差。因此当用截面数据作样本时,容易产生异方差。对于具有异方差性的建模问题,数据整理就是注意消除异方差性,这常与模型参数估计方法结合起来考虑。
应用回归分析-课后知识题目解析-何晓群

第二章一元线性回归2.14 解答:(1)散点图为:(2)x与y之间大致呈线性关系。
(3)设回归方程为01y xββ∧∧∧=+1β∧=12217()ni iiniix y n x yx n x--=-=-=-∑∑0120731y xββ-∧-=-=-⨯=-17y x∧∴=-+可得回归方程为(4)22ni=11()n-2i iy yσ∧∧=-∑2n01i=11(())n-2iy xββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75))[]1169049363110/3=++++=6.1σ∧=≈(5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=-可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x与y的决定系数22121()490/6000.817 ()niiniiy yry y∧-=-=-==≈-∑∑(7)ANOVAx平方和df 均方 F 显著性组间(组合)9.000 2 4.500 9.000.100 线性项加权的8.167 1 8.167 16.333 .056偏差.8331 .833 1.667 .326组内 1.000 2 .500总数10.000 4由于(1,3)F Fα>,拒绝H,说明回归方程显著,x与y有显著的线性关系。
应用回归分析整理课后习题参考答案

第二章 一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答: 假设1、解释变量X 是确定性变量,Y 是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性: E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关: Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi (i=1,2, …,n )仍满足基本假定。
求β1的最小二乘估计 解: 得:2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
证明:∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中:即: ∑e i =0 ,∑e i X i =021112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=0)ˆ(2ˆ111=--=∂∂∑=ii ni i eX X Y Q ββ)()(ˆ1211∑∑===ni i ni ii X Y X β01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回归方程E (Y )=β0+β1X 的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。
答:由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N (β0+β1X i , σ2 ) 最大似然函数:使得Ln (L )最大的0ˆβ,1ˆβ就是β0,β1的最大似然估计值。
同时发现使得Ln (L )最大就是使得下式最小,∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估计的目标函数相同。
应用回归分析第四版课后习题答案-全-何晓群-刘文卿精选全文完整版

可编辑修改精选全文完整版实用回归分析第四版第一章回归分析概述1.3回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章一元线性回归分析思考与练习参考答案2.1一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=σ2i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(X i, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, σ2) i=1,2, …,n2.3 证明(2.27式),∑e i =0 ,∑e i X i=0 。
证明:∑∑+-=-=niiiniXYYYQ12121))ˆˆ(()ˆ(ββ其中:即: ∑e i =0 ,∑e i X i =02.5 证明0ˆβ是β0的无偏估计。
证明:)1[)ˆ()ˆ(1110∑∑==--=-=ni i xxi ni i Y L X X X Y n E X Y E E ββ)] )(1([])1([1011i i xx i n i i xx i ni X L X X X n E Y L X X X n E εββ++--=--=∑∑==01010)()1(])1([βεβεβ=--+=--+=∑∑==i xxi ni i xx i ni E L X X X n L X X X n E 2.6 证明 证明:)] ()1([])1([)ˆ(102110i i xxi ni i xx i n i X Var L X X X n Y L X X X n Var Var εβββ++--=--=∑∑==222212]1[])(2)1[(σσxx xx i xx i ni L X n L X X X nL X X X n +=-+--=∑=2.7 证明平方和分解公式:SST=SSE+SSR证明:2.8 验证三种检验的关系,即验证: (1)21)2(r r n t --=;(2)2221ˆˆ)2/(1/t L n SSE SSR F xx ==-=σβ 证明:(1)01ˆˆˆˆi i i i iY X e Y Y ββ=+=-())1()1()ˆ(222122xx ni iL X n X XX nVar +=-+=∑=σσβ()()∑∑==-+-=-=n i ii i n i i Y Y Y Y Y Y SST 1212]ˆ()ˆ[()()()∑∑∑===-+--+-=ni ii ni i i i ni iY Y Y Y Y Y Y Y 12112)ˆˆ)(ˆ2ˆ()()SSE SSR )Y ˆY Y Y ˆn1i 2i i n1i 2i+=-+-=∑∑==0100ˆˆQQββ∂∂==∂∂ˆt======(2)2222201111 1111ˆˆˆˆˆˆ()()(())(()) n n n ni i i i xxi i i iSSR y y x y y x x y x x Lβββββ=====-=+-=+--=-=∑∑∑∑2212ˆ/1ˆ/(2)xxLSSRF tSSE nβσ∴===-2.9 验证(2.63)式:2211σ)L)xx(n()e(Varxxii---=证明:0112222222ˆˆˆvar()var()var()var()2cov(,)ˆˆˆvar()var()2cov(,())()()11[]2[]()1[1]i i i i i i ii i i ii ixx xxixxe y y y y y yy x y y x xx x x xn L n Lx xn Lβββσσσσ=-=+-=++-+---=++-+-=--其中:222221111))(1()(1))(,()()1,())(ˆ,(),())(ˆ,(σσσββxxixxiniixxiiiniiiiiiiiLxxnLxxnyLxxyCovxxynyCovxxyCovyyCovxxyyCov-+=-+=--+=-+=-+∑∑==2.10 用第9题证明是σ2的无偏估计量证明:2221122112211ˆˆ()()()22()111var()[1]221(2)2n ni ii in niii i xxE E y y E en nx xen n n Lnnσσσσ=====-=---==----=-=-∑∑∑∑第三章1.一个回归方程的复相关系数R=0.99,样本决定系数R2=0.9801,我们能2ˆ22-=∑neiσ判断这个回归方程就很理想吗? 答:不能断定这个回归方程理想。
《应用回归分析》课后题答案[整理版]
![《应用回归分析》课后题答案[整理版]](https://img.taocdn.com/s3/m/603529c1f242336c1eb95eca.png)
《应用回归分析》课后题答案[整理版] 《应用回归分析》部分课后习题答案第一章回归分析概述 1.1 变量间统计关系和函数关系的区别是什么, 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么, 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x 对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么, 答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么,答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2….Cov(εi,εj)=,σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么,在回归变量设置时应注意哪些问题,答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
《应用回归分析》第二版

x 图1. 2 y 与x 非确定性关系图
1 .2 回归方程与回归名称的由来
英国统计学家F.Galton(1822-1911年)。
F.Galton和他的学生、现代统计学的奠基者之一 K.Pearson(1856—1936年)在研究父母身高与其子女 身高的遗传问题时,观察了1 078对夫妇,
yˆ = 33.73 + 0.516x
yˆ = βˆ0 + βˆ1x
x
2 .2 参数β0、β1的估计
∑
∂Q
∂β0
β0
=
βˆ0
=
n
−2
i =1
( yi
− βˆ0
−
βˆ1xi )
=
0
∑ ∂Q
∂β1
β1
=
βˆ1
=
−2
n i =1
( yi
−
βˆ0
−
βˆ1xi )xi
=
0
经整理后,得正规方程组
∑ ∑ nβˆ0
n
+(
i =1
xi )βˆ1
2 .2 参数β0、β1的估计
一、普通最小二乘估计
(Ordinary Least Square Estimation,简记为OLSE)
最小二乘法就是寻找参数β0、β1的估计值使离差平方和达极小
∑n
Q ( βˆ0 , βˆ1 ) = ( y i − βˆ0 − βˆ1 xi ) 2
i =1
∑n
=
min
二、用统计软件计算 2. 例2.1用SPSS软件计算
Variables Entered/Removedb
2 .3 最小二乘估计的性质
三、βˆ0、βˆ1 的方差
《应用回归分析》课后题答案[整理版]
![《应用回归分析》课后题答案[整理版]](https://img.taocdn.com/s3/m/603529c1f242336c1eb95eca.png)
《应用回归分析》课后题答案[整理版] 《应用回归分析》部分课后习题答案第一章回归分析概述 1.1 变量间统计关系和函数关系的区别是什么, 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么, 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x 对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么, 答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么,答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2….Cov(εi,εj)=,σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么,在回归变量设置时应注意哪些问题,答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
《应用回归分析》课后题答案[整理版]
![《应用回归分析》课后题答案[整理版]](https://img.taocdn.com/s3/m/603529c1f242336c1eb95eca.png)
《应用回归分析》课后题答案[整理版] 《应用回归分析》部分课后习题答案第一章回归分析概述 1.1 变量间统计关系和函数关系的区别是什么, 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么, 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x 对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么, 答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么,答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2….Cov(εi,εj)=,σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么,在回归变量设置时应注意哪些问题,答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
应用回归分析-课后习题答案-何晓群
第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈(5)由于2 11(,)xxNLσββ∧:tσ∧==服从自由度为n-2的t分布。
因而/2|(2)1P t nαασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t tααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353即为:(2.49,11.5)22001()(,())xxxNn Lββσ-∧+:t∧∧==服从自由度为n-2的t分布。
因而/2(2)1P t nαα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1pβσββσα∧∧∧∧-<<+=-可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x与y的决定系数22121()490/6000.817()niiniiy yry y∧-=-=-==≈-∑∑(7)ANOVAx平方和df均方 F显着性组间(组合) 9.000 2 4.500 9.000 .100线性项加权的 8.167 1 8.167 16.333 .056偏差.833 1 .833 1.667.326组内 1.000 2 .500总数10.0004由于(1,3)F F α>,拒绝0H ,说明回归方程显着,x 与y 有显着的线性关系。
《应用回归分析》课后题答案解析

《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
应用回归分析第四版课后习题答案_全_何晓群_刘文卿

实用回归分析第四版第一章回归分析概述1.3回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章一元线性回归分析思考与练习参考答案2.1一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=σ2i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(X i, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, σ2) i=1,2, …,n2.3 证明(2.27式),∑e i =0 ,∑e i X i=0 。
证明:∑∑+-=-=niiiniXYYYQ12121))ˆˆ(()ˆ(ββ其中:即: ∑e i =0 ,∑e i X i =02.5 证明0ˆβ是β0的无偏估计。
证明:)1[)ˆ()ˆ(1110∑∑==--=-=ni i xxi n i i Y L X X X Y n E X Y E E ββ )] )(1([])1([1011i i xx i n i i xx i ni X L X X X n E Y L X X X n E εββ++--=--=∑∑==1010)()1(])1([βεβεβ=--+=--+=∑∑==i xx i ni i xx i ni E L X X X nL X X X n E 2.6 证明 证明:)] ()1([])1([)ˆ(102110i i xxi ni ixx i ni X Var L X X X n Y L X X X n Var Var εβββ++--=--=∑∑== 222212]1[])(2)1[(σσxx xx i xx i ni L X n L X X X nL X X X n +=-+--=∑=2.7 证明平方和分解公式:SST=SSE+SSR证明:2.8 验证三种检验的关系,即验证: (1)21)2(r r n t --=;(2)2221ˆˆ)2/(1/t L n SSE SSR F xx ==-=σβ 01ˆˆˆˆi i i i iY X e Y Y ββ=+=-())1()1()ˆ(222122xx ni iL X n X XX nVar +=-+=∑=σσβ()()∑∑==-+-=-=n i ii i n i i Y Y Y Y Y Y SST 1212]ˆ()ˆ[()()()∑∑∑===-+--+-=ni ii ni i i i ni iY Y Y Y Y Y Y Y 12112)ˆˆ)(ˆ2ˆ()()SSESSR )Y ˆY Y Y ˆn1i 2ii n1i 2i +=-+-=∑∑==0100ˆˆQQββ∂∂==∂∂证明:(1)ˆt======(2)2222201111 1111ˆˆˆˆˆˆ()()(())(()) n n n ni i i i xxi i i iSSR y y x y y x x y x x Lβββββ=====-=+-=+--=-=∑∑∑∑2212ˆ/1ˆ/(2)xxLSSRF tSSE nβσ∴===-2.9 验证(2.63)式:2211σ)L)xx(n()e(Varxxii---=证明:0112222222ˆˆˆvar()var()var()var()2cov(,)ˆˆˆvar()var()2cov(,())()()11[]2[]()1[1]i i i i i i ii i i ii ixx xxixxe y y y y y yy x y y x xx x x xn L n Lx xn Lβββσσσσ=-=+-=++-+---=++-+-=--其中:222221111))(1()(1))(,()()1,())(ˆ,(),())(ˆ,(σσσββxxixxiniixxiiiniiiiiiiiLxxnLxxnyLxxyCovxxynyCovxxyCovyyCovxxyyCov-+=-+=--+=-+=-+∑∑==2.10 用第9题证明是σ2的无偏估计量证明:2221122112211ˆˆ()()()22()111var()[1]221(2)2n ni ii in niii i xxE E y y E en nx xen n n Lnnσσσσ=====-=---==----=-=-∑∑∑∑第三章2ˆ22-=∑neiσ1.一个回归方程的复相关系数R=0.99,样本决定系数R 2=0.9801,我们能判断这个回归方程就很理想吗? 答:不能断定这个回归方程理想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章回归分析概述1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章一元线性回归分析思考与练习参考答案2.1一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=σ2i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(X i, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, σ2) i=1,2, …,n2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
证明:其中:即: ∑e i =0 ,∑e i X i =02.5 证明0ˆβ是β0的无偏估计。
证明:)1[)ˆ()ˆ(1110∑∑==--=-=ni i xx i n i iY L X X X Y n E X Y E E ββ )] )(1([])1([1011i i xx i n i i xx i ni X L X X X n E Y L X X X n E εββ++--=--=∑∑==1010)()1(])1([βεβεβ=--+=--+=∑∑==i xx i ni i xx i ni E L X X X nL X X X n E 2.6 证明 证明:)] ()1([])1([)ˆ(102110i i xx i ni i xx i ni X Var L X X X nY L X X X n Var Var εβββ++--=--=∑∑== 222212]1[])(2)1[(σσxxxx i xx i ni L X n L X X X nL X X X n +=-+--=∑=2.7 证明平方和分解公式:SST=SSE+SSR证明:∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ01ˆˆˆˆi i i i iY X e Y Y ββ=+=-())1()1()ˆ(222122xx ni iL X n X XX nVar +=-+=∑=σσβ()()∑∑==-+-=-=n i ii i n i i Y Y Y Y Y Y SST 1212]ˆ()ˆ[()()()∑∑∑===-+--+-=ni ii ni i i i ni iY Y Y Y Y Y Y Y 12112)ˆˆ)(ˆ2ˆ()()SSESSR )Y ˆY Y Y ˆn1i 2ii n1i 2i +=-+-=∑∑==0100ˆˆQQββ∂∂==∂∂2.8 验证三种检验的关系,即验证: (1)21)2(r r n t --=;(2)2221ˆˆ)2/(1/t L n SSE SSR F xx ==-=σβ 证明:(1)ˆt ======(2)22222011111111ˆˆˆˆˆˆ()()(())(())nnnni i ii xx i i i i SSR y y x y y x x y x x L βββββ=====-=+-=+--=-=∑∑∑∑2212ˆ/1ˆ/(2)xx L SSR F t SSE n βσ∴===-2.9 验证(2.63)式:2211σ)L )x x (n ()e (Var xx i i ---=证明:112222222ˆˆˆvar()var()var()var()2cov(,)ˆˆˆvar()var()2cov(,())()()11[]2[]()1[1]i i i i i i i iiiii i xx xxi xxe y yy y y y y x y y x x x x x x n L n L x x n L βββσσσσ=-=+-=++-+---=++-+-=--其中:222221111))(1()(1))(,()()1,())(ˆ,(),())(ˆ,(σσσββxxi xx i ni i xxii i ni i i ii i i i L x x n L x x n y L x x y Cov x x y n y Cov x x y Cov y y Cov x x y y Cov -+=-+=--+=-+=-+∑∑==2.10 用第9题证明是σ2的无偏估计量证明:2ˆ22-=∑n eiσ2221122112211ˆˆ()()()22()111var()[1]221(2)2n n i i i i n n i i i i xx E E y y E e n n x x e n n n L n n σσσσ=====-=---==----=-=-∑∑∑∑ 第三章1.一个回归方程的复相关系数R=0.99,样本决定系数R 2=0.9801,我们能判断这个回归方程就很理想吗? 答:不能断定这个回归方程理想。
因为:1. 在样本容量较少,变量个数较大时,决定系数的值容易接近1,而此时可能F 检验或者关于回归系数的t 检验,所建立的回归方程都没能通过。
2. 样本决定系数和复相关系数接近于1只能说明Y 与自变量X1,X2,…,Xp 整体上的线性关系成立,而不能判断回归方程和每个自变量是显著的,还需进行F 检验和t 检验。
3. 在应用过程中发现,在样本容量一定的情况下,如果在模型中增加解释变量必定使得自由度减少,使得 R 2往往增大,因此增加解释变量(尤其是不显著的解释变量)个数引起的R 2的增大与拟合好坏无关。
21ˆˆ*,1,2,...,)njj j i j pL X β====-∑jji j 其中: (X2.被解释变量Y 的期望值与解释变量k X X X ,,,21 的线性方程为:01122()k k E Y X X X ββββ=++++(3-2)称为多元总体线性回归方程,简称总体回归方程。
对于n 组观测值),,2,1(,,,,21n i X X X Y ki i i i =,其方程组形式为:01122,(1,2,,)i i i k ki i Y X X X i n ββββμ=+++++=(3-3) 即⎪⎪⎩⎪⎪⎨⎧+++++=+++++=+++++=nkn k n n n k k k k X X X Y X X X Y X X X Y μββββμββββμββββ 2211022222121021121211101 其矩阵形式为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n Y Y Y 21=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡kn n nk k X X X X X X X X X 212221212111111⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡k ββββ 210+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n μμμ 21即=+Y X βμ(3-4)其中=⨯1n Y ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n Y Y Y 21为被解释变量的观测值向量;=+⨯)1(k n X ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡kn n n k k X X X X X X X X X 212221212111111为解释变量的观测值矩阵;(1)1k +⨯=β⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡k ββββ 210为总体回归参数向量;1n ⨯=μ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n μμμ 21为随机误差项向量。
多元回归线性模型基本假定:课本P57第四章4.3 简述用加权最小二乘法消除一元线性回归中异方差性的思想与方法。
答:普通最小二乘估计就是寻找参数的估计值使离差平方和达极小。
其中每个平方项的权数相同,是普通最小二乘回归参数估计方法。
在误差项等方差不相关的条件下,普通最小二乘估计是回归参数的最小方差线性无偏估计。
然而在异方差的条件下,平方和中的每一项的地位是不相同的,误差项的方差大的项,在残差平方和中的取值就偏大,作用就大,因而普通最小二乘估计的回归线就被拉向方差大的项,方差大的项的拟合程度就好,而方差小的项的拟合程度就差。
由OLS 求出的仍然是的无偏估计,但不再是最小方差线性无偏估计。
所以就是:对较大的残差平方赋予较小的权数,对较小的残差平方赋予较大的权数。
这样对残差所提供信息的重要程度作一番校正,以提高参数估计的精度。
加权最小二乘法的方法:4.4简述用加权最小二乘法消除多元线性回归中异方差性的思想与方法。
答:运用加权最小二乘法消除多元线性回归中异方差性的思想与一元线性回归的类似。
多元线性回归加权最小二乘法是在平方和中加入一个适当的权数i w ,以调整各项在平方和中的作用,加权最小二乘的离差平方和为:220111ˆˆˆ()()N Nw i i i i i ii i Q w y y w y x ββ===-=--∑∑22__1_2__02222()()ˆ()ˆ1111,i i Nw iii w i wi www w w kx i ii imi i i miw xx y y x x y x w kx x kx w x σβββσσ==---=-=====∑∑1N i =11表示=或∑=----=ni ip p i i i p w x x y w Q 1211010)( ),,,(ββββββ(2)加权最小二乘估计就是寻找参数p βββ,,,10 的估计值pw w w βββˆ,,ˆ,ˆ10 使式(2)的离差平方和w Q 达极小。
所得加权最小二乘经验回归方程记做ppw w w w x x y βββˆˆˆˆ110+++= (3) 多元回归模型加权最小二乘法的方法:首先找到权数i w ,理论上最优的权数i w 为误差项方差2i σ的倒数,即21ii w σ=(4)误差项方差大的项接受小的权数,以降低其在式(2)平方和中的作用; 误差项方差小的项接受大的权数,以提高其在平方和中的作用。
