数据压缩实验指导书
数据压缩实验指导书
数据压缩实验指导书《数据压缩》实验指导书（24学时）实验一图像输入与输出基本操作（2学时）实验二图像预测编码（3学时）实验三图像熵编码与压缩（3学时）实验四图像dct变换编码与压缩（4学时）实验五图像小波变换编码与压缩（4学时）实验六jpeg编解码（4学时）实验七矢量量化图像压缩（4学时）实验一图像输出与输入基本操作一、实验题目：图像输出与输入操作方式二、实验目的自学在matlab环境下对图像文件的i/o操作方式，为加载各种格式的图像文件和后续进行图像处理打下基础。
三、实验内容利用matlab为用户提供的专门函数从图像格式的文件中读/写图像数据、显示图像，以及查询图像文件的信息。
四、预备知识熟识matlab研发环境。
五、实验原理（1）图像文件的加载利用imread函数可以完成图像文件的读取操作。
常用语法格式为：i=imread(‘filename’,‘fmt’)或i=imread(‘filename.fmt’)；其促进作用就是将文件名用字符串filename则表示的、扩展名用字符串fmt（则表示图像文件格式）则表示的图像文件中的数据念至矩阵i中。
当filename中不涵盖任何路径信息时，imread可以从当前工作目录中找寻并加载文件。
必须想要加载选定路径中的图像，最简单的方法就是在filename中输出完备的或相对的地址。
matlab积极支持多种图像文件格式的读、写和显示。
因此参数fmt常用的可能值有：‘bmp’windows图形格式‘jpg’or‘jpeg’联手图像专家组格式‘tif’or‘tiff’标志图像文件格式‘gif’图形互换格式‘pcx’windows画刷格式‘png’可移动网络图形格式‘xwd’xwindowdump格式比如，命令行>>i=imread(‘lena.jpg’);将jpeg图像lena读入图像矩阵i中。
（2）图像文件的写入（保存）利用imwrite顺利完成图像的输入和留存操作方式，也全然积极支持也全然积极支持上述各种图像文件的格式。
数据压缩实验报告
实验一常见压缩软件的使用一、实验目的使用一些常见的压缩软件，对数据压缩的概念、分类、技术和标准形成初步的认识和理解。
二、实验要求1．认真阅读实验指导书，按实验步骤完成实验内容。
2．实验过程中注意思考实验提出的问题，并通过实验解释这些问题。
3．通过实验达到实验目的。
三、实验环境计算机硬件：CPU处理速度1GHz以上，内存258M以上，硬盘10G以上软件：Windows操作系统2000或XP。
四、实验内容1．使用WinZip或WinRAR两种压缩软件分别对文本文件(.txt,.doc)、程序源代码文件(.c)、数据文件(.dat)、二进制目标代码文件(.obj)、图像文件(.bmp)、音频文件(.wav)和视频文件(.avi,.wmv)进行压缩，分别计算出压缩率，判断这两种压缩软件采用的是可逆压缩还是不可以压缩，猜测其可能用到了那些压缩（编码）技术？2．使用jpegimager、TAK和BADAK分别进行图像、音频和视频的压缩，体验其压缩效果。
3．使用bcl程序对文本文件、程序源代码文件、数据文件、二进制目标代码文件、图像文件等进行多种统计编码技术的压缩，包括香农-费诺(shannon-fano)编码、霍夫曼(huffman)编码、游程编码rle、字典编码lz等，记录每种压缩方法对不同类型文件的压缩效果并进行比较，结合所学知识，解释其中的原因。
五、实验步骤1、下载并打开WinZip和WinRAR两种压缩软件2、分别新建两个文档：qqjj.winzip 和winrar。
添加所要压缩的文件：文本文件(.txt,.doc)、程序源代码文件(.c)、数据文件(.dat)、二进制目标代码文件(.obj)、图像文件(.bmp)、音频文件(.wav)和视频文件(.avi,.wmv)进行压缩，如图所示：3、WinZip压缩软件可以直接看出各文件的压缩率，而winrar压缩软件不能直接看出各文件的压缩率，要在winrar压缩软件的屏幕上只显示一个压缩文件时，右健该压缩文件，点击显示信息方可看到该压缩文件的压缩率。
数据结构(5)_文件压缩
数据结构实验报告实验名称：文件压缩实验类型：综合性试验班级：20112111学号：2011211107姓名：冯若航实验日期：2003.6.19 下午4:001.问题描述文件压缩①基本要求哈夫曼编码是一种常用的数据压缩技术，对数据文件进行哈夫曼编码可大大缩短文件的传输长度，提高信道利用率及传输效率。
要求采用哈夫曼编码原理，统计文本文件中字符出现的词频，以词频作为权值，对文件进行哈夫曼编码以达到压缩文件的目的，再用哈夫曼编码进行译码解压缩。
●统计待压缩的文本文件中各字符的词频，以词频为权值建立哈夫曼树，并将该哈夫曼树保存到文件HufTree.dat中。
●根据哈夫曼树（保存在HufTree.dat中）对每个字符进行哈夫曼编码，并将字符编码保存到HufCode.txt文件中。
●压缩：根据哈夫曼编码，将源文件进行编码得到压缩文件CodeFile.dat。
●解压：将CodeFile.dat文件利用哈夫曼树译码解压，恢复为源文件。
2.数据结构设计此类问题，应设计文件的数据结构。
* 4 压缩头标记* 1 文件名长度* ns 文件名* 4 源文件长度* 1020 huffman树* 1021~EOF 文件内容赫夫曼树节点的数据结构typedef struct node{long w; //权short p,l,r; //父亲，左孩子，右孩子}HTNODE,*HTNP; //霍夫曼树的结点赫夫曼编码数组元素的数据结构设计typedef struct huffman_code{BYTE len; //长度BYTE *codestr; //字符串}HFCODE; //霍夫曼编码数组元素3.算法设计源代码#define_CRT_SECURE_NO_DEPRECATE#include<stdio.h>#include<string.h>#include<stdlib.h>typedef unsigned int UINT;typedef unsigned char BYTE;typedef struct node{long w; //权short p,l,r; //父亲，左孩子，右孩子}HTNODE,*HTNP; //霍夫曼树的结点typedef struct huffman_code{BYTE len; //长度BYTE *codestr; //字符串}HFCODE; //霍夫曼编码数组元素#define OK 1#define ERROR -1#define UNUSE -1 //未链接节点标志#define CHAR_BITS 8 //一个字符中的位数#define INT_BITS 32 //一个整型中的位数#define HUFCODE_SIZE 256 //霍夫曼编码个数#define BUFFERSIZE 256 //缓冲区大小大小#define UINTSIZE sizeof(UINT)#define BYTESIZE sizeof(BYTE)#define TAG_ZIGHEAD 0xFFFFFFFF //压缩文件头标#define MAX_FILENAME512//函数声明//压缩模块int Compress(char *SourceFilename,char *DestinationFilename);//压缩调用int Initializing(char *SourceFilename,FILE **inp,char *DestinationFilename,FILE **outp); //初始化文件工作环境long AnalysisFiles(FILE *in,long frequency[]);//计算每个不同字节的频率以及所有的字节数int CreateHuffmanTree(long w[],int n,HTNODE ht[]);//生成霍夫曼树int HuffmanTreeCoding(HTNP htp,int n,HFCODE hc[]);//霍夫曼编码int Search(HTNP ht,int n);//查找当前最小权值的霍夫曼树节点并置为占用BYTE Char2Bit(const BYTE chars[CHAR_BITS]);//将一个字符数组转换成二进制数字int Search(HTNP ht,int n);//查找当前最小权值的霍夫曼树节点并置为占用int WriteZipFiles(FILE *in,FILE *out,HTNP ht,HFCODE hc[],char* SourceFilename,long source_filesize);//写压缩文件//解压缩模块int DeCompress(char *SourceFilename,char *DestinationFilename);//解压缩调用int Initializing_Dezip(char *SourceFilename,FILE **inp,char*DestinationFilename,FILE **outp); //为处理解压缩流程初始化文件void ReadHuffmanTree(FILE* in,short mini_ht[][2]);//从待解压缩文件中读取huffman树int WriteDeZipFiles(FILE *in,FILE* out,short mini_ht[][2],long bits_pos,longDst_Filesize); //写解压缩文件void ErrorReport(int error_code);//报错//函数定义//函数实现//压缩int Compress(char *SourceFilename,char *DestinationFilename){FILE *in,*out; //输入输出流int i; //计数变量float Compress_rate; //存放压缩率HFCODE hc[HUFCODE_SIZE]; //存放256个字符的huffman编码HTNODE ht[HUFCODE_SIZE*2-1]; //256个字符的huffman树需要2*256-1=511个节点。
数据压缩实验报告4 (2)
桂林理工大学实验报告（2013~ 2014 学年度第一学期）班级: 学号 : 姓名: 实验名称: 实验四图像DCT变换编码与压缩日期: 2013年12月12日一、实验题目:图像DCT变换编码与压缩二、实验目的:（1）掌握离散余弦变换DCT的实现方法, 了解DCT的幅度分布特性, 从而加深对DCT变换的认识。
（2）掌握图像DCT变换编码的实现方法, 从而加深对变换编码压缩图像原理的理解。
三、实验内容:编程实现图像DCT变换编码。
四、预备知识:（1）熟悉DCT原理。
（2）熟悉变换编码原理。
（3）熟悉在MA TLAB环境下对图像文件的I/O操作。
五、实验原理:变换编码是在变换域进行图像压缩的一种技术。
图2.2.1显示了一个典型的变换编码系统。
压缩图像输入图像N×N图2.2.1 变换编码系统在变换编码系统中, 如果正变换采用DCT变换就称为DCT变换编码系统。
DCT用于把一幅图像映射为一组变换系数, 然后对系数进行量化和编码。
对于大多数的正常图像来说, 多数系数具有较小的数值且可以被粗略地量化（或者完全抛弃）, 而产生的图像失真较小。
DCT是仅次于K-L变换的次最佳正交变换, 且以获得广泛应用, 并成为许多图像编码国际标准的核心。
离散余弦变换的变换核为余弦函数, 计算速度快, 有利于图像压缩和其他处理。
对于N×N的数字图像, 二维DCT变换的正反变换可表示为：11001100(21)(21)(,)()()(,)cos cos222(21)(21)(,)()()(,)cos cos22N Nx yN Nu vx u y vF u v c u c v f x yN Nx u y vf x y c u c v F u vN N Nππππ--==--==++=++=∑∑∑∑（2.2.1）其中，00()()1,1,2,...,1u vc u c vu v N⎧==⎪==⎨=-⎪⎩或MA TLAB图像处理工具箱实现离散余弦变换有两种方法:（1）使用函数dct2, 该函数用一个基于FFT的算法来提高当输入较大的方阵时的计算速度。
JPEG图像压缩实验_百度文库.
JPEG 静态图像压缩实验指导书一、实验目的1. 了解多媒体通信中图像压缩技术2. 熟悉 JPEG 图像压缩编码过程3. 掌握二维 DCT 变换算法二、实验原理JPEG(Joint Photographic Experts Group 是一个由 ISO 和 ITU-T 两个组织机构联合组成的一个图像专家小组,负责制定静态的数字图像数据压缩编码标准, 这个专家组开发的算法称为 JPEG 算法,并且成为国际上通用的标准。
JPEG 是一个适用范围很广的静态图像数据压缩标准, 既可用于灰度图像又可用于彩色图像。
JPEG 不仅适于静止图像的压缩,电视图像的帧内图像的压缩编码,也常采用此算法。
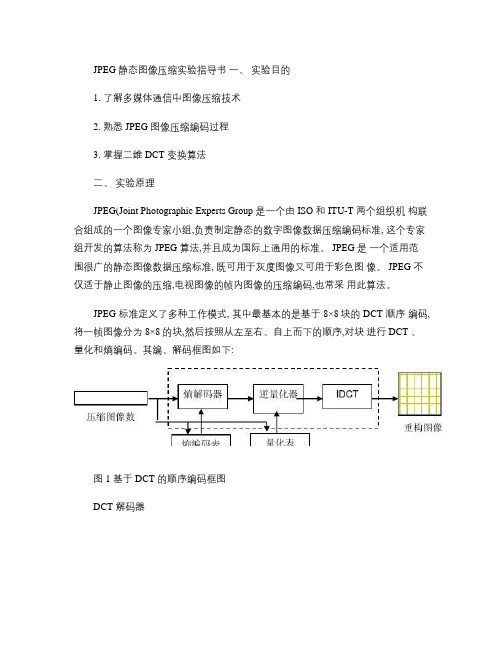
JPEG 标准定义了多种工作模式, 其中最基本的是基于 8×8块的 DCT 顺序编码,将一帧图像分为 8×8的块,然后按照从左至右、自上而下的顺序,对块进行 DCT 、量化和熵编码。
其编、解码框图如下:图 1 基于 DCT 的顺序编码框图DCT 解码器图 2 基于 DCT 的顺序解压缩框图JPEG 压缩编码算法的主要计算步骤:1 正向离散余弦变换 (FDCT。
2 量化 (quantization。
3 Z 字形编码 (zigzag scan。
4 使用差分脉冲编码调制 (differential pulse code modulation, DPCM 对直流系数(DC进行编码。
5 使用行程长度编码 (run-length encoding, RLE 对交流系数 (AC进行编码。
6 熵编码 (entropy coding。
三、实验内容按照上述压缩过程实现一幅图像的压缩,生成符合 JPEG 标准的图像文件 JPEG 图像编码流程如下:图 3 JPEG 图像编码流程1. DCT 变换对 8×8的图像数据块进行二维 DCT 的变换, 把能量集中在少数几个系数上,从而达到数据压缩的目的。
:DCT 变换公式 :DCT 反变换公式:其中:二维 DCT 变换可以分解为行和列的一维 DCT 变换的组合运算, 也可将 8×8的块分为更小的子块,直接对二维数据进行 2维快速余弦变换。
数据压缩实验
ok
数据压缩编码的分类
数据压缩方法根据不同的分类标准而不同 第一种，根据质量有无损失可分为：无损压缩和有损 压缩。 第二种，按照其作用域在空间域或频率域上分为：空 间方法、变换方法和混合方法。 第三种，根据是否自适应分为自适应性编码和非适应 性编码，一般来说，每一个编码方法都有其相应的自 适应算法。 第四种，按其原理分类也可分为：预测编码、变换编 码、量化与矢量量化编码、信息熵编码、分频带编码、 结构编码和基于知识的编码。
LZW压缩算法
LZW压缩算法是一种新颖的压缩方法，由 Lemple-Ziv-Welch 三人共同创造，用他们的名 字命名。它采用了一种先进的串表压缩，将每 个第一次出现的串放在一个串表中，用一个数 字来表示串，压缩文件只存贮数字，则不存贮 串，从而使图象文件的压缩效率得到较大的提 高。不管是在压缩还是在解压缩的过程中都能 正确的建立这个串表，压缩或解压缩完成后， 这个串表又被丢弃。
LZW压缩算法
LZW算法中，首先建立一个字符串表， 把每一个第一次出现的字符串放入串表 中，并用一个数字来表示，这个数字与 此字符串在串表中的位置有关，并将这 个数字存入压缩文件中，如果这个字符 串再次出现时，即可用表示它的数字来 代替，并将这个数字存入文件中。压缩 完成后将串表丢弃。
实现
参考代码LZW.java。
常用压缩编码算法的基本原理及实现技术
预测编码：编码器记录与传输的不是样本的真 实值，而是它与预测值的差。这一方法称为差 值脉冲编码调制（differential pulse code modulation，简称DPCM）方法 。 变换编码（K-L变换、DCT变换）：其主要思想 是利用图像块内像素值之间的相关性，把图像 变换到一组新的基上，使得能量集中到少数几 个变换系数上，通过存储这些系数而达到压缩 的目的 统计编码（Huffman编码、算术编码）：最常 用的统计编码是Huffman编码 。
实验报告-数据滤波和数据压缩实验
实验报告-数据滤波和数据压缩实验实验题⽬：使⽤Haar ⼩波和傅⾥叶变换⽅法滤波及数据压缩 1 实验⽬的（1）掌握离散数据的Haar ⼩波变换和傅⾥叶变换的定义，基本原理和⽅法（2）使⽤C++实现数据的Haar ⼩波变换和离散傅⾥叶变换（3）掌握数据滤波的基本原理和⽅法（4）掌握使⽤Haar ⼩波变换和离散傅⾥叶变换应⽤于数据压缩的基本原理和⽅法，并且对两种数据压缩进⾏评价2 实验步骤2.1 算法原理2.1.1 Haar ⼩波变换（1）平均，细节及压缩原理设{x1，x2}是⼀组两个元素组成的信号，定义平均与细节为(12)/2a x x =+，(12)/2d x x =-。
则可以将{a ，d}作为原信号的⼀种表⽰，且信号可由{a ，d}恢复，1x a d =+，2x a d =-。
由上述可以看出，当x1，x2⾮常接近时，d 会很⼩。
此时，{x1，x2}可以近似的⽤{a}来表⽰，由此实现了信号的压缩。
重构的信号为{a ，a}，误差信号为{|1|,|2|}{||,||}x a x a d d --=。
因此，平均值a 可以看做是原信号的整体信息，⽽d 可以看成是原信号的细节信息。
⽤{a}近似的表⽰原信号，可以实现对原信号的压缩，⽽且丢失的细节对于最终信号的重构不会有重⼤影响。
对于多元素的信号，可以看成是对于⼆元信号的⼀种推⼴。
（2）尺度函数和⼩波⽅程在⼩波分析中，引⼊记号[1,0)()()t X t φ=，其中，[1,0)()X t 表⽰区间[1，0]上的特征函数。
定义称()t φ为Haar 尺度函数。
由上式可知，,()j k t φ都可以由0,0()t φ伸缩和平移得到。
⼩波分析中，对于信号有不同分辨率的表⽰，当⽤较低分辨率来表⽰原始信号时，会丢失细节信息，需要找到⼀个函数来描述这种信息，该函数称之为⼩波函数。
基本的⼩波函数定义如下：则()(2)(21)t t t ψφφ=--。
()t ψ称为Haar ⼩波。
数据结构实验报告4文件压缩概要
数据结构与程序设计实验实验报告哈尔滨工程大学实验报告四一、问题描述哈夫曼编码是一种常用的数据压缩技术，对数据文件进行哈夫曼编码可大大缩短文件的传输长度，提高信道利用率及传输效率。
要求采用哈夫曼编码原理，统计文本文件中字符出现的词频，以词频作为权值，对文件进行哈夫曼编码以达到压缩文件的目的，再用哈夫曼编码进行译码解压缩。
统计待压缩的文本文件中各字符的词频，以词频为权值建立哈夫曼树，并将该哈夫曼树保存到文件HufTree.dat 中。
根据哈夫曼树（保存在HufTree.dat 中）对每个字符进行哈夫曼编码，并将字符编码保存到HufCode.txt 文件中。
压缩：根据哈夫曼编码，将源文件进行编码得到压缩文件CodeFile.dat。
解压：将CodeFile.dat 文件利用哈夫曼树译码解压，恢复为源文件。
二、数据结构设计由于哈夫曼树中没有度为1的结点，则一棵树有n个叶子结点的哈夫曼树共有2n-1个结点，可以存储在一个大小为2n-1的一维数组中，而且对每个结点而言，即需知双亲结点的信息，又需知孩子结点的信息，由此可采用如下数据结构。
1.使用结构体数组统计词频，并存储:typedef struct Node{int weight; //叶子结点的权值char c; //叶子结点int num; //叶子结点的二进制码的长度}LeafNode[N];2.使用结构体数组存储哈夫曼树:typedef struct{unsigned int weight;//权值unsigned int parent, LChild, RChild;}HTNode,Huffman[M+1]; //huffman树3.使用字符指针数组存储哈夫曼编码表：typedef char *HuffmanCode[2*M]; //haffman编码表三、算法设计1.读取文件，获得字符串void read_file(char const *file_name, char *ch){FILE *in_file = Fopen(file_name, "r");unsigned int flag = fread(ch, sizeof(char), N, in_file);if(flag == 0){printf("%s读取失败\n", file_name);fflush(stdout);}printf("读入的字符串是: %s\n\n", ch);Fclose(in_file);int len = strlen(ch);。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
目 录实验一用C/C++语言实现游程编码实验二用C/C++语言实现算术编码实验三用C/C++语言实现LZW编码实验四用C/C++语言实现2D-DCT变换13实验一用C/C++语言实现游程编码1. 实验目的1) 通过实验进一步掌握游程编码的原理；2) 用C/C++语言实现游程编码。
2. 实验要求给出数字字符，能正确输出编码。
3. 实验内容现实中有许多这样的图像，在一幅图像中具有许多颜色相同的图块。
在这些图块中，许多行上都具有相同的颜色，或者在一行上有许多连续的象素都具有相同的颜色值。
在这种情况下就不需要存储每一个象素的颜色值，而仅仅存储一个象素的颜色值，以及具有相同颜色的象素数目就可以，或者存储一个象素的颜色值，以及具有相同颜色值的行数。
这种压缩编码称为游程编码，常用(run length encoding，RLE)表示，具有相同颜色并且是连续的象素数目称为游程长度。
为了叙述方便，假定一幅灰度图像，第n行的象素值为：用RLE编码方法得到的代码为：0@81@38@501@40@8。
代码中用黑体表示的数字是游程长度，黑体字后面的数字代表象素的颜色值。
例如黑体字50代表有连续50个象素具有相同的颜色值，它的颜色值是8。
对比RLE编码前后的代码数可以发现，在编码前要用73个代码表示这一行的数据，而编码后只要用11个代码表示代表原来的73个代码，压缩前后的数据量之比约为7:1，即压缩比为7:1。
这说明RLE确实是一种压缩技术，而且这种编码技术相当直观，也非常经济。
RLE所能获得的压缩比有多大，这主要是取决于图像本身的特点。
如果图像中具有相同颜色的图像块越大，图像块数目越少，获得的压缩比就越高。
反之，压缩比就越小。
译码时按照与编码时采用的相同规则进行，还原后得到的数据与压缩前的数据完全相同。
因此，RLE是无损压缩技术。
RLE压缩编码尤其适用于计算机生成的图像，对减少图像文件的存储空间非常有效。
然而，RLE对颜色丰富的自然图像就显得力不从心，在同一行上具有相同颜色的连续象素往往很少，而连续几行都具有相同颜色值的连续行数就更少。
如果仍然使用RLE编码方法，不仅不能压缩图像数据，反而可能使原来的图像数据变得更大。
请注意，这并不是说RLE编码方法不适用于自然图像的压缩，相反，在自然图像的压缩中还真少不了RLE，只不过是不能单纯使用RLE一种编码方法，需要和其他的压缩编码技术联合应用。
4、思考题：①如果是英文字符，应该从哪几方面去进行考虑？②是否所有的字符都要RLE编码方法来进行编码？③如何区分字符与重复因子？实验二用C/C++语言实现算术编码1. 实验目的1) 通过实验进一步掌握算术编码的原理；2) 用C/C++语言实现算术编、解码。
2. 实验要求1) 能正确进行码字刷新及区间刷新；2) 合理输出码字；3) 能正确解码。
3. 实验内容[过程1] 假设信源符号为{00, 01, 10, 11}，这些符号的概率分别为{ 0.1, 0.4, 0.2, 0.3 }，根据这些概率可把间隔[0, 1)分成4个子间隔：[0, 0.1), [0.1, 0.5), [0.5, 0.7), [0.7, 1)，其中表示半开放间隔，即包含不包含。
上面的信息可综合在表1中。
编码时首先输入的符号是10，找到它的编码范围是[0.5,0.7)。
由于消息中第二个符号00的编码范围是[0, 0.1)，因此它的间隔就取[0.5, 0.7)的第一个十分之一作为新间隔[0.5, 0.52)。
依此类推，编码第3个符号11时取新间隔为[0.514, 0.52)，编码第4个符号00时，取新间隔为[0.514, 0.5146)，… 。
消息的编码输出可以是最后一个间隔中的任意数。
整个编码过程如图1所示。
图1 算术编码过程举例这个例子的编码和译码的全过程分别表示在表4-05和表4-06中。
根据上面所举的例子，可把计算过程总结如下。
考虑一个有M个符号的字符表集，假设概率，而。
输入符号用表示，第个子间隔的范围用表示。
其中，和，表示间隔左边界的值,表示间隔右边界的值，表示间隔长度。
编码步骤如下：步骤1：首先在1和0之间给每个符号分配一个初始子间隔，子间隔的长度等于它的概率，初始子间隔的范围用[，)表示。
令，和。
步骤2：L和R的二进制表达式分别表示为：和其中和等于“1”或者“0”。
比较和：①如果，不发送任何数据，转到步骤3；②如果，就发送二进制符号。
比较和：①如果，不发送任何数据，转到步骤3；②如果，就发送二进制符号。
这种比较一直进行到两个符号不相同为止，然后进入步骤3，步骤3：加1，读下一个符号。
假设第个输入符号为，按照以前的步骤把这个间隔分成如下所示的子间隔：令，和，然后转到步骤2。
假设有4个符号的信源，它们的概率如表4所示：[过程2] 假设有4个符号的信源，它们的概率如表4所示：概率。
它的编码过程，现说明如下。
输入第1个符号是，可知，定义初始间隔[，)＝[0.5, 0.75)，由此可知，左右边界的二进制数分别表示为：L ＝0.5=0.1(B)，R ＝0.7＝0.11… (B)。
按照步骤2，，发送1。
因，因此转到步骤3。
输入第2个字符，，它的子间隔，)＝[0.5, 0.625)，由此可得=0.125。
左右边界的二进制数分别表示为：L＝0.5=0.100 … (B)，R＝0.101… (B)。
按照步骤2，，发送0，而和不相同，因此在发送0之后就转到步骤3。
输入第3个字符，，, 它的子间隔[,)＝[0.59375, 0.609375)，由此可得=0.015625。
左右边界的二进制数分别表示为：＝0.59375=0.10011 (B)，＝0.609375=0.100111 (B)。
按照步骤2，，，，但和不相同，因此在发送011之后转到步骤3。
…发送的符号是：10011…。
被编码的最后的符号是结束符号。
图2 算术编码概念就这个例子而言，算术编码器接受的第1位是“1”，它的间隔范围就限制在[0.5, 1)，但在这个范围里有3种可能的码符,和，因此第1位没有包含足够的译码信息。
在接受第2位之后就变成“10”，它落在[0.5, 0.75)的间隔里，由于这两位表示的符号都指向开始的间隔，因此就可断定第一个符号是。
在接受每位信息之后的译码情况如下表5所示。
表5 译码过程表接受的数字间隔译码输出1[0.5, 1)-[0.5, 0.75)0[0.5,0.609375)1[0.5625,0.609375)-1[0.59375,0.609375)………度，因此译码器的译码过程不会无限制地运行下去。
实际上在译码器中需要添加一个专门的终止符，当译码器看到终止符时就停止译码。
在算术编码中需要注意的几个问题：1) 由于实际的计算机的精度不可能无限长，运算中出现溢出是一个明显的问题，但多数机器都有16位、32位或者64位的精度，因此这个问题可使用比例缩放方法解决。
2) 算术编码器对整个消息只产生一个码字，这个码字是在间隔[0, 1)中的一个实数，因此译码器在接受到表示这个实数的所有位之前不能进行译码。
3) 算术编码也是一种对错误很敏感的编码方法，如果有一位发生错误就会导致整个消息译错。
算术编码可以是静态的或者自适应的。
在静态算术编码中，信源符号的概率是固定的。
在自适应算术编码中，信源符号的概率根据编码时符号出现的频繁程度动态地进行修改，在编码期间估算信源符号概率的过程叫做建模。
需要开开发态算术编码的原因是因为事先知道精确的信源概率是很难的，而且是不切实际的。
当压缩消息时，我们不能期待一个算术编码器获得最大的效率，所能做的最有效的方法是在编码过程中估算概率。
因此动态建模就成为确定编码器压缩效率的关键。
实验三用C/C++语言实现LZW编码1. 实验目的1) 通过实验进一步掌握LZW编码的原理；2) 用C/C++语言实现LZW编、解码。
2. 实验要求给出字符，能正确输出编码，并能进行译码。
3. 实验内容1) 编码过程LZW编码是围绕称为词典的转换表来完成的。
这张转换表用来存放称为前缀(Prefix)的字符序列，并且为每个表项分配一个码字(Code word)，或者叫做序号，如表6所示。
这张转换表实际上是把8位ASCII字符集进行扩充，增加的符号用来表示在文本或图像中出现的可变长度ASCII字符串。
扩充后的代码可用9位、10位、11位、12位甚至更多的位来表示。
Welch的论文中用了12位，12位可以有4096个不同的12位代码，这就是说，转换表有4096个表项，其中256个表项用来存放已定义的字符，剩下3840个表项用来存放前缀(Prefix)。
LZW编码器(输入与输出之间的转换。
LZW编码器的输入是字符流(Charstream)，字符流可以是用8位ASCII字符组成的字符串，而输出是用n位(例如12位)表示的码字流(Codestream)，码字代表单个字符或多个字符组成的字符串。
LZW编码器使用了一种很实用的分析(parsing)算法，称为贪婪分析算法(greedy parsing algorithm)。
在贪婪分析算法中，每一次分析都要串行地检查来自字符流(Charstream)的字符串，从中分解出已经识别的最长的字符串，也就是已经在词典中出现的最长的前缀(Prefix)。
用已知的前缀(Prefix)加上下一个输入字符C也就是当前字符(Current character)作为该前缀的扩展字符，形成新的扩展字符串——缀-符串(String)：Prefix.C。
这个新的缀-符串(String)是否要加到词典中，还要看词典中是否存有和它相同的缀-符串String。
如果有，那么这个缀-符串(String)就变成前缀(Prefix)，继续输入新的字符，否则就把这个缀-符串(String)写到词典中生成一个新的前缀(Prefix)，并给一个代码。
LZW编码算法的具体执行步骤如下：步骤1：开始时的词典包含所有可能的根(Root)，而当前前缀P是空的；步骤2：当前字符(C) ：=字符流中的下一个字符；步骤3：判断缀-符串P+C是否在词典中(1) 如果“是”：P ：= P+C // (用C扩展P) ；(2) 如果“否”①把代表当前前缀P的码字输出到码字流;②把缀-符串P+C添加到词典;③令P：= C //(现在的P仅包含一个字符C);步骤4：判断码字流中是否还有码字要译(1) 如果“是”，就返回到步骤2；(2) 如果“否”①把代表当前前缀P的码字输出到码字流;②结束。
译码过程LZW译码算法中还用到另外两个术语：①当前码字(Current code word)：指当前正在处理的码字，用cW表示，用string.cW表示当前缀-符串；②先前码字(Previous code word)：指先于当前码字的码字，用pW表示，用string.pW表示先前缀-符串。