控制系统的极点配置实验报告
实验九控制系统极点的任意配置

东南大学自动化学院实 验 报 告课程名称: 自动控制实验名称: 控制系统极点的任意配置院 (系): 自动化 专 业: 自动化 姓 名: 学 号: 实 验 室: 实验组别: 同组人员: 实验时间:2016年 4月 30日 评定成绩: 审阅教师:一、实验目的1. 掌握用状态反馈的设计方法实现控制系统极点的任意配置;2. 用电路模拟的方法,研究参数的变化对系统性二、实验原理内容用全状态反馈实现二阶系统极点的任意配置,并用电路模拟的方法予予以实现; 理论证明,通过状态反馈的系统,其动态性能一定会优于只有输出反馈的系统。
设系统受控系统的动态方程为图6-1为其状态变量图。
图6-1 状态变量图令Kx r u -=,其中]...[21n k k k K =,r 为系统的给定量,x 为1⨯n 系统状态变量,u 为11⨯控制量。
则引入状态反馈后系统的状态方程变为相应的特征多项式为)](det[bK A SI --,调节状态反馈阵K 的元素]...[21n k k k ,就能实现闭环系统极点的任意配置。
图6-2为引入状态反馈后系统的方框图。
图6-2 引入状态变量后系统的方框图实验时,二阶系统方框图如6-3所示。
图6-3 二阶系统的方框图引入状态反馈后系统的方框图如图6-4所示。
根据状态反馈后的性能指标:20.0≤p δ,s 5.0Tp ≤,试确定状态反馈系数K1和K2图6-4 引入状态反馈后的二阶系统方框图三、实验步骤1. 引入输出单位反馈根据图6-3二阶系统的方框图,设计并组建该系统相应的模拟电路,如图6-9所示。
图6-9 引入状态反馈前的二阶系统模拟电路图在系统输入端加单位阶跃信号,虚拟示波器HBD-1观测c(t)输出点并记录相应的实验曲线,测量其超调量和过渡时间。
2.引入状态反馈根据图6-4引入状态反馈后的二阶系统的方框图,设计并组建该系统相应的模拟电路,如图6-10所示。
图6-10 状态反馈后的二阶系统模拟电路图在系统输入端加单位阶跃信号,虚拟示波器HBD-1观测c(t)输出点并记录相应的实验曲线,测量其超调量和过渡时间,然后分析其性能指标。
实验八控制系统极点的任意配置综合性设计性实验

实验八控制系统极点的任意配置(综合性设计性实验)
一、实验目的
1. 掌握用全状态反馈的设计方法实现控制系统极点的任意配置;
2. 用电路模拟的方法,研究参数的变化对系统性能的影响。
二、实验设备
同实验一。
三、实验内容
1. 用全状态反馈实现二阶系统极点的任意配置,并用电路模拟的方法予以实现;
2. 用全状态反馈实现三阶系统极点的任意配置,并通过电路模拟的方法予以实现。
四、实验原理(略)
五、实验步骤
请自行提出实验步骤,选择实验台上的通用电路单元设计并组建相应的模拟电路。
(K 值可参考取5,12,20等)。
完成实验报告,结合实验提出相应思考题。
现代控制实验报告

实验一控制系统极点的任意配置一、实验目的1.掌握用全状态反馈的方法实现控制系统极点的任意配置;2.用电路模拟与软件仿真的方法,研究参数的变化对系统性能的影响。
二、实验设备1.TBCC-1型信号与系统控制理论及计算机控制技术实验平台2.PC机一台(含上位机软件)37针通信线1根三、实验内容用全状态反馈实现二阶系统极点的任意配置,并分别用电路模拟与软件仿真予于实现四、实验原理由于控制系统的动态性能主要取决于它的闭环极点在S平面上的位置,因而人们常把对系统动态性能的要求转化为一组希望的闭环极点。
一个单输入单输出的N阶系统,如果金靠系统的输出量进行反馈,显然不能使系统的n个极点位于所希望的位置。
基于一个N阶系统有N个状态变量,如果把他们分别作为系统的反馈信号,则在满足一定的条件下就能实现对系统极点的任意配置,这个条件是系统能控。
理论证明,通关状态反馈的系统,其动态性能一定要优于只有输出反馈的系统。
本实验分别研究二阶系统状态反馈。
五、实验步骤1、设计一个二阶系统的模拟电路,测取其阶跃响应,并与软件仿真结果相比较。
2、根据上面的典型二阶系统,用极点配置的方法,设计一个全状态反馈的增益矩阵。
3、按确定的参数设计构建系统的模拟电路,测其阶跃响应,并与软件仿真结构相比较。
六、实验结果1.1二阶系统方框图1.2实验结果2.1引入状态反馈后的二阶系统方框图2.2实验结果七、思考题1.系统极点能任意配置的充要条件是什么?答:系统完全能控。
2.为什么引入状态反馈后的系统,其性能一定会优于只有输出反馈的系统?答:因为反馈后可以调整输入量,最后达到稳定输出。
3.典型二阶系统引入状态反馈后,能不能使输出的稳态值高于给定值?答:不能,最多等于给定值。
实验二状态观测器及其应用一、试验目的1.通关实验进一步了解状态观测器的原理与结构组成;2.用状态观测器的状态估计值对系统的极点进行任意配置。
二、实验设备1.TBCC-1型信号与系统控制理论及计算机控制技术实验平台2.PC机一台(含上位机软件)37针通信线1根三、实验内容1设计受控系统和相应状态观测器的模拟电路图。
线性系统的状态反馈及极点配置

现代控制理论实验(一)线性系统的状态反馈及极点配置——09级自动化本科一.实验目的1.了解和掌握状态反馈及极点配置的原理。
2.了解和掌握利用矩阵法及传递函数法计算状态反馈及极点配置的原理与方法。
3.掌握在被控系统中如何进行状态反馈及极点配置,构建一个性能满足指标要求的新系统的方法。
二.实验原理及说明一个控制系统的性能是否满足要求,要通过解的特征来评价,也就是说,当传递函数是有理函数时,它的全部信息几乎都集中表现为它的极点、零点及传递函数。
因此若被控系统完全能控,则可以通过状态反馈任意配置极点,使被控系统达到期望的时域性能指标。
若有被控系统如图3-3-61所示,它是一个Ⅰ型二阶闭环系统。
图3-3-61 被控系统如图3-3-61所示的被控系统的传递函数为:12021S 11)1(1)(a S a S b T TS T TS S T S i i i ++=++=++=φ (3-3-51) 采用零极点表达式为:))(()(210λλφ--=S S b S (3-3-52)进行状态反馈后,如图3-3-62所示,图中“输入增益阵”L 是用来满足静态要求。
图3-3-62 状态反馈后被控系统设状态反馈后零极点表达式为:))(()(21**--=λλφS S b S (3-3-53)1.矩阵法计算状态反馈及极点配置1)被控系统被控系统状态系统变量图见图3-3-63。
图3-3-63 被控系统状态系统变量状态反馈后的被控系统状态系统变量图见图3-3-64。
图3-3-64 状态反馈后的被控系统状态系统变量图图3-3-61的被控系统的状态方程和输出方程为:状态方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+-=+-=••1i 1i 2211X Y u T 1X T 1X X T 1X T 1X (3-3-54)⎪⎩⎪⎨⎧=+==•∑CxY u Ax X B C B A 0),,(式中[]01,T 10B 0T 1T 1T 1A ,i i 21=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=C x x x , 被控系统的特征多项式和传递函数分别为:12010a a b S b )(+++=S S S φB A)C(SI 1--=)(A -SI det a a )(f 0120=++=S S S 可通过如下变换(设P 为能控标准型变换矩阵): —x P X =将∑0C B A ),,(化为能控标准型 ),,(————C B A ∑,即: ⎪⎩⎪⎨⎧=+=•——————x C Y u x A B X 式中 ⎥⎦⎤⎢⎣⎡-==-101a -a 10AP P A — , ⎥⎦⎤⎢⎣⎡==-10B P B 1— , []10b b CP C ==— 2)被控系统针对能控标准型),,(————C B A ∑引入状态反馈:⎥⎦⎤⎢⎣⎡=-=—————式中10k k k xk u ν (3-3-55)可求得对—x 的闭环系统),,—————C B k B A (-∑的状态空间表达式: 仍为能控标准型,即: ⎪⎩⎪⎨⎧=+-=•————————)(x C Y u x B k B A X 式中 ⎥⎦⎤⎢⎣⎡+-+-=-)()(—————1100k a k a 10k B A则闭环系统),,(——————C B k B A -∑的特征多项式和传递函数分别为: )()(—————00112k k a k a k)B (A SI det )(f ++++=⎥⎦⎤⎢⎣⎡--=S S S )k a (k a b S b B )k B A (SI C )(00112011k ———————)(+++++=⎥⎦⎤⎢⎣⎡--=-S S S φ3)被控系统如图3-3-61所示:其中:05.01==T T i则其被控系统的状态方程和输出方程为:[]XY uX X 0110012020=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=期望性能指标为:超调量M P ≤20%;峰值时间t P ≤0.5秒。
综合性实验 极点配置全状态反馈控制指导书

综合性实验 极点配置全状态反馈控制一、实验目的1.学习并掌握用极点配置方法设计全状态反馈控制系统的方法。
2.用电路模拟与软件仿真方法研究参数对系统性能的影响。
二、实验内容1.设计典型二阶系统的极点配置全状态反馈控制系统,并进行电路模拟与软件仿真研究。
2.设计典型三阶系统的极点配置全状态反馈控制系统,并进行电路模拟与软件仿真研究。
三、实验前准备工作1 推导图1的数学模型(状态空间表达式),分析系统的能控性。
2 若系统期望的性能指标为:超调量25%p M ≤,峰值时间0.5p t ≤,求出期望的极点值。
根据以上性能指标要求设计出状态反馈控制器。
3 推导图2的数学模型(传递函数),求出其单位阶跃响应的动态性能指标(超调量、调节时间、静态速度误差系数)。
4 推导图4的数学模型(状态空间表达式),分析系统的能控性。
5考虑系统稳定性等要求,选择理想极点为:S 1=-9,S 2 =-2+j2,S 3=-2-j2, 根据以上性能指标要求思考如何设计状态反馈控制器。
6 推导图7的数学模型(传递函数)。
四、实验步骤1.典型二阶系统(1)对一已知二阶系统(见图1)用极点配置方法设计全状态反馈系数。
(2)见图2和图3,利用实验箱上的电路单元U9、U11、U12和U8,按设计参数设计并连接成系统模拟电路,测取阶跃响应,并与软件仿真结果比较。
(3)改变系统模拟电路接线,使系统恢复到图1所示情况,测取阶跃响应,并与软件仿真结果比较。
(4)对实验结果进行比较、分析,并完成实验报告。
2.典型三阶系统(1)对一已知三阶系统(见图4)用极点配置方法设计全状态反馈系数。
(2)见图5和图7,利用实验箱上的电路单元U9、U11、U12、U15和U8,按设计参数设计并连接成系统模拟电路,测取阶跃响应,并与软件仿真结果比较。
(3)改变系统模拟电路接线,使系统恢复到图5所示情况,测取阶跃响应,并与软件仿真结果比较。
软件仿真直接在MATLAB 中实现。
直线一级倒立摆系统的状态空间极点配置控制设计详细实验报告

一、直线一级倒立摆建模根据自控原理实验书上相关资料,直线一级倒立摆在建模时,一般忽略掉系统中的一些次要因素.例如空气阻力、伺服电机的静摩擦力、系统连接处的松弛程度等,之后可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示:倒立摆系统是典型的机电一体化系统,其机械部分遵循牛顿的力学定律,其电气部分遵守电磁学的基本定理.因此,可以通过机理建模方法得到较为准确的系统数学模型,通过实际测量和实验来获取系统模型参数.无论哪种类型的倒立摆系统,都具有3个特性,即:不确定性、耦合性、开环不稳定性. 直线型倒立摆系统,是由沿直线导轨运动的小车以及一端固定于小车上的匀质长杆组成的系统. 小车可以通过传动装置由交流伺服电机驱动. 小车导轨一般有固定的行程,因而小车的运动范围是受到限制的。
虽然倒立摆的形式和结构各异,但所有的倒立摆都具有以下的特性:1) 非线性倒立摆是一个典型的非线性复杂系统,实际中可以通过线性化得到系统的近似模型,线性化处理后再进行控制。
也可以利用非线性控制理论对其进行控制。
倒立摆的非线性控制正成为一个研究的热点。
2) 不确定性主要是模型误差以及机械传动间隙,各种阻力等,实际控制中一般通过减少各种误差来降低不确定性,如通过施加预紧力减少皮带或齿轮的传动误差,利用滚珠轴承减少摩擦阻力等不确定因素。
3) 耦合性倒立摆的各级摆杆之间,以及和运动模块之间都有很强的耦合关系,在倒立摆的控制中一般都在平衡点附近进行解耦计算,忽略一些次要的耦合量。
4) 开环不稳定性倒立摆的平衡状态只有两个,即在垂直向上的状态和垂直向下的状态,其中垂直向上为绝对不稳定的平衡点,垂直向下为稳定的平衡点。
由于机构的限制,如运动模块行程限制,电机力矩限制等。
为了制造方便和降低成本,倒立摆的结构尺寸和电机功率都尽量要求最小,行程限制对倒立摆的摆起影响尤为突出,容易出现小车的撞边现象。
由此,约束限制直线型一级倒立摆系统的实际控制要求可归结为3点:(1)倒立摆小车控制过程的最大位移量不能超过小车轨道的长度;(2)为保证倒立摆能顺利起立,要求初始偏角小于20°;(3)为保证倒立摆保持倒立的平衡态,要求控制系统响应速度足够快。
状态反馈与极点配置报告

自动控制原理(课程设计)一、题目用MATLAB创建用户界面,并完成以下功能:(1)由用户输入被控系统的状态空间模型、闭环系统希望的一组极点;(2)显示未综合系统的单位阶跃响应曲线;(3)显示采用一般设计方法得到的状态反馈矩阵参数;(4)显示闭环反馈系统的单位阶跃响应曲线;(5)将该子系统嵌入到寒假作业中程序中。
分别对固定阶次和任意阶次的被控系统进行设计。
分别给出设计实例。
二、运行结果界面:如图由用户输入被控系统的状态空间模型、闭环系统希望的一组极点例如,输入010001034A⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦,1B⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,[]2000C=,0D=,闭环系统希望的一组极点:22j-+、22j--、5-如图所示:被控系统的单位阶跃响应曲线闭环系统的单位阶跃响应曲线状态反馈矩阵显示三、讨论该闭环控制系统的状态反馈与极点配置设计系统可用于任意阶次的控制系统。
在此之前,我还做了一个固定阶次的控制系统状态反馈与极点配置的Matlab 控制台程序(见附录二)。
该系统的利用状态反馈进行极点任意配置所采用的方法为一般方法,其步骤如下:①判断受控系统是否完全能控;②由给定的闭环极点要求确定希望的闭环特征多项式的n个系数~i a;③确定原受控系统的特征多项式系数ia;④确定系统状态反馈矩阵~~~~[,,,]12nff fF=的诸元素~~11ii if a a-=--;⑤确定原受控系统化为能控标准形的变换阵的逆1P-,⑥确定受控系统完成闭环极点配置任务的状态反馈阵~1F F P-=。
四、参考文献[1]黄家英.《自动控制原理》.高等教育出版社,2010.5[2]唐向红,郑雪峰.《MATLAB及在电子信息类》.电子工业出版社,2009.6[3]吴大正,高西全.《MATLAB新编教程》.机械工业出版社,2008.4五、附录function varargout = tufeiqiang(varargin)%TUFEIQIANG M-file for tufeiqiang.fig% TUFEIQIANG, by itself, creates a new TUFEIQIANG or raises the existing% singleton*.%% H = TUFEIQIANG returns the handle to a new TUFEIQIANG or the handle to% the existing singleton*.%% TUFEIQIANG('Property','Value',...) creates a new TUFEIQIANG usingthe% given property value pairs. Unrecognized properties are passed via % varargin to tufeiqiang_OpeningFcn. This calling syntax produces a% warning when there is an existing singleton*.%% TUFEIQIANG('CALLBACK') and TUFEIQIANG('CALLBACK',hObject,...) call the% local function named CALLBACK in TUFEIQIANG.M with the given input % arguments.%% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one% instance to run (singleton)".%% See also: GUIDE, GUIDATA, GUIHANDLES% Edit the above text to modify the response to help tufeiqiang% Last Modified by GUIDE v2.5 20-May-2015 23:49:56% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @tufeiqiang_OpeningFcn, ...'gui_OutputFcn', @tufeiqiang_OutputFcn, ...'gui_LayoutFcn', [], ...'gui_Callback', []);if nargin && ischar(varargin{1})gui_State.gui_Callback = str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT% --- Executes just before tufeiqiang is made visible.function tufeiqiang_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% varargin unrecognized PropertyName/PropertyValue pairs from the% command line (see VARARGIN)% Choose default command line output for tufeiqianghandles.output = hObject;% Update handles structureguidata(hObject, handles);% UIWAIT makes tufeiqiang wait for user response (see UIRESUME)% uiwait(handles.figure1);% --- Outputs from this function are returned to the command line. function varargout = tufeiqiang_OutputFcn(hObject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT);% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Get default command line output from handles structurevarargout{1} = handles.output;function WZH_Callback(hObject, eventdata, handles)% hObject handle to WZH (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)A=get(handles.edit1,'String');A=char(A);A=str2num(A);B=get(handles.edit2,'String');B=char(B);B=str2num(B);C=get(handles.edit3,'String');C=char(C);C=str2num(C);D=get(handles.edit4,'String');D=char(D);D=str2num(D);sys = ss(A,B,C,D);axes(handles.axes1);set(handles.axes1,'unit','normalized');step(sys);%title('••×••••••••••••×•••ì•••ú••')set(findobj(gca,'Type','line','Color',[0 0 1]),...'Color','red',...'LineWidth',2)% --- Executes on button press in BFK.function BFK_Callback(hObject, eventdata, handles)% hObject handle to BFK (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)A=get(handles.edit1,'String');A=char(A);A=str2num(A);B=get(handles.edit2,'String');B=char(B);B=str2num(B);C=get(handles.edit3,'String');C=char(C);C=str2num(C);D=get(handles.edit4,'String');D=char(D);D=str2num(D);P=get(handles.edit5,'String');P=char(P);P=str2num(P);K = acker(A,B,P);at = A-B*K;bt = B;ct = C;dt = D;%[num,den]=zp2tf(z,p,k);%[num1,den1]=cloop(num,den);axes(handles.axes1);set(handles.axes1,'unit','normalized');%step(cloop(num,den));%rlocus(A,B,K,0)%step(num1,den1);sys = ss(at,bt,ct,dt);step(sys);title('±••··••••••••••••×•••ì•••ú••')set(findobj(gca,'Type','line','Color',[0 3 3]),...'Color','yellow',...'LineWidth',2)function FKC_Callback(hObject, eventdata, handles)% hObject handle to FKC (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)A=get(handles.edit1,'String');A=char(A);A=str2num(A);B=get(handles.edit2,'String');B=char(B);B=str2num(B);Z=get(handles.edit5,'String');Z=char(Z);Z=str2num(Z);Zif rank(ctrb(A,B)) == rank(A)N = acker(A,B,Z);Nstr=num2str(N)H = findobj('tag','edit6');set(H,'string',str);elsemsgbox('•••••••••••••••••••••••• ');endfunction pushbutton6_Callback(hObject, eventdata, handles)% hObject handle to pushbutton6 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)A=get(handles.edit1,'String');AA=char(A);AA=str2num(A);AB=get(handles.edit2,'String');BB=char(B);BB=str2num(B);BM = ctrb(A,B);if rank(M) == rank(A)msgbox('•••••ê••••••••••••••••••');%[num,den]=zp2tf(z,p,k);%[num1,den1]=cloop(num,den);%step(cloop(num,den));%rlocus(A,B,K,0)%step(num1,den1);elsemsgbox('•••••••••••••••••••••••• '); end。
自动控制原理学生实验:线性系统的状态反馈及极点配置
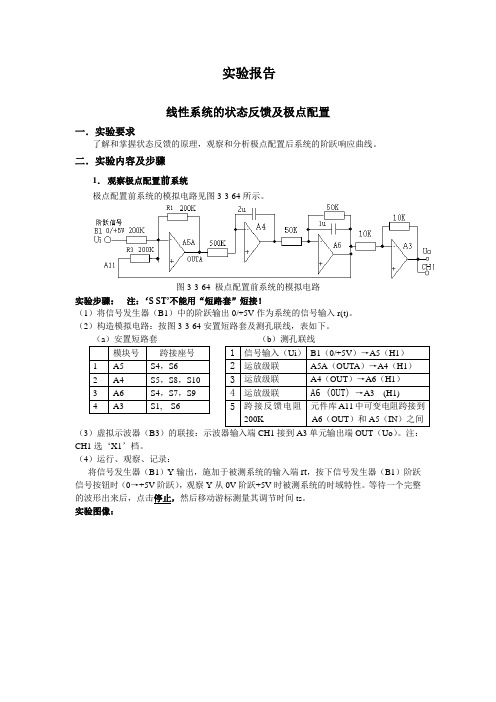
实验报告线性系统的状态反馈及极点配置一.实验要求了解和掌握状态反馈的原理,观察和分析极点配置后系统的阶跃响应曲线。
二.实验内容及步骤1.观察极点配置前系统极点配置前系统的模拟电路见图3-3-64所示。
图3-3-64 极点配置前系统的模拟电路实验步骤:注:‘S ST’不能用“短路套”短接!(1)将信号发生器(B1)中的阶跃输出0/+5V作为系统的信号输入r(t)。
(2)构造模拟电路:按图3-3-64安置短路套及测孔联线,表如下。
(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A3单元输出端OUT(Uo)。
注:CH1选‘X1’档。
(4)运行、观察、记录:将信号发生器(B1)Y输出,施加于被测系统的输入端rt,按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),观察Y从0V阶跃+5V时被测系统的时域特性。
等待一个完整的波形出来后,点击停止,然后移动游标测量其调节时间ts。
实验图像:由图得ts=3.880s 2.观察极点配置后系统 极点的计算:受控系统如图所示,若受控系统完全可控,则通过状态反馈可以任意配置极点。
受控系统设期望性能指标为:超调量M P ≤5%;峰值时间t P ≤0.5秒。
由1095.01t 707.0%5eM n n 2n p 1/p 2=≥⇒≤-==⇒≤=--ωωζωπζζζπ取因此,根据性能指标确定系统希望极点为:⎪⎩⎪⎨⎧--=+-=07.707.707.707.7*2*1j j λλ受控系统的状态方程和输出方程为:⎪⎩⎪⎨⎧=+=-----⋅-xC y b x A x μ式中][01,10,020120,21=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=----C b A x x x系统的传递函数为:202020a S a S βS β)(2012010++=+++=S S S G受控制系统的可控规范形为:[][]020T C C b T b a a T A T A X T X X C Y U b X A X K K i o K K KK k K K K ===⎥⎦⎤⎢⎣⎡==⎥⎦⎤-⎢⎣⎡-=⎥⎦⎤-⎢⎣⎡-===⎩⎨⎧=+=---10111,1020120010T ββ为变换阵),(式中当引入状态反馈阵K K =[K 0K 1]后,闭环系统()K K K K K C b K b A ,,-的传递函数为:()()()01201120120)20(20)(K S K S K a S K a S S S G o ++++=+++++=ββ而希望的闭环系统特征多项为:1001.14))(()(2*2*1**12*++=--=++=S S S S a S a S S f oλλ 令G K (S)的分母等于F #(S),则得到K K 为:[][]9.58010-==K K K k最后确定原受控系统的状态反馈阵K :由于 1-=T K K k求得和===---111,T C b T b T A T A K k K求得 ⎥⎥⎦⎤⎢⎢⎣⎡-=-1102011T所以状态反馈阵为: [][]9.59.91102019.580-=⎥⎥⎦⎤⎢⎢⎣⎡--=K极点配置系统如图所示:极点配置后系统根据极点配置后系统设计的模拟电路见下图所示。
自动控制原理实验四状态反馈设计报告

实验四、状态反馈设计一、实验目的1.掌握用状态空间法建立系统模型的方法。
2.掌握用状态反馈法进行极点配置的方法。
二、实验内容被控原系统如下图8-1所示,x1、x2为状态变量,以该状态变量建立系统的状态方程,用状态反馈法对原系统进行极点配置,期望性能为:Mp≤5%,tp≤0.5秒。
图8-1 被控原系统图8-2 极点配置后系统三、实验步骤1.建立状态空间模型。
2.从期望的性能指标,求出2阶系统的期望极点。
3.按照状态反馈法,设计反馈回路的参数。
4.在MA TLAB环境下,对极点配置后的系统性能进行仿真验证。
四、实验报告要求1.实验前进行理论设计,写出详细设计步骤。
2.记录实验有关数据及图表。
3.实验数据分析。
原系统:超调量: pos =16.0122上升时间: tr =1.7121调节时间:ts2 =7.8980峰值时间:tp =3.6980进行极点配置的计算:1.判断系统是否能控:跟根据原系统的传递函数,可得出A阵为,A = [ 0 1; -1 -1]A的转置为A’= [-1 0; -1 1]B阵为:b = [0; 1]C阵为:c = [1 0]Rank[Sc ]= Rank [A A*b]=2,为满秩,所以,系统可控。
Rank[ A ; A*c ]=2 为满秩,所以,系统可观测。
2.根据matlab程序计算出期望的极点:程序如下(其中超调取4%,峰值时间取0.45s)a=[0.1:0.01:0.99]; %%求出阻尼比,Wn;MP=exp(-pi.*a./sqrt(1-a.*a));a1=spline(MP,a,0.04)wn=pi./(0.45*sqrt(1-a1*a1))r=[1 2*wn*a1 wn*wn];g1=roots(r)A=[0 1;-1 -1] %%判断能控性b=[0;1]c=[1 0]Sc=[b A*b]rankk=rank(Sc)Ss=[c;c*A] %%判断能观察性rankkk=rank(Ss)k=[wn*wn-2*wn*a1-2 2*wn*a1-1] %%状态反馈增益阵[pos_1,tr_1,ts2_1,tp_1]=stepchar(t,y1) %%原系统与设计后系统的性能参数[pos_2,tr_2,ts2_2,tp_2]=stepchar(t,y2)得出:阻尼比a1 =0.7156wn =9.9952期望的极点为:S1=-7.1531 + 6.9813iS2=-7.1531 - 6.9813i所以,期望特征方程为:f*(s)=(S+7.1531)2+6.98132设:K=[k1 k2]反馈系统的特征方程为:f(s)=| SI-(A-b*k)|=[S -1; 1+k1 S+1+k2]=S2+(1+k2)S+(1+k1)令:f*(s)=f(s)求出K阵得出K=[83.5989 13.3061]极点配置后的系统:极点配置后系统性能指标:超调量:pos =4.1063上升时间:tr =0.1682调节时间:ts2 =0.5858峰值时间:tp =0.4754原系统与极点配置后系统比较:。
自控原理实验极点配置

实验3 控制系统极点的任意配置一、实验目的1. 掌握用全状态反馈的设计方法实现控制系统极点的任意配置2. 用电路模拟的方法,研究参数的变化对系统性能的影响二、实验设备1.THSSC-4型信号与系统·控制理论·计算机控制技术实验箱2.PC机一台(含上位机软件)、USB数据采集卡、37针通信线1根、16芯数据排线、USB接口线三、实验内容1. 用全状态反馈实现二阶系统极点的任意配置,并用电路模拟的方法予以实现2. 用全状态反馈实现三阶系统极点的任意配置,并通过电路模拟的方法予以实现四、实验原理由于控制系统的动态性能主要取决于它的闭环极点在S平面上的位置,因而人们常把对系统动态性能的要求转化为一组希望的闭环极点。
一个单输入单输出的N阶系统,如果仅靠系统的输出量进行反馈,显然不能使系统的n个极点位于所希望的位置。
基于一个N阶系统有N个状态变量,如果把它们作为系统的反馈信号,则在满足一定的条件下就能实现对系统极点任意配置,这个条件就是系统能控。
理论证明,通过状态反馈的系统,其动态性能一定会优于只有输出反馈的系统。
设系统受控系统的动态方程为=Axbux+y=cx图3-1为其状态变量图。
图3-1 状态变量图令Kx r u -=,其中]...[21n k k k K =,r 为系统的给定量,x 为1⨯n 系统状态变量,u 为1×1控制量。
则引入状态反馈后系统的状态方程变为bu x bK A x+-=)( 相应的特征多项式为)](det[bK A SI --,调节状态反馈阵K 的元素]...[21n k k k ,就能实现闭环系统极点的任意配置。
图3-2为引入状态反馈后系统的方框图。
图3-2 引入状态变量后系统的方框图1. 典型二阶系统全状态反馈的极点配置二阶系统方框图如3-3所示。
图3-3 二阶系统的方框图1.1 由图得)15.0(10)(+=S S S G ,然后求得:223.0=ξ,%48≈p δ同时由框图可得:2115.01)(X S X R =+- ,2110X X = 所以:R X X X 222212+--= R X X ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=2022100[]X X y 011==1.2 系统能控性[]242200=⎥⎦⎤⎢⎣⎡-=rank Ab b rank 所以系统完全能控,即能实现极点任意配置。
现代控制理论基础实验报告

现代控制理论基础实验报告专业:年级:姓名:学号:提交日期:实验一系统能控性与能观性分析1、实验目的:1. 通过本实验加深对系统状态的能控性和能观性的理解;2. 验证实验结果所得系统能控能观的条件与由它们的判据求得的结果完全一致。
2、实验内容:1•线性系统能控性实验 2.线性系统能观性实验。
3、实验原理:系统的能控性是指输入信号u 对各状态变量x 的控制能力。
如果对于系统任意的初始状态,可以找到一个容许的输入量,在有限的时间内把系统所有的状态变量转移到状态空间的坐标原 点。
则称系统是能控的。
系统的能观性是指由系统的输出量确定系统所有初始状态的能力。
如果在有限的时间内,根据 系统的输出能唯一地确定系统的初始状态,则称系统能观。
(10-1)i Ly=U c =[01]U c由上式可简写为x Ax bU y cxR 3对于图10-1所示的电路系统,设i L 和u c 分别为系统的两个状态变量,如果电桥中旦R 2 &则输入电压U 能控制i L 和U c 状态变量的变化,此时,状态是能控的;状态变量i L 与U c 有耦合关系, 输出U c 中含有i L 的信息,因此对U c 的检测能确定i L 。
即系统能观的。
R 1 R 3反之,当」时, R 2 R 4变i L 的大小,故系统不能控; 即系统不能观。
Ri R 31.1当13时R 2 R 4电桥中的由于输出R 31( R 1R 2 L (R , R 2R 3 R 4R3R4R 2c 点和d 点的电位始终相等,U c 不受输入U 的控制,u 只能改U c 和状态变量i L 没有耦合关系,故 U c 的检测不能确定i L ,丄(亠亠)C R R 2R 3 R 41 ( R 1R2 L (R R 2R 3 R 4R3R4I L U C(10-2)I LR 2R 1 R 2 i L式中X U C1 (L R 1 R 21 R2 ( —— C R 1 R 2 R3 R 4)R3 R 4R 3 R 4R 1 R 2 1 (L R 1 R 21 1 -( CR 1R 2R3 R 4) R 4 1 )R 3 R 4[0 1]由系统能控能观性判据得 ran k[b Ab] =2c rank cA 故系统既能控又能观。
实验三系统的能控性与能观性分析及状态反馈极点配置

实验三系统的能控性与能观性分析及状态反馈极点配置实验指导书一、实验目的加深理解能观测性、能控性、稳定性、最小实现等观念,掌握状态反馈极点配置方法,掌握如何使用MATLAB 进行以下分析和实现。
1、系统的能观测性、能控性分析;2、系统的最小实现;3、进行状态反馈系统的极点配置;4、研究不同配置对系统动态特性的影响。
二、实验原理、内容及步骤 1、系统能控性、能观性分析设系统的状态空间表达式如下:p m n R y R u R x DuCx y Bu Ax x ∈∈∈⎩⎨⎧+=+= (1-1)其中A 为n ×n 维状态矩阵;B 为n ×m 维输入矩阵;C 为p ×n 维输出矩阵;D 为p ×m 维传递矩阵,一般情况下为0。
系统的传递函数阵和状态空间表达式之间的关系如式(1-2)所示:D B A sI C s den s num s G +-==-1)()()(()( (1-2)式(1-2)中,)(s num 表示传递函数阵的分子阵,其维数是p ×m ;)(s den 表示传递函数阵的分母多项式,按s 降幂排列的后,各项系数用向量表示。
系统的能控性、能观测性分析是多变量系统设计的基础,包括能控性、能观测性的定义和判别。
系统状态能控性定义的核心是:对于线性连续定常系统(1-1),若存在一个分段连续的输入函数u(t),在有限的时间(t 1-t 0)内,能把任一给定的初态x(t 0)转移至预期的终端x(t 1),则称此状态是能控的。
若系统所有的状态都是能控的,则称该系统是状态完全能控的。
状态能控性判别方法分为2种:一般判别和直接判别法,后者是针对系统的系数阵A 是对角标准形或约当标准形的系统,状态能控性判别时不用计算,应用公式直接判断,是一种直接简易法;前者状态能控性分为一般判别是应用最广泛的一种判别法。
状态能控性判别式为:[]n B A AB B Rank RankQ n c==-1(1-3) 系统状态能观测性的定义:对于线性连续定常系统(1-1),如果对t 0时刻存在t a ,t 0<t a <∞,根据[t 0,t a ]上的y(t)的测量值,能够唯一地确定系统在t 0时刻的任意初始状态x 0,则称系统在t 0时刻是状态完全能观测的,或简称系统在[t 0,t a ]区间上能观测。
控制系统的极点配置实验报告

课程名称:控制理论乙指导老师:姚唯成绩:实验名称:控制系统的极点配置实验类型:同组学生姓名:郁明非一、实验目的和要求(必填)二、实验内容和原理(必填)三、主要仪器设备(必填)四、操作方法和实验步骤五、实验数据记录和处理六、实验结果与分析(必填)七、讨论、心得一、实验目的和要求1.掌握全状态反馈系统的极点配置方法2.在 Simulink 仿真环境中,研究极点配置对系统特性的影响二、实验内容和原理(一)实验内容1.一被控对象,其传递函数为10G ( s )( s 1)( s 2 )( s 3 )设计反馈控制器u=-kx ,使闭环系统的极点为12j 23,2 2 j 2 3 ,310 。
2.在 Simulink仿真环境下,用基本环节组成经过极点配置后的系统,通过图形观察环节,观察系统的各点响应。
(二)实验原理对一给定控制系统如果其状态完全可控,则可进行任意极点配置即通过设计反馈増益 K 使闭环系统具有期望的极点。
极点配置有二种方法:第一种方法是采用变换矩阵T,使系统具有期望的极点,从而求出矩阵K ;第二种方法基于 Caylay-Hamilton 理论,通过矩阵多项式φ(a),可求出 K(这种方法称为 Ackermann 公式)。
在 MATLAB 中,利用控制系统工具箱函数 place 和 acker 进行极点配置设计。
三、主要仪器设备一台 PC 电脑, matlab 仿真软件, simulink 仿真环境四、实验源代码及实验结果function jidianpeizhinum=[10];den=[1,6,11,6];[A,B,C,D]=tf2ss(num,den);J=[-2-j*2*sqrt(3),-2+j*2*sqrt(3),-10];K=place(A,B,J);Ksys=ss(A-B*K,[0;0;0],eye(3),0);t=0:0.01:4;X=initial(sys,[1;0;0],t);x1=[1,0,0]*X';x2=[0,1,0]*X';x3=[0,0,1]*X';subplot(3,1,1);plot(t,x2);grid on ;title('Reponse to initial condition'); ylabel('x1');subplot(3,1,2);plot(t,x2);grid on ;ylabel('x2');subplot(3,1,3);plot(t,x3);grid on ;ylabel('x3');xlabel('t(sec)');实验结果K =8.000045.0000 154.0000实验验证:>>num=[10];>>den=[1 6 11 6];>>[A,B,C,D]=tf2ss(num,den);>>J=[-2-j*2*sqrt(3),-2+j*2*sqrt(3),-10];>>K=place(A,B,J)K =8.000045.0000 154.0000>>A1=A-B*K;>>sys=ss(A1,B,C,D);>>G1=zpk(sys);>>G1=zpk(sys)G1 =10----------------------(s+10) (s^2 + 4s + 16)Continuous-time zero/pole/gain model.五、 simulink 仿真1.简单环节叠加仿真2.状态函数仿真六、心得、体会1.通过本次实验,掌握了状态反馈的概念,并且掌握了利用状态反馈进行极点配置的方法,学会了用MATLAB求解状态反馈矩阵。
自动控制理论实验课程6.3.1 极点配置仿真实验

极点配置(一)实验原理给定一个连续时间系统的状态空间模型:Bu Ax x += (1)其中:x 是系统的n 维状态向量,u 是m 维控制输入,A 和B 分别是适当维数的已知常数矩阵。
在状态反馈Kx -=u (2)作用下,闭环系统的状态方程是x BK A x )(-= (3)由线性时不变系统的稳定性分析可知,闭环系统(3)的稳定性由闭环系统矩阵A-BK 的特征值决定,即闭环系统(3)渐近稳定的充分必要条件是矩阵A-BK 的所有特征值都具有负实部。
而由经典控制理论知道,矩阵A-BK 的特征值也将影响诸如衰减速度、振荡、超调等过渡过程特性。
因此,若能找到一个适当的矩阵K ,使得矩阵A-BK 的特征值位于复平面上预先给定的特定位置,则以矩阵K 为增益矩阵的状态反馈控制器(2)就能保证闭环系统(3)是渐近稳定的,且具有所期望的动态响应特性。
这种通过寻找适当的状态反馈增益矩阵K ,使得闭环系统极点(即矩阵A-BK 的特征值)位于预先给定位置的状态反馈控制器设计问题称为是状态反馈极点配置问题,简称为极点配置问题。
对给定的线性定常系统(1)和一组给定的期望闭环极点},,{n 2,1λλλ =Ω,按以下步骤可以设计出使得闭环系统(3)具有给定极点},,{n 2,1λλλ =Ω的状态反馈控制器(2)。
第1步:检验系统的能控性。
如果系统是能控的,则继续第2步。
第2步:利用系统矩A 阵的特征多项式0111)det(a a a A I n n n +++=---λλλλ (4)确定的110,,,-n a a a 值。
第3步:确定将系统状态方程变换为能控标准形的变换矩阵T 。
若给定的状态方程已是能控标准形,那么T=I 。
非奇异线性变换矩阵T 可按如下方式确定:可控性矩阵:],b ,[1b A A b U n -= (5)计算1-U ,并记最后一行为h给出变换阵:112],,,h [--=n hA hA hA T (6)第4步:利用给定的期望闭环极点,可得期望的闭环特征多项式为011121)())((b b b n n n n +++=-----λλλλλλλλλ (7)并确定110,,,b -n b b 的值第5步:确定极点配置状态反馈增益矩阵K :T a b a b a b a b K n n n n ],,,[11221100--------= (8)也可以通过待定系数的方法来确定极点配置状态反馈增益矩阵K 。
控制系统极点的任意配置

检查能控性 0 2500 =2 50 −2500 所以系统完全能控,即具备极点任意配置的条件。 rank b Ab = rank λ I−A = 可知,原系统中 ζω n = 25 若要极点配置后系统的响应时间是原系统的5,且为临界阻尼则 ζω n = 125 ζ = 1,ω n = 125 希望的闭环特征多项式为: s 2 + 250s + 15625 引入状态反馈后系统的特征方程式为 s −50 sI − (A − bk) = 50 + 50k1 s + 50 + 50k 2 = s 2 + (50k 2 + 50)s + 2500k1 + 2500 = s2 + 250s + 15625 解得: k1 = 5.25,k 2 = 4 R1 = 3.81kΩ ,R 2 = 5kΩ 引入状态反馈后的方框图为
15625引入状态反馈后系统的特征方程式为si505050k250s156255k引入状态反馈后的方框图为系统框图可简化为62515625250s15625250015625625系统存在稳态误差需要在通过一个增益进行补偿可以通过反馈环路外的反相放大器来实现这样就不会改系统的性能
实验十六 控制系统极点的任意配置
实验步骤
1、 按照系统模拟电路图搭建原系统的模型 2、 运放电压为±15V,输入正负方波的幅值为 0.5V,频率为 1Hz,测量输入 和输出波形,观察输出对输入的跟踪情况,以及系统的阶跃响应。 3、 按照系统模拟电路图搭建控制器的模型,加入到原系统中。 4、 同样的输入下测量输出波形,并与校正前的系统比较,看是否满足题目 要求,是否与仿真结果相同。 5、 如果与仿真结果有差异,分析差异产生的原因,并作出调整。
最新东南大学极点配置实验名师指点资料

东南大学自动化学院实验报告课程名称:自动控制基础第9 次实验实验名称:控制系统极点的任意配置院(系):自动化学院专业:自动化姓名:高卓越学号:实验室:机械动力楼419 实验时间:2016 年4 月29 日评定成绩:审阅教师:目录一、实验目的和要求 (2)二、实验原理 (2)三、实验设备与器材配置 (3)四、预习思考题 (3)五、实验步骤 (4)六、实验结果 (5)七、实验总结 (8)一、 实验目的和要求1)掌握用状态反馈的设计方法实现控制系统极点的任意配置; 2)用电路模拟的方法,研究参数的变化对系统性。
二、 实验原理用全状态反馈实现二阶系统极点的任意配置,并用电路模拟的方法予以实现;理论证明,通过状态反馈的系统,其动态性能一定会优于只有输出反馈的系统。
设系统受控系统的动态方程为:bu Ax x+= cx y =下图为其状态变量图。
图6-1 状态变量图令Kx r u -=,其中]...[21n k k k K =,r 为系统的给定量,x 为1⨯n 系统状态变量,u 为11⨯控制量。
则引入状态反馈后系统的状态方程变为bu x bK A x+-=)( 。
相应的特征多项式为:)](det[bK A SI --,调节状态反馈阵K 的元素]...[21n k k k ,就能实现闭环系统极点的任意配置。
图6-2为引入状态反馈后系统的方框图。
图6-2 引入状态变量后系统的方框图实验时,二阶系统方框图如6-3所示。
图6-3 二阶系统的方框图引入状态反馈后系统的方框图如图6-4所示。
根据状态反馈后的性能指标:20.0≤p δ,试确定状态反馈系数K1和K2图6-4 引入状态反馈后的二阶系统方框图三、 实验设备与器材配置THBDC-1实验平台 THBDC-1虚拟示波器四、 预习思考题i.判断系统的能控性。
答:系统开环传递函数为:)15.0(1.01)(+=s s s G ,故系统状态方程为:⎪⎩⎪⎨⎧+==)(15.01)()(1.01)(221S R S S X S X S S X 即 ⎪⎪⎩⎪⎪⎨⎧===∙∙110)(2212x y x x t r x则⎥⎦⎤⎢⎣⎡-=20100A ,⎥⎦⎤⎢⎣⎡=20B ,[]01=C ,所以242200=⎥⎦⎤⎢⎣⎡-=c rankQ ,系统完全能控。
控制系统的极坐标图实验报告

自动控制原理实验报告一.实验目的1.利用计算机作出开环系统的极坐标图2.极坐标图系统分析二.实验步骤1.在Windows界面上用鼠标双击matlab图标,即可打开MATLAB命令平台。
2.练习相关M函数极坐标绘图函数:(nyquist图)格式1:nyquist(sys)格式2:nyquist(sys,w)格式3:[re,im,w]=nyquist(sys)函数功能:奈奎斯特轨线作图命令,即极坐标图。
格式1:给定开环系统的模型对象sys,作极坐标。
频率w的范围自动给定。
格式2:给定开环系统的模型对象sys,作极坐标。
频率w的范围人工给定。
格式3:返回极坐标图参数向量,不作图。
re为复变函数G(jω)的实部向量,re= real [G(jω)]。
im为复变函数的G(jω)虚部向量, im=imag[G(jω) ]。
w为频率向量,单位为[弧度]/秒。
例如,系统开环传递函数为作图程序为num=[0 0 10]; %作多项式模型den=[1 2 10];sys=tf(num,den); %系统对象nyquist(sys); %绘制极坐标图如果作图趋势不明显,可以采用下述方法改进:(1)使用命令axis()改变坐标显示范围axis([-1,1.5,-2,2]) %改变坐标显示范围(2)给定角频率变量w=0:0.1:100;nyquist(sys,w);三.实验内容1. )1(1)(+=s s s G 要求:作极坐标图。
程序: num=[0 0 1]; %作多项式模型den=[1 1 0];sys=tf(num,den); %系统对象nyquist(sys); %绘制极坐标图极坐标图如右图所示: 2. )1()(1+=Ts s K s G )1()(22+=Ts s K s G 要求:(1)作极坐标图。
(其中分别设定K 、T 的不同取值的情况)设K=1,T=2;程序:num1=[0 0 1]; %作多项式模型den1=[2 1 0];num2=[0 0 1]; %作多项式模型den2=[2 1 0 0];sys1=tf(num1,den1); %系统对象sys2=tf(num2,den2); %系统对象nyquist(sys1,sys2); %绘制极坐标图axis([-5,1,-10,10]) %改变坐标显示范围极坐标图如右图所示:(2) 比较两图的区别。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称: 控制理论乙 指导老师: 姚唯 成绩: 实验名称: 控制系统的极点配置 实验类型: 同组学生姓名: 郁明非 一、实验目的和要求(必填) 二、实验内容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理
六、实验结果与分析(必填)
七、讨论、心得
一、实验目的和要求
1.掌握全状态反馈系统的极点配置方法
2.在Simulink 仿真环境中,研究极点配置对系统特性的影响 二、实验内容和原理
(一)实验内容
1.一被控对象,其传递函数为
)
3)(2)(1(10
)(+++=
s s s s G
设计反馈控制器u=-kx ,使闭环系统的极点为3221j +-=μ,3222j --=μ,103-=μ。
2.
在Simulink 仿真环境下,用基本环节组成经过极点配置后的系统,通过图形观察环节,观察系统的各点响应。
(二)实验原理
对一给定控制系统如果其状态完全可控,则可进行任意极点配置即通过设计反馈増益K 使闭环系统具有期望的极点。
极点配置有二种方法:第一种方法是采用变换矩阵T ,使系统具有期望的极点,从而求出矩阵K ;第二种方法基于Caylay-Hamilton 理论,通过矩阵多项式φ(â),可求出K (这种方法称为Ackermann 公式)。
在MATLAB 中,利用控制系统工具箱函数place 和acker 进行极点配置设计。
三、主要仪器设备
一台PC 电脑,matlab 仿真软件,simulink 仿真环境 四、实验源代码及实验结果
function jidianpeizhi
num=[10];
den=[1,6,11,6];
[A,B,C,D]=tf2ss(num,den);
J=[-2-j*2*sqrt(3),-2+j*2*sqrt(3),-10]; K=place(A,B,J);
K
sys=ss(A-B*K,[0;0;0],eye(3),0);
t=0::4;
X=initial(sys,[1;0;0],t);
x1=[1,0,0]*X';
x2=[0,1,0]*X';
x3=[0,0,1]*X';
subplot(3,1,1);
plot(t,x2);
grid on;
title('Reponse to initial condition'); ylabel('x1');
subplot(3,1,2);
plot(t,x2);
grid on;
ylabel('x2');
subplot(3,1,3);
plot(t,x3);
grid on;
ylabel('x3');
xlabel('t(sec)');
实验结果
K =
实验验证:
>> num=[10];
>> den=[1 6 11 6];
>> [A,B,C,D]=tf2ss(num,den);
>> J=[-2-j*2*sqrt(3),-2+j*2*sqrt(3),-10]; >> K=place(A,B,J)
K =
>> A1=A-B*K;
>> sys=ss(A1,B,C,D);
>> G1=zpk(sys);
>> G1=zpk(sys)
G1 =
10
----------------------
(s+10) (s^2 + 4s + 16)
Continuous-time zero/pole/gain model.
五、simulink仿真
1.简单环节叠加仿真
2.状态函数仿真
六、心得、体会
1.通过本次实验,掌握了状态反馈的概念,并且掌握了利用状态反馈进行极点配置的方法,学会了用MATLAB求解状态反馈矩阵。
2.确定极点配置黄台反馈控制器的增益矩阵实现函数可以用两个来实现:place()和acker()函数。
函数acker是基于求解几点配置问题的艾克曼公式,它只能应用于单输入系统,要配置的闭环几点可以包括多重极点。
3.J是n个期望的闭环极点矩阵,除了用状态矩阵转化为传递函数之后求零极点来验证之外,还可以用命令[Q,D]=eig(A-B*K)来验证闭环几点,eig功能主要是求A-B*K这个矩阵的特征值与特征向量,Q为特征向量,D为特征值矩阵。
4.本次实验注重于对以前知识的学习以及对课本知识的巩固与加深理解。
Place函数在运用的时候,里面的变量需要是A,B两个状态矩阵,所以这就运用到了传递函数矩阵转化为状态矩阵的函数tf2ss;之后验证的过程中,需要算出传递函数GG,所以就运用了状态矩阵转化为传递函数的函数ss2tf以及tf函数;求出传递函数的零极点所需要的函数是zpk函数。
所以,本次实验可以说是对以前做过的实验的复习,也
是整个控制理论实验的提高。
