工程流体水力学第六章习题答案
哈工大建筑工业出版社伍悦滨工程流体力学(水力学)课后习题答案

P gh P ρρ==18、153.85kN ,0,0 19、28.85kN ,2.56 kN 20、0.114 21、不能 22、0.48m 第三章 1、35.86 m/s 2
2、36.27m/s 2二元/恒定 /非均匀流 3、ay-bx=c 4、x 2+y 2=c 5、3x -2y =3 6、y =0.242r 0 7、1,3不满足2满足 8、u x =-2xy -2x +f (y ) 9、4max 3Q bu = 10、18.05m/s, 22.25m/s 11、8.16 2.04 0.51 16.32 4.08 1.02 4.08 1.02 0.255 12、0.228kg/s 9.83m/s 13、4.77 m/s 14、0.158d 0.274d 0.354d 0.418d 0.474d ()21234520d u u u u u πρ++++ 15、0.056 m 16、300 mm 1.18m/s 17、Q 1/Q 2=0.28 18、2.64 kg/m 3 19、0xx yy zz εεε=== 0 xy yx z a εεω=== 有旋无角变形 ()() 2222222 2 222 0 xx yy zz xy z y x cxy cxy xyxycyxx y εεεεωωω-== =++-= ===+ 无旋有角变形 第四章 1、10.9 L/s 2、1.87m 3、235.5mm 4、0.8m B →A 5、3.85m/s 4.34m/s 6、12.7 L/s 7、11.8m 79.0kPa 8、68.1 -0.48 -20.1 0 kPa 9、1.23m 10、8.22 L/s 428mm 11、1.5 m 3/s 12、-64.5Pa 967.5Pa 13、143.24kN 14、25.05 L/s,8.35 L/s 1.97 kN 15、3.26kN ,5.26kN 16、2.322kN 17、527N 18、8.5 m 3/s, 22.42kN 19、98.35kN, 120.05kN 20、2509W 21、2 2y x x y ψ?=-=+ ()220.5 x y ψ?=+不存在 ψ?、均不存在
流体力学课后习题答案第六章

6-5 某蒸汽冷凝器内有250根平行的黄铜管,通过的冷却水流量Q =8 l /s ,水温为10oC ,为了使黄铜管内冷却水保持为紊流(此时黄铜管的热交换性能比层流时好),问黄铜管的直径不得超过多少?解:查表1.3有10℃的水621.310*10/m s ν-= 由214Q nd v π= ①及临界雷诺数R e 2300vdν== ② 联立有 14d m m = 即为直径最大值6.7 某管道的半径0r 15cm =,层流时的水力坡度J 0.15=,紊流时的水力坡度J 0.20=,试求管壁处的切应力0τ和离管轴r 10cm =轴处的切应力。
解:层流时:2f 3000h r r 1510ggJ 1.0109.80.15110.25Pa 2l 22τρρ-⨯===⨯⨯⨯⨯=23r 1010g J 1.0109.80.1573.5Pa 22τρ-⨯==⨯⨯⨯⨯=紊流时:2f 3000h r r 1510ggJ 1.0109.80.20147Pa 2l22τρρ-⨯===⨯⨯⨯⨯=2'3r1010gJ 1.0109.80.2098Pa 22τρ-⨯==⨯⨯⨯⨯=6.9为了确定圆管内径,在管内通过ν为0.013 cm 2/s 的水,实测流量为35cm 3/s ,长15m ,管段上的水头损失为2㎝水柱,试求此圆管的内径。
解: 设管内为层流42212832264gdlQgdl gd l d h f πνυνυυν===11441281280.013150035 1.949802f lQ d cm ghνππ⎛⎫⨯⨯⨯⎛⎫===⎪ ⎪⎪⨯⨯⎝⎭⎝⎭校核 1768013.094.13544Re =⨯⨯⨯===πνπνυd Qd 层流6-18 利用圆管层流Re64=λ,紊流光滑区25.0Re3164.0=λ和紊流粗糙区25.011.0⎪⎭⎫⎝⎛=d k s λ这三个公式,(1)论证在层流中0.1v∝f h ,光滑区75.1v∝f h ,粗糙区0.2v∝f h ;(2) 在不计局部损失h m 的情况下,如管道长度l 不变,若使管径d 增大一倍,而沿程水头损失h f 不变,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,流量各为原来的多少倍?(3) 在不计局部损失h m 的情况下, 如管道长度l 不变,通过流量不变,欲使沿程水头损失h f 减少一半,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,管径d 各需增大百分之几? 解:(1)由R e vdν=,22f l vh d gλ=有1232f l h v gdν=即在层流 1.0f h v∝由0.250.3164R eλ=得0.251.752 1.250.1582f lvh dgν=光滑区 1.752f h v∝由0.250.11s k d λ⎛⎫= ⎪⎝⎭得0.2523 1.250.0505sf k lh v dg=粗糙区 2.03f h v ∝(2)由214Q d v π=,以上公式变为14128f lQh d gνπ=Q 变为16倍0.251.752 4.751.750.7898f lQh dg νπ=Q 变为6.56倍0.2523 5.2520.808sf k lQh dg π=Q 变为6.17倍(3)由以上公式计算可知分别19%,16%,14%6-19 两条断面面积、长度、相对粗糙高度都相等的风管,断面形状分别为圆形和正方形,试求(1)若两者通过的流量相等,当其管内流动分别处在层流和紊流粗糙区两种情况下时,两种管道的沿程水头损失之比h f 圆/h f 方分别为多少?(2)若两者的沿程水头损失相等,且流动都处在紊流粗糙区,哪条管道的过流能力大?大多少? 解:(1)2214d a π=224a dπ=当量直径de a = 层流时 226464R e 22f l vlv h d gd gν==22220.7854f h de a h ddπ====圆方紊流粗糙区22f l vh d gλ=,λ相等0.886f h de a h dd====圆方(2)Q Q =圆方此时圆管流通能力大,大6%6.20 水管直径为50㎜,1、2两断面相距15 m ,高差3 m ,通过流量Q =6 l/s ,水银压差计读值为250㎜,试求管道的沿程阻力系数。
流体力学6,7,8章课后题答案

第六章 6-1解:层流状态下雷诺数Re 2000< 60.1Re 6.710vdv υ-⨯==⨯ ⇒60.120006.710v -⨯<⨯⇒62000 6.710/0.10.134(/)v m s -<⨯⨯= 即max 0.134/v m s =223max max max 0.13.140.1340.00105/ 1.05/44d Q Av v ms L sπ===⨯⨯≈=6-2解:层流状态下雷诺数Re 2000<3Re 20000.910120000.0450.1()vd d m d ρυ-=<⨯⨯⨯⇒<⇒<6-3解:3221.66100.21(/)0.13.1444Q v m s d π-⨯==≈⨯临界状态时Re 2000=52533Re Re0.210.1 1.0510(/)20001.05100.88109.2410()vd vd m s Pa s υυυμυρ---=⇒=⨯⇒==⨯⇒==⨯⨯⨯=⨯⋅ 6-4解:当输送的介质为水时:32210101270131444.(/)..Q v m s d π-⨯===⨯ 612701838632000151910..Re .vd υ-⨯===>⨯水 3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力粗糙。
当输送的介质为石油时:质量流量与水相等3310101010(/)Q kg s -=⨯⨯=31000118850.(/)Q m s == 2200118150********..(/)..Q v m s d π===⨯ 415030113184200011410..Re .vd υ-⨯===>⨯水3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力光滑。
6-5解:判断流态需先求出雷诺数()2900036009000088023144./..Re Q v m s Avd υ÷===⨯=冬季:421101./m s υ-⨯=40088021608820001110..Re ..vd υ-⨯===<⨯ ⇒ 流态为层流。
水力学第六章课后习题答案

7.14虹吸管将A 池中的水输入B 池,已知长度1l =3m ,2l =5m ,直径d =75mm ,两池水面高差H =2m ,最大超高h =1.8m ,沿程摩阻系数λ=0.02,局部损失系数:进口a ζ=0.5,转弯b ζ=0.2,出口c ζ=1,试求流量及管道最大超高断面的真空度。
解: 以下游水面为基准面,从上池水面到下池水面列伯努利方程:22222350.7 1.00.0222220.0752v l v v v v H g d g g g gζλζζ+⎛⎫=+++=++⨯ ⎪⎝⎭b c 进∴ 3.20v ==(m/s )23.200.07514.144Q vA π==⨯⨯=(L/s )从C 过流断面到下池水面列伯努利方程:2222222C C C C Cp v l v v z g g d g gαλζρ++=+ 取1C α= ∵C v v =∴251.8 2.010.02 1.00.0752a C C V p p p vH g g g ρρ-⎛⎫==-=++-⨯- ⎪⎝⎭25 3.203.80.02 3.100.07529.807=-⨯⨯=⨯m答:流量14.14Q =L/s ,管道最大超高断面的真空度为3.10m 。
7.16水从密闭容器A ,沿直径d =25mm ,长l =10m 的管道流入容器B ,已知容器A 水面的相对压强1p =2at ,水面高1H =1m ,2H =5m ,沿程摩阻系数λ=0.025,局部损失系数:阀门v ζ=4.0,弯头b ζ=0.3,试求流量。
解: 以地面为基准面,从A 池面到B 池面列伯努利方程:222111222123222v b p v p v l v H H g g g g d g ααζζζζλρρ⎛⎫++=+++++++ ⎪⎝⎭进出取120v v ==;20p =;0.5ζ=进; 1.0ζ=出,则有121122100.5 1.0 4.030.30.0250.025p g H H g v ρ⎡⎤⎛⎫+-⎢⎥⎪⎝⎭⎢⎥=⎢⎥⎛⎫+++⨯+⨯ ⎪⎢⎥⎝⎭⎣⎦ ()122120516.4g ⨯+-⎡⎤=⎢⎥⎣⎦4.37=(m/s )24.370.025 2.154Q vA π==⨯⨯=(l /s )答:流量 2.15Q =l /7.17水车由一直径d =150mm ,长l =80m 的管道供水,该管道中有两个闸阀和4个90°弯头(λ=0.03,闸阀全开a ζ=0.12,弯头b ζ=0.48)。
水力学 第六章课后题答案

思考题
6.6 明渠水流有哪三种流态,是如何定义的,判别标准是什么? 明渠恒定均匀流 、明渠恒定非均匀流 、明渠非恒定非均匀流。 明渠恒定均匀流:流速的大小和方向均不随时间及距离而变的明渠水流。 明渠恒定非均匀流:流速不随时间变化,但其大小和方向或二者之一沿程变化 的明渠水流。 明渠非恒定非均匀流:流动要素随时间变化且其大小和方向或二者之一沿程变 化的明渠水流。
2
2
R A 41.8 2.43m
17.24
C
1
1
R6
1
1
2.436 82.8m0.5 / s
n 0.014
Q CA Ri 82.8 41.8 2.43 0.002 241.3m3 / s
6.2 一梯形混凝土渠道,按均匀流设计。已知Q为35m3/s,b为8.2m,m为1.5 ,n为0.012及i为0.00012,求h(用试算——图解法和迭代法分别计算)。
6.10 何谓断面比能曲线?比能曲线有哪些特征? 答 水:深由的函Es 数h ,2g即QA22 知Es ,f (当h),流按量此Q和函过数水绘断出面的的断形面状比及能尺随寸水一深定变时化,的断关面系比曲能线仅即仅是是断 面比能曲线。 特征:是一条下端以水平线为渐近线,上端以过原点的 45o直线为渐近线的二次 抛物线;在K点有最小Esmin ,K点上部Es 随h增加而增大,K点下部 Es随h增加而减 小。
23
v Q 23 1.25m / s A 18.4
《工程流体力学(水力学)》第二版 禹华谦 课后习题答案 西南交通大学出版社

《工程流体力学(水力学)》第二版禹华谦课后习题答案西南交通大学出版社欢迎光临阳光大学生网, 提供最全面的大学生课后习题答案和复习试题免费下载,////0>.阳光大学生网我们希望呵护您的眼睛,关注您的成长,给您一片绿色的环境,欢迎加入我们,一起分享大学里的学习和生活感悟,免费提供:大学生课后答案 ,大学考试题及答案 ,大学生励志书籍。
《水力学》李炜徐孝平主编 2000 年 6 月武汉水利电力大学出版社共 12 章全部习题的解答第一章1-1 解:3 3 3ρ 1.03g cm 1030kg m , 比重s 1.03, γ 10.094kN m1-2 解:2γ9789N /m3ρ 998.88kg m ,g 9.8?3 2μ gμ9.8 ×1.002 ×10 N ?S /m?6 2ν 1.003 ×10 m /sργ 9789?4γ11.82 × 0.15 ×10?5 2以上为水,以下为空气μρνν 1.089 ×10 N ?S /m g 9.81-3 解:d ν9 7dp ?K ?2.19 ×10 × ?1% 2.19 ×10 Pav1-4 解:3 3γ G v 0.678 /10 678kgf /m①用工程单位制:2 4ργ g 678 / 9.8 69.18kgfs /mγγ ×9.8N kgf 6644.4N m②用国单位制: (SI 制) :3ργ g 678kg m1-5 解:du u 1.531流速梯度 3.75 ×10 3sdy δ 0.4 ×10u3 2切应力τμ 0.1 ×3.75 ×10 3.75 ×10 Paδ2活塞所受的摩擦阻力 F τ A τπdl 3.75 ×10 ×3.14 ×0.14 ×0.16 26.38N1-6 解:作用在侧壁上粘性切力产生的力矩du r 0.2M A μr 2 πr h μω+1 2 ×3.14 × 0.2 × 0.4 × μ×101 + 68.3 μdy δ 0.003M 4.905∴μ 0.072Pa ?S68.3 68.31-7 解:2设u Ay +By +c; ①根据实际流体的无滑移现象,当 y0 时 u0∴C 0 (第三个常数项为零); ②∵y0.04m 时,u1m/sdu2则有 1A ×0.04 +B ×0.04; ③E 点的流体切应力为零,有 2Ay +B 0 , dy10.0016A + 0.04B 1 A ?625?则由联立方程求得解得:0.08A +B 0 B 50?du du-3?6τμυρ 1.0 ×10 ×1000 × 2 Ay+B )1 ×10 (-1250y+50 )dy dy-2当y0 处,τ 5 ×10 Pa-2当y0.02 处,τ 2.5 ×10 Pa当 y0.04 处,τ0 Pa由此可见均匀流横断面上切应力是呈直线分布的。
武汉大学水力学教材答案第六章

第六章恒定管流1、并联管道中各支管的单位机械能损失相同,因而各支管水流的总机械能也应相等。
( )2、图示虹吸管中B点的压强小于大气压强。
( )3、恒定管流的总水头线沿流程下降,而测压管水头线沿流程可升可降。
( )4、在等直径圆管中一定发生均匀有压流动。
( )5、各并联支管的水头损失相同,所以其水力坡度也相同。
( )6、图示两个容器由两根直管相连,两管的管径、管长及糙率均相同,所以通过的流量相等。
( )7、设计管道时,若选用的糙率大于实际的糙率,则求得的管道直径偏小,不能通过要求的设计流量。
( )8、图示A、B 两点间有两根并联管道1 和2 。
设管1 的沿程水头损失为h f1,管 2 的沿程水头损失为h f2。
则h f1与h f2 的关系为()(1)h f1 >h f2;(2)h f1<h f2;(3)h f1 = h f2;(4)无法确定。
9、图示为坝身下部的三根泄水管a、b、c,其管径、管长、上下游水位差均相同,则流量最小的是()。
(1)a管;(2)b管;(3)c管;(4)无法确定。
10、在管道断面突然扩大处,测压管水头线沿程________________________________________________________;在管道断面突然缩小处,测压管水头线沿程____________________________________。
11、图示为一串联管段恒定流。
各管段流量q v1、q v2、q v3的关系为______________________。
各管段流速v1、v2、v3 的关系为____________________________________________________________。
12、对于有压管流出口为自由出流时,测压管水头线终点在_________________________________________________;出口为淹没出流时,若下游水池中流速v2=0,测压管水头线终点在____________________________,若v2≠0,测压管水头线应________________________________________________________________ ____下游水面。
流体力学4-6章答案 (2)

第四章 流体运动学和流体动力学基础4-15如图所示为一文丘里管和压强计,试推导体积流量和压强计读数之间的关系式。
解:对同在一条流线上的1、2两点列伯努利方程gu g p z g u g p z 2222222111 设测压管左侧液面坐标为z 3,1、2点的静压力满足gH H z z g p z z g p m 322311H z g p z g p m12211 代入伯努利方程可得4241/1/1124d d gH q m V4-16按图所示的条件求当H =30cm 时的流速u 。
解:设皮托管入口前方未受扰动处一点为点1,皮托管入口处一点为点2,由静压强分布可知x d g p p w 231x d H g p p w 242 gH p p w 8.043由以上三式,可得gH p p w 2.012由于1,2两点处于同一条流线上,对其列伯努利方程gp g u g p w w 2212 可得s m gH gp p g u w /084.13.08.94.04.0212 4-22如图所示,离心式水泵借一内径d =150mm 的吸水管以q V =60m 3/h 的流量从一敞口水槽中吸水,并将水送至压力水箱。
设装在水泵与吸水管接头上的真空计指示出负压值为39997Pa 。
水力损失不计,试求水泵的吸水高度H s 。
解:(1)取敞口水槽的自由液面与水泵出口之间的流体为控制体,令动能修正系数 1= 2=1,列伯努利方程gV g p H s 202222 吸水管内的平均流速为s m d q V V /943.015.03600/6044222可得 m g V g p H s 036.48.92943.08.910399972232224-29如图所示,一股射流以速度 0水平射到倾斜光滑平板上,体积流量为q V 0。
求沿板面向两侧的分流流量q V 1和q V 2的表达式,以及流体对板面的作用力。
忽略流体撞击的损失和重力影响,射流的压强分布在分流前后都没有变化。
水力学基础练习题六(含答案)

题4 图8-10中,水由封闭容器A沿垂直变直径管道流入下面的水池,容器内p0=2N/cm2且液面保持不变。若d1=50mm,d2=75mm,容器内液面与水池液面的高差H=1m(只计局部水头损失)。
求:(1)管道的流量Q;
(2)距水池液面处的管道内B点的压强。
图6-10
题5 采用内壁涂水泥砂浆的铸铁管供水,作用水头H=10m,管长l=1000m,管径d=200mm(如图8-12所示)。
(2)如泄流量Q'=25.14m3/s ,若管径与下游水位维持不变,由上游水位怎样变化?
(3)如流量Q'=25.14m2/s ,上、下游水位保持原状不变(即H=8m),问管径应如何变化?
图6-6
题3 一直径为d的水平直管从水箱引水、如图8-7所示,已知:管径d=0.1m,管长l=50m,H=4m,进口局部水头损失系数z1=0.5,阀门局部水头损失系数z2=2.5 ,今在相距为10m的1-1断面及2-2断面间设有一水银压差计,其液面差Δh=4cm,试求通过水管的流量Q。
求:(1)校验管道能否输水Q=50 l/s。
(2)如管道输水能力不足,为通过上述流量,在管道中加接部分并联管,取并联管l1=l2,又d1=d2=d,试求管长l1,l2。
(说明:本例中将用到管道比阻抗S0,,一般情况下可查水利计算手册。)
图6-12
题6 图8-13中,用长度为l的三根平行管路由A水池向B水池引水,管径d2=2d1,d3=3d1,管路的粗糙系数n均相等,局部水头损失不计,试分析三条管路的流量比。
问题6:在环状管网的任一闭合环路中,以顺时针方向的水流所引起的水头损失____逆时针方向的水流所引起的水头损失。
A.小于;
B.等于;
(完整word版)流体力学习题及答案-第六章

第六章 水波理论6-1 求波长为145m 的海洋波传播速度和波动周期,假定海洋是无限深的。
答:052.1514525.125.1=⨯==λc (m/s ),633.91458.08.0=⨯==λτ(s );即传播速度为15.052(m/s ),波动周期为9.633(s )。
6-2 海洋波以10m/s 移动,试求这些波的波长和周期。
答:6425.1/1025.1/2222===c λ(m ), 4.6648.08.0=⨯==λτ(s );即波长为64(m ),波浪周期为6.4(s )。
6-3 证明()t iH A z W Ω-+=ςλπ2cos )(为水深为H 的进行波的复势,其中iy x +=ς为复变数,y 轴垂直向上,原点在静水面上。
并证明λπλπHth 222=Ω(提示:()xshy i xchy iy x sin cos cos -=+)。
答:在图示坐标系中,平面进行波的速度势为:()()t kx chkHH y chk ag ωωϕ-+=sin 在x 、y 方向的速度分别为: ()()t kx shkHH y chk a x u ωωϕ-+=∂∂=cos , ()()t kx shkH H y shk a y v ωωϕ-+=∂∂=sin ; 由上述速度分布得到二维波浪运动的流函数为:()()()()()()()()t kx chkHH y shk ag t kx shkHH y shk k a dy t kx shkHH y chk a dx t kx shkH H y shk a udy vdx ωωωωωωωωψ-⋅+⋅=-⋅+⋅=-++-+-=+-=⎰⎰cos cos cos sin 因此,二维波浪运动的复势为:()()()()()()()()()()()[]t kx H y ishk t kx H y chk chkHag t kx chkHH y shk ag i t kx chkH H y chk ag t y x i t y x z W ωωωωωωωψϕ-++-+⋅=-+⋅+-+⋅=+=cos sin 1 cos sin ,,,, 在上式中,令:chkH ag A 1⋅=ω,t kx X ω-=,()H y k Y +=; 则可得到:()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⋅-⎪⎭⎫ ⎝⎛-⋅=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⋅+⎪⎭⎫ ⎝⎛-⋅=⋅+⋅=2sin 2cos 2sin 2cos cos sin ππππX ishY X chY A X ishY X chY A X ishY X chY A z W 由提示()xshy i xchy iy x sin cos cos -=+,可以得到:()()()⎥⎦⎤⎢⎣⎡--++=⎪⎭⎫ ⎝⎛++--=⎪⎭⎫ ⎝⎛+-=2cos 2cos 2cos πωπωπt ikH iy x k A H y ik t kx A iY X A z W6-4 在水深为d 的水平底部(即d z -=处),用压力传感器记录到沿x 方向传播的进行波的波压力为()t p 。
工程流体水力学第六章习题答案

第六章 量纲分析和相似原理答案6-1由实验观测得知,如图6-1所示的三角形薄壁堰的流量Q 与堰上水头H 、重力加速度g 、堰口角度θ以及反映水舌收缩和堰口阻力情况等的流量系数m 0(量纲一的量)有关。
试用π定理导出三角形堰的流量公式。
解:()00θ=,,,,f Q H g m 选几何学的量H ,运动学的量g 作为相互独立的物理量,有3个π项。
111πa H g Q β=,222a H g,3330πa H g m对1π,其量纲公式为11000-23-1L T M =L (LT )L T11L :03αβ=++,1T :021β=--解出152α=-,112β=-,则可得 152πQg H对2π,其量纲公式为220002L T M L (LT )22L :0αβ=+,2T :02β=-联立解上述方程组,可得02=α,02=β,02=γ,则可得2π对3π,其量纲公式为33000-2L T M L (LT )33L :0αβ=+,3T :02β=-联立解上述方程组,可得03=α,03=β,03=γ,则可得30πm123πππ0F ,,即052()0Q F m g H,,或1052()Q F m g H,2501),(H g m F Q θ=式中,θ要视堰口的实际角度而定,量纲一的量0m 要由实验来确定。
第十章三角形薄壁堰的理论分析解5204tan 252Qm gh 与上式形状相同。
6-2 根据观察、实验与理论分析,认为总流边界单位面积上的切应力τ0,与流体的密度ρ、动力粘度μ、断面平均流速v ,断面特性几何尺寸(例如管径d 、水力半径R )及壁面粗糙凸出高度Δ有关。
试用瑞利法求τ0的表示式; 若令沿程阻力系数8(,)λ∆=f Re d,可得208λτρ=v 。
解:351240τkv d将上式写成量纲方程形式后得35124-1-23-1-110dim ML T =(ML )(ML T )(LT )(L)(L)ααααατ--=根据量纲和谐原理可得:12M :1αα=+12345L :13ααααα-=--+++ 23T :2αα-=--选53αα、为参变量,联立解上述方程组可得:131αα=-,232αα=-,4352ααα=-+-。
流体力学课后习题答案第六章

6-5 某蒸汽冷凝器内有250根平行的黄铜管,通过的冷却水流量Q =8 l /s ,水温为10oC ,为了使黄铜管内冷却水保持为紊流(此时黄铜管的热交换性能比层流时好),问黄铜管的直径不得超过多少?解:查表1.3有10℃的水621.310*10/m s ν-= 由214Q nd v π= ①及临界雷诺数R e 2300vdν== ② 联立有 14d m m = 即为直径最大值6.7 某管道的半径0r 15cm =,层流时的水力坡度J 0.15=,紊流时的水力坡度J 0.20=,试求管壁处的切应力0τ和离管轴r 10cm =轴处的切应力。
解:层流时:2f 3000h r r 1510ggJ 1.0109.80.15110.25Pa 2l 22τρρ-⨯===⨯⨯⨯⨯=23r 1010g J 1.0109.80.1573.5Pa 22τρ-⨯==⨯⨯⨯⨯=紊流时:2f 3000h r r 1510ggJ 1.0109.80.20147Pa 2l22τρρ-⨯===⨯⨯⨯⨯=2'3r1010gJ 1.0109.80.2098Pa 22τρ-⨯==⨯⨯⨯⨯=6.9为了确定圆管内径,在管内通过ν为0.013 cm 2/s 的水,实测流量为35cm 3/s ,长15m ,管段上的水头损失为2㎝水柱,试求此圆管的内径。
解: 设管内为层流42212832264gdlQgdl gd l d h f πνυνυυν===11441281280.013150035 1.949802f lQ d cm ghνππ⎛⎫⨯⨯⨯⎛⎫===⎪ ⎪⎪⨯⨯⎝⎭⎝⎭校核 1768013.094.13544Re =⨯⨯⨯===πνπνυd Qd 层流6-18 利用圆管层流Re64=λ,紊流光滑区25.0Re3164.0=λ和紊流粗糙区25.011.0⎪⎭⎫⎝⎛=d k s λ这三个公式,(1)论证在层流中0.1v∝f h ,光滑区75.1v∝f h ,粗糙区0.2v∝f h ;(2) 在不计局部损失h m 的情况下,如管道长度l 不变,若使管径d 增大一倍,而沿程水头损失h f 不变,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,流量各为原来的多少倍?(3) 在不计局部损失h m 的情况下, 如管道长度l 不变,通过流量不变,欲使沿程水头损失h f 减少一半,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,管径d 各需增大百分之几? 解:(1)由R e vdν=,22f l vh d gλ=有1232f l h v gdν=即在层流 1.0f h v∝由0.250.3164R eλ=得0.251.752 1.250.1582f lvh dgν=光滑区 1.752f h v∝由0.250.11s k d λ⎛⎫= ⎪⎝⎭得0.2523 1.250.0505sf k lh v dg=粗糙区 2.03f h v ∝(2)由214Q d v π=,以上公式变为14128f lQh d gνπ=Q 变为16倍0.251.752 4.751.750.7898f lQh dg νπ=Q 变为6.56倍0.2523 5.2520.808sf k lQh dg π=Q 变为6.17倍(3)由以上公式计算可知分别19%,16%,14%6-19 两条断面面积、长度、相对粗糙高度都相等的风管,断面形状分别为圆形和正方形,试求(1)若两者通过的流量相等,当其管内流动分别处在层流和紊流粗糙区两种情况下时,两种管道的沿程水头损失之比h f 圆/h f 方分别为多少?(2)若两者的沿程水头损失相等,且流动都处在紊流粗糙区,哪条管道的过流能力大?大多少? 解:(1)2214d a π=224a dπ=当量直径de a = 层流时 226464R e 22f l vlv h d gd gν==22220.7854f h de a h ddπ====圆方紊流粗糙区22f l vh d gλ=,λ相等0.886f h de a h dd====圆方(2)Q Q =圆方此时圆管流通能力大,大6%6.20 水管直径为50㎜,1、2两断面相距15 m ,高差3 m ,通过流量Q =6 l/s ,水银压差计读值为250㎜,试求管道的沿程阻力系数。
工程流体力学-禹华谦-习题答案-第6章

第六章 理想流体动力学 6-1平面不可压缩流体速度分布为Vx=4x+1;Vy=-4y.(1) 该流动满足连续性方程否? (2) 势函数φ、流函数ψ存在否?(3)求φ、ψ 解:(1)由于044=-=∂∂+∂∂yVyx Vx ,故该流动满足连续性方程 (2)由ωz =21(y Vx x Vy ∂∂-∂∂)=)44(21+-=0, 故流动有势,势函数φ存在,由于该流动满足连续性方程, 流函数ψ存在,. (3)因 Vx yx ∂∂=∂∂=ψϕ=4x+1 Vy=y ∂∂φ=-x∂∂ψ=-4yd φ=x∂∂φdx+y ∂∂φdy=Vxdx+Vydy=(4x+1)dx+(-4y)dyφ=⎰d φ=⎰x∂∂φdx+y ∂∂φdy=⎰Vxdx+Vydy=⎰ (4x+1)dx+(-4y)dy=2x 2-2y 2+x d ψ=x∂∂ψdx+y ∂∂ψdy=-Vydx+Vxdy=4ydx+(4x+1)dyψ=⎰d ψ=⎰x∂∂ψdx+y ∂∂ψdy=⎰-Vydx+Vxdy=⎰ 4ydx+(4x+1)dy=4xy+y6-2 平面不可压缩流体速度分布:Vx=x 2-y 2+x; Vy=-(2xy+y).(1) 流动满足连续性方程否? (2) 势函数φ、流函数ψ存在否? (3)求φ、ψ . 解:(1)由于x Vx ∂∂+xVy∂∂=2x +1-(2x +1)=0,故该流动满足连续性方程,流动存在. (2)由ωz =21(y Vx xVy ∂∂-∂∂)=))2(2(21y y ---=0, 故流动有势,势函数φ存在,由于该流动满足连续性方程,流函数ψ也存在.(3)因 Vx=x∂∂φ =y ∂∂ψ= x 2-y 2+x, Vy=y ∂∂φ=-x ∂∂ψ=-(2xy+y).d φ=x∂∂φdx+y ∂∂φdy=Vxdx+Vydy=(x 2-y 2+x )dx+(-(2xy+y).)dyφ=⎰d φ=⎰x∂∂φdx+y ∂∂φdy=⎰Vxdx+Vydy =⎰ (x 2-y 2+x )dx+(- (2xy+y))dy=33x -xy 2+(x 2-y 2)/2 d ψ=x∂∂ψdx+y ∂∂ψdy=-Vydx+Vxdyψ=⎰d ψ=⎰x∂∂ψdx+y ∂∂ψdy=⎰-Vydx+Vxdy =⎰(2xy+y)dx+ (x 2-y 2+x)dy=x 2y+xy-y 3/36-3平面不可压缩流体速度势函数 φ=x 2-y 2-x,求流场上A(-1,-1),及B(2,2)点处的速度值及流函数值 解: 因 Vx=x ∂∂φ =y ∂∂ψ=2x-1,V y =y x y 2-=∂∂-=∂∂ψφ,由于x Vx ∂∂+xVy ∂∂=0,该流动满足连续性方程,流函数ψ存在d ψ=x∂∂ψdx+y ∂∂ψdy=-Vydx+Vxdyψ=⎰d ψ=⎰x∂∂ψdx+y ∂∂ψdy=⎰-Vydx+Vxdy=⎰2ydx+(2x-1)dy=2xy-y在点(-1,-1)处 Vx=-3; Vy=2; ψ=3 在点(2,2)处 Vx=3; Vy=-4; ψ=66-4已知平面流动速度势函数 φ=-π2qlnr,写出速度分量Vr,V θ,q 为常数。
水力学习题答案第六章.

选择题(单选题)1. 水在垂直管内由上向下流动,测压管水头差(a)h f=h;(b)h f=h+l ;(c)h f=l -h;(d)h f =l 。
2. 圆管流动过流断面上切应力分布为:(b)( a )在过流断面上是常数;( b )管轴处是零,且与半径成正比;( c )管壁处是零,向管轴线性增大;( d )按抛物线分布。
3. 圆管流的雷诺数(下临界雷诺数):(d)( a )随管径变化;( b )随流体的密度变化;(c)随流体的黏度变化;(d)不随以上各量变化。
5. 在圆管流中,层流的断面流速分布符合:(c)(a)均匀规律;(b)直线变化规律;(c)抛物线规律;(d)对数曲线规律。
6. 半圆形明渠半径r 0=4m,水力半径为:(c)(a)4m;(b)3m;( c )2m;(d)1m。
7. 变直径管流,细断面直径为d1,粗断面直径d2=2d1,粗细断面雷诺数的关系是:(d)(a)Re1=0.5 Re2;(b)Re1= Re2;(c)Re1=1.5 Re2;(d)Re1=2 Re2。
8. 圆管层流,实测管轴线上流速为4m/s ,则断面平均流速为: (c)(a)4 m/s ;(b) 3 .2m/s ;(c)2 m/s ;(d)1 m/s。
9. 圆管紊流过渡区的沿程摩阻系数λ:(c)(a)与雷诺数Re有关;(b)与管壁相对粗糙k s/ d有关;(c)与Re及k s/ d有关;(d)与Re和管长L 有关。
10. 圆管紊流粗糙区的沿程摩阻系数λ:(b)(a)与雷诺数Re有关;(b)与管壁相对粗糙k s/ d有关;4. 在圆管流中,紊流的断面流速分布符合:d)a)均匀规律;(b)直线变化规律;(c)抛物线规律;(d)对数曲线规律。
h,两断面间沿程水头损失,则:a)(c)与Re及k s/ d有关;(d)与Re和管长L 有关。
11. 工业管道的沿程摩阻系数λ ,在紊流过渡区随雷诺数的增加:(b)解: v4Q 4 16.3 2 2 0.2563 m d 2 3.14 0.1523600 Re vd0.2563 0.15 1922 0.2 10 4( a )增加; ( b )减小; ( c )不变; ( d )不定 计算题6.12 】水管直径 d=10cm ,管中流速 v=1m/s ,水温为 10℃,试判别流态。
流体第六章答案 大连民院

第三、四章 流体动力学基础习题及答案3-8已知流速场u x =xy 2, 313y u y =-, u z =xy, 试求:(1)点(1,2,3)的加速度;(2)是几维流动;(3)是恒定流还是非恒定流;(4)是均匀流还是非均匀流?解:(1)411633x x x x x x y z u u u u a u u u xy t x y z ∂∂∂∂=+++==∂∂∂∂25333213313233312163. 06m/s y y z x y a y u y a yu xu xy xy xy a =-===+=-==== (2)二元流动 (3)恒定流(4)非均匀流41xy 33-11已知平面流动速度分布为x y 2222cxu u x ycy x y =-=++,, 其中c 为常数。
求流线方程并画出若干条流线。
解:2222-xdx=ydyx ydx dydx dy cy cx u u x y x y =⇒-=⇒++积分得流线方程:x 2+y 2=c方向由流场中的u x 、u y 确定——逆时针3-17下列两个流动,哪个有旋?哪个无旋?哪个有角变形?哪个无角变形?(1)u x =-ay,u y =ax,u z =0 (2)z 2222,,0,a c x ycy cxu u u x y x y =-==++式中的、为常数。
z 2222,,0,a c x y cy cxu u u x y x y =-==++式中的、为常数。
解:(1)110 ()()22yx x y z u u a a a xy ωωω∂∂===-=+=∂∂有旋流动 xy 11()()0 22y x xy zx u u a a x y εεε∂∂=+=-==∂∂ 无角变形(2)222222222222222222211()2()2()22()()12()2()0 0 2()y x z x y u u x y c cx x y c cy x y x y x y c x y c x y x y ωωω∂⎡⎤∂+-+-=-=+⎢⎥∂∂++⎣⎦⎡⎤+-+====⎢⎥+⎣⎦无旋流动2222xy 22222112()()()022()()y x u u c x y c x y x y x y x y ε∂⎡⎤∂---=+==-≠⎢⎥∂∂++⎣⎦ 有角变形4—7变直径管段AB ,d A =0.2m,d B =0.4m ,高差△h=1.5m ,测得p A =30kPa ,p B =40kPa ,B 点处断面平均流速v B =1.5m/s ,试判断水在管中的流动方向。
最新工程流体力学 禹华谦 习题答案 第6章

第六章 理想流体动力学 6-1平面不可压缩流体速度分布为Vx=4x+1;Vy=-4y.(1) 该流动满足连续性方程否? (2) 势函数φ、流函数ψ存在否?(3)求φ、ψ 解:(1)由于044=-=∂∂+∂∂yVyx Vx ,故该流动满足连续性方程 (2)由ωz =21(y Vx x Vy ∂∂-∂∂)=)44(21+-=0, 故流动有势,势函数φ存在,由于该流动满足连续性方程, 流函数ψ存在,. (3)因 Vx yx ∂∂=∂∂=ψϕ=4x+1 Vy=y ∂∂φ=-x∂∂ψ=-4yd φ=x∂∂φdx+y ∂∂φdy=Vxdx+Vydy=(4x+1)dx+(-4y)dyφ=⎰d φ=⎰x∂∂φdx+y ∂∂φdy=⎰Vxdx+Vydy=⎰ (4x+1)dx+(-4y)dy=2x 2-2y 2+x d ψ=x∂∂ψdx+y ∂∂ψdy=-Vydx+Vxdy=4ydx+(4x+1)dyψ=⎰d ψ=⎰x∂∂ψdx+y ∂∂ψdy=⎰-Vydx+Vxdy=⎰ 4ydx+(4x+1)dy=4xy+y6-2 平面不可压缩流体速度分布:Vx=x 2-y 2+x; Vy=-(2xy+y).(1) 流动满足连续性方程否? (2) 势函数φ、流函数ψ存在否? (3)求φ、ψ . 解:(1)由于x Vx ∂∂+xVy∂∂=2x +1-(2x +1)=0,故该流动满足连续性方程,流动存在. (2)由ωz =21(y Vx xVy ∂∂-∂∂)=))2(2(21y y ---=0, 故流动有势,势函数φ存在,由于该流动满足连续性方程,流函数ψ也存在.(3)因 Vx=x∂∂φ =y ∂∂ψ= x 2-y 2+x, Vy=y ∂∂φ=-x ∂∂ψ=-(2xy+y).d φ=x∂∂φdx+y ∂∂φdy=Vxdx+Vydy=(x 2-y 2+x )dx+(-(2xy+y).)dyφ=⎰d φ=⎰x∂∂φdx+y ∂∂φdy=⎰Vxdx+Vydy =⎰ (x 2-y 2+x )dx+(- (2xy+y))dy=33x -xy 2+(x 2-y 2)/2 d ψ=x∂∂ψdx+y ∂∂ψdy=-Vydx+Vxdyψ=⎰d ψ=⎰x∂∂ψdx+y ∂∂ψdy=⎰-Vydx+Vxdy =⎰(2xy+y)dx+ (x 2-y 2+x)dy=x 2y+xy-y 3/36-3平面不可压缩流体速度势函数 φ=x 2-y 2-x,求流场上A(-1,-1),及B(2,2)点处的速度值及流函数值 解: 因 Vx=x ∂∂φ =y ∂∂ψ=2x-1,V y =y x y 2-=∂∂-=∂∂ψφ,由于x Vx ∂∂+xVy ∂∂=0,该流动满足连续性方程,流函数ψ存在d ψ=x∂∂ψdx+y ∂∂ψdy=-Vydx+Vxdyψ=⎰d ψ=⎰x∂∂ψdx+y ∂∂ψdy=⎰-Vydx+Vxdy=⎰2ydx+(2x-1)dy=2xy-y在点(-1,-1)处 Vx=-3; Vy=2; ψ=3 在点(2,2)处 Vx=3; Vy=-4; ψ=66-4已知平面流动速度势函数 φ=-π2qlnr,写出速度分量Vr,V θ,q 为常数。
《工程流体力学》 杨树人 第六章课后作业详解

0.02
Q2l hf 0.0826 5 4.58m d
则有
作业
【6-10】如图所示,某设备需润滑油的流量为Q=0.4cm3/s, 油从高位油箱经d=6mm,l=5m管道供给。设输油管道终 端为大气,油的运动粘度为1.5×10-4m2/s,(1)求沿程损 失是多少?(2)油箱液面高h应为多少?
作业
(2)列输油管道终端和自由液面的伯努利方程
v2 h (2 0.5) hf 2g
得
h 0.961m
作业
【6-13】如图示给水管路。已知L1=25m,L2=10m, D1=0.15m,D2=0.125m,λ1=0.037,λ2=0.039,闸门开启 1/4,其阻力系数ζ=17,流量为15L/s。试求水池中的水头 H。 【解】
2 v2 H hf hj 2g
其中
l1 l2 h f 0.0826Q (1 2 2 2 ) 0.464m d1 d2
2
2 2 2 v2 v12 A2 v2 v2 hj 0.5 0.5(1 ) ( 1) 1.4m 2g 2g A1 2 g 2g
故
H 1.864m
作业
【6-14】图示两水箱由一根钢管连通,管长100m,管径 0.1m。管路上有全开闸阀一个,R/D=4.0的90°弯头两个。 水温10℃。当液面稳定时,流量为6.5L/s,求此时液面差 H为若干?设△=0.15mm。 【解】此管路属长管,列两液 面的伯努利方程
H
H hf hj
(3)
Re
vd
4 0.2 =611621 6 1.308 10
/ d 2.5 103
查莫迪图得 0.025
工程流体力学答案(整理)
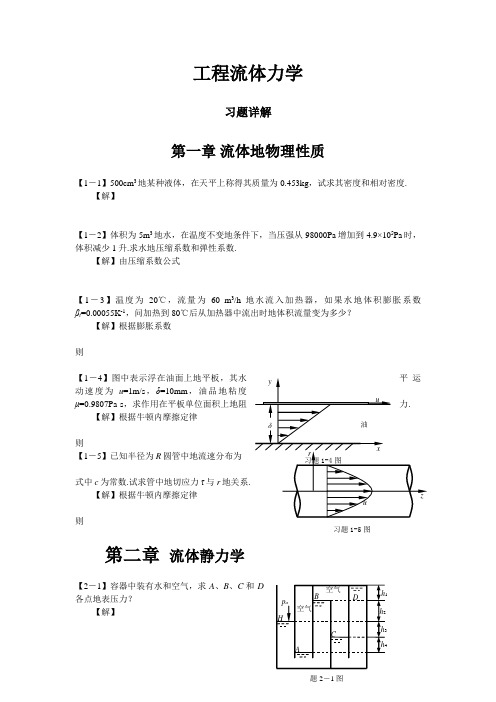
工程流体力学习题详解第一章流体地物理性质【1-1】500cm3地某种液体,在天平上称得其质量为0.453kg,试求其密度和相对密度.【解】【1-2】体积为5m3地水,在温度不变地条件下,当压强从98000Pa增加到4.9×105Pa时,体积减少1升.求水地压缩系数和弹性系数.【解】由压缩系数公式【1-3】温度为20℃,流量为60 m3/h地水流入加热器,如果水地体积膨胀系数βt=0.00055K-1,问加热到80℃后从加热器中流出时地体积流量变为多少?【解】根据膨胀系数则【1-4】图中表示浮在油面上地平板,其水动速度为u=1m/s,δ=10mm,油品地粘度μ=0.9807Pa·s,求作用在平板单位面积上地阻【解】根据牛顿内摩擦定律则【1-5】已知半径为R圆管中地流速分布为式中c为常数.试求管中地切应力τ与r地关系.【解】根据牛顿内摩擦定律则习题1-5图第二章流体静力学【2-1】容器中装有水和空气,求A、B、C和D【解】题2-1图【2-2】如图所示地U 形管中装有水银与水,试求:(1)A 、C 两点地绝对压力及表压力各为多少? (2)求A 、B 两点地高度差h ? 【解】 (1)(2)选取U 形管中水银地最低液面为等压面,则 得 【2-3】在一密闭容器内装有水及油,密度分别为ρw 及ρo ,油层高度为h 1,容器底部装有水银液柱压力计,读数为R ,水银面与液面地高度差为h 2,试导出容器上方空间地压力p 与读数R 地关系式.【解】选取压力计中水银最低液面为等压面,则得 【2-4】油罐内装有相对密度为0.7地汽油,为测定油面高度,利用连通器原理,把U 形管内装上相对密度为 1.26地甘油,一端接通油罐顶部空间,一端接压气管.同时,压力管地另一支引入油罐底以上地0.4m 处,压气后,当液面有气逸出时,根据U 形管内油面高度差△h =0.7m 来计算油罐内地油深H =?【解】选取U 形管中甘油最低液面为等压面,由气体各点压力相等,可知油罐底以上0.4m 处地油压即为压力管中气体压力,则得【2-5】图示两水管以U 形压力计相连,A 、B 两点高差1m ,U 形管内装有水银,若读数△h =0.5m ,求A 、B 两点地压力差为多少?【解】选取U 形管内水银最低液面为等压面,设B 点到水银最高液面地垂直高度为x ,则得【2-6】图示油罐发油装置,将直径为d 地圆管伸进罐内,端部切成45°角,用盖板盖住,盖板可绕管端上面地铰链旋转,借助绳系上来开启.已知油深H =5m ,圆管直径d =600mm ,油品相对密度0.85,不计盖板重力及铰链地摩擦力,求提升此盖板B题2-3图题2-4图所需地力地大小?(提示:盖板为椭圆形,要先算出长轴2b 和短轴2a ,就可算出盖板面积A =πab ).【解】分析如图所示以管端面上地铰链为支点,根据力矩平衡其中可得【2-7】图示一个安全闸门,宽为0.6m ,高为1.0m.距底边0.4m 处装有闸门转轴,使之仅可以绕转轴顺时针方向旋转.不计各处地摩擦力,问门前水深h 为多深时,闸门即可自行打开?水深h 小,即D 点上移.当D 好平衡.即得 【2-8】有一压力贮油箱(见图),其宽度(垂直于纸面方向)b =2m ,箱内油层厚h 1=1.9m ,密度ρ0=800kg/m 3,油层下有积水,厚度h 2=0.4m ,箱底有一U 型水银压差计,所测之值如图所示,试求作用在半径R =1m 地圆柱面AB 上地总压力(大小和方向).【解】分析如图所示,首先需确定自由液面,选取水银压差计最低液面为等压面,则由p B 不为零可知等效自由液面地高度曲面水平受力曲面垂直受力则【2-9】一个直径2m ,长5m 地圆柱体放置在图示地斜坡上.求圆柱体所受地水平力和浮力.【解】分析如图所示,因为斜坡地倾斜角为60°,故/ρo g题2-8题2-9经D 点过圆心地直径与自由液面交于F 点.BC 段和CD 段水平方向地投影面积相同,力方向相反,相互抵消,故 圆柱体所受地水平力圆柱体所受地浮力【2-10】图示一个直径D =2m ,长L =1m 地圆柱体,其左半边为油和水,油和水地深度均为1m.已知油地密度为ρ=800kg/m 3,求圆柱体所受水平力和浮力.【解】因为左半边为不同液体,故分别来分析AB 段和BC 段曲面地受力情况.AB 曲面受力BC 曲面受力则,圆柱体受力(方向向上)【2-11】图示一个直径为 1.2m 地钢球安装在一直径为1m 地阀座上,管内外水面地高度如图所示.试求球体所受到地浮力.【解】分析如图所示,图中实压力体(+)为一圆柱体,其直径为1.0m【2-12】图示一盛水地密闭容器,中间用隔板将其分隔为上下两部分.隔板中有一直径d =25cm 地圆孔,并用一个直径D =50cm 质量M =139kg 地圆球堵塞.设容器顶部压力表读数p M =5000Pa ,求测压管中水面高x 大于若干时,圆球即被总压力向上顶开?【解】分析如图所示,图中虚压力体(-)为一球体和圆柱体体积之和 根据受力分析可知则 ※【2-13】水车长3m ,宽 1.5m ,高1.8m ,盛水深1.2m ,见图2-2.试问为使水不益处,加速度a 地允许值是多少.【解】根据自由夜面(即等压面方程)题2-10图题2-11图图2-13图得第三章 流体运动学【3-1】已知流场地速度分布为 u =x 2y i -3y j +2z 2k(1)属几元流动?(2)求(x , y , z )=(3, 1, 2)点地加速度? 【解】(1)由流场地速度分布可知流动属三元流动. (2)由加速度公式得故过(3, 1, 2)点地加速度其矢量形式为:【3-2】已知流场速度分布为u x =x 2,u y =y 2,u z =z 2,试求(x , y , z )=(2, 4, 8)点地迁移加速度?【解】由流场地迁移加速度得故过(2, 4, 8)点地迁移加速度【3-3】有一段收缩管如图.已知u 1=8m/s ,u 2=2m/s ,l =1.5m.试求2点地迁移加速度.【解】由已知条件可知流场地迁移加速度为其中:则2点地迁移加速度为【3-4】某一平面流动地速度分量为u x =-4y ,u y =4x .求流线方程.【解】由流线微分方程得解得流线方程【3-5】已知平面流动地速度为,式中B 为常数.求流线方程.【解】由已知条件可知平面流动地速度分量题3-3 图代入流线微分方程中,则解得流线方程【3-6】用直径200mm地管输送相对密度为0.7地汽油,使流速不超过1.2m/s,问每秒最多输送多少kg?【解】由流量公式可知则【3-7】截面为300mm×400mm地矩形孔道,风量为2700m3/h,求平均流速.如风道出口处截面收缩为150mm×400mm,求该处断面平均流速.【解】由流量公式可知则如风道出口处截面收缩为150mm×400mm,则【3-8】已知流场地速度分布为u x=y+z,u y=z+x,u z=x+y,判断流场流动是否有旋?【解】由旋转角速度可知故为无旋流动.【3-9】下列流线方程所代表地流场,哪个是有旋运动?(1)2Axy=C(2)Ax+By=C(3)A ln xy2=C【解】由流线方程即为流函数地等值线方程,可得(1)速度分布旋转角速度可知故为无旋流动.(2)速度分布旋转角速度可知故为无旋流动.(3)速度分布旋转角速度可知故为有旋流动.【3-10】已知流场速度分布为u x =-cx ,u y =-cy ,u z =0,c 为常数.求:(1)欧拉加速度a =?;(2)流动是否有旋?(3)是否角变形?(4)求流线方程.【解】(1)由加速度公式得(2)旋转角速度可知故为无旋流动.(3)由角变形速度公式可知为无角变形.(4)将速度分布代入流线微分方程解微分方程,可得流线方程第四章 流体动力学【4-1】直径d =100mm 地虹吸管,位置如附图中所示.求流量和2、3地压力.不计水头损失.【解】选取4点所在断面和1点所在断面列伯努力方程,以过4点地水平线为基准线.得,则选取1、2点所在断面列伯努利方程,以过1点地水平线为基准线(v 2=v 4)得选取1、3点所在断面列伯努利方程,以过1点地水平线为基准线(v 3=v 4)得【4-2】一个倒置地U 形测压管,上部为相对密度0.8地油,用来测定水管中点地速度.若读数△h =200mm ,求管中流速u =?【解】选取如图所示1-1、2-2断面列伯努利方程,以水管轴线为基准线同时,选取U 形测压管中油地最高液面为等压面,则题 4-1图题 4-2图【4-3】图示为一文丘里管和压力计,试推导体积流量和压力计读数之间地关系式.当z 1=z 2时,ρ=1000kg/m 3,ρH =13.6×103kg/m 3,d 1=500mm ,d 2=50mm ,H =0.4m ,流量系数α=0.9时,求Q =?【解】列1-1、2-2所在断面地伯努利方程、以过1-1断面中心点地水平线为基准线.选取压力计中汞地最低液面为等压面,则 又由、,得所以【4-4】管路阀门关闭时,压力表读数为49.8kPa ,阀门打开后,读数降为9.8kPa.设从管路进口至装表处地水头损失为流速水头地2倍,求管路中地平均流速.【解】当管路阀门关闭时,由压力表度数可确定管路轴线到自有液面地高度H当管路打开时,列1-1和2-2断面地伯努利方程,则得【4-5】为了在直径D =160mm 地管线上自动掺入另一种油品,安装了如下装置:自锥管喉道处引出一个小支管通入油池内.若压力表读数为2.3×105Pa ,吼道直径d =40mm ,T 管流量Q =30 l/s ,油品地相对密度为0.9.欲掺入地油品地相对密度为0.8,油池油面距喉道高度H =1.5m ,如果掺入油量约为原输量地10%左右,B 管水头损失设为0.5m ,试确定B 管地管径.【解】列1-1和2-2断面地伯努利方程,则 其中得列3-3和4-4自有液面地伯努利方程,以4-4断面为基准面,则其中、,代入上式,得27mm 【4-6】一变直径地管段AB ,直径d A =0.2m ,d B =0.4m ,高差h =1.0m ,用压力表测得p A =70kPa ,p B =40kPa ,用流量计测得流量Q =0.2m 3/s.试判断水在管段中流动地方向.题 4-4图题 4-5图题 4-3图【解】列A 点和B 点所在断面地伯努利方程则故流动方向为A -B .【4-7】泄水管路如附图所示,已知直径d 1=125mm ,d 2=100mm ,d 3=75mm ,汞比压力计读数h =175mm ,不计阻力,求流量和压力表读数.【解】列1-1、2-2断面地波努利方程又由(即) 可得、、 列压力表所在断面和出口断面地伯努利方程可得【4-8】如图所示,敞开水池中地水沿变截面管路排出地质量流量Q m =14kg/s ,若d 1=100mm ,d 2=75mm ,d 3=50mm ,不计损失,求所需地水头H ,以及第二段管段中央M 点地压力,并绘制测压管水头线.【解】列1-1和3-3断面地伯努利方程,则其中 、 得列M 点所在断面2-2和3-3断面地伯努利方程,则 得【4-9】由断面为0.2m 2和0.1 m 2地两根管子组成地水平输水管系从水箱流入大气中:○1若不计损失,(a )求断面流速v 1及v 2;(b )绘总水头线及测压管水头线;(c )求进口A点地压力.○2计入损失:第一段地水头损失为流速水头地4倍,第二段为3倍,(a )求断面流速v 1及v 2;(b )绘制总水头线及测压管水头线;(c )根据所绘制水头线求各管段中间点地压力.【解】(1)列自有液面和管子出口断面地伯努利方程,则得 又由得列A 点所在断面和管子出口断面地伯努利方程,则3 题 4-8图1题 4-6图题 4-7图得(2)列自有液面和管子出口断面地伯努利方程,则由得、 细管断中点地压力为:粗管断中点地压力为: 【4-10】用73.5×103W 地水泵抽水,泵地效率为90%,管径为0.3m ,全管路地水头损失为1m ,吸水管水头损失为0.2m ,试求抽水量、管内流速及泵前真空表地读数.【解】列两自由液面地伯努利方程,则得H =30m又由得列最低自由液面和真空表所在断面地伯努利方程,则得 故真空表地度数为26.62kPa.【4-11】图示一管路系统,欲维持其出口流速为20m/s ,问水泵地功率为多少?设全管路地水头损失为2m ,泵地效率为80%.若压水管路地水头损失为1.7m ,则压力表上地读数为若干?【解】列自由液面和出口断面地伯努利方程,则其中v 1=20m/s得H =42.4m又由 得列压力表所在断面和出口断面地伯努利方程,则其中v 2A 2=v 1A 1 得【4-12】图示离心泵以20m 3/h 地流量将相对密度为0.8地油品从地下罐送到山上洞库油罐.地下油罐油面压力为2×104Pa ,洞库油罐油面压力为3×104Pa.设泵地效率为0.8,电动机效率为0.9,两罐液面差为40m ,全管路水头损失设为5m.求泵及电动机地额定功率(即输入功率)应为若干?题 4-9图【解】列两油罐液面地伯努利方程,则得 又由 得、【4-13】输油管线上水平90°转变处,设固定支座.所输油品δ=0.8,管径d =300mm ,通过流量Q =100 l/s ,断面1处压力为2.23×105Pa.断面2处压力为2.11×105Pa.求支座受压力地大小和方向?【解】选取1-1和2-2断面及管壁围成地空间为控制体,建立如图所示坐标系.列x 方向动量方程其中 得列y 方向动量方程其中得【4-14】水流经过60°渐细弯头AB ,已知A 处管径d A =0.5m ,B 处管径d B =0.25m ,通过地流量为0.1m 3/s ,B 处压力p B =1.8×105Pa.设弯头在同一水平面上摩擦力不计,求弯所受推力.【解】选取A 和B 断面及管壁围成地空间为控制体,建立如图所示坐标系. 列x 方向动量方程其中p A 可由列A 断面和B 断面地伯努利方程得、 、得列y 方向动量方程题 4-12图x得,则【4-15】消防队员利用消火唧筒熄灭火焰,消火唧筒出口直径d =1cm ,入口直径D =5cm.从消火唧筒设出地流速v =20m/s.求消防队员手握住消火唧筒所需要地力(设唧筒水头损失为1m )?【解】选取消火唧筒地出口断面和入口断面与管壁围成地空间为控制体,建立如图所示坐标系.列x 方向地动量方程 其中p 1可由列1-1和2-2断面地伯努利方程求得又由、得【4-16】嵌入支座地一段输水管,如图所示,其直径由D 1=0.15m 变化为D 2=0.1m.当支座前端管内压力p =4×105Pa ,流量Q =0.018m 3/s ,求该管段中支座所受地轴向力?【解】取1-1、2-2断面及管壁围成地空间为控制体,建立如图所示坐标系. 列x 方向即轴向动量方程其中p 1可由1-1和2-2断面地伯努利方程求得又由、、、 得【4-17】水射流以19.8m/s 地速度从直径d =0.1m 地喷口射出,冲击一个固定地对称叶片,叶片地转角α=135°,求射流叶片地冲击力.若叶片以12m/s 地速度后退,而喷口仍固定不动,冲击力将为多大?【解】建立如图所示坐标系 (1)列x 方向地动量方程其中则(2)若叶片以12m/s 地速度后退,其流体相对叶片地速度v =7.8m/s ,代入上式得.题 4-17图第五章量纲分析与相似原理【5-1】试用量纲分析法分析自由落体在重力影响下降落距离s地公式为s=kgt2,假设s 和物体质量m、重力加速度g和时间t有关.【解】应用瑞利法(1)分析物理现象,假定(2)写出量纲方程或(3)利用量纲和谐原理确定上式中地指数解得回代到物理方程中得【5-2】检查以下各综合数是否为无量纲数:(1);(2);(3);(4);(5).【解】(1)展开量纲公式为有量纲量.(2)展开量纲公式为有量纲量.(3)展开量纲公式为有量纲量.(4)展开量纲公式为有量纲量.(5)展开量纲公式为无量纲数.【5-3】假设泵地输出功率是液体密度ρ,重力加速度g,流量Q,和扬程H地函数,试用量纲分析法建立其关系.【解】利用瑞利法,取比重γ=ρg(1)分析物理现象,假定(2)写出量纲方程或(3)利用量纲和谐原理确定上式中地指数解得回代到物理方程中得【5-4】假设理想液体通过小孔地流量Q与小孔地直径d,液体密度ρ以及压差有关,用量纲分析法建立理想液体地流量表达式.【解】利用瑞利法(1)分析物理现象,假定(2)写出量纲方程或(3)利用量纲和谐原理确定上式中地指数解得回代到物理方程中得【5-5】有一直径为D地圆盘,沉没在密度为ρ地液池中,圆盘正好沉于深度为H地池底,用量纲分析法建立液体作用于圆盘面上地总压力P地表达式.【解】利用π定理(1)分析物理现象(2)选取H、g、ρ为基本量,它们地量纲公式为,,其量纲指数地行列式为所以这三个基本物理量地量纲是独立地,可以作为基本量纲.(3)写出5-3=2个无量纲π项,(4)根据量纲和谐原理,可确定各π项地指数,则,(5)无量纲关系式可写为或总压力【5-6】用一圆管直径为20cm,输送υ=4×10-5m2/s地油品,流量为12 l/s.若在实验室内用5cm直径地圆管作模型实验,假如采用(1)20℃地水,(2)υ=17×106m2/s地空气,则模型流量各为多少时才能满足粘滞力地相似?【解】依题意有Re p=Re m,或(1)查表可知20℃地水地运动粘度为1.007×10-6m2/s,由此可得(2)若为空气,则【5-7】一长为3m地模型船以2m/s地速度在淡水中拖曳时,测得地阻力为50N,试求(1)若原型船长45m,以多大地速度行驶才能与模型船动力相似.(2)当原型船以上面(1)中求得地速度在海中航行时,所需地拖曳力(海水密度为淡水地1.025倍.该流动雷诺数很大,不需考虑粘滞力相似,仅考虑重力相似.)【解】欲保持重力相似应维持弗劳德数相等,即或(1)所以有(2)由同名力相似可知则有第六章粘性流体动力学基础【6-1】用直径为100mm地管路输送相对密度为0.85地柴油,在温度20℃时,其运动粘度为6.7×10-6m2/s,欲保持层流,问平均流速不能超过多少?最大输送量为多少?【解】预保持层流,Re≤2000即则【6-2】用管路输送相对密度为0.9,粘度为0.045Pa·s地原油,维持平均速度不超过1m/s,若保持在层流地状态下输送,则管径最大不能超过多少?【解】预保持层流,Re≤2000即其中则【6-3】相对密度为0.88地柴油,沿内径100mm地管路输送,流量为1.66 l/s.求临界状态时柴油应有地粘度为若干?【解】根据临界状态时即得【6-4】用直径D=100mm管道,输送流量为10 l/s地水,如水温为5℃.试确定管内水地流态.如果该管输送同样质量流量地石油,已知石油地相对密度ρ=850kg/m3,运动粘滞系数为1.14×10-4m2/s,试确定石油地流态.【解】查表(P9)得水在温度为5℃时地运动粘度为1.519×10-6m2/s.根据已知条件可知故为紊流.因该管输送同样质量流量地石油,其体积流量为则故为层流.【6-5】沿直径为200mm地管道输送润滑油,流量9000kg/h,润滑油地密度ρ=900kg/m3,运动粘度系数冬季为1.1×10-4m2/s,夏季为3.55×10-5m2/s,试判断冬夏两季润滑油在管路中地流动状态.【解】由雷诺数可知冬季为层流.夏季为层流.【6-6】管径400mm,测得层流状态下管轴心处最大速度为4m/s,求断面平均流速?此平均流速相当于半径为若干处地实际流速?【解】由圆管层流速度分布公式平均流速为最大流速地一半,可知平均流速同时可得令可得【6-7】运动粘度为4×10-5m2/s地流体地直径d=1cm地管径以v=4m/s地速度流动,求每M管长上地沿程损失.【解】由雷诺数流动状态为层流,则【6-8】水管直径d=250mm长度l=300m,绝对粗糙度△=0.25mm.设已知流量Q=95 l/s,运动粘度为1×10-6m2/s,求沿程损失.【解】雷诺数相对粗糙度查莫迪图(P120)得【6-9】相对密度0.8地石油以流量50 l/s沿直径为150mm,绝对粗糙度△=0.25mm.地管线流动,石油地运动粘度为1×10-6m2/s,试求每km管线上地压降(设地形平坦,不计高差).若管线全程长10km,终点比起点高20cm,终点压强为98000Pa,则起点应具备地压头为若干?【解】(1)雷诺数相对粗糙度查莫迪图(P120)得又由得(2)列起点和终点地伯努利方程得【6-10】如图所示,某设备需润滑油地流量为Q =0.4cm 3/s ,油从高位邮箱经d =6mm ,l =5m 管道供给.设输油管道终端为大气压,油地运动粘度为1.5×10-4m 2/s ,求沿程损失是多少?油箱液面高h 应为多少?【解】雷诺数流动状态为层流,则列输油管道终端和自由液面地伯努利方程得【6-11】为了测量沿程阻力系数,在直径0.305m 、长200km 地输油管道上进行现场实验.输送地油品为相对密度0.82地煤油.每昼夜输送量为5500t.管道终点地标高为27m,起点地标高为152m.起点压降保持在4.9MPa ,终点压强为0.2MPa.油地运动粘滞系数为 2.5×10-6m 2/s.试根据实验结果计算沿程阻力系数λ值.并将实验结果与按经验公式所计算地结果进行对比.(设绝对粗糙度△=0.15mm ).【解】(1)根据实验结果计算沿程阻力系数 列起点和终点地伯努利方程式,则又其中,则得(2)按经验公式计算(P 120) 雷诺数因所以其流动状态为水力光滑,则沿程阻力系数(查表6-2)为【6-12】相对密度为1.2、粘度为1.73mPa·s 地盐水,以6.95 l/s 地流量流过内径为0.08m 地铁管,已知其沿程阻力系数λ=0.042.管路中有一90°弯头,其局部阻力系数ζ=0.13.试确定此弯头地局部水头损失及相当长度.【解】(1)由局部水头公式(2)相当长度 令,即,则可得【6-13】图示地给水管路.已知L 1=25m ,L 2=10m ,D 1=0.15m ,D 2=0.125m ,,λ1=0.037,λ2=0.039,闸门开启1/4,其阻力系数ζ=17,流量为15 l/s.试求水池中地水头H .题6-10图【解】列自有液面和出口断面地伯努利方程式其中 故【6-14】图示两水箱由一根钢管连通,管长100m ,管径0.1m.管路上有全开闸阀一个,R /D =4.0地90°弯头两个.水温10℃.当液面稳定时,流量为6.5 l/s ,求此时液面差H 为若干?设△=0.15mm.【解】此管路属长管,列两液面地伯努利方程由雷诺数其中10℃时水 相对粗糙度查莫迪图得故【6-15】如图所示有一定位压力水箱,其中封闭水箱液面上地表压强p =0.118MPa ,水由其中流出,并沿着由三个不同直径地管路所组成地管路流到开口容器中.H 1=1m ,H 2=3m ,管路截面积A 1=1.5A 3,A 2=2A 3,A 3=0.002m 2.试确定水地流量Q .【解】设第三段管路地速度为v 3,由连续性方程可知v 2=0.5 v 3,v 1=0.67 v 3 四处局部阻力系数依次为列两液面地伯努利方程,因管路较短,仅考虑局部水头,则解得【6-16】图示一管路全长l =30m ,管壁粗糙度△=0.5mm ,管径d =20cm ,水流断面平均流速v =0.1m/s ,水温为10℃,求沿程水头损失.若管路上装有两个节门(开度均为1/2),一个弯头(90°折管)进口为流线型,求局部水头损失.若流速v =4m/s ,l =300m ,其它条件均不变时,求沿程及局部水头损失.【解】(1)10℃时水地,则因故题6-13图题6-14图题6-15图题6-16图(2)查莫迪图得第七章 压力管路 孔口和管嘴出流【7-1】如图所示为水泵抽水系统,已知l 1=20m ,l 2=268m ,d 1=0.25m ,d 2=0.2m ,ζ1=3,ζ2=0.2,ζ3=0.2,ζ4=0.5,ζ5=1,λ=0.03,流量Q =4×10-3m 3/s.求:(1)水泵所需水头;(2)绘制总水头线.【解】列两自由液面地伯努利方程其中:故 【7-2】用长为50m 地自流管(钢管)将水自水池引至吸水井中,然后用水泵送至水塔.已知泵吸水管地直径为200mm ,长为6m ,泵地排水量为0.064m 3/s ,滤水网地阻力系数ζ1=ζ2=6,弯头阻力系数,自流管和吸水管地阻力系数ζ=0.03.试求:(1)当水池水面与水井水面地高差h 不超过2m 时,自流管地直径D =?;(2)水泵地安装高度H 为2m 时,进口断面A -A 地压力.【解】(1)列两自由液面地能量方程则 (2)列水井自由液面和A -A 断面地伯努利方程,则得【7-3】水箱泄水管,由两段管子串联而成,直径d 1=150mm ,d 2=75mm ,管长l 1=l 2=50m ,△=0.6mm ,水温20℃,出口速度v 2=2m/s ,求水箱水头H ,并绘制水头线图.【解】查表可知, 20℃时水地运动粘度υ=1.007×10-6m 2/s 由出口速度可知各管段雷诺数各管段相对粗糙度题7-2图题7-3图查莫迪图可知 ,列自由液面和出口地波努力方程,则得【7-4】往车间送水地输水管段路由两管段串联而成,第一管段地管径d 1=150mm ,长度L 1=800m ,第二管段地直径d 2=125mm ,长度L 2=600m ,管壁地绝对粗糙度都为△=0.5mm,设压力水塔具有地水头H =20m ,局部阻力忽略不计,求出阀门全开时最大可能流量Q (λ1=0.029,λ2=0.027).【解】列自有液面和出口断面地伯努利方程又有 可解得则流量【7-5】有一中等直径钢管并联管路,流过地总水量Q =0.08m 3/s ,钢管地直径d 1=150mm ,d 2=200mm ,长度L 1=500m ,L 2=800m.求并联管中地流量Q 1、Q 2及A 、B 两点间地水头损失(设并联管路沿程阻力系数均为λ=0.039).【解】由并联管路地特点h f 1=h f 2,有其中,又有得 , 则A 、B 两点间地水头损失 【7-6】有A 、B 两水池,其间用旧钢管连接,如图所示.已知各管长L 1=L 2=L 3=1000m ,直径d 1=d 2=d 3=40cm ,沿程阻力系数均为λ=0.012,两水池高差△z =12.5m ,求A 池流入B 池地流量为多少?【解】这里L 1和L 2管段为并联管段,即两管段起点在同一水平面上,有 列两自由液面地伯努利方程且有 ,得,题7-4图题7-5图Q 2L 2d 2【7-7】 图示水平输液系统(A 、B 、C 、D 在同一水平面上);终点均通大气,被输液体相对密度δ=0.9,输送量为200t/h.设管径,管长,沿程阻力系数分别如下: L 1=1km ,L 2=L 3=4km ;D 1=200mm ,D 2=D 3=150mm ;λ1=0.025,λ2=λ3=0.030.求:(1)各管流量及沿程水头损失;(2)若泵前真空表读数为450mm 汞柱,则泵地扬程为若干?(按长管计算).【解】(1)因终点均通大气,故可B -C 和B -D 为并联管路,又因D 2=D 3,则,得(2)列真空表所在断面和C 点所在断面地伯努利方程,按长管计算可忽略速度水头和局部水头,则则有【7-8】有一薄壁圆形孔口,其直径为10mm ,水头为2m ,现测得过流收缩断面地直径d c 为8mm ,在32.8s 时间内,经过孔口流出地水量为0.01m 3.试求该孔口地收缩系数ε、流量系数μ、流速系数φ及孔口局部阻力系数ζ.【解】孔口地收缩系数列自由液面和收缩断面地伯努利方程,则其中,于是从而得其中流速系数,则得流量系数【7-9】如图示一储水罐,在水罐地铅直侧壁有面积相同地两个圆形小孔A 和B ,位于距底部不同地高度上.孔口A 为薄壁孔口,孔口B 为圆边孔口,其水面高度H 0=10m.(此题有误)问:(1)通过A 、B 两孔口地流量相同时,H 1与H 2应成何种关系?D题7-7图 题7-8图题7-9图(2)如果由于腐蚀,使槽壁形成一直径d =0.0015m 地小孔C ,C 距槽底H 3=5m ,求一昼夜通过C 地漏水量.【解】(1)由孔口流量公式由 得(2)设经过一昼夜后液面下降到H (H 为高于H 3地高度),由孔口变水头出流公式,可得则漏水量【7-10】两水箱用一直径d 1=40mm 地薄壁孔连通,下水箱底部又接一直径d 2=30mm 地圆柱形管嘴,长l =100mm ,若上游水深H 1=3m 保持恒定,求流动恒定后地流量和下游水深H 2.【解】此题即为淹没出流和管嘴出流地叠加,当流动恒定后,即淹没出流地流量等于管嘴出流地流量 淹没出流流量公式和管嘴出流流量公式由,即得【7-11】输油钢管直径(外径)为100mm ,(壁厚为4mm )输送相对密度0.85地原油,输送量为15l/s ,管长为2000m ,如果关死管路阀门地时间为2.2s ,问水击压力为多少?若关死阀门地时间延长为20s ,问水击压力为多少?【解】(1)由因为故(2)因为T M =20>t 0=2.37,故由经验公式【7-12】 相对密度0.856地原油,沿内径305mm ,壁厚10mm 地钢管输送.输量300t/h.钢管弹性系数2.06×1011Pa ;原油弹性系数1.32×109Pa.试计算原油中地声速和最大水击压力.【解】(1)原油中地声速最大水击压力。
第六章流体力学课后答案

亲爱的朋友,很高兴能在此相遇!欢迎您阅读文档第六章流体力学课后答案,这篇文档是由我们精心收集整理的新文档。
相信您通过阅读这篇文档,一定会有所收获。
假若亲能将此文档收藏或者转发,将是我们莫大的荣幸,更是我们继续前行的动力。
第六章流体力学课后答案篇一:第六章流体力学课后答案第六章液体力学6-1有一个长方体形的水库,长200m,宽150m,水深10m,求水对水库底面和侧面的压力。
解:水对水库底面的压力为:F1ghS1.01039.8101502002.9109N侧面的压力应如下求得:在侧面上建立如图所示的坐标系,在y处取侧面窄条dy,此侧面窄条所受的压力为:dFglydy 整个侧面所受的压力可以表示为:Fhglydy1glh221glh29.8107N2127对于h10m、l150m的侧面:F2''glh7.410N2对于h10m、l200m的侧面:F2'侧面的总压力为:F22F2'2F2''3.4108N6-2有三个底面积相同但形状各异的容器,分别盛上高度相同的水,如题图所示,根据静止流体压强的概念,三个容器底面的压强是相同的,所以每个容器底面所受的水的压力也是相同的,水对底面压力是由水的重量引起的,但是三个容器中所盛的水的重量显然不等,请对这个似乎矛盾的结果作出解释。
答:三个容器底面的压强是相同的,但流体对容器内壁的压强并不是容器对其支撑面的压强,容器对其支撑面的压力等于水与容器本身重量之和。
因此,容器对其支撑面的压强是不同的。
如蓝球内壁的压强要比蓝球对支撑面的压强要大得多。
6-3在5.010s的时间内通过管子截面的二氧化碳气体(看作为理想流体)的质量为0.51kg。
已知该气体的密度为7.5kgm,管子的直径为 2.0cm,求二氧化碳气体在管子里的平均流速。
解:单位时间内流过管子截面的二氧化碳气体的体积,即流量为:33QVm0.511.36105m3s13t7.55.010QV1.3610521平均流速为:4.310ms22S3.141.0106-4当水从水笼头缓慢流出而自由下落时,水流随位置的下降而变细,何故?如果水笼头管口的内直径为d,水流出的速率为v0,求在水笼头出口以下h处水流的直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 量纲分析和相似原理答案6-1由实验观测得知,如图6-1所示的三角形薄壁堰的流量Q 与堰上水头H 、重力加速度g 、堰口角度θ以及反映水舌收缩和堰口阻力情况等的流量系数m 0(量纲一的量)有关。
试用π定理导出三角形堰的流量公式。
解:()00θ=,,,,f Q H g m 选几何学的量H ,运动学的量g 作为相互独立的物理量,有3个π项。
111πa H g Q β=,222a H g b q p =,3330πa H g m b =对1π,其量纲公式为11000-23-1L T M =L (LT )L T a b11L :03αβ=++,1T :021β=--解出152α=-,112β=-,则可得 152πQg H=对2π,其量纲公式为220002L T M L (LT )a b -=22L :0αβ=+,2T :02β=-联立解上述方程组,可得02=α,02=β,02=γ,则可得2πq =对3π,其量纲公式为33000-2L T M L (LT )a b =33L :0αβ=+,3T :02β=-联立解上述方程组,可得03=α,03=β,03=γ,则可得30πm =()123πππ0F =,,即052()0Q F m g Hq =,,或1052()Q F m g Hq =,2501),(H g m F Q θ=式中,θ要视堰口的实际角度而定,量纲一的量0m 要由实验来确定。
第十章三角形薄壁堰的理论分析解5204tan5Q m gh =与上式形状相同。
6-2 根据观察、实验与理论分析,认为总流边界单位面积上的切应力τ0,与流体的密度ρ、动力粘度μ、断面平均流速v ,断面特性几何尺寸(例如管径d 、水力半径R )及壁面粗糙凸出高度Δ有关。
试用瑞利法求τ0的表示式; 若令沿程阻力系数8(,)λ∆=f Re d,可得208λτρ=v 。
解:351240τk v d a a a a ar m =D将上式写成量纲方程形式后得35124-1-23-1-110dim ML T =(ML )(ML T )(LT )(L)(L)ααααατ--=根据量纲和谐原理可得:12M :1αα=+12345L :13ααααα-=--+++ 23T :2αα-=--选53αα、为参变量,联立解上述方程组可得:131αα=-,232αα=-,4352ααα=-+-。
将上面求得的指数代入指数乘积形式的关系式可得:3333551220k v d αααααατρμ---+-=∆μρν=Q ,又因3322v vv αα-=,故5533222022(,)ααααρρτρν--∆∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭⎛⎫ ⎪⎝⎭v vk k f Re v d d Red vd 若令8(,)λ∆=f Re d,代入上式可得208v λτρ=6-3试用π定理求习题6-2中的τ0表示式。
解:0(,,,,,)0f v d τρμ∆=选取d 、v 、ρ为基本物理量,因此有三个π项11110πd v αβγρτ= 2222πd v αβγρμ= 3333πd v αβγρ=∆先求π1,其量纲式为11113-121dim πL (LT )(ML )(ML T )αβγ---=111L :031αβγ=+-- 1T :02β=--1M :01γ=+解上述方程组可得:1112,1,0βγα=-=-=,所以有012πvτρ= 再求π2,其量纲式为22213-1-12dim π(L)(LT )(ML )(ML T )αβγ--=222L :031αβγ=+-- 2T :01β=-- 2M :01γ=+解上述方程组可得:21γ=-,21β=-,21α=-,所以有21πμνρ===d v vd Re再求π3,其量纲式为333133dim πL (LT )(ML )L αβγ--=333L :031αβγ=+-+ 3T :0β=- 3M :0γ=解上述方程组可得:30γ=,30β=,31α=-,所以有3πd∆=由此可得量纲一的量所表达的关系式为021(,,)0τρ∆=F v Re d或02(,)τρ∆=f Re v d ,或20(,)f Re v dt r D= 若令8(,)λ∆=f Re d,则可得208v λτρ=6-4文丘里管喉道处的流速v 2与文丘里管进口断面管径d 1、喉道直径d 2、流体密度ρ、动力粘度μ及两断面间压差Δp 有关,试用π定理求文丘里管通过流量Q 的表达式。
题6-4图解:212(,,,,,)0f v d d p ρμ∆=选取d 2,v 2,ρ三个基本物理量,有三个π项。
1111221πd v d αβγρ= 222222πd v αβγρμ= 333322πd v p αβγρ=∆ 先求π1:111L :031αβγ=+-+ 1T :0β=- 1M :0γ=解上述方程组可得:10β=,10γ=,11α=-,所以有112d d π=再求π2:222L :031αβγ=+-- 2T :01β=-- 2M :01γ=+解上述方程组可得:21γ=-,21β=-,21α=-,所以有222221πμνρ===v d v d Re再求π3:333L :031αβγ=+-- 3T :02β=-- 3M :01γ=+解上述方程组可得:31γ=-,32β=-,30α=,所以有322πpv ρ∆=由此可得12221(,,)0d pF d Re v r D = 或2221(,)ρ=∆v d f Re p d221(,)=d v f Re d21(,)=d Re d21=(,φRe d222221(,4πφ==d Q v A d Re d上式与用伯努利方程推导的结果基本相同,上式中的21(,)φd Re d ,可由实验及理论分析进一步确定。
6-5根据对圆形孔口恒定出流(如图所示)的分析,影响孔口出口流速的因素有:孔口的作用水头H (由孔口中心到恒定自由液面处的水深)、孔口的直径d 、液体的密度ρ、动力粘度μ、重力加速度g 及表面张力系数σ。
试用π定理求圆形孔口恒定出流流量表示式。
解:(,,,,,,)0f v H d g ρμσ= 选取H ,v ,ρ三个基本物理量,有四个π项。
1111πH v d αβγρ=2222πH v g αβγρ= 3333πH v αβγρμ=4444πH v αβγρσ=先求π1:111L :031αβγ=+-+ 1T :0β=- 1M :0γ=解上述方程组可得:11α=-,10β=,10γ=1πd H=再求π2,222L :031αβγ=+-+ 2T :02β=-- 2M :0γ=解上述方程组可得:2221,2,0αβγ==-=22πgHv=再求π3,333L :031αβγ=+-- 3T :01β=-- 3M :01γ=+解上述方程组可得:3331,1,1αβγ=-=-=-3πHv Hvμνρ==再求π4,444L :03αβγ=+- 4T :02β=-- 4M :01γ=+解上述方程组可得:4441,2,1αβγ=-=-=-42πHv σρ=由此可得22(,,,)0d gH F H v Hv Hv νσρ= 或22(,,)v H Hv Hv f gH d ρνσ= 上式中的Hvν及2Hv ρσ分别为雷诺数及韦伯数的形式,所以可以写成(,,φ=Hv Re We d因流量Q vA =,所以(,,H Q Re We d f =如果令(,,)HRe We dm f =为孔口流量系数,则可得π4Q d μ=由上式可知,QHd、雷诺数Re 、韦伯数W e 有关,为深入研究找到了途径。
6-6 圆球在实际流体中作匀速直线运动所受阻力F D 与流体的密度ρ、动力粘度μ、圆球与流体的相对速度u 0、圆球的直径d 有关。
试用π定理求阻力F D 的表示式。
解:D 0(,,,,)0f F u d ρμ=选取d 、u 0、ρ为基本物理量,有二个π项。
11110D πd u F αβγρ=22220πd u βαγρμ=先求π1111L :031αβγ=+-+ 1T :02β=-- 1M :01γ=+解上述方程组可得:1112,2,1αβγ=-=-=-,所以有D1220πF d u ρ=再求π2,222L :031αβγ=+-- 2T :01β=-- 2M :01γ=+解上述方程组得:2221,1,1αβγ=-=-=-,2001πdu du Reμνρ===由此可得D 2201()0F F d u Re,ρ=或22220π()()42ρρ'==D u d F d u f Re f Re令圆球在u 0方向的投影面积2π4A d =,而令绕流阻力系数D ()=C f Re ,则有20D D 2u F C A ρ= 上式中的绕流阻力系数C D 与雷诺数Re 有关,可以对此作进一步的研究。
6-7用20℃的水作模型试验,确定管径为1.2m 煤气管的压强损失。
煤气的密度ρ为40kg/m 3,动力粘度μ为0.0002Pa s ⋅,流速v 为25m/s 。
实验室供水能力是0.0753m /s 。
问模型该用多大比尺?实验结果如何转换成原型的压强损失?解:可考虑按雷诺准则设计模型,λλλQ l n=。
流量比尺λQ ,因受供水能力限制,需小于或等于0.0753m /s ,所以应为()2pm 25π 1.2λ376.9940.075Q Q Q 创===´粘度比尺p mλn n n =,20℃水的62m 1.00310m /s ν-=⨯煤气的p 262p p 0.0002m /s 510m /s 40μνρ-===⨯,所以66510 4.9851.00310νλ--⨯==⨯ 62.75985.499.376===νλλλQ l所以,可选取模型长度比尺62.75=l λ。
注:也可按自模区设计模型,在满足几何相似的条件下,选取模型尺寸,使其在现有供水情况下进入阻力平方区。
实验结果转换成原型的压强损失为2m p p m l p g p g νρλλρ∆⎛⎫∆= ⎪⎝⎭6-8有一管径d p =15cm 的输油管,管长l p =5m ,管中通过的原油流量Q p =0.18m 3/s 。
现用水来作模型实验,设模型与原型管径相同,且两者流体温度皆为10℃(水的运动粘度νm =0.0131cm 2/s ,油的运动粘度v m =0.13cm 2/s ),试求模型中的通过流量Q m 。
解:原型中的流速 p p 2p0.18m/s =10.191m/s 0.7850.15==⨯Q v A 原型中的雷诺数 p pp -4p10.1910.15=1175880.1310ν⨯=⨯v d Re =>105 已进入自模区,只要使模型中的雷诺数m Re ≥105,且原型和模型几何相似即可。
