最新特殊四边形(练习题+提高题+详细答案)
(完整版)特殊平行四边形练习题(答案已做)

特殊平行四边形专题练习1、练习:①矩形ABCD 的两条对角线相交于O ,∠AOD=120°,AB=4cm ,则矩形对角线AC 长为______cm .②.四边形ABCD 的对角线AC ,BD 相交于点O ,能判断它为矩形的题设是( )A .AO=CO ,BO=DOB .AO=BO=CO=DOC .AB=BC ,AO=COD .AO=CO ,BO=DO ,AC ⊥BD③.四边形ABCD 中,AD //BC ,则四边形ABCD 是 ___________,又对角线AC ,BD 交于点O , 若∠1=∠2,则四边形ABCD 是_______________.2、练习:①.如图,BD 是菱形ABCD 的一条对角线,若∠ABD=65°,则∠A=_____.②. 一个菱形的两条对角线分别是6cm ,8cm ,则这个菱形的周长等于 cm,面积= cm 2③.若菱形的周长为8cm,高为1cm,则菱形两邻角的度数比为(三)正方形:3.练习:①正方形的面积为4,则它的边长为____,对角线长为_____.②已知正方形的对角线长是4,则它的边长是 ,面积是 。
③如图所示,在△ABC 中,AB=AC ,点D ,E ,F 分别是边AB ,BC ,AC 的中点,连接DE ,EF ,要使四边形ADEF 是正方形,还需增加条件:_______.二、复习练习: (一)、选择题:1、矩形ABCD 的长AD=15cm ,宽AB=10cm ,∠ABC 的平分线分AD 边为AE 、ED两部分,这AE 、ED 的长分别为( )A .11cm 和4cmB .10cm 和5cmC .9cm 和6cmD .8cm 和7cm2、四边形ABCD 的对角线互相平分,要使它变为矩形,需要添加的条件是( ) A .AB=CD B .AD=BC C .AB=BC D .AC=BD3、如图,在正方形ABCD 的外侧,作等边三角形ADE ,则∠AEBO ( ) A. 10° B .15° C .20° D .12.5°4、如图,在菱形ABCD 中,E 、F 分别是AD 、BD 的中点,如果EF=2,那么菱形ABCD 的周长是( ) A. 4 B .8 C .12 D .16ABDECABCDEEF(二)、填空题5、已知正方形ABCD 对角线AC ,BD 相交于点O ,•且AC=•16cm ,•则DO=•_____cm , •BO=____cm ,∠OCD=____度.6、在平面直角坐标系中,四边形ABCD 是菱形,∠ABC=60°, 且点A 的坐标为(0,2),则点B 坐标( ), 点C 坐标为( ),点D 坐标为( )。
初中数学特殊的平行四边形50题(含答案)

特殊的平行四边形练习题(50题)菱形、矩形、正方形一、单选题(共18题;共36分)1.下列条件中,能判定一个四边形为矩形的条件是( )A. 对角线互相平分的四边形B. 对角线相等且平分的四边形C. 对角线相等的四边形D. 对角线相等且互相垂直的四边形【答案】B【解析】【解答】解:A、对角线互相平分的四边形是平行四边形,故A不符合题意;B、对角线相等且平分的四边形是矩形,故B符合题意;C、对角线相等的四边形不是矩形,故C不符合题意;D、对角线相等且互相垂直的四边形不是矩形,故D不符合题意.故答案为:B.【分析】根据矩形的判定方法,逐项进行判断,即可求解2.如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a ,EF=b ,NH= c ,则下列各式中正确的是()A. a > b > cB. a =b =cC. c > a > bD. b > c > a【答案】B【解析】【解答】解:连接OA、OD、OM,如图所示:则OA=OD=OM,∵四边形ABOC、DEOF、HNMO均为矩形,∴OA=BC=a,OD=EF=b,OM=NH=c,∴a=b=c;故答案为:B.【分析】连接OA、OD、OM,则OA=OD=OM,由矩形的对角线相等得出OA=BC=a,OD=EF=b,OM=NH=c,再由同圆的半径相等即可得出a=b=c.3.如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( )A. 1B. 2C.D.【答案】 D【解析】【解答】解:连接DE交AC于P,连接BD,BP,由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB,∴PE+PB=PE+PD=DE,即DE就是PE+PB的最小值,∵∠BAD=60°,AD=AB,∴△ABD是等边三角形,∴AD=BD,∵AE=BE=AB=1,∴DE⊥AB,在Rt△ADE中,DE=,∴ PE+PB的最小值是.故答案为:D.【分析】连接DE交AC于P,连接BD,BP,根据菱形的性质得出B、D关于AC对称,得出DE就是PE+PB 的最小值,根据等边三角形的判定与性质得出DE⊥AB,再根据勾股定理求出DE的长,即可求解.4.若正方形的对角线长为2 cm,则这个正方形的面积为()A. 4B. 2C.D.【答案】B【解析】【解答】解:设正方形的边长为xcm,根据题意得:x2+x2=22,∴x2=2,∴正方形的面积=x2=2(cm2).故答案为:B.【分析】设正方形的边长为xcm,利用勾股定理列出方程,求出x2=2,即可求出正方形的面积为2.5.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为()A. 72B. 24C. 48D. 96【答案】C【解析】【解答】解:∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD,∵DH⊥AB,∴∠BHD=90°,∴BD=2OH,∵OH=4,∴BD=8,∵OA=6,∴AC=12,∴菱形ABCD的面积= AC•BD=×12×8=48.故答案为:C.【分析】根据菱形的性质得O为BD的中点,再由直角三角形斜边上的中线等于斜边的一半,得BD的长度,最后由菱形的面积公式求得面积.6.将一张长方形纸片折叠成如图所示的形状,则∠ABC等于( )A. 73°B. 56°C. 68°D. 146°【答案】A【解析】【解答】如图,∵∠CBD=34°,∴∠CBE=180°﹣∠CBD=146°,由折叠的性质可得∠ABC=∠ABE= ∠CBE=73°.故答案为:A【分析】根据补角的知识可求出∠CBE,从而根据折叠的性质∠ABC=∠ABE= ∠CBE,可得出∠ABC的度数.7.如图,已知矩形AOBC的顶点O(0,0),A(0,3),B(4,0),按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OC,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠BOC内交于点F;③作射线OF,交边BC于点G,则点G的坐标为()A. (4,1)B. (4,)C. (4,)D. (4,)【答案】B【解析】【解答】解:∵四边形AOBC是矩形,A(0,3),B(4,0),∴OB=4,OA=BC=3,∠OBC=90°,∴OC==5,作GH⊥OC于H,如图,由题意可知:OG平分∠BOC,∵GB⊥OB,GH⊥OC,∴GB=GH,设GB=GH=x,由S△OBC=×3×4=×5×x+ ×4×x,解得:x=,∴G(4,).故答案为:B.【分析】根据勾股定理可得OC的长,作GH⊥OC于H,根据角平分线的性质可得GB=GH,然后利用面积法求出GB即可.8.如图1,在矩形ABCD中,点E在CD上,∠AEB=90°,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q,设点P运动的路程为x,PQ长为y,若y与x之间的函数关系图象如图2所示,当x=6时,PQ的值是( )A. 2B.C.D. 1【答案】B【解析】【解答】解:由图象可知:AE=3,BE=4,在Rt ABE中,∠AEB=90°AB= =5当x=6时,点P在BE上,如图,此时PE=4-(7-x)=x-3=6-3=3∵∠AEB=90°, PQ⊥CD∴∠AEB=∠PQE=90°,在矩形ABCD中,AB//CD∴∠QEP=∠ABE∴PQE BAE, ∴=∴=∴PQ=故答案为:B.【分析】由图象可知:AE=3,BE=4,根据勾股定理可得AB=5,当x=6时,点P在BE上,先求出PE的长,再根据△ PQE ∽△ BAE,求出PQ的长.9.如图,在平面直角坐标系中,已知点,.若平移点到点,使以点,,,为顶点的四边形是菱形,则正确的平移方法是()A. 向左平移1个单位,再向下平移1个单位B. 向左平移个单位,再向上平移1个单位C. 向右平移个单位,再向上平移1个单位D. 向右平移1个单位,再向上平移1个单位【答案】 D【解析】【解答】解:因为B(1,1)由勾股定理可得OB=,所以OA=OB,而AB<OA.故以AB为对角线,OB//AC,由O(0,0)移到点B(1,1)需要向右平移1个单位,再向上平移1个单位,由平移的性质可得由A(,0)移到点C需要向右平移1个单位,再向上平移1个单位,故选D.【分析】根据平移的性质可得OB//AC,平移A到C,有两种平移的方法可使O,A,B,C四点构成的四边形是平行四边形;而OA=OB>AB,故当OA,OB为边时O,A,B,C四点构成的四边形是菱形,故点A平移到C的运动与点O平移到B的相同.10.如图,把长方形ABCD沿EF对折,若∠1=500,则∠AEF的度数等于()A. 25ºB. 50ºC. 100ºD. 115º【答案】 D【解析】解析:∵把矩形ABCD沿EF对折,∴AD∥BC,∠BFE=∠2,∵∠1=50°,∠1+∠2+∠BFE=180°,∴∠BFE==65°,∵∠AEF+∠BFE=180°,∴∠AEF=115°.故选D11.在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是()A. ②③B. ③④C. ①②④D. ②③④【答案】 D【解析】【解答】∵AB=1,AD=,∴BD=AC=2,OB=OA=OD=OC=1.∴△OAB,△OCD为正三角形.AF平分∠DAB,∴∠FAB=45°,即△ABF是一个等腰直角三角形.∴BF=AB=1,BF=BO=1.∵AF平分∠DAB,∴∠FAB=45°,∴∠CAH=45°﹣30°=15°.∵∠ACE=30°(正三角形上的高的性质)∴∠AHC=15°,∴CA=CH由正三角形上的高的性质可知:DE=OD÷2,OD=OB,∴BE=3ED.所以正确的是②③④.故选D.【分析】这是一个特殊的矩形:对角线相交成60°的角.利用等边三角形的性质结合图中的特殊角度解答.本题主要考查了矩形的性质及正三角形的性质.12.矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB 上,当△CDE的周长最小时,点E的坐标为()A. (3,1)B. (3,)C. (3,)D. (3,2)【答案】B【解析】【解答】解:如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.∵D(,0),A(3,0),∴H(,0),∴直线CH解析式为y=﹣x+4,∴x=3时,y= ,∴点E坐标(3,)故选:B.【分析】如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,先求出直线CH解析式,再求出直线CH与AB的交点即可解决问题.本题考查矩形的性质、坐标与图形的性质、轴对称﹣最短问题、一次函数等知识,解题的关键是利用轴对称找到点E位置,学会利用一次函数解决交点问题,属于中考常考题型.13.如图,正方形ABCD的边长为4,M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为().A. 3B. 4C. 5D.【答案】C【解析】【分析】由正方形的对称性可知点B与D关于直线AC对称,连接BM交AC于N′点,N′即为所求在Rt△BCM中利用勾股定理即可求出BM的长即可.【解答】∵四边形ABCD是正方形,∴点B与D关于直线AC对称,连接BD,BM交AC于N′,连接DN′,N′即为所求的点,则BM的长即为DN+MN的最小值,∴AC是线段BD的垂直平分线,又CM=CD-DM=4-1=3,在Rt△BCM中,BM==5,故DN+MN的最小值是5.故选C.【点评】本题考查的是轴对称-最短路线问题及正方形的性质,先作出M关于直线AC的对称点M′,由轴对称及正方形的性质判断出点M′在BC上是解答此题的关键.14.将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是,则点C的坐标是()A. (4,2)B. (2,4)C. (,3)D. (3,)【答案】 D【解析】【解答】解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,过点A作AN⊥BF于点N,过点C作CM⊥x轴于点M,∵∠EAO+∠AOE=90°,∠AOE+∠MOC=90°,∴∠EAO=∠COM,又∵∠AEO=∠CMO,∴∠AEO∽△COM,∴=,∵∠BAN+∠OAN=90°,∠EAO+∠OAN=90°,∴∠BAN=∠EAO=∠COM,在△ABN和△OCM中∴△ABN≌△OCM(AAS),∴BN=CM,∵点A(−1,2),点B的纵坐标是,∴BN= ,∴CM= ,∴MO==2CM=3,∴点C的坐标是:(3, ).故选:D.【分析】次题主要考查了矩形的性质以及相似三角形的判定与性质以及结合全等三角形的判定与性质等知识.构造直角三角形,正确得出CM的长是解题的关键.15.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是()A. 1B. 2C. 3D. 4【答案】 D【解析】【解答】解:∵四边形ADEF为正方形,∴∠FAD=90°,AD=AF=EF,∴∠CAD+∠FAG=90°,∵FG⊥CA,∴∠C=90°=∠ACB,∴∠CAD=∠AFG,在△FGA和△ACD中,,∴△FGA≌△ACD(AAS),∴AC=FG,①正确;∵BC=AC,∴FG=BC,∵∠ACB=90°,FG⊥CA,∴FG∥BC,∴四边形CBFG是矩形,∴∠CBF=90°,S△FAB= FB•FG= S四边形CBFG,②正确;∵CA=CB,∠C=∠CBF=90°,∴∠ABC=∠ABF=45°,③正确;∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,∴△ACD∽△FEQ,∴AC:AD=FE:FQ,∴AD•FE=AD2=FQ•AC,④正确;故选:D.【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;证明四边形CBFG是矩形,得出S△FAB= FB•FG= S四边形CEFG,②正确;由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;证出△ACD∽△FEQ,得出对应边成比例,得出D•FE=AD2=FQ•AC,④正确.16.如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M 为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为()A. 5B.C.D.【答案】B【解析】【解答】设BE=x,则CE=6-x,∵四边形ABCD矩形,AB=4,∴AB=CD=4,∠C=∠B=90°,∴∠DEC+∠CDE=90°,又∵F是AB的中点,∴BF=2,又∵EF⊥ED,∴∠FED=90°,∴∠FEB+∠DEC=90°,∴∠FEB=∠CDE,∴△BFE∽△CED,∴=,∴=,∴(x-2)(x-4)=0,∴x=2,或x=4,①当x=2时,∴EF=2,DE=4,DF=2,∴AM=ME=,∴AE===2,②当x=4时,∴EF=2,DE=2,DF=2,∴AM=ME=,∴AE==2,AE==4,∴x=4不合题意,舍去故答案为:B.【分析】设BE=x,则CE=6-x,由矩形性质得出AB=CD=4,∠C=∠B=90°,又由EF⊥ED,根据同角的余角相等可得出∠FEB=∠CDE;由相似三角形的判定得出△BFE∽△CED,再根据相似三角形的性质得出=,由此列出方程从而求出x=2或x=4,分情况讨论:①当x=2时,由勾股定理算出AE===2,②当x=4时,由勾股定理算出AE==2,AE==4,故x=4不合题意,舍去.17.如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有()A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【解答】∵四边形ABCD是正方形,∴∠B=∠DCB=90°,AB=BC,∵AG=CE,∴BG=BE,由勾股定理得:BE=GE,∴①错误;∵BG=BE,∠B=90°,∴∠BGE=∠BEG=45°,∴∠AGE=135°,∴∠GAE+∠AEG=45°,∵AE⊥EF,∴∠AEF=90°,∵∠BEG=45°,∴∠AEG+∠FEC=45°,∴∠GAE=∠FEC,在△GAE和△CEF中∴△GAE≌△CEF,∴②正确;∴∠AGE=∠ECF=135°,∴∠FCD=135°﹣90°=45°,∴③正确;∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,∴∠FEC<45°,∴△GBE和△ECH不相似,∴④错误;即正确的有2个.故选B.【分析】根据正方形的性质得出∠B=∠DCB=90°,AB=BC,求出BG=BE,根据勾股定理得出BE=GE,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△GAE≌△CEF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.18.如图,P是正方形ABCD内一点,∠APB=135,BP=1,AP=,求PC的值()A. B. 3 C. D. 2【答案】B【解析】【分析】解答此题的关键是利用旋转构建直角三角形,由勾股定理求解.如图,把△PBC绕点B逆时针旋转90°得到△ABP′,点C的对应点C′与点A重合.根据旋转的性质可得AP′=PC,BP′=BP,△PBP′是等腰直角三角形,利用勾股定理求出,然后由∠APB=135,可得出∠APP′=90°,再利用勾股定理列式计算求出.故选B.二、填空题(共15题;共16分)19.如图所示,△ABC为边长为4的等边三角形,AD为BC边上的高,以AD为边的正方形ADEF的面积为________。
第一章 特殊平行四边形 单元测试(含答案)

第一章特殊平行四边形一、选择题1. 下列四边形对角线相等但不一定垂直的是( )A.平行四边形B.矩形C.菱形D.正方形2. 平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD3. 如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=4,BD=6,则菱形ABCD的周长为( )A.16B.24C.413D.8134. 如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )D.34 A.5B.4C.3425. 如图,菱形ABCD的对角线AC,BD的长分别为6 cm,8 cm,则这个菱形的周长为( )A.5 cm B.10 cm C.14 cm D.20 cm6. 如图,点P是矩形ABCD的边上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )A.4.8B.5C.6D.7.27. 如图,点E是正方形ABCD中CD上的一点,把△ADE绕点A顺时针旋转90∘到△ABF的位置,若四边形AECF的面积为16,DE=1,则EF的长是( )A.4B.5C.217D.348. 如图,在矩形ABCD中,EG垂直平分BD于点G,若AB=4,BC=3,则线段EG的长度是( )A.32B.158C.52D.39. 如图,正方形ABCD的边长为2,点E,F分别为边AD,BC上的点,且EF=5,点G,H 分别边AB,CD上的点,连接GH交EF于点P.若∠EPH=45∘,则线段GH的长为( )A.5B.2103C.253D.710. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )A.732B.4C.5D.92二、填空题11. 菱形的对角线长为6和8,则菱形的高为.12. 如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加条件,就能保证四边形EFGH是矩形.13. 在菱形ABCD中,对角线AC,BD交于点O,点F为BC中点,过点F作FE⊥BC于点F交BD于点E,连接CE,若∠BDC=34∘,则∠ECA=.14. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为.15. 在矩形ABCD中,AB=4,BC=3,折叠矩形ABCD,使点B与点D重合,则BF的长为.16. 如图,菱形ABCD中,AB=2,∠BAD=60∘,点E是边AB的中点,点P在对角线AC上移动.则PB+PE的最小值是.三、解答题17. 已知如图,在菱形ABCD中,对角线AC,BD相交于点O,DE∥AC,AE∥BD.(1) 求证:四边形AODE是矩形.(2) 若AB=6,∠BCD=120∘,求四边形AODE的面积.18. 如图,在正方形ABCD中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.(1) 若正方形ABCD边长为3,DF=4,求CG的长.(2) 求证:EF+EG=2CE.19. 在平行四边形ABCD中,对角线AC,BD相交于点O.EF过点O且与ABCD分别相交于点E,F.(1) 如图①,求证:OE=OF;(2) 如图②,若EF⊥DB,垂足为O,求证:四边形BEDF是菱形.20. 回答下列问题.(1) 提出问题:如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH.(2) 类比探究:如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG 于点O,探究线段EF与HG的数量关系,并说明理由.21. 如图,矩形ABCD中,点E,F分别在边AB,CD上,点G,H在对角线AC上,EF与AC相交于点O,AG=CH,BE=DF.(1) 求证:四边形EGFH是平行四边形.(2) 当EG=EH时,连接AF.①求证:AF=FC.②若DC=8,AD=4,求AE的长.答案一、选择题1. B2. B3. C4. D5. D6. A7. D8. B9. B10. D二、填空题11. 24512. AC⊥BD13. 2214. 615. 25816. 3三、解答题17.(1) 因为DE∥AC,AE∥BD,所以四边形AODE是平行四边形,因为在菱形ABCD中,AC⊥BD,所以∠AOD=90∘,所以四边形AODE是矩形.(2) 因为∠BCD=120∘,AB∥CD,所以∠ABC=180∘−120∘=60∘,因为AB=BC,所以△ABC是等边三角形,所以OA=12×6=3,OB=32×6=33,因为四边形ABCD是菱形,所以OD=OB=33,所以四边形AODE的面积=OA⋅OD=3×33=93.18.(1) ∵四边形ABCD是正方形,∴∠BCG=∠DCB=∠DCF=90∘,BC=DC,∵BE⊥DF,∴∠CBG+∠F=∠CDF+∠F,∴∠CBG=∠CDF,在△CBG和△CDF中,{∠BCG=∠DCF=90∘,BC=CD,∠CBG=∠CDF,∴△CBG≌△CDF(ASA),∴BG=DF=4,∴在Rt△BCG中,CG2+BC2=BG2,∴CG=42−32=7.(2) 过点C作CM⊥CE交BE于点M,∵△CBG≌△CDF,∴CG=CF,∠F=∠CGB,∵∠MCG+∠DCE=∠ECF+∠DCE=90∘,∴∠MCG=∠ECF,在 △MCG 和 △ECF 中,{∠MCG =∠ECF,CG =CF,∠F =∠CGB,∴△MCG ≌△ECF (ASA),∴MG =EF ,CM =CE ,∴△CME 是等腰直角三角形,∴ME =2CE ,又 ∵ME =MG +EG =EF +EG , ∴EF +EG =2CE .19.(1) ∵ 四边形 ABCD 是平行四边形, ∴OB =OD ,AB ∥CD ,∴∠EBO =∠FDO ,在 △OBE 与 △ODF 中,{∠EBO =∠FDO,OB =OD,∠BOE =∠DOF, ∴△OBE ≌△ODF (ASA),∴OE =OF ;(2) ∵OB =OD ,OE =OF , ∴ 四边形 BEDF 是平行四边形, ∵EF ⊥BD ,∴ 四边形 BEDF 是菱形.20.(1) ∵ 四边形 ABCD 是正方形, ∴AB =DA ,∠ABE =90∘=∠DAH , ∴∠HAO +∠OAD =90∘,∵AE⊥DH,∴∠ADO+∠OAD=90∘,∴∠HAO=∠ADO,在△ABE和△DAH中,{∠BAE=∠HDA,AB=AD,∠B=∠HAD,∴△ABE≌△DAH(ASA),∴AE=DH.(2) EF=GH,理由:将PE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH,∵EF⊥GH,∴AM⊥DN,根据(1)的结论得AM=DN,∴EF=GH.21.(1) ∵矩形ABCD中,AB∥CD,∴∠FCH=∠EAG,又∵CD=AB,BE=DF,∴CF=AE,且CH=AG,∠FCH=∠EAG,∴△AEG≌△CFH(SAS),∴GE=FH,∠CHF=∠AGE,∴∠FHG=∠EGH,∴FH∥GE,∴四边形EGFH是平行四边形.(2) ①连接AF,∵EG=EH,四边形EGFH是平行四边形,∴四边形GFHE为菱形,∴EF垂直平分GH,又∵AG=CH,∴EF垂直平分AC,∴AF=CF=AE.②设AE=x,则FC=AF=x,DF=8−x,在Rt△ADF中,AD2+DF2=AF2,∴42+(8−x)2=x2,解得x=5,∴AE=5.。
特殊四边形培优及答案

特殊四边形练习题及答案1.如下图,将一张边长为8的正方形纸片ABCD折叠,使点D落在BC的中点E处,点A落在点F处,折痕为MN,那么线段MN的长为〔〕2A.10 B.45 C.89 D.212.如图2,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,以下结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2.其中结论正确的个数是〔〕.〔A〕1个〔B〕2个〔C〕3个〔D〕4个3.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.那么以下结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是〔〕A.2 B.3 C.4 D.54.如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,那么这个最小值为〔〕A.2 B.3 C.335.如图,ABCD 为正方形,O 为AC 、BD 的交点,△DCE 为Rt △,∠CED=90°,∠DCE=30°,假设OE=,那么正方形的面积为〔 〕A .5B .4C .3D .26.如图,∠MON=90°,矩形ABCD 的顶点A 、B 分别在边OM ,ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1,运动过程中,点D 到点O 的最大距离为A .21B .5C .1455D .527.如图,正方形ABCD 的边长是4cm ,点G 在边AB 上,以BG 为边向外作正方形GBFE ,连接AE 、AC 、CE ,那么△AEC 的面积是 cm 2。
中考特殊四边形证明及计算提高练习(含答案)

中考特殊四边形证明及计算提高练习平行四边形1.(2012•威海)(1)如图①,▱ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.(2)如图②,将▱ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.2.(2011•贵阳)[阅读]在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为.[运用](1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为_________.(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.3.(2007•黑龙江)在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB.请直接应用上述信息解决下列问题:当点P分别在△ABC内(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明.4.(2006•泰安)如图,矩形ABCD的对角线交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F,连接AF,CE.(1)求证:四边形AECF是平行四边形;(2)若∠BAD的平分线与FC的延长线交于点G,则△ACG是等腰三角形吗?并说明理由.5.(2006•陕西)如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA到点D,使AD=AB.连接DE,DF.(1)求证:AF与DE互相平分;(2)若BC=4,求DF的长.6.如图,以△ABC三边为边在BC同侧作三个等边△ABD、△BCE、△ACF.请回答下列问题:(1)求证:四边形ADEF是平行四边形;(2)当△ABC满足什么条件时,四边形ADEF是矩形.菱形7.(2010•盘锦)如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE 交AB于点F.(1)若点D是BC边的中点(如图①),求证:EF=CD;(2)在(1)的条件下直接写出△AEF和△ABC的面积比;(3)若点D是BC边上的任意一点(除B、C外如图②),那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.8.(2011•海南)如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.(1)求证:△BDQ≌△ADP;(2)已知AD=3,AP=2,求cos∠BPQ的值(结果保留根号).9.(2009•龙岩)在边长为6的菱形ABCD中,动点M从点A出发,沿A⇒B⇒C向终点C运动,连接DM交AC 于点N.(1)如图1,当点M在AB边上时,连接BN:①求证:△ABN≌△ADN;②若∠ABC=60°,AM=4,∠ABN=α,求点M到AD的距离及tanα的值.(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x(6≤x≤12).试问:x为何值时,△ADN为等腰三角形.10.(2007•常德)如图1,已知四边形ABCD是菱形,G是线段CD上的任意一点时,连接BG交AC于F,过F作FH∥CD交BC于H,可以证明结论成立.(考生不必证明)(1)探究:如图2,上述条件中,若G在CD的延长线上,其它条件不变时,其结论是否成立?若成立,请给出证明;若不成立,请说明理由;(2)计算:若菱形ABCD中AB=6,∠ADC=60°,G在直线CD上,且CG=16,连接BG交AC所在的直线于F,过F作FH∥CD交BC所在的直线于H,求BG与FG的长.(3)发现:通过上述过程,你发现G在直线CD上时,结论还成立吗?11.(2001•河北)如图,在菱形ABCD中,AB=10,∠BAD=60度.点M从点A以每秒1个单位长的速度沿着AD 边向点D移动;设点M移动的时间为t秒(0≤t≤10).(1)点N为BC边上任意一点,在点M移动过程中,线段MN是否一定可以将菱形分割成面积相等的两部分并说明理由;(2)点N从点B(与点M出发的时刻相同)以每秒2个单位长的速度沿着BC边向点C移动,在什么时刻,梯形ABNM的面积最大并求出面积的最大值;(3)点N从点B(与点M出发的时刻相同)以每秒a(a≥2)个单位长的速度沿着射线BC方向(可以超越C点)移动,过点M作MP∥AB,交BC于点P.当△MPN≌△ABC时,设△MPN与菱形ABCD重叠部分的面积为S,求出用t表示S的关系式,井求当S=0时的值.矩形12.(2002•无锡)已知:如图,矩形ABCD中,AB=2,AD=3,E、F分别是AB、CD的中点.(1)在边AD上取一点M,使点A关于BM的对称点C恰好落在EF上.设BM与EF相交于点N,求证:四边形ANGM是菱形;(2)设P是AD上一点,∠PFB=3∠FBC,求线段AP的长.13.如图,在下列矩形ABCD中,已知:AB=a,BC=b(a<b),假定顶点在矩形边上的菱形叫做矩形的内接菱形,现给出(Ⅰ)、(Ⅱ)、(Ⅲ)三个命题:命题(Ⅰ):图①中,若AH=BG=AB,则四边形ABGH是矩形ABCD的内接菱形;命题(Ⅱ):图②中,若点E、F、G和H分别是AB、BC、CD和DE的中点,则四边形EFGH是矩形ABCD的内接菱形;命题(Ⅲ):图③中,若EF垂直平分对角线AC,变BC于点E,交AD于点F,交AC于点O,则四边形AECF是矩形ABCD的内接菱形.请解决下列问题:(1)命题(Ⅰ)、(Ⅱ)、(Ⅲ)都是真命题吗?请你在其中选择一个,并证明它是真命题或假命题;(2)画出一个新的矩形内接菱形(即与你在(1)中所确认的,但不全等的内接菱形).(3)试探究比较图①,②,③中的四边形ABGH、EFGH、AECF的面积大小关系.14.在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.(1)如图1,证明平行四边形ECFG为菱形;(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.15.如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE、AC和BE相交于点O.(1)判断四边形ABCE是怎样的四边形,说明理由;(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED 的面积.16.(2011•清远)如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.(1)求证:AB=DF;(2)若AD=10,AB=6,求tan∠EDF的值.17.(2010•大庆)已知:如图①,正方形ABCD与矩形DEFG的边AD、DE在同一直线l上,点G在CD上.正方形ABCD的边长为a,矩形DEFG的长DE为b,宽DG为3(其中a>b>3).若矩形DEFG沿直线l向左以每秒1个单位的长度的速度运动(点D、E始终在直线l上).若矩形DEFG在运动过程中与正方形ABCD的重叠部分的面积记作S,运动时间记为t秒(0≤t≤m),其中S与t的函数图象如图②所示.矩形DEFG的顶点经运动后的对应点分别记作D′、E′、F′、G′.(1)根据题目所提供的信息,可求得b=_________,a=_________,m=_________;(2)连接AG′、CF′,设以AG′和CF′为边的两个正方形的面积之和为y,求当0≤t≤5时,y与时间t之间的函数关系式,并求出y的最小值以及y取最小值时t的值;(3)如图③,这是在矩形DEFG运动过程中,直线AG′第一次与直线CF′垂直的情形,求此时t的值.并探究:在矩形DEFG继续运动的过程中,直线AG′与直线CF′是否存在平行或再次垂直的情形?如果存在,请画出图形,并求出t的值;否则,请说明理由.18.(2005•淮安)已知:平行四边形ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD,A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).(1)求证:四边形ABCD是矩形;(2)在四边形ABCD中,求的值.19.如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.(1)求证:四边形PMEN是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN是菱形;(3)四边形PMEN有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.20.如图:矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.(1)判断△BEC的形状,并说明理由?(2)判断四边形EFPH是什么特殊四边形?并证明你的判断;(3)求四边形EFPH的面积.正方形21.(2012•黑龙江)在△ABC中,∠BAC=90°,AB=AC,若点D在线段BC上,以AD为边长作正方形ADEF,如图1,易证:∠AFC=∠ACB+∠DAC;(1)若点D在BC延长线上,其他条件不变,写出∠AFC、∠ACB、∠DAC的关系,并结合图2给出证明;(2)若点D在CB延长线上,其他条件不变,直接写出∠AFC、∠ACB、∠DAC的关系式.22.(2012•常德)已知四边形ABCD是正方形,O为正方形对角线的交点,一动点P从B开始,沿射线BC运动,连接DP,作CN⊥DP于点M,且交直线AB于点N,连接OP,ON.(当P在线段BC上时,如图1:当P在BC 的延长线上时,如图2)(1)请从图1,图2中任选一图证明下面结论:①BN=CP;②OP=ON,且OP⊥ON;(2)设AB=4,BP=x,试确定以O、P、B、N为顶点的四边形的面积y与x的函数关系.23.(2011•来宾)已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点,(1)如果动点E、F满足BE=CF(如图1):①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);②证明:AE⊥BF;(2)如果动点E、F满足BE=OF(如图2),问当AE⊥BF时,点E在什么位置,并证明你的结论.24.(2011•河北)如图,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.(1)求证:①DE=DG;②DE⊥DG(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想:(4)当时,请直接写出的值.25.(2011•阜新)如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O 为AC中点.(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;(2)如图2,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由;(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形(尺规作图,保留作图痕迹,不写作法),并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.26.(2006•内江)如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连接E、F、G、H,把四边形EFGH 称为中点四边形.连接AC、BD,容易证明:中点四边形EFGH一定是平行四边形.(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD 的对角线满足AC=BD时,四边形EFGH为菱形.当四边形ABCD的对角线满足_________时,四边形EFGH为矩形;当四边形ABCD的对角线满足_________时,四边形EFGH为正方形;(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明;(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少?27.如图,四边形ABCD是正方形,点P是BC上任意一点,DE⊥AP于点E,BF⊥AP于点F,CH⊥DE于点H,BF的延长线交CH于点G.(1)求证:AF﹣BF=EF;(2)四边形EFGH是什么四边形?并证明;(3)若AB=2,BP=1,求四边形EFGH的面积.28.如图,在正方形ABCD中,点M在边AB上,点N在边AD的延长线上,且BM=DN.点E为MN的中点,DE的延长线与AC相交于点F.试猜想线段DF与线段AC的关系,并证你的猜想.29.在图1到图3中,点O是正方形ABCD对角线AC的中点,△MPN为直角三角形,∠MPN=90°.正方形ABCD 保持不动,△MPN沿射线AC向右平移,平移过程中P点始终在射线AC上,且保持PM垂直于直线AB于点E,PN垂直于直线BC于点F.(1)如图1,当点P与点O重合时,OE与OF的数量关系为_________;(2)如图2,当P在线段OC上时,猜想OE与OF有怎样的数量关系与位置关系?并对你的猜想结果给予证明;(3)如图3,当点P在AC的延长线上时,OE与OF的数量关系为_________;位置关系为_________.30.以△ABC的各边,在边BC的同侧分别作三个正方形.他们分别是正方形ABDI,BCFE,ACHG,试探究:(1)如图中四边形ADEG是什么四边形?并说明理由.(2)当△ABC满足什么条件时,四边形ADEG是矩形?(3)当△ABC满足什么条件时,四边形ADEG是正方形?初中数学中考特殊四边形证明及计算组卷参考答案与试题解析一.解答题(共30小题)1.(2012•威海)(1)如图①,▱ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.(2)如图②,将▱ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.考点:平行四边形的性质;全等三角形的判定与性质;翻折变换(折叠问题).分析:(1)由四边形ABCD是平行四边形,可得AD∥BC,OA=OC,又由平行线的性质,可得∠1=∠2,继而利用ASA,即可证得△AOE≌△COF,则可证得AE=CF.(2)根据平行四边形的性质与折叠性质,易得A1E=CF,∠A1=∠A=∠C,∠B1=∠B=∠D,继而可证得△A1IE≌△CGF,即可证得EI=FG.解答:证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,OA=OC,∴∠1=∠2,在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴AE=CF;(2)∵四边形ABCD是平行四边形,∴∠A=∠C,∠B=∠D,由(1)得AE=CF,由折叠的性质可得:AE=A1E,∠A1=∠A,∠B1=∠B,∴A1E=CF,∠A1=∠A=∠C,∠B1=∠B=∠D,又∵∠1=∠2,∴∠3=∠4,∵∠5=∠3,∠4=∠6,∴∠5=∠6,在△A1IE与△CGF中,,∴△A1IE≌△CGF(AAS),∴EI=FG.点评:此题考查了平行四边形的性质、折叠的性质以及全等三角形的判定与性质.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.2.(2011•贵阳)[阅读]在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为.[运用](1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为(2,1.5).(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.考点:平行四边形的性质;坐标与图形性质;矩形的性质.专题:几何综合题.分析:(1)根据矩形的对角线互相平分及点E的坐标即可得出答案.(2)根据题意画出图形,然后可找到点D的坐标.解答:解:(1)M(,),即M(2,1.5).(2)如图所示:根据平行四边形的对角线互相平分可得:设D点的坐标为(x,y),∵以点A、B、C、D构成的四边形是平行四边形,①当AB为对角线时,∵A(﹣1,2),B(3,1),C(1,4),∴BC=,∴AD=,∵﹣1+3﹣1=1,2+1﹣4=﹣1,∴D点坐标为(1,﹣1),②当BC为对角线时,∵A(﹣1,2),B(3,1),C(1,4),∴AC=2,BD=2,D点坐标为(5,3).③当AC为对角线时,∵A(﹣1,2),B(3,1),C(1,4),∴AB=,CD=,D点坐标为:(﹣3,5),综上所述,符合要求的点有:D'(1,﹣1),D″(﹣3,5),D″′(5,3).点评:本题考查了平行四边形的性质及矩形的性质,关键是掌握已知两点求其中点坐标的方法.3.(2007•黑龙江)在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB.请直接应用上述信息解决下列问题:当点P分别在△ABC内(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明.考点:平行四边形的性质.专题:探究型.分析:在图2中,因为四边形PEAF为平行四边形,所以PE=AF,又三角形FDC为等腰三角形,所以FD=PF+PD=FC,即PE+PD+PF=AC=AB,在图3中,PE=AF可证,FD=PF﹣PD=CF,即PF﹣PD+PE=AC=AB.解答:解:图2结论:PD+PE+PF=AB.证明:过点P作MN∥BC分别交AB,AC于M,N两点,∵PE∥AC,PF∥AB,∴四边形AEPF是平行四边形,∵MN∥BC,PF∥AB∴四边形BDPM是平行四边形,∴AE=PF,∠EPM=∠ANM=∠C,∵AB=AC,∴∠EMP=∠B,∴∠EMP=∠EPM,∴PE=EM,∴PE+PF=AE+EM=AM.∵四边形BDPM是平行四边形,∴MB=PD.∴PD+PE+PF=MB+AM=AB,即PD+PE+PF=AB.图3结论:PE+PF﹣PD=AB.点评:此题主要考查了平行四边形的性质,难易程度适中,读懂信息,把握规律是解题的关键.4.(2006•泰安)如图,矩形ABCD的对角线交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F,连接AF,CE.(1)求证:四边形AECF是平行四边形;(2)若∠BAD的平分线与FC的延长线交于点G,则△ACG是等腰三角形吗?并说明理由.考点:平行四边形的判定;全等三角形的判定;等腰三角形的判定;矩形的性质.专题:证明题;几何综合题;探究型.分析:(1)根据矩形的性质可知:AB=CD,∠ABE=∠CDF,∠AEB=∠CFD=90°,得到△ABE≌△CDF,所以AE∥CF,AE=CF,可证四边形AECF为平行四边形;(2)因为AE∥FG,得到∠G=∠GAE.利用AG平分∠BAD,得到∠BAG=∠DAG,从而求得∠ODA=∠DAO.所以∠CAG=∠G,可得△CAG是等腰三角形.解答:(1)证明:∵矩形ABCD,∴AB∥CD,AB=CD.∴∠ABE=∠CDF,又∠AEB=∠CFD=90°,∴AE∥CF,∴△ABE≌△CDF,∴AE=CF.∴四边形AECF为平行四边形.(2)解:△ACG是等腰三角形.理由如下:∵AE∥FG,∴∠G=∠GAE.∵AG平分∠BAD,∴∠BAG=∠DAG.又OA=AC=BD=OD,∴∠ODA=∠DAO.∵∠BAE与∠ABE互余,∠ADB与∠ABD互余,∴∠BAE=∠ADE.∴∠BAE=∠DAO,∴∠EAG=∠CAG,∴∠CAG=∠G,∴△CAG是等腰三角形.点评:本题考查三角形全等的性质和判定方法以及等腰三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.5.(2006•陕西)如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA到点D,使AD=AB.连接DE,DF.(1)求证:AF与DE互相平分;(2)若BC=4,求DF的长.考点:平行四边形的判定.专题:计算题;证明题.分析:(1)连接EF、AE,证四边形AEFD是平行四边形即可.(2)注意应用直角三角形斜边上的中线等于斜边的一半和平行四边形的性质:平行四边形的对边相等,求得AE长即可.解答:(1)证明:连接EF,AE.∵点E,F分别为BC,AC的中点,∴EF∥AB,EF=AB.又∵AD=AB,∴EF=AD.又∵EF∥AD,∴四边形AEFD是平行四边形.∴AF与DE互相平分.(2)解:在Rt△ABC中,∵E为BC的中点,BC=4,∴AE=BC=2.又∵四边形AEFD是平行四边形,∴DF=AE=2.点评:本题考查了平行四边形的判定,有中点时需考虑运用三角形的中位线定理或者直角三角形斜边上的中线等于斜边的一半.6.如图,以△ABC三边为边在BC同侧作三个等边△ABD、△BCE、△ACF.请回答下列问题:(1)求证:四边形ADEF是平行四边形;(2)当△ABC满足什么条件时,四边形ADEF是矩形.考点:平行四边形的判定;等边三角形的性质;矩形的判定.专题:证明题;探究型.分析:1、本题可根据三角形全等证得DE=AF,AD=EF,即可知四边形ADEF是平行四边形2、要使四边形ADEF是矩形,必须让∠FAD=90°,则∠BAC=360°﹣90°﹣60°﹣60°=150°解答:证明:(1)∵等边△ABD、△BCE、△ACF,∴DB=AB,BE=BC.又∠DBE=60°﹣∠EBA,∠ABC=60°﹣∠EBA,∴∠DBE=∠ABC.∴△DBE≌△CBA.∴DE=AC.又∵AC=AF,∴AF=DE.同理可证:△ABC≌△FCE,证得EF=AD.∴四边形ADEF是平行四边形.(2)假设四边形ABCD是矩形,∵四边形ADEF是矩形,∴∠DAF=90°.又∵等边△ABD、△BCE、△ACF,∴∠DAB=∠FAC=60°.∴∠BAC=360﹣∠DAF﹣∠FAC﹣∠DAB=150°.当△ABC满足∠BAC=150°时,四边形ADEF是矩形.点评:此题主要考查了等边三角形的性质和平行四边形的判定.7.(2010•盘锦)如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE 交AB于点F.(1)若点D是BC边的中点(如图①),求证:EF=CD;(2)在(1)的条件下直接写出△AEF和△ABC的面积比;(3)若点D是BC边上的任意一点(除B、C外如图②),那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.考点:平行四边形的判定与性质;全等三角形的判定与性质;等边三角形的性质.专题:证明题.分析:(1)根据△ABC和△AED是等边三角形,D是BC的中点,ED∥CF,求证△ABD≌△CAF,进而求证四边形EDCF是平行四边形即可;(2)在(1)的条件下可直接写出△AEF和△ABC的面积比;(3)根据ED∥FC,结合∠ACB=60°,得出∠ACF=∠BAD,求证△ABD≌△CAF,得出ED=CF,进而求证四边形EDCF是平行四边形,即可证明EF=DC.解答:(1)证明:∵△ABC是等边三角形,D是BC的中点,∴AD⊥BC,且∠BAD=∠BAC=30°,∵△AED是等边三角形,∴AD=AE,∠ADE=60°,∴∠EDB=90°﹣∠ADE=90°﹣60°=30°,∵ED∥CF,∴∠FCB=∠EDB=30°,∵∠ACB=60°,∴∠ACF=∠ACB﹣∠FCB=30°,∴∠ACF=∠BAD=30°,在△ABD和△CAF中,,∴△ABD≌△CAF(ASA),∴AD=CF,∵AD=ED,∴ED=CF,又∵ED∥CF,∴四边形EDCF是平行四边形,∴EF=CD.(2)解:△AEF和△ABC的面积比为:1:4;(3)解:成立.理由如下:∵ED∥FC,∴∠EDB=∠FCB,∵∠AFC=∠B+∠BCF=60°+∠BCF,∠BDA=∠ADE+∠EDB=60°+∠EDB∴∠AFC=∠BDA,在△ABD和△CAF中,∴△ABD≌△CAF(AAS),∴AD=FC,∵AD=ED,∴ED=CF,又∵ED∥CF,∴四边形EDCF是平行四边形,∴EF=DC.点评:此题主要考查学生对平行四边形的判定和性质、全等三角形的判定和性质、等边三角形的性质的理解和掌握.此题涉及到的知识点较多,综合性较强,难度较大.8.(2011•海南)如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.(1)求证:△BDQ≌△ADP;(2)已知AD=3,AP=2,求cos∠BPQ的值(结果保留根号).考点:菱形的性质;全等三角形的判定与性质;解直角三角形.专题:几何综合题.分析:(1)由四边形ABCD是菱形,可证得AD=AB,∠ABD=∠CBD=∠ABC,AD∥BC,又由∠A=60°,易得△ABD是等边三角形,然后由SAS即可证得△BDQ≌△ADP;(2)首先过点Q作QE⊥AB,交AB的延长线于E,然后由三角函数的性质,即可求得PE与QE 的长,又由勾股定理,即可求得PQ的长,则可求得cos∠BPQ的值.解答:(1)证明:∵四边形ABCD是菱形,∴AD=AB,∠ABD=∠CBD=∠ABC,AD∥BC,∵∠A=60°,∴△ABD是等边三角形,∠ABC=120°,∴AD=BD,∠CBD=∠A=60°,∵AP=BQ,∴△BDQ≌△ADP(SAS);(2)解:过点Q作QE⊥AB,交AB的延长线于E,∵BQ=AP=2,∵AD∥BC,∴∠QBE=60°,∴QE=QB•sin60°=2×=,BE=QB•cos60°=2×=1,∵AB=AD=3,∴PB=AB﹣AP=3﹣2=1,∴PE=PB+BE=2,∴在Rt△PQE中,PQ==,∴cos∠BPQ===.点评:此题考查了菱形的性质与勾股定理、三角函数的性质.此题难度适中,解题的关键是数形结合思想的应用.9.(2009•龙岩)在边长为6的菱形ABCD中,动点M从点A出发,沿A⇒B⇒C向终点C运动,连接DM交AC 于点N.(1)如图1,当点M在AB边上时,连接BN:①求证:△ABN≌△ADN;②若∠ABC=60°,AM=4,∠ABN=α,求点M到AD的距离及tanα的值.(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x(6≤x≤12).试问:x为何值时,△ADN为等腰三角形.考点:菱形的性质;全等三角形的判定;等腰三角形的判定;解直角三角形.专题:动点型.分析:(1)①三角形ABN和ADN中,不难得出AB=AD,∠DAC=∠CAB,AN是公共边,根据SAS即可判定两三角形全等.②通过构建直角三角形来求解.作MH⊥DA交DA的延长线于点H.由(1)可得∠MDA=∠ABN,那么M到AD的距离和∠α就转化到直角三角形MDH和MAH中,然后根据已知条件进行求解即可.(2)本题要分三种情况即:ND=NA,DN=DA,AN=AD进行讨论.解答:解:(1)①证明:∵四边形ABCD是菱形,∴AB=AD,∠1=∠2.又∵AN=AN,∴△ABN≌△ADN(SAS).②作MH⊥DA交DA的延长线于点H.由AD∥BC,得∠MAH=∠ABC=60°.在Rt△AMH中,MH=AM•sin60°=4×sin60°=2.∴点M到AD的距离为2.∴AH=2.∴DH=6+2=8.在Rt△DMH中,tan∠MDH=,由①知,∠MDH=∠ABN=α,∴tanα=;(2)∵∠ABC=90°,∴菱形ABCD是正方形.∴∠CAD=45°.下面分三种情形:(Ⅰ)若ND=NA,则∠ADN=∠NAD=45°.此时,点M恰好与点B重合,得x=6;(Ⅱ)若DN=DA,则∠DNA=∠DAN=45°.此时,点M恰好与点C重合,得x=12;(Ⅲ)若AN=AD=6,则∠1=∠2.∵AD∥BC,∴∠1=∠4,又∠2=∠3,∴∠3=∠4.∴CM=CN.∴AC=6.∴CM=CN=AC﹣AN=6﹣6.故x=12﹣CM=12﹣(6﹣6)=18﹣6.综上所述:当x=6或12或18﹣6时,△ADN是等腰三角形.点评:本题考查了等腰三角形的判定,全等三角形的判定,菱形的性质,正方形的性质等知识点,注意本题(2)中要分三种情况进行讨论,不要丢掉任何一种情况.10.(2007•常德)如图1,已知四边形ABCD是菱形,G是线段CD上的任意一点时,连接BG交AC于F,过F 作FH∥CD交BC于H,可以证明结论成立.(考生不必证明)(1)探究:如图2,上述条件中,若G在CD的延长线上,其它条件不变时,其结论是否成立?若成立,请给出证明;若不成立,请说明理由;(2)计算:若菱形ABCD中AB=6,∠ADC=60°,G在直线CD上,且CG=16,连接BG交AC所在的直线于F,过F作FH∥CD交BC所在的直线于H,求BG与FG的长.(3)发现:通过上述过程,你发现G在直线CD上时,结论还成立吗?考点:菱形的性质;勾股定理;平行线分线段成比例.专题:综合题;压轴题.分析:(1)借助中间比进行证明,根据平行线分线段成比例定理分别证明两个比都等于即可;(2)首先应画出两个不同的图形进行分析.构造30°的直角三角形,然后计算两条直角边的长,在两种情况中,GQ=16+3=19或16﹣3=13,然后根据勾股定理计算BG的长,进一步根据比例式求得FG的长;(3)成立,根据(2)中的过程,可以分别求得左右两个比,从而证明结论.解答:解:(1)结论成立证明:由已知易得FH∥AB,∴,∵FH∥GC,∴.(2)∵G在直线CD上,∴分两种情况讨论如下:①G在CD的延长线上时,DG=10,如图1,过B作BQ⊥CD于Q,由于四边形ABCD是菱形,∠ADC=60°,∴BC=AB=6,∠BCQ=60°,∴BQ=3,CQ=3,∴BG=.又由FH∥GC,可得,而△CFH是等边三角形,∴BH=BC﹣HC=BC﹣FH=6﹣FH,∴,∴FH=,由(1)知,∴FG=.②G在DC的延长线上时,CG=16,如图2,过B作BQ⊥CG于Q,∵四边形ABCD是菱形,∠ADC=60°,∴BC=AB=6,∠BCQ=60°.∴BQ=3,CQ=3.∴BG==14.又由FH∥CG,可得,∴.∵BH=HC﹣BC=FH﹣BC=FH﹣6,∴FH=.∵FH∥CG,∴.∴BF=14×÷16=.∴FG=14+.(3)G在DC的延长线上时,,,∴成立.结合上述过程,发现G在直线CD上时,结论还成立.点评:证明比例式的时候,可以利用相似或利用平行线分线段成比例定理进行证明.11.(2001•河北)如图,在菱形ABCD中,AB=10,∠BAD=60度.点M从点A以每秒1个单位长的速度沿着AD 边向点D移动;设点M移动的时间为t秒(0≤t≤10).(1)点N为BC边上任意一点,在点M移动过程中,线段MN是否一定可以将菱形分割成面积相等的两部分并说明理由;(2)点N从点B(与点M出发的时刻相同)以每秒2个单位长的速度沿着BC边向点C移动,在什么时刻,梯形ABNM的面积最大并求出面积的最大值;(3)点N从点B(与点M出发的时刻相同)以每秒a(a≥2)个单位长的速度沿着射线BC方向(可以超越C点)移动,过点M作MP∥AB,交BC于点P.当△MPN≌△ABC时,设△MPN与菱形ABCD重叠部分的面积为S,求出用t表示S的关系式,井求当S=0时的值.考点:菱形的性质;二次函数的最值;全等三角形的性质.专题:压轴题.分析:(1)菱形被分割成面积相等的两部分,那么分成的两个梯形的面积相等,而两个梯形的高相等,只需上下底的和相等即可.(2)易得菱形的高,那么用t表示出梯形的面积,用t的最值即可求得梯形的最大面积.(3)易得△MNP的面积为菱形面积的一半,求得不重合部分的面积,让菱形面积的一半减去即可.解答:解:(1)设:BN=a,CN=10﹣a(0≤a≤10)因为,点M从点A以每秒1个单位长的速度沿着AD边向点D移动,点M移动的时间为t秒(0≤t≤10)所以,AM=1×t=t(0≤t≤10),MD=10﹣t(0≤t≤10).所以,梯形AMNB的面积=(AM+BN)×菱形高÷2=(t+a)×菱形高÷2;梯形MNCD的面积=(MD+NC)×菱形高÷2=[(10﹣t)+(10﹣a)]×菱形高÷2当梯形AMNB的面积=梯形MNCD的面积时,即t+a=10,(0≤t≤10),(0≤a≤10)所以,当t+a=10,(0≤t≤10),(0≤a≤10)时,可出现线段MN一定可以将菱形分割成面积相等的两部分.(2)点N从点B以每秒2个单位长的速度沿着BC边向点C移动,设点N移动的时间为t,可知0≤t≤5,因为AB=10,∠BAD=60°,所以菱形高=5,AM=1×t=t,BN=2×t=2t.所以梯形ABNM的面积=(AM+BN)×菱形高÷2=3t×5×=t(0≤t≤5).所以当t=5时,梯形ABNM的面积最大,其数值为.(3)当△MPN≌△ABC时,则△ABC的面积=△MPN的面积,则△MPN的面积为菱形面积的一半为25;因为要全等必有MN∥AC,∴N在C点外,所以不重合处面积为×(at﹣10)2×∴重合处为S=25﹣,当S=0时,即PM在CD上,∴a=2.点评:本题考查了菱形以及相应的三角函数的性质,注意使用两条平行线间的距离相等等条件.12.(2002•无锡)已知:如图,矩形ABCD中,AB=2,AD=3,E、F分别是AB、CD的中点.(1)在边AD上取一点M,使点A关于BM的对称点C恰好落在EF上.设BM与EF相交于点N,求证:四边形ANGM是菱形;(2)设P是AD上一点,∠PFB=3∠FBC,求线段AP的长.考点:菱形的判定;矩形的性质.专题:计算题;证明题.分析:(1)设AG交MN于O,由题意易得AO=GO,AG⊥MN,要证四边形ANGM是菱形,还需证明OM=ON,又可证明AD∥EF∥BC.∴MO:ON=AO:OG=1:1,∴MO=NO;(2)连接AF,由题意可证得∠PFA=∠FBC=∠PAF,∴PA=PF,∴PA=,求得PA=.解答:(1)证明:设AG交MN于O,则∵A、G关于BM对称,∴AO=GO,AG⊥MN.∵E、F分别是矩形ABCD中AB、CD的中点,。
特殊四边形练习题及答案

特殊四边形练习题及答案一、填空题1、已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则的值为1 2 32、如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).3、如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .4、我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形。
则矩形的中点四边形是 .5、如图,在正方形中,点,分别在边,上,若,,,则正方形的面积等于.5 6 7 86、如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.7、如图,菱形ABCD中,E、F分别是BC、CD的中点,过点E作EG⊥AD于G,连接GF.若∠A=80°,则∠DGF的度数为.8、如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是.二、简答题9、如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E.求证:AE=CE.10、如图,正方形ABCD的边长为4,点E是正方形边上的点,AE=5,BF⊥AE,垂足为点F,求BF的长.11、如图,正方形ABCD中,E、F分别为BC、CD上的点,且AE⊥BF,垂足为G,求证:AE=BF.12、如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.(1)求证:BE=CD;(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明.13、如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.(1)求证:AE=CF;(2)若∠ABE=55°,求∠EGC的大小.14、如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)判断OE与OF的大小关系?并说明理由;(4分)(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;(4分)(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF会是正方形.不要写理由。
特殊四边形提高训练题
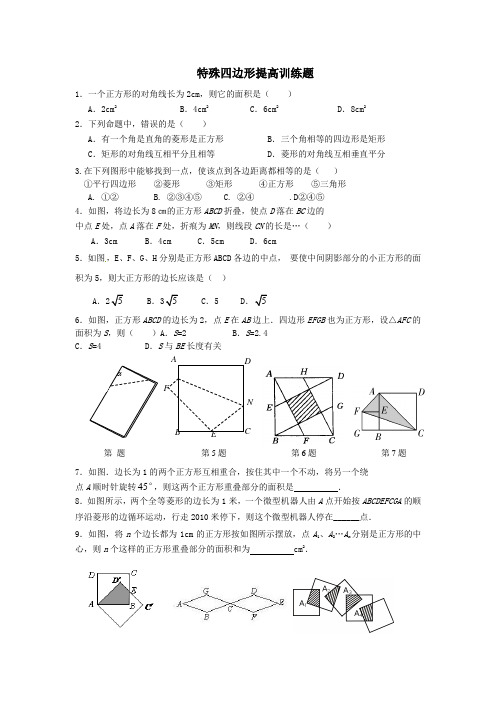
特殊四边形提高训练题1.一个正方形的对角线长为2cm ,则它的面积是( )A .2cm 2B .4cm 2C .6cm 2D .8cm 2 2.下列命题中,错误的是( ) A .有一个角是直角的菱形是正方形B .三个角相等的四边形是矩形C .矩形的对角线互相平分且相等D .菱形的对角线互相垂直平分3.在下列图形中能够找到一点,使该点到各边距离都相等的是( )①平行四边形 ②菱形 ③矩形 ④正方形 ⑤三角形A. ①②B. ②③④⑤C. ②④ .D ②④⑤4.如图,将边长为8㎝的正方形ABCD 折叠,使点D 落在BC 边的中点E 处,点A 落在F 处,折痕为MN ,则线段CN 的长是…( )A .3cmB .4cmC .5cmD .6cm5.如图,E 、F 、G 、H 分别是正方形ABCD 各边的中点,•要使中间阴影部分的小正方形的面积为5,则大正方形的边长应该是( )A .25B .35C . 5D .56.如图,正方形ABCD 的边长为2,点E 在AB 边上.四边形EFGB 也为正方形,设△AFC 的面积为S ,则( )A .S =2 B .S =2.4C .S =4D .S 与BE 长度有关7.如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕点A 顺时针旋转45°,则这两个正方形重叠部分的面积是 .8.如图所示,两个全等菱形的边长为1米,一个微型机器人由A 点开始按ABCDEFCGA 的顺序沿菱形的边循环运动,行走2010米停下,则这个微型机器人停在______点.9.如图,将n 个边长都为1cm 的正方形按如图所示摆放,点A 1、A 2…A n 分别是正方形的中心,则n 个这样的正方形重叠部分的面积和为 cm 2.NM F E D C B A 第5题 第 题 第6题 第7题10.如图,在正方形ABCD中,△PBC、△QCD是两个等边三角形,PB与DQ交于M,BP与CQ交于E,CP与DQ交于F.求证:PM=QM.11. 已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.(1)求证:AM=DM;(2)若DF=2,求菱形ABCD的周长.12.如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于H.(1)求证:①△BCG≌△DCE;②BH⊥DE.(2)试问当点G运动到什么位置时,BH垂直平分DE?请说明理由.13.在菱形ABCD中,∠B=60°,AC是对角线.(1)如图1,点E、F分别在边BC、CD上,且BE=CF.①求证:△ABE≌△ACF;②求证:△AEF是等边三角形.(2)若点E在BC的延长线上,在直线CD上是否存在点F,使△AEF是等边三角形?请证明你的结论(图2备用).AB=4,BC=25214.已知在矩形ABC 中,O 为BC 上一点,BO=如图所示,以BC 所在直线为x 轴,O 为坐标原点建立平面直角坐标系,M 为线段OC 上的一点.(1)若点M 的坐标为(1,0),如图①,以OM 为一边作等腰△OMP ,使点P 在矩形ABCD 的一边上,则符合条件的等腰三角形有几个?请直接写出所有符合条件的点P 的坐标;(2)若将(1)中的点M 的坐标改为(4,0),其它条件不变,如图②,那么符合条件的等腰三角形有几个?求出所有符合条件的点P 的坐标;(3)若将(1)中的点M 的坐标改为(5,0),其它条件不变,如图③,请直接写出符合条件的等腰三角形有几个.(不必求出点P 的坐标)15.如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF=BE .(1)求证:CE=CF ;(2)在图1中,若G 在AD 上,且∠GCE=45°,则GE=BE+GD 成立吗?为什么?(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图2,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B=90°,AB=BC=12,E 是AB 上一点,且∠DCE=45°,BE=4,求DE 的长.16.阅读材料:如图,△ABC 中,AB=AC ,P 为底边BC 上任意一点,点P 到两腰的距离分别为r 1,r 2,腰上的高为h ,连接AP ,则S △ARP +S △ACP =S △ABC ,即:1/2AB*r1+1/2AC*r2=1/2AC*h ∴r 1+r 2=h (定值).(1)理解与应用:如图,在边长为3的正方形ABCD 中,点E 为对角线BD 上的一点,且BE=BC ,F 为CE 上一点,FM ⊥BC 于M ,FN ⊥BD 于N ,试利用上述结论求出FM+FN 的长.(2)类比与推理:如果把“等腰三角形”改成“等边三角形”,那么P 的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:7 217.已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h(定值).(3)拓展与延伸:若正n边形A1A2…A n,内部任意一点P到各边的距离为r1r2…r n,请问r1+r2+…+r n是否为定值?如果是,请合理猜测出这个定值.18. 已知:△ABC的高AD所在直线与高BE所在直线相交于点F.(1)如图1,若△ABC为锐角三角形,且∠ABC=45°,过点F作FG∥BC,交直线AB于点G,求证:FG+DC=AD;(2)如图2,若∠ABC=135°,过点F作FG∥BC,交直线AB于点G,则FG、DC、AD 之间满足的数量关系是。
《特殊四边形》的专题复习1(有答案)

《特殊四边形》的专题复习1一、选择题(本大题共85小题,共255.0分。
在每小题列出的选项中,选出符合题目1. 下列说法错误的是( )A. 对角线相等是矩形具有而菱形不具有的性质B. 对角线互相垂直平分是正方形具有而菱形不具有的性质C. 每一条对角线平分一组对角是菱形具有而矩形不具有的性质D. 顺次连接任意四边形各边中点所得的四边形一定是平行四边形2. 关于▱ABCD的叙述,正确的是( )A. 若AC=BD,则▱ABCD是菱形B. 若AB=AD,则▱ABCD是矩形C. 若AB⊥BC,则▱ABCD是正方形D. 若AC⊥BD,则▱ABCD是菱形3. 矩形具有而菱形不一定具有的性质是( )A. 对边相等B. 对角线垂直C. 对角线相等D. 对角线互相平分4. 如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO.添加下列条件,不能判定四边形ABCD是菱形的是( )A. AB=ADB. AC=BDC. AC⊥BDD. ∠ABO=∠CBO5. 如图,E,F,G,H分别是四边形ABCD四条边的中点,要使四边形EFGH为矩形,四边形ABCD应具备的条件是( )A. AD//BCB. AC=BDC. AC⊥BDD. AD=AB6. 若以A(−0.5,0)、B(2,0)、C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在( )A. 第一象限B. 第C. 第二象限D. 第三象限四象限7. 如图,已知点E、F、G、H分别是菱形ABCD各边的中点,则四边形EFGH是( )A. 正方形B. 矩形C. 菱形D. 平行四边形8. 如图,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点.则下列说法中正确的个数是( )①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分.④若四边形EFGH是正方形,则AC与BD互相垂直且相等.A. 1B. 2C. 3D. 49. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )A. 当AB=BC时,它是菱形B. 当AC⊥BD时,它是菱形C. 当AC=BD时,它是矩形D. 当∠ABC=90°时,它是正方形10. 若一个多边形的内角和是1800∘,则这个多边形的边数是( )A. 5B. 8C. 10D. 1211. 在四边形ABCD中,给出下列条件:①AB//CD;②AD=BC;③∠A=∠C;④AD//BC.从以上选择两个条件使四边形ABCD为平行四边形的选法有( )A. 3种B. 4种C. 5种D. 6种12. 已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )A. ∠A=∠BB. ∠A=∠CC. AC=BDD. AB⊥BC13. 下列命题中,真命题是( )A. 两条对角线垂直的四边形是菱形B. 对角线垂直且相等的四边形是正方形C. 两条对角线相等的四边形是矩形D. 两条对角线相等的平行四边形是矩形14. 四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )A. AB=CDB. AD=BCC. AB=BCD. AC=BD15. 如图,□ABCD的对角线AC,BD相交于点O,EF过点O与AD,BC分别交于点E,F.若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长是( )A. 16B. 14C. 12D. 1016. 一个多边形的各个内角都等于120°,则它的边数为( )A. 3B. 6C. 7D. 817. 在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可能是( )A. 3:4:5:4B. 4:4:3:3C. 3:4:3:4D. 4:3:3:418. 一个多边形的内角和是外角和的2倍,则它是( )A. 四边形B. 五边形C. 六边形D. 八边形19. 下列说法正确的有几个( )①两组对角分别相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③对角线相等的平行四边形是矩形;④矩形的四个角是直角;⑤对角线互相垂直的四边形是菱形;⑥对角线互相垂直的平行四边形是菱形;⑦四条边相等的四边形是菱形.A. 6个B. 5个C. 4个D. 7个20. 如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为12cm,点B,D之间的距离为16cm,则线段AB的长为( )A. 9.6cmB. 10cmC. 20cmD. 12cm21. 如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为6,那么平行四边形ABCD的周长是( )A. 8B. 10C. 12D. 1822. 如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC 边上的中点,则MP+PN的最小值是( )A. 12B. 1C. √2D. 223. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )A. 125B. 245C. 12D. 2424. 下列属于矩形具有而菱形不具有的性质是( )A. 两组对边分别平行且相等B. 两组对角分别相等C. 对角线相互平分D. 四个角都相等25. 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )A. 6cmB. 7cmC. 8cmD. 9cm26. 如图,菱形ABCD的两条对角线AC,BD相交于点O,E是AB的中点,若AC=6,菱形ABCD的面积为24,则OE长为( )A. 2.5B. 3.5C. 3D. 427. 一个多边形的内角和等于它的外角和的3倍,则它是边形.( )A. 六B. 七C. 八D. 九28. 如图,在△ABC中,点E、D、F分别在边AB、BC、CA上,且DE//CA,DF//BA,下列四个判断中,不正确的是( )A. 四边形AEDF是平行四边形B. 如果∠BAC=90°,那么四边形AEDF是矩形C. 如果AD⊥BC且AB=AC,那么四边形AEDF是正方形D. 如果AD平分∠BAC,那么四边形AEDF是菱形29. 一个多边形的各个内角都等于120°,则它的边数为( )A. 3B. 6C. 7D. 830. 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=4,∠ABC=60°,则BD的长为( )A. 4√3B. 4C. 2√3D. 331. 如图所示,在矩形ABCD中,O是BC的中点,∠AOD=90°,若矩形ABCD的周长为30cm,则AB的长为( )A. 5cmB. 10cmC. 15cmD. 7.5cm32. 一个多边形从一个顶点出发,最多可以作2条对角线,则这个多边形是( )A. 四边形B. 五边形C. 六边形D. 七边形33. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥BC于点H,连接OH,若OA=4,OH的长为1.5,则S菱形ABCD=( )A. 24B. 12C. 8D. 634. 如图,两个大小一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到▵DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )A. 24B. 40C. 42D. 4835. 如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=( )A. √41B. √42C. 5√2D. 2√1336. 一个正多边形的内角和是900度,则这个多边形是( )A. 正六边形B. 正七边形C. 正八边形D. 正九边形37. 如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为( )A. 20B. 15C. 10D. 538. 如图,在▵ABCD中,AD=8,AB=5,AE平分∠BAD交边BC于点E,DF平分∠ADC 交边BC于点F,则EF=( )A. 2B. 3C. 3D. 3.539. 如图,在▱ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF//DE,交AB的延长线于点F,则BF的长为( )A. 5B. 4C. 3D. 240. 下面给出的四边形ABCD中,∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD 是平行四边形的条件是( )A. 3:4:3:4B. 3:3:4:4C. 2:3:4:5D. 3:4:4:341. 在平行四边形ABCD中,∠ABC的角平分线交AD所在直线于点E,若AE=6,DE=2,则ABCD周长为( )A. 28B. 20C. 28或20D. 28或2442. 一个多边形截去一个角后,形成一个六边形,那么原多边形边数为( )A. 5B. 5或6C. 5或7D. 5或6或743. 如图,矩形ABCD中,对角线AC,BD交于点O.若∠AOB=60°,BD=8,则AB的长为( )A. 4B. 4√3C. 3D. 544. 已知一个正多边形的每一个外角都是30∘,则这个正多边形的边数是( )A. 12B. 10C. 9D. 845. 如果一个多边形的内角和是540∘,那么这个多边形的对角线的条数是.( )A. 5B. 4C. 3D. 2答案和解析1.【答案】B2.【答案】D3.【答案】C4.【答案】B5.【答案】C6.【答案】C7.【答案】B8.【答案】A9.【答案】D10.【答案】D11.【答案】B12.【答案】B13.【答案】D14.【答案】D15.【答案】C16.【答案】B17.【答案】C18.【答案】C19.【答案】A20.【答案】B21.【答案】C22.【答案】B23.【答案】B24.【答案】D25.【答案】C26.【答案】A27.【答案】C28.【答案】C29.【答案】B30.【答案】A31.【答案】A32.【答案】B33.【答案】B34.【答案】D35.【答案】D36.【答案】B37.【答案】D38.【答案】A39.【答案】C40.【答案】A41.【答案】C42.【答案】D43.【答案】A44.【答案】A45.【答案】A。
专题1.7特殊的平行四边形单元提升卷-2024-2025学年九年级数学上册[含答案]
![专题1.7特殊的平行四边形单元提升卷-2024-2025学年九年级数学上册[含答案]](https://img.taocdn.com/s3/m/79053ba84793daef5ef7ba0d4a7302768f996f5a.png)
第1章 特殊的平行四边形单元提升卷【北师大版】考试时间:60分钟;满分:100分考卷信息:本卷试题共23题,单选10题,填空6题,解答7题,满分100分,限时60分钟,本卷题型针对性较高,覆盖面广,选题有深度,可衡量学生掌握本章内容的具体情况!一.选择题(共10小题,满分30分,每小题3分)(23-24九年级·四川泸州·期中)1.菱形具有而平行四边形不具有的性质是( )A .两组对边分别平行B .对角线互相平分C .两组对角线分别相等,对角线互相垂直D .对角线互相垂直(23-24九年级·河南焦作·期中)2.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm 的正方形ABCD 沿对角线BD 方向平移1cm 得到正方形A B C D ¢¢¢¢,形成一个“方胜”图案,则点D ,B ¢之间的距离为( )A .2cmBC .1)cmD .1)cm -(23-24九年级·重庆江津·期中)3.如图,在矩形ABCD 中,8AB =,4BC =,将矩形沿AC 折叠,点D 落在点D ¢处,则重叠部分AFC V 的面积为( )A .6B .8C .10D .12(23-24九年级·陕西渭南·期中)4.如图,四边形ABCD 是菱形,等边AMN V 的顶点M N 、分别在BC CD 、上,且AM BC =,则C Ð的度数为( )A .105°B .100°C .115°D .120°(23-24九年级·江西九江·期中)5.如图,矩形ABCD 的三个顶点的坐标分别为(1,3),(4,3),(4,1)A B C .若直线y x b =+平分矩形ABCD 的周长,则b 的值为( )A .12-B .1-C .12D .2(23-24九年级·河北保定·期中)6.将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD ,用拉紧的橡皮筋连接AC BD ,,转动这个四边形,使它的形状改变.当90ABC Ð=°时,如图1,测得AC =.当60ABC Ð=°时,如图2,此时BD AC -=( )A .B 1C .1D .(23-24九年级·河北廊坊·期中)7.如图,四边形ABCD 是由四个边长为1的正六边形所围成,则四边形ABCD 的面积是( )A B .1C D .2(23-24九年级·湖北孝感·期中)8.如图,D 是ABC V 内部一点,AC BD ^,依次取AB ,BC ,CD ,AD 的中点,并顺次连接得到四边形MNPQ ,若4BD =,6AC =,则四边形MNPQ 的面积为( )A .24B .18C .12D .6(23-24九年级·江苏苏州·期中)9.如图,已知菱形ABCD 的边长为6,点M 是对角线AC 上的一动点,且120ABC Ð=°,则MA MB MD ++的最小值是( )A .B .3+C .6D .(23-24·黑龙江大庆·三模)10.如图,已知四边形ABCD 为正方形,AB =E 为对角线AC 上一点,连接DE ,过点E 作EF DE ^,交BC 的延长线于点F ,以DE ,EF 为邻边作矩形DEFG ,连接CG .下列结论:①矩形DEFG 是正方形;②2CE CG +;③CG 平分DCF Ð;④CE CF =.其中结论正确的序号有( )A .①③B .②④C .①②③D .①②③④二.填空题(共6小题,满分18分,每小题3分)(23-24九年级·江苏扬州·期中)11.如图,在四边形ABCD 中,P 、Q 、M 、N 分别是AD 、BC 、BD 、AC 的中点,当四边形ABCD 满足 时(填写一个条件),PQ ⊥MN .(23-24九年级·湖北恩施·期末)12.如图,点P 是矩形ABCD 对角线AC 上一点,过点P 做EF BC ∥,分别交AB ,CD 于点E ,F ,连接,PB PD .若2AE =,9PF =,则图中阴影部分的面积为 .(23-24九年级·山东滨州·期末)13.以正方形ABCD 的边CD 为一边作等边CDE V ,则AEC Ð的度数是 .(23-24九年级·江苏苏州·期中)14.如图,菱形ABCD 的顶点A 恰好是矩形BCEF 对角线的交点,若菱形ABCD 的周长为8,则矩形BCEF 的面积是 .(23-24九年级·河南郑州·期末)15.如图,在等腰ABC V 中,3AB BC ==,AC =A ,B 分别在x 轴,y 轴上,且BC x ∥轴,将ABC V 沿x 轴向左平移,当点A 与点O 重合时,点B 的坐标为 .(23-24九年级·江苏·期中)16.已知矩形ABCD ,AB =6,AD =8,将矩形ABCD 绕点A 顺时针旋转θ(0°<θ<360°)得到矩形AEFG ,当θ= °时,GC =GB .三.解答题(共7小题,满分52分)(23-24九年级·浙江·专题练习)17.如图,四边形ABCD 是菱形,点C ,点D 的坐标分别是()4,0,()0,3.(1)请分别写出点A ,点B 的坐标;(2)求出该菱形的周长.(23-24九年级·广东潮州·期末)18.如图,菱形ABCD 对角线交于点O ,BE AC AE BD ∥,∥,EO 与AB 交于点F .(1)试判断四边形AEBO 的形状,并说明你的理由;(2)求证:EO DC =.(23-24九年级·湖北荆州·期中)19.下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.已知:四边形ABCD 是平行四边形.?求作:菱形ABEF (点E 在BC 上,点F 在AD 上).作法:①以A 为圆心,AB 长为半径作弧,交AD 于点F ;②以B 为圆心,AB 长为半径作弧,交BC 于点E ;③连接EF .所以四边形ABEF 为所求作的菱形.(1)根据小明的做法,使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明;证明:AF AB =Q ,BE AB =,\ = .在ABCD Y 中,AD BC ∥,即AF BE ∥,\四边形ABEF 为平行四边形( )(填推理的依据),AF AB =Q ,\四边形ABEF 为菱形( )(填推理的依据).(23-24九年级·广东广州·期中)20.如图,线段9AB =,射线BG AB ^,P 为射线BG 上一点,以AP 为边作正方形APCD ,且C 、D 与点B 在AP 两侧,已知DP 平分CPA Ð,在线段DP 取一点E ,使EAP BAP Ð=Ð,直线CE 与线段AB 相交于点F (点F 与点A 、B 不重合).(1)求证:AEP CEP △≌△;(2)判断CF 与AB 的位置关系,并说明理由;(3)求AEF △的周长.(23-24九年级·江苏常州·期中)21.图①、图②、图③均是106´的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A 、B 、C 、D 、P 均在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹.(1)在图①中,作以点P 为对称中心的平行四边形ABEF .(2)在图②中,在边AD 上找一点G ,在边BC 上找一点H ,连接CG ,AH ,使四边形CGAH 为矩形.(3)在图③中,在四边形ABCD 的边CD 上找一点N ,连接AN ,使45DAN Ð=o .(23-24九年级·广西桂林·期中)22.如图1,在矩形ABCD 中,对角线AC BD 、相交于点O ,606cm AOB AB Ð=°=,,点P 从点A 出发沿AB 以每秒1cm 的速度向点B 运动,同时点Q 从点C 出发沿CA 方向以每秒2cm 的速度向点A 运动,设运动的时间为t 秒,当点P 运动到点B 时,点Q 停止运动.过点Q 作QH BC ^于点H .(1)填空:ACB =∠ °,HQ = ,AQ = (用含有t 的式子表示);(2)是否存在某一时刻t ,使四边形APHQ 为菱形?若存在,求出t 的值,请说明理由;(3)若在某一时刻t ,平面内存在一点G ,使P 、Q 、G 、H 四点构成的四边形是矩形,求出t 的值.(23-24九年级·天津滨海新·期中)23.已知正方形ABCD 的边长为8,点E 是对角线AC 上的一点.(1)如图①,若点E 到AD 的距离为6,则点E 到AB 的距离为 ;(2)连接DE ,过点E 作EF ED ^,交AB 于点F .①如图②,以DE ,EF 为邻边作矩形DEFG .求证:矩形DEFG 是正方形;②如图③,在①的条件下,连接AG ,求AG AE +的值.1.D【分析】本题考查了菱形的性质,平行四边形的性质,掌握菱形的性质是解题的关键.由菱形的性质可直接求解.【详解】解:菱形的性质有:两组对边平行,两组对边相等,对角线互相垂直平分,平行四边形的性质有:两组对边分别平行,两组对边相等,对角线互相平分,∴菱形具有而平行四边形不具有的性质是对角线互相垂直,故选:D .2.D【分析】本题考查平移性质,正方形的性质,勾股定理,熟练掌握平移性质和正方形的性质是解答的关键,由题意得1cm BB ¢=,根据正方形的性质和勾股定理,求出BD ,进而求出答案即可;【详解】由题意得1cm BB ¢=,Q 四边形ABCD 是正方形,2cm,90AB AD A \==Ð=°,BD \=,()1cm DB BD BB ¢¢\=-=-,\点D ,B ¢之间的距离为()1cm -,故选:D .3.C【分析】本题考查了矩形的折叠问题,矩形的性质和折叠的性质,勾股定理,以及间接法求三角形的面积,解题的关键是利用勾股定理正确求出BF 的长度,先证明¢V AD F ≌CBF V ,得到AF CF =,设BF x =,则8AF CF x ==-,根据勾股定理,求出x ,然后利用ABC V 的面积减去CBF V 的面积,即可得到答案.【详解】解:由折叠和矩形的性质可知,90D D B ¢Ð=Ð=Ð=°,4¢==AD CB ,又∵¢Ð=ÐAFD CFB ,∴AD F ¢V ≌CBF V (AAS ),∴AF CF =,设BF x =,则8AF CF x ==-,在Rt CBF △中,由勾股定理,得:()22248x x +=-,解得:3x =,∴1184431022AFC ABC CBF S S S =-=´-´´=V V V ;故选:C .4.B【分析】由四边形ABCD 的四边都相等,可证得四边形ABCD 是菱形,又由等边AMN V 的顶点M 、N 分别在BC 、CD 上,且AM AB =,可设BAM NAD x Ð=Ð=,根据三角形的内角和定理得出方程()2180602180x x +°-°-=°,解此方程的解即可求出答案.【详解】解:Q 四边形ABCD 的四边都相等,\四边形ABCD 是菱形,B D \Ð=Ð,DABC Ð=Ð,//AD BC ,180DAB B \Ð+Ð=°,AMN Q △是等边三角形,AM AB =,60AMN ANM \Ð=Ð=°,AM AD =,B AMB \Ð=Ð,D AND Ð=Ð,由三角形的内角和定理得:BAM NAD Ð=Ð,设BAM NAD x Ð=Ð=,则180602D AND x Ð=Ð=°-°-,180NAD D AND Ð+Ð+Ð=°Q ,2(180602)180x x \+°-°-=°,解得:20x =°,22060100C BAD \Ð=Ð=´°+°=°.故选:B .【点睛】本题主要考查对菱形的判定和性质,等边三角形的性质,等腰三角形的性质,三角形的内角和定理以及平行线的性质等知识点.注意掌握方程思想的应用是解此题的关键.5.A【分析】连接,AC BD 相交于点E ,根据四边形ABCD 是矩形,可得点E 是AC 的中点,即可求出5,22E æöç÷èø,再将5,22E æöç÷èø代入y x b =+即可求出b 的值.【详解】解:连接,AC BD 相交于点E ,如下图所示,∵(1,3),(4,3)A B ,∴AB x ∥轴,∵四边形ABCD 是矩形,,AC BD 相交于点E ,∴AE CE =,点E 是AC 的中点,∴1431,22E ++æöç÷èø,即5,22E æöç÷èø,∵直线y x b =+平分矩形ABCD 的周长,∴直线y x b =+经过点5,22E æöç÷èø,∴522b +=,解得12b =-,故选:A .【点睛】本题主要考查了矩形的性质和一次函数,求出点E 的坐标是解题的关键.6.B【分析】本题考查了正方形的判定与性质,菱形的判定与性质,勾股定理,先根据正方形的性质求出AB ,再根据菱形的性质和勾股定理求出AC BD ,即可求解,掌握正方形和菱形的性质是解题的关键.【详解】解:如图1,当90ABC Ð=°时,AB BC CD DA ===,∴四边形ABCD 是正方形,又∵AC =,∴1AB =,如图2,AC 与BD 的交点为O ,当60ABC Ð=°时,,∴AB BC CD DA ===四边形ABCD 是菱形,∴90AOB Ð=°,1302ABO ABC =Ð=а,OA OC OB OD ==,,∴11122OA AB ==´=∴OB =∴12212AC OA ==´=,22BD OB ===∴1BD AC -=-,故选:B .7.C【分析】本题考查的是正多边形的内角与外角,菱形的性质与判定,勾股定理的应用,化为最简二次根式,先证明四边形ABCD 是菱形,18012060BAD Ð=°-°=°,如图,连接BD ,过点D 作DE AB ^交AB 于点E ,再进一步可得答案.【详解】解:如图,由正六边形的性质可得:18012060BAD Ð=°-°=°,1AB BC CD AD ====,∴四边形ABCD 是菱形,如图,连接BD ,过点D 作DE AB ^交AB 于点E ,∵四边形ABCD 是菱形,∴ABD BCD S S =△△,又∵60BAD Ð=°,∴ABD △为等边三角形,∵DE AB ^,∴1122AE AB ==,∴在Rt ADE V 中,DE ===,∴12ABD S AB DE △=´´,∴菱形ABCD 故选:C .8.D【分析】本题主要考查了三角形中位线定理,矩形的性质与判定,先根据三角形中位线定理可得1,22MQ BD MQ BD ==∥,1,22PN BD PN BD ==∥,1,32MN AC MN AC ==∥,从而可得,MQ PN MQ PN =∥,再根据平行四边形的判定可得四边形MNPQ 是平行四边形,然后根据平行线的性质可得MQ MN ^,根据矩形的判定可得平行四边形MNPQ 是矩形,最后利用矩形的面积公式求解即可得.【详解】解:Q 点,M Q 分别是AB ,AD 的中点,且4BD =,1,22MQ BD MQ BD \==∥,同理可得:1,22PN BD PN BD ==∥,1,32MN AC MN AC ==∥,,MQ PN MQ PN \=∥,\四边形MNPQ 是平行四边形,AC BD ^Q ,MQ AC \^,又M N AC Q ∥,MQ MN \^,\平行四边形MNPQ 是矩形,∴四边形MNPQ 的面积是236MQ MN ×=´=,故选:D .9.D【分析】过点D 作DE AB ^于点E ,连接BD ,根据垂线段最短,此时DE 最短,即MA MB MD ++最小,根据菱形性质和等边三角形的性质即可求出DE 的长,进而可得结论.【详解】解:如图,过点D 作DE AB ^于点E ,连接BD ,Q 菱形ABCD 中,120ABC Ð=°,60DAB \Ð=°,AD AB DC BC ===,ADB \V 是等边三角形,30MAE \Ð=°,2AM ME \=,MD MB =Q ,222MA MB MD ME DM DE \++=+=,根据垂线段最短,此时DE 最短,即MA MB MD ++最小,Q 菱形ABCD 的边长为6,DE \===2DE \=.MA MB MD ++\的最小值是故选:D .【点睛】本题考查了菱形的性质,等边三角形的判定与性质,解决本题的关键是掌握菱形的性质,等边三角形的判定与性质.10.A【分析】过E 作EM BC ^,过E 作EN CD ^于N ,如图所示,根据正方形性质得90BCD Ð=°,45ECN Ð=°,推出四边形EMCN 是正方形,由矩形性质得EM EN =,90DEN NEF MEF NEF Ð+Ð=Ð+Ð=°,根据全等三角形的性质得ED EF =,推出矩形DEFG 是正方形,故①正确;根据正方形性质得AD DC =,90ADE EDC Ð+Ð=°推出ADE CDG V V ≌,得到AE CG =,45DAE DCG Ð=Ð=°,由此推出CG 平分DCF Ð,故③正确;进而求得AC AE CE CE CG =+=+=,故②错误;当DE AC ^时,点C 与点F 重合,得到CE 不一定等于CF ,故④错误;故选A .【详解】过E 作EM BC ^,过E 作EN CD ^于N ,如图所示,∵四边形ABCD 是正方形,∴90BCD Ð=°,45ECN Ð=°,∴90EMC ENC BCD Ð=Ð=Ð=°,∴NE NC =,∴四边形EMCN 是正方形,∴EM EN =,∵四边形DEFG 是矩形,∴90DEN NEF MEF NEF Ð+Ð=Ð+Ð=°,∴DEN MEF Ð=Ð,在DEN V 和FEM △中,DNE FME EN EMDEN FEM Ð=Ðìï=íïÐ=Ðî,∴()DEN FEM ASA V V ≌,∴ED EF =,∴矩形DEFG 是正方形,故①正确;∴DE DG =,90EDC CDG Ð+Ð=°∵四边形ABCD 是正方形∴AD DC =,90ADE EDC Ð+Ð=°∴ADE CDGÐ=Ð在ADE V 和CDG V中AD CD ADE CDGDE DG =ìïÐ=Ðíï=î∴()ADE CDG SAS V V ≌∴AE CG =,45DAE DCG Ð=Ð=°∵90DCF Ð=°∴CG 平分DCF Ð,故③正确;∴AC AE CE CE CG =+=+=,故②错误;当DE AC ^时,点C 与点F 重合,∴CE 不一定等于CF ,故④错误.故选:A【点睛】本题考查了正方形的性质与判定,全等三角形的判定与性质,正确作出辅助线是解本题的关键.11.A B =CD【分析】根三角形中位线的性质,菱形的性质即可解答;【详解】解:∵P 、Q 、M 、N 分别是AD 、BC 、BD 、AC 的中点,∴PN 是△ACD 的中位线,PN =12CD , MQ 是△BCD 的中位线,MQ =12CD , ∴MQ =PN =12CD , 同理可得:NQ =PM =12AB ,当AB =CD 时,MQ =PN =NQ =PM ,四边形MQNP 是菱形,∵菱形对角线垂直平分,∴PQ ⊥MN ,故答案为:AB =CD ;【点睛】本题考查了三角形中位线的性质,菱形的判定和性质,掌握菱形的性质是解题关键.12.18【分析】本题考查了矩形的性质,过点P 作GH 分别交AB 、CD 于点G 、H ,证明GPFB EPHD S S =四边形四边形,从而1122GPFB EPHD S S =四边形四边形,即DPE PFB S S =△△,求出PFB S V 的值即可求出整个阴影部分的面积,熟练掌握矩形的性质定理是解题关键.【详解】解:过点P 作GH 分别交AB 、CD 于点G 、H ,如图所示:由矩形性质可知,ADC ABC S S =△△,PFC PHC S S =△△,AGP AEP S S =△△,ABC PFC AGP ADC PHC AEP S S S S S S \--=--△△△△△△,即GPFB EPHD S S =四边形四边形,\1122GPFB EPHD S S =四边形四边形,即DPE PFB S S =△△,2GP AE ==Q ,9PF =,12992PFB DPE S S \=´´==△△,即图中阴影面积为9918DPE PFB S S +=+=△△,故答案为:18.13.45°或135°【分析】分类讨论;当点E 在正方形内部,根据正方形的性质和等边三角形的性质可得AD DC DE ==,30ADE Ð=°,再根据等腰三角形的性质和三角形内角和定理即可求解;当点E 在正方形ABCD 的外部时, 根据正方形的性质和等边三角形的性质可得AD DE =,150ADE Ð=°,再根据等腰三角形的性质和三角形内角和定理即可求解.【详解】解:当点E 在正方形内部时,∵四边形ABCD 是正方形,∴90ADC Ð=°,AD DC =,∵DEC V 是等边三角形,∴DE DC =,60EDC DEC Ð=Ð=°,∴AD DC DE ==,30ADE Ð=°,∴18030752AED °-°Ð==°,∴==7560=135AEC AED DEC ÐÐ+а+°°;当点E 在正方形ABCD 的外部时,∵四边形ABCD 是正方形,∴90ADC Ð=°,AD DC =,∵DEC V 是等边三角形,∴60EDC DEC Ð=Ð=°,DC DE =,∴AD DE =,9060150ADE Ð=°+°=°,∴180150152AED °-°Ð==°, ∴=6015=45AEC а-°°,故答案为:45°或135°.【点睛】本题考查正方形的性质、等边三角形的性质、等腰三角形的性质、三角形内角定理,熟练掌握正方形的性质和等边三角形的性质,运用分类讨论思想解决问题是解题的关键.14.【分析】本题考查了矩形的性质,等边三角形的判定,菱形的性质,与性质,根据菱形的性质得出2AB BC ==,进而利用矩形的性质得出AB AC =,得出ABC V 是等边三角形,利用矩形的面积解答即可.【详解】解:Q 四边形ABCD 是菱形,2AB BC \==,Q 四边形BCEF 是矩形,FC BE \=,FA AC =,AE AB =,90ACB Ð=°,AB AC \=,1AB AC BC ===Q ,ABC \V 是等边三角形,60ABC \Ð=°,24BE AB \==,在Rt ECB V 中,EC ===\矩形BCEF 的面积2BC EC =×==故答案为:15.53æ-ççè【分析】本题考查勾股定理,矩形的判定与性质以及图形的平移,过点A 作AD BC ^,证明四边形OABD 是矩形,得到OA BD =,OB AD =,根据勾股定理求得BD 和OB 的长度,可得平移的距离,即可求解.【详解】解:如图,过点A 作AD BC ^,∵90AOB OBD BDA Ð=Ð=Ð=°,∴四边形OABD 是矩形,∴OA BD =,OB AD =,由勾股定理可得,2222AB BD AC DC -=-,∴()22983BD BD -=--,∴53BD =,∴53OA =,OB ==∴当点A 与点O 重合时,点A 向左移动53个单位,∴点B 的坐标为53æ-ççè,故答案为:53æ-ççè.16.60或300【分析】当GB =GC 时,点G 在BC 的垂直平分线上,分两种情况讨论,依据∠DAG =60°,即可得到旋转角θ的度数.【详解】解:当GB =GC 时,点G 在BC 的垂直平分线上,分两种情况讨论:①当点G 在AD 右侧时,取BC 的中点H ,连接GH 交AD 于M ,∵GC =GB ,∴GH ⊥BC ,∴四边形ABHM 是矩形,∴AM =BH =12AD =12AG ,∴GM 垂直平分AD ,∴GD =GA =DA ,∴△ADG 是等边三角形,∴∠DAG =60°,∴旋转角θ=60°;②当点G 在AD 左侧时,同理可得△ADG 是等边三角形,∴∠DAG =60°,∴旋转角θ=360°﹣60°=300°.故答案为60或300【点睛】本题考查了旋转的性质,矩形的性质,利用分类讨论思想解决问题是本题的关键.17.(1)()4,0A -,()0,3B -(2)20【分析】此题考查了菱形的性质,勾股定理,(1)首先根据菱形的性质得到OA OC =,OB OD =,AC BD ^,然后根据对称的性质求解即可;(2)首先求出4OC =,3OD =,然后利用勾股定理求出5CD ==,然后根据菱形的性质求解即可.【详解】(1)∵四边形ABCD 是菱形,∴OA OC =,OB OD =,AC BD ^,∴点A 与点C 关于点O 对称,点B 与点D 关于点O 对称,∵点C 、点D 的坐标分别是()4,0,()0,3,∴点()4,0A -,点()0,3B -;(2)∵点C 、点D 的坐标分别是()4,0,()0,3,∴4OC =,3OD =,在Rt COD V 中,由勾股定理得:5CD ==,∵四边形ABCD 是菱形,∴5AB BC AD CD ====,∴菱形ABCD 的周长44520CD ==´=.18.(1)矩形,见解析(2)见解析【分析】本题主要考查的是菱形的性质、矩形的性质和判定;(1)先证明四边形AEBO 为平行四边形,再由由菱形的性质可证明90BOA Ð=°,从而可证明四边形AEBO 是矩形;(2)依据矩形的性质可得到EO BA =,然后依据菱形的性质可得到AB CD =.【详解】(1)解:四边形AEBO 是矩形,证明如下:∵BE AC AE BD ∥,∥,\四边形AEBO 是平行四边形.又Q 菱形ABCD 对角线交于点OAC BD \^,即90AOB Ð=°.\四边形AEBO 是矩形.(2)证明:Q 四边形AEBO 是矩形EO AB \=,在菱形ABCD 中,AB DC =.EO DC \=.19.(1)见解析(2)AF ,BE ,一组对边相等且平行的四边形是平行四边形,一组邻边相等的平行四边形是菱形.【分析】本题考查作图-复杂作图,平行四边形的判定和性质,菱形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.(1)作图见解答过程;(2)AF ,BE ,一组对边相等且平行的四边形是平行四边形,邻边相等的平行四边形是菱形.【详解】(1)四边形ABEF 为所求作的菱形.(2)AF AB =Q ,BE AB =,AF BE \=,在ABCD Y 中,AD BC ∥.即AF BE ∥.\四边形ABEF 为平行四边形(一组对边相等且平行的四边形是平行四边形).AF AB =Q ,\四边形ABEF 为菱形(一组邻边相等的平行四边形是菱形.)故答案为:AF ,BE ,一组对边相等且平行的四边形是平行四边形,一组邻边相等的平行四边形是菱形.20.(1)见解析(2)CF AB ^.理由见解析(3)18【分析】此题考查了正方形的性质、矩形的判定和性质、全等三角形的判定和性质等知识,添加辅助线构造全等是解题的关键.(1)利用正方形的性质得到PC PA =,45APD CPD Ð=Ð=°,又由已知PE PE =,即可证明AEP CEP △≌△;(2)如图,设AP 与CF 相交于点M ,证明BAP FCP Ð=Ð,由90FCP CMP Ð+Ð=°,AMF CMP Ð=Ð,得到90AMF PAB Ð+Ð=°,即可证明结论;(3)过点C 作CN PB ^于点N ,则90CNP Ð=°.证明四边形CFBN 是矩形,则CN BF =,证明()AAS PCN APB V V ≌,则CN PB BF ==,PN AB =,又由AEP CEP △≌△得到AE CE =,利用等量代换得到218AE EF AF AB \++==,即可得到答案.【详解】(1)解:证明:Q 四边形APCD 为正方形,DP \平分APC Ð,PC PA =,90APC Ð=°,45APD CPD \Ð=Ð=°,又∵PE PE =,(SAS)AEP CEP \≌△△;(2)CF AB ^.理由如下:如图,设AP 与CF 相交于点M ,AEP CEP Q ≌△△,EAP ECP \Ð=Ð,EAP BAP Ð=ÐQ ,BAP FCP \Ð=Ð,90FCP CMP Ð+Ð=°Q ,AMF CMP Ð=Ð,90AMF PAB \Ð+Ð=°,90AFM \Ð=°,CF AB \^;(3)过点C 作CN PB ^于点N ,则90CNP Ð=°.∵18090CFB AFM Ð=°-Ð=°,∴90CFB CNP ABP Ð=Ð=Ð=°∴四边形CFBN 是矩形,∴CN BF =,∵90CPN PCN CPN APB Ð+Ð=Ð+Ð=°,∴PCN APB Ð=Ð,∵,90AB PN CNP PBA =Ð=Ð=°∴()AAS PCN APB V V ≌,CN PB BF \==,PN AB =,AEP CEP Q ≌△△,AE CE \=,218AE EF AF CE EF AF BN AF PN PB AF AB CN AF AB BF AF AB \++=++=+=++=++=++==即AEF △的周长为18.21.(1)见详解(2)见详解(3)见详解【分析】(1)利用网格特征连接,AP BP 并延长,即可作以点P 为对称中心的平行四边形ABEF ;(2)取格点E ,连接AE 交BC 于点H ,取格点F ,连接CF 交AD 于点G ,连接CG ,AH ,即可作四边形CGAH 为矩形;(3)取格点,,E P Q ,连接,,,AE PQ ED PQ 与ED 交于点F ,连接AF 并延长交CD 于点N 即可.【详解】(1)解:如图①中,平行四边形ABEF 即为所求;理由:BP FP AP EP ======Q ,∴四边形ABEF 是平行四边形.(2)解:如图②中,矩形CGAH 即为所求;理由:如图12903490Ð+Ð=°Ð+Ð=°Q ,,1234180Ð+Ð+Ð+Ð=\°,∵4CO AG ==,5BC AE ===,3BO EG ==,BCO EAG \V V ≌,∴13Ð=Ð,24ÐÐ=,1490\Ð+Ð=°,即90AHB Ð=°,同理可得90DGC Ð=°,5,CD AB CD AB ==∥Q ,ABCD \是平行四边形,,,B D AD BC AD BC \Ð=Ð=∥,,,90B D CD AB AHB DGC Ð=Ð=Ð=Ð=°Q ,()AHB CGD AAS \V V ≌,DG BH \=,,AG CH AG CH \=∥,\四边形CGAH 是矩形;(3)解:如图③中,45DAN Ð=o ,点N 即为所求.理由:5,3,4AE AD AG EH DG AH ======Q ,()AEH DAG SSS \V V ≌,12\Ð=Ð,2390Ð+Ð=°Q ,1390\Ð+Ð=°,90DAE \Ð=°,ADE \V 是等腰直角三角形,,DQ PE DQ PE =∥Q ,,FDQ FEP FQD FPE \Ð=ÐÐ=Ð,()FQD FPE ASA \V V ≌,DF EF \=,,AF DE AF \^平分DAE Ð,1452DAN DAE \Ð=Ð=°.【点睛】本题主要考查了中心对称图形,平行四边形的性质和判定,矩形的判定,全等三角形的性质和判定,勾股定理,等腰三角形的性质和判定等知识点,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.22.(1)30,t ,()122t -(2)存在,2t =时,四边形APHQ 是菱形(3)t 的值为3或245【分析】(1)证明AOB V 是等边三角形,推出60BAC Ð=°,可得结论;(2)存在,当AP AQ =时,四边形APHQ 是菱形,构建方程求解即可;(3)分两种情形,当90QPH Ð=°时,当90QPH Ð=°时,存在一点G ,使P 、Q 、G 、H 四点构成的四边形是矩形,分别构建方程求解.【详解】(1)解:∵四边形ABCD 是矩形,90AC BD OA OC ABC \==Ð=°,,,OA OB \=,60AOB Ð=°Q ,AOB \V 是等边三角形,60BAO \Ð=°,906030°°\Ð=-°=ACB ,6cm AB =Q ,212cm AC AB \==,QH CB ^Q ,90QHC \Ð=°,2cm CQ t =Q ,()122cm AQ t \=-,1cm 2QH CQ t ==,故答案为:30,t ,()122t -;(2)存在某一时刻t ,使四边形APHQ 为菱形由题意得:HQ AP ∥,cm AP QH t ==,\四边形APHQ 是平行四边形,当AP AQ =时,四边形APHQ 是菱形,122t t \=-,4t \=,4t \=时,四边形APHQ 是菱形;(3)当90PQH Ð=°时,存在一点P 、Q 、G 、H 四点构成的四边形是矩形,此时四边形PBHQ 是矩形,所以PB QH =,6t t \-=,3t \=;当90QPH Ð=°时,存在一点P 、Q 、G 、H 四点构成的四边形是矩形,根据解析(2)可知,四边形APHQ 为平行四边形,60QHP BAC \Ð=Ð=°,90QPH Ð=°Q ,30PQH \Ð=°,QH AP ∥Q ,30APQ PQH \Ð=Ð=°,2AP AQ \=,()2122t t \=-,245t \=,综上所述,满足条件的t 的值为3或245.【点睛】本题属于四边形综合题,考查了矩形的性质,菱形的判定和性质,等边三角形的判定与性质,矩形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.23.(1)6(2)①见解析;②【分析】本题考查了正方形的判定和性质,角平分线的性质,全等三角形的判定和性质,勾股定理等,掌握相关图形的判定和性质是解题的关键.(1)过点E 作EM AD ^于M ,利用角平分线的性质定理解决问题即可.(2)①连接EB ,证明DE EB =,EF EB =,可得结论;②证明SAS GDA EDC ≌()△△,推出AG EC =,可得结论.【详解】(1)解:如图①中,过点E 作EM AD ^于M ,EN AB ^于N .Q 四边形ABCD 是正方形,∴45EAM EAN Ð=Ð=°,Q EM AM ^,EN AN ^,∴6EM EN ==,∴点E 到AB 的距离为6,故答案为:6.(2)①证明:如图②中,连接EB .Q 四边形ABCD 是正方形,\CD CB =,45DCE BCE Ð=Ð=°,在DCE △和BCE V 中,CD CB DCE BCE CE CE =ìïÐ=Ðíï=î,\SAS DCE BCE ≌()△△,\DE EB =,CDE CBE =∠∠,Q 90ADC ABC Ð=Ð=°,\EBF ADE Ð=Ð,Q DE EF ^,\90DEF DAF Ð=Ð=°,\180ADE AFE Ð+Ð=°,Q 180AFE EFB °Ð+Ð=,\ADE EFB Ð=Ð,\EFB EBF Ð=Ð,\EF EB =,答案第23页,共23页\=DE EF ,Q 四边形DEFG 是矩形,\四边形DEFG 是正方形.②解:如图③中,Q 四边形DEFG ,四边形ABCD 都是正方形,\90ADC GDE Ð=Ð=°,DA DC =,DG DE =,\GDA EDC Ð=Ð,在GDA △和EDC △中,DG DE GDA EDC DA DC =ìïÐ=Ðíï=î,\SAS GDA EDC ≌()△△,\AG EC =,\AG AE EC AE AC +=+=,在Rt ADC V 中,AD CD =,由勾股定理有AC ====,\AG AE EC AE AC +=+===。
2024年中考数学真题汇编专题21 特殊的平行四边形+答案详解

2024年中考数学真题汇编专题21 特殊的平行四边形+答案详解(试题部分)一、单选题1.(2024·重庆·中考真题)如图,在矩形ABCD 中,分别以点A 和C 为圆心,AD 长为半径画弧,两弧有且仅有一个公共点.若4=AD ,则图中阴影部分的面积为( )A .328π−B .4πC .324π−D .8π2.(2024·甘肃临夏·中考真题)如图,O 是坐标原点,菱形ABOC 的顶点B 在x 轴的负半轴上,顶点C 的坐标为()3,4,则顶点A 的坐标为( )A .()4,2−B .()4C .()2,4−D .(− 3.(2024·湖北武汉·中考真题)小美同学按如下步骤作四边形ABCD :①画MAN ∠;②以点A 为圆心,1个单位长为半径画弧,分别交AM ,AN 于点B ,D ;③分别以点B ,D 为圆心,1个单位长为半径画弧,两弧交于点C ;④连接BC ,CD ,BD .若44A ∠=︒,则CBD ∠的大小是( )A .64︒B .66︒C .68︒D .70︒4.(2024·四川成都·中考真题)如图,在矩形ABCD 中,对角线AC 与BD 相交于点O ,则下列结论一定正确的是( )A .AB AD = B .AC BD ⊥ C .AC BD = D .ACB ACD ∠=∠5.(2024·黑龙江绥化·中考真题)如图,四边形ABCD 是菱形,5CD =,8BD =,AE BC ⊥于点E ,则AE 的长是( )A .245B .6C .485D .126.(2024·河北·中考真题)在平面直角坐标系中,我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”.如图,矩形ABCD 位于第一象限,其四条边分别与坐标轴平行,则该矩形四个顶点中“特征值”最小的是( )A .点AB .点BC .点CD .点D7.(2024·吉林·中考真题)如图,在平面直角坐标系中,点A 的坐标为()4,0−,点C 的坐标为()0,2.以OA OC ,为边作矩形OABC ,若将矩形OABC 绕点O 顺时针旋转90︒,得到矩形OA B C ''',则点B '的坐标为( )A .()4,2−−B .()4,2−C .()2,4D .()4,28.(2024·甘肃·中考真题)如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,60ABD ∠=︒,2AB =,则AC 的长为( )A .6B .5C .4D .39.(2024·四川眉山·中考真题)如图,在矩形ABCD 中,6AB =,8BC =,点E 在DC 上,把ADE V 沿AE 折叠,点D 恰好落在BC 边上的点F 处,则cos CEF ∠的值为( )A B C .34 D .5410.(2024·甘肃·中考真题)如图1,动点P 从菱形ABCD 的点A 出发,沿边AB BC →匀速运动,运动到点C 时停止.设点P 的运动路程为x ,PO 的长为y ,y 与x 的函数图象如图2所示,当点P 运动到BC 中点时,PO 的长为( )A.2 B .3 C D .11.(2024·甘肃临夏·中考真题)如图1,矩形ABCD 中,BD 为其对角线,一动点P 从D 出发,沿着D B C →→的路径行进,过点P 作PQ CD ⊥,垂足为Q .设点P 的运动路程为x ,PQ DQ −为y ,y 与x 的函数图象如图2,则AD 的长为( )A B .83 C D .11412.(2024·广西·中考真题)如图,边长为5的正方形ABCD ,E ,F ,G ,H 分别为各边中点,连接AG ,BH ,CE ,DF ,交点分别为M ,N ,P ,Q ,那么四边形MNPQ 的面积为( )A .1B .2C .5D .1013.(2024·内蒙古呼伦贝尔·中考真题)如图,边长为2的正方形ABCD 的对角线AC 与BD 相交于点O .E 是BC 边上一点,F 是BD 上一点,连接,DE EF .若DEF 与DEC 关于直线DE 对称,则BEF △的周长是( )A.B .2C .4−D 14.(2024·上海·中考真题)四边形ABCD 为矩形,过A C 、作对角线BD 的垂线,过B D 、作对角线AC 的垂线,如果四个垂线拼成一个四边形,那这个四边形为( )A .菱形B .矩形C .直角梯形D .等腰梯形15.(2024·四川德阳·的矩形叫黄金矩形,黄金矩形给我们以协调的美感,世界各国许多著名建筑为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形ABCD 是黄金矩形.()AB BC <,点P 是边AD 上一点,则满足PB PC ⊥的点P 的个数为( )A .3B .2C .1D .016.(2024·四川泸州·中考真题)如图,在边长为6的正方形ABCD 中,点E ,F 分别是边AB BC ,上的动点,且满足AE BF =,AF 与DE 交于点O ,点M 是DF 的中点,G 是边AB 上的点,2AG GB =,则12OM FG +的最小值是( )A .4B .5C .8D .1017.(2024·重庆·中考真题)如图,在边长为4的正方形ABCD 中,点E 是BC 上一点,点F 是CD 延长线上一点,连接AE ,AF ,AM 平分EAF ∠.交CD 于点M .若1BE DF ==,则DM 的长度为( )A .2BCD .125二、填空题18.(2024·福建·中考真题)如图,正方形ABCD 的面积为4,点E ,F ,G ,H 分别为边AB ,BC ,CD ,AD 的中点,则四边形EFGH 的面积为 .19.(2024·山东威海·中考真题)将一张矩形纸片(四边形ABCD )按如图所示的方式对折,使点C 落在AB 上的点C '处,折痕为MN ,点D 落在点D '处,C D ''交AD 于点E .若3BM =,4BC '=,3AC '=,则DN = .20.(2024·河南·中考真题)如图,在平面直角坐标系中,正方形ABCD 的边AB 在x 轴上,点A 的坐标为()20−,,点E 在边CD 上.将BCE 沿BE 折叠,点C 落在点F 处.若点F 的坐标为()06,,则点E 的坐标为 .21.(2024·广西·中考真题)如图,两张宽度均为3cm 的纸条交叉叠放在一起,交叉形成的锐角为60︒,则重合部分构成的四边形ABCD 的周长为 cm .22.(2024·天津·中考真题)如图,正方形ABCD 的边长为,AC BD 相交于点O ,点E 在CA 的延长线上,5OE =,连接DE .(1)线段AE 的长为 ;(2)若F 为DE 的中点,则线段AF 的长为 .23.(2024·内蒙古包头·中考真题)如图,在菱形ABCD 中,60ABC ∠=︒,6AB =,AC 是一条对角线,E 是AC 上一点,过点E 作EF AB ⊥,垂足为F ,连接DE .若CE AF =,则DE 的长为 .24.(2024·广东·中考真题)如图,菱形ABCD 的面积为24,点E 是AB 的中点,点F 是BC 上的动点.若BEF △的面积为4,则图中阴影部分的面积为 .25.(2024·浙江·中考真题)如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,53AC BD =.线段AB 与A B ''关于过点O 的直线l 对称,点B 的对应点B '在线段OC 上,A B ''交CD 于点E ,则B CE '与四边形OB ED '的面积比为26.(2024·黑龙江绥化·中考真题)在矩形ABCD 中,4cm AB =,8cm BC =,点E 在直线AD 上,且2cm DE =,则点E 到矩形对角线所在直线的距离是 cm .三、解答题27.(2024·陕西·中考真题)如图,四边形ABCD 是矩形,点E 和点F 在边BC 上,且BE CF =.求证:AF DE =.28.(2024·吉林长春·中考真题)如图,在四边形ABCD 中,90A B ∠=∠=︒,O 是边AB 的中点,AOD BOC ∠=∠.求证:四边形ABCD 是矩形.29.(2024·青海·中考真题)综合与实践顺次连接任意一个四边形的中点得到一个新四边形,我们称这个新四边形为原四边形的中点四边形......数学兴趣小组通过作图、测量,猜想:原四边形的对角线对中点四边形的形状有着决定性作用.以下从对角线的数量关系和位置关系两个方面展开探究.【探究一】如图1,在四边形ABCD中,E、F、G、H分别是各边的中点.求证:中点四边形EFGH是平行四边形.证明:∵E、F、G、H分别是AB、BC、CD、DA的中点,∴EF、GH分别是ABC和ACD的中位线,∴12EF AC=,12GH AC=(____①____)∴EF GH=.同理可得:EH FG=.∴中点四边形EFGH是平行四边形.结论:任意四边形的中点四边形是平行四边形.(1)请你补全上述过程中的证明依据①________【探究二】从作图、测量结果得出猜想Ⅰ:原四边形的对角线相等时,中点四边形是菱形.(2)下面我们结合图2来证明猜想Ⅰ,请你在探究一证明结论的基础上,写出后续..的证明过程. 【探究三】(3)从作图、测量结果得出猜想Ⅱ:原四边形对角线垂直时,中点四边形是②________.(4)下面我们结合图3来证明猜想Ⅱ,请你在探究一证明结论的基础上,写出后续..的证明过程. 【归纳总结】(5)请你根据上述探究过程,补全下面的结论,并在图4中画出对应的图形.结论:原四边形对角线③________时,中点四边形是④________.30.(2024·吉林长春·中考真题)【问题呈现】小明在数学兴趣小组活动时遇到一个几何问题:如图①,在等边ABC 中,3AB =,点M 、N 分别在边AC 、BC 上,且AM CN =,试探究线段MN 长度的最小值.【问题分析】小明通过构造平行四边形,将双动点问题转化为单动点问题,再通过定角发现这个动点的运动路径,进而解决上述几何问题.【问题解决】如图②,过点C 、M 分别作MN 、BC 的平行线,并交于点P ,作射线AP .在【问题呈现】的条件下,完成下列问题:(1)证明:AM MP =;(2)CAP ∠的大小为 度,线段MN 长度的最小值为________.【方法应用】某种简易房屋在整体运输前需用钢丝绳进行加固处理,如图③.小明收集了该房屋的相关数据,并画出了示意图,如图④,ABC 是等腰三角形,四边形BCDE 是矩形,2AB AC CD ===米,30ACB ∠=︒.MN 是一条两端点位置和长度均可调节的钢丝绳,点M 在AC 上,点N 在DE 上.在调整钢丝绳端点位置时,其长度也随之改变,但需始终保持AM DN =.钢丝绳MN 长度的最小值为多少米.31.(2024·河北·中考真题)情境 图1是由正方形纸片去掉一个以中心O 为顶点的等腰直角三角形后得到的.该纸片通过裁剪,可拼接为图2所示的钻石型五边形,数据如图所示.(说明:纸片不折叠,拼接不重叠无缝隙无剩余)操作 嘉嘉将图1所示的纸片通过裁剪,拼成了钻石型五边形.如图3,嘉嘉沿虚线EF ,GH 裁剪,将该纸片剪成①,②,③三块,再按照图4所示进行拼接.根据嘉嘉的剪拼过程,解答问题:(1)直接写出线段EF 的长;(2)直接写出图3中所有与线段BE 相等的线段,并计算BE 的长.探究淇淇说:将图1所示纸片沿直线裁剪,剪成两块,就可以拼成钻石型五边形.请你按照淇淇的说法设计一种方案:在图5所示纸片的BC 边上找一点P (可以借助刻度尺或圆规),画出裁剪线(线段PQ )的位置,并直接写出BP 的长.32.(2024·内蒙古呼伦贝尔·中考真题)如图,在平行四边形ABCD 中,点F 在边AD 上,AB AF =,连接BF ,点O 为BF 的中点,AO BC 于点E ,连接EE(1)求证:四边形ABEF 是菱形:(2)若平行四边形ABCD 的周长为22,1,120CE BAD =∠=︒,求AE 的长.33.(2024·河南·中考真题)如图,在Rt ABC △中,CD 是斜边AB 上的中线,∥BE DC 交AC 的延长线于点E .(1)请用无刻度的直尺和圆规作ECM ∠,使ECM A ∠=∠,且射线CM 交BE 于点F (保留作图痕迹,不写作法).(2)证明(1)中得到的四边形CDBF 是菱形34.(2024·贵州·中考真题)如图,四边形ABCD 的对角线AC 与BD 相交于点O ,AD BC ∥,90ABC ∠=︒,有下列条件:①AB CD ∥,②AD BC =.(1)请从以上①②中任选1个作为条件,求证:四边形ABCD 是矩形;(2)在(1)的条件下,若3AB =,5AC =,求四边形ABCD 的面积.35.(2024·吉林·中考真题)图①、图②均是44⨯的正方形网格,每个小正方形的顶点称为格点.点A ,B ,C ,D ,E ,O 均在格点上.图①中已画出四边形ABCD ,图②中已画出以OE 为半径的O ,只用无刻度的直尺,在给定的网格中按要求画图.(1)在图①中,面出四边形ABCD 的一条对称轴.(2)在图②中,画出经过点E 的O 的切线.36.(2024·吉林·中考真题)小明在学习时发现四边形面积与对角线存在关联,下面是他的研究过程:【探究论证】(1)如图①,在ABC 中,AB BC =,BD AC ⊥,垂足为点D .若2CD =,1BD =,则ABC S =______.(2)如图②,在菱形A B C D ''''中,4''=A C ,2B D ''=,则A B C D S ''''=菱形______.(3)如图③,在四边形EFGH 中,EG FH ⊥,垂足为点O .若5EG =,3FH =,则EFGH S =四边形______;若EG a =,FH b =,猜想EFGH S 四边形与a ,b 的关系,并证明你的猜想.【理解运用】(4)如图④,在MNK △中,3MN =,4KN =,5MK =,点P 为边MN 上一点.小明利用直尺和圆规分四步作图:(ⅰ)以点K 为圆心,适当长为半径画弧,分别交边KN ,KM 于点R ,I ;(ⅱ)以点P 为圆心,KR 长为半径画弧,交线段PM 于点I ';(ⅲ)以点I '为圆心,IR R ',点R ',K 在MN 同侧;(ⅳ)过点P 画射线PR ',在射线PR '上截取PQ KN =,连接KP ,KQ ,MQ .请你直接写出MPKQ S 四边形的值.37.(2024·四川广元·中考真题)如图,已知矩形ABCD .(1)尺规作图:作对角线AC 的垂直平分线,交CD 于点E ,交AB 于点F ;(不写作法,保留作图痕迹)(2)连接AE CF 、.求证:四边形AFCE 是菱形.38.(2024·黑龙江牡丹江·中考真题)在Rt ACB △中,90ACB ∠=︒,12BC =,8AC =,以BC 为边向ACB △外作有一个内角为60︒的菱形BCDE ,对角线BD CE ,交于点O ,连接OA ,请用尺规和三角板作出图形,并直接写出AOC 的面积.39.(2024·广东广州·中考真题)如图,Rt ABC △中,90B ??.(1)尺规作图:作AC 边上的中线BO (保留作图痕迹,不写作法);(2)在(1)所作的图中,将中线BO 绕点O 逆时针旋转180︒得到DO ,连接AD ,CD .求证:四边形ABCD 是矩形.40.(2024·广东广州·中考真题)如图,点E ,F 分别在正方形ABCD 的边BC ,CD 上,3BE =,6EC =,2CF =.求证:ABE ECF △△∽.41.(2024·四川遂宁·中考真题)康康在学习了矩形定义及判定定理1后,继续探究其它判定定理.(1)实践与操作①任意作两条相交的直线,交点记为O ;②以点O 为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段OA OB OC OD 、、、; ③顺次连结所得的四点得到四边形ABCD .于是可以直接..判定四边形ABCD 是平行四边形,则该判定定理是:______. (2)猜想与证明通过和同伴交流,他们一致认为四边形ABCD 是矩形,于是猜想得到了矩形的另外一种判定方法:对角线相等的平行四边形是矩形.并写出了以下已知、求证,请你完成证明过程.已知:如图,四边形ABCD 是平行四边形,AC BD =.求证:四边形ABCD 是矩形.42.(2024·重庆·中考真题)在学习了矩形与菱形的相关知识后,小明同学进行了更深入的研究,他发现,过矩形的一条对角线的中点作这条对角线的垂线,与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形,可利用证明三角形全等得到此结论.根据他的想法与思路,完成以下作图与填空:(1)如图,在矩形ABCD 中,点O 是对角线AC 的中点.用尺规过点O 作AC 的垂线,分别交AB ,CD 于点E ,F ,连接AF ,CE .(不写作法,保留作图痕迹)(2)已知:矩形ABCD ,点E ,F 分别在AB ,CD 上,EF 经过对角线AC 的中点O ,且EF AC ⊥.求证:四边形AECF 是菱形.证明:∵四边形ABCD 是矩形,∴AB CD .∴①,OCF OAE ∠=∠.∵点O 是AC 的中点,∴②.∴CFO AEO ≅△△(AAS ).∴③.又∵OA OC =,∴四边形AECF 是平行四边形.∵EF AC ⊥,∴四边形AECF 是菱形.进一步思考,如果四边形ABCD 是平行四边形呢?请你模仿题中表述,写出你猜想的结论:④. 43.(2024·吉林长春·中考真题)如图,在ABC 中,5AB AC ==,6BC =.点D 是边BC 上的一点(点D 不与点B 、C 重合),作射线AD ,在射线AD 上取点P ,使AP BD =,以AP 为边作正方形APMN ,使点M 和点C 在直线AD 同侧.(1)当点D 是边BC 的中点时,求AD 的长;(2)当4BD =时,点D 到直线AC 的距离为________;(3)连结PN ,当PN AC ⊥时,求正方形APMN 的边长;(4)若点N 到直线AC 的距离是点M 到直线AC 距离的3倍,则CD 的长为________.(写出一个即可) 44.(2024·甘肃·中考真题)【模型建立】(1)如图1,已知ABE 和BCD △,AB BC ⊥,AB BC =,CD BD ⊥,AE BD ⊥.用等式写出线段AE ,DE ,CD 的数量关系,并说明理由.【模型应用】(2)如图2,在正方形ABCD 中,点E ,F 分别在对角线BD 和边CD 上,AE EF ⊥,AE EF =.用等式写出线段BE ,AD ,DF 的数量关系,并说明理由.【模型迁移】(3)如图3,在正方形ABCD 中,点E 在对角线BD 上,点F 在边CD 的延长线上,AE EF ⊥,AE EF =.用等式写出线段BE ,AD ,DF 的数量关系,并说明理由.45.(2024·黑龙江大兴安岭地·中考真题)如图,在平面直角坐标系中,等边三角形OAB 的边OB 在x 轴上,点A 在第一象限,OA 的长度是一元二次方程2560x x −−=的根,动点P 从点O 出发以每秒2个单位长度的速度沿折线OA AB −运动,动点Q 从点O 出发以每秒3个单位长度的速度沿折线OB BA −运动,P 、Q 两点同时出发,相遇时停止运动.设运动时间为t 秒(0 3.6t <<),OPQ △的面积为S .(1)求点A 的坐标;(2)求S 与t 的函数关系式;(3)在(2)的条件下,当S =M 在y 轴上,坐标平面内是否存在点N ,使得以点O 、P 、M 、N 为顶点的四边形是菱形.若存在,直接写出点N 的坐标;若不存在,说明理由.2024年中考数学真题汇编专题21 特殊的平行四边形+答案详解(答案详解)一、单选题1.(2024·重庆·中考真题)如图,在矩形ABCD 中,分别以点A 和C 为圆心,AD 长为半径画弧,两弧有且仅有一个公共点.若4=AD ,则图中阴影部分的面积为( )A .328π−B .4πC .324π−D .8π 根据题意可得2AC AD =∵矩形ABCD ,∴AD =在Rt ABC △中,AB =2.(2024·甘肃临夏·中考真题)如图,O 是坐标原点,菱形ABOC 的顶点B 在x 轴的负半轴上,顶点C 的坐标为()3,4,则顶点A 的坐标为( )A .()4,2−B .()4C .()2,4−D .(−3.(2024·湖北武汉·中考真题)小美同学按如下步骤作四边形ABCD :①画MAN ∠;②以点A 为圆心,1个单位长为半径画弧,分别交AM ,AN 于点B ,D ;③分别以点B ,D 为圆心,1个单位长为半径画弧,两弧交于点C ;④连接BC ,CD ,BD .若44A ∠=︒,则CBD ∠的大小是( )A .64︒B .66︒C .68︒D .70︒【答案】C,AD BC ABD ∠44=︒,MBC A =∠=(11802CBD =故选:C .4.(2024·四川成都·中考真题)如图,在矩形ABCD 中,对角线AC 与BD 相交于点O ,则下列结论一定正确的是( )A .AB AD =B .AC BD ⊥ C .AC BD = D .ACB ACD ∠=∠5.(2024·黑龙江绥化·中考真题)如图,四边形ABCD 是菱形,5CD =,8BD =,AE BC ⊥于点E ,则AE 的长是( )A .245B .6C .485D .126.(2024·河北·中考真题)在平面直角坐标系中,我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”.如图,矩形ABCD 位于第一象限,其四条边分别与坐标轴平行,则该矩形四个顶点中“特征值”最小的是( )A .点AB .点BC .点CD .点D【答案】B 【分析】本题考查的是矩形的性质,坐标与图形,分式的值的大小比较,设(),A a b ,AB m =,AD n =,可得(),D a b n +,(),B a m b +,(),C a m b n ++,再结合新定义与分式的值的大小比较即可得到答案.【详解】解:设(),A a b ,AB m =,AD n =,7.(2024·吉林·中考真题)如图,在平面直角坐标系中,点A 的坐标为()4,0−,点C 的坐标为()0,2.以OA OC ,为边作矩形OABC ,若将矩形OABC 绕点O 顺时针旋转90︒,得到矩形OA B C ''',则点B '的坐标为( )A .()4,2−−B .()4,2−C .()2,4D .()4,28.(2024·甘肃·中考真题)如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,60ABD ∠=︒,2AB =,则AC 的长为( )A .6B .5C .4D .3 ,得到AOB 是等边三 ∴AOB 是等边三角形,2AB =,OA OB ==解得4AC =故选C .9.(2024·四川眉山·中考真题)如图,在矩形ABCD 中,6AB =,8BC =,点E 在DC 上,把ADE V 沿AE 折叠,点D 恰好落在BC 边上的点F 处,则cos CEF ∠的值为( )A B C .34 D .54【答案】A【分析】本题考查了矩形的性质,折叠的性质,勾股定理,求角的三角函数等知识点,正确利用折叠的性质是解题的关键.根据折叠的性质,可求得8AF AD ==,EF DE =,从而求得BF ,CF ,在Rt EFC △中,由勾股定理,得222EF CE CF =+,即可求得结果.【详解】解:四边形ABCD 是矩形,把10.(2024·甘肃·中考真题)如图1,动点P 从菱形ABCD 的点A 出发,沿边AB BC →匀速运动,运动到点C 时停止.设点P ,PO 的长为y ,y 与x 的函数图象如图2所示,当点P 运动到BC 中点时,PO 的长为( )A .2B .3CD .11.(2024·甘肃临夏·中考真题)如图1,矩形ABCD 中,BD 为其对角线,一动点P 从D 出发,沿着D B C →→的路径行进,过点P 作PQ CD ⊥,垂足为Q .设点P 的运动路程为x ,PQ DQ −为y ,y 与x 的函数图象如图2,则AD 的长为( )A .3B .83CD .114Rt BCD 中,()(24a −−解得:23a =,2AD a =+=故选:B .12.(2024·广西·中考真题)如图,边长为5的正方形ABCD ,E ,F ,G ,H 分别为各边中点,连接AG ,BH ,CE ,DF ,交点分别为M ,N ,P ,Q ,那么四边形MNPQ 的面积为( )A .1B .2C .5D .10 明()SAS ADG BAH ≌四边形MNPQ 是矩形,证明(AAS ADQ BAM ≌矩形MNPQ 是正方形,ADQ △中,利用勾股定理求出【详解】解:∵四边形ABCD 是正方形,AB BC CD DA ===CD ∥,AD BC ∥,分别为各边中点,DF BH ,∴四边形MNPQ 是平行四边形,CE ,1DGCG =,PQ ,∴()SAS ADG BAH ≌DAG ABH ∠=∠,90DAG GAB ∠+∠=90ABH GAB ∠+∠=︒,90QMN AMB ∠=∠=︒,同理∴平行四边形MNPQ 是矩形,∵90AQD AMB ∠=∠=︒,DAG ABH ∠=∠,AD BA =,∴()AAS ADQ BAM ≌,∴DQ AM =,又DQ PQ =,AM QM =, ∴DQ AM PQ QM ===,∴矩形MNPQ 是正方形,在Rt ADQ △中,222AD DQ AQ =+,∴()22252QM QM =+,∴25QM =,∴正方形MNPQ 的面积为5,故选:C .【点睛】本题考查了正方形的判定与性质,全等三角形判定与性质,平行线分线段成比例,勾股定理等知识,明确题意,灵活运用相关知识求解是解题的关键.13.(2024·内蒙古呼伦贝尔·中考真题)如图,边长为2的正方形ABCD 的对角线AC 与BD 相交于点O .E 是BC 边上一点,F 是BD 上一点,连接,DE EF .若DEF 与DEC 关于直线DE 对称,则BEF △的周长是( )A .B .2C .4−D∵DEF 与DEC 关于直线2DF DC ==,DFE ∠2BF BD DF =−=45FBE FEB ∠=∠=︒,222EF BF ==−(14.(2024·上海·中考真题)四边形ABCD 为矩形,过A C 、作对角线BD 的垂线,过B D 、作对角线AC 的垂线,如果四个垂线拼成一个四边形,那这个四边形为( )A .菱形B .矩形C .直角梯形D .等腰梯形 OBC OAD S S =,OC 再由菱形的判定即可得到答案.四边形OBC OAD S S ∴=,OC OB OA ==过A C 、作对角线BD 的垂线,过1122OBC OAD S S OC BF ∴==⋅=CH BF AE ===如果四个垂线拼成一个四边形,那这个四边形为菱形,15.(2024·四川德阳·的矩形叫黄金矩形,黄金矩形给我们以协调的美感,世界各国许多著名建筑为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形ABCD 是黄金矩形.()AB BC <,点P 是边AD 上一点,则满足PB PC ⊥的点P 的个数为( )A .3B .2C .1D .0设AB a =,BC b =,假设存在点P ,且在Rt ABP 中,2222BP AB AP a =+=在Rt PDC 中,222(PC PD CD b =+= PB PC ⊥,∴ 222BC BP PC =+,即222b a x =++整理得2x bx +− 24b ac ∆=−16.(2024·四川泸州·中考真题)如图,在边长为6的正方形ABCD 中,点E ,F 分别是边AB BC ,上的动点,且满足AE BF =,AF 与DE 交于点O ,点M 是DF 的中点,G 是边AB 上的点,2AG GB =,则12OM FG +的最小值是( )A .4B .5C .8D .10 先证明()SAS ADE BAF ≌12DF ,如图所示,在易证明()SAS FBG FBH ≌H 、D 、F 三点共线时,有最小值,最小值即为一半,求出8AH =,在Rt ADH 中,由勾股定理得10=,责任12OM +ABCD 是正方形,90ABC =︒,∴()SAS ADE BAF ≌ADE BAF ∠=∠,DOF ADO ∠=∠+∠∵点M 是DF 的中点,12OM DF =;∴()SAS FBG FBH ≌FH FG =,1122OM FG DF +=∴当H 、D 、F 三点共线时,Rt ADH 中,由勾股定理得12OM FG +的最小值为故选:B .17.(2024·重庆·中考真题)如图,在边长为4的正方形ABCD 中,点E 是BC 上一点,点F 是CD 延长线上一点,连接AE ,AF ,AM 平分EAF ∠.交CD 于点M .若1BE DF ==,则DM 的长度为( )A .2B C D .125【答案】D 【分析】本题主要考查了正方形的性质,全等三角形的性质与判定,勾股定理,先由正方形的性质得到904ABE ADC ADF C AB AD CD BC ====︒====∠∠∠∠,,再证明()SAS ABE ADF △≌△得到二、填空题18.(2024·福建·中考真题)如图,正方形ABCD 的面积为4,点E ,F ,G ,H 分别为边AB ,BC ,CD ,AD 的中点,则四边形EFGH 的面积为 .【答案】2【分析】本题考查正方形性质,线段中点的性质,根据正方形性质和线段中点的性质得到1HD DG ==,进而得到DGH S ,12AHE EFB CGF S S S ===,个小三角形面积求解,即可解题.【详解】解:正方形ABCD 的面积为4,点DGH S =同理可得12AHE EFB CGF S S S ===,四边形EFGH 的面积为11422−−故答案为:2.19.(2024·山东威海·中考真题)将一张矩形纸片(四边形ABCD )按如图所示的方式对折,使点C 落在AB 上的点C '处,折痕为MN ,点D 落在点D '处,C D ''交AD 于点E .若3BM =,4BC '=,3AC '=,则DN = .然后证明BC M AEC ''≌,得到中,利用222NE D E D N '+'=解题即可.Rt C BM '中,2C M C B '+'=5CM =,D C M D ∠=∠=∠'''是矩形,,E AEC '=∠∴BC M AEC ''≌,4BC AE '==,MC ='7AB CD C D ''===,84DE AD AE =−=−D N DN a '==,则EN 20.(2024·河南·中考真题)如图,在平面直角坐标系中,正方形ABCD 的边AB 在x 轴上,点A 的坐标为()20−,,点E 在边CD 上.将BCE 沿BE 折叠,点C 落在点F 处.若点F 的坐标为()06,,则点E 的坐标为 .Rt EGF 中,利用勾股定理构建关于的边长为a ,CD 与则四边形AOGD 是矩形,∴OG AD a ==,DG ∵折叠,∴BF BC a ==,CE =∵点A 的坐标为()20−,,点F 的坐标为()06,, ∴2AO =,6FO =,∴2BO AB AO a =−=−,在Rt BOF △中,222BO FO BF +=,∴()22226a a −+=,解得10a =,∴4FG OG OF =−=,8GE CD DG CE CE =−−=−,在Rt EGF 中,222GE FG EF +=,∴()22284CE CE −+=,解得5CE =,∴3GE =,∴点E 的坐标为()3,10,故答案为:()3,10.【点睛】本题考查了正方形的性质,坐标与图形,矩形的判定与性质,折叠的性质,勾股定理等知识,利用勾股定理求出正方形的边长是解题的关键.21.(2024·广西·中考真题)如图,两张宽度均为3cm 的纸条交叉叠放在一起,交叉形成的锐角为60︒,则重合部分构成的四边形ABCD 的周长为 cm .ABCD S =BC CD =∴四边形Rt ADN △22.(2024·天津·中考真题)如图,正方形ABCD 的边长为,AC BD 相交于点O ,点E 在CA 的延长线上,5OE =,连接DE .(1)线段AE 的长为 ;(2)若F为DE的中点,则线段AF的长为.)四边形Rt DOC中,DC=,32∴==OD OC OAOE=5∴AE OE OA=−=(2)延长AFAB=,AC是一条对角线,E 23.(2024·内蒙古包头·中考真题)如图,在菱形ABCD中,60ABC∠=︒,6=,则DE的长为.是AC上一点,过点E作EF AB⊥,垂足为F,连接DE.若CE AF先判断ABC,ACD都是等边三角形,的直角三角形的性质可得出【详解】解∶过D作DH∠=∵菱形ABCD中,ABC===,∠∴AB BC CD AD∴ABC,ACD都是等边三角形,==∴60EAF∠=︒,AC AB⊥,EF ABAEF∠=︒,30=,2AE AF24.(2024·广东·中考真题)如图,菱形ABCD 的面积为24,点E 是AB 的中点,点F 是BC 上的动点.若BEF △的面积为4,则图中阴影部分的面积为 .ADE S =8ABF S =,则可求出CDF 的面积,然后利用ADE BEF CDF S S S S S =−−阴影求解即可.【详解】解:连接AF BD 、,1122ADE ABD S S ==⨯28ABF BEF S S ==,设菱形ABCD 中BC 边上的高为12ABFABCDBF h S ⋅=菱形,即23BF BC =,2BF =ABFCDF SS =CDF =△10ADE BEF CDF S SS S =−−=,25.(2024·浙江·中考真题)如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,53AC BD =.线段AB 与A B ''关于过点O 的直线l 对称,点B 的对应点B '在线段OC 上,A B ''交CD 于点E ,则B CE '与四边形OB ED '的面积比为CEB OEB SS ''=,然后证明出(AAS A ED CEB ''≌明出()SSS ODE OB E '≌,得到ODE OB E SS '=,进而求解即可. 【详解】∵四边形ABCD 是菱形,53AC BD = 10AC a =,6BD a =152OA OC AC a ===,∵线段AB 与A B ''关于过点O 的直线∴12BOF COF BOB '∠=∠=∠=∴45AOG DOG ∠=∠=︒∴点A ',D ,O 三点共线∴2A D A O OD a ''=−=,B C 'CEB OEB S S ''=A D B '=CD AB ∥CDO ∠∴(AAS A ED CEB ''≌A E CE '=A B AB CD ''==DE B E '=又∵OD B O =',OE =∴()SSS ODE OB E '≌ODE OB E SS '= 3CEB CEB OEB ODE OB ED S S S S S ''''==++四边形故答案为:13. 26.(2024·黑龙江绥化·中考真题)在矩形ABCD 中,4cm AB =,8cm BC =,点E 在直线AD 上,且2cm DE =,则点E到矩形对角线所在直线的距离是cm.Rt AE F中,11=∠OAD ODARt E F D中,12在射线ADRt DCE中,2=∠CAD DCE+∠DCE DCA23Rt DE F 中,综上所述,点故答案为:25三、解答题27.(2024·陕西·中考真题)如图,四边形ABCD 是矩形,点E 和点F 在边BC 上,且BE CF =.求证:AF DE =.【答案】见解析【分析】本题考查了矩形的性质,全等三角形的判定和性质.根据矩形的性质得到AB CD =,90B C ∠=∠=︒,再推出BF CE =,利用SAS 证明ABF DCE ≌△△,即可得到AF DE =. 【详解】证明:∵四边形ABCD 是矩形, ∴AB DC =,90B C ∠=∠=︒, ∵BE CF =,∴BE EF CF EF +=+,即BF CE =, ∴()SAS ABF DCE ≌, ∴AF DE =.28.(2024·吉林长春·中考真题)如图,在四边形ABCD 中,90A B ∠=∠=︒,O 是边AB 的中点,AOD BOC ∠=∠.求证:四边形ABCD 是矩形.【答案】证明见解析.【分析】本题考查全等三角形的判定与性质、平行四边形的判定及矩形的判定,熟练掌握判定定理是解题关键.利用SAS 可证明AOD BOC ≌△△,得出AD BC =,根据90A B ∠=∠=︒得出AD BC ∥,即可证明四边形ABCD 是平行四边形,进而根据有一个角是直角的平行四边形是矩形即可证明四边形ABCD 是矩形. 【详解】证明:∵O 是边AB 的中点, ∴OA OB =,在AOD △和BOC 中,90A B OA OB AOD BOC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,∴AOD BOC ≌△△, ∴ADBC =, ∵90A B ∠=∠=︒, ∴AD BC ∥,∴四边形ABCD 是平行四边形, ∵90A B ∠=∠=︒, ∴四边形ABCD 是矩形.29.(2024·青海·中考真题)综合与实践顺次连接任意一个四边形的中点得到一个新四边形,我们称这个新四边形为原四边形的中点四边形......数学兴趣小组通过作图、测量,猜想:原四边形的对角线对中点四边形的形状有着决定性作用. 以下从对角线的数量关系和位置关系两个方面展开探究.如图1,在四边形ABCD 中,E 、F 、G 、H 分别是各边的中点. 求证:中点四边形EFGH 是平行四边形.证明:∵E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点, ∴EF 、GH 分别是ABC 和ACD 的中位线, ∴12EF AC =,12GH AC =(____①____)∴EF GH =. 同理可得:EH FG =.∴中点四边形EFGH 是平行四边形.结论:任意四边形的中点四边形是平行四边形. (1)请你补全上述过程中的证明依据①________ 【探究二】从作图、测量结果得出猜想Ⅰ:原四边形的对角线相等时,中点四边形是菱形.(2)下面我们结合图2来证明猜想Ⅰ,请你在探究一证明结论的基础上,写出后续..的证明过程. 【探究三】(3)从作图、测量结果得出猜想Ⅱ:原四边形对角线垂直时,中点四边形是②________. (4)下面我们结合图3来证明猜想Ⅱ,请你在探究一证明结论的基础上,写出后续..的证明过程. 【归纳总结】(5)请你根据上述探究过程,补全下面的结论,并在图4中画出对应的图形.。
中考数学专题训练:特殊平行四边形(附参考答案)

中考数学专题训练:特殊平行四边形(附参考答案)1.如图,在矩形ABCD和△BDE中,点A在BE上.若矩形ABCD的面积为20,△BDE的面积为24,则△ADE的面积为( )A.10 B.12C.14 D.162.如图,矩形ABCD的对角线AC,BD交于点O,AB=3,BC=4,过点O作OM⊥AC,交BC于点M,过点M作MN⊥BD,垂足为点N,则OM+MN的值为( )A.245B.165C.125D.653.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,E是AC 的中点,则BE的长为( )A.2 B.52C.√5D.34.关于菱形的性质,以下说法不正确的是( )A.四条边相等B.对角线相等C.对角线互相垂直D.是轴对称图形5.下列选项中能使□ABCD成为菱形的是( )A.AB=CD B.AB=BCC.∠BAD=90°D.AC=BD6.如图,在菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC-CD方向移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是( )A.直角三角形→等边三角形→等腰三角形→直角三角形B.直角三角形→等腰三角形→直角三角形→等边三角形C.直角三角形→等边三角形→直角三角形→等腰三角形D.等腰三角形→等边三角形→直角三角形→等腰三角形7.如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( )A.2 B.52C.3 D.48.如图,在菱形ABCD中,E,F分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( )A.2 B.3C.4 D.59.如图,将矩形ABCD对折,使边AB与DC,BC与AD分别重合,展开后得到四边形EFGH.若AB=2,BC=4,则四边形EFGH的面积为( )A.2 B.4C.5 D.610.一个四边形顺次添加下列条件中的三个条件便得到正方形:a.两组对边分别相等;b.一组对边平行且相等;c.一组邻边相等;d.一个角是直角.顺次添加的条件:①a→c→d ②b→d→c ③a→b→c,则正确的是( )A.仅①B.仅③C.①②D.②③11.如图,在正方形ABCD中,点E,F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则CG的长是( )A.2 B.√5C.3√22D.12512.如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( )A.BE=12AE B.PC=PDC.∠EAF+∠AFD=90°D.PE=EC13.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( )A.1 B.√2C.√3D.214.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则OE的长度为( )A.√6B.√62C.2√2D.2√315.如图,在△ABC中,D,E,F分别是边AB,BC和AC的中点,请添加一个条件________________________,使四边形BEFD为矩形.(填一个即可)16.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.若AC=12,BD=16,则OE的长为______.17.如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点,点FAC,连接EF.若AC=10,则EF=______.在对角线AC上,且AF=1418.如图,E是矩形ABCD边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为_____.19.如图,菱形ABCD的对角线AC,BD相交于点O,OE⊥AD,垂足为点E,AC=8,BD=6,则OE的长为______.20.如图,菱形ABCD的边长为6 cm,∠BAD=60°,将该菱形沿AC方向平移2√3 cm得到四边形A′B′C′D′,A′D′交CD于点E,则点E到AC的距离为_____cm.21.如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE 的中点,AF与DE相交于点G,则GF的长等于______.22.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°得到正方形AB1C1D1,则阴影部分的面积是_________.23.如图,在正方形ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于______.24.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是_______.参考答案1.C 2.C 3.C 4.B 5.B 6.C 7.B 8.B 9.B 10.C 11.D 12.C 13.C 14.B15.AB⊥BC(答案不唯一) 16.10 17.52 18.3 19.12520.221.√19422.2-2√3323.2α 24.8√5。
2024河南中考数学复习 (特殊)平行四边形的判定 强化精练 (含答案)

2024河南中考数学复习(特殊)平行四边形的判定强化精练基础题1.下列条件中,能判定四边形ABCD是平行四边形的是()A.AB∥CD,AD=BCB.∠A=∠B,∠C=∠DC.AB=AD,CB=CDD.AB∥CD,AB=CD2.如图,用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线AC,BD就可以判断,其推理依据是()第2题图A.矩形的对角线相等B.矩形的四个角是直角C.对角线垂直的平行四边形是矩形D.对角线相等的平行四边形是矩形3.(2023河南黑白卷)如图,在等腰Rt△ABC中,∠ACB=90°,AC=4,点D为AB中点,DE⊥BC,DF⊥AC,则四边形DECF的周长为()A.6B.8C.10D.12第3题图4.如图,将两张对边平行的纸条交叉叠放在一起,重合部分构成一个四边形ABCD,转动一张纸条的过程中,下列结论:①四边形ABCD的周长不变;②四边形ABCD的面积有变化;③AD=BC;④AD=AB;其中一定正确的是()第4题图A.②④B.②③C.①②D.①③5.[新考法——增加条件判定菱形](2023齐齐哈尔)如图,在四边形ABCD中,AD=BC,AC⊥BD于点O.请添加一个条件:________,使四边形ABCD成为菱形.第5题图6.如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.若AC=10,则四边形OCED的周长是________.第6题图7.如图,在等腰Rt△OAB中,OA=OB=2,∠AOB=90°,以AB为边向右侧作等腰Rt△ABC,连接OC,则OC的长为________.第7题图8.(2023岳阳)如图,点M在▱ABCD的边AD上,BM=CM,请从以下三个选项中①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使▱ABCD为矩形.(1)你添加的条件是________(填序号);(2)添加条件后,请证明▱ABCD为矩形.第8题图拔高题9.(2022辽宁)如图,CD是△ABC的角平分线,过点D分别作AC,BC的平行线,交BC于点E,交AC于点F.若∠ACB=60°,CD=43,则四边形CEDF的周长是______.第9题图10.如图,菱形ABCD的对角线AC,BD相交于点O,P为AB边上一动点(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,若AC=20,BD=10,则EF的最小值为________.第10题图11.(2023长春)将两个完全相同的含有30°角的直角三角板在同一平面内按如图所示位置摆放,点A,E,B,D依次在同一条直线上,连接AF,CD.(1)求证:四边形AFDC是平行四边形;(2)已知BC=6cm,当四边形AFDC是菱形时,AD的长为________cm.第11题图12.(2023丽水)某数学兴趣小组活动,准备将一张三角形纸片(如图)进行如下操作,并进行猜想和证明.(1)用三角板分别取AB,AC的中点D,E,连接DE,画AF⊥DE于点F;(2)用(1)中所画的三块图形经过旋转或平移拼出一个四边形(无缝隙无重叠),并用三角板画出示意图;(3)请判断(2)中所拼的四边形的形状,并说明理由.第12题图参考答案与解析1.D2.D【解析】推理依据是对角线相等的平行四边形是矩形.3.B【解析】∵△ABC为等腰直角三角形,∴AC=BC=4,∵DE⊥BC,DF⊥AC,∠ACB=90°,∴四边形CEDF为矩形,∴DF∥BC,又∵D为AB中点,∴DF=12BC=2,同理DE=12AC=2,∴四边形CEDF为正方形,∴正方形CEDF的周长为4DF=4×2=8.4.B【解析】由题意可知:AB∥CD,AD∥BC,∴四边形ABCD为平行四边形,DC到AB 的距离不会变化,AD=BC,随着纸条的转动,线段AB的长度发生变化,∴四边形ABCD 的面积有变化.5.AD∥BC(或AB=CD或OB=OD或∠ADB=∠CBD等)【解析】当添加“AD∥BC”时,∵AD=BC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD是菱形;当添加:“AB=CD”时,∵AD=BC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD 是菱形;当添加“OB=OD”时,∵AD=BC,AC⊥BD,∴Rt△ADO≌Rt△CBO(HL),∴AO =CO,DO=BO,∴四边形ABCD是菱形;当添加:“∠ADB=∠CBD”时,∴AD∥BC,∵AD=BC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD是菱形.6.20【解析】∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形,∴OC=DE,OD=CE,∵矩形ABCD的对角线AC,BD相交于点O,∴OC=12AC=5,OD=12BD,BD=AC,∴OC=OD=5,∴OC=OD=CE=DE,∴平行四边形OCED是菱形,∴菱形OCED的周长=4OC=4×5=20.7.22或25【解析】分两种情况:①当以AB为底边作等腰Rt△ABC时,如解图①,∵OA=OB=2,∠AOB=90°,∴∠OAB=∠ABO=45°.∵△ABC是等腰直角三角形,∴∠CAB =∠CBA=45°,∠ACB=90°,∴∠AOB=∠OAC=∠ACB=∠CBO=90°,又∵OA=OB,∴四边形AOBC是正方形,∴OC=AB=OA2+OB2=22;②当以AB为腰作等腰Rt△ABC时,当∠CAB=90°,如解图②,∴∠ABC=45°.∵OA=OB=2,∠AOB=90°,∴∠ABO=45°,AB=22.∴∠CBO=∠ABC+∠ABO=90°,∵△ABC是等腰直角三角形,∴BC=AB2+AC2=4,∴OC=OB2+BC2=22+42=25;当∠ABC=90°,如解图③,同理可得OC=25.综上所述,OC的长为22或25.第7题解图8.(1)解:①;(2)证明:∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,∴∠A+∠D=180°,在△ABM和△DCM中,AB=DC∠1=∠2BM=CM,∴△ABM≌△DCM(SAS),∴∠A=∠D,∴∠A=∠D=90°,∴▱ABCD为矩形.9.16【解析】如解图,连接EF交CD于点O,∵DE∥AC,DF∥BC,∴四边形CEDF是平行四边形,∵CD是△ABC的角平分线,∴∠FCD=∠ECD,∵DE∥AC,∴∠FCD=∠CDE,∴∠ECD=∠CDE,∴CE=DE,∴四边形CEDF是菱形,∴CD⊥EF,∠ECD=12∠ACB=30°,OC=12CD=23,在Rt△COE中,CE=OCcos30°=2332=4,∴四边形CEDF的周长是4CE=4×4=16.第9题解图10.25【解析】如解图,连接OP ,∵四边形ABCD 是菱形,AC =20,BD =10,∴AC ⊥BD ,AO =12AC =10,BO =12BD =5,∠AOB =90°,在Rt △ABO 中,由勾股定理得,AB =AO 2+BO 2=102+52=55,∵PE ⊥OA 于点E ,PF ⊥OB 于点F ,∴∠OEP =∠OFP =∠EOF =90°,∴四边形OEPF 是矩形,∴EF =OP ,当OP 取最小值时,EF 的值最小,∴当OP ⊥AB 时,OP 最小,此时,S △ABO =12OA ·OB =12AB ·OP ,∴OP =10×555=25,∴EF 的最小值为25.第10题解图11.(1)证明:∵△ACB ≌△DFE ,∴AC =DF ,∠CAB =∠FDE ,∴AC ∥DF ,∴四边形AFDC 是平行四边形;(2)解:18.【解法提示】如解图,连接CF 交AD 于点O ,∵∠ACB =90°,∠CAB =30°,BC =6cm ,∴AC =3BC =63(cm),∵四边形AFDC 是菱形,∴CF ⊥AD ,AD =2AO ,∴∠AOC =90°,∴AO =32AC =32×63=9(cm),∴AD =2AO =18(cm).第11题解图12.解:(1)画图如解图①;第12题解图①(2)画图如解图②,四边形MBCN 是所求的四边形;第12题解图②(3)矩形,理由如下:∵∠MDB +∠BDE =180°,∠DEC +∠NEC =180°,∴点M ,D ,E ,N 在一条直线上,如解图③,分别延长BD ,CE 交于点A ,过点A 作AF ⊥MN 于点F ,∵D ,E 分别是AB ,AC 的中点,∴DE 为△ABC 的中位线,∴DE ∥BC ,DE =12BC ,∵MD +EN =DE ,∴MN =MD +DE +EN =BC ,MN ∥BC ,∴四边形MBCN 为平行四边形,由题意可得:△MDB ≌△FDA ,△AFE ≌△CNE ,∴∠N =∠AFE =90°,∴四边形MBCN 为矩形.第12题解图③。
特殊四边形培优及答案

特殊四边形练习题及答案1.如图所示,将一张边长为8的正方形纸片ABCD折叠,使点D落在BC的中点E处,点A落在点F处,折痕为MN,则线段MN的长为()2A.10 B.45 C.89 D.212.如图2,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2.其中结论正确的个数是().(A)1个(B)2个(C)3个(D)4个3.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是()A.2 B.3 C.4 D.54.如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为()A.2 B.3 C. D5.如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=,则正方形的面积为()A.5 B.4 C.3 D.26.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为A1 B.5 D.527.如图,正方形ABCD的边长是4cm,点G在边AB上,以BG为边向外作正方形GBFE,连接AE、AC、CE,则△AEC的面积是 cm2。
8.顺次连接矩形四边中点所形成的四边形是.学校的一块菱形花园两对角线的长分别是6m和8m,则这个花园的面积为.9.如图,将矩形纸片ABCD折叠,使边AB、CD均落在对角线BD上,得折痕BE、BF,则∠EBF= .10.如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为.11.如图,在矩形ABCD 中,AB=4,BC=6,若点P 在AD 边上,连接BP 、PC ,△BPC 是以PB 为腰的等腰三角形,则PB 的长为 .12.如图,菱形ABCD 中,对角线AC=6,BD=8,M 、N 分别是BC 、CD 的中点,P 是线段BD 上的一个动点,则PM+PN 的最小值是 .13.在ABCD 中,ABCDS24=,AE 平分∠BAC ,交BC 于E. 沿AE 将△ABE 折叠,点B的对应点为F ,连结EF 并延长交AD 于G ,EG 将ABCD 分为面积相等的两部分. 则ABE S ∆= .14.如图,矩形ABCD 中,AD=10,AB=8,点P 在边CD 上,且BP=BC ,点M 在线段BP 上,点N 在线段BC 的延长线上,且PM=CN ,连接MN 交BP 于点F ,过点M 作ME ⊥CP 于E ,则EF= .15.如图,已知菱形AMNP 内接于△ABC ,M 、N 、P 分别在AB 、BC 、AC 上,如果AB =21 cm ,CA =15cm ,求菱形AMNP 的周长.(6分)变式1图PNMC B A16.(本题8分)如图,四边形ABCD 是正方形,BE ⊥BF ,BE=BF ,EF 与BC 交于点G.(1)求证:ABE CBF △≌△;(2)若50ABE ∠=°,求EGC ∠的大小.17.如图,菱形ABCD 中,E 、F 分别是边AD ,CD 上的两个动点(不与菱形的顶点重合),且满足CF=DE ,∠A=60°.(1)写出图中一对全等三角形:____________________. (2)求证:△BEF 是等边三角形; (3)若菱形ABCD 的边长为2,设△DEF 的周长为m ,则m 的取值范围为 (直接写出答案); (4)连接AC 分别与边BE 、BF 交于点M 、N,且∠CBF =15º,试说明:222AM CN MN =+ 18.如图所示,点O 是菱形ABCD 对角线的交点,CE ∥BD ,EB ∥AC ,连接OE ,交BC 于F . (1)求证:OE=CB ;(2)如果OC: OB=1:2,ABCD 的面积.ADCE GBF19.已知:如图,在中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:△DOE≌△BOF.(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.20.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AE∥BC,DE∥AB.证明:(1)AE=DC;(2)四边形ADCE为矩形.=90°,BC的垂直平分线EF交BC于点D,交21.如图,已知:在四边形ABFC中,ACBAB于点E,且CF=AE(1)试探究,四边形BECF是什么特殊的四边形;(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.(特别提醒:表示角最好用数字)22.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE ⊥AB于E,OF⊥AD于F.(1)对角线AC的长是,菱形ABCD的面积是;(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.23.如图,在四边形ABCD 中,点H 是BC 的中点,作射线AH ,在线段AH 及其延长线上分别取点E ,F ,使EH=FH ,连接BE ,CF . (1)求证:△BEH ≌△CFH .(2)当BH 与EH 满足什么关系时,四边形BFCE 是矩形? 请说明理由.24.(1)如图,正方形ABCD 中,点E ,F 分别在边BC ,CD 上,∠EAF=45°,延长CD 到点G ,使DG=BE ,连结EF ,AG .求证:EF=FG . (2)如图,等腰直角三角形ABC 中,∠BAC=90°,AB=AC ,点M ,N 在边BC 上,且∠MAN=45°,若BM=1,CN=3,求MN 的长.25.如图,在正方形ABCD 中,E 、F 分别是AB 、BC 上的点,且AE=BF .求证:CE=DF .图1图226.如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.(1)求证:四边形ADCF是菱形;(2)若BC=8,AC=6,求四边形ABCF的周长.27.【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.【探究展示】(1)证明:AM=AD+MC;(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.【拓展延伸】(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.28.如图,矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.29.如图,在矩形ABCD中,AB=4cm,BC=8cm.点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度都是1cm/s.连结PQ,AQ,CP.设点P、Q运动的时间为t(s).(1)当t 为何值时,四边形ABQP 是矩形. (2)当t 为何值时,四边形AQCP 是菱形.(3)分别求出(2)中菱形AQCP 的周长和面积.30.把一个含45°角的直角三角板BEF 和一个正方形ABCD 摆放在一起,使三角板的直角顶点和正方形的顶点B 重合,联结DF ,点M ,N 分别为DF ,EF 的中点,联结MA ,MN . (1)如图1,点E ,F 分别在正方形的边CB ,AB 上,请判断MA ,MN 的数量关系和位置关系,直接 写出结论;(2)如图2,点E ,F 分别在正方形的边CB ,AB 的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.BFNME CDA FCBEMNAD图1 图231.如图,已知正方形ABCD ,AC 、BD 相交于点O ,E 为AC 上一点,AH ⊥EB 交EB 于点H ,AH 交BD 于点F .(1)若点E 在图1的位置,判断OE 与OF 的数量关系,并证明你的结论;(2)若点E 在AC 的延长线上,请在图2中按题目要求补全图形,判断OE 与OF 的数量关系,并证明你的结论.32.提出问题:如图1,将三角板放在正方形ABCD 上,使三角板的直角顶点P 在对角线AC 上,一条直角边经过点B ,另一条直角边交边DC 与点E ,求证:PB=PE分析问题:学生甲:如图1,过点P 作PM ⊥BC ,PN ⊥CD ,垂足分别为M ,N 通过证明两三角形全等,进而证明两条线段相等.学生乙:连接DP ,如图2,很容易证明PD=PB ,然后再通过“等角对等边”证明PE=PD ,就可以证明PB=PE 了.解决问题:请你选择上述一种方法给予证明.问题延伸:如图3,移动三角板,使三角板的直角顶点P 在对角线AC 上,一条直角边经过点B ,另一条直角边交DC 的延长线于点E ,PB=PE 还成立吗?若成立,请证明;若不成立,请说明理由.33.如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF=BE . (1)求证:CE=CF ;(2)在图1中,若G 在AD 上,且∠GCE=45°,则GE=BE+GD 成立吗?为什么? (3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题: ①如图2,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B=90°,AB=BC=12,E 是AB 的中点,且∠DCE=45°,求DE 的长; ②如图3,在△ABC 中,∠BAC=45°,AD ⊥BC ,BD=2,CD=3,则△ABC 的面积为 _________ (直接写出结果,不需要写出计算过程).34.在正方形ABCD 中,点F 是BC 延长线上一点,过点B 作BE ⊥DF 于点E ,交CD 于点G ,连接CE.(1)若正方形ABCD 边长为3,DF=4,求CG 的长; (2)求证:EF+EG=2CE.35.(1)图①是将线段AB 向右平移1个单位长度,图②是将线段AB 折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形﹒GEABCDF(2)若长方形的长为a ,宽为b ,请分别写出三个图形中除去阴影部分后剩余部分的面积﹒(3)如图④,在宽为10m ,长为40m 的长方形菜地上有一条弯曲的小路,小路宽为1m ,求这块菜地的面积﹒36.如图,菱形ABCD 中,点E,M 在A,D 上,且CD=CM ,点F 为AB 上的点,且∠ECF=12∠B(1)若菱形ABCD 的周长为8,且∠D=67.5°,求△MCD 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩形、菱形、正方形知识点测试题
一、选择题
1.能判定四边形ABCD为平行四边形的题设是().
(A)AB∥CD,AD=BC; (B)∠A=∠B,∠C=∠D;
(C)AB=CD,AD=BC; (D)AB=AD,CB=CD
2.正方形具有而菱形不一定具有的性质是()
(A)对角线互相平分; (B)对角线相等;
(C)对角线平分一组对角; (D)对角线互相垂直
3.下列说法不正确的是()
(A)对角线相等且互相平分的四边形是矩形;
(B)对角线互相垂直平分的四边形是菱形;
(C)一组对边平行且不等的四边形是梯形;
(D)一边上的两角相等的梯形是等腰梯形
4.不能判定四边形ABCD为平行四边形的题设是()
(A)AB=CD,AD=BC (B)AB//CD
(C)AB=CD,AD∥BC (D)AB∥CD,AD∥BC
5.下列说法不正确的是()
(A)只有一组对边平行的四边形是梯形;
(B)只有一组对边相等的梯形是等腰梯形;
(C)等腰梯形的对角线相等且互相平分;
(D)在直角梯形中有且只有两个角是直角
(6)
二、填空题
6.如上图:矩形的对角线相交成的角中,有一个角是60°,这个角所对的边长为20cm,则其对角线长为______;该矩形的面积为________.
7.一个菱形的两条对角线长分别为6cm,8cm,这个菱形的边长为_______,•面积S=______.
8.如果一个四边形的四个角的比是3:5:5:7,则这个四边形是_____形.
9.如下图,等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AB=6,AD=5,则△CDE的周长是________.
综合提高题
一、填空题(5道题)
1.在平行四边形ABCD 中,已知对角线AC 和BD 相交于点O ,△ABO 的周长为17,AB =6,那么对角线AC +BD =
2.以正方形ABCD 的边BC 为边做等边△BCE,则∠AED 的度数为 .
3.延长正方形ABCD 的边AB 到E ,使BE =AC ,则∠E= °
4.已知菱形ABCD 的边长为6,∠A=60°,如果点P 是菱形内一点,且PB =PD =2那么AP 的长为 .
5.在平面直角坐标系中,点A 、B 、C 的坐标分别是A(-2,5),
B(-
3,-1),C(1,-1),在第一象限内找一点D ,使四边形 ABCD 是平行四边形,那么点D 的坐标是 .
二、选择题(10道题)
6.如图4在平行四边形ABCD 中,∠B=110°,延长AD 至F ,延长CD 至E ,连结EF ,则∠E+∠F=( )
A .110°
B .30° C.50° D .70°
7.菱形具有而矩形不具有的性质是 ( ) A .对角相等 B .四边相等 C .对角线互相平分 D .四角相等
8.平行四边形ABCD 中,对角线AC 、BD 交于点O ,
点E 是BC 的中点.若OE=3 cm ,则AB 的长为 ( ) A .3 cm B .6 cm C .9 cm D .12 cm
9.已知:如图,在矩形ABCD 中,E 、F 、G 、H 分别为边
AB 、BC 、CD 、DA 的中点.若AB =2,AD =4, 则图中阴影部分的面积为 ( ) A .8 B .6 C .4 D .3
E A D
H G
10.将两块能完全重合的两张等腰直角三角形纸片拼成下列图形:
①平行四边形(不包括菱形、矩形、正方形)②矩形③正方形
④等边三角形⑤等腰直角三角形 ( )
A.①③⑤ B.②③⑤ C.①②③ D.①③④⑤11.如图是一块电脑主板的示意图,每一转角处都是
直角,数据如图所示(单位:mm),则该主板的周长
是 ( )
A.88 mm B.96 mm C.80 mm D.
84 mm
12、如图,把矩形ABCD沿EF对折后使两部分重合,若150
∠=,则AEF
∠=()
A.110° B.115°
C.120° D.130°
13、某商店出售下列四种形状的地砖:①正三角形;②正方形;③
正五边形;④正六边形。
若只选购其中一种地砖镶嵌地面,可供选择的地砖共有().
(A)4种(B)3种(C)2种(D)1种
14、四边形ABCD,仅从下列条件中任取两个加以组合,使得ABCD 是平行四边形,一共有多少种不同的组合?()
AB∥CD BC∥AD AB=CD BC=AD
A.2组
B.3组
C.4组
D.6组
15、下列说法错误的是()
A.一组对边平行且一组对角相等的四边形是平行四边形.
B.每组邻边都相等的四边形是菱形.
C. 对角线互相垂直的平行四边形是正方形.
D.四个角都相等的四边形是矩形.
三、解答题(4道题)
16、如图9,四边形ABCD是菱形,对角线AC=8 cm ,
BD=6 cm, DH⊥AB于H,求:DH的长
F
E
D C B
A
A
B
D
C
E
P
F
(9)
(10)
(11)
(12)
17、已知:如图10,菱形ABCD的周长为16 cm,
∠ABC=60°,对角线AC和BD相交于点O,
求AC和BD的长.
18、如图11,在正方形ABCD中,P为对角线BD上一点,
PE⊥BC,垂足为E,PF⊥CD,垂足为F,
求证:EF=AP
19、在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
⑴试说明:DE=DF
⑵只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外添加辅助线,无需证明
参考答案
一、填空题
1、22
2、150°或15°
3、22.5°
4、4
5、(2 ,5)
6 7 8 9 10 11 12 13
14 15
D B C A B C A
B C D
E F
1
2
3
16、AC=4 cm , BD=4
17、证明:连结PC
∵四边形ABCD为平行四边形
∴AB=AC ,∠ABD=∠DPC ∠BCD=90°
∵BP=BP
∴△ABP≌△CBP
∴AP = CP
∵PE⊥BC,PF⊥DC
∴四边形PECF为矩形
∴EF=PC
∴EF=AP
18、证明:⑴连结AD
∵AB=AC,D为BC的中点
∴AD为∠BAC的平分线
∵DE⊥AB ,DF⊥AC
∴DE=DF
⑵∠BAC=90° DE⊥DF
19、菱形
∵四边形ABCD为平行四边形
∴AD∥BC ,∠2=∠3
∵AB∥EF
∴四边形ABED为平行四边形
∵∠2=∠1
∴∠1=∠3
∴AB=BE
∴四边形ABED为菱形。
