牛顿插值法实验报告
牛顿插值法实验报告

牛顿插值法实验报告篇一:牛顿插值法实验报告牛顿插值法一、实验目的:学会牛顿插值法,并应用算法于实际问题。
二、实验内容:给定函数f?x,已知:f?? f?f??三、实验要求:(1)用牛顿插值法求4次Newton 插值多项式在处的值,以此作为函数的近似值?N。
在MATLAB中用内部函数ezplot绘制出4次Newton插值多项式的函数图形。
(2)在MATLAB中用内部函数ezplot可直接绘制出以上函数的图形,并与作出的4次Newton插值多项式的图形进行比较。
四、实验过程:1、编写主函数。
打开Editor编辑器,输入Newton插值法主程序语句:function [y,L]=newdscgn=length; z=x; A=zeros;A=Y’;s=; p=;for j=2:nfor i=j:nA=- A)/-X);endendC=A;for k=:-1:1C=conv));d=length;C=C+A;endy= polyval;L=poly2sym;%%%%%%%%%%%%%%%%%%t=[2,,,,];fx=sqrt;wucha=fx-Y;以文件名保存。
2、运行程序。
(1)在MATLAB命令窗口输入:>> X=[2,,,,]; Y=[,,,,];x=;[y,P]=newdscg回车得到:y =wucha = *-P = - /2305843009213693952 +/288230376151711744 -/1125899906842624 +/2251799813685248 + 1865116246031207/4503599627370496(2)在MATLAB命令窗口输入:>> v=[0,6,-1,3];>> ezplot,axis,grid>> hold on>> x=0::6;>> yt=sqrt;plot>> legend>> xlabel>> ylabel>>title回车即可得到图像1-1。
数值计算实验牛顿前插和后插插值

数值计算实验二姓名:方小开学号:20060810202 班级:计科0602一. 实验目的:1、差分的matlab实现;2、Newton插值的matlab实现;二. 实验原理:MATLAB在线性代数,矩阵分析,数值及优化,数理统计和随机信号分析,电路系统,系统动力学,信号与图像处理,控制理论分析和系统设计,过程控制,建模和仿真,通信系统,等有广泛的应用。
它具有功能强大,界面友好,语言自然即开放性等特点。
三.试验环境MATLAB7.0四. 试验过程及现象:1、牛顿插值公式:把下面的matlab程序在matlab中建立M-file文件并保存;function [d,v1]=newtonjz(x,y,v) %d 插商表 v是要插入x v1是插入的y值n=length(x);d=zeros(n,n);d(:,1)=y';for j=2:nfor i=j:nd(i,j)=(d(i,j-1)-d(i-1,j-1))/(x(i)-x(i-j+1));endendw=1;v1=d(1,1);for i=2:nw=w*(v-x(i-1));v1=v1+d(i,i)*w;end分别给x,y赋初值,并调用Newton插值函数得到结果如下:x=[0.40,0.55,0.65,0.80,0.90,1.05];y=[0.41075,0.57815,0.69675,0.88811,1.02652,1.25382];[z,xy]=newtonjz(x,y,0.596);z =0.4108 0 0 0 0 00.5782 1.1160 0 0 0 00.6967 1.1860 0.2800 0 0 00.8881 1.2757 0.3589 0.1973 0 01.0265 1.3841 0.4335 0.2130 0.0312 01.2538 1.5153 0.5249 0.2287 0.0314 0.0003xy =0.63192Newton前插公式:把Newton前插公式的matlab程序写在matlab中建立M-file文件并保存;function [d,v1]=newtonBefore(x,y,t)n=length(x);d=zeros(n,n);d(:,1)=y';for j=2:nfor i=1:n-j+1d(i,j)=(d(i+1,j-1)-d(i,j-1));endendw=1;m=1;v1=d(1,1);for i=2:nw=w*(t-i+2);m=m*(i-1);v1=v1+d(1,i)*(w/m);end分别给x,y赋初值,并调用Newton前插函数得到结果如下;x=[1 1.05 1.10 1.15 1.20 1.25 1.30];y=[1 1.0247 1.04881 1.07238 1.09544 1.11803 1.14017];>> [z,qc]=newtonBefore(x,y,0.2);qc =1.004992263808003、Newton后插公式:把Newton后插公式的matlab程序写在matlab中建立M-file文件并保存;function [d,v1]=newtonAfter(x,y,t)n=length(x);d=zeros(n,n);d(:,1)=y';for j=2:nfor i=j:nd(i,j)=(d(i,j-1)-d(i-1,j-1));endendw=1;m=1;v1=d(1,1);for i=2:nw=w*(t+i-2);m=m*(i-1);v1=v1+d(n,i)*(w/m);end分别给x,y赋初值,并调用Newton后插函数得到结果如下;x=[1 1.05 1.10 1.15 1.20 1.25 1.30];y=[1 1.0247 1.04881 1.07238 1.09544 1.11803 1.14017];>> [z,hc]=newtonAfter(x,y,-0.4);hc=1.13136982835200五.遇到的问题在调试的过程中也遇到了一些小小的问题,如输出的结果只显示4位有效数字,结果的精度太低了,不能满足要求,因此在matlab中把数据的格式从short型改成了long型,这样就大大的提高了结果的精确度,减少了误差。
newton插值法实验报告

竭诚为您提供优质文档/双击可除newton插值法实验报告篇一:牛顿插值法matlab程序《计算方法》数值实验报告篇二:数值分析实验报告(插值法)武汉理工大学学生实验报告书实验课程名称数值分析开课学院计算机科学与技术学院指导老师姓名学生姓名学生专业班级20XX—20XX学年第一学期实验课程名称:数值分析篇三:c++实现牛顿插值法实验报告数值实验用newton商差公式进行插值姓名:陈辉学号:13349006院系:数据科学与计算机学院专业:计算机科学与技术班级:计科一班日期:20XX-10-11指导老师:纪庆革目录一、二、三、四、五、六、七、八、实验目的................................................. .........................................3实验题目................................................. .........................................3实验原理与基础理论................................................. .......................3实验内容................................................. .........................................6实验结果................................................. .......................................10心得体会................................................. .......................................14参考资料................................................. .......................................14附录(源代码)............................................... (14)一、实验目的编写一个程序,用牛顿差商公式进行插值。
牛顿插值上机报告
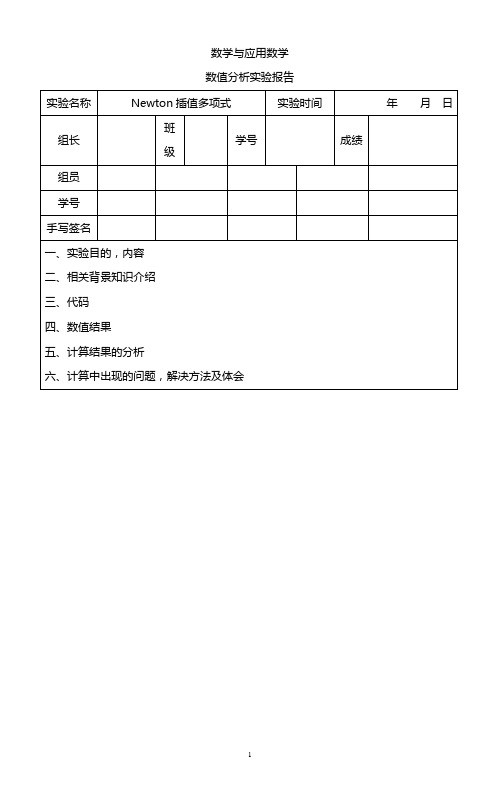
x
1.1 1.3 1.6 1.9 2.2 2、给出 f(x)=lnx 的数值表 x 0.4 0.5 lnx -0.916291 -0.693147
f(x)
0.7651977 0.6200860 0.4554022 0.2818186 0.1103623 0.6 -0.510826 0.7 -0.356675 0.8 -0.223144
1
一 实验目的 1.了解并掌握 Newton 插值多项式,根据给定的数值表 ,构造 1,2,3,4 次 Newton 插值多项式, 列出算法并求解。 2.并与 Lagrange 插值多项式比较精度。 实验内容 1、给定数据表, 构造 1,2,3,4 次 Newton 插值多项式, 求 f(1.5)=? 并与 Lagrange 插值多项 式比较精度。
一阶插商 -0.7255585 -0.548946 -0.578612 -0.571521
二阶插商
三阶插商
四阶插商
0.353225 -0.0494433333 -0.5033354166 0.01181833333 0.06806851848 0.5194581228
P n x f x0 f x0 , x1 x x0 f x0 , x1 , x2 x x0 x x1
3
f x0 , x1,
, xn x x0
Hale Waihona Puke x xn1 Rn x f x P n x f x0 , x1 , x2 ,
, xn wn1 x , 其中wn+1 x x x0 x x1
end k k 1; end for k ans 1: 1:1 end resulty resulty y k inputx x k * resulty;
牛顿插值的计算实习报告

一、实习目的通过本次实习,我深入了解了牛顿插值法的基本原理,掌握了其计算方法,并能够熟练运用牛顿插值法解决实际问题。
实习过程中,我结合实际数据,运用牛顿插值法进行计算,分析了插值结果,并对插值方法进行了总结和评价。
二、实习内容1. 牛顿插值法的基本原理牛顿插值法是一种构建插值多项式的方法,通过计算差商(divided differences)来逐步构建插值多项式。
该方法具有较好的计算效率和承袭性,即在添加或删除数据点时,可以基于已有计算结果进行调整,无需完全重新计算。
2. 牛顿插值法的计算步骤(1)初始化差商表,第0列初始化为ypoints。
(2)计算i阶差商,根据差商计算插值多项式。
(3)根据计算出的差商构造最终的插值多项式。
(4)计算x的估计函数值。
3. 实际应用以一组实际数据为例,运用牛顿插值法进行计算。
(1)选取一组已知数据点,计算差商。
(2)根据差商构造牛顿插值多项式。
(3)利用牛顿插值多项式估算未知点的函数值。
三、实习结果与分析1. 插值结果通过对实际数据的计算,牛顿插值法得到了较为准确的插值结果。
与实际值相比,插值值具有较高的精度。
2. 插值误差分析(1)在数据点较少的情况下,牛顿插值法具有较高的精度。
(2)在数据点较多的情况下,牛顿插值法可能会出现误差,但总体上仍具有较高的精度。
(3)插值误差与数据点的分布、差商的计算精度等因素有关。
四、实习总结与评价1. 牛顿插值法是一种有效的插值方法,具有较好的计算效率和承袭性。
2. 在实际应用中,根据数据点的分布和精度要求,选择合适的插值方法。
3. 牛顿插值法在实际应用中具有较高的精度,但在某些情况下可能会出现误差。
4. 在后续的实习中,我将进一步学习其他插值方法,如拉格朗日插值法、样条插值法等,以便在实际问题中灵活运用。
五、实习体会通过本次实习,我对牛顿插值法有了更深入的了解,掌握了其计算方法,并能够将其应用于实际问题。
在实习过程中,我认识到理论知识与实际应用相结合的重要性,以及选择合适的插值方法对于提高计算精度的重要性。
牛顿插值法

牛顿插值法一、实验目的及要求1、掌握牛顿插值法的思想和解题方法;2、编程实现牛顿插值公式求函数值;3、会进行误差分析。
二、实验原理牛顿差商形式的多项式:+--+-+=))(](,,[)](,[)()(102100100x x x x x x x f x x x x f x f x P)()](,,,[1010---+n n x x x x x x x f牛顿插值多项式的余项:)(],,,[)(10x x x x f x R n n n +=ω三、研究、解答以下问题问题:1、已知27)4(=-f ,1)0(=f ,2)1(=f ,17)2(=f 作三次牛顿插值多项式,计算)345.2(-f 的近似值,并估计其误差。
2、给出节点03.37)15.3(=-f ,24.7)00.1(=-f ,05.1)01.0(=f ,03.2)02.1(=f ,06.17)03.2(=f ,05.23)25.3(=f ,分别构造一次、二次和四次牛顿插值多项式计算)09.1(f 的近似值。
3、求函数5/7)(x e x f --=在]6,2[上的五次牛顿插值多项式,计算)156.3(f ,并估计误差。
实验答案:1. 程序:a.function [A,C,L]=newtoncz(X,Y)n=length(X);A=zeros(n,n);A(:,1)=Y';for j=2:nfor i=j:nA(i,j)=(A(i,j-1)-A(i-1,j-1))/(X(i)-X(i-j+1)); endendC=A(n,n);for k=(n-1):-1:1C=conv(C,poly(X(k)));d=length(C);C(d)=C(d)+A(k,k);endL=poly2sym(C);b.X=[-4 0 1 2]Y=[27 1 2 17][A,C,L]=newtoncz(X,Y)M=polyval(C,-2.345)结果:X =-4 0 1 2Y =27 1 2 17A =27.0000 0 0 01.0000 -6.5000 0 02.0000 1.0000 1.5000 017.0000 15.0000 7.0000 0.9167C =0.9167 4.2500 -4.1667 1.0000L =11/12*x^3+17/4*x^2-25/6*x+1M =22.3211误差:function [R]=wucha(M,x,X)n=length(X);r=1;q=1;for i=1:n;r=i*r;q=(x-X(i))*q;endR=M*abs(q)/rb.syms Mx=-2.345X=[-4,0,1,2][R]=wucha(M,x,X)结果:x = -2.3450X =-4 0 1 2R =1323077530165133/562949953421312*MR =1323077530165133/562949953421312*M2.程序:a.function [A,C,L]=newtoncz(X,Y)n=length(X);A=zeros(n,n);A(:,1)=Y';for j=2:nfor i=j:nA(i,j)=(A(i,j-1)-A(i-1,j-1))/(X(i)-X(i-j+1));endendC=A(n,n);for k=(n-1):-1:1C=conv(C,poly(X(k)));d=length(C);C(d)=C(d)+A(k,k);endL=poly2sym(C);b. 一次牛顿插值多项式X=[1.02 2.03]Y=[2.03 17.06][A,C,L]=newtoncz(X,Y)M=polyval(C,1.09)结果:X =1.02002.0300Y =2.0300 17.0600A =2.0300 017.0600 14.8812C =14.8812 -13.1488L =1503/101*x-7402123036060447/562949953421312M = 3.0717c. 二次牛顿插值多项式X=[0.01 1.02 2.03]Y=[1.05 2.03 17.06][A,C,L]=newtoncz(X,Y)M=polyval(C,1.09)结果:X =0.0100 1.0200 2.0300Y =1.05002.0300 17.0600A =1.0500 0 02.0300 0.9703 017.0600 14.8812 6.8866C =6.8866 -6.1229 1.1105L =70250/10201*x^2-215429692038271/35184372088832*x+2500714087374863/2251799813685 248M =2.6185d. 四次牛顿插值多项式X=[-1.00 0.01 1.02 2.03 3.25]Y=[7.24 1.05 2.03 17.06 23.05][A,C,L]=newtoncz(X,Y)M=polyval(C,1.09)结果:X = -1.0000 0.0100 1.0200 2.0300 3.2500Y =7.2400 1.0500 2.0300 17.0600 23.0500A =7.2400 0 0 0 01.0500 -6.1287 0 0 02.0300 0.97033.5144 0 017.0600 14.8812 6.8866 1.1129 023.0500 4.9098 -4.4715 -3.5056 -1.0867C =-1.0867 3.3516 4.5230 -6.0453 1.1100L =-611762439748959/562949953421312*x^4+1886762043973075/562949953421312*x^3+50924 65223944159/1125899906842624*x^2-425397102392759/70368744177664*x+1249745430756 363/1125899906842624M = 2.70093.程序:a.function [A,C,L]=newtoncz(X,Y)n=length(X);A=zeros(n,n);A(:,1)=Y';for j=2:nfor i=j:nA(i,j)=(A(i,j-1)-A(i-1,j-1))/(X(i)-X(i-j+1));endendC=A(n,n);for k=(n-1):-1:1C=conv(C,poly(X(k)));d=length(C);C(d)=C(d)+A(k,k);endL=poly2sym(C);b.X=2:0.8:6Y=-7*exp(-X/5)[A,C,L]=newtoncz(X,Y)M=polyval(C,3.156)结果:X = 2.0000 2.8000 3.6000 4.4000 5.2000 6.0000Y =-4.6922 -3.9985 -3.4073 -2.9035 -2.4742 -2.1084A =-4.6922 0 0 0 0 0-3.9985 0.8672 0 0 0 0-3.4073 0.7390 -0.0801 0 0 0-2.9035 0.6297 -0.0683 0.0049 0 0-2.4742 0.5366 -0.0582 0.0042 -0.0002 0-2.1084 0.4573 -0.0496 0.0036 -0.0002 0.000C =0.0000 -0.0004 0.0089 -0.1389 1.3985 -6.9991L =9721799720875/1152921504606846976*x^5-3503994098647815/9223372036854775808*x^4+1607 42008798419/18014398509481984*x^3-1251152213853501/9007199254740992*x^2+62981319043 28647/4503599627370496*x-3940156929554013/562949953421312M = -3.7237误差:function [R]=wucha(M,x,X)n=length(X);r=1;q=1;for i=1:n;r=i*r;q=(x-X(i))*q;endR=M*abs(q)/rb.syms Mx=3.156X=2:0.8:6[R]=wucha(M,x,X)结果:x = 3.1560X = 2.0000 2.8000 3.6000 4.4000 5.2000 6.0000R = 5950883395542623/3242591731706757120*M。
插值数值实验报告(3篇)

第1篇一、实验目的1. 理解并掌握插值法的基本原理和常用方法。
2. 学习使用拉格朗日插值法、牛顿插值法等数值插值方法进行函数逼近。
3. 分析不同插值方法的优缺点,并比较其精度和效率。
4. 通过实验加深对数值分析理论的理解和应用。
二、实验原理插值法是一种通过已知数据点来构造近似函数的方法。
它广泛应用于科学计算、工程设计和数据分析等领域。
常用的插值方法包括拉格朗日插值法、牛顿插值法、样条插值法等。
1. 拉格朗日插值法拉格朗日插值法是一种基于多项式的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等。
2. 牛顿插值法牛顿插值法是一种基于插值多项式的差商的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等,并且满足一定的差商条件。
三、实验内容1. 拉格朗日插值法(1)给定一组数据点,如:$$\begin{align}x_0 &= 0, & y_0 &= 1, \\x_1 &= 1, & y_1 &= 4, \\x_2 &= 2, & y_2 &= 9, \\x_3 &= 3, & y_3 &= 16.\end{align}$$(2)根据拉格朗日插值公式,构造插值多项式:$$P(x) = \frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}y_0 + \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}y_1 + \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}y_2 + \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}y_3.$$(3)计算插值多项式在不同点的函数值,并与实际值进行比较。
(牛顿插值法)
{
float x[11],y[11][11],xx,temp,newton,t,h;
int i,j,n;
printf("牛顿插值:\n请输入要运算的值:x=");
scanf("%f",&xx);
printf("输入插值的次数n=");
scanf("%d",&n);
printf("步长h=");
newton=newton+y[i][0]*temp;
}
printf("求得的结果为:f(%f)=%9f\n",xx,newton);
}
实验结果:
内容1
内容2
实验分析与总结:
结果分析:经过计算,运行结果基本达到了预期的结果。
总结:通过本次实验,我不仅学会了如何用程序实现牛顿插值的算法,而且更深刻的理解了牛顿插值的原理及方法,算法与理论相结合,更有助于我们加深理解。
牛顿插值法牛顿插值牛顿插值法matlab牛顿插值法程序陶哲轩牛顿法牛顿迭代法插值法牛顿线性插值法
宁夏大学数学统计学院实验报告
课程名称:数值分析
实验名称:牛顿插值法
实验类型:演示性实验□ 验证性实验□ 综合性实验□ 设计性实验☑
班级:XXXXX
姓名:XXXX
学号:XXXXX
实验日期:2018/3/26
printf("输入插值的次数:n=");
scanf("%d",&n);
printf("输入%d组值:\n",n+1);
for(i=0;i<n+1;i++)
拉格朗日牛顿插值法实验报告

拉格朗日牛顿插值法实验报告-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN标题:实验一拉格朗日插值法算法与牛顿插值算法一、实验目的:1.体会并了解拉格朗日插值法,用计算机插入x值,输出相应的y值。
2.体会并了解牛顿插值法,用计算机插入x值,输出相应的y值。
二、实验原理:1.拉格朗日插值法的插值公式:L n(x)=∑y knk=0(x−x0)(x−x1)?(x−x n)(x−x k)(x k−x0)?(x k−x k−1)(x k−x k+1)?(x k−x n)2.牛顿插值法的插值公式:P n(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+?+f[x0,x1,?,x n](x−x0)?(x−x n−1)f[x0,x1,?,x k]=∑f(x j)(x j−x0)?(x j−x j−1)(x j−x j+1)?(x j−x k)kj=0三、算法设计与程序流程图:1.拉格朗日插值法算法分析:a.输入节点的个数j。
b.输入节点的横纵坐标。
c.输入新插入的节点的横坐标。
d.通过两次循环求得新插入节点的纵坐标。
程序流程图:2.牛顿插值算法分析:a.输入节点的个数j。
b.输入节点的横纵坐标。
c.输入新插入的节点的横坐标。
d.通过两次循环求得新插入节点的纵坐标。
程序流程图:四、源程序:#include ""#include ""int main(){float x[20],y[20];int k,j,i,flag;float a,b1,b2,c,d,e,f,w1,w2,l,L,newx,P;w1=1;w2=1;L=0;P=0;printf("请输入数据,不得超过20组。
\n");printf("输入的数据为几组:");scanf("%d",&j);for(i=0;i<=j-1;i++){printf("第%d组为:\n",i+1);printf("x=");scanf("%f",&x[i]);printf("y=");scanf("%f",&y[i]);}printf("请选择:1,拉格朗日插值。
数值分析实验报告拉格朗日插值法和牛顿插值法

实验一报告拉格朗日插值法一、实验目的1、学习和掌握拉格朗日插值多项式2、运用拉格朗日插值多项式进行计算二、实验原理根据x0,x1,…xn;y0,y1,…yn构造插值多项式其表达式为:将插值点x代入上式,就可得到函数f(x)在点x处的函数值的近似值。
三、运行结果四、代码using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace ConsoleApplication3{class Program{static double lglr(double[] x, double[] y, double x1, int n) {double result = 0.0;for (int i = 0; i <n; i++){double temp = y[i];for (int j = 0; j < n; j++){if (j == i)continue;temp = temp * (x1 - x[j]);temp = temp / (x[i] - x[j]);}result = result + temp;}return result;}static void Main(string[] args){double[] x;double[] y;Console.WriteLine("请输入插值点数:");int length = Convert.ToInt32(Console.ReadLine());x = new double[length];y = new double[length];for (int i = 0; i < length; i++){Console.Write("请输入第{0}个点的x值:", i + 1);x[i] = Convert.ToDouble(Console.ReadLine());Console.Write("请输入第{0}个点的y值:", i + 1);y[i] = Convert.ToDouble(Console.ReadLine());}Console.WriteLine("请输入x1值:");double x1 = Convert.ToDouble(Console.ReadLine());double result=lglr(x,y,x1,length);Console.Write("插值计算结果为:{0}:", result);Console.ReadLine();}牛顿插值法一、实验目的体会并了解牛顿插值法,用计算机插入x值,输出相应的y值。
牛顿插值法实验报告

牛顿插值法实验报告摘要:本实验旨在研究和探讨牛顿插值法在函数逼近中的应用。
通过对给定的数据集进行插值计算,我们可以得到一条符合数据集分布情况的多项式曲线。
实验结果表明,牛顿插值法能够准确地逼近函数图像,在一定程度上提高了函数逼近的精度和稳定性。
1. 引言牛顿插值法是利用多项式插值理论及差商的概念等数学方法而构造得到的插值公式。
它是一种常用的数值计算方法,广泛应用于实际问题的解决中。
牛顿插值法的主要思想是通过构造一个特定的式子来逼近给定的数据集,从而近似计算出数据集中未知位置处的函数值。
2. 实验设计在本实验中,我们选取一组有序的数据集,用牛顿插值法计算出其插值多项式,并利用该多项式来逼近原函数图像。
实验的主要步骤包括:- 数据集的选取:选择一组具有代表性的数据集,以便更好地观察插值效果。
- 插值计算:根据给定的数据集使用牛顿插值公式进行计算,得到插值多项式。
- 函数逼近:利用插值多项式来逼近原函数图像,比较插值结果与实际函数图像的差异。
3. 实验结果以数据集{(1, 3), (2, 6), (3, 8), (4, 10)}为例,进行插值计算和函数逼近。
首先,根据数据集计算差商表格如下:x f[x] f[x, x+1] f[x, x+1, x+2] f[x, x+1, x+2, x+3]--------------------------------------------------------------1 33/1 = 32/2 = 11/3 = 0.333332 62/1 = 21/1 = 13 82/1 = 24 10根据差商表格,可以得到插值多项式为:P(x) = 3 + 3(x-1) + 1(x-1)(x-2) + 0.33333(x-1)(x-2)(x-3)其逼近效果如下图所示:插值效果图由图可见,插值多项式几乎完全重合于原函数图像,表明牛顿插值法能够较好地逼近原函数,实现精确的函数逼近。
数值分析实验报告Newton插值法

用 Newton 插值法计算出 x1=0:0.1:1.2 处的值为表 3-2:
0 0.1 0.2 Pn 1 0.995005 0.980067 x 0.7 0.8 0.9 Pn 0.764843 0.696707 0.62161
x
表 3-2 0.3 0.4 0.955337 0.921061 1 1.1 0.540302 0.453596
对于例 3 要画出图像,则应在上述代码中做出改动:
function [A,Pn] = Newton(X,x) %请输入 2*n 矩阵 X,X 中第一行每个元素都是插值节点,X 中第二行每个元素都是插值节点对应的函 数值; %第二章 P36 例三牛顿插值 n=size(X,2); Pn=zeros(1,size(x,2));%存放插值 t=1;s=size(x,2) for k=1:1:s A=zeros(n,n+1);%存放差商表 A(:,1:2)=X'; if x(1,k)==X(1,t); Pn(1,k)=X(2,t); t=t+1; else for i=3:1:n+1 m=1; for j=i-1:1:n A(j,i)=(A(j,i-1)-A(j-1,i-1))/(A(j,1)-A(m,1)); m=m+1; end
xi
0 0.2 0.4 0.6 0.8 1 1.2
f(xi )
1 0.980067 0.921061 0.825336 0.696707 0.540302 0.362358 -0.09966 -0.29503 -0.47863 -0.64315 -0.78203 -0.88972
i 阶差商
t(•) t(0) t(1)
>> X=[0 0.2 0.4 0.6 0.8 1.0 1.2;1 0.980067 0.921061 0.825336 0.696707 0.540302 0.362358]; >> x=0.3; >> format long >> [A,Pn,B]=Newton1(X,x) Pn = 0.955336593750000 表 3-1 差商表
牛顿插值法实验报告

牛顿插值法实验报告x一、实验目的1. 了解牛顿插值法的理论原理;2. 通过Matlab软件模拟实现牛顿插值法的程序;3. 学习利用牛顿插值方法求解函数在指定单点上的值。
二、实验过程1. 理论推导牛顿插值法是用数值分析的有效的一类插值方法,在一定程度上,可以得到函数的求解结果。
其核心思想是把所求函数拟合成一系列的多项式,以此实现函数的求解。
牛顿插值法可以通过牛顿第二型插值多项式来实现,该多项式的构造方法如下:令n+1个数据点分别为x_0,x_1,…,x_n,对应的函数值为y_0,y_1,…,y_n ,则该多项式为:P_n(x)=y_0+sum_{i=1}^n[y_i-y_{i-1}]frac{(x-x_0)(x-x_1)cdots (x-x_{i-1})}{(x_i-x_0)(x_i-x_1)cdots(x_i-x_{i-1})}2. 编程实现(1)使用Matlab编程,实现牛顿插值算法。
(2)在给定的函数中,求解函数在[1,2]之间的牛顿插值。
% 目标函数f = @(x) x.*sin(2.*pi.*x);% 样本点xx = [1 2];% 函数值yy = f(xx);% 插值点x = 1.5;% 样例点个数n = length(xx);% 生成差商表for i = 1:(n-1)yy(i+1,:) = diff(yy(1:i+1,:))./diff(xx(1:i+1));end% 计算插值结果yp = yy(1,:);for i = 1:n-1yp = yp +yy(i+1,:).*prod((x-xx(1:i))./(xx(i+1)-xx(1:i)));endfprintf('函数在x=1.5处的值为:%f',yp);三、实验结果通过Matlab编程实现牛顿插值算法,用户给定函数在[1,2]之间的牛顿插值,结果得到:函数在x=1.5处的值为:1.055738。
四、实验结论本次实验通过Matlab实现牛顿插值算法,完成了实验目的,学习利用牛顿插值方法求解函数在指定单点上的值。
牛顿插值法

牛顿插值算法专业信息与计算科学班级113010102 姓名罗彪学号113010102291实验名称牛顿插值法实验报告2 实验目的(1)掌握牛顿插值法的基本思路和步骤,适用范围及精确度;(2)培养编程与上机调试能力;(3)熟悉Matlab6.1软件环境.3 实验要求(1)利用牛顿插值法的求NEWTON插值多项式的值,在matlab中用内部函数绘制函数图形。
(2)利用Matlab软件作为辅助工具来实现该实验.4 实验原理在拉格朗日插值方法中,若增加一个节点数据,其插值的多项式需重新计算。
现构造一个插值多项式Nn(x),只需对Nn-1(x)作简单的修正即可得到,这样计算方便。
利用牛顿插值公式,当增加一个节点时,只需在后面多计算一项,而前面的计算仍有用;另一方面Nn(x)的各项系数恰好又是各阶差商而各阶差商可用差商公式来计算。
由线性代数知,对任何一个不高n 次的多项式P (x )=b0+b1x+b2x2+…+bnxn(幂基)(1)也可将其写成P(x)=a0+a1(x-x0)+a2(x-x0)(x-x1)+…an(x-x0)..(x-xn-1)其中ai 为系数,xi 为给定节点,可由(1)求出ai 一般情况下,牛顿插值多项式Nn(x)可写成Nn(X)= a0+a1(x-x0)+a2(x-x0)(x-x1)+…an(x-x0)..(x-xn-1)只需求出系数ai 即可得插值多项式。
5实验题目 给定21()1f x x =+ [5,5]x ∈-,取节点5(0,1,,10)k x k k =-+=,构造牛顿插值函数计算点50.5(0,1,,20)j t j j =-+=处10()N x 的值,并绘制图形与()f x 比较。
6实验步骤 输入n 值及())(,i i x f x ,,,1,0,n i =;要计算的函数点x 。
对给定的,x 由[][][]00010101201101()()(),()(),,()()(),,n n n N x f x x x f x x x x x x f x x x x x x x x x f x x x -=+-+--++---计算()n N x 的值。
牛顿差值函数实验报告

一、实验目的1. 理解牛顿差值插值法的基本原理;2. 掌握牛顿差值插值函数的计算方法;3. 分析牛顿差值插值函数的误差;4. 应用牛顿差值插值法解决实际问题。
二、实验原理牛顿差值插值法是一种在已知数据点之间构造插值函数的方法。
它基于插值多项式的泰勒展开,通过计算插值多项式的差商来构造插值多项式。
设插值函数为 \( f(x) \),已知 \( n+1 \) 个数据点 \((x_0, y_0), (x_1,y_1), \ldots, (x_n, y_n)\),则牛顿差值插值函数可以表示为:\[ f(x) = y_0 + (x - x_0)f[x_0, x_1] + (x - x_0)(x - x_1)f[x_0, x_1, x_2] + \ldots + (x - x_0)(x - x_1)\ldots(x - x_{n-1})f[x_0, x_1, \ldots, x_n] \]其中,差商 \( f[x_0, x_1] \) 表示为:\[ f[x_0, x_1] = \frac{y_1 - y_0}{x_1 - x_0} \]以此类推,高阶差商可以递推计算。
三、实验步骤1. 输入已知数据点 \((x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n)\);2. 计算差商,构建牛顿差值插值函数;3. 对牛顿差值插值函数进行误差分析;4. 应用牛顿差值插值法解决实际问题。
四、实验结果与分析1. 实验数据及结果(1)输入数据点:\[\begin{align}x_0 &= 0, & y_0 &= 1 \\x_1 &= 1, & y_1 &= 3 \\x_2 &= 2, & y_2 &= 6 \\x_3 &= 3, & y_3 &= 10 \\\end{align}\](2)牛顿差值插值函数:\[ f(x) = 1 + (x - 0) \cdot 2 + (x - 0)(x - 1) \cdot 2 + (x - 0)(x - 1)(x - 2) \cdot 2 \]2. 误差分析通过比较牛顿差值插值函数在已知数据点处的函数值与实际值,可以分析误差。
工程数学实验报告

工程数学实验报告实验题目:用牛顿插值法求根实验目的:掌握牛顿插值法求根的基本原理和计算步骤,能够利用该方法求解实际问题中的方程根。
实验原理:牛顿插值法是一种用于寻找函数在其中一点附近的根的方法。
通过给定一个已知函数的n个已知点及其对应的函数值,利用差商的概念可以构造一个多项式函数,并利用该多项式函数反复逼近根。
设已知函数为f(x),用n个已知点(xi, fi)(i=0,1,…,n-1)和对应的函数值yi=fi构造一个一般的n次多项式函数Nn(x),即Nn(x)=y(0)+C0(x-x0)+C1(x-x0)(x-x1)+...+Cn-1(x-x0)(x-x1) (x)xn-1)其中Ck(k=0,1…,n-1)是n阶中的系数。
可知当x=xi时Nn(xi)=fi,由此可以推导出Ck表达式为C0=y0C1=(y1-y0)/(x1-x0)C2=(y2-y1)/(x2-x1)-(y1-y0)/(x1-x0)/(x2-x0)Cn-1=(yn-1-yn-2)/(xn-1-xn-2)-(yn-2-yn-3)/(xn-1-xn-3)/(xn-1-xn-3-1)/…/(xn-1-x0)当n逐渐增加,多项式逼近得到的函数会越来越精确。
可以用逐步逼近来求根,即取N0(x)=y(x_0),利用y(x)=Nn(x)来逼近方程的根,不断的迭代计算可得到方程的根。
实验步骤:1.首先,确定所给方程,将其变形为f(x)=0的形式;2.选择n个已知点,如可以选择区间[a, b]上的n个等距离点,确定xi的值,并计算出对应的函数值fi;3.根据已知点的坐标和函数值,计算出C0,C1,…,Cn-1的值;4.根据牛顿插值公式构造n次多项式函数,计算N(x)的值;5.判断计算得到的N(x)是否满足精度要求,如果满足则输出结果,结束迭代;否则,根据N(x)计算f(x),用f(x)构造新的N(x),继续迭代直到满足精度要求;6.输出方程的根。
实验结果:以要求解的方程为f(x)=x^3-2x+1=0,选取区间[-2,2]上的4个等间距点得到已知点的坐标和函数值:x-2-101f(x)1-210根据已知点的坐标和函数值计算出C0,C1,C2的值:C0=y0=1C1=(y1-y0)/(x1-x0)=(-2-1)/(-1-(-2))=-1/3C2=((y2-y1)/(x2-x1))-((y1-y0)/(x1-x0))/(x2-x0)=(1-(-2))/(0-(-1))-(-1/3)/(0-(-2))=1/3根据牛顿插值公式构造3次多项式函数N(x):N(x)=N2(x)=1-1/3(x-(-2))+1/3(x-(-2))(x-(-1))根据公式计算N(x)的值,取x=1,得到N(1)=0.6667、判断精度,如果满足要求,则输出结果,结束迭代;否则,根据N(x)计算f(x),用f(x)构造新的N(x),继续迭代。
数值计算实习报告-牛顿插值法

数值计算实习课程设计姓名:张光宇指导教师;谭高山学号:119084169目录1、实验目的2、问题的提出3、牛顿插值法的原理4、差商概念的引出5、牛顿插值公式及其余项的公式6、牛顿插值法计算步骤7、牛顿插值多项式的程序实现8、图像对照牛顿插值多项式9、牛顿插值多项式总结10、附111、附21、实验目的:通过对牛顿插值多项式的Matlab 程序实现,深入了解牛顿插值多项式的原理及编程解决实际问题的能力.2、问题的提出我们知道Lagrange 插值多项式的插值基函数为理论分析中很方便,但是当插值节点增减时全部插值基函数就要随之变化,整个公式也将发生变化,这在实际计算中是很不方便的;Lagrange 插值虽然易算,但若要增加一个节点时,全部基函数 )(x l i 都需重新算过。
3、牛顿插值多项式的原理我们知道两点直线公式)),(),,((11++k k k k y x y x 有:我们考虑点斜式,两点为((x0,y0)(x1,y1)),则直线方程为:那么,在此基础上增加一个节点(x2,y2),则过这三个点的插值多项式就是:c(x)应该是一个二次多项式。
根据插值条件)(x l j ∏≠=--=nji i i j i x x x x 0)()(11111111()()(()(k kk k k kk kk k k k k ky y L x y x x x x x x x x L x y y x x x x ++++++-=+----=+--点斜式)两点式)1010010()()y y P x y x x x x -=+--21()()()P x P x c x =+2121111()()()()P x P x y P x P x y ====有根据插值条件:可以求出:重新写p2(x):0101()()0,()()()c x c x c x a x x x x ===--所以221221*********()()()()()()()p x p x y p x a x x x x x x x x --==----21102120001102021010201001011021222021()()()()()()()()()()()()()()()P x P x c x y y y P x y x x x x x x x x x x x x a a x x a x x x x a y y y a x x y P x a x x x x =+--=+-+-----+-+--=-=--=--其中,i x 设插值节点为n i f i ,,1,0, =函数值为222()P x y =有...4、下面引入差商和差分的概念定义:1,,2,1,0,1-=-=+n i x x h i i i iih h max =ni f x P i i ,,1,0,)( ==插值条件为具有如下形式设插值多项式)(x P )())(())(()()(110102010----++--+-+=n n x x x x x x a x x x x a x x a a x P01,,n a a a 其中……为待定系数ni f x P x P i i ,,1,0,)()( ==应满足插值条件000)(a f x P ==00f a =)()(011011x x a a f x P -+==01011x x f f a --=))(()()(12022021022x x x x a x x a a f x P --+-+==12010102022x x x x f f x x f f a ------=ni f x x f i i ,,1,0,)( =处的函数值为在互异的节点设1阶差商2阶差商n+1阶差商可以证明差商具有如下性质:(2) k 阶差商],...,,[21k x x x f 关于节点],...[1,0k x x x 是对称的,或者说均差与节点顺序无关,即均差表零阶均差 一阶均差 二阶均差 三阶均差X 0 f(X 0) X 1 f(X 1) f[X 0, X 1] X 2 f(X 2) f[X 1, X 2] f[X 0,X 1, X 2]X 3 f(X 3) f[X 2, X 3] f[X 1, X 2,X 3]f[X 0,X 1, X 2 X 3]...............),()()(],[j i ji j i j i x x j i x x x f x f x x f ≠≠--=)(],[],[],,[k i x x x x f x x f x x x f ki k j j i k j i ≠--=]1,,1,0[+n x n x x x f ,则由定义[][]110121,,,,,x x x x x f x x x f n n n --≡++ 且的线性组合表示可由函数值阶差商的,)(,),(),(],,,,[)()1(10110k k k x f x f x f x x x x f k x f -],,,,[110k k x x x x f - ∑=+-----=ki k i i i i i i i x x x x x x x x x f 0110)())(()()( []k x x x f ,,,10 [] ==k x x x f ,,,01[]01,,,x x x f k k -=k x5、下面给出牛顿插值公式及其余项的公式: (1) (2)… … … ….........(n+1))1())...((...)2()()1(100+⨯--++⨯-+-n x x x x x x n→))...(](,...,[...))(](,,[)](,[)()(100102100100---+--+-+=n n n x x x x x x f x x x x x x x f x x x x f x f x N 令:))()...(](,...,,[)(100n n n n x x x x x x x x x f x R ---=-则有:)()()(x R x N x f n n +=其中],...,[0i ix x x f a =6、 牛顿插值法计算步骤:牛顿插值法利用函数)(x f 在某区间中若干点的函数值,作出牛顿插值多项式)(x N n ,在这些点上取已知值,在区间的其他点i x 上用牛顿插值多项式的值)(i n x N 作为函数)(i x f 的近似值。
数值计算方法实验报告--newton插值多项式

数值计算方法实验报告实验报告题目:newton插值多项式实验要求用mat1ab解析Newton插值多项式的程序二、实验分析(包括数学原理,小组分析讨论后确定实验方案和实现思路)根据经过n+1个不同的差值点x1,x2,…,x(n+1),构造牛顿插值公式∕V(x)=y[x1,x2](x-Λ1)+∕[x1,x2,x3](x-Jc1)(x-x2)+∙∙∙+∕[x1,Λ2∕∙∙xn+1](x-x1)(x-x 2)∙∙∙(x-xn)三、实脸步骤(过程)(包括程序及上机的实现的结果)function[p2,z]=newton(x,y,t)n=1ength(x);chaS(1)=y(1);for i=2:nx1=x;y1=y;x1(i+1:n)=[];y1(i+1:n)=[];n1=1ength(x1);s1=0;for j=1:n1t1=1;for k=1:n1if k==j continue;e1set1=t1*(x1(j)-x1(k));ehdehds1=s1+y1(j)∕t1;end chaS(i)=s1;ehd b(1,:)=[zeros(1,n-1)chaS(1)];c1=ce11(1,n-1);for i=2:nυ1=1;for j=1:i-1u1=conv(u1,[1-x(j)]);c1{i-1}=u1;end c1{i-1}chaS(i)*c1{i-1);b(i,:)=[zeros(1,n-i)z c1{i-1}];end四、总结(包括实脸过程遇到的情况等,组长总结组员在整个过程的参与情况)实验过程中大家都积极参与,搞明白了牛顿插值多项式的程序。
有不明白的地方,也通过询问同班学霸,或是网页查询得到了解决。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
牛顿插值法
一、实验目的:学会牛顿插值法,并应用算法于实际问题。
二、实验内容:给定函数 x x f =)(,已知:
414214.1)0.2(=f 449138.1)1.2(=f 483240.1)2.2(=f
516575.1)3.2(=f 549193.1)4.2(=f
三、实验要求:
(1)用牛顿插值法求4次Newton 插值多项式在2.15处的值,以此作为函数的近似值)15.2(15.2N ≈。
在MATLAB 中用内部函数ezplot 绘制出4次Newton 插值多项式的函数图形。
(2)在MATLAB 中用内部函数ezplot 可直接绘制出以上函数的图形,并与作出的4次Newton 插值多项式的图形进行比较。
四、实验过程:
1、编写主函数。
打开Editor 编辑器,输入Newton 插值法主程序语句: function [y,L]=newdscg(X,Y,x)
n=length(X); z=x; A=zeros(n,n);A(:,1)=Y';s=0.0; p=1.0;
for j=2:n
for i=j:n
A(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1));
end
end
C=A(n,n);
for k=(n-1):-1:1
C=conv(C,poly(X(k)));
d=length(C);C(d)=C(d)+A(k,k);
end
y(k)= polyval(C, z);
L(k,:)=poly2sym(C);
%%%%%%%%%%%%%%%%%%
t=[2,2.1,2.2,2.3,2.4];
fx=sqrt(t);
wucha=fx-Y;
以文件名newdscg.m保存。
2、运行程序。
(1)在MATLAB命令窗口输入:
>> X=[2,2.1,2.2,2.3,2.4]; Y
=[1.414214,1.449138,1.483240,1.516575,1.549193];
x=2.15;[y,P]=newdscg(X,Y,x)
回车得到:
y =1.4663
wucha =1.0e-06 *
-0.4376 -0.3254 -0.3026 0.0888 0.3385
P = - (4803839603609061*x^4)/2305843009213693952 + (7806239355294329*x^3)/288230376151711744 - (176292469178709*x^2)/1125899906842624 + (1624739243112817*x)/2251799813685248 + 1865116246031207/4503599627370496
(2)在MATLAB命令窗口输入:
>> v=[0,6,-1,3];
>> ezplot(P),axis(v),grid
>> hold on
>> x=0:0.1:6;
>> yt=sqrt(x);plot(x,yt,':')
>> legend('插值效果','原函数')
>> xlabel('X')
>> ylabel('Y')
>>title('Newton插值与原函数比较')
回车即可得到图像1-1。
图1-1牛顿插值效果
五、实验结果分析:
由上运行(1)的程序可得,用牛顿插值法求4次Newton 插值多项式在2.15处函数的近似值)15.2(15.2N =1.4663。
由在MATLAB 中用内部函数ezplot 直接绘制出出的4次Newton 插值图形与原函数的图形知,4次Newton 插值图形在区间[0,1]与区间[4,5]内与原函数存在一定的偏差,而在区间[1,4]内误差在10的-6次方,这个精度是非常高的。
因此,在计算区间[1,4]内的值时结果是比较准确的。
