等腰三角形等腰三角形的性质 公开课一等奖课件
等腰三角形全国优质课一等奖完美PPT课件

直角三角形相关知识回顾
直角三角形的定义
有一个内角为90°的三角形 称为直角三角形。
2024/1/28
直角三角形的性质
直角三角形的两个锐角互 余,斜边是直角三角形的 最长边,且满足勾股定理 。
直角三角形的判定
若一个三角形满足有一个 内角为90°或满足勾股定理 ,则该三角形为直角三角 形。
21
相似三角形相关知识拓展
02
若一个三角形中有一个角为90度 ,且这个三角形的两条直角边相 等,则这个三角形是等腰直角三 角形。
13
其他特殊情况下判定方法
若一个三角形的三条边满足勾股定理, 即其中两条边的平方和等于第三条边的 平方,则这个三角形是直角三角形。若 此时直角边相等,则为等腰直角三角形
。
2024/1/28
若一个三角形的三条边满足 a:b:c=1:1:√2的关系(a、b为直角边, c为斜边),则这个三角形是等腰直角
顶角与底角的关系
顶角的度数是底角度数的两倍,即顶角 = 2 × 底 角。
3
高、中线与角平分线的关系
在等腰三角形中,高、中线和顶角的角平分线互 相重合。
2024/1/28
9
等腰三角形性质总结
对称性
等腰三角形是Hale Waihona Puke 对称图形,对 称轴是底边的垂直平分线。
2024/1/28
边角关系
在等腰三角形中,两底角相等 ,且顶角的度数是底角度数的 两倍。
3
课程背景与意义
三角形是初中数学的重要内容 ,等腰三角形作为特殊三角形 ,具有独特的性质和广泛的应 用。
2024/1/28
学习等腰三角形有助于学生理 解三角形的基本性质,掌握证 明方法,提高几何推理能力。
《等腰三角形的性质》优秀课件

全等识别
若两个三角形三边及三角分别相等,则这两个三角形全等。在等腰三角形中, 若两个等腰三角形的底边和腰长分别相等,则这两个等腰三角形全等。
2024/1/26
21
对后续知识点(如圆、三角函数)的铺垫作用
对圆的知识点铺垫
等腰三角形的性质与圆的性质有密切联系。例如,在等腰三角形中,底边上的中垂线同时也是底边所 在圆的直径;此外,在等腰三角形中引入外接圆和内切圆的概念,可以进一步探讨三角形的性质。
SAS全等判定
若两个三角形两边和夹角分别相等,则这两个三 角形全等。
3
HL全等判定(直角三角形)
在直角三角形中,若斜边和一条直角边分别相等 ,则这两个三角形全等。
2024/1/26
5
与其他特殊三角形关系
与等边三角形的关系
等边三角形是特殊的等腰三角形,三 边都相等。
与相似三角形的关系
若两个等腰三角形的顶角和底角分别 相等,则这两个三角形相似。
8
边角关系
等腰三角形中,两个等腰边所 对的两个底角相等,即等边对 等角。
2024/1/26
等腰三角形的顶角平分线、底 边上的中线、底边上的高相互 重合,即“三线合一”。
等腰三角形中,若有一个角是 60度,则这个三角形是等边三 角形。
9
面积计算公式
等腰三角形的面积可以通过以下公式计算
面积 = (底边长度 × 高) / 2。其中,底边长度是两个等腰边所夹的底边的长度, 高是从顶点到底边的垂直距离。
《等腰三角形的性质》 优秀课件
2024/1/26
1
目录
2024/1/26
• 等腰三角形基本概念 • 等腰三角形性质探究 • 等腰三角形在生活中的应用 • 等腰三角形相关定理证明 • 等腰三角形在几何变换中的地位和作用 • 典型例题解析与课堂互动环节
等腰三角形PPT市公开课一等奖省优质课获奖课件

A
你还记得我们探索过等腰三角形性 质吗?
定理:
B1
2C
等腰三角形两个底角相等(等边对等角).
定理: 等腰三角形顶角平分线,底边上中线,底 A
边上高相互重合.
你能利用已经有公理和定理证实这
些结论吗?
B
C
D
第2页
回顾与思索 A
定理:等腰三角形两个底角相等(等边对等角).
已知:如图,在△ABC中, AB=AC. 求证: ∠B=∠C.
∴BD=CE(全等三角形对应边相等).
第10页
命题证实
例2 求证:等腰三角形两腰上中线相等.
A
已知:如图,在△ABC中,AB=AC,BM,CN
是△ABC两腰上中线.求证:BM=CN. 证实:∵AC=AB (已知),
NM
∴∠ABC=∠ACB(等边对等角).
B
C
∴又C∵MC=MBN= (12等AC式,B性N质= )12.AB(已知),
证实:∵AB=AC(已知),
∴又∴∵∠∠∠A1=B1∠C==212∠(∠等AA式CBBC性(,∠等质2边).=对12 等∠角AC)B. (已知),
在△BDC与△CEB中 ∵∠ACB=∠ ABC(已知),
A
E B ●1
D 2● C
BC=CB(公共边),∠1=∠2(已证),
∴△BDC≌△CEB(ASA).
证实:∵AB=AC(已知),
Q
P
∴∠ABC=∠ACB(等边对等角).
B
C
又∵ BP,CQ是△ABC两腰上高(已知),
∴∠BPC=∠CQB=900(高定义).
在△BPC与△CQB中,
∵∠BPC=∠CQB(已证),
∠PCB=∠QBC(已证),BC=CB(公共边),
《等腰三角形的性质》优秀课件pptx

定义及特点定义有两边相等的三角形叫做等腰三角形,相等的两边叫做腰,另一边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角。
特点等腰三角形是轴对称图形,有一条对称轴,即底边的垂直平分线;两腰相等,两底角相等。
与等边三角形关系区别等边三角形的三边都相等,三个角都是60度;而等腰三角形只有两边相等,两底角相等,顶角可以是任意角度(小于180度)。
联系等边三角形可以看作是特殊的等腰三角形,即当等腰三角形的顶角为60度时,它就变成了等边三角形。
03在建筑设计中,等腰三角形常被用于构建具有对称美的结构,如尖顶房屋、桥梁的支撑结构等。
建筑学在机械设计和制造中,等腰三角形的稳定性被广泛应用,如三脚架、起重机的支撑结构等。
工程学在解决一些实际问题时,等腰三角形可以作为数学模型,帮助我们理解和解决问题,如测量高度、计算角度等。
数学建模实际应用举例01等腰三角形定义有两边相等的三角形称为等腰三角形。
02两边相等定理内容等腰三角形的两个底角相等。
03定理证明方法通过构造中线或高,利用全等三角形或相似三角形的性质进行证明。
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合,简称“三线合一”。
两角相等定理内容定理证明方法推论通过构造角平分线或中线,利用全等三角形或相似三角形的性质进行证明。
在等腰三角形中,若有一个角是60°,则这个三角形是等边三角形。
030201等腰三角形是轴对称图形,对称轴是底边的垂直平分线。
对称性在等腰三角形中,若两条边相等,则对应的两个角也相等。
对称性推论1在等腰三角形中,若一个角是另一个角的两倍,则这个三角形是直角三角形,且直角在顶角处。
对称性推论2在等腰三角形中,若底边两端点到对称轴的距离相等,则这两个点是底边的两个三等分点。
对称性推论3对称性及其推论两条边相等根据等腰三角形的定义,若一个三角形有两条边长度相等,则该三角形为等腰三角形。
两个角相等等腰三角形的两个底角相等,因此若一个三角形有两个角相等,则可根据此性质判定该三角形为等腰三角形。
等腰三角形的性质定理公开课获奖课件省赛课一等奖课件

目前请同学们把手中旳等腰三角形对折,使两腰 AB、AC重叠在一起,折痕为AD,你还能能找出那些线段相等?哪些角相等?
等腰三角形旳性质定理2 等腰三角形旳顶角平分线、底边上旳中线和高线相互重叠,简称等腰三角形三线合一
(1)假如AD是等腰三角形顶角旳平分线,那么AD也是 、 。
G
已知:如图,在D,E在BC上,AB=AC,AD=AE,则BD与CE相等吗?
E
A
B
C
D
H
练习5:
已知:在△ABC中,AB=AC, AD是BC边上旳中线, ∠ABC旳平分线BG交AD于点E,EF⊥AB,垂足为F.求证:EF=ED
A
E
F
G
D
C
B
练习6:
(2)假如AD是等腰三角形底边上旳中线,那么AD也是 、 。
(3)假如AD是等腰三角形底边上旳高线,那么AD也是 、 。
底边上旳高线
底边上旳中线
顶角旳平分线
底边上旳高线
底边上旳中线
顶角旳平分线
例1已知:如图,AD平分∠BAC,∠ADB=∠ADC 求证:AD⊥BC
等腰三角形旳性质
文字论述
几何语言
等腰三角形旳两底角相等(同一种三角形中,等边对等角)
∵AB=AC∴∠B=∠C
等腰三角形顶角旳平分线、底边上旳中线、高线相互重叠(简称等腰三角形三线合一)
∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD
对称轴顶角平分线底边高线底边中线所在直线
轴对称
练习4:已知:在△ABC中,AB=AC,D为CA延长线上一点,DF⊥BC,交AB于点E,求证:∠D=∠AED
E
1、已知:在 △ ABC中AB=AC,OB=OC, AO旳延长线交BC于点D,求证:AD⊥BC.
等腰三角形的性质优质课市公开课一等奖省优质课获奖课件
BD=CE.另两种选法可由证三角形全等而得
第10页
16.如图,在等腰三角形ABC中,AB=AC,点D在BC上,且AD=AE. (1)若∠BAC=90°,∠BAD=30°,求∠EDC度数; (2)若∠BAC=α(α>30°),∠BAD=30°,求∠EDC度数; (3)猜测∠EDC与∠BAD数量关系.(无须证实)
第11页
解:(1)∵∠BAC=90°,AB=AC,∴∠B=∠C=12(180°-∠BAC)=45 °,∴∠DAC=∠BAC-∠BAD=90°-30°=60°,∵AD=AE,∴∠
ADE=∠AED=12(180°-∠DAC)=60°,又∵∠ADC=∠B+∠BAD= 45°+30°=75°,∴∠EDC=∠ADC-∠ADE=75°-60°=15°,∴ ∠EDC 的度数是 15°
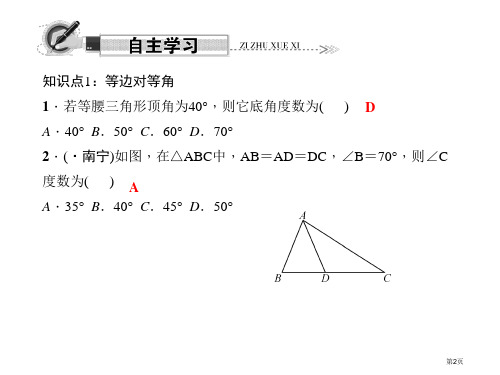
知识点1:等边对等角 1.若等腰三角形顶角为40°,则它底角度数为( ) D A.40° B.50° C.60° D.70° 2.(·南宁)如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C 度数为( ) A A.35° B.40° C.45° D.50°
第2页
3.如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB= AC,若∠1=20°,则∠2度数为( ) B A.25° B.65° C.70° D.75°
利用等腰三角形性质解题时,考虑不全方面而漏解.
第13页
第4页
知识点2:三线合一
6.等腰三角形是轴对称图形,它对称轴是( C)
A.过顶点直线
B.底边垂线
等腰三角形的性质 课件 公开课一等奖课件

C
底边上的中线,底边上的高互相重合 A 在△ABC中,AB =AC, 点 D在BC上
1、∵AD ⊥ BC 1 2 BD DC 。 ∴∠ 1 = ∠ ,____= 2、∵AD是中线, 1 1 2 2 AD BC 1 2 ∴ ⊥ ,∠ =∠ 。 3、∵AD是角平分线, B BD AD DC BC ∴ ⊥ , = 。 D 等腰三角形是轴对称图形.对称轴是底边上的 中线(顶角平分线,底边上的高)所在直线
• 活动2:探索等腰三角形性质
• 上面剪出的等腰三角形是轴对称图形吗? • 把剪出的等腰三角形ABC沿折痕AD对折,找出其中相等的线 段和角,填入下表
B
重合的线段
A C D
重合的角
AB 和 AC
∠B和 ∠C
和
和
和
和
你能发现等腰三角形有什么性质吗?说一
说你的猜想.
性质1:等腰三角形的 两底角相等。(简写成 “等边对等角” )
C
活动3:等腰三角形性质定理的证明
证明性质1:等腰三角形的两个底角相等 (等边对等角) 。
提问:这性质的条件和结论是什么?用数学符号如何 表达条件和结论?
已知:△ABC中,AB=AC 求证:∠B=C 分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形? 证明:在△ABC中,AB=AC,作底边 BC的中线AD, 在 △ BAD 与△ CAD 中 ∵ AB=___ AC CD BD=___ AD AD=___ B ∴ △ BAD ≌△ CAD( SSS ) ∠C ∠B= ___
青 春 风 采
高考总分:
692分(含20分加分) 语文131分 数学145分 英语141分 文综255分
毕业学校:北京二中 报考高校: 北京大学光华管理学 院 北京市文科状元 阳光女孩--何旋
等腰三角形PPT经典教学课件市公开课一等奖省优质课获奖课件

1.什么样三角形叫做等腰三角形?
有两条边相等三角形叫做等腰三角形。 A
2.它各部分名称分别是什么?
顶角
(1)相等两条边叫做腰。 (2)另一边叫底边。 (3)两腰夹角叫顶角。 (4)腰与底边夹角叫底角。
腰
底角
B 底边
腰
C
顶角是直角等腰三角形叫做等
2
A
解: 在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
B
D
C
∴∠B=∠C=(1800-∠A)=400(三角形内角和定理).
又∵AD⊥BC(已知),
∴∠BAD=∠CAD(等腰三角形顶角平分线与底边上高 相互重合).
∴∠BAD=∠CAD=500.
第9页
1.什么是等边三角形? 三边都相等三角形叫做等边三角形。
普通三角形
A
有这种性质
吗?
要注意是指顶角 平分线、底边上 高、底边上中线
这三线重合。
B
C
D
第7页
练习一
一、判断:
1、如图1:
B
∵AB=AC ∴∠1=∠2 (错)
A
12
D 图1 E A
2、如图2:
B
图2
∵AB=BC ∴∠B=∠C (错)
二、填空:如图3。依据等腰三角形性质定C理推
论, 在△ABC中,AB=AC时,
3
4
5
第4页
准备一张长方形纸片,按以下步骤剪出一个三角 形.
A
步骤1 对折
步骤2 画线
步骤3 沿线剪开
B DC
步骤4 展开铺平画出折痕
第5页
观察剪出△ABC,回答以下问题,并说明理由。
等腰三角形的判定 公开课比赛一等奖-ppt课件

角所对的边也相等 (简写成“等角对等边”)。
几何语言:
A
∵∠B =∠C (已知)
∴ AB=AC(等角对等边)
B
C
巩固练习:下列两个图形是否是等腰三角形? 300
400
400
750
例题讲解
例1 如图,在△ABC中,已知∠A=400,∠B=700.
求证:AB=AC
A
证明:∵∠A+∠B+∠C=1800(三角形的
12
证明: 画∠BAC的平分线交BC于点D
在△BAD和△CAD中 ∵∠1=∠2(角平分线的定义
B
DC
∠B=∠C(已知) AD=AD (公共边)
你还有其 他证法吗
∴ △BAD ≌ △CAD (A.A.S.)
?
∴ AB= AC (全等三角形的对应边相等)
等腰三角形的判定
注意:在同
一个三角形
如果一个三角形有两个角相等,那么中这应用两哟!个
1
B
A
D
2
C
例2 如图,AB∥CD,∠1=∠2.求证:AB=AC
A
D
证明:∵AB∥CD(已知)
∴∠B=∠2(两直线平行,
同位角相等)
12
B
C
又∵∠1=∠2(已知)
∴∠B=∠1(等量代换)
∴AB=AC(等角对等边)
练习2 已知如图,∠CAE是△ABC的外角,
∠1=∠2,AD∥BC.求证:AB=AC
学习重难点
重点:让学生掌握一个三角形是等腰三角形的条件 和正确应用.
难点:一个三角形是等腰三角形的条件的正确文字 叙述.
把“等腰三角形的两个底角相等”改写成“如 果------那么-----”形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13.3.1 等腰三角形的性质
2.等腰三角形性质的证明 如图 13-3-1 所示,等腰三角形 ABC 中,AB=AC.若 AD 是 BC 边上的高,则根据___H_._L_.__,可得△ABD ≌△ACD; 若 AD 是 BC 边上的中线,则根据___S_._S_._S_.__,同样可得△ABD ≌△ACD;若 AD 是顶角∠BAC 的平分线,则根据__S_._A_._S_.___, 也 可 以 得 到 △ABD ≌△ACD. 由 此 可 以 发 现 , ∠ B = ____∠__C____;若 AD 是底边上的高,则它也是_底__边__上__的__中__线_, 还是顶__角__的__平__分__线__;若 AD 是底边上的中线,则它是_底__边__上__的_,高 还是顶__角___的__平__分__线_;若 AD 是顶角的平分线,则它是底__边__上__的__高, 还是_底__边__上__的__中__线___.
13.3.1 等腰三角形的性质
活动2 教材导学
1.认识等腰三角形 阅读课本 P78 做一做,跟着操作,完成下列问题: (1) 等 腰 三 角 形 是 ___轴_____ 对 称 图 形 , 它 的 对 称 轴 是 _底__边__上__的__高__(_中__线__)_所__在__的__直__线__或__顶__角__的__平__分__线__所__在__的__直__线____. (2)由操作知∠BAD=∠__C__A_D___;∠B=___∠__C___;BD= __C__D____;∠ADB=∠___A_D__C__. ◆ 知识链接——[新知梳理]知识点一Biblioteka 13.3.1 等腰三角形的性质
[归纳总结]
边的性质 角的性质 轴对称性
重要线段
等腰三角形
等边三角形
两腰相等
三条边都相等
两底角相等
三个角都相等, 都等于60°
是轴对称图形, 有1条对称轴
是轴对称图形, 有3条对称轴
顶角的平分线、底边上的中 线和底边上的高互相重合(三 线合一),它所在的直线是等 腰三角形的对称轴
13.3.1 等腰三角形的性质
证明:过点 D 作 DF⊥BE 于点 F. ∵△ABC 是等边三角形, ∴∠ABC=∠ACB=60°. ∵D 为 AC 的中点,∴∠DBC=30°(三线合一). ∵∠BCD=60°=∠E+∠EDC,CE=CD, ∴∠E=30°, ∴∠DBC=∠E. 又∵∠BFD=∠EFD,DF=DF, ∴△BDF≌△EDF,∴BD=DE.
性质:(1)等边三角形的各个角都相等,并且每一个角都 等于6_0_°.(2)等边三角形的三条边都相等.(3)等边三角形是 轴对称图形,有__3__条对称轴.
13.3.1 等腰三角形的性 质
重难互动探究
探究问题一 等腰三角形的边、角计算 例 1 [课本例 1 变式题] (1)某等腰三角形的两条边长分 别为 3 cm 和 6 cm,则它的周长为( C ) A.9 cm B.12 cm C.15 cm D.12 cm 或 15 cm
13.3.1 等腰三角形的性质
13.3.1 等腰三角形的性质
探究新知
活动1 知识准备 1.下列图形不一定是轴对称图形的是( D ) A.圆 B.长方形 C.线段 D.三角形 2.(1)若等腰三角形的两边长为 2 和 5,则它的第三条边长 为____5____; (2) 若 等 腰 三 角 形 的 两 边 长 为 6 和 5 , 则 它 的 周 长 为 _1_7_或__1_6__.
[解析] 已知等腰三角形的一个内角为 70°,它可能是顶角, 也可能是底角,因此需要分类讨论;若内角为 110°,则它只能 是顶角,而不能是底角.
[归纳总结] (1)已知的边没确定为底边或腰时,要分情况 讨论求解,并注意三角形三边关系这一隐含条件.(2)已知的 角没确定为底角或顶角时,要分情况讨论求解,并注意三角形 内角和为 180°.
[解析] C 在没有明确腰长和底边长的情况下,要分两种情 况进行讨论,当腰长是 3 cm,底边长是 6 cm 时,由于 3+3 不 大于 6,所以不能组成三角形;当腰长是 6 cm,底边长是 3 cm 时,能组成一个三角形,这时其周长=6+6+3=15(cm).
13.3.1 等腰三角形的性质
(2)已知:等腰三角形有一个内角为 70°,则其他两个内角 的度数分别为_5_5_°__,__5_5°或70°,_4_0_°_;若有一个内角为 110°, 则其他两个内角的度数分别为3_5_°__,35°____.
? 想一想
今后我们应该怎样做?
公共场合,我们应该安静有序地排队等候。
课堂上我们应该静静的倾听,静静的思考
讨论问题的时候,我们要认真倾听 别人的意见,有序地发表自己的见解。
到室外或功能室上课前,迅速 有序列队,安静轻步走到上课地点,上 下楼梯靠右行。
让我们读一读
• 铃声响 速静心 进教室 坐端正 • 上下楼 靠右行 走廊里 步要轻 • 不追逐 不吵闹 休息好 讲文明 • 早操时 快静齐 课间时 也安静 • 管理班 守纪律 惜时间 勤学习 • 排路队 守秩序 不推挤 慢慢行 • 寻清静 现文明 好习惯 能养成
①已知等腰三角形底边上的中线,则它平分顶角,垂直底 边;
②已知等腰三角形顶角平分线,则它垂直平分底边; ③已知等腰三角形底边上的高,则它平分底边,平分顶角. (2)等腰三角形“三线合一”的性质常常可以用来证明角 相等、线段相等和线段垂直.在遇到等腰三角形的问题时,尝 试作这条辅助线,常常会有意想不到的效果. (3)证明线段的垂直问题,借助等腰三角形的性质很方便, 这是证明垂直问题的重要思路和方法.
静之内涵
• 文静有礼之仪态 • 安静宜人之环境 • 平静淡然之心境 • 冷静处事之素养
大自然之静
优雅安静的大自然能让人心情舒畅万物生存
人之静
安静祥和的校园能让我们静心思考、学习
? 想一想
在我们的校园以及身处的公共场所,有哪 些与“静”的内涵背道而驰的现象?
• 在教室或者楼道打闹 • 在厕所相互泼水嬉闹 • 有事没事把窗帘拉上又拉下 • 上课不认真听讲、讲话 • ......
安静是一种美德 的改变!
期待你
13.3.1 等腰三角形的性质
探究问题三 等边三角形的性质的运用 例 3 已知:如图 13-3-3,在等边三角形 ABC 的 AC 边上取中点 D,BC 的延长线上取一点 E,使 CE=CD.求证: BD=DE.
图 13-3-3 [解析] 要证明 BD=DE,可将 BD,DE 放到两个三角形 中,证这两个三角形全等即可.
13.3.1 等腰三角形的性质
探究问题二 利用等腰三角形的性质进行证明 例 2 如图 13-3-2 所示,AB=AC,BD=CD,AD
的延长线交 BC 于点 E.求证:AE⊥BC.
图 13-3-2 [解析] 要证 AE⊥BC,可以考虑证明∠AEB=∠AEC= 12∠BEC=90°,但是这样太麻烦.考虑到△ABC 是等腰三 角形,用等腰三角形的性质——等腰三角形的顶角平分线、 底边上的高互相重合去证明较方便.
? 想一想
大家说一说:这些现象有什么危害?
安静是什么
• 安静是修养。
•公共场所是公众活动的地方,任何人都不得以任何 理由对其进行任何形式的独占,而应自觉维护该场 所的秩序,遵守必须的社会公德。
安静是什么
• 安静是文化,是文明。
•文化可以引领人的发展。到了一个非常安静的场所 ,你忍心一个人制造大的声响来引起别人不必要的 注意吗?当大家都停下自己的活动看你时,你会感 觉到脸红,自觉融入到这安静的氛围之中。学校狠 抓安静校园的治理,就是为了建设良好的校园文化 ,提高文明水平。
每一条边上的中线、高和 所对角的平分线都三线合 一,它们所在的直线都是 等边三角形的对称轴
以下是赠送内容
如何让课堂秩序井然
-------“和美雅静”在行动
有读有思
我们可以安静一点吗?(节选)
• 德国摄影记者在东京旅行,拍下一辑东京地铁挤拥的照 片。许多日本人默默承受挤拥,不论西装笔挺,脸孔压在车 厢门的玻璃上,鼻扁嘴凸,面容扭曲,就是一副死忍,绝不 吭声半句。这个照片系列,成为日本国民性格的代表作。 • 日本人乘搭公共交通工具,不论地铁还是飞机,其恬静 是一大景观。手机不会响,为他人着想,固不必说,车厢里 鲜有交谈,即使有,声音也自觉低下来,令西方记者称奇。 • 日本火车与瑞士和欧洲各国的火车类似,就是乘客自觉 恬静,读书看报,或者上网工作。这方面,难怪日本早身在 西方文明国家之列,公共交通,首重一个“公”字,国民无 公德,国家再强,GDP再高,没有人心中真正看得起你。
安静是什么
• 安静是形象。
•文明程度比较高的国家,所有公共场所都是比较安 静的,对来自其他国的游客的喧哗吵闹感到非常惊 诧。如果是黄皮肤、黑头发的游客,就一定认为是 中国人,其潜台词就是:中国游客太闹,文明古国 来的人,文明程度并不高。这就是形象。
安静是什么
• 保持安静是一种习惯。
•习惯是养成的,除了必要的约束,还需要较长的时 间。行为养成习惯,习惯形成品质,品质决定人生。 自觉保持公共场所的安静,就是良好的行为,就能形 成良好的品质,就会对你的人生起到良好影响。
13.3.1 等腰三角形的性质
证明:在△BAD 与△CAD 中, AB=AC, AD=AD, BD=CD, ∴△BAD≌△CAD(S.S.S.), ∴∠BAE=∠CAE. 又∵AB=AC,∴△ABC 是等腰三角形, ∴AE⊥BC.
13.3.1 等腰三角形的性质
[归纳总结] (1)等腰三角形“三线合一”的性质包含多层 含义:
► 知识点二 等腰三角形的性质 性质:(1)等腰三角形的两底角_相_等__.(简写成“等边对
等角”) (2)等腰三角形底边上的高、中线及顶角的平分线互相重
合.(简称“三线合一”) (3)等腰三角形是轴对称图形,底边的垂直平分线是它的
