2017-2018北京市海淀区高三数学一模理科试题及答案
2017-2018学年北京市海淀区高三(上)期中数学试卷(理科)

2017-2018学年北京市海淀区高三(上)期中数学试卷(理科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)若集合A={x|x﹣2<0},B={x|e x>1},则A∩B=()A.R B.(﹣∞,2)C.(0,2) D.(2,+∞)2.(5分)下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是()A.f(x)=ln|x|B.f(x)=2﹣x C.f(x)=x3D.f(x)=﹣x23.(5分)已知向量=(1,0),=(﹣1,1),则()A.∥B.⊥C.()∥D.()⊥4.(5分)已知数列{a n}满足a1+a2+…+a n=2a2(n=1,2,3,…),则()A.a1<0 B.a1>0 C.a1≠a2D.a2=05.(5分)将的图象向左平移个单位,则所得图象的函数解析式为()A.y=sin2x B.y=cos2x C.D.+cosα>1”的()6.(5分)设α∈R,则“α是第一象限角”是“sinαA.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.(5分)设f(x)=e sinx+e﹣sinx(x∈R),则下列说法不正确的是()A.f(x)为R上偶函数 B.π为f(x)的一个周期C.π为f(x)的一个极小值点D.f(x)在区间上单调递减8.(5分)已知非空集合A,B满足以下两个条件.(ⅰ)A∪B={1,2,3,4,5,6},A∩B=?;(ⅱ)A的元素个数不是A中的元素,B的元素个数不是B中的元素,则有序集合对(A,B)的个数为()A.10 B.12 C.14 D.16二、填空题共6小题,每小题5分,共30分.9.(5分)定积分的值等于.10.(5分)设在海拔x(单位:m)处的大气压强y(单位:kPa),y与x的函数关系可近似表示为y=100e ax,已知在海拔1000m处的大气压强为90kPa,则根据函数关系式,在海拔2000m处的大气压强为kPa.11.(5分)能够说明“设x是实数,若x>1,则”是假命题的一个实数x的值为.12.(5分)已知△ABC是边长为2的正三角形,O,D分别为边AB,BC的中点,则①=;②若,则x+y=.13.(5分)已知函数(其中ω>0,)的部分图象如图所示,则ω=,φ=.14.(5分)已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2﹣ax+a,其中a∈R.①f(﹣1)=;②若f(x)的值域是R,则a的取值范围是.三、解答题共6小题,共80分.解答应写出文字说明,验算步骤或证明过程.15.(13分)已知函数.(Ⅰ)求的值;(Ⅱ)求f(x)在区间上的最大值和最小值.16.(13分)已知{a n}是等比数列,满足a2=6,a3=﹣18,数列{b n}满足b1=2,且{2b n+a n}是公差为2的等差数列.(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)求数列{b n}的前n项和.17.(13分)已知函数,其中a>0.(Ⅰ)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)求f(x)在区间[1,e]上的最小值.(其中e是自然对数的底数)18.(13分)如图,在四边形ACBD中,,且△ABC为正三角形.(Ⅰ)求cos∠BAD的值;(Ⅱ)若CD=4,,求AB和AD的长.19.(14分)已知函数(0<x<π),g(x)=(x﹣1)lnx+m(m ∈R)(Ⅰ)求f(x)的单调区间;(Ⅱ)求证:1是g(x)的唯一极小值点;(Ⅲ)若存在a,b∈(0,π),满足f(a)=g(b),求m的取值范围.(只需写出结论)20.(14分)若数列A:a1,a2,…,a n(n≥3)中a i∈N*(1≤i≤n)且对任意的2≤k≤n﹣1a k+1+a k﹣1>2a k恒成立,则称数列A为“U﹣数列”.(Ⅰ)若数列1,x,y,7为“U﹣数列”,写出所有可能的x,y;(Ⅱ)若“U﹣数列”A:a1,a2,…,a n中,a1=1,a n=2017,求n的最大值;(Ⅲ)设n0为给定的偶数,对所有可能的“U﹣数列”A:a1,a2,…,a n0,记M=max{a1,a2,…,a n0},其中max{x1,x2,…,x s}表示x1,x2,…,x s这s个数中最大的数,求M的最小值.。
2017-2018学年海淀区高三理科一学期期末练习

海淀区高三年级第一学期期末练习数学(理科)2018. 1本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题纸上,在试卷上作答无效。
考试结束后,将答题纸交回。
第一部分(选择题,共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)复数12+=ii(A )2-i(B )2+i(C )2--i(D )2-+i (2)在极坐标系Ox 中,方程2sin ρθ=表示的圆为xO1x O1xO1xO1(A )(B )(C )(D )(3)执行如图所示的程序框图,输出的k 值为(A ) 4 (B ) 5 (C ) 6 (D ) 7 (4)设m 是不为零的实数,则“0m >”是“方程221x y m m-=表示双曲线”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件(5)已知直线0x y m -+=与圆O :221x y +=相交于A ,B 两点,且OAB ∆为正三角形,则实数m 的值为(A )32(B )62(C )32或32- (D )62或62- (6)从编号分别为1,2,3,4,5,6的六个大小完全相同的小球中,随机取出三个小球,则恰有两个小球编号相邻的概率为(A )15(B )25(C )35(D )45开始a = 1 , k = 1a = 2a k = k +1结束a > 10 输出 k 否是(7)某三棱锥的三视图如图所示,则下列说法中:① 三棱锥的体积为16② 三棱锥的四个面全是直角三角形③ 三棱锥四个面的面积中最大的值是32所有正确的说法是(A )① (B )①② (C )②③ (D )①③(8)已知点F 为抛物线C :()220ypx p =>的焦点,点K 为点F 关于原点的对称点,点M 在抛物线C 上,则下列说法错误..的是 (A )使得MFK ∆为等腰三角形的点M 有且仅有4个 (B )使得MFK ∆为直角三角形的点M 有且仅有4个(C )使得4MKF π∠=的点M 有且仅有4个 (D )使得6MKF π∠=的点M 有且仅有4个第二部分(非选择题,共110分)二、填空题共6小题,每小题5分,共30分。
2017年北京市海淀区高三理科一模数学试卷

2017年北京市海淀区高三理科一模数学试卷一、选择题(共8小题;共40分)1. 已知集合,,则等于A. B.C. D. 或2. 已知复数,则“为纯虚数”的充分必要条件为A. B. C. , D. ,3. 执行如图所示的程序框图,输出的值为A. B. C. D.4. 设,若,则A. B. C. D.5. 已知,,,则,,的大小关系是A. B. C. D.6. 已知曲线(为参数),,,若曲线上存在点满足,则实数的取值范围为A. B. C. D.7. 甲、乙、丙、丁、戊五人排成一排,甲和乙都排在丙的同一侧,排法种数为A. B. C. D.8. 某折叠餐桌的使用步骤如图所示,有如图检查项目:项目①:折叠状态下(如图1),检查四条桌腿长相等;项目②:打开过程中(如图2),检查;项目③:打开过程中(如图2),检查;项目④:打开后(如图3),检查;项目⑤:打开后(如图3),检查.在检查项目的组合中,可以正确判断“桌子打开之后桌面与地面平行的是”A. ①②③B. ②③④C. ②④⑤D. ③④⑤二、填空题(共6小题;共30分)9. 若等比数列满足,,则公比 ______,前项和 ______.10. 已知,,满足的动点的轨迹方程为______.11. 在中,.① ______;②若,则 ______.12. 已知向量,,其中,,且,则向量和的夹角是______.13. 已知函数.若关于的方程在内有唯一实根,则实数的最小值是______.14. 已知实数,,,满足,则的最大值是______.三、解答题(共6小题;共78分)15. 已知是函数的一个零点.(1)求实数的值;(2)求的单调递增区间.16. 据报道,巴基斯坦由中方投资运营的瓜达尔港目前已通航.这是一个可以停靠万吨油轮的深水港,通过这一港口,中国船只能够更快到达中东和波斯湾地区,这相当于给中国平添了一条大动脉!在打造中巴经济走廊协议(简称协议)中,能源投资约亿美元,公路投资约亿美元,铁路投资约亿美元,高架铁路投资约亿美元,瓜达尔港投资约亿美元,光纤通迅投资约为亿美元.有消息称,瓜达尔港的月货物吞吐量将是目前天津、上海两港口月货物吞吐量之和,表格记录了2015年天津、上海两港口的月吞吐量(单位:百万吨):月月月月月月月月月月月月天津上海(1)根据协议提供信息,用数据说明本次协议投资重点;(2)从表中个月任选一个月,求该月天津、上海两港口月吞量之和超过百万吨的概率;(3)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过百万吨的概率,设为瓜达尔未来个月的月货物吞吐量超过百万吨的个数,写出的数学期望(不需要计算过程).17. 如图,由直三棱柱和四棱锥构成的几何体中,,,,,平面平面.(1)求证:;(2)若为的中点,求证: 平面;(3)在线段上是否存在点,使直线与平面所成的角为?若存在,求的值,若不存在,说明理由.18. 已知函数,其中实数.(1)判断是否为函数的极值点,并说明理由;(2)若在区间上恒成立,求的取值范围.19. 已知椭圆:,与轴不重合的直线经过左焦点,且与椭圆相交于,两点,弦的中点为,直线与椭圆相交于,两点(1)若直线的斜率为,求直线的斜率;(2)是否存在直线,使得成立?若存在,求出直线的方程;若不存在,请说明理由.20. 已知含有个元素的正整数集具有性质:对任意不大于(其中)的正整数,存在数集的一个子集,使得该子集所有元素的和等于.(1)写出,的值;(2)证明:“,,,成等差数列”的充要条件是“”;(3)若,求当取最小值时的最大值.答案第一部分1. A2. D3. B4. B5. C6. C7. D8. B第二部分9. ;10.11. ;12.13.14.第三部分15. (1)由题意可知,即,即,解得.(2)由(1)可得函数的递增区间为,.由,,得,,所以,的单调递增区间为,.16. (1)本次协议的投资重点为能源,因为能源投资为亿,占总投资亿的以上,所占比重大.(2)设事件:从个月中任选一个月,该月超过百万吨.根据提供的数据信息,可以得到天津、上海两港口的月吞吐量之和分别是:,,,,,,,,,,,,其中超过百万吨的月份有个,所以,.(3)的数学期望.17. (1)在直三棱柱中,平面,故,由平面平面,且平面平面,所以平面,又平面,所以.(2)在直三棱柱中,平面,所以,,又,所以,如图建立空间直角坐标系,,,,,,,所以,,设平面的法向量为,由即令,则,,于是,因为为中点,所以,所以,由,可得,所以与平面所成角为,即 平面.(3)由(2)可知平面的法向量为.设,则,.若直线与平面成角为,则,解得,故不存在这样的点.18. (1)由可得函数定义域为.,令,经验证,因为,所以的判别式,由二次函数性质可得,是函数的异号零点,所以是的异号零点,所以是函数的极值点.(2)已知,因为,又因为,所以,所以当时,在区间上,所以函数单调递减,所以有恒成立;当时,在区间上,所以函数单调递增,所以,所以不等式不能恒成立;所以时,有在区间恒成立.19. (1)由已知可知,又直线的斜率为,所以直线的方程为,设,,由解得所以中点,于是直线的斜率为.(2)假设存在直线,使得成立.当直线的斜率不存在时,的中点,所以,,矛盾;故可设直线的方程为,联立椭圆的方程,得,设,,则,,于是,点的坐标为,直线的方程为,联立椭圆的方程,得,设,则,由题知,,即,化简,得,故,所以直线的方程为,.20. (1),.(2)先证必要性:因为,,又,,,成等差数列,故有,所以;再证充分性:因为,,,,为正整数数列,故有,,,,,,所以,又,故,故,,,为等差数列.(3)先证明,假设存在,且为最小的正整数.依题意,则,又因为,故当时,不能等于集合的任何一个子集所有元素的和.故假设不成立,即成立,因此,即,所以.因为,则,若时,则当时,集合中不可能存在若干不同元素的和为,故,即,此时可构造集合.因为当时,可以等于集合中若干个元素的和;故当时,可以等于集合中若干不同元素的和;故当时,可以等于集合中若干不同元素的和;故当时,可以等于集合中若干不同元素的和;故当时,可以等于集合中若干不同元素的和;所以集合满足题设.所以当取最小值时,的最大值为.。
2018海淀区高中数学(理)一模试卷及答案-(17974)
海淀区高三年级第二学期期中练习数学(理科)2018. 4 本试卷共 4 页, 150 分。
考试时长 120 分钟。
考生务必将答案答在答题纸上,在试卷上作答无效。
考试结束后,将答题纸交回。
第一部分(选择题,共40 分)一、选择题共 8 小题,每小题 5 分,共 40 分。
在每小题列出的四个选项中,选出符合题目要求的一项。
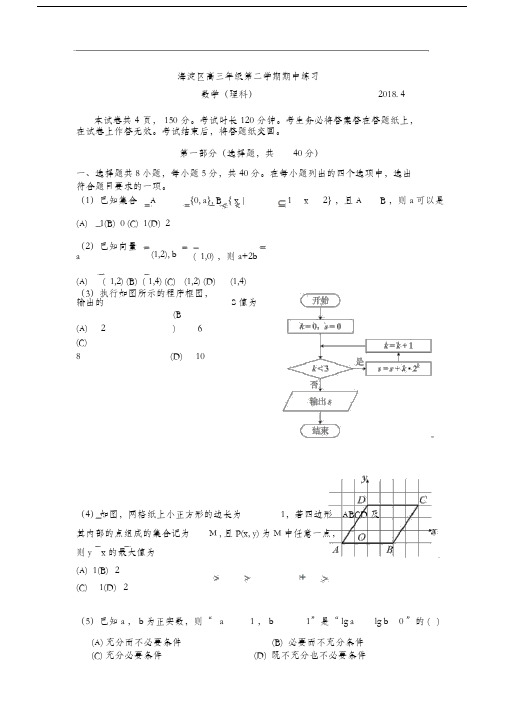
(1)已知集合 A {0, a}, B { x | 1 x 2} ,且 A B ,则 a 可以是(A)1(B) 0 (C) 1(D) 2(2)已知向量a (1,2),b ( 1,0) ,则 a+2b(A) ( 1,2) (B) ( 1,4) (C) (1,2) (D) (1,4)(3)执行如图所示的程序框图,输出的S值为(A) 2 (B) 6(C)8(D) 10(4)如图,网格纸上小正方形的边长为1,若四边形ABCD 及其内部的点组成的集合记为M , 且 P(x, y) 为 M 中任意一点,则 y x 的最大值为(A) 1(B) 2(C)1(D) 2(5)已知 a , b 为正实数,则“ a 1 , b 1”是“ lg a lg b 0 ”的 ( )(A) 充分而不必要条件(B) 必要而不充分条件(C) 充分必要条件(D) 既不充分也不必要条件第1 页共 15 页(6)如图所示,一个棱长为 1 的正方体在一个水平放置的转盘上转动,用垂直于竖直墙面的水平光线照射,该正方体在竖直墙面上的投影的面积记作S ,则 S 的值不可能是(A) 16 4 3(B) (C) (D)5 3 2(7)下列函数f ( x) 中,其图象上任意一点P( x, y) 的坐标都满足条件yx 的函数是(A) f (x) x3 (B) f ( x)x (C) f ( x)e x 1(D)f( x)ln( x 1)( 8)已知点 M 在圆 C1 :( x1)2( y1)2 1 上,点 N 在圆 C2 :( x 1)2( y 1)21上,则下列说法错误的是(A ) OM ON 的取值范围为[ 3 2 2,0](B) | OM ON | 的取值范围为[0,2 2](C) | OM ON |的取值范围为[2 2 2,2 2 2](D)若OM ON ,则实数的取值范围为[ 3 2 2, 3 2 2]第二部分(非选择题,共110分)二、填空题共 6 小题,每小题 5 分,共30 分。
高三试题—2017-2018学年北京市海淀区高三上学期理科期末数学试卷

4√2 M
是棱BC
的中点,点P
在底面ABC
D内,点Q在线段A
1C1上.若P
M
=
1
,则P Q长度的最小值为
.
14. 对任意实数 ,定义集合 . ⎧
∣⎧ x − y + 2 ⩾ 0
⎫
k
Dk
=
⎨(x, y) ∣⎨ x + y − 2
⎩
∣⎩
⩽
0
, x, y
∈
R⎬ ⎭
∣ kx − y ⩽ 0
①若集合Dk表示的平面区域是一个三角形,则实数k的取值范围是
置,使A1E = A1D如图2.
(1) 求证:平面A1ED⊥平面BC . DE (2) 求A1B与平面A1CD所成角的正弦值. (3) 设M 、N分别为A 和 1E BC 的中点,试比较三棱锥M − A1CD和三棱锥N − A1CD(图中未画出)的体积大小,
并说明理由.
18.
已知椭圆C
:2 x
+
2 2y
望 . E(X) (3) 经过了解,前6次测试是打开含有文字与表格的文件,后6次测试是打开含有文字与图片的文件.请你依据表中
数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
17.
如图 ,梯形 中, , , 1
ABC D
AD//BC C D⊥BC BC
=
CD
=
, 1 AD
=
2,E为AD中点.将△ABE沿BE翻折到△A1BE的位
B. 使得△MFK为直角三角形的点M 有且仅有4个
C. 使得△MKF = π 的点M 有且仅有4个
4
D. 使得△MKF = π 的点M 有且仅有4个
北京市海淀区2017-2018学年高三上学期期中考试数学理试题 Word版含解析

海淀区2017-2018学年高三年级第一学期期中练习数 学(理科)本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上 作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合{2}A x x =>,{(1)(3)0}B x x x =--<,则A B =A. {1}x x >B. {23}x x <<C. {13}x x <<D. {2x x >或1}x < 2. 已知向量(1,2),(2,4)=-=-a b ,则a 与b A. 垂直 B. 不垂直也不平行 C. 平行且同向D. 平行且反向3. 函数222x xy =+的最小值为A. 1B. 2C. D. 44. 已知:p 0c ∃>,方程20x x c -+= 有解,则p ⌝为 A. 0c ∀>,方程20x x c -+=无解 B. c ∀≤0,方程20x x c -+=有解 C. 0c ∃>,方程20x x c -+=无解 D. c ∃≤0,方程20x x c -+=有解5. 已知函数,,log x b c y a y x y x ===的图象如图所示,则A. a b c >>B. a c b >>C. c a b >>D. c b a >> 6. 设,a b 是两个向量,则“+>-a b a b ”是“0⋅>a b ”的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件D. 既不充分也不必要条件7. 已知函数42()cos sin f x x x =+,下列结论中错误..的是 A. ()f x 是偶函数 B. 函数()f x 最小值为34C.π2是函数()f x 的一个周期 D. 函数()f x 在π0,2()内是减函数 8.如图所示,A 是函数()2x f x =的图象上的动点,过点A 作直线平行于x 轴,交函数2()2x g x +=的图象于点B ,若函数()2x f x =的图象上存在点C 使得ABC ∆为等边三角形,则称A 为函数()2x f x =上的好位置点. 函数()2x f x =上的好位置点的个数为A. 0B. 1C. 2D. 大于2第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
高三试题—2017-2018学年北京市海淀区高三上学期理科期末数学试卷解析

(3)答案见解析
17. 【答】(1)证明见解析
(2) √6
4
(3)三棱锥M − A1C D 和三棱锥N − A1C D 的体积相等.
18. 【答案】(1)短轴长为2b = , 3√2
离心率为e = c = . √2
a
2
(2) . |T P | < |T M |
19. 【答案】(1)证明见解析 (2)证明见解析 (3)当0 < a < 1 时,f (x)有两个零点. 当a = 1 时,f (x)有一个零点; 当a > 1 时,f (x)有两个零点.
2017~2018学年北京海淀区高三上学期理科期末数学试卷
选择题:本大题共8小题,每小题5分,共40分.
1. 【答案】A 2. 【答案】D 3. 【答案】B 4. 【答案】A 5. 【答案】D 6. 【答案】C 7. 【答案】D 8. 【答案】C
填空题:本大题共6小题,每小题5分,共30分.
9. 【答案】 2 √5
20. 【答案】(1)2,1,1,2,2,3,1 (2)证明见解析 (3)证明见解析
5
10. 【答案】5050 11. 【答案】2 12. 【答案】6 13. 【答案】√− 3− 3
14. 【答案】1.(−1, 1) 2. 1
[−2, ] 5
解答题:本大题共6小题,共80分.
15. 【答案】(1)1 (2)− 2 √3
3
16. 【答案】(1) 7
12
(2)分布列见解析,期望为 3
20172018学年北京市海淀区高三(上)期中数学试卷(理科)

2017-2018学年北京市海淀区高三(上)期中数学试卷(理科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)若集合A={x|x﹣2<0},B={x|e x>1},则A∩B=()A.R B.(﹣∞,2)C.(0,2) D.(2,+∞)2.(5分)下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是()A.f(x)=ln|x|B.f(x)=2﹣x C.f(x)=x3D.f(x)=﹣x23.(5分)已知向量=(1,0),=(﹣1,1),则()A.∥B.⊥C.()∥D.()⊥4.(5分)已知数列{a n}满足a1+a2+…+a n=2a2(n=1,2,3,…),则()A.a1<0 B.a1>0 C.a1≠a2D.a2=05.(5分)将的图象向左平移个单位,则所得图象的函数解析式为()A.y=sin2x B.y=cos2x C.D.6.(5分)设α∈R,则“α是第一象限角”是“sinα+cosα>1”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.(5分)设f(x)=e sinx+e﹣sinx(x∈R),则下列说法不正确的是()A.f(x)为R上偶函数 B.π为f(x)的一个周期C.π为f(x)的一个极小值点D.f(x)在区间上单调递减8.(5分)已知非空集合A,B满足以下两个条件.(ⅰ)A∪B={1,2,3,4,5,6},A∩B=∅;(ⅱ)A的元素个数不是A中的元素,B的元素个数不是B中的元素,则有序集合对(A,B)的个数为()A.10 B.12 C.14 D.16二、填空题共6小题,每小题5分,共30分.9.(5分)定积分的值等于.10.(5分)设在海拔x(单位:m)处的大气压强y(单位:kPa),y与x的函数关系可近似表示为y=100e ax,已知在海拔1000m处的大气压强为90kPa,则根据函数关系式,在海拔2000m处的大气压强为kPa.11.(5分)能够说明“设x是实数,若x>1,则”是假命题的一个实数x的值为.12.(5分)已知△ABC是边长为2的正三角形,O,D分别为边AB,BC的中点,则①=;②若,则x+y=.13.(5分)已知函数(其中ω>0,)的部分图象如图所示,则ω=,φ=.14.(5分)已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2﹣ax+a,其中a∈R.①f(﹣1)=;②若f(x)的值域是R,则a的取值范围是.三、解答题共6小题,共80分.解答应写出文字说明,验算步骤或证明过程.15.(13分)已知函数.(Ⅰ)求的值;(Ⅱ)求f(x)在区间上的最大值和最小值.16.(13分)已知{a n}是等比数列,满足a2=6,a3=﹣18,数列{b n}满足b1=2,且{2b n+a n}是公差为2的等差数列.(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)求数列{b n}的前n项和.17.(13分)已知函数,其中a>0.(Ⅰ)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)求f(x)在区间[1,e]上的最小值.(其中e是自然对数的底数)18.(13分)如图,在四边形ACBD中,,且△ABC为正三角形.(Ⅰ)求cos∠BAD的值;(Ⅱ)若CD=4,,求AB和AD的长.19.(14分)已知函数(0<x<π),g(x)=(x﹣1)lnx+m(m ∈R)(Ⅰ)求f(x)的单调区间;(Ⅱ)求证:1是g(x)的唯一极小值点;(Ⅲ)若存在a,b∈(0,π),满足f(a)=g(b),求m的取值范围.(只需写出结论)20.(14分)若数列A:a1,a2,…,a n(n≥3)中a i∈N*(1≤i≤n)且对任意的2≤k≤n﹣1a k+1+a k﹣1>2a k恒成立,则称数列A为“U﹣数列”.(Ⅰ)若数列1,x,y,7为“U﹣数列”,写出所有可能的x,y;(Ⅱ)若“U﹣数列”A:a1,a2,…,a n中,a1=1,a n=2017,求n的最大值;(Ⅲ)设n0为给定的偶数,对所有可能的“U﹣数列”A:a1,a2,…,a n0,记M=max{a1,a2,…,a n0},其中max{x1,x2,…,x s}表示x1,x2,…,x s这s个数中最大的数,求M的最小值.2017-2018学年北京市海淀区高三(上)期中数学试卷(理科)参考答案与试题解析一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)若集合A={x|x﹣2<0},B={x|e x>1},则A∩B=()A.R B.(﹣∞,2)C.(0,2) D.(2,+∞)【解答】解:集合A={x|x﹣2<0}={x|x<2},B={x|e x>1}={x|x>0},则A∩B={x|0<x<2}=(0,2).故选:C.2.(5分)下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是()A.f(x)=ln|x|B.f(x)=2﹣x C.f(x)=x3D.f(x)=﹣x2【解答】解:函数f(x)=ln|x|是偶函数又在区间(0,+∞)上单调递增,满足题意;函数f(x)=2﹣x是非奇非偶函数,不满足题意;函数f(x)=x3是奇函数,不满足题意;函数f(x)=﹣x2是偶函数,但在区间(0,+∞)上单调递减,不满足题意;故选:A.3.(5分)已知向量=(1,0),=(﹣1,1),则()A.∥B.⊥C.()∥D.()⊥【解答】解:根据题意,依次分析选项:对于A、向量=(1,0),=(﹣1,1),1×1≠0×(﹣1),则∥不成立,A 错误;对于B、向量=(1,0),=(﹣1,1),•=1×(﹣1)+0×1≠0,则⊥不成立,B错误;对于C、向量=(1,0),=(﹣1,1),﹣=(2,﹣1),2×1≠(﹣1)×(﹣1),则(﹣)∥不成立,C错误;对于D、向量=(1,0),=(﹣1,1),﹣=(0,1),(+)•=0×1+1×0=0,则(+)⊥成立,D正确;故选:D.4.(5分)已知数列{a n}满足a1+a2+…+a n=2a2(n=1,2,3,…),则()A.a1<0 B.a1>0 C.a1≠a2D.a2=0【解答】解:数列{a n}满足a1+a2+…+a n=2a2(n=1,2,3,…),n=1时,a1=2a2;n=2时,a1+a2=2a2,可得a2=0.故选:D.5.(5分)将的图象向左平移个单位,则所得图象的函数解析式为()A.y=sin2x B.y=cos2x C.D.【解答】解:的图象向左平移个单位,得y=sin[2(x+)+],即y=sin[2x+]=cos2x,∴所得图象的函数解析式为y=cos2x.故选:B.6.(5分)设α∈R,则“α是第一象限角”是“sinα+cosα>1”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【解答】解:∵α是第一象限角,∴根据正弦和余弦线知,sinα+cosα>1,是充分条件,由“sinα+cosα>1“,也可推出α是第一象限角,是必要条件,故选:C.7.(5分)设f(x)=e sinx+e﹣sinx(x∈R),则下列说法不正确的是()A.f(x)为R上偶函数 B.π为f(x)的一个周期C.π为f(x)的一个极小值点D.f(x)在区间上单调递减【解答】解:∵f(x)=e sinx+e﹣sinx,∴f(﹣x)=e sin﹣x+e﹣sin﹣x=e sinx+e﹣sinx=f(x),即f(x)为R上偶函数,故A正确;f(x+π)=e sin(x+π)+e﹣sin(x+π)e sinx+e﹣sinx=f(x),故π为f(x)的一个周期,故B正确;f′(x)=cosx(e sinx﹣e﹣sinx),当x∈(,π)时,f′(x)<0,当x∈(π,)时,f′(x)>0,故π为f(x)的一个极小值点,故C正确;x∈时,f′(x)>0,故f(x)在区间上单调递增,故D错误;故选:D.8.(5分)已知非空集合A,B满足以下两个条件.(ⅰ)A∪B={1,2,3,4,5,6},A∩B=∅;(ⅱ)A的元素个数不是A中的元素,B的元素个数不是B中的元素,则有序集合对(A,B)的个数为()A.10 B.12 C.14 D.16【解答】解:若集合A中只有1个元素,则集合B中只有5个元素,则1∉A,5∉B,即5∈A,1∈B,此时有C40=1,若集合A中只有2个元素,则集合B中只有4个元素,则2∉A,4∉B,即4∈A,2∈B,此时有C41=4,若集合A中只有3个元素,则集合B中只有3个元素,则3∉A,3∉B,不满足题意,若集合A中只有4个元素,则集合B中只有2个元素,则4∉A,2∉B,即2∈A,4∈B,此时有C43=4,若集合A中只有5个元素,则集合B中只有1个元素,则5∉A,1∉B,即1∈A,5∈B,此时有C44=1,故有序集合对(A,B)的个数是1+4+4+1=10,故选:A二、填空题共6小题,每小题5分,共30分.9.(5分)定积分的值等于0.【解答】解:∵==﹣=0故答案为:010.(5分)设在海拔x(单位:m)处的大气压强y(单位:kPa),y与x的函数关系可近似表示为y=100e ax,已知在海拔1000m处的大气压强为90kPa,则根据函数关系式,在海拔2000m处的大气压强为81kPa.【解答】解:∵在海拔1000m处的大气压强为90kPa,∴90=100e1000a,即a=,当x=2000时,y=100e ax=100=81,故答案为:8111.(5分)能够说明“设x是实数,若x>1,则”是假命题的一个实数x的值为2.【解答】解:令x=2,则,故答案为:212.(5分)已知△ABC是边长为2的正三角形,O,D分别为边AB,BC的中点,则①=3;②若,则x+y=.【解答】解:∵△ABC是边长为2的正三角形,O,D分别为边AB,BC的中点,则①==•2•=3,②若,则==,即x=﹣,y=2,故x+y=故答案为:(1)3(2)13.(5分)已知函数(其中ω>0,)的部分图象如图所示,则ω=2,φ=﹣.【解答】解:由图象可知f(x)的周期为T==π,∴=π,解得ω=2.由图象可知f()=1,即=1,∴+φ=+kπ,k∈Z.∴φ=﹣+kπ,又,∴φ=﹣.故答案为:2,.14.(5分)已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2﹣ax+a,其中a∈R.①f(﹣1)=﹣1;②若f(x)的值域是R,则a的取值范围是(﹣∞,0]∪[4,+∞).【解答】解:①函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2﹣ax+a,其中a∈R,f(﹣1)=﹣f(1)=﹣(1﹣a+a)=﹣1;②若f(x)的值域是R,由f(x)的图象关于原点对称,可得当x>0时,f(x)=x2﹣ax+a,图象与x轴有交点,可得△=a2﹣4a≥0,解得a≥4或a≤0,即a的取值范围是(﹣∞,0]∪[4,+∞).故答案为:①﹣1 ②(﹣∞,0]∪[4,+∞).三、解答题共6小题,共80分.解答应写出文字说明,验算步骤或证明过程.15.(13分)已知函数.(Ⅰ)求的值;(Ⅱ)求f(x)在区间上的最大值和最小值.【解答】解:(Ⅰ)因为,=,=1.(Ⅱ),=,=2sinxcosx+2cos2x﹣1,=sin2x+cos2x,=,因为,所以,所以,故当,即时,f(x)有最大值当,即时,f(x)有最小值﹣1.16.(13分)已知{a n}是等比数列,满足a2=6,a3=﹣18,数列{b n}满足b1=2,且{2b n+a n}是公差为2的等差数列.(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)求数列{b n}的前n项和.【解答】(本题13分)解:(Ⅰ)设数列{a n}的公比为q,则…(2分)解得a1=﹣2,q=﹣3…(3分)所以,…(5分)令c n=2b n+a n,则c1=2b1+a1=2,c n=2+(n﹣1)×2=2n…(7分)…(9分)(Ⅱ)∵,∴数列{b n}的前n项和:S n=(1+2+3+…+n)+[(﹣3)0+[(﹣3)+(﹣3)2+(﹣3)3+…+(﹣3)n﹣1] =+,∴.…(13分)17.(13分)已知函数,其中a>0.(Ⅰ)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)求f(x)在区间[1,e]上的最小值.(其中e是自然对数的底数)【解答】解:(Ⅰ)当a=2时,,,…(1分)此时,f(1)=﹣1,f'(1)=0,…(2分)故曲线y=f(x)在点(1,f(1))处的切线方程为y=﹣1.…(3分)(Ⅱ)的定义域为(0,+∞)…(4分)…(5分)令f'(x)=0得,x=a或x=1…(6分)①当0<a≤1时,对任意的1<x<e,f'(x)>0,f(x)在[1,e]上单调递增…(7分)f(x)最小=f(1)=1﹣a…(8分)②当1<a<e时,x(1,a)a(a,e)f'(x)﹣0+f(x)↘极小↗…(10分)f(x)最小=f(a)=a﹣1﹣(a+1)•lna…(11分)②当a≥e时,对任意的1<x<e,f'(x)<0,f(x)在[1,e]上单调递减…(12分)…(13分)由①、②、③可知,.18.(13分)如图,在四边形ACBD中,,且△ABC为正三角形.(Ⅰ)求cos∠BAD的值;(Ⅱ)若CD=4,,求AB和AD的长.【解答】解:(Ⅰ)因为,∠CAD∈(0,π)所以所以cos∠BAD====(Ⅱ)设AB=AC=BC=x,AD=y,在△ACD和△ABD中由余弦定理得代入得解得或(舍)即,19.(14分)已知函数(0<x<π),g(x)=(x﹣1)lnx+m(m ∈R)(Ⅰ)求f(x)的单调区间;(Ⅱ)求证:1是g(x)的唯一极小值点;(Ⅲ)若存在a,b∈(0,π),满足f(a)=g(b),求m的取值范围.(只需写出结论)【解答】解:(Ⅰ)因为=,令f'(x)=0,得因为0<x<π,所以…(3分)当x变化时,f'(x),f(x)的变化情况如下:xf'(x)+0﹣f(x)↗极大值↘…(5分)故f(x)的单调递增区间为,f(x)的单调递减区间为…(6分)(Ⅱ)证明:∵g(x)=(x﹣1)lnx+m∴(x>0),…(7分)设,则故g'(x)在(0,+∞)是单调递增函数,…(8分)又∵g'(1)=0,故方程g'(x)=0只有唯一实根x=1…(10分)当x变化时,g'(x),g(x)的变化情况如下:x(0,1)1(1,+∞)g'(x)﹣0+g(x)↘极小值↗…(12分)故g(x)在x=1时取得极小值g(1)=m,即1是g(x)的唯一极小值点.(Ⅲ)…(14分)20.(14分)若数列A:a1,a2,…,a n(n≥3)中a i∈N*(1≤i≤n)且对任意的2≤k≤n﹣1a k+1+a k﹣1>2a k恒成立,则称数列A为“U﹣数列”.(Ⅰ)若数列1,x,y,7为“U﹣数列”,写出所有可能的x,y;(Ⅱ)若“U﹣数列”A:a1,a2,…,a n中,a1=1,a n=2017,求n的最大值;(Ⅲ)设n0为给定的偶数,对所有可能的“U﹣数列”A:a1,a2,…,a n0,记M=max{a1,a2,…,a n0},其中max{x1,x2,…,x s}表示x1,x2,…,x s这s个数中最大的数,求M的最小值.【解答】(本题14分)解:(Ⅰ)∵数列A:a1,a2,…,a n(n≥3)中a i∈N*(1≤i≤n)且对任意的2≤k≤n﹣1a k+a k﹣1>2a k恒成立,则称数列A为“U﹣数列”.+1数列1,x,y,7为“U﹣数列”,∴所有可能的x,y为,或.…(3分)(Ⅱ)n的最大值为65,理由如下…(4分)+a k﹣1>2a k⇔a k+1﹣a k>a k﹣a k﹣1一方面,注意到:a k+1对任意的1≤i≤n﹣1,令b i=a i+1﹣a i,则b i∈Z且b k>b k﹣1(2≤k≤n﹣1),故b k ≥b k+1对任意的2≤k≤n﹣1恒成立.(★)﹣1当a1=1,a n=2017时,注意到b1=a2﹣a1≥1﹣1=0,得b i=(b i﹣b i﹣1)+(b i﹣1﹣b i)+…+(b2﹣b1)+b1≥i﹣1(2≤i≤n﹣1)﹣2此时即,解得:﹣62≤n≤65,故n≤65…(7分)另一方面,取b i=i﹣1(1≤i≤64),则对任意的2≤k≤64,b k>b k﹣1,故数列{a n}为“U﹣数列”,此时a65=1+0+1+2+…+63=2017,即n=65符合题意.综上,n的最大值为65.…(9分)(Ⅲ)M的最小值为,证明如下:…(10分)当n0=2m(m≥2,m∈N*)时,﹣b k≥1,b m+k﹣b k=(b m+k﹣b m+k﹣1)+(b m+k﹣1﹣b m+k﹣2)一方面:由(★)式,b k+1+…+(b k﹣b k)≥m.+1此时有:(a1+a2m)﹣(a m+a m+1)=(b m+1+b m+2+…+b2m﹣1)﹣(b1+b2+…+b m﹣1)=(b m+1﹣b1)+(b m+2﹣b2)+…+(b2m﹣1﹣b m﹣1)≥m(m﹣1)•故…(13分)另一方面,当b1=1﹣m,b2=2﹣m,…,b m﹣1=﹣1,b m=0,b m+1=1,…,b2m﹣1=m ﹣1时,a k+1+a k﹣1﹣2a k=(a k+1﹣a k)﹣(a k﹣a k﹣1)=b k﹣b k﹣1=1>0取a m=1,则a m+1=1,a1>a2>a3>…>a m,a m+1<a m+2<…<a2m,且此时.综上,M的最小值为.…(14分)。
北京市海淀区高三数学一模理科试题及答案

海淀区高三年级第二学期期中练习数学(理)参考答案与评分标准、选择题共8小题,每小题 5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
注:第12、14题第一空均为3分,第二空均为2分。
三、解答题共6小题,共80分。
解答题应写出解答步骤。
15.(本题满分13分)(I) f ( )2』3 sin cos 2cos 1(□) f(X ) 、、3sin 2x cos2x因为函数y sinx的单调递增区间为2k -,2k-( k Z),令2k2x - 2k(k Z ),2 62解得kx k _ (k Z ),36故f (x)的单调递增区间为[k , k ]( k Z ).................. 13分3616.(本题满分13分)(I )设事件A :从上表12个月中,随机取出1个月,该月甲地空气 月平均相对湿度 有利于病毒繁殖和传 播•用A 表示事件抽取的月份为第i 月,则{A 1, A 2, A 3, A 4, A 5, A s , A 7, A s , A 9, A 10, A 1, A 2}共 12 个基本事件, A {A 2,A 6,A 8,A 9, AI 0,A 11}共 6 个基本事件,所以,P( A) 6- . ................................................................................. 4分 12 2(n)在第一季度和第二季度的6个月中,甲、乙两地 空气月平均相对湿度都有利于病毒繁殖和传播的月2018.46 6 62 .................................................................................................... •分份只有2月和6月,故X所有可能的取值为0 , 1, 2 .2随机变量的分布列为(川)的最大值为58%,最小值为54%. ................................................................-13分 17.(本题满分14分)(I )方法1 :设AC 的中点为0,连接BO ,PO .由题意PA PB PC 2, P0 1,AO BO CO 1因为 在 PAC 中,PA PC ,O 为AC 的中点 所以PO AC ,因为在 POB 中,PO 1,OB 1,PB 、、2 所以PO OB因为 AC^OB O ,AC,OB 平面 ABC 所以PO 平面ABC因为PO 平面PAC ............................................................................. 4分 所以平面PAC 平面ABC 方法2:设AC 的中点为O ,连接BO , PO . 因为 在 PAC 中,PA PC ,O 为AC 的中点所以 PO AC ,因为 PA PB PC , PO PO PO , AO BO CO所以 POA 也 POB 也 POC所以POAPOBPOC 90所以 PO OB因为 AC |>B O , AC,OB平面ABC所以 PO平面 ABC因为 PO 平面 PAC ................. 4分所以平面PAC 平面ABC 方法3:设AC 的中点为O ,连接PO ,因为在 PAC 中,PA PC , 所以PO ACP(X0)Cl6_ C !15 -,P(X 5C 1C 1 i )CC C 6 -,P(X152)1 15x设AB 的中点Q ,连接PQ , OQ 及OB . 因为 在 OAB 中,OA OB , Q 为AB 的中点 所以OQ AB .因为 在 PAB 中,PA PB , Q 为AB 的中点 所以PQ AB .因为 PQ^OQ Q , PQ,OQ 平面 OPQ 所以 AB 平面OPQ 因为 OP 平面OPQ 所以 OP AB因为 AB p| AC A , AB, AC 平面 ABC 所以PO 平面ABC因为PO 平面PAC ......................................................... 所以平面PAC 平面ABC(n)由PO 平面ABC , OB AC ,如图建立空间直角坐标系,则O(0,0,0) , C(1,0,0) , B(0,1,0), A( 1,0,0) , P(0,0,1) 由OB 平面APC ,故平面 APC 的法向量为O B 由 B C (1,1,0), P C (1,0,1)0得:1 2当[3刁时,设平面PBC 的法向量为n(x,y,z),则(0,1,0)令x 1,得y 1 (1,1,1)由二面角A PC B 是锐二面角, 所以二面角APC B 的余弦值为(出)设B N B P ,令B M AN1,则得(1(1) (1,□是关于 入的单调递增函数,所以 B N [I,:2]BP 4 514分18.(本题满分13分)(I)当a 0时,f(x)In x故 f'(x)In令 f '(x)1 ln x 2x0,得0故f (x)的单调递增区间为(0,e)(n)方法1: f'(x)x a ,ln x x ______彳 a i1 ln x x (x 令 g(x) 1 a .In xXa 1 x a -则 g2 2 0X XX由 g(e) a a 1a 0,g(e ) 1a 1(1 a)1a (F1)。
2017-2018年北京市海淀区高三(上)数学期中试卷和答案(理科)

)
【解答】解:函数 f(x)=ln|x|是偶函数又在区间(0,+∞)上单调递增,满足 题意; 函数 f(x)=2﹣x 是非奇非偶函数,不满足题意; 函数 f(x)=x3 是奇函数,不满足题意; 函数 f(x)=﹣x2 是偶函数,但在区间(0,+∞)上单调递减,不满足题意; 故选:A.
)
5. (5 分)将 式为( )
的图象向左平移
个单位,则所得图象的函数解析
A.y=sin2x B.y=cos2x C.
D. )
6. (5 分)设 α∈R,则“α 是第一象限角”是“sinα+cosα>1”的( A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
7. (5 分)设 f(x)=esinx+e﹣sinx(x∈R) ,则下列说法不正确的是( A.f(x)为 R 上偶函数 B.π 为 f(x)的一个周期 C.π 为 f(x)的一个极小值点 D.f(x)在区间 8. (5 分)已知非空集合 A,B 满足以下两个条件. (ⅰ)A∪B={1,2,3,4,5,6},A∩B=∅; 上单调递减
2. (5 分)下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( A.f(x)=ln|x| B.f(x)=2﹣x C.f(x)=x3 D.f(x)=﹣x2 )
3. (5 分)已知向量 =(1,0) , =(﹣1,1) ,则( A. ∥ B. ⊥ C. ( )∥ D. ( )⊥
4. (5 分)已知数列{an}满足 a1+a2+…+an=2a2(n=1,2,3,…) ,则( A.a1<0 B.a1>0 C.a1≠a2 D.a2=0
第 3 页(共 18 页)
2017-2018 学年北京市海淀区高三 (上) 期中数学试卷 (理 科)
2017北京高考海淀区一模理数试题分析

2017年海淀区一模考试理科数学试卷分析精华学校数学主讲教师白彦彬一、整体评价:从整体上看,本套试卷整体难度和分布与2016北京高考题基本相当,同时命题稳中求变、风格独特、适当创新、联系生活实际、与时俱进、背景深远,是一套比较好的模拟试卷。
(关键词:稳中求新,数学应用,与时俱进)二、具体分析:(1)考点分布:基本知识:集合与逻辑、函数与导数、三角函数与平面向量、数列与不等式、立体几何、解析几何、统计概率、复数与框图。
基本思想、方法:函数与方程、数形结合、分类讨论、化归与转化的思想、特殊与一般的思想、反证法等。
(2)试题难易分布得当,重点突出①基础题(知识点覆盖全面,求解办法易于得到,运算难度较低):1,2,3,4,5,6,9,10,11,12, 15,16, 19(1),20(1);②中档题(有一定的综合度,解题过程蕴含一定的数学思想方法,或背景有新意,或有一定的运算量):7,13,17,18,19(2),20(2)③难题(综合度或抽象度较大,解题过程常通过试验的方法探寻规律,蕴含深刻的数学思想方法):8,14,20(3)(3)具体精彩试题分析:①选择题第5题:非常创新地考查定积分的运算和定积分的几何意义;②选择题第7题:用分类讨论即可,注意不重不漏即可。
③选择题第8题:本题命题手法新颖,充分体现了数学的实用性,紧扣2017年北京市《考试说明》中加入对数学文化的考查,引导考生在实际生活发现数学问题,分析和解决问题的能力。
④填空题第13题:考查考生数形结合思想,难度不大。
⑤填空题第14题:作为填空题的压轴题,非常巧妙地考查了线性规划和平面解析,需要考生转化为向量内积运算,可以搞定。
此题比较好地考查考生的数形结合和化归与转化的数学思想。
⑥解答题第16题:本题考查统计与概率,延续了往年的特点,以真实事例作为背景命题,考查考生数学应用意识和数据处理能力。
体现了数学高考命题的方向:与时俱进,考查数学核心素养。
2017年北京市海淀区高考一模数学试卷(理科)【解析版】

2017年北京市海淀区高考数学一模试卷(理科)一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|x(x+1)≤0},集合B={x|x>0},则A∪B=()A.{x|x≥﹣1}B.{x|x>﹣1}C.{x|x≥0}D.{x|x>0} 2.(5分)已知复数z=i(a+bi)(a,b∈R),则“z为纯虚数”的充分必要条件为()A.a2+b2≠0B.ab=0C.a=0,b≠0D.a≠0,b=0 3.(5分)执行如图所示的程序框图,输出的x值为()A.0B.3C.6D.84.(5分)设a,b∈R,若a>b,则()A.<B.2a>2b C.lga>lgb D.sin a>sin b5.(5分)已知a=xdx,b=x2dx,c=dx,则a,b,c的大小关系是()A.a<b<c B.a<c<b C.b<a<c D.c<a<b6.(5分)已知曲线C:(t为参数),A(﹣1,0),B(1,0),若曲线C上存在点P满足•=0,则实数a的取值范围为()A.B.[﹣1,1]C.D.[﹣2,2] 7.(5分)甲、乙、丙、丁、戊五人排成一排,甲和乙都排在丙的同一侧,排法种数为()A.12B.40C.60D.808.(5分)某折叠餐桌的使用步骤如图所示,有如图检查项目:项目①:折叠状态下(如图1),检查四条桌腿长相等;项目②:打开过程中(如图2),检查OM=ON=O'M'=O'N';项目③:打开过程中(如图2),检查OK=OL=O'K'=O'L';项目④:打开后(如图3),检查∠1=∠2=∠3=∠4=90°;项目⑤:打开后(如图3),检查AB=A'B'=C'D'=CD.在检查项目的组合中,可以正确判断“桌子打开之后桌面与地面平行的是”()A.①②③B.②③④C.②④⑤D.③④⑤二、填空题(每题5分,满分30分,将答案填在答题纸上)9.(5分)若等比数列{a n}满足a2a4=a5,a4=8,则公比q=,前n项和S n=.10.(5分)已知F1(﹣2,0),F2(2,0),满足||PF1|﹣|PF2||=2的动点P的轨迹方程为.11.(5分)在△ABC中,c=a cos B.①A=;②若sin C=,则cos(π+B)=.12.(5分)若非零向量,满足•(+)=0,2||=||,则向量,夹角的大小为.13.(5分)已知函数f(x)=若关于x的方程f(x+a)=0在(0,+∞)内有唯一实根,则实数a的最小值是.14.(5分)已知实数u,v,x,y满足u2+v2=1,,则z=ux+vy的最大值是.三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)15.(13分)已知是函数f(x)=2cos2x+a sin2x+1的一个零点.(Ⅰ)求实数a的值;(Ⅱ)求f(x)的单调递增区间.16.(13分)据报道,巴基斯坦由中方投资运营的瓜达尔港目前已通航.这是一个可以停靠8~10万吨油轮的深水港,通过这一港口,中国船只能够更快到达中东和波斯湾地区,这相当于给中国平添了一条大动脉!在打造中巴经济走廊协议(简称协议)中,能源投资约340亿美元,公路投资约59亿美元,铁路投资约38亿美元,高架铁路投资约16亿美元,瓜达尔港投资约6.6亿美元,光纤通讯投资约为0.4亿美元.有消息称,瓜达尔港的月货物吞吐量将是目前天津、上海两港口月货物吞吐量之和.表格记录了2015年天津、上海两港口的月吞吐量(单位:百万吨):(Ⅰ)根据协议提供信息,用数据说明本次协议投资重点;(Ⅱ)从表中12个月任选一个月,求该月天津、上海两港口月吞吐量之和超过55百万吨的概率;(Ⅲ)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过55百万吨的概率,设X为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出X的数学期望(不需要计算过程).17.(13分)如图,由直三棱柱ABC﹣A1B1C1和四棱锥D﹣BB1C1C构成的几何体中,∠BAC=90°,AB=1,BC=BB1=2,C1D=CD=,平面CC1D⊥平面ACC1A1.(Ⅰ)求证:AC⊥DC1;(Ⅱ)若M为DC1中点,求证:AM∥平面DBB1;(Ⅲ)在线段BC上(含端点)是否存在点P,使直线DP与平面DBB1所成的角为?若存在,求的值,若不存在,说明理由.18.(13分)已知函数f(x)=x2﹣2ax+4(a﹣1)ln(x+1),其中实数a<3.(Ⅰ)判断x=1是否为函数f(x)的极值点,并说明理由;(Ⅱ)若f(x)≤0在区间[0,1]上恒成立,求a的取值范围.19.(14分)已知椭圆G:+y2=1,与x轴不重合的直线l经过左焦点F1,且与椭圆G相交于A,B两点,弦AB的中点为M,直线OM与椭圆G相交于C,D两点.(1)若直线l的斜率为1,求直线OM的斜率;(2)是否存在直线l,使得|AM|2=|CM|•|DM|成立?若存在,求出直线l的方程;若不存在,请说明理由.20.(14分)已知含有n个元素的正整数集A={a1,a2,…,a n}(a1<a2<…<a n,n≥3)具有性质P:对任意不大于S(A)(其中S(A)=a1+a2+…+a n)的正整数k,存在数集A的一个子集,使得该子集所有元素的和等于k.(Ⅰ)写出a1,a2的值;(Ⅱ)证明:“a1,a2,…,a n成等差数列”的充要条件是“S(A)=”;(Ⅲ)若S(A)=2017,求当n取最小值时a n的最大值.2017年北京市海淀区高考数学一模试卷(理科)参考答案与试题解析一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|x(x+1)≤0},集合B={x|x>0},则A∪B=()A.{x|x≥﹣1}B.{x|x>﹣1}C.{x|x≥0}D.{x|x>0}【解答】解:∵集合A={x|x(x+1)≤0}={x|﹣1≤x≤0},集合B={x|x>0},∴A∪B={x|x≥﹣1}.故选:A.2.(5分)已知复数z=i(a+bi)(a,b∈R),则“z为纯虚数”的充分必要条件为()A.a2+b2≠0B.ab=0C.a=0,b≠0D.a≠0,b=0【解答】解:复数z=i(a+bi)=ai﹣b(a,b∈R),则“z为纯虚数”的充分必要条件为﹣b=0,a≠0.故选:D.3.(5分)执行如图所示的程序框图,输出的x值为()A.0B.3C.6D.8【解答】解:x=0,y=9,≠,x=1,y=8,≠,x=2,y=6,=4≠,x=3,y=3,3=,输出x=3,故选:B.4.(5分)设a,b∈R,若a>b,则()A.<B.2a>2b C.lga>lgb D.sin a>sin b 【解答】解:a,b∈R,a>b,当a>0,b<0时,A不成立,根据指数函数的单调性可知,B正确,根据对数函数的定义,可知真数必需大于零,故C不成立,由于正弦函数具有周期性和再某个区间上为单调函数,故不能比较,故D不成立,故选:B.5.(5分)已知a=xdx,b=x2dx,c=dx,则a,b,c的大小关系是()A.a<b<c B.a<c<b C.b<a<c D.c<a<b【解答】解:a=xdx=|=,b=x2dx=|=,c=dx=|=,则b<a<c,故选:C.6.(5分)已知曲线C:(t为参数),A(﹣1,0),B(1,0),若曲线C上存在点P满足•=0,则实数a的取值范围为()A.B.[﹣1,1]C.D.[﹣2,2]【解答】解:∵A(﹣1,0),B(1,0),若曲线C上存在点P满足•=0,∴P的轨迹方程是x2+y2=1.曲线C:(t为参数),普通方程为x﹣y+a=0,由题意,圆心到直线的距离d=≤1,∴,故选:C.7.(5分)甲、乙、丙、丁、戊五人排成一排,甲和乙都排在丙的同一侧,排法种数为()A.12B.40C.60D.80【解答】解:根据题意,分2种情况讨论:①、甲和乙都排在丙的左侧,将甲乙安排在丙的左侧,考虑甲乙之间的顺序,有2种情况,排好后有4个空位,在4个空位中选一个安排丁,有4种情况,排好后有5个空位,在5个空位中选一个安排戊,有5种情况,则甲和乙都排在丙的左侧的情况有2×4×5=40种,②、甲和乙都排在丙的右侧,同理有40种不同的排法;故甲和乙都排在丙的同一侧的排法种数为40+40=80种;故选:D.8.(5分)某折叠餐桌的使用步骤如图所示,有如图检查项目:项目①:折叠状态下(如图1),检查四条桌腿长相等;项目②:打开过程中(如图2),检查OM=ON=O'M'=O'N';项目③:打开过程中(如图2),检查OK=OL=O'K'=O'L';项目④:打开后(如图3),检查∠1=∠2=∠3=∠4=90°;项目⑤:打开后(如图3),检查AB=A'B'=C'D'=CD.在检查项目的组合中,可以正确判断“桌子打开之后桌面与地面平行的是”()A.①②③B.②③④C.②④⑤D.③④⑤【解答】解:项目①:折叠状态下(如图1),四条桌腿长相等时,桌面与地面不一定平行;项目②:打开过程中(如图2),若OM=ON=O'M'=O'N',可以得到线线平行,从而得到面面平行;项目③:打开过程中(如图2),检查OK=OL=O'K'=O'L',可以得到线线平行,从而得到面面平行;项目④:打开后(如图3),检查∠1=∠2=∠3=∠4=90°,可以得到线线平行,从而得到面面平行项目⑤:打开后(如图3),检查AB=A'B'=C'D'=CD.桌面与地面不一定平行;故选:B.二、填空题(每题5分,满分30分,将答案填在答题纸上)9.(5分)若等比数列{a n}满足a2a4=a5,a4=8,则公比q=2,前n项和S n=2n﹣1.【解答】解:∵等比数列{a n}满足a2a4=a5,a4=8,∴,解得a1=1,q=2,∴前n项和S n==2n﹣1.故答案为:2,2n﹣1.10.(5分)已知F1(﹣2,0),F2(2,0),满足||PF1|﹣|PF2||=2的动点P的轨迹方程为.【解答】解:根据题意,F1(﹣2,0),F2(2,0),则|F1F2|=4,动点P满足||PF1|﹣|PF2||=2,即2<4,则P的轨迹是以F1、F2为焦点的双曲线,其中c=2,2a=2,即a=1,则b2=c2﹣a2=3,双曲线的方程为:;故答案为:.11.(5分)在△ABC中,c=a cos B.①A=90°;②若sin C=,则cos(π+B)=﹣.【解答】解:①∵c=a cos B.∴cos B==,整理可得:a2=b2+c2,∴A=90°;②∵sin C=,A=90°,∴B=90°﹣C,∴cos(π+B)=﹣cos B=﹣sin C=﹣故答案为:90°,.12.(5分)若非零向量,满足•(+)=0,2||=||,则向量,夹角的大小为120°.【解答】解:设向量,的夹角为θ,则θ∈[0°,180°];又•(+)=0,2||=||,∴+•=0,即+||×2||cosθ=0,解得cosθ=﹣,∴θ=120°,即向量,夹角为120°.故答案为:120°.13.(5分)已知函数f(x)=若关于x的方程f(x+a)=0在(0,+∞)内有唯一实根,则实数a的最小值是﹣.【解答】解:作出f(x)的函数图象如图所示:∵f(x+a)在(0,+∞)上有唯一实根,∴f(x)在(a,+∞)上有唯一实根,∴﹣≤a<1.故答案为.14.(5分)已知实数u,v,x,y满足u2+v2=1,,则z=ux+vy的最大值是2.【解答】解:约束条件的可行域如图三角形区域:A(2,1),B(2,﹣1),C(0,1),u2+v2=1设u=sinθ,v=cosθ,目标函数经过A时,z=2sinθ+2cosθ=2sin().目标函数经过B时,z=2sinθ﹣cosθ=sin(θ+β).(其中tanβ=).目标函数经过C时,z=sinθ≤1.所以目标函数的最大值为:2.故答案为:.三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)15.(13分)已知是函数f(x)=2cos2x+a sin2x+1的一个零点.(Ⅰ)求实数a的值;(Ⅱ)求f(x)的单调递增区间.【解答】解:(Ⅰ)由题意可知,即,即,解得.(Ⅱ)由(Ⅰ)可得==,函数y=sin x的递增区间为,k∈Z.由,k∈Z,得,k∈Z,所以,f(x)的单调递增区间为,k∈Z.16.(13分)据报道,巴基斯坦由中方投资运营的瓜达尔港目前已通航.这是一个可以停靠8~10万吨油轮的深水港,通过这一港口,中国船只能够更快到达中东和波斯湾地区,这相当于给中国平添了一条大动脉!在打造中巴经济走廊协议(简称协议)中,能源投资约340亿美元,公路投资约59亿美元,铁路投资约38亿美元,高架铁路投资约16亿美元,瓜达尔港投资约6.6亿美元,光纤通讯投资约为0.4亿美元.有消息称,瓜达尔港的月货物吞吐量将是目前天津、上海两港口月货物吞吐量之和.表格记录了2015年天津、上海两港口的月吞吐量(单位:百万吨):(Ⅰ)根据协议提供信息,用数据说明本次协议投资重点;(Ⅱ)从表中12个月任选一个月,求该月天津、上海两港口月吞吐量之和超过55百万吨的概率;(Ⅲ)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过55百万吨的概率,设X为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出X的数学期望(不需要计算过程).【解答】解:(Ⅰ)本次协议的投资重点为能源,因为能源投资为340亿,占总投资460亿的50%以上,所占比重大.(Ⅱ)设事件A:从12个月中任选一个月,该月超过55百万吨.根据提供的数据信息,可以得到天津、上海两港口的月吞吐量之和分别是:56,49,58,54,54,57,59,58,58,56,54,56,其中超过55百万吨的月份有8个,所以,.(Ⅲ)X的数学期望EX=8.17.(13分)如图,由直三棱柱ABC﹣A1B1C1和四棱锥D﹣BB1C1C构成的几何体中,∠BAC=90°,AB=1,BC=BB1=2,C1D=CD=,平面CC1D⊥平面ACC1A1.(Ⅰ)求证:AC⊥DC1;(Ⅱ)若M为DC1中点,求证:AM∥平面DBB1;(Ⅲ)在线段BC上(含端点)是否存在点P,使直线DP与平面DBB1所成的角为?若存在,求的值,若不存在,说明理由.【解答】解:(Ⅰ)证明:在直三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,故AC ⊥CC1,由平面CC1D⊥平面ACC1A1,且平面CC1D∩平面ACC1A1=CC1,所以AC⊥平面CC1D,又C1D⊂平面CC1D,所以AC⊥DC1.(Ⅱ)证明:在直三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,所以AA1⊥AB,AA1⊥AC,又∠BAC=90°,所以,如图建立空间直角坐标系A﹣xyz,依据已知条件可得A(0,0,0),,,B(0,0,1),B1(2,0,1),,所以,,设平面DBB的法向量为,由即令y=1,则,x=0,于是,因为M为DC1中点,所以,所以,由,可得,所以AM与平面DBB1所成角为0,即AM∥平面DBB1.(Ⅲ)解:由(Ⅱ)可知平面BB 1D的法向量为.设,λ∈[0,1],则,.若直线DP与平面DBB1成角为,则,解得,故不存在这样的点.18.(13分)已知函数f(x)=x2﹣2ax+4(a﹣1)ln(x+1),其中实数a<3.(Ⅰ)判断x=1是否为函数f(x)的极值点,并说明理由;(Ⅱ)若f(x)≤0在区间[0,1]上恒成立,求a的取值范围.【解答】解:(Ⅰ)由f(x)=x2﹣2ax+4(a﹣1)ln(x+1)可得函数f(x)定义域为(﹣1,+∞),=,令g(x)=x2+(1﹣a)x+(a﹣2),经验证g(1)=0,因为a<3,所以g(x)=0的判别式△=(1﹣a)2﹣4(a﹣2)=a2﹣6a+9=(a ﹣3)2>0,由二次函数性质可得,1是函数g(x)的异号零点,所以1是f'(x)的异号零点,所以x=1是函数f(x)的极值点.(Ⅱ)已知f(0)=0,因为,又因为a<3,所以a﹣2<1,所以当a≤2时,在区间[0,1]上f'(x)<0,所以函数f(x)单调递减,所以有f(x)≤0恒成立;当2<a<3时,在区间[0,a﹣2]上f'(x)>0,所以函数f(x)单调递增,所以f(a﹣2)>f(0)=0,所以不等式不能恒成立;所以a≤2时,有f(x)≤0在区间[0,1]恒成立.19.(14分)已知椭圆G:+y2=1,与x轴不重合的直线l经过左焦点F1,且与椭圆G相交于A,B两点,弦AB的中点为M,直线OM与椭圆G相交于C,D两点.(1)若直线l的斜率为1,求直线OM的斜率;(2)是否存在直线l,使得|AM|2=|CM|•|DM|成立?若存在,求出直线l的方程;若不存在,请说明理由.【解答】解:(1)由已知可知F1(﹣1,0),又直线l的斜率为1,所以直线l 的方程为y=x+1,设A(x1,y1),B(x2,y2),由解得或,所以AB中点,于是直线OM的斜率为.(2)假设存在直线l,使得|AM|2=|CM|•|DM|成立.当直线l的斜率不存在时,AB的中点M(﹣1,0),所以,,矛盾;故直线的斜率存在,可设直线l的方程为y=k(x+1)(k≠0),联立椭圆G的方程,得(2k2+1)x2+4k2x+2(k2﹣1)=0,设A(x1,y1),B(x2,y2),则,,于是,点M的坐标为,.直线CD的方程为,联立椭圆G的方程,得,设C(x0,y0),则,由题知,|AB|2=4|CM|•|DM|=4(|CO|+|OM|)(|CO|﹣|OM|)=4(|CO|2﹣|OM|2),即,化简,得,故,所以直线l的方程为,.20.(14分)已知含有n个元素的正整数集A={a1,a2,…,a n}(a1<a2<…<a n,n≥3)具有性质P:对任意不大于S(A)(其中S(A)=a1+a2+…+a n)的正整数k,存在数集A的一个子集,使得该子集所有元素的和等于k.(Ⅰ)写出a1,a2的值;(Ⅱ)证明:“a1,a2,…,a n成等差数列”的充要条件是“S(A)=”;(Ⅲ)若S(A)=2017,求当n取最小值时a n的最大值.【解答】解:(Ⅰ)由集合A={a1,a2,…,a n},}(a1<a2<…<a n,n≥3),由a n为正整数,则a1=1,a2=2.(Ⅱ)先证必要性:因为a1=1,a2=2,又a1,a2,…,a n成等差数列,故a n=n,所以;再证充分性:因为a1<a2<…<a n,a1,a2,…,a n为正整数数列,故有a1=1,a2=2,a3≥3,a4≥4,…,a n≥n,所以,又,故a m=m(m=1,2,…,n),故a1,a2,…,a n为等差数列.(Ⅲ)先证明(m=1,2,…,n).假设存在,且p为最小的正整数.依题意p≥3,则a1+a2+…+a p﹣1≤1+2+…+2p﹣2=2p﹣1﹣1,又因为a1<a2<…<a n,故当k∈(2p﹣1﹣1,a p)时,k不能等于集合A的任何一个子集所有元素的和.故假设不成立,即(m=1,2,…,n)成立.因此,即2n≥2018,所以n≥11.因为S=2017,则a1+a2+…+a n﹣1=2017﹣a n,若2017﹣a n<a n﹣1时,则当k∈(2017﹣a n,a n)时,集合A中不可能存在若干不同元素的和为k,故2017﹣a n≥a n﹣1,即a n≤1009.此时可构造集合A={1,2,4,8,16,32,64,128,256,497,1009}.因为当k∈{2,2+1}时,k可以等于集合{1,2}中若干个元素的和;故当k∈{22,22+1,22+2,22+3}时,k可以等于集合{1,2,22}中若干不同元素的和;…故当k∈{28,28+1,28+2,…,28+255}时,k可以等于集合{1,2,…,28}中若干不同元素的和;故当k∈{497+3,497+4,…,497+511}时,k可以等于集合{1,2,…,28,497}中若干不同元素的和;故当k∈{1009,1009+1,1009+2,…,1009+1008}时,k可以等于集合{1,2,…,28,497,1009}中若干不同元素的和,所以集合A={1,2,4,8,16,32,64,128,256,497,1009}满足题设,所以当n取最小值11时,a n的最大值为1009.。
北京市海淀区2017-2018学年度第一学期期中考试高三数学(理)

试卷编号:1732北京市海淀区2017-2018学年度第一学期期末考试高三数学(理)班级:_____学号:_____姓名:_____成绩:_____一、选择题共8小题。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.若集合A={x|x−2<0},B={x|e x>1},则A∩B=( )(A)R(B)(−∞,2)(C)(0,2)(D)(2,+∞)2.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )(A)f(x)=ln|x|(B)f(x)=2−x(C)f(x)=x3(D)f(x)=−x23.已知向量a=(1,0),b=(−1,1),则( )(A)a∥b(B)a⊥b(C)(a−b)∥b(D)(a+b)⊥a4.已知数列{a n}满足a1+a2+···+a n=2a2(n=1,2,3,···),则( )(A)a1<0(B)a1>0(C)a1 a2(D)a2=05.将y=sin(2x+π6)的图象向左平移π6个单位,则所得图象的函数解析式为( )(A)y=sin2x(B)y=cos2x(C)y=sin(2x+π3)(D)y=sin(2x−π6)6.设α∈R,则“α是第一象限角”是“sinα+cosα>1”的( )(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件7.设f(x)=e sin x+e−sin x(x∈R),则下列说法不正确的是( )(A)f(x)为R上偶函数(B)π为f(x)的一个周期(C)π为f(x)的一个极小值点(D)f(x)在区间(0,π2)上单调递减8.已知非空集合A,B满足以下两个条件:①A∪B={1,2,3,4,5,6},A∩B=∅;②A的元素个数不是A中的元素,B的元素个数不是B中的元素,则有序集合对(A,B)的个数为( )(A)10(B)12(C)14(D)16二、填空题共6小题。
2018北京市海淀区高三数学一模理科试题及答案

资料收集于网络,如有侵权请联系网站删除只供学习与交流.资料收集于网络,如有侵权请联系网站删除只供学习与交流.资料收集于网络,如有侵权请联系网站删除只供学习与交流.资料收集于网络,如有侵权请联系网站删除只供学习与交流.资料收集于网络,如有侵权请联系网站删除海淀区高三年级第二学期期中练习()参考答案与评分标准理数学2018.48540 分。
在每小题列出的四个选项中,选出符合题目要求的一项。
小题,每小题分,共一、选择题共121432 分。
注:第题第一空均为、分,第二空均为680 分。
解答题应写出解答步骤。
三、解答题共小题,共15. 13 分)(本题满分????2?2coscos1??f()23sin(Ⅰ)66662??133?23???2??1???? 222???2·3 ····················································································分f(x)?3sin2x?cos2x(Ⅱ)?)?2sin(2x?6??????x?siny?,2k2?k k?Z,因为函数)的单调递增区间为(??22????????k?2?2x2k??k?Z,令)(226??????kk?x?k?Z,()解得63??)x(f??]?,k[k?Z?k 1 3····························分()故的单调递增区间为6313 16.分)(本题满分只供学习与交流.请联系网站删除资料收集于网络,如有侵权A112有利于病毒繁殖和传月平均相对湿度:从上表个月,该月甲地空气个月中,随机取出(Ⅰ)设事件A i.月,则用表示事件抽取的月份为第播i},A,A,AAA,A,A,A,,A??{A,A,A,12 个基本事件,共1970468151213},A,A,AA?{A,A,A 6 个基本事件,共196218016?(A)?P. ·4···································································分所以,2126空气月平均相对湿度都有利于病毒繁殖和传播的月(Ⅱ)在第一季度和第二季度的个月中,甲、乙两地02X126. ,所有可能的取值为月,故份只有,月和2121CCCC18262424???0)?2)?P(XP(X?1)??P(X??,,22215CC15C155666X的分布列为随机变量21X182P1515558%54%M.3 ·······1··········································,最小值为分的最大值为(Ⅲ)17.14 分)(本题满分1 :(Ⅰ)方法PA OCB ACOBOPO. 由题意的中点为,设,连接AO?BO?CO?11PO?,,2PC?PA?PB??PACPA?PCOAC的中点因为中,在为,PO?AC,所以?POBOB?11PO?,中,在因为,2PB?OB?PO所以AC,OB?OACOB?ABC平面因为,PO?ABC平面所以PO?PAC4·································································平面分因为PACABC?平面平面所以只供学习与交流.请联系网站删除资料收集于网络,如有侵权2:方法PA OCBPOBOACO . ,,连接设的中点为ACO?PACPA?PC的中点中,,因为为在AC?PO,所以CO?PCAO?BOPA?PB?POPO?PO?,,因为POC??POB?POA≌≌所以??90POB??POC?POA??所以OBPO?所以?,OBACOOB?ACABC平面,因为ABCPO?平面所以PAC?PO·4 ································································平面分因为ABCPAC?平面所以平面3:方法PAOQCB ACOPO?PACPA?PC,的中点为,因为在,连接中,设PO?AC所以QPQOQ OB AB. 及,的中点,连接设QOB?OABOA?AB的中点因为为在,中,OQ?AB. 所以Q AB?PB?PABPA的中点中,在,为因为PQ?AB. 所以PQOQ?QPQ,OQ?OPQ平面因为,OPQ?AB 平面所以OPQ?OP平面因为只供学习与交流.请联系网站删除资料收集于网络,如有侵权BAOP?所以?ACAB,A?ABAC ABC平面因为,ABC?PO平面所以PACPO?··4 ·······························································平面分因为ABCPAC?平面平面所以ACABCOB?PO?,如图建立空间直角坐标系,则,平面(Ⅱ)由zP(0,0,1)?1,0,0)P(1,0,0)B(0,1,0)A(O(0,0,0)C,,,,APCOB?APC(0,1,0)OB?的法向量为平面由,故平面1)(1,0,?(1,?1,0)PC?BC?,由PBC),z?(x,yn,则设平面的法向量为0y?x???0n?BC??得:由?0PC?n?0?x?z??1?y1x?(1,1,1)?n1z?,即,得,令n?OB13??cos?n,OB??3||OBn|?|13?A?PC?B是锐二面角,由二面角3B?A?PC············································9 分所以二面角的余弦值为3?10???BPBN?,则(Ⅲ)设,????)1,,?(?1,0,1)?(1?BM?BC?CM?BC?CP?(1,?1,0)?????),??1,1)(1,1BN?AB?BP?(1,1,0)??(0,?ANAB?令0AN?BM????????)?01)?(11)??(??(1得?1???1?μλ的单调递增函数,是关于即,???11?只供学习与交流.资料收集于网络,如有侵权请联系网站删除1212??]?][,?[,,时,当53342BN1][,?·4 ······1·································································分所以5BP418. 13分)(本题满分xln?)(xf0a?时,(Ⅰ)当x1xln?x?xln1?故x??f'(x)0?f'(x)e?0?x,得22xx令)ex)(0,f(·4·······················································分故的单调递增区间为ax?ax??ln?lnx1 1 xx:(Ⅱ)方法?)?f'(x22)?a)a(x(x?ax??x)1?lng(令xax?a10??????g'(x)则22xxx1aa1a?0??(?1)?g(e)?1?(1?a?0g(e)?a)?,由0?(x)g0x)?g()x,??xx?(0,x)?(时,时,故当;当00 1?1?aa eee1?a0?(x)g)e?(e,x,故存在00)(0,x),??(xxx000?)xf'(0?)(xf↗↘极大值1?)f(x故02ea?0??lnx1??02?xe?x??0013···················································??,解得故分xln12ea????0??2e a?x?0a2.e的值为故只供学习与交流.资料收集于网络,如有侵权请联系网站删除1lnx1x?(0,??f(x))x?(0,??)?2,的最大值为,(Ⅱ)方法且存在:的充要条件为对任意的0x?(0,??))??x?(0,2xlnxa?e?的意价于对任得使,,且存在使得,等22e x?a e lnx10?20x?a e02lnx??e xa,00a2xlnx?)g(x?e.的最大值为等价于2e g'(x)??1,x g'(x)?02e?x.,得令)g(x↗↘极大值g(x)222222ee?elne?g(e)?ea?. ·13 ··························,即的最大值为故分1914 分)((本小题)41???1?22ba??222a?b?c?,(Ⅰ)由题意?c3???e?a2?6?c,,解得:2b??22a22yx C??1·5 ···················································分的标准方程为故椭圆821(x?2)y?1?l1)PTPTQQ(2,的方程为-则点或,点的坐标为直线(Ⅱ)假设直线或,的斜率不存在,21xy??2. 即222?yx??1??822?04?4?x?x,联立方程,得1?x?y?2??2 lC. 相切,不合题意此时,直线与椭圆只供学习与交流.资料收集于网络,如有侵权请联系网站删除TPTQ. 的斜率存在故直线和1 :方法),y)Q(xP(x,y,则设,22111y?12)x:y?1??(TP,直线2x?11y?22)y?1?x?(TQ:直线2x?22??x2x21?2ON?|OM|2?|?|,故1?1yy?2111t?y?xxPQ:?OT:y0?t)由直线,设直线(2222?yx1????28220??tx?2t?x4?2?联立方程,1?t?xy??2?2t2??x?x4?2tx?x?0??,当时,21212x?x?221)(??4?|OM||?|ON1y?y?1212?xx?221)(??4?111?x?t1tx??21221)??4(t2)(x?x)(xx?t?2112?4?1121)t?x)?(?xx?(t?1)(x22112421)t?t)?4(4?(t?2)(?22t???411221)(t?(?2t)?1)(2t?4)?(t??24?4.4 (1)分只供学习与交流.资料收集于网络,如有侵权请联系网站删除2 :方法TQ)yx,,y)Q(P(xkk TP和和,直线设的斜率分别为,21122111xPQ:y?x?tOT:y?t?0)由,设直线(2222?yx??1??8222?4?0tx?2?xt?2?联立方程,1?x??ty??22x?x??2tx?x?2t?40??,当时,2121y?1y?121??k?k21x?2x?22111x?t?1x?t?1 2122??x?2x?221xx?(t?2)(x?x)?4(t?1)2211?(x?2)(x?2)212?4?(t?2)(?2t)?2t4(t?1)?(x?2)(x?2)21?0TQ TP的斜率和为零故直线和直线?TMN??TNM故TM?TN故MNMNT2的中点横坐标为在线段故的中垂线上,即|OM|?|ON|?4·14·····································································故分20. 13 分)(本题满分N?N?N?BA”.3 ”“·“···········3 ”“·············数表数表,值分,其(Ⅰ)不是是为aa N?A”“,的值和均是数表(Ⅱ)假设ji,'',ji a?max{a,a,...,a}?max{a,a,...,a}?a'?ii;若,则①'i,j',1',ii,1',2i,2jni,ii',ni a?min{a,a,...,a}?min{a,a,...,a}?a'jj?;若②,则'jj1,''i2,ji,j'1,j',2,jnn,j,j j?j''i?i,则一方面,③若a?max{a,a,...,a}?a?min{a,a,...,a}?a,'ji',''ji,ni,1i,2i,ji,'j1,'2,j,nj另一方面只供学习与交流.资料收集于网络,如有侵权请联系网站删除a?max{a,a,...,a}?a?min{a,a,...,a}?a;j1,i',2jii',n',1j2,ji',j',ij',n,i N?N?A”““. ·····8 . ”··················是唯一的值,则其即若数表数表分是矛盾1 :(Ⅲ)方法A?(a)1931936121.…列的数表行,组成的对任意的由,,,1919i,j?jj)bB?(iiBA列,即如下,将数表的第的第定义数表列的元素写在数表行,第行,第19j,i19?b?a1?j?1919i?1?),(其中jij,i,显然有:31919361B21…列的数表,组成的,①,数表行是由,jjAB列的元素数表行的元素,即为数表②的第的第iiAB 行的元素③列的元素,即为数表数表的第的第j a i A列中的最小值④是第若数表行中的最大值,也是第中,ji,j b i B. 行中的最小值则数表是第中,列中的最大值,也是第ij,C?(c)B362 ,即定义数表如下,其与数表对应位置的元素的和为19?,i19j c?362?b1?j?19191?i?),(其中ii,jj,显然有31919361C21…列的数表数表,是由,①,行,组成的j b i B列中的最小值中,若数表列中的最大值,也是第②是第ij,j c i C列中的最大值中,列中的最小值,也是第是第则数表ij,A?(a)1919336121…列的数表行,,特别地,对由,,组成的1919i,j?31919361C21…列的数表,组成的,,①,数表行是由j a i A列中的最小值②是第若数表行中的最大值,也是第中,ji,j c i C 列中的最大值是第则数表列中的最小值,也是第中,ij,a1?j?19C??A??N??N191?i?””““值,其),则,且其即对任意的值,为(其中ji,1919c?362?b?362?a.为jj,i,iij,C?T(A)T(C)?AC?T(A)N?362A“”,的,即数表值记,则与数表之和为?N?362“”,值中的数表两两配对,使得每对数表的之和为故可按照上述方式对19E(X)?181X. ·3 ·1 ·························································的数学期望故分2 :方法19,20,21,...,341,342,343X.所有可能的取值为只供学习与交流.资料收集于网络,如有侵权请联系网站删除k?19,20,21,...,341,342,343n?kX?A,则中使得的数表,记的个数记作k19181822?C?C?[(18n?19)!].k?k361k?1218182n?19?C?C?[(18)!]?n,则则k?361?k?k1k362343343343????(362?nnk?kn)?k k362k?k19??k?19k19k?)??(EX,???(362?nk)n?k kk19?k19k?E(X)?181362)(2EX???. ·············343343343???nnn kkk19k?19?k?19k343343···13 分故,343343??nn kk19k19?k?只供学习与交流.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018北京市海淀区高三数学一模理科试题及答案海淀区高三年级第二学期期中练习数学(理)参考答案与评分标准2018.4 一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
二、填空题共6小题,每小题5分,共30分。
注:第12、14题第一空均为3分,第二空均为2分。
三、解答题共6小题,共80分。
解答题应写出解答步骤。
15. (本题满分13分)(Ⅰ)2()cos 2cos 16666f ππππ=+-2121222⎛⎫=⨯+⨯- ⎪ ⎪⎝⎭2= ··································· 3分(Ⅱ)()2cos 2f x x x=+ 2sin(2)6x π=+因为函数sin y x =的单调递增区间为2,222k k ππππ⎡⎤-+⎢⎥⎣⎦(k ∈Z ),令222262k x k πππππ-≤+≤+(k ∈Z ),解得 36k x k ππππ-≤≤+(k ∈Z ),故()f x 的单调递增区间为[,]36k k ππππ-+(k ∈Z ) 13分16. (本题满分13分)(Ⅰ)设事件A :从上表12个月中,随机取出1个月,该月甲地空气月平均相对湿度有利于病毒繁殖和传播. 用iA 表示事件抽取的月份为第i 月,则123456789101112{,,,,,,,,,,,}A A A A A A A A A A A A Ω=共12个基本事件,26891011{,,,,,}A A A A A A A =共6个基本事件,所以,61()122P A ==. ·························· 4分(Ⅱ)在第一季度和第二季度的6个月中,甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份只有2月和6月,故X 所有可能的取值为0,1,2.242662(0)155C P X C ====,1124268(1)15C C P X C ===,22261(2)15C P X C ===随机变量X 的分布列为(Ⅲ)M 的最大值为58%,最小值为54%. ······ 13分17.(本题满分14分) (Ⅰ)方法1:OPCAB设AC 的中点为O ,连接BO ,PO . 由题意PA PB PC ===1PO =,1AO BO CO ===因为 在PAC ∆中,PA PC =,O 为AC 的中点所以PO AC⊥,因为 在POB ∆中,1PO =,1OB =,PB =所以 PO OB⊥因为 AC OB O=,,AC OB ⊂平面ABC所以 PO ⊥平面ABC因为PO ⊂平面PAC ··························· 4分 所以 平面PAC ⊥平面ABC 方法2:OPCA设AC 的中点为O ,连接BO ,PO . 因为 在PAC ∆中,PA PC =,O 为AC 的中点 所以 PO AC⊥,因为 PA PB PC==,PO PO PO ==,AO BO CO ==所以POA∆≌POB ∆≌POC ∆所以90POA POB POC ∠=∠=∠=︒所以PO OB⊥因为AC OB O =,,AC OB⊂平面ABC所以PO⊥平面ABC因为PO⊂平面PAC···························4分所以平面PAC⊥平面ABC方法3:O PCA BQ设AC的中点为O,连接PO,因为在PAC∆中,PA PC=,所以PO AC⊥设AB的中点Q,连接PQ,OQ及OB.因为在OAB∆中,OA OB=,Q为AB的中点所以OQ AB⊥.因为在PAB∆中,PA PB=,Q为AB的中点所以PQ AB⊥.因为PQ OQ Q=,,PQ OQ⊂平面OPQ所以AB⊥平面OPQ因为 OP ⊂平面OPQ 所以 OP AB⊥因为 AB AC A=,,AB AC ⊂平面ABC所以 PO ⊥平面ABC因为PO ⊂平面PAC ··························· 4分 所以 平面PAC ⊥平面ABC(Ⅱ)由PO ⊥平面ABC ,OB AC ⊥,如图建立空间直角坐标系,则(0,0,0)O ,(1,0,0)C ,(0,1,0)B ,(1,0,0)A -,(0,0,1)P由OB ⊥平面APC ,故平面APC 的法向量为(0,1,0)OB = 由(1,1,0)BC =-,(1,0,1)PC =-设平面PBC 的法向量为(,,)n x y z =,则 由BC PC ⎧⋅=⎨⋅=⎩n n 得:00x y x z -=⎧⎨-=⎩令1x =,得1y =,1z =,即(1,1,1)n =cos ,||||3n OB n OB n OB ⋅<>===⋅由二面角A PC B --是锐二面角, 所以二面角A PC B-- ········ 9分(Ⅲ)设BN BP μ=,01μ≤≤,则(1,1,0)(1,0,1)(1,1,)BM BC CM BC CP λλλλ=+=+=-+-=--(1,1,0)(0,1,1)(1,1,)AN AB BN AB BP μμμμ=+=+=+-=-令0BM AN ⋅=得(1)1(1)(1)0λμλμ-⋅+-⋅-+⋅= 即1111λμλλ==-++,μ是关于λ的单调递增函数,当12[,]33λ∈时,12[,]45μ∈, 所以12[,]45BN BP ∈ ·································· 14分18.(本题满分13分)(Ⅰ)当0a =时,ln ()xf x x=故221ln 1ln '()x xx x f x x x ⋅--==令'()0f x >,得0x <<e故()f x 的单调递增区间为(0,)e ··········· 4分(Ⅱ)方法1:22ln 1ln '()()()x a ax xx x f x x a x a +-+-==++令()1ln ag x x x=+-则221'()0a x ag x x x x +=--=-<由()0a g =>e e,1111()1(1)(1)0a a a a g a a e e +++=+-+=⋅-<e故存在10(,)a x +∈e e ,0()0g x =故当0(0,)x x ∈时,()0g x >;当0(,)x x ∈+∞时,()0g x <故02()f x =e 故000201ln 0ln 1ax x x x a ⎧+-=⎪⎪⎨⎪=⎪+⎩e,解得202x a ⎧=⎪⎨=⎪⎩e e················· 13分故a 的值为2e . (Ⅱ)方法2:()f x 的最大值为21e 的充要条件为对任意的(0,)x ∈+∞,2ln 1x x a ≤+e且存在0(0,)x ∈+∞,使得020ln 1x x a =+e,等价于对任意的(0,)x ∈+∞,2ln a x x≥-e且存在0(0,)x ∈+∞,使得200ln a x x ≥-e ,等价于2()ln g x x x=-e的最大值为a.2'()1g x x=-e ,令'()0g x =,得2x =e .故()g x 的最大值为22222()ln g =-=e e e e e ,即2a =e .13分(19)(本小题14分)(Ⅰ)由题意22222411a b a b c c e a ⎧+=⎪⎪⎪-=⎨⎪⎪==⎪⎩,解得:a =b =c = 故椭圆C 的标准方程为22182x y += ········· 5分(Ⅱ)假设直线TP 或TQ 的斜率不存在,则P 点或Q点的坐标为(2,-1),直线l 的方程为11(2)2y x +=-,即122y x =-. 联立方程22182122x y y x ⎧+=⎪⎪⎨⎪=-⎪⎩,得2440xx -+=,此时,直线l 与椭圆C 相切,不合题意.故直线TP 和TQ 的斜率存在.方法1:设11(,)P x y ,22(,)Q x y ,则直线111:1(2)2y TP y x x --=--, 直线221:1(2)2y TQ y x x --=--故112||21x OM y -=--,222||21x ON y -=--由直线1:2OT y x =,设直线1:2PQ y x t =+(0t ≠) 联立方程,2222182224012x y x tx t y x t ⎧+=⎪⎪⇒++-=⎨⎪=+⎪⎩当∆>时,122x x t+=-,21224x x t ⋅=-||||OM ON +1212224()11x x y y --=-+--1212224()111122x x x t x t --=-++-+-121221212(2)()4(1)411(1)()(1)42x x t x x t x x t x x t +-+--=-+-++- 22224(2)(2)4(1)411(24)(1)(2)(1)42t t t t t t t t -+----=--+-⋅-+-4= ······················· 14分方法2:设11(,)P x y ,22(,)Q x y ,直线TP 和TQ 的斜率分别为1k 和2k由1:2OT y x =,设直线1:2PQ y x t =+(0t ≠)联立方程,2222182224012x y x tx t y x t ⎧+=⎪⎪⇒++-=⎨⎪=+⎪⎩当∆>时,122x x t+=-,21224x x t ⋅=-12k k +12121122y y x x --=+--121211112222x t x t x x +-+-=+--121212(2)()4(1)(2)(2)x x t x x t x x +-+--=-- 21224(2)(2)4(1)(2)(2)t t t t x x -+----=--=故直线TP 和直线TQ 的斜率和为零 故TMN TNM ∠=∠故TM TN =故T 在线段MN 的中垂线上,即MN 的中点横坐标为2 故||||4OM ON += ······························ 14分20. (本题满分13分)(Ⅰ)A 是“N -数表 ”,其“N -值”为3,B 不是“N -数表”. ······················································· 3分 (Ⅱ)假设,i ja 和','i j a 均是数表A 的“N -值”,① 若'i i =,则,,1,2,',1',2',','max{,,...,}max{,,...,}i ji i i n i i i n i j aa a a a a a a ===; ② 若'j j =,则,1,2,,1,'2,','','min{,,...,}min{,,...,}i jj j n j j j n j i j aa a a a a a a === ;③ 若'i i ≠,'j j ≠,则一方面,,1,2,,'1,'2,','','max{,,...,}min{,,...,}i j i i i n i j j j n j i j a a a a a a a a a =>>=,另一方面','',1',2',',1,2,,,max{,,...,}min{,,...,}i j i i i n i j j j n j i ja a a a a a a a a =>>=;矛盾. 即若数表A 是“N -数表”,则其“N -值”是唯一的. ···················································· 8分 (Ⅲ)方法1:对任意的由1,2,3,…,361组成的19行19列的数表,1919()i j A a ⨯=.定义数表,1919()j i B b⨯=如下,将数表A 的第i 行,第j 列的元素写在数表B 的第j 行,第i 列,即,,j i i jb a =(其中119i ≤≤,119j ≤≤)显然有:① 数表B 是由1,2,3,…,361组成的19行19列的数表② 数表B 的第j 行的元素,即为数表A 的第j 列的元素 ③ 数表B 的第i 列的元素,即为数表A 的第i 行的元素 ④ 若数表A 中,,i ja 是第i 行中的最大值,也是第j 列中的最小值则数表B 中,,j ib 是第i 列中的最大值,也是第j 行中的最小值. 定义数表,1919()j i C c ⨯=如下,其与数表B 对应位置的元素的和为362,即,,362j i j ic b =-(其中119i ≤≤,119j ≤≤)显然有① 数表C 是由1,2,3,…,361组成的19行19列的数表② 若数表B 中,,j ib 是第i 列中的最大值,也是第j 列中的最小值则数表C 中,,j ic 是第i 列中的最小值,也是第j 列中的最大值特别地,对由1,2,3,…,361组成的19行19列的数表,1919()i j A a ⨯=① 数表C 是由1,2,3,…,361组成的19行19列的数表② 若数表A 中,,i ja 是第i 行中的最大值,也是第j 列中的最小值则数表C 中,,j ic 是第i 列中的最小值,也是第j 列中的最大值即对任意的19A ∈Ω,其“N -值”为,i ja (其中119i ≤≤,119j ≤≤),则19C ∈Ω,且其“N -值”为,,,362362j ij i i jcb a =-=-.记()C T A =,则()T C A =,即数表A 与数表()C T A =的“N -值”之和为362,故可按照上述方式对19Ω中的数表两两配对,使得每对数表的 “N -值”之和为362,故X 的数学期望()181E X =. ···················· 13分 方法2:X 所有可能的取值为19,20,21,...,341,342,343.记19Ω中使得X k=的数表A的个数记作kn ,19,20,21,...,341,342,343k =,则218182136119[(18)!]k k k n C C --=⨯⨯⨯.则218182362361119[(18)!]k k k kn C C n ---=⨯⨯⨯=,则343343343362191919343343343191919(362)()kkkk k k kkkk k k nk nk nk E X nnn-======⋅⋅⋅-===∑∑∑∑∑∑,故34334319193433431919(362)2()362kkk k kkk k nknk E X nn====⋅⋅-=+=∑∑∑∑,()181E X =. ··· 13分。
