第十四章练习题及答案

合集下载

法考真题：马工程《民事诉讼法》第十四章普通程序练习题及答案

第十四章普通程序练习题及答案1. 张丽因与王旭感情不和，长期分居，向法院起诉要求离婚。

法院向王旭送达应诉通知书，发现王旭已于张丽起诉前因意外事故死亡。

关于本案，法院应作出下列哪一个裁判? ( )A. 诉讼终结的裁定B. 驳回起诉的裁定C. 不予受理的裁定D. 驳回诉讼请求的判决[解析]本题考查的是起诉条件。

2.何某因被田某打伤，向甲县法院提起人身损害赔偿之诉，法院予以受理。

关于何某起诉行为将产生的法律后果，下列哪一选项是正确的? ( )A.何某的诉讼时效中断B.田某的答辩期开始起算C.甲县法院取得排他的管辖权D_田某成为适格被告[解析]本题考查起诉的法律效果。

3.关于起诉与受理的表述，下列哪些选项正确的? ( )A.法院裁定驳回起诉的，原告再次起诉符合条件的，法院应当受理B.法院按撤诉处理后，当事人以同一诉讼请求再次起诉的，法院应当受理C.判决不准离婚的案件，当事人没有新事实和新理由再次起诉的，法院一律不予受理D.当事人超过诉讼时效起诉的，法院应当受理4.关于民事起诉状应当包括的内容，下列哪些选项是正确的? ( )A. 双方当事人的基本情况B.案由C.诉讼请求D.证据和证据来源[解析]本题考查民事起诉状的法定内容。

5.王某以借款纠纷为由起诉吴某。

经审理，法院认为该借款关系不存在，王某交付吴某的款项为应支付的货款，王某与吴某之间存在买卖关系而非借用关系。

法院向王某作出说明，但王某坚持己见，不予变更诉讼请求和理由。

法院遂作出裁定，驳回王某的诉讼请求。

关于本案,下列哪一说法是正确的? ( )A.法院违反了不告不理原则B.法院适用裁判形式错误C.法院违反了辩论原则D.法院违反了处分原则6.下列哪一选项不是民事起诉状的法定内容? ( )A. 双方当事人的基本情况B.案由C. 诉讼请求和所依据的事实与理由D. 证据和证据来源，证人姓名与住所7. 常年居住在 Y 省 A 县的王某早年丧妻，独自一人将两个儿子和一个女儿养大成人。

八年级数学上册《第十四章乘法公式》同步练习题及答案(人教版)

八年级数学上册《第十四章乘法公式》同步练习题及答案（人教版）一、选择题（共8题）1.下列计算正确的是( )A．a2⋅a3=a6B．3a2+2a3=5a5C．a3÷a2=a D．(a−b)2=a2−b22.若x2−6x+y2+4y+13=0，则y x的值为( )A．8B．−8C．9D．193.下列算式能用平方差公式计算的是( )A．(x−2)(x+1)B．(2x+y)(2y−x)C．(−2x+y)(2x−y)D．(−x−1)(x−1)4.若x2−mx+4是完全平方式，则m的值为( )A．2B．4C．±2D．±45.如图，在边长为a的正方形中挖掉一个边长为b的小正方形，把余下的部分拼成一个长方形（无重叠部分），通过计算两个图形中阴影部分的面积，可以验证的一个等式是( )A．a2−b2=(a+b)(a−b)B．a(a−b)=a2−abC．(a−b)2=a2−2ab+b2D．a(a+b)=a2+ab6.对于代数式：x2−2x+2，下列说法正确的是( )A．有最大值1B．有最小值1C．有最小值2D．无法确定最大最小值7.在下列多项式中，与−x−y相乘的结果为x2−y2的多项式是( )A．−x+y B．x+y C．x−y D．−x−y8.已知一个正方形的边长为a，将该正方形的边长增加1，则得到的新正方形的面积为( )A．a2+2a+1B．a2−2a+1C．a2+1D．a+1二、填空题（共5题）9.计算：(a+2)(a−2)=．10.已知m=√2+1，n=√2−1则代数式m2+n2−3mn的值为．11.定义：形如a+bi的数称为复数（其中a和b为实数，i为虚数单位，规定i2=−1 )，a称为复数的实部，b称为复数的虚部，复数可以进行四则运算，运算的结果还是一个复数．如(1+ 3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i−9=−8+6i，因此(1+3i)2的实部是−8，虚部是6．已知复数(3−mi)2的虚部是12，则实部是．12.根据图①到图②的变化过程可以写出一个整式的乘法公式，这个公式是．13.有两个正方形A，B现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的边长之和为．三、解答题（共6题）14.计算：(1) (ab)3⋅(−23a4b5)÷32a2b5．(2) (2x−y+5)(2x+y−5)．15.数学课堂上，张老师写出了下面四个等式，仔细观察下列等式，你会发现什么规律：1×5+4=32，2×6+4=42，3×7+4=52，4×8+4=62⋯⋯(1) 请你按照这个规律再写出第5个，第6个等式：、．(2) 请将你写出第n个等式．(3) 说出这个等式成立的理由：16.已知代数式(ax−3)(2x+4)−x2−b化简后，不含有x2项和常数项．(1) 求a，b的值．(2) 求(b−a)(−a−b)+(−a−b)2−a(2a+b)的值．17.先化简后求值：(x−2y)2−(x+2y)(x−2y)，其中x=−1，y=2．18.如图所示，某市有一块长为(3a+b)米，宽为(2a+b)米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当a=3，b=2时的绿化面积．19.学习整式乘法时，老师拿出三种型号卡片，如图1．(1) 选取1张A型卡片，6张C型卡片，则应取张B型卡片才能用它们拼成一个新的正方形，新的正方形的边长是（请用含a，b的代数式表示）；(2) 选取4张C型卡片在纸上按图2的方式拼图，并剪出中间正方形作为第四种D型卡片，由此可验证的等量关系为；(3) 选取1张D型卡片，3张C型卡片按图3的方式不重叠地放在长方形MNPQ框架内，已知NP的长度固定不变，MN的长度可以变化，图中两阴影部分（长方形）的面积分别表示为S1，S2，若S=S1−S2，且S为定值，则a与b有什么关系？请说明理由．答案1. C2. B3. D4. D5. A6. B7. A8. A9. a2−410. 311. 512. (a+b)(a−b)=a2−b213. 514.(1)(ab)3⋅(−23a4b5)÷32a2b5=−23a7b8÷32a2b5=−49a5b3.(2)(2x−y+5)(2x+y−5)=[2x−(y−5)][2x+(y−5)] =4x2−(y−5)2=4x2−(y2−10y+25)=4x2−y2+10y−25.15.(1) 5×9+4=72；6×10+4=82(2) 第n个：n×(n+4)+4=(n+2)2．(3) 左边=n×(n+4)+4=n2+4n+4=(n+2)2=右边；即n×(n+4)+4=(n+2)2成立．16.(1) 原式=ax (2x +4)−3(2x +4)−x 2−b=2ax 2+4ax −6x −12−x 2−b =(2a −1)x 2+(4a −6)x −12−b,∵ 不含 x 2 项和常数项∴2a −1=0，−12−b =0∴a =12，b =−12． (2) 原式=−(b −a )(a +b )+[−(a +b )]2−2a 2−ab=−(b 2−a 2)+a 2+2ab +b 2−2a 2−ab =a 2−b 2+a 2+2ab +b 2−2a 2−ab =ab,当 a =12，b =−12 时原式=12×(−12)=−6．17. 原式=x 2−4xy +4y 2−(x 2−4y 2)=x 2−4xy +4y 2−x 2+4y 2=−4xy +8y 2.当 x =−1，y =2 时原式=−4×(−1)×2+8×22=40．18. 绿化面积S=(3a +b )(2a +b )−(a +b )2=6a 2+5ab +b 2−a 2−b 2−2ab =5a 2+3ab(平方米).当 a =3，b =2 时S =5×32+3×3×2=63（平方米）．19.(1) 9；a +3b(2) (a −b )2=(a +b )2−4ab(3) 设 MN 长为 xS 1=(a −b )[x −(a −b )]=ax −bx −a 2+2ab −b 2S 2=3b (x −a )=3bx −3abS =S 1−S 2=(a −4b )x −a 2+5ab −b 2由题意得，若S为定值，则S将不随x的变化而变化可知当a−4b=0时，即a=4b时，S=−a2+5ab−b2为定值．故答案为：a=4b时，S为定值．。

第14章测试题及答案语文

第14章测试题及答案语文一、选择题（每题2分，共20分）1. 下列词语中，书写完全正确的一项是（）。

A. 翩跹起舞B. 心旷神怡C. 一愁莫展D. 风声鹤唳2. “落霞与孤鹜齐飞，秋水共长天一色”出自哪位诗人的作品？A. 李白B. 杜甫C. 王维D. 杜牧3. “不以物喜，不以己悲”体现了哪种人生态度？A. 乐观主义B. 悲观主义C. 现实主义D. 悲观现实主义4. 下列句子中，使用了拟人修辞手法的是（）。

A. 春风又绿江南岸B. 明月几时有，把酒问青天C. 疑是地上霜D. 独在异乡为异客5. “床前明月光”是哪位诗人的诗句？A. 李白B. 杜甫C. 王之涣D. 孟浩然二、填空题（每题2分，共10分）6. 《滕王阁序》的作者是______。

7. “春眠不觉晓，处处闻啼鸟”出自《______》。

8. “但愿人长久，千里共婵娟”是______的诗句。

9. “山重水复疑无路，柳暗花明又一村”出自《______》。

10. “夜来风雨声，花落知多少”是______的诗句。

三、简答题（每题10分，共30分）11. 请简述《岳阳楼记》中“先天下之忧而忧，后天下之乐而乐”的含义。

12. 请分析《出师表》中诸葛亮对刘备的忠诚表现。

13. 请解释“不以物喜，不以己悲”所体现的人生态度。

四、阅读理解题（每题15分，共30分）14. 阅读以下段落，回答问题：“山不在高，有仙则名。

水不在深，有龙则灵。

斯是陋室，惟吾德馨。

苔痕上阶绿，草色入帘青。

谈笑有鸿儒，往来无白丁。

可以调素琴，阅金经。

无丝竹之乱耳，无案牍之劳形。

南阳诸葛庐，西蜀子云亭。

孔子云：何陋之有？”（1）请解释“斯是陋室，惟吾德馨”的含义。

（2）文中提到的“南阳诸葛庐，西蜀子云亭”分别指的是什么？15. 阅读以下段落，回答问题：“独在异乡为异客，每逢佳节倍思亲。

遥知兄弟登高处，遍插茱萸少一人。

”（1）请解释“每逢佳节倍思亲”的含义。

（2）这首诗表达了作者怎样的情感？五、作文题（20分）16. 以“我眼中的秋天”为题，写一篇不少于800字的作文。

初中数学人教版八年级上册第十四章同步练习题带答案

初初初初初初初初初初初初初初初初初初初初初初初初14.1整式的乘法一、选择题1.计算3a2⋅a3的结果是()A. 4a5B. 4a6C. 3a5D. 3a62.要使(x2+ax+5)⋅(−6x3)的展开式中不含x4的项，则a应等于()D. 1A. −1B. 0C. 163.下列计算错误的是()A. (−a)⋅(−a)2=a3B. (−a)2⋅(−a)2=a4C. (−a)3⋅(−a)2=−a5D. (−a)3⋅(−a)3=a64.已知(x−3)(x2+mx+n)的乘积项中不含x2和x项，则m，n的值分别为()A. m=3，n=9B. m=3，n=6C. m=−3，n=−9D. m=−3，n=95.下列各式中，计算结果错误的是()．A. (x+2)(x−3)=x2−x−6B. (x−4)(x+4)=x2−16C. (2x+3)(2x−6)=2x2−3x−18D. (2x−1)(2x+2)=4x2+2x−26.若(x+m)(x+n)=x2−5x−15，则()A. m，n同时为正B. m，n同时为负C. m，n异号且绝对值小的为负D. m，n异号且绝对值大的为负7.已知a m=5，a n=2，则a m+n的值等于()A. 25B. 10C. 8D. 78.下列计算正确的是()A. (x3)2=x5B. (x3)2=x6C. (x n+1)2=x2n+1D. x3⋅x2=x6二、填空题9.若4x=3，则4x+2=________．10.若−x a+b y5与3x4y2b−a的和是单项式，则(2a+2b)(a−3b)的值为．11.若x3n=5，y2n=3，则x6n y4n的值为．12.计算：(m−n)·(n−m)3·(n−m)4=________．13.若m为正偶数，则(a−b)m⋅(b−a)n与(b−a)m+n的结果(填“相等”或“互为相反数”)．三、计算题14.计算：(1)(m−2n)(−m−n);(2)(x+1)(x2−x+1);(3)(a−b)(a2+ab+b2);(4)x(x2+x−1)−(2x2−1)(x−4)．四、解答题15.小明有一块长为m米，宽为n米的长方形玻璃，长、宽各裁掉a米后恰好能铺盖一张办公桌台面(玻璃与台面的大小相同)，则台面面积是多少？16.(1)已知m+4n−3=0，求2m⋅16n的值;(2)已知x2m=2，求(2x3m)2−(3x m)2的值．17.若x=2m+1，y=3+4m．(1)请用含x的式子表示y;(2)如果x=4，求此时y的值．18.(1)已知−2x3m+1y2n与4x n−2y6−m的积和−4x4y2是同类项，求m，n的值；a xb y+8与单项式4a2y b3x−y的和为单项式，求这两个单项式的积．(2)已知单项式−23答案和解析1.【答案】C【解析】解：3a2⋅a3=3a5．故选：C．直接利用单项式乘以单项式运算法则化简得出答案．此题主要考查了单项式乘以单项式运算，正确掌握相关运算法则是解题关键．2.【答案】B【解析】【分析】本题主要考查单项式乘多项式．先展开，然后根据不含x4项可知x4项的系数为0，计算即可．【解答】解：(x2+ax+5)⋅(−6x3)=−6x5−6ax4−30a3，∵展开式中不含x4的项，∴−6a=0，∴a=0，故选B．3.【答案】A【解析】【分析】本题考查了同底数幂的乘法，解答本题的关键是掌握同底数幂的乘法法则．根据同底数幂的乘法法则，结合选项进行判断即可．【解答】解：A、(−a)⋅(−a)2=−a3，原式计算错误，故本选项正确；B、(−a)2⋅(−a)2=a4，计算正确，故本选项错误；C、(−a)3⋅(−a)2=−a5，计算正确，故本选项错误；D、(−a)3⋅(−a)3=a6，计算正确，故本选项错误；故选A．4.【答案】A【解析】【分析】本题考查了多项式乘多项式法则，合并同类项时要注意项中的指数及字母是否相同．多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．不含某一项就是说这一项的系数为0．【解答】解：∵原式=x3+(m−3)x2+(n−3m)x−3n，又∵乘积项中不含x2和x项，∴(m−3)=0，(n−3m)=0，解得，m=3，n=9．故选A．5.【答案】C【解析】【分析】本题主要考查多项式乘多项式，根据多项式乘多项式的运算法则：用多项式的每一项去乘另一个多项式的每一项，再把所得的积相加，逐项计算即可求解．【解答】解：A.(x+2)(x−3)=x2−3x+2x−6=x2−x−6，故正确；B.(x−4)(x+4)=x2−4x+4x−16=x2−16，故正确；C.(2x+3)(2x−6)=4x2−12x+6x−18=4x2−6x−18，故错误；D.(2x−1)(2x+2)=4x2+4x−2x−2=4x2+2x−2，故正确；故选C．6.【答案】D【解析】【分析】本题主要考查多项式乘多项式．根据多项式乘多项式展开，求出m+n=−5，mn=−15，判断即可．【解答】解：(x+m)(x+n)=x2+(m+n)x+mn，∴m+n=−5，mn=−15，∵mn=−15<0，∴m，n异号，又∵m+n=−5<0，∴m，n中负数的绝对值大，故选D．7.【答案】B【解析】【分析】本题考查了同底数幂的乘法，同底数幂的乘法：底数不变指数相加，根据同底数幂的乘法，可得答案．【解答】解：∵a m=5，a n=2，∴a m+n=a m⋅a n=10，故选B．8.【答案】B【解析】【分析】本题主要考查同底数幂的乘法、幂的乘方、积的乘方的应用，着重培养学生的运算能力.解题的关键是会利用同底数幂的乘法、幂的乘方、积的乘方计算．【解答】A.(x3)2=x6，故A错误；B.(x3)2=x6，故B正确；C.(x n+1)2=x2n+2，故C错误；D.x3⋅x2=x3+2=x5，故D错误．故选B．9.【答案】48【解析】【分析】本题考查同底数幂的运算性质，代数式求值．根据a m●a n=a m+n，将所求代数式变形为4x+2=4x×42，再把4x=3代入计算即可．【解答】解：∵4x=3，∴4x+2=4x×42=3×16=48．故答案为48．10.【答案】−64【解析】【分析】此题考查了多项式乘多项式，以及合并同类项，熟练掌握同类项性质及运算法则是解本题的关键．根据题意得到两式为同类项，确定出a与b的值，代入原式计算即可求出值．【解答】解：∵−x a+b y5与3x4y2b−a的和是单项式，∴−x a+b y5与3x4y2b−a为同类项，即a+b=4①2b−a=5②①+②得b=3，再代入①得a=1，则(2a+2b)(a−3b)=(2+6)×(1−9)=−64，故答案为：−6411.【答案】225【解析】【分析】本题主要考查同底数幂的乘法、幂的乘方、积的乘方的应用。

八年级数学上册《第十四章幂的乘方》练习题附答案-人教版

八年级数学上册《第十四章幂的乘方》练习题附答案-人教版一、选择题1.已知3a＝1，3b＝2，则3a＋b的值为( )A.1B.2C.3D.272.下列运算正确的是( )A.2a+3b=5abB.a2•a3=a5C.(2a)3=6a3D.a6+a3=a93.下列运算正确的是( )A.a2•a3=a6B.(﹣a)4=a4C.a2+a3=a5D.(a2)3=a54.下列计算正确的是( )A.a3•a2=a6B.(﹣a2)3=a6C.a3+a4=a7D.a2•(a3)4=a145.计算(－a3)2的结果是( )A.－a5B.a5C.a6D.－a66.如果(a3)2=64，则a等于( )A.2B.-2C.±2D.以上都不对7.下列计算正确的是( )A.a﹣(b﹣c+d)=a+b+c﹣dB.3x﹣2x=1C.﹣x•x2•x4=﹣x7D.(﹣a2)2=﹣a48.计算(x2)3的结果为( )A.3x2B.x6C.x5D.x89.下列四个算式：(1)(x4)4=x4+4=x8；(2)[(y2)2]2=y2×2×2=y8； (3)(﹣y2)3=y6； (4)[(﹣x)3]2=(﹣x)6=x6.其中正确的有( )A.0个B.1个C.2个D.3个10.若m=2100，n=375，则m、n的大小关系正确的是（）A.m＞nB.m＜nC.相等D.大小关系无法确定二、填空题11.已知a3n=2，则a9n=_________.12.已知(x m)n＝x5，则mn(mn﹣1)的值为_______.13.计算：[(-x)2] n·[-(x3)n]=______．14.若5m=3，5n=2，则52m+n= ．15.计算：(x n)2+(x2)n﹣x n•x2=_______．16.如果1284×83=2n，那么n=________．三、解答题17.计算:a2·a4+(a2)318.计算:a3·a5+(－a2)4－3a819.计算：[(x＋y)3]6＋[(x＋y)9]2.20.计算：x4·x5·(－x)7＋5(x4)4－(x8)2；21.已知a＝12，mn＝2，求a2•(a m)n的值.22.已知a m＝5，a n＝3，求a2m＋3n的值．23.在比较216和312的大小时，我们可以这样来处理：∵216=(24)4=164，312=(33)4=274又∵16＜27∴164＜274，即216＜312.你能类似地比较下列各组数的大小吗？(1)2100与375；(2)3555，4444与5333.参考答案1.C2.B3.B4.D5.C6.C7.C8.B9.C10.B11.答案为：812.答案为：2013.答案为：-x5n；14.答案为：18.15.答案为：2x2n﹣x n+2．16.答案为：3717.解：原式=2a6；18.解：原式=-a8；19.解：原式=(x＋y)18＋(x＋y)18=2(x＋y)18.20.解：原式=－x16＋5x16－x16=3x16.21.解：原式=a2•a mn=a2+mn=(12)4=116.22.解：因为a m=5，a n=3所以a2m+3n=a2m·a3n=(a m)2·(a n)3 =52×33=25×27=675．23.解：(1)∵2100=(24)25=1625，375=(33)25=2725又∵16＜27∴1625＜2725，即2100＜375.(2)∵3555=(35)111=243111，4444=(44)111=256111，5333=(53)111=125111又∵125＜243＜256∴125111＜243111＜256111. 即5333＜3555＜4444.。

答案：第十四章练习题-健康管理服务营销

第十四章：健康管理服务营销1.（多选）正确答案：ABCE，消费者在购买、使用商品和接受服务时享有人身、财产安全不受损害的权利；享有自主选择商品或者服务的权利；享有公平交易的权利；享有依法成立维护自身合法权益的社会团体的权利；享有获得有关消费和消费者权益保护方面的知识的权利；消费者因购买、使用商品或者接受服务受到人身、财产损害的，享有依法获得赔偿的权利；在购买、使用商品和接受服务时，享有其人格尊严、民族风俗习惯得到尊重的权利；享有对商品和服务以及保护消费者权益工作进行监督的权利。

消费者有权检举、控告侵害消费者权益的行为和国家机关及其工作人员在保护消费者权益工作中的违法失职行为，有权对保护消费者权益提出批评、建议，但不包括没收不合格商品的权利。

2.（多选）正确答案：AC，消费者在购买、使用商品和接受服务时，享有其人格尊严、民族风俗习惯得到尊重的权利。

3.（多选）正确答案：ABCD，消费者在购买、使用商品和接受服务时享有人身、财产安全不受损害的权利；有权要求经营者提供的商品和服务，符合保障人身、财产安全的要求；4.（多选）正确答案：ABCD，消费者在购买、使用商品和接受服务时享有人身、财产安全不受损害的权利。

消费者有权要求经营者提供的商品和服务，符合保障人身、财产安全的要求。

消费者享有知悉其购买、使用的商品或者接受的服务的真实情况的权利。

消费者有权根据商品或者服务的不同情况，要求经营者提供商品的价格、产地、生产者、用途、性能、规格、等级、主要成分、生产日期、有效期限、检验合格证明、使用方法说明书、售后服务，或者服务的内容、规格、费用等有关情况。

消费者享有自主选择商品或者服务的权利。

消费者在自主选择商品或者服务时，有权进行比较、鉴别和挑选。

消费者享有公平交易的权利。

即知悉真实情况、自主选择、公平交易和获得赔偿的权利。

5.（单选）正确答案：B，《中华人民共和国民法通则》第17条规定：无民事行为能力或者限制民事行为能力的精神病人，由下列人员担任监护人：（一）配偶；（二）父母；（三）成年子女；（四）其他近亲属；（五）关系密切的其他亲属、朋友愿意承担监护责任，经精神病人的所在单位或者住所地的居民委员会、村民委员会同意的。

八年级数学上册《第十四章公式法》练习题附答案-人教版

八年级数学上册《第十四章公式法》练习题附答案-人教版一、选择题1.下列各式中，能用平方差公式因式分解的是( )A.x2+4y2B.x2﹣2y2+1C.﹣x2+4y2D.﹣x2﹣4y22.计算：852﹣152=( )A.70B.700C.4900D.70003.因式分解的结果是(2x－y)(2x＋y)的是 ( )A.－4x2＋y2B.4x2＋y2C.－4x2－y2D.4x2－y24.已知x2-y2=6，x-y=1，则x+y等于( )A.2B.3C.4D.65.下列因式分解正确的是( )A.6x＋9y＋3＝3(2x＋3y)B.x2＋2x＋1＝(x＋1)2C.x2﹣2xy﹣y2＝(x﹣y)2D.x2＋4＝(x＋2)26.下列各式中不能用完全平方公式因式分解的是( )A.-x2+2xy-y2B.x4-2x3y+x2y2C.(x2-3)2-2(3-x2)+1D.x2-xy+12y27.若多项式x2+mx+4能用完全平方公式分解因式，则m的值可以是( )A.4B.﹣4C.±2D.±48.若a+b=3,a-b=7,则b2-a2的值为( )A.-21B.21C.-10D.109.小明在抄因式分解的题目时，不小心漏抄了x的指数，他只知道该数为不大于10的正整数，并且能利用平方差公式因式分解，他抄在作业本上的式子是x□﹣4y2(“□”表示漏抄的指数)，则这个指数可能的结果共有( )A.2种B.3种C.4种D.5种10.如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“和谐数”如(8=32﹣12，16=52﹣32，即8，16均为“和谐数”)，在不超过2017的正整数中，所有的“和谐数”之和为( )A.255054B.255064C.250554D.255024二、填空题11.因式分解：m2﹣4= .12.因式分解：(2a+b)2﹣(a+2b)2= .13.计算：2 019×2 021-2 0202=__________.14填空根据题意填空：x2﹣6x+(______)=(x﹣______)215.已知x＋y＝0.2，x＋3y＝1，则代数式x2＋4xy＋4y2的值为________.16.观察下列各式：(1)42－12=3×5；(2)52－22=3×7；(3)62－32=3×9；………则第n(n是正整数)个等式为_____________________________.三、解答题17.因式分解：5x2+10x+518.因式分解：x2(x﹣y)+(y﹣x)19.因式分解：2a3-12a2＋18a20.因式分解：9a2(x﹣y)+4b2(y﹣x)21.在一块边长为a cm的正方形纸板中，四个角分别剪去一个边长为b cm的小正方形，利用因式分解计算：当a＝98 cm，b＝27 cm时，剩余部分的面积是多少？22.已知x－y=2，y－z=2，x＋z=4，求x2－z2的值.23.已知x2+y2﹣4x+6y+13=0，求x2﹣6xy+9y2的值.24.两位数相乘：19×11=209,18×12=216,25×25=625,34×36=1 224，47×43=2 021，…(1)认真观察，分析上述各式中两因数的个位数字、十位数字分别有什么联系，找出因数与积之间的规律，并用字母表示出来；(2)验证你得到的规律.25.中国古贤常说万物皆自然，而古希腊学者说万物皆数.同学们还记得我们最初接触的数就是“自然数”吧!在数的学习过程中，我们会对其中一些具有某种特性的自然数进行研究，我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“n喜数”.定义：对于一个两位自然数，如果它的个位和十位上的数字均不为零，且它正好等于其个位和十位上的数字的和的n倍(n为正整数)，我们就说这个自然数是一个“n喜数”.例如：24就是一个“4喜数”，因为24=4×(2+4)；25就不是一个“n喜数”因为25≠n(2+5).(1)判断44和72是否是“n喜数”？请说明理由；(2)试讨论是否存在“7喜数”若存在请写出来，若不存在请说明理由.参考答案1.C2.D3.D4.D5.B.6.D7.D8.A9.D10.D11.答案为：(m+2)(m﹣2).12.答案为：3(a+b)(a﹣b).13.答案为：-114.答案为：9，3；15.答案为：0.36.16.答案为：(n+3)2-n2=3(2n+3)17.解：原式=5(x2+2x+1)=5(x+1)2；18.解：原式=x2(x﹣y)+(y﹣x)=(x﹣y)(x2﹣1)=(x﹣y)(x+1)(x﹣1)；19.解：原式=2a(a-3)220.解：原式=(x﹣y)(3a+2b)•(3a﹣2b).21.解：根据题意，得剩余部分的面积是：a2－4b2＝(a＋2b)(a－2b)＝152×44＝6 688(cm2). 22.解：由x－y=2，y－z=2，得x－z=4.又∵x＋z=4∴原式=(x＋z)(x－z)=16.23.解：∵x2+y2﹣4x+6y+13=(x﹣2)2+(y+3)2=0∴x﹣2=0，y+3=0，即x=2，y=﹣3则原式=(x﹣3y)2=112=121.24.解：(1)上述等式的规律是：两因数的十位数字相等，个位数字相加等于10而积后两位是两因数个位数字相乘、前两位是十位数字相乘，乘积再加上这个十位数字之和；如果用m表示十位数字，n表示个位数字的话则第一个因数为10m＋n，第二个因数为10m＋(10－n)，积为100m(m＋1)＋n(10－n)；表示出来为：(10m＋n)[10m＋(10－n)]=100m(m＋1)＋n(10－n)；(2)∵左边=(10m＋n)(10m－n＋10)=(10m＋n)[10(m＋1)－n]=100m(m＋1)－10mn＋10n(m＋1)－n2=100m(m＋1)－10mn＋10mn＋10n－n2=100m(m＋1)＋n(10－n)=右边∴(10m＋n)[10m＋(10－n)]=100m(m＋1)＋n(10－n)，成立.25.解：(1)44不是一个“n喜数”，因为44≠n(4+4)72是一个“8喜数”，因为72=8(2+7)；(2)设存在“7喜数”，设其个位数字为a十位数字为b，(a，b为1到9的自然数)由定义可知：10b+a=7(a+b)化简得：b=2a因为a，b为1到9的自然数∴a=1，b=2；a=2，b=4；a=3，b=6；a=4，b=8；∴“7喜数”有4个：21、42、63、84.。

八年级数学上册《第十四章整式的乘法》练习题附带答案-人教版

八年级数学上册《第十四章整式的乘法》练习题附带答案-人教版一、选择题1.计算a·5ab=( )．A．5ab B．6a2b C．5a2b D．10ab2.计算：(﹣x)3•2x的结果是( )A.﹣2x4B.﹣2x3C.2x4D.2x33.若□×3xy＝3x2y，则□内应填的单项式是( )A.xyB.3xyC.xD.3x4.计算－3x(2x2－5x－1)的结果是( )A.－6x3＋15x2＋3xB.－6x2－15x2－3xC.－6x3＋15x2D.－6x3＋15x2－15.如果一个长方体的长为(3m－4)，宽为2m，高为m，则它的体积为( )A.3m3－4m2B.m2C.6m3－8m2D.6m2－8m6.满足2x(x－1)－x(2x－5)=12的x的值为( )A.0B.1C.2D.47.如果(x﹣2)(x＋3)＝x2＋px＋q，那么p、q的值为( )A.p＝5，q＝6B.p＝1，q＝﹣6C.p＝1，q＝6D.p＝5，q＝﹣68.若(x＋a)与(x＋3)的乘积中不含x的一次项，则a的值为( )A.3B.﹣3C.1D.﹣19.计算(2x－1)(5x＋2)等于( )A.10x2－2B.10x2－x－2C.10x2＋4x－2D.10x2－5x－210.请你计算:(1﹣x)(1＋x),(1﹣x)(1＋x＋x2),(1﹣x)(1＋x＋x2＋x3),…,猜想(1﹣x)(1＋x ＋x2＋…＋x n)的结果是( )A.1﹣x n＋1B.1＋x n＋1C.1﹣x nD.1＋x n二、填空题11.计算：．12.如果x n y4与2xy m相乘的结果是2x5y7，那么mn= ．13.计算：2x(3x2-x+1)=14.如图是一个L形钢条的截面，它的面积为________15.计算(1＋a)(1-2a)＋a(a-2)=________.16.已知x2+2x=3，则代数式(x+1)2﹣(x+2)(x﹣2)+x2的值为_____.三、解答题17.化简：(－3ab2)3·(－13 ac)218.化简：ab(3a﹣2b)+2ab2．19.化简：(2x﹣5)(3x＋2)；20.化简：x(4x＋3y)－(2x＋y)(2x－y)21.市环保局将一个长为2×106分米，宽为4×104分米，高为8×102分米的长方体废水池中的满池废水注入正方体贮水池净化，那么请你想一想，能否恰好有一个正方体贮水池将这些废水刚好装满？若有，求出正方体贮水池的棱长；若没有，请说明理由.22.先化简，再求值：3ab[(－2ab)2－3b(ab－a2b)＋ab2]，其中a=－1，b=13 .23.王老师家买了一套新房，其结构如图所示(单位：米)．他打算将卧室铺上木地板，其余部分铺上地砖．(1)木地板和地砖分别需要多少平方米？(2)如果地砖的价格为每平方米x元，木地板的价格为每平方米3x元，那么王老师需要花多少钱？24.若关于x的多项式(x2＋x-n)(mx-3)的展开式中不含x2和常数项，求m，n的值.25.将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内，未被覆盖的部分恰好分割为两个长方形，面积分别为S1和S2.已知小长方形纸片的长为a，宽为b，且a＞b.当AB长度不变而BC变长时，将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内，S1与S2的差总保持不变，求a，b满足的关系式.(1)为解决上述问题，如图3，小明设EF＝x，则可以表示出S1＝_______，S2＝_______；(2)求a，b满足的关系式，写出推导过程.参考答案1.C2.A.3.C4.A5.C6.D7.B.8.B.9.B10.A11.答案为：12.答案为：1213.答案为：6x3-2x2+2x.14.答案为：ac+bc-c2.15.答案为：-a2-3a＋116.答案为：817.原式=－3a5b6c218.原式=3a2b﹣2ab2+2ab2=3a2b．19.原式＝6x2＋4x﹣15x﹣10＝6x2﹣11x﹣10.20.原式=3xy＋y2；21.解：有.因为长方体废水池的容积为(2×106)×(4×104)×(8×102)=64×1012=(4×104)3所以正方体水池的棱长为4×104分米22.解：原式=21a3b3-6a2b3.将中a=－1，b=13代入，原式=-1.23.解：(1)卧室的面积是2b(4a﹣2a)＝4ab(平方米)厨房、卫生间、客厅的面积和是b·(4a ﹣2a﹣a)＋a·(4b﹣2b)＋2a·4b＝ab＋2ab＋8ab＝11ab(平方米)即木地板需要4ab平方米，地砖需要11ab平方米.(2)11ab·x＋4ab·3x＝11abx＋12abx＝23abx(元)，即王老师需要花23abx元.24.解：原式=mx3＋(m-3)x2-(3＋mn)x＋3n由展开式中不含x2和常数项，得到m-3=0，3n=0解得m=3，n=0.25.解：(1)a(x＋a)，4b(x＋2b)；(2)由(1)知：S1＝a(x＋a)，S2＝4b(x＋2b)∴S1－S2＝a(x＋a)－4b(x＋2b)＝ax＋a2－4bx－8b2＝(a－4b)x＋a2－8b2∵S1与S2的差总保持不变∴a－4b＝0.∴a＝4b.。

八年级数学上册《第十四章积的乘方》练习题附答案-人教版

八年级数学上册《第十四章积的乘方》练习题附答案-人教版一、选择题1.计算(-2a2)3的结果是( )A.-6a2B.-8a5C.8a5D.-8a62.计算(﹣2a2b)3的结果是（）A.﹣6a6b3B.﹣8a6b3C.8a6b3D.﹣8a5b33.下列计算正确的是( )A.(a2)3=a5B.2a﹣a=2C.(2a)2=4aD.a•a3=a44.计算(﹣3x2)3的结果是（）A.9x5B.﹣9x5C.27x6D.﹣27x65.计算﹣(﹣3a2b3)4的结果是( )A.81a8b12B.12a6b7C.﹣12a6b7D.﹣81a8b126.如果(a n•b m b)3=a9b15，那么( )A.m=4，n=3B.m=4，n=4C.m=3，n=4D.m=3，n=37.如果(2a m•b m+n)3=8a9b15，则( )A.m=3，n=2B.m=3，n=3C.m=6，n=2D.m=2，n=58.﹣x n与(﹣x)n的正确关系是( )A.相等B.互为相反数C.当n为奇数时它们互为相反数，当n为偶数时相等D.当n为奇数时相等，当n为偶数时互为相反数9.已知a=1.6×109，b=4103，则a2×2b=（）A.2×107B.4×1014C.3.2×105D.3.2×101410.已知2a=3，2b=6，2c=12，则a，b，c的关系为：①b=a+1；②c=a+2；③a+c=2b；④b+c=2a+3.其中正确的个数有( )A.1个B.2个C.3个D.4个二、填空题11.若x n＝2，y n＝3，则(xy)n＝________．12.计算：(﹣2xy2)3= ．13.填空：45×(0.25)5= (________×________)5= ________5= ________.14.计算：(-3a2)3= ．15.已知2m+5n-3=0，则4m×32n的值为．16.已知2a=5,2b=10,2c=50,那么a、b、c之间满足的等量关系是 .三、解答题17.计算：[(－3a2b3)3]2；18.计算：(2x2)3－x2·x419.计算：(－2xy2)6＋(－3x2y4)3；20.已知273×94=3x，求x的值．21.已知n是正整数，且x3n= 2，求(3x3n)3＋(－2x2n)3的值.22.已知x3m=2，y2m=3，求(x2m)3＋(y m)6－(x2y)3m·y m的值.23.(1)若2x+5y-3=0，求4x•32y的值.(2)若26=a2=4b，求a+b值.参考答案1.D2.B3.D4.D5.D6.A7.A8.D9.D10.D11.答案为：6.12.答案为：﹣8x3y6．13.答案为：4 0.25 1 114.答案为：-27a6．15.答案为：8.16.答案为：a+b=c.17.解：原式=729a12b18.18.解：原式=7x6；19.解：原式=37x6y12；20.解：因为273×94=(33)3×(32)4=39×38=39+8=317即3x=317，所以x=17．21.解：(3x3n)3＋(－2x2n)3= 33×(x3n)3＋(－2)3×(x3n)2= 27×8＋(－8)×4= 184.22.解：原式=－5.23.解：(1)8；(2)11或-5；。

八年级数学上册《第十四章因式分解》同步练习题及答案(人教版)

八年级数学上册《第十四章因式分解》同步练习题及答案(人教版)班级姓名学号一、单选题1．下列说法正确的是（）.A．不论x取何值，（x-1）0=1 B．6226的值比3224大C．多项式x2+x+1是完全平方式D．4´3100-399是11的倍数2．下列各式从左到右的变形属于因式分解的是（）A．x2−9=(x+3)(x−3)B．6x2y3=2x2⋅3y3C．(x+2)(x−3)=x2−x−6D．x2+2x+1=x(x+2)+13．已知m=1+√2，n=1−√2，且(7m2−14m+a)(3n2−6n−7)=8，则a的值等于（）A．－5 B．5 C．－9 D．94．若x3+x2+x+1=0，则x27+x26+…+x+1+x+…x26+x27的值是（）A．1 B．0 C．-1 D．25．如果二次三项式x2+px−6可以分解因式为（x+q）·（x-2），那么(p−q)2的值为（）A．2 B．3 C．4 D．96．a、b、c为某一三角形的三边，且满足a2+b2+c2=6a+8b+10c﹣50，则三角形是（）A．直角三角形B．等边三角形C．等腰三角形D．锐角三角形7．下列分解因式正确的是（）A．2x2−xy−x=2x(x−y−1)B．−xy2+2xy−3y=−y(xy−2x−3)C．x(x−y)−y(x−y)=(x−y)2D．x2−x−3=x(x−1)−38．小南是一位密码编译爱好者，在他的密码手册中有这样一条信息：a−b，x−1，3，x2+1，a，x+ 1分别对应下列六个字：你、爱、中、数、学、国，现将3a(x2−1)−3b(x2−1)因式分解，结果呈现的密码信息可能是（）A．你爱数学B．你爱学C．爱中国D．中国爱你二、填空题9．计算21×3.14+79×3.14的结果为．10．因式分解：ab2−4ab+4a=.11．若 mn = 1， m - n = 2，则 m2n - mn2的值是．12．有下列说法：①在同一平面内，过直线外一点有且只有一条直线与已知直线平行；②无论k取任何实数，多项式x2−ky2总能分解成两个一次因式积的形式；③已知二元一次方程组{x+y=6ax+y=4的解也是二元一次方程x−3y=−2的解，则a的值是2；④若x=2m+1，y=4m−3，则y=x2−4；其中正确的说法是.13．已知：整式A＝（n2﹣1）2+（2n）2，整式B＞0．尝试化简整式A．发现A＝B2，求整式B．联想由上可知，B2＝（n2﹣1）2+（2n）2，当n＞1时，n2﹣1，2n，B为直角三角形的三边长，如图．填写下表中B的值：直角三角形三边n2﹣1 2n B勾股数组Ⅰ/ 8勾股数组Ⅱ35 /三、解答题14．已知；a、b、c是△ABC的三边的长，且满足a3+ab2+bc2=ac2+a2b+b3，试判断△ABC的形状．15．用平方差公式因式分解（1）−3xy3+27x3y（2）4a2x2−16a2y2（3）(a+2)(a−8)+6a（4）81x4−y416．（1）因式分解：2a3−8a．（2）如图AB//CD，∠A=40°，∠D=45°求∠1和∠2的度数．17．如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字，与从个位到最高位依次排出的一串数字完全相同，那么我们把这样的自然数称为“和谐数”．例如自然数12321，从最高位到个位依次排出的一串数字是：1，2，3，2，1，从个位到最高位依次排出的一串数字仍是：1，2，3，2，1，因此12321是一个“和谐数”，再加22，545，3883，345543…都是“和谐数”．（1）请你直接写出3个四位“和谐数”；请你猜想任意一个四位“和谐数”能否被11整除？并说明理由；（2）已知一个能被11整除的三位“和谐数”，设其个位上的数字x（1≤x≤4，x为自然数），十位上的数字为y，求y与x的函数关系式．18．如图，在一块长为2x米，宽为x米的长方形广场中心，留一块长为2y米，宽为y米的活动场地，其余的地方做花坛．（1）求花坛的面积；（2）当x=45，y=35且修建花坛每平方米需花费50元时，则修建整个花坛需要多少元？19．阅读材料：将（x+y）2+2（x+y）+1分解因式．解：将x+y看成整体，令x+y＝A，则原式＝A2+2A+1＝（A+1）2，再将A还原，原式＝（x+y+1）2．上述材料解题过程用到了整体思想，整体思想是数学中的常用方法，请根据上面方法完成下列各小题．（1）因式分解：（m+n）2﹣6（m+n）+9；（2）设M＝（a﹣b）（a﹣b﹣2）+1．①因式分解M；②若M＝0，求a﹣b的值．参考答案1．D2．A3．C4．C5．C6．A7．C8．D9．31410．a(b−2)211．212．①13．15；3714．解：∵a3+ab2+bc2=ac2+a2b+b3∴（a3﹣a2b）+（ab2﹣b3）+（bc2﹣ac2）=0a2（a﹣b）+b2（a﹣b）﹣c2（a﹣b）=0（a﹣b）（a2+b2﹣c2）=0∴a=b或a2+b2=c2则三角形是等腰三角形或直角三角形．15．（1）解：原式=-3xy(y2-9x2)=-3xy(y+3x)(y-3x)（2）解：原式=4a2(x2-4y2)=4a2(x+2y)(x-2y)（3）解：原式=a2-8a+2a-16+6a=a2-16=(a+4)(a-4)（4）解：原式=(9x2+y2)(9x2-y2)= (9x2+y2)(3x+y)(3x−y)16．（1）解：原式=2a(a2−4)=2a(a+2)(a−2)．（2）解：∵AB//CD∴∠1=∠A=40°∵∠D=45°∴∠2=∠1+∠D=85°．17．（1）【解答】解：四位“和谐数”：1221，1331，1111，6666…（答案不唯一）任意一个四位“和谐数”都能被11整除，理由如下：设任意四位“和谐数”形式为：abcd，则满足：最高位到个位排列：d，c，b，a个位到最高位排列：a，b，c，d．由题意，可得两组数据相同，则：a=d，b=c则abcd11=1000a+100b+10c+d11=1000a+100b+10b+a11=91a+10b为正整数．∴四位“和谐数”能被11整数又∵a，b，c，d为任意自然数∴任意四位“和谐数”都可以被11整除；（2）【解答】设能被11整除的三位“和谐数”为：xyz，则满足：个位到最高位排列：x，y，z．最高位到个位排列：z，y，x．由题意，两组数据相同，则：x=z故 xyz=xyx=101x+10y故xyz11=101x+10y11=99x+11y+2x−y11=9x+y+2x−y11为正整数．故y=2x（1≤x≤4，x为自然数）．18．（1）解：根据题意可知长方形广场的面积为2x2平方米活动场地的面积为2y2平方米故花坛的面积为(2x2−2y2)平方米；（2）解：当x=45，y=35时2x2−2y2=2(x+y)(x−y)=2(45+35)(45−35)=2×80×10= 160050×1600=80000（平方米）答：修建整个花坛需要80000元．19．（1）解：令m+n＝A原式＝A2﹣6A+9＝（A﹣3）2再将A还原原式＝（m+n﹣3）2；（2）解：①M＝（a﹣b）（a﹣b﹣2）+1 =（a﹣b）[（a﹣b）﹣2]+1令a﹣b＝C则M＝C（C﹣2）+1＝C2﹣2C+1＝（C﹣1）2＝（a﹣b﹣1）2；②∵M＝0∴（a﹣b﹣1）2＝0∴a﹣b﹣1＝0∴a﹣b＝1∴a﹣b的值为1．。

第十四章胶体分散系统和大分子溶液练习题及答案

第十四章胶体分散系统和大分子溶液练习题一、选择题1．溶胶与大分子溶液的区别主要在于：(A) 粒子大小不同；(B) 渗透压不同；(C) 丁铎尔效应的强弱不同；(D) 相状态和热力学稳定性不同。

2．以下说法中正确的是：(A) 溶胶在热力学和动力学上都是稳定系统；(B) 溶胶与真溶液一样是均相系统；(C) 能产生丁达尔效应的分散系统是溶胶；(D) 通过超显微镜能看到胶体粒子的形状和大小。

3．由过量KBr与AgNO3溶液混合可制得溶胶，以下说法正确的是：(A) 电位离子是Ag+(B) 反号离子是NO3-(C) 胶粒带正电(D) 它是负溶胶。

4．将含0.012 dm3 NaCl 和0.02 mol·dm-3 KCl 的溶液和100 dm3 0.005 mol·dm-3的AgNO3液混合制备的溶胶，其胶粒在外电场的作用下电泳的方向是:(A) 向正极移动(B) 向负极移动(C) 不作定向运动(D) 静止不动5．将橡胶电镀到金属制品上，应用的原理是：(A) 电解(B) 电泳(C) 电渗(D) 沉降电势6．在大分子溶液中加入大量的电解质, 使其发生聚沉的现象称为盐析, 产生盐析的主要原因是：(A) 电解质离子强烈的水化作用使大分子去水化(B) 降低了动电电位(C) 由于电解质的加入，使大分子溶液处于等电点(D) 动电电位的降低和去水化作用的综合效应7．在H3AsO3的稀溶液中，通入过量的H2S 气体，生成As2S3溶胶。

用下列物质聚沉，其聚沉值大小顺序是：(A) Al(NO3)3＞MgSO4＞K3Fe(CN)6(B) K3Fe(CN)6＞MgSO4＞Al(NO3)3(C) MgSO4＞Al(NO3)3＞K3Fe(CN)6(D) MgSO4＞K3Fe(CN)6＞Al(NO3)38．对亚铁氰化铜负溶胶而言, 电解质KCl, CaCl2, K2SO4, CaSO4的聚沉能力顺序为：(A) KCl > CaCl2 > K2SO4 > CaSO4(B) CaSO4 > CaCl2 > K2SO4 > KCl(C) CaCl2 > CaSO4 > KCl > K2SO4(D) K2SO4 > CaSO4 > CaCl2 > KCl9．将大分子电解质NaR 的水溶液用半透膜和水隔开，达到Donnan 平衡时，膜外水的pH值：(A) 大于7 (B) 小于7 (C) 等于7 (D) 不能确定10．只有典型的憎液溶胶才能全面地表现出胶体的三个基本特性, 但有时把大分子溶液也作为胶体化学研究的内容, 一般地说是因为它们：(A) 具有胶体所特有的分散性,不均匀(多相)性和聚结不稳定性(B) 具有胶体所特有的分散性(C) 具有胶体的不均匀(多相)性(D) 具有胶体的聚结不稳定性11．溶胶的电学性质由于胶粒表面带电而产生,下列不属于电学性质的是：(A) 布朗运动(B) 电泳(C) 电渗(D) 沉降电势12．溶胶的聚沉速度与电动电位有关, 即:(A) 电动电位愈大，聚沉愈快(B) 电动电位愈小，聚沉愈快(C) 电动电位为零，聚沉愈快(D) 电动电位愈负，聚沉愈快13．Donnan平衡产生的本质原因是：(A) 溶液浓度大，大离子迁移速度慢；(B) 小离子浓度大，影响大离子通过半透膜；(C) 大离子不能透过半透膜且因静电作用使小离子在膜两边浓度不同；(D) 大离子浓度大，妨碍小离子通过半透膜。

2023-2024学年八年级数学上册《第十四章-乘法公式》同步练习题含答案(人教版)

2023-2024学年八年级数学上册《第十四章乘法公式》同步练习题含答案(人教版）学校:___________班级：___________姓名：___________考号：___________一、选择题：（本题共8小题，每小题5分，共40分．）1．下列运算正确的是（）A．B．C．D．2．计算:852-152等于( )A．70 B．700 C．4 900 D．7 0003．下列各式中，能用平方差公式计算的是（）（1）（a－2b）（－a+2b）；（2）（a－2b）（－a－2b）；（3）（a－2b）（a+2b）；（4）（a－2b）（2a+b）．A．（1）（2）B．（2）（3）C．（3）（4）D．（1）（4）4．已知a﹣b=5，（a+b）2=49，则a2+b2的值为（）A．25 B．27 C．37 D．44 5．···的个位数是（）A．4 B．5 C．6 D．86．有3张边长为a的正方形纸片，8张边长分别为a、b（b＞a）的矩形纸片，10张边长为b的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成个正方形（按原纸张进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（）A．a+5b B．a+4b C．2a+2b D．a+3b7．已知实数、、满足，下列结论正确的是（）A．可能为B．若、、中有两个数相等，则C．若，则D．若，则8．如图①，边长为a的大正方形中有四个边长均为b的小正方形，小华将阴影部分拼成了一个长方形（如图②），则这个长方形的面积为（）A．a2﹣4b2B．（a+b）（a﹣b）C．（a+2b）（a﹣b）D．（a+b）（a﹣2b）二、填空题：（本题共5小题，每小题3分，共15分．）9．计算：．10．已知(a＋b)2＝7，(a－b)2＝4，则 ab 的值为.11．七中有一正方形花坛，边长为am，现在把花坛边长增加3m，则这个花坛面积增加m．12．运用平方差公式计算：．13．如图，点M是AB的中点，点P在MB上.分别以AP，PB为边，作正方形APCD和正方形PBEF，连结MD和ME.设AP＝a，BP＝b，且a+b＝10，ab＝15.则图中阴影部分的面积为.三、解答题：（本题共5题，共45分）14．化简：.15．化简：．16．先化简，再求值(3a+2b)(2a﹣3b)﹣(a﹣2b)(2a﹣b)，其中．17．已知：关于x，y的二元一次方程组的解满足，求的值.18．有一张边长为厘米的正方形桌面，因为实际需要，需将正方形边长增加厘米，木工师傅设计了如图所示的三种方案：善于观察思考的小明发现：利用图形面积关系这三种方案都能验证公式：．对于方案一，小明是这样验证的：因为大正方形的面积可以看成：，又可以看成所以．解答下列问题：（1）公式验证：请根据方案二、方案三，分别写出公式的验证过程．方案二：方案三：（2）公式应用，已知实数a，均为正数，且a-b=2，ab=3，求的值．参考答案：1．【答案】D 2．【答案】D 3．【答案】B 4．【答案】C 5．【答案】C 6．【答案】D 7．【答案】D 8．【答案】A9．【答案】10．【答案】11．【答案】6a+912．【答案】25513．【答案】4514．【答案】解：.15．【答案】解：原式．16．【答案】解：(3a+2b)(2a﹣3b)﹣(a﹣2b)(2a﹣b)=(6a2+4ab﹣9ab﹣6b2)﹣(2a2-4ab﹣ab+2b2)=6a2+4ab﹣9ab﹣6b2﹣2a2+4ab+ab﹣2b2=4a2﹣8b2当a=﹣1.5 ，b= 时原式=4×( )2﹣8×( )2=9-= ．17．【答案】解：①+②得：②+①得：③+④得：又x+y=a∴，则a=9即x+y=9③-④得：∴x-y=7∴.18．【答案】（1）解：方案二：∵大正方形面积可以看成又可以看成∴；方案三：∵大正方形面积可以看成，又可以看成∴；（2）解：∵a-b=2∴∴∵ab=3∴∴，即∴a+b=±4。

八年级数学上册《第十四章同底数幂的乘法》练习题附带答案-人教版

八年级数学上册《第十四章同底数幂的乘法》练习题附带答案-人教版一、选择题1.式子a2m＋3不能写成( )A．a2m·a3 B．a m·a m＋3 C．a2m＋3 D．a m＋1·a m＋22.计算a6•a2的结果是( )A.a12B.a8C.a4D.a33.化简﹣b•b3•b4的正确结果是( )A.﹣b7B.b7C.-b8D.b84.若m·23=26，则m等于( )A.2B.4C.6D.85.若x m-5x2n-x6=0，则m、n的关系是（）A. m-n=6B.2m+n=5C.m+2n=11D.m-2n=76.下列各式中，计算过程正确的是（）A. x3+x3=x3+3=x6B.x3·x3=2x3=x6C. x·x3·x5=x0+3+5=x8D.x·(-x)3= -x2+3= -x57.x·x6·( )=x12，括号内填( )A.x6B.x2C.x5D.x8.如果a2n﹣1a n+5=a16，那么n的值为( )A.3B.4C.5D.69.若(a m+1b n+2)(a2n-1b2m)=a5b3，则m+n的结果是（）A.1B.2C.3D.-310.已知x+y﹣4=0，则2y•2x的值是( )A.16B.﹣16C.D.8二、填空题11.计算a3•a的结果是.12.计算：3a·a2＋a3=_______．13.计算 -a×(-a)2×(-a)3=______14.若a m=2,a n=3，则a m+n= ．15.若2x＋1＝16，则x＝______．16.已知4×5x+3=n，则用含n的代数式表示5x为____.三、解答题17.计算：a3•a2•a4+(﹣a)2；18.计算：10×10+102×102；19.计算：－x2·(－x)4·(－x)3；20.计算：(m－n)·(n－m)3·(n－m)4；21.已知4x=8，4y=32，求x＋y的值．22.已知4×2a×2a+1=29，且2a+b=8，求a b的值．23.已知(a＋b)a·(b＋a)b=(a＋b)5，且(a－b)a＋4·(a－b)4－b=(a－b)7，求a a b b的值.24.阅读下列材料：小明为了计算1＋2＋22＋…＋22017＋22018的值，采用以下方法：设S＝1＋2＋22＋…＋22017＋22018①则2S＝2＋22＋…＋22018＋22019②②－①得2S－S＝S＝22019－1∴S＝1＋2＋22＋…＋22017＋22018＝22019－1请仿照小明的方法解决以下问题：(1)1＋2＋22＋…＋29＝________；(2)3＋32＋…＋310＝________；(3)求1＋a＋a2＋…＋a n的和(a＞0，n是正整数，请写出计算过程).参考答案1.C2.B3.C4.D5.B6.D7.C8.B9.B10.A11.答案为：a 4.12.答案为：4a 313.答案为：a 6；14.答案为：6.15.答案为：3.16.答案为：500n 17.解：原式=a 9+a 2；18.原式=2000019.原式=－x 2·x 4·(－x 3)=x 2·x 4·x 3=x 9.20.原式=－(n －m)·(n －m)3·(n －m)4=－(n －m)1＋3＋4=－(n －m)8.21.解：4x ·4y =8×32=256=44而4x ·4y =4x ＋y ∴x ＋y=4.22.解：由题意得，2a+3=9解得：a=3则b=8﹣2a=8﹣6=2a b =9.23.解：∵(a ＋b)a ·(b ＋a)b =(a ＋b)5，(a －b)a ＋4·(a －b)4－b =(a －b)7∴⎩⎨⎧a ＋b ＝5，a ＋4＋4－b ＝7.解得⎩⎨⎧a ＝2，b ＝3.∴a a b b =22×33=108.24.解：(1)设S ＝1＋2＋22＋ (29)则2S＝2＋22＋ (210)②－①得2S－S＝S＝210－1∴S＝1＋2＋22＋…＋29＝210－1；(2)设S＝3＋32＋33＋34＋…＋310①，则3S＝32＋33＋34＋35＋…＋311②，②－①得2S＝311－3，所以S＝311－32，即3＋32＋33＋34＋ (310)311－32；(3)设S＝1＋a＋a2＋a3＋a4＋…＋a n①，则aS＝a＋a2＋a3＋a4＋…＋a n＋a n＋1②，②－①得：(a －1)S＝a n＋1－1，a＝1时，不能直接除以a－1，此时原式等于n＋1；a不等于1时，a－1才能做分母，所以S＝a n＋1－1a－1，即1＋a＋a2＋a3＋a4＋…＋a n＝a n＋1－1a－1.。

八年级数学上册《第十四章乘法公式》同步练习题及答案(人教版)

八年级数学上册《第十四章乘法公式》同步练习题及答案(人教版）学校:___________班级：___________姓名：___________考号：___________一、选择题：1．下列运算中，正确的是（） A ．336x x x ⋅= B ．235()x x = C ．232x x x ÷=D ．222()x y x y -=-2．设（a+b ）2=（a ﹣b ）2+A ，则A=（） A ．2ab B ．4ab C ．abD ．﹣4ab 3．若4a 2+kab+9b 2是完全平方式，则常数k 的值为（） A ．6 B ．12 C ．6±D ．12± 4．无论x ，y 取何值，多项式x 2+y 2-4x+6y+13的值总是（） A ．都是整数 B ．都是负数 C ．是零 D ．是非负数5．若()()22221135a b a b +++-=，则22a b +=（） A ．3B ．6C ．3±D ．6±6．我们把形如+b （a ，b +1型无理数，则2是（）A 型无理数B C D 型无理数7．已知： ()2(1)5a a a b ---=-. 求：代数式 222a b ab +- 的值为（）A ．-5B ．5C ．252D ．258．如图，大正方形的边长为m ，小正方形的边长为n ，x ，y 表示四个相同长方形的两边长（x>y ），则①x-y=n ；②xy= 224m n - ；③x 2-y 2=mn ；④x 2+y 2= 222m n - 中，正确的是（）A ．①②③B ．①②④C ．①③①D ．①②③①二、填空题：9．计算()()11a a +-的结果是 .10．多项式 2264x mx ++ 是完全平方式，则m= . 11．已知a+b=7，ab=6，则a 2+b 2的值为． 12．若 2111322a k a a ⎛⎫⎛⎫-=+- ⎪⎪⎝⎭⎝⎭ ，则k= . 13．杨辉三角，又称贾宪三角，是二项式系数在三角形中的一种几何排列，如图，观察下面的杨辉三角：按照前面的规律，则（a+b ）5= ．三、解答题：14．计算：32)(32)x y c x y c -+++（．15．计算下列各题（1）()222(2)x y xy -⋅-（2）24(1)(25)(25)x x x +-+-16．先化简，再求值： ()()()22235a b a b a b b +-+--，其中 12a =- 和 2b = ．17．已知4m n -=和3mn =-．（1）计算：22m n +；（2）求()()2244m n --的值；（3）求28324m n m n +⋅÷的值．18．当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图1可得等式：（a+2b）（a+b）＝a2+3ab+2b2．（1）由图2可得等式：．（2）利用（1）中所得到的结论，解决下面的问题：已知a+b+c＝13，ab+bc+ac＝52，求a2+b2+c2的值．（3）利用图3中的纸片（足够多），画出一种拼图，使该拼图可用来验证等式：（3a+b）（a+3b）＝3a2+10ab+3b2．参考答案：1．A 2．B 3．D 4．D 5．B 6．B 7．C 8．A 9．a 2-1 10．±8 11．37 12．3413．1a 5+5a 4b+10a 3b 2+10a 2b 3+5ab 4+1b 514．解：原式= ()()2323x c y x c y +-++⎡⎤⎡⎤⎣⎦⎣⎦ = ()()2223x c y +- = 222449x cx c y ++- . 15．（1）解： ()222(2)x yxy -⋅-42=4(2)x y xy ⋅- 53=8x y - ；（2）解： 24(1)(25)(25)x x x +-+-22=4(21)(425)x x x ++--22=484425x x x ++-+=829x + ．16．解：原式=a 2+4ab+4b 2﹣3a 2+ab ﹣3ab+b 2﹣5b 2 =﹣2a 2+2ab 当a 12=-，b=2时，原式 15222=--=-17．（1）解：4m n -= 3mn =-22m n ∴+ 2()2m n mn =-+()2423=+⨯- 166=- 10=；（2）解：()()2244m n --()222()416mn m n =-++当3mn =-，2210m n +=时原式2(3)41016=--⨯+94016=-+ 15=-；（3）28324m n m n +⋅÷3522(2)(2)(2)m n m n +=⋅÷3524222m n m n +=⋅÷ 352422m n m n ++=÷ 35242m n m n +--= 2m n +=4m n -= 3mn =-2()m n ∴+ 2()4m n mn =-+()2443=+⨯- 1612=- 4=2m n ∴+=或2- 2m n +∴ 22=或22-4=或14．18．（1）（a+b+c ）2＝a 2+b 2+c 2+2ab+2ac+2bc （2）解：∵a+b+c ＝13，ab+bc+ac ＝52 ∴（a+b+c ）2＝a 2+b 2+c 2+2（ab+ac+bc ）即（13）2＝a 2+b 2+c 2+2×52 ∴a 2+b 2+c 2＝65（3）解：如图：。

《生理学》第十四章心血管系统疾病的生物化学检验练习题及答案

第十四章心血管系统疾病的生物化学检验练习题及答案一、学习目标1.掌握：肌酸激酶及其同工酶、乳酸脱氢酶及其同工酶、心肌肌钙蛋白、肌红蛋白、心型脂肪酸结合蛋白、C-反应蛋白、同型半胱氨酸、缺血修饰性白蛋白测定的方法学评价、临床意义和应用评价。

2.熟悉：B型利钠肽及B型利钠肽原N端肽测定的临床意义和应用评价。

3.了解：心脏的结构和功能；心血管系统疾病的病理生理机制；理想的心肌损伤标志物的特点。

二、习题（一）填空题1.AST在AMI发生后升高，达高峰。

2.血清CK-MB活性水平在AMI发病后开始出现增高，即可达到峰值。

3.血清LDH有5种同工酶，AMI发生后升高更为明显是，并导致比值升高。

4.肌钙蛋白是横纹肌的结构蛋白，存在于心肌和骨骼肌肌原纤维的细丝中，与钙结合的部分称为肌钙蛋白C，含抑制因子部分称为，与原肌球蛋白结合的部分称为。

5.肌红蛋白是一种，广泛存在于骨骼肌、心肌和平滑肌中，分子量大约为17.8 kD，小于乳酸脱氢酶，且位于细胞质内，故心肌损伤后。

6.判断再灌注干预效果，应动态检测或，确定有无冲洗小峰或高且持续时间长的再灌注损伤新峰。

（二）单项选择题A型题1.心肌损伤标志物中，用于排除AMI发生的较好指标是A.MbB.cTnIC.CK-MBD.cTn TE.CK2.血清CK-MB活性水平在AMI发病后达到峰值的时间是A.2～4小时B.4～6小时C.6～9小时D.9～24小时E.24～48小时3.AMI发病后能够判断再梗死的心肌酶是A.CK-MMB.CK-MBC.CK-BBD.LDHE.AST4.检测血清CK- MB特异性最佳的方法是A.单克隆抗体法（质量检测法）B.离子交换色谱法C.免疫抑制法D.电泳法E.比色法5.组成LDH2的亚基为A.M4 B.HM3C.H2M2D.H3M E.H46.诊断心肌梗死发生一周以上的心肌酶是A.CK-MMB.CK-MBC.CK-BBD.ASTE.LDH7.肌钙蛋白由几种亚基组成A.2B.3C.4D.5E.68.诊断心肌损伤确定性标志物是A.LDHB.CK-MBC.CK-MMD.cTnE.AST9.肌红蛋白（Mb）在AMI后出现在血清中的时间为A.1小时B.2小时C.3小时D.4～6小时E.8～12小时10.有关肌钙蛋白的评价，下列说法正确的是A.cTn在溶栓治疗成功后立即下降B.cTn检测对于微小心肌损伤的敏感度低于CKC.cTn在AMI发作时，只在6～48小时内维持增高D.cTn可敏感地测出小灶可逆性心肌损伤的存在E.cTn定量测定对于判断急性心肌梗死面积大小无意义11.下列心肌损伤标志物中，具有较好的阴性预测值，用于排除AMI的较好指标是A.CKB.CK-MBC.LDHD.cTnE.Mb12.以下为冠心病明确危险因素的是A.ALP升高B.白蛋白增高C.糖耐量异常D.HDL升高E.ALT增高13.下列关于CRP的说法，正确的是A.是炎症时淋巴因子刺激肝脏和上皮细胞合成，在感染、创伤、手术时可增高B.在AMI发生过程中最先升高C.CRP降低反映动脉粥样硬化存在明显的炎症过程和粥样斑块破裂脱落D.AMI患者hs- CRP检测可明确诊断E.溶栓治疗AMI患者的CRP升高与心梗范围密切相关14.下列有关BNP特征的描述正确的是A.BNP有很高的阴性预测价值，BNP正常可排除心力衰竭的存在B.BNP升高程度和CHF严重程度不一致C.BNP在机体中起保钠、利尿、收缩血管的生理作用D.怀疑AMI患者检查BNP，可行早期诊断E.对于呼吸困难患者，BNP不是一个将来发生CHF的预示因子15.胸痛发作12小时疑为急性心肌梗死者，推荐检测的心肌标志物是A.CKB.MbC.ASTD. cTnTE.LDH16.可用于微小心肌损伤诊断的标志物是A.CKB.ASTC.LDHD.ALTE.cTn T17.胸痛发作2小时疑为急性心肌梗死者，推荐检测的心肌标志物是A.CKB.MbC.ASTD.cTn TE.LDH118.下列血清心肌标志物升高持续时间最长的是A.MbB.CK-MBC.cTn ID.H-FABPE.AST19.急性心肌梗死时，最先恢复正常的酶是A.ALTB.LDHC.CKD.ASTE.α-HBDH20.下列属传统心肌酶谱项目而现趋于淘汰的是A.ALTB.BNPC.CK-MBD.ASTE.ALP21.心肌损伤时血清LDH同工酶的变化为A.LDH1>LDH2B.LDH2> LDH1C.LDH3>LDH2D.LDH4 > LDH3E.LDH5>LDH422.下述心肌损伤标志物中分子量最小的是A.H-FABPB.cTn IC.CK-MBD.cTn TE.Mb23.CK作为心脏标志物的叙述中，不正确的是A.快速、经济、有效，是当今应用最广泛的心肌损伤标志物B.其浓度与急性心肌梗死面积有一定关联，可大致判断梗死范围C.诊断特异性强，对心肌微小损伤敏感D.能用于测定心肌再梗死E.能用于判断再灌注损伤24.下列有关CRP的描述，不正确的选项是A.CRP和冠心病密切相关，被看作独立的危险因素B.CRP和冠脉不良预后关系密切，是冠心病一个长期或短期的危险因素C.在AMI发生后6小时在血中才能测得升高的CRPD.CRP和TC/HDL联合分析，可大大提高预测冠心病的准确性E.CRP的升高反映动脉硬化存在低度的炎症过程和粥样斑块的脱落25.通常不能用来评估溶栓疗效的指标是A.cTn TB.cTn IC.CK-MBD.LDHE.CK26.下列有关肌钙蛋白应用评价的说法不正确的是A.cTn敏感度高于CKB.cTn检测特异性高于CK-MB活性检测C.cTn可用于判断再灌注是否成功D.cTn用于诊断近期发生再梗死效果最好E.窗口期较CK长，有利于诊断迟到的急性心肌梗死和不稳定型心绞痛27. IFCC建议将心肌损伤标志物测定周期控制在多长时间之内较合适A.4小时B.3小时C.2小时D.1小时E.0.5小时28.下列关于脂肪酸结合蛋白（FABP）的特性描述，不正确的是A.FABP是分子量较肌红蛋白更小的胞质蛋白B.心肌内FABP含量较Mb低C.FABP能和脂肪酸结合，在心肌脂代谢中起重要作用D.FABP诊断早期AMI的敏感性与Mb相近，比CK-MB高E.临床用Mb/FABP可用于区分心肌损伤及骨骼肌损伤29. BNP与下列哪项指标联合应用，对急性不稳定性心力衰竭(HF)的危险分层更准确A.CK-MBB.MbC.cTnD.LDHE.MLC30.以下不是冠心病危险因子的是A.纤维蛋白原增高B.C反应蛋白增高C.HDL增高D.凝血因子增高E.血胆固醇( TCH)增高B型题（1～3题共用备选答案）A.免疫抑制法B.电泳法C.酶联-紫外连续监测法D.层析法E.荧光法1.目前临床检测LDH同工酶常用的方法是B2.目前临床检测CK-MB常用的方法是A3.目前临床检测AST常用的方法是C（4～7题共用备选答案）D.cTnE.MbA.CKB.CK-MBC.LDH14.与碳酸酐酶Ⅲ联合检测可提高AMI诊断特异性的是E5.目前作为心肌损伤确诊标志物的是D6.AMI发生后，血中出现最早的损伤标志物是E7.AMI发生后，血中出现高峰浓度最晚的标志物是C（8～9题共用备选答案）E.ASTA.CKB.MbC.LDHD.LDH18.诊断AMI特异性最差的是E9.用于心肌再灌注损伤判断的较好指标是A（三）简答题1.简述免疫抑制法测定CK- MB的方法原理。

八年级数学上册《第十四章因式分解》同步练习及答案-人教版

八年级数学上册《第十四章因式分解》同步练习及答案-人教版学校:___________班级：___________姓名：___________考号：___________一、单选题1．已知x+y=−4，xy=3，则x2+y2=（）．A．22B．10C．13D．52．下列等式从左到右变形，属于因式分解的是（）A．x3−x2=x(x2−1)B．x2−2x+1=(x−1)2)D．x2+6x+8=x(x+6)+8C．2a−1=a(2−1a⋅(m2−1)的结果是（）3．计算2÷1+m1−mA．﹣m2﹣2m﹣1 B．2(m﹣1)2C．2m2﹣4m﹣2 D．﹣2m2+4m﹣24．下列多项式中，不能用提公因式法因式分解的是（）A．x3﹣x+1 B．（a﹣b）﹣4（b﹣a）2C．11a2b﹣7b2D．5a（m+n）﹣3b2（m+n）5．下列因式分解正确的是（）A．x2+y2=（x+y）2B．y2﹣x2=（x+y）（y﹣x）C．x2+2xy﹣y2=（x﹣y）2D．x2﹣2xy+y2=（x+y）（x﹣y）6．多项式m2－4n2与m2－4mn＋4n2的公因式是（）A．（m＋2n）（m－2n) B．m＋2nC．m－2n D．（m＋2n）（m－2n）27．已知多项式ax2+bx+c因式分解的结果为(x−1) . (x+4)则abc为（）A．12 B．9 C．-9 D．-128．如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“友好数”如（8=32−12,16= 52−32，即8,16均为“友好数”），在不超过2020的正整数中，所有的“友好数”之和为（）A．255054 B．255064 C．250554 D．255024二、填空题9．因式分解：4a3﹣16a= ．10．已知m−n=3，则m2−n2−6n的值11．多项式9x2+1加上单项式后,能成为一个含x的三项式的完全平方式.12．已知ab=2，2a−b=−3则代数式2a2b−ab2的值为.13．如图，边长为a，b的长方形的周长为16，面积为10，则a²b+ab²= 。

八年级上册生物第十四章丰富多彩的生物世界 1至4节知识点+习题与答案解析

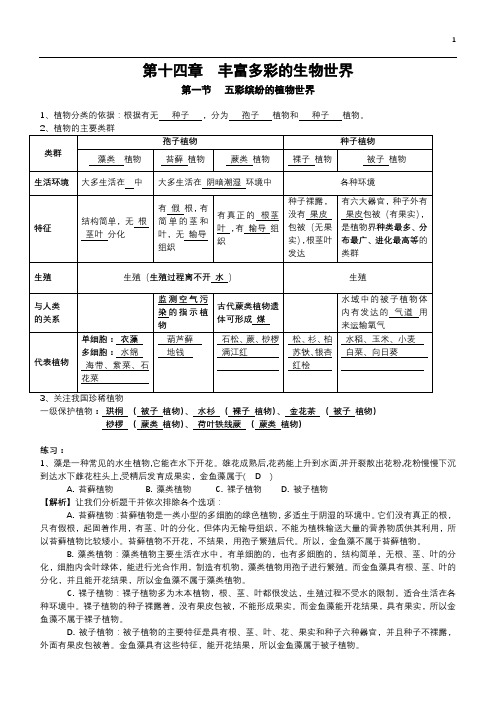
第十四章丰富多彩的生物世界第一节五彩缤纷的植物世界1、植物分类的依据：根据有无种子，分为孢子植物和种子植物。

一级保护植物：珙桐（被子植物）、水杉（裸子植物）、金花茶（被子植物）桫椤（蕨类植物）、荷叶铁线蕨（蕨类植物）练习：1、藻是一种常见的水生植物,它能在水下开花。

雄花成熟后,花药能上升到水面,并开裂散出花粉,花粉慢慢下沉到达水下雌花柱头上,受精后发育成果实，金鱼藻属于( D)A. 苔藓植物B. 藻类植物C. 裸子植物D. 被子植物【解析】让我们分析题干并依次排除各个选项：A. 苔藓植物：苔藓植物是一类小型的多细胞的绿色植物，多适生于阴湿的环境中。

它们没有真正的根，只有假根，起固着作用，有茎、叶的分化，但体内无输导组织，不能为植株输送大量的营养物质供其利用，所以苔藓植物比较矮小。

苔藓植物不开花，不结果，用孢子繁殖后代。

所以，金鱼藻不属于苔藓植物。

B. 藻类植物：藻类植物主要生活在水中，有单细胞的，也有多细胞的，结构简单，无根、茎、叶的分化，细胞内含叶绿体，能进行光合作用，制造有机物，藻类植物用孢子进行繁殖。

而金鱼藻具有根、茎、叶的分化，并且能开花结果，所以金鱼藻不属于藻类植物。

C. 裸子植物：裸子植物多为木本植物，根、茎、叶都很发达，生殖过程不受水的限制，适合生活在各种环境中。

裸子植物的种子裸露着，没有果皮包被，不能形成果实。

而金鱼藻能开花结果，具有果实，所以金鱼藻不属于裸子植物。

D. 被子植物：被子植物的主要特征是具有根、茎、叶、花、果实和种子六种器官，并且种子不裸露，外面有果皮包被着。

金鱼藻具有这些特征，能开花结果，所以金鱼藻属于被子植物。

综上所述，金鱼藻属于被子植物。

故答案为：D. 被子植物。

2【分析】苔藓植物，有茎叶的分化，无根，用孢子繁殖后代；蕨类植物有了根、茎、叶的分化，并且体内开始有了输导组织，因此一般比较高大，用孢子繁殖后代；裸子植物用种子繁殖后代，种子外无果皮包被着；被子植物用种子繁殖后代，种子外有果皮包被着。

第十四章练习题及答案

法考真题：马工程《民事诉讼法》第十四章 普通程序练习题及答案

八年级数学上册《第十四章 乘法公式》同步练习题及答案(人教版)

第14章测试题及答案语文

初中数学人教版八年级上册第十四章同步练习题带答案

八年级数学上册《第十四章 幂的乘方》练习题附答案-人教版

答案：第十四章练习题-健康管理服务营销

八年级数学上册《第十四章 公式法》练习题附答案-人教版

八年级数学上册《第十四章整式的乘法》练习题附带答案-人教版

八年级数学上册《第十四章 积的乘方》练习题附答案-人教版

八年级数学上册《第十四章 因式分解》同步练习题及答案(人教版)

第十四章胶体分散系统和大分子溶液练习题及答案

2023-2024学年八年级数学上册《第十四章-乘法公式》同步练习题含答案(人教版)

八年级数学上册《第十四章同底数幂的乘法》练习题附带答案-人教版

八年级数学上册《第十四章 乘法公式》同步练习题及答案(人教版)

《生理学》第十四章心血管系统疾病的生物化学检验练习题及答案

八年级数学上册《第十四章 因式分解》同步练习及答案-人教版

八年级上册生物 第十四章 丰富多彩的生物世界 1至4节知识点+习题与答案解析

法考真题：马工程《民事诉讼法》第十四章普通程序练习题及答案

八年级数学上册《第十四章乘法公式》同步练习题及答案(人教版)

八年级数学上册《第十四章幂的乘方》练习题附答案-人教版

八年级数学上册《第十四章公式法》练习题附答案-人教版

八年级数学上册《第十四章积的乘方》练习题附答案-人教版

八年级数学上册《第十四章因式分解》同步练习题及答案(人教版)

八年级数学上册《第十四章乘法公式》同步练习题及答案(人教版)

八年级数学上册《第十四章因式分解》同步练习及答案-人教版

八年级上册生物第十四章丰富多彩的生物世界 1至4节知识点+习题与答案解析