最小二乘法的基本原理和多项式拟合
最小二乘多项式拟合

最小二乘多项式拟合最小二乘多项式拟合,是一种常用的数据拟合方法,在各个学科领域都有广泛的应用。
它通过寻找最佳拟合曲线来近似描述一组离散数据点的趋势和规律。
在工程、统计学、经济学等领域,这种方法被广泛用于数据分析、曲线预测和模型建立。
首先,我们来看一下最小二乘拟合的基本原理。
在数据拟合过程中,我们通常假设数据是由一个未知函数生成的,而我们的目标是找到一个多项式函数,使得该多项式函数与数据之间的拟合误差最小。
为了达到这个目标,最小二乘拟合采用了最小化残差平方和的策略。
残差即为观测值与拟合值之间的差值,通过求解残差平方和的最小值,我们可以得到最佳拟合曲线的参数。
在最小二乘多项式拟合中,我们通常假设待拟合的数据点(x,y)满足下述形式的多项式方程:y=a0+a1*x+a2*x^2+...+ an*x^n,其中a0,a1,a2,...,an为待求的参数。
我们可以通过求解该多项式方程的系数,得到最佳拟合曲线。
在实际应用中,为了选择最佳的多项式次数,我们需要考虑过拟合和欠拟合的问题。
过拟合指的是模型过于复杂,过度适应了训练数据,但对新数据的预测效果较差;欠拟合则代表模型过于简单,无法很好地拟合数据的真实规律。
为此,我们可以引入交叉验证等方法,来选择合适的多项式次数,以平衡模型的复杂度和拟合能力。
此外,最小二乘多项式拟合还可以应用于数据的预测和模型建立。
对于已知的数据点,我们可以通过最小二乘方法拟合得到多项式函数,进而预测未知数据点的值。
这在实际中有很多应用,比如股票市场预测、天气预测等。
同时,最小二乘拟合还可以作为其他模型的基础,用于构建更复杂的模型,如神经网络、支持向量机等。
最后,最小二乘多项式拟合方法还有一些应注意的问题。
由于数据的分布情况和噪声的存在,最小二乘拟合可能对异常值比较敏感,因此需要在拟合过程中进行数据清洗和异常值处理。
此外,最小二乘拟合假设了数据之间是无相关的,因此在某些情况下,如时间序列数据的拟合中,可能并不适用。
直线拟合的四种方法

直线拟合的四种方法直线拟合是一种常见的数据分析方法,用于找到一条直线来描述数据集中的趋势。
在实际应用中,直线拟合常用于回归分析、统计建模、机器学习等领域。
下面将介绍四种常用的直线拟合方法。
1. 最小二乘法(Least Squares Method)最小二乘法是最常见的直线拟合方法之一、该方法的基本思想是通过最小化实际观测数据点与直线的残差平方和来确定最佳拟合直线。
具体步骤如下:(1)给定包含n个数据点的数据集;(2) 设直线方程为y = ax + b,其中a为斜率,b为截距;(3)计算每个数据点到直线的垂直距离,即残差;(4)将残差平方和最小化,求解a和b的值。
2. 总体均值法(Method of Overall Averages)总体均值法也是一种常用的直线拟合方法。
该方法的基本思想是通过计算数据集的x和y的均值,将直线拟合到通过这两个均值点的直线上。
具体步骤如下:(1)给定包含n个数据点的数据集;(2) 计算x和y的均值,即x_mean和y_mean;(3) 利用直线方程y = a(x - x_mean) + y_mean拟合数据。
3. 多项式拟合法(Polynomial Fitting Method)多项式拟合法是一种常见的直线拟合方法,适用于数据集中存在非线性趋势的情况。
该方法的基本思想是通过将数据拟合到多项式模型,找到最佳拟合直线。
具体步骤如下:(1)给定包含n个数据点的数据集;(2) 设多项式方程为y = a0 + a1*x + a2*x^2 + ... + an*x^n;(3) 通过最小二乘法求解a0, a1, a2, ..., an的值;(4)通过求解得到的多项式方程进行数据拟合。
4. 支持向量机(Support Vector Machine)支持向量机是一种经典的机器学习方法,适用于直线拟合问题。
该方法的基本思想是找到离数据集最近的点,然后构建一条平行于这两个点的直线。
具体步骤如下:(1)给定包含n个数据点的数据集;(2)将数据点划分为两个类别,如正类和负类;(3)找到离两个类别最近的点,将其作为支持向量;(4)根据支持向量构建一条平行于两个类别的直线,使得两个类别之间的间隔最大化。
最小二乘法原理

最小二乘法原理1. 概念 最小二乘法多项式曲线拟合,根据给定的m 个点,并不要求这条曲线精确地经过这些点,而是曲线y=f(x)的近似曲线y= φ(x)。
2. 原理给定数据点pi(xi,yi),其中i=1,2,…,m 。
求近似曲线y= φ(x)。
并且使得近似曲线与y=f(x)的偏差最小。
近似曲线在点pi 处的偏差δi= φ(xi)-yi ,i=1,2,...,m 。
常见的曲线拟合方法:1. 是偏差绝对值最小11min (x )y m mi i i i i φδφ===-∑∑ 2. 是最大的偏差绝对值最小min max (x )y i i i iφδϕ=- 3. 是偏差平方和最小2211min ((x )y )m mii i i i φδϕ===-∑∑ 按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。
推导过程:1. 设拟合多项式为:01...k k y a a x a x =+++2. 各点到这条曲线的距离之和,即偏差平方和如下:22011(...)m k i i k i i R y a a x a x =⎡⎤=-+++⎣⎦∑ 3. 为了求得符合条件的a 值,对等式右边求ak 偏导数,因而我们得到了:0112(...)0m k i k i i y a a x a x =⎡⎤--+++=⎣⎦∑0112(...)0m k ik i i y a a x a x x =⎡⎤--+++=⎣⎦∑……..0112( 0k k i k i i y a a x a x x =⎡⎤--+++=⎣⎦∑4. 将等式简化一下,得到下面的式子01111...n n nki k ii i i i a n a x a x y ===+++=∑∑∑ 21011111...n n n nk i ik i i i i i i i a x a x a x y x +====+++=∑∑∑∑ ……12011111...n n n nkk k k ii k i i i i i i i a x a x a x y x +====+++=∑∑∑∑ 5. 把这些等式表示成矩阵形式,就可以得到下面的矩阵:11102111111121111.........n n n k i i i i i i n n n n k i i i i i i i i i n n n n k k k k k i i i i i i i i i n x x y a a x x x x y a x x x x y ===+====+====⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦∑∑∑∑∑∑∑∑∑∑∑ 6. 将这个范德蒙矩阵化简后得到:011112221...1...1...k k k k n n n a y x x a y x x a y x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦。
最小二乘法的基本原理和多项式拟合matlab实现_0

---------------------------------------------------------------最新资料推荐------------------------------------------------------ 最小二乘法的基本原理和多项式拟合matlab实现最小二乘法的基本原理和多项式拟合 matlab 实现最小二乘法的基本原理和多项式拟合一、最小二乘法的基本原理从整体上考虑近似函数 p(x) 同所给数据点(xi, yi) (i=0, 1, , m) 误差 ri p(xi) yi(i=0, 1, , m) 的大小,常用的方法有以下三种:一是误差 riri p(xi) yi(i=0, 1, , m) 绝对值的最大值max0 i m,即误差向量 r (r0, r1, rm) T 的范数;二是误差绝对值的和i 0mri,即误差向量 r 的 1范数;三是误差平方和 i 0 rm2i 的算术平方根,即误差向量 r 的 2范数;前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑 2范数的平方,因此在曲线拟合中常采用误差平方和 i 0 体大小。
rm2i 来度量误差 ri(i=0, 1,, m) 的整数据拟合的具体作法是:对给定数据 (xi, yi) (i=0, 1, , m) ,在取定的函数类中,求 p(x) , 使误差 ri p(xi) yi(i=0, 1, , m)的平方和最小,即 i 0 rm2i i 0 p(x) y iim2 min 从几何意义上讲,就是寻求与给定点(xi, yi) (i=0, 1, , m) 的距离平方和为最小的曲线y p(x) (图 6-1)。
函数 p(x) 称为拟合函数或最小二乘解,求拟合函数 p(x) 的1 / 15方法称为曲线拟合的最小二乘法。
在曲线拟合中,函数类可有不同的选取方法 .61 二多项式拟合为所有次数不超过 n(n m) 的多项式构假设给定数据点(xi, yi) (i=0, 1, , m) , pn(x) akxkk 0n 成的函数类,现求一 m , 使得 2 I pn(xi) yi i 0 2 n akxik yi mini 0 k0 (1) m 当拟合函数为多项式时,称为多项式拟合,满足式(1)的 pn(x) 称为最小二乘拟合多项式。
最小二乘法的原理及在建模中的应用分析

最小二乘法的原理及在建模中的应用分析最小二乘法(least squares method)是一种数学优化方法,用于解决线性回归和非线性回归问题,通过求取使得误差平方和最小化的参数估计值。
它的原理是寻找一条最佳拟合曲线或平面,使得观测值与拟合值之间的误差最小。
在线性回归问题中,最小二乘法可以用来估计回归模型的参数。
假设我们有n个样本点{(x1, y1), (x2, y2), ..., (xn, yn)},其中yi是对应的观测值,我们想要找到一个线性模型y = ax + b,使得拟合值与观测值之间的误差最小。
这个问题可以通过最小化误差平方和来求解。
误差平方和定义为E(a, b) = Σ(yi - (axi + b))^2,我们需要找到使得E(a, b)最小的a和b。
∂E/∂a = -2Σ(xi(yi - (axi + b))) = 0∂E/∂b = -2Σ(yi - (axi + b)) = 0将上述方程进行化简,可以得到如下的正规方程组:Σ(xi^2)a + Σ(xi)b = Σ(xi yi)Σ(xi)a + nb = Σ(yi)解这个方程组,可以得到最小二乘估计的参数值。
1.线性回归分析:最小二乘法可以用于估计线性回归模型的参数。
通过最小二乘估计,可以得到最佳拟合直线,并用这条直线来预测因变量。
2.时间序列分析:最小二乘法可以用于拟合时间序列模型。
通过寻找最佳拟合函数,可以识别出序列中的趋势和周期性变化。
3.统计数据处理:最小二乘法可以用于数据平滑和滤波处理。
通过拟合一个平滑曲线,可以去除数据中的噪声和不规则波动,从而提取出数据中的趋势信息。
4.多项式拟合:最小二乘法可以用于多项式拟合。
通过最小二乘估计,可以拟合出多项式函数,将其用于数据拟合和函数逼近。
5.曲线拟合:最小二乘法可以用于非线性曲线拟合。
通过选择合适的函数形式,并通过最小二乘估计求解参数,可以拟合出复杂的非线性曲线。
总之,最小二乘法是一种常用的参数估计方法,可以用于线性回归、非线性拟合、时间序列分析等多种建模问题。
多项式最小二乘拟合

多项式最小二乘拟合是一种常见的数学方法,可以用于解决数据分析和预测问题。
本文将详细介绍的原理、应用以及注意事项。
一、原理是一种基于最小二乘法的数学方法。
最小二乘法是一种寻找函数与数据拟合的方法,它试图寻找一个函数来最小化数据点和该函数之间的距离之和。
最小二乘法通常用于数据拟合、回归分析、统计模型构建和信号处理等领域。
是在多项式模型的基础上使用最小二乘法拟合数据。
多项式模型一般形式为:y = a0 + a1*x + a2*x^2 + …… + an*x^n其中y为因变量,x为自变量,a0、a1、a2……an是待定系数,n为多项式的阶数。
的目标是寻找一组系数a0、a1、a2……an,使得对于给定的数据点(xi, yi),拟合函数f(xi)与实际值yi的偏差最小。
二、应用可以应用于很多领域,例如:1. 数据分析:可以用于分析数据,找出数据中的规律和趋势。
2. 预测分析:可以用于预测未来的趋势和走势。
3. 信号处理:可以用于处理信号,找出信号中的噪声和信号。
4. 工程应用:可以应用于工程设计、系统优化等领域。
三、注意事项1. 数据要求:需要一组数据来进行拟合计算,因此数据质量很重要。
数据应该尽量准确、完整、真实。
2. 模型选择:中的多项式阶数对于模型的精度和复杂度有很大的影响。
因此,在选择模型时应该考虑到模型与数据的适应性和效率。
3. 拟合误差:中的误差也是需要考虑的问题。
拟合误差越小,模型的预测精度就越高。
当拟合误差过大时,需要重新检验数据和模型选择。
四、总结是一种基于最小二乘法的数学方法,可以用于解决数据分析和预测问题。
在实际应用中,应该注重数据的质量、模型的选择和拟合误差的控制,以确保拟合结果的准确性和可靠性。
最小二乘法多项式拟合原理

最小二乘法多项式拟合原理最小二乘法多项式拟合原理最小二乘法是一种数学方法,用于寻找一个函数,使得该函数与已知数据点的残差平方和最小化。
尤其在数据分析和统计学中广泛应用,其中特别重要的应用是曲线拟合。
本文将介绍最小二乘法在多项式拟合中的原理。
多项式拟合多项式拟合是一种常见的曲线拟合方法,它将数据点逼近为一个固定次数的多项式。
假设有N个数据点(x1,y1),(x2,y2),…,(xN,yN),希望找到一个关于x的M次多项式函数y=a0+a1x+a2x^2+...+aMx^M,最小化拟合曲线与数据点之间的残差平方和,即S(a0,a1,…,aM)=∑i=1N(yi−P(x))2其中P(x)=a0+a1x+a2x^2+...+aMx^M。
最小二乘法最小二乘法是一种优化方法,通过最小化残差平方和,寻找最优的拟合函数参数。
在多项式拟合中,残差平方和的最小值可以通过相应的求导数为零来计算拟合函数参数。
设残差平方和S的导数为零得到的方程组为∑xi0,…,xiMaM=∑yi⋅xi0,…,xiM,其中M+1个未知量为a0,a1,…,aM,共有M+1个方程,可以使用线性代数解决。
拟合错误与选择问题使用较高次数的多项式进行拟合,可能会导致过度拟合,使得拟合函数更接近每个数据点,因此更难以预测它们之间的关系。
另一方面,使用过低次数的多项式无法反映出数据点之间的较细节的关系。
因此,在实践中,我们需要权衡多项式次数和误差,以找到一个最合适的拟合结果。
总结最小二乘法是一种常用的曲线拟合方法,在多项式拟合中广泛应用。
通过最小化残差平方和,可以找到最优的拟合函数参数,权衡多项式次数和误差,可以得出最合适的拟合结果。
加权最小二乘法 拟合多项式 matlab

加权最小二乘法(Weighted Least Squares, WLS)是一种经典的拟合方法,用于处理数据中的噪声和异常值。
在拟合多项式的过程中,加权最小二乘法能够更好地适应不同的数据权重,从而得到更准确、更可靠的拟合结果。
结合Matlab强大的数学计算和可视化工具,我们可以更方便、更高效地实现加权最小二乘法拟合多项式。
一、加权最小二乘法的基本原理1. 加权最小二乘法的概念在拟合多项式过程中,常常会遇到数据噪声较大或者部分数据异常值较大的情况。
此时,普通的最小二乘法可能无法有效地拟合数据,因此需要引入加权最小二乘法。
加权最小二乘法通过为每个数据点赋予不同的权重,对异常值和噪声进行更有效的处理。
2. 加权最小二乘法的数学原理加权最小二乘法的数学原理主要是在最小化误差的基础上,引入权重矩阵来调整不同数据点的重要性。
通过优化残差的加权和,可以得到适应不同权重的拟合结果。
二、Matlab中的加权最小二乘法1. Matlab工具Matlab提供了丰富的数学计算和拟合工具,通过内置的polyfit函数和curve fitting工具箱,可以方便地实现加权最小二乘法拟合多项式。
Matlab还提供了丰富的可视化工具,可以直观展示加权最小二乘法的拟合效果。
2. 加权最小二乘法的实现在Matlab中,可以通过指定权重向量来调用polyfit函数,实现加权最小二乘法拟合多项式。
利用Matlab内置的拟合评估工具,可以对拟合效果进行全面评估和优化。
三、实例分析以实际数据为例,我们可以在Matlab环境下进行加权最小二乘法的拟合多项式实例分析。
通过构建数据模型、指定权重、调用polyfit函数并结合可视化工具,可以全面了解加权最小二乘法在拟合多项式中的应用效果。
四、个人观点和总结在实际工程和科学研究中,加权最小二乘法拟合多项式是一种非常有效和重要的数据处理方法。
结合Matlab强大的数学计算和可视化工具,可以更方便、更高效地实现加权最小二乘法拟合多项式。
最小二乘法的原理

最小二乘法的原理
最小二乘法是一种统计学中常用的参数估计方法,用于拟合数据并找到最适合数据的数学模型。
其原理是通过最小化实际观测值与预测值之间的误差平方和,来确定模型参数的取值。
具体而言,假设有一组数据点,其中每个数据点包括自变量(即输入值)和因变量(即输出值)的配对。
我们要找到一条最佳拟合曲线(或者直线),使得曲线上的预测值尽可能接近实际观测值。
而最小二乘法的目标就是使得残差的平方和最小化。
假设要拟合的模型为一个一次多项式:y = β0 + β1*x,其中β0和β1是待估计的参数,x是自变量,y是因变量。
我们要找到
最优的β0和β1,使得拟合曲线的误差最小。
为了使用最小二乘法,我们首先需要构建一个误差函数。
对于每个数据点,误差函数定义为实际观测值与预测值之间的差,即e = y - (β0 + β1*x)。
我们的目标是最小化所有误差的平方和,即最小化Sum(e^2)。
通过对误差函数求导,并令导数为0,可以得到最小二乘法的
正规方程组。
解这个方程组可以得到最优的参数估计值,即
β0和β1的取值。
最终,通过最小二乘法,我们可以得到一条最佳拟合曲线(或直线),使得曲线的预测值与实际观测值的误差最小。
这条拟
合曲线可以用于预测新的因变量值,或者理解自变量与因变量之间的关系。
最小二乘拟合多项式

最小二乘拟合多项式最小二乘拟合多项式导言在数学和统计学中,最小二乘法是一种常见的数学优化和统计估计技术。
它被广泛应用于曲线拟合、参数估计和回归分析等领域。
其中,最小二乘拟合多项式是最常见和基础的应用之一。
本文将深入探讨最小二乘拟合多项式的原理、应用以及其在实际问题中的意义。
一、最小二乘法简介1.1 原理最小二乘法是一种通过最小化误差平方和来确定模型参数的方法。
在最小二乘法中,通过寻找最佳的参数估计使得模型预测值与观测值之间的差异最小化。
这样,我们可以得到一个最优的拟合曲线或函数,以便能够更好地描述观测到的数据。
1.2 应用最小二乘法在各个领域中都有广泛的应用。
在物理学中,最小二乘法常被用于拟合实验数据以确定物理定律的参数。
在工程学中,最小二乘法可用于估计信号的隐含参数,如音频信号处理中的频率分量估计。
在金融学、经济学和生物学等领域,最小二乘法也被用于回归分析、模式识别和图像处理等问题中。
二、最小二乘拟合多项式原理2.1 多项式拟合多项式拟合是最小二乘法的一种应用,用于构建一个多项式函数来拟合观测数据。
通过选择最适合的多项式次数,我们可以更好地逼近数据,并获得最优的拟合结果。
2.2 最小二乘拟合多项式最小二乘拟合多项式的目标是选择最佳的多项式来拟合给定的数据。
具体而言,它通过最小化残差平方和来确定最优的多项式系数,使得拟合曲线与观测数据之间的误差最小化。
这样,我们可以得到一个最优的拟合多项式,以便更好地描述数据的分布和趋势。
三、最小二乘拟合多项式的应用3.1 数据拟合最小二乘拟合多项式在数据拟合问题中有着广泛的应用。
通过拟合数据点,我们可以通过最小二乘法来估计数据的分布规律以及趋势。
这对于数据分析和预测具有重要意义,能够帮助我们更好地理解和利用数据。
3.2 预测与模型验证除了数据拟合,最小二乘拟合多项式还可以用于预测和模型验证。
通过构建拟合多项式,我们可以预测未来的数值或事件,并验证模型的准确性和可靠性。
最小二乘法在数学建模中的应用

最小二乘法在数学建模中的应用
最小二乘法在数学建模中的应用
最小二乘法(Least Squares Method,LSM)是一种用来近似拟
合数据的算法,它能够有效地从一组数据中求出最佳拟合的参数。
它的应用广泛,可以用于各种类型的数据拟合,如线性回归,逻辑函数拟合,多项式拟合等等。
这篇文章旨在介绍最小二乘法在数学建模中的应用。
最小二乘法的基本原理是:给定一组数据坐标点,寻找一组参数,使得模型函数与所有数据点的距离的平方和最小。
最小二乘法可以用于找到上述最佳参数,从而求出模型函数的最优拟合。
最小二乘法是一种直观而有效的拟合方法,可以通过给定数据解决许多问题,如多项式拟合,曲线拟合,线性回归等等。
最小二乘法可以用于数学建模中的不同手段。
下面介绍其在数学建模中的三种典型应用:
(1)多项式拟合。
多项式拟合是最小二乘法的一种重要应用。
在数学建模中,多项式拟合可以用来描述数据集的趋势,让测量者以把握变化的方式进行测量。
最小二乘法可以用来找出最佳多项式参数,从而优化拟合精度。
(2)线性回归分析。
线性回归是建模的常用方法,它可以用来
预测一个变量和多个变量之间的关系。
最小二乘法可以用来拟合这种多变量关系,确定线性回归模型的最优参数,从而进行预测。
(3)逻辑函数拟合。
最小二乘法可以用来适应数据集,并找出
符合数据趋势的函数模型。
逻辑函数拟合就是其中之一,它可以用来求解复杂的数学问题。
最后,最小二乘法在数学建模中的应用十分广泛,它可以帮助更好地估计数据模型的参数,用来更精准地拟合分析数据,并有助于精细地控制数学建模过程的结果。
最小二乘法c语言程序

最小二乘法c语言程序最小二乘法(Least Squares Method)是一种常用的数学统计方法,用于求解线性回归问题。
它通过最小化残差平方和来确定回归系数的估计值,从而得到最佳拟合的直线。
在本文中,我们将介绍最小二乘法的原理和应用,并给出一个基于C语言的最小二乘法程序示例。
一、最小二乘法原理最小二乘法的核心思想是通过选择最优的回归系数,使得观测值与拟合值之间的残差平方和最小。
对于给定的数据集,我们希望找到一条直线 y = mx + b,使得所有观测点到该直线的距离之和最小。
具体而言,对于给定的n个数据点(xi, yi),我们可以通过以下步骤求解最小二乘法的回归系数:1. 计算数据集的均值:x̄ = (x1 + x2 + ... + xn)/n,ȳ = (y1 + y2 + ... + yn)/n;2. 计算样本数据的协方差:cov(x, y) = (∑(xi - x̄)(yi - ȳ))/(n-1);3. 计算回归系数:m = cov(x, y)/var(x),b = ȳ - m * x̄。
二、最小二乘法的应用最小二乘法被广泛应用于各个领域,特别是在数据分析和机器学习中。
它可以用于拟合曲线、求解方程组、估计参数等问题。
以下是一些常见的应用场景:1. 线性回归:最小二乘法可以用于求解线性回归问题,求得最佳拟合直线;2. 多项式拟合:最小二乘法可以拓展到多项式回归问题,通过增加高次项来适应更复杂的数据分布;3. 数据预测:最小二乘法可以根据历史数据来预测未来的趋势和数值,比如股票价格预测、天气预报等;4. 参数估计:最小二乘法可以用于估计模型中的参数,比如通过观测数据来估计某一物理量的真实值;5. 数据平滑:最小二乘法可以用于平滑数据,去除噪声和异常点,得到更加真实和可靠的数据。
三、最小二乘法的C语言程序示例下面是一个基于C语言的最小二乘法程序示例,用于求解线性回归问题:```c#include <stdio.h>void leastSquares(int x[], int y[], int n, float *m, float *b) {int i;float sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;for (i = 0; i < n; i++) {sumX += x[i];sumY += y[i];sumXY += x[i] * y[i];sumX2 += x[i] * x[i];}*m = (sumXY - sumX * sumY / n) / (sumX2 - sumX * sumX / n);*b = sumY / n - *m * sumX / n;}int main() {int x[] = {1, 2, 3, 4, 5};int y[] = {2, 4, 6, 8, 10};int n = sizeof(x) / sizeof(x[0]);float m, b;leastSquares(x, y, n, &m, &b);printf("The linear regression equation is: y = %.2fx + %.2f\n", m, b);return 0;}```以上程序通过最小二乘法求解给定数据集的线性回归方程。
最小二乘法的基本原理和多项式拟合

最小二乘法的基本原理和多项式拟合1. 建立模型:首先需要确定要拟合的模型形式,可以选择线性模型或多项式模型等适应数据的形式。
多项式拟合是其中一种常见的形式。
多项式模型是一种多项式方程,表示为:y = a0 + a1x + a2x^2 + ... + anx^n,其中y是因变量,x是自变量,a0, a1, ..., an是要估计的参数。
2.确定误差:通过计算观测值与模型预测值之间的差异,来度量拟合程度。
误差可以通过残差来表示,即实际观测值与预测值之间的差异。
对于多项式拟合,可以使用观测点的纵坐标与拟合曲线的纵坐标之间的距离来描述误差。
3. 构建目标函数:通过最小化误差的平方和来确定最佳拟合曲线。
这可以通过构建一个目标函数来实现,该函数是误差平方和的函数。
目标函数是一个关于参数a0, a1, ..., an的函数,通过选择合适的参数值,可以使得目标函数达到最小值。
4.最小化目标函数:通过计算目标函数对参数的偏导数,设置偏导数为零,得到关于参数的一系列线性方程。
通过求解这个线性方程组,可以得到最佳参数的估计值。
5.进行拟合:将得到的最佳参数估计值带入模型中,得到最佳拟合曲线。
这条曲线将是观测值与预测值之间的最佳拟合线。
多项式拟合是一种常见的最小二乘法应用。
它的基本原理是通过拟合多项式函数来逼近数据点。
多项式拟合可以通过设置多项式的阶数来调整拟合的灵活性。
较低阶数的多项式可能无法很好地拟合数据,而较高阶数的多项式则可能会产生过拟合问题。
多项式拟合具体的步骤包括:1.选择多项式阶数:首先需要选择合适的多项式阶数。
低阶的多项式通常比较简单,但可能无法很好地拟合数据。
高阶的多项式可以更好地适应数据,但可能会存在过拟合问题。
选择合适的多项式阶数需要在简单性和拟合度之间进行权衡。
2. 构建多项式模型:根据选择的多项式阶数,构建多项式模型。
多项式模型是一个多项式方程,表示为:y = a0 + a1x + a2x^2 + ... + anx^n。
最小二乘法的基本原理和多项式拟合
最小二乘法的基本原理和多项式拟合一最小二乘法的基本原理从整体上考虑近似函数P(x)同所给数据点(X i,y i)(i=o,i,…,m)误差ri 二呛)—y i(i=0,1,…,m)ri= P(X i)-y i(i=0,1,…,m)绝对值的最大值maX m r i,即误差向量m/ 、T》仃r =(「0,「1,…r m)的X—范数;二是误差绝对值的和 7 ,即误差向量r的1 —m2Z r i范数;三是误差平方和 7 的算术平方根,即误差向量r的2—范数;前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑2—范数的平方,m2送r i r因此在曲线拟合中常采用误差平方和V 来度量误差r i(i=0 , 1,…,m)的整体大小。
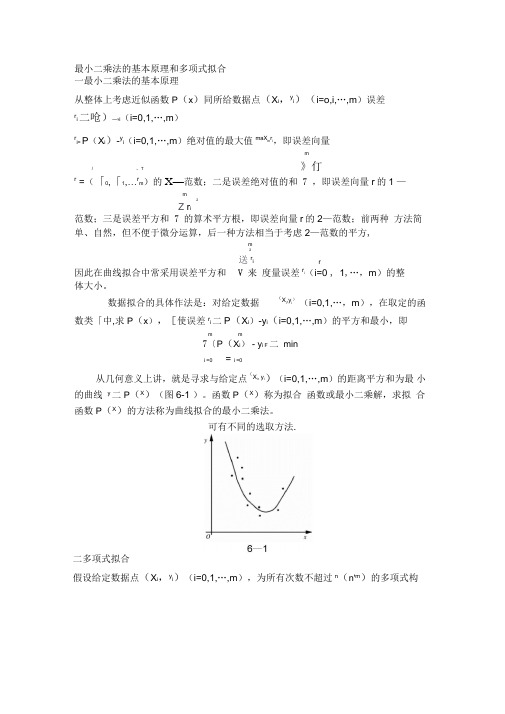
数据拟合的具体作法是:对给定数据(X i,y i)(i=0,1,…,m),在取定的函数类「中,求P(x),[使误差r i二P(X i)-y i(i=0,1,…,m)的平方和最小,即m m7〔P(X i) - y i F 二mini =0 = i =0从几何意义上讲,就是寻求与给定点(X i, y i)(i=0,1,…,m)的距离平方和为最小的曲线y二P(X)(图6-1 )。
函数P(X)称为拟合函数或最小二乘解,求拟合函数P(X)的方法称为曲线拟合的最小二乘法。
可有不同的选取方法.二多项式拟合假设给定数据点(X i,y i)(i=0,1,…,m),为所有次数不超过n(n'm)的多项式构nP n (X )=送 a k X k成的函数类,现求一心m,使得n送 k | a k X i -y i = minV.k=0 丿(1)当拟合函数为多项式时,称为多项式拟合,满足式(1)的P n (X )称为最小二乘 拟合多项式。
特别地,当n=1时,称为线性拟合或直线拟合。
I =送 bn(X i ) —y i 2i =0显然I 7 (' a k X k- y i )2i -0 k -0为a 0,a i ,…a n 的多元函数,因此上述问题即为求1 = l(a 0,a i 「a n )的极值 问题。
excel表格最小二乘法拟合

excel表格最小二乘法拟合一、最小二乘法拟合原理1. 基本概念- 在Excel表格中进行最小二乘法拟合,首先要理解最小二乘法的基本原理。
最小二乘法是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。
- 对于一组给定的数据点(x_i,y_i)(i = 1,2,·s,n),假设我们要拟合的函数为y = f(x),那么误差e_i=y_i - f(x_i)。
最小二乘法的目标就是使∑_{i = 1}^ne_{i}^2最小。
2. 线性拟合(以一元线性为例)- 对于一元线性函数y = ax + b,我们要根据给定的数据点(x_i,y_i)确定a和b 的值。
- 根据最小二乘法原理,a和b的计算公式为:- a=frac{n∑_{i = 1}^nx_iy_i-∑_{i = 1}^nx_i∑_{i = 1}^ny_i}{n∑_{i =1}^nx_{i}^2-(∑_{i = 1}^nx_i)^2}- b=frac{∑_{i = 1}^ny_i - a∑_{i = 1}^nx_i}{n}二、Excel中的操作步骤(以线性拟合为例)1. 准备数据- 在Excel中输入要拟合的数据,将自变量x的值放在一列(例如A列),因变量y的值放在另一列(例如B列)。
2. 绘制散点图- 选中数据(包括x和y的值),点击“插入”选项卡,选择“散点图”。
这一步可以直观地观察数据的分布情况。
3. 添加趋势线(进行拟合)- 在散点图上右键单击其中一个数据点,选择“添加趋势线”。
- 在弹出的“设置趋势线格式”对话框中:- 选择“线性”类型(如果是进行线性拟合)。
- 勾选“显示公式”和“显示R平方值”。
“显示公式”会给出拟合得到的线性方程y = ax + b的具体表达式,“显示R平方值”可以用来评估拟合的好坏,R^2的值越接近1,说明拟合效果越好。
三、实例演示假设我们有以下一组数据:x y1 23 44 55 61. 数据输入- 在Excel的A1 - A5单元格分别输入1、2、3、4、5,在B1 - B5单元格分别输入2、3、4、5、6。
最小二乘法多项式曲线拟合原理与实现

最小二乘法多项式曲线拟合原理与实现一、引言最小二乘法多项式曲线拟合是一种常用的数据拟合方法,它可以通过一组离散的数据点来拟合出一个多项式函数,从而达到对数据进行预测和分析的目的。
本文将详细介绍最小二乘法多项式曲线拟合的原理与实现。
二、最小二乘法最小二乘法是一种数学优化方法,它可以通过最小化误差平方和来求解未知参数。
在多项式曲线拟合中,我们需要求解多项式函数中各个系数的值,使得该函数与给定数据点之间的误差平方和最小。
三、多项式曲线拟合多项式曲线拟合是指通过一组离散的数据点来拟合出一个多项式函数,该函数能够较好地描述这些数据点之间的关系。
在实际应用中,我们通常使用低阶的多项式函数来进行拟合,例如一次、二次或三次多项式函数。
四、最小二乘法多项式曲线拟合原理假设我们有n个离散的数据点(x1,y1),(x2,y2),...,(xn,yn),其中xi表示自变量,yi表示因变量。
我们希望通过这些数据点来拟合出一个m次多项式函数y=f(x),其中m为多项式的阶数。
我们可以将多项式函数表示为如下形式:f(x)=a0+a1x+a2x^2+...+amxm其中a0,a1,...,am为待求解的系数。
我们需要通过最小二乘法来求解这些系数的值。
首先,我们需要定义误差平方和E(a0,a1,...,am):E(a0,a1,...,am)=∑i=1n(yi−f(xi))^2然后,我们需要求解使得误差平方和最小的系数值。
为了方便计算,我们可以将误差平方和展开:E(a0,a1,...,am)=∑i=1n(yi−a0−a1xi−a2xi^2−...−amxm)^2接下来,我们需要对误差平方和进行求导,并令导数等于零,从而得到使得误差平方和最小的系数值。
具体来说,我们需要分别对每个系数进行求导:∂E/∂a0=−2∑i=1n(yi−a0−a1xi−a2xi^2−...−amxm)∂E/∂a1=−2∑i=1n(xi(yi−a0−a1xi−a2xi^2−...−amxm))...∂E/∂am=−2∑i=1n(xmi(yi−a0−a1xi−a2xi^2−...−amxm))然后,我们将每个导数等于零,得到一个线性方程组:∑j=0maijaj=∑i=1nyi×xi^j其中aij表示第j个系数的第i次幂。
最小二乘法的基本原理

最小二乘法的基本原理
最小二乘法是一种常用的数据拟合方法,通过最小化观测值与理论模型值之间的残差平方和来确定模型中的未知参数。
其基本原理如下:
1. 建立模型:首先需要根据问题的特点建立一个数学模型,其中包含了待求的未知参数。
2. 收集数据:通过实验或者观测,收集到一组数据,这些数据包括自变量和对应的因变量。
3. 假设函数形式:假设要拟合的函数形式,通常是一个线性函数或者多项式函数。
4. 构建观测方程:根据所建立的模型和假设的函数形式,将观测数据代入方程中,得到一个由未知参数构成的方程组。
5. 设置目标函数:以观测方程中的残差平方和作为目标函数,定义为所有观测数据的残差平方之和。
6. 最小化目标函数:通过最小化目标函数,求解出最优的未知参数,使得观测方程的残差平方和最小。
7. 模型评估:检验拟合效果,包括残差分析、计算决定系数等。
最小二乘法常用于解决各种问题,如数据拟合、曲线拟合、参数估计等。
它的优点是计算简便、结果稳定可靠,但也有一些
限制和假设条件,如误差满足独立同分布、误差服从正态分布等。
在实际应用中,需要根据具体问题和数据情况选择适合的模型和方法。
最小二乘法的基本原理和多项式拟合

最小二乘法的基本原理和多项式拟合Document number:NOCG-YUNOO-BUYTT-UU986-1986UT最小二乘法的基本原理和多项式拟合一最小二乘法的基本原理从整体上考虑近似函数同所给数据点 (i=0,1,…,m)误差(i=0,1,…,m)的大小,常用的方法有以下三种:一是误差(i=0,1,…,m)绝对值的最大值,即误差向量的∞—范数;二是误差绝对值的和,即误差向量r的1—范数;三是误差平方和的算术平方根,即误差向量r的2—范数;前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和来度量误差 (i=0,1,…,m)的整体大小。
数据拟合的具体作法是:对给定数据 (i=0,1,…,m),在取定的函数类中,求,使误差(i=0,1,…,m)的平方和最小,即=从几何意义上讲,就是寻求与给定点 (i=0,1,…,m)的距离平方和为最小的曲线(图6-1)。
函数称为拟合函数或最小二乘解,求拟合函数的方法称为曲线拟合的最小二乘法。
在曲线拟合中,函数类可有不同的选取方法.6—1二多项式拟合假设给定数据点 (i=0,1,…,m),为所有次数不超过的多项式构成的函数类,现求一,使得(1)当拟合函数为多项式时,称为多项式拟合,满足式(1)的称为最小二乘拟合多项式。
特别地,当n=1时,称为线性拟合或直线拟合。
显然为的多元函数,因此上述问题即为求的极值问题。
由多元函数求极值的必要条件,得(2)即(3)(3)是关于的线性方程组,用矩阵表示为(4)式(3)或式(4)称为正规方程组或法方程组。
可以证明,方程组(4)的系数矩阵是一个对称正定矩阵,故存在唯一解。
从式(4)中解出 (k=0,1,…,n),从而可得多项式(5)可以证明,式(5)中的满足式(1),即为所求的拟合多项式。
我们把称为最小二乘拟合多项式的平方误差,记作由式(2)可得(6)多项式拟合的一般方法可归纳为以下几步:(1) 由已知数据画出函数粗略的图形——散点图,确定拟合多项式的次数n;(2) 列表计算和;(3) 写出正规方程组,求出;(4) 写出拟合多项式。
最小二乘法曲线数据拟合

最小二乘法曲线数据拟合
首先,最小二乘法的基本原理是通过最小化拟合曲线与实际数
据之间的误差平方和来确定最佳拟合曲线的参数。
这意味着拟合曲
线的参数将被调整,以使拟合曲线上的点与实际数据点的残差之和
最小化。
其次,最小二乘法可以用于拟合各种类型的曲线,例如线性曲线、多项式曲线、指数曲线等。
对于线性曲线拟合,最小二乘法可
以得到最佳拟合直线的斜率和截距;对于多项式曲线拟合,最小二
乘法可以确定最佳拟合多项式的系数;对于指数曲线拟合,最小二
乘法可以找到最佳拟合曲线的底数和指数。
此外,最小二乘法还可以通过添加约束条件来进行拟合。
例如,可以通过添加正则化项来控制拟合曲线的复杂度,以避免过拟合问题。
常见的正则化方法包括岭回归和Lasso回归。
在实际应用中,最小二乘法曲线数据拟合可以用于许多领域,
如经济学、统计学、物理学等。
它可以用于分析趋势、预测未来值、估计参数等。
例如,在经济学中,最小二乘法可以用于拟合经济模型,以评估不同因素对经济指标的影响。
最后,最小二乘法的计算通常可以通过数值方法来实现,例如
使用最小二乘法的矩阵形式求解线性方程组,或者使用迭代算法来
拟合非线性曲线。
总结起来,最小二乘法是一种常用的数据拟合方法,通过最小
化拟合曲线与实际数据之间的误差平方和来确定最佳拟合曲线的参数。
它可以适用于各种类型的曲线拟合,并可以通过添加约束条件
来进行拟合。
在实际应用中,最小二乘法可以用于分析趋势、预测
未来值、估计参数等。
最小二乘法的计算可以通过数值方法来实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008-12-29
第一节 最小二乘法的基本原理和多项式拟合
Page 6 of 8
a 0 = a1 = L a n = 0 ,与齐次方程组有非零解的假设矛盾。因此正规方程组(4)必有唯一解
解得 a 0 = 13.4597, 故拟合多项式为 y = 13.4597 − 3.6053 + 0.2676 x 2 *三 最小二乘拟合多项式的存在唯一性 定理1 设节点 x0 , x1 , L , x n 互异,则法方程组(4)的解存在唯一。 证 由克莱姆法则,只需证明方程组(4)的系数矩阵非奇异即可。 用反证法,设方程组(4)的系数矩阵奇异,则其所对应的齐次方程组
ri ,即误差 向量 r = ( r , r , L r ) T 的∞—范数;二是误差绝对值的和 ∑ 值 max m 0 1 0≤i ≤ m i =0
m
ri
,即误差向
∑r 量r的1—范数;三是误差平方和
i =0
m
2
i
的算术平方根,即误差向量r的2—范数;前两种方法
简单、自然,但不便于微分运算 ,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合
∑ xi ∑x
i =0 i =0 m 2 i
m
∑x
i =0
m
M
n +1 i
⎤ ⎡ m ⎤ yi ⎥ ⎥ ∑ ⎢ i =0 i =0 ⎥ ⎡a0 ⎤ ⎢ m ⎥ m n +1 ⎥ ⎢ a ⎥ ⎢ ⎥ L ∑ xi ⎢ 1 ⎥ x y ∑ i i = ⎥ ⎢ ⎥ i =0 ⎢ M ⎥ ⎢ i =0 ⎥ M M ⎥ ⎥ ⎢a ⎥ ⎢ m ⎥ m ⎣ n⎦ ⎢∑ xin y i ⎥ L ∑ xi2 n ⎥ ⎢ ⎥ ⎥ ⎣ i =0 ⎦ (4) i =0 ⎦ L
其中
p n ( x) = ∑ a k x k
k =0 n
所以 p n ( xi ) = 0 (i=0,1,…,m) pn ( x) 是次数不超过n的多项式,它有m+1>n个相异零点,由代数基本定理,必须有
mhtml:file://C:\Documents and Settings\邵雷\桌面\最小二乘法\第一节 最小二乘...
m
L
有非零解。式(7)可写为
∑ (∑ xij + k )a k = 0,
k =0 i =0
n
m
j = 0,1, L , n
(8)
将式(8)中第j个方程乘以 a j (j=0,1,…,n),然后将新得到的n+1个方程左右两端分别 相
⎡ n m j+k ⎤ a ( x ) a 0 =0 ∑ j ⎢∑ ∑ i k ⎥ 加,得 j =0 ⎣k =0 i=0 ⎦
解 画出散点图(图6-2),可见测得的数据接近一条直线,故取n=1,拟合函数为 R = a 0 + a1T 列表如下 i 0 1 2 3 4 5 6 Ti 19.1 25.0 30.1 36.0 40.0 45.1 50.0 245.3 Ri 76.30 77.80 79.25 80.80 82.35 83.90 85.10 565.5
第一节 最小二乘法的基本原理和多项式拟合
Page 1 of 8
第一节 最小二乘法的基本原理和多项式拟合 一 最小二乘法的基本原理 从整体上考虑近似函数 p ( x ) 同所给数据点 ( xi , y i ) (i=0,1,…,m)误差 ri = p ( xi ) − y i (i=0,1, …,m) 的大小,常用的方法有以下三种:一是误差 ri = p ( xi ) − y i (i=0,1,…,m)绝对值的最大
6-2 例2 已知实验数据如下表 i xi 0 1 10 1 3 5 2 4 4 3 5 2 4 6 1 5 7 1 6 8 2 7 9 3 8 10 4
yi
试用最小二乘法求它的二次拟合多项式。 解 设拟合曲线方程为
2 y = a 0 + a1 x + a 2 x
列表如下 I 0 1 2 3 4 5 6 7 8 xi 1 3 4 5 6 7 8 9 10 53 yi 10 5 4 2 1 1 2 3 4 32
∑r 中常采用误差平方和
i =0
m
2
i
来 度量误差 ri (i=0,1,…,m)的整体大小。
数据拟合的具体作法是:对给定数据 ( xi , y i ) (i=0,1,…,m),在取定的函数类 Φ 中,求
p ( x) ∈ Φ ,使误差 ri = p ( xi ) − y i (i=0,1,…,m)的平方和最小,即
线拟合的最小二乘法。 在曲线拟合中,函数类 Φ 可有不同的选取方法.
6—1 二 多项式拟合 假设给定数据点 ( xi , y i ) (i=0,1,…,m), Φ 为所有次数不超过 n(n ≤ m) 的多项式构成的函数
p n ( x) = ∑ a k x k ∈ Φ
k =0 n
类,现求一
,使得
mhtml:file://C:\Documents and Settings\邵雷\桌面\最小二乘法\第一节 最小二乘...
j = 0,1, L , n
(2)
即 k =0
∑ (∑ xij + k ) a k = ∑ xij y i ,
i =0 i =0
n
m
m
j = 0,1, L , n
(3)
(3)是关于 a 0 , a1 , L a n ⎢ x i ⎢∑ i =0 ⎢ M ⎢m ⎢∑ xin ⎢ ⎣ i =0
∑x
m
n i
式(3)或式(4)称为正规方程组或法方程组。 可以证明,方程组(4)的系数矩阵是一个对称正定矩阵,故存在唯一解。从式(4)中 解出 a k (k=0,1,…,n),从而可得多项式
p n ( x) = ∑ a k x k
k =0 n
(5)
可以证明,式(5)中的 p n ( x ) 满足式(1),即 p n ( x ) 为所求的拟合多项式。我们把
∑[p
i =0
m
n
( xi ) − y i ]
2
称为最小二乘拟合多项式 p n ( x ) 的平方误差,记作
r
2 2
= ∑ [ p n ( xi ) − y i ]
i =0
m
2
由式(2)可得
mhtml:file://C:\Documents and Settings\邵雷\桌面\最小二乘法\第一节 最小二乘...
2008-12-29
第一节 最小二乘法的基本原理和多项式拟合
Page 3 of 8
r
2 2
= ∑ y i2 − ∑ a k (∑ xik y i )
i =0 k =0 i =0
m
n
m
(6)
多项式拟合的一般方法可归纳为以下几步: (1) 由已知数据画出函数粗略的图形——散点图,确定拟合多项式的次数n; (2) 列表计算
∑ ri2
i =0
m
=
∑ [ p( x ) − y ]
i =0 i i
m
2
= min
从几何意义上讲,就是寻求与给定点 ( xi , y i ) (i=0,1,…,m)的距离平方和为最小的曲线
y = p ( x) (图6-1)。函数 p ( x ) 称为拟合 函数或最小二乘解,求拟合函数 p ( x ) 的方法称为曲
n
因为
m m n n ⎡ n m j+k ⎤ m n n k j j+k a ( x ) a = a a x = ( a x )( a x ) = [ p n ( xi )]2 ∑ ∑ ∑ ∑ ∑ k i j i k ⎥ ∑ ∑∑ k j i j ⎢∑ ∑ i i =0 j =0 i =0 k =0 j =0 ⎣ k =0 i =0 ⎦ i =0 j =0 k =0 n
x i2 x i3 x i4
xi y i 10 15 16 10 6 7 16 27 40 147
xi2 y i
∑
1 9 16 25 36 49 64 81 100 381
1 27 64 125 216 343 512 729 1000 3017
1 81 256 625 1296 2401 4096 6561 10000 25317
∑ xij
i =0
m
( j = 0,1, L ,2n)
和
∑x
i =0
m
j i
yi
( j = 0,1, L ,2n)
;
(3) 写出正规方程组,求出 a 0 , a1 , L a n ;
p n ( x) = ∑ a k x k
k =0 n
(4) 写出拟合多项式
。
在实际应用中, n < m 或 n ≤ m ;当 n = m 时所得的拟合多项式就是拉格朗日或牛顿插值多项 式。 例1 测得铜导线在温度 Ti (℃)时的电阻 Ri (Ω) 如表6-1,求电阻R与温度 T的近似函数关 系。 i Ti (℃) Ri (Ω) 0 19.1 76.30 1 25.0 77.80 2 30.1 79.25 3 36.0 80.80 4 40.0 82.35 5 45.1 83.90 6 50.0 85.10
I = ∑ (∑ a k xik − y i ) 2
i =0 k =0 m n
为 a 0 , a1 , L a n 的多元函数,因此上述问题即为求 I = I (a 0 , a1 ,L a n ) 的极值 问题。由多元函数 求极值的必要条件,得
m n ∂I = 2∑ (∑ a k xik − y i ) xij = 0, ∂a j i =0 k =0
10 45 64 50 36 49 128 243 400 1025
得正规方程组
