上海交通大学版大学物理学习题答案之8机械波习题思考题
大学物理机械波习题附答案
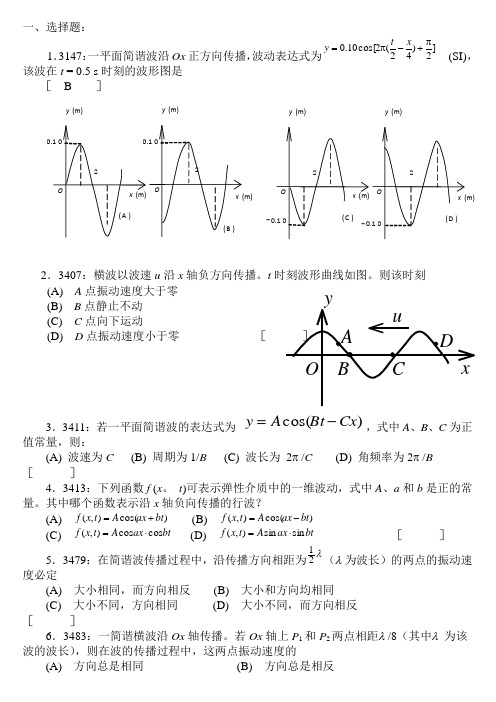
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) btax A t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C)大小不同,方向相同 (D) 大小不同,而方向相反 [ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反y (m) y (m) - y (m) y (m)(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长(B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
《大学物理学》答案(上海交大版)上下册

习 题1-1. 已知质点位矢随时间变化的函数形式为)ωt sin ωt (cos j i +=R r其中ω为常量.求:(1)质点的轨道;(2)速度和速率。
解:1) 由)ωt sin ωt (cos j i +=R r 知 t cos R x ω= t sin R y ω=消去t 可得轨道方程 222R y x =+2) j rv t Rcos sin ωωt ωR ωdtd +-==i R ωt ωR ωt ωR ωv =+-=2122])c o s ()s i n [(1-2. 已知质点位矢随时间变化的函数形式为j i r )t 23(t 42++=,式中r 的单位为m ,t 的单位为s .求:(1)质点的轨道;(2)从0=t 到1=t 秒的位移;(3)0=t 和1=t 秒两时刻的速度。
解:1)由j i r )t 23(t 42++=可知2t 4x =t 23y +=消去t 得轨道方程为:2)3y (x -=2)j i rv 2t 8dtd +==j i j i v r 24)dt 2t 8(dt 11+=+==⎰⎰Δ3) j v 2(0)= j i v 28(1)+=1-3. 已知质点位矢随时间变化的函数形式为j i r t t 22+=,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
解:1)j i rv 2t 2dt d +== i va 2dtd ==2)212212)1t (2]4)t 2[(v +=+= 1t t 2dtdv a 2t +==n a ==1-4. 一升降机以加速度a 上升,在上升过程中有一螺钉从天花板上松落,升降机的天花板与底板相距为d ,求螺钉从天花板落到底板上所需的时间。
解:以地面为参照系,坐标如图,升降机与螺丝的运动方程分别为20121at t v y += (1) 图 1-420221gt t v h y -+= (2)21y y = (3) 解之t =初速度0v 水平抛出,求:1-5. 一质量为m 的小球在高度h 处以(1)小球的运动方程;(2)小球在落地之前的轨迹方程; (3)落地前瞬时小球的t d d r ,t d d v ,tv d d . 解:(1) t v x 0= 式(1)2gt 21h y -= 式(2)j i r )gt 21-h (t v (t)20+=(2)联立式(1)、式(2)得 22v 2gx h y -=(3)j i rgt -v t d d 0= 而 落地所用时间 gh 2t = 所以j i r 2gh -v t d d 0= j v g td d -= 2202y 2x )gt (v v v v -+=+=212220[()]g t dvdt v gt ==+1-6. 路灯距地面的高度为1h ,一身高为2h 的人在路灯下以匀速1v 沿直线行走。
《大学物理》习题库试题及答案___05_机械波习题

一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是 [ b ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动 (D) D 点振动速度小于零[ d ]3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B[ c ]u=λ/T C=ϖ/u4.3413:下列函数f (x 。
t)可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播-的行波?(A) )A(bt),tf-=cos(xaxax(bt),Atf+xcos(=(B) )(C) bttAaxxf sin(⋅),sin==(D) btt(⋅axxA),cosf cos[a]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反(B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反[ a ]6.3483:一简谐横波沿Ox轴传播。
若Ox轴上P1和P2两点相距λ /8(其中λ为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同(B) 方向总是相反(C) 方向有时相同,有时相反(D) 大小总是不相等[ c ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则(A) 振动频率越高,波长越长(B) 振动频率越低,波长越长(C) 振动频率越高,波速越大(D) 振动频率越低,波速越大[ B ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
《大学物理学》机械波练习题

《大学物理学》机械波部分自主学习材料(解答)一、选择题10-1.图(a )表示0t =时的简谐波的波形图,波沿x 轴正方向传播,图(b )为一质点的振动曲线,则图(a )中所表示的0x =处质点振动的初相位与图(b )所表示的振动的初相位分别为( C ) (A )均为2π; (B )均为π-; (C )π与π-; (D )2π-与2π。
【提示:图(b )为振动曲线,用旋转矢量考虑初相角为2π-,图(a )为波形图,可画出过一点时间的辅助波形,可见0x =处质点的振动为由平衡位置跑向负方向,则初相角为2π】10-2.机械波的表达式为0.05cos(60.06)y t x ππ=+,式中使用国际单位制,则( C ) (A )波长为5m ; (B )波速为110m s -⋅;(C )周期为13秒; (D )波沿x 正方向传播。
【提示:利用2k πλ=知波长为1003λ=m ,利用u k ω=知波速为1100u m s -=⋅,利用2T πω=知周期为13T =秒,机械波的表达式中的“+”号知波沿x 负方向传播】10-3.一平面简谐波沿x 轴负方向传播,角频率为ω,波速为u ,设4Tt =时刻的波形如图所示,则该波的表达式为( D )(A )cos[()]xy A t u ωπ=-+; (B )cos[()]2x y A t u πω=--;(C )cos[()]2x y A t u πω=+-;(D )cos[()]xy A t uωπ=++。
【提示:可画出过一点时间的辅助波形,可见在4Tt =时刻,0x =处质点的振动为由平衡位置向正方向振动,相位为2π-,那么回溯在0t=的时刻,相位应为π】10-4.如图所示,波长为λ的两相干平面简谐波在P 点相遇,波在点1S 振动的初相是1ϕ,到P 点的距离是1r 。
波在点2S 振动的初相是2ϕ,到P 点的距离是2r 。
以k 代表零或正、负整数,则点P 是干涉极大的条件为( D )OO1S 2S r(A )21r r k π-=; (B )212k ϕϕπ-=; (C )212122r r k ϕϕππλ--+=;(D )122122r r k ϕϕππλ--+=。
大学物理波动篇机械波复习题及答案课件

种不同的媒质中传播, 在分界面上的 P 点
相遇, 频率n = 200Hz, 振幅A1=A2=2.00 10-
2m, S2 的位相比 S1 落后 /2。在媒质1中
波速 u1= 800 m s-1, 在媒质2中波速 u2=
1000 m s-1 , S1P=r1=4.00m,
静止的点。求两波的波长和两波源间最 小位相差。
o
S1
S2
x
d
29
解: 设S1 和 S2的振动初位相分别为 1 和 2在 x1点两波引起的振动位相差
2 2 d x1/ 1 2 x1 / 2k 1
2 1 2 d 2 x1/ 2k 1 (1)
在x2点两波引起的振动位相差
2 2 d x2/ 1 2 x2 / 2k 3
波分别通过图中的 o1和 o2 点,通过 o1 点 的简谐波在 M1M2 平面反射后,与通过 o2 点的简谐波在 P 点相遇,假定波在M1M2平 面反射时有半波损失,o1 和 o2 两点的振动
方程为,y10=Acos(2t) 和 y20=Acos(2t) , 且 o1m+mp=16,o2P = 6 (为波长) 求:
(A)波速为C/B; (B)周期为 1/B;
(C)波长为C/2 ; (D)圆频率为 B。
[]
5
5.一平面简谐波沿正方相传播, t=0 时刻的
波形如图所示, 则 P 处质点的振动在 t=0 时
刻的旋转矢量图是
y
u
A
x
o
P
( A)
o
x
A
(B)
o
x
A
(C ) A o
x
A
(D)
大学物理机械波习题及答案解析
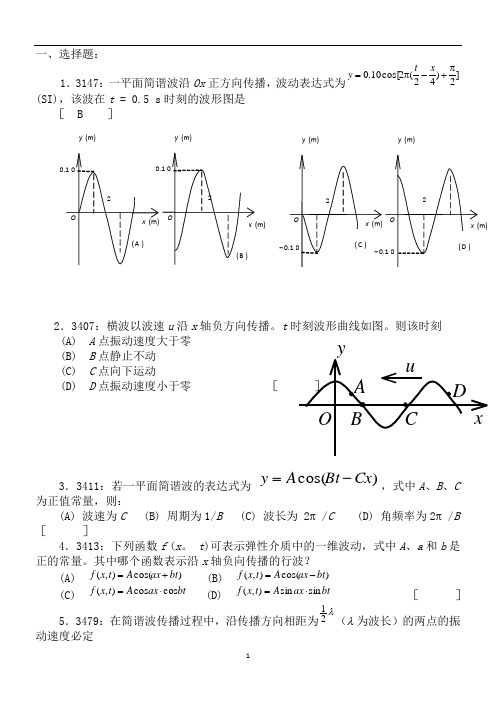
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为(SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻 (A) A 点振动速度大于零 (B) B 点静止不动(C) C 点向下运动(D) D 点振动速度小于零 [ ] 3.3411:若一平面简谐波的表达式为 ,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B [ ]4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) (B)(C) (D) [ ]5.3479:在简谐波传播过程中,沿传播方向相距为(λ 为波长)的两点的振动速度必定]2)42(2cos[10.0π+-π=x t y )cos(Cx Bt A y -=)cos(),(bt ax A t x f +=)cos(),(bt ax A t x f -=bt ax A t x f cos cos ),(⋅=bt ax A t x f sin sin ),(⋅=λ21 x u A y B C D Ox (m) O 2 0.1 0y (m) ( A ) x (m) O 2 0.1 0 y (m) ( B )x (m) O 2- 0.1 0 y (m) ( C ) x (m)O 2 y (m)( D ) - 0.1 0(A) 大小相同,而方向相反 (B) 大小和方向均相同(C) 大小不同,方向相同 (D) 大小不同,而方向相反 [ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
大物 上海交大课后答案 第八章

习题88-1.如图所示,金属圆环半径为R ,位于磁感应强度为B的均匀磁场中,圆环平面与磁场方向垂直。
当圆环以恒定速度v在环所在平面内运动时,求环中的感应电动势及环上位于与运动方向垂直的直径两端a 、b 间的电势差。
解:(1)由法拉第电磁感应定律i d dtεΦ=-,考虑到圆环内的磁通量不变,所以,环中的感应电动势0i ε=; (2)利用:()aab bv B dl ε=⨯⋅⎰,有:22ab Bv R Bv R ε=⋅=。
【注:相同电动势的两个电源并联,并联后等效电源电动势不变】8-2.如图所示,长直导线中通有电流A I 0.5=,在与其相距cm 5.0=d 处放有一矩形线圈,共1000匝,设线圈长cm 0.4=l ,宽cm 0.2=a 。
不计线圈自感,若线圈以速度cm/s 0.3=v 沿垂直于长导线的方向向右 运动,线圈中的感生电动势多大?解法一:利用法拉第电磁感应定律解决。
首先用0lB dl I μ⋅=∑⎰ 求出电场分布,易得:02I B rμπ=, 则矩形线圈内的磁通量为:00ln22x axI I l x al dr r xμμππ++Φ=⋅=⎰, 由i d Nd t εΦ=-,有:011()2i N I l d x x a x dtμεπ=--⋅+ ∴当x d =时,有:041.92102()i N I l a v V d a μεπ-==⨯+。
解法二:利用动生电动势公式解决。
由0lB dl I μ⋅=∑⎰ 求出电场分布,易得:02I B rμπ=, 考虑线圈框架的两个平行长直导线部分产生动生电动势, 近端部分:11NB l v ε=, 远端部分:22NB lv ε=, 则:12εεε=-=00411() 1.921022()N I N I al v l v V d d a d d a μμππ--==⨯++。
8-3.如图所示,长直导线中通有电流强度为I 的电流,长为l 的金属棒ab 与长直导线共面且垂直于导线放置,其a 端离导线为d ,并以速度v平行于长直导线作匀速运动,求金属棒中的感应电动势ε并比较U a 、U b 的电势大小。
大学物理机械波习题附答案
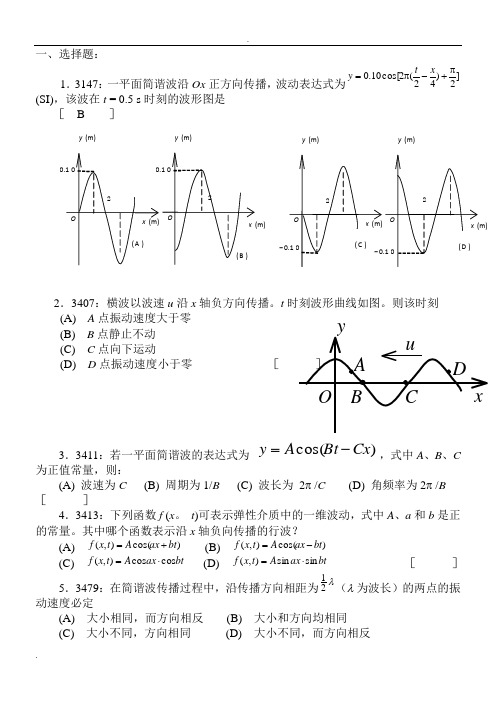
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt axA t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反y (m) y (m) - y (m) y (m)[ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长 (B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
上海交通大学版大学物理学习题答案之8机械波习题思考题

习题8-1、沿一平面简谐波的波线上,有相距2.0m的两质点A与B, B点振动相位比A点洛后一,已知振动周期为2.0s,求波长与波速。
6解:根据题意,对于A、B两点,21 , x 2m6而相位与波长之间又满足这样的关系: 2 1 X2 Xi 2x轴正向传播,距坐标原点O为X1处P点的振动式为y Acos( t ),波速为u,求:(1) 平面波的波动式;⑵若波沿x轴负向传播,波动式又如何?解:(1)根据题意,距坐标原点O为乂1处P点就是坐标原点的振动状态传过来的,其O点振动状态传到p点需用t 互,也就就是说t时刻p处质点的振动状u—x态重复t -时刻O处质点的振动状态。
换而言之,0处质点的振动状态相当于ut x ru时刻p处质点的振动状态,则0点的振动方程为y Acos[x1(t -)u]波动方程为:y Acos[ (t 'u?] Acos[ (t 口为)]代入数据,可得:波长入=24m。
又已知T=2s,所以波速u=入/T=12m/s 8-2.已知一平面波沿点的振动规律为y Acos(2 t),试写出:(1) 该平面简谐波的表达式;(2) B 点的振动表达式(B 点位于A 点右方d 处)。
解:(1)仿照上题的思路,根据题意,A 点的振动规 律为y Acos(2 t ),它的振动就是 0点传过来的,所以0点的振动方程为:y ACOS[2 ( t -)] ulx那么该平面简谐波的表达式为 :y A COS[2 ( t — —)]u u(2) B 点的振动表达式可直接将坐标X d l ,代入波动方程:IIy Acos[2 ( t 一 --------- )] Acos[2 ( t —)]u u u也可以根据B 点的振动经过—时间传给A 点的思路来做。
u8-4、已知一沿X 正方向传播的平面余弦波,tT 为 2s 、(1) 写出0点的振动表达式; (2) 写出该波的波动表达式;动状态,则0点的振动方程为:y A cos[x 1、(t -)]波动方程为:y Acos[ ( t 虫-)u u]Acos[ (t 3)] u⑵若波沿x 轴负向传播,0处质点的振动状态相当于t 冬 时刻p 处质点的振u8-3、一平面简谐波在空间传播,如图所示,已知A1s 时的波形如图所示,且周期(3)写出A点的振动表达式;(4)写出A点离0点的距离。
大学物理_机械波答案

机械波1.提示:1(,)cos[2()]t xy x t A T πϕλ=-+,2012(,)cos[2()]x t y x t A T λπϕλ+=-+,1sin[2()],dy t xv A dtTωπϕλ==--+2112sin[2()]x dy t v A v dtTλωπϕλ+==--+=-2.提示:波速取决于媒质的性质,振动速度是媒质中质元的运动速度3.提示:由图可知O 点处质元的运动方向向下,00,0,,t t y v A ω===-sin[2],dy t v A dtTωπϕ==-+0sin(0),2v A A πωϕωϕ=-+=-=4.提示:由图可知:8,160/,3,m u m s A m λ===则120,240uH Z v T νωππλ=====由图可知O 点处质元的运动方向向上,则当0,0,sin[2()],dy t xt x v A A dtT ωπϕωλ====--+=时可得2πϕ=-5.提示:在最大位移处,胁变最小,它的速度为0,因此动能为0,对于简谐波动能等于势能。
6.提示:对于A 点的上下运动可当作机械振动,在其偏离平衡位置最大位移处其动能为0,因此A 点在向平衡位置方向运动,则可知波沿X 轴负方向传播 7.提示:12,2πϕϕ-=2121122224r r πϕϕπϕπππλλ⎛⎫⎛⎫∆=---=--⨯=- ⎪ ⎪⎝⎭⎝⎭8.提示:由波腹条件22xk k x πλπλ=±⇒=±二、填空题 1.CB ,Bπ2,Cπ2,lC ,lC -提示:将已知波的方程与波的标准方程2(,)cos[]xy x t A t πωϕλ=-+或(,)cos[()]xy x t A t uωωϕ=-+对比可得波长和波速,位相差为:222[()][]t r d t r d cdπππωϕωϕλλλ-++--+==2.Lλπϕ2-;Nk k x x ∈±=,1λ;zk k x x ∈++=,)21(1λ。
大学物理学习指导答案08草稿(例题、练习题答案)

第八章 波动【例题】例8-1 如图,一平面波在介质中以波速u = 20 m/s 沿x 轴负方向传播, 已知A 点的振动方程为 t y π⨯=-4c o s 1032 (SI). (1) 以A 点为坐标原点写出波的表达式;(2) 以距A 点5 m 处的B 点为坐标原点,写出波的表达式. 【解】(1) 坐标为x 点的振动相位为)]/([4u x t t +π=+φω)]/([4u x t +π=)]20/([4x t +π=波的表达式为 )]20/([4cos 1032x t y +π⨯=- (SI)(2) 以B 点为坐标原点,则坐标为x 点的振动相位为 ]205[4-+π='+x t t φω (SI) 波的表达式为 ])20(4cos[1032π-+π⨯=-x t y (SI) 例8-2 已知波长为λ 的平面简谐波沿x 轴负方向传播.x = λ /4处质点的振动方程为 ut A y ⋅π=λ2cos(SI)(1) 写出该平面简谐波的表达式. (2) 画出t = T 时刻的波形图.【解】(1) 如图A ,取波线上任一点P ,其坐标设为x ,由波的传播特性,P 点的振动落后于λ /4处质点的振动.波的表达式 )]4(22cos[x utA y -π-π=λλλ )222cos(x ut A λλπ+π-π= (SI) (2) t = T 时的波形和 t = 0时波形一样. t = 0时 )22cos(x A y λπ+π-=)22cos(π-π=x A λ 按上述方程画的波形图见图B .例8-3某质点作简谐振动,周期为2 s ,振幅为0.06 m ,t = 0 时刻,质点恰好处在负向最大位移处,求:(1) 该质点的振动方程; (2) 此振动以波速u = 2 m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3) 该波的波长.【解】(1) 振动方程 )22c o s (06.00π+π=ty )c o s (06.0π+π=t (SI) . (2) 波动表达式 ])/(cos[06.0π+-π=u x t yABOxPxλ/4 u图A])21(cos[06.0π+-π=x t (SI) (3) 波长 4==uT λ m例8-4 一平面简谐波沿Ox 轴正向传播,波动表达式为 ]4/)/(cos[π+-=u x t A y ω,则x 1 = L 1处质点的振动方程是 ;x 2 = -L 2处质点的振动和x 1 = L 1处质点的振动的相位差为φ2 - φ1 = .]4/)/(cos[11π+-=u L t A y ωuL L )(21+ω例8-5 一平面简谐波的表达式为 )37.0125cos(025.0x t y -= (SI),其波速u = ;波长λ = .338 m/s 17.0 m例8-6 已知一平面简谐波的表达式为 )cos(bx at A -,(a 、b 均为正值常量),则波长为 ;波沿x 轴传播的速度为 .2π / b a /b例8-7 一平面简谐波的表达式为 )/(2c o sλνx t A y -π=.在t = 1 /ν 时刻,x 1 = 3λ /4与x 2 = λ /4二点处质元速度之比是(A) -1. (B)31. (C) 1. (D) 3. [ A ] 例8-8 沿x 轴负方向传播的平面简谐波在t = 2 s 时刻的波形曲线 如图所示,设波速u = 0.5 m/s . 求:原点O 的振动方程.【解】由图,λ = 2 m , 又 ∵u = 0.5 m/s ,∴ ν = 1 /4 Hz ,T = 4 s .题图中t = 2 s =T 21. t = 0时,波形比题图中的波形倒退λ21,见图.此时O 点位移y 0 = 0(过平衡位置)且朝y 轴负方向运动,∴ π=21φ∴ )2121c o s (5.0π+π=t y (SI) 例8-9 一平面简谐波沿x 轴正向传播,波的振幅A = 10 cm ,波的角频率ω = 7π rad/s.当t = 1.0 s 时,x = 10 cm 处的a 质点正通过其平衡位置向y 轴负方向运动,而x = 20 cm 处的b 质点正通过y = 5.0 cm 点向y 轴正方向运动.设该波波长λ >10 cm ,求该平面波的表达式. 【解】设平面简谐波的波长为λ,坐标原点处质点振动初相为φ,则波的表达式可写成 )/27c o s(1.0φλ+π-π=x t y (SI) t = 1 s 时 0])/1.0(27cos[1.0=+π-π=φλyx (m)y (m) 0u0.5 12t = 0 -1因此时a 质点向y 轴负方向运动,故 π=+π-π21)/1.0(27φλ ① b 质点正通过y = 0.05 m 处向y 轴正方向运动,应有05.0])/2.0(27cos[1.0=+π-π=φλy且 π-=+π-π31)/2.0(27φλ ②由①、②两式联立得 λ = 0.24 m 3/17π-=φ∴ 该平面简谐波的表达式为 ]31712.07cos[1.0π-π-π=x t y (SI) 例8-10 图示一简谐波在t = 0时刻与t = T /4时刻(T 为周期)的波形图,则o 处质点振动的初始相位为 ;x 1处质点的振动方程为 . π /2 )22cos(1π-π=t T A y x 例8-11 图所示为一平面简谐波在t = 0 时刻的波形图,设此简谐波的频率为250 Hz ,且此时质点P 的运动方向向下,求:(1) 该波的表达式;(2) 在距原点O 为100 m 处质点的振动方程与振动速度表达式.【解】(1) 由P 点的运动方向,可判定该波向左传播.原点O 处质点,t = 0 时φc o s 2/2A A =, 0sin 0<-=φωA v所以 4/π=φO 处振动方程为 )41500c o s (0π+π=t A y (SI) 由图可判定波长λ = 200 m ,故波动表达式为]41)200250(2cos[π++π=x t A y (SI) (2) 距O 点100 m 处质点的振动方程是 )45500cos(1π+π=t A y振动速度表达式是 )45500cos(500π+ππ-=t A v (SI)例8-12 一平面简谐波在弹性媒质中传播时,某一时刻媒质中某质元在负的最大位移处,则它的能量是(A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. [ B ]例8-13 设入射波的表达式为 )(2cos 1Tt x A y +π=λ,在x = 0处发生反射,反射点为一固定端.设反射时无能量损失,求:(1) 反射波的表达式 (2) 合成的驻波的表达式. 【解】(1) 入射波在x=0处振动:10cos2t y A T=π,/4反射点是固定端,所以反射有相位突变π,反射波在x=0处振动:20cos(2)ty A Tπ=+π, 反射波振幅为A ,沿x 轴正向传播故反射波的表达式为 ])//(2cos[2π+-π=T t x A y λ(2) 驻波的表达式是21y y y += )21/2c o s ()21/2c o s (2π-ππ+π=T t x A λ 例8-14 如果入射波的表达式是)//(2cos 1λx T t A y +=π,在x = 0处发生反射后形成驻波,反射点为波腹.设反射后波的强度不变,则反射波的表达式y 2 = ; 在x = 2λ /3处质点合振动的振幅等于 .)(2cos λxT t A -π A 【解】入射波在x=0处振动:10cos2t y A T=π, 反射点是波腹,所以反射无相位突变π,反射波在x=0处振动:20cos(2)t y A T=π, 反射波振幅为A ,沿x 轴正向传播故反射波的表达式为 2cos[2(//)]y A x t T λ=-π 将x = 2λ /3带入上式,计算得出 A例8-15 在固定端x = 0处反射的反射波表达式是)/(2cos 2λνx t A y -π=. 设反射波无能量损失,那么入射波的表达式是y 1 = ;形成的驻波的表达式是y = . 解法同例8-13, ])/(2cos[π++πλνx t A )212cos()21/2cos(2π+ππ+πt x A νλ 例8-16 驻波表达式为t x A y ωλcos )/2cos(2π=,则2/λ-=x 处质点的振动方程是 ;该质点的振动速度表达式是 .将2/λ-=x 带入t x A y ωλcos )/2cos(2π=,得t A y ωcos 21-= 对t 求导得 t A ωsin 2=v例8-17 在驻波中,两个相邻波节间各质点的振动(A) 振幅相同,相位相同. (B) 振幅不同,相位相同.(C) 振幅相同,相位不同. (D) 振幅不同,相位不同. [ B ]例题答案【练习题】8-1 一横波沿绳子传播,其波的表达式为:)2100c o s(05.0x t y π-π= (SI)(1) 求此波的振幅、波速、频率和波长.(2) 求绳子上各质点的最大振动速度和最大振动加速度. (3) 求x 1 = 0.2 m 处和x 2 = 0.7 m 处二质点振动的相位差. 解:(1) 已知波的表达式为)2100cos(05.0x t y π-π=与标准形式)/22cos(λνx t A y π-π= 比较得A = 0.05 m , ν = 50 Hz , λ = 1.0 m u = λν = 50 m/s(2) 7.152)/(max max =π=∂∂=A t y νv m /s 322m a x 22m a x 1093.44)/(⨯=π=∂∂=A t y a ν m/s 2 (3) π=-π=∆λφ/)(212x x ,二振动反相8-2 一平面简谐波,其振幅为A ,频率为ν .波沿x 轴正方向传播.设t = t 0刻波形如图所示.则x = 0处质点的振动方程为(A) ]21)(2cos[0π++π=t t A y ν. (B) ]21)(2cos[0π+-π=t t A y ν. (C) ]21)(2cos[0π--π=t t A y ν. (D)])(2cos[0π+-π=t t A y ν. [ B ] 8-3 已知一平面简谐波的表达式为 )cos(dx bt A y -=,(b 、d 为正值常量),则此波的频率ν = ;波长λ = .b / 2π 2π / d8-4 一平面简谐机械波沿x 轴正方向传播,波动表达式为)2/cos(2.0x t y ππ-= (SI),则波速u = ;x = -3 m 处媒质质点的振动加速度a 的表达式为 .2 m/s )23cos(2.02x t a π+ππ-= (SI) 8-5 一平面简谐波沿x 轴正向传播,其振幅和角频率分别为A 和ω ,波速为u ,设t = 0时的波形曲线如图所示.(1) 写出此波的表达式. (2) 求距O 点为λ/8处质点的振动方程.(3) 求距O 点为λ/8处质点 在t = 0时的振动速度.解:(1) 以O 点为坐标原点.由图可知,该点振动初始条件为 0cos 0==φA y , 0s i n 0<-=φωA v所以 π=21φ 波的表达式为 ]21)/(c o s [π+-=u x t A y ωω (2) 8/λ=x 处振动方程为]21)8/2(cos[π+π-=λλωt A y )4/cos(π+=t A ωx(3) )21/2sin(/d d π+π--=λωωx t A t y t = 0,8/λ=x 处质点振动速度 ]21)8/2sin[(/d d π+π--=λλωA t y 2/2ωA -= 8-6 如图所示,有一平面简谐波沿x 轴负方向传播,坐标原点O 的振动规律为)cos(0φω+=t A y ),则B 点的振动方程为(A) ])/(cos[0φω+-=u x t A y . (B) )]/([cos u x t A y +=ω. (C) })]/([cos{0φω+-=u x t A y . (D) })]/([cos{0φω++=u x t A y . [ D ]8-7 已知一平面简谐波的表达式为 )24(cos x t A y +π= (SI). (1) 求该波的波长λ ,频率ν 和波速u 的值; (2) 写出t = 4.2 s 时刻各波峰位置的坐标表达式,并求出此时离坐标原点最近的那个波峰的位置.解:(1) 由波数 k = 2π / λ 得波长 λ = 2π / k = 1 m由 ω = 2πν 得频率 ν = ω / 2π = 2 Hz 波速 u = νλ = 2 m/s(2) 波峰的位置,即y = A 的位置.由 1)24(c o s=+πx t 有 π=+πk x t 2)24( ( k = 0,±1,±2,…) 解上式,有 t k x 2-=. 当 t = 4.2 s 时, )4.8(-=k x m . 所谓离坐标原点最近,即| x |最小的波峰.在上式中取k = 8, 可得 x = -0.4 的波峰离坐标原点最近.8-8某质点作简谐振动,周期为2 s ,振幅为0.06 m ,t = 0 时刻,质点恰好处在负向最大位移处,求:(1) 该质点的振动方程; (2) 此振动以波速u = 2 m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3) 该波的波长.解:(1) 振动方程 )22c o s (06.00π+π=ty )c o s (06.0π+π=t (SI) . (2) 波动表达式 ])/(cos[06.0π+-π=u x t y])21(cos[06.0π+-π=x t (SI)(3) 波长 4==uT λ m8-9 一平面简谐波沿Ox 轴正方向传播,波长为λ.若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ,则P 2点处质点的振动方程为 ;与P 1点处质点振动状态相同的那些点的位置是 .])(2cos[212φλν++-π=L L t A y λk L x +-=1 ( k = ± 1, ± 2, …) 8-10 一平面简谐波在弹性媒质中传播,媒质质元从平衡位置运动到最大位移处的过程中: (A) 它的动能转换成势能. (B) 它的势能转换成动能.xOP 1 P 2 L 1 L 2(C) 它从相邻的一段质元获得能量其能量逐渐增大.(D) 它把自己的能量传给相邻的一段质元,其能量逐渐减小. [ D ] 8-11 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是(A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. [ C ] 8-12 一平面简谐波沿Ox 轴正方向传播,波的表达式为 )/(2cos λνx t A y -π=, 而另一平面简谐波沿Ox 轴负方向传播,波的表达式为 )/(2cos 2λνx t A y +π=, 求:(1) x = λ/4 处介质质点的合振动方程; (2) x = λ/4 处介质质点的速度表达式.解:(1) x = λ /4处 )212cos(1π-π=t A y ν , )212cos(22π+π=t A y ν ∵ y 1,y 2反相 ∴合振动振幅A A A A s =-=2, 合振动的初相φ 和y 2的初相一样为π21.合振动方程 )212c o s (π+π=t A y ν (2) x = λ /4处质点的速度 )212sin(2/d d π+ππ-== v t A t y νν)2cos(2π+ππ=t A νν8-13 在绳子上传播的平面简谐入射波表达式为)2cos(1λωxt A y π+=,入射波在x = 0处绳端反射,反射端为自由端.设反射波不衰减,证明形成的驻波表达式为:t xA y ωλcos )2cos(2π=证明:入射波在x = 0处引起的振动方程为 t A y ωcos 10=,由于反射端为自由端,所以反射波在O 点的振动方程为 t A y ωcos 20=∴ 反射波为 )2c o s (2λωxt A y π-=驻波方程21y y y +=)2cos(λωx t A π+=)2cos(λωxt A π-+t x A ωλcos )2cos(2π=8-14 如图所示,两相干波源在x 轴上的位置为S 1和S 2,其间距离为d = 30 m ,S 1位于坐标原点O .设波只沿x 轴正负方向传播,单独传播时强度保持不变.x 1 = 9 m 和x 2 = 12 m 处的两点是相邻的两个因干涉而静止的点.求两波的波长和两波源间最小相位差.解:设S 1和S 2的振动相位分别为φ 1和φ 2.在x 1点两波引起的振动相位差 ]2[]2[1112λφλφx x d π---π-π+=)12(K 即 π+=-π--)12(22)(112K x d λφφ ①在x 2点两波引起的振动相位差 ]2[]2[2122λφλφx x d π---π-π+=)32(K即 π+=-π--)32(22)(212K x d λφφ ②②-①得 π=-π2/)(412λx x 6)(212=-=x x λ m由① π+=-π+π+=-)52(22)12(112K x d K λφφ当K = -2、-3时相位差最小 π±=-12φφ【练习题答案】。
大学物理机械波习题附问题详解
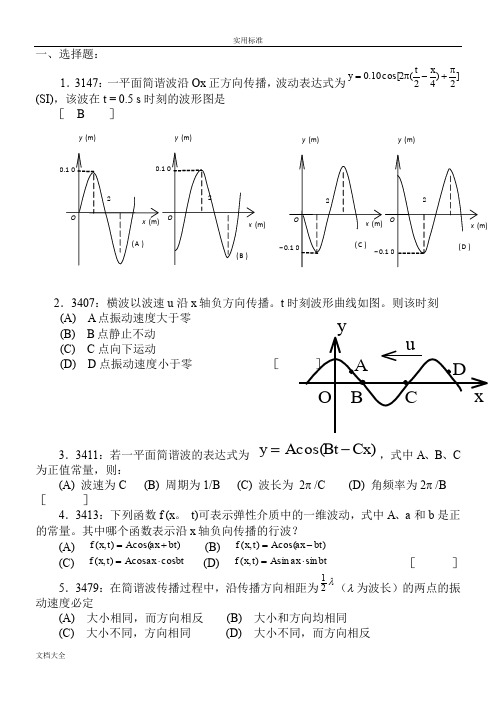
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt axA t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反y (m) y (m) - y (m) y (m)[ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长 (B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
上海交通大学版大学物理学习题答案之机械振动习题思考题

习题77-1.原长为m 5.0的弹簧,上端固定,下端挂一质量为kg 1.0的物体,当物体静止时,弹簧长为m 6.0.现将物体上推,使弹簧缩回到原长,然后放手,以放手时开始计时,取竖直向下为正向,写出振动式。
(g 取9.8)解:振动方程:cos()x A t ωϕ=+,在本题中,kx mg =,所以9.8k =;ω===振幅是物体离开平衡位置的最大距离,当弹簧升长为0.1m 时为物体的平衡位置,以向下为正方向。
所以如果使弹簧的初状态为原长,那么:A=0.1,当t=0时,x=-A,那么就可以知道物体的初相位为π。
所以:0.1cos x π=+)即)x =−7-2.有一单摆,摆长m 0.1=l ,小球质量g 10=m .0=t 时,小球正好经过rad 06.0−=θ处,并以角速度rad/s 2.0=•θ向平衡位置运动。
设小球的运动可看作简谐振动,试求:(g 取9.8)(1)角频率、频率、周期;(2)用余弦函数形式写出小球的振动式。
解:振动方程:cos()x A t ωϕ=+我们只要按照题意找到对应的各项就行了。
(1)角频率: 3.13/rad s ω===,频率:0.5Hz ν===,周期:22T s ===(2)根据初始条件:Aθϕ=0cos 象限)象限)4,3(02,1(0{sin 0<>−=ωθϕA ̇可解得:32.2088.0−==ϕ,A 所以得到振动方程:0.088cos 3.13 2.32t θ=−()7-3.一竖直悬挂的弹簧下端挂一物体,最初用手将物体在弹簧原长处托住,然后放手,此系统便上下振动起来,已知物体最低位置是初始位置下方cm 0.10处,求:(1)振动频率;(2)物体在初始位置下方cm 0.8处的速度大小。
解:(1)由题知2A=10cm,所以A=5cm;1961058.92=×=∆=−x g m K 又ω=14196==mk,即ππν721==m k (2)物体在初始位置下方cm 0.8处,对应着是x=3cm 的位置,所以:03cos 5x A ϕ==那么此时的04sin 5v A ϕω=−=±那么速度的大小为40.565vA ω==7-4.一质点沿x 轴作简谐振动,振幅为cm 12,周期为s 2。
大学物理机械波练习习题思考题包括答案.doc

习题 88-1.沿一平面简谐波的波线上,有相距 2.0 m 的两质点A与B,B点振动相位比 A 点落后,已知振动周期为 2.0 s ,求波长和波速。
6解:根据题意,对于A、 B 两点,21 , x 2m ,2 6而x 24m , u 12m/sT8-2 .已知一平面波沿x 轴正向传播,距坐标原点O 为x1处 P 点的振动式为y A cos( t) ,波速为 u ,求:(1)平面波的波动式;(2)若波沿x轴负向传播,波动式又如何解:( 1)设平面波的波动式为y Acos[ (t x)0 ] ,则 P 点的振动式为:x 1 )uy P A cos[ ( t 0 ] ,与题设P点的振动式 y P Acos( t ) 比较,x1 ux x1有:0 ,∴平面波的波动式为:y Acos[ (t ) ] ;u u ( 2)若波沿x轴负向传播,同理,设平面波的波动式为:y A cos[ ( t x0 ] ,则P点的振动式为:)uy P A cos[ ( t x1)0 ] ,与题设P点的振动式 y P Acos( t ) 比较,x1 uxx1 )有:0 ,∴平面波的波动式为:y A cos[ (tu ] 。
u8-3 .一平面简谐波在空间传播,如图所示,已知A点的振动规律为y A cos(2 t ) ,试写出:( 1)该平面简谐波的表达式;( 2)B点的振动表达式( B 点位于 A 点右方 d 处)。
解:( 1)仿照上题的思路,根据题意,设以O 点为原点平面简谐波的表达式为:y A cos[2 (t x )0 ] ,则 A 点的振动式:uy A A cos[2 (tl ) 0]u题设 A 点的振动式 yA cos(2t) 比较,有:2 l 0,lx )u∴ 该平面简谐波的表达式为:yAcos[ 2 ( t ]u u( 2) B 点的振动表达式可直接将坐标x d l ,代入波动方程:l d l ] A cos[2 ( tdy Acos[ 2 ( tu )) ]uu8-4.已知一沿 x 正方向传播的平面余弦波, t1s 时的波形如图所示, 且周期 T3为 2s 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题8-1. 沿一平面简谐波的波线上,有相距m 0.2的两质点A 与B ,B 点振动相位比A 点落后6π,已知振动周期为s 0.2,求波长和波速。
解:根据题意,对于A 、B 两点,m x 2612=∆=-=∆,πϕϕϕ而相位和波长之间又满足这样的关系:πλπλϕϕϕ221212xx x ∆-=--=-=∆代入数据,可得:波长λ=24m 。
又已知 T=2s ,所以波速u=λ/T=12m/s8-2. 已知一平面波沿x 轴正向传播,距坐标原点O 为1x 处P 点的振动式为)cos(ϕω+=t A y ,波速为u ,求:(1)平面波的波动式;(2)若波沿x 轴负向传播,波动式又如何?解:(1)根据题意,距坐标原点O 为1x 处P 点是坐标原点的振动状态传过来的,其O 点振动状态传到p 点需用 ux t 1=∆,也就是说t 时刻p 处质点的振动状态重复ux t -时刻O 处质点的振动状态。
换而言之,O 处质点的振动状态相当于ux t 1+ 时刻p 处质点的振动状态,则O 点的振动方程为:]cos[1ϕω++=)(u x t A y 波动方程为:11cos[]cos[()]x x x xy A t A t uu uωϕωϕ-=+-+=-+()(2)若波沿x 轴负向传播, O 处质点的振动状态相当于ux t 1-时刻p 处质点的振动状态,则O 点的振动方程为:]cos[1ϕω+-=)(ux t A y波动方程为:11cos[]cos[()]x x x xy A t A t u u uωϕωϕ+=--+=-+()8-3. 一平面简谐波在空间传播,如图所示,已知A 点的振动规律为)2cos(ϕπν+=t A y ,试写出:(1)该平面简谐波的表达式;(2)B 点的振动表达式(B 点位于A 点右方d 处)。
解:(1)仿照上题的思路,根据题意,A 点的振动规律为)2cos(ϕπν+=t A y ,它的振动是O 点传过来的,所以O 点的振动方程为:]2cos[ϕπν++=)(u l t A y那么该平面简谐波的表达式为:]2cos[ϕπν+++=)(u x u l t A y(2)B 点的振动表达式可直接将坐标x d l =-,代入波动方程:]2cos[]2cos[ϕπνϕπν++=+-++=)()(u d t A ul d u l t A y也可以根据B 点的振动经过ud 时间传给A 点的思路来做。
8-4. 已知一沿x 正方向传播的平面余弦波,s 31=t 时的波形如图所示,且周期T 为s 2.(1)写出O 点的振动表达式;(2)写出该波的波动表达式;(3)写出A 点的振动表达式; (4)写出A 点离O 点的距离。
解:由图可知A=0.1m ,λ=0.4m ,由题知T= 2s ,ω=2π/T=π,而u=λ/T=0.2m/s 。
波动方程为:y=0.1cos [π(t-x/0.2)+Ф0]m 关键在于确定O 点的初始相位。
(1) 由上式可知:O 点的相位也可写成:φ=πt+Ф0由图形可知: s 31=t 时y 0=-A/2,v 0<0,∴此时的φ=2π/3, 将此条件代入,所以:03132ϕππ+= 所以30πϕ=O 点的振动表达式y=0.1cos [πt+π/3]m(2)波动方程为:y=0.1cos [π(t-x/0.2)+π/3]m (3)A 点的振动表达式确定方法与O 点相似由上式可知:A 点的相位也可写成:φ=πt+ФA0由图形可知: s 31=t 时y 0=0,v 0>0,∴此时的φ=-π/2,将此条件代入,所以:0312A ϕππ+=-所以650πϕ-=AA 点的振动表达式y=0.1cos [πt-5π/6]m(4)将A 点的坐标代入波动方程,可得到A 的振动方程,与(3)结果相同,所以: y=0.1cos [π(t-x/0.2)+π/3]= 0.1cos [πt-5π/6]可得到:m x A 233.0307==8-5. 一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播。
已知原点的振动曲线如图所示。
试写出:(1)原点的振动表达式; (2)波动表达式;(3)同一时刻相距m 1的两点之间的位相差。
解:由图可知A=0.5cm ,原点处的振动方程为:y=Acos (ωt+φ)时 y=A/2 v>0 可知其相位为φ1=3π-时 y=0 v<0 可知其相位为φ2=2π代入振动方程, φ=3π-ω+φ=2π可得:ω=65π T=2π/ω=12/5则 y=0.5cos (65πt-3π)cm (2)沿x轴负方向传播,波动表达式:555y=0.5cos[(t+)-]=0.5cos[(t+)-]a 63643x x u ππππcm (3)根据已知的T=12/5,m/s 8.0=u ,可知:m 2548=λ 那么同一时刻相距m 1的两点之间的位相差: 3.27rad 24252==∆=∆πλπϕx8-6. 一正弦形式空气波沿直径为cm 14的圆柱形管行进,波的平均强度为m)J/(s 100.93⋅⨯-,频率为Hz 300,波速为m/s 300。
问波中的平均能量密度和最大能量密度各是多少?每两个相邻同相面间的波段中含有多少能量? 解:(1)∵ I=w u ∴uI w ==9.0×10-3/300=3×10-5 J ·m -3w max =2w =0.6×10-4 J ·m -3 (2) W=νπλπωudwd wV 224141===3×10-5×1π/4×(0.14)2×300/300=4.62×10-7J8-7. 一弹性波在媒质中传播的速度m/s 103=u ,振幅m 100.14-⨯=A ,频率H z 103=ν。
若该媒质的密度为3kg/m 800,求:(1)该波的平均能流密度;(2)1分钟内垂直通过面积24m 100.4-⨯=S 的总能量。
解:ω=2πγ=2π310⨯(1))()()(s m J A u I ∙⨯=⨯⨯⨯⨯==-252324322/1058.110210800102121πωρ(2)1分钟内垂直通过面积24m 100.4-⨯=S 的总能量 W=ISt J 3451079.3601041058.1⨯=⨯⨯⨯⨯=-8-8. 1S 与2S 为左、右两个振幅相等相干平面简谐波源,它们的间距为4/5λ=d ,2S 质点的振动比1S 超前2π. 设1S 的振动方程为t TA y π2c o s 10=,且媒质无吸收,(1)写出1S 与2S 之间的合成波动方程;(2)分别写出1S 与2S 左、右侧的合成波动方程。
解:(1))2cos(1101r t A y λπϕω-+= )2cos(2202r t A y λπϕω-+=由题意:φ20-φ10=2π设它们之间的这一点坐标为x ,则 )2cos(101x t A y λπϕω-+=)()(x t A x t A y λπϕωλλππϕω2cos ]4522cos[10102++=--++= 相当于两列沿相反方向传播的波的叠加,合成为驻波。
合成波为:t Tx A y y y πλπ2cos2cos221=+=(2) 在S 1左侧的点距离S 1为x : )2cos(101x t A y λπϕω++=)()(x t A x t A y λπϕωλλππϕω2cos ]4522cos[10102++=++++= 合成波为:)(λπxT t A y y y +=+=2cos 221在S 2右侧的点距离S 1为x : )2cos(101x t A y λπϕω-+= )()(x t A x t A y λπϕωλλππϕω2cos ]4522cos[10102-+=--++= 两列波正好是完全反相的状态,所以合成之后为0。
8-9. 设1S 与2S 为两个相干波源,相距41波长,1S 比2S 的位相超前2π。
若两波在在1S 、2S 连线方向上的强度相同且不随距离变化,问1S 、2S 连线上在1S 外侧各点的合成波的强度如何?又在2S 外侧各点的强度如何? 解:由题意:φ1-φ2=2π, r 1在S 1左侧的点: AS 1=r 1, AS 2=r 2,∆φ=πλλππλπϕϕ-=--=---4/12221212r rr 2所以A=A 1-A 2=0,I=0; S 1 S 2 A 在S 2左侧的点: AS 1=r 1, AS 2=r 2, r 1∆φ=04/12221212=---=---λλππλπϕϕr r所以A=A 1+A 2=2A ,I=4I 0;8-10. 测定气体中声速的孔脱(Kundt )法如下:一细棒的中部夹住,一端有盘D 伸入玻璃管,如图所示。
管中撒有软木屑,管的另一端有活塞P ,使棒纵向振动,移动活塞位置直至软木屑形成波节和波腹图案。
若已知棒中纵波的频率ν,量度相邻波节间的平均距离d ,可求得管内气体中的声速u 。
试证:d u ν2=。
证明:根据驻波的定义,相邻两波节(腹)间距:2λ=∆x ,再根据已知条件:量度相邻波节间的平均距离d ,所以:2λ=d 那么:d 2=λ所以波速d u νλν2==8-11. 图中所示为声音干涉仪,用以演示声波的干涉。
S 为声源,D 为声音探测器,如耳或话筒。
路径SBD 的长度可以变化,但路径SAD 是固定的。
干涉仪内有空气,且知声音强度在B 的第一位置时为极小值100单位,而渐增至B 距第一位置为cm 65.1的第二位置时,有极大值900单位。
求:(1)声源发出的声波频率;(2)抵达探测器的两波的振幅之比。
解:根据驻波的定义,相邻两波节(腹)间距:2λ=∆x相邻波节与波腹的间距:4λ=∆x 可得:cm x 6.64=∆=λ声音的速度在空气中约为340m/s ,所以:)。
(hz u5151106.63402=⨯==-λν根据强度是振幅的平方的关系:声音强度在B 的第一位置时为极小值100单位, 在第二位置有极大值900单位,所以振幅的相对大小为10与30单位。
极小值的原因是两个振幅相减(A 1-A 2=10 ) ,极大值的原因是两个振幅相加(A 1+A 2=30 )。
那么A 1:A 2=2:1 。
8-12. 绳索上的波以波速m/s 25=v 传播,若绳的两端固定,相距m 2,在绳上形成驻波,且除端点外其间有3个波节。
设驻波振幅为m 1.0,0=t 时绳上各点均经过平衡位置。
试写出:(1)驻波的表示式;(2)形成该驻波的两列反向进行的行波表示式。
解:根据驻波的定义,相邻两波节(腹)间距:2λ=∆x ,如果绳的两端固定,那么两个端点上都是波节,根据题意除端点外其间还有3个波节,可见两端点之间有四个半波长的距离,224=⨯=∆λx ,所以波长m 1=λ,m/s 25=v ,所以)。
