高等数学1.3函数的极限PPT
合集下载
《高等数学极限》课件

THANK YOU
无穷级数与无穷积分的收敛性
总结词
收敛性是无穷级数和无穷积分最重要的性质之一,它 表示无穷级数或无穷积分的和是有限的。收敛性的判 定是高等数学中的一个重要问题,需要用到多种数学 方法和技巧。
详细描述
收敛性是无穷级数和无穷积分最重要的性质之一,它 表示无穷级数或无穷积分的和是有限的。如果一个无 穷级数或无穷积分是收敛的,那么它的和就是有限的 ,否则就是发散的。收敛性的判定是高等数学中的一 个重要问题,需要用到多种数学方法和技巧,如比较 判别法、柯西判别法、阿贝尔判别法等。对于不同的 级数和积分,需要采用不同的方法和技巧进行收敛性 的判定。
03
导数与连续性
导数的定义与性质
导数的定义
导数是函数在某一点的变化率的极限 ,表示函数在该点的切线斜率。
导数的性质
导数具有线性、可加性、可乘性和链 式法则等性质,这些性质在研究函数 的单调性、极值和曲线的几何特性等 方面具有重要应用。
导数的计算方法
基本初等函数的导数
对于常数、幂函数、指数函数、三角函数和反三角函 数等基本初等函数,需要熟记其导数公式。
限的。
无穷积分的定义与性质
总结词
无穷积分是数学中另一个重要的概念,它是由无穷多个 定积分的和组成的积分。无穷积分具有一些重要的性质 ,如可加性、可乘性和可微性等。
详细描述
无穷积分是由无穷多个定积分的和组成的积分,这些定 积分可以是积分限不同的积分。无穷积分在数学中也有 着广泛的应用,如求解面积、体积和曲线长度等。无穷 积分具有一些重要的性质,如可加性、可乘性和可微性 等。其中,可加性表示无穷积分可以拆分成若干个部分 的和,可乘性和可微性则表示无穷积分可以与函数进行 运算和求导。
高等数学 函数的极限课件

函数极限的定义可以用数学符号表示为:lim f(x) = A,表示当x趋近 于某个值时,f(x)趋近于A。
函数极限的性质
01
唯一性
函数的极限是唯一的,即如果 lim f(x) = A和lim f(x) = B,则
A = B。
02
有界性
函数的极限是有界的,即存在 一个正数M,使得当x在某点附 近时,f(x)的绝对值小于M。
高等数学 函数的极限课件
目录
• 函数极限的基本概念 • 函数极限的运算性质 • 无穷小与无穷大 • 函数的连续性 • 极限的应用
01
函数极限的基本概念
函数极限的定义
01
02
函数极限的定义是高等数学中的基本概念,它描述了函数在某一点的 变化趋势。具体来说,如果当自变量趋近于某一值时,函数值无限接 近于一个确定的数,则称该数为函数的极限。
求复合函数极限的方法
通过将复合函数分解为基本初等函数或已知极限的函数,利用极限的四则运算性质和已知极限,求得 复合函数的极限。
反函数的极限
反函数极限的定义
设函数y=f(x)在点x0有定义且f'(x0)=1,其反函数为x=g[f(x)],如果lim(y→y0) x=lim(y→y0) g[f(x)],则称反函 数在点y0处存在极限。
03
局部保号性
如果lim f(x) = A且A > 0,则 在某点附近存在一个正数δ, 使得当x满足一定条件时,f(x)
> 0。
函数极限的存在性定理
函数极限的存在性定理是高等数学中一个重要的定理,它给出了函数极限存在的 充分条件。根据这个定理,如果函数在某点的左右极限存在且相等,则函数在该 点有极限。
连续性的几何意义
高等数学(同济第六版)课件 第一章 3.函数的极限(一)

且a >b, (或a<b)
则正数X, 当x<-X时, 都有f(x) >b . (或f(x)<b) 当x>X时, 当|x|>X时,
(4) 充要条件:
lim lim lim f ( x ) A x f ( x ) A且 x f ( x ) A.
x
证: " " 0, X 1 0, 当x>X1 时,成立 f ( x ) A .
得 | x x0 |
x0
当 | x x0 | x0 时,才能使x>0, 取 min{ x0 , x0 } 当 0 x x0 时, 成立 | x x0 |
lim x
x x0
x0
" "定义
x x0
lim f ( x ) A
2 x2 x 1 3 lim x 1 x 1 2 x2 x 1 3 | 2 | x 1 | ( x 1) 0, | x 1 2 x2 x 1 3 | 当x与1多么接近时? | x 1 | x 1 | 2
2 x2 x 1 0, 当 0 | x 1 | 时, 成立 | 3 | 2 x 1
lim f ( x ) 0, 则 lim f ( x ) g( x ) 0
x x
1 x (7) 重要极限:lim (1 ) e x x
特点:(1)1 型 (2)底数减1等于指数的倒数 。
例2 求下列极限
2 x3 3 x2 5 (1) lim 3 2 x 7 x 4 x 1
二、 自变量趋向有限值时函数的极限 若当x无限接近于x0时,函数f(x)无限接近于常数A, 称常数A为当x趋于x0时,函数f(x)的极限。 记作 lim f ( x ) A
函数的极限【高等数学PPT课件】

A(或f
( x0
0)
A)
右极限: 定理1
lim
xx0
f (x)
A(或f (x0
0)
A)
lim f (x) A lim f (x) lim f (x) A
xx0
xx0
xx0
x sin x, x 0
例1
试问函数f ( x)
10, x 0
(c) Sketch the graph of F.
例2 lim sin x不存在 x
lim sin 1 不存在.
x0
x
y sin 1 x
思考与练习
1. 若极限 lim f ( x) 存在, 是否一定有
x x0
lim f ( x) f ( x0 ) ?
x x0
2. 设函数 f ( x) a x2, x 1 且 2x 1, x 1
lim f ( x)
x1
存在, 则 a 3 .
3.Let F (x) x 2 1 .
x 1
(a) Find (i) lim F (x) x 2 1 .
x1
x 1
(ii) lim x1
F(x)
x2 1 .
x 1
(b) Does lim F(x). exist?
x1
lim f ( x) lim f ( x) lim f ( x) 不存在.
x0
x0
x0
二、函数极限的性质
1.惟一性
定理1 (极限的惟一性) 如果函数极限
存在,则极限值惟一.
2.有界性
定理2 (局部有界性)
如果极限 lim f (x) xx0
高等数学的教学课件1-3函数的极限

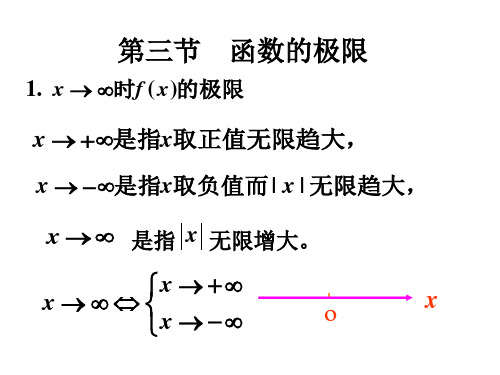
自变量无限变化的过程有如下几种形式:
一、x 无限增大,记为x 1 x 0且 x 无限增大,记为x 2 x 0且 x 无限增大,记为x
二、x无限接近某定值 x0,记为x x0 1 x x0且x x0,记为x x0 2 x x0且x x0,记为x x0
一、自变量趋向无穷大时函数的极限
x0
x0
f (0 ) f (0 ) 1, lim f ( x) 1. x0
例13
x 1, x 0 假设f ( x) ax b, 0 x 1
2 x, x 1
试确定a、b之值,使得lim f ( x)及 lim f ( x)都存在
x0
x1
解 f (0 ) lim (x 1) 0 1 1.
x
2
证
任给 0,
要使 arctan x arctan x ,
22
即 arctanx ,
2
故只需 x tan( ).
2
取G tan( ),
2
当x G时,
就有 arctan x , 证毕。
2
lim arctanx
x
2
lim arctanx
x
2
典型极限
例12
x0
x0 x
点x0的去心邻域, 体现x接近x0程度.
1. 定义 :
定义 2 如果对于任意给定的正数 (不论它多么小),
总存在正数 ,使得对于适合不等式0 x x0 的 一切x ,对应的函数值 f ( x)都满足不等式
f (x) A ,
那末常数 A就叫函数 f ( x)当x x0 时的极限,记作
例5
证明
lim
x x0
x
x0 .
证 f ( x) A x x0 , 任给 0, 取 ,
一、x 无限增大,记为x 1 x 0且 x 无限增大,记为x 2 x 0且 x 无限增大,记为x
二、x无限接近某定值 x0,记为x x0 1 x x0且x x0,记为x x0 2 x x0且x x0,记为x x0
一、自变量趋向无穷大时函数的极限
x0
x0
f (0 ) f (0 ) 1, lim f ( x) 1. x0
例13
x 1, x 0 假设f ( x) ax b, 0 x 1
2 x, x 1
试确定a、b之值,使得lim f ( x)及 lim f ( x)都存在
x0
x1
解 f (0 ) lim (x 1) 0 1 1.
x
2
证
任给 0,
要使 arctan x arctan x ,
22
即 arctanx ,
2
故只需 x tan( ).
2
取G tan( ),
2
当x G时,
就有 arctan x , 证毕。
2
lim arctanx
x
2
lim arctanx
x
2
典型极限
例12
x0
x0 x
点x0的去心邻域, 体现x接近x0程度.
1. 定义 :
定义 2 如果对于任意给定的正数 (不论它多么小),
总存在正数 ,使得对于适合不等式0 x x0 的 一切x ,对应的函数值 f ( x)都满足不等式
f (x) A ,
那末常数 A就叫函数 f ( x)当x x0 时的极限,记作
例5
证明
lim
x x0
x
x0 .
证 f ( x) A x x0 , 任给 0, 取 ,
高等数学-函数的极限PPT课件

则A是 f (x)当 x 的极限. 记为: lim f ( x) A. x
或者记为:当 x 时,f ( x) A.
从定义中得到: x X 包含了 x X 和x X .
所以: x 包含了 x 和 x . 于是有
定理:lim f ( x) A lim f ( x) A且 lim f ( x) A.
x
x
x
则有:lim(2 1 ) 2, limarctan x 不存在.
x
x
x
.
7
注意: 证明极限存在时,关键是任意给定 0, 寻找X.
求X的方法: 由 f (x) A 解出x
几何解释:
Aε f (x) Aε
AA
X
A X
或者记为:当 x 时,f ( x) A.
则有:lim (2 1 ) 2, limarctan x π
x
x
x
2
对于 y 2 1 ,lim (2 1 ) 2,lim (2 1 ) 2,那么 lim(2 1 ) ?
x x
x
x
或者从x0的两边同时接近于x0.
.
12
函数极限的几何意义
lim f ( x) A 0, 0, 使得当
xБайду номын сангаас x0
0 x x0 时, 恒有 f ( x) A 成立.
0
当 x U ( x0 ) 时,
函数f(x)的图形完全
y
y f (x)
落在以直线y=A为中
定义:如果 0, X 0, 使当 x X 时,恒有 f (x) A ,
高教社2024高等数学第五版教学课件-1.3 两个重要极限

则若有函数()在0 的某邻域内恒有
() ≤ () ≤ (),
那么当 → 0 时,有 ≤ () ≤ (),
即
故
≤ () ≤ ,
() = .
→0
= 1.
(−)
证:因为
−
−
−
=
=
,
所以我们只需讨论 → 0+ 的情形,
→∞
→∞ 2 + 1
1+
= 1 +
→∞
方法二
2 + 3
→∞ 2 + 1
=
2
2+1
2
2+1
3
1+
2
=
1
→∞
1+
2
+1
→∞
→∞
1+
1+
3
2
1
2
2 3
3 ×2
1
2×2
2+1
2
2+1
2
⋅ 1+
2
2+1
∙ 1 +
→∞
1
2
2
2+1
1
2
= ⋅ 1 = .
+1
∙ 1+
∙ 1+
3
2
1
2
=
3
2
×1
1
2
×1
=
→0
例3 计算
解
≠ 0, ≠ 0)
→0
=
() ≤ () ≤ (),
那么当 → 0 时,有 ≤ () ≤ (),
即
故
≤ () ≤ ,
() = .
→0
= 1.
(−)
证:因为
−
−
−
=
=
,
所以我们只需讨论 → 0+ 的情形,
→∞
→∞ 2 + 1
1+
= 1 +
→∞
方法二
2 + 3
→∞ 2 + 1
=
2
2+1
2
2+1
3
1+
2
=
1
→∞
1+
2
+1
→∞
→∞
1+
1+
3
2
1
2
2 3
3 ×2
1
2×2
2+1
2
2+1
2
⋅ 1+
2
2+1
∙ 1 +
→∞
1
2
2
2+1
1
2
= ⋅ 1 = .
+1
∙ 1+
∙ 1+
3
2
1
2
=
3
2
×1
1
2
×1
=
→0
例3 计算
解
≠ 0, ≠ 0)
→0
=
高等数学函数的极限课程课件
则称当x x0时,函数f ( x)以a为极限,记作
lim f ( x) a 或
x x0
f (x) a(x x0 )
此时, 亦称当 x x0 时 f ( x) 存在极限
(或收 敛且收 敛 于 a ).
注 1 : 定义中的“0 | x x0 | ”表明: 当 x x0 时, f ( x) 有无极限以及极限值为多少均与 f ( x) 在 x0 有无定义无关.
xk
1
但 lim f ( x)不 存 在
2
xk
函数极限与数列极限的联系(某个桥梁):
定理3.1(Heine定理)
设f
: N ( x0 )
R为一函数,则 lim x x0
f (x)
a的
充要条件为对于N ( x0 )中的任何数列xn,
只要xn x0 (n ),
相应的函数值数列f ( xn )都收敛于a.
例3.2 问limarctanx是否存在? x
解 因为 lim arctan x ,
x
2
lim arctan x ,
x
2
lim arctan x lim arctan x,
x +
x
所以 limarctanx不存在.
x
y arctanx图象如图:
y
2
y arctan x
o
x
2
2. x x0时f ( x)的极限
都有 | f ( x) | L.
证明 设 lim f ( x) a, x x0 对 1, 0, 当0 x x0 时,
有 | f ( x) a | 1
所以当x ( x0 , x0 ) ( x0, x0 ) 时,
有a 1 f ( x) a 1
高等数学教案PPt

注 有时平面曲线用极坐标方程表示非
常简便.
例如,圆 x2 y2 R2,其极坐标方程为
rR
y
R
x 圆 x2 y2 2ax 的极坐标方程为
r 2a cos
上页 下页 返回
§1.1 函数
几个特殊的函数举例
例2 分段函数
设
f (x)
1 x2
x
1,
,
1 0
x 0, x 1.
y
其定义域为 [1,1).
y (1)x y a
y ax
(a 1)
(0,1)
O
x
定义域为 (, ),值域为(0, ).
上页 下页 返回
§1.1 函数
(3) 对数函数
y loga x
y
(a 0, a 1)
y log a x
(a 1)
(1,0)
O
x
y log 1 x
a
定义域为 (0, ), 值域为 (, ).
第一章 函数与极限
§1.1 函数 §1.2 函数的极限 §1.3 极限运算法则 §1.4 极限存在准则与两个重要极限 §1.5 无穷小与无穷大
上页 下页 返回
第一章 函数与极限
§1.6 函数的连续性与连续函数的运算 §1.7 初等函数的连续性及闭区间上连续
函数的性质
上页 下页 返回
§1.1 函数
如果 D1 x (x)U , x D ,则对每个x D1
通过函数u (x) 有确定的 u U 与之对应,又
通过函数 y f (u)有确定的实数y 与u 对应,从而
得到一个以为x自变量,y为因变量定义在 D1上的函
数,称它为由函数 y f (u) 与 u (x) 复合而成的
大学高等数学 1_3 函数的极限

则 A 0.
( f ( x) 0)
( A 0)
假设 A < 0 , 则由定理 1,
与已知
证: 用反证法.
存在
的某去心邻域 , 使在该邻域内 (同样可证 f ( x) 0 的情形)
条件矛盾, 所以假设不真, 故 A 0 . 思考: 若定理 2 中的条件改为 f ( x) 0, 是否必有 A 0 ?
解: 利用定理 3 . 因为
x 0 x 0
y x 1
x
lim f ( x) lim ( x 1) 1
x0
lim f ( x) lim ( x 1) 1
x 0 x 0
Page 12
显然 f (0 ) f (0 ) , 所以 lim f ( x) 不存在 .
a
3
.
Page 16
lim f ( x) A 或
当 时, A
y f (x)
这表明:
极限存在
x0 x0 x
函数局部有界 (P36定理2)
Page 3
例1. 证明
证:
f ( x) A
时,
故 0 , 对任意的 0 , 当 总有 因此
Page 4
例2. 证明
二、自变量趋于无穷大时函数的极限
定义2 . 设函数 大于某一正数时有定义, 若 则称常数 时的极限, 记作
0 , X 0 ,
A 为函数
x
lim f ( x) A
x X 或x X
几何解释:
y
A A
A f ( x) A
y f (x)
因此
x x0
lim
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
近于某个确定的常数A,那么就称当 x x0时函数
f x 的极限是A,亦称函数 f x 在点 x0 的极限是A,
记为
x x0
lim f x A或者f x A x x0 ;
如果这样的常数A不存在,就称当 x x0时函 数 f x 没有极限,亦称函数 f x 在点 x0 处没 有极限,习惯上也常常表达为 lim f x 不存在。
定义2 设函数 f x 在点 x0 的一个右领域内有定义。
如果当
时,函数值 x x0
x f无限接近于某确定
的右极限是 x f
的常数A,那么称为
A,亦称函数
x x0
时,函数 x x0
在点 x f
x0 处的右极限是 A,记为
lim f x A或者f x0 A
第三节 函数的极限
一、函数极限的概念 二、函数极限的性质
1.自变量 x x0 函数的极限
问题: 函数 y f ( x ) 在 x x0 的过程中 , 对应 函数值 f ( x ) 无限趋近于确定值 A.
例1 设有函数 f x 2 x 1 。定点 x0 2。不难看出,
渐近线.
2.另两种情形:
f ( x) A 10 . x 情形 : xlim
0, X 0, 使当x X时, 恒有 f ( x ) A .
2 . x 情形 : lim f ( x ) A
0
x
0, X 0, 使当x X时, 恒有 f ( x ) A .
当 x x0 ,对应的函数值 f x 2 x 1 无限接近于5
然而,譬如说对于函数
2 x 1, x 2 g x 1, x 2 或者对于函数
不难看出,当 x x0 时,对应的函数值 g x 或者
h x 依然无限接近于常数5 h x 2 x 1, x 2,
o
x0
x0
x0
x
显然, 找到一个后,越小越好.
定理 : lim f ( x ) A f ( x0 ) f ( x0 ) A.
x x0
x 例6 验证 lim 不存在. x0 x
x x lim lim 证 x 0 x x 0 x
y
1
lim ( 1) 1
x x0
0
f ( x ) 0(或f ( x ) 0), 则A 0(或A 0).
例8 证明下列极限:
(1) lim x x0 , 其中, x0 R;
x x0
( 2) lim x
x x0
x0 , 其中, x0 R ;
π ( 3) lim arctan x . x 2
f x A x .
定义类似地,我们有 命题2
x
lim f x A的充分必要条件是lim f x A且 lim f x A
x x
例6
1 由于当x 时,函数值f x 无限接近于0,所 x 1 1 以有 lim 0,以及直线y 0是曲线y 的一条水平 x x x
x
lim f x A 或者
f x A x ;
设函数f x 当x小于某一负数时有定义 ,如果当 x 时,函数值f x 无限接近于某个确定的 常数A,那么就称当x 时,函数值f x 的极 限是A, 记为
x
lim f x A 或者
左极限与右极限称为单侧极限.
1.函数极限与 f ( x )在点x0是否有定义无关 ; 注意:
2. 与任意给定的正数 有关.
2.几何解释:
当x在x0的去心 邻 域时,函数y f ( x ) 图形完全落在以直 线y A为中心线, 宽为2的带形区域内.
A
A
y
y f ( x)
A
1 例2 设有函数 f x ,定点 x0 1 ,不难 x 1 1 看出,当 x x0 时,对应的函数值 f x x 1
的绝对值无限制地增大,不能无限接近于任何一
个确定的常数
定义1 设函数 f x 在点 x0 的一个去心邻域 u x0 内
有定义。如果当 x x0时,函数值 f x 无限接
lim f ( x ) A且 x lim f ( x ) A. 定理 : lim f ( x) A x x
3.几何解释:
y
A
sin x x
X
X
当x X或x X时, 函数 y f ( x )图形完全落在以 直线y A为中心线, 宽为2的带形区域内.
通过上面演示实验的观察: sin x 当 x 无限增大时, f ( x ) 无限接近于 0. x
定义3
设函数f x 当 x 大于某一正数时有定义 。如果 当x 时,函数值f x 无限接近于某个确定 的常数A,那么,就称当 x 时,函数f x 的 极限是A,并称函数f x 在无穷远处的极限是 A, 记为
二、函数极限的性质
1.有界性
定理 若在某个过程下 , f ( x ) 有极限 , 则存在 过程的一个时刻,在此时刻以后 f ( x ) 有界.
2.唯一性
定理 若lim f ( x )存在,则极限唯一.
3.不等式性质
定理(保序性)
0
设 lim f ( x ) A, lim g( x ) B.
x x0 x x0
若 0, x U ( x0 , ), 有f ( x ) g( x ), 则A B .
推论
设 lim f ( x ) A, lim g( x ) B, 且A B
x x0 x x0 0
则 0, x U ( x0 , ), 有f ( x ) g( x ).sin x 来自0. 例1 证明 lim x x
1 sin x sin x 1 证 , 0 x X x x
0, 取 X ,
sin x 0 , x
x
y
sin x x
1
则当 x X时恒有
sin x 故 lim 0. x x
定义 : 如果 lim f ( x ) c , 则直线 y c是函数y f ( x ) 的图形的水平渐近线 .
定理(保号性)
若 lim f ( x ) A, 且A 0(或A 0),
x x0 0
则 0,当x U ( x0 , )时, f ( x ) 0(或f ( x ) 0).
推论
若 lim f ( x ) A, 且 0,当x U ( x0 , )时,
x x0
定义2 设函数 f x 在点 x0 的一个左领域内有定义。
如果当
时,函数值 x x0
x f无限接近于某确定 x f的左极限是
的常数A,那么称为
A,亦称函数
x x0
时,函数 x x0
x f在点
x0 处的左极限是 A,记为
lim f x A或者f x0 A
x 0
o
1
x
x x lim 1 1 lim lim x 0 x 0 x x 0 x
f ( x ) 不存在. 左右极限存在但不相等, lim x0
2.自变量趋向无穷大时函数的极限
sin x 观察函数 当 x 时的变化趋势. x
播放
问题: 函数 y f ( x ) 在 x 的过程中, 对应 函数值 f ( x ) 无限趋近于确定值 A.
lim f x A 或者
x
f x A x .
类似于函数 f x 在 x0 处的左、右极限,我们有
,如果当 定义4 设函数f x 当x大于某一正数时有定义 x 时,函数值f x 无限接近于某个确定的 常数A,那么就称当x 时,函数值f x 的极 限是A, 记为
