算法合集之《伸展树的基本操作与应用》
数据结构及应用算法教程修订版

20
假如中序遍历二叉排序树,所得序列将是有 序旳,即实现了对原始数据旳排序,二叉排序 树即由此得名。
原始序列数据 (49,38,65,76,49,13,27,52)
构造旳二叉排序树 49
38
65
13
49
7627Leabharlann 52中序遍历二叉排序树
for ( i=H.length; i>1; --i ) { // 调整堆来实现排序 H.r[1]←→H.r[i]; // 将堆顶统计和目前未经排序子序列 // H.r[1..i]中最终一种统计相互互换 HeapAdjust(H.r, 1, i-1); // 对 H.r[1] 进行筛选
} 13
} // HeapSort
13
s->data = T ->data;
s->next = head->next;
38
head->next = s; degression(T ->rchild ); } }
s 插入结点
旳指针操作
40
降序排列旳动态模型演示
49
38
76
13
40
134738069
1343890
143308
3138
13
32
字母集: s, t, a, e, i
出现频度: 5, 6, 2, 9, 7
编码: 101, 00, 100, 11, 01
29
0
1
电文: eat
13 01
16 01
6 00
7 01
7 0
1
9 11
浙教版五年级上册信息技术第15课算法的应用(共19张PPT)

五年级上
第十五课 算法的应用
01 学习目标 02 本课内容 03 课堂总结 04 练习一下
2
01
学习目标
3
学习目标
你将学习
1.最短距离算法的应用。 2.算法思维在生活中的应用。
4
02
本课内容
5
本课学习
课堂引入
6
小组讨论
学习了最短距离算法后,生活 中哪些问题可以应用这种算法来解 决?
9
二、灵活运用 算法指导生活
10
11
三、 应用算法思维 优化生活
12
13
14
03
课堂总结
15
课堂总结 使用算法结果解决问题 灵活运用算法指导生活 应用算法思维优化生活
16
04
练习一下
17
Thank you for wat是解决问题的方法及其步骤。经过验证后,使用正确的算法可以解 决特定的生活问题。同一种算法也可以用于解决其他类似问题,还可以采用在 设计算法过程中的思维方法来进一步优化生活。
使用算法结果 解决问题
灵活运用算法 指导生活
应用算法思维 优化生活
……
一、使用算法结 果解决问题
伸展树代码(pascal)

3.如果当前结点,当前结点的父亲结点,当前结点的父亲结点的父亲结点三点成一折线,
则连续旋转当前结点两次(按不同方向)。
旋转的方向一定要画图确定,只需记住最终要把x移到这一堆的根上即可
如x,y都是它们父亲的左孩子,则先左旋y,再左旋x,
又如y是父亲z的右孩子,x是父亲y的左孩子,则先右旋x,再左旋x.
end;
if father[x]=0 then root:=x;
end;
{//插入一个数w的过程,第一种实现
procedure insert(w:longint);
var x:longint;
begin
if total=0 then //如果为空树,则初始化此树
2.更改各子树指针
1)x的子树先移动
x的右孩子变成了y的左儿子,如果此孩子不为空则它的父亲为y
2)关于x的修改
x代替了y,成为了原先y的父亲的儿子
如果y不是y的指针
A B C D
根据sgybi大牛的总结,其实什么zig-zag,zig-zig都是浮云
只要牢记以下几条规律即可保证清晰明了:
1.如果当前结点是根节点的孩子,直接旋转一次即可。
2.如果当前结点,当前结点的父亲结点,当前结点的父亲结点的父亲结点三点成一直线,
{伸展操作图解如下:
z x
/ \ / \
y D A y
/ \ / \
x C ---> B z
/ \ zig-zig / \
end;
//w=1求以x为根的子树中最小值,w=2求x的子树中最大值
具体地,(单)旋转分为以下几个步骤:
伸展树(SplayTree)的实现

伸展树(SplayTree)的实现优点:伸展树(splay tree)是⼀种能⾃我调整的⼆叉搜索树(BST)。
虽然某⼀次的访问操作所花费的时间⽐较长,但是平摊(amortized)之后的访问操作(例如旋转)时间能达到O(logn)的复杂度。
对于某⼀个被访问的节点,在接下来的⼀段时间内再次频繁访问它(90%的情况下是这样的,即符合90-10规则,类似于CPU内或磁盘的cache设计原理)的应⽤模式来说,伸展树是⼀种很理想的数据结构。
另外⼀点与其他平衡⼆叉树的区别是,伸展树不需要存储任何像AVL树中平衡因⼦(balance factor)那样的平衡信息,可以节省空间的开销。
缺点:不像其他平衡⼆叉树那样即使最坏情况下也能达到O(logn)访问时间,它的最坏情况下只有O(n),跟单向链表⼀样。
另外,伸展树的查找操作会修改树的结构,这与普通意义上的查找为只读操作习惯不太⼀样。
实现⽅式:伸展树的实现有两种⽅式,⼀是⾃底向上(bottom-up),另外⼀种是⾃顶向下(top-down)。
考虑到实现的难易程度,⾃顶向下的实现⽅式⽐较简单,因为⾃底向上需要保存已经被访问的节点,⽽⾃顶向下可以在搜索的过程中同时完成splay操作。
虽然两者得出的树结构不太⼀样,但是它们的平摊时间复杂度都是O(logn)。
两种实现的基本操作就是splay,splay将最后被访问到的节点提升为根节点。
在⾃顶向下(top-down)的实现中,需要将输⼊的树拆成三颗树,分别为左树L,中树M和右树R。
其中M树维护当前还未被访问到的节点,L树中所有节点的值都⼩于M树中的任何节点值,R树中所有节点的值都⼤于M树中的任何节点值。
L树中只需要知道当前的最⼤节点(leftTreeMax),⽽R树中只需要知道当前的最⼩节点(rightTreeMin)。
左右两棵树的根节点分别可以通过nullNode节点(它是leftTreeMax和rightTreeMin的初始值,⽽且splay过程中变量nullNode本⾝未变化,只改变它的左右孩⼦节点)的右和左孩⼦节点得到,因为leftTreeMax中加⼊⼀个新的节点或⼦树时都是将新的节点作为leftTreeMax的右孩⼦,⽽不是左孩⼦(注意这⾥的顺序),rightTreeMin跟leftTreeMax相反。
第3章 伸展树与跳表

• p的右子树做g的左子 树,然后g做p的右子树; • 第1步:将p右旋转(zig) 到g,即pg两节点换位; • q的右子树做p的左子 树,然后p做q的右子树; • 第2步:接着将q右旋转 到p
1 2
双重旋转
2. zigzag旋转
• q的左子树做p的右子 树,然后p做q的右子树; • 第1步:将q左旋转(zag) 到p,即pq两节点换位; • 第2步: q的右子树做g 的左子树,然后g做q的 右子树;
– – – –
根节点右孩子为空 等于根节点的右孩子 小于根节点的右孩子 大于根节点的右孩子
3.1.6 插入运算的实现
• 插入30
一 空树 二 30 三 43 30 四 43 五 43 六 43
50
32
50
3
50
四 23
五 23
六
23
3
30
50
3
25
问题:要插入节点30
1. 2. 3. 树为空--新建节点,值为30,作为根 树的根节点就等于30,直接返回 duplicate 30小于根节点时:
类中成员函数的实现
#include "Stack.h" Stack::Stack(int s) { data=new int[s]; size=s; memNum=0; } Stack::~Stack() { delete[] data; } int Stack::pop(int &num) { if(memNum==0) return 0; num=data[--memNum]; return 1; } int Stack::push(int mem) { if(memNum==size) return 0; data[memNum++]=mem; return 1; }
伸展树的原理

伸展树的原理伸展树(Splay Tree)是一种自平衡的二叉搜索树,它在执行插入、查找、删除等操作时,会通过伸展操作将最近访问的节点调整到根节点位置,以提高访问效率。
伸展树的原理主要包括以下几个方面:二叉搜索树、伸展操作和如何维持平衡。
一、二叉搜索树伸展树是一种二叉搜索树,每个节点都有一个关键字和两个子节点(左子节点和右子节点)。
对于每个节点,它的左子节点的关键字小于等于它的关键字,而右子节点的关键字大于它的关键字。
这样的特性使得通过比较节点的关键字可以高效地进行查找和插入操作。
二、伸展操作伸展操作是伸展树的关键操作,它通过一系列的旋转操作将最近访问的节点调整到根节点位置。
当执行查找、插入或删除操作时,伸展树会将要操作的节点旋转到根节点位置,这样可以将频繁访问的节点保持在近乎根节点的位置,提高了整体的访问效率。
伸展操作主要包括两种旋转:zig和zig-zig。
1. Zig旋转:当要旋转的节点是根节点的直接子节点时,执行zig旋转。
假设要旋转的节点为X,其父节点为P,X是P的左子节点。
在zig旋转后,X会被旋转至根节点的位置,P成为X的右子节点,X的左子节点成为P的右子节点。
示意图如下:P X/ / \X ===> L P/ \ \L R R2. Zig-zig旋转:当要旋转的节点的父节点和祖父节点都是根节点的直接子节点时,执行zig-zig旋转。
假设要旋转的节点为X,其父节点为P,祖父节点为G,X是P的左子节点,P是G的左子节点。
在zig-zig旋转后,X会被旋转至根节点的位置,P成为X的右子节点,G成为P的右子节点,X的左子节点成为P 的左子节点,P的左子节点成为G的右子节点。
示意图如下:G X/ / \P ==> P G/ \ / \X C L R/ \L R通过不断地执行zig和zig-zig旋转,伸展操作可以将最近访问的节点调整至根节点位置。
这样可以使得频繁访问的节点保持在近乎根节点的位置,提高查找的效率。
算法与数据结构公开课一等奖课件省赛课获奖课件

章 内 容
4.3 数据构造及表达
2学
时
4.4 惯用数据构造及表达(表、树、图) 6学时
4.5 查找与排序
4学
时
4.6 文献与文献操作
2学
时
4.7 应用举例
2学
时
软件
技术
算法历史小知识
基础
算法的中文名称出自周髀算经;而英文名称Algorithm 来自于9 世纪波斯数学家比阿勒.霍瓦里松的名字al-Khwarizmi,由于比 阿勒.霍瓦里松在数学上提出了算法这个概念。他写的书《aljabr w’al muqabalah》(代数学)演变成为现在中学的代数教科 书。Ad-Khwarizmi强调求解问题是有条理的环节。如果他能活 到今天的话,他一定会被以他的名字而得名的办法的进展所感 动。
Towers(1, Source, Target, Interm); Towers(n-1, Interm, Target, Source); } }
软件
技术
基础
贪心法 基本思想
先根据题目的部分条件拟定答案的范畴, 在此范畴内对全部可能的状况逐个验证,直到 全部状况验证完毕,若每个状况使验证题目符 合条件,则为本题的一种答案,若全部状况验 证完毕后均不符合题目的条件,则题目无解。
算 法
•2程)序可不读性含(语R法ead错ab误ilit;y)
的 评
••3程 程)算序序强法对对健的性几精第(组心一ro输 选b目u入 择s的tn数 的e是s据 、s)为典了型阅的读、和交流;能 生产 满
价 原 则
苛数•应算的4解间程)刻据含 法 输可可决 是序高有 应 出的;速 矛读读对效容 对 成度 盾、性性率一错 其 果快 的带有有与切解 作 。; 、有助助低决出合存实刁存于 于功反储际法储难对 对效映容问的量性。,算 算量题输当而的小的法 法入输不。求几的 的数入是时解组理 调据非产间往输解试法生和往入;和数 莫空 是修据 名时 其改, 妙。足 格 求 结规 要 的 果
伸展树(Splaytree)的基本操作与应用

伸展树(Splaytree)的基本操作与应⽤伸展树的基本操作与应⽤【伸展树的基本操作】 伸展树是⼆叉查找树的⼀种改进,与⼆叉查找树⼀样,伸展树也具有有序性。
即伸展树中的每⼀个节点 x 都满⾜:该节点左⼦树中的每⼀个元素都⼩于 x,⽽其右⼦树中的每⼀个元素都⼤于 x。
与普通⼆叉查找树不同的是,伸展树可以⾃我调整,这就要依靠伸展操作 Splay(x,S)。
伸展操作 Splay(x,S) 伸展操作 Splay(x,S)是在保持伸展树有序性的前提下,通过⼀系列旋转将伸展树 S 中的元素 x 调整⾄树的根部。
在调整的过程中,要分以下三种情况分别处理: 情况⼀:节点 x 的⽗节点 y 是根节点。
这时,如果 x 是 y 的左孩⼦,我们进⾏⼀次 Zig(右旋)操作;如果 x 是 y 的右孩⼦,则我们进⾏⼀次 Zag(左旋)操作。
经过旋转,x 成为⼆叉查找树 S 的根节点,调整结束。
如图 1 所⽰: 情况⼆:节点 x 的⽗节点 y 不是根节点,y 的⽗节点为 z,且 x 与 y 同时是各⾃⽗节点的左孩⼦或者同时是各⾃⽗节点的右孩⼦。
这时,我们进⾏⼀次Zig-Zig 操作或者 Zag-Zag 操作。
如图 2 所⽰: 情况三:节点 x 的⽗节点 y 不是根节点,y 的⽗节点为 z,x 与 y 中⼀个是其⽗节点的左孩⼦⽽另⼀个是其⽗节点的右孩⼦。
这时,我们进⾏⼀次 Zig-Zag 操作或者 Zag-Zig 操作。
如图 3 所⽰: 如图 4 所⽰,执⾏ Splay(1,S),我们将元素 1 调整到了伸展树 S 的根部。
再执⾏ Splay(2,S),如图 5 所⽰,我们从直观上可以看出在经过调整后,伸展树⽐原来“平衡”了许多。
⽽伸展操作的过程并不复杂,只需要根据情况进⾏旋转就可以了,⽽三种旋转都是由基本得左旋和右旋组成的,实现较为简单。
伸展树的基本操作 利⽤ Splay 操作,我们可以在伸展树 S 上进⾏如下运算: (1)Find(x,S):判断元素 x 是否在伸展树 S 表⽰的有序集中。
c++算法大全

算法大全目录【程序1-1】欧几里德递归算法 (1)【程序1-2】欧几里德迭代算法 (1)【程序1-3】Gcd的连续整数检测算法 (1)【程序1-4】求F n (1)【程序1-5】逆序输出正整数的各位数 (1)【程序1-6】汉诺塔问题 (1)【程序1-7】排列产生算法 (2)【程序2-1】求数组元素累加之和的迭代程序 (2)【程序2-2】求数组元素累加之和的递归程序 (3)【程序2-3】矩阵乘法 (3)【程序3-1】伸展树类 (3)【程序3-2】旋转函数 (4)【程序3-3】伸展树插入 (4)【程序3-4】跳表结点类 (5)【程序3-5】跳表类 (5)【程序3-6】构造函数 (6)【程序3-7】级数分配 (6)【程序3-8】插入运算 (6)【程序4-1】ENode类 (7)【程序4-2】图的广度优先遍历 (8)【程序4-3】图的深度优先搜索 (8)【程序4-4】计算d和Low (9)【程序4-5】求双连通分量 (9)【程序4-6】与或树及其结点类型 (9)【程序4-7】判断与或树是否可解算法 (10)【程序4-8】广度优先生成解树的算法框架 (10)【程序5-1】分治法 (11)【程序5-2】一分为二的分治法 (11)【程序5-3】可排序表类 (11)【程序5-5】分治法求最大、最小元 (12)【程序5-6】二分搜索算法框架 (13)【程序5-7】对半搜索递归算法 (13)【程序5-8】对半搜索的迭代算法 (13)【程序5-9】Merge函数 (14)【程序5-10】两路合并排序 (14)【程序5-11】分划函数 (14)【程序5-12】快速排序 (15)【程序5-13】Select函数 (15)【程序5-14】线性时间选择算法 (15)【程序6-1】贪心法 (16)【程序6-2】背包问题的贪心算法 (16)【程序6-3】带时限作业排序的贪心算法 (17)【程序6-4】带时限的作业排序程序 (17)【程序6-5】使用并查集的带时限作业排序程序 (17)【程序6-6】两路合并最佳模式的贪心算法 (18)【程序6-7】最小代价生成树的贪心算法 (18)【程序6-8】普里姆算法 (19)【程序6-9】克鲁斯卡尔算法 (20)【程序6-10】迪杰斯特拉算法 (20)【程序6-11】多带最优存储 (21)【程序7-1】多段图的向前递推算法 (22)【程序7-2】弗洛伊德算法 (22)【程序7-3】矩阵连乘算法 (22)【程序7-4】矩阵连乘的备忘录方法 (23)【程序7-5】求LCS的长度 (24)【程序7-6】构造最长公共子序列 (24)【程序7-7】构造最优二叉搜索树 (25)【程序7-8】0/1背包的递归算法 (25)【程序7-9】0/1背包算法的粗略描述 (26)【程序7-10】0/1背包最优解值算法 (26)【程序7-11】0/1背包最优解算法 (28)【程序7-12】Johnson算法 (28)【程序8-1】递归回溯法 (28)【程序8-2】迭代回溯法 (29)【程序8-3】蒙特卡罗算法 (29)【程序8-4】n-皇后问题的回溯算法 (29)【程序8-5】子集和数的回溯算法 (30)【程序8-6】图的m-着色算法 (30)【程序8-7】哈密顿环算法 (31)【程序8-8】0/1背包算法 (31)【程序8-9】批处理作业调度算法 (33)【程序9-2】基于上下界函数的FIFO分枝限界法 (34)【程序9-3】基于上下界的LC分枝限界法 (35)【程序9-4】带时限的作业排序 (35)【程序9-5】类声明 (36)【程序9-6】上下界函数 (37)【程序9-7】0/1背包问题的LC分枝限界法 (38)【程序9-8】批作业类和活结点结构 (38)【程序9-9】下界函数 (39)【程序9-10】批处理作业调度LCBB算法 (40)【程序10-1】不确定搜索算法 (41)【程序10-2】不确定排序算法 (41)【程序10-3】最大集团判定问题不确定算法 (41)【程序10-4】可满足性问题的不确定算法 (41)【程序11-1】标识重复元素的拉斯维加斯算法 (42)【程序11-2】伪素数测试 (42)【程序11-3】合数性检测 (42)【程序11-4】素数测试的蒙特卡罗算法 (43)【程序11-5】快速排序舍伍德算法 (43)【程序12-1】平面图着色近似算法 (43)【程序12-2】最小顶点覆盖近似算法 (43)【程序12-3】集合覆盖近似算法 (43)【程序12-4】子集和数算法 (44)【程序12-5】修正表L为新表 (44)【程序12-6】子集和数近似方案 (44)【程序1-1】欧几里德递归算法intRGc d(int m,int n){if(n==0)re turn m;else re turnR Gc d(n,m%n);}【程序1-2】欧几里德迭代算法int Gc d(int m,int n){if (m==0)re turn n;if (n==0)re turn m;if (m>n) Swa p(m,n);while(m>0){int c=n%m;n=m;m=c;}return n;}【程序1-3】Gcd的连续整数检测算法int Gc d(int m,int n){if (m==0)re turn n;if (n==0)re turn m;int t=m>n?n:m;while (m%t || n%t) t--;return t;}【程序1-4】求F nlo ng F ib( lo ng n){if(n<=1) re turn n;else re turn F ib(n-2)+F ib(n-1);}【程序1-5】逆序输出正整数的各位数#inc lude<ios trea m.h>vo id P rintDig it(uns ig ne d int n){ //设k位正整数为d1d2 d k,按各位数的逆序d k d k 1 d1形式输出cout<<n%10; //输出最后一位数d kif(n>=10) P rintDig it(n/10); //以逆序输出前k-1位数}vo id ma in(){uns ig ne d int n;cin>>n;PrintDig it(n);}【程序1-6】汉诺塔问题#inc lude <ios trea m.h>enum tower { A='X', B='Y', C='Z'};vo id Mo ve(int n,towe r x,towe r y){ //将第n个圆盘从塔座x移到塔座y的顶部cout << "T he disk "<<n<<" is mo ve d fro m "<<c ha r(x) << " to to p of tower " << c ha r(y) << e ndl;}vo id Ha no i(int n, tower x, to wer y, towe r z){ // 将塔座x上部的n个圆盘移到塔座y上,顺序不变。
算法总结 伸展树Splay
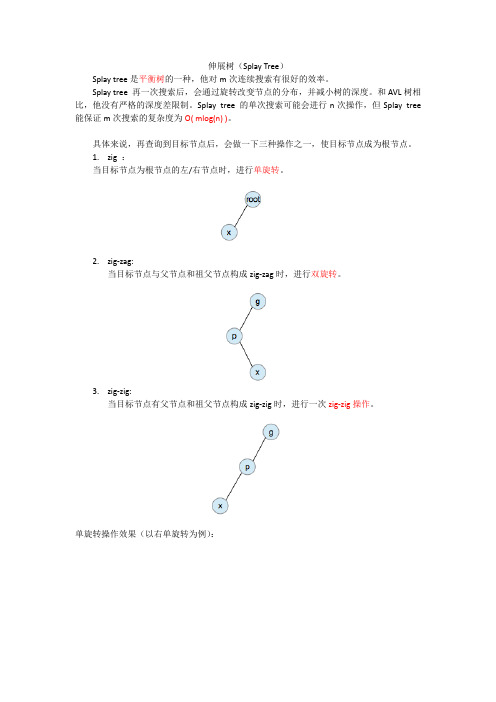
伸展树(Splay Tree)Splay tree是平衡树的一种,他对m次连续搜索有很好的效率。
Splay tree 再一次搜索后,会通过旋转改变节点的分布,并减小树的深度。
和AVL树相比,他没有严格的深度差限制。
Splay tree 的单次搜索可能会进行n次操作,但Splay tree 能保证m次搜索的复杂度为O( mlog(n) )。
具体来说,再查询到目标节点后,会做一下三种操作之一,使目标节点成为根节点。
1.zig:当目标节点为根节点的左/右节点时,进行单旋转。
2.zig-zag:当目标节点与父节点和祖父节点构成zig-zag时,进行双旋转。
3.zig-zig:当目标节点有父节点和祖父节点构成zig-zig时,进行一次zig-zig操作。
单旋转操作效果(以右单旋转为例):双旋转操作效果:Zig-zig操作效果:在Splay tree中,zig-zig操作基本上代替的AVL tree 中的单旋转。
下面用一个具体的例子示范:(搜索节点2)原树zig-zag (double rotation)zig-zigzig (single rotation at root)上面的第一次查询需要n次操作。
然而经过一次查询后,2节点成为了根节点,树的深度大减小。
整体上看,树的大部分节点深度都减小。
此后对各个节点的查询将更有效率。
伸展树的另一个好处是将最近搜索的节点放在最容易搜索的根节点的位置。
在许多应用环境中,比如网络应用中,某些固定内容会被大量重复访问。
伸展树可以让这种重复搜索以很高的效率完成。
代码:#include <cstdio>#include <iostream>using namespace std;template<typename T>class SplayTree{public:SplayTree();~SplayTree();void del(const T &x);void insert(const T &x);const T & max(){Node * p = root;while(p->rch != nullnode)p = p->rch;splay(root,p->key);return p->key;}const T & min(){Node * p = root;while(p->lch != nullnode)p = p->lch;splay(root,p->lch);return p->key;}private:struct Node{T key;Node *lch,* rch;Node(){}Node(const T & x) : key(x){}}* nullnode,* root;void left_rotate(Node * & x);void right_rotate(Node * & x);void splay(Node * &root,const T & x); };template<typename T>SplayTree<T>::SplayTree(){nullnode = new Node;nullnode->lch = nullnode;nullnode->rch = nullnode;root = nullnode;}template<typename T>SplayTree<T>::~SplayTree(){while(root != nullnode)del(max());delete nullnode;}template<typename T>void SplayTree<T>::del(const T & x) {Node * newroot;splay(root,x);if(x != root->key)return; // No found...if(root->lch == nullnode)newroot = root->rch;else{newroot = root->rch;splay(newroot,x);newroot->rch = root->rch;}delete root;root = newroot;}template<typename T>void SplayTree<T>::insert(const T & x) {Node * newroot = new Node(x);if(root == NULL){newroot->lch = nullnode;newroot->rch = nullnode;root = newroot;return;}splay(root,x);if(x < root->key){newroot->lch = root->lch;root->lch = nullnode;newroot->rch = root;root = newroot;}else{newroot->rch = root->rch;root->rch = nullnode;newroot->lch = root;root = newroot;}}template <typename T>void SplayTree<T>::left_rotate(Node * & x){Node * y = x->rch;x->rch = y->lch;y->lch = x;x = y;}template <typename T>void SplayTree<T>::right_rotate(Node * & x){Node * y = x->lch;x->lch = y->rch;y->rch = x;x = y;}template <typename T>void SplayTree<T>::splay(Node * &root,const T & x) {Node head,*ltree = & head,*rtree = & head; head.lch = nullnode;head.rch = nullnode;while(x != root->key){if(x < root->key){if(root->lch != nullnode&& x < root->lch->key) right_rotate(root);if(root->lch == nullnode)break;rtree->lch = root;rtree = root;root = root->lch;}else{if(root->rch != nullnode&& x > root->rch->key) left_rotate(root);if(root->rch == nullnode)break;ltree->rch = root;ltree = root;root = root->rch;}}ltree->rch = root->lch;root->lch = head.rch;rtree->lch = root->rch;root->rch = head.lch;}int main(){SplayTree<int>st;st.insert(1);cout<<st.max() <<endl;st.insert(78);cout<<st.max() <<endl;st.insert(12);cout<<st.max() <<endl;st.insert(45);cout<<st.max() <<endl;st.insert(10);cout<<st.max() <<endl;st.insert(12720);cout<<st.max() <<endl;return 0;}。
算法合集之《线段树的应用》

线段树的应用广西柳铁一中林涛【摘要】在竞赛解题中,常遇到与区间有关的操作,比如统计若干矩形并的面积,记录一个区间的最值、总量,并在区间的插入、删除和修改中维护这些最值、总量。
线段树拥有良好的树形二分结构,能够高效的完成这些操作,本文将介绍线段树的各种操作以及一些推广。
本文通过3个例子:《蛇》、《空心长方体》、《战场统计系统》,讲述线段树中基本的插入、删除、查找操作,和不规则的修改和删除操作,以及到二维的推广。
关键字:线段树二分子树收缩叶子释放面积树【正文】1. 线段树的定义及特征定义1:线段树一棵二叉树,记为T (a,b),参数a,b表示该节点表示区间[a,b]。
区间的长度b-a记为L。
递归定义T[a,b]:若L>1 :[a, (a+b) div 2]为T的左儿子[(a+b) div 2,b]为T的右儿子。
若L=1 :T为一个叶子节点。
表示区间[1, 10]的线段树表示如下:(以下取对数后均向上取整)定理1:线段树把区间上的任意一条线段都分成不超过2log L条线段证明:(1)在区间(a,b)中,对于线段(c,d),如果(c<=a) 或(d>=b),那么线段在(a,b)中被分为不超过log(b-a)。
用归纳法证明,如果是单位区间,最多被分为一段,成立。
如果区间(a,b)的左儿子与右儿子成立,那么如果当c<=a时,1.若d<=(a+b)div2那么相当与其左儿子分该线段,所分该线段数树不超过log((a+b)div 2-a),即不超过log(b-a),成立。
2.若d>(a+b) div 2那么相当于该线段被分为它左儿子表示的线段,加上右儿子分该线段,线段数不超过1+log(b-(a+b) div 2),也不超过log(b-a),成立。
对于d>=b的情况证明类似,不再赘述。
(2)在区间(a,b)中,对于任意线段也用归纳法证明。
对于单位区间,最多分为一段,成立。
伸展树算法

伸展树学习1、access(i,t):如果i在树t中,则返回指向它的指针,否则返回空指针。
为了实现access(i,t),可以从树t的根部向下查找i。
如果查找操作遇到了一个含有i的节点x,就在x处进行splay操作,并返回指向x的指针,访问结束。
如果遇到了空指针,表示i不在树中,此时就在最后一个非空节点处进行splay操作,然后返回空指针。
如果树是空的,将忽略掉splay操作。
2、insert(i,t):将条目i插入树t中(假设其尚不存在)。
为了实现insert(i,t),首先执行split(i,t),然后把t换成一个由新的包含有i的根节点组成的树,这个根节点的左右子树分别是split返回的树t1和t2。
3、delete(i,t):从树t中删除条目i(假设其已经存在)。
为了实现delete(i,t),首先执行access(i,t),然后把t换成其左子树和右子树join之后的新树。
4、join(t1,t2):将树t1和t2合并成一棵树,其中包含之前两棵树的所有条目,并返回合并之后的树。
这个操作假设t1中的所有条目都小于t2 中的条目,操作完成之后会销毁t1和t2。
为了实现join(t1,t2),首先访问t1中最大的条目i。
访问结束之后,t1的根节点中包含的就是i,它的右孩子显然为空。
于是把t2作为这个根节点的右子树并返回完成之后的新树即可实现join操作。
5、split(i,t):构建并返回两棵树t1和t2,其中t1包含t中所有小于等于i的条目,t2包含t中所有大于i的条目。
操作完成之后销毁t。
为了实现split(i,t),首先执行access(i,t),然后根据新根节点中的值是大于还是小于等于i来切断这个根节点的左链接或右链接,并返回形成的两棵树。
另外insert和delete方法有更好的实现,时间复杂度更小:1、insert(i, t):查找i,把遇到的空指针替换成一个含有i的新节点,然后再在新节点处对树进行splay操作。
算法合集之《基本数据结构在信息学竞赛中的应用》

h(x-1,y)+1, 方格(x,y)上是 0 且 x>1. 这个递推式的正确性是十分显然的,这里就不加证明了。 现在的任务是,对于矩阵的每一行,在求出这行中所有 h(x,y)的值后,需要得到每 一条悬线能够最多往左往右各延伸多长的距离而不碰到障碍“1” (这里用 left(x,y)记录 (x,y)格上的悬线能够向左延伸的最长距离,用 right(x,y)记录能够延伸的最长距离). 与 王知昆同学论文中的动态规划算法不同, 这里将运用一种基本数据结构——栈来解决问 题。
可以很容易证明,队列的各项基本操作的时间复杂度均为 O(1). 除了栈和队列之外,还有一种限定性数据结构是双端队列。在双端队列中,每个端 点都可以只输出、 只输入或同时输出输入。 因此前面所介绍的队列可以看成是双端队列 的一种特殊情况。 除了上面介绍的数据结构以外,基本数据结构还包括串、有根树的存储结构等。限 于文章篇幅,这里不进行具体介绍,而将重点阐述栈、队列以及线性表的应用。
三、 队列
和栈相反,队列是一种先进先出(First In First Out,缩写为 FIFO )的线性表。它 只允许在表的一端进行插入,而在另一端删除元素。在队列中,允许插入的一端叫做队 尾,允许删除的一端则称为队头。 图 6 为队列的示意图。
出队列 a1 a2 a3 …… an
入队列
队头 图6
队尾
head
ZHAO
QIAN 图4
SUN
可以很容易证明, 在线性表的链式存储结构中, 删除与插入任意一个已经定位 的元素的时间复杂度为 O(1),而定位一个元素的时间复杂度为 O(N).
二、 栈
栈是限定仅在表尾进行插入或删除操作的线性表。 因此, 表尾端称为栈顶, 相应地, 表头端称为栈底。不含元素的空表称为空栈。 根据图 5 可以很明显地看出,栈的修改是按后进先出的原则进行的。因此,栈又称 后进先出(Last In First Out)的线性表(简称 LIFO 结构) 。 栈的基本操作有: INISTACK(S) 初始化操作 EMPTY(S) 判栈空操作
算法合集之《伸展树的基本操作与应用》

11
时间复杂度分析—会计方法
对某个节点的 访问和旋转
用1元钱表示一个单位时间代价。
伸展树不变量:在任意时刻,伸展树中的任
意节点x都至少有μ(x)元的存款。
12
时间复杂度分析
在Splay调整过程中,费用将会用在以下两个
方面: (1)为使用的时间付费。也就是每一次单位时 间的操作,要支付1元钱。 (2)当伸展树的形状调整时,需要加入一些钱 或者重新分配原来树中每个节点的存款,以 保持不变量继续成立。
13
时间复杂度分析
用μ(x)和μ’(x)分别表示在进行一次旋转操作
前后节点x处的存款。
分三种情况分析旋转操作的花费:
(1)Zig 或 Zag (2)Zig-Zig 或 Zag-Zag (3)Zig-Zag 或 Zag-Zig
14
时间复杂度分析 情况1
Zig或Zag
为了保持伸展树不变量继续成立,需要花费:
时间复杂度O(n2),不能在时限内出解
用线段树记录输入的数
空间要求很大,需要一个大数组
红黑树或平衡二叉树
编程太复杂,调试不方便
21
伸展树的应用
算法描述
这题中,涉及到对于有序集的三种操作:
插入、求前趋、求后继
每次读入一个数p,将p插入伸展树S,同时p也被调整 到伸展树的根节点。 求出p点左子树中的最大值和右子树中的最小值,这两 个数就分别是有序集中p的前趋和后继。 进而求得最小差值,加入最后结果T。
3(μ(S)-μ(x))+1 3(μ’(x)-μ(x)) 3(μ’(x)-μ(x))
基本操作 Splay(x,S)
3(μ(S)-μ(x))+1 O(log2n)
BST 拓展与伸展树 (Splay) 一日通

完整的复杂度分析参见任何一本均摊分析的教科书 (伸展树的分析和并查集的分析是两个均摊分析的 经典之作), 这里只给出一些结论. (1) 插入, 删除, 查找
数据结构 时间复杂度
BST 平均 O(logn) Treap 期望 O(logn) Splay 均摊 O(logn) AVL 严格 O(logn) (2) 在伸展树中, 连续访问一段长度为 m 的区间的均摊代价是 O(m+logn) 而不仅仅是 O(mlogn) . 这个结论蕴含前驱, 后继的查找都是均摊 O(1) . (3) 如果存在非随机访问 (有规律的, 比如按顺序插入), 伸展树的形态可能相当不平衡 (极端情况下, 一条链). 但是一旦沿着这条链花费 O(n) 时间走过一次, 树的结构又会变得平衡许多. 而这次 O(n)的代 价, 可以通过前 n 次不必旋转节省的开销来弥补. 有趣的是, 如果存在非随机访问, 伸展树要比上面提到 的所有平衡树都要快. 例如, 如果用 splay 维护一个双端队列 (只在两端增删节点), 上面的所有操作都 是均摊 O(1) 的. (4) 由于均摊复杂度的局限性, 伸展树在生活中的应用受到限制. 想像下面的场景: -我已经等了整整五十九分钟了!你们的服务怎么这么慢! -我们的服务均摊复杂度是每人一分钟, 也就是六十个人一个小时. 一个小时之前, 在你前面排队的五
6. C++ 实现 点击查看程序代码 Code: #include <cstdio> using namespace std; const int maxint=~0U>>1;
struct node {
int key,size; node *c[2]; node():key(0),size(0){c[0]=c[1]=this;} node(int key_,node* c0_,node* c1_):
最小生成树算法及其应用word资料12页

最小生成树算法及其应用1.基础篇1.1定义在电路设计中,常常需要把一些电子元件的插脚用电线连接起来。
如果每根电线连接两个插脚,把所有n个插脚连接起来,只要用n-1根电线就可以了。
在所有的连接方案中,我们通常对电线总长度最小的连接方案感兴趣。
把问题转化为图论模型就是:一个无向连通图G=(V,E),V是插脚的集合,E是插脚两两之间所有可能的连接的集合。
给每条边(u,v)一个权值w(u,v),表示连接它们所需的电线长度。
我们的目标就是找到一个无环的边集T,连接其中所有的点且使总权值最小。
总权值既然T是连接所有点的无环边集,它一定是一棵树。
因为这棵树是从图G 中生成出来的,我们把它叫做生成树。
如果一棵生成树在所有生成树中总权值最小,我们就把它称作最小生成树。
1.2求最小生成树的一般算法解决最小生成树问题有没有一般的方法呢?下面我们就介绍一种贪心算法。
该算法设置了集合A,该集合一直是某最小生成树的子集。
算法执行的每一步,都要决策是否把边(u,v)添加到集合A中,能够添加的条件是保证A∪{(u,v)}仍然是最小生成树的子集。
我们称像(u,v)这样的边为A的安全边,或称这样的边对集合A是安全的。
求最小生成树的一般算法流程如下:GENERIC-MST(G,w)1.A←Ф2.while A没有形成一棵生成树3.do找出A的一条安全边(u,v)4.A←A∪{(u,v)}5.return A一开始A为Ф,显然满足最小生成树子集的条件。
之后,每一次循环都把一条A的安全边加入A中,A依然是最小生成树。
本节的余下部分将提出一条确认安全边的规则(定理1),下一节将具体讨论运用这一规则寻找安全边的两个有效的算法。
图1一个图的割(S,V-S)首先定义几个概念。
有向图G=(V,E)的割(S,V-S)是V的一个分划。
当一条边(u,v)∈E的一个端点属于S而另一端点属于V-S,我们说边(u,v)通过割(S,V-S)。
若集合A中没有边通过割,就说割不妨碍集合A。
伸展树的原理及应用

伸展树的原理及应用1. 什么是伸展树伸展树(Splay Tree)是一种自调整的二叉搜索树。
它在进行插入、删除、查找等操作后会通过旋转和重新排序使得被访问频率高的节点上升到根节点附近,从而提高了它们的访问效率。
2. 伸展树的原理伸展树的原理非常简单,当某个节点被访问后,就将它旋转到根节点的位置。
这个过程会导致树的结构发生变化,被访问的节点上升到根节点附近,从而提高对该节点的后续访问效率。
3. 伸展树的操作伸展树主要有以下几种操作:3.1 查找查找操作是伸展树最基本的操作之一。
当进行查找操作时,伸展树会根据被访问的节点的位置进行旋转和重新排序,将它移动到距离根节点更近的位置。
这样可以保证后续的查找操作更加高效。
3.2 插入插入操作将一个新的节点插入到伸展树中。
在插入操作中,伸展树会先进行普通的二叉搜索树插入操作,然后根据被插入节点的位置进行旋转和重新排序,将它移动到距离根节点更近的位置。
3.3 删除删除操作是将一个节点从伸展树中删除。
在删除操作中,伸展树会先进行普通的二叉搜索树删除操作,然后根据被删除节点的位置进行旋转和重新排序,将与被删除节点相邻的节点移动到距离根节点更近的位置。
4. 伸展树的应用伸展树在实际应用中有着广泛的应用。
它主要应用于以下几个方面:4.1 字典伸展树可以用作字典的实现。
字典是一种将键与值关联起来的数据结构,它可以快速插入、删除和查找键值对。
伸展树作为一种自调整的二叉搜索树,在实现字典时可以提供较好的性能。
4.2 缓存伸展树可以用作缓存的实现。
缓存是一种存储数据的临时存储器,它可以用来提高数据的访问速度。
伸展树作为一种自调整的二叉搜索树,可以根据数据的访问频率自动调整节点的位置,从而提高缓存的性能。
4.3 排序伸展树可以用作排序算法的实现。
排序是将一组数据按照某种规则进行排列的过程,伸展树作为一种自调整的二叉搜索树,可以根据数据的访问频率自动调整节点的位置,从而提高排序的性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
伸展树的基本操作与应用安徽省芜湖一中杨思雨目录【关键字】 (2)【摘要】 (2)【引言】 (2)【伸展树的基本操作】 (2)伸展操作Splay(x,S) (3)伸展树的基本操作 (4)时间复杂度分析 (5)【伸展树的应用】 (7)【总结】 (8)【参考书目】 (9)【附录】 (9)【关键字】伸展树基本操作应用【摘要】本文主要介绍了伸展树的基本操作以及其在解题中的应用。
全文可以分为以下四个部分。
第一部分引言,主要说明了二叉查找树在信息学竞赛中的重要地位,并且指出二叉查找树在某些情况下时间复杂度较高,进而引出了在时间复杂度上更为优秀的伸展树。
第二部分介绍了伸展树的基本操作。
并给出了对伸展树时间复杂度的分析和证明,指出伸展树的各种基本操作的平摊复杂度均为O(log n),说明伸展树是一种较平衡的二叉查找树。
第三部分通过一个例子介绍了伸展树在解题中的应用,并将它与其它树状数据结构进行了对比。
第四部分指出了伸展树的优点,总结全文。
【引言】二叉查找树(Binary Search Tree)能够支持多种动态集合操作。
因此,在信息学竞赛中,二叉排序树起着非常重要的作用,它可以被用来表示有序集合、建立索引或优先队列等。
作用于二叉查找树上的基本操作的时间是与树的高度成正比的。
对一个含n 各节点的完全二叉树,这些操作的最坏情况运行时间为O(log n)。
但如果树是含n个节点的线性链,则这些操作的最坏情况运行时间为O(n)。
而有些二叉查找树的变形,其基本操作在最坏情况下性能依然很好,比如红黑树、A VL树等等。
本文将要介绍的伸展树(Splay Tree),也是对二叉查找树的一种改进,虽然它并不能保证树一直是“平衡”的,但对于伸展树的一系列操作,我们可以证明其每一步操作的平摊复杂度都是O(log n)。
所以从某种意义上说,伸展树也是一种平衡的二叉查找树。
而在各种树状数据结构中,伸展树的空间要求与编程复杂度也都是很优秀的。
【伸展树的基本操作】伸展树是二叉查找树的一种改进,与二叉查找树一样,伸展树也具有有序性。
即伸展树中的每一个节点x都满足:该节点左子树中的每一个元素都小于x,而其右子树中的每一个元素都大于x。
与普通二叉查找树不同的是,伸展树可以自我调整,这就要依靠伸展操作Splay(x,S)。
伸展操作Splay(x,S)伸展操作Splay(x,S)是在保持伸展树有序性的前提下,通过一系列旋转将伸展树S中的元素x调整至树的根部。
在调整的过程中,要分以下三种情况分别处理:情况一:节点x的父节点y是根节点。
这时,如果x是y的左孩子,我们进行一次Zig(右旋)操作;如果x是y的右孩子,则我们进行一次Zag(左旋)操作。
经过旋转,x成为二叉查找树S的根节点,调整结束。
如图1所示图1情况二:节点x的父节点y不是根节点,y的父节点为z,且x与y同时是各自父节点的左孩子或者同时是各自父节点的右孩子。
这时,我们进行一次Zig-Zig操作或者Zag-Zag操作。
如图2所示图2情况三:节点x的父节点y不是根节点,y的父节点为z,x与y中一个是其父节点的左孩子而另一个是其父节点的右孩子。
这时,我们进行一次Zig-Zag操作或者Zag-Zig操作。
如图3所示图3如图4所示,执行Splay(1,S),我们将元素1调整到了伸展树S的根部。
再执行Splay(2,S),如图5所示,我们从直观上可以看出在经过调整后,伸展树比原来“平衡”了许多。
而伸展操作的过程并不复杂,只需要根据情况进行旋转就可以了,而三种旋转都是由基本得左旋和右旋组成的,实现较为简单。
图 4 Splay(1,S)图 5 Splay(2,S)伸展树的基本操作利用Splay操作,我们可以在伸展树S上进行如下运算:(1)Find(x,S):判断元素x是否在伸展树S表示的有序集中。
首先,与在二叉查找树中的查找操作一样,在伸展树中查找元素x。
如果x 在树中,则再执行Splay(x,S)调整伸展树。
(2)Insert(x,S):将元素x插入伸展树S表示的有序集中。
首先,也与处理普通的二叉查找树一样,将x插入到伸展树S中的相应位置上,再执行Splay(x,S)。
(3)Delete(x,S):将元素x从伸展树S所表示的有序集中删除。
首先,用在二叉查找树中查找元素的方法找到x的位置。
如果x没有孩子或只有一个孩子,那么直接将x删去,并通过Splay操作,将x节点的父节点调整到伸展树的根节点处。
否则,则向下查找x的后继y,用y替代x的位置,最后执行Splay(y,S),将y调整为伸展树的根。
(4)Join(S1,S2):将两个伸展树S1与S2合并成为一个伸展树。
其中S1的所有元素都小于S2的所有元素。
首先,我们找到伸展树S1中最大的一个元素x,再通过Splay(x,S1)将x调整到伸展树S1的根。
然后再将S2作为x节点的右子树。
这样,就得到了新的伸展树S。
如图6所示图6(5)Split(x,S):以x为界,将伸展树S分离为两棵伸展树S1和S2,其中S1中所有元素都小于x,S2中的所有元素都大于x。
首先执行Find(x,S),将元素x调整为伸展树的根节点,则x的左子树就是S1,而右子树为S2。
如图7所示图7除了上面介绍的五种基本操作,伸展树还支持求最大值、求最小值、求前趋、求后继等多种操作,这些基本操作也都是建立在伸展操作的基础上的。
时间复杂度分析由以上这些操作的实现过程可以看出,它们的时间效率完全取决于Splay操作的时间复杂度。
下面,我们就用会计方法来分析Splay操作的平摊复杂度。
首先,我们定义一些符号:S(x)表示以节点x为根的子树。
|S|表示伸展树S 的节点个数。
令μ(S) = [ log|S| ],μ(x)=μ(S(x))。
如图8所示图8我们用1元钱表示单位代价(这里我们将对于某个点访问和旋转看作一个单位时间的代价)。
定义伸展树不变量:在任意时刻,伸展树中的任意节点x都至少有μ(x)元的存款。
在Splay调整过程中,费用将会用在以下两个方面:(1)为使用的时间付费。
也就是每一次单位时间的操作,我们要支付1元钱。
(2)当伸展树的形状调整时,我们需要加入一些钱或者重新分配原来树中每个节点的存款,以保持不变量继续成立。
下面我们给出关于Splay操作花费的定理:定理:在每一次Splay(x,S)操作中,调整树的结构与保持伸展树不变量的总花费不超过3μ(S)+1。
证明:用μ(x)和μ’(x)分别表示在进行一次Zig、Zig-Zig或Zig-Zag操作前后节点x处的存款。
下面我们分三种情况分析旋转操作的花费:情况一:如图9所示图9我们进行Zig或者Zag操作时,为了保持伸展树不变量继续成立,我们需要花费:μ’(x) +μ’(y) -μ(x) -μ(y) = μ’(y) -μ(x)≤μ’(x) -μ(x)≤3(μ’(x) -μ(x))= 3(μ(S) -μ(x))此外我们花费另外1元钱用来支付访问、旋转的基本操作。
因此,一次Zig 或Zag操作的花费至多为3(μ(S) -μ(x))。
情况二:如图10所示图10我们进行Zig-Zig操作时,为了保持伸展树不变量,我们需要花费:μ’(x) +μ’(y) +μ’(z) -μ(x) -μ(y) -μ(z) = μ’(y) +μ’(z) -μ(x) -μ(y)= (μ’(y) -μ(x)) + (μ’(z) -μ(y))≤(μ’(x) -μ(x)) + (μ’(x) -μ(x))= 2 (μ’(x) -μ(x))与上种情况一样,我们也需要花费另外的1元钱来支付单位时间的操作。
当μ’(x) <μ(x) 时,显然 2 (μ’(x) -μ(x)) +1 ≤3 (μ’(x) -μ(x))。
也就是进行Zig-Zig操作的花费不超过3 (μ’(x) -μ(x))。
当μ’(x) =μ(x)时,我们可以证明μ’(x) +μ’(y) + μ’(z) <μ(x) +μ(y) +μ(z),也就是说我们不需要任何花费保持伸展树不变量,并且可以得到退回来的钱,用其中的1元支付访问、旋转等操作的费用。
为了证明这一点,我们假设μ’(x) +μ’(y) + μ’(z) >μ(x) +μ(y) +μ(z)。
联系图9,我们有μ(x) =μ’(x) =μ(z)。
那么,显然μ(x) =μ(y) =μ(z)。
于是,可以得出μ(x) =μ’(z) =μ(z)。
令a = 1 + |A| + |B|,b = 1 + |C| + |D|,那么就有[log a] = [log b] = [log (a+b+1)]。
①我们不妨设b≥a,则有[log (a+b+1)] ≥[log (2a)]= 1+[log a]> [log a] ②①与②矛盾,所以我们可以得到μ’(x) =μ(x) 时,Zig-Zig操作不需要任何花费,显然也不超过3 (μ’(x) -μ(x))。
情况三:与情况二类似,我们可以证明,每次Zig-Zag操作的花费也不超过3 (μ’(x) -μ(x))。
以上三种情况说明,Zig操作花费最多为3(μ(S)-μ(x))+1,Zig-Zig或Zig-Zag 操作最多花费3(μ’(x)-μ(x))。
那么将旋转操作的花费依次累加,则一次Splay(x,S)操作的费用就不会超过3μ(S)+1。
也就是说对于伸展树的各种以Splay操作为基础的基本操作的平摊复杂度,都是O(log n)。
所以说,伸展树是一种时间效率非常优秀的数据结构。
【伸展树的应用】伸展树作为一种时间效率很高、空间要求不大的数据结构,在解题中有很大的用武之地。
下面就通过一个例子说明伸展树在解题中的应用。
例:营业额统计Turnover (湖南省队2002年选拔赛)题目大意Tiger最近被公司升任为营业部经理,他上任后接受公司交给的第一项任务便是统计并分析公司成立以来的营业情况。
Tiger拿出了公司的账本,账本上记录了公司成立以来每天的营业额。
分析营业情况是一项相当复杂的工作。
由于节假日,大减价或者是其他情况的时候,营业额会出现一定的波动,当然一定的波动是能够接受的,但是在某些时候营业额突变得很高或是很低,这就证明公司此时的经营状况出现了问题。
经济管理学上定义了一种最小波动值来衡量这种情况:该天的最小波动值= min { | 该天以前某一天的营业额-该天的营业额| } 当最小波动值越大时,就说明营业情况越不稳定。
而分析整个公司的从成立到现在营业情况是否稳定,只需要把每一天的最小波动值加起来就可以了。
你的任务就是编写一个程序帮助Tiger来计算这一个值。
注:第一天的最小波动值为第一天的营业额。
数据范围:天数n≤32767,每天的营业额ai≤1,000,000。
最后结果T≤231。
初步分析题目的意思非常明确,关键是要每次读入一个数,并且在前面输入的数中找到一个与该数相差最小的一个。
