chapter 3-有穷状态自动机
第三章有穷自动机

例:将图示的DFA M最小化。
a
b
6
4
a
a
a
b
a
1
ab
5a
7
b3
b
b
2 b
1、将M状态分为两个子集: P0=({1,2,3,4},{5,6,7})
2、{1,2,3,4}读入a后划为: P1=({1,2},{3,4},{5,6,7})
3、进一步划分: P2=({1,2},{3},{4},{5,6,7})
对M的状态集S进行划分的步骤:
①把S的终态与非终态分开,分成两个子集, 形成基本划分,属于这两个不同子集的 状态是可区别的。
②假定某个时候已含m个子集,记={I(1) , I(2) , …,I(m) }且属于不同子集的状态是可 区别的,再检查中的每个I能否进一步划 分,对于某个I(i) ,令I(i) ={S1,S2,…,Sk}, 若存在一个输入字符使得move(I(i) ,a)不包 含在现行的某一子集I(i)中,则将I(i)一分 为二。
若M的某些结既是初态结,又是终态结,
或者存在一条从某个初态结到某个终态结 的道路,则空字可为M所接受。
例: NFA M=({0,1,2,3,4},{a,b},f,{0},{2,4})
f(0,a)={0,3} f(2,b)={2} f(0,b)={0,1}
f(3,a)={4} f(1,b)={2} f(4,a)={4}
M’=(K, ,f,S,Z)
一个含有m个状态和n个输入字符的NFA 可表示为一张状态转换图,该图含有m个 状态结,每个结可射出若干条 箭弧与别的 结点相连接,每条弧用*中的一个字(不 一定要不同的字,且可以为空字)作标记 (称输入字),整个图至少含有一个初态 结以及若干个终态结。
第三章有穷自动机-PPT课件

自动机接受(收)字符串
• 3)自动机接收语言 自动机 M所能接收的串组成一个集合, 则称该集合为自动机 M所能接收(识别)的 语言。 用L(M)表示: L ( M ) = {ω ∣ t(q0, ω )∈ F , ω ∈ * }
3.2.4 自动机的等价性
•定义3.2 M和M是等价的,当且仅当 对每一个串x,M接收x当且仅当M接收x。 •定义3.3 如果M仅通过重新标记它的 状态就能转换称M,则M和M称为同构的 (Isomorphic)。 •FSA的一个基本定理是:对每一个自动 机M,存在一个等价的具有最少状态个 数的自动机M,而且对于每一个其状态 个数与M相同且等价于M的自动机M″, 必是与M同构的。换句话说,M在结构 上是唯一的。
3.2.5 非确定有穷状态自动机
•定义3.4 一个非确定有穷自动机NDFSA是一个
五元组
NDFSA=(Q, , t, q0, F) 其中,Q是一个非空有穷状态集, 是一个非空有穷输入字母集, 映射t为QQ的子集(即t是一个多值映射), Q0Q是开始状态集, FQ是终止状态集。 •同样的,NDFSA也可以用状态转换表和状态转换 图表示。
3.2.3 构形和移动(2)
• 构形(q0,ω)称为初始构形,其中q0 是初始状态,ω是由该自动机可接 收或拒绝的任何输入串。构形(q, ) 称为终止构形,其中是空串, qF(终态集)。 • 自动机的移动(记为├)是从一种构 形到另一种构形的转换。 • DFSA的工作过程就是一系列的移动 过程。 • 记号├+称为├的传递闭包;├*称为 ├的自反闭包。 ├*表示“0次或多 次移动”;├+表示“一次或多次移 动”。
第三章有穷自动机

有穷自动机分为两类: (1)确定的有穷自动机
(Deterministic Finite Automata简称DFA) (2)不确定的有穷自动机
(Nondeterministic Finite Automata简称 NFA) 。
第三章有穷自动机
3.1.1 确定有穷自动机的形式定义
一个DFA M=(K,Σ,f,S,Z),其中
假定I是M中状态集的一个子集,定义 _closure(I)如下: ➢ 若qI,则q_closure(I); ➢ 若q_closure(I),q是由q出发经多条 弧到达的状态,则q_closure(I)。
第三章有穷自动机
定义:假定I是NFA M中状态集的一个子集,
a,定义
Ia=_closure(J) 其中J是所有那些可从子集I中的任一状态 出发,经过一条a连线(跳过a连线前的ε连 线)而到达的状态(结)的全体。
④ 将由上述过程得到的最终形式的表看作一 个状态转换表,即把其中第一列中的元素 作为状态,把Ia ,Ib分别看作是输入符号a, b,把其余信息看作是状态转换函数之值。 这个表唯一地刻画了一个确定的有穷状态 自动机M,其初态是该表第一行第一列的 元素,其终态是该表中所有那些含有原终 态的元素。可以证明,这个DFA M和NFA M是等价的。 第三章有穷自动机
3.1.4 自动机的等价性
为了讨论自动机的等价性,先对DFA 中的映射进行扩充。
扩充的转换函数f
➢ 设QK,函数f(Q, )=Q,即如果输入字符 是空串,则仍停留在原来的状态上。
➢ 对QK,T,t1*,f(Q,Tt1)=f(f(Q,T), t1) 该定义是一个递归定义,说明当自动机处 在状态Q且面临某个输入串Tt1时,则先应 用函数 f(Q,T)=P,然后应用函数f(P,t1)。
第3章 有穷状态自动机 计算机专业 形式语言课件

状态说明
状态
输入字符
0
开始状态
q0
q1
q1
q2
终止状态
q2
q1
2020/10/3
13
3.2有穷状态自动机
M2=({q0,q1,q2,q3},{0,1,2},δ2,q0,{q2}) δ2(q0,0)= q1,δ2(q1,0)= q2 δ2(q2,0)= q1,δ2(q3,0)= q3 δ2(q0,1)= q3,δ2(q1,1)= q3 δ2(q2,1)= q3,δ2(q3,1)= q3 δ2(q0,2)= q3,δ2(q1,2)= q3 δ2(q2,2)= q3,δ2(q3,2)= q3
2020/10/3
8
3.1 语言的识别
• 相应的物理模型
一个右端无穷的输入带。 一个有穷状态控制器(finite state control,FSC) 。 一个读头。
• 系统的每一个动作由三个节拍构成:读入 读头正注视的字符;根据当前状态和读入 的字符改变有穷控制器的状态;将读头向 右移动一格。
2020/10/3
q0——q0∈Q,是M的开始状态(initial state), 也可叫做初始状态或者启动状态。
2020/10/3
11
3.2有穷状态自动机
δ——状态转移函数(transition function),有 时候又叫做状态转换函数或者移动函数。δ: Q×∑Q,对(q,a)∈Q×∑,δ(q,a)=p 表示:M在状态q读入字符a,将状态变成p, 并将读头向右移动一个带方格而指向输入 字符串的下一个字符。
第3章 有穷状态自动机
• 主要内容 • 确定的有穷状态自动机(DFA)
– 作为对实际问题的抽象、直观物理模型、形式 定义,DFA接受的句子、语言,状态转移图。
03有穷状态自动机

set(q0)={x | x∈∑*,x=ε 或者x以1结尾} set(q1)={x | x∈∑*,x=0或者x以10结尾} set(q2)={x | x∈∑*,x=00或者x以100结尾} set(q3)={x | x∈∑*,x以000结尾} set(q4)={x | x∈∑*, x以001结尾} 这5个集合是两两互不相交。
M2=({q0,q1,q2,q3},{0,1,2},δ2,q0,{q2}) δ2(q0,0)= q1,δ2(q1,0)= q2,δ2(q2,0)= q1,δ2(q3,0)= q3 δ2(q0,1)= q3,δ2(q1,1)= q3 ,δ2(q2,1)= q3,δ2(q3,1)= q3 δ2(q0,2)= q3,δ2(q1,2)= q3 ,δ2(q2,2)= q3,δ2(q3,2)= q3 表3-2 δ 2转换函数 状态说明 开始状态 终止状态 状态 0 q0 q1 q2 q3 q1 q2 q1 q3 输入字符 1 q3 q3 q3 q3 2 q3 q3 q3 q3
8
例3-1
下面是一个有穷状态自动机 M1=({q0 ,q1 ,q2}, {0}, δ1 , q0 , {q2}) 其中,δ1(q0,0)= q1 ,δ1(q1,0)= q2 , δ1(q2,0)= q1 用表3-1表示δ1。
状态说明
状态
输入字符 0
开始状态
终止状态
q0 q1
q2
q1 q2
q1
9
Hale Waihona Puke 例3-110扩展的状态转移函数
将δ 扩充为
ˆ : Q * Q
对任意的 q∈Q,w∈∑*,a∈∑,定义
ˆ (1) (q, ) q ˆ ˆ (2) (q, wa ) ( (q, w), a)
3 FA 语言与自动机导论

A
i FA M
B
状态 A i B d F
FA f (A, i) = B f (B, i) = B f (B, d) = B (B为终止状态)
RG AiB BiB BdB Bε
B
B
B
1
状态转换矩阵
11
FA的状态转换图
状态转换图显示了一个由状态、转换组成的状态 机。
有限自动机的状态转换图说明系统的动态视图。 状态图强调一个对象按事件次序发生的行为。
22
例3.3扩:接受语言{x000 | x {0,1}*} ∪{x001 | x {0,1}*}的 FA
解:该语言定义的句子以000或001结尾。设q0为DFA的开 始状态,用q1记住结尾串中的第一个0;用q2记住在q1之 后紧接着又读到的一个0;用q3记住在q2后紧接着又读到 的一个0,用q4记住在q2后紧接着又读到的一个1,识别 该语言的FA如下图(3-5):
则 A也作为终止状态
13
3.2 有穷状态自动机
主要内容:
1、DFA的形式化定义
2、DFA的仿真算法(伪代码描述)
14
一.有穷自动机的形式化定义
1. 确定的有穷自动机DFA
一个确定的有穷自动机DFAM是一个五元组(5-tuple): M=(K,Σ, δ ,q0,F) 其中:K:状态的非空有穷集 Σ:有穷输入字母表 δ:K× Σ到K的一个映射(是单值函数)
q0∈K 是开始状态
F K 是终止状态集
15
例3-2:构造一个DFA,识别语言{x000y | x,y {0,1}*} 解:该语言定义的句子都会有三个连续的0。设q0为DFA 的开始状态,用q1记住子串“000”的第一个0;用q2记住 在q1之后紧接着又读到的一个0,这可能是子串“000”的 第2个0;用q3记住在q2后紧接着又读到的一个0,发现子 串“000”即识别结束。识别该语言的确定的有穷状态自 动机如下图:
第03章有穷状态自动机-电子科技大学

作为对DFA的修改
q1 0
0
0,1
S q0
10
1
1 q3
q2
构造接受语言
L={x| x{0,1}*,且 x含有子串00或11}的DFA
“直接”的FA
0,1 0 q1
0
0,1
S q0
1
1 q3
q2
希望是接受语言
L={x| x{0,1}*,且 x含有子串00或11}的FA
与DFA的区别
并不是对于所有的(q, a) Q ,(q, a)
M = (Q, , , q0, F)
其中,Q, , q0, F 状态的意义同DFA(定义3-1)
—状态转移函数。 : Q 2Q。 对(q, a) Q ,(q, a)={p1, p2, …, pm} 表示M在
状态q读入字符a,可以选择地将状态变成p1, p2, …, 或者pm,并将读头向右移动一个带方格而指向输入 字符串的下一个字符。
状态说明 状态
开始状态 [q0] [q1] [q2]
即时描述
设M = (Q, , , q0, F)为一个FA,x, y *,
(q0, x)=q,xqy称为M的一个即时描述。
它表示xy是M 正在处理的一个字符串,x引导M
从q0启动并到达状态q,当前正指向y的首字符。
如果xqay是M的一个即时描述,且(q, a)=p,则
经过字符a的处理后,即时描述变为xapy。这一 过程记作:
NFA不适于构造“不包含子串…”, “不满足条件…”的语言,在这些情况 下它可能退化为DFA。
定理3-1
NFA与DFA等价。 ➢ NFA与DFA等价是指NFA和DFA能识
别相同的语言类。 ➢ 回顾等价的概念:
第3章 有穷自动机

33
正规文法FA
给定文法G[S]: S→aS|aA|bB A→bA|cC B→aB|dD C →cC|c D →dD|d 给出其对应的状态转换图。S是开始状 态,Z是终止状态.图3.16 FA
34
FA正规文法
①自动机A中的每一个状态均作为G的非终结符号,
q1 q2
q5 q6 q6 q4 q6
26
q3 q4 q3
NFA到DFA的转换 ③ 利用子集法构造确定的有穷自动机
假设已知的NFA为(Q′,Σ′,t′,Q0′,F′)。与NFA等 价的DFA为(Q,Σ,t,Q0,F)。 Σ:可由NFA所含有的输入字母集合得到。 Q:由Q ′的一些子集组成。 Q0:是包含NFA的开始状态在内的Q ′的一个子集。 F:由包含NFA的终止状态F ′在内的Q ′的一些子集组 成。
31
DFA化简举例
G 0 0 I
0
start
F 1
1
0
1
0
H
1
J
1
32
3.3 正规文法与FA
由正规文法G[S]可直接构造一个与之等价的FA A。
令G的终结符号集为A的字母表;
G的非终结符号作为A的状态,G的开始符号为A的开始 状态;
增加一个终止状态Z(ZVN);
形如U→a的规则,引一条从状态U到终止状态Z的标记为a 的 弧;
a T U T V W S b
a a Z b
15
a b
B a
a
3.1.4非确定的有穷自动机NDFA的形式定义 非确定的有穷自动机NFA
NFA=(Q,∑,t, Q0,F) Q——有穷非空的状态集 。
自动机与形式语言_第三章_DFA_NFA解析

2019/8/24
6
3.1 语言的识别
• 识别系统(模型) • ⑴ 系统具有有穷个状态,不同的状态代表
不同的意义。按照实际的需要,系统可以 在不同的状态下完成规定的任务。 • ⑵ 我们可以将输入字符串中出现的字符汇 集在一起构成一个字母表。系统处理的所 有字符串都是这个字母表上的字符串。
2019/8/24
F——FQ,是M的终止状态(final state)集 合。q∈F,q称为M的终止状态,又称为 接受状态(accept state)。
2019/8/24
13
3.2有穷状态自动机
• 例 3-1 下面是一个有穷状态自动机
M1=({q0,q1,q2},{0},δ1,q0,{q2}) 其中,δ1(q0,0)= q1,δ1(q1,0)= q2,δ1(q2,0)= q1 用表3-1表示δ1。
q0——q0∈Q,是M的开始状态(initial state), 也可叫做初始状态或者启动状态。
2019/8/24
12
3.2有穷状态自动机
δ——状态转移函数(transition function), 有时候又叫做状态转换函数或者移动函数。 δ:Q×∑Q,对(q,a)∈Q×∑,δ(q, a)=p表示:M在状态q读入字符a,将状态 变成p,并将读头向右移动一个带方格而指 向输入字符串的下一个字符。
18
3.2有穷状态自动机
• 将δ 扩充为
ˆ : Q * Q
对任意的q∈Q,w∈∑*,a∈∑,定义
(1)ˆ(q, ) q (2)ˆ(q, wa) (ˆ(q, w),a)
2019/8/24
19
q1
q2
0
2019/8/24
15
3.2有穷状态自动机
编译原理:第3章 有穷自动机

编译原理第3章内容简介学习目标第3章有穷自动机3.1 有穷自动机的形式定义3.1 有穷自动机的形式定义DFA的表示举例——状态转换表DFA的表示举例——状态转换图 3.13.1 FA的形式定义有穷自动机识别的符号串举例DFA A3.1 有穷自动机的形式定义 3.1 有穷自动机的形式定义NFA举例 3.13.1用NFA识别符号串yFA的构造FA的构造举例—1FA的构造举例—2FA的构造举例—3请构造一个有穷自动机FA的构造举例—4 3.1请构造一个有穷自动机FA的等价性举例3.2 NFA到DFA的转换 3.2 NFA到DFA的转换—NFA确定化3.2 NFA到DFA的转换3.2 NFA到DFA的转换—NFA确定化——ε闭包状态子集I的ε闭包——举例状态子集I的状态子集I的ε闭包——举例状态子集I的——Ia 子集3.2 NFA到DFA的转换Ia子集——举例Ia子集——举例 3.2 NFA到DFA的转换NFA到DFA的转换——子集法NFA=(Q NFA到DFA的转换——举例1aNFA到DFA的转换——举例2NFA DFA DFA NFA DFA DFADFA化简举例1DFA化简——注意NFA到最小化DFA的转换——举例33.3 正规文法与FA3.3 正规文法与FAFA⇒右线性正规文法FA⇒右线性正规文法——举例1y3.4 正规表达式RE与FA 正规表达式与有穷自动机3.4 RE与FA——RE的性质 3.4 RE与FA—RE⇒FARE⇒FA举例1RE⇒FA举例23.4 RE与FA——FA⇒RE FA⇒REFA⇒RE FA⇒RE举例FA⇒RE举例正规文法到正规表达式正规文法到正规表达式DFA的程序实现DFADFA的程序实现DFA DFA的程序实现lDFA的程序实现l第3章内容小结第3章内容小结参考文献。
第3章 有穷状态自动机 计算机专业 形式语言课件

2021/4/26
19
3.2有穷状态自动机
• 例 3-2 构造一个DFA,它接受的语言为 {x000y|x,y∈{0,1}*}
q0——M的启动状态; q1—第—1个M0读;到了一个0,这个0可能是子串“000”的
q2—是—子M串在“q001后0”紧的接第2着个又0;读到了一个0,这个0可能
q3—符—串M含在有q子2后串紧“接00着0”又;读因到此了,一这个个0状,态发应现该输是入字终 止状态。
2021/4/26
7
3.1 语言的识别
• ⑷ 系统中有一个状态,它是系统的开始状 态,系统在这个状态下开始进行某个给定 句子的处理。
• ⑸ 系统中还有一些状态表示它到目前为止 所读入的字符构成的字符串是语言的一个 句子,把所有将系统从开始状态引导到这 种状态的字符串放在一起构成一个语言, 该语言就是系统所能识别的语言。
– 定义。 – ε-NFA与DFA的等价性。
• FA是正则语言的识别器
– 正则文法(RG)与FA的等价性。 – 相互转换方法。 – 带输出的有穷状态自动机。 – 双向有穷状态自动机。
2021/4/26
2
第3章 有穷状态自动机
• 重点:DFA的概念,DFA、NFA、ε-NFA 、 RG之间的等价转换思路与方法。
第3章 有穷自动机共45页

(c)
空移环路的消除
• 找到空移环路之后,要消除它只要把空移环路上 所有结点q1,q2,…,qn合成一个结点,并消除它们 所有的弧。如果其中的某一个结点qi(i=1或 2,…,n)是开始结点或终止结点,则将此合并后的 新结点相应地设置为开始状态或终止状态。
例3.8
q0
a
q1
q2
则L(A)=L(B)={(ab)n|n1}, 所以自动机A,B等价。
非确定的有穷自动机NDFA
• 定义3.5 一个非确定的有穷自动机是一个五 元组,NDFA=Q,,t,Q0,F,其中Q 为状态的有穷非空集, 为有穷输入字母 表,t为Q 到Q的子集(多值映射), Q0Q是初始状态集,F Q为终止状态集。
例3.5 DFA A=({q0,q1}, {a,b}, t, q0, {q0} ), 其中 t(q0,a)=q1, t(q1,b)=q0.
DFA B=({q0’,q1’,q2’}, {a,b}, t’, q0’, {q2’} ), 其中 t’(q0’,a)=q1’, t’(q1’,b)=q2’, t’(q2’,a)=q1’.
有穷自动机DFA定义:
一个确定的有穷自动机(DFA)M是一个五元组:M=(Q, Σ,t,q0,F)其中
✓ 1 Q是一个有穷集,它的每个元素称为一个状态;
✓ 2 Σ是一个有穷字母表,它的每个元素称为一个输入符 号,所以也称Σ为输入符号字母表;
✓ 3 t是转换函数,是在Q×Σ→Q上的映射,即,如 t(qi, a)=qj,(qi,qjQ)就意味着,当前状态为qi,输入 符为a时,将转换为下一个状态qj,我们把qj称作qi的一 个后继状态;
例子
NDFA N=({S,P,Z},{0,1},t,{S,P}, {Z})
第三章有穷自动机

例:将图示的DFA M最小化。
a
b
6
4
a
a
a
b
a
1
a
b
5a
7
b3
b
b
2 b
第三章有穷自动机
1、将M状态分为两个子集: P0=({1,2,3,4},{5,6,7})
2、{1,2,3,4}读入a后划为: P1=({1,2},{3,4},{5,6,7})
3、进一步划分: P2=({1,2},{3},{4},{5,6,7})
② 检查Ia 和Ib,看它们是否已在表的第一列 中出现,把未曾出现者之一填入下一空行 的第一列上,再计算该行的第二、第三列 上的Ia 和Ib。
第三章有穷自动机
③ 重复第二步,直至表中所有第二、第三列 上的元素全部再第一列出现为止。
因为M中的状态(子集)的个数是有限的,所 以上述三步必定在有限步骤内终止。
f(V,a)=U f(V,b)=Q U Q V
f(Q,a)=Q f(Q,b)=Q V U Q
QQQ
第三章有穷自动机
3.1.3 状态转换图
图中标有的为开始状态,标有双圈的状态为终止 状态。
若f(Ki,a)=Kj,则从状态结点Ki到状态Kj画标记为a
的弧。
a
q0
q1
a
bb
bb
a
q3
q2
a
第三章有穷自动机
➢ NFA有一个开始状态集,而DFA只有一个 开始状态。
➢ NFA的映射是QQ的子集,是一个多 值映射,而DFA的映射是QQ,是一 个单值映射。
➢ DFA是NFA的特例,对于每个NFA M,存 在一个DFA M’,使得L(M)=L(M’)。
03 有穷状态自动机

13
例3-2
构造一个 DFA,它接受的语言为{ x000y | x, y∈{0, 1}* }。 关键:是否出现了子串“000”? q0——M 的启动状态; q1——M 读到了一个 0,这个 0 可能是子串“000”的第 1 个0; q2——M 在 q1 后紧接着又读到了一个 0,这个 0 可能是子串 “000”的第 2 个0; q3——M 在 q2 后紧接着又读到了一个 0,发现输入字符串含 有子串“000”;因此,这个状态应该是终止状态。 可以给出 M 的状态转移函数的部分定义: δ(q0 ,0)=q1——M 读到了一个0,这个 0 可能是子串 “000”的 第1个0。 δ(q1,0)=q2——M 又读到了一个 0,这个 0 可能是子串 “000” 的第2个0。 δ(q2 ,0)=q3——M 找到了子串 “000”。
14
例3-2
δ(q0,1)=q0——M 在 q0 读到了一个 1,它需要继续在 q0 “等待” 可能是子串“000”的第 1 个 0 的输入字符 0; δ(q1,1)=q0——M 在刚刚读到了一个 0 后,读到了一个 1,表明 在读入这个 1 之前所读入的 0 并不是子串“000”的第 1 个 0, 因此,M 需要重新回到状态 q0,以寻找子串“000”的第1个0; δ(q2,1)=q0——M 在刚刚发现了00后,读到了一个1,表明在读入 这个1之前所读入的00并不是子串“000”的前两个0,因此, M 需要重新回到状态 q0,以寻找子串“000”的第 1 个 0; δ(q3,0)=q3——M 找到了子串“000”,只用读入该串的剩余部分。 δ(q3,1)=q3——M 找到了子串“000”,只用读入该串的剩余部分。
开始状态
状态
q0 q1
输入字符
第03章有穷状态自动机-电子科技大学

即时描述
设M = (Q, , , q0, F)为一个FA,x, y *, (q0, x)=q,xqy称为M的一个即时描述。 它表示xy是M 正在处理的一个字符串,x引导M 从q0启动并到达状态q,当前正指向y的首字符。 如果xqay是M的一个即时描述,且(q, a)=p,则 经过字符a的处理后,即时描述变为xapy。这一 过程记作: xqay
证明思路
(1) 显然,DFA是NFA的特殊形式;即所有 的DFA已经用NFA的形式表示; (2) 需要证明对于任意给定的NFA,存在与 之等价的DFA。
根据NFA构造DFA,将状态集合从Q变换到2Q, 这样DFA中的任意一个状态实际上是NFA中某 些状态的组合(这里避免使用术语“集合”)。 使用归纳法证明DFA与NFA的状态转移存在一 一对应关系。 证明由DFA和NFA能识别相同的语言。 L(M1) = L(M2)
作为对DFA的修改 q1 0 0 S 1 0 q0 1 1 q2
构造接受语言
0,1
q3
L={x| x{0,1}*,且 x含有子串00或11}的DFA
“直接”的FA
q1
0,1
S q0
0 1
0 1
0,1
q3
q2 希望是接受语言 L={x| x{0,1}*,且 x含有子串00或11}的FA
与DFA的区别
当这个子集为空时,表示没有状态与之对应;
当这个子集的元素个数大于1时,表示有多个状 态与之对应。
第03章 有穷状态自动机-19、20、21节课-2011-10-22
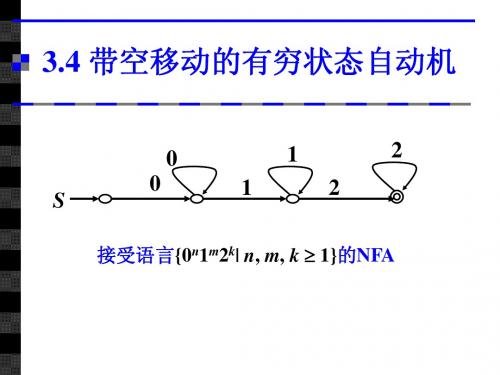
q0 0q1
q1 0q1 | 1q2 q2 1q2 | 2q3| 2 q3 2q3| 2
练习(见习题)
20(左图)
习题评讲
q0 0q1 | 1q3 | 1 q1 0q0 | 1q3| 1 q2 1q0 | 0q3| 0 q3 0q1 | 1q1
Ø {q1} Ø Ø Ø {q2}
M接受(识别)的语言
M接受(识别)的语言 对于x∈∑*,仅当
时,称x被M接受。
*
ˆ ( q0 , x ) F
ˆ L(M ) {x | x 并且 (q0 , x) F }
定理3-2
-NFA与NFA等价。
证明思路: (1) 显然, NFA是-NFA的特殊形式;即所 有的NFA 已经用-NFA的形式表示; (2) 需要证明对于任意给定的-NFA ,存在 与之等价的NFA 。
定理3-4(续)
对(a,A)∈T×V
{B|AaB∈P}∪{Z} 如果Aa∈P 如果AaP
δ(A,a)=
{B|AaB∈P}
用B∈δ(A,a)与产生式AaB对应 用Z∈δ(A,a)与产生式Aa对应。
注意
ε-CLOSURE(q)与δ(q,ε)不同
定义3-9
带空移动的不确定的有穷状态自动机(nondeterministic finite automaton with -moves, NFA) M是一个五元组: M = (Q, , , q0, F) 其中,Q, , q0, F 状态的意义同DFA (定义3-1)。
定理3-2(续)
设有-NFA M1 = (Q, , 1, q0, F) (1) 构造与之等价的NFA 取 NFA M2 = (Q, , 2, q0, F2),其中 F2 = F {q0} 如果F -CLOSURE(q0) Ø F 如果F -CLOSURE(q0) =Ø
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 0 q1 1 q2 0
0 1 q3
0,1
q4
第三章、有穷状态自动机
例2、假设字母表为{0,1},构造一个识别含有001子串的所有 字符串的DFA的状态图。
1 0 q1 1 q2 0
0 1 q3
0,1
q4
第三章、有穷状态自动机
关键问题:DFA与NFA等价吗?
第三章、有穷状态自动机
第三章、有穷状态自动机
NFA与DFA的等价性
NFA与DFA等价是指两种模型识别相同的语言类(正则语言)。 对于任意给定的DFA,存在一个NFA与之等价; 对于任意给定的NFA,存在一个DFA与之等价。 DFA本身就是一种NFA,所以,要证明DFA与NFA等价,只需证明 对于任意给定的NFA,存在一个DFA与之等价。 下面根据给定的NFA构造一个DFA: 这里M2=(Q2,Σ,δ,q0,F ),Q2 =P(Q),
第三章、有穷状态自动机
δ1
q01 q1 q2
0 1
q1 q2 q1
0 q02 q3 q4
q01 q1 Q2
1 q3 q4 q5
δ2
q02 q3 q4
q5
q5
q5
第三章、有穷状态自动机
下面构造M= (Q,Σ,δ,q,F), (1)Q={(r1,r2) ∣ r1∈Q1且r2∈Q2}; (2)Σ= {0,1}; (3)转移函数 δ((r1,r2) ,a)= δ (δ1 (r1,a) ,δ 2(r2,a)), 如下页表所示; (4)q0=(q01,q02)是M的起始状态; (5)F={(q2,q02),(q2,q3),(q2,q4),(q2,q5),(q01,q4), (q1,q4)}。
第三章、有穷状态自动机
定理:正则语言类在并运算下封闭。 证明:思路:即假设A,B正则,再证明A∪B正则。 设自动机M1,M2分别识别A,B ,造一个M识别A∪B即可。 M1=(Q1,Σ,δ1,q1,F1), M2=(Q2,Σ,δ2,q2,F2),下面开始构造一个 M=(Q,Σ,δ,q0,F)使其符合要求。 (1)Q={(r1,r2) ∣r1∈A1且r2∈A2}=Q1×Q2; (2) Σ相同,若不同,则Σ= Σ1 ∪ Σ2; (3)转移函数δ:任意(r1,r2) ∈Q,a ∈ Σ,令 δ ((r1,r2) ,a)= δ (δ1 (r1,a) ,δ 2(r2,a)), 于是, δ 取M的一个状态和一个输入符号,返回M的下一个状 态; (4)q0是有序对(q1,q2); (5)F={(r1,r2) ∣r1∈F1或r2∈F2} (注意,F≠F1×F2) 综上,我们构造了自动机M。
第三章、有穷状态自动机
例6、假设字母表为{0,1},构造一个识别L(E)={0,ε}的DFA的 状态图。
0
q1
1 0,1
q2
q3
0,1
第三章、有穷状态自动机
0 0
1
q1 1
比如例1的自动机的形式描述: (1)、Q={q1,q2}; (2)、 Σ={0,1}; (3)、 δ (q1,0)=q1, δ (q1,1)=q2, δ (q2,0)=q2, δ (q2,1)=q1; (4)、q1为起始状态; (5)、F={q2}为接受状态集。
第三章、有穷状态自动机
四、非确定性
前面所有的有穷自动机都是确定性的,记为DFA,特点是必须每个符
号都有相应的运算结果,自然的,考虑非确定性NFA,为推广,它在
任何一点,下一个状态可能存在若干个选择。那么,区别在哪里呢?
1
1 0 0
1
q01
0,1
q1
0
q2
0,1
q01
0,ε
q1
0
q2
第三章、有穷状态自动机
第三章、有穷状态自动机
例如:教室外面的饮料销售机,就是典型的有穷状态自动机, 投币,选择饮料,找零,出口,大家试着解析一下它的工作过 程,进行数学语言描述或者画出机器草图。
条件:2元雪碧,3元橙汁,4元vc汁,红色圈表示接受状态。
请大家上来画设计图!
第三章、有穷状态自动机
这就是我们天天见到的售货机,也称为自动机。
第三章、有穷状态自动机
该定理不仅证明了这个结论,更重要的是为我们的运算提供了方法。 例2、通过运算构造DFA: L(M)={w ∣w含偶数个0或二个1}。 解:令L(M1)={w ∣w含偶数个0}, L(M2)={w ∣w含二个1}。 则L(M)= L(M1) ∪ L(M2),其中,
1
1
0 0
1
q01
第三章、有穷状态自动机
0 1
0
q1 1
q2
0,1
q3 1
例如机器运行时:010: reject 11: accept 010100100100100: accept 010000010010: reject : reject
第三章、有穷状态自动机
二、设计有穷自动机
就是针对给定的语言,你来设计一台自动机,并且准确识别这 个语言。确定性的有穷自动机记为DFA。 定义:如果一个语言被一台有穷自动机识别,则称它是正则语 言。
例3、假设字母表为{0,1},构造一个识别从1开始以0结束的 所有字符串的DFA的状态图。
1
0 0
q0
0
1
q1
1
q2
q3
0,1
第三章、有穷状态自动机
例4、假设字母表为{0,1},构造一个识别空集Ф的DFA的状态图。
q1
例5、假设字母表为{0,1},构造一个识别L(E)={ε}的DFA的状态图。
q1
2 q1 3
q2
4
余额
q3 q4 q5
q6
第三章、有穷状态自动机
一、有穷状态自动机的形式定义
定义1、 确定的有穷状态自动机是一个五元组(Q, Σ, δ, q0, F ),其 中 (1)、 Q是有限状态集; (2) 、Σ是字母表; (3)、 Δ:Q× Σ→Q称为状态转换函数,它是状态集与字 母表的笛卡尔积到状态集的一个映射; (4) 、q0∈Q是初始状态; (5) 、 F是终止状态集。
q2
第三章、有穷状态自动机
问题(讨论):
1、DFA如何进行运算?
第三章、有穷状态自动机
三、正则运算
在算术中,基本对象是数,工具是处理数的运算,如+, ×;在计算理论中,对象是语言,工具是处理语言所设计的 如下3种运算,称作正则运算。 定义:设A和B为语言,则下列3种运算称作正则运算。 (1)并:A∪B={x∣x∈A或x ∈B} (2)连接:AB={xy∣x∈A且x ∈B} (3)星号:A*={x1 x2…xk∣xi∈A,i=1, …k,k≧0} 例1、Σ={0,1},A={01,11},B={001,100},则 A∪B={01,11,001,100}; AB={01001,01100,11001,11100}; A*={ε,01,11,0101,0111,1101,1111,010101,…}。 注意:Ф ∪ Ф = Ф , Ф Ф = Ф , Ф *={ε}, A Ф = Ф
第三章、有穷状态自动机
δ (q01,q02) (q01,q3) (q01,q4) (q01,q02) (q1,q02) (q1,q3) (q1,q4) (q1,q5) (q2,q02) (q2,q3) (q2,q4) (q2,q5) 0 (q1,q02) (q1,q3) (q1,q4) (q1,q5) (q2,q02) (q2,q3) (q2,q4) (q2,q5) (q1,q02) (q1,q3) (q1,q4) (q1,q5) 1 (q01,q3) (q01,q4) (q01,q5) (q01,q5) (q1,q3) (q1,q4) (q1,q5) (q1,q5) (q2,q3) (q2,q4) (q2,q5) (q2,q5)
例1、假设字母表为{0,1},所考虑的语言由所以含有奇数个1的字 符串组成,构造一个识别这个语言的所有字符串的DFA的状 态图。 大家先设计。
第三章、有穷状态自动机
0 1
0
q1 1
q2
第三章、有穷状态自动机
例2、假设字母表为{0,1},构造一个识别含有001子串的所有 字符串的DFA的状态图。
第三章、有穷状态自动机
第三章、有穷状态自动机
考虑非确定性NFA,为DFA的推广,它在任何一点,下一个状态 可能存在若干个选择。那么,区别在哪里呢?主要是转移函数δ, 有很多计算分支,如果这些子过程中至少有一个接受,那么整个 计算接受。为了适应,大家运算一下010001110,100110, 11111111。非确定性NFA比DFA构造容易,实际上也是对能力更强 的计算模型的非确定性的一个很好的引入。
第三章、有穷状态自动机
(q01,q02)
0
0
(q1,q02) (q2,q02)
1
(q01,q3)
1
0
(q1,q3)
0 0 0 0 0 0
1
(q2,q3)
1
(q01,q4)
1
0
(q1,q4)
1
(q2,q4)
1
(q01,q5)
1 0
(q1,q5)
1
(q2,q5)
1
1
0
1
那么,还可以证明,连接运算与星运算也是封闭的。
q1
0
M1
q2
第三章、有穷状态自动机
0 0
1
0
1
0,1
1
q02
q3
q4
q5
M2
M1=(Q1,Σ,δ1,q1,F1), M2=(Q2,Σ,δ2,q2,F2), (1)、Q1={q01,q1,q2 }, Q2={q02,q3,q4,q5}; (2)、 Σ= {0,1}; (3)、转移函数δ1, δ2如下表; (4)、q01,q02分别是M1,M2的起始状态; (5)、F1={q2}, F2={q4}.
