第一课最优化共轭梯度法
最优化方法-共轭方向和共轭梯度法

由3式可以看出
2020/3/6
16
2.共轭方向-共轭方向法
• 基本定义
利用共轭方向作为搜索方向的无约束极小化算法
• 通用步骤:
(1)任取X 0 ,以及在X 0的下降方向P0 , k 0; (1)求解一维搜索问题
min f ( X k Pk ),为最优步长,是个数值.
(3) X k1 X k k Pk ;
X
T QX
bT
X
c, Q正定,
X 0是初始点,
P0
f
(X0)
X k1 X k k Pk , k 0,1...m 1, k是最优步长,且
Pk1 f ( X k1) ak Pk (这是构造的结果)
其中ak
f
( X k1)T QPk PkT QPk
,
P0
(
X
)T
k 1
Pk
)T
PkT f ( X k1)
f ( X k1) QX k1 b Q( X k k Pk ) b, ( X k 1 X k k Pk )
f ( X k1) (QX k b) kQPk f ( X k ) kQPk
当m 2时 所以,P0,P1, Pm1是线性无关的。
P0T QP1
P0T Q f ( X 1 )
f ( X 1 )T QP0 P0T QP0
P0
P0T Qf ( X 1 ) f ( X 1 )T QP0 0
表明,P0与P1共轭。
2020/3/6
2020/3/6
4
1.共轭方向法的基本原理
• 已知 X1 点是在 X 0 点在直线 l0 上沿 P0 搜索方向的一个极小 点。(l0 与 P0 是平行的)
共轭梯度法

•基本思想:把共轭性与最速下降法相结合,利用已 知点处的梯度构造一组共轭方向,并沿着这组方 向进行搜索,求出目标函数的极小点
4.4共轭梯度法
先讨论对于二次凸函数的共轭梯度法,考虑问题
min f (x) 1 xT Ax bT x c
3, giT d (i) giT gi (蕴涵d (i) 0)
证明: 显然m1,下用归纳法(对i)证之.
当i 1时,由于d (1) g1,从而3)成立,对i 2时, 关系1)和2)成立,从而3)也成立.
4.4共轭梯度法
设对某个i<m,这些关系均成立,我们证明对于i+1
也成立.先证2),
因此
2 / 3 1 5/ 9
d (2)
1/ 1
3
1 9
2 0
5/9 1
从x(2)出发,沿方向d (2)进行搜索,求步长2,使满足 :
f
( x (1)
2d (1) )
min
0
f
(x(2)
d (2))
2 0
4.4共轭梯度法
显然, d (1)不是目标函数在x(1)处的最速下降方向.
下面,我们用FR法构造两个搜索方向.
从x(1)出发,沿方向d (1)进行搜索,求步长1,使满足 :
f
( x (1)
1d (1) )
min
0
f
( x (1)
d (1) )
得1 2 3
A正定,故x是f(x)的极小值点.
共轭方向与共轭梯度法-最优化方法

f (X1)T P0 0 ,所以 f (X1)T P0 1P1TQ P0 0
P1TQ P0 0
(1)
以上就是搜索方向P1所必须满足的(必要) 条件。这也是使X2是极小点的充分条件。 P1,P2称为关于Q的共轭方向。
讨论表明 对于二维的具有正定矩阵Q的 二次函数f(X),从任一初始点出发,依次沿关 于Q共轭的两个方向进行一维搜索,必可达到 f(X)的无约束精确极小点。
Pk 1
0
且对j 0,1 , k 2, 有
PjT QPk PjT Q f ( X k ) k1Pk1
PjT Qf
(X
k
)
k
PT
1 j
QPk
1
f ( X k )T QPj
f ( X k )T f ( X j1) f ( X j ) j
f ( X k1 ) QX k1 b Q( X k k Pk ) b (2)
f ( X k1 ) f ( X k ) k QPk
所以
f ( X m ) f ( X m1) m1QPm1
f ( X m2 ) m2QPm2 m1QPm1
其中1 是最优步长,1>0 .因为 X * 是无约束极小点。
故 f ( X * ) 0 即 QX * b 0
f (X1) QX1 b
Q( X * 1P1) b (QX * b) 1QP1 1QP1
又因为 X1是f(X)沿P0方向的直线l0上的极小点,故
设 X En ,
,Q为对称正定矩阵,P0,
P1,···,Pm-1是关于Q共轭的m个共轭方向,
最优化共轭梯度法

x1 x2
,
A
4 0
0 2
.
f ( x) ( 4x1 , 2x2 )T .
第 1 次迭代:
令 d (1) g1 ( 8, 4 )T ,
而
1
g1T d (1) d (1)T Ad (1)
(
8
,
4
)
8 4
(
8
,
4
)
2. 共轭梯度法
Fletcher R eeves 共轭梯度法 :
min f ( x) 1 xT Ax bT x c 2
其中 x Rn , A是对称正定矩阵,b Rn,c 是常数。
基本思想:将共轭性和最速下降方向相结合,利用已知迭 代点 处的梯度方向构造一组共轭方向,并沿此方向进行搜索,求出 函数的极小点。
取最速下降方向作为第一个搜索方向,开始下一轮搜索。
注 在共轭梯度法中,也可采用其它形式的公式计算i ,如
i
giT1( gi1 giT gi
gi )
( PRP共轭梯度法)。
i
|| gi1 || d (i)T gi
(Dixon共轭梯度法)。
i
gi
T 1
(
gi1
gi
)
d (i)T ( gi1 gi )
||
gi1 ||2 d (i)T gi
|| gi1 ||2 || gi ||2
(4)
FR算法步骤:
1. 任取初始点x(1) ,精度要求 ,令k 1。 2. 令g1 f ( x(1) ),若 || g1 || ,停止,x(1)为所求极小点;
共轭梯度法

2 2 min f ( x ) = x1 + 2x2 x
⎛1⎞ 给定初始点 x (0) = ⎜ ⎜1⎟ ⎟。 ⎝ ⎠
13
⎛ 2 x1 ⎞ ⎛ 2 0⎞ 2 首先, ∇f ( x ) = ⎜ ⎜ 0 4⎟ ⎟ ,以下利用(4.14)确定 β k 。 ⎜ 4x ⎟ ⎟ ,H= ∇ f ( x ) = ⎜ ⎝ ⎠ ⎝ 2⎠ k=0:
0
k +1
) 与搜索方向 s 0 ," , s k 均正交。同时,利用引理 4.1 马上
设 H ∈ R n×n 是对称正定阵,s ," , s
0
n −1
0
n −1
是非零 G—共轭方向组,x ∈ R 。 若对问题(UQP),
0
n
从 x 出发,依次沿 s ," , s
0
进行最优一维搜索,最终得到 x ,则 x 是(UQP)的最优解。
为保证 H-共轭性,在 x 处必须取 s 为搜索方向,而不能取 α s (α > 0) 为搜索方向。
k k
k
利用定理 4.3,马上得到上述算法的有限终止性。 定理 4.4 设 H ∈ R n×n 是对称正定阵。若用凸二次规划的共轭梯度法求解 (UQP) 时产生迭代点
x1 ," , x K ,则 x K 是(UQP)的最优解,并且 K ≤ n 。
首先由(4.7)知, g = ∇f ( x ) ( j = 0, " , k -1)是 s ," , s 的线性组合,因此根据定理 4.2,
j j 0 j
( g k )T g j =0, j = 0, " , k -1
由于
共轭梯度法详细解读

共轭梯度法详细解读
嘿,朋友们!今天咱就来好好唠唠共轭梯度法。
你想想啊,咱平常解决问题就像走迷宫似的,有时候会在里面转来转去找不到出路,而共轭梯度法呀,就像是在迷宫里给咱指了一条明路!比如说你想找一条最快从山这头到那头的路,共轭梯度法就能帮上大忙啦!
它可不是随随便便就出现的哦,那可是数学家们绞尽脑汁研究出来的宝贝呢!就好比一个超级英雄,专门来打救我们这些在复杂问题里苦苦挣扎的人。
在实际应用里,它可厉害着呢!比如说在工程计算中,要设计一个最完美的结构,共轭梯度法就能迅速算出最优解。
哇塞,这不就相当于有个超厉害的军师在帮咱出谋划策嘛!
你再想想,我们日常生活中很多事情都可以类比成用共轭梯度法来解决问题呀。
比如说你要规划一次旅行,怎么安排路线最合理,不就是在找那个最优的旅行路径嘛,这时候共轭梯度法的思路就能派上用场啦!它就像一个隐藏在幕后的高手,默默地为我们排忧解难。
而且哦,一旦你掌握了它,那种感觉就像是你突然掌握了一种绝世武功,能在各种难题面前游刃有余。
这可太酷了吧!
哎呀呀,共轭梯度法真的是太神奇、太有用啦!大家可一定要好好去了
解它、运用它呀,你绝对会被它的魅力折服的!相信我,没错的!。
共轭梯度法在优化问题中的应用

共轭梯度法在优化问题中的应用共轭梯度法是一种高效的优化算法,在许多优化问题中都得到了广泛的应用。
它是一种迭代方法,用于解决最小化二次函数的优化问题。
在本文中,我将介绍共轭梯度法的原理和算法,并探讨它在优化问题中的应用。
一、共轭梯度法的原理共轭梯度法的核心思想是通过迭代的方式,找到一个与之前迭代步骤方向相互垂直的搜索方向,以加快收敛速度。
在每一次迭代中,共轭梯度法根据当前的搜索方向更新搜索点,直到找到最优解或达到预定的收敛标准。
具体来说,共轭梯度法从一个初始搜索点开始,计算对应的梯度,并沿着负梯度方向进行搜索。
通过一定的方法找到一个与之前搜索方向相互垂直的新搜索方向,并以一定步长更新搜索点。
迭代过程将重复进行,直到满足收敛标准或达到最大迭代次数。
二、共轭梯度法的算法共轭梯度法的算法包括以下几个步骤:1. 初始化搜索点x0和梯度g0,设置迭代次数k=0。
2. 计算当前搜索方向d_k=-g_k(k为当前迭代次数)。
3. 通过一维搜索方法找到最佳步长α_k。
4. 更新搜索点x_k+1 = x_k + α_k * d_k。
5. 计算更新后的梯度g_k+1。
6. 判断是否满足收敛标准,若满足则算法停止,否则转到步骤7。
7. 计算新的搜索方向β_k+1。
8. 将迭代次数k更新为k+1,转到步骤3。
这个算法保证了每一次迭代中的搜索方向都是彼此相互垂直的,从而加快了收敛速度。
三、共轭梯度法的应用共轭梯度法在优化问题中有广泛的应用,特别是在二次规划、线性规划和非线性规划等领域。
在二次规划问题中,共轭梯度法可以高效地求解线性系统Ax=b,其中A是一个对称正定的矩阵。
由于共轭梯度法的特性,它只需要进行n 次迭代,其中n是问题的维度,就能得到精确的解。
这使得共轭梯度法在大规模线性系统求解中具有重要的应用价值。
在线性规划问题中,共轭梯度法可以用于求解带有线性约束的最小二乘问题。
共轭梯度法通过将线性约束转化为一系列的正交子空间,从而在求解最小二乘问题时能够更快地收敛。
共轭梯度法

f ( x1)T p0 0
现在找方向p1直接指向最优解x * ,
如何找呢 ?
x● 0
等值线
x*
● p1
p0
x● 1
(1) 方向p1满足的条件
设从x沿p到x*的最佳步长为( ),
则有
x* x p
因此
f ( x* ) f ( x) Qp
由于 f (x* ) Qx* b
所以 f ( x) Qp 0
f (xk
k
dk
)
min
R
f (xk
dk )
注意:这里的搜索是在整个实数轴上进行,因为共轭
方向不一定是下降方向
下面的定理说明了共轭方向法如何求出解
定理5.1.2
设函数f由(.)给出, 非零向量组d , d,
,
d
关于
n
矩阵Q相互共轭. x Rn , 设迭代格式
xk xk k dk , k , , , n - 其中步长k由精确搜索计算. 则
等值线
由此解得
所以
p0T Qf ( x1 ) p0T Qp0
p1
-f (x1)
p0T Qf ( x1 ) p0T Qp0
p0
x*
f (x1)
●
p1
p0
x● 0
x●
p0
1
从上面的(1)和(2)可以得出稍后要介绍的共轭方向
法或共轭梯度法的基本原理
返回
共轭方向的定义
考察二次函数极小化问题
min f (x) 1 xTQx qT x 2
唯楚有材
於斯为盛
最优化
主讲:刘陶文
学好最优化,走遍天下都不怕
课件制作:刘陶文
第五章 无约束问题算法(III) — 共轭梯度法
共轭梯度法课件

4.3共轭梯度法4.3.1共轭方向法定义4.3.1设A 是n ×n 对称正定矩阵,d 1,d 2,是n 维非零矢量,如果d 1T Ad 2=0则称d 1和d 2是A-共轭的,简称共轭的设d 1,d 2,...,d m 是R n 中一组非零向量,如果d i T Ad j =0,i ≠j ,j,i=1,2,...,k则d 1,d 2,...,d m 是A-共轭的,简称共轭的,也称它们是一组A 共个方向定理4.3.3设x 0∈Rn 是任意初始点,对于极小化二次函数min f(x)=1/2 x T Ax-b T x 共轭方向法至多经n 步精确线性搜索终止;且每一x i+1都是f(x)在x 0和方向d 1,d 2,....,di, 所张成的线性流形{|x x=x 0+,0j i j j da ∑=j a ∀}中的极小点。
4.3.4共轭梯度法共轭梯度法是一个典型的共轭方向法,他的每一个搜索方向是相互共轭的,而这些搜索方向d k 仅仅是负梯度方向-g k 与上一次迭代的搜索方向d k-1组合。
因此,存储量小,计算方便。
定理4.3.6对于正定二次函数,采用精确线性搜索的共轭梯度法在m ≦n 步后终止,且对1≦i≦n成立下列关系式:d i T Ad j=0,j=0,1,...,i-1,g i T Ag j=0,j=0,1-1,d i T Ag i= - g i T g I[g0,g1,...,g i]=[g0,Ag0,,...,A i g0][d0,d1,...,d i]=[g0,Ag0,,...,A i g0]其中[g0,g1,...,g i]和[d0,d1,...,d i]分别表示g0,g1,...,g i及d0,d1,...,d i张成的子空间,[g0,Ag0,,...,A i g0]表示g0的i阶Krylov子空间。
定理4.3.9(FR共轭梯度法的总体收敛性定理)假定f R n R在有界水平集L={x R n|f(x)≦f(x0)}上连续可微,且有下界,那么采用精确线性搜索的F-R共轭梯度法产生的序列{x k}至少有一个聚点是驻点,即1当{x k}是有穷数列时,其最后一个点是f(x)的驻点;2当{x k}是无穷数列时,它必有聚点,且任一聚点都是f(x)的驻点。
共轭梯度法

3. 算法的 MATLAB 实现
在 MATLAB 中编程实现的共轭梯度法函数为: min GETD 功能:用共轭梯度法求解多维函数的极值。
调用格式: [ x, min f ] min GETD( f , x0, var, eps) 其中, f :目标函数;
x0 :初始点; :自变量向量; var x :目标函数取最小值时的自变量值;
(6) 若 k 1 n ,令 x(0) x( n ) ,转步骤(3) ,否则转步骤(7) ;
(7) 令 p
( k 1)
f ( x
( k 1)
) k p
(k )
, k
f ( x ( k 1) ) f ( x )
(k )
2 2
, 置 k k 1, 转步骤 (4) 。
t 0
(k ) ( k ) (4) 用 一 维 搜 索 法 求 t k , 使 得 f ( x kt p ) m i n f
( ) 5; x( k 1 ) x k( ) kt p k,转步骤
k( ) x
) 令, tk p( ,
(5) 若 f ( x
( k 1)
) ,停止,极小值点为 x ( k 1) ,否则转步骤(6) ;
1 f ( X ) d1 + x1 -x1* 2 1 =d1 + x1 -x1* 2
2
*
2
1 d1 a x1 -x1* 2
2b x1 -x1*
x -x c x -x
2
2b x1 -x1*
最优化方法3-5共轭梯度法和共轭方向法

算法 3.5.1
设目标函数为 f (x) 1 xTGx bT x c,其中G 正定。 2
给定控制误差 。
Step1. 给定初始点 x0及初始下降方向 p0,令k 0。
Step2. 作精确一维搜索,求步长k
f
( xk
k
pk )
min
0
f
( xk
pk
)
Step3. 令 xk1 xk k pk 。
称 Fletcher-Reeves 公式,简称 FR 公式。
k 1
gkT Gpk1 pkT1Gpk 1
Gpk 1
1
k 1
(gk
g
k 1 ) ,
gkT Gpk1
1
k 1
gkT
(gk
g
k 1)
,
pkT1Gpk 1
1
k 1
(g
k1 k2
pk2 )T
(gk
g
k 1)
1
k 1
g
g T
k 1 k
1
(2)Polak-Ribiere-Polyak 公式
故
k 1
g
T k
(
gk
g
k 1)
gkT1gk 1
此式是 Polak 和 Ribiere 以及 Polyak 分别于 1969
年提出的,故称 Polak-Ribiere-Polyak 公式,简称 PRP
0,i
1,2,L
,k
(ii) xk1是二次函数在k 维超平面Hk 上的极小点。
证明 由引理 3.5.2,只需证明(i),
数值最优化(共轭梯度)ppt课件

所以
29
PRP算法 FR算法中: (2)Polak-Ribiere-Polyak公式
由于gkTgk-1=0,所以有 对于二次函数,这两个函数是等价的,但对于一般的函数,根 据这两个公式的出的算法的计算效果有差异.
注:对于这两个算法,可以证明pkTgk= -gkTgk<0,因而都是下 降算法.
min f (x0+ p0)=1600 4+42-4+1的极小点, 得0 =0.080632,(精确一维搜索方法求得,e =10-5,) 于是x1=x0+ 0 p0=(0.161264,0)T,
第五章 无约束问题 算法(III)
——共轭梯度法
1
共轭方向法的思路
对于简单的二次函数
1 xT x bT x c 1 ( x b)T ( x b) c bTb
2
2
任给一个初始向量x(0),沿着方向e1=(1,0,···,0)T进行搜索,即 求解下面问题
由于
min 1
f1 (1 )
( x(0)
z
x(1) O
x(3) =x* x(2) y
x(0)
x
5
共轭方向法的思路
上面的方法对一般的二次函数是否适用呢?
考虑问题
其中
G
1 2
2 5
易见G是正定的,f(x)的极小点为(0,0)T.
以x(0)=(-1,-1)T为初始点,在方向e1=(1,0)T上进行一维搜索. 即求解问题
易求得1*=3,x(1)=x(0)+1*e1=(2,-1)T.
是f(x)在x1与p1,p2,···,pk所生成的k维超平面Hk上唯一极小点的充 分必要条件是
共轭梯度法

v
i 0
p Api
n
i T i
pi
证明:
任意向量 v (v R ) 可以表示成
v c j Pj
j 0
n 1
用 Pi A
T
(i 1,2,,n-1) 左乘式(1)得
n 1 j 0
PiT Av c j PiT APj ci PiT APi
ci P iT Av P i APi
共轭梯度法
(Fletcher-Reeves)
梯度法的特点 优点 迭代过程简单,编制程序较易,一次迭代的工作量较少,计 算机内存量小。 函数值下降方向明确,对初始点没有严格要求。 缺点 跌代过程中走许多弯路,有些情况下,收敛速度较慢。
d ( k ) -f (x ( k ) ) f (x ( k 1) ) d ( k ) 0
f (x )
(1)
f (x* ) A (x(1) 1d1 ) B A x (1) B 1Ad1 0
=
d (1)
f (x(1) ) 1Ad1 0
x*
1d (1)
d (f (x d f (x
( 0) T (0) T
(1)
) 1Ad(1) )
提供共轭向量系的方法有多种,如共轭梯度法,Powell方法等。
(二)共轭梯度法
Fletcher & Reeves (1964)
构造共轭方向的具体方法
x
(k )
x
( 0)
id(i )
i 0
k 1
(1) 初始搜索方向的确定 选定初始点
x (0) ,下降方向 d (0)
取
x (0) 处的负梯度方向;
梯度法和共轭梯度法

极小点,其中Bk{ x Nhomakorabeax k
id (i) ,i
R}
i 1
是由 d (1) , d (2) ,, d (k) 生成的子空间。特别地,当k n时,x(n1)是
f ( x)在Rn上的唯一极小点。
推论 在上述定理条件下,必有 f ( x(k1) )T d (i) 0, i 1, 2,, k。
3、共轭方向法
i
g
i
T 1
(
gi1
gi
)
d (i)T ( gi1 gi )
||
gi1 ||2 d (i)T gi
|| gi1 ||2 || gi ||2
(4)
FR算法步骤:
1. 任取初始点x(1) ,精度要求 ,令k 1。 2. 令g1 f ( x(1) ),若 || g1 || ,停止,x(1)为所求极小点;
上式两边同时左乘d jT A,则有
k
id
jT Ad i
0,
i 1
因为d 1 , d 2 ,, d k 是 k 个 A共轭的向量,所以上式可化简为
j d jT Ad j 0 .
因为d j 0,而 A是正定矩阵,所以d jT Ad j 0,
所以
j 0, j 1, 2,, k。
因此 d1 ,d 2 ,,d k 线性无关。
2. 共轭方向
定义 设 A 是 n n的对称正定矩阵,对于Rn中的两个非零向量 d1 和 d 2, 若有 d1T Ad 2 0,则称d 1和d 2关于A共轭。 设 d1 , d 2 ,,d k 是 Rn 中一组非零向量,如果它们两两关于A 共轭,即 d iT Ad j 0, i j , i , j 1, 2,, k。 则称这组方向是关于A共轭的,也称它们是一组A共轭方向。
最优化课程练习-共轭梯度法
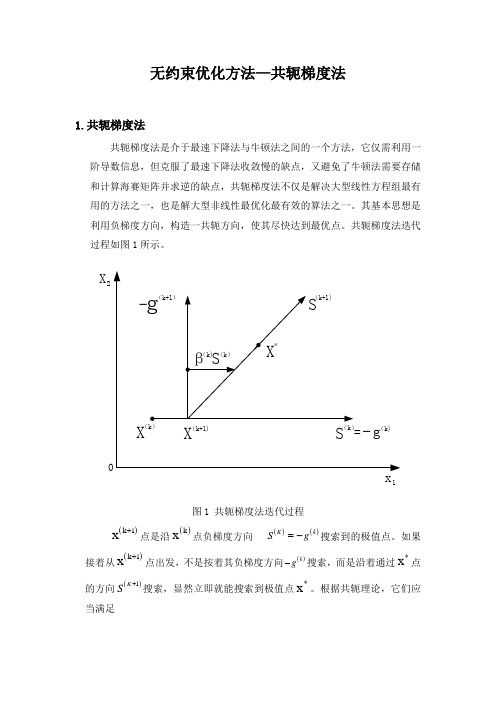
无约束优化方法—共轭梯度法1.共轭梯度法共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算海赛矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。
其基本思想是利用负梯度方向,构造一共轭方向,使其尽快达到最优点。
共轭梯度法迭代过程如图1所示。
1X 2图1 共轭梯度法迭代过程()k 1x +点是沿()k x 点负梯度方向()()K k Sg =-搜索到的极值点。
如果接着从()k 1x +点出发,不是按着其负梯度方向()kg -搜索,而是沿着通过*x 点的方向()1K S +搜索,显然立即就能搜索到极值点*x 。
根据共轭理论,它们应当满足()()(1)1k Tk SAS+=即()KS 与()1K S +是互为共轭方向,新构造的共轭方向()1K S +,可由矢量合成,()(1)(1)()()2k k k k SgSβ++=-+()k β值可根据在极值点附近目标函数等值线近似为二次型函数的道理,推到出:()(1)(1)(1)2()()()()2||||3||||k T k k k k T k k gg g g g g β+++==利用两个点的梯度()k g和(1)k g+,就可以构造一个与梯度矢量为共轭的矢量()1K S +,沿着该方向搜索,即可求得极值点。
共轭梯度法程序框图如图2所示。
图2 共轭梯度法程序框图2. 共轭梯度法的应用用共轭梯度法计算22121212()52410f X x x x x x x =+---+ 的最优解,其中:初始点()0[1,1]T X =。
收敛精度ε=0.0001(1).共轭梯度法程序设计#include "stdio.h" #include "math.h"double fun1(double x1,double x2) {double y;y=x1*x1+x2*x2-5*x1*x2-2*x1-4*x2+10; return y; }double fun2(double g[],double d[]) {double buchang;buchang=-(g[0]*d[0]+g[1]*d[1])/(d[0]*(2*d[0]-5*d[1])+d[1]*(-5*d[0]+2*d[1])); return buchang; }main(){ double t, beta,x1=1,x2=1,d[2],g[4], y, m,e=0.0001; int k=1;g[0]=2*x1-5*x2-2; g[1]=2*x2-5*x1-4; m=(sqrt(g[0]*g[0]+g[1]*g[1]));while(m>e&&k<=200) { if (k==1) {d[0]=-g[0]; d[1]=-g[1];beta=0; } else {beta=(g[0]*g[0]+g[1]*g[1])/(g[2]*g[2]+g[3]*g[3]); d[0]=-g[0]+beta*d[0]; d[1]=-g[1]+beta*d[1]; }t=fun2(g,d); x1=x1+d[0]*t; x2=x2+d[1]*t; g[2]=g[0]; g[3]=g[1];g[0]= 2*x1-5*x2-2;g[1]= 2*x2-5*x1-4;m=sqrt(g[0]*g[0]+g[1]*g[1]); k++; }y=fun1(x1,x2);printf("迭代次数为k=%d\n",k);printf("分别输出x1=%f,x2=%f\n",x1,x2); printf("极小值y=%f",y); }(2).程序运行结果(3).结 论用共轭梯度法计算22121212()52410f X x x x x x x =+---+的最优解为*( 1.142857,0.857143)X =-- ,*()12.857143F X = 。
共轭梯度法

共轭梯度法对于任意形式的目标函数()f X ,在极值点*X 附近展开成泰勒级数,且取前三项,有()()()****2**1()...2TT f X f Xf X X X X X f X X X ⎡⎤⎡⎤⎡⎤⎡⎤≈+∇-+-∇-⎣⎦⎣⎦⎣⎦⎣⎦因在极值点*X 处()*0f X ∇=,而()2**()f X H X ∇=为()f X 在*X 的二阶偏导数矩阵,即Hessian 矩阵,故()****1().().2T f X f X X X H X X X ⎡⎤⎡⎤≈+--⎣⎦⎣⎦ 对于二次函数来说,若令()()()2*2*2*221122,,f X f X f X a b c x x x x ∂∂∂===∂∂∂∂则()**1(),a b H X f X d b c ⎡⎤==⎢⎥⎣⎦而—常数 则,得到()()()()()()()()()()()()()()11221212121122*1**112*2**12**112**1222****11122-1()+--2---1=+--2--1-2---2x x a b f X d x x x x b c x x a x x b x x d x x x x b x x c x x d a x x b x x x x c x x ⎡⎤⎡⎤⎢⎥⎡⎤≈⎢⎥⎣⎦⎢⎥⎣⎦⎣⎦⎡⎤+⎢⎥⎡⎤⎣⎦⎢⎥+⎣⎦⎡⎤=+++⎢⎥⎣⎦由上式可知,当12*1**2x x X X x x ⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦时,得到目标函数的极小值()*1()f X f X d ==,当22(),,...f X d d =时,则有等值线族。
令2()f X d =,代入上式,则有()()()()112222****2111221()-2---2f X d d a x x b x x x x c x x ⎡⎤=≈+++⎢⎥⎣⎦所以目标函数()f X 在*X 点附近的等值线方程为()()()()112222****1122-2---0a x x b x x x x c x x d +++=式中,122()d d d =-=常数。
共轭梯度法求解优化问题

共轭梯度法求解优化问题
共轭梯度法是一种用于求解优化问题的迭代算法。
它主要应用于求解大规模线
性方程组和最小二乘问题,特别适用于对称正定矩阵。
共轭梯度法的基本思想是利用梯度信息来进行迭代优化。
它的优点在于每次迭
代只需要计算一次梯度,相对于其他常见的优化算法,如梯度下降法,它的收敛速度更快。
具体来说,共轭梯度法首先需要确定一个初始点和一个初始搜索方向,然后通
过不断迭代来逼近最优解。
在每次迭代中,它会沿着当前搜索方向移动一定的步长,并更新下一个搜索方向。
这个搜索方向是通过利用上一次的梯度和当前梯度之间的差异来确定的,这样可以确保在每次迭代中找到一个相互正交的搜索方向,从而加快收敛速度。
在实际求解中,共轭梯度法通常与预处理技术相结合,以进一步提高求解效率。
预处理技术通过对矩阵进行变换,将其转化为更容易求解的形式。
常见的预处理技术包括对角预处理、不完全Cholesky分解预处理等。
总结来说,共轭梯度法是一种高效的优化算法,特别适用于求解大规模线性方
程组和最小二乘问题。
它通过利用梯度信息来迭代逼近最优解,并通过寻找相互正交的搜索方向来加快收敛速度。
在实际应用中,我们可以结合预处理技术来进一步提高求解效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知迭代点x(k)和搜索方向d (k) ,利用一维搜索确定最优步长k ,
即求解
min f ( x(k ) d (k ) ) 。
记 ( ) f ( x(k) d (k) ),
令 ( ) f ( x(k) d (k) )T d (k) 0,
即有 [ A( x(k) d (k) ) b ]T d (k) 0,
则函数 f ( x) 的等值面 1 ( x x)T A( x x) c 2
是以 x 为中心的椭球面。
由于 f ( x) A( x x) 0,
而 2 f ( x) A,
因为A 正定,所以2 f ( x ) A 0,
x
因此 x 是 f ( x)的极小点。
设 x(0) 是在某个等值面上的一点,d (1) 是 Rn中的一个方向, x(0)沿着d (1) 以最优步长搜索得到点x(1) 。
4 0
0 8 2 4
5 18
所以
x(2) x(1) 1 d (1)
( 2, 2 )T 5 ( 8, 4 )T ( 2 , 8 )T
18
99
第 2次迭代:
g2 1
( 8 ,16 )T .
|| ||
9 g2 g1
9 ||2 ||2
得到点x(2) , x(3) ,, x(k1) ,则 x(k1) 是函数 f ( x)在 x(1) Bk 上的
极小点,其中
Bk
{ x|x
k
id (i),i R}
i 1
是由 d (1) , d (2) ,, d (k) 生成的子空间。特别地,当k n时,x(n1)是
其中 i
|| f ( x(i1) ) ||2 。 || f ( x(i) ) ||2
(2) 搜索步长i不能利用公式(3)计算,需由一维搜索确定。
精品课件!
精品课件!
(3) 算法在有限步迭代后不一定能满足停止条件,此时可采取 如下措施: 以 n 次迭代为一轮,每次完成一轮搜索后,如果还没有求 得极小点,则以上一轮的最后一个迭代点作为新的初始点,
令 k : k 1。
4. 利用公式(3)计算k ,令 x(k1) x(k) k d (k) ,转3。
例 用FR 算法求解下述问题:
min f ( x) 2x12 x22
初始点取为x(1) ( 2, 2 )T。
解:
f
(
x)
1 2
(
x1
,
x2
)
4 0
0 2
x1 x2
,
A
4 0
0 2
.
f ( x) ( 4x1 , 2x2 )T .
第 1 次迭代:
令 d (1) g1 ( 8, 4 )T ,
而
1
g1T d (1) d (1)T Ad (1)
(
8
,
4
)
8 4
(
8
,
4
)
j d jT Ad j 0 . 因为d j 0,而 A是正定矩阵,所以d jT Ad j 0,
所以
j 0, j 1, 2,, k。
因此 d1 ,d 2 ,,d k 线性无关。
几何意义
设有二次函数 f ( x) 1 ( x x)T A( x x) 2
其中 A 是 n n 对称正定矩阵, x 是一个定点。
x(k1) x(k) k d (k)
f (x(k)
k
d (k) )
min
f
( x(k )
d(k))
直到某个x(k) 满足f ( x(k) ) 0。
注 由定理2可知,利用共轭方向法求解上述极小化问题,至多经过 n 次迭代必可得到最优解。
如何选取一组共轭方向?
否则,令d (1) g1 ,利用公式(3)计算1 ,令x(2) x(1) 1 d (1)。
3. 令gk1 f ( x(k1) ),若 || gk1 || ,停止,x(k1)为所求极小点; 否则,令d (k1) gk1 k d (k) ,其中 k用公式(4)计算。
则d (1)是点 x(1)所在等值面的切向量。
该等值面在点x(1) 处的法向量为 f ( x(1) ) A( x(1) x).
则 d (1) 与 f ( x(1) ) 正交,
即 d (1)Tf ( x(1) ) 0, 令 d (2) x x(1) , 所以 d (1)T Ad (2) 0,
定理 1. 设 A是 n阶对称正定矩阵,d 1 ,d 2 ,,d k 是 k 个 A共轭的非零
向量,则这个向量组线性无关。
证明
设存在实数1 ,2 ,,k ,使得
k
id i
0,
i 1
上式两边同时左乘d jT A,则有
k
id
jT Ad i
0,
i 1
因为d 1 ,d 2 ,,d k 是 k 个 A共轭的向量,所以上式可化简为
f ( x)在Rn上的唯一极小点。
推论 在上述定理条件下,必有 f ( x(k1) )T d (i) 0, i 1, 2,, k。
共轭方向法
对于极小化问题 min f ( x) 1 xT Ax bT x c , 2
其中 A是正定矩阵,称下述算法为共轭方向法 :
(1) 取定一组A共轭方向d (1) , d (2) ,, d (n) ; (2) 任取初始点x(1) ,依次按照下式由x(k)确定点x(k1) ,
2. 共轭梯度法
Fletcher R eeves 共轭梯度法 :
min f ( x) 1 xT Ax bT x c 2
其中 x Rn , A是对称正定矩阵,b Rn,c 是常数。
基本思想:将共轭性和最速下降方向相结合,利用已知迭 代点 处的梯度方向构造一组共轭方向,并沿此方向进行搜索,求出 函数的极小点。
3. 用于一般函数的共轭梯度法
min f ( x) s.t. x Rn
对用于正定二次函数的共轭梯度法进行修改:
(1) 第一个搜索方向仍取最速下降方向,即d (1) f ( x(1) )。
其它搜索方向按下式计算:
d (i1) f ( x(i1) ) i d (i) ,
(
8)2 9
82
(16)2 9
42
4 81
.
d (2) g2 1 d (1)
( 8 , 16 )T 4 ( 8, 4 )T
99
81
40 (1, 4 )T 81
2
g2T d (2) d (2)T Ad (2)
40 8 16 1
( 81
9
, 9 ) 4
9
(
40 81
)2
(
1
,
4
)
4 0
0 1 2 4
20
x(3) x(2) 2 d (2)
( 2 , 8 )T 9 40 (1, 4 )T 9 9 20 81
( 0,0 )T
g3 ( 0, 0 )T x(3)即为所求极小点。
(4) 由定理3,FR算法中i的计算公式可以简化。
i
d (i)T A gi1 d (i)T Ad (i)
gi
T 1
A
d
(i)
d (i)T Ad (i)
gi
T 1
A[ (
x ( i 1)
x(i)
)/
i ]
d (i)T A[( x(i1) x(i) ) / i ]
gi f ( x(i) ) A x(i) b .
i
gi
T 1
(
gi1
gi
)
d (i)T ( gi1 gi )
||
gi1 ||2 d (i)T gi
|| gi1 ||2 || gi |Байду номын сангаас2
(4)
FR算法步骤:
1. 任取初始点x(1) ,精度要求 ,令k 1。 2. 令g1 f ( x(1) ),若 || g1 || ,停止,x(1)为所求极小点;
(1)
如何确定 k?
要求d (k1) 和d (k) 关于 A共轭。
则在(1)式两边同时左乘d (k)T A,得
0 d (k)T Ad (k1) d (k)T Agk1 k d (k)T Ad (k)
解得
k
d (k)T A gk1 d (k)T Ad (k)
(2)
(3) 搜索步长的确定 :
令 gk f ( x(k) ) Ax(k) b,则有
解得
[ gk Ad (k) ]T d (k) 0,
k
d
gkT
(k )T
d (k Ad
) (k
)
(3)
定理 3 对于正定二次函数 f ( x) 1 xT Ax bT x c,FR算法在m n次 2
一维搜索后即终止,并且对所有的 (i 1 i m),下列关系成立 (1) d (i)T Ad ( j) 0, j 1, 2,, i 1; (2) giT g j 0, j 1, 2,, i 1; (3) giT d (i) giT gi 。
