八年级数学等腰三角形专项练习
八年级上册《数学》三角形专项练习题(含答案)

八年级上册《数学》三角形专项练习题11.1.1三角形的边一、能力提升1.如图,在图形中,三角形有()A.4个B.5个C.6个D.7个2.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为()A.2B.3C.5D.133.若一个三角形的两条边长分别为3和8,而第三条边长为奇数,则第三条边长为()A.5或7B.7C.9D.7或94.在△ABC中,若三条边长均为整数,周长为11,且有一条边长为4,则这个三角形最长边可能取值的最大值是()A.7B.6C.5D.45.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC 为公共边的“共边三角形”有对.6.若等腰三角形的腰长为6,则它的底边长a的取值范围是.7.用7根相同的火柴棒首尾顺次连接摆成一个三角形,能摆成的不同的三角形的个数为.8.已知等腰三角形的两边长分别为3cm和7cm,求这个三角形的周长.9.已知等腰三角形的周长是16cm.(1)若其中一边的长为4cm,求另外两边的长;(2)若其中一边的长为6cm,求另外两边的长.10.若a,b,c是△ABC的三边长,请化简|a-b-c|+|b-c-a|+|c-a-b|.11.已知等腰三角形的周长为20cm,设腰长为xcm.(1)用含x的式子表示底边长.(2)腰长x能否为5cm,为什么?(3)求x的取值范围.二、创新应用12.在平面内,分别用3根、5根、6根、…小棒首尾依次相接,能搭成什么形状的三角形?通过尝试,形状如表所示.小棒数目3 5 6 ……示意图……形状等边三角形等腰三角形等边三角形……(1)4根小棒能搭成三角形吗?(2)8根、12根小棒能搭成几种不同形状的三角形?并画出它们的示意图.答案一、能力提升1.B2.B;由题意知2+x>13,且x<13+2,解得11<x<15,因为x为正整数,所以x 可以是12,13,14.故选B.3.D;由题意知第三条边长大于5小于11.因为第三条边长为奇数,所以它的大小为7或9.4.C由题意知三角形的三条边长分别为2,4,5或3,4,4,所以最长边可能取值的最大值为5.5.3;△BDC与△BEC,△BDC与△BAC,△BEC与△BAC,共3对.6.0<a<12.7.2.8.解:若腰长为3cm,则三边长分别为3cm,3cm,7cm,而3+3<7,此时不能构成三角形;若腰长为7cm,则三边长分别为3cm,7cm,7cm.此时能构成三角形,其周长为3+7+7=17(cm).故这个三角形的周长为17cm. 9.解:(1)若腰长为4cm,则底边长为16-4-4=8(cm).三边长分别为4cm,4cm,8cm,不符合三角形的三边关系,所以应该是底边长为4cm.所以腰长为(16-4)÷2=6(cm).三边长分别为4cm,6cm,6cm,符合三角形的三边关系.所以另外两边的长都为6cm.(2)若腰长为6cm,则底边长为16-6-6=4(cm).三边长分别为4cm,6cm,6cm,符合三角形的三边关系.所以另外两边的长分别为6cm 和4cm.若底边长为6cm,则腰长为(16-6)÷2=5(cm).三边长分别为6cm,5cm,5cm,符合三角形的三边关系.所以另外两边的长都为5cm.10.解:因为a,b,c是△ABC的三边长,所以a<b+c,b<c+a,c<a+b,即a-b-c<0,b-c-a<0,c-a-b<0.所以|a-b-c|+|b-c-a|+|c-a-b|=-(a-b-c)-(b-c-a)-(c-a-b)=a+b+c.11.解:(1)底边长为(20-2x)cm.(2)不能.理由如下:若腰长为5cm,则底边长为20-2×5=10(cm).因为5+5=10,不满足三角形的三边关系.所以腰长不能为5cm.(3)根据题意,得解得0<x<10.由三角形的三边关系,得x+x>20-2x,解得x>5.综上所述,x的取值范围是5<x<10.二、创新应用12.解:(1)4根小棒不能搭成三角形.(2)8根小棒能搭成一种三角形,示意图如图甲;12根小棒能搭成三种不同形状的三角形,示意图如图乙.11.1.2三角形的高、中线与角平分线一、能力提升1.若一个三角形中仅有一条高在三角形的内部,则该三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.直角三角形或钝角三角形2.如图,AE⊥BC于点E,BF⊥AC于点F,CD⊥AB于点D.在△ABC中,边AC上的高是线段()A.AEB.CDC.BFD.AF3.如图,线段AE是△ABC的中线,已知EC=6,DE=2,则线段BD的长为()A.2B.3C.4D.64.如图,在△ABC中,∠C=90°,D,E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是()A.线段BC是△ABE的高B.线段BE是△ABD的中线C.线段BD是△EBC的角平分线D.∠ABE=∠EBD=∠DBC5.如图,在△ABC中,E,F分别是AB,AC的中点,△CEF的面积为2.5,则△ABC的面积为()A.6B.7C.8D.106.如图,BD和CE是△ABC的两条角平分线,且∠DBC=∠ECB=31°,则∠ABC=度,∠ACB=度.7.如图,线段AD,CE分别是△ABC中边BC,AB上的高.若AD=10,CE=9,AB=12,则BC的长是.8.如图,在△ABC中,AB=AC,线段AD是△ABC的中线,△ABC的周长为34cm,△ABD的周长为30cm,求AD的长.9.已知在等腰三角形ABC中,AB=AC,若腰AC上的中线BD将等腰三角形ABC的周长分成15和6两部分,求三角形ABC的腰长及底边长.10.如图,AD是△CAB的角平分线,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是△EDF的角平分线吗?如果是,请给予证明;如果不是,请说明理由.二、创新应用11.有一块三角形优良品种试验基地,如图,由于引进四个优良品种进行对比试验,需将这块土地分成面积相等的四块,请你制定出两种以上的划分方案供选择.(画图即可)答案一、能力提升1.D;直角三角形和钝角三角形都只有一条高在三角形的内部.2.C3.C4.D5.D;∵F为AC的中点,∴线段EF为△AEC的中线,∴S△AEC=2S△CEF=5.∵E为AB的中点,∴线段CE为△ABC的中线,∴S△ABC=2S△AEC=10.6.62;62.7.10.8;S△ABC=BC·AD=AB·CE,则BC===10.8.8.解:∵线段AD是△ABC的中线,∴BC=2BD.∵AB=AC,△ABC的周长为34cm,∴2AB+2BD=34cm,即AB+BD=17cm.又△ABD的周长为30cm,即AB+BD+AD=30cm,∴AD=13cm.9.解:设AB=AC=2x,则AD=CD=x.当AB+AD=15,BC+CD=6时,有2x+x=15,所以x=5,AB=AC=2x=10,BC=6-5=1.当BC+CD=15,AB+AD=6时,有2x+x=6,所以x=2,AB=AC=2x=4,BC=13.因为4+4<13,所以不能组成三角形.故三角形ABC的腰长为10,底边长为1.10.解:DO是△EDF的角平分线.证明如下:∵AD是△CAB的角平分线,∴∠EAD=∠FAD.∵DE∥AB,DF∥AC,∴∠EDA=∠FAD,∠FDA=∠EAD.∴∠EDA=∠FDA,即DO是△EDF的角平分线.二、创新应用11.解:如图(答案不唯一).11.1.3三角形的稳定性一、能力提升1.如图,桥梁的斜拉钢索是三角形的结构,主要是为了()A.节省材料,节约成本B.保持对称C.利用三角形的稳定性D.美观漂亮2.下列不是利用三角形稳定性的是()A.伸缩晾衣架B.三角形房架C.自行车的三角形车架D.矩形门框的斜拉条3.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短4.王师傅用四根木条钉成一个四边形木架.如图,要使这个木架不变形,他至少还要再钉上()根木条.A.0B.1C.2D.35.如图,要使四边形木条框架ABCD变“活”(具有不稳定性),应将木条拆除.6.伸缩铁门能自由伸缩,主要是应用了四边形的.7.我们所用的课桌和所坐的凳子,时间长了总是摇摇晃晃的,这是什么原因?要使自己用的桌凳不晃动应该怎么办?如图,如果有六边形木框,要使它不变形,应该怎么办?二、创新应用8.如图,我们知道要使四边形木架不变形,至少要钉一根木条.那么要使五边形木架不变形,至少要钉几根木条?要使七边形木架不变形,至少要钉几根木条?要使n边形木架不变形,又至少要钉多少根木条呢?答案一、能力提升1.C.2.A.3.A;打开的那一扇窗户下边的一部分OB、窗户框下边的一部分OA 及AB组成一个三角形,根据三角形的稳定性,知可用AB固定窗户.4.B.5.AC.6.不稳定性.7.解:这是因为课桌和凳子的四个侧面都是四边形木架,当交接处松动后就具有不稳定性.解决这类问题的方法是在每个侧面加上一根木条(或木板),使之成为三角形.要使六边形木框不变形,至少应加3根木条使其划分为三角形.二、创新应用8.解:要使五边形木架不变形,至少要钉2根木条;要使七边形木架不变形,至少要钉4根木条;要使n边形木架不变形,至少要钉(n-3)根木条.11.2.1三角形的内角一、能力提升1.在△ABC中,∠A=55°,∠B比∠C大25°,则∠B的度数为()A.50°B.75°C.100°D.125°2.如图,CD∥AB,∠1=120°,∠2=80°,则∠E等于()A.40°B.60°C.80°D.120°3.(2020·辽宁锦州中考)如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是()A.80°B.90°C.100°D.110°4.在△ABC中,若∠A=∠B+∠C,则∠A的度数是.5.如图,点B,C,D在同一条直线上,CE∥AB,∠ACB=90°.如果∠ECD=36°,那么∠A的度数是.6.如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2的度数是.7.在△ABC中,若最大角∠A等于最小角∠C的两倍,最大角又比另一个角大20°,则△ABC的三个角的度数分别是多少?8.如图,E是△ABC中边AC上的一点,过点E作ED⊥AB,垂足为D.若∠1=∠2,则△ABC是直角三角形吗?为什么?9.如图,在△ABC中,D是BC上一点,F是BA延长线上一点,连接DF交AC于点E,且∠B=42°,∠C=59°,∠DEC=47°,求∠F的度数.二、创新应用10.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点D.(1)若∠ABC+∠ACB=110°,则∠BDC=;(2)若∠A=100°,则∠BDC=;(3)若∠A=n°,求∠BDC的度数.答案一、能力提升1.B;设∠C的度数为x°,则∠B的度数为x°+25°,则55°+x°+x°+25°=180°,解得x=50,则∠B=75°.2.A;∵CD∥AB,∠1=120°,∴∠CDB=∠1=120°,∴∠EDC=60°.∵∠2=80°,∴∠E=180°-80°-60°=40°.3.C∵∠A=30°,∠B=50°,∴∠ACB=180°-∠A-∠B=100°.又CD平分∠ACB,∴∠ACD=∠ACB=50°.∴∠ADC=180°-∠A-∠ACD=100°.4.90°.5.54°.6.270°.由三角形三内角之间的关系,得∠3+∠4=90°,所以∠1+∠2=(180°-∠3)+(180°-∠4)=2×180°-(∠3+∠4)=360°-90°=270°.7.解:设∠C=x°,则∠A=2x°,∠B=2x°-20°,根据三角形的内角和定理,有2x+(2x-20)+x=180,解得x=40,即∠C=40°.所以2x=80,∠A=80°,2x-20=60,∠B=60°.故△ABC的三个角的度数分别为∠A=80°,∠B=60°,∠C=40°.8.解:△ABC是直角三角形.理由如下:∵ED⊥AB,∴∠ADE=90°,∴∠1+∠A=90°.又∠1=∠2,∴∠2+∠A=90°.∴△ABC是直角三角形.9.解:在△EDC中,∠EDC=180°-(∠C+∠DEC)=180°-(59°+47°)=74°.∴∠FDB=180°-∠EDC=180°-74°=106°.在△BDF中,∠F=180°-(∠B+∠FDB)=180°-(42°+106°)=32°.二、创新应用10.解:(1)125°.(2)140°.(3)∵∠A=n°,∴∠ABC+∠ACB=180°-n°.∵BD平分∠ABC,CD平分∠ACB,∴∠DBC+∠DCB=∠ABC+∠ACB=(∠ABC+∠ACB)=×(180°-n°)=90°-.∴∠BDC=180°-(∠DBC+∠DCB)=180°-=90°+.11.2.2三角形的外角一、能力提升1.一副三角尺有两个直角三角形,如图叠放在一起,则∠α的度数是()A.165°B.120°C.150°D.135°2.如图,在△ABC中,AD为边BC上的中线,在△ABD中,AE为边BD上的中线,在△ACD中,AF为边DC上的中线,则下列结论错误的是()A.∠1>∠2>∠3>∠CB.BE=ED=DF=FCC.∠1>∠4>∠5>∠CD.∠1=∠3+∠4+∠53.如图,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于()A.120°B.115°C.110°D.105°4.(2020·湖北中考)将一副三角尺按如图摆放,点E在AC上,点D在BC 的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是()A.15°B.20°C.25°D.30°5.如图,∠ABC的平分线与∠ACD的平分线相交于点P.若∠A=60°,则∠P等于()A.30°B.40°C.50°D.60°6.(2020·湖北黄冈中考)如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD=.7.如图,已知在△ABC中,D是AB上一点,E是AC上一点,BE与CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°,则∠BDC=,∠BFC=.8.如图,D,E,F分别是△ABC三边延长线上的点,求∠D+∠E+∠F+∠1+∠2+∠3的度数.9.如图,在△ABC中,E是AC延长线上的一点,D是BC上的一点.求证:(1)∠BDE=∠E+∠A+∠B.(2)∠BDE>∠A.10.如图,在△ABC中,D是边BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.二、创新应用11.如图①,有一个五角形图案ABCDE,你能说明∠A+∠DBE+∠C+∠D+∠E=180°吗?如果点B向下移动到AC上(如图②)或AC的另一侧(如图③),上述结论是否依然成立?请说明理由.答案一、能力提升1.A如图,∵∠2=90°-45°=45°,∴∠1=∠2-30°=15°.∴∠α=180°-∠1=165°.2.C由三角形的一个外角大于与它不相邻的内角,知∠1>∠2>∠3>∠C,故选项A正确;根据三角形中线的定义,知BE=ED=DF=FC,故选项B正确;∠4与∠5的大小不能判定,故选项C错误;根据三角形的一个外角等于与它不相邻两个内角的和,知∠1=∠2+∠4,∠2=∠3+∠5,所以∠1=∠3+∠4+∠5,故选项D正确.3.B4.A5.A利用三角形的外角性质,得∠P=∠PCD-∠PBD=(∠ACD-∠ABC)=∠A=30°.6.30°.7.97°;117°.8.解:∵∠D+∠3=∠CAB,∠E+∠1=∠ABC,∠F+∠2=∠ACB,∴∠D+∠E+∠F+∠1+∠2+∠3=∠CAB+∠ABC+∠ACB=180°.9.证明:(1)∵∠BDE,∠DCE分别是△CDE,△ABC的一个外角,∴∠BDE=∠E+∠DCE,∠DCE=∠A+∠B,∴∠BDE=∠E+∠A+∠B.(2)由(1)得∠BDE=∠E+∠A+∠B,∴∠BDE>∠A.10.解:∵∠3是△ABD的外角,∴∠3=∠1+∠2.∵∠1=∠2,∠3=∠4,∴∠4=2∠2.在△ABC中,∵∠2+∠4=180°-∠BAC=180°-63°=117°,∴∠1=∠2=117°÷(1+2)=39°.∴∠DAC=∠BAC-∠1=63°-39°=24°.二、创新应用11.解:在题图①中,∠A+∠C=∠DNM, ①∠DBE+∠E=∠DMN, ②①+②,得∠A+∠DBE+∠C+∠E=∠DNM+∠DMN.∵∠D+∠DNM+∠DMN=180°,∴∠A+∠DBE+∠C+∠D+∠E=180°.在题图②、题图③中,上述结论仍然成立,理由与题图①完全相同.11.3.1多边形一、能力提升1.在下列关于正多边形的特征说法中,错误的是()A.每一条边都相等B.每一个内角都相等C.每一个外角都相等D.所有对角线都相等2.过多边形的一个顶点可以引2017条对角线,则这个多边形的边数是()A.2017B.2018C.2019D.20203.如果过多边形的一个顶点的对角线把多边形分成8个三角形,那么这个多边形的边数为()A.8B.9C.10D.114.将一个四边形截去一个角后,它不可能是()A.三角形B.四边形C.五边形D.六边形5.在n边形的一边上任取一点(不包含顶点)与各顶点相连,可得三角形的个数是()A.nB.n-2C.n-1D.n+16.过m边形的一个顶点有7条对角线,n边形没有对角线,则m n=.7.已知一个多边形的边数恰好是从这个多边形的一个顶点出发所作的对角线的条数的2倍,求此多边形的边数.二、创新应用8.观察下面图形,解答下列问题:(1)在上面第四个图中画出六边形的所有对角线;(2)观察规律,把下表填写完整.边数 3 4 5 6 7 …n对角线条0 2 5 …数答案一、能力提升1.D2.D3.C4.D一个多边形截去一个角后,可能出现三种情况:少一个角、角的个数不变或多一个角.5.C6.1000;从m边形的一个顶点出发有(m-3)条对角线,由m-3=7,得m=10. n边形没有对角线,所以n=3.所以m n=103=1000.7.解:设这个多边形的边数为n,则从多边形的一个顶点出发所作的对角线的条数为n-3.依题意,得n=2(n-3),解得n=6.二、创新应用8.解:(1)(2)边数 3 4 5 6 7 …n对角线条数0 2 5 9 14 …n(n-3)11.3.2多边形的内角和一、能力提升1.如果一个正多边形的每一个外角都是锐角,那么这个正多边形的边数一定不小于()A.3B.4C.5D.62.(2020·山东济宁中考)一个多边形的内角和是1080°,则这个多边形的边数是()A.9B.8C.7D.63.若一个多边形的边数由5增加到11,则内角和增加的度数是()A.1080°B.720°C.540°D.360°4.如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是()A.110°B.108°C.105°D.100°5.如果一个多边形的内角和是其外角和的一半,那么这个多边形是()A.六边形B.五边形C.四边形D.三角形6.若凸n边形的内角和为1260°,则从一个顶点出发引的对角线条数是.7.如图,在四边形ABCD中,∠A+∠B=210°,且∠ADC的平分线与∠DCB的平分线相交于点O,则∠COD的度数是.8.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和内角和.9.如图,求∠A+∠B+∠OCD+∠ODC+∠E+∠F的度数.二、创新应用10.在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.(1)如果这个多边形是五边形,请求出这个外角的度数;(2)是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.答案一、能力提升1.C每个外角都是锐角,即小于90°,设边数为n,则这些锐角的和一定小于n×90°.而外角和为360°,所以360°<n×90°,n>4,即n不小于5.2.B设这个多边形的边数是n,则(n-2)×180°=1080°,解得n=8.3.A因为每增加一条边,内角和增加180°,所以增加6条边,内角和增加180°×6=1080°.4.D由题意知∠AED的补角为80°,则∠AED=100°.5.D多边形的外角和是360°,内角和等于外角和的一半,则内角和是180°,可知此多边形为三角形.6.6因为凸n边形的内角和为1260°,所以(n-2)×180°=1260°,得n=9.故从一个顶点出发引的对角线的条数为9-3=6.7.105°∵四边形的内角和为360°,∠A+∠B=210°,∴∠ADC+∠BCD=360°-210°=150°.∵DO,CO分别为∠ADC与∠BCD的平分线,∴∠ODC=∠ADC,∠OCD=∠BCD.∴∠ODC+∠OCD=(∠ADC+∠BCD)=×150°=75°.∴∠COD=180°-75°=105°.8.解:由题意知这个多边形的内角和为3×360°-180°=900°.设这个多边形的边数为n,根据题意,得(n-2)×180°=900°,解得n=7.故这个多边形的边数为7.9.解:如图,连接BE,则在△COD与△BOE中,∠ODC+∠OCD+∠COD=180°,∠OBE+∠OEB+∠BOE=180°.∵∠COD与∠BOE是对顶角,∴∠COD=∠BOE.∵∠ODC+∠OCD=180°-∠COD,∠OBE+∠OEB=180°-∠BOE,∴∠ODC+∠OCD=∠OBE+∠OEB.∴题图中的∠A+∠B+∠OCD+∠ODC+∠E+∠F等于上图中的∠A+∠F+∠ABC+∠DEF+∠OBE+∠OEB=∠A+∠F+∠ABE+∠BEF=360°,即所求六个角的和为360°.二、创新应用10.解:(1)设这个外角的度数是x°,则(5-2)×180-(180-x)+x=600,解得x=120.故这个外角的度数是120°.(2)存在.设边数为n,这个外角的度数是x°,则(n-2)×180-(180-x)+x=600,整理得x=570-90n.因为0<x<180,即0<570-90n<180,并且n为正整数,所以n=5或n=6.故这个多边形的边数是6,这个外角的度数为30°.。
初二数学上册第二单元等腰三角形专项练习题

初二数学上册第二单元等腰三角形专项练习题篇一:初二数学上册第二单元等腰三角形专项练习题初二数学上册第二单元等腰三角形专项练习题一、选择题1已知一个等腰三角形的底边长为5,这个等腰三形的腰长为_,则_的取值范围是() A .0_lt;__lt;52B ._≥52C _>52D 0_lt;__lt;10 2.等腰三角形的底角为15°,腰长为a,则此三角形的面积为()A a2B1a22C 1 a2 D2 a2图543将一张长方形的纸片ABCD如图(4)那样折起,使顶点C落在F处.其中AB=4,若∠FED=30°,则折痕ED的长为( )A. 4 B 4C 8D 53 10.如图(5),在△ABC中,BC=8㎝,AB的垂直平分线交AB于点D,交AC于点E, △ABC的周长为18㎝,则AC的长等于( )A 6㎝B 8㎝C 10㎝D 12㎝4下列图形中,不是轴对称图形的是() A有两个内角相等的三角形 B 有一个内角是45°直角三角形 C. 有一个内角是30°的直角三角形 D. 有两个角分别是30°和120°的三角形 5、下列图形中,轴对称图形有()个A.1B.2C. 3D.4 6、等腰三角形周长是29,其中一边是7,则等腰三角形的底边长是() A 15B15或7 C 7 D 11 7、在△ABC中,AB=AC,BD平分∠ABC,若∠BDC=75°,则∠A的度数为()A、30°B、40°C、45 °D、60°8、下列图形中,不是轴对称图形的是() A 角 B 等边三角形 C 线段 D不等边三角形9、正△ABC的两条角平分线BD和CE交于点I,则∠BICAADFDBB为() A.60 B.90 C.120 D.150° 10、下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;?③三个外角(每个顶点处各取一个外角)都相等的三角形;?④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有()A①②③ B①②④ C①③ D①②③④ 11、如图1,D、E、F分别是等边△ABC各边上的点,且AD=BE=CF,则△DEF?的形状是()A形C.直角 D.不等边三角形 12Rt△ABC中,CD是斜边AB上的高,∠图5B=30°, AD=2cm,则AB的长度是()A.2cm B.4cm C.8cm D.16cm 13如图2,E是等边△ABC中AC边上的点,∠1= 2,BE=CD,则对△ADE的形状判断准确的是() A.等腰三角形B.等边三角形 C.不等边三角形 D.不能确定形状图(1) 图(2)二、填空题1、△ABC中,AB=AC,∠A=∠C,则∠B=_______.2、已知AD是等边△ABC的高,BE是AC边的中线,AD与BE交于点F,则∠AFE=______.3、△ABC中,∠B=∠C=15°,AB=2cm,CD⊥AB交BA的延长线于点D,?则CD?的长度是_______.4、如图(3),在ΔABC中AB=AC,∠A=36°,BD平分∠ABC,则∠1=________, 图中有_______个等腰三角形。
苏科版八年级数学上册《2.5等腰三角形的轴对称性》同步练习题-带答案

苏科版八年级数学上册《2.5等腰三角形的轴对称性》同步练习题-带答案一、单选题1.如图,在Rt△ABC 中,△ACB =90°,△CAB=36°,以C 为原点,C 所在直线为y 轴,BC 所在直线为x 轴建立平面直角坐标系 ,在坐标轴上取一点M 使△MAB 为等腰三角形,符合条件的 M 点有( )A .6个B .7个C .8个D .9个2.如图,等腰△ABC ,AB=AC ,∠BAC=120°,AD ⊥BC 于点D .点P 是BA 延长线上一点,O 点是线段AD 上一点,OP=OC ,下面的结论:△AC 平分△PAD ;△△APO=△DCO ;△△OPC 是等边三角形;△AC=AO+AP.其中正确结论的个数为( )A .4B .3C .2D .13.如图,在四边形ABCD 中,△BAD =△BCD =90°,△ADC =45°,BD =2a ,E 为BD 中点,给出下列结论:△AE =a , △△CAE =45°,△AC = 2a ,△取AC 的中点F , 则EF △AC , 其中正确的个数是( )A .1个B .2个C .3个D .4个4.如图,在ABC 中,AB=AC ,分别以点A 、点B 为圆心,以大于12AB 长为半径画弧,两弧交点的连线交AC 于点D ,交AB 于点E ,连接BD ,若40A ∠=︒,则DBC ∠=( )A.40︒B.50︒C.20︒D.30︒∠的度数为()5.如图,ABC中,已知AB AC=,DE垂直平分AC,40∠=︒则BCDAA.15︒B.30︒C.50︒D.65︒6.已知A和B两点在线段EF的中垂线上,且△EBF=100°,△EAF=70°,则△AEB等于() A.95°B.15°C.95°或15°D.170°或30°7.等腰三角形的顶角是50°,则它的底角是()A.65°B.80°C.50°或65°D.50°或80°8.已知等腰三角形的一个内角是50︒,则这个三角形顶角的度数是()A.130︒B.50︒C.80︒D.50︒或80︒⊥于D点,点E、F分别是AD的三等分点,若ABC的面积为9.如图,在ABC中,AB=AC,AD BC18,则图中阴影部分面积为()A.6B.8C.9D.10∠,若AB=m,10.如图,ABC中,∠B=2∠C,AD是BC边上的高,E是BA延长线上一点,AC平分DAEBC=p,BD=q,则下列等式一定成立的是()A .m q p +=B .2m q p +=C .2m q p +=D .12q m p +=二、填空题11.在等边三角形ABC 中,点E 在直线AB 上,点D 在直线BC 上,且ED =EC ,若三角形ABC 的边长为1,AE =2,则CD 的长为 .12.若等腰三角形的周长为30cm ,一边长为6cm ,则腰长为 .13.如图,CA 1是等腰Rt △ABC 斜边AB 上的高,以CA 1为直角边构造等腰Rt △CA 1B 1(点C ,A 1,B 1按顺时针方向排列),△A 1CB 1=90°,称为第一次构造;CA 2是Rt △CA 1B 1斜边上的高,再以CA 2为直角边构造等腰Rt △CA 2B 2(点C ,A 2,B 2按顺时针方向排列),△A 2CB 2=90°,称为第二次构造…,以此类推,当第n 次构造的Rt △CAnBn 的边CBn 与△ABC 的边CB 第二次重合时,构造停止,若S △ABC =1,则构造出的最后一个三角形的面积为 .14.等腰三角形的一个角的度数是36︒,则它的底角的度数是 .15.如图,在ABC 中,AB=AC ,AD 是BC 边上的中线,ABC ∠的平分线交AD 于点E ,EF AB ⊥于点F ,若5EF =,则ED 的长度为 .三、解答题16.已知等腰三角形的周长为15cm ,一腰上的中线把等腰三角形分成周长之差为3cm 的两个三角形,求等腰三角形的腰长.17.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒,OA OB 组成,两根棒在O 点相连并可绕O 转动、C 点固定OC CD DE ==点D E 、可在槽中滑动.若75BDE ∠=︒,请求出CDE ∠的度数.18.(1)如图1,在四边形ABCD 中,AD//BC ,G 为CD 上一点,连接AG ,BG .△若AG 平分DAB ∠,BG 平分ABC ∠,求AGB ∠的度数;△若90ABC ∠=︒,AD+BC=AB ,G 为CD 中点,求证:ABG 为等腰直角三角形;(2)某工程队需要在A ,B 两棵树的前方建立一座八角亭.按如下方法选址:如图2,甲工人从C 点直走到树A 处,然后向右转90后再直走一段路等于AC 的长度到点D 处;乙工人从C 点直走到树B 处,然后向左转90后再直走一段路等于BC 的长度到点E 处.工程队队长打算把八角亭建在DE 的中点G 处.过几天,工程队带着建筑材料来施工,却发现忘记标记起始点C ,正当大家懊恼时,队长说:别急,只要找到A ,B 两棵树连线的中点F ,由点F 引AB 的垂线,再往A ,B 两棵树前方量出AB 的长度的一半,就能找到之前的G 点(如图3所示).你觉得队长的方法对吗?为什么?19.如图,一条船上午6时从海岛A 出发,以15海里/时的速度向正北方向航行,上午8时到达海岛B 处,分别从A ,B 处望灯塔C ,测得30NAC ∠=︒ 60NBC ∠=︒.(1)求海岛B到灯塔C的距离;(2)若这条船继续向正北航行,问上午几时小船与灯塔C的距离最短?20.某中学八年级学生到野外开展数学综合实践活动,在营地看到一个不规则的建筑物,为测量该建筑物两端A,B间的距离,但同学们给出了以下建议:(1)甲同学的方案如下:先在平地上取一个可直接到达A,B的点O,连接AO,BO,并分别延长AO至点C,,DO=BO,最后测出CD的长即为A,B间的距离,请你说说该方案可行的理延长BO至点D,使CO AO由;(2)由于在EF处有一堵墙阻挡了路线,使得无法按照甲同学的方案直接测量出A,B间的距离,但同学们测得∠EOC=65°,∠C=80°,∠OEF=145°,CF=127m,EF=78m,请求出该建筑物两端A,B之间的距离.参考答案1.C2.B3.D4.D5.B6.C7.A8.D9.C10.B11.1或3/3或112.12cm13.1612 14.36︒或72°15.516.4cm 或6cm17.80︒18.(1)△90︒△略;(2)队长说法正确,略 19.(1)海岛B 到灯塔C 的距离为30海里(2)上午9时小船与灯塔C 的距离最短 20.(1)甲同学的方案可行;略(2)该建筑物两端A ,B 之间的距离为205m .。
八年级数学 等腰三角形与直角三角形专项习题(含答案)

1.已知等腰三角形的两边长是4cm 和9cm ,则此三角形的周长是()A .17cm B .13cmC .22cmD .17cm 或22cm 2.等腰三角形一腰上的高与另一腰的夹角为60°,则等腰三角形的底角度数为()A .15°B .30°C .15°或75°D .30°或150°3.如图,在Rt △ABC中,∠C =90°,AB =10,BC =6.点F 是边BC 上一动点,过点F 作FD∥AB 交AC 于点D ,E 为线段DF 的中点,当BE 平分∠ABC 时,AD 的长度为.4.如图,在△ABC 中,∠ACB =90°,点D 、E 、F 分别是AB 、BC 、CA 的中点.若CD =2,则线段EF 的长是.八年级数学等腰三角形与直角三角形专项习题(含答案)5.(有难度)在Rt△ABC中,∠C=90°,有一个锐角为60°,AB=6,若点P在直线AB上(不与点A,B重合),且∠PCB=30°,则AP的长为.6.如图所示,△ABC中,AB=BC,DF⊥BC于点D,交AC于F,DE⊥AB于点E.⑴若∠AFD=155°,求∠EDF的度数;⑵若点F是AC的中点,求证:∠CFD=1∠B.1.解:①4cm 是腰长时,三角形的三边分别为4cm 、4cm 、9cm ,∵4+4=8<9,∴不能组成三角形;②4cm 是底边时,三角形的三边分别为4cm 、9cm 、9cm ,能够组成三角形,周长=4+9+9=22cm ,综上所述,三角形的周长22cm .故选:C .2.解:在等腰△ABC 中,AB =AC ,BD 为腰AC 上的高,∠ABD =60°,当BD 在△ABC 内部时,如图1,∵BD 为高,∴∠ADB =90°,∴∠BAD =90°-60°=30°,∵AB =AC ,∴∠ABC =∠ACB =12(180°-30°)=75°;当BD 在△ABC 外部时,如图2,∵BD 为高,∴∠ADB =90°,∴∠BAD =90°-60°=30°,∵AB =AC ,∴∠ABC =∠ACB ,而∠BAD =∠ABC +∠ACB ,∴∠ACB =12∠BAD =15°,综上所述,这个等腰三角形底角的度数为75°或15°.故选:C .3.解:设AD =x ,∵∠C =90°,AB =10,BC =6,∴AC ==8,∴CD =8-x ,∵DF ∥AB ,∴AD :AC =BF :BC ,∴x :8=BF :6,∴BF =34x ,∵BF 平分∠ABC ,∴∠FBE =∠ABE ,∵FD ∥AB ,∴∠FEB =∠ABE,∴∠FBE =∠FEB,∴FE =BF,∵E 是FD 中点,∴DF =2EF ,答案解析4.解:∵Rt△ABC中,∠ACB=90°,D是AB的中点,即CD是直角三角形斜边上的中线,∴AB=2CD=2×2=4,又∵E、F分别是BC、CA的中点,即EF是△ABC的中位线,∴EF=12AB=12×2=2,故答案为:2.5.解:当∠A=30°时,∵∠C=90°,∠A=30°,∴∠CBA=60°,BC=AB=×6=3,由勾股定理得,AC=3,①点P在线段AB上,∵∠PCB=30°,∠CBA=60°∴∠CPB=90°,∴∠CPA=90°,在Rt△ACP中,∠A=30°,∴PC=AC=×3=.∴在Rt△APC中,由勾股定理得AP=.②点P在线段AB的延长线上,∵∠PCB=30°,∴∠APC=90°+30°=120°,∵∠A=30°,∴∠CPA=30°.∵∠PCB=30°,∴∠PCB=∠CPA,∴BP=BC=3,∴AP=AB+BP=6+3=9.当∠ABC=30°时,∵∠C=90°,∠ABC=30°,∴∠A=60°,AC=AB=×6=3,由勾股定理得,BC=3,①点P在线段AB上,∵∠PCB=30°,∴∠ACP=60°,∴△ACP是等边三角形,∴AP=AC=3.②点P在线段AB的延长线上,∵∠PCB=30°,∠ABC=30°,∴CP∥AP这与CP与AP交于点P矛盾,舍去.综上所得,AP的长为,9或3.故答案为:,9或3.6.解:⑴∵∠AFD=155°,∴∠DFC=25°,∵DF⊥BC,DE⊥AB,∴∠FDC=∠AED=90°,在Rt△FDC中,∴∠C=90°-25°=65°,∵AB=BC,∴∠C=∠A=65°,∴∠EDF=360°-65°-155°-90°=50°.⑵连接BF,∵AB=BC,且点F是AC的中点,∴BF⊥AC,∠ABF=∠CBF=12∠ABC,∴∠CFD+∠BFD=90°,∠CBF+∠BFD=90°,∴∠CFD=∠CBF,∴∠CFD=12∠ABC.。
专题13.4等腰三角形【十大题型】-2024-2025学年八年级数学上册举一反三系[含答案]
![专题13.4等腰三角形【十大题型】-2024-2025学年八年级数学上册举一反三系[含答案]](https://img.taocdn.com/s3/m/ca6a144e53d380eb6294dd88d0d233d4b14e3f0d.png)
试卷第 11 页,共 15 页
(1)求证: VBEC 是等腰三角形;
(2)用等式表示线段 AB、AC、BD 之间的数量关系,并证明.
②若 ÐCMD = 30° , CD = 3 ,求 V BCM 的周长;
(2)若 BC = 8 ,且 V ABC 的面积为 40,求 VCDM 周长的最小值.
【题型 4 利用三线合一证明】
【例 4】
(23-24 八年级·辽宁锦州·期中)
13.如图,在 V ABC 中, AD 是 BC 边上的高线, CE 是中线,且 DG ^ CE 于 G ,
PA、PB、PC ,则图中有
个等腰三角形.
【变式 6-2】
(23-24 八年级·吉林白山·期中)
23.如图,在四边形 ABCD 中, AD ∥ BC , AB = CD , ÐBDC = ÐBCD ,点 E 是线段 BD
上一点,且 BE = AD .
(1)求证: △ADB≌Байду номын сангаасEBC ;
(2)直接写出图中所有的等腰三角形.
专题 13.4 等腰三角形【十大题型】
【华东师大版】
【题型 1 利用等边对等角求解】
【题型 2 利用等边对等角进行证明】
【题型 3 利用三线合一求解】
【题型 4 利用三线合一证明】
【题型 5 格点中画等腰三角形】
【题型 6 找出图中的等腰三角形】
【题型 7 利用等角对等边证明等腰三角形】
【题型 8 利用等角对等边求边长或证明边相等】
(23-24 八年级·陕西西安·期末)
26.如图,在 V ABC 中, ÐACB = 90o , CE 是斜边 AB 上的高,角平分线 BD 交 CE 于点
M .求证: VCDM 是等腰三角形.
人教版-八年级数学上册《第十三章 等腰三角形》同步练习题及答案

人教版-八年级数学上册《第十三章等腰三角形》同步练习题及答案学校班级姓名学号一、选择题:(本题共8小题,每小题5分,共40分.)1.等腰三角形的一个底角为,则它的顶角为()A.B.C.D.或2.一个等腰三角形两边长分别为20和10,则周长为()A.40 B.50 C.40或50 D.不能确定3.如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是()A.AB=2BD B.AD⊥BC C.AD平分∠BAC D.∠B=∠C4.如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,且BD=BE,CD=CF,∠A=70°,那么∠FDE等于()A.40°B.45°C.55°D.35°5.如图,已知中,AB=AC,E、D分别为、上的点,连接BD,DE,若AD=DE=BE,∠C=70°,则的度数为()A.50°B.60°C.70°D.80°6.如图,在等边△ABC中,点D、E分别是BC、AB边上的点,且AE=BD,AD与CE交于点F,则∠DFC 的度数为()A.45°B.60°C.65°D.75°7.如图,点B和点C是对应顶点,记,当时,与之间的数量关系为()A.B.C.D.8.如图,△ABC是边长为2的等边三角形,点P在AB上,过点P作PE⊥AC,垂足为E,延长BC到点Q,使CQ=PA,连接PQ交AC于点D,则DE的长为()A.0.5 B.0.9 C.1 D.1.25二、填空题:(本题共5小题,每小题3分,共15分.)9.在△ABC中,∠C=90°,∠A=30°,AB=16,则BC的长是.10.△ABC中,AB=AC,∠BAC=40°,点D在直线BC上,CD=CA,则∠DAB的度数为.11.如图,在中,∠C=90°,AD=ED,∠CDE=72°,则的大小等于度.12.如图,在等边中,BD=CE,与交于P,,垂足为,PD=2,PQ=6,则的长为.13.如图,在中,点在边上,于点,若的面积为6,则的面积为.三、解答题:(本题共5题,共45分)14.已知,如图,等边△ABC中,点D为BC延长线上一点,点E为CA延长线上一点,且AE=DC,求证:AD=BE.15.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AB于E,求EB:EA的值.16.如图,和是顶角相等的等腰三角形,BC,DE分别是这两个等腰三角形的底边.求证.17.如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧,CE与BD交于点F,连接BE,按要求将图形补完整;(1)求证:△ADC≌△BDE;(2)求证:BD垂直平分CE.18.如图,在中,AB=AC,D为的中点,于点E,于点F,且DE=DF,连接,点G在的延长线上,且CD=CG.(1)求证:是等边三角形;(2)若,求的长.参考答案:1.C 2.B 3.A 4.C 5.B 6.B 7.B 8.C9.810.75°或15°11.5412.1413.1014.证明:在等边△ABC中,AB=CA,∠BAC=∠ACB=60°,∴∠EAB=∠DCA=120°.在△EAB和△DCA 中,∴△EAB≌△DCA(SAS),∴AD=BE15.解:如图,连接AD∵AB=AC,∠BAC=120°,D为BC的中点∴∠BAD=60°,AD⊥BC∴∠B=90°﹣60°=30°∵DE⊥AB∴∠ADE=90°﹣60°=30°设EA=x在Rt△ADE中,AD=2EA=2x在Rt△ABD中,AB=2AD=4x∴EB=AB﹣EA=4x﹣x=3x∴EB:EA=3x:x=3.16.证明:和是顶角相等的等腰三角形,得出∴AB=AC,AD=AE,∠BAD=∠CAE在和中,.17.(1)解:补充图形如下:∵和都是等边三角形∴,CD=ED,∠ADB=∠CDE∴∴在和中∴(2)解:由(1)得∴在等腰中有∴由已知在等边三角形中有∴为的垂直平分线即垂直平分.18.(1)证明:∵,DF⊥BC∴∵D为的中点∴在与中∴∴∴∵∴∴是等边三角形;(2)解:由(1)知,是等边三角形∴∴∵∴连接,则∴∴∵∴∵∴∴∴CG=2。
初中数学等腰三角形专项练习

试卷第1页,总4页…………外……………内…绝密★启用前等腰三角形课后练习等腰三角形考试范围:等腰三角形;考试时间:100分钟;命题人:陈泽咏注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、单选题1.下列说法中错误的是( ) A .等腰三角形的底角一定是锐角 B .等腰三角形顶角的外角是底角的2倍 C .等腰三角形至少有两个角相等D .等腰三角形的顶角一定是锐角2.下列关于等腰三角形的性质叙述错误的是( ) A .等腰三角形的两底角相等 B .等腰三角形的两边相等 C .等腰三角形是轴对称图形D .等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合 3.关于等腰三角形,有以下说法:(1)有一个角为46︒的等腰三角形一定是锐角三角形 (2)等腰三角形两边的中线一定相等(3)两个等腰三角形,若一腰以及该腰上的高对应相等,则这两个等腰三角形全等 (4)等腰三角形两底角的平分线的交点到三边距离相等 其中,正确说法的个数为( ) A .1个B .2个C .3个D .4个4.如图所示的方格纸中,每个方格均为边长为1的小正方形,我们把每个小正方形的顶点称为格点,现已知A 、B 、C 、D 都是格点.则下列结论中正确的是( )A .ABC ∆、ABD ∆都是等腰三角形试卷第2页,总4页B .ABC ∆、ABD ∆都不是等腰三角形C .ABC ∆是等腰三角形,ABD ∆不是等腰三角形 D .ABC ∆不是等腰三角形,ABD ∆是等腰三角形 5.“等腰三角形两底角相等”的逆命题是( ) A .等腰三角形“三线合一” B .底边上高和中线重合的三角形等腰 C .两个角互余的三角形是等腰三角形 D .有两个角相等的三角形是等腰三角形 6.下列说法中错误的是( )A .等腰三角形底边上的高所在的直线是它的对称轴B .等腰三角形底边上的中线所在的直线是它的对称轴C .等腰三角形顶角的平分线所在的直线是它的对称轴D .等腰三角形一定有三条对称轴7.已知等腰三角形的两边长x ,y 满足2|4|(8)0x y -+-=,则这个等腰三角形的周长为( ) A .16B .20C .16或20D .以上都不对8.已知一个等腰三角形的腰长是5,底边长是8,这个等腰三角形的面积是( ) A .24B .20C .15D .129.等腰三角形的一边长为5,周长为20.则这个等腰三角形的底边长为( ) A .5B .10C .5或10D .5或7.510.已知等腰三角形的一个内角为80︒,则这个等腰三角形的底角为( ) A .50︒B .80︒C .50︒或80︒D .50︒或100︒11.等腰三角形一腰上的高与腰长之比为1:2,则等腰三角形顶角的度数为( ) A .30B .60︒C .30或150︒D .60︒或120︒12.若等腰三角形一腰上的高与另一腰的夹角为30°,则这个等腰三角形的底角是( ) A .60°或30°B .60°C .30°或120°D .60°或120°13.等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形底边的长为( ) A .17cm B .5cmC .5cm 或17cmD .无法确定第II 卷(非选择题)请点击修改第II 卷的文字说明试卷第3页,总4页…………○…:___________班级:…………○…二、填空题14.等腰三角形的一个外角为100°,则这个等腰三角形的顶角为________;等腰三角形一腰上的高与腰的夹角为36°,则该等腰三角形的顶角为______.15.已知等腰三角形一腰上的中线将这个等腰三角形的周长分为9cm 和15cm 两部分,则这个等腰三角形的腰长为__________cm .16.规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k ,若14k =,则该等腰三角形的底角为______. 17.已知等腰三角形的周长为29,一边长为7,则此等腰三角形的腰长为__________.18.已知等腰三角形的两边长,x y 满足方程组28210x y x y +=⎧⎨+=⎩,则此等腰三角形的周长为_____.三、解答题19.已知:如图,等腰三角形ABC 中,90ACB ∠=︒,等腰三角形DCE 中,90DCE ∠=︒,点D 在AB 上,连接AE .求证:EA AB ⊥.20.用一根长度为20cm 的细绳围成一个等腰三角形.(1)如果所围等腰三角形的腰长是底边长的2倍,则此时的底边长度是多少? (2)所围成的等腰三角形的腰长不可能等于4cm ,请简单说明原因. (3)若所围成的等腰三角形的腰长为a ,请求出a 的取值范围.21.定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段....叫做这个三角形的三分线.(1)图①是顶角为36︒的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为36︒的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);试卷第4页,总4页……○………………○…………………○……※※装※※订※※线答※※题※※……○………………○…………………○……(2)图③是顶角为45︒的等腰三角形,请你在图③中画出顶角为45︒的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.(3)ABC 中,30B ∠=︒,AD 和DE 是ABC 的三分线,点D 在BC 边上,点E 在AC 边上,且AD BD =,DE CE =,设c x ∠=︒,则x 所有可能的值为_________. 22.如图,已知AC BC ⊥,BD AD ⊥,AC 与BD 交于O ,AC BD =.连接AB .求证:OAB 是等腰三角形.本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
八年级数学等腰三角形中的分类讨论专项练习

八年级数学等腰三角形中的分类讨论专项练习类型一:遇角需讨论1.若等腰三角形的一个外角等于110°则底角的度数为()A.70°或40° B.40°或55° C.55°或70° D.70°2.已知等腰三角形一腰上的高线与另一腰的夹角为50°,那么这个等腰三角形的底角的度数为()A.15°或75° B.70° C.20° D.70°或20°3.若等腰三角形一腰上的高与底边的夹角为70°,则顶角的度数为___________________.4.数学课上,张老师举了下面的例题:例1 等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)例2 等腰三角形ABC中,∠A=40°,求∠B的度数.(答案:40°或70或100°)张老师启发同学们进行变式,小敏编了如下一题:变式等腰三角形ABC中,∠A=80°,求∠B的度数.(1)请你解答以上的变式题;(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.5.【定义】数学课上,陈老师对我们说:如果1条线段将一个三角形分成2个等腰三角形,那么这条线段就称为这个三角形的“好线”;如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.【理解】(1)如图①,在△ABC中,∠A=27°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数;(2)如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.【应用】(3)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形中最大内角的所有可能值为____________________________________________;(4)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在边BC上,点E 在边AB上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.类型二:遇边需讨论6.若一个等腰三角形的一边长为6cm,周长为30cm,则它的另两边长分别为()A.6cm.,18 cm B.12 cm,12 cmC.6 cm,12 cm D.6 cm,18 cm 或12cm,12 cm a,相交于点O,∠1=50°,点A在直线a上,直线b存在点B,使以点O,7.如图,直线bA,B为顶点的三角形是等腰三角形,这样的点B有()A.1个B.2个C.3个D.4个8.如图,有一个三角形纸片ABC,∠A=80°,D是边AC上一点,沿BD方向剪开三角形纸片后,发现所得两纸片均为等腰三角形,则∠C的度数可以是_________________________.9.在等腰三角形ABC中,如果过顶角的顶点A的一条直线AD将△ABC分割成两个等腰三角形,那么∠BAC=_________________________.10.如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:画出3种不同的示意图,并在所画等腰三角形长为3的边上标注数字3)类型三:遇中线需讨论11.已知等腰三角形的底边长为10cm,一腰上的中线把这个等腰三角形的周长分为两部分,其中一部分比另一部分长5cm,那么这个等腰三角形的腰长为____________________cm.12.已知等腰三角形一腰上的中线将三角形的周长分成了21和27两个部分,求等腰三角形的底边长和腰长.参考答案CD140°5、6、B7、D 8、15。
八年级数学从等腰三角形看分类讨论专题练习

八年级数学从等腰三角形看分类讨论专题练习1.(本小题10分)某等腰三角形的两条边长分别为3cm和6cm,则它的周长为()A. 9cmB. 12 cC. 15cmD. 12cm或15cm2.(本小题10分)若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为()A. 50°B. 80°C. 65°或50°D. 50°或80°3.(本小题10分)等腰三角形的两角之差为30°,求该三角形顶角的度数为()∙ A. 80°B. 40°C. 40°或80°D. 50°或80°4.(本小题10分)如图,在等腰三角形ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连结BE,则∠CBE等于( )∙ A. 80°B. 70°C. 60°D. 50°5.(本小题10分)等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( ) ∙ A. 60°B. 120°C. 60°或150°D. 60°或120°6.在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为()A. 7B. 11C. 7或11D. 157.在△ABC中,AB=AC,AB的中垂线与AC所在直线相交所得的锐角为50°,则底角∠B=( )A. 70°B. 50C. 70°或20°D. 20°8. 等腰三角形的周长是16,其中两边之差为2,求它的腰长为()A. B. 6 C. 8 D. 6或9. 已知线段AB,以点A和点B为其中两个点作位置不同的等腰直角三角形,一共可以作( )A. 2个B. 4C. 6个D. 8个10. 等腰三角形周长是29,其中一边是7,则等腰三角形的底边长是()∙ A. 15 B. 15或7 C. 7 D. 1111. 已知一等腰三角形的两个内角的度数之比为1:4,求等腰三角形底角的度数()∙ A. 30° B. 80° C. 30°或80° D. 90°12. 等腰三角形一腰上的高与一边的夹角为50°,则该等腰三角形的底角度数()∙ A. 50° B. 40°或20°或70° C. 70°或20° D. 40°或70°。
部编数学八年级上册专题09等腰等边三角形问题(解析版)含答案

2023--2024学年度人教版数学八年级上册期末复习核心考点三种题型精炼专题09 等腰等边三角形问题选择题一、选择题1. (2023贵州省)5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为120°,腰长为12m ,则底边上的高是( )A. 4mB. 6mC. 10mD. 12m【答案】B 【解析】作AD BC ^于点D ,根据等腰三角形的性质和三角形内角和定理可得()1180302B C BAC Ð=Ð=°-Ð=°,再根据含30度角的直角三角形的性质即可得出答案.如图,作AD BC ^于点D ,Q ABC V 中,120BAC Ð=°,AB AC =,\()1180302B C BAC Ð=Ð=°-Ð=°,Q AD BC ^,\11126m 22AD AB ==´=,故选B .【点睛】本题考查等腰三角形的性质,三角形内角和定理,含30度角的直角三角形的性质等,解题的关键是掌握30度角所对的直角边等于斜边的一半.2.如图,点F 在正五边形ABCDE 的内部,ABF V 为等边三角形,则AFC Ð等于( )A. 108°B. 120°C. 126°D. 132°【答案】C【解析】根据多边形内角和公式可求出∠ABC的度数,根据正五边形的性质可得AB=BC,根据等边三角形的性质可得∠ABF=∠AFB=60°,AB=BF,可得BF=BC,根据角的和差关系可得出∠FBC的度数,根据等腰三角形的性质可求出∠BFC的度数,根据角的和差关系即可得答案.∵ABCDE是正五边形,∴∠ABC=(52)1805-´°=108°,AB=BC,∵ABFV为等边三角形,∴∠ABF=∠AFB=60°,AB=BF,∴BF=BC,∠FBC=∠ABC-∠ABF=48°,∴∠BFC=1(180)2FBC°-Ð=66°,∴AFCÐ=∠AFB+∠BFC=126°,【点睛】本题考查多边形内角和、等腰三角形的性质、等边三角形的性质,熟练掌握多边形内角和公式是解题关键.3. 如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )A.AC>BC B.AC=BC C.∠A>∠ABC D.∠A=∠ABC【答案】A【解析】本题考查了等腰三角形的性质:等腰三角形的两腰相等;等腰三角形的两个底角相等;等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.根据等腰三角形的两个底角相等,由AD=BD 得到∠A=∠ABD ,所以∠ABC >∠A ,则对各C 、D 选项进行判断;根据大边对大角可对A 、B 进行判断.∵AD=BD ,∴∠A=∠ABD ,∴∠ABC >∠A ,所以C 选项和D 选项错误;∴AC >BC ,所以A 选项正确;B 选项错误.4. 如图所示,直线a ∥b ,点A 在直线a 上,点B 在直线b 上,AC =BC ,∠C =120°,∠1=43°,则∠2的度数为( )A. 57°B. 63°C. 67°D. 73°【答案】D 【解析】根据等腰三角形的性质可求出30ABC Ð=°,可得出+173ABC ÐÐ=°,再根据平行线的性质可得结论.∵AC =BC ,∴ABC D 是等腰三角形,∵=120C а ∴11(180)(180120)3022ABC C Ð=°-Ð=°-°=° ∴1304373ABC Ð+Ð=°+°=°∵a ∥b ,∴2173ABC Ð=Ð+Ð=°故选:D【点睛】本题主要考查了等腰三角形的判定与性质,以及平行线的性质,求出173ABC Ð+Ð=°是解答本题的关键.二、填空题1. 如图,屋顶钢架外框是等腰三角形,其中AB AC =,立柱AD BC ^,且顶角120BAC Ð=°,则C Ð大小为 .【答案】30°##30度【解析】先由等边对等角得到B C Ð=Ð,再根据三角形的内角和进行求解即可.AB AC =Q ,B C \Ð=Ð,120BAC Ð=°Q ,180BAC B C Ð+Ð+Ð=°,180120302C °-°\Ð==°,故答案为:30°.【点睛】本题考查了等腰三角形的性质及三角形的内角和定理,熟练掌握知识点是解题的关键.2. 如图,在ABC V 中,40ABC Ð=°,80BAC Ð=°,以点A 为圆心,AC 长为半径作弧,交射线BA 于点D ,连接CD ,则BCD Ð的度数是 .【答案】10°或100°【解析】分两种情况画图,由作图可知得AC AD =,根据等腰三角形的性质和三角形内角和定理解答即可.如图,点D 即为所求;的在ABC D 中,40ABC Ð=°,80BAC Ð=°,180408060ACB \Ð=°-°-°=°,由作图可知:AC AD =,1(18080)502ACD ADC \Ð=Ð=°-°=°,605010BCD ACB ACD \Ð=Ð-Ð=°-°=°;由作图可知:AC AD =¢,ACD AD C \Т=Т,80ACD AD C BAC Т+Т=Ð=°Q ,40AD C \Т=°,1801804040100BCD ABC AD C \Т=°-Ð-Т=°-°-°=°.综上所述:BCD Ð度数是10°或100°.故答案为:10°或100°.【点睛】本题考查了作图-复杂作图,三角形内角和定理,等腰三角形判定与性质,解题的关键是掌握基本作图方法.3.如图,在△ABC 中,AB=AC=2a ,∠ABC=∠ACB=15°,CD 是腰AB 上的高.则CD 的长为 .【答案】a【解析】观察图形可以发现,在Rt △ADC 中,AC=2a ,而∠DAC 是△ABC 的一个外角, 则∠DAC=15°×2=30°,根据在直角三角形中,30°角所对的边是斜边的一半, 可求出CD .∵∠ABC=∠ACB=15°,∴∠DAC=∠ABC+∠BAC=30°.的的∴CD=AC=a(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半).4.在等腰ABC D 中,AD BC ^交直线BC 于点D ,若12AD BC =,则ABC D 的顶角的度数为 .【答案】30°或150°或90°..【解析】①BC 为腰,∵AD ⊥BC 于点D ,AD=12BC ,∴∠ACD=30°,如图1,AD 在△ABC 内部时,顶角∠C=30°,如图2,AD 在△ABC 外部时,顶角∠ACB=180°﹣30°=150°,②BC 为底,如图3,∵AD ⊥BC 于点D ,AD=12BC ,∴AD=BD=CD ,∴∠B=∠BAD ,∠C=∠CAD ,∴∠BAD+∠CAD=12×180°=90°,∴顶角∠BAC=90°,综上所述,等腰三角形ABC 的顶角度数为30°或150°或90°.5.在直角三角形中,如果一个锐角等于30°, 那么它所对的直角边等于斜边的 _.【答案】一半。
第02讲 等腰三角形(1个知识点+5大题型+18道强化训练)(教师版) 24-25学年八年级数学上册
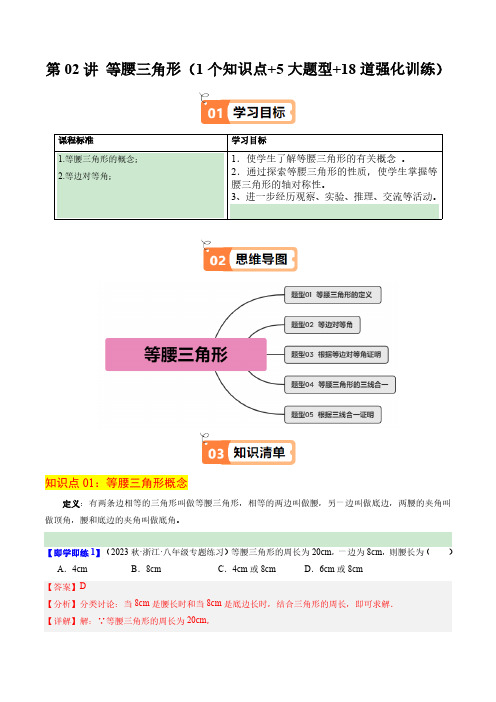
第02讲 等腰三角形(1个知识点+5大题型+18道强化训练)知识点01:等腰三角形概念定义:有两条边相等的三角形叫做等腰三角形,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
【即学即练1】(2023秋·浙江·八年级专题练习)等腰三角形的周长为20cm ,一边为8cm ,则腰长为( )A .4cmB .8cmC .4cm 或8cmD .6cm 或8cm【答案】D【分析】分类讨论:当8cm 是腰长时和当8cm 是底边长时,结合三角形的周长,即可求解.【详解】解:∵等腰三角形的周长为20cm ,题型01 等腰三角形的定义1.有5根小棒,长度分别为3、3、4、6、6,用其中的3根做等腰三角形的边,可以搭出( )种不同的等腰三角形.A.5B.4C.3D.2【答案】C【分析】此题考查了三角形的特性中的三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.【详解】解:根据三角形的特性:任意两边之和大于第三边;可以组成的三角形有:①3、3、4;②3、6、6③4、6、6所以,搭出3种不同的等腰三角形.故选:C.2.(比例的应用)一个等腰三角形的一条腰长是20厘米,其中有两条边的长度比是2:5,这个等腰三角形的周长是()厘米.A.90B.120C.48D.48或120【答案】C【分析】本题考查了等腰三角形的判定和性质,构成等腰三角形的条件,根据题意,分类讨论,当腰长与底边的比是2:5时,根据构成等腰三角形的条件判定,不符合题意;当底边与腰长的比是2:5时,符合题意,由此即可求解.【详解】解:当腰长与底边的比是2:5时,∵等腰三角形一条腰长为20厘米,∴等腰三角形的另一条腰长也为20厘米,则底边长为50厘米,+<,∵202050∴不能构成等腰三角形,不符合题意;当底边与腰长的比是2:5时,∴底边长为8厘米,∴等腰三角形的三边长为20厘米,20厘米,8厘米,能构成等腰三角形,符合题意;++=(厘米),∴这个等腰三角形的周长为2020848故选:C .3.等腰三角形的一个底角和顶角的比是1:4,则它的顶角是度.【答案】120【分析】首先要知道三角形的内角和是180°,根据等腰三角形的特点,两底角相等,所以三个角的比是++=份,先求出一份的度数,再求顶角的度数即可.此题考查了1:1:4,把这个三角形的内角和看作1146有关三角形内角和的知识,以及按比例分配应用题的解法.¸++´,【详解】解:180(114)4=¸´,18064=(度).120答:它的顶角是120度.故答案为:120.4|2|0b -=,则以a b ,为边长的等腰三角形的周长为 .(1)有两边长分别为4cm ,6cm ;(2)有两边长分别为4cm ,8cm .【答案】(1)三角形的周长为14cm 或16cm(2)三角形的周长为20cm【分析】本题考查了等腰三角形的性质和三角形的三边关系;(1)根据等腰三角形的定义,分情况并利用三角形的三边关系求解即可.(2)根据等腰三角形的定义,分情况并利用三角形的三边关系求解即可.【详解】(1)解:若三角形的腰长为4cm ,则底边长为6cm ,能组成三角形,此三角形的周长为()44614cm ++=,若三角形的腰长为6cm ,则底边长为4cm ,能组成三角形,此三角形的周长为()66416cm ++=.综上可知,三角形的周长为14cm 或16cm .(2)若三角形的腰长为4cm ,则底边长为8cm ,不能组成三角形;若三角形的腰长为8cm ,则底边长为4cm ,能组成三角形,此三角形的周长为()88420cm ++=.题型02 等边对等角1.等腰ABC V 中,AB AC =,若70A Ð=°,则B Ð=( )A .40°B .55°C .65°D .60°【答案】B【分析】本题考查了等边对等角、三角形内角和定理,根据等边对等角结合三角形内角和定理计算即可得出答案.【详解】解:∵AB AC =,∴B C Ð=Ð,∵70A Ð=°,∴()18070255B Ð=°-°¸=°.故选:B .2.在ABC V 中,AB AC =,点D 在BC 上,AD CD =,若120BAC Ð=°,则BDA Ð的度数为( )A .30°B .45°C .60°D .80°,则它的一个底角是.当20°的角为等腰三角形的底角时,其底角为20°,故它的底角的度数是80°或20°.故答案为:80°或20°.4.一个等腰三角形一腰上的高与另一腰的夹角为50°,则该等腰三角形的顶角度数为.【答案】40°或140°【分析】本题主要考查了等腰三角形的性质,三角形外角的性质,三角形内角和定理,解题的关键是根据题意画出图形,并注意分类讨论.要注意分类讨论,等腰三角形可能是锐角三角形也可能是钝角三角形,然后根据三角形的内角和以及三角形的外角的性质即可求解.【详解】解:若三角形为锐角三角形时,如图,AB AC =,50ACD Ð=°,CD 为高,即90ADC Ð=°,此时180A ACD ADC Ð+Ð+Ð=°,∴180905040A Ð=°-°-°=°,若三角形为钝角三角形时,如图,AB AC =,50ACD Ð=°,CD 为高,即90ADC Ð=°,此时9050140BAC D ACD Ð=Ð+Ð=°+°=°,综上,等腰三角形的顶角的度数为40°或140°.故答案为:40°或140°.5. 如图,在ABC V 中,AB AC =,AD BC ^于点D ,E 为AD 上一点,连接CE ,使CE AE =,65B Ð=°,求ECD Ð的度数.【答案】40°【分析】本题考查了等腰三角形的性质,三角形内角和定理应用.根据等边对等角得出65ACB B Ð=Ð=°,根据三角形内角和定理得出180656550BAC Ð=°-°-°=°,根据等腰三角形三线合一的性质得出题型03 根据等边对等角证明1.如图,分别是小明、小颖和小亮三位同学用尺规作AOB Ð的平分线的图示,对于三人不同的作法, 其中正确的个数是( )A .0个B .1 个C .2个D .3个【答案】D 【分析】本题主要考查了全等三角形的性质与判定,平行线的尺规作图,线段的尺规作图,等边对等角等等,根据对应的作图痕迹结合全等三角形的性质与判定条件证明即可.【详解】解:小明的作图中OD OC DE CE OE OE ===,,,∴()SSS ODE OCE △≌△,∴DOE COE Ð=Ð,∴OE 平分AOB Ð,故小明的作法正确;小颖的作图中OD OC OF OG DOF COG ===,,∠,∴()SAS DOF COG △≌△,∴OGE OFE Ð=Ð,∵OF OC OG OD -=-,∴DG CF =,又∵DEG CEF Ð=Ð,∴DEG CEF △≌△,∴=GE FE又∵OE OE =,∴FOE GOE △≌△,DOE COE Ð=Ð,∴OE 平分AOB Ð,故小颖的作法正确;小亮的作图中,EF BD OF EF =∥,,∴FOE FEO BOE ==∠∠∠,∴OE 平分AOB Ð,故小亮的作法正确;故选:D .2.如图,甲、乙两艘船同时从海上点P 处出发,甲船沿点P 的正南方向匀速航行,乙船沿点P 的北偏东70°方向匀速航行,甲、乙两船的速度相同,则乙船在甲船的( )A .北偏东10°B .北偏东30°C .北偏东35°D .北偏东40°3.如图,在ABC V 中,AB AC =,50A Ð=°,点D 是ABC V 内的一点,连接BD ,CD .若12Ð=Ð,则D Ð的度数为 .DAE Ð= .【答案】80°/80度【分析】本题考查垂直平分线的性质,三角形内角和定理,根据DM 、EN 分别垂直平分AB 和AC 得到AD BD =,AE CE =,从而得到C BCAE Ð=Ð,B BAD Ð=Ð,结合130BAC Ð=°与三角形内角和定理即可得到答案;【详解】解:∵DM 、EN 分别垂直平分AB 和AC ,∴AD BD =,AE CE =,∴C CAE Ð=Ð,B BAD Ð=Ð,∵130BAC Ð=°,∴130BAD CAE DAE Ð+Ð+Ð=°,∵180B C BAC Ð+Ð+Ð=°,∴50B C Ð+Ð=°,∴50BAD CAE Ð+Ð+=°,∴80DAE Ð=°.故答案为:80°.5.如图,已知,,C E AC AE CAD EAB Ð=Ð=Ð=Ð.求证:ABD ADB Ð=Ð.【答案】见解析【分析】此题重点考查全等三角形的判定与性质、“等边对等角”等知识.由CAD EAB Ð=Ð,推导出CAB EAD Ð=Ð,即可根据“ASA ”证明CAB EAD ≌V V ,可得AB AD =,即可求证.【详解】证明:∵CAD EAB Ð=Ð,∴CAD BAD EAB BAD Ð-Ð=Ð-Ð,∴CAB EAD Ð=Ð,在CAB △和EAD V 中,∵,,CAB EAD AC AE C E =ÐÐ==ÐÐ,∴()ASA CAB EAD ≌V V ,∴AB AD =,∴ABD ADB Ð=Ð.题型04 等腰三角形的三线合一1.如图,在ABC V 中,AB AC =.在AB ,AC 上分别截取AP ,AQ ,使AP AQ =.再分别以点P ,Q 为圆心,以大于12PQ 的长为半径作弧,两弧在BAC Ð内交于点R ,作射线AR ,交BC 于点D .若6BD =,则BC 的长为( )A .12B .3C .8D .10【答案】A 【分析】本题主要考查了角平分线的尺规作图和等腰三角形的性质,根据作图过程可得,AD 平分BAC Ð,根据等腰三角形三线合一的性质求解即可.解题的关键在于能够准确判断出AD 平分BAC Ð.【详解】解:根据作图过程可得,AD 平分BAC Ð,又∵AB AC =,∴212BC BD ==,故选:A .2.如图:ABC V 中,D 点在BC 上,现有下列四个命题:①若AB AC =,则B C Ð=Ð.②若AB AC =,BAD CAD Ð=Ð,则AD BC ^,BD DC =.③若AB AC =,BD DC =,则AD BC ^,BAD CAD Ð=Ð.④若AB AC =,AD BC ^,则BD DC =,BAD CAD Ð=Ð.其中正确的有( )A .1个B .2个C .3个D .4个【答案】D 【分析】本题考查了命题与定理:判断一件事情的语句,叫做命题.也考查了等腰三角形的性质.根据等腰三角形的性质对①进行判断;根据等腰三角形的“三线合一”对②③④进行判断.【详解】解:若AB AC =,则B C Ð=Ð,所以①正确;若AB AC =,BAD CAD Ð=Ð,即AD 为顶角的平分线,则AD BC ^,BD DC =,所以②正确;若AB AC =,BD DC =,即AD 为底边上的中线,则AD BC ^,BAD CAD Ð=Ð,所以③正确;若AB AC =,AD BC ^,即AD 为底边上的高,则BD DC =,BAD CAD Ð=Ð,所以④正确.故选:D .3.如图,在ABC V 中,AB AC =,AD 平分BAC Ð,点E 在边AB 上,且BD BE =.若100BAC Ð=°,则ADE Ð的大小为 .Ð=°.BDE题型05 根据三线合一证明.最近粉色二七塔邂逅玉兰花火出了圈,郑州市民纷纷围观打卡.如图,二七塔的顶端可看作等腰三角形,,=是边BC上的一点.下列条件不能说明AD是ABCABC AB AC DV的角平分线的是()A .ADB ADCÐ=ÐB .BD CD =C .2BC AD=D .ABD ACDS S =V V 【答案】C 【分析】本题主要考查了等腰三角形的性质,熟练掌握等腰三角形“三线合一”的性质是解题的关键.根据等腰三角形“三线合一”的性质,逐项判断即可求解.【详解】解:A 、ADB ADC Ð=ÐQ ,180ADB ADC Ð+Ð=°,90ADB ADC \Ð=Ð=°,即AD 是ABC V 的高线,ABC QV 是等腰三角形,AB AC =,AD \是ABC V 的角平分线,故A 选项不符合题意;B 、ABC QV 是等腰三角形,BD CD =,AD \是ABC V 的角平分线,故B 选项不符合题意;C 、若2BC AD =,不能说明AD 是ABC V 的角平分线,故C 选项符合题意;D 、ABD ACD S S =Q △△,BD CD \=,∴AD 是ABC V 的角平分线,故D 选项不符合题意;故选:C .2.如图,在ABC V 中,AB AC =,D 是BC 的中点,下列结论不一定正确的是( )A .B CÐ=ÐB .12AD AB =C .BAD CAD Ð=ÐD .AD BC^90,6cm EDF BE Ð=°=,则AF = .【答案】6cm /6厘米【分析】本题考查了等腰直角三角形的性质、全等三角形的判定和性质.利用等腰直角三角形的性质和已知条件证明AFD BED ≌△△即可得到BE AF =.【详解】解:∵,90AB AC BAC =Ð=°,点D 是BC 的中点,∴,45AD CD BD FAD B ==Ð=Ð=°,∴AD BD =,90EDF Ð=°Q ,∴90ADF ADE Ð+Ð=°,90ADE EDB Ð+Ð=°Q ,∴ADF EDB Ð=Ð,在AFD △和BED V 中,,∵45FAD B Ð=Ð=°,AD BD =,ADF EDB Ð=Ð,∴()ASA AFD BED V V ≌BE AF \=,∵6cm BE =,∴6cm AF =.故答案为:6cm4.如图,在ABC V 中,AB AC =,点D 为BC 边的中点,127Ð=°,则C Ð= °.【答案】63【分析】本题考查的是等腰三角形的性质,熟知等腰三角形三线合一的性质是解答此题的关键.由等腰三角形的三线合一性质可知70BAC Ð=°,再由三角形内角和定理和等腰三角形两底角相等的性质即可得出结论.【详解】解:AB AC =Q ,D 为BC 中点,∴AD 是BAC Ð的平分线,B C Ð=Ð,∵127Ð=°,∴2154BAC Ð=Ð=°,连接DE ,DF .(1)求证:ADE ADF V V ≌;(2)若80BAC Ð=°,求BDE Ð的度数.1.等腰三角形中有一内角等于80°,那么这个三角形的最小内角的度数为( )度A .50B .20C .40或50D .20或50A .42°B .84°C .90°D .96°【答案】B 【分析】本题考查的是线段垂直平分线的性质,等腰三角形性质,三角形的外角的性质,解题的关键是掌握线段的垂直平分线上的点到线段的两个端点的距离相等.根据线段垂直平分线的性质得到AD CD =,根据等腰三角形的性质得到DCA A Ð=Ð,再根据三角形的外角的性质计算即可.【详解】解:Q 线段AC 的垂直平分线交AB 于点D ,AD CD \=,Q 42A Ð=°,42DCA A Ð=°\Ð=,\84A BDC DCA Ð=°Ð=Ð+.故选:B .3.如图,直线a b ∥,点A 在直线a 上,点B 在直线b 上,AC BC =,120C Ð=°,144Ð=°,则2Ð的度数为( )A .64°B .74°C .56°D .66°∴(12ABC BAC Ð=Ð=´∵144Ð=°,∴1ABD ABC Ð=Ð+Ð=∵a b ∥,A .67°B .135°C .67.5°D .67.5°或22.5°【答案】D【分析】本题考查等边对等角,三角形的内角和定理以及三角形的外角,分高在等腰三角形的内部和外部,两种情况进行讨论求解即可.【详解】解:当三角形的高线在三角形的内部时,如图:,AB AC BD AC =^,45ABD Ð=°,则:45A Ð=°∴(11802ABC ACB Ð=Ð=当三角形的高线在三角形的外部时,如图:∵,45ABC ACB DAB ABC ACB Ð=ÐÐ=Ð+Ð=∴22.5ABC ACB Ð=Ð=°;故选D .5.如图,在ABC V 中,DM EN 、分别垂直平分20DAE Ð=°,则BAC Ð的度数为( )A .100°B .105°C .110°D .120°【答案】A 【分析】本题主要考查了线段垂直平分线的性质,三角形内角和定理,等腰三角形的性质.根据线段垂直平分线的性质,可得,DB DA EA EC ==,再由等腰三角形的性质,可得,B DAB C EAC Ð=ÐÐ=Ð,再由三角形内角和定理,即可求解.【详解】解:∵DM EN 、分别垂直平分AB 和AC ,∴,DB DA EA EC ==,∴,B DAB C EAC Ð=ÐÐ=Ð,∵20,180DAE B C BAC Ð=°Ð+Ð+Ð=°,∵18020160B BAD C EAC Ð+Ð+Ð+Ð=°-°=°,∴22160BAD EAC Ð+Ð=°,∴80BAD CAE Ð+Ð=°,∴8020100BAC BAD CAE DAE Ð=Ð+Ð+Ð=°+°=°.故选:A .6.如图,ABF △中,60A Ð=°,40F Ð=°;点C ,D ,E 在AB 的延长线上,且BC BG =,CD CH =,DE DP =,则E Ð等于( )A .30°B .20°C .15°D .10°,则它的周长为 .【答案】22cm 或26cm【分析】本题主要考查了等腰三角形的定义,三角形三边之间的关系等知识点,熟练掌握分类讨论思想是解题的关键.分情况讨论即可.【详解】解:①当6cm 为腰,10cm 为底时,6610+>Q ,6106+>,\能构成三角形,\等腰三角形的周长661022cm =++=;②当10cm 为腰,6cm 为底时,10106+>Q ,10610+>,\能构成三角形,\等腰三角形的周长1010626cm =++=;故答案为:22cm 或26cm .8.如图,一个小孩坐在秋千上,若秋千绕点O 旋转了80°,小孩的位置从A 点运动到了B 点,则OAB Ð的度数为 .【答案】50°/50度【分析】本题主要考查了等腰三角形的性质和三角形内角和定理.先根据题意得到OA OB =,80AOB Ð=°,再根据等腰三角形的性质和三角形内角和定理进行解答即可.【详解】解:由题意可知:OA OB =,80AOB Ð=°,OA OB =Q ,OAB OBA \Ð=Ð,180OAB OBA AOB Ð+Ð+Ð=°Q ,18080100OAB OBA \Ð+Ð=°-°=°,50OAB OBA \Ð=Ð=°,故答案为:50°.9.如图,80AOB Ð=°,在OA 上取点C ,以点C 为圆心,CO 长为半径画弧交OB 于点D ,连接CD ;以点D 为圆心,DC 长为半径画弧交OB 于点E ,连接CE ,DCE Ð的度数为 .【答案】40°/40度【分析】本题考查了作图-基本作图,等腰三角形的性质以及三角形外角的性质.由作图可知,CO CD =,DC DE =,根据等腰三角形的性质以及三角形外角的性质即可求解.【详解】解:由作图可知,CO CD =,DC DE =.CO CD =Q ,80ODC COD \Ð=Ð=°,80DCE CED ODC \Ð+Ð=Ð=°,DC DE =Q ,40DCE CED \Ð=Ð=°.故答案为:40°.10.如图,点E 在AB 上,AC 与DE 相交于点F ,ABC DEC ≌△△,30A Ð=°,70B Ð=°,则DFA Ð的度数为 .【答案】70°/70度【分析】本题主要考查全等三角形的性质、等边对等角和三角形内角和定理,根据题意得ACB Ð,结合全等三角形的性质有CED B Ð=Ð和CB CE =,利用等边对等角和三角形内角和定理可求得ECB Ð和ACE Ð,即可求得答案.【详解】解:∵30A Ð=°,70B Ð=°,∴80ACB Ð=°,∵ABC DEC ≌△△,∴70CED B Ð=Ð=°,CB CE =,∴70CEB B Ð=Ð=°,∴18040ECB B CEB Ð=°-Ð-Ð=°,则40ACE ACB ECB Ð=Ð-Ð=°,那么,18070DFA CFE CED ACE Ð=Ð=°-Ð-Ð=°.故答案为:70°.11.如图,100BAC Ð=°,若MP 和NQ 分别垂直平分AB 和AC ,则PAQ Ð=【答案】20°/20度【分析】本题考查了线段垂直平分线的性质,三角形内角和,等边对等角,解题的关键是熟练掌握并运用相关知识.根据MP 和NQ 分别垂直平分AB 和AC ,可得B BAP Ð=Ð,C CAQ Ð=Ð,结合三角形内角和即可得到80BAP CAQ B C Ð+Ð=Ð+Ð=°,从而可求得PAQ Ð的值.【详解】解:PM Q 垂直平分AB ,PA PB \=,B BAP \Ð=Ð,同理:QC QA =,C CAQ \Ð=Ð,100BAC Ð=°Q ,18080B C BAC \Ð+Ð=°-Ð=°,80BAP CAQ \Ð+Ð=°,20PAQ BAC BAP CAQ \Ð=Ð-Ð-Ð=°.故答案为:20°.12.如图,在五边形ABCDE 中,12590BAE B E Ð=°Ð=Ð=°,,AB BC AE DE ==,,在BC DE 、上分别找一点M 、N ,使得AMN V 周长最小时,AMN ANM Ð+Ð的度数为 .【答案】110°/110度【分析】本题考查了轴对称的性质、等腰三角形的性质、两点之间线段最短等知识点,正确找出AMN V 的周长最小时,点M 、N 的位置是解题关键.先根据轴对称的性质可得,A M A A N AM N ¢¢¢==,再根据三角形的周长公式、两点之间线段最短可得当点,,,A M N A ¢¢¢在同一条直线上时,AMN V 的周长最小,然后利用等腰三角形的性质、三角形的外角性质即可得.【详解】如图,作点A 关于BC 的对称点A ¢,关于DE 的对称点A ¢¢,连接A M ¢、A N ¢¢,则,A M A A N AM N ¢¢¢==,AMN \V 的周长为AM MN AN A M MN A N ¢¢¢++=++,由两点之间线段最短可知,当点,,,A M N A ¢¢¢在同一条直线上时,AMN V 的周长最小,125BAE Ð=°Q ,18055A A BAE ¢¢¢\Ð+Ð=°-Ð=°,,AM A M AN A N ¢¢¢==Q ,,A A AM A A AN ¢¢¢¢¢¢\Ð=ÐÐ=Ð,AMN ANM A A AM A A AN ¢¢¢¢¢¢\Ð+Ð=Ð+Ð+Ð+Ð,22A A ¢¢¢=Ð+Ð,()2A A =Ð+Т¢¢,110=°,故答案为:110°.13.在ABC V 中,7,2AB BC ==.(1)求AC 长度的取值范围;(2)若ABC V 的周长为偶数,求ABC V 的周长,并判断此时ABC V 的形状.【答案】(1)59AC <<(2)ABC V 的周长为16,是等腰三角形【分析】本题考查三角形的三边关系,三角形的分类:(1)根据三角形的三边关系进行求解即可;(2)根据(1)中的范围,结合ABC V 的周长为偶数,得到7AC =,即可得出结论.【详解】(1)解:∵在ABC V 中,7,2AB BC ==∴AB BC AC AB BC -<<+,∴59AC <<;(2)∵ABC V 的周长为偶数,9AB BC +=为奇数,∴AC 的长为奇数,∵59AC <<,∴7AC AB ==,∴ABC V 的周长为9716+=,是等腰三角形.14.如图,在ABC V 中,AB AC =,D 是AC 上一点,连接BD ,75BDA Ð=°,11ABD Ð=°,求DCB Ð的度数.【答案】43°【分析】本题考查了三角形内角和定理,等腰三角形的性质两个知识点,掌握这两个知识点是解题的关键;(1)若40A Ð=°,求DBC Ð的度数;(2)若3AE =,CBD △的周长为10,求BC 的长.点F .(1)若5AB =,则CMN V 的周长为 ___________;(2)若70MFN Ð=°,求MCN Ð的度数.【答案】(1)5;(2)40°【分析】本题考查了垂直平分线的性质、等腰三角形的性质等知识点,掌握相关结论即可.(1)由题意得,CM AM CN BN ==,据此即可求解;(2)根据()MCN ACB ACM BCN Ð=Ð-Ð+Ð,()180ACB A B Ð=°-Ð+Ð即可求解;【详解】(1)解:∵DM EN ,分别垂直平分边AC 和边BC ,∴,CM AM CN BN==∴CMN V 的周长5CM MN CN AM MN BN AB =++=++==故答案为:5(2)解:∵,CM AM CN BN ==,∴,A ACM B BCNÐ=ÐÐ=Ð∵70MFN Ð=°,∴180110FMN FNM MFN Ð+Ð=°-Ð=°∴110AMD BNE Ð+Ð=°∵90ADM BEN Ð=Ð=°∴70A B ACM BCN Ð+Ð=Ð+Ð=°∵()MCN ACB ACM BCN Ð=Ð-Ð+Ð,()180ACB A B Ð=°-Ð+Ð∴()()18040MCN A B ACM BCN Ð=°-Ð+Ð-Ð+Ð=°17.如图1,在等腰直角三角形ABC 中,AB AC =,90BAC Ð=°,点D 在BC 边上,连接AD ,AE AD ^,AE AD =,连接CE ,DE .(1)45ACE B Ð=Ð=°,请你说明理由.(2)求BCE Ð的度数.(3)点A 关于直线CE 的对称点为1A ,连接1CA ,1EA .补全图形,判断1EA C Ð与BAD Ð之间的数量关系并说明理由.【答案】(1)理由见解析(2)90BCE Ð=°(3)补全图形见解析,1EA C BAD Ð=Ð,理由见解析【分析】本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质、轴对称的性质等知识,熟练掌握全等三角形的判定与性质是解题关键.(1)首先根据等腰直角三角形的性质可得45B ACB Ð=Ð=°,再证明ABD ACE △△≌,由全等三角形的性质即可证明结论;(2)由(1)可知,45ACE Ð=°,45ACB Ð=°,然后由BCE ACE ACB Ð=Ð+Ð求解即可;(3)根据题意补画图形,结合轴对称的性质可得1EA EA =,1CA CA =,CE CE =,进而证明1ACE A CE ≌△△,易得1EA C EAC Ð=Ð,结合ABD ACE △△≌可知CAE BAD Ð=Ð,即可获得答案.【详解】(1)证明:∵AB AC =,90BAC Ð=°,∴45B ACB Ð=Ð=°,∵90BAC DAE Ð=Ð=°,∴BAD DAC CAE DAC Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,又∵AB AC =,AD AE =,∴()SAS ABD ACE V V ≌,∴45ACE B Ð=Ð=°;(2)解:由(1)可知,45ACE Ð=°,45ACB Ð=°,∴454590BCE ACE ACB Ð=Ð+Ð=°+°=°;(3)如图,1EA C BAD Ð=Ð,理由如下:∵点A 与1A 关于CE 对称,∴1EA EA =,1CA CA =,CE CE =,∴()1SSS ACE ACE V V ≌,∴1EA C EAC Ð=Ð,∵ABD ACE △△≌,∴CAE BAD Ð=Ð,∴1EA C BAD Ð=Ð.18.(1)如图1,在ABC V 中,AB AC =,90BAC Ð=°,CD 平分ACB Ð,BE CD ^,垂足为E ,试探究线段BE 和CD 之间的数量关系,并写出你的理由.(2)如图2,把条件改为:“在ABC V 中,AB AC =,90BAC Ð=°,点D 在BC 上,12EDB C Ð=Ð,BE ED ^,DE 与AB 相交于F 点,则线段BE 和FD 之间的数量关系如何?并证明你的结论.”【答案】(1)2CD BE =,理由见解析;(2)2DF BE =,理由见解析【分析】该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造全等三角形.(1)如图,延长BE,CA 交于点F ,证明ADC AFB V V ≌,得到DC BF =;再证明EFC EBC ≌△△,得到EF BE =,即可解决问题;(2)如图,作DG AC ∥,交BE 的延长线于点G ,则BDG C Ð=Ð,证明HFD HGB △≌△,得到DF BG =;证明EGD EBD △≌△,得到BE GE =,即可解决问题.【详解】解:(1)2CD BE =,理由如下:如图,延长BE ,CA 交于点F ,∵90BAC Ð=°,BE CD ^,则90BEC FEC Ð=Ð=°,∴180FED FAD Ð+Ð=°,∴180ADE F Ð+Ð=°,∵180ADE ADC Ð+Ð=°,∴ADC F Ð=Ð,在ADC △与AFB △中,DAC FAB ADC F AC AB Ð=ÐìïÐ=Ðíï=î,∵12EDB C Ð=Ð,则EDB Ð∴DE 平分BDG Ð;∵DG AC ∥,∴90BHD A Ð=Ð=°,=,∴EG BE∴2=.DF BE。
八年级数学上册专题13.6 等腰三角形的证明及计算大题专项训练(50道)(举一反三)(人教版)(原卷

专题13.6 等腰三角形的证明及计算大题专项训练(50道)【人教版】考卷信息:本套训练卷共50题,题型针对性较高,覆盖面广,选题有深度,可深化学生对等腰三角形工具的应用及构造等腰三角形!一.解答题(共50小题)1.(2022秋•勃利县期末)如图:△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC 于E,且BD=BE,求证:△ABC为等腰三角形.2.(2022秋•淮安区期末)如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于点D,交AB于点E,求∠DBC的度数.3.(2022秋•林州市期末)已知△ABC的两边长a和b满足√a−9+(b﹣4)2=0.(1)若第三边长为c,求c的取值范围.(2)若△ABC是等腰三角形,求△ABC的周长.4.(2022秋•河东区校级期中)如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB 与y轴交于D点,∠CAO=90°﹣∠BDO.(1)求证:AC=BC;(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长.5.(2022秋•武冈市期中)已知如图,△ABC中,EF∥BC,交AB、AC于E、F,∠B的平分线交EF于O 点.(1)求证:EO=BE;(2)若EF=BE+CF,求证:OC平分∠ACB.6.(2022秋•盘龙区期末)如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE =CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=50°时,求∠DEF的度数.BC,若D是AC的7.(2022秋•大石桥市期末)如图,△ABC是等边三角形,延长BC到点E,使CE=12中点,连接ED并延长交AB于点F.(1)若AF=3,求AD的长;(2)证明:DE=2DF.8.(2022春•大埔县期末)如图,△ABC是等边三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F为BC中点,连接AF.(1)直接写出∠BAE的度数为;(2)判断AF与CE的位置关系,并说明理由.9.(2022秋•宁明县期末)如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证:△CEB为等边三角形.10.(2022春•二七区校级期中)在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠BCE=β.(1)如图(1),点D在线段BC上移动时,①角α与β之间的数量关系是;②若线段BC=2,点A到直线BC的距离是3,则四边形ADCE周长的最小值是;(2)如图(2),点D在线段BC的延长线上移动时,①请问(1)中α与β之间的数量关系还成立吗?如果成立,请说明理由;②线段BC、DC、CE之间的数量是.11.(2022秋•台江区期末)如图,已知∠ABC=∠ADC=90°,BC=CD,CA=CE.(1)求证:∠ACB=∠ACD;(2)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P.①连接PE,交AM于点N,证明AM垂直平分PE;②点O是直线AE上的动点,当MO+PO的值最小时,证明点O与点E重合.12.(2022春•市南区期末)如图,Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB 的垂线交AC于点E,求证:BE垂直平分CD.13.(2022秋•平房区期末)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.(1)求证:AB=AC;(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.14.(2022秋•河西区期末)如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.15.(2022秋•巩义市期末)如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B 出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A 同时出发,运动的时间为ts.(1)用含t的式子表示线段AP、AQ的长;(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?(3)当t为何值时,PQ∥BC?16.(2022秋•清江浦区校级月考)如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,AC=20cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.(1)BP=(用t的代数式表示)(2)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形?(3)当点Q在边CA上运动时,出发秒后,△BCQ是以BC或BQ为底边的等腰三角形?17.(2022春•渠县校级期末)已知:如图,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形.18.(2022秋•北仑区期中)(1)如图1,△ABC中,作∠ABC、∠ACB的角平分线相交于点O,过点O 作EF∥BC分别交AB、AC于E、F.①求证:OE=BE;②若△ABC的周长是25,BC=9,试求出△AEF的周长;(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,试探求∠BAC与∠P AC的数量关系式.19.(2022秋•余干县期中)如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC.求证:BC=DC.20.(2022春•焦作期末)如图,在等边三角形ABC中∠B,∠C的平分线相交于点O,作BO,CO的垂直平分线分别交BC于点E和点F.小明说:“E,F是BC的三等分点.”你同意他的说法吗?请说明理由.21.(2022秋•工业园区期末)已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点.(1)求证:△BED是等腰三角形:(2)当∠BCD=°时,△BED是等边三角形.22.(2022春•梅州校级期末)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1.将三角板中30°角的顶点D放在AB边上移动,使这个30°角的两边分别与△ABC的边AC,BC相交于点E,F,且使DE始终与AB垂直.(1)△BDF是什么三角形?请说明理由;(2)设AD=x,CF=y,试求y与x之间的函数关系式;(不用写出自变量x的取值范围)(3)当移动点D使EF∥AB时,求AD的长.23.(2022秋•阳新县校级期末)如图1,在Rt△ACB中,∠ACB=90°,∠ABC=30°AC=1点D为AC 上一动点,连接BD,以BD为边作等边△BDE,EA的延长线交BC的延长线于F,设CD=n,(1)当n=1时,则AF=;(2)当0<n<1时,如图2,在BA上截取BH=AD,连接EH,求证:△AEH为等边三角形.24.(2022•宁德一模)如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,BC长为半径的弧分别交AC,AB于点D,E,连接BD,ED.(1)写出图中所有的等腰三角形;(2)若∠AED=114°,求∠ABD和∠ACB的度数.25.(2022秋•平舆县期末)如图,在△ABC中,∠ABC=45°,点P为边BC上的一点,BC=3BP,且∠P AB=15°,点C关于直线P A的对称点为D,连接BD,又△APC的PC边上的高为AH(1)求∠BPD的大小;(2)判断直线BD,AH是否平行?并说明理由;(3)证明:∠BAP=∠CAH.26.(2022春•本溪县期中)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠BAE=40°,求∠C的度数;(2)若△ABC周长为20cm,AC=8cm,求DC长.27.(2022秋•澧县期末)如图,一只船从A处出发,以18海里/时的速度向正北航行,经过10小时到达B 处.分别从A、B处望灯塔C,测得∠NAC=42°,∠NBC=84度.求B处与灯塔C距离.28.(2022春•西安期末)如图,在△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为17cm,求△ABC的周长.29.(2022春•嵩县期末)如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.(1)若MN=20cm,求△PEF的周长.(2)若∠AOB=35°,求∠EPF的度数.30.(2022秋•沂南县期末)如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF 交AD于点O.(1)求证:AD垂直平分EF;(2)若∠BAC=60°,写出DO与AD之间的数量关系,不需证明.31.(2022秋•张家港市校级期末)如图:AD为△ABC的高,∠B=2∠C,用轴对称图形说明:CD=AB+BD.32.(2022春•锦江区校级期末)操作实验:如图,把等腰三角形沿顶角平分线对折并展开,发现被折痕分成的两个三角形成轴对称.所以△ABD≌△ACD,所以∠B=∠C.归纳结论:如果一个三角形有两条边相等,那么这两条边所对的角也相等.根据上述内容,回答下列问题:思考验证:如图(4),在△ABC中,AB=AC.试说明∠B=∠C的理由;探究应用:如图(5),CB⊥AB,垂足为B,DA⊥AB,垂足为A.E为AB的中点,AB=BC,CE⊥BD.(1)BE与AD是否相等,为什么?(2)小明认为AC是线段DE的垂直平分线,你认为对吗?说说你的理由;(3)∠DBC与∠DCB相等吗?试说明理由.33.(2022•海丰县模拟)如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:BE=CE(要求:不用三角形全等的方法)34.(2022春•余杭区期末)如图,已知△ABC中,AB=AC,BC=6,AM平分∠BAC,D为AC的中点,BC.E为BC延长线上一点,且CE=12(1)求ME的长;(2)求证:△DMC是等腰三角形.35.(2022•白城校级模拟)在△ABC中,AB=AC,点D是线段BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,如果∠BAC=90°,则∠BCE=;(2)如图2,设∠BAC=α,∠BCE=β.当点D在线段BC上移动时,请写出α,β之间的数量关系,请说明理由.36.(2022秋•乐亭县期末)若a、b是△ABC的两边且|a﹣3|+(b﹣4)2=0(1)试求a、b的值,并求第三边c的取值范围.(2)若△ABC是等腰三角形,试求此三角形的周长.(3)若另一等腰△DEF,其中一内角为x°,另一个内角为(2x﹣20)°试求此三角形各内角度数.37.(2022秋•盂县期末)将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.求证:△CDO是等腰三角形.38.(2022秋•龙门县期中)如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE =CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)求证:∠B=∠DEF;(3)当∠A=40°时,求∠DEF的度数.39.(2022春•静安区校级期末)已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.求证:AC﹣AB=2BE.40.(2022秋•秦淮区校级期中)在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于D,AE⊥BD,垂足为E.求证:AC=2BE.41.(2022秋•滑县校级期末)已知△ABC为等边三角形,D为AC的中点,∠EDF=120°,DE交线段AB于E,DF交直线BC于F.(1)如图(1),求证:DE=DF;BC.(2)如图(2),若BE=3AE,求证:CF=14AE,则CF=BC;在图(1)中,若BE=4AE,则CF=BC.(3)如图(3),若BE=1342.(2022春•峄城区期末)如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.(1)求证:△CEF是等腰三角形;(2)若CD=2,求DF的长.43.(2022秋•红山区期末)如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P 从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)何时△PBQ是直角三角形?(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ 变化吗?若变化,则说明理由,若不变,则求出它的度数.44.(2022•南京模拟)数一数甲图中有几个角(小于平角)?乙图中有几个等腰三角形?丙图中有几对全等三角形?丁图中有几对等边三角形?45.(2022秋•五河县期末)如图,过等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且P A=CQ,连PQ交AC边于D.(1)求证:PD=DQ;(2)若△ABC的边长为1,求DE的长.46.(2022•南京模拟)如图,∠BAC=30°,点P是∠BAC的平分线上的一点,PD⊥AC于D,PE∥AC 交AB于E,已知AE=10cm,求PD的长度.47.(2022春•青浦区校级期末)如图,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的两侧,D在A,E之间,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.48.(2022秋•龙华区期末)如图,已知直线l1∥l2∥l3,点E、F分别在l3、l1上,Rt△ABC的直角顶点C 在直线l1上,点B在直线l2上,点A在直线l3上,l2与AC交于点D,且∠BAC=25°,∠BAE=25°.(1)求证:△ABD是等腰三角形;(2)求∠BCF的度数.49.(2022春•电白区期末)如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则(1)BP=cm,BQ=cm.(用含t的代数式表示)(2)当t为何值时,△PBQ是直角三角形?50.(2022•南京模拟)如图,在等边△ABC的三边上分别取点D、E、F,使AD=BE=CF.(1)试说明△DEF是等边三角形;(2)连接AE、BF、CD,两两相交于点P、Q、R,则△PQR为何种三角形?试说明理由.。
初中数学 八年级上册等腰三角形练习题

八年级上册等腰三角形练习题一. 选择题:1. 等腰三角形的一个角是94°,则腰与底边上的高的夹角为()A. 43°B. 53°C. 47°D. 90°2. 等腰三角形周长为13cm,其中一边长为3cm,则该等腰三角形底边长()A. 7cmB. 3cmC. 7cm或3cmD. 5cm3. 等腰三角形的两个内角的比是1:2,则这个等腰三角形是()A. 锐角三角形B. 直角三角形C. 锐角三角形或直角三角形D. 以上结论都不对4. 已知等腰三角形的一个外角等于70°,则底角的度数为()A. 110°B. 55°C. 35°D. 不能确定5. 等腰三角形一腰上的高与底边所成角为36°,这个等腰三角形的顶角为()A. 36°B. 72°C. 36°或72°D. 54°二. 填空题:1. 如果等腰三角形一个角是45°,那么另外两个角的度数为2. 等腰三角形一个外角等于110°,则底角的度数是3. 等腰三角形互相重合4. 等腰三角形底边长为10,则其腰长x的范围是5. 等腰三角形的底边长为5,一腰上中线把这个三角形周长分为两部分,它们的差为3,则腰长为三. 解答题:1. 如图,△ABC中,AB=AC,BC=BD,AD=DE=EB求∠A的度数2.如图,CA=CB,DF=DB,AE=AD 求∠A的度数A B3. 如图,△ABC中,AB=AC,D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,求∠AFD的度数4. 如图,△ABC中,AB=AC,BC=BD=ED=EA 求∠A的度数设∠A为xC FDB5. 如图,△ABC 中,AD 平分∠BAC ,若AC=AB+BD求∠B :∠C 的值四、证明题:7. 如图,△ABC 中,∠ABC,∠CAB 的平分线交于点P ,过点P 作DE ∥AB ,分别交BC 、AC 于点D 、E求证:DE=BD+AE8. 如图,△DEF 中,∠EDF=2∠E ,FA ⊥DE 于点A ,问:DF 、AD 、AE 间有什么样的大小关系C B ADE P B CD A D F E9. 如图,△ABC中,∠B=60°,角平分线AD、CE交于点O求证:AE+CD=AC10. 如图,△ABC中,AB=AC, ∠A=100°,BD平分∠ABC, 求证:BC=BD+AD OABCDEAC。
八年级数学上册《第十三章 等腰三角形》同步练习题及答案(人教版)

八年级数学上册《第十三章 等腰三角形》同步练习题及答案(人教版)学校:___________班级:___________姓名:___________考号:___________一、选择题:1.若等腰三角形的两边长分别为4和8,则它的周长为( )A .12B .16C .20D .16或202.如图,是屋架设计图的一部分,立柱BC 垂直于横梁AC ,AB =12m ,∠A =30°,则立柱BC 的长度为( )A .4mB .6mC .8mD .12m3.如图ABC 、ADE 中C 、D 两点分别在边AE 、AB 上,BC 与DE 相交于F 点.若BD CD CE == 104ADC ACD ∠+∠=︒则DFC ∠的度数为( ).A .104︒B .118︒C .128︒D .136︒4.如图 ABC 中 90ACB ∠=︒ , 60CAB ∠=︒ 动点P 在斜边AB 所在的直线m 上运动,连结PC ,那点P 在直线m 上运动时,能使图中出现等腰三角形的点P 的位置有( )A .6个B .5个C .4个D .3个5.如图,△ABC 是等边三角形,点D 是BC 边上任意一点,DE ⊥AB 于点E ,DF ⊥AC 于点F ,若等边三角形的高为4,则DE+DF =( )A .1B .2C .3D .46.如,AOB ADC ≌,90O D ∠∠︒==记αOAD ∠=,βABO ∠=当BC OA 时,α与β之间的数量关系为( )A .αβ=B .α2β=C .αβ90+︒=D .α2β180+︒=7.如图,CD 是等腰三角形ABC 底边AB 上的中线,BE 平分ABC ∠,交CD 于点E ,AC=6,DE=2则BCE 的面积是( )A .4B .6C .8D .128.如图,已知△ABC 中,∠B =50°,P 为△ABC 内一点,过点P 的直线MN 分别交AB ,BC 于点M 、N .若M 在PA 的中垂线上,N 在PC 的中垂线上,则∠APC 的度数为( )A .100°B .105°C .115°D .120°二、填空题:9.在△ABC 中,AB=AC ,其周长为20cm ,若AB=8cm ,则BC= cm.10.如图,在ABC 中70A ∠=︒,30C ∠=︒点D 为AC 边上一点,过点D 作DE //AB ,交BC 于点E ,且DE BE =,连接BD ,则BDC ∠的度数是 .11.如图,在Rt △ABC 中90ACB ∠=︒,AC=BC=2,△ACD 为等边三角形,连接BD ,则△BCD 的面积为 .12.如图,在△ABC 中,∠ABC 的角平分线和∠ACB 相邻的外角平分线CD 交于点D ,过点D 作DE ∥BC 交AB 于E ,交AC 于G ,若EG=2,且GC=6,则BE 长为 .13.如图,在△ABC 中,AB=20cm ,AC=12cm ,点P 从点B 出发以每秒3cm 速度向点A 运动,点Q 从点A 同时出发以每秒2cm 速度向点C 运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ 是以PQ 为底的等腰三角形时,运动的时间是 秒.三、解答题:14.如图,点0是∠ABC ,∠ACB 的平分线的交点,OE ∥AB 交BC 于点E ,OF ∥AC 交BC 于点F ,BC=5.求△OEF 的周长.15.如图,已知D 是∠ABC 的平分线与△ABC 的外角平分线的交点,DE ∥BC ,交AB 于点E ,交AC 于点F.求证:EF=BE-CF16.如图,在ABC 中11AB AC ==,120BAC ∠=︒且AD 是ABC 的中线,AE 是ADB 的角平分线,DF AB交AE的延长线于点F,求DF的长.17.如图,在四边形 ABCD 中,AB=AD,∠BAD=120°,∠ABC=∠ADC=90°,E,F 分别是 BC, CD 上的点,且∠EAF=60°.(1)若 BE=DF,求证:△AEF 为等边三角形;(2)求证:EF=BE+DF.18.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC 的平分线交BC于点G,连接FG.(1)求∠DFG的度数.(2)设∠BAD=θ,当θ为何值时,△DFG为等腰三角形参考答案:1.C 2.B 3.C 4.C 5.D 6.B 7.B 8.C 9.410.110°11.112.813.414.解:∵OB,OC分别是∠ABC,∠ACB的平分线∴∠1=∠2,∠4=∠5∵OE∥AB,OF∥AC∴∠1=∠3,∠4=∠6∴∠2=∠3,∠5=∠6∴BE=OE,OF=FC∴BC=BE+EF+FC=OF+OE+EF∵BC=5∴OF+OE+EF=5∴△OEF的周长=OF+OE+EF=5.15.证明:∵BD平分∠ABC∴∠ABD=∠CBD∵DE∥BC∴∠EDB=∠CBD∴∠ABD=∠EDB∴DE=BE同理DF=CF∵EF=DE-DF∴EF=BE-CF.16.解:∵△ABC是等腰三角形,D为底边的中点∴AD⊥BC,∠BAD=∠CAD∵∠BAC=120°∴∠BAD=60°,∠ADB=90°∵AE是∠BAD的角平分线∴∠DAE=∠EAB=30°.∵DF//AB∴∠F=∠BAE=30°.∴∠DAF=∠F=30°∴AD=DF.∵AB=11,∠B=30°∴1111 5.522AD AB==⨯=∴DF=5.517.(1)证明:∵∠ABC=∠ADC= 90︒,BE=DF,AB=AD∴△ABE≌△ADF∴AE=AF又∵∠EAF= 60︒∴△AEF为等边三角形;(2)证明:如图,延长CD至G,使得DG=BE,连接AG,可得到∵AD⊥DF∴∠ABE=∠ADG= 90︒∵AB=AD,DG=BE∴△ABE≌△ADG∴AE=AG,∠BAE=∠GAD又∵∠BAE+∠EAD= 120︒∴∠GAD+∠EAD= 120︒又∵∠EAF= 60︒∴∠GAF= 60︒ =∠EAF又∵AE=AG,AF=AF∴△EAF≌△GAF∴EF=GF=GD+DF=BE+DF∴EF=BE+DF.18.(1)解:∵AB=AC,∠BAC=100°∴∠B=∠C=40°.∵△ABD和△AFD关于直线AD对称∴△ADB≌△ADF∴∠B=∠AFD=40°,AB=AF∠BAD=∠FAD=θ∴AF=AC.∵AG平分∠FAC∴∠FAG=∠CAG.在△AGF和△AGC中{AF=AC∠FAG=∠CAG AG=AG∴△AGF≌△AGC(SAS) ∴∠AFG=∠C.∵∠DFG=∠AFD+∠AFG∴∠DFG=∠B+∠C=40°+40°=80°.答:∠DFG的度数为80°;(2)解:当GD=GF时∴∠GDF=∠GFD=80°.∵∠ADG=40°+θ∴40°+80°+40°+θ+θ=180°∴θ=10°.当DF=GF时∴∠FDG=∠FGD.∵∠DFG=80°∴∠FDG=∠FGD=50°.∴40°+50°+40°+2θ=180°∴θ=25°.当DF=DG时∴∠DFG=∠DGF=80°∴∠GDF=20°∴40°+20°+40°+2θ=180°∴θ=40°.∴当θ=10°,25°或40°时,△DFG为等腰三角形。
八年级数学上册《第二章 等腰三角形》练习题-含答案(湘教版)

八年级数学上册《第二章 等腰三角形》练习题-含答案(湘教版)一、选择题1.等腰三角形的一边长为3 cm ,周长为19 cm ,则该三角形的腰长为( )A.3 cmB.8 cmC.3 cm 或8 cmD.以上答案均不对2.在等腰三角形ABC 中,AB=AC,其周长为20cm,则边AB 的取值范围是( ).A.1cm<AB<4cmB.5cm<AB<10cmC.4cm<AB<8cmD.4cm<AB<10cm3.已知等腰△ABC 的底边BC=8,且|AC-BC|=2,那么腰AC 的长为( )A.10或6B.10C.6D.8或64.若a,b 为等腰△ABC 的两边,且满足520a b --=,则△ABC 的周长为 ( )A.9B.12C.15或12D.9或125.若三角形三个内角的比为1:2:3,则这个三角形是( )A.锐角三角形B.直角三角形C.等腰三角形D.钝角三角形6.在△ABC 中,∠A=70°,∠B=55°,则△ABC 是( )A.钝角三角形B.等腰三角形C.等边三角形D.等腰直角三角形7.等腰三角形的两边长分别为5和11,则它的周长为( )A .21B .21或27C .27D .258.在等腰△ABC 中,AB=AC ,其周长为20cm ,则AB 边的取值范围是( )A .1cm <AB <4cm B .5cm <AB <10cmC .4cm <AB <8cmD .4cm <AB <10cm二、填空题9.如果等腰三角形的周长为29,其中一边长为7,则这个等腰三角形的底边长是 .10.已知等腰△ABC 的周长为10,若设腰长为x ,则x 的取值范围是 .11.一个等腰三角形的底边长为5 cm ,一腰上的中线把这个三角形的周长分成的两部分之差是3 cm ,则它的腰长是12.如图,l ∥m ,等腰直角三角形ABC 的直角顶点C 在直线m 上,若∠β=20°,则∠α的度数为________13.一副三角形叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为度;14.若等腰三角形的腰长为6,则它的底边长a的取值范围是________;若等腰三角形的底边长为4,则它的腰长b的取值范围是_______.三、解答题15.已知等腰三角形一腰上的中线把这个三角形的周长分成 9cm和 15cm两部分求这个三角形的腰长。
人教版八年级数学上册 等腰三角形专题练习(无答案)

等腰三角形专题练习一、等腰三角形中分类问题.知识点:①无图;②边或角指代不明确;③三角形形状不确定.1.(1)等腰三角形一边长为4cm,周长为14cm,则另两边长为.(2)等腰三角形一边长为4cm,周长为16cm,则另两边长为_ .2.(1)等腰三角形一角为40°,则另两角的度数为_ .(2)等腰三角形一外角为100°,则三个内角的度数为.3.等腰三角形一腰上的高等于腰长的一半,则其顶角度数为.4.等腰三角形一腰上的高与腰边的夹角为40°,则这个三角形的顶角的度数为_.5.等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为50°,则其底角度数为_ _.6.等腰三角形的底边长为10cm,自底边的一个顶点作腰的中线,将这个三角形的周长分成两部分,如果一部分比另一部分长3cm,那么这个等腰三角形的腰长为.7.若两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形第三边所对的角之间的关系是.8.如图,已知直线m⊥直线n于点O,点A到m、n的距离相等,在直线m或n上确定一点P,使 OAP为等腰三角形.试回答:(1)符合条件的点P共有______ 个;(2)若符合条件的点P在直线m上,请直接写出∠OAP的所有可能的度数.二、等腰三角形中角度计算问题1.如图,△ABC中,AB=AC,BC=BD=DA,则∠A=.2.如图,△ABC中,AD=AC,BE=BC,且∠A+∠B=50°,则∠ECD=_.3.如图,△ABC中,AB=AC=CE,且AE=BE,AD⊥BC于D,则∠BAD=.4.如图,△ABC中,D、E是BC上的点,且分别在AB、AC的垂直平分线上,若∠BAC=110°,则∠DAE=.5.如图,等边△ABC中,BD中线,延长BC至E使CE=CD,则∠E=.6.如图,等边OABC中,DA=DB,∠DBE=∠DBC,且BE=BA,则∠E=.三、等腰三角形中周长问题知识点:等覆三角形、垂直平分战等性质的应用,关键是相等边的转换1.△ABC中,AB=AC,AC+BC=13.DE垂直平分AB,则△BCE的周长为_ _.2.BD平分∠ABC,CD平分∠ACB,过D作EF∥BC,EF=8cm,则BE+CF=_.3.BD平分∠ABC,CD平分∠ACB,DE∥BC,DF∥AC,若BC=10 cm,则△DEF的周长为_ _.4.△ABC中,D、E在BC上,且D、E分别在AB、AC的垂直平分线上,△ADE周长为10cm,则BC=_ .5.等腰Rt△ABC中,∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC,若BC=18cm,则△CDE的周长为__6.如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合;若∠ADB=30°,EH=4cm,BC = . 7.如图,∠MAN=16°,A1点在AM上,在AN上取一点A2,使A2A1=AA1,再在AM上取一点A3使A3A2=A2A1,如此一直作下去,到不能再作为止.那么作出的最后一点是8.如图,已知∠AOB=15°,点M在边OB上,且OM=4,点N和点P分别是OM和OA上的一个动点,则PM+PN的最小值为 .9.点C为∠AOB内一点.(1)在OA上求作点D,OB上求作点E,使△CDE的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB=30°,OC=10,求△CDE周长的最小值和此时∠DCE的度数.10 .如图,△ABC中,AB=AC=2,∠B=∠C=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BAD=20°时,∠EDC=_____°;(2)当DC等于多少时,△ABD≌△DCE?试说明理由;(3)△ADE能成为等腰三角形吗?若能,请求出此时∠BAD的度数;若不能,请说明理由.。
华东师大版八年级数学上册《13.3 等腰三角形》练习题及答案

华东师大版八年级数学上册《13.3 等腰三角形》练习题及答案班级:姓名:学号:分数:一、选择题1.等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )A.55°,55°B.70°,40°或70°,55°C.70°,40°D.55°,55°或70°,40°2.如果等腰三角形的一个底角为α,那么( )A.α不大于45°B.0°<α<90°C.α不大于90°D.45°<α<90°3.如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )A.∠B=∠CB.AD⊥BCC.AD平分∠BACD.AB=2BD4.等腰三角形的一条边长为6,另一边长为13,则它的周长为( )A.25B.25或32C.32D.195.若(a﹣4)2+|b﹣6|=0,则以a、b为边长的等腰三角形的周长为( )A.14B.16C.13D.14或166.如图,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )A.∠EBC=∠BACB.∠EBC=∠ABEC.AE=ECD.AE=BE7.在△ABC中,AB=c,BC=a,AC=b,下列条件不能判定△ABC是等腰三角形的是( )A.∠A∶∠B∶∠C=1∶1∶3B.a∶b∶c=2∶2∶3C.∠B=50°,∠C=80°D.2∠A=∠B+∠C8.如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( )A.1个B.3个C.4个D.5个9.如图,是四张形状不同的纸片,用剪刀沿一条直线将它们分别剪开(只允许剪一次),不能得到两个等腰三角形纸片的是( )om10.如图,在Rt△ABC中,∠C=30°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )A.4B.5C. 6D.7二、填空题11.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为 .12.等腰△ABC中,AB=AC,若∠A=40°,则∠B=_______.13.某中学的同学用下面的方法检测教室的房梁是否水平:在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点,同学们确信房梁是水平的,理由是.14.如图,在△ABC中,AD⊥BC于点D,请你再添加一个条件,确定△ABC是等腰三角形.你添加的条件是 .15.如图,OB、OC分别平分∠ABC与∠ACB,MN∥BC,若AB=24,AC=36,则△AMN 周长是 .16.如图,∠BOC=9°,点A在OB上,且OA=1.按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=.三、解答题17.如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.18.如图,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.19.如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.求证:△BDE是等腰三角形.20.如图,△ABC中,AB=AC,D、E分别是AB及AC延长线上的点,且BD=CE,连接DE交BC于点O.过点D作DH⊥BC,过E作EK⊥BC,垂足分别为H、K.(1)求证:DH=EK;(2)求证:DO=EO.21.如图,在△ABC中,AB=AC,点D、E、F分别在边AB,BC,AC上,且BD=CE,BE=CF.(1)求证:ED=EF;(2)当点G是DF的中点时,请判断EG和DF的位置关系,并说明理由.22.如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,连接DA并延长,交y轴于点E.①△OBC与△ABD全等吗?判断并证明你的结论;②当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?答案1.D2.B3.D.4.C5.D.6.A.7.D.8.D9.B10.C.11.答案为:3cm.12.答案为:70°.13.答案为:等腰三角形的底边上的中线、底边上的高重合.14.答案为:BD=CD(答案不唯一).15.答案为:60.16.答案为:9.17.解:∵AB=AC,DA=DB∴∠B=∠C=∠BAD∵CA=CD∴∠CDA=∠CAD又∠CDA=∠B+∠BAD=2∠B=2∠C∴∠CAD=2∠C在△ACD中,∠C+∠CDA+∠CAD=180°∴2∠C+2∠C+∠C=180°∴∠C=36°∴∠BAD=36°,∠CAD=2∠C=72°∴∠BAC=∠BAD+∠CAD=36°+72°=108°.18.解:EF⊥BC,理由为:证明:∵AB=AC,AD⊥BC∴∠BAD=∠CAD∵AE=AF∴∠E=∠EFA∵∠BAC=∠E+∠EFA=2∠EFA∴∠EFA=∠BAD∴EF∥AD∵AD⊥BC∴EF⊥BC则EF与BC的位置关系是垂直.19.证明:∵AD平分∠BAC∴∠BAD=∠DAC∵DE∥AC∴∠ADE=∠DAC.∴∠BAD=∠ADE∵AD⊥BD∴∠ADB=90°∴∠BAD+∠B=90°.∵∠BDE+∠ADE=90°∴∠B=∠BDE∴BE=DE∴△BDE是等腰三角形.20.解:(1)∵DH⊥BC,EK⊥BC∴∠DHB=∠K=90°∵AB=AC∴∠B=∠ACB又∵∠ACB=∠ECK∴∠B=∠ECK在△BDH和△CEK中∵∠ACB=∠ECK,∠B=∠ECK,BD=CE ∴△BDH≌△CEK(AAS).∴DH=EK.(2)∵DH⊥AC,EK⊥BC∴∠DHO=∠K=90°由(1)得EK=DH在△DHO和△EKO中∵∠DHO=∠K,∠DOH=∠EOK,DH=EK∴△DHO≌△EKO(AAS)∴DO=EO.21.证明:(1)∵AB=AC∴∠B=∠C在△BDE和△CEF中∴△BDE≌△CEF∴ED=EF;(2)又∵点G是DF的中点,则EG垂直平分DF. 理由是:等腰三角形底边上的高线与中线重合.22.解:(1)△OBC≌△ABD.证明:∵△AOB,△CBD都是等边三角形∴OB=AB,CB=DB,∠ABO=∠DBC∴∠OBC=∠ABC在△OBC和△ABD中∴△OBC≌△ABD(SAS);(2)∵△OBC≌△ABD∴∠BOC=∠BAD=60°又∵∠OAB=60°∴∠OAE=180°﹣60°﹣60°=60°∴∠EAC=120°,∠OEA=30°∴以A,E,C为顶点的三角形是等腰三角形时,AE和AC是腰∵在Rt△AOE中,OA=1,∠OEA=30°∴AE=2∴AC=AE=2∴OC=1+2=3∴当点C的坐标为(3,0)时,以A,E,C为顶点的三角形是等腰三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图,在△ABC中,AB=AC=10,AD=BD,△BCD的周长为17,那么BC的长是()A.5B.7C.12D.以上都不对2.如图,在△ABC中,AB=AC,BD⊥AC,则∠DBC等于()A.∠ABC B.2∠A C.∠A D.∠A3.如图,下列条件不能推出△ABC是等腰三角形的是()A.∠B=∠C B.AD⊥BC,∠BAD=∠CADC.AD⊥BC,BD=CD D.AD⊥BC,∠BAD=∠ACD4.在平面直角坐标系中,点A坐标为(2,2),点P在x轴上运动,当以点A,P、O为顶点的三角形为等腰三角形时,点P的个数为()A.2个B.3个C.4个D.5个5.如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为()A.5B.5或8C.D.4或6.如图,在△MBC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为()A.7B.8C.9D.107.如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有()A.3个B.4个C.5个D.6个8.如图,在△ABC中,BD平分∠ABC,ED∥BC,已知AB=5,AD=2,则△AED 的周长为()A.4B.5C.6D.79.如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=36°,那么∠BED 的度数为()A.108°B.120°C.126°D.144°10.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC 交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BGC=90°+∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,=mn.其中正确的结论有()则S△AEFA.①②④B.①③④C.①②③D.①②③④11.如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.随x,m,n的值而定12.等腰三角形一腰上的中线将其周长分为8和12两部分,则它的底边长是.13.如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=17cm,则△ODE的周长是cm.14.如图,若B,D,F在AN上,C,E在AM上,且AB=BC=CD=ED=EF,∠A=20o,则∠FEM=.15.如图,△ABC为等边三角形,∠BAD=15°,∠DAE=80°,AD=AE,则∠EFC=°.16.如图,在△ABC中,AB=BC=4,AC=3,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E、D,则DE的长为.17.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC 是等腰三角形的是.①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.18.设a、b分别是等腰三角形的两条边的长,m是这个三角形的周长,当a、0b、m满足方程组时,m的值是.19.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得的锐角为46°,则底角∠B的大小为.20.如图所示,在△ABC中,∠B=∠C,D是BC上一点,E是AC上一点,连接AD、DE,若∠ADE=∠AED,∠EDC=15°,则∠BAD=.21.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:(1)EF⊥AB;(2)△ACF为等腰三角形.22.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.(1)点M、N运动几秒后,M、N两点重合?(2)点M、N运动几秒后,可得到等边三角形△AMN?(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.23.如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.(1)试求∠DAE的度数.(2)如果把原题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?为什么?24.如图,在△ABC中,AB=AC,∠B=30°,D为BC边上一点,∠DAB=45°.(1)求∠DAC的度数;(2)请说明:AB=CD.25.如图,在△ABC中,AD是BC边上的高线,BE⊥AC于点E,∠BAD=∠CBE.求证:AB=AC.26.现在给出两个三角形,请你把图(1)分割成两个等腰三角形,把图(2)分割成三个等腰三角形.要求:在图(1)、(2)上分割:标出分割后的三角形的各内角的度数.27.如图1,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC的平分线BD交边AC 于点D.(1)求证:△BCD为等腰三角形;(2)若∠BAC的平分线AE交边BC于点E,如图2,求证:BD+AD=AB+BE;(3)若∠BAC外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立?直接写出正确的结论.28.如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC 上,且AD=AE,连接DE.(1)如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;(2)如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;(3)当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE 的数量关系,并说明理由.参考答案与试题解析一.选择题(共11小题)1.如图,在△ABC中,AB=AC=10,AD=BD,△BCD的周长为17,那么BC的长是()A.5B.7C.12D.以上都不对【解答】解:∵AD=BD,AC=AD+CD,∴BD+CD=AD+CD=AC,=BC+CD+BD=BC+AC=BC+10=17,∴C△BCD∴BC=7.故选:B.2.如图,在△ABC中,AB=AC,BD⊥AC,则∠DBC等于()A.∠ABC B.2∠A C.∠A D.∠A【解答】解:∵AB=AC,∴∠ABC=∠C=(180°﹣∠A),∵BD⊥AC,∴∠DBC=90°﹣∠C=90°﹣(180°﹣∠A)=∠A,故选:C.3.如图,下列条件不能推出△ABC是等腰三角形的是()A.∠B=∠C B.AD⊥BC,∠BAD=∠CADC.AD⊥BC,BD=CD D.AD⊥BC,∠BAD=∠ACD【解答】解:A、∵∠B=∠C,∴AB=AC,即△ABC是等腰三角形,故本选项不符合题意;B、∵AD⊥BC,∴∠ADB=∠ADC=90°,在△ADB和△ADC中∴△ADB≌△ADC(ASA),∴AB=AC,即△ABC是等腰三角形,故本选项不符合题意;C、∵AD⊥BC,BD=CD,∴AB=AC,即△ABC是等腰三角形,故本选项不符合题意;D、根据AD⊥BC和∠BAD=∠ACD不能推出△ABC是等腰三角形,故本选项符合题意;故选:D.4.在平面直角坐标系中,点A坐标为(2,2),点P在x轴上运动,当以点A,P、O为顶点的三角形为等腰三角形时,点P的个数为()A.2个B.3个C.4个D.5个【解答】解:如图,当OA=OP时,可得P1、P2满足条件;当PA=PO时,可得P3满足条件;当AO=AP时,可得P4满足条件,故选:C.5.如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为()A.5B.5或8C.D.4或【解答】解:如图,∵在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,∴由勾股定理,得BC==6cm.①当AP=AC时,2t=8,则t=4;②当AP=PC时,过点P作PD⊥AC于点D,则AD=CD,PD∥BC,∴PD是△ABC的中位线,∴点P是AB的中点,∴2t=5,即t=;③若AC=PC=8cm时,与PC<AC矛盾,不和题意.综上所述,t的值是4或;故选:D.6.如图,在△MBC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为()A.7B.8C.9D.10【解答】解:∵BO为∠ABC的平分线,CO为∠ACB的平分线,∴∠ABO=∠CBO,∠ACO=∠BCO,∵MN∥BC,∴∠MOB=∠OBC,∠NOC=∠BCO,∴∠ABO=∠MOB,∠NOC=∠ACO,∴MB=MO,NC=NO,∴MN=MO+NO=MB+NC,∵AB=4,AC=6,∴△AMN周长为AM+MN+AN=AM+MB+AN+NC=AB+AC=10,故选:D.7.如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有()A.3个B.4个C.5个D.6个【解答】解:∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠DBC=36°,∴∠BDC=180°﹣36°﹣72°=72°,∵DE∥AB,∴∠EDB=∠ABD=36°,∴∠EDC=72°﹣36°=36°,∴∠DEC=180°﹣72°﹣36°=72°,∴∠A=∠ABD,∠DBE=∠BDE,∠DEC=∠C,∠BDC=∠C,∠ABC=∠C,∴△ABC、△ABD、△DEB、△BDC、△DEC都是等腰三角形,共5个,故选:C.8.如图,在△ABC中,BD平分∠ABC,ED∥BC,已知AB=5,AD=2,则△AED 的周长为()A.4B.5C.6D.7【解答】解:∵BD平分∠ABC,∴∠ABD=∠CBD,∵ED∥BC,∴∠EDB=∠CBD,∴∠ABD=∠EDB,∴EB=ED,∴△AED的周长=AE+DE+AD=AE+BE+AD=AB+AD=7,故选:D.9.如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=36°,那么∠BED 的度数为()A.108°B.120°C.126°D.144°【解答】解:∵AE平分∠BAC∴∠BAE=∠CAE=36°∵ED∥AC∴∠CAE+∠DEA=180°∴∠DEA=180°﹣36°=144°∵∠AED+∠AEB+∠BED=360°∴∠BED=360°﹣144°﹣90°=126°.故选:C.10.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC 交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BGC=90°+∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,=mn.其中正确的结论有()则S△AEFA.①②④B.①③④C.①②③D.①②③④【解答】解:①∵∠ABC和∠ACB的平分线相交于点G,∴∠EBG=∠CBG,∠BCG=∠FCG.∵EF∥BC,∴∠CBG=∠EGB,∠BCG=∠CGF,∴∠EBG=∠EGB,∠FCG=∠CGF,∴BE=EG,GF=CF,∴EF=EG+GF=BE+CF,故本小题正确;②∵∠ABC和∠ACB的平分线相交于点G,∴∠GBC+∠GCB=(∠ABC+∠ACB)=(180°﹣∠A),∴∠BGC=180°﹣(∠GBC+∠GCB)=180°﹣(180°﹣∠A)=90°+∠A,故本小题正确;③∵∠ABC和∠ACB的平分线相交于点G,∴点G是△ABC的内心,∴点G到△ABC各边的距离相等,故本小题正确;④连接AG,∵点G是△ABC的内心,GD=m,AE+AF=n,∴S=AE•GD+AF•GD=(AE+AF)•GD=nm,故本小题错误.△AEF故选:C.11.如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.随x,m,n的值而定【解答】解:将△ABM绕点B顺时针旋转60°得到△CBH.连接HN.∵△ABC是等边三角形,∴∠ABC=∠ACB=∠A=60°,∵∠MON=30°,∴∠CBH+∠∠ABM+∠CBN=30°,∴∠NBM=∠NBH,∵BM=BH,BN=BN,∴△NBM≌△NBH,∴MN=NH=x,∵∠BCH=∠A=60°,CH=AM=n,∴∠NCH=120°,∴x,m,n为边长的三角形△NCH是钝角三角形,故选:C.二.填空题(共9小题)12.等腰三角形一腰上的中线将其周长分为8和12两部分,则它的底边长是或4.【解答】解:设等腰三角形的腰长是x,底边是y.根据题意,得:或,解得或.所以它的底边是或4.故答案为:或4.13.如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=17cm,则△ODE的周长是17cm.【解答】解:∵BO平分∠ABC,∴∠ABO=∠DBO,又OD∥AB,∴∠ABO=∠DOB,∴∠DBO=∠DOB,∴OD=BD,同理OE=CE,∵BC=17cm,则△ODE的周长c=OD+DE+OE=BD+DE+EC=BC=17cm.故答案为17.14.如图,若B,D,F在AN上,C,E在AM上,且AB=BC=CD=ED=EF,∠A=20o,则∠FEM=100°.【解答】解:∵∠A=20°,AB=BC,∴∠A=∠ACB=20°,∠CBD=∠A+∠ACB=20°+20°=40°;∵BC=CD,∴∠CBD=∠CDB=40°,∴∠ECD=∠A+∠CDA=30°(外角定理);∵CD=DE,∴∠DCE=∠DEC=60°,∴∠EDF=∠A+∠AED=80°;又∵DE=EF,∴∠EDF=∠EFD=80°,∴∠FEM=∠A+∠EFD=20°+80°=100°.故答案为100°.15.如图,△ABC为等边三角形,∠BAD=15°,∠DAE=80°,AD=AE,则∠EFC=85°.【解答】解:∵△ABC是等边三角形,∠BAD=15°,∠DAE=80°,∴∠CAE=∠BAE﹣∠BAC=15°+80°﹣60°=35°∵∠DAE=80°,AD=AE,∴∠ADE=∠E=(180°﹣80°)=50°,∵∠EFC是△AEF的外角,∴∠EFC=∠CAE+∠E=35°+50°=85°.故答案为85.16.如图,在△ABC中,AB=BC=4,AC=3,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E、D,则DE的长为7.【解答】解:∵DE∥BC,∴∠E=∠EBC.∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠E=∠ABE,∴AB=AE.同理可得:AD=AC,∴DE=AD+AE=AB+AC=4+3=7,故答案为:717.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC 是等腰三角形的是②③④.①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.【解答】解:应添加的条件是②③④;证明:②当∠BAD=∠CAD时,∵AD是∠BAC的平分线,且AD是BC边上的高;则△ABD≌△ACD,∴△BAC是等腰三角形;③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF;∵AB+BD=CD+AC,∴DE=DF,又AD⊥BC;∴△AEF是等腰三角形;∴∠E=∠F;∵AB=BE,∴∠ABC=2∠E;同理,得∠ACB=2∠F;∴∠ABC=∠ACB,即AB=AC,△ABC是等腰三角形;④△ABC中,AD⊥BC,根据勾股定理,得:AB2﹣BD2=AC2﹣CD2,即(AB+BD)(AB﹣BD)=(AC+CD)(AC﹣CD);∵AB﹣BD=AC﹣CD①,∴AB+BD=AC+CD②;∴①+②得:,2AB=2AC;∴AB=AC,∴△ABC是等腰三角形故答案为:②③④.18.设a、b分别是等腰三角形的两条边的长,m是这个三角形的周长,当a、0b、m满足方程组时,m的值是5或.【解答】解:①若a是腰长,b是底边,则2a+b=m,∵a、b、m满足方程组,把b=m﹣2a代入解得:m=4,a=1,b=2,∵a+a=1+1<2=b,不符合三角形任意两边之和大于第三边,∴m=4舍去;②若b是腰长,a是底边,则2b+a=m,∵a、b、m满足,把a=m﹣2b代入解得:m=5,b=.③若a=b,则a、b是腰,则,解得m=,a=,+>2,符合三角形的三边关系.故答案为:5或.19.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得的锐角为46°,则底角∠B的大小为68°或22°.【解答】解:(1)当AB的中垂线MN与AC相交时,∵∠AMD=90°,∴∠A=90°﹣46°=44°,∵AB=AC,∴∠B=∠C==68°;(2)当AB的中垂线MN与CA的延长线相交时,∴∠DAB=90°﹣46°=44°,∵AB=AC,∴∠B=∠C=∠DAB=22°.故答案为:68°或22°.20.如图所示,在△ABC中,∠B=∠C,D是BC上一点,E是AC上一点,连接AD、DE,若∠ADE=∠AED,∠EDC=15°,则∠BAD=30°.【解答】解:∵∠AED=∠C+∠EDC=∠C+15°,∠ADE=∠AED,∴∠ADC=∠ADE+∠EDC=∠AED+∠EDC=∠C+30°.又∠ADC=∠B+∠BAD,∠B=∠C,∴∠BAD=30°.故答案为30°.三.解答题(共8小题)21.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:(1)EF⊥AB;(2)△ACF为等腰三角形.【解答】证明:(1)∵AB=AC,∠BAC=36°,∴∠ABC=72°,又∵BD是∠ABC的平分线,∴∠ABD=36°,∴∠BAD=∠ABD,∴AD=BD,又∵E是AB的中点,∴DE⊥AB,即FE⊥AB;(2)∵FE⊥AB,AE=BE,∴FE垂直平分AB,∴AF=BF,∴∠BAF=∠ABF,又∵∠ABD=∠BAD,∴∠FAD=∠FBD=36°,又∵∠ACB=72°,∴∠AFC=∠ACB﹣∠CAF=36°,∴∠CAF=∠AFC=36°,∴AC=CF,即△ACF为等腰三角形.22.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.(1)点M、N运动几秒后,M、N两点重合?(2)点M、N运动几秒后,可得到等边三角形△AMN?(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.【解答】解:(1)设点M、N运动x秒后,M、N两点重合,x×1+12=2x,解得:x=12;(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图①,AM=t×1=t,AN=AB﹣BN=12﹣2t,∵三角形△AMN是等边三角形,∴t=12﹣2t,解得t=4,∴点M、N运动4秒后,可得到等边三角形△AMN.(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,由(1)知12秒时M、N两点重合,恰好在C处,如图②,假设△AMN是等腰三角形,∴AN=AM,∴∠AMN=∠ANM,∴∠AMC=∠ANB,∵AB=BC=AC,∴△ACB是等边三角形,∴∠C=∠B,在△ACM和△ABN中,∵,∴△ACM≌△ABN,∴CM=BN,设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,∴CM=y﹣12,NB=36﹣2y,CM=NB,y﹣12=36﹣2y,解得:y=16.故假设成立.∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M、N运动的时间为16秒.23.如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.(1)试求∠DAE的度数.(2)如果把原题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?为什么?【解答】解:(1)∵△ABC中,∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,∵BD=BA,CE=CA.∴∠BAD=(180°﹣45°)÷2,∠CAE=45°÷2,∴∠DAE=90°﹣∠BAD+∠CAE=45°.(2)不变.∠DAE=90°﹣+∠ACB=(∠B+∠ACB)=45°,从上式可看出当AB和AC不相等时,∠B+∠ACB也是定值为90°.所以不变.24.如图,在△ABC中,AB=AC,∠B=30°,D为BC边上一点,∠DAB=45°.(1)求∠DAC的度数;(2)请说明:AB=CD.【解答】(1)解:∵AB=AC,∴∠B=∠C=30°,∵∠C+∠BAC+∠B=180°,∴∠BAC=180°﹣30°﹣30°=120°,∵∠DAB=45°,∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;(2)证明:∵∠DAB=45°,∴∠ADC=∠B+∠DAB=75°,∴∠DAC=∠ADC,∴DC=AC,∵AB=AC,∴AB=CD.25.如图,在△ABC中,AD是BC边上的高线,BE⊥AC于点E,∠BAD=∠CBE.求证:AB=AC.【解答】证明:∵在△ABC中,AD是BC边上的高线,BE⊥AC于点E,∴∠ADB=∠BEC=90°.∴∠ABC+∠BAD=∠C+∠CBE=90°.又∵∠BAD=∠CBE,∴∠ABC=∠C.∴AB=AC.26.现在给出两个三角形,请你把图(1)分割成两个等腰三角形,把图(2)分割成三个等腰三角形.要求:在图(1)、(2)上分割:标出分割后的三角形的各内角的度数.【解答】解:如图所示:27.如图1,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC的平分线BD交边AC 于点D.(1)求证:△BCD为等腰三角形;(2)若∠BAC的平分线AE交边BC于点E,如图2,求证:BD+AD=AB+BE;(3)若∠BAC外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立?直接写出正确的结论.【解答】证明:(1)如图1,在△ABC中,∠BAC=75°,∠ACB=35°,∴∠ABC=180°﹣∠BAC﹣∠ACB=70°,(2分)∵BD平分∠ABD,∴∠DBC=∠ABD=35°,(3分)∴∠DBC=∠ACB=35°,∴△BCD为等腰三角形;(4分)(2)证法一:如图2,在AC上截取AH=AB,连接EH,由(1)得:△BCD为等腰三角形,∴BD=CD,∴BD+AD=CD+AD=AC,(6分)∵AE平分∠BAC,∴∠EAB=∠EAH,∴△ABE≌△AHE,∴BE=EH,∠AHE=∠ABE=70°,(8分)∴∠HEC=∠AHE﹣∠ACB=35°,∴EH=HC,∴AB+BE=AH+HC=AC,∴BD+AD=AB+BE;(10分)证法二:如图3,在AB的延长线上取AF=AC,连接EF,由(1)得:△BCD为等腰三角形,且BD=CD,∴BD+AD=CD+AD=AC,∵AE平分∠BAC,∴∠EAF=∠EAC,∴△AEF≌△AEC,∴∠F=∠C=35°,(8分)∴BF=BE,∴AB+BE=AB+BF=AF,∴BD+AD=AB+BE;(10分)(3)正确结论:BD+AD=BE﹣AB,理由是:如图4,在BE上截取BF=AB,连接AF,∵∠ABC=70°,∴∠AFB=∠BAF=35°,∵∠BAC=75°,∴∠HAB=105°,∵AE平分∠HAB,∴∠EAB=∠HAB=52.5°,∴∠EAF=52.5°﹣35°=17.5°=∠AEF=17.5°,∴AF=EF,∵∠AFC=∠C=35°,∴AF=AC=EF,∴BE﹣AB=BE﹣BF=EF=AC=AD+CD=AD+BD.(12分)28.如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC 上,且AD=AE,连接DE.(1)如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;(2)如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;(3)当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE 的数量关系,并说明理由.【解答】解:(1)∵∠B=∠C=35°,∴∠BAC=110°,∵∠BAD=80°,∴∠DAE=30°,∴∠ADE=∠AED=75°,∴∠CDE=180°﹣35°﹣30°﹣75°=40°;(2)∵∠ACB=75°,∠CDE=18°,∴∠E=75°﹣18°=57°,∴∠ADE=∠AED=57°,∴∠ADC=39°,∵∠ABC=∠ADB+∠DAB=75°,∴∠BAD=36°;(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β①如图1,当点D在点B的左侧时,∠ADC=x°﹣α,∴,(1)﹣(2)得2α﹣β=0,∴2α=β;②如图2,当点D在线段BC上时,∠ADC=y°+α,∴,(2)﹣(1)得α=β﹣α,∴2α=β;③如图3,当点D在点C右侧时,∠ADC=y°﹣α,∴,(2)﹣(1)得2α﹣β=0,∴2α=β.综上所述,∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.。
