职业高校统计学课件平均指标作业答案
统计学(第二版)课件及习题答案《统计学》参考答案

《统计学》(教育部教材)习题参考答案第一章统计概述一、填空题1.数量方面定量认识2.统计总体同质性差异性大量性3.总体单位数量标志品质标志不变标志可变标志4.总体指标名称指标数值5.总量指标相对指标平均指标数量指标质量指标静态指标动态指标二、单项选择题1.B 2.C 3.A 4.B 5.B三、多项选择题1.ABDE 2.ABC 3.ABCD 4.ABD 5.ABD四、问答题1.什么是指标?指标和标志有何区别和联系?①统计指标简称指标,是指综合反映现象总体数量特征的概念(及其数值)。
②指标与标志有两点区别:一是说明的对象范围不同,即指标是说明总体特征的,标志是说明总体单位特征的;二是具体表现的表示方式不同,即指标的具体表现都用数值表示,标志的具体表现只有数量标志用数值表示,品质标志则用文字表示。
③指标与标志有密切联系:一是标志表现是计算指标数值的基础;二是两者随研究目的不同具有转化关系。
2.指标有哪些具体分类?指标按表现形式分为总量指标、相对指标和平均指标;按性质或内容分为数量指标和质量指标;按时间状况分为静态指标和动态指标。
3.什么是指标体系?设置指标体系有何意义?指标体系是指一系列相互联系的指标组成的整体。
单项指标的局限性和社会经济现象的复杂性,决定了在统计中必须科学地设置指标体系,以便从不同角度、不同侧面来反映现象的全貌和事物间的联系。
4. 统计工作过程分哪几个阶段?如何理解统计“质—量—质”的认识过程?统计工作过程大致分为统计设计、统计调查、统计整理和统计分析四个相对独立、相互衔接的阶段。
四个阶段基本体现了统计“质—量—质”的认识过程。
统计首先要对现象进行初步的定性(质的)认识,作出统计设计;然后根据设计要求去进行量的调查和整理;最后通过统计分析,揭示现象的本质特征及其变化规律性,达到高一级的质的认识,实现统计之目的。
第二章统计调查一、填空题1.准确及时全面(系统或经济)2.调查项目3.全部工业生产设备每台工业生产设备每个工业企业4.单一表一览表表头表体表脚5.调查得到的统计数字客观现象实际数量表现登记性代表性二、单项选择题1.A 2.C 3.C 4.C 5.B三、多项选择题1.BCDE 2.BCDE 3.ABD 4.ABCDE 5.ACE四、问答题1.什么是统计调查?统计调查有哪些种类?统计调查是根据统计设计的要求,采用科学的方式和方法,有计划、有组织地向总体单位登记其有关标志表现,以获取统计研究所需要的原始资料的工作过程。
统计学原理作业答案(1).doc

宁大专科《统计学原理》作业第一次作业一、单项选择题1、社会经济统计学研究对象(C )。
A、社会经济现象总体B、社会经济现象个体C、社会经济现象总体的数量方面D、社会经济现象的数量方面2、统计研究在( B )阶段的方法属于大量观察法。
A、统计设计B、统计调查C、统计整理D、统计分析3、、研究某市工业企业生产设备使用状况,那么,统计总体为( A )。
A、该市全部工业企业B、该市每一个工业企业C、该市全部工业企业每一台生产设备D、该市全部工业企业所有生产设备4、下列标志属于品质标志的是( C )。
A、工人年龄B、工人工资C、工人性别D、工人体重5、下列变量中,属于连续变量的是( C )。
A、企业数B、职工人数C、利润额D、设备台数6、把一个工厂的工人组成总体,那么每一个工人就是( A )。
A、总体单位B、数量标志C、指标D、报告单位7、几位工人的工资分别为1500元、1800元和2500元,这几个数字是( C )。
A、指标B、变量C、变量值D、标志8、变异的涵义是( A )。
A、统计中标志的不同表现。
B、总体单位有许多不同的标志。
C、现象总体可能存在各种各样的指标。
D、品质标志的具体表现。
9、销售额和库存额两指标( D )。
A、均为时点指标B、均为时期指标C、前者是时点指标,后者是时期指标D、前者是时期指标,后者是时点指标10、下列指标中属于时期指标的有( B )。
A、机器台数B、产量C、企业数D、库存额11、不同时点的指标数值( B )。
A、具有可加性B、不具有可加性C、可加或可减D、以上都不对12、某企业计划规定劳动生产率比上年提高5%,实际提高8%,则该企业劳动生产率计划完成程度为( B )。
A、86%B、102.86%C、60%D、160%13、某市2004年重工业增加值为轻工业增加值的85%,该指标是( C )。
A、比较相对指标B、结构相对指标C、比例相对指标D、计划相对指标二、简答题1、什么是总体和单位,举例说明。
统计学高教课后习题标准答案

统计学高教课后习题标准答案————————————————————————————————作者:————————————————————————————————日期:第一章1.什么是统计学?怎样理解统计学与统计数据的关系?答:统计学是一门收集、整理、显示和分析统计数据的科学。
统计学与统计数据存在密切关系,统计学阐述的统计方法来源于对统计数据的研究,目的也在于对统计数据的研究,离开了统计数据,统计方法以致于统计学就失去了其存在意义。
2.简要说明统计数据的来源答:统计数据来源于两个方面:直接的数据:源于直接组织的调查、观察和科学实验,在社会经济管理领域,主要通过统计调查方式来获得,如普查和抽样调查。
间接的数据:从报纸、图书杂志、统计年鉴、网络等渠道获得。
3.简要说明抽样误差和非抽样误差答:统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的,从理论上看,这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差,它是不可避免的,但可以控制的。
4.答:(1)有两个总体:A品牌所有产品、B品牌所有产品(2)变量:口味(如可用10分制表示)(3)匹配样本:从两品牌产品中各抽取1000瓶,由1000名消费者分别打分,形成匹配样本。
(4)从匹配样本的观察值中推断两品牌口味的相对好坏。
第二章、统计数据的描述思考题1描述次数分配表的编制过程答:分二个步骤:(1)按照统计研究的目的,将数据按分组标志进行分组。
按品质标志进行分组时,可将其每个具体的表现作为一个组,或者几个表现合并成一个组,这取决于分组的粗细。
按数量标志进行分组,可分为单项式分组与组距式分组单项式分组将每个变量值作为一个组;组距式分组将变量的取值范围(区间)作为一个组。
统计分组应遵循“不重不漏”原则(2)将数据分配到各个组,统计各组的次数,编制次数分配表。
2.解释洛伦兹曲线及其用途答:洛伦兹曲线是20世纪初美国经济学家、统计学家洛伦兹根据意大利经济学家帕累托提出的收入分配公式绘制成的描述收入和财富分配性质的曲线。
统计学课后习题答案(全)

<<统计学>>课后习题参考答案第四章1. 计划完成相对指标==⨯++%100%51%81102.9% 2. 计划完成相对指标=%9.97%100%41%61=⨯-- 3.4.5.解:(1)计划完成相对指标=%56.115%1004513131214=⨯+++(2)从第四年二季度开始连续四季的产量之和为:10+11+12+14=47天完成任务。
个月零该产品总共提前天完成的天数已提前完成任务,提前该产品到第五年第一季1510459010144514121110∴=--+++=6.解:计划完成相对指标=%75.126%100%1.0102005354703252795402301564=⨯⨯⨯++++++(2)156+230+540+279+325+470=2000(万吨) 所以正好提前半年完成计划。
7.8.略第五章 平均指标与标志变异指标1.甲X =.309343332313029282726=++++++++乙X =44.319403836343230282520=++++++++ AD 甲=}22.29303430333032303130303029302830273026=-+-+-+-+-+-+-+-+-AD 乙=}06.594044.313844.313644.313444.313244.313044.312844.312544.3120=-+-+-+-+-+-+-+-+-R 甲=34-26=8 R 乙=40-20=20σ甲 =9)3334()3033()3032()3031()3030()3029()3028()3027()3026(222222222-+-+-+-+-+-+-+-+-=2.58 σ乙=9)44.3140()44.3138()44.3136()44.3134()44.3132()44.3130()44.3128()44.3125()44.3120(222222222-+-+-+-+-+-+-+-+-=6.06V 甲=1003058.2⨯%=8.6% V 乙=%3.19%10044.3106.6=⨯ 所以甲组的平均产量代表性大一些. 2.解:计算过程如下表:甲X =.)(5.101780元= 乙X =(元)9708077600= 3.解:计算过程如下表:甲X =.4.11980=(件) 乙X =8.120809660=(件) σ甲=06.98075.6568=(件) σ乙=81.10809355=(件) V 甲=1004.11906.9⨯%=7.58% V 乙=%94.8%1008.12081.10=⨯ 所以甲厂工人的平均产量的代表性要高些.4. 解:()()94.761018102457047.7610121871871870775121873595128518757653550=⨯-+==⨯-+--+==++++⨯+⨯+⨯+⨯+⨯=e M M X 5.解:(1)上期的平均计划完成程度为:()()第六章元解解度为下期的平均计划完成程tH V P X P P P P /3.2884102950943.5062900255.3212800604.43210943.506255.321604.432:.7%1.32%1009067.0291.0291.0%67.901%67.90%67.90%67.90%10030028300:.6%37.103%1031400%1011200%107810%110961400120081096:)2(%67.99%1001500100070080%951500%1001000%108700%1108044=⨯⎪⎭⎫ ⎝⎛++⨯++==⨯==-⨯====⨯-==++++++=⨯+++⨯+⨯+⨯+⨯σ1.()())(7.788%67.41500:2000%67.41500600:.6)(6.62126907106557306806702650600269071061527106556552655730620273068060026806706402670650:2)(7.62327107006907206806202680610271070062527006906452690720640272068062026806206002620680:)1(:.5%63.79%10026206005802580257646245002435:.4%85.105%100%113385%102350%97463%120485%105412%112410%98368%106350%105310%110324%102306%101303385350463485412410368350310324306303::.3872232122221030980329809002290010201210208402284067022670600.2104万吨年该县粮食产量为平均增长速度解元工人的月平均工资为乙工区上半年建筑安装元工人的月平均工资为甲工区上半年建筑安装解解度为全年月平均计划完成程解=+⨯=-==++++++⨯++⨯++⨯++⨯++⨯++⨯+=++++++⨯++⨯++⨯++⨯++⨯++⨯+=⨯++++++==⨯++++++++++++++++++++++=+++++⨯++⨯++⨯++⨯++⨯++⨯+=C a 7解:计算过程如下表:)(94.6653.444.45:1994:3.46025844.4594092万元年的地方财政支出额为则直线趋势方程为=⨯++=======∑∑∑bta y t tyb ny a二次曲线方程为:y = 0.0108x 2 + 4.1918x + 24.143(过程略) 指数曲线方程为:y = 26.996e 0.0978x8.解:计算过程如下表:9.解:(1)同季平均法求季节比率的过程如下表:(2)趋势剔除法测定的季节变动如下表:第七章 统计指数()()()()01001011111175000124000081138.44%5000012350008750002540000182138.03%500002535000181075000940000390.98%127500084000022750002540000425qqzpk q z q zq p q p q z kq z p q k p q⨯+⨯===⨯+⨯⨯+⨯===⨯+⨯⨯+⨯===⨯+⨯⨯+⨯==∑∑∑∑∑∑∑∑111111110102.12%75000184000015602.108.8%1200360110%105%pp q p q k p q p q p p=⨯+⨯====+∑∑∑∑11111560.135.65%1150135.65%124.68%108.8%.120%1800115%90096%6003.114.27%330042003300111.38%114.27%.pqpq qpqpq p qp q k p qk k k q q p q p q k q p q pkk k======⨯+⨯+⨯=======∑∑∑∑∑∑ 110101001013200005.100%128%250000128%123.1%14%320000307692.3104%307692.325000057692.3320000307692.312307.pq pqq PpK K K p qp q K p q p qq p q =⨯====+===-=-=-=-=∑∑∑∑∑∑1解:K 零售量变动对零售额变动影响的绝对值为:(万元)零售物价变动对零售总额变动影响的绝对值为:p 1110010000107350000120%120%180000110%110%116%116%17.6%107.6%350000291666.67120%180000163636.36.110%1pq pq q q pq pq q q K q K q p q Kq p q K p q p q ==+===+==+==+========⨯=∑∑∑∑∑∑∑∑城1城农城农1农1城城城1农农农城城城(万元)6.解:已知p ,,p ,,K ,K p 则p K 0010111101001116%291666.67338333.33107.6%163636.36176072.72350000180000103.03%338333.33176072.723%q pp q p q p q q q k p q p q p q ⨯==⨯=⨯=++====++∴∑∑∑∑∑∑∑∑农农农11城农城农K p p 该地区城乡价格上涨了。
第三章平均指标练习及答案

第三章平均指标练习及答案第三章平均指数和标记变异指数1,填写问题1。
平均指数是一种统计指数,表明某个标记在特定的时间、地点和条件下达到_ _ _ _ _ _ _ _ _ _,也称为平均值2。
权重对算术平均值的影响不是由权重的大小决定的,而是由权重的大小决定的3。
几何平均数是n的n根。
这是最适合计算和平均速度的方法。
4。
当标记值较大且次数较多时,平均值接近标记值较大的一侧;当标志值小且次数大时,平均值接近标志值较小的一侧。
5。
当加权算术平均值等于简单算术平均值时6.使用组中值计算加权算术平均值时,假设每个组中的标记值都是分布的,计算结果为1 7。
中位数是位于可变序列中的标记值,模式是群体中出现次数的标记值中位数和众数也可以称为平均数8。
调和平均是一种平均,它是9。
当变量序列中的算术平均值大于模式时,变量序列的分布是分布的;另一方面,当算术平均值小于模式时,变量序列的分布是分布的10。
更常用的趋势指标是、、、、11.标准偏差系数是12。
据了解,XXXX一季度某一系列商品的平均销售数量按商品销售情况分为以下几类:按商品销售情况(低于2万-30元)公司20家店铺商品销售的平均差价是()如果店铺数量为1.530-40.9 40-50超过3 2(数)甲7万元乙10万元丙12万元丁3万元9当数据集高度倾斜时,哪个平均值更具代表性?()算术平均值b中值c模式d几何平均值14。
方差为()A绝对偏差平均值B平方偏差平均值C平方偏差平均值D绝对偏差平均值15。
一组数据的偏度系数为1.3。
显示这组数据的分布是()正态分布b 平顶分布c左偏置分布d右偏置分布16。
当一组数据属于左偏置分布时,则()A均值、中值和模式组合成左侧的一个B模式和右侧的C模式。
平均值越小,平均值越大。
d模式在右侧,平均值为17。
四分位偏差排除了序列两端()单位标志值的影响A1096B 15% C25 % D35 %18。
优势比是代表_ _ _ _ _ _ _ _ _ _ _规模的指标。
统计学课件及习题答案05第五章 平均指标与变异指标-61页精选文档

职工人数(人)
15 30
50
100
平均工资(元) 2800 > 2500 > 2000 > 1256
平均指标的作用------利用平均指标进行估计推算(3)
若某地区 “十二五”计划期间经济平均增长速 度为7%,那么该地区到2019年GDP就会达到2.6万 亿,若人口2019年该地区人口为8500万人,则人 均30588元。
本章主要内容
一一
二
三
综合分析 平的均意指义标 和特点
计算和. 应用 平均指标
的原则
变异指标
第一节 平均指标
平均指标的 概念及作用
平均指标的 计算方法
一、平均指标的概念及作用
平均指标:简单地说就是若干变量值的平均。
静态
平 平均指标 均
指
标
动态
平均指标
反映总体各单位在 某一数量标志下标志值
的一般水平
8.4
x
xf f
168 20
8.4(件)
x
f
f
8.(4 件)
注意
⑴以比重为权数计算的结果 与用绝对数计算结果完全一样。 ⑵本例为单项数列资料。若为组
距数列,需先算组中值。
【加权算术平均法计算步骤】
各组 标志值 乘次数得 各组标志 总量
加总 得到 总体 标志 总量
计算 总体 单位 总量
总体 标志总量
教学目的与要求
通过本章学习,了解平均指标和变异指标的意义 和种类,掌握各种计算方法及其应用条件,能够应用 平均指标和变异指标进行基本的统计分析。
教学重点与难点
重点:各种加权平均数的计算方法和应用条件; 理解计算和应用平均指标的原则;标准差的计算;
难点:正确理解加权平均计算方法中的权数; 权数的正确选择;变异系数计算的必要性。
相对指标与平均指标习题含参考答案

第五章相对与平均指标一、填空题1.总量指标的表现形式是__绝对数___,其数值随着___总体范围__大小而增加或减少。
2.根据总量指标所反映的社会经济现象总体内容不同,可将总量指标分为___总体单位总量__和___总体标志总量__两种。
3.总量指标是计算__相对指标, 平均指标___的基础。
4.某高校在校生人数是__时点___指标,其数值__不可___相加;毕业生人数是__时期___指标,其数值__可以___相加。
5.价值指标的特点是具有广泛的__综合性___和__概括性___。
6.属于同一总体对比的相对指标有__结构___、__比例___和___计划完成__;属于不同总体对比的相对指标有__比较___和__强度___。
7.相对指标的计量形式有两种,即:__无名数___和__复名数___,其中,除强度相对指标用__复名数___表示外,其余都用__无名数___表示。
8.检查长期计划执行情况时,如计划指标是按计划期末应达到的水平下达的,应采用___水平__法计算;如计划指标是按整个计划期累计完成总数下达的,应采用_累计___法计算。
9.某校在校生中男女之比为:1,这是___比例__相对指标。
其中,男生所占比重为60%,这是___结构__相对指标。
10.同类指标数值在不同空间作静态对比形成__比较相对___指标;而同类指标数值在不同时间对比形成__动态相对___指标。
11.统计中的平均指标主要有__算术平均数___、__调和平均数___、__几何平均数___、__中位数___和___众数__五种。
1.12.简单算术平均数是加权算术平均数的__特殊形式___,事实上简单算术平均数也有___权数__存在,只不过各变量值出现的__权数___均相等。
2.13.各变量值与其算术平均数的__平方和___等于最小值。
3.14.权数对于平均数的影响作用,决定于作为权数的__各组单位数__的比重大小。
4.15.在某市范围内以企业为单位研究企业平均规模时,各企业职工人数总和是__标志___总量指标。
第5章 平均指标及答案

第五章平均指标一、本章重点1.平均指标反映了总体分布的共性或一般水平,和标志变异指标一起分别从集中趋势和离中趋势两个方面来描述总体分布的特征。
平均指标有动态上的平均指标和静态上的平均指标之分。
静态上的平均数有算术平均数、调和平均数、几何平均数、中位数和众数。
2.算术平均数是平均数的基本形式,是总体标志总量与总体单位总量之比。
有简单算术平均数和加权算术平均数之分。
权数的大小,并不是以权数本身值的大小而言的,而是指各组单位数占总体单位数的比重,即权重系数。
每一个标志值与其算术平均数离差之和为零,每一个标志值与其算术平均数离差的平方和为最小,是算术平均数两个最重要的性质。
3.调和平均数也叫倒数平均数,是根据标志值的倒数计算的,它是标志值倒数的算术平均数的倒数。
是在缺乏算术平均数基本公式分母部分的资料时所采用的。
4.几何平均数是计算平均比率和平均速度最适用的一种方法。
是n个标志值连乘积的n次方根,有简单调和平均数与加权调和平均数之分。
5.中位数和众数是根据标志值的位置计算的,所以也叫位置平均数。
把标志值从小到大排列起来处于中间位置上的数就是中位数,在一个变量数列中出现次数最多的哪个数就是众数。
要掌握组距数列确定中位数和众数的方法。
众数、中位数、算术平均数存在一定的关系,无论左偏还是右偏,中位数总是居于两者中间。
在偏斜适度的情况下,中位数与算术平均数之差约等于众数与算术平均数之差的1/3。
6.只有在同质总体内才能计算和应用平均指标;用组平均数补充说明总平均指标;用分配数列补充说明平均数是计算和应用平均指标的三个基本原则。
二、难点释疑1.算术平均数通常用来反映总体分布的集中趋势,调和平均数往往只作为算术平均数的变形来使用,即在已知标志总量而未知总体单位总量的情况下计算调和平均数;而几何平均数较适用于计算平均比例和平均速度。
2.调和平均数虽然是根据标志值的倒数计算的,但其结果不等于算术平均数的倒数。
在计算和应用平均指标时,除了考虑数理方面的要求外,更重要的是要考虑其现实的经济意义。
统计学平均数与变异指标计算题答案PPT课件

5 1875
12 5100
10 4750
20 10500
35 20125
18 11250
100 53600
x2 f (% ) Σf
703125 2167500 2256250 5512500 11571875 7031250 29242500
【解】五、2、(2)
σ乙
Σx 2f Σf
(
Σxf Σf
甲 企 业 工 人 数 (人 )
50 80
100 120 200
80
乙 企 业 工 人 结 构 (%)
5 12 10 20 35 18
合计
630
100
(1) 分别计算甲、乙两企业职工的平均工资; (2) 分别计算甲、乙两企业职工工资的标准差; (3) 比较甲、乙两企业职工平均工资的代表性大小。
【解】五、2、(1)
)2
292425 536 2
5129 71.62(元)
.
13
【解】五、2、(3)
V甲x572.4.101831.42% 4 V乙x751 .632613 .36 %
因为V甲> V乙,所以乙企业职工 平均工资的代表性较甲大。
.
14
五、3 题
某工厂生产某种零件,要经过四 道工序,各道工序的合格率分别为 98%、95%、92%、90%。试求该 零件的平均合格率。
第四章 综合指标习题
(二) 平均指标与标志变异指标
任课教师:汤来香 tanglx2000@
五、1 某产品资料如下:
等级
单 价 (元)
一级品 1.20
二级品 1.05
三级品 0.90
合计 —
收购量 (公斤)
职业高校统计学课件总量指标作业答案6P
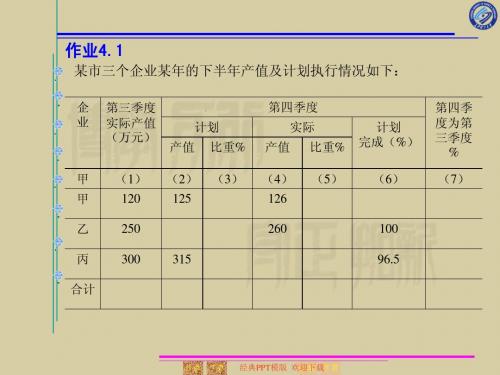
某市三个企业某年的下半年产值及计划执行情况如下:
企 业 第三季度 实际产值 (万元) (1) 120 250 300 315 第四季度 计划 产值 (2) 125 比重% (3) 实际 产值 (4) 126 260 100 96.5 比重% (5) 计划 完成(%) (6) 第四季 度为第 三季度 % (7)
下页上页下页目录经典ppt模版欢迎下载企业第三季度实际产值万元第四季度第四季度为第三季计划实际计划完成产值比重产值比重12012517861261826100810502502603714260376810001040300315450030444069651013合计67070010000690100009861030作业41解下页上页下页目录经典ppt模版欢迎下载1计算见上表35是结构相对数
目录 下页 经典PPT模版 欢迎下载 上页 下页
目录 下页
经典PPT模版 欢迎下载 上页 下页
目录 下页
经典PPT模版 欢迎下载 上页 下页
目录 下页
经典PPT模版 欢迎下载 上页 下页
目录 下页
经典PPT模版 欢迎下载 上页 下页
目录 下页
经典PPT模版 欢迎下载 上页 下页
作业4.1解
第三季度 企业 实际产值 (万元) (1) 第四季度 计划 产值 (2) 实际 产值 (4) 第四季度 为第三季 度的% (7)
比重 %
(3)
比重 %
(5)
计划 完成 % (6 )
甲
乙 丙 合计
120
250 300 670
125
260 315 700
17.86
37.14 45.00 100.00
126
260 304 690
(完整版)第三章平均指标练习及答案

第三章平均指标与标志变异指标一、填空题1.平均指标是表明__________某一标志在具体时间、地点、条件下达到的_________的统计指标,也称为平均数。
2.权数对算术平均数的影响作用不决定于权数的大小,而决定于权数的________的大小。
3.几何平均数是n个__________的n次方根,.它是计算和平均速度的最适用的一种方法。
4.当标志值较大而次数较多时,平均数接近于标志值较的一方;当标志值较小而次数较多时,平均数靠近于标志值较的一方。
5.当时,加权算术平均数等于简单算术平均数。
6.利用组中值计算加权算术平均数是假定各组内的标志值是分布的,其计算结果是一个。
7.中位数是位于变量数列的那个标志值,众数是在总体中出现次数的那个标志值。
中位数和众数也可以称为平均数。
8.调和平均数是平均数的一种,它是的算术平均数的。
9.当变量数列中算术平均数大于众数时,这种变量数列的分布呈分布;反之算术平均数小于众数时,变量数列的分布则呈分布。
10.较常使用的离中趋势指标有、、、、、。
11.标准差系数是与之比。
12.已知某数列的平均数是200,标准差系数是30%,则该数列的方差是。
13.对某村6户居民家庭共30人进行调查,所得的结果是,人均收入400元,其离差平方和为5100000,则标准差是,标准差系数是。
14.在对称分配的情况下,平均数、中位数与众数是的。
在偏态分配的情况下,平均数、中位数与众数是的。
如果众数在左边、平均数在右边,称为偏态。
如果众数在右边、平均数在左边,则称为偏态。
15.采用分组资料,计算平均差的公式是,计算标准差的公式是。
二、单项选择题1.加权算术平均数的大小( )A受各组次数f的影响最大B受各组标志值X的影响最大C只受各组标志值X的影响 D受各组次数f和各组标志值X的共同影响2,平均数反映了( )A总体分布的集中趋势 B总体中总体单位分布的集中趋势C总体分布的离散趋势 D总体变动的趋势3.在变量数列中,如果标志值较小的一组权数较大,则计算出来的算术平均数( )A接近于标志值大的一方 B接近于标志值小的一方C不受权数的影响D无法判断4.根据变量数列计算平均数时,在下列哪种情况下,加权算术平均数等于简单算术平均数( )A各组次数递增 B各组次数大致相等 C各组次数相等 D各组次数不相等5.已知某局所属12个工业企业的职工人数和工资总额,要求计算该局职工的平均工资,应该采用( )A简单算术平均法 B加权算术平均法 C加权调和平均法 D几何平均法6.已知5个水果商店苹果的单价和销售额,要求计算5个商店苹果的平均单价,应该采用( )A简单算术平均法 B加权算术平均法 C加权调和平均法 D几何平均法7.计算平均数的基本要求是所要计算的平均数的总体单位应是( )A大量的 B同质的 C差异的 D少量的8.某公司下属5个企业,已知每个企业某月产值计划完成百分比和实际产值,要求计算该公司平均计划完成程度,应采用加权调和平均数的方法计算,其权数是( )A计划产值 B实际产值 C工人数 D企业数9.由组距变量数列计算算术平均数时,用组中值代表组内标志值的一般水平,有一个假定条件,即( )A各组的次数必须相等 B各组标志值必须相等C各组标志值在本组内呈均匀分布 D各组必须是封闭组10.离中趋势指标中,最容易受极端值影响的是( )A极差 B平均差 C标准差 D标准差系数11.平均差与标准差的主要区别在于( )A指标意义不同 B计算条件不同 C计算结果不同 D 数学处理方法不同12.某贸易公司的20个商店本年第一季度按商品销售额分组如下:则该公司20个商店商品销售额的平均差为( )A 7万元B 1万元C 12 万元D 3万元13.当数据组高度偏态时,哪一种平均数更具有代表性? ( )A算术平均数 B中位数 C众数 D几何平均数14.方差是数据中各变量值与其算术平均数的( )A离差绝对值的平均数 B离差平方的平均数C离差平均数的平方 D离差平均数的绝对值15.一组数据的偏态系数为1.3,表明该组数据的分布是( )A 正态分布 B平顶分布 C左偏分布 D右偏分布16.当一组数据属于左偏分布时,则( )A平均数、中位数与众数是合而为一的 B众数在左边、平均数在右边C众数的数值较小,平均数的数值较大 D众数在右边、平均数在左边17.四分位差排除了数列两端各( )单位标志值的影响。
平均指标练习题

平均指标练习题一、选择题1. 下列哪个指标属于平均指标?A. 总量指标B. 相对指标C. 平均指标D. 比率指标2. 在一组数据中,若众数、中位数和平均数相等,则这组数据的分布特点是:A. 偏态分布B. 正态分布C. 平峰分布D. U型分布A. ΣXi / fiB. ΣXi / nC. Σfi / nD. ΣXi × fi / n4. 下列哪个指标适用于品质数据?A. 算术平均数B. 几何平均数C. 中位数D. 众数二、填空题1. 平均指标是反映__________的一般水平或典型特征的统计指标。
2. 算术平均数是所有__________之和除以__________。
3. 几何平均数适用于__________变量,其计算公式为__________。
4. 中位数是将一组数据按大小顺序排列后,位于__________位置的数值。
三、计算题1. 某班级5名学生的成绩分别为:80、85、90、85、88,求该班级学生的平均成绩。
2. 某公司员工月工资分别为:3000、3500、4000、4500、5000元,求该公司员工月平均工资。
3. 某商店连续5天的销售额分别为:2000、2500、2200、2400、2300元,求该商店这5天的平均销售额。
4. 已知一组数据的众数为500,中位数为450,求该组数据的平均数。
四、应用题1. 某企业生产A、B、C三种产品,产量分别为200、300、500件,求该企业平均每种产品的产量。
2. 某地区居民消费水平调查,甲、乙、丙三个家庭的月均消费分别为3000、4000、5000元,求这三个家庭的平均消费水平。
3. 某班级学生的身高数据如下:160cm、165cm、170cm、175cm、180cm,求该班级学生的平均身高。
4. 某城市今年四个季度的GDP分别为1000亿元、1100亿元、1200亿元、1300亿元,求该城市全年平均GDP。
五、判断题1. 平均数是所有数据加总后除以数据的个数,因此它一定能够代表所有数据的特征。
大学课程《统计学原理》PPT课件:第六章 平均指标与标志变异指标

二、标志变异的测度
(一)极差 (二)四分位差 (三)平均差 (四)方差和标准差 (五)是非标志的标准差 (六)变异系数
第三节 分布的偏度和峰度
一、偏度
偏度是用于衡量分布的不对称程度或偏 斜程度的指标。如果用矩法方式测定,偏 度指标α是变量的三阶中心动差除以标 准差三次方。
图6-5 偏度
第三节 分布的偏度和峰度
二、峰度
峰度是用于衡量分布的集中程度或分布曲 线的尖峭程度的指标。
图6-6 峰度
第四节 运用平均指标的原则
一、总体各单位必须是同质的
在统计研究中之所以需要计算平均数, 是因为总体的各个单位在数量标志上 存在着差异,通过平均,它们之间个别的、 偶然的差异可以相互抵消,从而反映出 整个总体的特征。
第六章 平均指标与标志变 异指标
目录
1 平均指标 2 标志变异指标——分布的离中趋势 3 分布的偏度和峰度 4 运用平均指标的原则
第一节 平均指标
一、平均指标概述
(一)平均指标的含义
在统计总体中,各个统计单位有表明其 属性和特征的标志,但这些标志在各统 计单位中的表现往往是不同的。
平均指标是将总体各单位标志值的差 异抽象化,反映总体在具体条件下各单 位标志值所达到的一般水平。
第一节 平均指标
(二)平均指标的作用
1.反映总体各单位变量分布的集中趋势 和一般水平
2.比较同类现象在不同单位的发展水平
3.比较同类现象在不同时期的发展变化 趋势或规律
4.分析现象之间的依存关系
(三)平均指标的分类
根据设置平均指标的方法的不同,可以将 平均指标划分为数值平均数和位置平均 数。
数量关系的经验公式为:算术平均数x和 众数Mo的距离约等于算术平均数x与中 位数Me距离的3倍。
统计学平均数与变异指标计算题答案

设一组数据为x1, x2, ..., xn,则算术平 均数计算公式为:M = (x1 + x2 + ... + xn) / n。例如,10个人的年龄数据 为15, 20, 25, ..., 60,则其算术平均数 计算公式为:(15 + 20 + 25 + ... + 60) / 10。
几何平均数的实例计算题答案
四分位数间距的实例计算题答案
总结词
四分位数间距反映了一组数据的离散程度。
详细描述
设一组数据为x1, x2, ..., xn,则四分位数间距计算公式为:Q3 - Q1。例如,某 个班级的分数数据为60分、70分、80分、90分、100分,则其四分位数间距计 算公式为:90分 - 60分。
感谢观看
THANKS
统计学平均数与变异
指标计算题答案
汇报人:
2023-12-01
• 平均数的计算 • 变异指标的计算 • 平均数与变异指标的关联 • 实例计算题答案
目录
01
平均数的计算
算术平均数
定义
算术平均数是所有数值的和除以数值的个数。
公式
$\frac{\sum_{i=1}^{n} x_i}{n}$
例子
如果一个班级有5个学生,他们的分数分别是80, 90, 85, 92, 88,那么他们的算术平均分是86。
详细描述
标准差是各数据点与其平均数之差的平方和的平均数的平方根,它可以帮助我们了解数据的波动范围和程度。标 准差越大,数据点越分散;标准差越小,数据点越集中。
方差
总结词
方差是衡量一组数据离散程度的另一个指标,它是各数据点与其平均数之差的平方和的平均数。
详细描述
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录 下页
上页 下页
作业5.2解
车间 废品率 产量(件) 产品制造总工时
xf1
xf2
%x
f2
f1甲Leabharlann 3701500
45
2.10
乙
2
20
3000
60
0.40
丙
4
90
500
20
3.60
合计
--
--
5000
125
6.10
目录 下页
上页 下页
(1)三种产品的综合废品率:三种产品的产量不能相加,所以 只能以产品制造总工时为权数加权。
上页 下页
乙工人计算资料
偏差
零件数 组中值
f
x
xf
x- x (x- x )2 (x- x )2f
9.6以下
1
9.5 9.5 -0.46 0.2116
0.2116
9.6-9.8
2
9.7 19.4 -0.26 0.0676
0.1352
9.8-10.0
2
9.9 19.8 -0.06 0.0036
0.0072
710
1.15 816.5 617.4
3
40
1.25
50
32
115
2850
- 3012.5 2711.8
目录 下页
上页 下页
〈1〉该地区各企业产值计划平均完成程度
x=
xf f
3012 .5 2850
=105.7%
〈2〉如果表中所给资料不是计划产值而是 实际产值,则产值计划平均完成程度为
H=
10.0-10.2 3
10.1 30.3 0.14 0.0196
0.0588
10.2-10.4 2
10.3 20.6 0.34 0.1156
0.2312
合计
10
- 99.6 --
--
0.644
目录 下页
上页 下页
甲工人:平均偏差为
xf
x= f
99.2 10
=9.92
2
标准差 δ甲= x x f 0.516 =0.2272
x xf1 125 2.5% f1 5000
(2)假定三个车间生产的是同一产品,产品的综合废品率。由于 假定三个车间生产的是同一产品,产品的产量能相加,可以以产量 为权数加权。
x xf2 6.1 3.39% f 2 180
(3)假定三个车间是连续加工,产品的平均废品率。
f
10
标准差系数V甲= 0.2272 =2.29%
x 9.92
用同样方法,可计算乙工人: 平均偏差
x =9.96
标准差δ乙=0.2538 标准差系数V乙=2.55% 所以,甲工人零件偏差的平均水平小,而且标准差系数小, 说明甲工人零件质量好,而且质量稳定。
目录 下页
上页 下页
作业5.4
某企业工人工资资料如下:
G 1 3 0.97 0.98 0.96 3%
目录 下页
上页 下页
作业5.3
对某车间甲、乙两工人当日产品中各抽取10件产品进行质量检查,得 资料如下:
偏差 (微米)
9.6以下 9.6-9.8 9.8-10.0 10.0-10.2 10.2-10.4 合计
零件数(件)
甲工人
乙工人
目录 下页
上页 下页
作业5.1解
计划完成程 度(%) 90以下
90-100
100-110
110-120 120以上
合计
企业数 (个)
计划产值 (万元)
组中值x
xf
f
f x
7
140
0.85
119 164.7
22
310
0.95 294.5 326.3
57
1650
1.05 1732.5 1571.4
26
1
1
2
2
3
2
3
3
1
2
10
10
试比较甲乙两工人谁生产的零件质量较稳定。
目录 下页
上页 下页
作业5.3解
甲工人计算资料
x 偏差
零件数 组中值 xf
f
x
x-
9.6以下
1
9.6-9.8
2
9.5 9.5 -0.42 9.7 19.4 -0.22
9.8-10.0 3
9.9 29.7 -0.02
10.0-10.2 3
f
f x
2850 2711 .8 =105.1%
目录 下页
上页 下页
作业5.2
已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:
车间 甲 乙 丙
合计
废品率% 3 2 4 --
产量(件) 70 20 90 --
产品制造总工时 1500 3000 500 5000
计算:(1)三种产品的平均废品率;(2)假定三个车 间生产的是同一产品,但独立完成,产品的平均废品率是 多少;(3)假定三个车间是连续加工某一产品,产品的平 均废品率是多少。
工人 类别
技术工人 普通工人
合计
月工资水平(元)
基期
报告期
700
750
400
450
工人数(人)
基期
报告期
300
400
200
600
500
1000
要求:
(1)分别计算基期工人总平均工资和报告期工人总平均工资 填入上表空格处;(2)说明报告期工人总平均工资比基期工 人总平均工资降低(或提高)的原因。
目录 下页
作业5.1
已知某地区各工业企业产值计划完成情况以及计划产值资料如下:
计划完成程度(%) 90以下 90-100 100-110 110-120 120以上 合计
企业个数(个) 7 22 57 26 3 115
计划产值(万元) 140 310 1650 710 40 2850
要求:(1)根据上述资料计算该地区各企业产值计划的 平均完成程度。(2)如果在上表中所给资料不是计划产值 而是实际产值,试计算产值计划平均完成程度。
10.1 30.3 0.18
10.2-10.4 1
合计
10
10.3 10.3 0.38 - 99.2 --
(x- x )2
0.1764 0.0484 0.0004 0.0324 0.1444
--
x (x- )2f
0.1764 0.0968 0.0012 0.0972 0.1444 0.516
目录 下页
上页 下页
作业5.4解
(1)基期、报告期平均工资
工人 类别
技术工人 普通工人
合计
月工资水平(元)
基期x0 报告期x1
700
750
400
450
580
570
工人数(人)
基期f0 300
报告期f1 400
200
600
500
1000
工资总额(元)
x0f0
x1f1
210000 300000
80000 270000
290000 570000
基期平均工资 x0 x0 f0 290000 580
f0
500
报告期平均工资 x1 x1 f1 570000 570 f1 1000
目录 下页
上页 下页
(2)报告期平均工资比基期平均工资下降原因分析
由上述计算结果可知:
报告期平均工资比基期平均工资下降了10元。这是由 于:尽管技术工人和普通工人报告期比基期工资都提 高了50元,这一因素影响本来应该使报告期平均工资 比基期平均工资提高50元,但是,由于工人数结构的 变化反而使平均工资下降了。工人数结构变化为:平 均工资高的技术工人由基期的60%下降为报告期的40 %,而平均工资低的普通工人由基期的40%上升为报 告期的60%。
