24630_解直角三角形单元测试.doc
单元测试:解直角三角形2

解直角三角形 全章测试班级 姓名 学号一、选择题(本题共8小题,每小题4分,共32分) 1. 60cos 的值等于( )A .21 B .22 C .23 D .12.在Rt △ABC 中, ∠C=90︒,AB=4,AC=1,则tanA 的值是( )A .154B .14C .15D .43.已知α为锐角,且23)10sin(=︒-α,则α等于( )A .︒50B .︒60C .︒70D .︒804.已知直角三角形ABC 中,斜边AB 的长为m ,40B ∠= ,则直角边BC 的长是( ) A .sin 40mB .cos 40mC .tan 40mD .tan 40m5.在Rt ABC △中,90C ∠= ,5BC =,15AC =,则A ∠=( )A .90B .60C .45D .306.如图,小雅家(图中点O 处)门前有一条东西走向的公路,经测得有一水塔(图中点A 处)位于她家北偏东60度500m 处,那么水塔所在的位置到公路的距离AB 是( )A .250m.B . 250.3 m.C .500.33 m.D .3250 m. 7.直角三角形纸片的两直角边长分别为6,8,现将ABC △如图那样折叠,使点A 与点B 重合,折痕为DE ,则tan CBE ∠的值是( )A .247B .73C .724D .1368CEABD(第7题)第6题(第10题)(图1)(图2) AB C 8.因为1sin 302=,1sin 2102=- ,所以sin 210sin(18030)sin30=+=- ;因为2sin 452=,2sin 2252=-,所以sin 225sin(18045)sin 45=+=- ,由此猜想,推理知:一般地当α为锐角时有sin(180)sin αα+=-,由此可知:sin 240=( )A .12- B .22-C .32-D .3-二、填空题(本题共5小题,每小题4分,共20分)9.2cos45°-21tan60°= ;10.如图是一张Rt △ABC 纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形(图2),那么在Rt △ABC 中,sin B ∠的值是 ; 11.林业工人为调查树木的生长情况,常用一种角卡为工具,可以很快测出大树的直径,其工作原理如图所示.现已知5380.5BAC AB =︒=∠′,米,则这棵大树的直径约为_________米;(结果精确到0.1米)12.在正方形网格中,ABC △的位置如图所示,则cos B ∠的值为 ; 13.如图,梯形ABCD 是拦水坝的横断面图,(图中1:3i =是指坡面的铅直高度DE 与水平宽度CE 的比),60B ∠= ,6AB =,4AD =,拦水坝的横断面ABCD的面积是 (结果保留三位有效数字,参考数据:3 1.732=,2 1.414=)三、解答题(共48分)14.(8分)在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,且a=3,b=3,解这个三角形.15.(8分)如图所示,课外活动中,小明在离旗杆AB 10米的C 处,用测角仪测得旗杆顶部A 的仰角为40︒,已知测角仪器的高CD =1.5米,求旗杆AB 的高. (精确到0.1米) (供选用的数据:sin 400.64≈ ,cos 400.77≈ ,tan 400.84≈ )16.(10分)热气球的探测器显示,从热气球看一栋高楼顶部的仰角为︒30,看这栋高楼底部的俯角为︒60,热气球与高楼的水平距离为66m ,这栋高楼有多高?(结果精确到0.1 m ,参考数据:73.13≈)17.(10分)如图是某宾馆大厅到二楼的楼梯设计图,已知6BC =米,9AB =米,中间平台宽度DE 为2米,DM EN ,为平台的两根支柱,DM EN ,垂直于AB ,垂足分别为M N ,,30EAB ∠= ,45CDF ∠= .求DM 和BC 的水平距离BM .(精确到0.1米,参考数据:2 1.41≈,3 1.73≈)FCED C AB40︒E D CBA(第19题)18.(12分)为了加强视力保护意识,小明想在长为3.2米,宽为4.3米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计方案新颖,构思巧妙.(1)甲生的方案:如图1,将视力表挂在墙ABEF 和墙ADGF 的夹角处,被测试人站立在对角线AC 上,问:甲生的设计方案是否可行?请说明理由. (2)乙生的方案:如图2,将视力表挂在墙CDGH 上,在墙ABEF 上挂一面足够大的平面镜,根据平面镜成像原理可计算得到:测试线应画在距离墙ABEF 米处.(3)丙生的方案:如图3,根据测试距离为5m 的大视力表制作一个测试距离为3m 的小视力表.如果大视力表中“E ”的长是3.5cm ,那么小视力表中相应“E ”的长是多少cm ?(附加题5分)19.如图,正方形ABCD 中,E 是BC 边上一点,以E 为圆心、EC 为半径的半圆与以A 为圆心,AB 为半径的圆弧外切,则sin EAB 的值为 。
解直角三角形单元测试.doc

解直角三角形单元测试班别 姓名 座号 评分一、填空题(每题5分,共25分)1.在△ABC 中,∠C =90°,135sin =B ,则cosB =___________. 2.若23sin =a ,则锐角a =__________度. 3.Rt △ABC 中,∠C =90°,220,20==c a ,则∠B =_________度.4.△ABC 中,∠C =90°,10,54sin ==AB A ,则AC =_________. 5.在离大楼15m 的地面上看大楼顶部仰角为60°,则大楼高约__________m(精确到lm).二、选择题(每题5分,共20分)6.直角三角形的两条边长分别为3、4,则第三条边长为 ( )A .5B .7C .7D .5或77.如图19—7l ,菱形ABCD 的对角线AC =6,BD =8,∠ABD =a ,则下列结论正确的是 ( )A .54sin =aB .53cos =aC .34tan =aD .34cot =a 8.如图19—72,在Rt △ABC 中,∠C =90°,BC =4,AC =3,CD ⊥AB 于D ,设∠ACD =a ,则cos a 的值为 ( )A .54B .43C .34D .539.如图19—73,钓鱼竿AC 长6m ,露在水面上的鱼线BC 长23m ,某钓者想看看鱼钓上的情况,把鱼竿AC 转动到C A '的位置,此时露在水面上的鱼线C B ''为33,则鱼竿转过的角度是 ( )A .60°B .45°C .15°D .90°三、解答题10.(5分)计算2cos30°+cot60°-2tan45°·tan60°11.(10分)如图19—74,求下列各直角三角形中字母的值.12.(10分)如图19—76,梯形ABCD 中,AB ⊥BC ,∠BAC =60°,∠ADC =135°,312 BC ,求梯形的面积和周长.13.(10分)如图,某公园入口处原有三阶台阶,每级台阶高为20cm,深为30cm.为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A ,斜坡的起始点为C ,现将斜坡的坡角∠BCA 设计为12°,求AC 的长度。
沪科版九上第25章《解直角三角形》word同步测试

第25章《解直角三角形》整章测试sin( 180 比sin ,由此可知:sin 240 二()7•如图,客轮在海上以30km/h 的速度由B 向C 航行,在B 处测得灯塔A 的方位角为北偏东80,测得C 处的方位角为南偏东 25,航 行1小时后到达C 处,在C 处测得A 的方位角为北偏东 20,则C 到 A 的距离是( )(A) 15.6 km(B)15.2km一、选择题(每小题 -分,共24分) 1.在 Rt △ ABC 中,/ C=90 , AB=4, AC=1,则 C OS A 的值是( )(A )(B) 1 (C) .15 (D) 4442.计算:,(tan 30 -1)2=()P 3(A ) 1 (B) 3-1 (C3 d) 1(D)l —3(A )直角三角形(B )钝角三角形COS B=_2」打ABC 的形状()2(C 锐角三角形(D )不能确定4. 如图,在 Rt △ ABC 中,tanB ' - , BC =2、、3,则 AC 等于()2(A ) 3( B ) 4(C ) 4 .3(D ) 65.如图,小颖利用有一个锐角是 30°的三角板测量一棵树的高度,已知她与树之间的水平距离 BE 为5m AB 为1.5m (即小颖的眼睛距地面的距离),那么这棵树高是()(A) (5 L 33) m (B)( 5.3 - ) m (C)5'3m (D)4m3 2231t 1所以 sin210; = sin(180 30 )二一sin 3o ;因为 sin45 =, sin225; = ,所以 2 2sin225 = sin(180 45'') = -sin45‘ ,由此猜想,推理知:一般地当〉为锐角时有 (A )(B)W33 3.在二ABC 中,—A,._B 都是锐角,且sinA =—,2CCA 3 (B10 DBCE米A AbDBhacBC C(EE Ba(1)(C) 15(、、6 s/2) km(D) 5(:.f6 3、,2)8.如图,在 Rt△ ABC 中,.A =90:, AC = 6cm , AB = 8cm ,把 AB 边翻折,使 AB 边15.(本题 8 分)计算:2(2cos 45「sin 60 ) 244含有a, b, c, 一:字母的式子表示)落在BC 边上,点A 落在点E 处,折痕为BD , 、填空题(每小题 3分,共24分)9•计算Sin60- tan45^的值是 cos30〔11.在 Rt△ ABC 中,.C =90 , BC:AC=3:4,则 cosA =12•如图,一架梯子斜靠在墙上,若梯子到墙的距离AC =3 米,3cos BAC ,则梯子AB 的长度为4三、解答题(本大题共 52 分)种测量方法,如下图所示•图中a, b, c 表示长度,[表示角度.请你求出AB 的长度(用 (C)症7314.如图,在菱形 ABCD 中, DEIAB,垂足为 E , DE=6cm16.(本题10分)某校数学兴趣小组在测量一座池塘边上A, B 两点间的距离时用了以下三则sin . DBE 的值为((D)卫10sinA=|,则菱形ABCD 的面积是cm 21(A)-3I -r — Jt 1卜丄■亠,\A ---------- C_____________(1) AB = _____ (2) AB = _____________ (3) AB = ______________17.(本题10分)小强家有一块三角形菜地,量得两边长分别为40m, 50m 第三边上的高为30m 请你帮小强计算这块菜地的面积(结果保留根号)20.(本题满分8分)如图,在某建筑物 AC 上,挂着“构建和谐社会,创建平安厦门”的测得仰角为60.求宣传条幅BC 的长•(小明的身高不计, 结果精确到0.1米)18.(本题12分)海中有一个小岛 P ,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东 航行,在点A 测得小岛P 在北偏东60°方向上,航行12海里到达B 点,这时测得小岛 P 在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.Aa宣传条幅BC ,小明站在点 F 处,看条幅顶端 B ,测得仰角为30,再往条幅方向前行 20米到达点E 处,看到条幅顶端 B ,第25章《解直角三角形》整章测试答案: 一、1 〜8 BABA ACDD 二、 9.0 10. > 11.312. 4 13.515. 3 .2,225; 16. 12 尺,13 尺三、 17.解:原式二 2(2 一32 622418.解:(1)AB 二.b 2-a 2(2)AB =a [J tan 一:19•解:分两种情况:(1 )当.ACB 为钝角时,BD 是高, .ADB = 90; • 在 Rt△ BCD 中,BC =40, BD =30CD = BC 2-BD 2= 1600-900 =10.7 •在 Rt△ ABD 中,AB =50,.AD =、; AB 2 - BD 2=40 • AC 二 AD -CD =40-10、7 ,S AABC 」ACL B D =丄(40-10、一 7) 30 =(600 -150、,7)(m 2) • 22(2)当• ACB 为锐角时,丁 BD 是高,ADB "BDC =90〃 ,在 Rt △ ABD 中,AB =50, BD =30 ,AD =::;AB 2 -BD 2 =40•同理 CD 二町BC2- BD 2= :1600-900=10 7 ,AC 二 AD CD =(40 10、7),.S A ABC = 1ACLBD =-(40 101 7) 30 =(600 150、7)(m 2) • 2 2综上所述:S A ABC =(600_150-7)(m 2).20.解:有触礁危险.2_^ J-2 2=2没有 14. 60(3) ABac理由:过点P作PD丄AC于D.设PD为X,在Rt△ PBD中,/ PBD=90 —45°= 45°.BD= PD= x .在Rt△ PAD中,•••/ PAD= 90°—60°= 30°,…AD = ---- 3x.tan 30 °••• AD = AB BD , . 3x =12 x.12 一.x 6( 3 ■ 1).3 -1T 6(. 3 1)< 18,•••渔船不改变航线继续向东航行,有触礁危险.。
解直角三角形章节检测题.doc
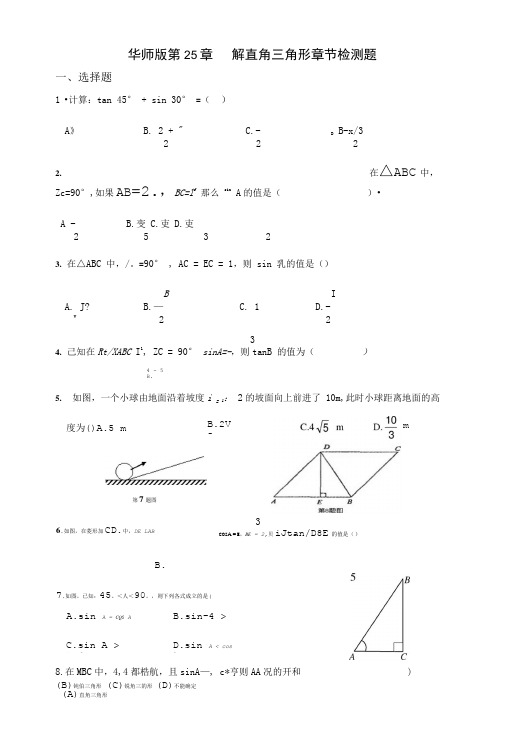
4 -5 B.度为()A.5 mB.2V 56.如图,在菱形加CD.中,DE LAB3COS A = E ,BE = 2,贝iJtan/D8E的值是( )B.27.如图,已知:45。
<人<90。
,则下列各式成立的是(A.sin A = CQS AB.sin-4 > cosC.sin A >tan AD.sin A < cosA8.在MBC 中,4,4都梏航,且sinA —, c*亨则AA 况的开和 )(B)钝伯三角形 (C)锐角三的形 (D)不能确定 (A)直角三角形华师版第25章 解直角三角形章节检测题一、选择题1 •计算:tan 45° + sin 30° =( ) A 》B. 2 + "C.- DB-x/32222.在△ABC 中,Zc=90°,如果AB =2.,BC=l f 那么 sin A 的值是( )•A - B.变 C.吏 D.吏25 323. 在△ABC 中,/。
=90° , AC = EC = 1,则 sin 乳的值是()B I A. J?B.—C. 1D.- V2234. 己知在Rt/XABC I 1, ZC = 90° sinA=-,则tanB 的值为()5. 如图,一个小球由地面沿着坡度i = 1: 2的坡面向上前进了 10m,此时小球距离地面的高第7题图m(C) 20 米(D)22 米D 久0 、z 0 w0 -V 0 \ \□ 0□LJ LJ10.如图,客轮在海上以30km/h 的速度由B 向C 航行,在B 处测得灯塔A 的方位角为北(A)(b)-T(C)W(D) -V3落在8C 边上,(A)l 3 折痕为BD,则sin ADBE 的值为( )(C )3^73739.如图,两建筑物水平距离为32米,从点4测得对点C 的俯角为30°,对点D 的俯角为45。
,则建筑物CD 的高约为().(A)14米(B)17米偏东80',测得C 处的方位角为南偏东25°,航行1小时后到达。
解直角三角形测试

17.sin55°、cos36°、sin56°的大小关系是____<____<____。
18.若 cos43°24'=0.7266,则 sin46°36'=______.
19.一个直角三角形有两条边长为 3 和 4,则较小锐角的正切值是_________。
20.tan230°+tan260°-cos30°·sin60°=______.
27.(8分)
如图,在等腰梯形ABCD中,AB 5 10,tgB 3,CB 25,求梯形面积
28、(8分)如图,在△ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,AD =103 3 cm,求∠B,AB,BC。
4
29.(本题8分):
在△ABC中,D为AB的中点,CD⊥AC,sin∠BCD 1,AC 5 ,求BC长. 4
解直角三角形单元测试题
一、选择题(每题2分,共30分)
1、在 Rt△ABC 中,∠C=90°,a=1,c=4,则 sinA 的值是(
)
15 A. 15
1 B. 3
1 C. 4
15 D. 4
2.若为锐角,且sin 4 ,则tg为 ( ) 5
A.9 B.3 C.3 D.4
高为_________米.
3
24、某人沿坡度为 1:3 的斜坡前进了 100 米,则他上升的最大高度为
米。
sinx+2cosx 25、已知:tanx=2 ,则2sinx-cosx =____________.
三、解答题(共50分):
sin 30 (1 tan 30)2 tan 45 26.(8分)计算: sin 60 cos45
43
12
sin 30 三、 26、解原式= sin 60 cos45
解直角三角形 测试Microsoft Office Word 文档

解直角三角形测试一.选择题(共3小题)1.(2013•昭通)如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为().B.C.D.2.(2013•贵阳)如图,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于().B.C.D.3.(2013•连云港)在Rt△ABC中,∠C=90°,若sinA=,则cosA的值为().B.C.D.二.填空题(共15小题)4.(2013•淄博)如图,AB是⊙O的直径,,AB=5,BD=4,则sin∠ECB=_________.5.用“>”、“=”、“<”填空:sin31°_________cos31°.6.(2002•西城区)如果α是锐角,且sin2α十cos235°=1,那么α=_________度.7.(2013•杭州)在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=;②cosB=;③tanA=;④tanB=,其中正确的结论是_________(只需填上正确结论的序号)8.(2013•贵港)如图,AB是⊙O的弦,OH⊥AB于点H,点P是优弧上一点,若AB=2,OH=1,则∠APB的度数是_________.9.(2013•扬州)在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC=_________.10.(2013•荆门)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE=_________.11.(2011•襄阳)在207国道襄阳段改造工程中,需沿AC方向开山修路(如图所示),为了加快施工进度,要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,BD=1000m,∠D=50°.为了使开挖点E在直线AC上,那么DE=_________m.(供选用的三角函数值:sin50°=0.7660,cos50°=0.6428,tan50°=1.192)12.(2013•成都)如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为_________米.13.(2013•西宁)如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为_________米.14.(2013•孝感)如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为_________m(结果不作近似计算).15.(2013•牡丹江)如图,AC是操场上直立的一个旗杆,从旗杆上的B点到地面C涂着红色的油漆,用测角仪测得地面上的D点到B点的仰角是∠BDC=45°,到A点的仰角是∠ADC=60°(测角仪的高度忽略不计)如果BC=3米,那么旗杆的高度AC=_________米.16.(2012•广西)如图,为测量旗杆AB的高度,在与B距离为8米的C处测得旗杆顶端A的仰角为56°,那么旗杆的高度约是_________米(结果保留整数).(参考数据:sin56°≈0.829,cos56°≈0.559,tan56°≈1.483)17.(2010•孝感)如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是_________海里(不近似计算).18.(2009•怀化)如图,小明从A地沿北偏东30°方向走100m到B地,再从B地向正南方向走200m到C地,此时小明离A地_________m.三.解答题(共9小题)19.(2012•永州)如图,AC是⊙O的直径,PA是⊙O的切线,A为切点,连接PC交⊙O 于点B,连接AB,且PC=10,PA=6.求:(1)⊙O的半径;(2)cos∠BAC的值.20.(2010•黔东南州)已知α为锐角,且,求的值.21.在△ABC中,(1)若∠的值;(2)若∠A=35°,∠B=65°,试比较cosA与sinB大小,说明理由.22.已知Rt△ABC中,∠C=90°,sinA、sinB是关于x的一元二次方程m(x2﹣2x)+5(x2+x)+12=0的两个实根,求实数m的值.23.(2013•昭通)计算:.24.(2013•岳阳)某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行改造,降低坡度,拟修新楼梯AD,使∠ADC=30°.(1)求舞台的高AC(结果保留根号);(2)在楼梯口B左侧正前方距离舞台底部C点3m处有一株大树,修新楼梯AD时底端D 是否会触到大树?并说明理由.25.(2013•随州)为了维护海洋权益,新组建的国家海洋局加强了海洋巡逻力度.如图,一艘海监船位于灯塔P的南偏东45°方向,距离灯塔100海里的A处,沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处.(1)在这段时间内,海监船与灯塔P的最近距离是多少?(结果用根号表示)(2)在这段时间内,海监船航行了多少海里?(参数数据:, 1.732,2.449.结果精确到0.1海里)26.(2012•黔南州)已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.(1)求证:CD为⊙O的切线;(2)过点C作CE⊥AB于E.若CE=2,cosD=,求AD的长.27.(2012•青海)如图,AB是⊙O的直径,弦CD⊥AB于点N,点M在⊙O上,∠1=∠C(1)求证:CB∥MD;(2)若BC=4,sinM=,求⊙O的直径.。
解直角三角形测试题及答案

《解直角三角形》整章测试一.选择题(每小题3分,共24分)1.在Rt △ABC 中, ∠C=90︒,AB=4,AC=1,则cos A 的值是( ) (A )154(B)14(C)15 (D)42.盘算:2)130(tan -︒=( )(A)331-(B)13- (C)133-(D )1-33.在ABC ∆中,,A B ∠∠都是锐角,且sinA =21, cosB =23,则ABC ∆的外形( )(A )直角三角形 (B )钝角三角形 (C )锐角三角形(D )不克不及肯定4.如图,在Rt ABC △中,3tan 2B =,23BC =,则AC 等于( ) (A )3(B )4(C )43(D )65.如图,小颖应用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的程度距离BE 为5m,AB 为1.5m (即小颖的 眼睛距地面的距离),那么这棵树高是( ) (A)(53332+)m (B)(3532+)m (C)533m (D)4m6.因为1sin 302=,1sin 2102=-,所以sin 210sin(18030)sin30=+=-;因为2sin 452=,2sin 2252=-,所以sin 225sin(18045)sin 45=+=-,由此猜测,推理知:一般地当α为锐角时有sin(180)sin αα+=-,由此可知:sin 240=( )北东ABC(A )12-(B)22-(C)32-(D)3- 7.如图,客轮在海上以30km/h 的速度由B 向C 航行,在B 处测得 灯塔A 的方位角为北偏东80,测得C 处的方位角为南偏东25,航 行1小时后到达C 处,在C 处测得A 的方位角为北偏东20,则C 到A 的距离是( )(A)156km (B)152km (C)15(62)+km (D)5(632)+km8.如图,在Rt ABC △中,906cm A AC ∠==,,8cm AB =,把AB 边翻折,使AB 边落在BC 边上,点A 落在点E 处,折痕为BD ,则sin DBE ∠的值为()(A)13(B)310(C)37373(D)1010二.填空题(每小题3分,共24分) 9.盘算sin 60tan 45cos30-的值是.10. 用“>”或“<”号填空:1sin 50cos 402-0.(可用盘算器盘算)Rt ABC △中,90C ∠=,:3:4BC AC =,则cos A =.12.如图,一架梯子斜靠在墙上,若梯子到墙的距离AC =3米,3cos 4BAC ∠=,则梯子AB 的长度为米. 13.如图,一汽船由南向北航行到O 处时,发明与汽船相距40海里的A 岛在北偏东33偏向.已知A 岛四周20海里水域有暗礁, 假如不转变航向,汽船(填“有”或“没有”)触暗礁 的安全.(可应用科学盘算器)ABCDEA BC14. 如图,在菱形ABCD 中,DE ⊥AB,垂足为E,DE=6cm,3sin 5A =,则菱形ABCD 的面积是__________2cm .15.依据指令[s,A](s ≥0,0°≤A <360°)机械人在平面上能完成如下动作:先在原地逆时针扭转角度A,再朝其面临的偏向沿直线行走距离s .如今机械人在平面直角坐标系的原点,且面临y 轴的负偏向,为使其移动到点(-3,3),应下的指令是.16. 有古诗“葭生池中”今有方池一丈,葭生个中心,出水一尺,引葭赴岸,适与岸齐,问:水深.葭长各几何?(1丈=10尺)答复:水深,葭长. 17.(本题8分)盘算:242(2cos 45sin 60)4︒-︒+. 18.(本题10分)某校数学兴致小组在测量一座池塘边上A B ,两点间的距离时用了以下三种测量办法,如下图所示.图中a b c ,,暗示长度,β暗示角度.请你分离求出AB 的长度(用含有a b c β,,,字母的式子暗示).(1)______AB = (2)______AB = (3)______AB =19.(本题10分)小强家有一块三角形菜地,量得双方长分离为40m,50m,第三边上的高为30m,请你帮小强盘算这块菜地的面积(成果保存根号). 20.(本题12分)海中有一个小岛P,它的四周18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A 测得小岛P 在北偏东60°偏向上,航行12海里到达B 点,这时测得小岛P 在北偏东45°偏向上.假如渔船不转变航路持续向东航行,有没有触礁安全?请解释来由.21.(本题12分)如图,AC 是某市环城路的一段,AE,BF,CD 都是南南偏向的街道,其与环城路AC 的交叉路口分离是A,B,C .经测量花草世界D 位于点A(1AC B a b(2ACB a β (3AC B a DE c b BC中山路文化路D和平路45° 15°30°EF的北偏东45°偏向.点B 的北偏东30°偏向上,AB =2km,∠DAC=15°.(1)求B,D 之间的距离; (2)求C,D 之间的距离.四.附加题(本题20分)22. 现代家居设计的“推拉式”钢窗,应用了轨道滑行技巧,纱窗装卸时应用了平行四边形的不稳固性,操纵步调如下: (1)将矩形纱窗转化成平行四边形纱窗后,纱窗上边框嵌入窗框的上轨道槽(如图1).(2)将平行四边形纱窗的下边框瞄准窗框的下轨道槽(如图2).(3)将平行四边形纱窗还原成矩形纱窗,同时下边框嵌入窗框的下轨道槽(如图3).在装卸纱窗的进程中,如图所示α∠的值不得小于81,不然纱窗受损.现将高96cm 的矩形纱窗正好装配在上.下槽深分离为0.9cm,高96cm (上.下槽底间的距离)的窗框上.试求合理装配纱窗时α∠的最大整数值.(下表供给的数据可供应用)sin810.987=0.990=sin830.993=sin840.995=cos90.987=0.990=0.993=0.995=25章《解直角三角形》整章测试答案:15.225⎡⎤⎣⎦ 16. 12尺,13尺三.17.解:原式18.解:(1)AB =图2 图3(2)tan AB a β= (3)ac AB b=. 19.解:分两种情形: (1)当ACB ∠为钝角时,BD 是高,90ADB ∴∠=.在Rt BCD △中,40BC =,30BD =∴CD ==在Rt ABD △中,50AB =,∴40AD ==.40AC AD CD ∴=-=-,新课标第一网∴211(4030(600)22ABC S AC BD ==-⨯=-△. (2)当ACB ∠为锐角时,BD 是高,90ADB BDC ∴∠=∠=,在Rt ABD △中,5030AB BD ==,,40AD ∴==.同理CD ==∴(40AC AD CD =+=+,∴211(4030(600)22ABC S AC BD ==+⨯=+△. 综上所述:2(600)ABC S =±△.20.解:有触礁安全.来由: 过点P 作PD ⊥AC 于D .设PD 为x,在Rt △PBD 中,∠PBD=90°-45°=45°. ∴BD =PD =x .在Rt △PAD 中,∵∠PAD =90°-60°=30°, ∴x .xAD 330tan =︒=∵BD ,AB AD +=∴x .x +=123 ∴)13(61312+=-=x .∵,<18)13(6+∴渔船不转变航路持续向东航行,有触礁安全.21. 解:(1)由题意得,∠EA D =45°,∠FBD=30°. ∴∠EAC=∠EA D +∠DA C =45°+15°=60°. ∵ AE∥BF∥CD,∴ ∠FBC=∠EAC =60°. ∴ ∠DBC=30°.又∵ ∠DBC=∠DAB+∠ADB, ∴ ∠ADB=15°.∴∠DAB=∠ADB.∴ BD=AB=2. 即B,D 之间的距离为2km .(2)过B 作BO⊥DC,交其延伸线于点O, 在Rt△DBO 中,BD=2,∠DBO=60°. ∴ DO=2×sin60°=2×323=,BO=2×cos60°=1.在Rt△CBO 中,∠CBO=30°,CO=BOtan30°=33,∴ CD=DO-CO=332333=-(km ).即C,D 之间的距离为332km .22. 解:可以或许合理装上平行四边形纱窗时的最大高度:960.995.1-=(cm )可以或许合理装上平行四边形纱窗时的高:96sin α∠或96cos(90)α-∠·° 当81α∠=°时,纱窗高:96sin 81960.98794.75295.1=⨯=<°∴此时纱窗能装进去,当82α∠=°时,纱窗高:96sin82960.99095.0495.1=⨯=<°∴此时纱窗能装进去.当83α∠=°时,纱窗高:96sin 83960.99395.32895.1=⨯=>°∴此时纱窗装不进去.是以能合理装上纱窗时α∠的最大值是82°.。
解直角三角形单元测试题含答案

解直角三角形单元测试题一、选择题:1、在△ABC中,若三边BC、CA、AB满足 BC:CA:AB=5:12:13,则sinA的值是( )A. B. C. D.2、已知∠A为锐角,且sinA≤,则()°≤A≤60°°≤A <90°°<A ≤30°°≤A≤90°3、在Rt△ABC中,∠C=90°,∠B=60°,那么sinA+cosB的值为()B. C. D.4、已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为()A. B. C. D.5、如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧上的一点,则cos∠APB的值是()A.45° B.1 C. D.无法确定6、如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为()A. B. C. D.7、如图,已知在△ABC中,cosA=,BE、CF分别是AC、AB边上的高,联结EF,那么△AEF和△ABC的周长比为()A.1:2 B.1:3 C.1:4 D.1:98、如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4 m,测得仰角为60°.已知小敏同学身高(AB)为 m,则这棵树的高度约为(结果精确到 m,≈( )A. m B. m C. m D. m9、如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )A.10海里 B.(10-10)海里 C.10海里 D.(10-10)海里10、如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )A. B.-1 C.2- D.11、如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )米米米 D. 24米12、如图,在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD是()(结果可以保留根号)A.30(3+)米 B.45(2+)米C.30(1+3)米 D.45(1+)米二、填空题:13、求值:sin60°•tan30°= .14、如图,∠1的正切值等于.15、如图,在菱形ABCD中,DE⊥AB,,BE=2,则________.16、如图,一人乘雪橇沿坡比1:的斜坡笔直滑下72米,那么他下降的高度为米.17、如图,小岛在港口的南偏东45°方向、距离港口81海里处.甲船从出发,沿方向以9海里/h的速度驶向港口;乙船从港口出发,沿南偏西60°方向,以18海里/h的速度驶离港口.现两船同时出发,当甲船在乙船的正东方向时,行驶的时间为h.(结果保留根号)18、如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是.三、计算题:19、.20、计算:21、已知顶点为A(2,一1)的抛物线与y轴交于点B,与x轴交于C、D两点,点C坐标(1,O);(1)求这条抛物线的表达式;(2)连接AB、BD、DA,求cos∠ABD的大小;(3)点P在x轴正半轴上位于点D的右侧,如果∠APB=45°,求点P的坐标.22、如图,在△ABC中,∠ACB=90°,AB=5,tanA=,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E;(1)求△ABC的面积;(2)求sin∠CBE的值.23、如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:(1)BC的长;(2)sin∠ADC的值.24、先化简,再求代数式的值÷(﹣),其中a=2cos30°﹣tan45°,b=2sin30°.25、如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到)(参考数据:≈,≈)26、南沙群岛是我国的固有领土,现在我南海渔民要在南沙群岛某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+)海里的C处,为防止某国的巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.27、如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:,AB 的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到米).(参考数据:sin42°≈,cos42°≈,tan42°≈)参考答案1、C2、C3、A4、A5、C6、B7、B8、D9、D10、A11、B12、A13、答案为:.14、答案为:.15、答案为:216、答案为:3617、答案为:18、答案为:2,19、.20、=1+2-(+1)-+2=221、解:(1)∵顶点为A(2,﹣1)的抛物线经过点C(1,0),∴可以假设抛物线的解析式为y=a(x﹣2)2﹣1,把(1,0)代入可得a=1,∴抛物线的解析式为y=x2﹣4x+3.(2)令y=0,x2﹣4x+3=0,解得x=1或3,∴C(1,0),D(3,0),令x=0,y=3, ∴B(0,3)∵OB=OD=3,∴∠BDO=45°,∵A(2,﹣1),D(3,0),∴∠ADO=45°,∴∠BD A=90°,∴(3)∵∠BDO=∠DPB+∠DBP=45°,∠APB=∠DPB+∠DPA=45°,∴∠DBP=∠APD,∵∠PDB=∠ADP=135°,∴△PDB∽△ADP,∴PD2=BD•AD=3=6,∴PD=,∴OP=3+,∴点P(3+,0).22、解:(1)∵∠ACB=90°,tanA=,∴=,∴AC=2BC,在Rt△ABC中,BC2+AC2=AB2,即BC2+4BC2=25,解得BC=,所以,AC=2,△ABC的面积=AC•BC=××2=5;(2)设CE=x,则AE=AC﹣CE=2﹣x,∵△ABC沿直线l翻折点A与点B重合,∴BE=AE=2﹣x,在Rt△BCE中,BC2+CE2=BE2,即2+x2=(2﹣x)2,解得x=,所以,CE=,BE=2﹣x=2﹣=,所以,sin∠CBE===.23、(1)过点A作AE⊥BC于点E,∵cosC=,∴∠C=45°.∴在Rt△ACE中,CE=AC·cosC=1.∴AE=CE=1.在Rt△ABE中,tanB=,即=,∴BE=3AE=3.∴BC=BE+CE=4.(2)∵AD是△ABC的中线,∴CD=BC=2.∴DE=CD-CE=1.∵AE⊥BC,DE=AE,∴∠ADC=45°.∴sin∠ADC=.24、解:原式=÷=×=,当a=2cos30°﹣tan45°=2×﹣1=﹣1,b=2sin30°=2×=1时,原式===.25、解:如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.则DE=BF=CH=10m,在直角△ADF中,∵AF=80m﹣10m=70m,∠ADF=45°,∴DF=AF=70m.在直角△CDE中,∵DE=10m,∠DCE=30°,∴CE===10(m),∴BC=BE﹣CE=70﹣10≈70﹣≈(m).答:障碍物B,C两点间的距离约为.∠ACB=45°,在Rt△ADC中,CD=AD=x,在Rt△ADB中∵=tan30°,∴BD=AD=x,∵BC=CD+BD=x+x=20(1+),即x+x=20(1+),解之得x=20,∴AC=AD=20.∴A、C之间的距离为20海里.27、解:延长CB交PQ于点D.∵MN∥PQ,BC⊥MN,∴BC⊥PQ.∵自动扶梯AB的坡度为1:,∴.设BD=5k米,AD=12k米,则AB=13k米.∵AB=13米,∴k=1,∴BD=5米,AD=12米.在Rt△CDA中,∠CDA=90゜,∠CAD=42°,∴CD=AD•tan∠CAD≈12×≈米,∴BC≈米.答:二楼的层高BC约为米.。
《解直角三角形》.doc

《解直角三角形》1、已知:在Rt △ABC 中,a=3,b=4,则cosA= ,tanA= 。
2、若△ABC 三边长度之比为a :b :c=3:4:5,则sinB= 。
3、设∠α为锐角,且cos α=54,则cot α= 。
4、计算0230cos 1-的值是 。
5、计算:1-sin 2240-cos 224= ,tan320·tan450·tan580= .6、在Rt △ABC 中 ,∠A=600,AB=14cm ,则AB 边上的高为 cm 。
7、在Rt △ABC 中,∠C=900,∠A=300,AB=4cm ,则BC= cm 。
8、等腰三角形的周长为32+,腰长为1,则底角等于 度。
9、已知α是锐角,若tan 3+(α+200)=3,则α= 。
10、某人沿着坡度i=1:3的山坡走了50米,则他离地面 米。
11、在Rt △ABC 中,各边都扩大5倍,则角A 的三角函数值( )A 、不变B 、扩大5倍C 、缩小5倍D 、不能确定12、在△ABC 中,若0)cos 23(1sin 2=-+-B A ,则∠C=( ) A 、750 B 、600 C450 D 、30013、当300<α≤600时,以下结论正确的是( )A 、21≤sin α≤23B 、21<cos α≤23 C 、33≤tan α≤3 D 、33≤cot α≤3 14、设α是锐角,则sin α+cos α的值一定( )A 、小于1B 、大于1C 、等于1D 、小于或等于115、如果α、β都是锐角,下面式子中正确的是( )A 、sin (α+β)=sin α+sin βB 、cos(α+β)=21时,α+β=600C 、若α≥β时,则cos α≥cos βD 、若cos α>sin β,则α+β>90016、当∠A 为锐角,且cotA 的值小于3时,∠A ( )A 、小于300B 、大于300C 、小于600D 、大于600解答题1、在Rt △ABC 中,∠C=900,a=2,b=1, 求∠A 的四个三角函数值。
解直角三角形单元测试题附答案

解直角三角形 单元测试 (时间:100分钟 满分:150分)一、填空题(每题3分,共30分)1.若直角三角形两条直角边长分别为5和12,则斜边上的中线长为________. 2.若等腰直角三角形的一边长是2,则它的面积为___________. 3.△ABC 中,∠C =90°,a =6,b =8,则sinA =_____________. 4.在△ABC 中,∠C =90°,135sin =B ,则cosB =___________. 5.若23sin =a ,则锐角a =__________度. 6.Rt △ABC 中,∠C =90°,220,20==c a ,则∠B =_________度. 7.△ABC 中,∠C =90°,10,54sin ==AB A ,则AC =_________. 8.在离大楼15m 的地面上看大楼顶部仰角为60°,则大楼高约__________m(精确到lm). 9.在电线杆离地面8m 的地方向地面拉一条缆绳以固定电线杆,如果缆绳与地面成 60°角,那么需要缆绳__________m(忽略打结部分).10.一个斜坡的坡度是1:3,高度是4m ,则他从坡底到坡顶部所走的路程大约是___________m .二、选择题(每题4分,共20分)11.直角三角形的两条边长分别为3、4,则第三条边长为 ( ) A .5 B .7 C .7 D .5或712.如图,菱形ABCD 的对角线AC =6,BD =8,∠ABD =a ,则下列结论正确的是 ( ) A .54sin =a B .53cos =a C .34tan =a D .34cot =a第12题 第13题13.如图,在Rt △ABC 中,∠C =90°,BC =4,AC =3,CD ⊥AB 于D ,设∠ACD =a ,则cos a 的值为 ( )A .54B .43C .34D .5314.△ABC 中,∠C =90°,且a ≠b ,则下列式子中,不能表示△ABC 面积的是 ( )A .ab 21B .B ac sin 21C .A b tan 212D .B A c cos sin 212⋅15.如图,钓鱼竿AC 长6m ,露在水面上的鱼线BC 长23m ,某钓者想看看鱼钓上的情况,把鱼竿AC 转动到C A '的位置,此时露在水面上的鱼线C B ''为33,则鱼竿转过的角度是 ( )A .60°B .45°C .15°D .90°三、解答题(每题10分,共50分)16.计算(1)2cos30°+cot60°-2tan45°·tan60°(2)()︒-︒-︒⋅︒︒+︒30sin 60sin 330cot 30tan 45cos 45sin 2217.如图,求下列各直角三角形中字母的值.18.如图是直线y =-2x+5的图象,求锐角a 的四个三角函数值.19.如图,梯形ABCD 中,AB ⊥BC ,∠BAC =60°,∠ADC =135°,312 BC ,求梯形的面积和周长.20.身高相同的甲、乙、丙三人放风筝,各人放出的线长分别为300m、250m、200m,线与地平面所成的角分别为30°、45°、60°(假设风筝线是拉直的),问三人所放的风筝谁的最高?21.(本题15分)分别以直角三角形的三边为边长向外作图形,如图,甲是作三个正方形,乙是作三个正三角形,丙是作三个半圆,丁是作三个等腰直角三角形.分别探索这四个图形工、Ⅱ、Ⅲ的面积之间的关系,并证明。
解直角三角形单元检测试题含答案)

解直角三角形单元检测试题一、填空题:1、如下图,表示甲、乙两山坡的情况, ___ __坡更陡。
(填“甲”或“乙”)α β121334甲乙2、在Rt△ABC中,∠C=90°,若AC=3,AB=5,则cosB的值为__________。
3、在Rt△ABC中,∠C=90°.若sinA=22,则sinB= 。
4、计算:tan245°-1=。
5、在△ABC中,AB=AC=10,BC=16,则tanB=___ __。
6、△ABC中,∠C=90°,斜边上的中线CD=6,sinA=31,则S△ABC=______。
7、菱形的两条对角线长分别为23和6,则菱形较小的内角为______度。
8、如图2是固定电线杆的示意图。
已知:CD⊥AB,CD33=m,∠CAD=∠CBD=60°,则拉线AC的长是__________m。
9、升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为30°,若双眼离地面1.5米,则旗杆的高度为______米。
(用含根号的式子表示)10、如图3,我校为了筹备校园艺术节,要在通往舞台的台阶上铺上红色地毯.如果地毯的宽度恰好与台阶的宽度一致,台阶的侧面如图所示,台阶的坡角为30o,90BCA∠=o台阶的高BC为2米,那么请你帮忙算一算需要米长的地毯恰好能铺好台阶.(结果精确到0.1m,取2 1.414=3 1.732=)11、如图4,如果△APB绕点B按逆时针方向旋转30°后得到△A'P'B,且BP=2,那么PP'的长为____________.(不取近似值. 以下数据供解题使用:sin15°=426-62+)二、选择题:12、在ABC ∆中,︒=∠90C ,AB=15,sinA=13,则BC 等于( )A 、45B 、5C 、15D 、14513、李红同学遇到了这样一道题:3tan(α+20°)=1,你猜想锐角α的度数应是( )A.40°B.30°C.20°D.10°14、身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300 m ,250 m ,200 m ;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝( )A.甲的最高B.乙的最低C.丙的最低D.乙的最高 15、在△ABC 中,若tanA=1,sinB=22,你认为最确切的判断是( ) A.△ABC 是等腰三角形 B.△ABC 是等腰直角三角形 C.△ABC 是直角三角形 D.△ABC 是一般锐角三角形 16、如图5,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8 m ,要在窗子外面上方安装水平挡光板AC ,使午间光线不能直接射入室内,那么挡光板的宽度AC 为( )A.1.8tan80°mB.1.8cos80°mC.︒80sin 8.1 mD.︒80tan 8.1 m 17、如图6,四边形ABCD 中,∠A=135°,∠B=∠D=90°,BC=23,AD=2,则四边形ABCD 的面积是( )A.42B.43C.4D.6三、解答题: 18、计算:(1)3cos30°+2sin45°(2)6tan 2 30°-3sin 60°-2sin 45°19、根据下列条件,求出Rt △ABC(∠C=90°)中未知的边和锐角.(1)BC=8,∠B=60°. (2)AC=2,AB=220、如图7,在Rt △ABC 中,∠C=90°,AC=8,∠A 的平分线AD=3316 求∠B 的度数及边BC 、AB 的长.21、等腰三角形的底边长20 cm ,面积为33100 cm 2,求它的各内角.22、同学们对公园的滑梯很熟悉吧!如图是某公园在“六•一”前新增设的一台滑梯,该滑梯高度AC =2m ,滑梯着地点B 与梯架之间的距离BC =4m 。
解直角三角形测试题(三套)

解直角三角形单元测试卷1姓名------------一、填空题:1.若锐角α、β互余且cos α=4/5,则sin β=________,cos β=__________。
2.在直角三角形ABC 中,∠C =60°,斜边BC =14 cm ,则BC 边上的高为____ cm 。
3.等边三角形的面积为,则边长为 ,高为_________.4.Rt △ABC 中,∠C =90°,CD ⊥AB 于D ,sinB =3/4,则tan ∠DCA =__________5. 三角形的一锐角A满足关系式20cos A,则A = .6.三角形三边为3,7,102,则最大锐角的余弦值为__________。
7..直角三角形的周长为24cm ,一个锐角的正弦值为3/5,则面积为__________。
二、选择题:8、已知:α为锐角,且tan α= ) A.030α︒<<︒ B.3045α︒<<︒ C. 4560α︒<<︒ D. 6090α︒<<︒9.在锐角ABC ∆中,tan 0B -=,且AB=4,则ABC ∆的面积等于( )A.4B.10、已知等腰三角形顶角为120°,底上的高为5,则一腰上的高为( ) (A )5 (B )52 (C )53 (D )10 11、下列各式正确的是( )(A )sin20°+sin20°=sin40° (B )cot 31°=tan (90°-59°) (C )sin 2A +cos 2(90°-A )=1 (D )sin2B A +=cos2C (其中A+B+C =180°)12. Rt △ABC 中,∠C=90°,D 为BC 一点,∠DAC=30°,BD =2,AB =23, AC 长是( )A.3B.22C.3D.32313. 上午9时,一条船从A 处出发,以每小时40海里的速度向正东方向航行,9时30分到达B 处,从A 、B 两处分别测得小岛M 在北偏东45°和北偏东15°方向,则在B 处船与小岛M 的距离是( ) A.20海里 B.202海里 C.153海里 D.203三、解答题:14.计算 cos 245°+sin60°·tan 30°15.如图,三角形△ABC 中,∠B =45°,∠C =60°,AB =23,AD ⊥BC 于D ,求CDABCD16.如图,已知四边形ABCD 中,BC =CD =DB ,∠ADB=90°,cos ∠ABD=4/5, 求S △ABD :S △BCD .BC17.如图,在上海黄埔江东岸,矗立着亚洲第一的电视塔“东方明珠”,某校学生在浦江西岸B处,测得塔尖D的仰角为,后退340米到A点测得塔尖D仰角为,设塔底C与B、A在一直线上,试求该塔的高度18.已知ABC∆中,AB=AC,CH是AB边上的高,且3,5CH AB BC==求tan B的值和CH的长.19.在△ABC中,∠C=90°,若b+c=90,∠A-∠B=30°,解这个直角三角形。
初中数学解直角三角形 单元测试.docx

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)试题1:在Rt△ABC中,∠C=90°,下列式子不一定成立的是()A.sinA=sinB B .cosA=sinB C.sinA=cosB D.∠A+∠B=90°试题2:直角三角形的两边长分别是6,8,则第三边的长为()A.10 B.2 C.10或2 D.无法确定试题3:已知锐角α,且sinα=cos37°,则a等于()A.37° B.63° C.53° D.45°试题4:在Rt△ABC中,∠C=90°,当已知∠A和a时,求c,应选择的关系式是()A.c= B.c= C.c=a・tanA D.c=试题5:如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB的中点N的最短路线是()A.8 B.2 C.2 D.2+2试题6:已知∠A是锐角,且sinA=,那么∠A等于()A.30° B.45° C.60° D.75°试题7:当锐角α>30°时,则cosα的值是()A.大于 B.小于 C.大于 D.小于试题8:小明沿着坡角为30°的坡面向下走了2米,那么他下降()A.1米 B.米 C.2 D.试题9:已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AC等于()A.6 B. C.10 D.12试题10:已知sinα=,求α,若用计算器计算且结果为“”,最后按键() A.AC10N B.SHIET C.MODE D.SHIFT “”试题11:如图,3×3•网格中一个四边形ABCD,•若小方格正方形的边长为1,•则四边形ABCD的周长是_______.试题12:计算2sin30°+2cos60°+3tan45°=_______.试题13:若sin28°=cosα,则α=________.试题14:已知△ABC中,∠C=90°,AB=13,AC=5,则tanA=______.试题15:如图所示的一只玻璃杯,最高为8cm,将一根筷子插入其中,杯外最长4厘米,•最短2厘米,那么这只玻璃杯的内径是________厘米.试题16:由下列条件解题:在Rt△ABC中,∠C=90°:(1)已知a=4,b=8,求c.(2)已知b=10,∠B=60°,求a,c.(3)已知c=20,∠A=60°,求a,b.试题17:计算sin230°+cos245°+sin60°・tan45°;试题18:计算+tan60°试题19:计算tan2°tan4°・tan6°…tan88°试题20:已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠A的四种三角函数值.试题21:如图所示,平地上一棵树高为5米,两次观察地面上的影子,•第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长多少米?试题22:如图所示的燕服槽一个等腰梯形,外口AD宽10cm,燕尾槽深10cm,AB的坡度i=1:1,求里口宽BC及燕尾槽的试题23:如图,AB是江北岸滨江路一段,长为3千米,C为南岸一渡口,•为了解决两岸交通困难,拟在渡口C处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸的最短的桥长多少?(精确到0.试题24:请你设计一个方案,测量一下你家周围的一座小山的高度.•小山底部不能到达,且要求写出需要工具及应测量数据.试题25:如图所示,学校在楼顶平台上安装地面接收设备,为了防雷击,在离接收设备3米远的地方安装避雷针,接收设备必须在避雷针顶点45•°夹角范围内,才能有效避免雷击(α≤45°),已知接收设备高80厘米,那么避雷针至少应安装多高?试题1答案:A试题2答案:C [点拨]长为8的边即可能为直角边,也可能为斜边.试题3答案:C [点拨]tanα=cot37°,所α+37°=90°即α=53°.试题4答案:A试题5答案:C试题6答案:C试题7答案:D试题8答案:A试题9答案:A试题10答案:D试题11答案:3+2试题12答案:.4+试题13答案:62°试题14答案:2.4试题15答案:6 [点拨]根据条件可得筷子长为12厘米,如图AC=10,BC== =6.试题16答案:解:(1)c= =4;(2)a=b×cotB=10×=,c=(3)a=c×sinA=20×=10,b=c×cos60°=10×=5.试题17答案:原式=()2+()2+××1=++=+试题18答案:原式=+=+试题19答案:原式=tan2°・tan4°・tan6°・…cot6°・cot4°・cot2°=(tan2°・cot2°)(tan4°・cot4°)・(tan6°・cot6°)…=1试题20答案:解:如下图,AD⊥BC,CE⊥AB,AB=AC.因为AD⊥BC,AB=AC,所以BD=CD=5.在直角三角形ABD中,AD==12.S△ABC=×AB×CE=×BC×AD,所以×13×CE=×10×12,CE=.在直角三角形ACE中,AE==.在直角三角形ACE中,sin∠CAE=,cos∠CAE=,tan∠CAE=,cot∠CAE=.试题21答案:第一次观察到的影子长为5×cot45°=5(米);第二次观察到的影子长为5•×cot30°=5(米).两次观察到的影子长的差是5-5米.试题22答案:解:如下图,作DF⊥BC于点F.由条件可得四边形AEFD是矩形,AD=EF=10.AB的坡角为1:1,所以=1,所以BE=10.同理可得CF=10.里口宽BC=BE+EF+FC=30(厘米).截面积为×(10+30)×10=200(平方厘米).试题23答案:过点C作CD⊥AB于点D.CD就是连接两岸最短的桥.设CD=x米.在直角三角形BCD中,∠BCD=45°,所以BD=CD=x.在直角三角形ACD中,∠ACD=30°,所以AD=CD×tan∠ACD=x・tan30°=x.因为AD+DB=AB,所以x+x=3,x=≈1.9(米).试题24答案:略.试题25答案:解:如图,AE⊥CD于点E,AB=CE=0.8,AE=BC=3.在直角三角形ADE中,cotα=,DE=AE×cotα=3cotα.因为α≤45°,所以cotα≥1,所以DE>3.CD=CE+DE>3.8(米).因此,避雷针最少应该安装3.8米高.。
解直角三角形 单元测试

§25 解直角三角形 单元测试(第2次)(总分100分)班级 姓名 座号 成绩一、选择题(本题共7小题,每小题3分,共21分) 1. sin60°的值等于( )A .21 B .22 C .23 D .12.α∠在方格纸中的位置如图所示,则tan α的值是( )A .34B .43C .35D .453. 已知Rt △ABC 中,∠C=90︒,边BC 的长为m ,∠B=50°,则AB 的长是( )A .︒50sin mB .︒50cos mC .︒50sin m D .︒50cos m4. 在Rt △ABC 中, ∠C=90︒,AB=3,AC=1,则sinA 的值是( )A.31 B .322 C .22 D .425. 已知在R t ABC △中,390sin 5C A ∠==°,,则tan B 的值为( )A .43 B .45 C .54D .346. 如图,先锋村准备在坡度为1:2的山坡上栽树,要求相邻两树之间的水平距离为4米,那么这两树在坡面上的距离AB 为 ( ) A. 4米 B. 2米 C.5米 D.52米7. 菱形O A B C 在平面直角坐标系中的位置如图所示,452AOC OC ∠==°,,则点B的坐标为( )A .(21),B .(12),C .(211)+,D .(121)+,二、填空题(本题共8小题,每小题4分,共32分)8. ︒⋅+︒⋅tan303sin452= ;9. 如图,在直角坐标系中,P 是第一象限的点,其坐标是(6,y ),且OP 与x 轴的正半轴的夹角α的正切值是34,则y= ;xyO CBAα4米ABα第2题 第6题第7题(第9题)10. 如图,某商场一楼与二楼之间有一手扶电梯.其中AB ,CD 分别表示一楼.二楼地面,∠ABC =150°,BC 的长是8 m ,则乘电梯从点B 到点C 上升的高度h 是 m ; 11. 某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为 米;12. 如图,菱形ABCD 的周长为20cm ,DE ⊥AB ,垂足为E ,54cos =C ,则DE= cm13. 在△ABC 中,AB=6,BC=8,∠B=30°,则这个三角形的面积为14. 在一次夏令营活动中,小亮从位于A 点的营地出发,沿北偏东60°方向走了5km 到达B 地,然后再沿北偏西30°方向走了5千米到达C 地,则C 点和A 点的距离为 km 15. 如图,在A B C △中,C ∠9060B D =∠=°,°,是A C 上一点, D E A B ⊥于E ,CD=2,DE=21,则B C的长为 ;三、解答题(共47分)16.(5分)计算: ︒⋅︒︒tan4545cos -30cos 2217.(5分)在△ABC 中,∠C 为直角,AB=4,∠A =45°,解这个直角三角形.CBAABCDEAB CD150°h第9题第10题第11题第12题第13题第14题 第15题C BA30°60°418. (7分)如图所示,课外活动中,小明在离旗杆AB 10米的C 处,用测角仪测得旗杆顶部A 的仰角为20°,已知测角仪器的高CD =1.5米,求旗杆AB 的高. (精确到0.1米) (供选用的数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)19.(7分)京杭运河修建过程中,某村考虑到安全性,决定将运河边一河埠头的台阶进行改造.在如图的台阶横断面中,将坡面A B 的坡角由45°减至30°.已知原坡面的长为6m (BC 所在地面为水平面)(1)改造后的台阶坡面会缩短多少?(结果保留根号)(2)改造后的台阶高度会降低多少?(结果保留根号)20.(7分)如图,梯形ABCD 是拦水坝的横断面图,AD ∥BC ,坡面AB 的坡度1:3=i ,︒=∠30C ,CD=8,AD=4,求拦水坝的横断面A B C D 的面积(结果保留根号)CDBA21.(8分)如图,小芸在自家楼房的窗户A 处,测量楼前的一棵树CD 的高. 现测得树顶C 处的俯角为45°,树底D 处的俯角为60°,楼底到大树的距离BD 为20米.请你帮助小芸计算树的高度(精确到0.1米).22.(8分)如图,已知一次函数b kx y +=的图象经过)1,2(--A ,)3,1(B 两点,并且交x 轴于点C ,交y 轴于点D , (1)求该一次函数的解析式; (2)求OCD ∠tan 的值;45°A BCD60° BD C AO 1 1yx。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形单元测试题
一、判断题
1、ctgl5°·ctg75°=ctg45°();
2、(2sin3O°-1)2=1();
3、sin75°=sin(45°+30°)=sin45°+sin30°();
4、在△ABC中,,则∶∶=3∶6∶8();
5、锐角A>B,则sinA>cosB ();
6、若α,β均为锐角,sinα-cosβ=0,则α+β=90°();
7、三角形的一锐角A满足关系式,则A=45°();
8、sinα的值随角α的不断增大而增大,cosα的值随角α的不断增大而减小();
9、直角三角形ABC中,sinA/sinB=a/b,故直角三角形中,边长与其对角成正比();
10、在0°<α<90°时,tgα<sinα()。
二、填空题:
11、可用三角形内锐角的正弦表示成__________。
12、A为一锐角,若sinA=,则cosA=__________,又若cosA=,则tgA =__________。
13、三边长分别为5、12、13的三角形的外接圆半径为________,内切圆半径为________。
14、顶角为锐角的正弦值为,周长为18cm的等腰三角形的底边长是
__________,腰长是__________。
15、A、B为直角三角形ABC的两锐角,sinA和sinB是方程的两个根,则=__________,sin2A+sin2B=__________。
16、在直角三角形ABC中,∠C=60°,斜边BC=14 cm,则BC边上的高为
__________ cm 。
三、选择题
17、α为锐角,则=()。
(A)1-sinα-cosα(B)l+sinα+cosα
(C)0 (D)sinα+cosα-1
18、正六边形的两条对边相距12cm,那么这个正六边形的边长为()。
(A)7.5 cm (B)cm (C)cm (D)cm
19、A、B为Rt△ABC的两锐角,∠C=90°,则有()。
(A)sinA=sinB (B)cosA=cosB (C)sinB=cosC (D)sinA=cosB
20、正三角形边长为,则其外接圆半径等于()。
(A)(B)(C)(D)
21、若0°<α<90°,则的值等于()。
(A)0 (B)1 (C)2 (D)3
四、计算和解答题
22、计算:
(1);
(2);
(3)已知,求的值;
(4)已知Rt△ABC,∠C=90°,∠A=60°,=2,求B,,。
23、解答题:
(5)甲、乙两楼相距100米,从乙楼底望甲楼顶仰角为60°,从甲楼顶望乙楼顶俯角为30°,求两楼的高度(精确到0.1米),要求画出正确图形。
(6)已知直角三角形的两条直角边的长是方程的两个
根的值,若这个直角三角形的斜边上的中线长6.5cm,求它的周长、面积和斜边上的高。
