运筹案例分析及实验报告
运筹学案例分析报告

运筹学案例分析报告班级:姓名:学号:完成日期:问题一、一、问题描述京成畜产品有限公司计划在市区的东、南、西、北四区建立销售部部门市场,拟议中有10个位置A j(j=1,2,3,4,...,10)可供选择,考虑到各地区居民的消费水平及居民居住密集度,规定:在东区由A1,A2,A3三个点至多选择两个;在西区由A4,A5两个点中至多选一个;在南区由A6,A7两个点中至少选一个;在北区由A8,A9,A10三个点中至少选两个。
A j各点的设备投资及每年可获利润由于地点不同而不同,预测情况如下表(单位:万元)。
但投资总额不超过720万元,问应选择哪几个销售点,可使年利润最大?二、模型建立设0-1变量X i=1(点被选用)或0(A i点没被选用)。
建立数学模型:目标函数:maxZ=36X1+40X2+50X3+22X4+20X5+30X6+25X7+48X8+58X9+61X10约束条件:100X1+120X2+150X3+80X4+70X5+90X6+80X7+149X8+160X9+180X10<=720X1+X2+X3<=2X4+X5>=1X6+X7>=1X8+X9+X10>=2X i>=0,且X i为0-1变量,i=1,2,3,...,10其lingo程序为:model:sets:row/1..5/:b;col/1..10/:c,x;links(row,col):a;endsetsdata:b=720 2 -1 -1 -2;c=36 40 50 22 20 30 25 48 58 61;a=100 120 150 80 70 90 80 140 160 1801 1 1 0 0 0 0 0 0 00 0 0 -1 -10 0 0 0 00 0 0 0 0 -1-1 0 0 00 0 0 0 0 0 0 -1 -1 -1;enddatamax=@sum(col(j):c(j)*x(j));@for(row(i):@sum(col(j):a(i,j)*x(j))<=b(i));@for(col(j):@bin(x));end三、模型求解与分析通过lingo程序的求解,我们可以获得如下数据:Global optimal solution found.Objective value: 245.0000 Objective bound: 245.0000 Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostB( 1) 720.0000 0.000000B( 2) 2.000000 0.000000B( 3) -1.000000 0.000000B( 4) -1.000000 0.000000B( 5) -2.000000 0.000000C( 1) 36.00000 0.000000C( 2) 40.00000 0.000000C( 3) 50.00000 0.000000C( 4) 22.00000 0.000000C( 5) 20.00000 0.000000C( 6) 30.00000 0.000000C( 7) 25.00000 0.000000C( 8) 48.00000 0.000000C( 9) 58.00000 0.000000C( 10) 61.00000 0.000000X( 1) 1.000000 -36.00000X( 2) 1.000000 -40.00000X( 3) 0.000000 -50.00000X( 4) 0.000000 -22.00000X( 5) 1.000000 -20.00000X( 6) 1.000000 -30.00000X( 7) 0.000000 -25.00000X( 8) 0.000000 -48.00000X( 9) 1.000000 -58.00000X( 10) 1.000000 -61.00000A( 1, 1) 100.0000 0.000000A( 1, 3) 150.0000 0.000000 A( 1, 4) 80.00000 0.000000 A( 1, 5) 70.00000 0.000000 A( 1, 6) 90.00000 0.000000 A( 1, 7) 80.00000 0.000000 A( 1, 8) 140.0000 0.000000 A( 1, 9) 160.0000 0.000000 A( 1, 10) 180.0000 0.000000 A( 2, 1) 1.000000 0.000000 A( 2, 2) 1.000000 0.000000 A( 2, 3) 1.000000 0.000000 A( 2, 4) 0.000000 0.000000 A( 2, 5) 0.000000 0.000000 A( 2, 6) 0.000000 0.000000 A( 2, 7) 0.000000 0.000000 A( 2, 8) 0.000000 0.000000 A( 2, 9) 0.000000 0.000000 A( 2, 10) 0.000000 0.000000 A( 3, 1) 0.000000 0.000000 A( 3, 2) 0.000000 0.000000 A( 3, 3) 0.000000 0.000000 A( 3, 4) -1.000000 0.000000 A( 3, 5) -1.000000 0.000000 A( 3, 6) 0.000000 0.000000 A( 3, 7) 0.000000 0.000000 A( 3, 8) 0.000000 0.000000 A( 3, 9) 0.000000 0.000000 A( 3, 10) 0.000000 0.000000 A( 4, 1) 0.000000 0.000000A( 4, 3) 0.000000 0.000000A( 4, 4) 0.000000 0.000000A( 4, 5) 0.000000 0.000000A( 4, 6) -1.000000 0.000000A( 4, 7) -1.000000 0.000000A( 4, 8) 0.000000 0.000000A( 4, 9) 0.000000 0.000000A( 4, 10) 0.000000 0.000000A( 5, 1) 0.000000 0.000000A( 5, 2) 0.000000 0.000000A( 5, 3) 0.000000 0.000000A( 5, 4) 0.000000 0.000000A( 5, 5) 0.000000 0.000000A( 5, 6) 0.000000 0.000000A( 5, 7) 0.000000 0.000000A( 5, 8) -1.000000 0.000000A( 5, 9) -1.000000 0.000000A( 5, 10) -1.000000 0.000000Row Slack or Surplus Dual Price1 245.0000 1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.000000 由此我们可以分析得出最优目标函数值为245.最优解为:X1=1,X2=1,X3=0,X4=0,X5=1,X6=1,X7=0,X8=0,X9=1,X10=1.四、结论当选择A1,A2,A5,A6,A10几个销售点时可获得最大利润245万元。
管理运筹学实训报告案例

一、实训背景随着市场竞争的日益激烈,企业对于管理运筹学的需求日益增长。
为了提高企业内部管理效率,培养具备运筹学知识的应用型人才,我校组织了一次管理运筹学实训活动。
本次实训旨在通过实际案例,让学生深入了解运筹学在实际工作中的运用,提高学生的实践能力。
二、实训目标1. 理解运筹学的基本概念和原理,掌握运筹学的基本方法。
2. 通过案例分析,了解运筹学在企业管理中的应用。
3. 培养学生运用运筹学解决实际问题的能力。
4. 增强学生的团队协作精神和沟通能力。
三、实训内容本次实训以某企业为例,该企业面临以下问题:1. 生产部门生产计划不合理,导致产能过剩或不足。
2. 仓库管理混乱,物资储备过多,增加库存成本。
3. 销售部门业绩不佳,客户满意度低。
针对以上问题,我们将运用运筹学中的线性规划、库存管理、销售预测等方法进行分析和解决。
四、实训过程1. 案例分析(1)生产计划问题根据企业历史数据,建立线性规划模型,确定生产计划,实现产能均衡。
(2)库存管理问题运用库存管理方法,建立最优库存模型,降低库存成本。
(3)销售预测问题运用时间序列分析法,预测未来一段时间内销售情况,为销售部门提供决策依据。
2. 模型求解(1)生产计划问题利用Excel求解线性规划模型,得出最优生产计划。
(2)库存管理问题利用库存管理软件,进行库存优化,降低库存成本。
(3)销售预测问题利用Excel中的时间序列分析工具,预测销售情况。
3. 案例实施(1)生产计划实施根据最优生产计划,调整生产部门的生产计划,实现产能均衡。
(2)库存管理实施根据最优库存模型,调整库存管理策略,降低库存成本。
(3)销售预测实施根据销售预测结果,调整销售部门的市场营销策略,提高客户满意度。
五、实训结果1. 生产部门的生产计划得到优化,产能得到均衡。
2. 库存成本得到有效降低,物资储备合理。
3. 销售部门业绩得到提升,客户满意度提高。
4. 学生在实训过程中,掌握了运筹学的基本方法,提高了实践能力。
运筹学实践教学报告范文(3篇)

第1篇一、引言运筹学作为一门应用数学分支,广泛应用于经济管理、工程技术、军事决策等领域。
本报告旨在通过运筹学实践教学,验证理论知识在实际问题中的应用效果,提高学生的实践能力和创新能力。
以下是对本次实践教学的总结和反思。
二、实践教学内容1. 线性规划问题本次实践教学选择了线性规划问题作为研究对象。
通过建立线性规划模型,我们尝试解决生产计划、资源分配等实际问题。
- 案例一:生产计划问题某公司生产A、B两种产品,每单位A产品需消耗2小时机器时间和3小时人工时间,每单位B产品需消耗1小时机器时间和2小时人工时间。
公司每天可利用机器时间为8小时,人工时间为10小时。
假设A、B产品的利润分别为50元和30元,请问如何安排生产计划以获得最大利润?- 建模:设A产品生产量为x,B产品生产量为y,目标函数为最大化利润Z = 50x + 30y,约束条件为:\[\begin{cases}2x + y \leq 8 \\3x + 2y \leq 10 \\x, y \geq 0\end{cases}\]- 求解:利用单纯形法求解该线性规划问题,得到最优解为x = 3,y = 2,最大利润为240元。
- 案例二:资源分配问题某项目需要分配三种资源:人力、物力和财力。
人力为50人,物力为100台设备,财力为500万元。
根据项目需求,每种资源的需求量如下:- 人力:研发阶段需20人,生产阶段需30人;- 物力:研发阶段需30台设备,生产阶段需50台设备;- 财力:研发阶段需100万元,生产阶段需200万元。
请问如何合理分配资源以满足项目需求?- 建模:设人力分配量为x,物力分配量为y,财力分配量为z,目标函数为最大化总效用U = x + y + z,约束条件为:\[\begin{cases}x \leq 20 \\y \leq 30 \\z \leq 100 \\x + y + z \leq 500\end{cases}\]- 求解:利用线性规划软件求解该问题,得到最优解为x = 20,y = 30,z = 100,总效用为150。
运筹学实验报告
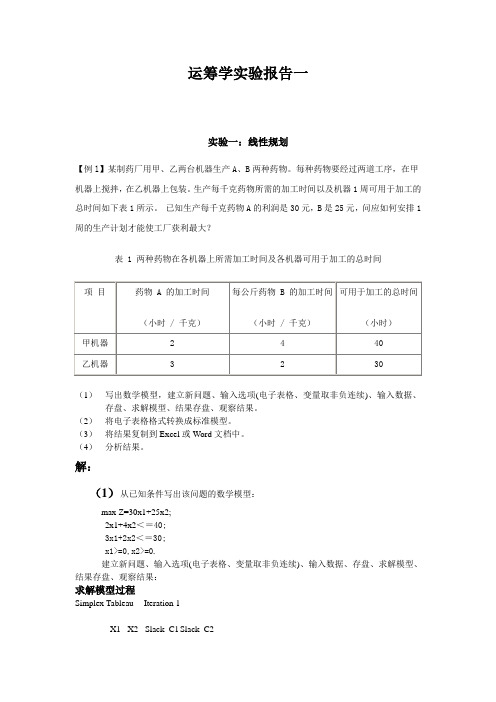
运筹学实验报告一实验一:线性规划【例l】某制药厂用甲、乙两台机器生产A、B两种药物。
每种药物要经过两道工序,在甲机器上搅拌,在乙机器上包装。
生产每千克药物所需的加工时间以及机器1周可用于加工的总时间如下表1所示。
已知生产每千克药物A的利润是30元,B是25元,问应如何安排1周的生产计划才能使工厂获利最大?表 1 两种药物在各机器上所需加工时间及各机器可用于加工的总时间(1)写出数学模型,建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果。
(2)将电子表格格式转换成标准模型。
(3)将结果复制到Excel或Word文档中。
(4)分析结果。
解:(1)从已知条件写出该问题的数学模型:max Z=30x1+25x2;2x1+4x2<=40;3x1+2x2<=30;x1>=0,x2>=0.建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果:求解模型过程Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 3X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioX2 25.0000 0 1.0000 0.3750 -0.2500 7.5000X1 30.0000 1.0000 0 -0.2500 0.5000 5.0000C(j)-Z(j) 0 0 -1.8750 -8.7500 337.5000(2)将电子表格格式转换成标准模型。
运筹学实验报告

运筹学实验报告导言运筹学是一门研究如何有效地进行决策、规划、控制和优化的学科。
它在不同领域中都有广泛应用,例如物流管理、生产调度、资源分配等。
本实验报告将介绍一个基于运筹学方法的实际案例,展示其在实践中的应用和效果。
问题描述我们选取了一个假设情景作为研究案例:一家电子公司正在考虑如何优化其供应链。
供应链的核心问题是如何在最小的时间和成本内将产品从制造商运送到最终客户手中。
该公司一直面临着供应链效率低下、库存过高等问题,因此需要进行优化。
方法选择为了解决供应链问题,我们选择了线性规划方法进行建模和求解。
线性规划是一种经典的运筹学方法,通过建立目标函数和约束条件来实现优化。
我们将考虑运输成本、库存成本和交货时间等因素,以最小化总成本为目标进行优化。
数据收集与分析首先,我们需要收集与供应链相关的数据,包括产品库存量、制造商的运输能力、客户的需求等信息。
通过对这些数据进行分析,我们可以获得对供应链瓶颈和优化潜力的洞察。
模型建立与求解根据数据分析的结果,我们可以建立数学模型来描述供应链的运作。
假设有n个制造商和m个客户,我们需要决策每个制造商向每个客户运送的产品数量。
我们定义决策变量x_ij表示制造商i 向客户j运送的产品数量。
通过设定合适的约束条件,如制造商的运输能力限制、客户的需求限制等,我们可以建立如下的线性规划模型:minimize ∑(c_ij * x_ij) for all i, jsubject to:∑(x_ij) <= supply_i for all i∑(x_ij) >= demand_j for all jx_ij >= 0 for all i, j其中c_ij表示从制造商i到客户j运输一个产品的成本,supply_i表示制造商i的运输能力,demand_j表示客户j的需求。
接下来,我们可以使用线性规划求解器对模型进行求解。
求解过程将得到最优的运输方案,包括每个制造商向每个客户运输的产品数量。
运筹学实验报告

运筹学实验报告实验目的:了解及掌握运筹学一些常用软件,如excel,WinQsb:实验步骤1用Excel求解数学规划例:求max=2x1+x2+x34x1+2x2+2x2≥42x1+4x2≤204x1+8x2+2x3≤4步骤:1.输入模型数据制E3的公式到E4-E6:3.从“工具”菜单中选择“规划求解”,将弹出的“规划求解参数”窗口中的目标单元格设为$E$3,可变单元格设为$B$2:$D$2,目标为求最大值: 4.添加约束:由于本例的约束条件类型分别为<=、>=和=,因此要分3次设置,每次设置完毕后都要单击“添加”按钮,如下图。
添加完成后选择“确定”返回。
5.单击“选项”按钮,将“规划求解选项”窗口中的“采用线性模型”和“假定非负”两项选中后点“确定”返回,设置好参数的界面如下图:6.单击“求解”按钮,得到问题的最优解为:x1 =1,x2=0,x3=0,max Z=2。
2.winQSB求解线性规划及整数规划[例]求解线性规划问题:Minz=2x1—x2+2x32x1+2x2+x3=43x1+x2+x4=6第1步:生成表格选择“程序,生成对话框:第2步:输入数据单击“OK”,生成表格并输入数据如下第3步:求解):x1,x2,x3决策变量(Decision Variable最优解:x1=2,x2=0,x3=0目标系数:c1=2,c2= -1,c3=2最优值:4;其中x1贡献4、x2,x3贡献0;检验数(Reduced Cost):0,0,1.75。
目标系数的允许减量(Allowable Min.c[j])和允许增量(Allowable Max.c[j]):目标系数在此范围变量时,最优基不变。
约束条件(Constraint):C1、C2;左端(Left Hand Side):4,6右端(Right Hand Side):4,6松驰变量或剩余变量(Slack or Surplus):该值等于约束左端与约束右端之差。
运筹学实验报告

运筹学实验报告运筹学实验报告一、引言运筹学是一门研究如何有效地进行决策和规划的学科。
它利用数学、统计学和计算机科学的方法,帮助解决各种实际问题。
本次实验旨在通过实际案例,探讨运筹学在实践中的应用。
二、问题描述我们选择了一个物流配送问题作为本次实验的研究对象。
假设有一家电商公司,需要将一批商品从仓库分配给不同的客户。
每个客户的需求量和距离仓库的距离都不同。
我们的目标是找到一种最优的配送方案,以最小化总配送成本。
三、数学模型为了解决这个问题,我们采用了整数规划模型。
首先,我们定义了以下变量:- Xij:表示将商品从仓库i分配给客户j的数量- Di:表示仓库i的供应量- Dj:表示客户j的需求量- Cij:表示将商品从仓库i分配给客户j的单位运输成本然后,我们建立了以下约束条件:1. 每个仓库的供应量不能超过其库存量:∑Xij ≤ Di2. 每个客户的需求量必须得到满足:∑Xij ≥ Dj3. 分配的商品数量必须是非负整数:Xij ≥ 0最后,我们的目标是最小化总配送成本:Minimize ∑Cij*Xij四、实验步骤1. 收集数据:我们收集了仓库的库存量、客户的需求量和单位运输成本的数据,并进行了整理和清洗。
2. 建立数学模型:根据收集到的数据,我们建立了上述的整数规划模型。
3. 求解模型:我们使用了运筹学软件对模型进行求解,并得到了最优的配送方案和总配送成本。
4. 分析结果:我们对结果进行了分析,比较了不同方案的优劣,并提出了一些建议。
五、实验结果与分析经过运筹学软件的求解,我们得到了最优的配送方案和总配送成本。
通过与其他方案的比较,我们发现该方案在成本上具有明显的优势。
同时,我们还发现一些仓库和客户之间的距离较远,可能会导致运输时间和成本增加。
因此,我们建议公司可以考虑优化仓库和客户的布局,以减少运输成本。
六、实验总结本次实验通过运筹学的方法,解决了一个物流配送问题。
我们通过建立数学模型、求解模型和分析结果,得出了最优的配送方案和总配送成本。
运筹学实验报告(1)

运筹学实验报告一、实验目的:通过实验熟悉单纯形法的原理,掌握matlab循环语句的应用,提高编程的能力和技巧,体会matlab在进行数学求解方面的方便快捷。
二、实验环境:Matlab2012b,计算机三、实验内容(包含参数取值情况):构造单纯形算法解决线性规划问题Min z=cxs.t. Ax=bxj>=0,j=1,…,n函数功能如下:function[S,val]=danchun(A1,C,N)其中,S为最优值,Val为最优解,A1为标准形式LP问题的约束矩阵及最后一列为资源向量(注:资源向量要大于零),A1=[A+b];C是目标函数的系数向量,C=c;N为初始基的下标(注:请按照顺序输入,若没有初始基则定义N=[])。
先输入A1,C,N三个必要参数,然后调用danchun(A1,C,N)进行求解。
在此函数中,首先判断N的长度是否为空,若为空,则flag=1,进入初始解问题的迭代求值,添加辅助问题,构建单纯形表,求g所对应的RHS值,若其>0,则返回该问题无解,若其=0,则返回A1,C,N三个参数,继续构造单纯形表求解。
A1为经过变换后的系数及资源向量,C为单纯形表的第一行,N为经过辅助问题求解之后的基的下标。
否则,直接构建单纯形表,对该问题进行求解,此时flag=2,多次迭代后找到解。
另外,若在大于零的检验数所对应的系数均小于零时,会显示“此问题无界”。
若找到最优解和最优值时,会输出“val”和“S=”以及具体数值。
四、源程序(在matlab中输入edit后回车,写在.M文件中,并保存为danchun.M)function[S,val]=danchun(A1,C,N)if(length(N)==0)gN=zeros(1,length(A1(:,1)));gC=[-C,gN,0];%原文题的检验数的矩阵G=[zeros(1,length(C)),-ones(1,length(gN)),0];val=zeros(1,length(C));%val为最优解;for i=(length(C)+1):length(C)+length(A1(:,1))%生成基变量gN(i-length(C))=i;endNn=gN;%%%%%%%ll=zeros(1,length(N));%比值最小原则%生成除了最上端两行的表的矩阵gb=A1(:,length(C)+1);A1(:,length(C)+1)=[];l=zeros(length(gN),length(gN));gA=[A1,l,gb];for i=1:length(gb)gA(i,gN(i))=1;endfor i=1:length(gN)%J为基本可行基所对应的检验数J(i)=G(gN(i));endfor i=1:length(gN)%找到基本可行基的检验数,将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);endendflag=1;elseflag=2;A=A1;Z=[-C,0];%单纯形表的第一行val=zeros(1,length(C));%val为最优解;ll=zeros(1,length(N));%比值最小原则end%%初始解问题while flag==1for i=1:length(gN)%J为基本可行基所对应的G的检验数J(i)=G(gN(i));JZ(i)=Z(gN(i));%JZ为基本可行基所对应的Z的检验数endfor i=1:length(gN)%找到基本可行基的检验数,将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);Z=Z-(JZ(i)/gA(i,gN(i)))*gA(i,:);endG1=G;%G1为检验数G1(:,length(G1))=[];D=max(G1);%找到检验数的最大值if(D<=0)%检验数都小于0if(G(length(G))>=1)disp('此情况无解');flag=0;elseif(G(length(G))>=0)for i=1:length(gN)if(max(gN)<=length(A1(1,:)));flag=2;for j=1:length(Nn)a=Nn(1);gA(:,a)=[];Z(a)=[];endA=gA;N=gN;break;endendendendelse%检验数大于0for i=1:length(G)if(G(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(gN)if(gA(j,i)>0)ll(j)=gA(j,length(G))/gA(j,i);%求比值elsell(j)=10000;endendd=min(ll);for k=1:length(ll)%找到进基和离基if(ll(k)==d)gN(k)=i;gA(k,:)=gA(k,:)/gA(k,i);for m=1:k-1gA(m,:)=-(gA(m,i)/gA(k,i))*gA(k,:)+gA(m,:);endfor n=k+1:length(ll)gA(n,:)=-(gA(n,i)/gA(k,i))*gA(k,:)+gA(n,:);endbreak;endendendendendendwhile(flag==2)for i=1:length(N)%J为基本可行基所对应的检验数J(i)=Z(N(i));endfor i=1:length(N)%找到基本可行基的检验数,将其赋值为0if(J(i)~=0)Z=Z-(J(i)/A(i,N(i)))*A(i,:);endendZ1=Z;%Z1为检验数Z1(:,length(Z1))=[];D=max(Z1);%找到检验数的最大值if(D<=0)%检验数都小于0disp('已找到最优解和最优值')for i=1:length(N)val(N(i))=A(i,length(Z));endS=Z(length(Z));disp('val');disp(val);flag=0;else%检验数大于0for i=1:length(Z)if(Z(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(N)if(A(j,i)>0)ll(j)=A(j,length(Z))/A(j,i);%求比值elsell(j)=10000;endendd=min(ll);if(d==10000)disp('此问题无界')flag=0;break;endfor k=1:length(ll)%找到进基和离基if(ll(k)==d)N(k)=i;A(k,:)=A(k,:)/A(k,i);for m=1:k-1A(m,:)=-(A(m,i)/A(k,i))*A(k,:)+A(m,:);endfor n=k+1:length(ll)A(n,:)=-(A(n,i)/A(k,i))*A(k,:)+A(n,:);endbreakendendendendendend五、运行结果与数据测试参考例题:例1:Min z=3x1+x2+x3+x4s.t. -2x1+2x2+x3=43x1+2x+x4=6Xj>=0,j=1,2,3,4在workspace中写入,形式如下:>> A=[-2 2 1 0 43 1 0 1 6]A =-2 2 1 0 43 1 0 1 6>> C=[3 1 1 1]C =3 1 1 1>> N=[3 4]N =3 4>> danchun(A,C,N)已找到最优解和最优值val0 2 0 4ans =6例2:初始解问题Min z=5x1+21x3s.t. x1-x2+6x3-x4=2x1+x2+2x3-x5=1xj>=0,j=1,…,5在workspace中写入,形式如下:>> A=[1 -1 6 -1 0 21 12 0 -1 1]A =1 -1 6 -1 0 21 12 0 -1 1 >> C=[5 0 21 0 0]C =5 0 21 0 0>> N=[]N =[]>> danchun(A,C,N)已找到最优解和最优值val0.5000 0 0.2500 0 0ans =7.7500六、求解实际问题(即解决附件中的实验题目)实验题目列出下列问题的数学模型,并用你自己的单纯形算法程序进行计算,最后给出计算结果。
运筹学案例分析报告

导言:每一个企业都是为了赚取利润,想要赚取更多的利润就要想办法节约自己的成本,那怎么节约自己的成本呢?运筹学是一门用纯数学的方法来解决最优方法的选择安排的学科。
运输是配送的必需条件,但是怎么才干让武城万事达酒水批发厂在运输问题是节约运输成本呢?我们就运用运筹学的方法来进行分析。
我们对他原来的运输路线进行调查,计算原来需要的运输成本,对它的运输方式我们进行研究然后确定新的运输路线为他节约运输成本。
武城万事达酒水批发有四个仓库存储啤酒分别为 1、2、3、4,有五个销地A、B、C、D、E,各仓库的库存与各销售点的销售量(单位均为 t),以及各仓库到各销售地的单位运价(元/t)。
半年中, 1、2、3、4 仓库中分别有 300、400、500、300 吨的存量,半年内 A、B、C、D、E 五个销售地的销量分别为 170、370、500、340、120 吨。
且从 1 仓库分别运往 A、B、C、D、E 五个销售地的单位运价分别为 300、350、280、380、310 元,从 2 仓库分别运往 A、B、C、D、E 五个销售地的单位运价分别 310、270、390、320、340 元,从 3 仓库分别运往A、B、C、D、E 五个销售地的单位运价分别 290、320、330、360、300 元,从 4 仓库分别运往 A、B、C、D、E 五个销售地的单位运价分别 310、340、320、350、320 元。
具体情况于下表所示。
求产品如何调运才干使总运费最小?仓库销地123存量300400500 A B D EC武城万事达酒水批发原来的运输方案:E 销售地的产品从 1 仓库供给, D 销售地的产品全由 2 仓库供给, C 销售地 全由 3 仓库供给, A 、B 销售地产品全由4 仓库供给。
即:产生的运输费用为 Z1Z =310*120+320*340+330*500+340*370+310*170=48950011、决策变量的设置设所有方案中所需销售量为决策变量 X ij (i=1、2、3、4,j=A 、B 、C 、D 、E) , 即:方案 1:是由仓库 1 到销售地 A 的运输量 X 1A方案 2:是由仓库 1 到销售地 B 的运输量 X 1B方案 3:是由仓库 1 到销售地 C 的运输量 X 1C方案 4:是由仓库 1 到销售地 D 的运输量 X 1D方案 5:是由仓库 1 到销售地 E 的运输量 X 1E方案 6:是由仓库 2 到销售地 A 的运输量 X 2A方案 7:是由仓库 2 到销售地 B 的运输量 X 2B方案 8:是由仓库 2 到销售地 C 的运输量 X 2C方案 9:是由仓库 2 到销售地 D 的运输量 X 2D方案 10:是由仓库 2 到销售地 E 的运输量 X 2E方案 11:是由仓库 3 到销售地 A 的运输量 X 3A4 300销量 170 370 500 340 120 1500方案 12:是由仓库 3 到销售地 B 的运输量 X3B方案 13:是由仓库 3 到销售地 C 的运输量 X3C方案 14:是由仓库 3 到销售地 D 的运输量 X3D方案 15:是由仓库 3 到销售地 E 的运输量 X3E方案 16:是由仓库 4 到销售地A 的运输量 X4A方案 17:是由仓库 4 到销售地B 的运输量 X4B方案 18:是由仓库 4 到销售地 C 的运输量 X4C方案 19:是由仓库 4 到销售地D 的运输量 X4D方案 20:是由仓库 4 到销售地E 的运输量 X4E2、目标函数的确定问题是求在运输过程中使总运费最小目标函数为:Min:Z=300X +350X +280X +380X +310X +310X +270X +390X +320X +340 1A 1B 1C 1D 1E 2A 2B 2C 2DX +290X +320X +330X +360X +300X +310X +340X +320X +350X +320X2E 3A 3B 3C 3D 3E 4A 4B 4C 4D 3A3、约束条件:X +X +X +X +X =3001A 1B 1C 1D 1EX +X +X +X +X =4002A 2B 2C 2D 2EX +X +X +X +X =5003A 2B 3C 3D 3EX +X +X +X +X =3004A 4B 4C 4D 4EX +X +X +X =1701A 2A 3A 4AX +X +X +X =3701B 2B 3B 4BX +X +X +X =5001C 2C 3C 4CX +X +X +X =3401E 2E 3E 4Eij4、运用表上作业法对模型求解:检验是否为最优解:仓库 销地3003501 300 300 20 20 10 10 1030370400 40 10 10 10 10200500 10 10 10 10 10300300 10 10 10 10 10150销量【50】【40】【30】4 517010 10 10 10 【10】12010 10 10 【10】行罚数 1 2 3 4 534030 30 50040 存 量列罚数1 23 370 17012010 A B D EC 4231D 2D 3D 4DX +X +X +X =120 X (i=1、2、3、4,j=A 、B 、C 、D )≥ 0X =X -X +X -X =300-290+360-280=901A 1A 3A 3C 1CX =X -X +X -X =310-290+360-320=602A 2A 3A 4D 2DX =X -X +X -X =310-350+360-290=304A 4A 4D 3D 3AX =X -X +X -X =320-360+320-270=103B 3B 3D 2D 2BX =X -X +X -X =340-350+320-270=404B 4B 4D 2D 2BX =X -X +X -X =390-330+360-320=1002C 2C 3C 3D 2DX =X -X +X -X =320-350+360-330=04C 4C 4D 3D 2CX =X -X +X -X =380-360+330-280=701D 1D 3D 3C 1CX =X -X +X -X =310-300+330-280=601E 1E 3E 3C 1CX =X -X +X -X =340-300+360-320=802E 2E 3E 3D 2DX =X -X +X -X =320-350+360-300=304E 4E 4D 3D 3E我们运用表上作业发对模型求得的一个解我们用闭合回路发进行检验,因为检验数全部是非负的,所以我们找出的解是最优解,最优解为:由 1 仓库运往 C 销地 300 吨, 2 仓库运往 B 地 370 吨, 2 仓库运往 D 地 30 吨, 3 仓库运往 A 销地 170 吨, 3 仓库运往 C 销地 200 吨, 3 仓库运往 D 销地 10吨, 3 仓库运往 E 销地 120 吨, 4 仓库运往 D 销地 300 吨.通过上述计算可知:原武城万事达酒水批发运输方案为: E销售地的产品全部由仓库1供给, D销售地的产品全部由仓库2供给, C销售地的产品全部由仓库3供给, A、 B销售地的产品全部由仓库4供给。
运筹学论文-运筹学案例分析报告

运筹学论文-运筹学案例分析报告一、背景运筹学是一门研究解决实际问题的科学,它专注于提高组织、企业和政府的生产效率,优化执行过程,使其能够有效地获得最大价值。
本案例旨在探讨一个具体的现实例子,概述如何使用运筹学进行解释以及识别和解决可能存在的潜在问题。
二、案例概述本案例涉及解决一个具体的实际问题,即如何利用有限的资源,有效的改变一个公司的业务流程,以降低其成本。
该方案涉及一家名为“关爱社会”的非营利组织,致力于为社会弱势群体提供支持和帮助。
该机构的活动主要集中在受支持者的社区中,提供技能培训、帮扶活动、营养指导和教育补助等服务。
该机构最近发现,其资金有限,从而导致社会服务无法有效现实受助者的需求。
通过运筹学方法分析,可以辨别机构拥有资源的可用性,从而重新安排和调整该机构对社会服务的投入,以优化执行过程。
三、运筹学原理运筹学方法可以帮助分析和解决实际问题。
运用运筹学,可以避免直接决策而遭受不必要的损失,改善组织的绩效,使其能够有效的改善锁定的资源,同时有效地改变业务流程,以获得最大价值。
四、案例分析针对本案例,我们首先对“关爱社会”机构的资源进行评估和分析,这包括人力资源、金融资源、工作经验和机构的实力等。
这样,我们可以更好的识别和分配公司的资源,以实现最优的结果。
在进而分析资源可用性的基础上,另一项重要的工作是对“关爱社会”机构所提供的服务的全面审查和审查。
由于公司的资源有限,因此必须仔细考虑每一项服务的重要性,并以此来决定机构把资源投入在哪里。
调整业务流程,将投入重点放到最需要的领域上是提高服务质量的最佳选择。
五、结论通过本次运筹学案例分析,我们有了更清晰的认识,即如何使用运筹学方法有效的改善现有的业务流程,使其能够更好的服务于受支持者的社区。
只有有效的资源安排和有效调整,“关爱社会”才能真正实现自身的价值,而运筹学正能够提供这样的解决方案。
1运筹学案例分析报告

1运筹学案例分析报告
运筹学是一门研究决策者在复杂问题中如何制定最优决策的学科,它综合了多种技术、理论,如概率论、搜索算法、贪婪算法、动态规划、属性优化、二进制编码、深层编码等,应用于各种重大决策分析、工程设计、社会模拟等不同领域。
比如一个城市发展规划,要想做到最少的投资,最大限度地实现城市发展,就需要使
用运筹学领域的方法来分析模拟,帮助决策者考虑到发展时存在的资源、财力、空间、利
益方等等复杂条件,以及贯彻社会发展路线、乃至政策影响,系统地把握实施步骤和过程,把握规划全过程的起伏变化,有效地降低到达最佳目标的风险空间。
比如车辆调度规划,从起点到终点,需要以最短的路径调度最多的车辆,以实现效率
最大化;又或者军事策略实施,在某个区域展开攻击时要考虑敌情分析、全局影响和战略
决策整合等因素,寻求出达到最大威慑力和节约资源的最优解;又或者能源配置,要求最
优化电力分配,来实现最佳能源利用,减少能耗等。
这些复杂系统的运筹学问题,通过计算技术的应用,可以把各种元素和因素进行归纳
组合,分析系统规律及各因素之间的关联,为决策者提供准确便捷的解决方案,实现最优
化模型解决。
哈工大运筹学实验报告实验

哈工大运筹学实验报告实验实验一:货物运输问题的数学建模与求解实验目的:1.了解货物运输问题的数学建模方法;2.掌握货物运输问题的线性规划求解方法;3.学会使用运筹学软件求解货物运输问题。
实验原理:货物运输问题属于线性规划问题的一种,其目标是在满足供需平衡和运输容量限制的前提下,使运输成本最小化。
实验内容:1.问题描述:公司有m个供应点和n个需求点,其中每个供应点的供应量为si (i=1,2,…,m),每个需求点的需求量为dj (j=1,2,…,n)。
公司希望通过运输将货物从供应点送到需求点,各供应点到需求点的单位运输成本为aij (i=1,2,…,m; j=1,2,…,n)。
公司希望确定每个供应点与需求点之间的货物运输量xij,以及总运输成本C,使总运输成本最小。
2.数学建模:设xij表示从第i个供应点到第j个需求点的货物运输量,C表示总运输成本,则该问题的数学模型可以描述为:min C = ∑(i=1 to m) ∑(j=1 to n) aij * xijsubject to:∑(j=1 to n) xij = si, i=1,2,…,m∑(i=1 to m) xij = dj, j=1,2,…,nxij ≥ 0, i=1,2,…,m; j=1,2,…,n3.求解方法:利用运筹学软件求解上述线性规划问题,得到最优解。
实验步骤:1.在运筹学软件中新建一个线性规划模型;2.设定决策变量、目标函数和约束条件,并输入相应参数;3.运行求解算法,得到最优解。
实验结果:根据实验步骤,通过运筹学软件求解货物运输问题,得到最优解如下:供应点1到需求点1的运输量为x11=200;供应点1到需求点2的运输量为x12=150;供应点2到需求点1的运输量为x21=100;供应点2到需求点2的运输量为x22=250;总运输成本最小为C=900。
实验总结:通过本次实验,我了解了货物运输问题的数学建模方法,并掌握了线性规划求解的基本步骤。
运筹学实训实验报告

一、实验背景运筹学是一门应用数学的分支,它运用数学模型和算法来解决各种优化问题。
随着现代科技的发展,运筹学在各个领域的应用越来越广泛,如生产管理、物流运输、资源分配等。
为了提高学生运用运筹学知识解决实际问题的能力,我们开展了运筹学实训实验。
二、实验目的1. 熟悉运筹学的基本概念和常用方法;2. 掌握线性规划、整数规划、运输问题、目标规划等运筹学模型;3. 学会运用计算机软件解决实际问题;4. 培养学生的团队合作精神和创新意识。
三、实验内容本次实验主要包括以下内容:1. 线性规划:以生产计划问题为例,建立数学模型,并运用Excel规划求解器求解最优解。
2. 整数规划:以人员排班问题为例,建立数学模型,并运用Lingo软件求解最优解。
3. 运输问题:以物流配送问题为例,建立数学模型,并运用Lingo软件求解最优解。
4. 目标规划:以投资组合问题为例,建立数学模型,并运用Lingo软件求解最优解。
四、实验步骤1. 线性规划实验(1)问题分析:某企业需要生产甲、乙两种产品,已知生产甲、乙两种产品所需的原料、劳动力及设备等资源消耗量,以及产品的售价和利润。
(2)模型建立:根据问题分析,建立线性规划模型,目标函数为最大化利润,约束条件为资源消耗量不超过限制。
(3)求解:运用Excel规划求解器求解最优解。
2. 整数规划实验(1)问题分析:某公司需要安排员工值班,要求每天至少有3名员工值班,且员工值班时间不能超过一周。
(2)模型建立:根据问题分析,建立整数规划模型,目标函数为最小化员工值班成本,约束条件为员工值班时间不超过限制。
(3)求解:运用Lingo软件求解最优解。
3. 运输问题实验(1)问题分析:某物流公司需要将货物从A、B两个仓库运送到C、D两个销售点,已知各仓库的货物量、各销售点的需求量以及运输成本。
(2)模型建立:根据问题分析,建立运输问题模型,目标函数为最小化运输成本,约束条件为各仓库的货物量不超过需求量。
运筹学案例分析报告.doc

运筹学案例分析报告运筹学案例分析报告篇1:一、研究目的及问题表述(一)研究目的:公司、企业或项目单位为了达到招商融资和其它发展目标之目的,在经过前期对项目科学地调研、分析、搜集与整理有关资料的基础上,向读者全面展示公司和项目目前状况、未来发展潜力的书面材料。
这是投资公司在进行投资前非常必要的一个过程。
所以比较有实用性和研究性。
(二)问题表述:红杉资本于1972年在美国硅谷成立。
从2005年9月成立至今,在科技,消费服务业,医疗健康和新能源/清洁技术等投资了众多具有代表意义的高成长公司。
在2011年红杉资本投资的几家企业项目的基础上,规划了未来五年在上述基础上扩大投资金额,以获得更多的利润与合作效应。
已知:项目1(受资方:海纳医信):从第一年到第四年每年年初需要投资,并于次年末收回本利115%项目2(受资方:今世良缘):第三年年初需要投资,到第五年末能收回本利125%,但规定最大投资额不超过40万元。
项目3(受资方:看书网):第二年年初需要投资,到第五年末能收回本利140%,但规定最大投资额不超过30万元。
项目4(受资方:瑞卡租车):五年内每年年初可购买公债,于当年末归还,并加息6%。
该企业5年内可用于投资的资金总额为100万元,问他应如何确定给这些项目的每年投资使得到第五年末获得的投资本例总额为最大?(三)数据来源:以下的公司于受资方等都是在投资网中找到的,其中一些数据为机密部分,所以根据资料中红杉资本所投资的金额的基础上,去编织了部分的数据,以完成此报告研究。
二、方法选择及结果分析(一)方法选择:根据自身的知识所学,选用了运筹学线性规划等知识,再结合Lindo软件,也有其他的方法与软件,但是线性规划为运筹学中比较基本的方法,并且运用起来比较方便简捷,也确保了方法的准确性。
(二)求解步骤:解:设xi1,xi2,xi3,xi4(i=1,2,3,4,5)为第i年初给项目1,2,3,4的投资额,他们都是待定的未知量。
管理运筹学有关最优方案的案例分析报告

第一部分一、案例名称:北方印染公司应如何合理使用技术培训费。
二、案例目的:确定培养方案,使企业增加的产值最多。
三、案例分析:由案例给出的信息,可以设十三个变量,分别为x1、x2、x3、x4、x5、x6、x7、x8、x9、x10、x11、x12、x13。
其分别代表的含义是,第一年由高中生培养初级工的人数,第二年由高中生培养初级工的人数,第三年由高中生培养初级工的人数,由高中生培养中级工的人数,由高中生培养高级工的人数,第一年由初级工培养中级工的人数,第二年由初级工培养中级工的人数,第三年由初级工培养中级工的人数,第一年由初级工培养高级工的人数,第二年由初级工培养高级工的人数,第一年由中级工培养高级工的人数,第二年由中级工培养高级工的人数,第三年由中级工培养高级工的人数。
为了更加直观的各个变量的含义,可以用如下表格展现各个变量的含义,以便于理解和分析。
根据培养一名初级工在高中毕业后需要一年,费用为1000元;培养一名中级工,高中毕业后第一年费用为3000元;培养一名高级工,高中毕业后第一年费用为3000元;由初级工培养为中级工需一年且费用为2800元;由初级工培养为高级工第一年且费用为2000元;由中级工培养为高级工需一年且费用为3600元。
并且根据第一年的投资为55万。
可以列出如下约束条件:1000x1+3000x4+3000x5+2800x6+2000x9+3600x11≤550000。
根据培养一名初级工在高中毕业后需要一年,费用为1000元;培养一名中级工,高中毕业后第二年费用为3000元;培养一名高级工,高中毕业后第一年费用为2000元;由中级工培养为高级工需一年且费用为3600元;由初级工培养为中级工需一年且费用为2800元;由初级工培养为高级工第一年且费用为2000元;由中级工培养为高级工需一年且费用为3600元。
并且根据第二年的投资为45万。
可以列出如下约束条件:1000x2+3000x4+2000x5+2800x7+3200x9+2000x10+36 00x12≤450000。
运筹案例分析总结

运筹案例分析总结案例背景运筹是一门涵盖了多个领域的学科,它通过数学建模与算法等方法,以优化问题为核心,研究如何在资源有限的情况下,使得系统能够达到最优的效果。
在实际应用中,运筹帮助企业和组织解决了众多复杂的问题,提高了效率、降低了成本。
本文将对几个运筹案例进行分析,并总结出一些关键点和经验教训。
案例一:生产计划优化公司在某次生产计划中遇到了一个问题,他们需要制定一个最优的生产计划,以便在资源有限的情况下提高产能,并同时满足客户的交货期要求。
为了解决这个问题,他们采用了运筹相关的方法。
方法与结果首先,他们对生产流程进行了详细的分析,找出了瓶颈环节和关键资源。
然后,他们使用数学建模的方法,将生产计划问题转化为一个线性规划问题,并使用了相应的算法进行求解。
通过优化生产计划,他们成功地提高了产能,并在满足客户需求的前提下,降低了生产成本。
教训与经验这个案例告诉我们,在处理生产计划优化问题时,我们需要充分了解整个生产流程,找出关键环节和资源瓶颈。
在数学建模和算法选择方面,我们需要选择合适的模型和算法,以求得最优解。
案例二:物流配送路径优化一家物流公司面临一个配送路径优化的问题。
他们需要确定一条最优的配送路径,以减少行驶距离,提高效率,并保证货物能够准时送达目的地。
方法与结果他们采用了运筹中的启发式算法和近似算法来优化配送路径。
首先,他们利用GIS地理信息系统采集了物流网络的数据,并进行了预处理和清洗。
然后,他们使用模拟退火算法和遗传算法等方法,对物流配送路线进行了求解。
通过优化配送路线,他们成功地减少了行驶距离,提高了效率,并准时送达了货物。
教训与经验通过这个案例我们学到,在处理物流配送问题时,使用GIS地理信息系统是非常有帮助的。
此外,启发式算法和近似算法在求解大规模配送路径问题时也非常有效。
然而,我们需要注意算法的参数调优和收敛性的检验,以求得较好的结果。
案例三:投资组合优化一家投资公司面临一个投资组合优化的问题。
运筹学案例的分析

运筹学案例的分析一、案例背景介绍本案例涉及一家制造业公司,该公司生产和销售汽车零部件。
由于市场竞争激烈,公司面临着多个挑战,如供应链管理、生产调度和库存管理等方面存在问题。
为了解决这些问题,公司决定运用运筹学方法进行分析和优化。
二、问题分析1. 供应链管理问题公司的供应链管理存在一些瓶颈,如供应商选择、物流运输和库存管理等方面存在问题。
如何优化供应链,降低成本,提高效率是一个亟待解决的问题。
2. 生产调度问题公司的生产线存在一些瓶颈,导致生产效率低下和交货周期延长。
如何优化生产调度,提高生产效率,缩短交货周期是公司急需解决的问题。
3. 库存管理问题公司面临着库存管理方面的挑战,如库存过高、库存周转率低等问题。
如何优化库存管理,降低库存成本,提高库存周转率是公司亟需解决的问题。
三、运筹学方法的应用为了解决上述问题,公司决定运用运筹学方法进行分析和优化。
具体应用如下:1. 供应链管理优化通过对供应链进行建模和分析,确定关键节点和瓶颈环节,优化供应商选择和物流运输方案,以降低成本和提高效率。
同时,建立合理的库存管理模型,通过合理的库存控制策略,降低库存成本,提高库存周转率。
2. 生产调度优化通过对生产线进行建模和分析,确定生产瓶颈和瓶颈环节,优化生产调度方案,提高生产效率和缩短交货周期。
同时,建立合理的生产计划和排程模型,通过合理的生产计划和排程策略,提高生产效率和减少交货周期。
3. 库存管理优化通过对库存管理进行建模和分析,确定库存管理的关键指标和影响因素,优化库存管理策略,降低库存成本和提高库存周转率。
同时,建立合理的库存控制模型和库存管理系统,通过合理的库存控制和管理策略,降低库存成本和提高库存周转率。
四、数据分析和模型建立为了进行运筹学分析和优化,公司需要收集相关的数据,并建立相应的模型。
数据可以包括供应链的各个环节的成本、时间和效率等指标,生产线的各个环节的生产能力和效率等指标,以及库存管理的各个环节的库存成本和库存周转率等指标。
运筹学实践教学报告模板(3篇)

第1篇一、引言运筹学作为一门应用广泛的学科,其核心在于运用数学模型和算法解决实际问题。
为了更好地理解和掌握运筹学的理论和方法,本次实践教学报告以XX项目为例,详细阐述运筹学在实际问题中的应用过程。
二、项目背景与目标1. 项目背景XX项目是XX公司为提高生产效率、降低成本而提出的一个优化问题。
公司现有生产线,由于设备老旧、工艺流程不合理等原因,导致生产效率低下,成本较高。
为了解决这一问题,公司决定运用运筹学方法进行生产线优化。
2. 项目目标通过运筹学方法,对XX项目生产线进行优化,实现以下目标:- 提高生产效率,降低生产周期;- 降低生产成本,提高企业经济效益;- 优化生产线布局,提高生产线柔性。
三、运筹学方法选择与应用1. 方法选择针对XX项目的特点,本次实践选择了以下运筹学方法:- 线性规划(Linear Programming,LP)- 整数规划(Integer Programming,IP)- 模拟退火算法(Simulated Annealing,SA)2. 方法应用(1)线性规划首先,根据XX项目实际情况,建立了线性规划模型。
模型中包含决策变量、目标函数和约束条件。
通过求解线性规划模型,得到了最优的生产方案,包括各设备的生产能力分配、生产顺序安排等。
(2)整数规划由于部分设备的生产能力为整数,因此采用整数规划方法对模型进行改进。
通过求解整数规划模型,进一步优化了生产方案,使得设备利用率达到最大化。
(3)模拟退火算法为了提高生产方案的鲁棒性,采用模拟退火算法对优化后的生产方案进行全局搜索。
通过模拟退火算法,得到了一组更加优化的生产方案,提高了生产线的柔性。
四、结果与分析1. 结果经过运筹学方法的应用,XX项目生产线优化取得了以下成果:- 生产效率提高了XX%;- 生产周期缩短了XX天;- 生产成本降低了XX%;- 生产线柔性得到了显著提高。
2. 分析(1)线性规划方法的应用使得生产线设备利用率得到最大化,从而提高了生产效率;(2)整数规划方法的应用确保了设备生产能力的合理分配,避免了生产过程中的资源浪费;(3)模拟退火算法的应用使得生产方案具有更好的鲁棒性,提高了生产线的柔性。
运筹实验报告--样板

实验一线性规划-生产计划1.1实验目的·理解线性规划的概念。
·建立线性规划问题的数学模型。
·把线性规划数学模型转化为ILOG OPL模型进行求解。
1.2实验指导1.2.1案例内容派公司是一个生产高尔夫器材的小型公司,公司决定生产高中价位的高尔夫袋。
分销商对新产品十分感兴趣,并且同意买进派公司下3个月内的全部产品。
在对整个高尔夫袋生产步骤进行了详细的调查以后,管理阶层明确了高尔夫袋的生产过程:(1)切割并印染原材料(2)缝合(3)成型(插入支撑架、球棒分离装置等)(4)检测和包装生产制定者详细分析生产过程的每一步,得出以下结论,生产一个标准高尔夫袋需要用:0.7小时完成切割并印染原材料,用0.5小时完成缝合,用1小时完成成型,用0.1小时检测和包装。
生产高级袋则需要:用1小时完成切割和印染,用0.8小时完成缝合,用0.7小时完成成型,用0.25小时检测和包装。
生产信息列于下表:表1.1 生产每个高尔夫袋所需要的时间生产耗时部门标准袋高档袋切割并印染原材料0.7 1缝合0.5 0.8成型 1 0.7检测和包装0.1 0.25派公司的生产还受各个部门生产能力的限制。
经过对整个生产部门工作量的研究。
生产制定者分析得出,3个月内每个部门的最大生产时间分别是:切割印染630小时,缝合600小时,成型708小时,检测包装135小时。
会计部门经过对生产数据、各种生产成本的分析得出了以下的结论,生产一个标准袋的利润是10美元,生产一个高级袋的利润是9美元。
问:派公司如何制定生产计划,使公司获得最大利润(不考虑产量是否是整数)。
1.2.2问题分析目标本题的目标就是使产品的利润最大。
约束条件对于生产时间来说,一共有4个约束条件,它们制约着两种高尔夫袋的生产。
约束条件 1 用于切割和印染的总时间必须小于等于切割和印染部所能承受的最大工作时间。
约束条件2 用于缝合的总时间必须小于等于缝合部所能承受的最大工作时间。
运筹学案例分析报告示例

食油生产问题(案例一)分析报告一、模型构造1.1 变量设置设两种硬质油代号分别为HD1、HD2(HD代表Hard),三种软质油代号分别为SF1、SF2、SF3(SF代表Soft)。
每种油的采购(Buy)、耗用(Use)和储存(Store)量分别在油品的代号前加B、U和S表示。
1—6月份5种油品的采购、耗用和储存量分别在油品代号后面加1—6表示。
总产量用PROD(Product)表示。
第一种硬质油六个月的采购量、耗用量、月末储存量共有17变量,其中,六月末的存储量为500吨。
BHD11,BHD12,BHD13,BHD14,BHD15,BHD16;UHD11,UHD12,UHD13,UHD14,UHD15,UHD16;SHD11,SHD12,SHD13,SHD14,SHD15;第二种硬质油六个月的采购量、耗用量、月末储存量共有17变量,其中,六月末的存储量为500吨。
BHD21,BHD22,BHD23,BHD24,BHD25,BHD26;UHD21,UHD22,UHD23,UHD24,UHD25,UHD26;SHD21,SHD22,SHD23,SHD24,SHD25;第一种软质油六个月的采购量、耗用量、月末储存量共有17变量,其中,六月末的存储量为500吨。
BSF11,BSF12,BSF13,BSF14,BSF15,BSF16;USF11,USF12,USF13,USF14,USF15,USF16;SSF11,SSF12,SSF13,SSF14,SSF15;第二种软质油六个月的采购量、耗用量、月末储存量共有17变量,其中,六月末的存储量为500吨。
BSF21,BSF22,BSF23,BSF24,BSF25,BSF26;USF21,USF22,USF23,USF24,USF25,USF26;SSF21,SSF22,SSF23,SSF24,SSF25;第三种软质油六个月的采购量、耗用量、月末储存量共有17变量,其中,六月末的存储量为500吨。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学案例分析:向市场运送木材阿拉巴马大西洋公司(Alabama Atlantic)是一个拥有三个木材资源区和五个需要供应的市场的木材公司。
木材资源区1、2、3每年所能够生产的木材量分别为15、20、1500万板英尺(board feet)。
每年市场1、2、3、4、5能够销售的木材量分别为11、12、9、10、800万板英尺。
过去,这个公司通过火车来运输木材。
然而,由于使用火车的运输成本已经上升了,所以可以考虑使用水运的方式来运输其中的一部分木材。
但是这种方式却需要公司要在水运方面进行投资。
使用火车运输的单位成本(单位:1千美元)使用轮船运输的单位成本(单位:1千美元)
出发地对于向市场运输木材的轮船的单位资金投入(单位:1千美元)
考虑到轮船的预计使用期限(大约30年)和货币的时间价值,年金成本大约是当年投入资金的十分之一。
公司的目标是要制订出一个全面运输计划,使总年金成本最小(包括运输成本)。
现在,如果你是公司管理科学小组的负责人。
那么所需要做的工作是根据下面所给出的三种选择分别制订出这种能够使得年金成本最小的运输计划。
选择l :继续使用火车来运输木材,并仅使用这一种方式。
选择2 :仅使用轮船运输木材(只能使用火车的地方除外)。
选择3 :根据在每一条特定的路线上哪种方式的运输成本比较低来选择使用火车还是轮船来运输木材。
找出在每一种情况下你的答案,并比较一下那种方案比较好。
要求:
1. 列出各种选择的数学模型;
2. 使用MATLAB求解你的模型;
3. 对各种选择进行简要评价,并给出你的最终运输方案。
