信号与系统仿真
地铁信号系统的仿真研究

地铁信号系统的仿真研究1. 引言1.1 地铁信号系统的仿真研究地铁信号系统的仿真研究是针对地铁列车信号系统进行的一项重要研究领域。
地铁作为城市中重要的公共交通方式,其安全性和效率对城市运行具有至关重要的作用。
而地铁信号系统作为地铁运行的核心部分,直接影响着地铁列车的运行安全和运行效率。
对地铁信号系统进行仿真研究,可以帮助地铁运营单位更好地了解信号系统的运行情况,提前发现潜在问题,优化信号系统参数,提高地铁列车的运行效率和安全性。
地铁信号系统的仿真研究不仅可以为地铁运营提供重要参考,还可以为地铁信号系统的设计和改进提供科学依据。
通过对地铁信号系统的仿真研究,可以进一步提高地铁运行的安全性、减少故障发生的可能性,提高运行效率,提升乘客的出行体验,为城市的发展和交通运输的改善做出贡献。
2. 正文2.1 地铁信号系统的仿真模型构建地铁信号系统的仿真模型构建是地铁信号系统仿真研究中的关键环节。
在进行仿真模型构建时,需要考虑到地铁信号系统的各个部分如信号灯、轨道、列车等之间的相互作用,以及其在不同情况下的运行状态。
首先,需要对地铁信号系统的结构和功能进行深入的了解,包括各种传感器、控制设备以及信号传输系统等。
然后根据地铁信号系统的实际运行情况,建立相应的数学模型,包括信号传输模型、列车运行模型等。
这些模型需要考虑到不同因素对地铁信号系统的影响,如列车的加速度、制动距离、人流量等。
在模型构建过程中,还需要考虑到地铁信号系统中可能存在的故障和异常情况,以及应对这些情况的应急措施。
通过对模型的验证和优化,可以不断提高仿真的准确性和可靠性,为地铁信号系统的运行和管理提供参考依据。
总的来说,地铁信号系统的仿真模型构建是一个复杂而繁琐的过程,但是通过科学的方法和技术手段,可以有效地模拟地铁信号系统的运行情况,为实际运营提供重要的支持和指导。
2.2 地铁信号系统的仿真参数设置地铁信号系统的仿真参数设置是整个仿真研究中至关重要的一部分。
信号与系统MATLAB仿真-2012

[4-4]
1 1 生成正弦信号 x(n) sin ( 5 n 4 )
8
clear; n=0:10; w0=pi/5;w1=pi/4; x=sin(w0*n+w1); stem(n,x); title(‘正弦型序列'); line([0,10],[0,0]); xlabel('n');ylabel('x(n)');
20
clear; x=[0.5,1.5,1,-0.5]; n0=-1:2; x1=2*ones(1,6); n1=0:5; [y1,n2]=sigmult(x1,n1,x,n0); [y2,n3]=sigadd(x1,n1,x,n0); subplot(411); stem(n0,x); ylabel('x');axis([-1 6 -2 3]); subplot(412);stem(n1,x1); ylabel('x1');axis([-1 6 -2 3]); subplot(413);stem(n2,y1); ylabel('y1=x*x1');axis([-1 6 -2 3]); subplot(414);stem(n3,y2); ylabel('y2=x+x1');axis([-1 6 0 5]);
3
[4-2] 比较不同的实指数信号
4
clear; n=0:1:10; a1=0.5;a2=-0.5;a3=1.2;a4=-1.2; x1=a1.^n;x2=a2.^n; x3=a3.^n;x4=a4.^n; subplot(2,2,1),stem(n,x1); title(‘实指数序列(0<a1<1)'); xlabel('n');ylabel('x1(n)'); subplot(2,2,2),stem(n,x2); title('实指数序列(-1<a2<0)'); line([0,10],[0,0]); xlabel('n');ylabel('x2(n)'); subplot(2,2,3),stem(n,x3); title('实指数序列(1<a3)'); xlabel('n');ylabel('x3(n)'); subplot(2,2,4),stem(n,x4); line([0,10],[0,0]); title('实指数序列(a4<-1)'); xlabel('n');ylabel('x4(n)'3];den=[1,0.4,1]; [num,den]=eqtflength(num,den); [z,p,k]=tf2zp(num,den);
信号与系统仿真作业

nGDOU-B—11—112广东海洋大学学生实验报告书(学生用表)课程名称课程号学院(系)信息学院专业班级学生姓名学号实验地点04002 实验日期实验一连时间信号的MATLAB表示和连续时间LTI系统的时域分析一、实验目的1.掌握MA TLAB产生常用连续时间信号的编程方法,并熟悉常用连续时间信号的波形和特性;2.运用MATLAB符号求解连续系统的零输入响应和零状态响应;3.运用MATLAB数值求解连续系统的零状态响应;4.运用MATLAB求解连续系统的冲激响应和阶跃响应;5.运用MATLAB卷积积分法求解系统的零状态响应。
二、实验原理1. 连续信号MATLAB实现原理从严格意义上讲,MA TLAB数值计算的方法并不能处理连续时间信号.然而,可用连续信号在等时间间隔点的取样值来近似表示连续信号,即当取样时间间隔足够小时,这些离散样值能够被MATLAB处理,并且能较好地近似表示连续信号.MATLAB提供了大量生成基本信号的函数.比如常用的指数信号、正余弦信号等都是MATLAB的内部函数。
为了表示连续时间信号,需定义某一时间或自变量的范围和取样时间间隔,然后调用该函数计算这些点的函数值,最后画出其波形图.三、实验内容1.实例分析与验证根据以上典型信号的MA TLAB函数,分析与验证下列典型信号MA TLAB程序,并实现各信号波形图的显示,连续信号的图形显示使用连续二维图函数plot().(1)正弦信号:用MA TLAB命令产生正弦信号2sin(2/4)ππ+,并会出时间0≤t≤3的波形图。
程序如下:K=2;w=2*pi ;phi=pi/4;t=0:0.01:3;ft=K*sin (w*t+phi );plot(t,ft ),grid on ;axis ([0,3,-2。
2,2.2])title (’正弦信号’)(2) 抽样信号:用MA TLAB 中的sinc(t)函数命令产生抽样信号Sa(t),并会出时间为66t ππ-≤≤的波形图。
“信号与系统”仿真演示系统设计

电气 电子 教学 学报
J OUR NAL OF E E E
Vo . 4 N . 13 o 1 F b2 1 e .0 2
“ 号与 系统 " 真 演 示 系统 设 计 信 仿
俎 云 霄,贾 越 ,李 奔 , 李 勇
( 北京 邮 电大学 电子 工程 学院 , 北京 107 ) 0 86
界 面 。主模块 界 面包 括 “ 续 时 间信 号 与 系 统 ” 连 和
修稿 日 : 1 - - ; 期 2 1 6 8 修回 日 :0 1 9 2 基金项 目: 0 00 期 21- - 0 2 北京市高等学校教育教学改革项 目( 目 : 0 - ) 项 号 2 72 0 9
第一作者 : 俎云霄 (9 4 ) 女 , 16 . , 博士 , 教授 , 主要从事信号与系统 、 电路分 析的教学和科研工作 , — i: y@tnh a eu c Ema z x s gu .d . a lu i
形 。整 个 系统界 面 直观清 晰 。
移 t= .37 。 0 2 2 1的频 谱 图 。调 节 图 中上 部 中间 的 滑 动 条可 改变 t。点 击 右 下 角 的 “ 闭 ” 钮 可 以 退 。 关 按
出此 界 面 。 图 中 , 域 波 形 的 横 轴 表 示 时 间 , 单 时 其 位是 “ ” 幅度 频 谱 的 横 轴 表 示 角 频 率 , 位 是 秒 。 单 “ 弧度/ ” 纵 轴表 示频 谱 幅 度 ; 位频 谱 的横 轴 与 秒 , 相 幅度 频谱 相 同 , 轴 表 示 相 位 , 位 是 “ ” 随后 纵 单 度 。
图 2和 图 3的坐标 均 与此相 同 , 不再重 复 。
:
信号与系统课程虚拟仿真教学探索与实践

信号与系统课程虚拟仿真教学探索与实践杨宗长【摘要】Along with the development of information technology, computer simulation has been one of important approaches in CAI (computer aided instruction). The course of signal and system is a key course of specialty in electronic information science. With considering the characteristics of the signal and system course and focusing on improving the teaching effect and upgrading the practical teaching efficacy, seven typical virtual simulation teaching projects are designed based on teaching experiences. The projects can be divided into: basic ones, comprehensive ones, exploratory and innovative ones. Design and implementation of the virtual simulation projects are done in the MatLab Simulink visual environment. Simulink-based simulation and practical teaching feedbacks show that the virtual simulation projects are intuitive and easy to operate, and good response results are received from the students. Finally, two possible teaching reforms are proposed for reference and consideration.%伴随着信息技术的发展,计算机仿真方法已成为现代教育技术的重要手段之一.信号与系统课程是电子信息类本科专业的一门核心基础课程.针对信号与系统课程特点,着眼于提高教学效果和改进实践教学,并结合教学实践经验,设计了多类型的虚拟仿真教学项目,其大致可分为:入门基础型、综合型以及探索创新型等.虚拟仿真项目采用MatLab Simulink 软件,在可视化仿真设计环境中实现.MatLab Simulink仿真以及实践教学反馈结果表明:所设计的虚拟仿真教学项目过程直观明了、可操作性强,近年来在所任教的信号与系统课程教学实践中反馈良好.同时,结合学生反馈建议和意见以及教学实践经验,提出了两种教改方案,以供同行参考.【期刊名称】《中国现代教育装备》【年(卷),期】2018(000)021【总页数】5页(P42-45,48)【关键词】计算机辅助教学;信号与系统;MatLab/Simulink;虚拟仿真教学【作者】杨宗长【作者单位】湖南科技大学信息与电气工程学院湖南湘潭 411201【正文语种】中文信号与系统课程是电子信息类本科专业的一门核心专业基础课程[1-5]。
基于MATLAB的信号与系统仿真实验毕业设计

基于MATLAB的信号与系统仿真实验毕业设计信号与系统是电子信息类专业的一门重要课程,它是其他课程的基础和前提。
为了更好地理解信号与系统的理论知识,掌握信号的分析和处理方法,实验仿真是非常重要的手段之一、MATLAB作为一款强大的数学软件,被广泛应用于信号与系统的实验仿真中。
本文将基于MATLAB,介绍一个基于信号与系统的仿真实验的毕业设计。
该设计主要包括以下几个方面的内容:实验目的、实验原理、实验步骤和实验结果及分析。
实验目的:本次实验的主要目的是通过MATLAB软件,实现信号与系统的仿真分析,掌握信号与系统的基本概念和分析方法,培养学生对信号与系统的实际应用能力。
实验原理:本实验主要涉及信号的生成与采样、信号的查表和存储、信号的线性时不变系统等方面的内容。
通过对不同种类的信号进行分析,可以更好地理解信号的特性,并通过系统的分析,了解线性时不变系统对信号的作用及特性。
实验步骤:1.信号的生成与采样:在MATLAB中,通过给定信号的频率、振幅及采样率等参数,利用正弦函数或方波函数生成模拟信号,并对信号进行采样。
2.信号的查表和存储:将生成的信号通过查表和存储的方式保存为数据文件,并通过MATLAB读取这些数据文件,进行后续的处理和分析。
3.信号的线性时不变系统:通过设计不同的线性时不变系统,如低通滤波器或高通滤波器等,对信号进行滤波处理。
可以分析系统的频率响应、幅频响应等参数,并观察滤波后信号的变化。
实验结果及分析:通过对生成的信号进行采样、查表和存储,并对信号进行线性时不变系统的处理,在MATLAB中可以得到相应的结果。
根据实验结果,可以对信号的特性进行分析,比较不同信号和系统对信号的影响,进一步了解信号与系统的相关知识。
综上所述,本次基于MATLAB的信号与系统仿真实验毕业设计主要是通过对信号的生成、采样、查表和存储以及对信号进行线性时不变系统的处理,来掌握信号与系统的分析方法和应用能力。
通过实验结果的分析,可以进一步理解信号与系统的概念和特性,提高对信号与系统的理解和应用能力。
“信号与系统”Matlab实验仿真教学系统设计

“信号与系统”Matlab实验仿真教学系统设计作者:张尤赛,马国军,黄炜嘉,周稳兰来源:《现代电子技术》2010年第18期摘要:针对“信号与系统”课程硬件实验教学不够深入和灵活的缺点,在分析理论教学和工程实际需求的基础上,利用Matlab和Simulink,建立了“信号与系统”实验仿真教学系统,并从系统设计、内容设计、界面设计、开发工具、二次开发等五个方面对该系统进行了阐述。
实验教学表明,该系统可以克服硬件实验系统的局限性,加深和拓宽了实验内容和实验层次,增强了实验的灵活性,有利于培养学生的实验动手能力和创新能力。
关键词:信号与系统; Matlab; 实验仿真教学; Simulink中图分类号:TN911.7-34; G642.4文献标识码:A文章编号:1004-373X(2010)18-0057-03Design of Mtalab Experimental Simulation Teaching System in Signals and SystemsZHANG You-sai, MA Guo-jun, HUANG Wei-jia, ZHOU Wen-lan(School of Electronics and Information, Jiangsu University of Science and Technology, Zhenjiang 212003, China)Abstract: Aiming at the disadvantages of hardware experimental teaching in Signals and Systems, the experimental simulation teaching system of Signals and Systems based on Matlab and Simulink is established by emphasizing experimental teaching requirements of theoretical teaching and actual engineering. Thus, the system design, content design, interface design, development tools and repeatedly development are studied respectively. The effects of experimental teaching show that it overcomes the limitation of hardware experiment, expands experimental contents and level, improves students hands-on ability and comprehensive quality.Keywords: signals and systems; Matlab; experimental simulation teaching; Simulink0 引言信号与系统的基本概念、基本理论与分析方法在不同学科、专业之间有着广泛应用和交叉渗透[1]。
信号与系统MATLAB仿真——信号及其运算

信号与系统MATLAB仿真——信号及其运算1. 知识回顾(1)信号的分类:确定信号与随机信号;周期信号与⾮周期信号;周期信号在时间上必须是⽆始⽆终的f(t)=f(t+T)f[k]=f[k+N]连续时间信号和离散时间信号;连续信号是指在信号的定义域内,除若⼲个第⼀类间断点外,对于任意时刻都由确定的函数值的信号离散信号是指在信号的定义域内,只在某些不连续规定的时刻给出函数值,⽽在其他时刻没有给出函数的信号能量信号、功率信号与⾮功率⾮能量信号;时限与频限信号;物理可实现信号。
(2)信号能量:E=limT→∞∫T−T f2(t)dtP=limT→∞12T∫T−Tf2(t)dtE=limN→∞N∑k=−N|f[k]|2P=limN→∞12N+1N∑k=−N|f[k]|2能量信号:0<E<∞,P=0;功率信号:0<P<∞,E=∞。
(3)冲激函数的性质加权特性(筛选特性):f(t)δ(t−t0)=f(t0)δ(t−t0)取样特性:∫+∞−∞f(t)δ(t−t0)=f(t0)偶函数:f(t)=f(−t)展缩特性:δ(at)=1|a|δ(t)δ(at−t0)=1|a|δ(t−t0a)导数及其特性。
(4)正弦两个频率相同的正弦信号相加,即使其振幅和相位各不相同,但相加后结果仍是原频率的正弦信号;若⼀个正弦信号的频率是另⼀个正弦信号频率的整数倍时,则合成信号是⼀个⾮正弦周期信号,其周期等于基波的周期。
正弦型序列:f[k]=A sin(Ω0k+φ)2π/Ω0是正整数:周期序列,周期为N;2π/Ω0为有理数,2π/Ω0=N/m:周期序列,周期N=m(2π/Ω0);2π/Ω0为⽆理数:⾮周期序列,但包络仍为正弦函数。
(5)抽样信号Sa(t)=sin t t偶函数;Sa(0)=1;t=kπ为其零点;∫+∞−∞Sa(t)dt=π;limt→±∞Sa(t)=0。
(6)信号的分解分解为直流分量与交流分量;奇偶分解;分解为实部和虚部;分解为基本信号的有限项之和;因⼦分解;连续信号分解为矩形脉冲序列;正交分解。
基于LabVIEW的“信号与系统”仿真实验系统设计

基于LabVIEW的“信号与系统”仿真实验系统设计“信号与系统”是电子信息类专业的重要专业基础课,概念多,理论性强,比较抽象。
为便于学生理解和掌握,设计了基于LabVIEW的信号与系统仿真实验系统。
详细介绍了系统构架、设计方法及主要知识点的演示示例。
标签:LabVIEW;信号与系统;仿真;实验一引言“信号与系统”是高等院校电子信息类专业的一门非常重要的基础课,但由于概念多、推导多、理论抽象,所以学生学习起来普遍感到不能很好地理解和掌握其基本理论与分析方法。
如何让学生深刻理解课程中的基本概念、基本原理,牢固掌握基本分析方法以及学会灵活运用这一理论工具,是值得研究和探讨的一个问题。
在课堂教学中适时引入仿真实验,可以帮助学生很好地理解理论理念,建构知识,提高教学质量。
本研究以LabVIEW作为仿真软件构建了“信号与系统”仿真实验系统,该系统界面友好、功能齐全,紧密结合“信号与系统”课程[1,2],主要面向讲授和学习“信号与系统”课程的教师和同学,不仅便于教师在课堂上进行教学演示,而且还便于学生在课后进行自学或复习。
二系统构架及设计1 系统构架仿真实验系统与“信号与系统”课程内容基本对应,共分为四大模块,分别是“连续时间信号分析”、“傅里叶级数和傅里叶变换”、“调制,滤波器,离散时间信号分析”和“声音信号及其波形”。
四个模块在内容上依次递进,如图1所示。
模块1是基础,主要介绍基本信号及其时域性质;模块2是对基本信号的频域性质分析;模块3主要是信号与系统的基本知识在通信中的应用;模块4是关于声音的采集、播放及其波形,是扩展部分。
每个模块中又根据实验内容分为几个子程序。
各模块中的实验内容如表1所示。
整个系统采用模块化的设计思路,每个程序均由如下几个模块构成:(1)信号产生模块(2)信号处理模块(3)结果显示模块。
信号产生模块负责产生若干个特定信号,该信号经过信号处理模块进行处理,例如卷积、滤波、FFT等,最后经过结果显示模块显示信号波形,或使喇叭发音。
信号与系统实验指导书(matlab软件仿真)

信号与系统实验指导书(MATLAB仿真)目录实验一MATLAB 基本应用 (2)实验二信号的时域表示 (7)实验三连续信号卷积 (11)实验四典型周期信号的频谱表示 (18)实验五傅立叶变换性质研究 (23)实验六离散信号分析 (26)实验七离散系统的Z域分析 (29)Matlab相关符号及函数说明 (37)实验一MATLAB 基本应用一、实验目的:学习MATLAB的基本用法,了解 MATLAB 的目录结构和基本功能以及MATLAB在信号与系统中的应用。
二、实验内容:例一已知x的取值范围,画出y=sin(x)的图型。
参考程序:x=0:0.05:4*pi;y=sin(x);plot(y)例二计算y=sin(π/5)+4cos(π/4)例三已知z 取值范围,x=sin(z);y=cos(z);画三维图形。
z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)xlabel('x')ylabel('y')zlabel('z')例四已知x的取值范围,用subplot函数绘图。
参考程序:x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(2,2,1),plot(x,y1),title('sin(x)')subplot(2,2,2),plot(x,y2),title('1.5*cos(x)')subplot(2,2,3),plot(x,y3),title('sin(2*x)')subplot(2,2,4),plot(x,y4),title('5*cos(2*x)')连续信号的MATLAB表示1、指数信号:指数信号Ae at在MATLAB中可用exp函数表示,其调用形式为:y=A*exp(a*t) (例取A=1,a=-0.4)参考程序:A=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;注:grid on是一个函数,表示在画图的时候添加网格线。
信号与系统仿真实验的研究

从 图中可以看 出, 虚拟仪器的编程采用 了全新 的 G语言 , 与传统的编程语言( c语言) 如 有着极大 地 区别 。从 文本 编 程 转 变 为 图形 编 程 , 与此 时 正 在
8 6
电气电子教 学学报
第3 3卷
学 习的 电路 系统方 框 图非 常类 似 , 程序 关 系 非 常清
2 借 助 Lb IW 完成 仿真 研究 ) aVE
图1 S a函数 及 其 频 谱
借助 Lb IW 的信号分析处理能力 , aVE 可以生成 连续信号和离散时间信号 , 生成周期信号及非周期
信号 , 对信 号 进 行 频 谱 分 析 , 究 信 号 时 域 与 频 域 研
2 2 简 洁 的 系统 构成 .
际的频谱分析仪器价格昂贵, 一般 不可能做到学生 人手一台。但在虚拟实验中, 能轻而易举地获得 却 这些 虚拟 仪 器 , 建 实验平 台。 搭 图 1 非周期信号 的卷 积运 算及其频谱” 是“ 实 验项 目的前面板 图。该项 目可 以对 冲激信号 、 单脉 冲信号 、 斜坡信号 、 三角信号 、 单周期 正弦波 、a函 s
第3 3卷 第 6期 21 0 1年 l 2月
电气 电子 教 学 学 报
J 0URN EE AL OF E
V0 _ 3 No 6 l3 . DC . 01 e 2 1
信 号与 系统仿 真 实验 的研 究
刘舒 帆 ,张 小虹 ,石 琼
( 解放 军理 工大 学 理 学院 , 苏 南京 2 10 ) 江 111
运行… ; Lb IW 与其他设备 的互连能力强 , ⑤ aVE 具
有标 准化 的总线 或 通信 接 口 , 以方便 地 与 其 它 电 可 路连 接 , 成数 据 的采 集与 输入输 出 J 完 。
信号与系统Sinmulink仿真

信号
?
系统
响应
3.5
信号与系统的Sinmulink仿真
Simulink提供了一个建立模型方块图的 图形用户接口(GUI) ,建模过程只需单 击和拖动鼠标操作就能完成,而且用户 可以立即看到系统的仿真结果。本次实 验掌握用Sinmulink建立仿真模型,并完 成系统响应的仿真。
信号
?
系统
响应
1.Simulink 基本操作
信号
?
系统
响应
例3:
(6)运行仿真 双击各模块可对系统中各模块参数进 行设置,各模块参数进行正确设置后, 单击系统模型编辑器上的Play图标(黑 色三角)或选择Simulation菜单下的 Start便可以对系统进行仿真分析。仿真 结束后双击Scope模块以显示系统仿真的 输出结果,如图所示。
信号
?
系统
响应
3.设置仿真参数
用鼠标双击指定模块图标,打开模块对 话框,根据对话框栏目中提供的信息进 行参数设置或修改。例如双击模型窗口 的传递函数模块,弹出对话框,在对话 框中分别输入分子、分母多项式的系数, 点击OK键,完成该模型的设置。
信号
?
系统
响应
4. 模块文件的取名和保存
模块文件的取名和保存选择模型窗口菜 单FileSave as后弹出一个“Save as”对话框,填入模型文件名,按保存 即可。
(1)启动Simulink 点击工具栏中的彩色图标 或在MATLAB环 境下输入simulink命令,会弹出一个名 “simulink library browser”的浏览 器窗口,如图所示,
信号
?
系统
响应
地铁信号系统的仿真研究

地铁信号系统的仿真研究【摘要】本文通过对地铁信号系统的仿真研究,探讨了其在城市轨道交通中的重要性和作用。
首先介绍了地铁信号系统的概述,包括其基本原理和结构。
然后详细分析了地铁信号系统的功能和主要问题,指出了系统中存在的一些瓶颈和挑战。
接着介绍了地铁信号系统的仿真方法,包括建模和仿真工具的选择。
最后展示了仿真结果,阐明了通过仿真研究可以提升地铁信号系统的效率和性能。
在结论部分总结了地铁信号系统的仿真研究成果,并提出了未来发展的方向。
本文旨在为城市轨道交通系统的优化和改进提供理论支持和方法指导。
【关键词】地铁信号系统、仿真研究、研究背景、研究意义、概述、功能、主要问题、仿真方法、仿真结果、成果、未来发展方向、总结1. 引言1.1 研究背景地铁信号系统作为地铁运行的重要组成部分,对地铁运行的安全和效率起着至关重要的作用。
随着城市化进程的加快,地铁交通系统的发展迅速,地铁线路的增多和运行的复杂性也在不断增加。
地铁信号系统的稳定性和可靠性问题变得愈发突出。
在过去的研究中,地铁信号系统存在着许多问题,例如系统的运行效率低下、信号干扰频繁等,这些问题直接影响到地铁线路的运行安全和时效性。
有必要对地铁信号系统进行深入的研究和分析,以寻找解决这些问题的有效方法。
在这样的背景下,本文将对地铁信号系统的仿真研究进行探讨,通过对地铁信号系统的概述、功能、主要问题以及仿真方法和结果进行详细分析,以期为地铁信号系统的稳定运行和发展提供一定的参考和指导。
希望通过本文的研究,可以为地铁交通系统的安全运行和效率提升做出一定的贡献。
1.2 研究意义地铁信号系统是地铁运行中至关重要的一环,它直接关系到地铁列车的运行安全和运行效率。
对地铁信号系统进行仿真研究有着重要的意义。
通过仿真可以模拟各种复杂情况,包括人员乘坐密度、列车运行速度、信号灯控制等,从而更好地评估地铁信号系统的性能和稳定性。
仿真可以帮助我们找出地铁信号系统存在的问题,及时进行改进和优化,提高地铁运行效率和安全性。
《信号与系统》MATLAB仿真实验讲义

《信号与系统》MATLAB仿真实验讲义(第二版)肖尚辉编写宜宾学院电信系电子信息教研室《信号与系统》课程2004年3月 宜宾使用对象:电子专业02级3/4班(本科)实验一 产生信号波形的仿真实验一、实验目的:熟悉MATLAB软件的使用,并学会信号的表示和以及用MATLAB来产生信号并实现信号的可视化。
二、实验时数:3学时+3学时(即两次实验内容)三、实验内容:信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。
对信号进行时域分析,首先需要将信号随时间变化的规律用二维曲线表示出来。
对于简单信号可以通过手工绘制其波形,但对于复杂的信号,手工绘制信号波形显得十分困难,且难以绘制精确的曲线。
在MATLAB中通常用三种方法来产生并表示信号,即(1)用MATLAB软件的funtool符合计算方法(图示化函数计算器)来产生并表示信号;(2)用MATLAB软件的信号处理工具箱(Signal Processing Toolbox)来产生并表示信号;(3)用MATLAB软件的仿真工具箱Simulink中的信号源模块。
(一) 用MATLAB软件的funtool符合计算方法(图示化函数计算器)来产生并表示信号在MATLAB环境下输入指令funtool,则回产生三个视窗。
即figure No.1:可轮流激活,显示figure No.3的计算结果。
figure No.2:可轮流激活,显示figure No.3的计算结果。
figure No.3:函数运算器,其功能有:f,g可输入函数表达式;x是自变量,在缺省时在[-2pi,2pi]的范围内;自由参数是a;在分别输入完毕后,按下面四排的任一运算操作键,则可在figure No.1或figure No.2产生相应的波形。
学生实验内容:产生以下信号波形3sin(x)、5exp(-x)、sin(x)/x、1-2abs(x)/a、sqrt(a*x)(二) 用MATLAB软件的信号处理工具箱(Signal Processing Toolbox)来产生并表示信号一种是用向量来表示信号,另一种则是用符合运算的方法来表示信号。
系统仿真信号实验报告

系统仿真信号实验报告系统仿真信号实验报告1. 引言系统仿真是一种通过计算机模拟系统行为的方法,可以对系统进行预测和优化。
在工程领域中,系统仿真有着广泛的应用,可以用于电子电路设计、通信网络规划、交通流模拟等方面。
本实验旨在通过系统仿真,研究信号的传输和处理过程,探索信号的特性和优化方法。
2. 实验目的本实验的主要目的是通过系统仿真,研究信号的传输和处理过程。
具体包括以下几个方面:- 了解信号的基本概念和特性;- 研究不同信号的传输特性;- 探索信号处理方法和优化策略。
3. 实验方法本实验采用MATLAB软件进行系统仿真。
在仿真过程中,我们将使用不同的信号类型,如正弦信号、方波信号和脉冲信号,并对其进行传输和处理。
4. 实验过程4.1 生成信号首先,我们使用MATLAB生成不同类型的信号。
通过调整信号的频率、幅度和相位等参数,我们可以得到不同特性的信号。
4.2 信号传输在信号传输过程中,我们将模拟信号在传输介质中的衰减和失真情况。
通过改变传输介质的特性和信号的传输距离,我们可以观察到信号的变化。
4.3 信号处理在信号处理过程中,我们将对传输后的信号进行滤波、降噪和增强等操作。
通过选择不同的信号处理算法和参数,我们可以改善信号质量并提取出所需的信息。
5. 实验结果与分析在实验过程中,我们得到了不同类型信号的传输和处理结果。
通过分析实验数据,我们可以得出以下结论:- 正弦信号在传输过程中受到较小的衰减和失真,适合用于远距离传输;- 方波信号在传输过程中会出现较大的失真,需要采取补偿措施;- 脉冲信号在传输过程中容易受到噪声干扰,需要进行滤波处理。
6. 结论与展望通过本实验,我们深入了解了信号的传输和处理过程,并探索了信号的特性和优化方法。
系统仿真为我们提供了一种有效的研究手段,可以在实际操作之前进行模拟和预测。
未来,我们可以进一步研究不同类型信号的传输特性和处理方法,以应对不同场景下的需求。
7. 参考文献[1] Smith, S. W. (1997). The Scientist and Engineer's Guide to Digital Signal Processing. California Technical Publishing.[2] Proakis, J., & Manolakis, D. (2006). Digital Signal Processing: Principles, Algorithms, and Applications. Pearson Education.8. 致谢感谢实验指导老师的悉心指导和支持,感谢实验室的同学们的合作,使本次实验取得了圆满的结果。
信号与系统MATLAB仿真——LTI连续系统的时域分析

信号与系统MATLAB仿真——LTI连续系统的时域分析1. 知识回顾(1)经典时域分析⽅法线性时不变(LTI)系统是最常见最有⽤的⼀类系统,描述这类系统的输⼊-输出特性的是常系数线性微分⽅程。
\begin{array}{l} {y^{(n)}}(t) + {a_{n - 1}}{y^{(n - 1)}}(t) + \cdot \cdot \cdot + {a_1}{y^{(1)}}(t) + {a_0}y(t) = \\ {b_m}{f^{(m)}}(t) + {b_{m - 1}}{f^{(m - 1)}}(t) + \cdot \cdot \cdot + {b_1}{f^{(1)}}(t) + {b_0}f(t) \end{array}齐次解:{y^{(n)}}(t) + {a_{n - 1}}{y^{(n - 1)}}(t) + \cdot \cdot \cdot + {a_1}{y^{(1)}}(t) + {a_0}y(t) = 0特征⽅程:{\lambda ^n} + {a_{n - 1}}{\lambda ^{n - 1}} + \cdot \cdot \cdot + {a_1}\lambda + {a_0} = 0均为单根:{y_h}(t) = \sum\limits_{i = 1}^n {{C_i}{e^{{\lambda _i}t}}}有重根(r重根):{y_h}(t) = \sum\limits_{i = 1}^r {{C_i}{t^{i - 1}}{e^{{\lambda _1}t}}}共轭复根({\lambda _{1,2}} = \alpha \pm j\beta ):{e^{\alpha t}}({C_1}\cos \beta t + {C_2}\sin \beta t)r重复根:{e^{\alpha t}}(\sum\limits_{i = 1}^r {{C_{1i}}{t^{i - 1}}} \cos \beta t + \sum\limits_{i = 1}^r {{C_{2i}}{t^{i - 1}}} \sin \beta t)特解:f(t) = {t^m}所有的特征根均不等于0:{y_p}(t) = {P_m}{t^m} + {P_{m - 1}}{t^{m - 1}} + \cdot \cdot \cdot + {P_1}t + {P_0}有r重等于0的特征根:{y_p}(t) = {t^r}[{P_m}{t^m} + {P_{m - 1}}{t^{m - 1}} + \cdot \cdot \cdot + {P_1}t + {P_0}] f(t) = {e^{\alpha t}}:\alpha 不是特征根:{y_p}(t) = P{e^{\alpha t}}\alpha 是特征单根:{y_p}(t) = {P_1}t{e^{\alpha t}} + {P_0}{e^{\alpha t}}\alpha 是r重特征根:{y_p}(t) = ({P_r}{t^r} + {P_{r - 1}}{t^{r - 1}} + \cdot \cdot \cdot + {P_1}t + {P_0}){e^{\alpha t}} f(t) = \cos \beta t或\sin \beta t:所有特征根均不等于 \pm j\beta :{y_p}(t) = {P_1}\cos \beta t + {P_2}\sin \beta t\pm j\beta 是特征单根:{y_p}(t) = t[{P_1}\cos \beta t + {P_2}\sin \beta t]全解:y(t) = {y_h}(t) + {y_p}(t)(2)零输⼊响应与零状态响应y(t) = {y_{zi}}(t) + {y_{zs}}(t)(3)冲激响应和阶跃响应\left\{ \begin{array}{l} \delta (t) = \frac{{{\rm{d}}\varepsilon (t)}}{{{\rm{d}}t}}\\ \varepsilon (t) = \int_{ - \infty }^t {\delta (\tau ){\rm{d}}\tau } \end{array} \right. \left\{ \begin{array}{l} h(t) = \frac{{{\rm{d}}g(t)}}{{{\rm{d}}t}}\\ g(t) = \int_{ - \infty }^t {h(\tau ){\rm{d}}\tau } \end{array} \right.(4)卷积积分y(t) = {f_1}(t) * {f_2}(t) = \int_{ - \infty }^{ + \infty } {{f_1}(\tau ){f_2}(t - } \tau ){\rm{d}}\tau系统的零状态响应:{y_{zs}}(t) = f(t) * h(t)卷积积分的性质:交换律分配率结合律任意函数与单位冲激函数卷积的结果仍是函数本⾝:f(t) * \delta (t) = f(t)2. 利⽤MATLAB求LTI连续系统的响应LTI连续系统以常微分⽅程描述,如果系统的输⼊信号及初始状态已知,便可以求出系统的响应。
信号与系统MATLAB仿真题目
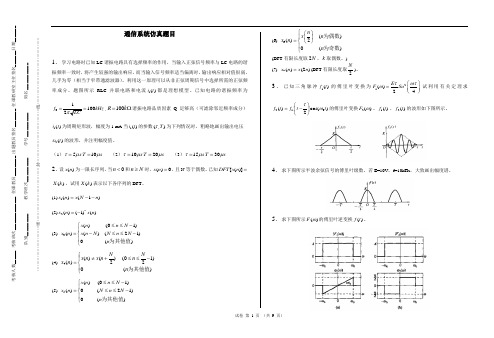
考核人数______ 考核班次_______________ 任课教员_________ 出题教员签名________ 任课教研室主任签名_______日期_______ 队别__________ 教学班次___________ 学号___________ 姓名____________…………………………密………………………………封………………………………线………………………………………通信系统仿真题目1.学习电路时已知LC 谐振电路具有选择频率的作用,当输入正弦信号频率与LC 电路的谐振频率一致时,将产生较强的输出响应,而当输入信号频率适当偏离时,输出响应相对值很弱,几乎为零(相当于窄带通滤波器)。
利用这一原理可以从非正弦周期信号中选择所需的正弦频率成分。
题图所示RLC 并联电路和电流1()i t都是理想模型。
已知电路的谐振频率为0100f kHz ==,100R k =Ω谐振电路品质因素Q 足够高(可滤除邻近频率成分)1()i t 为周期矩形波,幅度为1 mA 当1()i t 的参数(,)T τ为下列情况时,粗略地画出输出电压2()t υ的波形,并注明幅度值。
(1)510s T s τμμ== (2)1020s T s τμμ== (3)1530s T s τμμ==2.设()x n 为一限长序列,当0n <和n N ≥时,()0x n =,且N 等于偶数。
已知[()]DFT x n =()X k ,试用()X k 表示以下各序列的DFT 。
(1)1()(1)x n x N n =-- (2)2()(1)()n x n x n =-(3) 3()(01)()()(21)0()x n n N x n x n N N n N n ≤≤-⎧⎪=-≤≤-⎨⎪⎩为其他值(4) 4()()(01)()22()N N x n x n n x n n ⎧≠+≤≤-⎪=⎨⎪⎩为其他值 (5) 5()(01)()0(21)0()x n n N x n N n N n ≤≤-⎧⎪=≤≤-⎨⎪⎩为其他值 (6) 6()()20()n x n x n n ⎧⎛⎫⎪ ⎪=⎝⎭⎨⎪⎩为偶数为奇数(DFT 有限长度取2N ,k 取偶数。
《信号与系统教程》教案信号与系统的MATLAB仿真

《信号与系统教程》教案信号与系统的MATLAB仿真信号与系统是电子信息类专业以及相关领域常见的一门重要课程,是学生建立系统性的信号与系统理论知识体系的基础课程。
在学习信号与系统的过程中,MATLAB仿真是一个非常重要的工具,通过仿真可以更直观地理解信号与系统的原理和性质,加深学生对课程内容的理解和掌握。
一、实验目的:1.掌握使用MATLAB进行信号与系统仿真的基本方法;2.熟练掌握MATLAB中信号处理和系统分析的基本函数;3.理解信号与系统的基本性质和特点;4.通过仿真实验加深对信号与系统理论的理解。
二、实验内容:1.基本信号的生成与显示通过MATLAB编程生成并显示几种基本信号,如冲激信号、阶跃信号、正弦信号等,并观察它们的波形和频谱特性。
2.离散信号的处理与显示利用MATLAB进行离散信号的加减运算、时域缩放和频域移位等操作,并观察信号在时域和频域上的变化。
3.模拟系统的搭建与分析通过MATLAB建立一个简单的模拟系统,如一阶低通滤波器或者二阶高通滤波器,然后仿真系统的频率响应和时域响应。
4.离散系统的搭建与分析以差分方程形式给出一个离散系统的描述,用MATLAB实现系统的差分方程求解,并分析系统的频率响应和稳定性。
三、实验步骤:1.编写MATLAB代码生成基本信号,并绘制信号波形和频谱图;2.对生成的基本信号进行加减运算、缩放和移位等处理,并观察处理后的信号波形和频谱;3.建立一个模拟系统的传递函数或状态空间方程,利用MATLAB进行系统的频率响应和时域响应仿真;4.建立一个离散系统的差分方程描述,用MATLAB求解系统的时域响应,并分析系统的频谱特性和稳定性;四、实验结果:1.完成了基本信号的生成和显示,能够准确地观察不同信号的时域波形和频谱特性;2.成功实现了对离散信号的处理和显示,掌握了信号的加减、缩放和移位方法;3.实现了一个模拟系统的频率响应和时域响应仿真,了解了系统的性能和特点;4.成功建立了一个离散系统的差分方程模型,通过MATLAB求解得到系统的时域响应,并对系统的频谱和稳定性进行了分析。
信号与系统仿真实验报告

信号与系统仿真实验报告班级:学号:姓名:学院:实验一一、实验者姓名: 二、实验时间: 三、实验地点:四、实验题目:求三阶系统8106)65(5)(232+++++=s s s s s s H 的单位阶跃响应,并绘制响应波形图。
五、解题分析:要知道求单位阶跃响应需知道所用函数,以及产生波形图所需要用到的函数。
六、试验程序:num=[5 25 30]; den=[1 6 10 8]; step(num,den,10);title(‘Step response ’)七、实验结果:实验所得波形图如下:八、实验心得体会:通过本次试验了解学会了一些新的函数的应用。
了解到了N 阶系统的单位阶跃响应的计算方法,和系统的响应波形图的函数应用和绘制方法。
为后面的实验打下基础,并对信号仿真和《信号与系统》这门课程之间的联系有所增加,对《信号与系统》这门课里的问题也有了更加深入地了解。
九、实验改进想法:无。
0123456789100.511.522.533.544.5Step responseTime (sec)A m p l i t u d e实验二一、实验者姓名: 二、实验时间: 三、实验地点:四、实验题目:一个因果线性移不变系统)2()()2(81.0)(--+-=n x n x n y n y ,求:(1))(z H ;(2)冲激响应)(n h ;(3)单位阶跃响应)(n u ;(4))(ωj e H ,并绘出幅频和相频特性。
五、解题分析:离散卷积是数字信号处理中的一个基本运算,MTLAB 提供的计算两个离散序列卷积的函数是conv ,其调用方式为 y=conv(x,h) 。
其中调用参数x,h 为卷积运算所需的两个序列,返回值y 是卷积结果。
MATLAB 函数conv 的返回值y 中只有卷积的结果,没有y 的取值范围。
由离散序列卷积的性质可知,当序列x 和h 的起始点都为k=0时,y 的取值范围为k=0至length(x)+length(h)-2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统仿真电气工程学院09级1班2009302540017于岳川综述:本仿真课共有五个试验内容,内容涉及到冲击响应,阶跃响应,DFT,FFT,IFFT等内容。
本人通过所学知识和查阅相关资料,对每个试验都进行了扩展试验,写在解题分析部分,目的在于验证仿真结果的准确性并同时对题目进行更深入的分析。
其中一些试验,本人运用了对比的方法,验证了课本上所学的一些知识,对理论进行了验证和巩固。
由于本人水平有限,时间仓促,谬误之处在所难免,请老师批评指正,如果时间允许,希望能得到老师的评价。
本人邮箱:yuyuechuan1990@实验一一、实验题目:求三阶系统H(s)=5(s^2+5s+6)/(s^3+6s^2+10s+8)的单位阶跃相应,并绘制响应波形图。
二、Matlab编程b=[5 25 30];a=[1 6 10 8];sys=tf(b,a);%求传递函数t=0:0.01:10;u=step(sys,t); %绘制输出函数图象plot(t,u),grid;title('单位阶跃响应')三.改进方法同样对于此题,可以用simulink进行仿真,仿真结果如下:可见结果一致,且使用起来比编程方便一些。
四.解题分析:对令分母=0.解此方程,得到:>> p=[1 6 10 8];>> x=roots(p)x =-4.0000-1.0000 + 1.0000i-1.0000 - 1.0000i可见系统的极点都在左半开平面,因此系统是稳定的,这在两张阶跃响应的图上也得到了验证。
另外,在编程中使用了tf求传递函数。
实验二一、实验题目一个因果线性移不变系统求:y(n)=0.81y(n-2)+x(n)-x(n-2) (1)H(z);(2)冲激响应;(3)单位阶跃响应;(4)H(e^jw),并绘出幅频和相频特性二.Matlab编程b=[1 0 -1];a=[1 0 -0.81];figure(1);subplot(2,1,1);dimpulse(b,a),grid %求冲击响应title('冲击响应')%求阶跃响应subplot(2,1,2);dstep(b,a) %求阶跃响应title('阶跃响应')w=[0:0.01:1]*pi;figure(2);freqz(b,a,w) %求频率特性title(‘频率响应’)图2.1图2.2三.改进方法1.在第一次编程时,没有设置单位冲击响应和阶跃响应的时间(dimpulse(b,a),grid;dstep(b,a),grid)所以所绘制的图2.1在30秒和50秒后图象基本与横轴重合,无法辨认,因此重设响应时间为30s和50s,重新运行结果如下:可见图形更加容易辨认2.前边程序还有也缺点就是不能输出H(z)的表达式,使用符号变量可以实现,故加写程序如下:syms zHz=(1-z^-2)/(1-0.81*z^-2)pretty(Hz)运行结果:Hz =(1/z^2 - 1)/(81/(100*z^2) - 1)1-- - 12z----------81------ - 12100 z四.解题分析此题分析了差分方程描述的单位冲击响应和单位阶跃响应,学习了绘制频率特性的函数freqz. 此函数将幅频特性和相频特性分开绘制。
此外,本人还由系统函数Z反变换求解了h(n)的表达式,具体办成如下:syms n zHz=((1-z^-2)/(1-0.81*z^-2));%定义系统函数fn=iztrans(Hz,n)%求Z反变换pretty(fk);%美化输出表达式运行结果如下:fn =(100*kroneckerDelta(n, 0))/81 - (19*(9/10)^n)/162 -(19*(-9/10)^n)/162/ 9 \k / 9 \k19 | -- | 19 | - -- |100 kroneckerDelta(k, 0) \ 10 / \ 10 /------------------------ - ---------- - ------------81 162 162关于上边出现的kroneckerDelta函数,我再网上找到一些资料,但是还是没弄清楚。
可能是我做的有错误。
实验三一、实验题目:模拟信号x(t)=2sin(4pi*t)+5cos(8pi*t),求N=64的DFT的幅值谱和相位谱。
二.Matlab编程:N=64;%采样点数N=64;%计64点DFTt=(0:N-1)*0.1;x=2*sin(4*pi*t)+5*cos(8*pi*t);xk=fft(x,N);k=t*2*pi/N;subplot(2,1,1),stem(k,abs(xk)),title('64点DFT的幅值谱');subplot(2,1,2),stem(k,angle(xk)),title('64点DFT的相位谱');三、改进方法:通过观察所做出的图形可以发现,图形虽然是对的,但是横轴超过1.2左右的部分是空白的,因此使图形不对称,也不美观,另外没有X,Y的坐标,看起来很不方便,因此改写后程序如下:(下划线为修改后的程序)int nN=100;t=(0:N-1)*0.2;x=2*sin(4*pi*t)+5*cos(8*pi*t);xk=fft(x,N);k=t*2*pi/N;subplot(2,1,1),stem(k,abs(xk)),axis([0 1.26 0 300]);%限定坐标轴范围,下同xlabel('n');ylabel('|x(n)|');title('64点DFT的幅值谱');subplot(2,1,2),stem(k,angle(xk)),axis([0 1.26 -4 4]);xlabel('n');ylabel('φ(n)');title('64点DFT的相位谱'));重新运行后入行如下:可见图形更加对称且有了横纵坐标单位后图形表示的意义更加清晰。
四、解题分析此题对连续信号做DFT近似分析,而FFT是DFT的快速算法,因此二者从概念上是等价的。
因此编程时使用了FFT函数。
从幅度谱可以看到,出现了明显的频谱泄露现象。
从两个图也可以看出,当采样持续时间从0.1秒提高到0.2秒时,频率分辨率提高了。
即可以明显地看出原连续信号中的频率分量。
说明延长采样时间可以提高频率分辨率。
但是当t=0.1一定,靠增加采样点书数N到100,发现频谱密度提高了,但是却没有提高模拟域的频率分辨率,只是改善了栅栏效应。
实验四一、实验题目将信号x(t)=sin(240pi*t)做离散序列,比较原序列与经过FFT和IFFT变换后的序列,并做出说明。
二、matkab编程N=100;t=(0:N-1)*0.0001;x=sin(240*pi*t);subplot(2,1,1),stem(t,x);%输出100点离散序列title('100点离散序列’);xk=fft(x,N);%求100点FFTy=ifft(xk);%求IFFTsubplot(2,1,2),stem(t,y),title('IFFT变换图像')三.改进方法从上面的图像中可以看到,当采样点数较少是,难以从IFFT图象中看出元连续函数的变化趋势,因此改进后增加求包络线的步骤,改进后的程序如下;N=100;t=(0:N-1)*0.0001;x=sin(240*pi*t);subplot(3,1,1),stem(t,x);%输出100点离散序列title('100点离散序列’);xk=fft(x,N);%求100点FFTy=ifft(xk);%求IFFTsubplot(3,1,2),stem(t,y),title('IFFT变换图像')y1=hilbert(y);subplot(3,1,3),plot(t,y1)%画IFFT的包络线title('IFFT的包络')运行结果:三、解题分析此题属于用FFT近似分析连续信号,试验中可以发现,做IFFT变换后的序列与原序列的抽样序列基本相同。
且其包络线与原来的连续信号波形比较相似。
同时也可以发现,改变抽样间隔和抽样时间也可以使信号还原得更准确,当然这是显而易见的。
此外,这次实验也初次了解hilbert函数在信号处理中的作用。
实验五一、实验题目已知带通滤波器的系统函数为H(s)=2s/[(s+1)^2+10000],激励信号x(t)=(1+cos)*cos(100t),求(1)带通滤波器的频率响应;(2)输出稳态响应并绘制图形。
二、matlab编程b=[2 0];a=[1 2 10001];figure(1)freqs(b,a);%求频率响应¦title('频率响应')figure(2),bode(b,a),grid;%画带通滤波器的bode图title('bode图')W=[ 99 100 101];H=freqs(b,a,W);t1=0:0.01:10;x=0.5*cos(99*t1)+cos(100*t1)+0.5*cos(101*t1);y1=0.5*abs(H(1))*cos(99*t1+angle(H(1)))...+abs(H(2))*cos(100*t1+angle(H(2)))...+0.5*abs(H(3))*cos(101*t1+angle(H(3)));figure(3)subplot(2,1,1),plot(t1,x),grid, title('输入x的图像')subplot(2,1,2),plot(t1,y1),grid, title('稳态响应y(t)的图像')三.改进方法为了检验结果的正确性,用simulink重做上述实验:将输出函数分解为0.5cos(99t)+cos(100t)+0.5cos(101t),利用加法器将输入信号合成,通过传递函数后经过示波器观察波形输入信号波形输出信号波形可以发现结果是完全一致的,检验了编程的正确性。
三、解题分析本次试验内容为带通滤波器的仿真测试,通过BODE图和频率特性曲线,可以发现,带通滤波器在F=100HZ时增益最大,而输入信号的频率正好在99,100,101这三个点,因此,通过对比输入和输出的图像可以发现,输入信号通过带通滤波器后的失真很小。
说明仿真结果是正确的.而输出信号y(t)的描述,则是用了正弦信号通过系统后仍是正弦函数,只是幅值变为系统函数的模倍,相角加上系统函数的相角这一性质。
