简述基于MATLAB设计巴特沃斯低通滤波器
用 MATLAB 设计巴特沃斯低通滤波器
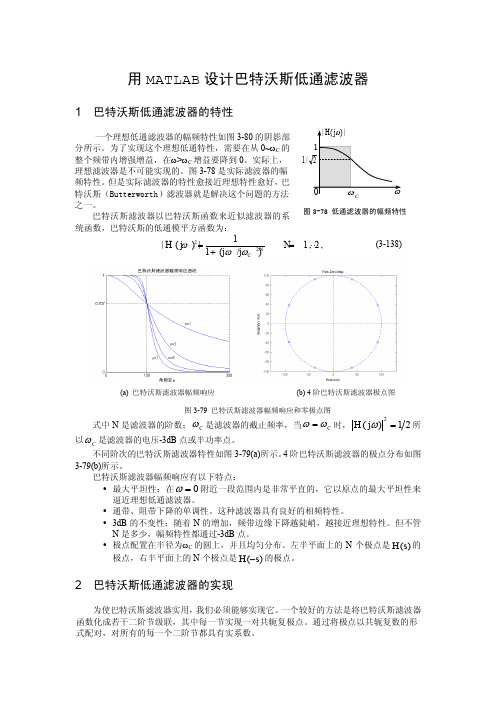
用MATLAB 设计巴特沃斯低通滤波器1 巴特沃斯低通滤波器的特性一个理想低通滤波器的幅频特性如图3-80的阴影部分所示。
为了实现这个理想低通特性,需要在从0~ωC 的整个频带内增强增益,在ω>ωC 增益要降到0。
实际上,理想滤波器是不可能实现的。
图3-78是实际滤波器的幅频特性。
但是实际滤波器的特性愈接近理想特性愈好,巴特沃斯(Butterworth )滤波器就是解决这个问题的方法之一。
巴特沃斯滤波器以巴特沃斯函数来近似滤波器的系统函数,巴特沃斯的低通模平方函数为:221|()|1,2,,1(/)NC H j N j j ωωω==+ (3-138)式中以C ω是滤波器的电压-3dB 点或半功率点。
不同阶次的巴特沃斯滤波器特性如图3-79(a)所示。
4阶巴特沃斯滤波器的极点分布如图3-79(b)所示。
巴特沃斯滤波器幅频响应有以下特点:• 最大平坦性:在0=ω附近一段范围内是非常平直的,它以原点的最大平坦性来逼近理想低通滤波器。
• 通带、阻带下降的单调性。
这种滤波器具有良好的相频特性。
• 3dB 的不变性:随着N 的增加,频带边缘下降越陡峭,越接近理想特性。
但不管N 是多少,幅频特性都通过-3dB 点。
• 极点配置在半径为ωC 的圆上,并且均匀分布。
左半平面上的N 个极点是)(s H 的极点,右半平面上的N 个极点是)(s H -的极点。
2 巴特沃斯低通滤波器的实现为使巴特沃斯滤波器实用,我们必须能够实现它。
一个较好的方法是将巴特沃斯滤波器函数化成若干二阶节级联,其中每一节实现一对共轭复极点。
通过将极点以共轭复数的形式配对,对所有的每一个二阶节都具有实系数。
1图3-78 低通滤波器的幅频特性图3-80所示运算放大器电路为实现一对共轭极点提供了很好的方法。
电路的系统函数为202202121121122121)(1)11(1)(ωωω++=+++=s Qs C C R R s C R C R s C C R R s H (3-139)式中,ω0是S 平面原点与极点之间的距离,Q 被称为电路的“品质因数”,它提供了对响应峰值尖锐程度的一种度量。
利用MATLAB设计巴特沃斯低通数字滤波器

利用MATLAB设计巴特沃斯低通数字滤波器引言数字滤波器是数字信号处理中的重要组成部分,可以用于去除信号中的噪音和不需要的频率成分。
巴特沃斯滤波器是一种常见的数字滤波器,被广泛应用于信号处理领域。
本文将介绍如何利用MATLAB设计巴特沃斯低通数字滤波器,并给出详细的步骤和示例代码。
设计步骤利用MATLAB设计巴特沃斯低通数字滤波器主要包括以下步骤:1.设计滤波器的参数2.计算滤波器的传递函数3.绘制滤波器的幅频响应曲线4.通过频域图像观察滤波器的性能下面将分别介绍每个步骤的详细操作。
设计滤波器的参数巴特沃斯低通数字滤波器的参数包括截止频率和阶数。
截止频率决定了滤波器的通频带,阶数决定了滤波器的陡峭程度。
通过MATLAB的butter()函数可以方便地设计巴特沃斯低通数字滤波器。
该函数的参数为滤波器的阶数和截止频率。
示例代码如下:order = 4; % 阶数cutoff_freq = 0.4; % 截止频率[b, a] = butter(order, cutoff_freq);计算滤波器的传递函数通过设计参数计算得到滤波器的传递函数。
传递函数是一个复数,包括了滤波器的频率响应信息。
使用MATLAB的freqz()函数可以计算滤波器的传递函数。
该函数的参数为滤波器的系数b和a,以及频率取样点的数量。
示例代码如下:freq_points = 512; % 频率取样点数量[h, w] = freqz(b, a, freq_points);绘制滤波器的幅频响应曲线经过计算得到的传递函数能够提供滤波器的幅频响应信息。
通过绘制幅频响应曲线,可以直观地观察滤波器的频率特性。
使用MATLAB的plot()函数可以绘制滤波器的幅频响应曲线。
该函数的参数为频率点和传递函数的幅值。
示例代码如下:magnitude = abs(h); % 幅值plot(w/pi, magnitude);xlabel('归一化频率');ylabel('幅值');title('巴特沃斯低通数字滤波器幅频响应');通过频域图像观察滤波器的性能通过绘制滤波器的频域图像,可以直观地观察滤波器对不同频率的信号的响应情况。
用matlab实现巴特沃斯低通滤波器

通信系统综合设计与实践题目基于MATLAB的低通滤波器设计院(系)名称信院通信系专业名称通信工程学生姓名学生学号指导教师2012年 5 月21 日目录摘要 (2)1.巴特沃斯低通数字滤波器简介 (3)1.1选择巴特沃斯低通滤波器及双线性变换法的原因 (3)1.2巴特沃斯低通滤波器的基本原理 (3)1.2.1巴特沃斯低通滤波器的基本原理 (3)1.2.2双线性变换法的原理............... .. (4)1.3数字滤波器设计流程图............... (6)1.4数字滤波器的设计步骤............... (6)2.巴特沃斯低通数字滤波器技术指标的设置 (8)3.用matlab实现巴特沃斯低通数字滤波器的仿真并分析 (9)3.1用matlab实现巴特沃斯低通数字滤波器的仿真 (9)3.2波形图分析............... ............... (9)4.用Simulink实现巴特沃斯低通数字滤波器的仿真并分析 (10)4.1 Simulink简介............... ............... . (10)4.2用Simulink实现巴特沃斯低通数字滤波器的仿真 (10)4.3波形图分析............... ............... . (10)4.3.1 Simulink波形图分析............... ....................... .. (10)4.3.2与matlab波形的比较............... .. (13)5.总结与体会.............................. (15)6.附录 (16)附录A (16)附录B (17)教师评语 (17)摘要低通滤波器是让某一频率以下的信号分量通过,而对该频率以上的信号分量大大抑制的电容、电感与电阻等器件的组合装置。
巴特沃斯滤波器是电子滤波器的一种,特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
巴特沃斯滤波器matlab自定义函数

巴特沃斯滤波器matlab自定义函数众所周知,巴特沃斯滤波器是一种常用的数字信号处理滤波器,可以用于去除信号中的噪音。
在MATLAB中,我们可以通过自定义函数来实现巴特沃斯滤波器,从而对信号进行滤波处理。
本文将介绍如何在MATLAB中编写自定义函数来实现巴特沃斯滤波器,并给出相应的使用案例。
一、巴特沃斯滤波器原理1.1 基本原理巴特沃斯滤波器是一种频域滤波器,其基本原理是通过设定截止频率和滤波器阶数来实现对信号频谱的调整,从而达到去除噪音的目的。
截止频率越低,滤波效果越好;滤波器的阶数越高,滤波效果也越好。
1.2 数学表达巴特沃斯滤波器的数学表达式如下所示:H(u, v) = 1 / [1 + (D(u, v) / D0) ^ (2n)]其中,H(u, v)为频域滤波器的传递函数,D(u, v)为频域点(u, v)到频谱中心的距离,D0为滤波器的截止频率,n为滤波器的阶数。
1.3 巴特沃斯滤波器的特点巴特沃斯滤波器具有平坦的幅频特性和相位特性,能够有效地保持信号的频率分量,对实时信号传输和快速信号处理具有重要的意义。
二、巴特沃斯滤波器MATLAB自定义函数的编写2.1 函数输入参数为了实现一个通用的巴特沃斯滤波器自定义函数,我们需要定义一些输入参数,以便灵活地调整滤波器的截止频率和阶数。
在MATLAB中,可以通过函数的输入参数来实现这一目的。
一般情况下,巴特沃斯滤波器自定义函数的输入参数包括:- 输入信号- 截止频率D0- 滤波器阶数n2.2 函数输出结果巴特沃斯滤波器自定义函数的输出结果通常是滤波处理后的信号,以便后续的信号分析和处理。
在MATLAB中,可以通过函数的输出参数来返回滤波处理后的信号。
巴特沃斯滤波器自定义函数的输出参数通常是滤波处理后的信号。
2.3 函数实现步骤在MATLAB中编写巴特沃斯滤波器自定义函数的实现步骤如下:- 读取输入参数,包括输入信号、截止频率D0和滤波器阶数n;- 计算输入信号的二维傅里叶变换,得到输入信号的频谱;- 根据巴特沃斯滤波器的数学表达式,计算频域滤波器的传递函数H(u, v);- 将输入信号的频谱与频域滤波器的传递函数相乘,得到滤波处理后的频谱;- 对滤波处理后的频谱进行反傅里叶变换,得到滤波处理后的信号;- 返回滤波处理后的信号作为函数的输出参数。
matlab巴特沃斯低通滤波函数

matlab巴特沃斯低通滤波函数巴特沃斯低通滤波是一种常用的数字滤波方法,用于滤除信号中高频成分,保留低频信号。
在MATLAB中,可以通过调用内置函数`butter`来实现巴特沃斯低通滤波。
本文将介绍这个函数的使用方法,并给出一个简单的示例。
## 巴特沃斯低通滤波概述巴特沃斯低通滤波器是一种无限脉冲响应(IIR)滤波器,它的频率响应曲线为-3dB截止频率。
在信号处理中,巴特沃斯低通滤波器可以用于去除信号中的高频噪声,使得信号更加平滑。
## MATLAB中的`butter`函数MATLAB提供了`butter`函数来设计巴特沃斯滤波器。
该函数的基本语法格式如下:```[b, a] = butter(n, Wn, 'type')```其中,`n`是滤波器阶数,`Wn`为归一化的截止频率,范围为[0, 1],具体取值要根据实际需求设定。
参数`'type'`用来指定滤波器类型,可选的值有'low'、'high'、'bandpass'、'stop'。
`butter`函数将返回滤波器的分子系数`b`和分母系数`a`,用于滤波器的差分方程表达式。
## 示例假设我们有一个包含噪声的信号`x`,现在希望设计一个巴特沃斯低通滤波器来去除信号中的高频成分。
下面是具体的步骤:1. 生成一个包含噪声的信号`x`,作为示例输入信号。
```matlabFs = 1000; % 采样率t = 0:1/Fs:1; % 时间长度x = sin(2*pi*50*t) + sin(2*pi*120*t) + randn(size(t));```2. 设计巴特沃斯低通滤波器。
```matlabfc = 150; % 截止频率Wn = fc/(Fs/2); % 归一化的截止频率n = 6; % 滤波器阶数[b, a] = butter(n, Wn, 'low');```3. 使用设计好的巴特沃斯低通滤波器对信号进行滤波。
毕业设计(论文)-基于MATLAB做巴特沃斯低通滤波器

分类号编号烟台大学毕业论文基于MATLAB设计巴特沃斯低通滤波器The Design of Butterworth Low-passing Filter Based on MA TLAB申请学位:院系:专业:姓名:学号:指导老师:2011年05 月26日烟台大学基于MA TLAB设计巴特沃斯低通滤波器姓名:导师:2011年05月26日烟台大学烟台大学毕业论文任务书院(系):光电信息科学技术学院[摘要]滤波器设计是数字信号处理的重要内容。
在MATLAB软件中有丰富的滤波器设计的相关命令,掌握相关的方法后可以提高我们的工作效率。
首先对巴特沃斯低通滤波器的特性进行研究,然后用MATLAB信号处理工具箱提供的函数设计出巴特沃斯低通滤波器模型,并对具体实例进行分析,使得巴特沃斯滤波器的设计更加快捷、直观、简单。
[关键词]巴特沃斯低通滤波器; MATLAB仿真;[Abstract]First,analyse the characteristics of Butterworth low-pass filter, second use MATLAB signal processing toolbox design the mode of Butterworth low - pass filter ,to study it though an explme. The method makes the design of Butterw orth filter quicklier ,more intuitively,and simp -lier.[Keywords] Butterworth low-pass filter; MATLAB simulation;目录1 绪论 (1)1.1 引言 (1)1.2 数字滤波器的设计原理 (1)1.3数字滤波器的应用 (2)1.4MATLAB的介绍 (3)1.5本文的工作及安排 (3)2 滤波器分类及比较 (5)2.1滤波器的设计原理 (5)2.2 滤波器分类 (5)2.3四种类型模拟滤波器的比较 (9)3巴特沃斯低通滤波器 (11)3.1巴特沃斯低通滤波器的设计原理 (11)4 MATLAB仿真及分析 (15)4.1 MATLAB工具箱函数 (15)4.2 巴特沃斯低通滤波器的MATLAB仿真 (15)5 结论与展望 (19)5.1 总结 (19)5.2 展望 (19)致谢 (20)参考文献 (21)1 绪论1.1 引言凡是有能力进行信号处理的装置都可以称为滤波器。
基于matlab 的巴特沃斯低通滤波器的实现讲课教案

基于m a t l a b的巴特沃斯低通滤波器的实现基于matlab 的巴特沃斯低通滤波器的实现一、课程设计的目的运用MATLAB实现巴特沃斯低通滤波器的设计以及相应结果的显示,另外还对多种低通滤波窗口进行了比较。
二、课程设计的基本要求1)熟悉和掌握MATLAB 的基本应用技巧。
2)学习和熟悉MATLAB相关函数的调用和应用。
3)学会运用MATLAB实现低通滤波器的设计并进行结果显示。
三、双线性变换实现巴特沃斯低通滤波器的技术指标:1.采样频率10Hz。
2.通带截止频率fp=0.2*pi Hz。
3.阻带截止频率fs=0.3*pi Hz。
4.通带衰减小于1dB,阻带衰减大于20dB四、使用双线性变换法由模拟滤波器原型设计数字滤波器程序代码:T=0.1; FS=1/T;fp=0.2*pi;fs=0.3*pi;wp=fp/FS*2*pi;ws=fs/FS*2*pi;Rp = 1; % 通带衰减As = 15; % 阻带衰减OmegaP = (2/T)*tan(wp/2); % 频率预计OmegaS = (2/T)*tan(ws/2); % 频率预计%设计巴特沃斯低通滤波器原型N = ceil((log10((10^(Rp/10)-1)/(10^(As/10)-1)))/(2*log10(OmegaP/OmegaS))); OmegaC = OmegaP/((10^(Rp/10)-1)^(1/(2*N)));[z,p,k] = buttap(N); %获取零极点参数p = p * OmegaC ;k = k*OmegaC^N;B = real(poly(z));b0 = k;cs = k*B; ds = real(poly(p));[b,a] = bilinear(cs,ds,FS);% 双线性变换figure(1);% 绘制结果freqz(b,a,512,FS);%进行滤波验证figure(2); % 绘制结果f1=50; f2=250;n=0:63;x=sin(2*pi*f1*n)+sin(2*pi*f2*n);subplot(2,2,1);stem(x,'.'); title ('输入信号');y=filter(b,a,x);subplot(2,2,2);stem(y,'.') ;wd1=boxcar(N)';b1=hd.*wd1;wd2=hanning(N)';b2=hd.*wd2;wd3=blackman(N)';b3=hd.*wd3;wd4=hamming(N)';b4=hd.*wd4;[h1,w]=freqz(b1,1);[h2,w]=freqz(b2,1);[h3,w]=freqz(b3,1);[h4,w]=freqz(b4,1);plot(w,20*log10(abs(h1)),w,20*log10(abs(h2)),':',w,20*log10(abs(h3)),'-.',w,20*log10(abs(h4)),'--')legend('矩形窗','汉宁窗','布莱克曼窗','汉明窗');结果显示;00.51 1.52 2.53 3.5-160-140-120-100-80-60-40-20020六、总结及心得:基于matlab 的巴特沃斯低通滤波器的实现姓名:学号: S20100 专业:日期: 2010年06月08日。
matlab做低通滤波器设计思路

设计低通滤波器是数字信号处理领域中的一项关键任务,而Matlab 作为一款强大的数学建模与仿真软件,为我们提供了丰富的工具和函数来完成这一任务。
在本篇文章中,我们将介绍在Matlab中设计低通滤波器的思路和具体步骤。
设计低通滤波器主要涉及以下几个方面:1. 确定滤波器的规格要求在设计任何一种滤波器之前,我们首先需要明确滤波器的规格要求,包括截止频率、通带最大衰减、阻带最小衰减等。
这些规格要求将直接影响到滤波器的设计参数和性能。
在Matlab中,可以利用Signal Processing Toolbox提供的函数来帮助我们确定滤波器的规格要求。
2. 选择滤波器的类型根据实际的应用需求,我们需要选择合适的滤波器类型。
常见的低通滤波器包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等。
每种类型的滤波器都有其适用的场景和特点。
在Matlab中,我们可以利用Filter Design and Analysis工具箱中的函数来选择合适的滤波器类型。
3. 根据规格要求设计滤波器一旦确定了滤波器的类型,我们就可以根据规格要求来设计滤波器。
在Matlab中,可以利用Filter Design and Analysis工具箱中的函数来实现滤波器设计,包括巴特沃斯滤波器设计函数butter()、切比雪夫滤波器设计函数cheby1()和cheby2()、椭圆滤波器设计函数ellip()等。
4. 分析和优化滤波器性能设计完成滤波器后,我们需要对滤波器的性能进行分析和优化。
在Matlab中,可以利用Filter Design and Analysis工具箱中的函数来对滤波器的频率响应、相位响应、裙延迟等进行分析,并根据实际需求对滤波器进行优化。
5. 验证滤波器的性能我们需要对设计完成的滤波器进行性能验证。
在Matlab中,可以利用Signal Processing Toolbox提供的函数来对设计的滤波器进行信号处理和性能评估,以确保滤波器能够满足实际需求。
基于Matlab的IIR Butterworth低通数字滤波器设计

问题:信号滤波是一个非常重要的信号处理手段,大量的信号处理系统中,信号滤波的质量将直接影响到系统整体性能。
现在有家医院向你提出一个问题,她们的心电图信号记录仪器由于受到了比较严重的电源干扰(50Hz附近),记录到的心电图ECG波形有较大的畸变,请问如何设计一个干扰滤除系统,让记录下的ECG数据继续可以进行疾病诊断。
(ECG的波形信息非常重要,设计滤波器需要注意这一点)基于Matlab的IIR Butterworth低通数字滤波器设计0 引言心电信号是心脏电活动在人体体表的表现,它一般比较微弱,其频率为0.05Hz~ 100Hz(能量集中在0. 05Hz~ 44Hz),幅度为几百微伏至几毫伏。
因此,在心电信号的采集过程中,极易受到内、外界环境的干扰,其中50Hz的工频干扰尤为突出。
心电图信号的干扰对心电图数据分析和压缩有一定影响。
如何消除50Hz工频干扰,成为处理心电信号的首要任务。
为了消除ECG数据中的主要干扰,保留有用信号或者从干扰中“抽取”有用信号,人们提出了许多方法,诸如,平滑滤波,中心频率固定的带阻滤波器,自适应滤波,低通数字滤波等等。
这些信号处理方法各有优缺点,平滑滤波算法简单,处理速度快,滤波效果较好,但存在一定的削峰作用;中心频率固定的带阻滤波器原理简单,能较大程度地抑制50Hz工频干扰,但存在“群延时”现象;自适应滤波器的中心频率能够跟随工频信号的频率幅度变化而自动调节并抵消工频干扰,但需要附加参考信号通道,算法相对复杂,难以用于实时处理。
考虑到工频干扰是50Hz的低频信号,假设要处理的ECG信号为0.05HZ~44HZ段信号,且Matlab软件中有一个数字滤波器软件包,可以直接进行调用处理信号,所以本文设计IIR巴特沃斯(Butterworth)低通数字滤波器来实现人体ECG信号的滤波。
1 数字滤波器介绍数字滤波器是一种用来过滤时间离散信号的数字系统,它可以用软件(计算机程序)或用硬件来实现,而且在两种情况下都可以用来过滤实时信号或非实时信号(记录信号)。
MATLAB-巴特沃斯滤波器

MATLAB-巴特沃斯滤波器fp=0.2*pi;fs=0.3*pi;Rp=1;Rs=15;Fs=1000;Wp=2*pi*fp;Ws=2*pi*fs;Nn=256;n=(0:100-1);[N,Wn]=buttord(Wp,Ws,Rp,Rs,'s'); [b,a]=butter(N,Wn,'s');w=linspace(1,300,100)*2*pi;H=freqs(b,a,w);figure(1);plot(w/(2*pi),20*log10(abs(H)));title('巴特沃斯模拟滤低通波器幅频特性'); xlabel('频率/Hz');ylabel('幅度/db');[bz,az]=impinvar(b,a,Fs);figure(2);zplane(bz,az);title('冲击响应不变法零极点分布图') figure(3)Subplot(2,1,1);freqz(bz,az,Nn,Fs);grid on;title('巴特沃斯数字滤波器幅频特性'); xlabel('幅度/Hz');ylabel('频率/db'); Subplot(2,1,2);title('巴特沃斯数字滤波器相频特性'); xlabel('幅度/Hz');ylabel('频率/db');ws1=0.2*pi;wp1 = 0.35*pi;wp2 = 0.65*pi;wc = [wp1/pi,wp2/pi];B=wp1-ws1;N = ceil(8/0.15);n=0:N-1;%%rectangle窗window=rectwin(N);[h1,w]=freqz(window,1);subplot(121);stem(window);xlabel('n');title('rectangle窗函数');hn = fir1(N-1,wc,Boxcar(N));[h2,w]=freqz(hn,1,512);figure(1)subplot(122);plot(w/pi,20*log(abs(h2)/abs(h2(1)))); grid; xlabel('w/pi');ylabel('幅度(dB)');title('rectangle滤波器的幅度特性'); ;%%blackman窗window=hamming(N);[h1,w]=freqz(window,1);figure(2)subplot(121);stem(window);title('hamming窗函数');hn = fir1(N-1,wc,hamming(N));[h2,w]=freqz(hn,1,512);subplot(122);plot(w/pi,20*log(abs(h2)/abs(h2(1)))); grid; xlabel('w/pi');ylabel('幅度(dB)');title('hamming滤波器幅度特性'); %%hanning窗window=hanning(N);[h1,w]=freqz(window,1);figure(3)subplot(121);stem(window);xlabel('n');title('blackman窗函数');hn = fir1(N-1,wc,hanning(N));[h2,w]=freqz(hn,1,512);subplot(122);plot(w/pi,20*log(abs(h2)/abs(h2(1))));grid;xlabel('w/pi');ylabel('幅度(dB)');title('hanning滤波器的幅度特性'); %%blackman窗window=blackman(N);[h1,w]=freqz(window,1);figure(4)subplot(121);stem(window);xlabel('n');title('blackman窗函数');hn = fir1(N-1,wc,blackman(N));[h2,w]=freqz(hn,1,512);subplot(122);plot(w/pi,20*log(abs(h2)/abs(h2(1)))); grid; xlabel('w/pi');ylabel('幅度(dB)');title('blackman滤波器的幅度特性'); 第四题第五题。
基于MATLAB的巴特沃斯低通滤波器的设计

H (s)
1
(s p(1))( s p(2))(s p(n))
所以事实上 z 为空阵。上述零极点形式可以化为:
H (s)
sn
k bni s n1
b1s b0
其中 b0
n c
,令
c
1rad / s ,得到巴特沃斯滤波器归一化结果,如表
1
所示。
表 1 n 1 ~ 8阶的巴特沃斯滤波器系数
h(n)= ha(nT) 其中 T 是抽样周期。 如果令 Ha(s)是 ha(t)的拉普拉斯变换,H(z)为 h(n)的 z 变换,利用 抽样序列的 z 变换与模拟信号的拉普拉斯变换的关系,得:
X (z) zesT
1 T
Xa
k
(s
jks )
1 T
k
X
a
s
姓名: 班级: 学号: 时间:2011 年 6 月
设计题目
基于 MATLAB 的巴特沃斯低通滤波器的设计
设计要求
1. 通过实验加深对巴特沃斯低通滤波器基本原理的理解。 2.学习编写巴特沃斯低通滤波器的 MATLAB 仿真程序 3. 滤波器的性能指标如下:通带截止频率 fp=5kHz,通带最大衰减 p =2dB,阻带截止频率 fs=12kHz,阻带最小衰减 s =30dB
滤波器的性能指标如下:通带截止频率 fp=5kHz,通带最大衰减 p =2dB,
阻带截止频率 fs=12kHz,阻带最小衰减 s =30dB
3.1MATLAB 中所需函数
ATLAB 的信号处理工具箱提供了滤波器的函数 buttap、buttord、butter。 由[z,p,k] = buttap(n)函数可设计出 n 阶巴特沃斯低通滤波器原型,其传递函数 为
matlab巴特沃斯滤波器设计

1. 引言在信号处理领域中,滤波器是一种重要的工具,用于去除噪音、增强信号质量或者提取感兴趣的信号成分。
巴特沃斯滤波器作为一种经典的滤波器类型,在信号处理中有着广泛的应用。
本文将围绕matlab中巴特沃斯滤波器的设计展开讨论,帮助读者更深入地理解该主题。
2. 巴特沃斯滤波器介绍巴特沃斯滤波器是一种基于极点和零点的滤波器,其频率响应曲线呈现出平坦的特性。
在频域中,巴特沃斯滤波器的幅频特性具有极为明显的特点,有助于实现对信号的精确处理和控制。
在matlab中,我们可以利用相应的工具和函数来设计和实现巴特沃斯滤波器,以达到特定的信号处理目的。
3. matlab中的巴特沃斯滤波器设计在matlab中,我们可以使用butter函数来设计巴特沃斯滤波器。
该函数提供了灵活的参数设置,可以根据需求来定制滤波器的截止频率、通带和阻带的衰减等参数。
通过调用butter函数,我们可以轻松地实现对巴特沃斯滤波器的设计和生成,为信号处理提供了便利的工具和方法。
4. 巴特沃斯滤波器在信号处理中的应用巴特沃斯滤波器在信号处理领域具有广泛的应用,例如在通信系统中常用于滤除噪声和干扰,提高信号的传输质量;在生物医学工程中常用于生物信号的提取和分析,帮助医生进行疾病诊断和治疗;在声音处理中用于去除环境噪音,提高音频质量等。
巴特沃斯滤波器通过其特殊的频率响应特性,为各种信号处理应用提供了有效的解决方案。
5. 我的个人观点和理解对于巴特沃斯滤波器,我认为其在信号处理中的作用举足轻重。
其平坦的频率响应曲线和灵活的参数设计,使其成为处理复杂信号的重要工具。
在matlab中,利用butter函数可以快速、方便地实现滤波器的设计,为信号处理的研究和应用提供了便利。
在实际应用中,巴特沃斯滤波器不仅可以用于去除噪音、增强信号质量,还可以用于提取感兴趣的信号成分,具有极大的实用价值。
6. 总结通过本文的讨论,我们对matlab中的巴特沃斯滤波器设计有了更深入的理解。
基于MATLAB的巴特沃思和切比雪夫低通滤波器的设计

第一章数字滤波器及MATLAB语言概述数字滤波是语音和图像处理、模式识别、谱分析等应用中的一个基本处理算法,在数字信号处理中占有极其重要的地位。
研究基于Matlab 环境下的IIR数字滤波器的设计与实现,给出了相应的Matlab函数命令,并将滤波器应用于图像噪声的去除,取得了不同的效果,就其结果做出了进一步的解释和说明。
数字滤波器是具有一定传输选择性的数字信号处理装置,其输入、输出均为数字信号,实质上是一个由有限精度算法实现的线性不变离散系统。
它的基本工作原理是利用离散系统特性对系统输入信号进行加工和变换,改变输入序列的频谱或信号波形,让有用频率的信号分量通过,抑制无用的信号输出分量。
MATLAB是美国MathWorks公司推出的一套用于工程计算的可视化高性能语言与软件环境。
MATLAB为数字滤波的研究和应用提供了一个直观、高效、便捷的利器。
它以矩阵运算为基础,把计算、可视化、程序设计融合到了一个交互式的工作环境中。
MATLAB推出的工具箱使各个领域的研究人员可以直观方便地进行科学研究、工程应用,其中的信号处理(signalproeessing)、图像处理(imageproeessing)、小波(wavelet)等工具箱为数字滤波研究的蓬勃发展提供了有力的工具。
数字滤波器与模拟滤波器相比,具有精度高、稳定、体积小、重量轻、灵活、不要求阻抗匹配以及能实现模拟滤波器无法进行的特殊滤波等优点。
本文主要介绍有限冲激响应数字滤波器(FIR)和无限冲激响应数字滤波器(IIR)的设计原理、方法、步骤以及在MATLAB中的实现,并以实例形式列出设计程序和仿真结果。
第二章 方案提取和技术要求第一节 方案提取IIR 数字滤波器是一种离散时间系统,其系统函数为假设M ≤N ,当M >N 时,系统函数可以看作一个IIR 的子系统和一个(M-N)的FIR 子系统的级联。
IIR 数字滤波器的设计实际上是求解滤波器的系数和 ,它是数学上的一种逼近问题,即在规定意义上(通常采用最小均方误差准则)去逼近系统的特性。
基于MATLAB和STM32的IIR巴特沃兹四阶低通滤波器设计
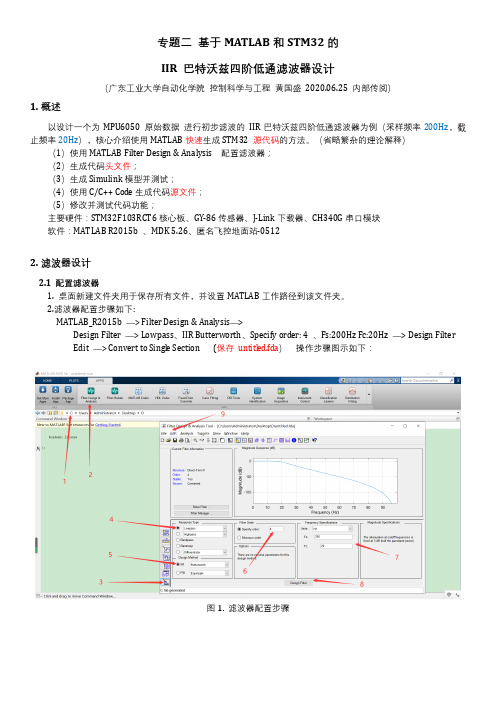
专题二基于MATLAB和STM32的IIR 巴特沃兹四阶低通滤波器设计(广东工业大学自动化学院控制科学与工程黄国盛2020.06.25 内部传阅)1.概述以设计一个为MPU6050 原始数据进行初步滤波的IIR巴特沃兹四阶低通滤波器为例(采样频率200Hz,截止频率20Hz),核心介绍使用MATLAB快速生成STM32 源代码的方法。
(省略繁杂的理论解释)(1)使用MATLAB Filter Design & Analysis 配置滤波器;(2)生成代码头文件;(3)生成Simulink模型并测试;(4)使用C/C++ Cod e生成代码源文件;(5)修改并测试代码功能;主要硬件:STM32F103RCT6核心板、GY-86传感器、J-Link下载器、CH340G串口模块软件:MATLAB R2015b 、MDK 5.26、匿名飞控地面站-05122.滤波器设计2.1 配置滤波器1. 桌面新建文件夹用于保存所有文件,并设置MATLAB工作路径到该文件夹。
2.滤波器配置步骤如下:MATLAB_R2015b —> Filter Design & Analysis—>Design Filter —> Lowpass、IIR Butterworth、Specify order: 4 、Fs:200Hz Fc:20Hz —> Design FilterEdit —> Convert to Single Section (保存untitl ed.fda)操作步骤图示如下:图1. 滤波器配置步骤2.2 生成代码头文件Targets —> generate C header —>修改参数:Numerator: b_20Hz、Denominator: a_20HzSingle-precision fl oat —> Generate (保存fdacoefs.h)操作步骤图示如下:图2. 代码头文件生成步骤生成的fdacoefs.h文件如下所示:图3. 生成的头文件2.3 生成Simulink模型并测试Realize Model —>Block name: IIR_Butterworth_IV_LPFBuil d model using basic elements —> Realize Model (保存Untitl ed.slx)操作步骤图示如下:图4. Simulink模型生成步骤生成的Untitled.slx文件如下所示:(双击模块可查看内部两个二阶节结构并对比头文件参数)图5. 生成的Simulink模型添加模块并测试滤波效果:其中Sine Wave1 、Sine Wave2、Sine Wave3、Model configuration parameters配置参数如下(详见下图):Sine Wave1:1A 15Hz 0 1/200Sine Wave2:0.5A 30Hz 15 1/200Sine Wave3:0.5A 60Hz 23 1/200Model configuration parameters: 0.5s Sine Wave1和输出比较OK!!!!!!!!图6. 仿真参数配置运行后的仿真波形效果如图:图7. 仿真效果2.4 使用C/C++ Code生成代码源文件配置流程:Code —> C/C++ Code —> Embed ded Cod e Quick Start—> Subsystem—> C code —>—> Custom Processor —> Custom8 16 3232 64 3232—> RAM / Execution生成的文件夹IIR_Butterworth_IV_LPF_ert_rtw中主要文件有两个:IIR_Butterworth_IV_LPF.c 和IIR_Butterworth_IV_LPF.h图8. 使用C/C++ Cod e生成的文件IIR_Butterworth_IV_LPF.c 、IIR_Butterworth_IV_LPF.h 中的核心代码如下:、图9. 生成的核心代码3.修改并测试代码功能3.1 代码修改至此生成三个核心代码文件:fdacoefs.h、IIR_Butterworth_IV_LPF.c 、IIR_Butterworth_IV_LPF.h我们还要对IIR_Butterworth_IV_LPF_step()进行修改,添加相应的输入输入接口,将具体数据参数化。
基于Matlab的巴特沃斯IIR数字滤波器设计

பைடு நூலகம்
基于 Matlab 的巴特沃斯 IIR 数字滤波器设计
1.低通 Wp=0.2; Rp=1; Ws=0.3; Rs=15; [N,Wc]=buttord(Wp,Ws,Rp,Rs) [Bz,Az]=butter(N,Wc)
给出的滤波器的幅度和增益曲线。 参考曲线如下:
低通滤波器
ω/π
ω/π
幅度
增益 dB
给出的滤波器的幅度和增益曲线。 参考曲线如下:
带通滤波器
ω/π ω/π
增益 dB
幅度
4.带阻
Wp=[0.2,0.8]; Rp=1; Ws=[0.3,0.7]; Rs=15; [N,Wc]=buttord(Wp,Ws,Rp,Rs) [Bz,Az]=butter(N,Wc,'stop')
给出的滤波器的幅度和增益曲线。 参考曲线如下:
带阻滤波器
ω/π ω/π
某输入信号如下:
N=128; t=0:N-1; fs=1000; x1=sin(2*pi*50*t/fs); x2=sin(2*pi*150*t/fs); x3=sin(2*pi*250*t/fs); xn=x1+x2+x3;
对 xn 进行滤波处理: 1)设计低通滤波器,滤除 x2 和 x3,给出的滤波器的幅度、增益曲线和输出波形;(参 考过渡带:0.15π-0.25π) 2)设计高通滤波器,滤除 x1 和 x2,给出的滤波器的幅度、增益曲线和输出波形;(参 考过渡带:0.35π-0.45π) 3)设计带通滤波器,滤除 x1 和 x3,给出的滤波器的幅度、增益曲线和输出波形;(参 考过渡带:0.15π-0.25π和 0.35π-0.45π) 4)设计带阻滤波器,滤除 x2,给出的滤波器的幅度、增益曲线和输出波形;(参考 过渡带:0.15π-0.25π和 0.35π-0.45π) 5)调解 1)中的 as,使滤波器阶数 N=4; 6)调解 4)中的过渡带,改善输出波形;
数字信号处理课程设计-基于MATLAB的巴特沃斯低通滤波器以切贝雪夫低通滤波器的设计

各专业全套优秀毕业设计图纸吉首大学信息科学与工程学院课程设计报告书课程:数字信号处理教程课题:基于MATLAB的巴特沃斯低通滤波器以切贝雪夫低通滤波器的设计姓名:学号:专业:通信工程年级: 2012级指导教师:基地指导教师:2014年12 月一、项目介绍与设计目的1.通过实验加深对巴特沃斯低通滤波器以及切贝雪夫低通滤波器基本原理的理解。
2.学习编写巴特沃斯低通滤波器和切比雪夫的MATLAB仿真程序。
3.滤波器的性能指标如下:通带截止频率fp=3kHz,通带最大衰减Rp=2dB,阻带截止频率fst=6kHz,阻带最小衰减As=30db二、设计方案1.项目环境要求MATLAB 软件2.设计内容一.理论设计:模拟巴特沃思低通滤波器的设计1.有技术指标可求的设计参数Ωp=6000πrad/s; Ωst=12000πrad/s;Rp=2db; As=30 db2.求N;=5.369取N=63.确定参数=1971.114.求系统函数Han(s)=1/(1+3.8637033S+7.4641016S^2+9.141620S^3+7.4641016S^4+3.8637033S^5+S^6)5.去归一化H(s)=Han(s/Ωc)=0.7648/(0.7648+3.0910s^5+6.2424s^4+7.9947S^3+6.6300S^2+0.6949)化简可得Ha(s)=5.8650*10^25/(s^6+7.6158*10^4s^5+2.9000*10^9s^4+7.0010*10^13s^3+1.12 67*10*18s^2+1.1496*10^32s+5.8650*10^25)切比雪夫低通滤波器1.由技术指标可得ε=1/(10^0.1As)=0.031N>=arcch[]/arch()取N=4系统函数为:Ha(s)=0.0316s^4+3.5954*10^8S^2+5.1099*10^17/(S^4+6.6533*10^4S^3+2.2247*10^9S^2+4.365 9*10^13S+5.1099*10^17)二.程序设计(1)巴特沃斯低通滤波器程序:clc,clear all;OmegaP=2*pi*3000;OmegaS=2*pi*6000;Rp=2;As=30;N=ceil(log10((10^(As/10)-1)/(10^(Rp/10)-1))/(2*log10(OmegaS/OmegaP)))OmegaC=OmegaP/((10^(Rp/10)-1)^(1/(2*N)));[z0,p0,k0]=buttap(N);p=p0*OmegaC;a=real(poly(p))k=k0*OmegaC^N;b0=real(poly(z0));b=k*b0w0=[OmegaP,OmegaS];[H,w]=freqs(b,a);Hx=freqs(b,a,w0);dbHx=-20*log10(abs(Hx)/max(abs(H)))plot(w/(2*pi)/1000,20*log10(abs(H)));xlabel('f(kHz)');ylabel('dB');axis([-1,12,-55,1])set(gca,'xtickmode','manual','xtick',[0,1,2,3,4,5,6,7,8,9,10]);Set(gca,'ytickmode','maunal','ytick',[-50,-40,-30,-2,-10,0]);grid;输出结果N=6b=5.8650e+25a=1 7.5158e+04 2.9000e+09 7.0010e+13 1.1267e+18 1.1496e+22 5.8650e+25 dbHx=2.0000 33.7692在matlab中显示如下:程序运行结果如下故系统函数为:Ha(s)=5.8650*10^25/(s^6+7.6158*10^4s^5+2.9000*10^9s^4+7.0010*10^13s^3+1.12 67*10*18s^2+1.1496*10^32s+5.8650*10^25)(2)切贝雪夫型低通滤波器此低通滤波器的系统函数为:Ha(s)=0.0316s^4+3.5954*10^8S^2+5.1099*10^17/(S^4+6.6533*10^4S^3+2.2247*10^9S^2+4.365 9*10^13S+5.1099*10^17)。
IIR低通滤波器的设计matlab程序
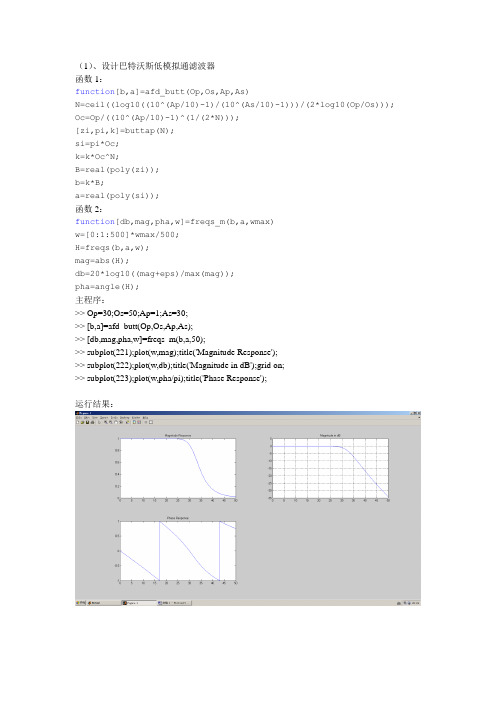
(1)、设计巴特沃斯低模拟通滤波器函数1:function[b,a]=afd_butt(Op,Os,Ap,As)N=ceil((log10((10^(Ap/10)-1)/(10^(As/10)-1)))/(2*log10(Op/Os))); Oc=Op/((10^(Ap/10)-1)^(1/(2*N)));[zi,pi,k]=buttap(N);si=pi*Oc;k=k*Oc^N;B=real(poly(zi));b=k*B;a=real(poly(si));函数2:function[db,mag,pha,w]=freqs_m(b,a,wmax)w=[0:1:500]*wmax/500;H=freqs(b,a,w);mag=abs(H);db=20*log10((mag+eps)/max(mag));pha=angle(H);主程序:>> Op=30;Os=50;Ap=1;As=30;>> [b,a]=afd_butt(Op,Os,Ap,As);>> [db,mag,pha,w]=freqs_m(b,a,50);>> subplot(221);plot(w,mag);title('Magnitude Response');>> subplot(222);plot(w,db);title('Magnitude in dB');grid on;>> subplot(223);plot(w,pha/pi);title('Phase Response');运行结果:(2)、用脉冲响应不变法设计巴特沃斯低通数字滤波器函数1:(同上)函数2:(同上)函数3:function[db,mag,pha,w]=freqz_m(bz,az)[H,w]=freqz(bz,az,1000,'Whole');H=(H(1:501))';w=(w(1:501))';mag=abs(H);db=20*log10((mag+eps)/max(mag));pha=angle(H);主程序:>> Wp=0.2*pi;Ws=0.3*pi;Ap=1;As=15;T=1;>> Op=Wp/T;Os=Ws/T;>> [b,a]=afd_butt(Op,Os,Ap,As);>> [db,mag,pha,Omega]=freqs_m(b,a,pi);>> subplot(224);plot(Omega/pi,db);title('模拟滤波器幅度响应');grid on; >> [ai,si,k]=residue(b,a);>> zi=exp(si*T);>> [bz,az]=residuez(ai,zi,k);>> bz=real(bz)*T;>> az=real(az);>> [db,mag,pha,w]=freqz_m(bz,az);>> subplot(221);plot(w/pi,mag);title('数字滤波器幅度响应');>> subplot(222);plot(w/pi,db);title('数字滤波器幅度响应db');grid on; >> subplot(223);plot(w/pi,pha/pi);title('数字滤波器相位响应');>> Op=(2/T)*tan(Wp/2);Os=(2/T)*tan(Ws/2);运行结果:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MATLAB 设计巴特沃斯低通滤波器
摘 要: 首先分析了巴特沃斯低通滤波器的特性。
然后用MATLAB 的信号处理工具箱提供的函 数设计了巴特沃斯低通滤波器,使得巴特沃斯滤波器的设计变得更加简单、快捷、直观。
巴特沃斯(Butterworth)滤波器是一种具有最大平坦幅度响应的低通滤波器,它在通信领域里已有广应用,在电测中也具有广泛的用途,可以作检测信号的滤波器。
MATLAB 语言是一种面向科学与工程计算的语言。
它编程效率高,测试程序手段丰富,扩展能力强,内涵丰富。
它的信号处理工具箱(Signal Processing Toolbox)提供了设计巴特沃斯滤波器的函数,本文充分利用这些函数,进行了巴特沃斯滤波器的程序设计,并将其作为函数文件保存,可方便地进行调用。
1. 巴特沃斯低通滤波器的特性
巴特沃斯低通滤波器的平方幅度响应为: n c j H 22)(11
)(ωωω+=
其中,n 为滤波器的阶数,ωc 为低通滤波器的截止频率。
该滤波器具有一些特殊
的性质:
① 对所有的n ,都有当 ω=0时,|H(j0)|2 =1;
② 对所有的n ,都有当ω=ωc 时,|H(j ωc )|2 =0.5 ,即在ωc 处有3dB 的衰减;
③|H(j ω)|2 是ω的单调递减函数,即不会出现幅度响应的起伏;
④ 当n →+∞时,巴特沃斯滤波器趋向于理想的低通滤波器;
⑤ 在ω=0处平方幅度响应的各级导数均存在且等于0,因此|H(j ω)|2 在该点上取得最大值,且具有最大平坦特性。
图l 展示了2阶、4阶、8阶巴特沃斯低通滤波器的幅频特性。
可见阶数n 越高,其幅频特性越好,低频检测信号保真度越高。
巴特沃斯与贝塞尔(Besse1)、切比雪夫(Cheby.shev)滤波器的特性差异如图2所示。
从图2可以看出,巴特沃斯滤波器在线性相位、衰减斜率和加载特性三个方面具有特性均衡的优点,因此在实际使用中,巴特沃斯滤波器已被列为首选。
2 .巴特沃斯低通滤波器的MATLAB实现
MATLAB的信号处理工具箱提供了有关巴特沃斯滤波器的函数buttap、buttord、butter。
2.1 用buttap函数设计归一化的巴特沃斯低通滤波器系数
[z,P,k]=bttap(n)可设计出n阶巴特沃斯低通滤波器原型,其传递函数为:
))(())2())(1(()(n p s p s p s k
s H -∧--=
因此实际上Z 为空阵。
上述零极点形式可以化为: 0
1110
)(b s b s b s b s H n n n ++∧++=--
其中n b 00ω=,巴特沃斯滤波器的归一化结果,如表1所示。
2.2 设计巴特沃斯滤波器的程序实现
buttord 函数可在给定滤波器性能的情况下,选择巴特沃斯滤波器的阶数n 和截止频率ωc , 从而可利用butter 函数设计巴特沃斯滤波器的传递函数。
[n,ωc ]=buttord(ωp ,ωs ,R p ,R s ,'s')可得到满足性能的模拟巴特沃斯滤波器的最小阶数n 及截止频率ωc , 其中ωp 为通带的拐角频率,ωs 为阻带的拐角频率,
ωp 和ωs 的单位均为rad/s ;R s 为通带区的最大波动系数,R p 为R s 阻带区的最小衰减系数,R p 和R s 的单位都为dB 。
[b ,a]=butter(n ,ωc ,'s' )可设计截止频率为ωc 的n 阶低通模拟巴特沃斯滤波器为:
)1()2()1()2()1()()()(11++∧++++∧++==--n a s a s n b s b s b s A s B s H n n n n
利用buttord 函数、buuer 函数编制设计巴特沃斯低通滤波器的MATLAB 函数文件butterdesign .m ,其清单如下:
Function[Nbutt ,Wcbutt ,bbutt ,abutt]=butterdesign(Wp ,Rp ,Ws ,As)
[Nbutt ,Wcbutt]=buttord(Wp ,Ws ,Rp ,As ,’S’);
[bbutt ,abutt]=butter(Nbutt ,Wcbutt ,’S’);
[hbutt ,Wbutt]=freqs(bbutt ,abutt);
subplot(2,1,1);plot(WbuR ,abs(hbutt));
subplot(2,1,2);plot(W'butt ,angle(hbutt));
为了使程序更通用,采用以下命令从键盘上输入巴特沃斯滤波器的性能指标。
Wp=input(’Please input passband comer frequencyin rad /s Wp=’)
Rp=input(’Please input passband ripple in dB Rp= ’)
Ws=input(’Please input stopb and comer frequency in rad /s Ws=’)
As=input(’Please input stopband attenuation in dB As=’)
调用butterdesign 函数就可设计出满足性能指标的巴特沃斯滤波器,其主程序文件名为buttermain .m 。
下面举例说明巴特沃斯滤波器的计算机辅助设计过程。
设计一模拟巴特沃斯低通滤波器,其通带的拐角频率ωp 为0.2π,通带区的最大波动系数R p 为7dB ,阻带的拐角频率ωs 为0.3π,阻带区的最小衰减系数R s 为16dB 。
在MATLAB 命令窗口中输入buttermain ,根据屏幕上的提示分别输入0.2*pi ,7,0.3*pi ,16,就可得到满足性能指标的巴特沃斯低通滤波器的最小阶数n=3,截止频率ωc =0.5122rad /s ,其传递函数为:
1344.05247.00244.11344
.0)(23+++=s s s s H
同时得到图3所示的巴特沃斯低通滤波器曲线。
3. 结束语
利用本文的butterdesign函数就可以轻而易举地设计出满足性能指标要求的巴特沃斯滤波器的最小阶数n及截止频率ωc ,并绘制出巴特沃斯滤波器的频率特性曲线,使得巴特沃斯滤波器的设计变得更加简单、快捷、直观。
参考文献
[1] 张殿龙,王福文.巴特沃斯低通滤波器在电动机测试中的应用[J].电测与仪表,2001.
[2] 王永初.Buttworth滤波器在过程控制中的应用[J].工业仪表与自动化装置,1994,6.
[3] 陈思.巴特沃斯低通滤波器的简化快速设计[J].信阳师范学院学报(自然科学版),1997.
[4] 楼顺天,李博菡.基于MATLAB的系统分析与设计——信号处理[M].西安电子科技大学出版社,1998.。
