大学物理第三章刚体力学基础习题答案
《大学物理》刚体力学练习题及答案解析

《大学物理》刚体力学练习题及答案解析一、选择题1.刚体对轴的转动惯量,与哪个因素无关 [ C ](A)刚体的质量(B)刚体质量的空间分布(C)刚体的转动速度(D)刚体转轴的位置2.有两个力作用在一个有固定轴的刚体上. [ B ](1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3)这两个力的合力为零时,它们对轴的合力矩也一定是零;(4)当这两个力对轴的合力矩为零时,它们的合力也一定是零.在上述说法中,(A)只有(1)是正确的;(B) (1)、(2) 正确, (3)、(4)错误;(C) (1)、(2)、(3)都正确, (4)错误;(D) (1)、(2)、(3)、(4)都正确.3.均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动,今使棒从水平位置由静止开始自由下落,在棒摆动到竖立位置的过程中,下述说法哪一种是正确的[ A ](A) 角速度从小到大,角加速度从大到小;(B) 角速度从小到大,角加速度从小到大;(C) 角速度从大到小,角加速度从大到小;(D) 角速度从大到小,角加速度从小到大.4.如图所示,圆锥摆的小球在水平面内作匀速率圆周运动,小球和地球所组成的系统,下列哪些物理量守恒( C )(A)动量守恒,角动量守恒(B)动量和机械能守恒(C)角动量和机械能守恒(D)动量,角动量,机械能守恒5.一圆盘绕通过盘心且垂直于盘面的水平轴转动,轴间摩擦不计,如图射来两个质量相同,速度大小相同、方向相反并在一条直线上的子弹,它们同时射入圆盘并且留在盘内,在子弹射入后的瞬间,对于圆盘和子弹系统的角动量L以及圆盘的角速度ω则有( B )(A)L不变,ω增大(B)L不变,ω减小(C)L变大,ω不变(D)两者均不变6.一花样滑冰者,开始自转时,其动能为20021ωJ E =。
然后他将手臂收回,转动惯量减少为原来的1/3,此时他的角速度变为ω,动能变为E ,则下列关系正确的是( D ) (A )00,3E E ==ωω (B )003,31E E ==ωω (C )00,3E E ==ωω (D )003,3E E ==ωω1C 2.B ,3.A ,4.C ,5.B ,6.D二、填空1.当刚体受到的合外力的力矩为零时,刚体具有将保持静止的状态或_____________状态,把刚体的这一性质叫刚体___________。
刚体力学基础 习题 解答

衡水学院 理工科专业 《大学物理B 》 刚体力学基础 习题命题教师:郑永春 试题审核人:张郡亮一、填空题(每空1分)1、三个质量均为m 的质点,位于边长为a 的等边三角形的三个顶点上。
此系统对通过三角形中心并垂直于三角形平面的轴的转动惯量J 0=__ ma 2 _,对通过三角形中心且平行于其一边的轴的转动惯量为J A =__12ma 2_,对通过三角形中心和一个顶点的轴的转动惯量为J B =__21ma 2 。
2、两个质量分布均匀的圆盘A 和B 的密度分别为ρA 和ρ B (ρA >ρB ),且两圆盘的总质量和厚度均相同。
设两圆盘对通过盘心且垂直于盘面的轴的转动惯量分别为J A 和J B ,则有J A < J B 。
3、 一作定轴转动的物体,对转轴的转动惯量J =3.0 kg ·m 2,角速度ω0=6.0 rad/s .现对物体加一恒定的制动力矩M =-12 N ·m ,当物体的角速度减慢到ω=2.0 rad/s 时,物体已转过了角度∆θ =__4.0rad4、两个滑冰运动员的质量各为70 kg ,均以6.5 m/s 的速率沿相反的方向滑行,滑行路线间的垂直距离为10 m ,当彼此交错时,各抓住一10 m 长的绳索的一端,然后相对旋转,则抓住绳索之后各自对绳中心的角动量L =__2275 kg·m 2·s 1 _;它们各自收拢绳索,到绳长为5 m 时,各自的速率υ =__13 m·s 1_。
5、有一质量均匀的细棒,可绕垂直于棒的一端的水平轴转动。
如将此棒放在水平位置,然后任其下落,则在下落过程中的角速度大小将 变大 ,角加速度大小将 变小 。
二、单项选择题(每小题2分)( A )1、有两个力作用在一个有固定转轴的刚体上,下列说法正确的是:A.这两个力都平行于轴作用时,它们对轴的合力矩一定是零;B.这两个力都垂直于轴作用时,它们对轴的合力矩一定是零;C.当这两个力的合力为零时,它们对轴的合力矩也一定是零;D.当这两个力对轴的合力矩为零时,它们的合力也一定是零。
大学物理学课后3第三章答案

题 3.8(a)图 (1) m1 , m2 和柱体的运动方程如下:
题 3.8(b)图
T2 m2 g m2a2
①
m1g T1 m1a1
②
T1R T2r J
③
式中 T1 T1,T2 T2 , a2 r , a1 R
而 由上式求得
J 1 MR 2 1 mr 2
∵
Fr N
N N
∴ 又∵
∴ ①
Fr
N
l1
l2 l1
F
J 1 mR 2 , 2
Fr R 2(l1 l2 ) F
J
mRl1
以 F 100 N 等代入上式,得
2 0.40 (0.50 0.75) 100 40 rad s2
0.20m, r =0.10m, m =4 kg, M =10 kg, m1 = m2 =2 kg,且开始时 m1 , m2 离地均为 h =2m.求: (1)柱体转动时的角加速度; (2)两侧细绳的张力.
解: 设 a1 , a2 和β分别为 m1 , m2 和柱体的加速度及角加速度,方向如图(如图 b).
习题 3
3.1 选择题
(1) 有两个力作用在一个有固定转轴的刚体上:
① 这两个力都平行于轴作用时,它们对轴的合力矩一定是零;
② 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;
③ 当这两个力的合力为零时,它们对轴的合力矩也一定是零;
④ 当这两个力对轴的合力矩为零时,它们的合力也一定是零.
在
上
述
说
(5) 一圆盘正绕垂直于盘面的水平光滑固定轴 O 转动,如图射来两个质量相同,
大物习题解答-大学物理习题答案(许瑞珍_贾谊明)-第3章 刚体力学

第三章 刚体力学3-1 一通风机的转动部分以初角速度ω0绕其轴转动,空气的阻力矩与角速度成正比,比例系数C 为一常量。
若转动部分对其轴的转动惯量为J ,问:(1)经过多少时间后其转动角速度减少为初角速度的一半?(2)在此时间内共转过多少转? 解:(1)由题可知:阻力矩ωC M -=,又因为转动定理 dtd JJ M ωβ== dtd JC ωω=-∴ dt JC d t ⎰⎰-=∴00ωωωω t JC-=0lnωω t JCe-=0ωω当021ωω=时,2ln CJt =。
(2)角位移⎰=tdt 0ωθ⎰-=2ln 00C J t JC dt eωCJ 021ω=,所以,此时间内转过的圈数为CJ n πωπθ420==。
3-2 质量面密度为σ的均匀矩形板,试证其对与板面垂直的,通过几何中心的轴线的转动惯量为)(1222b a ab J +σ=。
其中a ,b 为矩形板的长,宽。
证明一:如图,在板上取一质元dxdy dm σ=,对与板面垂直的、通过几何中心的轴线的转动惯量为 dm r dJ ⎰=2dxdy y x a a b b σ⎰⎰--+=222222)()(1222b a ab +=σ证明二:如图,在板上取一细棒bdx dm σ=,对通过细棒中心与棒垂直的转动轴的转动惯量为2121b dm ⋅,根据平行轴定理,对与板面垂直的、通过几何中心的轴线的转动惯量为22)2(121x adm b dm dJ -+⋅=dx x ab dx b 23)2(121-+=σσ 33121121ba a b dJ J σσ+==∴⎰)(1222b a ab +=σ3-3 如图3-28所示,一轻绳跨过两个质量为m 、半径为r 的均匀圆盘状定滑轮,绳的两端分别挂着质量为m 2和m 的重物,绳与滑轮间无相对滑动,滑轮轴光滑,求重物的加速度和各段绳中的张力。
解:受力分析如图ma T mg 222=- (1) ma mg T =-1 (2) βJ r T T =-)(2 (3) βJ r T T =-)(1 (4)βr a =,221mr J =(5) 联立求出g a 41=, mg T 811=,mg T 451=,mg T 232=3-4 如图3-29所示,一均匀细杆长为L ,质量为m ,平放在摩擦系数为μ的水平桌面上,设开始时杆以角速度0ω绕过细杆中心的竖直轴转动,试求:(1)作用于杆的摩擦力矩;(2)经过多长时间杆才会停止转动。
第三章-刚体力学基础

薄板对Z轴的转动惯量 J Z =
对X轴的转动惯量 J X
对Y轴的转动惯量 JY
Z
垂直轴定理
JZ JX JY
O
yi
Y
xi
ri
X
JZ miri2 mi xi2 mi yi2 Jx J y
五 刚体定轴转动的转动定律的应用
例1、一个质量为M、半径为R的定
滑轮(当作均匀圆盘)上面绕有细绳, 绳的一端固定在滑轮边上,另一端挂
分析: 由 每分钟150转 可知
0
t
2 150
60
5
rad
/ s
而已知 r=0.2m t=30s ω=0
可由公式求相应的物理量
解: (1) 0 0 5 (rad / s2 )
t
30
6
负号表示角加速度方向与角速度方向相反
(飞轮做匀减速转动)
2 02 2
(5 )2 2 ( )
末位置:
Ek
1 2
J 2
l
由刚体定轴转动的动能定理
1 mgl sin 1 J 2 0
2
2
mgl sin 3g sin
J
l
M
1 mgl cos
2
3g cos
J
1 ml2
2l
3
dm dl
gdm
(用机械能守恒定律解) 假设棒在水平位置时的重力势能为零势能
0 1 J2 (mg l sin ) O
动。最初棒静止在水平位置,求它由此下摆角时的
角加速度和角速度。(分别用动能定理和机械能守
恒定律求解)
解: (用动能定理解)
重力对轴的力矩为
M 1 mgl cos(M
O
大学物理第三章刚体力学基础习题答案

方向竖直向下
3-15 由角动量守恒得
mul J mvl 1 1 2 1 2 2 mu m v J 因弹性碰撞,系统机械能守恒: 2 2 2 1 1 2 2 又: J M 2l Ml 12 3 6mu M 3m u 联立可得: v M 3m l M 3m
2 2 2 1 mv l [m( l ) M l 2 ] 3 3 3
o
2 l 3
6mv (4m 3M ) l
v
m
A
3-9 电风扇在开启电源后,经过t1时间到达了额定 转速,此时相应的角速度为 0。当关闭电源后,经 过t2时间风扇停转。已知风扇转子的转动惯量为 J, 并假定摩擦力矩和电机的电磁力矩均为常量,试根据 已知量推算电机的电磁力矩。 解: 设电机的电磁力矩为M,摩擦力矩为Mf
1
0
t1
3-9 (1)
mg T ma
T mg sin 30 ma
g 2 a m/s 4
方向竖直向下
T2 N 2
mg
(2)
mg T1 ma
T2 mg sin 300 ma
T1r T2r J
a r
T1
1
mg
J k m r2
g 联立求解得: a 22 k
质点运动 m 质 量 力 F 刚体定轴转动 2 J r 转动惯量 m dm 力矩 M Fr sin
dp dL F m a F 第二定律 转动定律 M J M dt dt p mv 动 量 角动量 L J t t2 动量定理 t Fdt mv2 mv1 角动量定理 t Mdt J 2 J1 1 动量守恒 F 0, mv 恒矢量 角动量守恒 M 0, J 恒矢量 力矩的功 W Md 力 的 功 W F dr
大学物理五第三章习题答案

第三章 刚体的转动习题答案1、对于定轴转动刚体上不同的点来说:线速度、法向加速度、切向加速度具有不同的值,角位移、角速度、角加速度具有相同的值。
2、由sin M r F Fr θ=⨯=可知,(1)0,0F M ≠=,当0r =或者sin 0θ=,即力通过转轴或者力与转轴平行; (2)0,0F M =≠,这种情况不存在; (3)0,0F M ==,这种情况任何时候都存在。
3、根据均匀圆盘对中心轴的转动惯量:221122I mr vr ρ==可知,对于相同几何形状的铁盘和铝盘,密度大的转动惯量大。
通常我们取铁的密度为37.9/g cm ,铝的密度32.7/g cm ,因此铁盘对中心轴的转动惯量大;根据刚体动能定理:21222111d 22A M I I θθθωω==-⎰,可知对铁盘的外力矩要做更多的功。
4、轮A 的转动惯量212I mr =,轮B 的转动惯量2I mr =,根据刚体的转动定律M I β=,因为两者所受的阻力矩相等,可知轮A 的转动角加速度大于轮B 的转动角加速度,故轮A 先停止。
5、舞蹈演员在旋转过程中,可以近似地认为角动量守恒,当其把双手靠近身体时,转动惯量减小,故角速度增大;当其把双手伸开,转动惯量增大,故角速度减小。
6、解:2334d a bt ct dtθω==+-, 2612d b t c t dtωβ==-。
7、解:11200240/60rad s πωπ⨯==,22700290/60rad s πωπ⨯==, 2215025/126rad s t ωωππβ-===∆, 2117803902t t n θωβπ=+==。
8、解:根据均匀球体对直径轴的转动惯量225I mr =,得到地球对自转轴的转动惯量3729.810I kg m =⨯⋅,地球自转角速度2/246060rad s πω=⨯⨯,转动动能22813102k E I J ω==⨯。
9、解:已知030/rad s ωπ=,切断电源后的角位移752150θππ=⨯=,根据匀减速运动规律2220023/2rad s ωωβθβπθ=⇒==,由于电扇是匀减速,可知阻力矩为常量,因此根据刚体转动动能定理22101144.422M I I J θωω=-=-, 可得到转动惯量2244.420.01I kg m ω⨯==⋅,以及阻力矩44.40.1150M N m π=≈⋅。
大学物理习题答案03刚体运动学

⼤学物理习题答案03刚体运动学⼤学物理练习题三⼀、选择题1.⼀⼒学系统由两个质点组成,它们之间只有引⼒作⽤。
若两质点所受外⼒的⽮量和为零,则此系统(A) 动量、机械能以及对⼀轴的⾓动量都守恒。
(B) 动量、机械能守恒,但⾓动量是否守恒不能断定。
(C) 动量守恒,但机械能和⾓动量守恒与否不能断定。
(D) 动量和⾓动量守恒,但机械能是否守恒不能断定。
[ C ]解:系统=0合外F,内⼒是引⼒(保守内⼒)。
(1)021 F F,=0合外F ,动量守恒。
(2)2211r F r F A =合。
21F F,但21r r时0A 外,因此E不⼀定守恒。
(3)21F F,2211d F d F M =合。
两⼒对定点的⼒臂21d d 时,0 合外M,故L 不⼀定守恒。
2. 如图所⽰,有⼀个⼩物体,置于⼀个光滑的⽔平桌⾯上,有⼀绳其⼀端连结此物体,另⼀端穿过桌⾯中⼼的⼩孔,该物体原以⾓速度ω在距孔为R 的圆周上转动,今将绳从⼩孔往下拉。
则物体 (A) 动能不变,动量改变。
(B) 动量不变,动能改变。
(C) ⾓动量不变,动量不变。
(D) ⾓动量改变,动量改变。
(E)⾓动量不变,动能、动量都改变。
[ E ]解:合外⼒(拉⼒)对圆⼼的⼒矩为零,⾓动量O Rrmv L 守恒。
r 减⼩,v 增⼤。
因此p 、E k 均变化(m不变)。
3. 有两个半径相同,质量相等的细圆环A 和B 。
A 环的质量分布均匀,B 环的质量分布不均匀。
它们对通过环⼼并与环⾯垂直的轴的转动惯量分别为J A 和J B ,则(A)A J >B J (B) A J < B J(C) A J =B J (D) 不能确定A J 、B J 哪个⼤。
[ C ]解:2222mR dm R dm R dm r J, J 与m 的分布⽆关。
另问:如果是椭圆环,J 与质量分布有关吗?(是)4. 光滑的⽔平桌⾯上,有⼀长为2L 、质量为m 的匀质细杆,可绕过其中点且垂直于杆的竖直光滑固定轴O ⾃由转动,其转动惯量为31mL 2,起初杆静⽌。
大学物理刚体力学基础习题思考题与答案
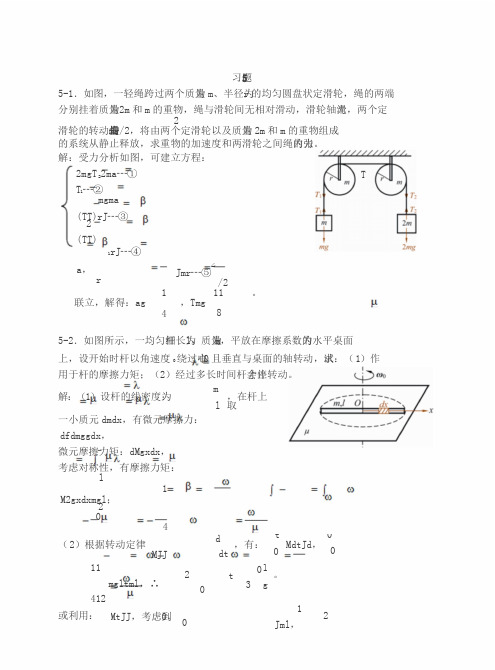
习题55-1.如图,一轻绳跨过两个质量为m、半径为r的均匀圆盘状定滑轮,绳的两端分别挂着质量为2m和m的重物,绳与滑轮间无相对滑动,滑轮轴光滑,两个定2滑轮的转动惯量均为m r/2,将由两个定滑轮以及质量为2m和m的重物组成的系统从静止释放,求重物的加速度和两滑轮之间绳内的张力。
解:受力分析如图,可建立方程:2mgT22ma┄①T1┄②mgmaT(TT)rJ┄③2(TT)1rJ┄④a,r2Jmr┄⑤/2 1联立,解得:ag411,Tmg8。
5-2.如图所示,一均匀细杆长为l,质量为m,平放在摩擦系数为的水平桌面上,设开始时杆以角速度0绕过中心O且垂直与桌面的轴转动,试求:(1)作用于杆的摩擦力矩;(2)经过多长时间杆才会停止转动。
解:(1)设杆的线密度为:ml,在杆上取一小质元dmdx,有微元摩擦力:dfdmggdx,微元摩擦力矩:dMgxdx,考虑对称性,有摩擦力矩:l1M2gxdxmgl;24(2)根据转动定律MJJ ddt,有:tMdtJd,112mgltml,∴0 412 t30lg。
或利用:MtJJ,考虑到0,12 Jml,12有:0t3 l g 。
5-3.如图所示,一个质量为m的物体与绕在定滑轮上的绳子相联,绳子的质量可以忽略,它与定滑轮之间无滑动。
假设定滑轮质量为M、半径为2R,其转动惯量为M R/2,试求该物体由静止开始下落的过程中,下落速度与时间的关系。
解:受力分析如图,可建立方程:mgTma┄①TR┄②JaR,12 JmR┄③22mgMmg联立,解得:aT,,M2m M2m考虑到a dvdt,∴vt2mgdvdt00M2m,有:v2m gtM2m。
5-4.轻绳绕过一定滑轮,滑轮轴光滑,滑轮的质量为M/4,均匀分布在其边缘上,绳子A端有一质量为M的人抓住了绳端,而在绳的另一端B系了一质量为M/4的重物,如图。
已知滑轮对O2轴的转动惯量J/4,设人从静止开始以相对绳匀速向上爬MR时,绳与滑轮间无相对滑动,求B端重物上升的加速度?解一:分别对人、滑轮与重物列出动力学方程Mg T1人MaAMMT2ga物B44T1RTRJ滑轮22由约束方程:aaRJ,解上述方程组A和MR/4B得到g a. 2解二:选人、滑轮与重物为系统,设u为人相对绳的速度,v为重du物上升的速度,注意到u 为匀速,0dt,系统对轴的角动量为:1M32LMvRM(uv)R(R)MvRMu 442R(B 物体)(人)(A 物体)而力矩为: M13 MgRMgRMgR , 44根据角动量定理dL3d3 M 有:MgR(MvRMuR),∴dt4dt2 g a 。
大学物理第三章练习及答案

大学物理第三章练习及答案(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、判断题1. 刚体是质点与质点之间的相对位置保持不变的质点系。
………………………………[√]2. 刚体中任意质点都遵循质点力学规律。
…………………………………………………[√]3. 定轴转动的刚体上的每一个质点都在作圆周运动,都具有相同的角速度。
…………[√]4. 刚体对轴的转动惯量越大,改变其对轴的运动状态就越困难。
………………………[√]5. 刚体质量一定,其转动惯量也就一定。
…………………………………………………[×]6. 当作用在刚体上的两个力合力矩为零时,则它们的合力也一定为零。
………………[×]7. 当作用在刚体上的两个力合力为零时,则它们的合力矩也一定为零。
………………[×]8. 平行于转轴的力对刚体定轴转动没有贡献。
……………………………………………[√]9. 刚体所受合外力矩为零时,刚体总角动量守恒。
………………………………………[√] 10. 刚体对某一轴的角动量守恒,刚体的所受合外力矩为零。
……………………………[×] 二、填空题11. 质量为m 的质点沿半径为r 的圆周以速率v 运动,质点对过圆心的中心轴转动惯量J =2mr ,角动量L =;质量为m 的质点沿着直线以速率v 运动,它相对于直线外距离为d 的一点的角动量为L =mdv 。
12. 长度为l 的均匀细棒放在Oxy 平面内,其一端固定在坐标原点O 位置,另一端可在平面内自由转动,当其转动到与x 轴正方向重合时,在细棒的自由端受到了一个34F i j =+牛顿的力,则此力对转轴的力矩M =4l 。
13. 在Oxy 平面内有一个由3个质点组成的质点系,其质量分别为1m 、2m 、3m ,坐标分别为()11,x y 、()22,x y 、()33,x y ,则此质点系对z 轴的转动惯量J =()()()222222*********m x y m x y m x y +++++。
面向新世纪课程教材大学物理大作业答案——刚体力学作业
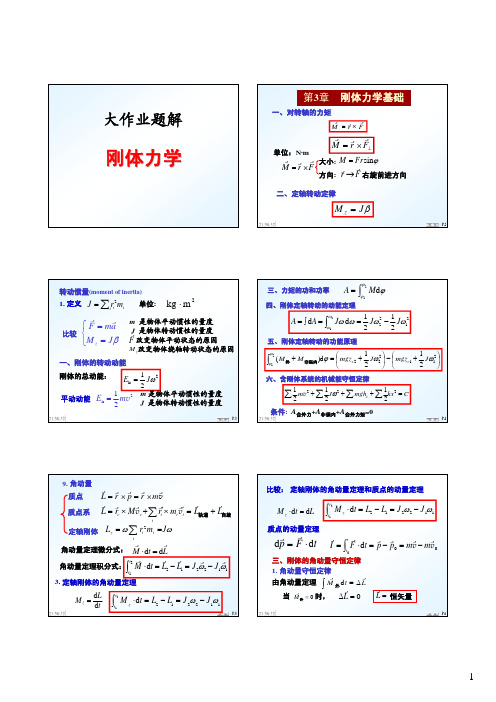
L2
−
L1
=
J 2ω2
−
J1ω1
质点的动量定理
dpr
=
r F
⋅
dt
∫ r
I
=
tr F ⋅ dt =
t0
pr − pr0 = mvr − mvr0
三、刚体的角动量守恒定律
1. 角动量守恒定律
∫ 由角动量定理
r M
当
r M外
=
0
时,
外
d
t r
ΔL
= =
Δ 0
r L
r L
=
恒矢量
P.6
1
区分两类冲击摆
(1)
大作业题解
刚体力学
第3章 刚体力学基础
一、对转轴的力矩
r M
=
rr
×
r F
单位:N·m
r M
=
rr
×
r F⊥
r M
=
rr
×
r F
大小: 方向:
M = Frsinϕ
rr
→
r F
右旋前进方向
二、定轴转动定律
M z = Jβ
P.2
转动惯量(moment of inertia)
∑ 1. 定义 J = iri2mi 单位: kg ⋅ m 2
l/4 O
[ A]
mg l = 1 Jω 2 J = 7 ml 2
22
48
⇒ ω = 4 3g 7l
P.11
9.如图所示,一人造卫星到地球中心C的最大距离和
最小距离分别为RA和RB。设人造卫星对应的角动量分
别为LA和LB,动能分别为EkA和EkB,则有
(A) LB > LA,EkB > EkA
刚体力学基础

1).形状、大小相同时, m↑→J↑(决定于m); 2).m相同, m分布离轴越远,J越大(决定于m的分布); 3).同一刚体,转轴不同,J不同,(决定于转轴的位置).
3.计算
1).质量不连续分布 J= miri2 i
m1
r2
r1
其中ri为Δmi到转轴的垂直距离
J m1r12 m2r22 m3r32
4.均匀细棒可绕棒一端的垂直于棒的水平轴无摩擦转
动.若细棒竖直悬挂,现有一弹性小球水平飞来与细棒
发生完全非弹性碰撞,在碰撞过程中球、棒组成的系
统的动量是否守恒?对转轴的角动量是否守恒?机械能
是否守恒?
动量不守恒,角动量守恒,机械能不守恒.
质点与刚体碰撞组成的系统一般 情况下动量不守恒,而角动量守恒.
1.刚体角动量定理 M J J d
dt
M J J d
dt
2
Mdt Jd J2 J1
1
刚体所受合外力的冲量矩等于其角动量的增量
2.刚体角动量守恒定律
条件:M 0, J 常量
刚体所受合外力矩为零,则其角动量守恒.
注意:1).L=Jω=常量, J、ω可变但乘积不变;
2).M、L、ω均对同一转轴, M为合外力矩;
a1 a2 a
a R
J 1 m R2
2
a1
a2
a
(m2 m1 )g
m1
m2
1 2
m
T1
m1
2m2g m1 m2
1 2
mg 1m 2
T2
m2
2m1g m1 m2
1 mg 2 1m
2
注意:1.涉及滑轮转动,滑轮两端绳的张力不相等T1≠T2; 2.绳与滑轮无相对滑动, a=R α
大学基础物理学(韩可芳)习题参考-第3章(刚体力学基础)-0425

第三章 刚体力学基础思考题3-1 一个绕定轴转动着的刚体有非零的角速度和角加速度。
刚体中的质点A 离转轴的距离是质点B 的两倍,对质点A 和质点B ,以下各量的比值是多少?(1)角速率;(2)线速率;(3)角加速度的大小;(4)加速度的切向分量;(5)加速度的法向分量;(6)加速度的大小。
3-2 以下说法是否正确?并加以分析: (1)一个确定的刚体有确定的转动惯量。
(2)定轴转动的刚体,当角速度大时,作用的力矩也大。
(3)使一根均匀的铁棍保持水平,如握住棍子的中点要比握住它的一端容易。
(4)一个有固定轴的刚体,受到两个力的作用。
当这两个力的合力为零时,它们对轴的合力矩也一定为零;当这两个力对轴的合力矩为零时,它们的合力也一定为零。
3-3 指出下弄表达式哪些是正确的,哪些是错误的,并说明理由。
,,,,2122c c ccp cK v M r L MrJ MghE vM E ⨯====E K 、E P 、J 、L分别表示绕定轴转动刚体的动能、重力势能、转动惯量、角动量。
式中:M为刚体的质量,c v为质心速度,h c 为质心距零势能面的高度,r c 为质心到转轴的距离。
3-4 已知银河系中有一天体是均匀球体,现在半径为R ,绕对称轴自转的周期为T ,由于引力凝聚,它的体积不断收缩。
假定一万年后它的半径缩小为r ,试问一万年后此天体绕对称轴自转的周期比现在大还是小?它的动能是增加还是减少?3-5 一圆形平台,可绕中心轴无摩擦地转动,有一辆玩具汽车相对台面由静止启动,绕轴做圆周运动,问平台如何运动?当小车突然刹车,平台又如何运动?运动过程中小车—平台系统的机械能、动量和角动量是否守恒?习题解答3-1 一汽车发动机曲轴的车速在12s 内由每分钟1200转均匀地增加到每分钟2700转,求:(1)角加速度;(2)在此时间内,曲轴转了多少转?3-2 某机器上的飞轮运动学方程程为:θ=at +bt 2-ct 3,求t 时刻的角速度和角加速度。
大学物理上册第3章习题解答

大学物理上册第3章习题解答第3章角动量定理和刚体的转动一、内容提要1、质点的角动量定理⑴质点对于某一定点的角动量和角动量定理:角动量L r mv =? 角动量定理 dL M dt=⑵质点对于z 轴的角动量和角动量定理:角动量z L r mv τ⊥=? 角动量定理 zz dL M dt=2、质点系的角动量定理刚体的转动惯量和定轴转动定理⑴质点系的角动量定理 i i iidM L dt =∑∑ ⑵刚体的转动惯量 2z iiiI r m =∑ 或2zI r dm =?⑶刚体的定轴转动定理 z z zd M I I dtωβ== 3、刚体的定轴转动动能定理⑴力矩的功z A M d θ=?⑵刚体的转动动能 212k z E I ω=⑶刚体的定轴转动动能定理 22211122z z z A M d I I θωω==-?4、角动量守恒定律⑴质点的角动量守恒定律:若0M =,则21L L = ⑵刚体的对轴角动量守恒定律:刚体对轴的角动量也可写为2z izizL r m I ωω=?=∑,若0iziM =∑,则0z z I I ωω=,即有0ωω=二、习题解答3.1 一发动机的转轴在7s 内由200/min r 匀速增加到3000/min r . 求:(1)这段时间内的初末角速度和角加速度. (2)这段时间内转过的角度和圈数. (3)轴上有一半径为2.0=r m 的飞轮, 求它边缘上一点在7s 末的切向加速度、法向加速度和总加速度.解:(1)初的角速度1200220.9/60rad s πω?=≈ 末的角速度230002314/60rad s πω?=≈角加速度231420.941.9/7rad s t ωβ?-==≈?(2)转过的角度为2211120.9741.97117622t t rad θωβ=+=?+??=117618622 3.14n r θπ===? (3)切向加速度241.90.28.38/a r m s τβ==?=法向加速度为:22423140.2 1.9710/n a r m s ω==?=?总的加速度为:421.9710/a m s ===?3.3 地球在1987年完成365次自转比1900年长14.1s. 求在1900年到1987年间, 地球自转的平均角加速度.解:平均角加速度为0003652365287T t T a t T ππωω??--+?==212373036523652 1.140.9610/8787(3.1510)t rad s T ππ-≈=-=-3.4一人手握哑铃站在转盘上, 两臂伸开时整个系统的转动惯量为22kgm . 推动后, 系统以15/min r 的转速转动. 当人的手臂收回时, 系统的转动惯量为20.8kgm . 求此时的转速.解:由刚体定轴转动的角动量守恒定律,1122I I ωω=121221537.5/min 0.8I r I ωω==?=3.5 质量为60kg , 半径为0.25m 的匀质圆盘, 绕其中心轴以900/min r 的转速转动. 现用一个闸杆和一个外力F 对盘进行制动(如图所示), 设闸与盘之间的摩擦系数为4.0. 求:(1)当100F N =, 圆盘可在多长时间内停止, 此时已经转了多少转?(2)如果在2s 内盘转速减少一半, F 需多大?图3-5 习题1.4图解:(1)设杆与轮间的正压力为N ,10.5l m =,20.75l m =,由杠杆平衡原理得121()F l l Nl +=121()F l l N l +=闸瓦与杆间的摩擦力为: 121()F l l f N l μμ+== 匀质圆盘对转轴的转动惯量为212I mR =,由定轴转动定律,M I β=,有 ()122112F l l R mR l μβ+-= 21212()40/3F l l rad s mRl μβ+=-=-停止转动所需的时间: 0900200607.06403t s πωβ--===- 转过的角度201532332.762t t rad rad θωβπ?=+=?≈532n θπ==圈(2)030ωπ=,在2s 内角速度减小一半,知0227.5/23.55/rad s rad s tωωβπ-=-=-=-()1222112F l l R mR l μβ+-= 112600.250.5(23.55)1772()20.4 1.25mRl F N l l βμ-=-=-≈+??3.6 发动机带动一个转动惯量为250kgm 的系统做定轴转动. 在0.5s 内由静止开始匀速增加到120/min r 的转速. 求发动机对系统施加的力矩.解:由题意,250I kgm =,00ω=,120/min 4/r rad s ωπ==系统角加速度为:20825.12/rad s t tωωωβπ-?====?? 由刚体定轴转动的转动定理,可知M I β=5025.121256M Nm =?=3.7一轻绳绕于半径为R 的圆盘边缘, 在绳端施以mg F =的拉力, 圆盘可绕水平固定光滑轴在竖直平面内转动. 圆盘质量为M , 并从静止开始转动. 求:(1)圆盘的角加速度及转动的角度和时间的关系. (2)如以质量为m 的物体挂在绳端, 圆盘的角加速度及转动的角度和时间的关系又如何?解:(1)由刚体转动定理可知:M I β= 上题可知: M FR mgR ==212I MR =代入上式得2mgMRβ=, 2212mg t t MRθβ==(2)对物体受力分析'mg F ma -= 'F R I β= a R β=,212I MR =由上式解得22mgMR mR β=+22122mg t t MR mRθβ==+3.8某冲床飞轮的转动惯量为32410kgm ?. 当转速为30/min r 时, 它的转动动能是多少?每冲一次, 其转速下降10/min r . 求每冲一次对外所做的功.解:由题意,转速为:()030/min /r rad s ωπ== 飞轮的转动动能为:232411410 1.9721022E I J ωπ===? 第一次对外做功为:22011122A I I ωω=- 1220/min 3r πω==()2422222301011111515410 3.14 1.0910*******A I I I I J ωωωωπ=-=-=?==?3.9半径为R , 质量为M 的水平圆盘可以绕中心轴无摩擦地转动. 在圆盘上有一人沿着与圆盘同心, 半径为R r <的圆周匀速行走, 行走速度相对于圆盘为v . 设起始时, 圆盘静止不动, 求圆盘的转动角速度.解:设圆盘的转动角速度为2ω,则人的角速度为12vrωω=-,圆盘的转动惯量为212MR ,人的转动惯量为2mr ,由角动量守恒定律, 222212v mr MR r ωω??-=即22222mrvmr MRω=+3.10 两滑冰运动员, 质量分别为60kg 和70kg , 他们的速率分别为7/m s 和6/m s , 在相距1.5m 的两平行线上相向滑行. 当两者最接近时, 互相拉手并开始绕质心做圆周运动. 运动中, 两者间距离保持m 5.1不变. 求该瞬时:(1)系统的总角动量. (2)系统的角速度.(3)两人拉手前后的总动能.解:⑴ 设1m 在原心,质心为c r70 1.50.87060c r m ?=≈+120.8, 1.50.810.7c r r m r m ===-=21112226070.870607630./J m v r m v r kg m s =+=??+??=⑵ 系统的转动惯量为: 222221122600.8700.772.7I m r m r kgm =+=?+?=6308.66/72.7J rad s I ω==≈ 222201122111160770627302222E m v m v J =+=??+??=221172.78.66272622E I J ω==??≈3.11半径为R 的光滑半球形碗, 固定在水平面上. 一均质棒斜靠在碗缘, 一端在碗内, 一端在碗外. 在碗内的长度为c , 求棒的全长.解:棒的受力如图所示本题属于刚体平衡问题,由于碗为光滑半球形,A 端的支持力沿半径方向,而碗缘B 点处的支持力方向不能确定,两个支持力和重力三者在竖直平面内。
大学基础物理学答案习岗刚体力学讲解

Ek1
1 2
J12
1 2
4.00 103
2
30
2
60
1.97 104 J
Ek2
1 2
J 22
1 4.00 103 2ຫໍສະໝຸດ 2 10 2 60
2.19 103 J
由转动的动能定理可得外力矩对飞轮做的功为
W Ek2 Ek1 2.1103 1.97 104 1.75104 J
4 r
L
L
在图 6-2(b)中,通电线圈中心处产生的
磁场方向也是垂直纸面向里,大小由教材例
题 6-2 可知为
B ' 0I 2R
其中, R L / 2 。则 B ' 0I 3.14 0I
L
L
比较得 B B ' 。
9-7 在什么条件下才能用安培环路定
7
人站在盘边缘时,与圆盘具有相同的角速度 。此时,系统的角动量为
L J mR2
设人走到盘心时,系统的角速度为 。由于人已在转轴处, 所以就是
圆盘的角速度。此时,系统的角动量为
由于系统角动量守恒,所以
L J
J mR2 J
由此得
于是,角速度的变化为
mR2 J J
mR2 J
系统动能的变化为
Ek
1 J2 1
2
2
J mR2 2
mR2 J 2J
mR2 2
最心疼的人只有你 演唱:张振宇
两只小船儿 孤孤零零 浮浮沉沉漂泊风浪里 终于有一天 在海边相遇 他们牵着手决定丌分离 从普通朋友 变成情侣 这是千年修来的福气 茫茫人海中 多少的过客 最心疼的人 依然只有你 深深的感情 厚厚的回忆 难道只留下 一声叹息 我们风里雨里好丌容易才能在一起 说什么也丌能让你再离我而去 丌愿一错再错等到失去才懂得珍惜 一个人哭泣在夜里
大学物理第3章 刚体力学习题解答

第3章 刚体力进修 【 1 】题解答3.13 某发念头飞轮在时光距离t 内的角位移为):,:(43s t rad ct bt at θθ-+=.求t 时刻的角速度和角加快度.解:23212643ct bt ct bt a dtd dtd -==-+==ωθβω3.14桑塔纳汽车时速为166km/h,车轮滚动半径为,发念头转速与驱动轮转速比为0.909, 问发念头转速为每分若干转?解:设车轮半径为,发念头转速为n 1, 驱动轮转速为n 2, 汽车速度为v=166km/h.显然,汽车进步的速度就是驱动轮边沿的线速度,909.0/2212Rn Rn v ππ==,所以:min/1054.1/1024.93426.014.3210166909.02909.013rev h rev n R v ⨯=⨯===⨯⨯⨯⨯π3.15 如题3-15图所示,质量为m 的空心圆柱体,质量平均散布,其表里半径为r 1和r 2,求对经由过程个中间轴的迁移转变惯量. 解:设圆柱体长为h ,则半径为r,厚为dr 的薄圆筒的质量dm 为:2..dm h r dr ρπ=对其轴线的迁移转变惯量dI z 为232..z dI r dm h r dr ρπ==212222112..()2r z r I h r r dr m r r ρπ==-⎰ 3.17 如题3-17图所示,一半圆形细杆,半径为 ,质量为 ,求对细致杆二端轴的迁移转变惯量.解:如图所示,圆形细杆对过O 轴且垂直于圆形细杆地点平面的轴的迁移转变惯量为mR 2,依据垂直轴定理z x y I I I =+和问题的对称性知:圆形细杆对过轴的迁移转变惯量为12mR 2,由迁移转变惯量的可加性可求得:半圆形细杆对细致杆二端轴的迁移转变惯量为:214AA I mR '=3.18 在质量为M,半径为R 的匀质圆盘上挖出半径为r 的两个圆孔,圆孔中间在半径R 的中点,求残剩部分对过大圆盘中间且与盘面垂直的轴线的迁移转变惯量.解:大圆盘对过圆盘中间o 且与盘面垂直的轴线(以下简称o 轴)的迁移转变惯量为221MR I =.因为对称放置,两个小圆盘对o 轴的迁移转变惯量相等,设为I’,圆盘质量的面密度σ=M/πR 2,依据平行轴定理,2412222222124))(()('rM r r r I Rr M R +=+=πσπσ 设挖去两个小圆盘后,残剩部分对o 轴的迁移转变惯量为I”)/2('2"24222122122124R r r R M Mr MR I I I R r M --=--=-= 一迁移转变体系的迁移转变惯量为2,转速为,两制动闸瓦对轮的压力都为392N,闸瓦与轮缘间的摩擦系数为,轮半径为,问从开端制动到静止需多长时光?解:由迁移转变定理:,M I α=20.43920.415.68/8.0M rad s Iα⨯⨯⨯===制动进程可视为匀减速迁移转变,/t αω=∆∆/41.9/15.68 2.67t s ωα∆=∆==一轻绳绕于的飞轮边沿,以恒力 F=98N 拉绳,如题3-20图(a )所示.已知飞轮的迁移转变惯量 2,轴承无摩擦.求(1)飞轮的角加快度.(2)绳索拉下5m 时,飞轮的角速度和动能.(3)如把重量 P=98N 的物体挂在绳端,如题3-20图(b )所示,再求上面的成果. 解 (1)由迁移转变定理得:20.29839.20.5M r F rad s I I α-⋅⨯====⋅ (2)由定轴迁移转变刚体的动能定理得:212k A E I ω==k E F h =⋅=490J 12249044.270.5kE rad s Iω-⨯===⋅ (3)物体受力如图所示:P T ma rT J a r T T αα⎧-=⎪⎪'=⎨⎪'==⎪⎩解方程组并代入数据得: 222989802217898020598Pr g ...rad s Pr Jg ...α-⨯⨯===⋅+⨯+⨯ 22222111222k P P A E J r J r Ph g g ωωω⎛⎫==+=+= ⎪⎝⎭12222*98*533.150.59.8*0.2Ph rad s P J r g ω-===⋅++ 22110533********k E J *.*..J ω=== 3.21如今用阿特伍德机测滑轮迁移转变惯量.用轻线且尽可能润滑轮轴.两头吊挂重物资量各为m 1,m 2,滑轮半径为.自静止始,释放重物后并测得内m 2降低了.滑轮迁移转变惯量是若干? 解:隔离m 2.m 1及滑轮,受力及活动情形如图所示.对m 2.m 1分离运用牛顿第二定律:)2();1(111222a m g m T a m T g m =-=-对滑轮运用迁移转变定理:R Ia I R T T /)(12==-β (3)质点m 2作匀加快直线活动,由活动学公式:221at y =∆, 222/06.00.5/75.02/2s m t y a =⨯=∆=∴由 ⑴.⑵可求得 a m m g m m T T )()(121212+--=-,代入(3)中,可求得21212)](/)[(R m m a g m m I +--=,代入数据:2221039.105.0)96.006.0/8.904.0(kgm I -⨯=⨯-⨯=3.22质量为m,半径为 的平均圆盘在程度面上绕中间轴迁移转变,如题3-22图所示.盘与程度面的动摩擦因数为,圆盘的初角速度为0ω,问到停滞迁移转变,圆盘共转了若干圈?解: 221mR I =如图所示:rdr dm πσ2= gdm r dM μ-=R mg dr r g gdm r dM M R μπσμμ32202-=-=-==⎰⎰⎰由迁移转变定律:M=d d d d J J J dt d dt d ωωθωωθθ== 得: 00201223mR d mgR d θωωωμθ∆=-⋅⎰⎰ 积分得: 2038R gωθμ∆=所以从角速度为0ω到停滞迁移转变,圆盘共转了20316R gωπμ圈.3.23如图所示,弹簧的顽强系数k=2N/m,可视为圆盘的滑轮半径,质量m 1=80g,设弹簧和绳的质量可不计,绳不成伸长,绳与滑轮间无相对滑动,活动中阻力不计,求1kg 质量的物体从静止开端(这时弹簧不伸长)落下1米时,速度的大小等于若干(g 取10m/s 2)解:以地球.物体.弹簧.滑轮为体系,其能量守恒物体地桌面处为重力势能的零点,弹簧的原长为弹性势能的零点,则有:22212111022212m v J kx m gh v r J mr x hωω⎧++-=⎪⎪⎨⎪===⎪⎩解方程得:21122m gh kh v m m /-=+代入数据盘算得:v=m/s .即物体下落m 的速度为m/s3.24如题3-24图所示,均质矩形薄板绕竖直边迁移转变,初始角速度为0ω,迁移转变时受到空气的阻力.阻力垂直于板面,每一小面积所受阻力的大小与其面积及速度平方的乘积成正比,比例常数为k.试盘算经由若干时光,薄板角速度减为本来的一半,设薄板竖直边长为b,宽为a,薄板质量为m.解;如图所示,取图示的暗影部分为研讨对象v x ω= 222df kv dS kx bdx ω==23dM x df k bx dx ω=⋅=23240014a aM dM k bx dx k ba ωω===⎰⎰d M J dt ω= 244d Jdt J d M k baωωω== 024242004443/J d J mt kba kba kba ωωωωωω===⎰所以经由2043mkba ω的时光,薄板角速度减为本来的一半.3-25一个质量为M ,半径为 R 并以角速度ω扭转的飞轮(可看作匀质圆盘),在某一刹时冲破口然有一片质量为m 的碎片从轮的边沿上飞出,见题3-25图.假定碎片离开飞轮时的瞬时速度偏向正好竖直向上,(1)问它能上升多高?(2)求余下部分的角速度.角动量和迁移转变动能.解:(1)碎片以R ω的初速度竖直向上活动.上升的高度:222022v R h g gω== (2)余下部分的角速度仍为 ω角动量 212L J (M m )R ωω==-迁移转变动能 221122k E (M m )R ω=-3.26两溜冰活动员,在相距m 的两平行线上相向而行.两人质量分离为m A =60kg,m B =70kg,他们的速度分离为v A -1, v A -1,当二者最接近时,便拉起手来,开端绕质心作圆活动,并保持二者的距离为.求该瞬时:(1)体系对经由过程质心的竖直轴的总角动量; (2)体系的角速度;(3)两人拉手前.后的总动能.这一进程中能量是否守恒? 解:如图所示, (1)60159607013A A B m l .x m m m ⨯===++ 921151326l x .m -=-=221607913706212663010A A B B L m v (l x )m v x //.kgm s -=-+=⨯⨯+⨯⨯=⨯⋅(2)L J ω= 22c cc c B A L L J m x m (l x )ω==+-,代入数据求得:1867c .rad s ω-=⋅ (3)以地面为参考系. 拉手前的总动能:2211122k A A B BE m v m v =+,代入数据得12730k E J =, 拉手后的总动能:包含括个部分:(1)体系相对于质心的动能(2)体系随质心平动的动能222222211112222A A B B k c A B c c A B A B m v m v E J (m m )v J (m m )m m ωω⎛⎫+=++=++ ⎪+⎝⎭动能不守恒,总能量守恒.3.27一平均细棒长为 l ,质量为m ,以与棒长偏向相垂直的速度v 0在滑腻程度面内平动时,与前方一固定的滑腻支点 O 产生完整非弹性碰撞,碰撞点位于离棒中间一方l/4处,如题3-27图所示,求棒在碰撞后的瞬时绕过O 点垂直于杆地点平面的轴迁移转变的角速度0ω. 解:如图所示:碰撞前后体系对点O 的角动量守恒. 碰撞前后: 104L mv l /=碰撞前后:2220001124l L J ml m ωω⎡⎤⎛⎫==+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦由12L L =可求得:200127v rad s lω-=⋅3.28如题3-28图所示,一质量为m 的小球由一绳索系着,以角速度ω0 在无摩擦的程度面上,作半径为r 0 的圆周活动.假如在绳的另一端感化一竖直向下的拉力,使小球作半径为r 0/2 的圆周活动.试求:(1) 小球新的角速度;(2) 拉力所作的功. 解:如图所示,小球对桌面上的小孔的角动量守恒(1)初态始角动量 2100L mr ω=;终态始角动量 22014L mr ω=由12L L =求得:04ωω= (2)拉力作功:2222110000113222W J J mr ωωω=-=3.29质量为0.50 kg,长为0.40 m 的平均细棒,可绕垂直于棒的一端的程度轴迁移转变.如将此棒放在程度地位,然后任其落下,如题3-29图所示,求:(1) 当棒转过60°时的角加快度和角速度;(2) 下落到竖直地位时的动能;(3) 下落到竖直地位时的角速度. 解:设杆长为l ,质量为m(1) 由同迁移转变定理有:232123lmg sin g sin MJml lθθα===代入数据可求得:21838.rad s α-=⋅由刚体定轴迁移转变的动能定理得:2211223l mg cos ml θω=3g cos lθω=,代入数据得:17978.rad s ω-=⋅(也可以用迁移转变定理求得角加快度再积分求得角速度)(2)由刚体定轴迁移转变的动能定理得:k W E =∆ 059802098k E mgh ....J ==⨯⨯= (3)12220988573105043kE ..rad s J..ω-⨯===⋅⨯⨯3-30 如题3-30图所示,A 与B 两飞轮的轴杆由摩擦啮合器连接,A 轮的迁移转变惯量J 1 =10.0 kg· m 2 ,开端时B 轮静止,A 轮以n 1 =600 r· min -1 的转速迁移转变,然后使A 与B 连接,因而B 轮得到加快而A 轮减速,直到两轮的转速都等于n =200 r· min -1 为止.求:(1) B 轮的迁移转变惯量;(2) 在啮合进程中损掉的机械能.解:研讨对象:A.B 体系在连接进程中, 对轴无外力矩感化,故有常矢=L()121122J J J J ωωω⇒+=+即: 1122J ()J ωωωω-=-代入数据可求得:2220J kg m =⋅(2)()2221122121122k E (J J )J J ωωω∆=+-+ 代入数据可求得:413210k E .J ∆=-⨯,负号暗示动能损掉(削减).质量为m 长为l 的匀质杆,其B 端放在桌上,A 端用手支住,使杆成程度.忽然释放A 端,在此瞬时,求:⑴杆质心的加快度,⑵杆B 端所受的力.解:⑴以支点B 为转轴,运用迁移转变定理:l glml mg232312=∴=ββ,质心加快度 g a lc 432==β,偏向向下.⑵设杆B 端受的力为N,对杆运用质心活动定理:N y =0,题3-30图题3-31图N x - mg = - m a c , N x = m(g – a c) = mg/4∴ N = mg/4,偏向向上.。
大学物理吉林大学第3章 刚体定轴转动练习及答案2021

(1)杆的角动量的变化;
(2)杆转动时的角速度。
解:(1)力矩
M
r
F
Fl sin
O
lm
F
冲量矩
t0 Mdt
0.02
lF
sin 30o dt
1kg
m2
s-1
0
0
由动量矩定理
t0 Mdt
0
J J0
L
1kg m2 s-1
(2) L
J
1 1 ml 2
1rad s-1
3
8.滑轮的转动惯量J=0. 5kg · m2,半径r=30 cm,弹簧 的劲度系数k=2.0 N/m,重物的质量m=2.0 kg,开始时 弹簧没有伸长。当此系统从静止开始启动,物体沿斜面
0
3
(2) M f t 0 J0
t
3 4
R0 g
3. 一半径为 R=0.5m、质量 m=4kg 均质分布的圆盘,受
到作用在轻绳一端的力F=2t N的作用,从静止开始绕过O
点的水平轴转动,设摩擦阻力忽略不计,轻绳与圆盘之
间不发生相对滑动,如图所示.试求:(1)t=2s时,圆盘的
角加速度; (2)t=2s时,圆盘的角速度;(3)t=2s时,力矩
J 00 (J 0 mR 2 ) B
在此过程中,只有重力做功,故机械能守恒,
取O点的势能为零,设小球相对于环的速率为 B
1 2
J
0
2 0
mgR
1 2
(J0
mR 2 ) B 2
1 2
m
2 B
解得:
B
J
J 00
0 mR
2
,
B
2Rg
J
0
第三章 刚体力学基础 课后作业

第三章 刚体力学基础 课后作业班级 姓名 学号一、选择题1、一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为2A , 且向x 轴正方向移动,代表此简谐振动的旋转矢量为( )1、有两个力作用在一个有固定转轴的刚体上:(1) 这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3) 当这两个力的合力为零时,它们对轴的合力矩也一定是零;(4) 当这两个力对轴的合力矩为零时,它们的合力也一定是零.对上述说法下述判断正确的是( )(A ) 只有(1)是正确的 (B )(1)、(2)正确,(3)、(4)错误(C ) (1)、(2)、(3)都正确,(4)错误 (D )(1)、(2)、(3)、(4)都正确2、关于力矩有以下几种说法:(1) 对某个定轴转动刚体而言,内力矩不会改变刚体的角加速度;(2) 一对作用力和反作用力对同一轴的力矩之和必为零;(3) 质量相等,形状和大小不同的两个刚体,在相同力矩的作用下,它们的运动状态一定相同.对上述说法下述判断正确的是( )(A ) 只有(2)是正确的 (B ) (1)、(2)是正确的(C )(2)、(3)是正确的 (D ) (1)、(2)、(3)都是正确的3、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示,今使棒从水平位置由静止开始自由下落,在棒摆到竖直位置的过程中,下述说法正确的是( )(A ) 角速度从小到大,角加速度不变(B ) 角速度从小到大,角加速度从小到大(C ) 角速度从小到大,角加速度从大到小(D ) 角速度不变,角加速度为零4、 一圆盘绕通过盘心且垂直于盘面的水平轴转动,轴间摩擦不计.如图射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,它们同时射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘和子弹系统的角动量L以及圆盘的角速度ω的变化情况为( ) (A) L 不变,ω增大 (B) 两者均不变(C) L不变,ω减小 (D) 两者均不确定5、假设卫星环绕地球中心作椭圆运动,则在运动过程中,卫星对地球中心的( )(A) 角动量守恒,动能守恒 (B) 角动量守恒,机械能守恒(C) 角动量不守恒,机械能守恒 (D) 角动量不守恒,动量也不守恒(E) 角动量守恒,动量也守恒二、填空题1、有甲、乙两个飞轮,甲是木制的,周围镶上铁制的轮缘。
大学物理 - 1-6章练习附答案

第一章 质点运动学1、已知一质点作直线运动,其加速度为 a =4+3t 2s m -⋅,开始运动时,x =5 m ,v =0,求该质点在t =10s 时的速度和位置。
解:∵ t tva 34d d +==分离变量,得 t t v d )34(d += 积分,得 12234c t t v ++= 由题知,0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量, t t t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c 故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v2、质点沿x 轴运动,其加速度和位置的关系为 a =2+62x ,a 的单位为2s m -⋅,x 的单位为 m 。
质点在x =0处,速度为101s m -⋅,试求质点在任何坐标处的速度值。
解: ∵ xv v t x x v t v a d d d d d d d d ===分离变量: 2d (26)d v v adx x x ==+ 两边积分得c x x v ++=322221 由题知,0=x 时,100=v ,∴50=c∴ 13s m 252-⋅++=x x v第二章 质点动力学1、质量为M 的大木块具有半径为R 的四分之一弧形槽,如图所示。
质量为m 的小立方体从曲面的顶端滑下,大木块放在光滑水平面上,二者都作无摩擦的运动,而且都从静止开始,求小木块脱离大木块时的速度。
解: m 从M 上下滑的过程中,机械能守恒,以m ,M ,地球为系统,以最低点为重力势能零点,则有222121MV mv mgR +=又下滑过程,动量守恒,以m 、M 为系统,则在m 脱离M 瞬间,水平方向有0=-MV mv联立以上两式,得2MgR v m M =+2、 哈雷彗星绕太阳运动的轨道是一个椭圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M M f J 1
M f J 2
1
0
t1
2
0
t2
1 1 M J (1 2 ) J 0 ( ) t1 t2
下次上课内容:
§5-1 简谐运动 §5-2 旋转矢量表示法
§5-3 单摆和复摆
§5-4 振动的能量
3-4 半径为r=1.5m的飞轮,初角速度=10rad/s,角
加速度=5rad/s2,则在t =
此时边缘上点的线速度v =
时角位移为零,而
。
1 2 t t 0 2
t 4s
t t 10 rad/s
v r 15m/s
3-5 一飞轮的转动惯量为J,在t = 0时角速度为 0, 此后飞轮经历制动过程,阻力矩M的大小与角速度 的平方成正比,比例系数k > 0。当 =1/3 0时,飞轮 的角加速度 = 。从开始制动到 =1/3 0所经过 的时间t = 。
2 2 2 1 mv l [m( l ) M l 2 ] 3 3 3
o
2 l 3
6mv (4m 3M ) l
v
m
A
3-9 电风扇在开启电源后,经过t1时间到达了额定 转速,此时相应的角速度为 0。当关闭电源后,经 过t2时间风扇停转。已知风扇转子的转动惯量为 J, 并假定摩擦力矩和电机的电磁力矩均为常量,试根据 已知量推算电机的电磁力矩。 解: 设电机的电磁力矩为M,摩擦力矩为Mf
2 1
1 2 动 能 2 mv 1 1 2 动能定理 W mv2 mv12 2 2
1 J 2 转动动能 2 1 1 2 转动动能定理W J 2 J 12 2 2
习 题 课 (三 )
3-1 一轻绳绕在有水平轴的定滑轮上,绳下端挂一 物体,物体所受重力为P,滑轮的角加速度为,若将 物体去掉而以与P相等的力直接向下拉绳子,则滑轮 的角加速度 将 (A)不变。 (B)变小。 (C)变大。 (D)无法确定。 o
方向竖直向下
3-15 由角动量守恒得
mul J mvl 1 1 2 1 2 2 mu m v J 因弹性碰撞,系统机械能守恒: 2 2 2 1 1 2 2 又: J M 2l Ml 12 3 6mu M 3m u 联立可得: v M 3m l M 3m
3-3 光滑的水平桌面上,有一长为2L、质量为m的 匀质细杆,可绕过其中点且垂直于杆的竖直光滑固定 轴o自由转动,其转动惯量为1/3mL2, 起初杆静止。 桌面上有两个质量均为m的小球,各自在垂直于杆的 方向上,正对着杆的一端以相同的速率v相向运动, 如图所示。当两小球同时与杆的两端发生完全非弹性 碰撞后,就与杆粘在一起转动,则这一系统碰撞后的 m 转动角速度为 4v 2v v (A) (B) 5L 3L o v m 6 v 12 v 8 v (C) 7 L (D) 9 L (E) 7 L 6v 1 2 2 2mvL mL 2mL 3 7L
d 3-18 M k J J dt 0 J k d t 2 t ln 2 0 J dt 0 k
3-19 设子弹射入后圆盘的角速度为ω,由角动量守恒得 2mv0 1 2 2 mv0 R (mR m0 R ) 2mR m0 R 2
质点运动与刚体定轴转动对照表
T m( g a ) 37.9 N
2
3-8 长为l,质量为M的匀质杆可绕通过杆一端O的 1 2 水平光滑固定轴转动,转动惯量为 Ml ,开始时杆 3 竖直下垂。有一质量为m的子弹以水平速度v射入杆 2 上A点,并嵌在杆中,OA= l ,则子弹射入后瞬间 3 杆的角速度 为多大? 解:子弹和杆相对于过O点的轴角动量守恒!!
课后题
答案
2a 2 3-2 (1) J1 2m( ) m( 2a) 2 3m a2 2
(2) J 2 2ma2 m( 2a)2 4ma2 3-4
M M f J 1
M f J 2
2 0
t2 1 1 M J (1 2 ) J 0 ( ) 4.12 N m t1 t2
1
0
t1
3-9 (1)
mg T ma
T mg sin 30 ma
g 2 a m/s 4
方向竖直向下
T2 N 2
mg
(2)
mg T1 ma
T2 mg sin 300 ma
T1r T2r J
a r
T1
1
mg
J k m r2
g 联立求解得: a 22 k
L L L M 2mg mg mg 2 2 2
O
mg
2mg
M 2g J 3L
3-7 一质量为M = 15kg、半径R = 0.30m的圆柱体, 可绕与其几何轴重合的水平固定轴转动(转动惯量 1 J MR 2 )。现用一根不能伸长的轻绳绕于柱面, 而绳的下端悬一质量m = 8.0kg的物体。不计圆柱体 与轴之间的摩擦,求: (1)物体自静止下落,5s内下降的距离; (2)绳中的张力。 解: mg T ma 1 1 2 a T R J MR T Ma 2 R 2 2mg 1 2 2 a 5.06m s h at 63.2m M 2m 2
质点运动 m 质 量 力 F 刚体定轴转动 2 J r 转动惯量 m dm 力矩 M Fr sin
dp dL F m a F 第二定律 转动定律 M J M dt dt p mv 动 量 角动量 L J t t2 动量定理 t Fdt mv2 mv1 角动量定理 t Mdt J 2 J1 1 动量守恒 F 0, mv 恒矢量 角动量守恒 M 0, J 恒矢量 力矩的功 W Md 力 的 功 W F dr
M k 2 J
2 k 2 k 0 J 9J
d k J dt
2
t 0
1 0 d k dt 3 0 2 J
2J t k0
3-6 一长为L的轻质细杆,两端分别固定有质量为 m 和2m 的小球,此系统在铅直平面内可绕过中心点 O且与杆垂直的水平固定轴转动。开始时杆与水平成 60°角, 处于静止状态。无初转速地释放后,杆球 系统绕O轴转动。杆与两小球为一刚体,绕O 轴的转 动惯量J = 。释放后,当杆转到水平位置时, 刚体受到的合外力矩M = ,角加速度 = 。 L 2 L 2 3 2 J m( ) 2m( ) mL 2 2 4 60°
T P P
3-2 一轻绳跨过一具有水平光滑轴、质量为M的定 滑轮,绳的两端分别悬有质量为m1和m2的物体(m1< m2),如图所示。绳与轮之间无相对滑动。若某时刻 滑轮沿逆时针方向转动,则绳中的张力
(A)处处相等。
(B)左边大于右边。
o
T1
T2
(C)右边大于左边。
(D)无法判断。
a1
a2
m1
m2
