Matlab8个例子
matlab for循环例子

matlab for循环例子MATLAB 是一种高级语言和交互式环境,广泛应用于科学、工程、金融和其他行业。
其中 for 循环是 MATLAB 中的一种基本结构,它可用于重复执行一段代码,以达到某种特定的目的。
这里我们将介绍几个 for 循环的例子,供大家参考。
1. 从 1 到 10 输出所有偶数下面是一个使用 for 循环实现的输出所有偶数的程序:```matlabfor i = 1:10if mod(i,2)==0disp(i)endend```首先,我们将 i 初始化为 1,所以循环的第一次迭代将 i 设为 1。
然后计算 i 是否为偶数,如果是则输出,否则进入下一次迭代,将 i 递增。
这样就可以输出所有从 1到 10 的偶数了。
2. 计算一组数据的平均值程序首先定义了一个包含一组数据的向量 data,然后将 total 初始化为 0。
接下来,用 length(data) 函数获取数据长度 N,然后将 for 循环的索引 i 初始化为 1,循环次数为 N。
循环中,每次将 data(i) 加到 total 上,并递增 i,最后计算平均值并输出。
```matlabA = [1 2 3; 4 5 6; 7 8 9];[m,n] = size(A);average = zeros(m,1);for i = 1:mfor j=1:naverage(i) = average(i) + A(i,j);endaverage(i) = average(i)/n;enddisp(average)```程序首先定义一个 3x3 的矩阵 A,然后用 size(A) 函数获取其大小,分别赋值给 m 和 n。
接下来,定义一个 m 行 1 列的零向量 average,用两个循环分别取出 A 矩阵每一行的值,并将它们相加。
最后,将平均值赋值给 average 向量,并输出。
4. 斐波那契数列```matlabn = 10;fibonacci = zeros(n,1);fibonacci(1) = 0;fibonacci(2) = 1;for i = 3:nfibonacci(i) = fibonacci(i-1) + fibonacci(i-2);enddisp(fibonacci')```程序首先定义了一个变量 n,表示斐波那契数列的项数。
matlab中uint8函数用法

matlab中uint8函数用法
在MATLAB中,uint8函数是一种数据类型转换函数,它将输入的数据转换为8位无符号整数类型。
该函数的语法如下:
uint8(X)
其中,X表示要转换的数据,可以是一个数值、向量、矩阵或多维数组。
uint8函数将X中的每个元素转换为8位无符号整数类型,并返回一个与X相同大小的数组。
下面是一些使用uint8函数的示例:
1. 将一个double类型的数值转换为8位无符号整数类型:
```
x = 123.456;
y = uint8(x);
```
2. 将一个矩阵中的所有元素转换为8位无符号整数类型:
```
A = [1.2, 3.4; 5.6, 7.8];
B = uint8(A);
```
3. 将一个RGB图像转换为8位无符号整数类型:
```
img = imread('test.jpg');
img_uint8 = uint8(img);
```
在这个例子中,imread函数用于读取一张RGB图像,然后将其转换为8位无符号整数类型。
需要注意的是,uint8函数会将输入数据中的小数部分直接截断,因此可能会导致精度丢失。
此外,如果输入数据中存在负数,uint8函数会将其转换为0。
总之,uint8函数是MATLAB中常用的数据类型转换函数之一,它可以将不同类型的数据转换为8位无符号整数类型,方便进行后续的计算和处理。
matlab数学建模100例

matlab数学建模100例Matlab是一种强大的数学建模工具,广泛应用于科学研究、工程设计和数据分析等领域。
在这篇文章中,我们将介绍100个使用Matlab进行数学建模的例子,帮助读者更好地理解和应用这个工具。
1. 线性回归模型:使用Matlab拟合一组数据点,得到最佳拟合直线。
2. 多项式拟合:使用Matlab拟合一组数据点,得到最佳拟合多项式。
3. 非线性回归模型:使用Matlab拟合一组数据点,得到最佳拟合曲线。
4. 插值模型:使用Matlab根据已知数据点,估计未知数据点的值。
5. 数值积分:使用Matlab计算函数的定积分。
6. 微分方程求解:使用Matlab求解常微分方程。
7. 矩阵运算:使用Matlab进行矩阵的加减乘除运算。
8. 线性规划:使用Matlab求解线性规划问题。
9. 非线性规划:使用Matlab求解非线性规划问题。
10. 整数规划:使用Matlab求解整数规划问题。
11. 图论问题:使用Matlab解决图论问题,如最短路径、最小生成树等。
12. 网络流问题:使用Matlab解决网络流问题,如最大流、最小费用流等。
13. 动态规划:使用Matlab解决动态规划问题。
14. 遗传算法:使用Matlab实现遗传算法,求解优化问题。
15. 神经网络:使用Matlab实现神经网络,进行模式识别和预测等任务。
16. 支持向量机:使用Matlab实现支持向量机,进行分类和回归等任务。
17. 聚类分析:使用Matlab进行聚类分析,将数据点分成不同的类别。
18. 主成分分析:使用Matlab进行主成分分析,降低数据的维度。
19. 时间序列分析:使用Matlab进行时间序列分析,预测未来的趋势。
20. 图像处理:使用Matlab对图像进行处理,如滤波、边缘检测等。
21. 信号处理:使用Matlab对信号进行处理,如滤波、频谱分析等。
22. 控制系统设计:使用Matlab设计控制系统,如PID控制器等。
matlab化学计算例子

matlab化学计算例子一、化学计算在MATLAB中的应用MATLAB是一种功能强大的数值计算软件,广泛应用于各个领域,包括化学。
化学计算是指利用数学方法和计算机技术来解决化学问题,如计算化学反应的速率常数、热力学性质、电子结构等等。
下面将介绍一些在MATLAB中常见的化学计算例子。
1. 化学反应速率常数的计算:在化学反应动力学中,化学反应速率常数是描述化学反应速率的重要参数。
利用MATLAB可以通过拟合实验数据来计算化学反应速率常数,从而得到反应动力学模型。
2. 热力学性质的计算:热力学性质是描述物质热学行为的参数,如热容、焓、熵等。
利用MATLAB可以计算物质的热力学性质,比如通过拟合实验数据来计算热容和焓值。
3. 分子轨迹模拟:分子轨迹模拟是研究分子运动的重要方法。
利用MATLAB可以进行分子轨迹模拟,通过求解分子的运动方程来模拟分子的运动轨迹。
4. 电子结构计算:电子结构是描述分子和固体中电子分布的重要参数。
利用MATLAB可以进行电子结构计算,如利用密度泛函理论计算分子的电子结构。
5. 化学反应动力学模拟:化学反应动力学是研究化学反应速率和机理的重要方法。
利用MATLAB可以进行化学反应动力学模拟,通过求解反应动力学方程来模拟化学反应的速率。
6. 化学平衡计算:化学平衡是研究化学反应在一定条件下达到平衡的重要方法。
利用MATLAB可以进行化学平衡计算,如利用平衡常数和反应方程来计算平衡浓度和平衡常数。
7. 化学反应机理优化:化学反应机理是描述化学反应过程的详细步骤和反应物之间的相互作用的模型。
利用MATLAB可以进行化学反应机理优化,通过对反应机理参数的拟合和优化来得到最佳的反应机理模型。
8. 化学反应路径分析:化学反应路径是描述化学反应过程中各个中间体和过渡态的生成和消失关系的模型。
利用MATLAB可以进行化学反应路径分析,通过求解反应路径方程来分析化学反应过程中不同反应路径的贡献。
matlab

45.产生极坐标图象的命令为:polar ( theta, r)。此命令用法类似于plot,很多plot 可用的选项polar 同样可用。
46.plot 的很多选项在loglog 中也可以使用。我们还有另外两个选择可用,第一个是semilogx(x, y),它产生的图象x 轴使用对数值,y 轴仍然用直接值;相应地,semilogy(x, y)产生的图象y 轴使用对数值,x 使用直接值。
40.fplot和plot的区别:fplot 函数绕过选择用来绘图的时间间隔,而自动为我们决定绘图的点数。一般地,fplot 为你产生尽可能精确的的图象,同时它也帮助我们绕过像这样的错误。调用fplot 的形式如 fplot('function string', [xstart, xend]) 。
y)完全一样。要产生堆合柱状图,我们写成bar(x, y, 'stacked')。
59.在等号“=”前面加上否定号“~”表示“不相等”,if sizex(2) ~= sizeN(2)。
60.使用disp命令在屏幕上打印出错误信息。disp('错误:数据必须具有相同的维数。')
61.求中位数:>> md = median(A);
42.添加图例:专业的图象总是附有图例,告诉读者某个曲线是什么。legend('sinh(x)','cosh(x)')
43.令如何设置绘图范围。可以通过调用axis 命令:axis ( [xmin xmax ymin ymax] )
44.子图即是在一个图上显示多于一个图象。绘制子图使用命令subplot(m, n, p),这里m 和n 告诉MATLAB 产生的产生的子图有m 行和n 列,p 用来告诉MATLAB 我们所要贴上去的某个已经绘制的图形窗口。
matlab解决小问题例子和代码

MATLAB是一种用于数学计算、数据可视化和编程的高级技术计算语言和交互式环境。
它是许多工程和科学领域中的首选工具之一,能够帮助用户快速解决各种小问题。
本文将通过例子和代码,介绍MATLAB是如何解决小问题的。
1. 读取和绘制数据假设我们有一组实验数据,保存在一个名为"data.csv"的文件中。
我们可以使用MATLAB的csvread函数读取数据,然后使用plot函数绘制图形,如下所示:```matlabdata = csvread('data.csv'); % 读取数据plot(data(:,1), data(:,2)); % 绘制数据xlabel('x轴'); % 添加x轴标签ylabel('y轴'); % 添加y轴标签title('数据可视化'); % 添加标题```2. 拟合曲线现在我们想对这组数据进行曲线拟合,以便更好地理解数据的特征。
我们可以使用MATLAB的polyfit函数来进行多项式拟合,然后使用polyval函数绘制拟合曲线,如下所示:```matlabp = polyfit(data(:,1), data(:,2), 2); % 二次多项式拟合y_fit = polyval(p, data(:,1)); % 计算拟合曲线的值plot(data(:,1), data(:,2)); % 绘制原始数据hold on;plot(data(:,1), y_fit, 'r--'); % 绘制拟合曲线xlabel('x轴'); % 添加x轴标签ylabel('y轴'); % 添加y轴标签title('数据拟合'); % 添加标题legend('原始数据', '拟合曲线'); % 添加图例```3. 解方程假设我们需要解一个简单的方程,例如x^2-5x+6=0。
matlab典型例子(吐血整理)
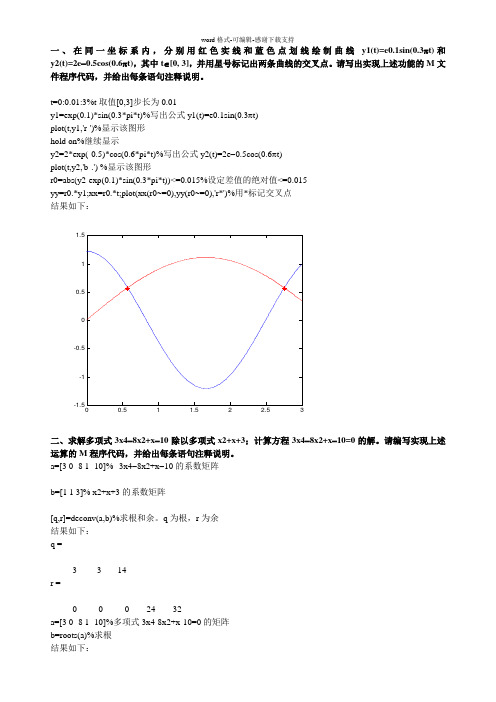
一、在同一坐标系内,分别用红色实线和蓝色点划线绘制曲线y1(t)=e0.1sin(0.3πt)和y2(t)=2e -0.5cos(0.6πt),其中t ∈[0, 3],并用星号标记出两条曲线的交叉点。
请写出实现上述功能的M 文件程序代码,并给出每条语句注释说明。
t=0:0.01:3%t 取值[0,3]步长为0.01y1=exp(0.1)*sin(0.3*pi*t)%写出公式y1(t)=e0.1sin(0.3πt) plot(t,y1,'r-')%显示该图形 hold on%继续显示y2=2*exp(-0.5)*cos(0.6*pi*t)%写出公式y2(t)=2e -0.5cos(0.6πt) plot(t,y2,'b-.') %显示该图形r0=abs(y2-exp(0.1)*sin(0.3*pi*t))<=0.015%设定差值的绝对值<=0.015 yy=r0.*y1;xx=r0.*t;plot(xx(r0~=0),yy(r0~=0),'r*')%用*标记交叉点 结果如下:-1.5-1-0.50.511.5二、求解多项式3x4-8x2+x -10除以多项式x2+x+3;计算方程3x4-8x2+x -10=0的解。
请编写实现上述运算的M 程序代码,并给出每条语句注释说明。
a=[3 0 -8 1 -10]%3x4-8x2+x -10的系数矩阵b=[1 1 3]% x2+x+3的系数矩阵[q,r]=deconv(a,b)%求根和余。
q 为根,r 为余 结果如下: q =3 -3 -14 r =0 0 0 24 32a=[3 0 -8 1 -10]%多项式3x4-8x2+x-10=0的矩阵 b=roots(a)%求根 结果如下:b =-1.9319 1.8581 0.0369 + 0.9629i 0.0369 - 0.9629i三、编写M 文件,计算下题:取自变量x 的区间为[-6,6],数据间隔为0.01,有函数y=sin(x)+0.5, z=f(x,y)=3sin(x)-y/10,绘制三维曲线图z 。
matlab对变量运算

在MATLAB 中,你可以执行各种数学运算来操作变量。
以下是一些常见的例子:1. 加法:你可以使用"+" 符号来执行加法运算。
例如,如果你有两个变量a 和b,你可以通过"a + b" 来计算它们的和。
2. 减法:你可以使用"-" 符号来执行减法运算。
例如,"a - b" 将返回a 和b 的差。
3. 乘法:你可以使用"*" 符号来执行乘法运算。
例如,"a * b" 将返回a 和b 的乘积。
4. 除法:你可以使用"/" 符号来执行除法运算。
例如,"a / b" 将返回a 除以b 的结果。
5. 指数运算:你可以使用"^" 符号来执行指数运算。
例如,"a ^ 2" 将返回a 的平方。
6. 开方运算:你可以使用"sqrt" 函数来执行开方运算。
例如,"sqrt(a)" 将返回a 的平方根。
7. 对数运算:你可以使用"log" 或"ln" 函数来执行对数运算。
例如,"log(a)" 将返回以e 为底的对数,而"ln(a)" 将返回以自然对数e 为底的对数。
8. 正弦、余弦和正切运算:你可以使用"sin"、"cos" 和"tan" 函数来执行这些运算。
例如,"sin(a)" 将返回 a 的正弦值,其中 a 是以弧度计的角度。
9. 其他三角函数:你可以使用"asin"、"acos" 和"atan" 函数来计算反正弦、反余弦和反正切值。
10. 绝对值:你可以使用"|" 符号来获取一个数的绝对值,或者使用"abs" 函数。
matlab编程例题

matlab编程例题Matlab是一种高级的计算机编程语言和数学计算软件。
它具有强大的数据处理和可视化功能,可以用于各种科学计算、数据分析、模拟和建模等领域。
本文将介绍一些常见的Matlab编程例题,帮助初学者掌握Matlab的基本编程技能。
1. 矩阵运算矩阵是Matlab中最基本的数据类型之一,可以进行各种数学运算。
下面是一些矩阵运算的例子:a = [1 2 3; 4 5 6; 7 8 9]; %定义一个3×3的矩阵b = [10 20 30; 40 50 60; 70 80 90]; %定义另一个3×3的矩阵c = a + b; %矩阵加法d = a - b; %矩阵减法e = a * b; %矩阵乘法f = a' %矩阵转置运行上面的代码,可以得到以下结果:c =11 22 3344 55 6677 88 99d =-9 -18 -27-36 -45 -54-63 -72 -81e =300 360 420660 810 9601020 1260 1500f =1 4 72 5 83 6 92. 绘图Matlab具有强大的绘图功能,可以绘制各种二维和三维图形。
下面是一些绘图的例子:x = linspace(0, 2*pi, 100); %生成一个包含100个点的等间隔向量y = sin(x); %计算sin函数plot(x, y); %绘制sin函数图像z = peaks(25); %生成一个25×25的山峰矩阵surf(z); %绘制3D山峰图像运行上面的代码,可以得到以下结果:sin函数图像:3D山峰图像:3. 文件读写Matlab可以读写各种文件格式,包括文本文件、Excel文件、图像文件等。
下面是一些文件读写的例子:fid = fopen('data.txt', 'r'); %打开名为“data.txt”的文本文件data = fscanf(fid, '%f'); %读取文件中的数据fclose(fid); %关闭文件plot(data); %绘制数据图像A = xlsread('data.xlsx'); %读取名为“data.xlsx”的Excel 文件plot(A(:, 1), A(:, 2)); %绘制Excel文件中的数据图像运行上面的代码,可以得到以下结果:文本文件数据图像:Excel文件数据图像:4. 函数编写Matlab中的函数是一种可重复使用的代码块,可以让程序更加模块化和可读性更高。
matlab基本用法

matlab基本用法MATLAB基本用法1. 创建变量和赋值•使用等号(=)可以将值赋给变量,例如:x = 5•变量名可以是字母、数字和下划线的任意组合,但必须以字母开头2. 数组和矩阵操作•MATLAB中的数组和矩阵可以使用方括号([])进行定义,例如:A = [1, 2, 3]•使用冒号(:)可以生成等差数列,例如:x = 1:3生成数组[1, 2, 3]•通过索引可以访问数组和矩阵中的元素,索引从1开始,例如:A(1)访问矩阵A中的第一个元素3. 矩阵运算•MATLAB提供了各种矩阵运算的函数,例如矩阵相乘A * B、矩阵转置A'等•使用.运算符可以对矩阵中的每个元素进行逐元素操作,例如矩阵各元素相加:A + B4. 函数和脚本文件•使用function关键字可以定义函数,例如:function y = myFunction(x)y = x^2;end•使用.m扩展名保存函数或脚本文件,例如``•通过运行脚本文件或函数名来执行代码,例如:myScript或myFunction(4)5. 控制流程•使用if-elseif-else结构可以进行条件判断,例如:if x > 0disp('x is positive');elseif x < 0disp('x is negative');elsedisp('x is zero');end•使用for循环可以重复执行一段代码,例如:for i = 1:5disp(i);end•使用while循环可以在满足条件时重复执行代码块,例如:while x > 0disp(x);x = x - 1;end6. 图形绘制•使用plot函数可以绘制二维曲线图,例如:x = 0::10;y = sin(x);plot(x, y);•使用scatter函数可以绘制散点图,例如:x = [1, 2, 3, 4];y = [2, 4, 1, 3];scatter(x, y);•使用imshow函数可以展示图像,例如:image = imread('');imshow(image);以上是MATLAB基本用法的一些例子和详细讲解。
matlab数据处理例子

matlab数据处理例子一、数据导入和处理1.读取Excel文件数据:使用MATLAB的xlsread函数可以读取Excel文件中的数据。
例如,可以使用以下代码读取名为“data.xlsx”的Excel文件中的第一个工作表中的所有数据:data = xlsread('data.xlsx');2.导入CSV文件数据:使用MATLAB的csvread函数可以读取CSV文件中的数据。
例如,可以使用以下代码读取名为“data.csv”的CSV文件中的所有数据:data = csvread('data.csv');3.数据清洗:在处理大量数据时,往往需要对数据进行清洗。
可以使用MATLAB提供的一些函数对数据进行清洗,例如去除重复数据、去除空值等。
例如,可以使用以下代码去除数据中的重复项:data = unique(data,'rows');4.数据筛选:在处理数据时,往往需要根据特定的条件筛选出符合要求的数据。
可以使用MATLAB提供的一些函数对数据进行筛选,例如根据某一列数据的大小筛选数据。
例如,可以使用以下代码筛选出第一列数据大于10的所有数据:data = data(data(:,1)>10,:);5.数据转换:在处理数据时,往往需要将数据转换成特定的格式。
可以使用MATLAB提供的一些函数对数据进行转换,例如将字符串转换成数值型数据。
例如,可以使用以下代码将第一列数据转换成字符串类型:data(:,1) = num2str(data(:,1));二、数据可视化1.散点图:散点图是一种常用的数据可视化方式,可以帮助我们快速了解数据的分布情况。
可以使用MATLAB的scatter函数绘制散点图。
例如,可以使用以下代码绘制以第一列数据为横坐标、第二列数据为纵坐标的散点图:scatter(data(:,1),data(:,2));2.折线图:折线图可以显示数据随时间或其他变量的变化趋势。
matlab 程序例子

例5-1 在0≤x≤2π区间内,绘制曲线 y=2e -0.5x cos(4πx) 程序如下: x=0:pi/100:2*pi;y=2*exp(-0.5*x).*cos(4*pi*x); plot(x,y)例5-2 绘制曲线 。
程序如下: t=0:0.1:2*pi; x=t.*sin(3*t); y=t.*sin(t).*sin(t); plot(x,y);例5-3 分析下列程序绘制的曲线。
x1=linspace(0,2*pi,100); x2=linspace(0,3*pi,100); x3=linspace(0,4*pi,100); y1=sin(x1); y2=1+sin(x2); y3=2+sin(x3); x=[x1;x2;x3]'; y=[y1;y2;y3]'; plot(x,y,x1,y1-1)例5-4 用不同标度在同一坐标内绘制曲线y1=0.2e -0.5x cos(4πx) 和y2=2e -0.5x cos(πx)。
程序如下: x=0:pi/100:2*pi;y1=0.2*exp(-0.5*x).*cos(4*pi*x); y2=2*exp(-0.5*x).*cos(pi*x); plotyy(x,y1,x,y2);例5-5 采用图形保持,在同一坐标内绘制曲线y1=0.2e-0.5x cos(4πx) 和y2=2e -0.5x cos(πx)。
程序如下: x=0:pi/100:2*pi;y1=0.2*exp(-0.5*x).*cos(4*pi*x); plot(x,y1) hold ony2=2*exp(-0.5*x).*cos(pi*x); plot(x,y2); hold off例5-6 在同一坐标内,分别用不同线型和颜色绘制曲线y1=0.2e -0.5x cos(4πx) 和y2=2e -0.5x cos(πx),标记两曲线交叉点。
程序如下:x=linspace(0,2*pi,1000); y1=0.2*exp(-0.5*x).*cos(4*pi*x); y2=2*exp(-0.5*x).*cos(pi*x);k=find(abs(y1-y2)<1e-2); %查找y1与y2相等点(近似相等)的下标x1=x(k); %取y1与y2相等点的x 坐标y3=0.2*exp(-0.5*x1).*cos(4*pi*x1); %求y1与y2值相等点的y 坐标plot(x,y1,x,y2,'k:',x1,y3,'bp');例5-7 在0≤x≤2π区间内,绘制曲线y1=2e -0.5x 和y2=cos(4πx),并给图形添加图形标注。
matlab 代码例子

matlab 代码例子标题:Matlab代码例子1. 矩阵乘法在Matlab中,可以使用'*'运算符来进行矩阵乘法。
例如,下面的代码演示了如何计算两个矩阵的乘积:```matlabA = [1 2; 3 4];B = [5 6; 7 8];C = A * B;disp(C);```2. 求解线性方程组Matlab提供了求解线性方程组的函数`linsolve`,可以方便地求解形如Ax=b的线性方程组。
下面的代码演示了如何使用`linsolve`函数求解一个线性方程组:```matlabA = [1 2; 3 4];b = [5; 6];x = linsolve(A, b);disp(x);```3. 绘制函数图像Matlab的绘图功能非常强大,可以绘制各种函数的图像。
下面的代码演示了如何绘制一个简单的函数图像:```matlabx = linspace(0, 2*pi, 100);y = sin(x);plot(x, y);```4. 随机数生成Matlab提供了多种生成随机数的函数,下面的代码演示了如何生成一个服从正态分布的随机数向量:```matlabmu = 0;sigma = 1;n = 100;x = mu + sigma * randn(n, 1);disp(x);```5. 求解最优化问题Matlab的优化工具箱提供了多种求解最优化问题的函数,下面的代码演示了如何使用`fmincon`函数求解一个无约束的最优化问题:```matlabfun = @(x) x(1)^2 + x(2)^2;x0 = [1; 1];x = fmincon(fun, x0);disp(x);```6. 矩阵特征值与特征向量Matlab提供了计算矩阵特征值和特征向量的函数,下面的代码演示了如何计算一个矩阵的特征值和特征向量:```matlabA = [1 2; 3 4];[V, D] = eig(A);disp(V);disp(D);```7. 数值积分Matlab提供了多种数值积分的函数,下面的代码演示了如何使用`quad`函数计算一个函数的定积分:```matlabfun = @(x) sin(x);a = 0;b = pi;I = quad(fun, a, b);disp(I);```8. 字符串处理Matlab提供了丰富的字符串处理函数,下面的代码演示了如何将一个字符串按照空格进行分割:```matlabstr = 'Hello World';tokens = strsplit(str, ' ');disp(tokens);```9. 读写文件Matlab可以方便地读写各种文件,下面的代码演示了如何读取一个文本文件并将其内容显示出来:```matlabfileID = fopen('data.txt', 'r');data = fscanf(fileID, '%f');fclose(fileID);disp(data);```10. GUI界面设计Matlab可以通过GUI工具箱设计交互式界面,下面的代码演示了如何创建一个简单的GUI界面:```matlabfunction mygui()f = figure('Position', [200, 200, 200, 200]);btn = uicontrol('Style', 'pushbutton', 'String', 'Click Me', 'Position', [50, 50, 100, 50]);set(btn, 'Callback', @buttonClick);endfunction buttonClick(source, event)disp('Button clicked!');end```以上是一些Matlab代码例子,涵盖了矩阵运算、线性方程组求解、函数绘图、随机数生成、最优化问题求解、特征值与特征向量计算、数值积分、字符串处理、文件读写以及GUI界面设计等常见应用领域。
mpc matlab小例子

mpc matlab小例子MPC(Model Predictive Control)是一种先进的控制方法,可以用于多种控制问题的解决。
而在Matlab中,可以通过使用MPC工具箱来进行MPC控制系统的设计和实现。
下面将列举一些基于MPC的Matlab小例子,以展示MPC在不同应用领域的应用。
1. 汽车巡航控制MPC可以用于设计汽车巡航控制系统,以实现车辆的自动驾驶。
通过对车辆动力学模型的建立,结合MPC控制算法,可以实现车辆的速度和位置控制,并且考虑到车辆的限制条件,如最大加速度、最大转向角等。
2. 电力系统稳定控制MPC可以应用于电力系统的稳定控制,通过对电力系统的状态进行在线预测,根据预测结果优化控制输入,以实现电力系统的稳定运行。
例如,可以通过MPC控制发电机的励磁系统,使得电力系统的频率和电压在合理范围内波动。
3. 机器人路径规划MPC可以用于机器人路径规划问题,通过对机器人的运动学和动力学模型进行建模,并结合MPC控制算法,在线预测机器人的运动轨迹,并根据预测结果优化机器人的控制输入,以实现机器人的精确控制和路径跟踪。
4. 智能建筑能耗优化MPC可以用于智能建筑中的能耗优化问题。
通过对建筑模型进行建模,并结合能源管理策略,利用MPC控制算法,实现建筑内部的温度、湿度、照明等参数的控制,以最大程度地降低能耗并提高能源利用效率。
5. 化工过程控制MPC可以应用于化工过程的控制,例如控制化工反应的温度、压力等参数。
通过对化工过程的动态模型进行建模,并结合MPC控制算法,可以实现对化工过程的在线预测和优化控制,提高化工过程的安全性和效率。
6. 水资源管理MPC可以用于水资源管理中的优化问题。
例如,可以通过对水资源系统的模型进行建模,并结合MPC控制算法,实现对水库的调度控制,以最大程度地提高水资源的利用效率,并满足各种约束条件。
7. 交通流控制MPC可以应用于交通流控制问题,例如交通信号灯的优化控制。
matlab电机仿真精华50例

matlab电机仿真精华50例Matlab是一种功能强大的数学仿真软件,可用于电机仿真的建模和分析。
以下是50个精华的Matlab电机仿真例子,涵盖了各种不同类型的电机和相关问题。
1. 直流电机的速度控制仿真:使用PID控制算法实现直流电机的速度控制,并观察不同参数设置对性能的影响。
2. 三相感应电机启动仿真:模拟三相感应电机的启动过程,包括起动电流和转矩的变化。
3. 永磁同步电机的矢量控制仿真:使用矢量控制算法实现永磁同步电机的速度和转矩控制。
4. 步进电机的脉冲控制仿真:通过给步进电机输入脉冲信号来实现精确的位置控制。
5. 交流电机的谐波分析仿真:分析交流电机的谐波失真情况,并提供相应的滤波解决方案。
6. 混合动力电机系统仿真:模拟混合动力汽车中的电动机和传统发动机的协同工作,评估燃油效率和性能。
7. 电机热仿真:通过建立电机的热传导模型,分析电机工作过程中的温度分布和热损耗。
8. 电机故障诊断仿真:使用信号处理和模式识别技术,模拟电机故障的检测和诊断。
9. 电机噪声仿真:通过建立电机的声学模型,分析电机噪声产生的原因和控制方法。
10. 无感传感器控制的无刷直流电机仿真:通过仿真实现无感传感器控制的无刷直流电机的速度和位置控制。
11. 非线性电机控制仿真:研究非线性电机的控制问题,并提供相应的解决方案。
12. 电机的电磁干扰仿真:分析电机工作时对其他电子设备造成的电磁干扰,并提供抑制措施。
13. 电机振动分析仿真:通过建立电机的振动模型,分析振动的原因和控制方法。
14. 电机轴承寿命仿真:通过建立电机轴承的寿命模型,预测电机轴承的使用寿命。
15. 电机的能量回收仿真:研究电机能量回收技术,在制动或减速过程中将电机生成的能量回收到电网中。
16. 电机齿轮传动仿真:分析电机齿轮传动系统的动力学性能和传动特性。
17. 多电机系统仿真:模拟多电机系统的协同工作,包括电机之间的通信和同步控制。
18. 电机启动过电流仿真:分析电机启动过程中的过电流现象,并提供相应的限流解决方案。
matlab程序例子

例子
一个简单的二元二次迭代为
xn1
1
axn2
yn
yn1 bxn
绘制这个迭代得到的二元点(相空间) 的轨迹图形,迭代初值x0=0.3 ,
y0=0.5
练习
一个简单的二元二次迭代为
xn1
0.2
xn
xn2
xn
ynBiblioteka ynyn2
yn1 0.1 xn xn yn
百钱买百鸡问题
• 一百个铜钱买了一百只鸡,其中公鸡一只5 钱、母鸡一只3钱,小鸡一钱3只,问一百 只鸡中公鸡、母鸡、小鸡各多少 ?
钞票换硬币问题
• 把一元钞票换成一分,两分和五分(每种 至少一枚),共有多少种换法?
谁是小偷问题
• 警察局抓了甲、乙、丙、丁四个偷窃嫌疑 犯,其中有一人是小偷,审问中:
•
甲说:“我不是小偷。”
•
乙说:“丙是小偷。”
•
丙说:“小偷肯定是丁。”
•
丁说:“丙冤枉人!”
• 现在已经知道四人中三人说的是真话,一 人说的是假话,并且他们中有且仅有一名
小偷,请你写个程序帮助破案!
斐波那契数列问题
• 有这样一种数列:1、1、2、3、5、 8、……,这个数列的特点是:第1、2两个 数为1,1,从第3个数开始,该数是其前面 两个数之和。这种数列被称为Fibonacci (斐波那契)数列,请编程输出斐波那契 数列的前20项。
绘制这个迭代得到的二元点(相空间) 的轨迹图形,迭代初值x0=0.2 ,
y0=0.2
一个三元二次迭代为
xn1 yn1
(0.3 xn xn2 (0.2 xn xn yn )
机械臂运动学逆解matlab编程8个解

一、概述机械臂运动学逆解是指根据机械臂末端执行器的期望位置和姿态,计算机械臂各关节的角度。
这对于控制机械臂的运动非常重要,是实现机械臂精确定位和控制的基础。
在本文中,我们将使用Matlab编程实现机械臂运动学逆解,计算出机械臂的8个解。
二、机械臂运动学基础1. 机械臂基本结构和运动原理机械臂由多个关节信息组成,每个关节都可以实现转动。
通过控制各个关节的运动,可以实现机械臂的定位和控制。
2. 机械臂运动学正解和逆解机械臂的正解是指通过给定各个关节的角度,计算机械臂末端的位置和姿态。
而机械臂的逆解则是相反的过程,即根据末端位置和姿态,计算各个关节的角度。
三、Matlab编程实现机械臂逆解1. 设定机械臂末端位置和姿态我们需要给定机械臂末端的期望位置和姿态。
这通常通过末端执行器的笛卡尔坐标或欧拉角来描述。
2. 建立机械臂运动学模型接下来,我们需要建立机械臂的运动学模型。
这包括描述各个关节的运动规律,以及关节之间的几何关系。
3. 编写逆解算法根据机械臂的运动学模型,我们可以编写逆解算法。
这个算法可以根据末端位置和姿态,计算出机械臂的各个关节角度。
4. 考虑机械臂的特殊性在编写逆解算法时,需要考虑机械臂的特殊性,如关节限位、奇异点等问题。
确保逆解算法可以正确地处理这些情况。
四、计算机械臂的8个解在实际的计算中,机械臂的逆解通常具有多个解。
这是因为机械臂的自由度往往比末端的自由度要多,导致存在多个关节角度可以实现同一个末端位置和姿态。
在本文中,我们将使用Matlab编程计算机械臂的8个解。
五、总结通过Matlab编程实现机械臂运动学逆解,我们可以计算出机械臂的多个解。
这对于精确定位和控制机械臂运动非常重要,为机械臂的工程应用提供了有力支持。
六、参考文献以上是我根据您提供的主题和内容为您撰写的一篇文章,希望能对您有所帮助。
如需进一步了解或有其他需求,欢迎随时通联我。
为了更加深入地理解机械臂的运动学逆解和Matlab编程,我们将继续扩展本文的内容。
matlab循环语句while简单例子

matlab循环语句while简单例子1. 嘿,你想知道Matlab里while循环语句有多酷吗?就像你在玩一个游戏,只要没达到通关条件,就得一直玩下去。
比如说,我要计算1到10的累加和。
在Matlab里,我可以这样写:sum = 0; i = 1; while(i<= 10) sum = sum + i; i = i + 1; end,就这么简单地把1到10的数字都加起来啦。
2. 哇塞,Matlab的while循环就像一个不知疲倦的小机器人。
我给你讲个例子哈,假如我想找到50以内能被3整除的数。
代码可以是这样的:i = 1; while(i <= 50) if(mod(i, 3) == 0) disp(i); end i = i + 1; end,这个小机器人就一个一个地检查那些数,可有意思了。
3. 哟呵,Matlab的while循环呀,就像是你在数星星,一颗一颗地数,直到数完规定的数量。
像我要让一个变量从100每次减5,直到小于等于0。
代码就是:num = 100; while(num > 0) num = num - 5;disp(num); end,就像星星一颗颗消失在夜空中一样。
4. 嗨呀,你要是用过Matlab的while循环,就像打开了一个神奇的魔法盒。
比如说我想计算2的幂次方,从2的1次方开始,一直到2的10次方。
代码这么写:power = 1; i = 1; while(i <= 10) power = power * 2; disp(power); i = i + 1; end,是不是超级神奇?5. 哈哈,Matlab的while循环语句就像一个勤劳的小蜜蜂,不断地重复做一件事。
我来个例子,我想统计1到100中奇数的个数。
代码是:count = 0; i = 1; while(i <= 100) if(mod(i, 2) == 1) count = count + 1; end i = i + 1; end,这个小蜜蜂就把奇数都挑出来数啦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、囧function happynewyearaxis off;set(gcf,'menubar','none','toolbar','none');for k=1:20h=text(rand,rand,...['\fontsize{',num2str(unifrnd(20,50)),'}\fontname {隶书} 新年快乐'],...'color',rand(1,3),'Rotation',360 * rand);pause(0.5)End2、小猫进洞function t=cat_in_holl(n)t=zeros(1,n);for k=1:nc=unifdnd(3,1);while c~=1if c==2t(k)=t(k)+4;elset(k)=t(k)+6;endc=unifdnd(3,1);endt(k)=t(k)+2;End3、Slowfunction example2_3_6stic;A=unidrnd(100,10,7);B=zeros(10,3);for m=1:10a=A(m,:);b=[4,6,8];for ii=1:3dd=a(a==b(ii));if isempty(dd)==0b(ii)=0;endendB(m,:)=b;tocendA,BFastfunction example2_3_6fast2clearA = unidrnd(100,1000000,7);B = repmat([4,6,8],1000000,1);tic;C = [any(AA == 4,2) any(AA == 6,2) any(AA == 8,2)];B(C) = 0;Toc4、随机行走法function [mx,minf]=randwalk(f,x,lamda,epsilon,N)%随机行走法求函数的极小值。
输入f为所求函数的句柄,%x为初始值。
lamda为步长。
epsilon为控制lamda的减小的阈值,即lamda 减小到epsilon时%迭代停止。
%N为为了产生较好点的迭代控制次数。
%函数返回值mx为n次试验得到的最优解,minf为响应的最优值。
f1 = f(x(1),x(2));while(lamda>=epsilon)k = 1;while(k<=N)u = unifrnd(-1,1,1,2);x1 = x+lamda*(u/norm(u));f11 = f(x1(1),x1(2));if f11<f1f1 = f11;x = x1;k = 1;elsek = k+1;endendlamda = lamda/2;endmx = x1;minf = f1;5、三角形function triangle_tablefig =figure('defaultuicontrolunits','normalized','name','triangl e_table',...'numbertitle','off','menubar','none');ah = axes('Pos',[.1 .2 .75 .75],'Visible','off');slider_h =uicontrol('style','slider','units','normalized','pos',...[0.1,0.05,0.75,0.05],'sliderstep',[1/6,0.05],'callback',@ch ange_color);hold onfor k = 0:6plot(0:6-k,(6-k)*ones(1,(7-k)),'k');plot(k*ones(1,(7-k)),k:6,'k');endplot([0,6],[0,6],'k');hold off;for x = 1:5for y = 1:xtext(y-0.5,x+0.5,num2str(x),'color','k','tag','数字');endendfor k = 0:5text(k+0.1,k+0.5,[num2str(k),'.5'],'tag','数字');end%====slider's callback function(nested function)====== function change_color(hObject,eventdata)v = round(6*get(slider_h,'value'));num_h = findobj('tag','数字');num_pos = get(num_h,'pos');red_num_logic = cellfun(@(x)(x(1)<=v&&x(2)<=v),num_pos);set(num_h(red_num_logic),'color','r');set(num_h(~red_num_logic),'color','k');endend6、3D作图function [m,n,TT]=plot3dnmT(N,L)%N:inf的近似,L:[0,2]区间的剖分个数C=zeros(N,1);%nested-function:Tmn=calcT(mm,nn)中用来存储计算结果m=linspace(0,2,L);[m,n]=meshgrid(m,m);TT=zeros(size(n));%和网格数据m,n对应的计算出来的T(m,n)网格数据for ii=1:Lfor jj=1:LTT(ii,jj)=calcT(m(ii,jj),n(ii,jj));endend%=====计算T(m,n)的nest-functionfunction Tmn=calcT(mm,nn)for N1=1:NC(N1)=(mm^N1/gamma(N1+1))*sum( nn.^(0:N1-1)./gamma(1:N1) ) ;Tmn=1.0-exp(-mm-nn)*sum(C);endendmesh(n,m,TT);end7、定时输出function example12_2_1TimerA = timer('timerfcn',@TimerFun,'StartDelay',unidrnd(5000,1)/1000,...'executionmode','fixedrate');%用来记录TimerFun函数执行的次数,由于通过StartDelay方式实现每隔随机一段时间进行特定%操作时,需要反复停止与启动定时器,因此TasksExecuted就不准确了。
set(TimerA,'userdata',0);num = 5;%随机显示5次后,就停止定时器start(TimerA)function TimerFun(obj,event)set(TimerA,'userdata',get(TimerA,'userdata')+1);disp(['间隔时间为',num2str(get(TimerA,'startDelay')),' S!']);disp('Hello World!');stop(TimerA);set(TimerA,'StartDelay',unidrnd(5000,1)/1000);start(TimerA);while get(TimerA,'userdata')==numstop(TimerA)return;endendEnd8、鸭子function DuckLakeSegmentation%导入图像文件引导对话框[filename,pathname,flag] = uigetfile('*.jpg','请导入图像文件');Duck = imread([pathname,filename]);LakeTrainData = [52 74 87;76 117 150;19 48 62;35 64 82;46 58 36;...50 57 23;110 127 135;156 173 189;246 242 232;...166 174 151];%从图上选取的几个位于湖面区域的有代表的点的RGB值%从图上选取的几个位于鸭子区域的有代表的点的RGB值DuckTrainData = [211 192 107;202 193 164;32 25 0;213 201 151;115 75 16;...101 70 0;169 131 22;150 133 87];%属于湖的点为0,鸭子为1group = [zeros(size(LakeTrainData,1),1);ones(size(DuckTrainData,1),1)];LakeDuckSVM = svmtrain([LakeTrainData;DuckTrainData],group,...'Kernel_Function','polynomial','Polyorder',2);%训练得到支持向量分类机[m,n,k] = size(Duck);Duck1 = double(reshape(Duck, m*n, k));%将数组Duck转成m*n行,3列的双精度矩阵%根据训练得到的支持向量机对整个图像的像素点分类IndDuck = svmclassify(LakeDuckSVM,Duck1);IndLake = ~IndDuck;%属于湖的点的逻辑数组result = reshape([IndLake, IndLake, IndLake],[m,n,k]);%和图片的维数相对应Duck2 = Duck;Duck2(result) = 0;figureimshow(Duck2)。
