指数平滑法及其在负荷预测中的应用
电力负荷预测常用方法的分析比较与应用

电力负荷预测常用方法的分析比较与应用电力负荷预测是指对未来一段时间内的电力负荷进行预测,以便电力公司合理安排发电计划、优化电网运行和保障用电需求。
电力负荷预测方法主要分为统计方法、基于模型的方法和机器学习方法,下面对这些方法进行详细分析比较与应用。
统计方法是电力负荷预测中最简单直接的方法之一,常用的统计方法有平均值法、移动平均法和指数平滑法。
这些方法通过历史负荷数据的统计特征来进行预测,在数据量较大、负荷变化较为平稳的情况下有一定的预测准确性。
然而,在面对复杂的负荷变化模式和非线性关系时,统计方法的预测效果较差。
基于模型的方法是利用电力负荷与影响其变化的相关因素之间的数学模型进行预测。
常见的基于模型的方法有回归模型、时序模型和神经网络模型。
回归模型通过建立负荷与时间、气温等因素之间的关系来进行预测,优点是简单易懂;时序模型将负荷视为一个时间序列,利用时间序列分析方法进行预测,适用于具有明显周期性的负荷变化;神经网络模型则通过训练神经网络来对负荷进行预测,可以较好地处理非线性关系。
基于模型的方法需要依赖较为完整和准确的数据,并且参数调整和模型选择较为困难,但在一些特定场景和较为规律的负荷变化中有较好的预测效果。
机器学习方法是近年来在电力负荷预测中得到广泛应用的一类方法。
这些方法通过训练预测模型来预测未知负荷,其中常见的机器学习方法有支持向量回归(SVR)、随机森林(RF)和深度学习模型等。
SVR是一种回归算法,通过非线性映射将输入数据映射到高维空间中,并在高维空间中寻找最优超平面,从而进行预测;RF基于集成学习的思想,通过随机产生多个决策树并利用投票方式进行预测;深度学习模型则是基于神经网络的一类算法,通过多层次的网络结构进行特征学习和预测。
相对于传统的统计方法和基于模型的方法,机器学习方法能够更好地处理非线性关系和复杂的负荷变化模式,在数据量较大和样本复杂的情况下取得了很好的效果。
在实际应用中,电力负荷预测方法的选择需要考虑多个因素,包括数据的可靠性、预测的时间范围、负荷变化的规律性等。
指数平滑法及其在负荷预测中的应用

指数平滑法及其在负荷预测中的应用
陈娟;吉培荣;卢丰
【期刊名称】《三峡大学学报(自然科学版)》
【年(卷),期】2010(32)3
【摘要】指数平滑法是电力系统负荷预测的主要方法之一,该方法的准确性取决于平滑系数α.对采用厚近薄远原则与远近相同原则优选α进行对比研究,结果表明采用厚近薄远原则优选α有更好的结果.在此基础上,结合相关分析,给出了厚近薄远的具体方案,并给出了负荷预测的具体实例.
【总页数】5页(P37-41)
【作者】陈娟;吉培荣;卢丰
【作者单位】三峡大学,电气与新能源学院,湖北,宜昌,443002;三峡大学,电气与新能源学院,湖北,宜昌,443002;荆州供电公司,湖北,荆州,434023
【正文语种】中文
【中图分类】TM715
【相关文献】
1.指数平滑法在电力系统负荷预测中的应用 [J], 吉博文;吴张傲
2.温斯特线性与季节性指数平滑法在电力负荷预测中的应用及改进 [J], 叶舟;陈康民
3.温斯特线性与季节性指数平滑法在电力负荷预测中的应用及改进 [J], 叶舟;陈康民
4.DF8003基于指数平滑法的短期电力负荷预测应用探讨 [J], 张云菊
5.指数平滑法在短期负荷预测中的应用 [J], 田德胜;刘厚法
因版权原因,仅展示原文概要,查看原文内容请购买。
电力系统中的电力负荷预测算法和模型优化

电力系统中的电力负荷预测算法和模型优化随着电力需求的不断增长和电力系统规模的扩大,电力负荷预测成为了电力系统运行和规划的关键。
准确的电力负荷预测可以帮助电力系统管理者合理安排电力供应,提高电力系统的可靠性和效率。
电力负荷预测是根据历史负荷数据和其他影响因素,通过建立预测模型来预测未来一段时间内的负荷需求。
在电力系统中,负荷预测涉及多种因素,包括天气状况、季节变化、节假日等。
为了提高电力负荷预测的准确性和精确度,研究人员提出了各种预测算法和模型优化方法。
下面将介绍一些常用的电力负荷预测算法和模型优化技术。
1. 时间序列分析方法时间序列分析是一种常用的电力负荷预测方法,它利用历史负荷数据的时间趋势和周期性来预测未来的负荷需求。
常用的时间序列分析方法包括ARIMA模型(自回归移动平均模型)和指数平滑模型。
ARIMA模型是一种基于统计学的负荷预测方法,它通过建立负荷数据的自回归和移动平均模型,来对未来的负荷进行预测。
指数平滑模型则是一种根据过去负荷数据的加权平均来预测未来负荷的方法,它对最近的负荷数据给予更高的权重。
2. 机器学习方法近年来,随着机器学习技术的快速发展,越来越多的研究人员开始将机器学习方法应用于电力负荷预测。
机器学习方法根据历史负荷数据和其他影响因素,通过训练模型来预测未来的负荷需求。
常用的机器学习方法包括支持向量机(SVM)、神经网络和决策树等。
支持向量机是一种常用的分类和回归分析方法,它通过构建超平面来对负荷数据进行分类和预测。
神经网络模型模拟了人脑的神经元连接,通过训练和优化权重来实现负荷预测。
决策树模型则通过建立一系列的决策规则来对负荷数据进行分类和预测。
3. 基于模型优化的方法除了选择适当的预测算法,模型优化也是提高负荷预测准确性的重要手段。
模型优化包括特征选择、参数优化和模型融合等技术。
特征选择是在建立预测模型时,选择最具相关性和重要性的特征进行建模。
通过剔除冗余和不相关的特征,可以提高模型的泛化能力和预测准确性。
电力系统中的电力负荷预测方法教程

电力系统中的电力负荷预测方法教程电力负荷预测是电力系统运行的重要组成部分,准确的负荷预测是保持电力系统的稳定运行、合理调度电力资源的关键。
在电力系统中,负荷预测的主要目标是预测未来一段时间内的电力负荷需求。
本文将介绍几种常用的电力负荷预测方法,包括传统的时间序列方法和基于机器学习的方法。
1. 时间序列方法时间序列方法是电力负荷预测中最常用的方法之一。
它基于历史负荷数据分析未来负荷的变化趋势。
时间序列方法需要建立模型来捕捉负荷数据的周期性和趋势性。
以下是一些常见的时间序列方法:1.1 移动平均法移动平均法是最简单的时间序列方法之一。
它通过计算每个时间点前几个时间点的负荷平均值来进行预测。
移动平均法适用于负荷呈现稳定的周期性变化的情况,但对于具有较大波动的负荷数据可能表现不佳。
1.2 指数平滑法指数平滑法是一种适用于具有趋势性的负荷数据的时间序列方法。
它根据历史数据的权重来预测未来负荷。
指数平滑法通过调整平滑系数来提高模型的准确性。
常见的指数平滑方法有简单指数平滑法和双指数平滑法。
1.3 季节分解法季节分解法是一种将负荷数据分解为趋势、季节和随机成分的方法。
该方法适用于数据存在明显的季节性变化的情况。
通过将负荷数据分解为不同的成分,可以更好地分析和预测负荷的未来变化。
2. 基于机器学习的方法随着机器学习算法的发展,越来越多的研究者开始将其应用于电力负荷预测领域。
相比于传统的时间序列方法,基于机器学习的方法可以更好地捕捉数据之间的非线性关系和复杂模式。
以下是一些常见的基于机器学习的方法:2.1 神经网络神经网络是基于人工智能领域的一种强大的模型,可用于负荷预测。
神经网络可以通过学习大量的历史负荷数据来预测未来负荷。
神经网络具有强大的适应性和非线性建模能力,但对于数据量较小的情况可能存在过拟合的问题。
2.2 支持向量机支持向量机是一种常用的机器学习算法,它可以通过寻找一个最优超平面来进行分类和回归问题。
电力系统中的负荷预测与调度方法

电力系统中的负荷预测与调度方法一、引言电力系统是现代社会不可或缺的基础设施之一,负荷预测与调度是电力系统运行中不可或缺的环节。
准确的负荷预测和合理的负荷调度能够提高电力系统的运行效率,保障供电的可靠性和稳定性。
本文将探讨电力系统中的负荷预测与调度方法,从而为电力系统的优化运行提供支持。
二、负荷预测方法负荷预测是指通过对历史数据的分析和建模,预测未来一段时间内的负荷需求。
常见的负荷预测方法包括统计方法、时间序列方法和人工智能方法。
1. 统计方法统计方法是根据历史数据进行统计分析和推断,预测出未来的负荷需求。
常用的统计方法包括回归分析、指数平滑法和趋势法。
回归分析通过建立负荷与影响因素之间的回归关系来预测负荷需求。
指数平滑法根据历史数据的加权平均值进行预测,适用于短期负荷预测。
趋势法则通过寻找历史数据中的趋势来预测未来负荷需求。
2. 时间序列方法时间序列方法是基于一系列数据随时间变化的规律性进行预测。
常用的时间序列方法包括移动平均法、指数平滑法、ARIMA模型和回归模型。
移动平均法通过计算历史数据的平均值来预测未来负荷需求。
指数平滑法通过对历史数据的加权平均来预测未来负荷需求。
ARIMA模型是一种常用的时间序列模型,可以捕捉到负荷的季节性和趋势性。
回归模型则通过建立负荷与影响因素之间的回归关系进行预测。
3. 人工智能方法人工智能方法包括神经网络、支持向量机和遗传算法等。
神经网络是一种模拟人脑神经元工作方式的机器学习算法,可以通过对历史数据的学习来预测未来负荷需求。
支持向量机是一种监督学习算法,能够建立负荷与影响因素之间的非线性回归关系。
遗传算法则是一种基于生物进化原理的优化算法,可以用于寻找最优的负荷预测模型参数。
三、负荷调度方法负荷调度是指在不同时间段内对电力系统中的发电机组和负荷进行合理安排和调度,以满足电力供需平衡和经济运行的要求。
1. 优化调度方法优化调度方法通过建立数学模型,以最小化电力系统的运行成本为目标,确定最优的发电机组出力和负荷供需平衡。
电力系统中的负荷预测算法与模型构建

电力系统中的负荷预测算法与模型构建随着工业化和城市化的快速发展,电力需求也不断增长。
为了满足日益增长的电力需求,电力系统必须能够准确预测未来的负荷,以便进行合理的发电规划和运行调度。
本文将介绍电力系统中常用的负荷预测算法和模型构建方法,并探讨它们的优缺点。
1. 基于统计方法的负荷预测算法基于统计方法的负荷预测算法是使用历史负荷数据进行预测的一种方法。
常用的统计方法包括移动平均法、指数平滑法和回归分析法。
移动平均法是一种简单的算法,它通过计算历史负荷数据的平均值来进行预测。
然而,这种方法没有考虑到负荷数据的趋势和季节性变化,因此在长期预测上效果较差。
指数平滑法是一种常见的算法,它通过加权计算历史负荷数据的平均值来进行预测。
这种方法考虑了近期数据的权重,能够较好地预测短期变化,但对于长期趋势的预测效果有限。
回归分析法是一种使用回归模型进行预测的方法。
它根据历史负荷数据和其他影响因素的关系,建立了一个数学模型来进行预测。
这种方法能够较好地考虑到各种因素对负荷的影响,预测精度相对较高。
2. 基于机器学习的负荷预测算法随着机器学习技术的快速发展,越来越多的电力系统开始采用基于机器学习的负荷预测算法。
基于机器学习的负荷预测算法可以通过训练模型来学习历史负荷数据和其他影响因素之间的复杂关系,从而实现更准确的负荷预测。
常用的基于机器学习的负荷预测算法包括支持向量机(SVM)、人工神经网络(ANN)和决策树等。
支持向量机是一种监督学习算法,它通过构造一个最优划分超平面来进行分类或回归。
在负荷预测中,支持向量机可以通过训练模型来学习历史负荷数据和其他影响因素之间的关系,并进行未来负荷的预测。
人工神经网络是一种模拟人脑神经元工作方式的算法。
它通过建立具有多个神经元的网络结构来进行学习和预测。
在负荷预测中,人工神经网络可以通过训练模型来学习历史负荷数据和其他影响因素之间的复杂关系,并进行准确的负荷预测。
决策树是一种基于树形结构的分类和回归算法。
电力电量负荷预测方法及应用分析

电力电量负荷预测方法及应用分析作者:刘慷来源:《科技资讯》2012年第33期摘要:为了进一步提高预测精度,则需要对传统方法进行一些改进,使预测结果具有更高的参考价值,本文主要探讨了时间序列预测法以及其实际运用。
关键词:负荷预测时间序列法中图分类号:TM93 文献标识码:A 文章编号:1672-3791(2012)11(c)-0105-02电力负荷预测具有十分重要的作用,其是调度中心制订发电计划及发电厂报价的依据,同时其也可以为发电计划程序、离线网络分析和合理的调度安排提供数据,而其准确率的高低对电力系统的运行、控制和生产计划都有着非常重要的影响。
为了更加准确的预测市场对电力电量的需求,现如今已有很多预测方法被用于电力电量的预测,各种方法都有其优缺点。
随着电力市场的发展,人们对负荷预测精度的要求也越来越高。
为了进一步提高预测精度,则需要对传统方法进行一些改进,使预测结果具有更高的参考价值。
随着现代科学技术的不断进步,理论研究的逐步深入,以灰色理论、时间序列理论、模糊数学等为代表的新兴交叉学科理论的出现,为负荷预测的飞速发展提供了坚实的理论依据和数学基础。
1 负荷预测及分类电力负荷实质上是指电力的需求量或用电量,即能量的时间变化率,也可以被定义为发电厂、供电地区或电网在某一瞬间所承担的工作负荷。
电力负荷往往具有以下一些特点:(1)电力负荷往往以天为单位不断起伏的,具有较大的周期性;(2)电力负荷的变化过程一般不会有较大的突变,属于连续性变化;(3)电力负荷对一些因素会比较敏感,比如季节、温度、天气等。
在对负荷进行预测时,需要考虑系统的运行特性、增容决策等因数,以便更加准确的确定未来某特定时刻的负荷数据。
就负荷本身而言,其主要是指电力需求量或用电量。
电力电量预测对电力系统安全经济运行和国名经济发展具有重要意义。
由于对电力负荷进行预测的目的会有所不同,所以将其分为四类即:(1)超短期负荷预测,主要是用于对未来一小时以内的负荷进行预测;(2)短期负荷预测,主要是指日负荷预测和周负荷预测,分别用于安排日调度计划和周调度计划;(3)中期负荷预测,主要是指一个月到一年的负荷预测,主要用于确定机组运行方式和设备的大规模修理计划等情况;(4)长期负荷预测,主要指未来3~5年甚至更长时间内的负荷预测,主要是用于电网规划部门。
指数平滑预测法及其在经济预测中的应用
中图分 类号 : F 2 2
文献标志码 : A 文章编 号 : 1 6 7 3 — 2 9 1 X( 2 0 1 3 ) 0 4 — 0 0 1 1 - 0 3
一
、
时 间序 列分 析
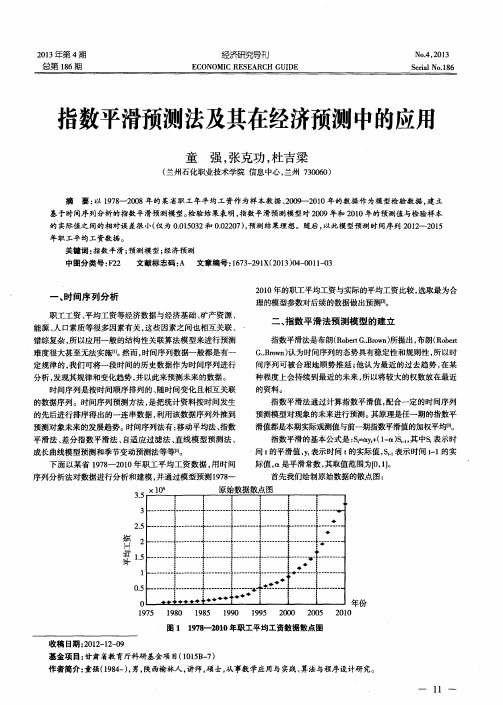
2 0 1 0 年 的职工平均工资与实际的平均工资 比较 , 选取最为合 理的模型参数对后续的数据做 出预测网 。
表1 所示 ) , 2 0 0 9 年和 2 0 1 0 年的数据作 为模型 的检验数据 。
1 9 8 1 3 2 o 0 8 3 0
年份编号 1 9 8 0 2
根据 经验 、 实 际运算 分 析和 观察 , 选取 — 5 6 — 6 + 6 3 『 2 _ 一 + 一 7 4 5 = 6 4 7 . 6 7 , 并 分 别 选 取0 【 = o _ 3 , 仅 = o . 2 5 , 0 l = O . 2 , 仅 = 0 . 1 5 , n = 0 . 1 对 原 始 数 据 做 指 数 平 滑, 预 测 情 况
摘
要: 以1 9 7 8 -2 0 0 8年的 某省 职工年平 均工资作为样本数据 、 2 0 0 9 - - 2 0 1 0年 的数据作 为模 型检 验数据 , 建立
基于时间序列分析的指数平滑预测模型。 检验结果表明 , 指数平 滑预测模型对 2 0 0 9 年和 2 0 1 0 年的预 测值 与检验样本
指数平滑 的基本公式是 : S t =  ̄ y t + ( 1 - a ) S 其 中s 表示时
间t 的平滑值 , y t 表示时间 t 的实际值 , s 。 表示时间 卜1 的实 际值 , 是平 滑常数 , 其取值范围为【 O , 1 】 。 首先我们绘制原始数据的散点图 :
( 见表 2 ) : 表2 指 数 平 滑 预 测 结 果
电力系统中的长期电力负荷预测方法研究

电力系统中的长期电力负荷预测方法研究引言在电力系统运行中,准确预测长期电力负荷是至关重要的,这对于确保电力供应的可靠性和经济性都具有重要意义。
然而,由于电力负荷具有复杂的非线性特征和受许多因素的影响,预测长期电力负荷一直是一个具有挑战性的问题。
本文将介绍电力系统中的长期电力负荷预测方法的研究进展。
一、时间序列分析方法时间序列分析方法是最常用于预测电力负荷的方法之一。
其基本假设是未来的负荷与过去的负荷具有相关性。
常用的时间序列分析方法有移动平均法、指数平滑法和ARIMA模型等。
移动平均法通过计算历史负荷数据的平均值来进行预测,适用于负荷具有明显趋势和季节性的情况。
指数平滑法则是通过对历史负荷数据进行加权平均来预测未来负荷,适用于负荷波动较为平稳的情况。
ARIMA模型则是一种结合了自回归(AR)、差分(I)和滑动平均(MA)的模型,能够对负荷的趋势、季节性和随机性进行建模和预测。
二、神经网络方法神经网络方法是近年来在电力负荷预测中应用较多的方法之一。
神经网络具有良好的非线性逼近能力和自适应学习能力,能够对复杂的电力负荷数据进行建模和预测。
常用的神经网络模型有多层感知器(MLP)、循环神经网络(RNN)和长短期记忆网络(LSTM)等。
多层感知器是最基本的神经网络模型,其通过多个神经元层次的连接来进行信息处理和学习。
循环神经网络则具有记忆能力,能够处理序列数据,并且可以捕捉到序列数据中的长期依赖关系。
长短期记忆网络则是对循环神经网络的改进,解决了长期依赖问题,适合于电力负荷数据的建模和预测。
三、支持向量机方法支持向量机方法是一种基于统计学习理论的预测方法,具有较好的泛化能力。
支持向量机通过在特征空间中构建一个最优分类超平面来进行分类和回归。
在电力负荷预测中,支持向量机方法可以通过训练数据样本集来拟合一个预测模型,然后利用该模型对未来的电力负荷进行预测。
支持向量机方法的优点是能够处理高维数据和非线性问题,但是其也存在训练时间较长和对参数的选择较为敏感的问题。
供电系统中的电力负荷预测方法的教程

供电系统中的电力负荷预测方法的教程随着电力需求的不断增长和电网的发展,准确预测电力负荷成为了保障供电系统稳定运行的关键。
电力负荷预测是指根据历史负荷数据、天气因素以及其他相关因素,利用数学和统计模型来预测未来一段时间内的电力负荷。
本教程将介绍一些常用的电力负荷预测方法,并详细阐述其原理和应用。
一、基于时间序列分析的电力负荷预测方法时间序列分析是指对一组连续观测值按照时间先后顺序进行统计分析的方法。
在电力负荷预测中,时间序列分析常用于分析和预测负荷的季节性、周期性和趋势变化。
其中最常用的模型包括ARIMA模型和指数平滑模型。
1. ARIMA模型ARIMA模型是自回归滑动平均模型(Autoregressive Integrated Moving Average Model)的缩写。
它基于时间序列数据的自相关和趋势性,将未来的观测值与过去的观测值和误差进行组合,通过最小化残差的平方和来求得最优模型。
ARIMA模型的预测准确性较高,适用于负荷变化较为平稳的情况。
2. 指数平滑模型指数平滑模型是根据时间序列数据的加权平均值来进行预测的一种简单方法。
它常用于处理负荷有明显季节性变化或趋势变化的情况。
指数平滑模型包括简单指数平滑、二次指数平滑和霍尔特线性指数平滑等,通过调整平滑系数来适应不同的负荷变化趋势。
二、基于机器学习的电力负荷预测方法随着机器学习技术的快速发展,越来越多的研究者开始将其应用于电力负荷预测中。
机器学习方法通常基于大量样本数据,通过学习样本数据的模式和规律,并将其应用到未知数据中进行预测。
1. 神经网络模型神经网络模型是一种模仿人脑神经元构造的数学模型,广泛应用于电力负荷预测中。
它通过构建多层神经元网络和定义适当的激活函数,学习输入特征和输出负荷之间的非线性关系。
神经网络模型的预测准确性较高,适用于处理较为复杂的负荷变化。
2. 支持向量机模型支持向量机模型是一种常用的分类和回归分析方法,在电力负荷预测中也有广泛应用。
电力负荷预测中的时间序列分析与模型预测

电力负荷预测中的时间序列分析与模型预测在电力系统运营中,准确地预测电力负荷对于合理调度电力资源、保障电力供应和优化运营具有重要意义。
为了实现高效的电力负荷预测,时间序列分析和模型预测成为一种常用的方法。
时间序列分析是指对一组有序的数据按时间顺序进行建模和分析的统计技术。
在电力负荷预测中,时间序列分析可以帮助我们揭示出负荷数据的周期性和趋势性,为后续的模型预测提供依据。
常用的时间序列分析方法包括移动平均法、指数平滑法和季节调整法。
移动平均法是一种简单的平滑预测方法,它通过计算过去一段时间内的平均负荷量来预测未来的负荷。
移动平均法考虑了历史数据的整体变化趋势,但没有考虑到季节性和周期性的变化。
指数平滑法是一种适用于短期预测的方法,它将较大权值赋予近期数据,并逐渐减小权值的大小。
指数平滑法能够灵活地适应数据的变化,但同样没有考虑到季节性和周期性的影响。
季节调整法可以将负荷数据按季节性特征进行分解,并对不同季节的数据进行分别分析和预测。
季节调整法考虑了季节性的影响,但对于长期趋势的预测效果相对较差。
除了时间序列分析,模型预测也是电力负荷预测中常用的方法之一。
模型预测是基于历史数据和其他相关因素构建数学模型,通过模型来预测未来负荷变化。
常用的模型预测方法包括回归分析、人工神经网络和支持向量机。
回归分析是一种简单而直观的模型预测方法,它通过建立自变量和因变量的函数关系来进行预测。
回归分析可以对各种因素对负荷变化的影响进行量化,并进行预测。
然而,回归分析假设因变量和自变量之间存在线性关系,因此对于非线性关系的应用效果较差。
人工神经网络是一种模拟人脑神经网络结构和功能的数学模型,它能够通过学习和训练来建立输入和输出之间的复杂关系。
人工神经网络能够对非线性问题进行较好的建模和预测,但需要大量的数据进行训练,且模型较为复杂。
支持向量机是一种基于统计学习理论的模型预测方法,它通过寻找最优超平面将数据划分为不同的类别,并通过支持向量来进行预测。
指数平滑法在短期负荷预测中的应用

应用改进后的方法,以每个预测日 之前20 天的实际负荷作为历史资料,对
泗阳电网2003年1~12月的负荷进行了预 应性、精确性等方面都有好的效果。
测,实际预测结果表明,这种预测方法
⑵改进后的指数平滑法主要应用于
的预测效果是良好的,将预测值与2003 电网日负荷值的预测,对节假日负荷值
2005 年 第 02 期 总第 213 期
37
就可以在一定的置信程度下推断预测过程 平滑误差应很小,即追踪信号应接近于
中存在系统偏差。当追踪信号反应出预测 零;反之,预测结果存在着系统偏差,追
过程中有系统偏差以后,意味着时间序列 踪信号将会接近于-1或1。由上述计算步
发生了变化,此时重新修正平滑常数α的 骤可以看出,在实际计算过程中,平滑参
取值,使预测模型自动响应这种变化,并 对预测重新加以调整,从而合理解决前面 提出的问题。这就是自调整平滑参数的单 指数平滑法。这里α为平滑参数是因为α 将随着每一时期实际观测值的变化而被修 正,不再是固定不变的常数了。此方法的 具体计算步骤如下。
需求侧管理
DSM
指数平滑法在短期负荷预测中的应用
田德胜,刘厚法 (泗阳县供电公司,江苏 泗阳 223700)
Z
H
A
I
Y
A
O
摘要:针对泗阳电网的负荷预测问题,引进了改进的指数平滑法,应用于实际负荷预测问题中,获得了满意的效果。
关键词:电力系统;负荷预测;指数平滑法
中图分类号:T M 7 1 5
文献标志码:A
现不出明显的趋势或周期来。对于这种非 平稳随机过程,或称非平稳时间序列,采 用单指数平滑法进行负荷预测实际上只考 虑趋势项,而忽略了周期性以及随机波动 项,当原始数据波动较大时,预测模型一 般很难通过假设检验。所以在预测前,需 对原始数据序列进行处理。
电力系统中的负荷预测算法

电力系统中的负荷预测算法电力系统的负荷预测算法在能源领域扮演着重要的角色。
准确的负荷预测可帮助电力公司更好地规划电力供应,提高运营效率,并降低运营成本。
本文将讨论电力系统中常见的负荷预测算法,并介绍它们的原理和优势。
一、简单移动平均法简单移动平均法是最常见的负荷预测算法之一。
该算法基于过去一段时间的负荷数据来预测未来的负荷趋势。
算法的原理很简单,即将过去若干个时间点的负荷数据求平均,然后将平均值作为未来时间点的负荷预测值。
该算法的优势在于简单易懂,计算速度快,适用于对负荷变化率不大的情况。
然而,它忽略了负荷数据的季节性变化和趋势性变化,因此在某些情况下预测结果可能不够准确。
二、指数平滑法指数平滑法是另一种常用的负荷预测算法。
该算法基于指数平滑模型,通过给予过去负荷数据不同的权重,来预测未来的负荷趋势。
指数平滑法的原理是:预测值等于上一个时间点的实际值与上一个时间点的预测值之间的加权平均。
通过权重的调整,可以使得算法对过去数据的依赖程度不同,更加适应不同数据变化的趋势。
该算法的优势在于能够捕捉数据的趋势性变化,并且较好地适应季节性变化。
然而,指数平滑法对于负荷的突变和异常值比较敏感,这在某些情况下可能导致预测结果的不准确。
三、ARIMA模型ARIMA(自回归综合移动平均模型)是一种常用的时间序列分析方法,也是电力系统中负荷预测的重要算法之一。
该算法结合了自回归(AR)和移动平均(MA)的特点,能够更准确地预测负荷的趋势。
ARIMA模型的原理是通过分析时间序列数据的自相关性和平稳性,建立数学模型,并利用该模型对未来的负荷进行预测。
ARIMA模型能够较好地适应负荷数据的季节性变化和趋势性变化。
该算法的优势在于能够对负荷数据的季节性变化进行较好的建模,并且对于突变和异常值有较好的鲁棒性。
然而,ARIMA模型的参数估计和模型选择比较复杂,需要较长的计算时间,且对数据的平稳性要求较高。
综上所述,电力系统中的负荷预测算法有多种选择,每种算法都有其适用的场景和优势。
浅谈配网规划中负荷预测的几种方法

浅谈配网规划中负荷预测的几种方法负荷预测是电力系统中配网规划的重要组成部分,它对于合理规划电网设备和优化电网运行具有重要的意义。
本文将从时间序列分析、统计回归、人工神经网络和混合方法四个方面介绍负荷预测的几种方法。
一、时间序列分析时间序列分析是一种常用的负荷预测方法。
它通过对历史负荷数据进行分析,建立起负荷与时间的关系模型,从而预测未来一段时间内的负荷情况。
常见的时间序列分析方法有移动平均法、指数平滑法和季节性模型法等。
1.移动平均法移动平均法是一种简单的时间序列分析方法,它通过计算过去一段时间内负荷的平均值,并将这个平均值作为未来负荷的预测值。
移动平均法重视历史数据的平均趋势,适用于负荷变化比较平缓的情况。
2.指数平滑法指数平滑法是一种根据历史数据的加权平均值来预测未来负荷的方法。
它通过给历史数据设置不同的权重,将较大权重放在近期数据,较小权重放在远期数据,从而更加重视近期负荷数据的变化情况。
3.季节性模型法季节性模型法考虑到负荷的季节性变化,将负荷数据分为季节性和非季节性两个部分,并分别建立相应的模型。
季节性模型法通过对历史数据的季节性部分进行分析,得出未来负荷的季节性预测值,并与非季节性部分相加得出最终的负荷预测值。
二、统计回归统计回归是一种常用的负荷预测方法,它通过建立负荷与其他影响因素之间的关系模型,从而预测未来负荷情况。
常见的统计回归方法有简单线性回归、多元线性回归和逐步回归等。
1.简单线性回归简单线性回归是一种最简单的回归分析方法,它假设负荷与单个影响因素之间的关系是线性的,通过拟合负荷与单个影响因素之间的散点图,得出拟合直线的斜率和截距,从而得出负荷与影响因素之间的线性关系。
2.多元线性回归多元线性回归是一种考虑多个影响因素的回归分析方法,它假设负荷与多个影响因素之间的关系是线性的,通过拟合负荷与多个影响因素之间的散点图,得出拟合平面的系数,从而得出负荷与影响因素之间的线性关系。
用电负荷计算方法

用电负荷计算方法电负荷计算是电力系统设计与规划的重要环节,可以帮助用户准确、合理地评估电力需求,为电网规划和电力设备的选型提供参考依据。
电负荷计算主要包括负荷分类、负荷估算和负荷预测三个方面。
本文将详细介绍电负荷计算方法及其应用。
一、负荷分类电负荷按照其性质和使用方式可以分为稳定负荷、间歇性负荷和突变负荷。
1.稳定负荷:稳定负荷是指电力系统中相对恒定、不发生较大变化的负荷,如工厂的基础负荷、城市的居民用电负荷等。
稳定负荷一般不会对电力系统产生较大的冲击,其计算方法主要是基于历史数据和实际测量数据。
2.间歇性负荷:间歇性负荷是指电力系统中以间隔时间出现、持续时间相对较短的负荷,如空调、电梯、电炉等。
间歇性负荷的计算需要考虑负荷启停特性和使用频率,一般可以通过测量和统计分析来获取。
3.突变负荷:突变负荷是指电力系统中突然出现和消失的负荷,如启动大电动机、短时间内大量用电设备同时启动等。
突变负荷对电系统运行稳定性和设备的选择均有较大影响,其计算方法一般采用模拟和推算的方式。
二、负荷估算负荷估算是指在缺乏实际测量数据的情况下,通过对负荷特征和系统参数的分析与计算,预测电力系统在未来一段时间内的负荷情况。
负荷估算分为静态负荷估算和动态负荷估算两种方法。
1.静态负荷估算:静态负荷估算主要通过对历史数据和实际测量数据的分析,推算出负荷的基本特征,如负荷的平均值、峰值、谐波内容等。
静态负荷估算一般用于短期负荷预测和负荷曲线的绘制。
2.动态负荷估算:动态负荷估算是指通过建立电力系统负荷模型,结合外部条件和负荷特征的变化,对未来负荷进行逐时、逐日或逐月的预测。
动态负荷估算可以基于统计学方法、智能算法、指数平滑法等进行。
三、负荷预测负荷预测是指根据历史负荷数据、外部环境、经济发展等因素,通过建立预测模型,对未来电力系统的负荷进行预测。
负荷预测可以帮助电力系统规划者合理安排电力资源,提高电力系统的可靠性和经济性。
1.统计学方法:统计学方法是对历史负荷数据进行统计分析,寻找负荷与时间、气温、经济因素等因素的关系,并据此建立预测模型,进行负荷预测。
指数平滑法在电力系统负荷预测中的应用

指数平滑法在电力系统负荷预测中的应用电力负荷预测是电力部门的重要工作之一,它对电力系统的规划、建设和运行起重要作用。
文章用指数平滑方法进行中期电力负荷预测,所得结果对实际工作有积极作用。
标签:电力系统;负荷预测;指数平滑预测模型Abstract:Power load forecasting is one of the most important work in power sector,which plays an important role in the planning,construction and operation of power system. In this paper,the exponential smoothing method is used for medium term power load forecasting,and the result has positive effect on the practical work.Keywords:power system;load forecasting;exponential smoothing forecasting model1 概述电能的生产和消费对社会经济的发展有重要作用,电能通过电力网进行传输和分配。
发电机组、电力传输网、电力用户或电气设备在某一时间点或时间范围需要承担或者消耗的电功率以及电能量被称为电力负荷,简称为负荷。
负荷预测,对保证社会的用电需求、提高电力企业经济效益和社会效益有重要意义,还对未来电力网的发展起决定性作用。
负荷预测是电力部门的重要工作之一。
负荷预测的原则包括:(1)可知行原则。
人们对于预测对象的过去、现在和将来的发展趋势是有所了解的,可以根据事物发展情况,对未来进行预测。
(2)相似性原则。
人们可以把已经经历过的事物的发展情况的过程和变化规律作为参照,再对另一相同事物的发展情况按照这一规律进行预测。
基于等维新息指数平滑法模型的中长期负荷预测

S yn (1 ) yn 1 ,..., (1 ) n 1 y1
1 (1 ) n S 0
2 优选平滑系数
平滑系数的选择直接影响着预测结果的精 度。根据比较过去常用的试凑法[12]、经验估计法、 0.618 优选法和最近提出的贡献率法和半衰期法的 优缺点[13-14]。本文选用 0.618 优选法来确定 值。 文献 [10] 选用平均绝对百分误差作为目标函 数,其计算公式为
(15) (16) 这种新陈代谢的数据处理方式即为等维新息技 术,用上述处理方法可以使指数平滑法预测模型得 到优化,不过等维新息模型存在最佳维数区,所以 寻找最佳的维数,可以使等维新息指数平滑预测模 型得到更佳的优化,预测精度得到提高,更好地体 现负荷发展趋势。 经等维新息数据处理后的指数平滑法的负荷预 测总体流程图如图 1 所示。
1.2 二次曲线指数平滑模型 二次曲线指数平滑模型公式为
由式(14)知道 WMAE 是平滑系数 的函数, 通过 0.618 法对 进行搜寻, 求出每个小区间中 对 应 WMAE 的最小值, 这个最小值对应的平滑系数 就是通过对各期误差赋权得到的优选平滑系数。 0.618 法的具体步骤是: (0,1) 分成 10 个等距子区 设 ε=0.01,将 间,即
S yt (1 ) S
1 t 1 n
1 t 1 ,t=1,2,
次 和 三 次 平 滑 值 , 且 S S12 S13 X 1 。 其 中
1 1
…,n
(1)
反复利用式(1)递推可得
F3 ( 3 ,..., (n 1)(n 2) 3 (1 ) n / 2) 。
3 (4 3 ) S n ] / 2(1 ) 2
指数平滑法负荷预测

目录中文摘要 (1)英文摘要 (2)1引言 (3)1.1 负荷预测 (3)1.2 电力负荷预测常用方法 (4)1.3负荷预测的研究现状及发展 (5)1.4毕业设计主要工作 (6)2基于指数平滑法的短期负荷预测模型 (7)2.1 指数平滑法 (7)2.2基于指数平滑法的短期负荷预测模型 (10)3短期负荷预测的软件实现 (11)3.1 C语言简介 (11)3.2短期负荷预测软件实现 (12)4负荷预测结果分析 (17)4.1 原始数据处理 (17)4.2 输入变量 (18)4.3 一次指数平滑法负荷预测 (19)4.4 二次指数平滑法负荷预测 (21)4.5 负荷预测比较分析 (25)5结论 (29)5.1 结论 (29)5.2 展望 (29)谢辞 (31)参考文献 (32)附录一程序代码 (33)基于指数平滑法的短期负荷预测摘要:负荷预测是电力系统领域的一个传统研究问题,随着我国电力事业的发展,电网的管理日趋现代化,电力系统负荷预测问题的研究也越来越引起人们的注意。
指数平滑法是一种简单常用的负荷预测方法,他能用较少的原始数据,对未来的负荷情况进行预测。
本文将使用这种方法进行短期负荷预测。
选取某地某年全年每小时的负荷数据作为可参加运算的数据,用选择的方式,对以小时为单位或者以一整天为单位的负荷进行预测,最后输出结果,计算误差及误差率。
并用C语言程序设计对其进行实现。
本设计以探究输入变量对一、二次指数平滑法负荷预测的影响,选用适当的数据,改变各个输入变量(平滑常数a,参与计算的数据量t等)得到具体的结果,通过对结果的分析,得到这些输入变量对一、二次指数平滑法负荷预测的影响。
关键词:短期负荷预测;一次指数平滑法;二次指数平滑法;C语言;输入变量的影响。
Based on Exponential Smoothing Short-term Load ForecastingAbstract:The field of power system load forecasting is a traditional research problem, as China's power industry development, the management of anincreasingly modern power grid, power system, the problem of loadforecasting are increasingly attracting attention.Exponential smoothing method is a simple, common load forecastingmethod, he can use less of the original data, to predict the future loadconditions. This article will use this method for short-term loadforecasting. Select the year, somewhere, the hourly load data as the datamay participate in operations, with the choice of method of in hours or in aday's load forecast for the unit, the final output, error and error ratecalculation . And use C language programming to achieve them. Toexplore the design of the input variables on the first and second loadforecasting exponential smoothing effect, choose the appropriate data,changing the various input variables (smoothing constant a, t the amountof data involved in the calculation, etc.) are concrete results, through theresults analysis, these input variables on the first and second loadforecasting exponential smoothing effect.Keywords:Short-term Load Forecasting; An Exponential Smoothing; Double Exponential Smoothing Method; C Language;Input Variables.1引言电力负荷预测是电力系统规划决策、经济运行的前提和基础,电力负荷的准确预测对电力系统的经济运行和国民经济的发展具有重要意义。
电力负荷预测第四章 平移法与平滑法

移动平均预测法 与平滑预测法
一. 时间序列的概念、构成 二. 移动平均法 三. 指数平滑法
教学要求 :
●清楚时间序列的概念与构成及该方法的优缺点;
●掌握移动平均的计算(简单、加权、差分)与
递推公式,及优、缺点; ●清楚指数平滑法的计算(简单、二次、三次),
掌握平滑系数的含义,及该方法的优、缺点;
(3)三重指数平滑——抛物线变化时
St (1) Yt (1 )St 1(1)
St (2) St (1) (1 )St 1(2)
St (3) St (2) (1 )St 1(3)
Yt k at bt k ct k 2
●混合型:
Yt=Tt St Ct It
● ● ●
Yt=St + Tt Ct It
● ●
3.时间序列的分类
●确定型:
只考虑各期数量的大小;
不考虑可能出现的大小(如移动平移、指数平滑)。
●随机型:实际变量按时间先后次序排列。
期望(均值)
自协方差
平稳的: E(yt)=a,E[(yt+k-a)(yt-a)]=rk, rk仅与k有关 非平稳的:均值平稳,但方差不平稳 均值不平稳,但方差平稳 或都不平稳 均值不平稳的处理办法:1)季节差分▽s yt= yt –yt-s 2)一阶差分▽ yt= yt –yt-1 方差不平稳的处理方法:Zt =lnyt或者
C3=b3-b2
D6=average(c3:c5)
e6=b5+d6
一阶差分移动平均算例的原始曲线与趋势线
电量
25
20
线性 趋势线
15
10
5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E
| Xt - X ^t | Xt
( 17)
以上 4 个公式都有一个共同点, 即把各期的模型 误差不分远近同等看待, 但实际上 , 近期的误差对预 测的影响比远期的误差要大 . 应该这样说, 衡量外推
第 32 卷
第3期
陈
娟等
指数 平滑法及其在负荷预测中的应用
39
预测误差大小的判据与衡量曲线的拟合程度, 判据应 该有所不同 , 后者可对各期的绝对误差值采用等权的 算术平均计算, 而前者宜采用/ 厚近薄远0 的加权算术 平均[ 3] , / 厚近薄远0可以体现近期误差比较重要的特 点. 2. 2 采用/ 厚近薄远0 原则优选 A 值时权重大小及判 据公式的选择 / 厚近薄远0 原则的物理意义是 , 物理量未来的变 化趋势更多地取决于历史时段中近期的发展规律, 远 期的历史数据与未来发展趋势的相关性较弱 [ 4] . / 厚近薄远0 的具体做法有多种 , 本文采用的方法 如下 : 给定一个 B( 0< B < 1) , 将模型误差用下列各式 确定 : 加权平均平方和误差 : WMSE = 1 n 加权均方根误差 : WRMSE = , St 为第 t 期的平滑值; x t 为第 t 期的实际观察 值; S t- 1 为第 t - 1 期的平滑值 ; A为平滑常数 , 其取值 范围为 ( 0, 1) ; 将 St - 1 = A x t - 1 + ( 1- A ) St - 2 , S t - 2 = A x t- 1 + ( 1- A ) St - 3 , St - 3 = A x t - 1 + ( 1- A ) St - 4 , , 代 入公式( 1) 可得 : St = A xt + A (1- A ) x t- 1 + A (1- A ) x t- 2 + A (1- A ) 3 x t- 3 + , + A (1- A ) t- 1 x 1 + ( 1 - A ) tS 0 上述公式中各项系数和为 A+ A ( 1- A )+ A (1- A ) + , + A ( 1- A )
摘要 : 指数平滑法是电力系统负荷预测的主要方法之一, 该方法的准确性取决于平滑系数 A . 对采 用厚近薄远原则与远近相同原则优选 A 进行对比研究, 结果表明采用厚近薄远原则优选 A 有更好 的结果. 在此基础上, 结合相关分析, 给出了厚近薄远的具体方案, 并给出了负荷预测的具体实例 . 关键词: 负荷预测 ; 中图分类号: TM715 指数平滑法 ; 平滑系数; 优选 文章编号 : 16722948X( 2010) 0320037205 文献标识码: A
.
电力系统负荷预测理论和方法随时代的发展而 进步 , 如今在深度和广度上都有了长足的进步. 负荷 预测总的来说可分为非数学和数学方法两大类 . 非数 学方法有国际比较法、 专家估计法等 , 数学方法主要 包括相关法和外推法两类 . 相关法有回归分析法和投 入产出法; 外推法有指数平滑法、 时间序列法、 卡尔曼 滤波法等 . 指数平滑法作为外推法中的一种重要类型 , 运用 尤为普遍 . 原因在于这种方法建立的模型较简单, 计 算简便、 需要存贮的数据少, 通过近期的观察值能很 快地计算出新的预测值 . 在电力负荷预测方面, 它既 可用于对未来周日以小时负荷为统计样本的短期预
第 32 卷 第 3 期 2010 年 6 月
三峡 大学学报 ( 自然科学版 ) J of China Three Gor ges Univ. ( Natura l Sciences)
Vol 1 32 No 13 Jun1 2010
指数平滑法及其在负荷预测中的应用
陈 娟1 吉培荣1 卢 丰2
434023) ( 1. 三峡大学 电气与新能源学院, 湖北 宜昌 443002; 2. 荆州供电公司, 湖北 荆州
1
1. 1
指数平滑法介绍
指数平滑法基本原理 指数平滑法的一般公式是 : St = A xt + (1- A ) S t- 1 ( 1)
a t = 3S (t 1) - 3S (t 2) + S(t 3) bt = A ( 1) [ ( 6- 5A )St 2( 1 - A )2
( 8)
2( 5 - 4A ) S(t 2) + ( 4 - 3 A ) S(t 3) ] ct = A ( 1) - 2S(t 2) + S(t 3) ] 2 [ St 2( 1- A )
accuracy of t he met hod depends on smoot hing coefficient A . In t his paper, a st udy of how to seek t he best A is given. T he results show t hat the use of principle of valueing near errors and cont empt ing far error s can get a bet t er model. On this basis, combined wit h correlat ive analysis, a met hod of how t o value near er rors and cont empt far err ors is proposed. A pract ical example of load forecasting is also shown here. Keywor ds load forecast ing; exponent ial smoot hing met hod; smoot hing coefficient ; opt imum seeking
Exponential Smoothing Method and Its Application to Load Forecasting
Chen Juan1 Ji Peirong1 Lu Feng2
( 1. Col lege of Elect rical Engineering & Renewable Energy, China Three Gorges Univ. , Yichang 443002, China; 2. Jingzhou Power Supply Company, Jingzhou 434023, China) Abstr act Exponent ial smoot hing met hod is one of the main load forecasting met hods for power syst em; the
t 2 t- 1 2
以上各式 中, S(t 1) 、 S (t 2) 、 S(t 3) 分别 为 t 期的一 次平滑 值、 二次平滑值、 三次平滑值. 各次平滑 值计算公式 为: 一次指数平滑值: S (t 1) = A X t + (1- A ) S (t-1)1 二次指数平滑值: S(t 2) = A X (t 1) + ( 1 - A ) S(t-2)1 三次指数平滑值: S(t 3) = A X (t 2) + ( 1 - A ) S(t-3)1 ( 13)
nWMAE = 1 E | et | B n t= 1 加权平均绝对百分比误差 : n t n t= 1
Ee B
n t= 1
2 n- t t
( 18)
图 1 优 选过程的流程图
1 n
E eB
2 t
n- t
( 19)
3
实验研究
( 20)
以下 6 组数据分别为确定性数据 ( 数据 [ 1] ) 、 有 随机偏差数据 ( 数据 [ 2] - [ 4] ) 和实际年度负荷数据 ( 数据[ 5] - [ 6] ) . 数据 [ 1] : 10, 10. 5, 11, 11. 5, 12, 12. 5, 13, 13. 5, 14, 14. 5, 15, 15. 5. 数据 [ 2] : 6, 14, 16, 24, 26, 34, 36, 44, 46, 54, 56, 64. 数据 [ 3] : 1, 2, 9, 11, 24, 28, 46, 54, 76, 88, 114, 130. 数据 [ 4] : 2, 6, 10, 8, 15, 25, 31, 49, 67, 86, 97, 95. 数据 [ 5] : 10. 2, 14. 3, 17. 6, 21. 4, 26. 9, 27. 7, 28. 9, 30. 4, 32. 1, 35. 7, 39. 9, 45. 2 ( 河 南 省 某 市 1992~ 2003 年用电量数据 ) . 数据 [ 6] : 142. 879, 164. 962, 187. 018, 223. 645, 259. 477, 279. 949, 299. 731, 320. 195, 353. 370, 401. 515, 439. 186, 496. 839( 福建省 1991~ 2002 年全社会用电 量数据) . 实验过程中, 分别采用 MA PE 和 WMAPE 作为 优选平滑系数 A 的目标函数 . 实验程序用 Delphi 语 言编制 , 用前 11 个 ( 年 ) 的数据按照远近相同原则和 厚近薄远的原则优选出的平滑系数 A值 , 见表 1. 从表 1 可以看出 , 对于确定性的数据 , 建模时采用远近相 同原则和厚近薄远的原则优选出的 A 值是一样的 ; 而 对非确定性的数据 , 总体上看两种原则优选出的平滑 系数是不一样的. 对非确定性的数据, 当 B\ 0. 95 时,
( 1) t- 1
( 11) ( 12)
+ ( 2)
t 1- (1- A ) t (1- A ) = A 1- (1- A ) ) + ( 1- A t
以上各式中 , X t 为 t 期的观察值 , S 、 S 期、 t- 1 期的一次平滑值, S 、 S 期的二次平滑值 , S 、 S 次平滑值 .
