第4章 移动平均法和指数平滑法(2)
时间序列预测的常用方法及优缺点分析

时间序列预测的常用方法及优缺点分析一、常用方法1. 移动平均法(Moving Average)移动平均法是一种通过计算一系列连续数据的平均值来预测未来数据的方法。
这个平均值可以是简单移动平均(SMA)或指数移动平均(EMA)。
SMA是通过取一定时间窗口内数据的平均值来预测未来数据,而EMA则对旧数据赋予较小的权重,新数据赋予较大的权重。
移动平均法的优点是简单易懂,适用于稳定的时间序列数据预测;缺点是对于非稳定的时间序列数据效果较差。
2. 指数平滑法(Exponential Smoothing)指数平滑法是一种通过赋予过去观测值不同权重的方法来进行预测。
它假设未来时刻的数据是过去时刻的线性组合。
指数平滑法可以根据数据的特性选择简单指数平滑法、二次指数平滑法或霍尔特线性指数平滑法。
指数平滑法的优点是计算简单,对于较稳定的时间序列数据效果较好;缺点是对于大幅度波动的时间序列数据预测效果较差。
3. 季节分解法(Seasonal Decomposition)季节分解法是一种将周期性、趋势性和随机性分开处理的方法。
它假设时间序列数据可以被分解为这三个不同的分量,并独立预测各分量。
最后将这三个分量合并得到最终的预测结果。
季节分解法的优点是可以更准确地预测具有强烈季节性的时间序列数据;缺点是需要根据具体情况选择合适的模型,并且较复杂。
4. 自回归移动平均模型(ARMA)自回归移动平均模型是一种统计模型,通过考虑当前时刻与过去时刻的相关性来进行预测。
ARMA模型考虑了数据的自相关性和滞后相关性,能够对较复杂的时间序列数据进行预测。
ARMA模型的优点是可以更准确地预测非稳定的时间序列数据;缺点是模型参数的选择和估计比较困难。
5. 长短期记忆网络(LSTM)长短期记忆网络是一种深度学习模型,通过引入记忆单元来记住时间序列数据中的长期依赖关系。
LSTM模型可以有效地捕捉时间序列数据中的非线性模式,具有很好的预测性能。
LSTM模型的优点是适用于各种类型的时间序列数据,可以提供较准确的预测结果;缺点是对于数据量较小的情况,LSTM模型容易过拟合。
时间序列的平滑预测法

时间序列的平滑预测平滑法:简单平均法,移动平均法、指数平滑法。
平滑法既可以用于对时间序列进行平滑以描述序列的趋势,也可对平稳时间序列进行短期预测。
1、 简单平均法根据过去已有的观测值通过简单平均来预测下一期的值;舍时间序列已有的t 期观测值为y1、y2………yt ,那么t+1期的预测值1t F +值为:112111111t+2111(.......),11,1t+2=,t+1tt t i i t t t t t i i F y y y y t t t t e F F y +=+++++==++=++=-∑∑当到了期时,有了期的实际值y 就可以计算误差y 那么期的预测值就为以此类推。
2、 移动平均法通过对时间序列逐期递移求得平均数作为趋势值或者预测值的一种平滑预测方法。
移动平均又包括简单移动平均和加权移动平均。
简单移动平均就是将最近K 期的观测值进行平均,作为下一期的预测值;1<K<t.1211231t+21........,........t k t k t tt t t k t k t t t y y y y F y ky y y y F y k-+-+-+-+-+++++++==++++==同理均方误差MSE 的计算公式为:MSE =误差平方和误差个数移动平均法只使用最近K 期的数据,每次计算都是使用最近K 期数据;这一方法比较适合较为平稳的时间序列数据。
实际中选取不同的K ,比较MSE 的大小来选择合适的步长。
3、 指数平滑法一次指数平滑就是以一段时期的预测值和观测值的线性组合作为t+1期的预测值,预测模型为:说明:通常将11F y =。
1(1)t t t F y F αα+=+-其中,0<<1t t y t t αα为期实际观测值,F 为期的预测值;为平滑系数()。
211111322212433321=(1)(1)=(1)(1)=(1)1-+(1)F y F y y y F y F y y F y F y y F αααααααα∂+-=∂+-=∂+-=∂+-∂+-=∂+-第二期预测值:第三期预测值:第四期预测值:()y 依此类推。
移动平均法和平滑法

5.5 温特线性和季节性指数平滑法
一、温特线性和季节性指数平滑法旳基本原理 温特线性和季节性指数平滑法利用三个方 程式,其中每一种方程式都用于平滑模型旳三 个构成部分(平稳旳、趋势旳和季节性旳), 且都具有一种有关旳参数。
回总目录 回本章目录
温特法旳基础方程式:
St
xt ItL
1 St1
bt1
回总目录 回本章目录
设时间序列为 x1, x2 ,..., 移动平均法能够表达为:
1 t
Ft1
xt xt1 ... xtN 1
/
N
N
xi
t N 1
式中: xt 为最新观察值;
Ft 1为下一期预测值;
由移动平均法计算公式能够看出,每
一新预测值是对前一移动平均预测值旳修
正,N越大平滑效果愈好。
Ft1 xt (1 )Ft
回总目录 回本章目录
由一次指数平滑法旳通式可见: 一次指数平滑法是一种加权预测,权数为
α。它既不需要存储全部历史数据,也不需要
存储一组数据,从而能够大大降低数据存储问 题,甚至有时只需一种最新观察值、最新预测
值和α值,就能够进行预测。它提供旳预测值
是前一期预测值加上前期预测值中产生旳误差 旳修正值。
回总目录 回本章目录
计算公式:
St axt 1 a St1
St aSt 1 a St1
St为一次指数平滑值;St 为二次指数平滑值;
at 2St St
bt
1
St St
Ftm at bt m
m为预测超前期数
回总目录 回本章目录
二、霍尔特双参数线性指数平滑法 其基本原理与布朗线性指数平滑法相 似,只是它不用二次指数平滑,而是对趋 势直接进行平滑。
时间序列预测的方法与分析

时间序列预测的方法与分析时间序列预测是一种用于分析和预测时间相关数据的方法。
它通过分析过去的时间序列数据,来预测未来的数据趋势。
时间序列预测方法可以分为传统统计方法和机器学习方法。
下面将分别介绍这两种方法以及它们的分析步骤。
1. 传统统计方法传统统计方法主要基于时间序列数据的统计特征和模型假设进行分析和预测。
常用的传统统计方法包括移动平均法、指数平滑法和ARIMA模型。
(1) 移动平均法:移动平均法通过计算不同时间段内的平均值来预测未来的趋势。
该方法适用于数据变动缓慢、无明显趋势和周期性的情况。
(2) 指数平滑法:指数平滑法通过对历史数据进行加权平均,使得近期数据具有更大的权重,从而降低对过时数据的影响。
该方法适用于数据变动较快、有明显趋势和周期性的情况。
(3) ARIMA模型:ARIMA模型是一种常用的时间序列预测模型,它结合了自回归(AR)、差分(I)和滑动平均(MA)的概念。
ARIMA模型可以用于处理非平稳时间序列数据,将其转化为平稳序列数据,并通过建立ARIMA模型来预测未来趋势。
2. 机器学习方法机器学习方法通过训练模型来学习时间序列数据的特征和规律,并根据学习结果进行预测。
常用的机器学习方法包括回归分析、支持向量机(SVM)和神经网络。
(1) 回归分析:回归分析通过拟合历史数据,找到数据之间的相关性,并建立回归模型进行预测。
常用的回归算法包括线性回归、多项式回归和岭回归等。
(2) 支持向量机(SVM):SVM是一种常用的非线性回归方法,它通过将数据映射到高维空间,找到最佳分割平面来进行预测。
SVM可以处理非线性时间序列数据,并具有较好的泛化能力。
(3) 神经网络:神经网络是一种模仿人脑神经元组织结构和工作原理的计算模型,它通过训练大量的样本数据,学习到数据的非线性特征,并进行预测。
常用的神经网络包括前馈神经网络、循环神经网络和长短期记忆网络等。
对于时间序列预测分析,首先需要收集并整理时间序列数据,包括数据的观测时间点和对应的数值。
指数平滑法

指数平滑法,也叫指数移动平均法,是移动平均预测法加以发展的一种特殊加权移动平均预测法。
一次指数平滑法是以本期的实际值和一次指数平滑预测值的加权平均作为下一期的市场现象预测值的方法。
一次指数平滑公式的实际意义是,被研究市场现象某一期的预测值,等于它前一期的一次指数平滑预测值,加上以平滑系数调整后的市场现象前一期的观察值与一次平滑值的离差。
模型平滑指数的确定指数平滑法是以首项系数为,公比为的等比数列的和为权数的加权平均法。
在计算过程中,越接近预测期的权数越大,越远离的权数越小.的取值在0到1之间,在一次预测中,同时选择几个值进行预测,并分别计算预测误差,最后选择误差小的初始值的确定一般将定义为应用某企业的历史销售资料如下,用一次指数平滑法预测2009年的销售额(1)确定平滑指数,选定0.3、0.5、0.8(2)确定第一个平滑值,即1997年的一次指数平滑值(3)分别计算不同平滑系数下各年的预测值以0.3的平滑系数为例,预测2009年销售额趋势预测法原理趋势预测法,也叫趋势外推预测,就是利用时间序列所具有的直线或曲线趋势,通过建立预测模型进行预测的方法。
模型直线趋势预测法直线方程Y=a+bXX为自变量,为按照自然数顺序排列的时间序数Y为因变量,为预测对象按照时间排列的数据趋势外推法,就是通过预测对象和时间的对应关系,用拟合方程的方法寻找参数,建立预测模型进行预测。
应用已知某企业某种产品1993年-2006年的销售数据,请用趋势外推预测法预测企业2007年的销售量。
一元线性回归模型例题进行预测2008年固定投资为298亿元,预计国内生产总值为市场调查方案范文分享(一)调研背景近年来,宝洁公司凭借其强大的品牌运作能力以及资金实力,在洗发水市场牢牢地坐稳了第一把交椅。
但是随着竞争加剧,局势慢慢起了变化,联合利华强势跟进,夏士莲、力士等多个洗发水品牌从宝洁手中夺走了不少消费者。
花王旗下品牌奥妮和舒蕾占据了中端市场,而低端的市场则归属了拉芳、亮庄、蒂花之秀、好迪等后起之秀。
指数平滑法

(2)指数平滑法指数平滑法是从移动平均法发展而来的,它是以预测期的上期实际值和预测值为基数,分别给两者不同的权数,计算出加权平均数作为预测期的预测值的方法。
其计算公式如下:式中:Yt--预测期的预测值;Yt-1--预测期的前期预测值;Xt-1--预测期的前期实际值;a--平滑系数(0≤a≤1)。
因为从这个公式可以看出,只要有上期的预测值Yt-1和上期的实际值Xt-1,就可以求得预测期的预测值Yt。
故同理有:将 Yt-1和Yt-2代入Yt,就可以得到:由此可见,指数平滑法实质上就是一种加权移动平均法。
在计算时分别以a、a(1-a)、a(1-a)2……对过去各期的实际值进行了加权,权数反映各期实际值对预测值的不同影响。
近期的影响较大,加权数也较大;远期的影响较小,加权数也较小。
由于加权数是指数形式,因此这种方法被称作指数平滑法。
在指数平滑法中,平滑系数a是很重要的参数,它通常是根据预测者的经验确定的。
一般来讲,a值越大,则近期实际值的趋向性变动的影响也越大;a值越小,则近期实际值的趋向性变动的影响也越小。
a一般在0.01至0.30之间,合适的a值要根据过去的数据经过试算和调整求得。
例如,某企业本季度销售额预测值为6000万元,实际销售额为6500万元,a假定=0.1,则下季度销售额的预测值为:=0.1×6500+(1-0.1)×6000=6050万元(3)趋势延伸法趋势延伸法就是根据时间序列数据,运用数学的最小二乘法求得变动趋势线,并使其延伸,借以预测未来的发展趋势的方法,因而又叫最小二乘法。
趋势延伸法适用于长期预测,常用的主要有直线趋势法和曲线趋势法。
这里主要介绍直线趋势法,曲线趋势法请参考有关教材书籍。
直线趋势法适用于历史数据随时间的发展变化趋势近于直线的情况。
其方程式为:式中:Y--预测理论值;X--时间序数;a、b--待定系数。
根据最小二乘法原理,当∑X=0时,有:例题:某企业1999年1-5月份的销售额资料为:试预测该企业6月份的销售额。
移动平均与指数平滑

— 203.8 206.9 213.8 216.8 218.0 212.1 210.8 216.1 213.2 217.3 226.5
— 203.8 209.0 230.0 226.9 223.8 211.1 209.5 219.0 212.8 219.8 233.8
设时间序列为x1,x2, …: 移动平均法可以表示为:
( xt xt 1 xt N 1 ) 1 t Ft 1 xi N N t N 1
式中:
xt为最新观察值; Ft+1为下一期预测值;
由移动平均法计算公式可以看出,每一新预测值是对
前一移动平均预测值的修正,N越大平滑效果愈好。
(1)移动平均法有两种极端情况
在移动平均值的计算中包括的过去观察值的实
际个数N=1,这时利用最新的观察值作为下一期
的预测值;
N=n ,这时利用全部 n个观察值的算术平均值作
为预测值。
当数据的随机因素较大时,宜选用较大的N,这样有
利于较大限度地平滑由随机性所带来的严重偏差;
当数据的随机因素较小时,宜选用较小的N,这有利 于跟踪数据的变化,并且预测值滞后的期数也少。
(1)一次指数平滑法的初值的确定有几种方法: 取第一期的实际值为初值; 取最初几期的平均值为初值。
一次指数平滑法比较简单,但也有问题。问题之 一便是力图找到最佳的 α 值,以使均方差最小,这需 要通过反复试验确定。
例:用一次指数平滑法对1981年1月我国平板玻璃月产量进行预
测(α=0.3,0.5 ,0.7)。并选择使均方误差最小的α进行预测
0.7 259 .5 0.3 240 .1 253 .68
移动平均法和平滑法

回总目录 回本章目录
例题分析
•例 1
分析预测我国平板玻璃月产量。 下表是我国1980-1981年平板玻璃月产量,试选用N=3 和N=5用一次移动平均法进行预测。计算结果列入表中。
时间 1980.1 1980.2 1980.3 1980.4 1980.5 1980.6 1980.7 1980.8 1980.9 1980.10 1980.11 1980.12 序号 1 2 3 4 5 6 7 8 9 10 11 12 实际观测值 203.8 214.1 229.9 223.7 220.7 198.4 207.8 228.5 206.5 226.8 247.8 259.5 三个月移动平均值 215.9 222.6 224.8 214.6 209.0 211.6 214.3 220.6 227.0 五个月移动平均值 218.4 217.4 216.1 215.8 212.4 213.6 223.5
回总目录 回本章目录
5.2 线性二次移动平均法
一、线性二次移动平均法 (1)基本原理 为了避免利用移动平均法预测有趋势 的数据时产生系统误差,发展了线性二次 移动平均法。这种方法的基础是计算二次 移动平均,即在对实际值进行一次移动平 均的基础上,再进行一次移动平均。
回总目录 回本章目录
(2)计算方法 线性二次移动平均法的通式为:
Ft+m = ( St + bm) It−L+m t
回总目录 回本章目录
使用此方法时一个重要问题是如何确 定α、β和γ的值,以使均方差达到最小。 通常确定α、β和γ的最佳方法是反复试 验法。
回总目录 回本章目录
回总目录 回本章目录
5.3 线性二次指数平滑法
• 一次移动平均法的两个限制因素在线性二 次移动平均法中也才存在,线性二次指数 平滑法只利用三个数据和一个α值就可进 行计算; • 在大多数情况下,一般更喜欢用线性二次 指数平滑法作为预测方法。
指数平滑法+移动平均法等

指数平滑法一次指数平滑法公式如下:为t+1期的指数平滑趋势预测值;为t期的指数平滑趋势预测值;为t期实际观察值;为权重系数。
通用公式可以写成如下形式:1)简单移动平均法在市场预测中,经常遇到按时间排列的统计数据,如按月份、季度和年度统计的数据,称为时间序列。
时间序列预测方法包括简单移动平均法、指数平滑法、趋势外推法等。
1)简单移动平均法。
是预测将来某一时期的平均预测值的一种方法。
该方法按对过去若干历史数据求算术平均数,并把该数据作为以后时期的预测值。
简单移动平均法可以表述为:n —在计算移动平均值时所使用的历史数据的数目,即移动时间的长度.为了进行预测,需要对每一个t计算出相应的,所有计算得出的数据形成一个新的数据序列。
经过两到三次同样的处理,历史数据序列的变化模式将会被揭示出来。
这个变化趋势不及原始数据上下变化的幅度大,一般是在原始数据序列所描绘的曲线下方.因此,移动平均法从方法论上分类属于平滑技术.移动平均法只适用于短期预测,在大多数情况下只用于以月度或周为单位的近期预测。
优点:简单易行,容易掌握.缺点:只是在处理水平型历史数据时才有效,每计算一次移动平均需要最近的n个观测值。
而在现实生活中,历史数据的类型远比水平型复杂,这就大大限制了移动平均法的应用范围。
简单移动平均法的另一个主要用途是对原始数据进行预处理,以消除数据中的异常因素或除去数据中的周期变动成分。
例题9某商品在2005年1-12月份的销量如下表所示,请用简单移动平均法预测2006年第一季度该商场电视机销售量。
移动平均法计算表时间t—时序实际销售量(台)3个月移动平均预测2005。
1 1 532005。
2 2 462005.33 282005.44 35 42 2005。
55 48 36 2005。
36 50 37 2005。
77 38 44 2005.8834 45 2005.99 58 41 2005.1010 64 43 2005.1111 45 52 2005.1212 42 56弹性系数分析法9300*(0。
信息分析方法__指数平滑法

第四节 指数平滑法指数平滑法是在移动平均法基础上发展而来的一种时间序列分析预测法,它是通过计算指数平滑值,配合一定的时间序列预测模型,对现象的未来进行预测。
它既可用于市场趋势变动预测,也可用于市场季节变动预测。
在市场趋势变动预测中,根据平滑次数不同,指数平滑法又可分为一次指数平滑法、二次指数平滑法、三次指数平滑法。
一、 一次指数平滑法一次指数平滑法,是指根据本期观察和上期一次指数平滑值,计算其加权平均值,并将其作为下期预测值的方法。
它仅适用于各期数据大体呈水平趋势变动的时间序列的分析预测,并且仅能向下作一期预测。
(一) 平滑公式和预测模型设时间序列各期观察值为Y 1、Y 2,…,Y n ,则一次指数平滑公式为(1)1-t t (1)t)S -(1Y S αα+= (7-16)式中:(1)tS 为第t 期的一次指数平滑值;α为平滑系数,且0<α<1;Y t 为第t 期的观察值。
将第t 期的一次指数平滑值(1)t S 作为第t+1期的预测值1t Y ˆ+,即 )1(1ˆtt S Y =+ (7-17) 为进一步说明指数平滑法的实质,现将(7-16)式展开。
由于(1)1-t t (1)t)S -(1Y S αα+=(1)2-t 1-t (1)1-t )S -(1Y S αα+=… …(1)01(1)1)S -(1Y S αα+=所以 (1)1-t t 1t )S -(1Y Y ˆαα+=+ ])S -(1Y )[-(1Y (1)2-t 1-t t αααα++=(1)0t 11-t 1-t t S )-(1Y )-(1)Y -(1Y αααααα++++=(1)0t 1j -t j S )-(1Y )-(1ααα++=∑-=t j (7-18)由于0<α<1,当t →∞时,(1-α)t →0,于是将(7-27)式改写为∑∞=+=0j -t j 1t Y )-(1Y ˆj αα (7-19) 由于∑-==1j1)-(1t j αα,各期权数由近及远依指数规律变化,且又具有平滑数据功能,指数平滑法由此而得名。
指数平滑法

指数平滑法的基本公式
指数平滑法的基本公式是:
St · yt (1 )St 1
式中, St--时间t的平滑值; yt--时间t的实际值; St − 1--时间t-1的平滑值; α--平滑常数,其取值范围为[0,1]
由该公式可知: 1.St是yt和 St − 1的加权算数平均数,随着 α取值的 大小变化,决定yt和 St − 1对St的影响程度,当α 取1时,St = yt;当 取0时,St = St − 1。 2.St具有逐期追溯性质,可探源至St − t + 1为止,包 括全部数据。其过程中,平滑常数以指数形式递 减,故称之为指数平滑法。指数平滑常数取值至 关重要。平滑常数决定了平滑水平以及对预测值 与实际结果之间差异的响应速度。
S
(1) t
(1 ) yt j (1 ) S
j t j 0
ቤተ መጻሕፍቲ ባይዱ
t 1
(1) 0
由于0< <1,当 t→∞时, (1 )t→0,于是上述公 变为:
S
(1) t
(1 ) j yt j
j 0
由此可见 St(1) 实际上是 yt , yt i ,..., yt j ... 的加权平均。 (1 ), 加权系数分别为 , (1 )2 ,…,是按几何级 数衰减的,愈近的数据,权数愈大,愈远的数据, 权数愈小,且权数之和等于1,即
指数平滑

指数平滑法一、指数平滑法简介指数平滑法是布朗(Robert G..Brown)所提出,布朗(Robert G..Brown)认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到最近的未来,所以将较大的权数放在最近的资料。
指数平滑法是生产预测中常用的一种方法。
也用于中短期经济发展趋势预测,所有预测方法中,指数平滑是用得最多的一种。
简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用;移动平均法则不考虑较远期的数据,并在加权移动平均法中给予近期资料更大的权重;而指数平滑法则兼容了全期平均和移动平均所长,不舍弃过去的数据,但是仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
也就是说指数平滑法是在移动平均法基础上发展起来的一种时间序列预测分析法,它是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。
其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。
二、指数平滑法的基本公式指数平滑法的基本公式是:式中,∙S t--时间t的平滑值;∙y t--时间t的实际值;∙S t− 1--时间t-1的平滑值;∙a--平滑常数,其取值范围为[0,1];由该公式可知:1.S t是y t和S t−1的加权算术平均数,随着a取值大小变化,决定y t和S t−1对S t的影响程度,当a取1时,S t = y t;当a取0时,S t = S t− 1。
2.S t具有逐期追溯性质,可探源至S t−t+ 1为止,包括全部数据。
其过程中,平滑常数以指数形式递减,故称之为指数平滑法。
指数平滑常数取值至关重要。
平滑常数决定了平滑水平以及对预测值与实际结果之间差异的响应速度。
平滑常数a越接近于1,远期实际值对本期平滑值影响程度的下降越迅速;平滑常数a 越接近于 0,远期实际值对本期平滑值影响程度的下降越缓慢。
由此,当时间数列相对平稳时,可取较大的a;当时间数列波动较大时,应取较小的a,以不忽略远期实际值的影响。
第4章 移动平均法和指数平滑法(2)

4.3 指数平滑法
一次指数平滑公式的展开如下 :
ˆ ˆ aY 1a Y Y t 1 t t ˆ 1 aYt 1a aY a Y t 1 t1 ˆ aYt a1a Yt1 1a Y t 1
2
aYt a1a Yt1 a1a Yt2 a1a Yt3
例4-4:音像店每周的出租量y
740 660 0 680 y 700 720
5 t
10
15
如果依然使用一次移动平均法进行预测,会产生什 么后果?
4.2 平均值预测法
所谓二次移动平均,就是将一次移动平均序列再进行 一次移动平均。二次移动平均值的计算公式为:
M t M t 1 M t k 1 M k
Y12 Y11 Y10 ˆ ˆ 15.3(万元) Y2003.1 Y13 3
4.2 平均值预测法
一次移动平均法的应用:P101例4.3 采用5期移动平均的方法进行预测 预测方法选择是否合适?预测的效果如何?
4.2 平均值预测法
可对预测误差(残差)进行自相关检验: • 例4.3残差的自相关系数检验图
(2)趋势估算值:
Tt Lt Lt 1 1 Tt 1
(3)未来p期的预测值:
ˆ L pT Y t p t t
表示水平的平滑系数, 表示趋势估算值的平滑系数
4.3 指数平滑法
有关霍特法平滑系数和初始值的说明:
两个平滑系数 与 ,既可以通过主观选择,也可以通过软件 最小化预测误差自动选择 初始值的设定有两种方法: • 方法一:水平的初始值L0=Y1,T0=0 • 方法二:将前几期的观测值作为因变量,时间t作为自变量进 行回归,回归结果中常数项的估计值作为L0,斜率系数作为 趋势的初始值T0 (Stata默认前一半的观测值作为回归的样本 量)
电力负荷预测第四章 平移法与平滑法讲解

S (1) t
Yt
(1 )St
(1) 1
S (2) t
St (1)
(1
)St
(2) 1
S (3) t
St (2)
(1 )St
(3) 1
Yt k at bt k ct k 2
推导 (略)
a 3S 3S S (1)
(2)
递推式
Yt 1 Yt Yt 1 ...... Yt N 1 Yt Yt Yt N
1
N 1
Yt
j
N
N
N J 1
Yt
—(t+1)期预测
1
Yt — t期观察值
紧凑式
N — 移动平均期数(移动跨距)
年电量变化曲线
电量 18 16 14 12 10 8 6 4 2 0 81年 82年 83年 84年 85年 86年 87年 88年 89年 90年 91年 92年 93年
或都不平稳
均值不平稳的处理办法:1)季节差分▽s yt= yt –yt-s 2)一阶差分▽ yt= yt –yt-1
方差不平稳的处理方法:Zt =lnyt或者 Zt yt
4.时序分析的特点
●时序数据是多因素综合作用的结果。 ●不必考虑去寻找影响因素,以及识别主要因素、
次要因素。 ●与回归相比,不需要对随机扰动项的限定,在实
电量 10 12 13 16 16 15 16 17 15 14 13 14
N=3
11.7 13.3 15 15.7 16 16 16 15.3 14 13.7
N=3加权
12.7 13.1 14.3 15.5 15.7 16.3 15.8 13.8 13.6 13.6
移动平均法and指数平滑法

移动平均法and指数平滑法感谢:⼀、移动平均法(Moving average , MA)移动平均法⼜称滑动平均法、滑动平均模型。
⽤处:⼀组最近的实际数据值->[预测]->未来⼀期或⼏期内公司产品需求量/公司产能。
分类:简单移动平均和加权移动平均思想:根据时间序列资料,逐项推移,依次计算包含⼀定项数的序时平均值,以反映长期趋势。
好处:时间序列数值受周期变动和随机波动影响起伏较⼤,不容易显⽰事件发展趋势, MA可以消除这些因素影响。
(⼀)简单移动平均法各个元素的权重相等。
公式如下:Ft=(At-1 + At-2 + At-3 + ... + At-n) / n[简单的滑动窗⼝](⼆)加权移动平均法加权移动平均给固定跨越期限内的每个变量值以不同的权重。
其原理是:历史各期产品需求的数据信息对预测未来期内的需求量的作⽤不⼀样。
Ft=w1At-1 + w2At-2 + w3At-3 + ... + wnAt-n⼆、指数平滑法(Exponential Smoothing, ES)指数平滑法认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到最近的未来,所以将较⼤的权数放在最近的资料。
指数平滑法是⽣产预测中常⽤的⼀种⽅法,⽤于中短期经济发展趋势预测,所有预测⽅法中指数平滑⽤得最多。
简单的全期平均法:全部平均。
移动平均法:不考虑较远期数据,并在加权移动平均法中给予近期资料更⼤权重。
指数平滑法:兼容全期平均和移动平均所长,不舍弃过去的数据,仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
指数平滑法在移动平均法基础上发展起来的⼀种时间序列分析预测法,通过计算指数平滑值,配合⼀定的时间序列预测模型对现象的未来进⾏预测。
任⼀期的指数平滑值都是本期实际观察值与前⼀期指数平滑的加权平均。
(⼀)指数平滑法的公式S_t = a \c dot y_t + (1-a)S_{t-1}S_t:时间t的平滑值y_t: 时间t的实际值S_t-1: 时间t-1的平滑值a--平滑常数,取值范围[0, 1](⼆)指数平滑的预测公式根据平滑次数不同,指数平滑法分为:⼀次指数平滑法、⼆次指数平滑法和三次指数平滑法等(1)⼀次指数平滑y_t+1(predict) = a* y_t(actual) + (1-a) * y_t(predict)(2)⼆次指数平滑预测yt+m=(2+am/(1-a))yt'-(1+am/(1-a))yt=(2yt'-yt)+m(yt'-yt) a/(1-a)其中yt= ayt-1'+(1-a)yt-1,就是⼀次指数平滑的再平滑。
应用时间序列第四章习题解答1-4

t x x x x x t 1 t (1 ) t 1 (1 ) t 1 (1 ) t 1 ……○ t t t t t t
令 A lim
t
t x t
1 式两端取极限,得: ○
lim
t
(2)
ˆ21 x 20 x20 (1 ) x19 (1 )2 x18 … (1 )19 x1 x
0.4 13 0.4 0.6 11 0.4 0.62 10 … 0.4 0.619 10 11.79240287
t x x lim (1 ) lim t 1 t t t t
即 A (1 ) A
lim
t
xt A 1。 t
另解:根据指数平滑的定义有(1)式成立, (1)式等号两边同乘 (1 ) 有(2)式成立
t t (t 1) (1 ) (t 2) (1 ) 2 (t 2) (1 )3 (1) x t (1 ) x t (1 ) (t 1) (1 ) 2 (t 2) (1 )3 (2)
1 1 ˆ21 ( x20 x19 x18 x17 x16 ) (13 11 10 10 12) 11.2 解:(1) x 5 5
1 1 ˆ22 ( x ˆ21 x20 x19 x18 x17 ) (11.2 13 11 10 10) 11.04 x 5 5
a
6 25 6 4 0.16 。 25 25
b a 0.4
4. 现有序列 xt t , t 1, 2,… ,使用平滑系数为 的指数平滑法
《市场调查与分析》教材(第二版)模块四习题及答案(已修改)

模块四作业参考答案一.选择题1.分析市场信息,使之集中化、有序化成为可利用的信息,这一过程是( D )。
A.市场调查B.市场分析C.市场预测D.整理资料2.在资料整理阶段,资料分类时要注意同一资料的( B )。
A.差异性B.共同性C.统计性D.详尽性3.列表分析技术主要有(AB )。
A.单变量频数表技术B.交叉列表分析技术C.饼图技术D.柱形图技术4.交叉制表的优点有(ABCD )A.使统计数据清晰、简洁B.使统计内容简明易懂C.便于各变量间的对比,便于计算D.方便核查各数据的正确性和完整性5.资料录入时,对其编码的做法有( AB )。
A.事前编码B.事后编码C.结构编码D.精确编码6.用直线将各数据点连接起来而组成的图形,以折线方式显示数据的变化趋势的统计图是( B )。
A.饼形图B.折线图C.散点图D.柱形图7.资料分组的类型有(ABCD)。
A.质量标志分组B.数量标志分组C.空间标志分组D.时间标志分组8.比率或速度的平均应采用( C )来进行计算。
A. 简单算术平均数B. 加权算术平均数C. 几何平均数D. 调和平均数9.在下列两两组合的指标中,两个指标完全不受极端数值影响的一组是( D )。
A. 算术平均数和调和平均数B. 几何平均数和众数C. 调和平均数和众数D. 众数和中位数10.一项关于大学生体重的调查显示,男生的平均体重是60千克,标准差为5千克;女生的平均体重是50千克,标准差为5千克。
据此数据可以推断 ( B )。
A. 男生体重的差异较大B. 女生体重的差异较大C. 男生和女生的体重差异相同D. 无法确定11.比例相对指标是用以反映总体内部各部分之间内在的( C )。
A. 质量关系B. 计划关系C. 密度关系D. 数量关系12.相关分析研究的是( C )。
A. 变量之间的数量关系B. 变量之间的变动关系C. 变量之间相互关系的密切程度D. 变量之间的因果关系13.集合意见法的预测者是( AB )。
第四章 时间序列平滑预测法

ˆ ( N 3) X t 1 ˆ ( N 5) X
t 1
Xt
423 358 434
445 527 429 426 502 480 384 427 446
419 448
月份
1
2
3
4
5
6
7
8
9
10
11
12
13
ˆ ( N 3) X t 1 ˆ ( N 5) X
t 1
Xt
423 358 434 445 527 429 426 502 480 384 427 446 405 412 469 467 461 452 469 455 430 419 437 439 452 466 473 444 444 448
1 (1) ˆ X t 1 ( N 3) M t (3) ( X t X t 1 X t 2 ) 3
1 (1) ˆ X t 1 ( N 5) M t (5) ( X t X t 1 X t 2 X t 3 X t 4 ) 5
月份 1 2 3 4 5 6 7 8 9 10 11 12 13
实际销售量 三期移动平均预测 五期移动平均预测
只
550 500 450 400 350 300 0 1 2 3 4 5 6 7
下个月的 预测销售 量——
419 or 448
8 9 10 11 12 13
月份
?
N 的选取
在实用上,一般用对过去数据预测的均方误差S 来作为选取N 的准则。
N=3 N=5
不能归因于其他三种成分 的时间序列的变化
时间坐标若不是 季度,就是年
往往,一个时间序列,是由四种因素(T、 S、C、I)综合作用的结果。 这四种因素对时间序列变化的影响有两种基 本假设→
预测与决策第四章答案
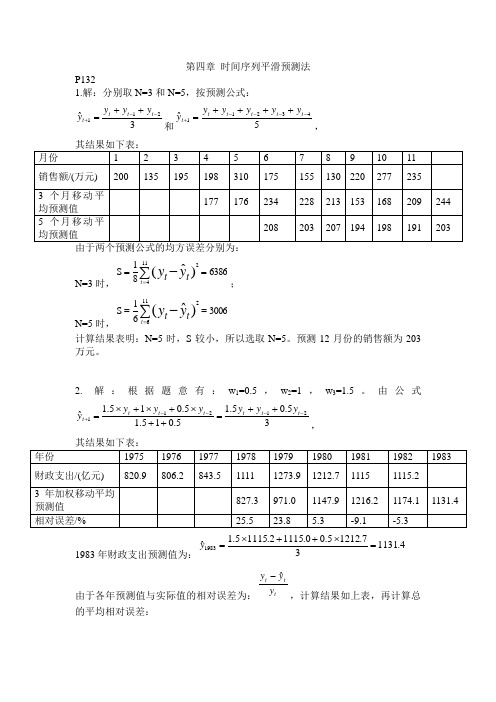
第四章 时间序列平滑预测法P1321.解:分别取N=3和N=5,按预测公式:3ˆ211--+++=t t t t y y y y和5ˆ43211----+++++=t t t t t t y y y y y y,N=3时,638681S 1142)ˆ(==∑-=t t t y y ;N=5时,300661S 1162)ˆ(==∑-=t t t y y计算结果表明:N=5时,S 较小,所以选取N=5。
预测12月份的销售额为203万元。
2. 解:根据题意有:w 1=0.5,w 2=1,w 3=1.5。
由公式35.05.15.015.15.015.1ˆ21211----+++=++⨯+⨯+⨯=t t t t t t t y y y y y y y,1983年财政支出预测值为:4.113137.12125.00.11152.11155.1ˆ1983=⨯++⨯=y由于各年预测值与实际值的相对误差为:t t t y yy ˆ-,计算结果如上表,再计算总的平均相对误差:%4.8%100)8.58274.53361(%100)ˆ1(=⨯-=⨯-∑∑tt y y由于总预测值的平均值比实际值低8.4%,所以可将1983年的预测值修正为6.1235%4.814.1131=-)(因此,1983年的财政支出为1235.6亿元。
3. 解:采用指数平滑法,取13ˆ0.13S 3.0)1(010====S y 。
即,α。
按预测模型:t t t y y y ˆ)1(ˆ1αα-+=+,预测结果如下表因此,预测1981。
4. 解:08.122310.11117.12297.13297.13235.1217.1347.142)2(8)1(8=++==++=M M ,则86.14308.12297.13222)2(8)1(88=-⨯=-=M M a 89.1008.12297.132)(132)2(8)1(88=-=--=M M b于是,得t=8时,直线趋势预测模型为:T y T 89.1086.143ˆ8+=+(2)利用移动平滑预测法当7.87S S 3.02010===)()(,初始值α,45.10745.122)2(8)1(8==S S ,则45.13745.10745.12222)2(8)1(88=-⨯=-=S S a 43.6)45.10745.122(7.03.0)(7.013.0)2(8)1(88=-=--=S S b于是,得t=8时,直线趋势预测模型为:T y T 43.645.137ˆ8+=+当7.87S S 6.02010===)()(,初始值α,根据上表计算得,64.12932.136)2(8)1(8==S S ,则99.14264.12932.13622)2(8)1(88=-⨯=-=S S a 01.10)64.12932.136(4.06.0)(4.016.0)2(8)1(88=-=--=S S b 于是,得t=8时,直线趋势预测模型为: T y T 01.1099.142ˆ8+=+(3) 三个模型的拟合误差分别为: 趋势移动平均法:()72.403174.122ˆ318621==-=∑=t t t y y S指数平滑法:()58.153713.1075ˆ71,3.08622==-==∑=t t t y y S α()99.67790.475ˆ71,6.08623==-==∑=t t t y y S αN=3的趋势移动平均法误差最小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.3 指数平滑法
一次指数平滑公式的展开如下 :
ˆ ˆ aY 1a Y Y t 1 t t ˆ 1 aYt 1a aY a Y t 1 t1 ˆ aYt a1a Yt1 1a Y t 1
2
aYt a1a Yt1 a1a Yt2 a1a Yt3
•
表4-1 化妆品销售额及一次移动平均法计算表(单位:万元)
年 2002 月 1 2 3 4 5 6 7 8 9 10 11 12 2003 1 t 1 2 3 4 5 6 7 8 9 10 11 12 13 销售额 Yt 15.0 16.5 14.7 16.2 13.8 12.9 14.0 14.4 15.3 14.7 16.5 14.7 预测值 15.4 15.8 14.9 14.3 13.6 13.8 14.6 14.8 15.5 15.3 0.8 -2.0 -2.0 -0.3 0.8 1.5 0.1 1.7 -0.8 15.2 14.8 14.3 14.3 14.1 14.3 15.0 15.1 -2.3 -0.8 0.1 1.0 0.6 2.2 0.3 k=3
练习:见书P106页表4-5(例4.4)
4.2 平均值预测法
关于二次移动平均法的小结: 该方法不是用二次移动平均值直接进行预测,而是 在二次移动的基础上,利用滞后偏差建立线性预测模 型,然后再用所得到的模型进行预测 该方法适用于平稳时间序列ST,以及存在线性变化 的趋势数据 该方法可以进行远期预测,但预测误差一般都较大, 因为at,bt实际上存在近期的局限性
Yt Yt 1 Yt k 1 ˆ Yt 1 M t k
(t k )
移动平均法下,每期观测结果的权重都相同 移动平均法只处理已知的最近k期数据,新的观测值 不断被纳入计算平均值,同时去掉早期的观测值 1阶移动平均MA(1)是4.1节公式(1)中的朴素预测法
4.2 平均值预测法
1.00 -1.00 1 Autocorrelations of e -0.50 0.00 0.50
2
3 Lag
4
5
6
Bartlett's formula for MA(q) 95% confidence bands
4.2 平均值预测法
• 例4.3残差自相关系数的Q检验结果 • • • • • • • • LAG AC 1 2 3 4 5 6 0.5063 0.0786 -0.2986 -0.6028 -0.6426 -0.2195 PAC 0.5137 -0.2146 -0.3971 -0.5096 -0.6381 0.0669 Q 7.2093 7.3904 10.126 21.807 35.745 37.456 Prob>Q 0.0073 0.0248 0.0175 0.0002 0.0000 0.0000
Yt Yt 1 Yt k 1 Mt k
(t k )
其中k为移动平均的期数,表示k阶移动平均 移动平均的作用在于修匀数据,消除一些随机干扰, 使长期趋势显露出来,从而可用于趋势分析及预测
4.2 平均值预测法
如果时间序列没有明显的周期变化和趋势变化,可 用第t 期的移动平均值作为第t+1期的预测值,即:
4.3 指数平滑法
用一次指数平滑法进行预测,除了选择合适的a外, 还要确定平滑序列的初始值 S0 ,初始值是由预测者 估计或指定的,具体方法是: (1)选取第一期观测值作为初始值,即:
ˆ S Y Y 1 0 1
(2)选取最初几期观测值的平均值作为初始值,即:
k 1 ˆ S Y Y t 1 0 k t 1
4.2 平均值预测法
• 当k=3时, • 当k=5时,
1 12 ˆ MSE Yt Y t 7 t 6
1 12 ˆ MSE Yt Y t 9 t 4
2
15.16 1.68 9
2
12.23 1.75 7
• 计算结果表明:k=3时,MSE较小,故选取k=3。预 测2003年1月份的化妆品销售额为:
Y12 Y11 Y10 ˆ ˆ 15.3(万元) Y2003.1 Y13 3
4.2 平均值预测法
一次移动平均法的应用:P101例4.3 采用5期移动平均的方法进行预测 预测方法选择是否合适?预测的效果如何?
4.2 平均值预测法
可对预测误差(残差)进行自相关检验: • 例4.3残差的自相关系数检验图
4.2 平均值预测法
关于一次移动平均法的小结: 一次移动平均法只处理已知的最近k期数据 局限: 该方法只能对后续相邻的那一项进行预测 该方法只适用于平稳时间序列ST,对趋势或季节型数 据的处理并不出色 当时间序列呈上升趋势时,预测值偏低;当时间序列 呈下降趋势时,预测值偏高
4.2 平均值预测法
为了解决大量数据储存的问题,还可以使用如下公式:
ˆ Y t 2 ˆ Y tY t 1 t 1 t 1
当时间序列是平稳的,简单平均法是一种适宜的预测 方法(例如处于成熟期的产品数量)
4.2 平均值预测法
4.2.2 一次移动平均法
定义:所谓一次移动平均法(moving average) ,就 是取时间序列的k个连续观测值予以平均,并依次滑动, 直至将数据处理完毕,得到一个平均值序列,即:
4.2.3 二次移动平均法
如果数据具有线性趋势,则一次移动平均数预测值 和实际值之间大都存在滞后的偏差,为解决存在线性趋 势的预测,需要使用二次移动平均法 该方法并不是用二次移动平均值直接进行预测,而是 在二次移动的基础上,利用滞后偏差建立线性预测模型, 然后再用所得到的模型进行预测
4.2 平均值预测法
历史观测值丧失其影响的速度取决于a的大小:a越大, 预测值对时间序列的反应速度也越快;反之则越慢。 因此选择合适的 a 值是得出精确预测结果的关键。 一般地,若序列变化较平稳,则 a 值应小一些;若序 列波动较大,则 a 值应大一些。除了人为选择a的取 值外,还可以通过软件的迭代法,自动选择产生最小 预测误差(例如MSE)的a值。
第4章 移动平均法和指数平滑法
4.1 朴素法 4.2 平均值预测法 4.3 指数平滑法 4.4 Stata软件操作
4.2 平均值预测法
4.2.1 简单平均法
定义:所谓简单平均法(simple average) ,就是采 用所有相关历史观测值的平均值作为下一期的预测,即:
t 1 ˆ Y Y t 1 i t i 1
例4-4:音像店每周的出租量y
740 660 0 680 y 700 720
5 t
10
15
如果依然使用一次移动平均法进行预测,会产生什 么后果?
4.2 平均值预测法
所谓二次移动平均,就是将一次移动平均序列再进行 一次移动平均。二次移动平均值的计算公式为:
M t M t 1 M t k 1 M k
4.3 指数平滑法
4.3.2 霍特法(Holt):趋势调整
霍特线性指数平滑法,主要考虑了随时间而变化的局 部线性趋势,即水平值和趋势斜率系数都会随时间而 改变
4.3 指数平滑法
用于霍特法的三个公式是: (1)现时水平估算值:
Lt aYt 1 a Lt 1 Tt 1
(2)趋势估算值:
Tt Lt Lt 1 1 Tt 1
(3)未来p期的预测值:
ˆ L pT Y t p t t
表示水平的平滑系数, 表示趋势估算值的平滑系数
4.3 指数平滑法
有关霍特法平滑系数和初始值的说明:
两个平滑系数 与 ,既可以通过主观选择,也可以通过软件 最小化预测误差自动选择 初始值的设定有两种方法: • 方法一:水平的初始值L0=Y1,T0=0 • 方法二:将前几期的观测值作为因变量,时间t作为自变量进 行回归,回归结果中常数项的估计值作为L0,斜率系数作为 趋势的初始值T0 (Stata默认前一半的观测值作为回归的样本 量)
4.3 指数平滑法
4.3.1 一次指数平滑法
指数平滑法(exponential smoothing):是根据更近 的经验不断修正预测值的一种方法
ˆ S aY 1 a Y ˆ Y ˆ a (Y Y ˆ) Y t 1 t t t t t t
a为平滑系数(0<a<1) 第t+1期的预测值等于在第t期的预测值的基础之上, 再对第t期的预测误差进行a 倍调整
ˆ Y t
k=5
ˆ Yt Y t
ˆ Y t
ˆ Yt Y t
4.2 平均值预测法
• 预测误差可以通过均方误差MSE来度量,即:
1 n 2 ˆ MSE (Yt Yt ) n k t k 1
其中,n为时间序列的项数 • 如在本例中,要预测化妆品的销售额,究竟应取 k=3还是k=5合适,可通过计算这两个预测公式的均 方误差MSE,选取使MSE较小的那个k。
4.3 指数平滑法
移动平均法只考虑最近的观测结果,且对每期观测 值都赋予相同的权重 指数平滑法是对时间序列由近及远采取具有逐步衰减 性质的加权处理,使得近期的数据以较大的权数,远 期的数据以较小的权数,是对移动平均法的改进 指数平滑法的分类: 一次指数平滑法 霍特法(Holt):趋势调整 温特法(Winters) :趋势和季节调整
' t
其中 M t'和M t分别表示第t期的二次移动平均值和一次 移动平均值 M t 从第k项开始有数据, M t' 从(2k-1)项开始有数据
4.2 平均值预测法
为了消除滞后偏差对预测的影响,可在一次、二次移 动平均值的基础上,利用滞后偏差的规律来建立线性趋 势模型,利用线性趋势模型进行预测 预测步骤为: (1)对时间序列 yt 计算出 M t 和M t' (2)利用 M t 和M 计算线性趋势模型的截距 t 和斜率 bt at M t M t M t' 2 M t M t' 2 ' bt M M t t k 1 k表示移动平均值的期数
