为什么样本方差里面要除以(n-1)而不是n
为什么样本标准差使用被称为自由度的n-1

为什么样本标准差使用被称为自由度的n-1
自由度的定义:
“自由度(degrees of freedom)”指的是,在一定的约束条件下,样本所能提供的独立的信息的个数。
考虑样本量为n的样本(n个数),如果我们知道样本均值,那么我们只需要知道前n-1个数,就可以得知全部信息,因为最后一个数可以借助均值计算得出。
所以,在给定样本均值(约束条件)的情况下,我们相当于在原本n个数的基础上消减了一个自由度,样本提供的信息只有n-1个独立的部分。
当样本数据的个数为n时,若样本平均数x拔确定后,则附加给n个观测值的约束个数就是1个,一次只有n-1个数据可以自由取值,其中必有一个数据不能自由取值。
按照这一逻辑,如果对n个观测值附加的约束个数为k个,自由度则为n-k。
例如假设样本有3个值,即x1=2,x2=4,x3=9,则当x拔=5确定后,x1、x2、x3只有两个数据可以自由取值,另一个则不能自由取值,比如x1=6,x2=7,那么x3必然取2,而不能取其他值。
样本方差自由度为什么为n-1呢,因为在计算离差平方和∑(xi -x)2 时,必须先求出样本平均数 x拔,而 x拔则是附加给∑(xi -x)2 的一个约束,因此,计算离差平方和时只有n-1个独立的观测值,而不是n个。
方差估计常用公式推导

方差估计常用公式推导
嘿,咱今天就来好好聊聊方差估计常用公式推导!先来说说总体方差的估计公式吧,就像射击打靶一样,要衡量一群数据的离散程度。
比如咱有一组数 1,3,5,7,9,这中间的波动有多大呢,就得用公式啦!
总体方差的估计公式就是:样本方差 = 各数据与样本均值的差的平方和除以样本个数。
哎呀,是不是听起来有点晕乎?举个例子哈,这组数 1,3,5,7,9,先算出均值是 5,然后算每个数和 5 的差值的平方,再把这些平方和加起来,最后除以 5,这不就得出方差啦!
还有个样本方差公式呢,就好像是给总体方差打了个折扣!公式是:样本方差 = 各数据与样本均值的差的平方和除以(样本个数 - 1)。
咦,为啥要除以(样本个数 - 1)呢?这就像给计算加了点调料,让结果更靠谱呀!比如说另一组数 2,4,6,8,它的样本方差就得按照这个公式好好算一算啦!
咋样,是不是感觉方差估计也不是那么难理解啦?加油哦,你肯定能掌握的!。
证明样本方差的时候除以n是一个一致的估计量

证明样本方差的时候除以n是一个一致的估计量
样本方差是统计分析中常常使用的量,它是用来描述一组数据的离散程度,并且可以用来衡量数据之间的差异。
在统计学中,方差是一种重要的度量,但是由于其计算复杂性,通常会有所出入。
《证明样本方差的时候除以n是一个一致的估计量》这个问题,研究人员普遍认为,当样本方差除以n时,这一估计量是一致的。
这就是说,当数据组大小越大,样本方差的估计值越接近真实方差。
要解释这一结论,我们可以从理论上和实证上来考虑这个问题。
实证上,我们可以利用不同大小的样本,对样本方差的估计量进行检验,假设真实方差为θ。
实验结果表明,当样本大小增加时,样本方差的估计值的确是一致的,即:
估计量S / n趋于θ
从这个实证上,我们很容易得出结论:当样本方差除以n时,这一估计量是一致的。
理论上,这一结论也可以由大数定律和中心极限定理给出证明,即大数定律指出,任何统计量的样本平均都会收敛到总体平均,而中心极限定理则指出,总体平均的样本方差会收敛到总体方差。
因此,由此可以推出,当样本方差除以n时,这一估计量是一致的。
由以上理论和实证的论述可知,当样本方差除以n时,这一估计量是一致的,这也是大多数研究人员普遍认可的,由此可见,这一结论是可信的。
总结一下,本文的主要内容是:证明样本方差的时候除以n是一
个一致的估计量。
从理论和实证上来看,当样本方差除以n时,这一估计量是一致的,这也是大多数研究人员普遍认可的,由此可见,这一结论是可信的。
样本方差公式中N-1的思考

样本方差公式中N-1的思考蒲智勇摘要:样本方差是来判断数据的稳定性的,在生活中应用样本方差来做出选择,直接关系着事件的成功与否。
本文通过文件检索等方法,分析了的意义与来源,得出样本方差公式中N-1是对标准方差的修正的结果。
关键词:样本样本方差统计量无偏性Sample variance formula for N - 1Abstract:the stability of the sample variance is to judge the data, application sample variance in life to make a choice, directly related with the success of the event. In these paper, through methods of document retrieval, analyzes the meaning and origin, draw a sample variance formula for N - 1 is the result of a modification to the standard variance.Keywords:sample sample variance statistics magnitude unbiasedness前言:目前许多教材上,对样本方差是如何来的都未做出解释,即使有也一笔带过,大学上课的老师提都未提。
大学是来做学问的地方,怎么不去探讨它?当接触这样本方差公式时,就在想是不是,样本的平均值与观察值相等的原因引起的。
就随便列举了一组观察值,恰好观察值与样本均值相等,就草率的认为明白了这公式。
但心里还是对这个公式感觉怪怪的,怎么跟以前的方差公式不一样,以前是N,怎么现在变成了N-1?一直想从其他角度推出这个公式,因为个人因素,未能如愿。
那就只有从侧面去解释这个原因一、样本方差中的基本概念为无偏估计。
贝塞尔公式 n-1

贝塞尔公式 n-1
什么是贝塞尔公式 n-1?
在统计学中,贝塞尔公式 n-1 常常被用来对样本统计量的方差进行校正。
而对于需要进行参数估计的问题,常常需要使用样本较小的情况下,
通过样本均值来估计总体均值。
然而,当我们使用样本平均数来进行参数估计时,可能会出现估计偏
差的问题。
这是因为我们所计算的样本均值只是样本中所有数据相加
后所得到的平均数,并未考虑到样本数据集在相加的过程中出现了随
机误差。
为了避免这样的估计偏差,我们需要对样本统计量的方差进
行校正。
在这种情况下,我们将采用贝塞尔公式,这个公式在统计学中是非常
重要的。
事实上,许多人都认为贝塞尔公式是统计学的艺术之一。
不
过初学者也不要害怕,它对于我们的数据分析提供了一种重要的手段,帮助我们更加准确地估计出样本数据的总体参数。
就像之前所说的,贝塞尔公式用于校正样本统计量的方差。
具体地说,贝塞尔公式是将样本方差乘以一个校正因子来得到修正后的样本方差,这个校正因子通常是 (n-1)/n,其中 n 代表样本数据点的总数。
使用贝塞尔公式校正样本统计量的方差的好处是显然的,它可以帮助
我们更加准确地估计总体参数。
然而,也需要注意到贝塞尔公式使用
的范围是有限的。
当样本数据点数量趋近于总体数据点数量时,贝塞尔公式的偏差会变得非常小,因此它的效果也会减弱。
总之,贝塞尔公式对于样本数据的方差校正是非常有用的,这样我们就可以得到更加准确的总体参数估计。
它是统计学中的一道精妙的工具,在实际数据分析过程中也经常被使用。
为什么样本方差里面要除以(n-1)而不是n?

前段日子重新整理了一下这个问题的解答,跟大家分享一下,如果有什么错误的话希望大家能够提出来,我会及时改正的,话不多说进入正题:首先,我们来看一下样本方差的计算公式:刚开始接触这个公式的话可能会有一个疑问就是:为什么样本方差要除以(n-1)而不是除以n?为了解决这个疑惑,我们需要具备一点统计学的知识基础,关于总体、样本、期望(均值)、方差的定义以及统计估计量的评选标准。
有了这些知识基础之后,我们会知道样本方差之所以要除以(n-1)是因为这样的方差估计量才是关于总体方差的无偏估计量。
这个公式是通过修正下面的方差计算公式而来的:修正过程为:我们看到的其实是修正后的结果:对于这种修正的话是有相关的公式推导的。
下面都会一一给出。
为了方便叙述,在这里说明好数学符号:前面说过样本方差之所以要除以(n-1)是因为这样的方差估计量才是关于总体方差的无偏估计量。
在公式上来讲的话就是样本方差的估计量的期望要等于总体方差。
如下:但是没有修正的方差公式,它的期望是不等于总体方差的也就是说,样本方差估计量如果是用没有修正的方差公式来估计总计方差的话是有偏差的下面给出比较好理解的公式推导过程:也就是说,除非否则一定会有需要注意的是不等式右边的才是的对方差的“正确”估计,但是我们是不知道真正的总体均值是多少的,只能通过样本的均值来代替总体的均值。
所以样本方差估计量如果是用没有修正的方差公式来估计总计方差的话是会有偏差,是会低估了总体的样本方差的。
为了能无偏差的估计总体方差,所以要对方差计算公式进行修正,修正公式如下:这种修正后的估计量将是总体方差的无偏估计量,下面将会给出这种修正的一个来源;为了能搞懂这种修正是怎么来的,首先我们得有下面几个等式:1.方差计算公式:2.均值的均值、方差计算公式:对于没有修正的方差计算公式我们有:因为:所以有:在这里如果想修正的方差公式,让修正后的方差公式求出的方差的期望为总体方差的话就需要在没有修正的方差公式前面加上来进行修正,即:所以就会有这样的修正公式:而我们看到的都是修正后的最终结果:这就解释了为什么要对方差计算公式进行修正,且为什么要这样修正。
多元统计
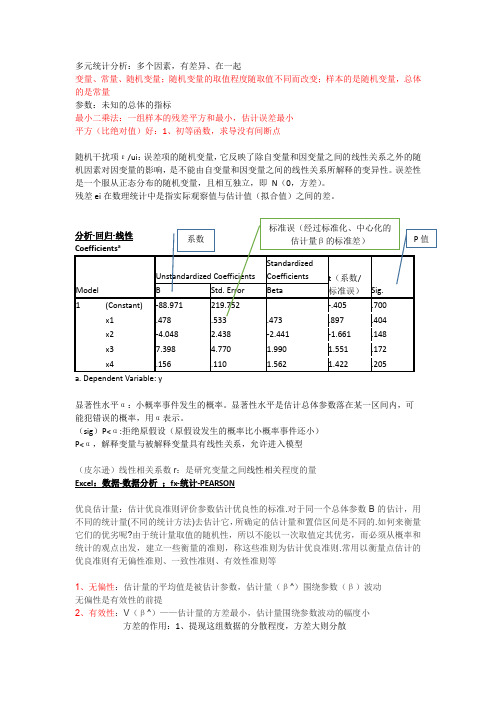
多元统计分析:多个因素,有差异、在一起变量、常量、随机变量;随机变量的取值程度随取值不同而改变;样本的是随机变量,总体的是常量参数:未知的总体的指标最小二乘法:一组样本的残差平方和最小,估计误差最小平方(比绝对值)好:1、初等函数,求导没有间断点随机干扰项ε/ui:误差项的随机变量,它反映了除自变量和因变量之间的线性关系之外的随机因素对因变量的影响,是不能由自变量和因变量之间的线性关系所解释的变异性。
误差性是一个服从正态分布的随机变量,且相互独立,即N(0,方差)。
残差ei在数理统计中是指实际观察值与估计值(拟合值)之间的差。
优良估计量:估计优良准则评价参数估计优良性的标准.对于同一个总体参数B的估计,用不同的统计量(不同的统计方法)去估计它,所确定的估计量和置信区间是不同的.如何来衡量它们的优劣呢?由于统计量取值的随机性,所以不能以一次取值定其优劣,而必须从概率和统计的观点出发,建立一些衡量的准则,称这些准则为估计优良准则.常用以衡量点估计的优良准则有无偏性准则、一致性准则、有效性准则等1、无偏性:估计量的平均值是被估计参数,估计量(β^)围绕参数(β)波动无偏性是有效性的前提2、有效性:V(β^)——估计量的方差最小,估计量围绕参数波动的幅度小方差的作用:1、提现这组数据的分散程度,方差大则分散3、样本容量越大越好为什么样本方差是除以n-1:自由度df:相互独立的变量个数标准化的好处:1、同一量纲2、不再有水平和分散程度的不同(均值0方差1)分析-描述统计-描述-将标准化得分另存为变量z标准化回归:线性回归中-选项-把在等式中包含常量的√去掉(随机)向量(x,y):把独立(随机)变量x、y放在一起形成一个整体行向量*列向量=一个数列向量*行向量=一个矩阵假设检验:假设的是总体,假设是具体的总检验:F统计量线性回归结果-方差分析表ANOVA有n个样本,i个解释变量,最小二乘法有n-(i+1)个方程,i+1是因为除了参数还有截距项。
样本方差与方差的关系

样本方差与方差的关系样本方差和方差是统计学中常用的两个概念。
它们都是用来衡量数据的离散程度的指标。
本文将介绍样本方差和方差的概念、计算方法以及它们之间的关系。
我们来了解一下样本方差和方差的定义。
样本方差是指在统计学中,用来衡量一组样本数据的离散程度的统计量。
它表示数据与其均值之间的偏离程度。
用公式表示为:样本方差=∑(xi-x̄)²/n-1,其中xi表示样本中的每个数据点,x̄表示样本的均值,n表示样本的个数。
方差是指在统计学中,用来衡量一组数据的离散程度的统计量。
它表示数据与其均值之间的偏离程度。
用公式表示为:方差=∑(xi-μ)²/n,其中xi表示每个数据点,μ表示总体的均值,n表示数据的个数。
从定义可以看出,样本方差和方差的计算公式非常相似,只是分母上的n-1和n有所不同。
这是因为样本方差是用来估计总体方差的,而总体方差是用来描述整个总体数据的离散程度的。
而在计算样本方差时,为了使样本方差更接近总体方差,需要用n-1来代替n,这样可以更好地估计总体的离散程度。
样本方差和方差的关系可以从两个方面来进行解释。
首先,从计算公式上看,样本方差和方差的计算方法非常相似,只是分母上的n-1和n有所不同。
其次,从概念上看,样本方差和方差都是用来衡量数据的离散程度的指标,都表示数据与其均值之间的偏离程度。
因此,可以说样本方差是方差的一种估计。
在实际应用中,样本方差和方差都有着重要的作用。
它们可以帮助我们了解数据的离散程度,进而进行数据分析和决策。
比如,在财务领域,可以用方差来衡量投资组合的风险;在生产领域,可以用样本方差来衡量产品的质量稳定性;在医学领域,可以用方差来衡量药物的疗效稳定性。
样本方差和方差是用来衡量数据的离散程度的统计量。
它们在计算公式和概念上都非常相似,只是分母上的n-1和n有所不同。
样本方差是用来估计总体方差的,而方差是用来描述整个总体数据的离散程度的。
它们在实际应用中有着重要的作用,可以帮助我们了解数据的离散程度,进行数据分析和决策。
证明样本方差的时候除以n是一个一致的估计量

证明样本方差的时候除以n是一个一致的估计量统计学中,方差是一个重要的概念,它可以用来衡量一个随机变量在不同值上的离散程度,从而帮助我们更好地了解数据中变量之间的关系。
方差的估计量是我们用来测量方差的重要方法,其中最常用的方法是除以n的样本方差估计量,本文将探讨它的特性。
首先,我们来解释什么是除以n的样本方差估计量,简单来说,就是根据一个样本的数据,通过计算每个值与样本均值之间的差值的平方和,然后除以n,得到的结果就是样本方差估计量。
其次,我们来讨论除以n的样本方差估计量的一致性,根据大数定律,当样本总量n不断增加时,样本方差估计量也会趋于某个不变的量。
也就是说,当样本量n增大时,样本方差估计量将逐渐接近真实的总体方差的值,于是当n足够大时,样本方差估计量就是一致的。
在数学论文中,我们经常用表示一致性的符号来证明一个结论,例如用符号$s_n^2$表示样本方差估计量,在数学论文中,我们常常用符号$sigma^2$表示总体方差,那么我们可以利用符号表示出一致性的公式:$lim_{nrightarrowinfty}s_n^2=sigma^2$最后,我们要证明除以n的样本方差估计量是一致的,首先,我们要知道总体方差$sigma^2$的表达式:$sigma^2=frac{sum_{i=1}^nE(X_i-mu)^2}{n}$其中,$mu$是总体的平均值,$X_i$是样本每一个样本值,$E$表示期望。
我们将$E(X_i-mu)^2$替换成实际样本值$x_i-bar x$,而$bar x$是样本的平均值,那么总体方差$sigma^2$的表达式变为:$sigma^2=frac{sum_{i=1}^n(x_i-bar x)^2}{n}$而我们以前提到,除以n的样本方差估计量也是:$s_n^2=frac{sum_{i=1}^n(x_i-bar x)^2}{n}$我们可以发现,$sigma^2$和$s_n^2$是一样的,于是,当我们把$n$取足够大的时候,$s_n^2$的值就会趋近于$sigma^2$,也就达到了一致的要求,于是证明了除以n的样本方差估计量是一致的。
关于求方差时为什么要除以n

关于求方差时为什么要除以n-1,而不是除以n的问题
无论你采用哪种抽样方法,样本都不可能覆盖全体对象,所以为了补偿误差,便除以n-1。
比如统计一个国家人民的身高的时候,整个国家里应该有最高与最矮的人,但是你自己确定的样本里,往往很难取到这么稀有的数值,所以你根据样本算出的波动区间往往小于实际波动区间,所以便除以n-1来补偿。
一般都能够理解样本计算出的结果和实际结果之间的误差,但不明白的是如果要补偿误差的话,为什么是n-1而不是n-2或n-3、甚至其他的数,这些数不是同样可以增大结果吗?
具体说来,抽样,实际上也就是通过样本去估计总体。
用样本去估计总体,当然就要评估估计的好坏如何。
首先,评估方面就是先要评估这个估计是有偏估计还是无偏估计,无偏估计更为有效。
除以n所得到的样本方差虽然也是总体方差的估计量,但并不是无偏估计量,而除以n-1所得到的样本标准方差则是无偏估计量。
正因为除以n-1所得到的样本标准方差是总体的无偏估计,所以它更科学,误差更小。
若除以n-2或n-3的话,首先未必能保证这就是总体方差的估计量,即使是,也不会是无偏估计。
之所以选择n-1,这个不是巧合,而是数学推导下的结果。
更进一步说的话,若发现两个估计量都是无偏估计量,那就得评估这两个估计量的方差的大小,也就是有效性问题,谁的方差小,谁就更有效。
方差为什么要除以n-1

样本方差为什么是除以n‐1不要bs……话说这个问题从中学开始就困扰着我,可是课本上通常都是语焉不详一笔带过,似乎是很显然的样子,搞得我一度无限怀疑自己的智商。
最近仔细看了看书,整理了一下思路,终于把它推倒了。
赶紧记下来,请各位过路的大牛指教。
下面的推倒过程需要两个结论,在这里不加证明了,基本上概率书上都有。
(1)对于任意两个随机变量X,Y都有 E(X+Y) = E(X) + E(Y),和的期望等于期望的和 (2) V(X) = E(X^2) – E(X)^2,方差等于平方的期望减去期望的平方。
(3)若X,Y独立,有V(X+Y) = V(X) + V(Y)。
另外还有E(aX+b) = aE (X) + b, V(aX+b) = a^2*V(X)从头来说,有这么个随机变量X,我们不知道它的分布,但是我们可以获得很多个满足同样分布的样本Xi,现在我们要从这些样本里估计这个随机分布的一些信息,比如它的均值(所谓总体均值)和方差(所谓总体方差)。
当然我们想让我们的估计尽可能地准确,判断准确与否的一个标准(不是唯一标准)就是看它是不是“无偏估计”(unbiased estimation),所谓无偏估计就是说这个估计的期望值(每个样本都是一个随机变量,估计值是由这样样本算出来的,所以也是个随机变量,也有期望方差等等概念)就是真实值。
比如最简单的,样本均值 就是一个无偏估计,因为我们可以证明:这里第三个等号用到了结论(1)。
这个样本均值比较自然而符合直观,加起来一除自然是平均值。
但下面不太符合直观的来了,样本方差的无偏估计是这里的就是上面那个样本均值。
这里就比较别扭了,因为感觉上应该是除以n才对,怎么会冒出一个n1来?但是下面我们可以证明 .推倒前还需要一个东西,的方差:下面可以开始了:这里后面那个E分成了三部分,第一部分这里第二个等号利用结论(2)关于第二部分和第三部分,实际上有这个只要把代入展开就可以发现,所以后面两项就只剩下了,而代入起来就有。
样本方差、变异系数、极差的概念

一、样本方差的概念样本方差是描述一个数据集中各个数据与其均值之间的离散程度的统计量。
它的计算公式为:样本方差=Σ(xi- x̄)²/(n-1),其中Σ代表求和,xi代表第i个数据,x̄代表样本均值,n代表样本容量。
样本方差的计算过程主要包括以下几个步骤:1. 计算样本均值:将所有数据相加,然后除以样本容量。
2. 求出每个数据与样本均值的差,然后平方。
3. 将所有差的平方相加,然后除以样本容量减1,即得到样本方差。
样本方差的大小反映了数据的离散程度。
当样本方差较大时,说明数据的波动范围较大,数据之间的差异性较明显;反之,当样本方差较小时,说明数据的波动范围较小,数据之间的差异性较小。
样本方差在统计分析中有着重要的作用。
二、变异系数的概念变异系数是一种用来比较不同数据集变异程度的统计量,它消除了数据的量纲和数量级的影响,能够更加客观地比较不同样本之间的变异程度。
变异系数的计算公式为:变异系数=(标准差/均值)×100。
变异系数的数值越小,说明数据的相对离散程度越小,数据的稳定性越高;反之,变异系数的数值越大,说明数据的相对离散程度越大,数据的稳定性越低。
变异系数常常用于进行不同样本的变异程度比较,特别是在对数据的稳定性进行评估时,变异系数具有很好的应用效果。
三、极差的概念极差是描述一个数据集中最大值与最小值之间距离的统计量。
它是最简单直观的离散程度的度量,计算公式为:极差=最大值-最小值。
极差反映了数据的全距大小,当极差较大时,说明数据的波动范围较大,数据之间差异性明显;反之,当极差较小时,说明数据的波动范围较小,数据之间的差异性较小。
结语样本方差、变异系数和极差是统计学中常用的描述数据分布情况的统计量,它们分别从不同角度描述了数据的离散程度和变异程度。
在实际的数据分析中,我们可以根据具体的需求选择合适的统计量来描述数据的分布情况,并且需要综合考虑这些统计量的特点,以便更加准确地分析和解释数据的特征。
总体方差和样本方差公式

总体方差和样本方差公式方差这个概念在数学统计里可重要啦!咱们今天就来好好唠唠总体方差和样本方差公式。
先来说说总体方差公式。
总体方差呢,它反映的是整个总体数据的离散程度。
假如咱们把一个总体里所有的数据都看作是一个大家庭的成员,那总体方差就是衡量这个大家庭成员之间差异大小的一个重要指标。
总体方差的公式是:\(\sigma^2 = \frac{\sum_{i=1}^{N}(X_i -\mu)^2}{N}\) 。
这里的\(X_i\)表示总体中的第\(i\)个数据,\(\mu\)是总体的均值,\(N\)是总体中数据的个数。
举个例子哈,比如说咱们要研究一个班级所有同学的数学成绩,这所有同学的成绩就构成了一个总体。
假设这个班级有 50 个同学,他们的数学成绩分别是 85、90、88、92、78…… 那咱们先算出这 50 个成绩的平均值\(\mu\),然后用每个成绩\(X_i\)减去平均值\(\mu\),再平方,把这 50 个平方值加起来,最后除以 50 ,这就算出总体方差啦。
再说说样本方差公式。
样本方差呢,是基于从总体中抽取的一部分数据来估计总体方差的。
就好像咱们没办法把整个班级同学的成绩都了解清楚,只能先抽取一部分同学的成绩来研究。
样本方差的公式是:\(s^2 = \frac{\sum_{i=1}^{n}(x_i - \overline{x})^2}{n - 1}\) 。
这里的\(x_i\)是样本中的第\(i\)个数据,\(\overline{x}\)是样本的均值,\(n\)是样本中数据的个数。
我记得之前有一次,我们做一个关于学生身高的调查。
因为全校学生太多了,没法一个个都测量,所以就随机抽取了 30 个同学的身高作为样本。
这 30 个同学的身高有高有矮,参差不齐。
我们先算出这 30个身高数据的平均值\(\overline{x}\),然后每个身高数据\(x_i\)都减去平均值\(\overline{x}\),再平方,把这些平方值加起来,最后除以 29 ,就得到了样本方差。
样本均值方差为什么除以n-1

样本均值⽅差为什么除以n-1设样本均值为,样本⽅差为,总体均值为,总体⽅差为,那么样本⽅差有如下公式:很多⼈可能都会有疑问,为什么要除以n-1,⽽不是n,但是翻阅资料,发现很多都是交代到,如果除以n,对样本⽅差的估计不是⽆偏估计,⽐总体⽅差要⼩,要想是⽆偏估计就要调⼩分母,所以除以n-1,那么问题来了,为什么不是除以n-2、n-3等等。
所以在这⾥彻底总结⼀下,⾸先交代⼀下⽆偏估计。
⽆偏估计以例⼦来说明,假如你想知道⼀所⼤学⾥学⽣的平均⾝⾼是多少,⼀个⼤学好⼏万⼈,全部统计有点不现实,但是你可以先随机挑选100个⼈,统计他们的⾝⾼,然后计算出他们的平均值,记为。
如果你只是把作为整体的⾝⾼平均值,误差肯定很⼤,因为你再随机挑选出100个⼈,⾝⾼平均值很可能就跟刚才计算的不同,为了使得统计结果更加精确,你需要多抽取⼏次,然后分别计算出他们的平均值,分别记为:然后在把这些平均值,再做平均,记为:,这样的结果肯定⽐只计算⼀次更加精确,随着重复抽取的次数增多,这个期望值会越来越接近总体均值,如果满⾜,这就是⼀个⽆偏估计,其中统计的样本均值也是⼀个随机变量,就是的⼀个取值。
⽆偏估计的意义是:在多次重复下,它们的平均数接近所估计的参数真值。
介绍⽆偏估计的意义就是,我们计算的样本⽅差,希望它是总体⽅差的⼀个⽆偏估计,那么假如我们的样本⽅差是如下形式:那么,我们根据⽆偏估计的定义可得:由上式可以看出如果除以n,那么样本⽅差⽐总体⽅差的值偏⼩,那么该怎么修正,使得样本⽅差式总体⽅差的⽆偏估计呢?我们接着上式继续化简:(Var(X^)为什么等于σ2/n?推导公式:D(X把)=D(1/n∑Xi)=1/n²D(∑Xi)=1/n²∑D(Xi)=(1/n²)nσ²=σ²/n )到这⾥得到如下式⼦,看到了什么?该怎修正似乎有点眉⽬。
如果让我们假设的样本⽅差乘以,即修正成如下形式,是不是可以得到样本⽅差是总体⽅差的⽆偏估计呢?则:因此修正之后的样本⽅差的期望是总体⽅差的⼀个⽆偏估计,这就是为什么分母为何要除以n-1。
样本变异数的公式为何是除以n-1?_详全文

樣本變異數的公式為何是除以n-1?淡江大學數學系 鄭惟厚教授高中數學課本中提到,假設母體數據n x x x ,,,21 的平均數等於µ,則母體變異數為()nx n i i ∑=−=122µσ,標準差為()nx n i i ∑=−=12µσ。
但是如果n x x x ,,,21 是抽自某一母體的樣本數據,則其樣本變異數等於 ()1122−−=∑=n x xs n i i ,標準差()1122−−==∑=n x x s s n i i 。
同樣都是在計算變異數,為何一個公式是除以n,另一個公式卻是除以n-1呢?除以n 很自然,因為通常求平均都是除以n 的,所以母體變異數的公式相當「正常」,相對來說,樣本變異數的分母n-1,就顯得怪怪的。
要了解n-1的背後原因,首先必須知道,母體和樣本的角色不同、「地位」也就不一樣。
母體是我們的關心對象,通常我們會想要知道有關它的資訊。
比如我們可能有興趣知道,全國成年民眾當中,贊成把集會遊行改成報備制的,占多少百分比。
但是就如同這個例子的「全國成年民眾」,母體通常都很龐大,幾乎不可能對它蒐集完整資訊,通常只能從其中抽取樣本,再從樣本裡面找相關資訊。
樣本變異數2s 的角色,除了可以提供我們有關樣本數據的散佈情況之外,還有一個重要功能,就是當作母體變異數2σ的估計。
當作估計的量,我們會希望它不要系統性的高估、或者系統性的低估,也就是要求估計量有「不偏」性質。
用秤體重來比喻的話,如果體重計有時把我們秤重了些、有時又秤輕了些,但是若秤了許許多多次之後,平均起來就等於我們的真實體重的話,就相當於有不偏性質。
但是假如我家體重計無法正確歸零,常常把我的體重「加碼」,量很多次下來,平均把我多秤了半公斤,這樣就叫做系統性高估,而非「不偏」了。
假設樣本變異數2s 公式的分母是用n 而非n-1的話,如果把它當作母體變異數2σ的估計,常常會低估,不符合「不偏」的條件,但是如果把n 改成n-1,樣本變異數就會是母體變異數的不偏估計,這件事實是可以用數學證明出來的。
n-1的概念

n-1的概念
n-1的概念可用于描述一种常见的模式或规则,其中n表示某
一集合或群体的总数,而n-1表示该集合或群体中的自由度或
可变因素的数量。
在许多统计学和研究领域中,n-1常用于计算样本的自由度。
自由度指的是可以独立变动的数值的个数,其中n表示样本的总数。
在计算统计学指标和执行假设检验时,使用n-1的自由
度可以更准确地估计总体参数。
例如,在计算样本的方差时,通常会使用n-1作为自由度。
这
是因为在样本中,只有n-1个数据点可以做出独立的选择,而
最后一个数据点的值是由前n-1个数据点决定的。
另一个应用n-1的领域是网络拓扑结构中的最小生成树。
最小
生成树是一个连接所有节点的无环子图,它的边的数量为n-1,其中n是节点的总数。
这个概念在通信网络、电力网络和交通网络等领域中被广泛使用。
总之,n-1的概念适用于各种不同领域,其中它代表了一个集
合或群体中可变因素的数量。
这种概念通常用于计算自由度、估计总体参数和描述网络拓扑结构等应用中。
方差的两种公式

方差的两种公式
方差是统计学中一个重要的概念,它可以用来衡量一组数据的离散程度。
方差可以用两种公式来计算:一种是总体方差的公式,另一种是样本方差的公式。
总体方差的公式是:σ2=Σ(X-μ)2/N,其中X表示总体中的每个样本值,μ表示总体的均值,N表示总体的样本数。
这个公式表明,总体方差是由每个样本值与总体均值之差的平方和除以总体样本数得到的。
样本方差的公式是:s2=Σ(X-x)2/n-1,其中X表示样本中的每个样本值,x
表示样本的均值,n表示样本的样本数。
这个公式表明,样本方差是由每个样本值与样本均值之差的平方和除以样本样本数减一得到的。
总体方差和样本方差都是用来衡量一组数据的离散程度,但是它们的计算方法是不同的。
总体方差是由每个样本值与总体均值之差的平方和除以总体样本数得到的,而样本方差是由每个样本值与样本均值之差的平方和除以样本样本数减一得到的。
总体方差和样本方差都是统计学中重要的概念,它们可以用来衡量一组数据的离散程度,从而帮助我们更好地理解数据。
数理统计中自由度的理解和应用

数理统计中自由度的理解和应用摘要:数理统计是一门以概率论为基础的应用学科,应用于许多领域。
文章对数理统计作出了一个深入浅出的介绍,并对数理统计中自由度的理解作了较为全面的阐述,并在此基础上给了自由度科学的定义。
通过列举自由度在统计学中的应用,旨在全面认识自由度。
关键字:数理统计;自由度数理统计是数学的一个分支学科,是一门以概率论为基础的应用学科。
随着研究随机现象规律性的科学—概率论的发展,应用概率论的结果更深入地分析研究统计资料,通过对某些现象的频率的观察来发现该现象的内在规律性,并作出一定精确程度的判断和预测;将这些研究的某些结果加以归纳整理,逐步形成一定的数学概型,这些组成了数理统计的内容。
数理统计在自然科学、工程技术、管理科学及人文社会科学中得到越来越广泛和深刻的应用,其研究的内容也随着科学技术和政治、经济与社会的不断发展而逐步扩大,但概括地说可以分为两大类:⑴试验的设计和研究,即研究如何更合理更有效地获得观察资料的方法;⑵统计推断,即研究如何利用一定的资料对所关心的问题作出尽可能精确可靠的结论,当然这两部分内容有着密切的联系,在实际应用中更应前后兼顾。
它以随机现象的观察试验取得资料作为出发点,以概率论为理论基础来研究随机现象.根据资料为随机现象选择数学模型,且利用数学资料来验证数学模型是否合适,在合适的基础上再研究它的特点、性质和规律性。
例如灯泡厂生产灯泡,将某天的产品中抽出几个进行试验,试验前不知道该天灯泡的寿命有多长,概率和其分布情况.试验后得到这几个灯泡的寿命作为资料,从中推测整批生产灯泡的使用寿命、合格率等。
为了研究它的分布,利用概率论提供的数学模型进行指数分布,求出值,再利用几天的抽样试验来确定指数分布的合适性。
简而言之,数理统计以概率论为基础,根据试验或观察得到的数据,来研究随机现象统计规律性的学科。
它的任务就是研究有效地收集数据,科学地整理与分析所获得的有限的资料,对所研究的问题,尽可能地作出精确而可靠的结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为什么样本方差里面要除以(n-1)而不是n?(---by小马哥整理)
首先,我们来看一下样本方差的计算公式:
(1) 刚开始接触这个公式的话可能会有一个疑问就是:为什么样本方差要除以(n-1)而不是除以n?为了解决这个疑惑,我们需要具备一点统计学的知识基础,关于总体、样本、期望(均值)、方差的定义以及统计估计量的评选标准。
有了这些知识基础之后,我们会知道样本方差之所以要除以(n-1)是因为这样的方差估计量才是关于总体方差的无偏估计量。
这个公式是通过修正下面的方差计算公式而来的。
公式(2)是我们按照正常的思维, 思考的应该有的方差的计算公式,也就是除以n的情况:
(2)
公式(3)是我们经过修正得到的式子, 修正过程为:
(3)
我们在课本上看到的其实是修正后的结果:
(4) 下面详细(推导)讲, 为啥会要乘以前面那个(1/n-1), 来对公式(2)进行修正.
为了方便叙述,在这里说明好数学符号:
(5) 前面说过样本方差之所以要除以(n-1)是因为这样的方差估计量才是关于总体方差的无偏估计量。
在公式上来讲的话就是样本方差的估计量的期望要等于总体方差。
如下:
(6) 但是没有修正的方差公式,它的期望是不等于总体方差的(下面会讲解详细原因, 就是下面那个公式推导!)
(7) 也就是说,样本方差估计量如果是用没有修正的方差公式来估计总计方差的话是有偏差的
下面给出比较好理解的公式推导过程:
(8) 也就是说,除非否则一定会有
(9) 需要注意的是不等式右边的才是的对方差的“正确”估计,但是我们是不知道真正的总体均值是多少的,只能通过样本的均值来代替总体的均值。
所以样本方差估计量如果是用没有修正的方差公式来估计总计方差的话是会有偏差,是会低估了总体的样本方差的。
为了能无偏差的估计总体方差,所以要对方差计算公式进行修正,修正公式如下:
(10) 这种修正后的估计量将是总体方差的无偏估计量,下面将会给出这种修正的一个来源;
为了能搞懂这种修正是怎么来的,首先我们得有下面几个等式:
1.方差计算公式:
(11) 2. 均值的均值、方差计算公式:
(12) 对于没有修正的方差计算公式我们有:
(13)
因为:
(14) 所以有:
(15) 在这里如果想修正的方差公式,让修正后的方差公式求出的方差的期望为总体方差的话就需要在没有修正的方差公式前面加上来进行修正,即:
(16) 所以就会有这样的修正公式:
(17) 而我们看到的都是修正后的最终结果:
(18)。
