在线索二叉树中如何求先序
先序线索化转圈问题

先序线索化转圈问题先序线索化转圈问题是一种经典的数学问题,它可以帮助我们探索数学中的先序遍历、线索化和环的概念。
让我们来了解一下先序遍历和线索化的含义。
我们将研究如何将这些概念应用到转圈问题上,并通过一些具体的例子来进一步理解。
1. 先序遍历在二叉树中,先序遍历是指先访问根节点,然后遍历左子树,最后遍历右子树。
这个遍历顺序可以用一个节点序列来表示,我们可以把先序遍历的结果存储在一个数组中。
在这个数组中,根节点的位置总是在左子树和右子树之前。
2. 线索化线索化是将二叉树中的空指针调整为指向前驱节点或后继节点的方式。
通过线索化,我们可以用指针在树中前进而不需要使用递归或栈。
对于一个二叉树的节点,如果它没有左子树,我们可以把它的左指针指向它的前驱节点;如果它没有右子树,我们可以把它的右指针指向它的后继节点。
3. 先序线索化转圈问题现在让我们来考虑一个有趣的问题:如何将一棵已经线索化的二叉树转化为一个环形链表呢?我们需要把每一个节点的右指针指向它的后继节点,并使得最后一个节点的后继节点指向第一个节点。
为了解决这个问题,我们可以使用先序遍历的思想。
我们可以从根节点开始,依次遍历每个节点,并将它的右指针指向它的后继节点。
我们还需要记录前一个访问的节点,以便将它的后继节点指向当前节点。
具体的步骤如下:- 如果当前节点为根节点,将它的右指针指向它的后继节点,并记录当前节点为前一个节点。
- 如果当前节点有左子树,递归处理左子树。
- 如果当前节点有右子树,继续遍历它的右子树。
通过这种方式,我们可以将一个已经线索化的二叉树转化为一个环形链表。
这个环形链表可以让我们在任意节点中,通过右指针循环遍历所有节点。
在实际应用中,先序线索化转圈问题可以用于优化二叉树的遍历算法。
由于线索化的特性,我们可以避免使用递归或栈,从而提高遍历的效率。
通过对先序线索化转圈问题的深入研究,我们可以更好地理解先序遍历、线索化和环的概念。
这个问题不仅提供了一个数学的挑战,还具有一定的实际应用价值。
二叉树序列口诀

二叉树序列口诀
二叉树的序列化和反序列化是二叉树算法中的核心操作,也是面试中的重点考察内容。
对于初学者来说,掌握二叉树的序列化和反序列化需要掌握以下口诀:
一、二叉树序列口诀
1.前序序列化
①根节点放前面,输出数值;
②递归左子树,输出左子树的序列化结果;
③递归右子树,输出右子树的序列化结果。
2.中序序列化
①递归左子树,输出左子树的序列化结果;
②根节点放中间,输出数值;
③递归右子树,输出右子树的序列化结果。
3.后序序列化
①递归左子树,输出左子树的序列化结果;
②递归右子树,输出右子树的序列化结果;
③根节点放后面,输出数值。
二、二叉树反序列口诀
1.前序反序列化
①读取当前节点的值,生成新节点;
②递归读取左子树,将左子树连接到新节点;
③递归读取右子树,将右子树连接到新节点。
2.中序反序列化
①递归读取左子树,将左子树连接到当前节点;
②读取当前节点的值,生成新节点;
③递归读取右子树,将右子树连接到新节点。
3.后序反序列化
①递归读取左子树,将左子树连接到当前节点;
②递归读取右子树,将右子树连接到当前节点;
③读取当前节点的值,生成新节点。
总之,掌握好二叉树的序列化和反序列化操作,可以为你的算法之路打下坚实的基础,让你在职场中游刃有余,赢得更多的机会和成就。
二叉树前驱后继的查找

线索二叉树的运算1.查找某结点*p在指定次序下的前趋和后继结点(1)在中序线索二叉树中,查找结点*p的中序后继结点在中序线索二叉树中,查找结点*p的中序后继结点分两种情形:①若*p的右子树空(即p->rtag为Thread),则p->rchild为右线索,直接指向*p的中序后继。
【例】下图的中序线索二叉树中,结点D的中序后继是A。
②若*p的右子树非空(即p->rtag为Link),则*p的中序后继必是其右子树中第一个中序遍历到的结点。
也就是从*p的右孩子开始,沿该孩子的左链往下查找,直至找到一个没有左孩子的结点为止,该结点是*p的右子树中"最左下"的结点,即*P的中序后继结点。
【例】上图的中序线索二叉树中:A的中序后继是F,它有右孩子;F的中序后继是H,它无右孩子;B的中序后继是D,它是B的右孩子。
在中序线索二叉树中求中序后继结点的过程可【参见动画演示】,具体算法如下:BinThrNode *InorderSuccessor(BinThrNode *p){//在中序线索树中找结点*p的中序后继,设p非空BinThrNode *q;if (p->rtag==Thread) //*p的右子树为空Return p->rchild;//返回右线索所指的中序后继else{q=p->rchild;//从*p的右孩子开始查找while (q->ltag==Link)q=q->lchild;//左子树非空时,沿左链往下查找return q;//当q的左子树为空时,它就是最左下结点} //end if}该算法的时间复杂度不超过树的高度h,即O(h)。
(2)在中序线索二叉树中查找结点*p的中序前趋结点中序是一种对称序,故在中序线索二叉树中查找结点*p的中序前趋结点与找中序后继结点的方法完全对称。
具体情形如下:①若*p的左子树为空,则p->1child为左线索,直接指向*p的中序前趋结点;【例】上图所示的中序线索二叉树中,F结点的中序前趋结点是A②若*p的左子树非空,则从*p的左孩子出发,沿右指针链往下查找,直到找到一个没有右孩子的结点为止。
二叉树前中后序遍历做题技巧

二叉树前中后序遍历做题技巧在计算机科学中,二叉树是一种重要的数据结构,而前序、中序和后序遍历则是二叉树遍历的三种主要方式。
下面将分别对这三种遍历方式进行解析,并提供一些解题技巧。
1.理解遍历顺序前序遍历顺序是:根节点->左子树->右子树中序遍历顺序是:左子树->根节点->右子树后序遍历顺序是:左子树->右子树->根节点理解每种遍历顺序是解题的基础。
2.使用递归或迭代二叉树的遍历可以通过递归或迭代实现。
在递归中,每个节点的处理函数会调用其左右子节点的处理函数。
在迭代中,可以使用栈来模拟递归过程。
3.辨析指针指向在递归或迭代中,需要正确处理指针的指向。
在递归中,通常使用全局变量或函数参数传递指针。
在迭代中,需要使用栈或其他数据结构保存指针。
4.学会断点续传在处理大规模数据时,为了避免内存溢出,可以采用断点续传的方式。
即在遍历过程中,将中间结果保存在文件中,下次遍历时从文件中读取上一次的结果,继续遍历。
5.识别循环和终止条件在遍历二叉树时,要识别是否存在循环,并确定终止条件。
循环可以通过深度优先搜索(DFS)或广度优先搜索(BFS)避免。
终止条件通常为达到叶子节点或达到某个深度限制。
6.考虑边界情况在处理二叉树遍历问题时,要考虑边界情况。
例如,对于空二叉树,需要进行特殊处理。
又如,在处理二叉搜索树时,需要考虑节点值的最小和最大边界。
7.优化空间使用在遍历二叉树时,需要优化空间使用。
例如,可以使用in-place排序来避免额外的空间开销。
此外,可以使用懒加载技术来延迟加载子节点,从而减少内存占用。
8.验证答案正确性最后,验证答案的正确性是至关重要的。
可以通过检查输出是否符合预期、是否满足题目的限制条件等方法来验证答案的正确性。
如果可能的话,也可以使用自动化测试工具进行验证。
线索化二叉树前序

#include <stdio.h>#include <malloc.h>#include <stdlib.h>#include <assert.h>#include <string.h>#include "Stack.h"typedef enum{LINK,THEAD} PointTag;typedef struct ThBTnode{char data;PointTag Ltag,Rtag;ThBTnode* left;ThBTnode* right;}ThBTnode, * ThTree;ThBTnode * BuyNode(){ThBTnode* s = (ThBTnode*)malloc(sizeof(ThBTnode));assert(s !=NULL);memset(s,0,sizeof(ThBTnode));s->Ltag = s->Rtag = LINK;return s;}ThBTnode* CreatTheadTree(char *& str){ThBTnode *s = NULL;if(str==NULL){return NULL;}if(*str!='#'){s=BuyNode();s->data =*str;s->left = CreatTheadTree(++str);s->right = CreatTheadTree(++ str);}return s;}ThBTnode* first_Pri(ThBTnode * ptr){return ptr;}ThBTnode * next_Pri(ThBTnode * ptr){if(ptr ==NULL){return NULL;}if(ptr->Ltag!=THEAD){return ptr->left;}else{return ptr->right;}}void PriOrder_Thread_fn(ThBTnode* ptr){ThBTnode * p =NULL;for(p=first_Pri(ptr);p!=NULL;p=next_Pri(p)){printf("%c ",p->data);}printf("\n");}ThBTnode *Parent(ThBTnode* ptr,ThBTnode* p){if(ptr ==NULL||ptr ==p){return NULL;}if(ptr->Ltag ==THEAD &&ptr->Rtag ==THEAD){return NULL;}if( ptr->left ==p &&ptr->Ltag !=THEAD || ptr->right == p &&ptr->Rtag!=THEAD) {return ptr;}else{ThBTnode *q =NULL;if(ptr->Ltag !=THEAD){q=Parent(ptr->left,p);}if(NULL == q && ptr->Rtag !=THEAD){q =Parent(ptr->right,p);}return q;}}ThBTnode * last_Pri(ThBTnode *ptr){while(ptr !=NULL && ptr->Rtag!=THEAD){ptr=ptr->right;if(ptr->Rtag==THEAD && ptr->Ltag!=THEAD){ptr=ptr->left;}}return ptr;}ThBTnode * pri_Pri(ThBTnode*root, ThBTnode *ptr) {if(ptr ==NULL || ptr==root){return NULL;}if(ptr->Ltag ==THEAD && ptr->Rtag ==THEAD){return ptr->left;}else{ThBTnode*s = Parent(root,ptr);if(s->Ltag ==THEAD&&s->Rtag ==LINK){return s;}if(s->Rtag ==THEAD&& s->Ltag ==LINK){return s;}else{if(s->Ltag==LINK &&s->Rtag ==LINK && s->right ==ptr){return last_Pri(s->left);}else{return s;}}}}void PriOrder_Thread_lp(ThBTnode * ptr){ThBTnode * p =NULL;for(p=last_Pri(ptr);p!=NULL;p=pri_Pri(ptr,p)){printf("%c ",p->data);}printf("\n");}void PriOr_ThTree(ThBTnode * ptr,ThBTnode *&p){ThBTnode *s =NULL;ThBTnode *q =NULL;if(ptr !=NULL){s=ptr->left;q=ptr->right;if(ptr->left ==NULL && p!=NULL){ptr->left =p;ptr->Ltag = THEAD;}if(p!=NULL && p->right ==NULL){p->right = ptr;p->Rtag=THEAD;}p=ptr;PriOr_ThTree(s,p);PriOr_ThTree(q,p);}}void ThreadTree_pri(ThBTnode * ptr) {ThBTnode* p=NULL;if(ptr!=NULL){PriOr_ThTree(ptr,p);}p->Rtag = THEAD;p->right = NULL;}。
二叉树先序遍历算法

二叉树先序遍历算法
二叉树先序遍历是一种树的遍历算法,先序遍历过程如下:
1. 先访问根节点;
2. 再访问左子节点;
3. 再访问右子节点;
二叉树先序遍历是一种树状数据结构的深度优先搜索(DFS)算法。
先序遍历对
树状数据结构中的每个节点仅进行一次访问,且访问的次序是从上到下,从左到右的方式。
先序遍历属于深度优先搜索,它以一定的次序访问树或图的每个节点,然后递归访问其子节点,深度优先搜索可以按一定方式去遍历有向图、二叉树等数据结构,对节点都进行一定次序的编号或标签,访问顺序是按从小到大的顺序,从而把BST全部访问一次。
二叉树先序遍历的时间复杂度为O(n),空间复杂度为O(logn),应用范围很广,常用于二叉查找树的构造或查找、求树的高度和深度、树的前中后序遍历等,其中在建立二叉查找树时,往往我们都会使用先序遍历;同时,也可用先序遍历来求二叉树的节点数,计算树的深度等。
因此,二叉树先序遍历是一种基本而又重要的数据结构遍历算法,在许多应用
场景中都可以被朂泛使用,深受各个计算机领域的热捧。
二叉树遍历(前中后序遍历,三种方式)

⼆叉树遍历(前中后序遍历,三种⽅式)⽬录刷题中碰到⼆叉树的遍历,就查找了⼆叉树遍历的⼏种思路,在此做个总结。
对应的LeetCode题⽬如下:,,,接下来以前序遍历来说明三种解法的思想,后⾯中序和后续直接给出代码。
⾸先定义⼆叉树的数据结构如下://Definition for a binary tree node.struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}};前序遍历,顺序是“根-左-右”。
使⽤递归实现:递归的思想很简单就是我们每次访问根节点后就递归访问其左节点,左节点访问结束后再递归的访问右节点。
代码如下:class Solution {public:vector<int> preorderTraversal(TreeNode* root) {if(root == NULL) return {};vector<int> res;helper(root,res);return res;}void helper(TreeNode *root, vector<int> &res){res.push_back(root->val);if(root->left) helper(root->left, res);if(root->right) helper(root->right, res);}};使⽤辅助栈迭代实现:算法为:先把根节点push到辅助栈中,然后循环检测栈是否为空,若不空,则取出栈顶元素,保存值到vector中,之后由于需要想访问左⼦节点,所以我们在将根节点的⼦节点⼊栈时要先经右节点⼊栈,再将左节点⼊栈,这样出栈时就会先判断左⼦节点。
代码如下:class Solution {public:vector<int> preorderTraversal(TreeNode* root) {if(root == NULL) return {};vector<int> res;stack<TreeNode*> st;st.push(root);while(!st.empty()){//将根节点出栈放⼊结果集中TreeNode *t = st.top();st.pop();res.push_back(t->val);//先⼊栈右节点,后左节点if(t->right) st.push(t->right);if(t->left) st.push(t->left);}return res;}};Morris Traversal⽅法具体的详细解释可以参考如下链接:这种解法可以实现O(N)的时间复杂度和O(1)的空间复杂度。
c语言二叉树的先序,中序,后序遍历
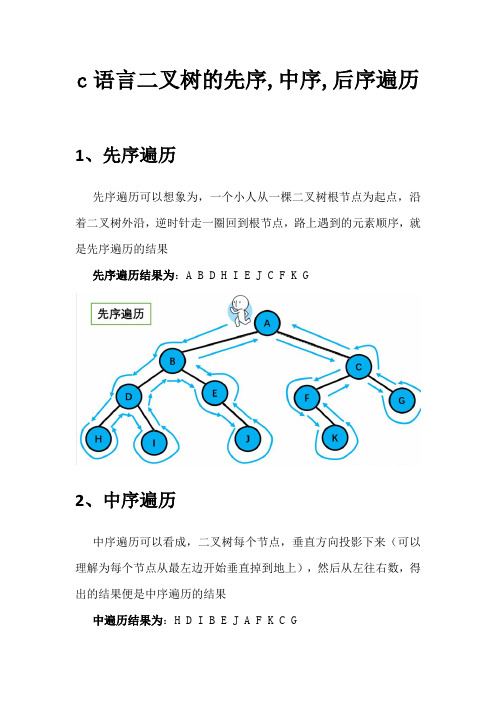
c语言二叉树的先序,中序,后序遍历1、先序遍历先序遍历可以想象为,一个小人从一棵二叉树根节点为起点,沿着二叉树外沿,逆时针走一圈回到根节点,路上遇到的元素顺序,就是先序遍历的结果先序遍历结果为:A B D H I E J C F K G2、中序遍历中序遍历可以看成,二叉树每个节点,垂直方向投影下来(可以理解为每个节点从最左边开始垂直掉到地上),然后从左往右数,得出的结果便是中序遍历的结果中遍历结果为:H D I B E J A F K C G3、后序遍历后序遍历就像是剪葡萄,我们要把一串葡萄剪成一颗一颗的。
还记得我上面提到先序遍历绕圈的路线么?(不记得翻上面理解)就是围着树的外围绕一圈,如果发现一剪刀就能剪下的葡萄(必须是一颗葡萄)(也就是葡萄要一个一个掉下来,不能一口气掉超过1个这样),就把它剪下来,组成的就是后序遍历了。
后序遍历中,根节点默认最后面后序遍历结果:H I D J E B K F G C A4、口诀先序遍历:先根再左再右中序遍历:先左再根再右后序遍历:先左再右再根这里的根,指的是每个分叉子树(左右子树的根节点)根节点,并不只是最开始头顶的根节点,需要灵活思考理解5、代码展示#include<stdio.h>#include<stdlib.h>typedef struct Tree{int data; // 存放数据域struct Tree *lchild; // 遍历左子树指针struct Tree *rchild; // 遍历右子树指针}Tree,*BitTree;BitTree CreateLink(){int data;int temp;BitTree T;scanf("%d",&data); // 输入数据temp=getchar(); // 吸收空格if(data == -1){ // 输入-1 代表此节点下子树不存数据,也就是不继续递归创建return NULL;}else{T = (BitTree)malloc(sizeof(Tree)); // 分配内存空间T->data = data; // 把当前输入的数据存入当前节点指针的数据域中printf("请输入%d的左子树: ",data);T->lchild = CreateLink(); // 开始递归创建左子树printf("请输入%d的右子树: ",data);T->rchild = CreateLink(); // 开始到上一级节点的右边递归创建左右子树return T; // 返回根节点}}// 先序遍历void ShowXianXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}printf("%d ",T->data);ShowXianXu(T->lchild); // 递归遍历左子树ShowXianXu(T->rchild); // 递归遍历右子树}// 中序遍历void ShowZhongXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}ShowZhongXu(T->lchild); // 递归遍历左子树printf("%d ",T->data);ShowZhongXu(T->rchild); // 递归遍历右子树}// 后序遍历void ShowHouXu(BitTree T) // 后序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}ShowHouXu(T->lchild); // 递归遍历左子树ShowHouXu(T->rchild); // 递归遍历右子树printf("%d ",T->data);}int main(){BitTree S;printf("请输入第一个节点的数据:\n");S = CreateLink(); // 接受创建二叉树完成的根节点printf("先序遍历结果: \n");ShowXianXu(S); // 先序遍历二叉树printf("\n中序遍历结果: \n");ShowZhongXu(S); // 中序遍历二叉树printf("\n后序遍历结果: \n");ShowHouXu(S); // 后序遍历二叉树return 0;}。
前序后序中序详细讲解

前序后序中序详细讲解1.引言1.1 概述在数据结构与算法中,前序、中序和后序是遍历二叉树的三种基本方式之一。
它们是一种递归和迭代算法,用于按照特定的顺序访问二叉树的所有节点。
通过遍历二叉树,我们可以获取有关树的结构和节点之间关系的重要信息。
前序遍历是指先访问根节点,然后递归地访问左子树,最后递归地访问右子树。
中序遍历是指先递归地访问左子树,然后访问根节点,最后递归地访问右子树。
后序遍历是指先递归地访问左子树,然后递归地访问右子树,最后访问根节点。
它们的不同之处在于访问根节点的时机不同。
前序遍历可以帮助我们构建二叉树的镜像,查找特定节点,或者获取树的深度等信息。
中序遍历可以帮助我们按照节点的大小顺序输出树的节点,或者查找二叉搜索树中的某个节点。
后序遍历常用于删除二叉树或者释放二叉树的内存空间。
在实际应用中,前序、中序和后序遍历算法有着广泛的应用。
它们可以用于解决树相关的问题,例如在Web开发中,树结构的遍历算法可以用于生成网页导航栏或者搜索树结构中的某个节点。
在图像处理中,前序遍历可以用于图像压缩或者图像识别。
另外,前序和后序遍历算法还可以用于表达式求值和编译原理中的语法分析等领域。
综上所述,前序、中序和后序遍历算法是遍历二叉树的重要方式,它们在解决各种与树有关的问题中扮演着关键的角色。
通过深入理解和应用这些遍历算法,我们可以更好地理解和利用二叉树的结构特性,并且能够解决更加复杂的问题。
1.2文章结构文章结构是指文章中各个部分的布局和组织方式。
一个良好的文章结构可以使读者更好地理解和理解文章的内容。
本文将详细讲解前序、中序和后序三个部分的内容和应用。
首先,本文将在引言部分概述整篇文章的内容,并介绍文章的结构和目的。
接下来,正文部分将分为三个小节,分别对前序、中序和后序进行详细讲解。
在前序讲解部分,我们将定义和解释前序的意义,并介绍前序在实际应用中的场景。
通过详细的解释和实例,读者将能更好地理解前序的概念和用途。
数据结构二叉树先序中序后序考研题目

数据结构二叉树先序中序后序考研题目在考研所涉及的数据结构中,二叉树以及与之相关的先序、中序和后序遍历是一个重要的考察点。
通过对二叉树的各种遍历方式的理解和掌握,可以帮助考生更好地理解树这个数据结构,提高解题的效率和正确率。
本文将针对数据结构中关于二叉树先序、中序和后序遍历的考研题目进行深入探讨,并希望能为考生提供一些帮助和启发。
一、先序、中序和后序遍历的概念在开始具体讨论考研题目之前,我们先来回顾一下先序、中序和后序遍历的概念。
在二叉树中,所谓的先序、中序和后序遍历,是指对二叉树中的节点进行遍历的顺序方式。
1. 先序遍历:先访问根节点,然后依次递归地访问左子树和右子树。
在遍历过程中,对于任一节点,先访问该节点,然后再访问其左右子树。
2. 中序遍历:先递归地访问左子树,然后访问根节点,最后再递归地访问右子树。
在遍历过程中,对于任一节点,先访问其左子树,然后访问该节点,最后再访问其右子树。
3. 后序遍历:先递归地访问左子树,然后再递归地访问右子树,最后再访问根节点。
在遍历过程中,对于任一节点,先访问其左右子树,然后再访问该节点。
二、考研题目解析1. 题目一:给出一个二叉树的中序遍历和后序遍历序列,构建该二叉树。
这是一个典型的二叉树重建题目,考查对中序和后序遍历结果的理解和利用。
解题的关键在于根据后序遍历序列确定根节点,在中序遍历序列中找到对应的根节点位置,然后再将中序遍历序列分为左右两个子树部分,分别递归构建左右子树。
考生需要对二叉树遍历的特点有清晰的认识,以及对递归构建树结构有一定的掌握。
2. 题目二:给出一个二叉树的先序遍历和中序遍历序列,构建该二叉树。
这个题目与上一个题目相似,同样是考察对二叉树重建的理解和应用。
解题思路也类似,首先根据先序遍历的结果确定根节点,在中序遍历序列中找到对应的根节点位置,然后递归构建左右子树。
需要注意的是,先序遍历序列的第一个元素即为根节点,而中序遍历序列中根节点的左边是左子树,右边是右子树。
二叉树的遍历【NOIP2001普及组】洛谷P1030求先序排列

⼆叉树的遍历【NOIP2001普及组】洛⾕P1030求先序排列题⽬链接模板题先讲⼀下⼆叉树的遍历⼆叉树的遍历分类性质求法分为三类:1. 先序遍历(PreOrder):根节点→左⼦树→右⼦树2. 中序遍历(InOrder):左⼦树→根节点→右⼦树3. 后序遍历(PostOrder):左⼦树→右⼦树→根节点我们可知:**序遍历实际上是指根节点的位置⽆论哪种遍历顺序,左⼦树都在右⼦树的前⾯在前序遍历中,第⼀个点是根节点在后序遍历中,最后⼀个点是根节点例如这样⼀个⼆叉树:它的先序遍历:A--B--D--E--X--C--F--Y--Z它的中序遍历:D--B--X--E--A--Y--F--Z--C它的后序遍历:D--X--E--B--Y--Z--F--C--A求后序遍历⽤到递归的思想,求整个⼆叉树的后序遍历就是求每个⼦树的后序遍历,最后连接起来即可。
1 #include<iostream>2using namespace std;3string z,q;4int len,cnt;5void PostOrder(int l,int r){//求中序遍历中l到r这个⼦树的后序遍历6if(l>r) return; //边界条件7int i;8char ans=q[cnt++]; //先序遍历的第⼀个是根节点9for(i=l;i<=r;i++){10if(z[i]==ans) break;//找到根节点在中序遍历中的位置11 }12 PostOrder(l,i-1); //递归左⼦树13 PostOrder(i+1,r); //递归右⼦树14 cout<<ans; //注意后序遍历是左右根的顺序,所以最后输出根15 }16int main()17 {18 cin>>z>>q; //z是中序遍历,q是先序遍历19 len=z.length()-1;20 PostOrder(0,z.length()-1);//⼀开始是整个⼦树21return0;22 }求先序遍历这⽐求后序遍历稍微有些复杂,需要保留根节点,即:PreOrder(左端点,右端点,根节点)。
线索二叉树

6·4 线索二叉树1、线索二叉树的结点结构二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构,使每个结点都有了唯一前驱和后继(第一个结点无前驱,最后一个结点无后继)。
对于二叉树的一个结点,查找其左右子女是方便的,其前驱后继只有在遍历中得到。
为了容易找到前驱和后继,有两种方法。
一是在结点结构中增加向前和向后的指针fwd和bkd,这种方法增加了存储开销,不可取;二是利用二叉树的空链指针。
现将二叉树的结点结构重新定义如下:其中:ltag=0 时ltag=1 时lchild指向前驱;rtag=0 时rchild指向左子女;rtag=1 时rchild指向后继;以这种结点结构构成的二叉链表作为二叉树的存储结构,叫做线索链表,指向前驱和后继的指针叫线索,加上线索的二叉树叫线索二叉树,对二叉树进行某种形式遍历使其变为线索二叉树的过程叫线索化。
学习线索化时,有三点必须注意:一是何种“序”的线索化,是先序、中序还是后序;二是要“前驱”线索化、“后继”线索化还是“全”线索化(前驱后继都要);三是只有空指针处才能加线索。
2、对二叉树进行中序线索化的算法bithptr *pre; /* 全程变量*/void INTHREAD(bithptr *p){if(p!=NULL){ INTHREAD(p->lchild); /* 左子树线索化*/if(p->lchild==NULL) { p->ltag=1;p->lchild=pre;}if(p->rchild==NULL) p->rtag=1;if(pre!=NULL && pre->rtag==1) pre->rchild=p;pre=p; /* 前驱指向当前结点*/INTHREAD(p->rchild); /* 右子树线索化*/}3、在线索二叉树上查找前驱和后继(1)中序线索二叉树:若结点的ltag=1,lchild指向其前驱;否则,该结点的前驱是以该结点为根的左子树上按中序遍历的最后一个结点。
线索二叉树

void InThreading(BiThrTree p) { if ( p ) { InThreading ( p -> lchild ); //左子树中序线索化 左子树中序线索化 if ( p->lchild = = NULL ) { p->LTag=Thread; p->lchild= pre; } //左线索为 ; 左线索为pre 左线索为 if ( pre->rchild == NULL ) { pre->RTag=Thread; pre->rchild= p ;} //后继线索 后继线索 pre = p; //保持 指向 的前驱 保持pre指向 保持 指向p的前驱 InThreading(p -> rchild ); //右子树中序线索化 右子树中序线索化 } }//InThreading
指向该线性序列中的“前驱”和 “后继” 的指针 指针,称作“线索” 线索” 指针 线索
A B C D E F G H K
^B
C^ E^
^D^
包含 “线索” 的存储 结构,称作 “线索链 线索链 表” 与其相应的二叉树, 线索二叉树” 称作 “线索二叉树 线索二叉树中序线索二叉树源自A0 1B
C
NULL
Status InOrderThreading (BiThrTree &Thrt , BiThrTree T ) { //将二叉树 改变为其中序线索二叉树 将二叉树T改变为其中序线索二叉树 if ( !Thrt = (BiThrTree ) malloc (sizeof(BiThrNode))) exit ( OVERFLOW ); Thrt-> LTag = Link ; Thrt ->RTag = Thread; Thrt -> rchild = Thrt; if ( !T ) Thrt -> lchild = Thrt; //空树 空树 else { Thrt -> lchild = T ; pre = Thrt ; InTreading( T ); //中序遍历进行中序线索化 中序遍历进行中序线索化 pre-> rchild = Thrt; pre->RTag= Thread; Thrt -> rchild = pre; } return OK; }
二叉树前序和中序遍历求后序 表格法

二叉树前序和中序遍历求后序表格法1.概述二叉树是计算机科学中常见的数据结构,它可以用来表示树形结构的数据。
在二叉树的遍历中,前序遍历、中序遍历和后序遍历是三种重要的遍历方式。
本文将介绍如何通过前序遍历和中序遍历的结果来求出二叉树的后序遍历结果,以及如何使用表格法来进行求解。
2.二叉树遍历的概念在二叉树中,前序遍历指的是首先访问根节点,然后再递归地前序遍历左子树和右子树;中序遍历指的是先递归地中序遍历左子树,然后访问根节点,最后再递归地中序遍历右子树;后序遍历指的是先递归地后序遍历左子树和右子树,最后再访问根节点。
在本文中,我们将讨论如何通过前序遍历和中序遍历的结果来求出后序遍历的结果。
3.二叉树的定义我们需要了解二叉树的定义。
二叉树是一种树形结构,它的每个节点最多有两个子节点,分别为左子节点和右子节点。
对于任意一个节点,它的左子树和右子树也分别是二叉树。
如果一个节点没有左子树或者右子树,我们称其为叶子节点。
二叉树一般用递归的方式来定义,并且可以通过链式存储结构或者顺序存储结构来实现。
4.二叉树前序和中序遍历求后序接下来,我们将介绍如何通过二叉树的前序遍历和中序遍历结果来求出后序遍历的结果。
4.1 基本思路我们知道前序遍历的顺序是根节点、左子树、右子树,中序遍历的顺序是左子树、根节点、右子树。
假设我们已经知道了二叉树的前序遍历序列和中序遍历序列,那么我们可以通过这两个序列来确定二叉树的结构。
具体地,我们可以通过前序遍历序列找到根节点,然后在中序遍历序列中找到该根节点的位置,这样就可以确定左子树和右子树的中序遍历序列。
再根据左子树和右子树的节点数目,我们可以在前序遍历序列中确定左子树和右子树的前序遍历序列。
我们可以递归地对左子树和右子树进行求解,直到最终得到二叉树的后序遍历序列。
4.2 具体步骤具体地,通过前序遍历序列和中序遍历序列求后序遍历序列的步骤如下:1)在前序遍历序列中找到根节点2)在中序遍历序列中找到根节点的位置,确定左子树和右子树的中序遍历序列3)计算左子树和右子树的节点数目,确定左子树和右子树的前序遍历序列4)递归地对左子树和右子树进行求解5)最终得到二叉树的后序遍历序列4.3 表格法求解除了上述的基本思路和具体步骤外,我们还可以通过表格法来求解二叉树的后序遍历序列。
线索二叉树(图)

线索二叉树:遍历二叉树:实际上是对二叉树(非线性结构)进行的线性化操作,即以一定规则将二叉树中的结点排列成一个线性序列(先序序列、中序序列和后序序列)。
举例:图6.9所示的二叉树中的结点,按中序遍历可得到中序序列:a+b*c-d-e/f,其中‘c’的前驱为‘*’,后继为‘-’。
当以二叉链表作为二叉树的存储结构时,只能找到结点的左右孩子信息,而不能直接得到结点在任一线性序列中的前驱和后继信息,因为这种信息只有在遍历的动态过程中才能得到。
如何保存这种在遍历过程中得到的结点的前驱和后继信息呢?方法一:在二叉链表的每个结点上增加两个指针域fwd和bkwd,分别指向在依任一次序遍历时得到的前驱和后继信息。
(大大影响存储密度)方法二:利用二叉链表中的空链域来存放结点的前驱和后继信息。
(在有n个结点的二叉链表中必定存在n+1个空链域!)(不影响存储密度)为此,可以将二叉链表中的结点结构作如下修改:lchild LTag data RTag rchild其中:Ltag = 0 lchild域指示结点的左孩子1 lchild域指示结点的前驱Rtag = 0 rchild域指示结点的右孩子1 rchild域指示结点的后继我们把如此修改后的二叉链表称为二叉树的线索链表,其中指向结点前驱和后继的指针称为线索。
相应地,把添加线索后的二叉树称为线索二叉树(Threaded Binary Tree)。
对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。
举例:图6.11(a)所示为中序线索二叉树,与其对应的中序线索链表如图 6.11(b)所示。
其中实线为指针(指向左、右子树),虚线为线索(指向前驱和后继)。
在线索树上进行遍历,只要找到序列中的第一个结点,然后依次找结点的后继直到其后继为空时而停止。
关键是如何在线索树中找结点的后继?二叉树的二叉线索存储表示:(p133-134)线索二叉树的遍历:(以中序线索二叉树为例,即中序遍历二叉线索树)算法6.5二叉树的线索化:(以中序线索化为例,即通过中序遍历建立中序线索链表)算法6.6,算法6.7。
前序序列和后续序列确定二叉树

前序序列和后续序列确定⼆叉树⼆叉树:已知前序与后序建树那么我们换⼀种思考⽅式,我们先来看看先序与后序序列的排布规律。
以下⾯这棵树来举例:其先序序列为: 1 2 3 4 6 7 5后序序列为:2 6 7 4 5 3 1⾸先我们要知道:先序序列遍历顺序是:根结点-左⼦树-右⼦树后序序列遍历顺序是:左⼦树-右⼦树-根结点很明显,我们可以看出结点在先、后序列中的排布有以下这些特征:【1】、在先序序列中,根结点在⼦树中的结点前⾯,在后序序列中,根结点在⼦树中的结点后⾯。
【2】、以任⼀节点为根结点时,其⼦树在先序后序序列中排布都是先左⼦树后右⼦树,⽽根结点排在最后。
那么,反过来思考,已知这个先序与后序序列所确定的树是唯⼀的吗?进⼀步推⼴:怎么通过先序与后序序列判断是否存在唯⼀的树呢?现在,我们来⼀步步分析已知先序与后序的建树过程:①、根据特征【1】可知:根结点为先序序列第⼀个节点以及后序序列最后⼀个结点,因此根结点为1。
②、先序序列中第⼆个结点为2,其在后序序列中的位置是第⼀个,那么根据特征【2】我们可以知道结点2是没有⼦树的,⽽且结点2要么在根结点的左⼦树,要么在右⼦树。
假设结点2在右⼦树,那么由特征【2】可知根结点1没有左⼦树,⽽且先序序列中结点2后⾯的结点全部为结点2的⼦树上的结点。
再看后序序列,由特征【2】可知,结点2后⾯的结点不可能是其⼦树上的结点。
因此,假设显然与已知⽭盾。
这样,我们⼜知道结点2是结点1的左孩⼦,且结点2没有⼦结点。
③、先序序列第三个位置上的结点为3,该结点在后序序列中排倒数第⼆个。
由②可知,结点3必然是根结点1的右孩⼦。
④、先序序列第四个位置上的结点为4,该结点在后序序列中排第四个。
因为结点4在先序序列中排在结点3后⾯,⼜因为结点3是根结点1的右孩⼦,所以结点4只可能在结点3的⼦树上。
结点3的⼦树可能出现的情况是:只有左⼦树,只有右⼦树,左右⼦树都有。
因为在后序序列中,结点4左边是结点6、7,右边是结点5。
二叉树的先序,中序,后序遍历的递归写法

二叉树的先序,中序,后序遍历的递归写法一、前言二叉树是数据结构中最基础、最重要的一种数据结构之一,如何遍历二叉树是每一个数据结构学习者需要掌握的技能。
本文将介绍二叉树的三种遍历方式:前序遍历、中序遍历和后序遍历,以及它们的递归写法。
二、先序遍历二叉树的先序遍历顺序是:根节点→ 左子树→ 右子树。
1.递归写法(1)基本思路先访问根节点,然后递归遍历左子树,最后递归遍历右子树。
(2)代码实现public void preOrderTraversal(TreeNode root) {if (root == null) return;System.out.println(root.val);preOrderTraversal(root.left);preOrderTraversal(root.right);}2.中序遍历二叉树的中序遍历顺序是:左子树→ 根节点→ 右子树。
1.递归写法(1)基本思路递归遍历左子树,然后访问根节点,最后递归遍历右子树。
(2)代码实现public void inOrderTraversal(TreeNode root) {if (root == null) return;inOrderTraversal(root.left);System.out.println(root.val);inOrderTraversal(root.right);}3.后序遍历二叉树的后序遍历顺序是:左子树→ 右子树→ 根节点。
1.递归写法(1)基本思路递归遍历左子树,然后递归遍历右子树,最后访问根节点。
(2)代码实现public void postOrderTraversal(TreeNode root) {if (root == null) return;postOrderTraversal(root.left);postOrderTraversal(root.right);System.out.println(root.val);}三、总结本文介绍了二叉树的三种遍历方式以及它们的递归写法。
先序中序后序遍历算法

先序中序后序遍历算法
先序、中序和后序遍历是二叉树遍历的三种基本方法,它们可以帮助我们按照不同顺序访问树中的节点。
下面我会分别介绍这三种遍历算法。
1. 先序遍历:
先序遍历是指先访问根节点,然后递归地对左子树进行先序遍历,最后递归地对右子树进行先序遍历。
因此,先序遍历的顺序是根-左-右。
2. 中序遍历:
中序遍历是指先递归地对左子树进行中序遍历,然后访问根节点,最后递归地对右子树进行中序遍历。
因此,中序遍历的顺序是左-根-右。
3. 后序遍历:
后序遍历是指先递归地对左子树进行后序遍历,然后递归地
对右子树进行后序遍历,最后访问根节点。
因此,后序遍历的顺序
是左-右-根。
这三种遍历算法都是基于递归的思想实现的,它们在不同的应
用场景下都有各自的优势。
例如,先序遍历常用于复制整棵树,中
序遍历常用于二叉搜索树的查找操作,后序遍历常用于计算表达式
树的值等。
除了递归实现外,这三种遍历算法也可以通过迭代的方式实现,通常使用栈来辅助实现。
在实际应用中,根据具体的问题和数据结
构的特点,选择合适的遍历算法可以提高算法的效率和准确性。
总之,先序、中序和后序遍历算法是树结构中常用的基本算法,它们在数据结构和算法领域具有重要的意义,对于理解树的结构和
实现树相关的操作非常重要。
希望以上介绍能够帮助你更好地理解
这三种遍历算法。
数据结构——已知先序中序求后序,已知中序后序求先序

数据结构——已知先序中序求后序,已知中序后序求先序 总结下⼆叉树的已知两种遍历⽅式求第三种遍历顺序的⽅法,已知先序和中序遍历或者后序与中序遍历后⼆叉树是唯⼀确定的,下⾯介绍怎么求出第三种遍历顺序。
先序遍历顺序为:根结点——左⼦结点——右⼦结点,中序遍历为:左⼦结点——根结点——右⼦结点,我们注意到,先序遍历的第⼀个元素就是⼆叉树根结点,我们在中序遍历中以该元素分为左右两部分,则左边为左⼦树,右边为右⼦树,递归即可还原⼆叉树,这个过程中可直接输出后序遍历的顺序。
同理,可以⽤后序与中序还原出先序遍历的顺序。
代码及测试数据如下:1 #include <iostream>2 #include <cstdio>3 #include <cstring>4 #include <algorithm>5 #include <malloc.h>6 #include <string>7 #include <vector>8 #include <stack>9 #include <queue>10 #include <set>11 #include <map>1213#define FRER() freopen("in.txt", "r", stdin);1415using namespace std;1617//函数状态码定义18#define TRUE 119#define FALSE 020#define OK 121#define ERROR 022#define INFEASIBLE -123#define OVERFLOW -22425 typedef char TElemType;26 typedef int Status;2728 typedef struct BiNode {29 TElemType data;30struct BiNode *lchild, *rchild;31 }BiNode, *BiTree;3233 BiTree BinaryTreeFormorderings(char *, char *, int);34 BiTree BinaryTreePostorderings(char *, char *, int);3536/*37ABDECFG38DBEAFCG39DEBFGCA40*/4142int main()43 {44 FRER()45int n;46char str[100], ptr[100];47 cin >> n >> str >> ptr;48 BinaryTreePostorderings(str, ptr, n);49return0;50 }5152 BiTree BinaryTreeFormorderings(char *pre, char *in, int len) {53if(len <= 0)54return NULL;55 BiNode *node = new BiNode;56 node->data = *pre;57int idx = 0;58while(idx < len) {59if(*(in + idx) == *pre)60break;61 ++idx;62 }63 node->lchild = BinaryTreeFormorderings(pre + 1, in, idx);64 node->rchild = BinaryTreeFormorderings(pre + idx + 1, in + idx + 1, len - (idx + 1));65 cout << node->data << '';66return node;67 }6869 BiTree BinaryTreePostorderings(char *in, char *post, int len) {70if(len == 0)71return NULL;72 BiNode *node = new BiNode;73 node->data = *(post + len - 1);74 cout << node->data << '';75int idx = 0;76while(idx < len) {77if(*(in + idx) == *(post + len - 1))78break;79 ++idx;80 }81 node->lchild = BinaryTreePostorderings(in, post, idx);82 node->rchild = BinaryTreePostorderings(in + idx + 1, post + idx, len - (idx + 1)); 83return node;84 }。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1在线索二叉树中如何求先序、中序的前驱、后继,为什么后续线索二叉树是不完备的?先序前驱:若左标志为1,则左链为线索,指示其前驱;否则
a) 若该结点是二叉树的根,则其前驱为空;
b) 若该结点是其双亲的左孩子或是其双亲的右孩子且其双亲没有左子树,则其前驱为其双亲;
c) 若该结点是其双亲的右孩子且其双亲有左子树,则其前驱为其双亲的左子树中的先序遍历列出的最后一个结点。
先序后继:若右标志为1,则右链为线索,指示其后继;否则,如果有左子树则遍历左子树第一个访问的结点,为其后继;如果没有左子树则遍历右子树第一个访问的结点,为其后继;
中序前驱:若左标志为1,则左链为线索,指示其前驱;否则,遍历其左子树最后访问
的结点,为其前驱
中序后继:若右标志为1,则右链为线索,指示其后继;否则,遍历其右子树第一个访问的结点,为其后继
后续后继:
a) 若该结点是二叉树的根,则其后继为空;
b) 若该结点是其双亲的右孩子或是其双亲的左孩子且其双亲没有右子树,则其后继为其双亲;
c) 若该结点是其双亲的左孩子且其双亲有右子树,则其后继为其双亲的右子树中的后序遍历列出的第一个结点。
求后续后继需要知道双亲结点,而二叉链表无法找到双亲,因此不完备:
5如果只想得到一个序列中前k(k>=5)个最小元素的部分排序序列,可以采用哪些排序方法,最好采用哪种排序方法?
1插入、快速、归并需要全体排序不合适
2起泡、简单选择、堆可以。
堆完成查找总时间:4n+klogn,起泡和简单选择总时间kn,因此堆较好。
5荷兰国旗
问题分析:
这个问题我们可以将这个问题视为一个数组排序问题,这个数组分为前部,中部和后部三个部分,每一个元素(红白蓝分别对应0、1、2)必属于其中之一。
由于红、白、蓝三色小球数量并不一定相同,所以这个三个区域不一定是等分的,也就是说如果我们将整个区域放在[0,1]的区域里,由于三色小球之间数量的比不同(此处假设1:2:2),可能前部为[0,0.2),中部为[0.2,0.6),后部为[0.6,1]。
我们的思路如下:将前部和后部各排在数组的前边和后边,中部自然就排好了。
具体的:
设置两个标志位begin和end分别指向这个数组的开始和末尾,然后用一个标志位current从头开始进行遍历:
1)若遍历到的位置为0,则说明它一定属于前部,于是就和begin位置进行交换,然后current向前进,begin也向前进(表示前边的已经都排好了)。
2)若遍历到的位置为1,则说明它一定属于中部,根据总思路,中部的我们都不动,然后current向前进。
3)若遍历到的位置为2,则说明它一定属于后部,于是就和end位置进行交换,由于交换完毕后current指向的可能是属于前部的,若此时current前进则会导致该位置不能被交换到前部,所以此时current不前进。
而同1),end向后退1。
1. void swap (int &var1, int &var2)
2. {
3. int temp = var1;
4. var1 = var2;
5. var2 = temp;
6. }
7.
8. void shuffle(int *array)
9. {
10. int current = 0;
11. int end = N-1;
12. int begin = 0;
13. while( current<=end )
14. {
15. if( array[current] ==0 )
16. {
17. swap(array[current],array[ begin]);
18. current++;
19. begin++;
20. }
21. else if( array[current] == 1 )
22. {
23. current++;
24. }
25. else{//When array[current] = 2
26. swap(array[current],array[ end]);
27. end--;
28. }
29. }
30. }
8对含有n个互不相同的元素的线性表,能否以低于2n-3次比较同时找出最大元素和最小元素?如果能请详细说明算法思想,如果不能说明原因
可以实现。
选用锦标赛算法。
两两元素比较,淘汰较小的,形如一棵二叉树。
树根为最大值(此时用掉n-1次比较)。
而最小者一定位于首次被淘汰之列。
故只有⎡ n/2⎤个。
一共需n-1+⎡ n/2⎤次比较。
9在什么条件下,MSD基数排序比LSD基数排序效率更高?
【解答】由于高位优先的MSD方法是递归的方法,就一般情况来说,不像低位优先的LSD方法那样直观自然,而且实现的效率较低。
但如果待排序的排序码的大小只取决于高位的少数几位而与大多数低位无关时,采用MSD方法比LSD方法的效率要高。
10若对有n个元素的有序顺序表和无序顺序
表进行顺序搜索, 试就下列三种情况分别讨论两者在等搜索概率时的平均搜索长度是否相同?
(1) 搜索失败;
(2) 搜索成功, 且表中只有一个关键码等于给定值k的对象;
(3) 搜索成功, 且表中有若干个关键码等于给定值k的对象, 要求一次搜索找出所有对象
【解答】
(1) 不同。
因为有序顺序表搜索到其关键码比要查找值大的对象时就停止搜索,报告失败信息,不必搜索到表尾;而无序顺序表必须搜索到表尾才能断定搜索失败。
(2) 相同。
搜索到表中对象的关键码等于给定值时就停止搜索,报告成功信息。
(3) 不同。
有序顺序表中关键码相等的对象相继排列在一起,只要搜索到第一个就可以连续搜索到其它关键码相同的对象。
而无序顺序表必须搜索全部表中对象才能确定相同关键码的对象都找了出来,所需时间就不相同了。
11m*n阶二维整形数组B在行和列方向上都是递增排列的,整数x在B中存在,编写一个时间复杂度不超过O(m+n)的算法,找出x 在B中的位置
V oid F(int b[m][n],int x,int &i,int &j)
{
i=0;j=n-1;
while(b[i][j]!x)
if(b[i][j]<x)i++;
else j--;
}。
