MATLAB数学建模算法学习笔记
Matlab学习笔记(全)

Matlab学习笔记——《MATLAB与科学计算》王正盛国防工业出版社一.MA TLAB入门 (4)who、whos和永久变量 (4)显示格式 (4)图形 (4)二.MA TLAB数值计算 (5)1.常用命令: (5)2.矩阵的保存和获取 (5)3.矩阵的运算和数组的运算 (5)4.线性方程组 (5)5.多项式 (6)6.数值积分 (6)7.一般非线性方程组求解 (6)8.微分方程的数值求解 (7)三.MATLAB的符号计算 (7)1.符号变量和符号表达式 (7)2.微积分运算 (7)3.解方程 (8)4.化简和代换 (8)5.MA TLAB的符号表达式命令 (8)四.MA TLAB的图形和可视化 (9)1.二维图形 (9)2图形标记 (9)3.特殊坐标和图形 (9)4.其他命令 (9)5.填充命令 (10)6.三维图形 (10)7.符号绘图 (10)8.其他 (10)五.MA TLAB程序设计 (10)1.概述: (10)2.命令文件 (11)3.程序文件 (11)六.MA TLAB图形用户界面(GUI)设计 (11)七.基于MA TLAB的大规模矩阵计算 (11)1.稀疏矩阵 (11)八.基于MA TLAB的最优化问题求解 (12)1.线性规划问题 (12)2.非线性问题 (12)3.二次规划问题 (12)九.基于MA TLAB的数据插值和拟合 (12)1.一维数据插值 (12)2.二维数据插值 (13)3.曲线拟合 (13)十.基于MA TLAB的图像处理初步 (13)1.图像分类 (13)2.图像的读取和显示 (13)一.MATLAB入门who、whos和永久变量who 变量名%检查内存变量。
Whos %检查驻留变量的详细情况。
MATLAB自定义的永久变量:eps %计算机中的最小正数inf %无穷大pi %圆周率NaN %不定量flops %浮点运算次数i,j%虚数单位显示格式MATLAB中以短格式(5个有效数字)显示计算结果,可以用format命令改变数字显示格式1.变量的存储和调用1)存储当前工作空间中的变量Save %将所有的变量存入文件MATLAB.mat中Save mydate %将所有变量存入指定文件Save mydate x y z %将指定的变量存入指定的文件中2)将数据文件的变量载入当前的工作空间将save换作load即可图形1.二维图形绘制命令Plot(x,y);2.三维图形绘制命令Mesh(z);2.用户目录的建立在命令窗口输入:cd c:\mydir二.MATLAB数值计算1.常用命令:Reshape命令X=1:1:6; %产生6个元素的行向量Reshape(x,2,3); %利用X行向量产生一个2*3的向量diag命令:ar=rand(4,4) %产生一个4*4的0-1均匀随机向量d=diag(ar)%用ar的主对角元形成向量dD=diag(d)%利用d构成对角矩阵DSize:获取矩阵的行数和列数2.矩阵的保存和获取1)利用m文件利用文件编辑器编辑矩阵AM=[1 2 3;4 5 6;7 8 9]——》保存为在自己的目录下名的matrix.m ——》在MATLAB命令窗口中只要输入matrix就可以调用AM矩阵2)通过mat文件Mat文件是MA TLAB中保存数据的一种标准格式二进制文件,通过save和load执行,如前所述3)利用外部数据文件装入到指定矩阵中假如磁盘中已有名为c:\mydir\date.dat的二进制数据文件,利用load c:\mydir\date.dat命令可以在MATLAB工作空间中产生一个名为date的矩阵3.矩阵的运算和数组的运算矩阵运算是按矩阵的运算法则进行的;数组运算无论何种操作都是对元素逐个进行的,数组运算需要在运算符前加点号。
MATLAB学习记录

MATLAB学习记录1.mean()函数求平均值ExamplesA = [1 2 3; 3 3 6; 4 6 8; 4 7 7];mean(A)ans =3.00004.5000 6.0000mean(A,2)ans =2.00004.00006.00006.00002. lower(type)Convert string to lowercase 转换为⼩写字母lower('MathWorks') is mathworks.3.grid 绘图时划分⽹格,配合figure使⽤grid ongrid off grid grid(axes_handle,...) grid minor4.fliplr 矩阵左右翻转If A is the 3-by-2 matrix,A =1 42 53 6then fliplr(A) produces4 15 26 3If A is a row vector,A = 1 3 5 7 9then fliplr(A) produces 9 7 5 3 15. cat() Concatenate arrays along specified dimension 连接函数cat(2, A, B) is the same as [A, B], and cat(1, A, B) is the same as [A; B]. GivenA = B =1 2 5 63 4 7 8concatenating along different dimensions produces6. legend()Graph legend for lines and patches符号表,注明图像legend('Former','latter')7.sign函数正负号函数Signum functionY = sign(X)DescriptionY = sign(X) returns an array Y thesame size as X, where each element of Y is:1 if the corresponding element of X isgreater than zero0 if the corresponding element of X equals zero-1 if the corresponding element of X is less than zeroFor nonzero complex X, sign(X) = X./abs(X).For example:rin(k)=sign(sin(2*pi*k*ts)); %Squar Wave Signal8. axis([0,200,0,0.6]);限制坐标轴的现实范围轴的控制axis([xmin, xmax, ymin, ymax])⽤命令axis auto 使MATLAB重新⾃动选择范围。
MATLAB学习笔记[优秀范文五篇]
![MATLAB学习笔记[优秀范文五篇]](https://img.taocdn.com/s3/m/21be7d054a73f242336c1eb91a37f111f1850da1.png)
MATLAB学习笔记[优秀范文五篇]第一篇:MATLAB学习笔记读取excel表格中的数据%%excel表格需要存储在特定的目录下才能访问得到x=xlsread('training_data.xls',['A1:G2']);%提取excel表格中第一行A列到第2行G列之间矩阵内的数据y=xlsread('training_data.xls',['A2:G2']);%提取excel表格中第二行A列到第2行G列之间矩阵内的数据inputs=x';%将X转置后赋值给INPPUTStargets=y';%将Y转置后赋值给TARGETS2各种取整函数如ceil()、round()、floor()等之间的区别randperm(6)表示随机生产从1到6的整数串如[2 4 5 6 1 3 ]若A为矩阵A=[1 2 3;1 2 3;1 2 3],则sum(A,1)=[3 6 9]表示将每列相加之和作为列元素;sum(A,2)=[6;6;6]表示将每行相加之和作为行元素5自定义函数Function F=f(x)F=x^2+2*x+1;调用时:f(1);f(2);t= f(1);t= f(2);…..6将一段程序转化成注释:选中程序后按ctrl+t和ctrl+r相互转化。
7向量b=cumsum(向量a)若向量a=[1 2 3 4],则向量b=[1 3 6 10].第二篇:matlab学习心得体会数值运算1.cd显示当前的工作目录,dir列出当前目录下的子文件或子目录,home将光标移动到左上角,type列出所有的文件内容。
2.特殊矩阵的生成:3.linspace生成矩阵:(1)linspace(a,b):生成100个数据的向量;(2)linspace(a,b,n):生成n个元素的向量,线性分布;4.logspace生成矩阵:(1)logspace(a,b)生成50个对数元素的向量,x(1)=10^a,x(50)=10^b;(2)logspace(a,b,n):同linspace的用法; 5.指数与对数函数:6.复数函数:7.基本数组函数:8.矩阵变换函数:9.数据的输出格式由format命令来控制,但是只是影响其显示的结果,对计算结果或者是存储没有影响:10.常用的变量和常量:eps:浮点运算的精确程度,是MATLAB中的计算误差;realmax:计算机能够显示的最大的浮点数;realmin:同其相对应;11.一些特殊的标识符:12.bar条形图:13.几种特殊的图形颜色矩阵:14.照相制图的函数:15.axis ij:设置坐标为矩阵格式,坐标原点在左上角;axis为默认值; 16.坐标设置命令:17.光源设置:18.字符处理函数:19.矩阵分解:20.矩阵函数:21.第三篇:学习matlab总结(定稿)绘图函数 bar 竖直条图 barh 水平条图 hist 直方图histc 直方图计数 hold 保持当前图形 loglog x,y对数坐标图 pie 饼状图 plot 绘二维图 polar 极坐标图semilogy y轴对数坐标图 semilogx x轴对数坐标 subplot 绘制子图 bar3 数值3D竖条图 bar3h 水平3D条形图 comet3 3D慧星图cylinder 圆柱体fill3 填充的3D多边形 plot3 3维空间绘图quiver3 3D震动(速度)图 slice 体积薄片图 sphere 球stem3 绘制离散表面数据 waterfall 绘制瀑布 trisurf 三角表面clabel 增加轮廓标签到等高线图中datetick 数据格式标记 grid 加网格线gtext 用鼠标将文本放在2D图中 legend 图注plotyy 左右边都绘Y轴 title 标题xlabel X轴标签 ylabel Y轴标签 zlabel Z轴标签 contour 等高线图 contourc 等高线计算 contourf 填充的等高线图 hidden 网格线消影meshc 连接网格/等高线mesh 具有参考轴的3D网格 peaks 具有两个变量的采样函数 surf 3D阴影表面图surface 建立表面低层对象 surfc 海浪和等高线的结合 surfl 具有光照的3D阴影表面 trimesh 三角网格图多项式与插值conv 卷积和多项式乘法 roots 多项式的根poly 具有设定根的多项式 polyder 多项式微分 polyeig 多项式的特征根 polyfit 多项式拟合polyint 解析多项式积分 polyval 多项式求值polyvalm 矩阵变量多项式求值 residue 部分分式展开 interp1 一维插值 interp2 二维插值 interp3 三维插值interpft 使用FFT的一维插值 interpn 多维插值meshgrid 为3维点生成x和y的网格 ndgrid 生成多维函数和插值的数组 pchip 分段3次Hermite插值多项式 ppval 分段多项式的值spline 3次样条数据插值3、基本矩阵和矩阵操作blkding 从输入参量建立块对角矩阵 eye 单位矩阵linespace 产生线性间隔的向量logspace 产生对数间隔的向量numel 元素个数ones 产生全为1的数组 rand 均匀颁随机数和数组 randn 正态分布随机数和数组zeros 建立一个全0矩阵 colon)等间隔向量cat 连接数组diag 对角矩阵和矩阵对角线 fliplr 从左自右翻转矩阵 flipud 从上到下翻转矩阵 repmat 复制一个数组 reshape 改造矩阵 roy90 矩阵翻转90度 tril 矩阵的下三角triu 矩阵的上三角 dot 向量点集 cross 向量叉集ismember 检测一个集合的元素 intersect 向量的交集 setxor 向量异或集 setdiff 向是的差集 union 向量的并集数值分析和傅立叶变换 cumprod 累积 cumsum 累加cumtrapz 累计梯形法计算数值微分 factor 质因子inpolygon 删除多边形区域内的点 max 最大值mean 数组的均值 mediam 中值 min 最小值perms 所有可能的转换 polyarea 多边形区域 primes 生成质数列表 prod 数组元素的乘积 rectint 矩形交集区域 sort 按升序排列矩阵元素 sortrows 按升序排列行 std 标准偏差 sum 求和trapz 梯形数值积分 var 方差del2 离散拉普拉斯 diff 差值和微分估计 gradient 数值梯度 cov 协方差矩阵 corrcoef 相关系数 conv2 二维卷积conv 卷积和多项式乘法 filter IIR或FIR滤波器deconv 反卷积和多项式除法 filter2 二维数字滤波器cplxpair 将复数值分类为共轭对 fft 一维的快速傅立叶变换 fft2 二维快速傅立叶变换fftshift 将FFT的DC分量移到频谱中心ifft 一维快速反傅立叶变换 ifft2 二维傅立叶反变换 ifftn 多维快速傅立叶变换 ifftshift 反FFT 偏移nextpow2 最靠近的2的幂次 unwrap 校正相位角2、基本数学函数abs 绝对值和复数模长acos,acodh 反余弦,反双曲余弦acot,acoth 反余切,反双曲余切 acsc,acsch 反余割,反双曲余割 angle 相角asec,asech 反正割,反双曲正割 secant 正切asin,asinh 反正弦,反双曲正弦atan,atanh 反正切,双曲正切tangent 正切atan2 四象限反正切 ceil 向着无穷大舍入 complex 建立一个复数conj 复数配对cos,cosh 余弦,双曲余弦 csc,csch 余切,双曲余切 cot,coth 余切,双曲余切 exp 指数fix 朝0方向取整 floor 朝负无穷取整 gcd 最大公因数 imag 复数值的虚部 lcm 最小公倍数 log 自然对数log2 以2为底的对数 log10 常用对数 mod 有符号的求余nchoosek 二项式系数和全部组合数real 复数的实部 rem 相除后求余round 取整为最近的整数 sec,sech 正割,双曲正割 sign 符号数sin,sinh 正弦,双曲正弦 sqrt 平方根tan,tanh 正切,双曲正切1、特殊变量与常数 ans 计算结果的变量名computer 确定运行的计算机 eps 浮点相对精度 Inf 无穷大 I 虚数单位inputname 输入参数名 NaN 非数nargin 输入参数个数 nargout 输出参数的数目 pi 圆周率nargoutchk 有效的输出参数数目 realmax 最大正浮点数 realmin 最小正浮点数varargin 实际输入的参量varargout 实际返回的参量操作符与特殊字符 + 加实线 c 亮青色 : 点线 m 锰紫色-.点虚线--虚线七、注解xlabel('Input Value');% x轴注解 ylabel('Function Value');% y轴注解title('Two Trigonometric Functions');% 图形标题legend('y = sin(x)','y = cos(x)');% 图形注解 grid on;% 显示格线八、二维绘图函数 bar 长条图errorbar 图形加上误差范围fplot 较精确的函数图形 polar 极座标图 hist 累计图rose 极座标累计图 stairs 阶梯图 stem 针状图 fill 实心图 feather 羽毛图 compass 罗盘图 quiver 向量场图第四篇:MATLAB学习感想学习感想环科141 邢碧枞在科技飞速发展的今天,各行各业都离不开计算机的使用,而作为以科研为主的环境科学,更是离不开对计算机及软件的学习。
MATLAB基础知识

精心整理一、 1、数学建模基础知识及常用命令一、界面窗口介绍:1 命令窗口(command window ),窗口中输入命令,回车实现计算或绘图功能。
先级,加减法具有相同的低优先级,括号可以用来改变优先次序。
大家可以进行几个普通计算(练习10分钟)1、325+47⨯÷ 2、459+986-2.7+55-1033.5+20⨯()29() 2、数据显示格式默认情况下,matlab显示小数点后4位小数,可以利用format命令改变显示格式(一般写在要改变的数值的命令前):format short 小数点后4位format long 小数点后15位format bank 小数点后2位(以上为三个常用的)>> pians =3.1416三、matlab变量1、变量赋值形式变量=表达式(数值)或表达式(数值)其中,“=”为赋值符号,将右边表达式的值赋给左边变量(上面左的含义),当不指定输出变量时,matlab将表达式的值赋给临时变量ans(右的含义)。
同一行可以有多个变量赋值,用分号(不显示结果)或逗号(显示结果)分隔。
如取第二个元素a(2)ans = -5(2)利用符号“:”建立等差数组。
格式:x=初值:步长:终值(步长为1时可省略,步长也可以为如建立一个1至6,步长为1的等差数组:a=1:1:6a = 1 2 3 4 5 64、数组的运算y =a*x - b/x + 52、字符变量在matlab中用单引号括起来的一串字符称为字符串,字符串赋给变量,就构成字符变量。
ans =hello五、常用函数sin(x) 正弦函数asin(x) 反正弦函数ans =0.4223六、因式分解的命令factor(eq)例1、232++x xsyms x; y=x^2+3*x+2; factor(y)或者syms x; factor(x^2+3*x+2)七、多项式展开的命令expand(eq)例2、10x(1)求导,x可省略,直接用diff(y,n)指令即可;如果是一阶导数,则n 可以省略,直接用diff(y,x)或diff(y)即可。
Matlab学习笔记

第一讲 MATLAB基本知识【↑】可用于调出前一个命令行,【↓】可调出后一个命令行,这样避免了重新输入的麻烦。
当然历史窗口也具有此功能。
MATLAB文件格式有M、Mat、Mex等。
扩展名为“.m”的文件称为M文件(程序文件)。
顾名思义,该文件是解决问题的程序命令集合,工具箱中的函数大部分是M文件。
扩展名为“.mat”的文件称为MAT文件(数据文件),用来保存工作空间的数据变量。
扩展名为“.mex”的文件称为MEX文件(可执行文件),由MATLAB的编译器对M文件进行编译后产生。
表1-2 常见的文件管理命令命令说明what 显示当前目录中的MATLAB文件which文件主名显示指定的M文件的路径type文件主名显示指定的M文件内容save文件名存储定义的变量或演算结果到指定的文件名diary文件名以ASCII码形式记录所有的输入和屏幕上输出的内容cd.. 显示当前工作目录cd 子目录名进入子目录dir 显示当前目录中所有文件mkdir 建子目录Load filename 寻找名称为filename.mat的档案,并以二进制格式载入当用户在MATLAB命令窗口输入一条命令后,MATLAB按照一定次序寻找相关的文件。
基本的搜索过程是:①检查该命令是不是一个变量;②检查该命令是不是一个内部函数;③检查该命令是否当前目录下的M文件;④检查该命令是否是MATLAB搜索路径中其他目录下的M文件。
(意即可直接调用M文件) 变量的命名的规则是:①变量名区分大小写;②变量名以字母开头,可以由字母、数字、下画线组成,但不能使用标点;③变量名长度不超过63位,最多只能含有63个字符,后面的字符无效。
“%”是注释符,“%”后面的内容为注释,对MATLAB的计算不产生任何影响。
MATLAB是基于矩阵运算的,单一的数也是1×1的矩阵。
MATLAB将所有变量均保存为double的形式,在“Command Window”的状态下,所有的变量均存在于工作空间中。
数学建模matlab笔记

数据基本操作一般要处理的数据量都比较大,所以需要将数据导入。
读入图片:[X,map]=imread('filename.后缀');X 是一个三维的数据阵。
显示图片:imshow(X);将真彩转换成灰度:x1=grb2gray(X);将三维转化成二维。
翻转图片(翻转矩阵):x2=flipud(x1);上下翻转ud x3=fliplr(x1);左右翻转lr例:x1 = 1 2 3 4 5 6 7 8 9 x3 =3 2 1 6 54 9 8 7从Excel 中导入数据:b=xlsread('filename.xls');载入ASC 码文件(txt or six)并赋值给X: X=load('filename.后缀'); 导入同时赋值给X ,如果不想赋值可以这样写:load filename.后缀; 上述导入数据的前提是事先将数据文件放入matlab 的work 文件夹下。
如果没有放在work 文件夹下还可以这样:X=load('文件路径');设定观察区域:axis([-2 8 -6 12])横坐标最小值为-2,最大值为8;纵坐标最小值为-6,最大值为12fzero 的用法: x=fzero(@cos,[1,2]) 求cos(x)在区间[1,2]区间内的零点。
clear all ,clc;x=fzero(@cos,[1 2]) 结果:x =1.5708如果函数非系统内置,则需自己编写函数文件,格式如下: function y=myfun(x)%函数声明 y=x.*sin(x)+exp(x);%函数定义写完后保存并运行,文件名默认为函数名,不要更改,本例文件名即为myfun 函数求导:diff()(x f ,n); n 表示n 阶导数。
求不定积分: int ()(x f ); 求定积分:quad (fun ,n ,m );fun 为被积函数句柄(被积函数写成函数文件),m 、n 分别为积分上下限。
MATALB数学建模常用技巧总结

MATALB数学建模常用技巧总结MATLAB数学建模常用技巧总结引言在数学建模领域,MATLAB是一种被广泛应用的工具,其强大的计算能力和丰富的函数库使得它成为许多研究者和工程师的首选。
然而,要充分发挥MATLAB的优势并有效解决问题,我们需要掌握一些常用的技巧。
本文将总结一些MATLAB数学建模中常用的技巧,希望能够对读者有所帮助。
一、数据处理与可视化1. 数据导入与导出在数学建模中,数据处理是一个必不可少的过程。
MATLAB提供了丰富的数据导入与导出函数,可以轻松地从各种文件格式中导入数据,并将结果导出到合适的格式。
2. 数据清洗与处理对于实际问题中复杂的数据,我们常常需要对其进行清洗和处理。
MATLAB 提供了一系列强大的函数,如去除异常值、归一化、滤波等,可以帮助我们对数据进行预处理。
3. 数据可视化数据可视化是理解和传达数据的重要方式。
MATLAB的绘图功能非常强大,可以绘制各种类型的图形,如散点图、曲线图、柱状图等。
此外,还可以通过添加标注、调整颜色和线条等来美化图形。
二、数学建模方法1. 数值求解在实际问题中,我们常常需要求解各种数学方程和微分方程。
MATLAB提供了许多数值求解函数,如fsolve、ode45等,可以帮助我们解决这些问题。
2. 构建模型数学建模的关键在于构建恰当的数学模型。
MATLAB提供了丰富的函数和工具,可以帮助我们构建各种复杂的数学模型,如线性回归、非线性优化等。
3. 参数估计与拟合在实际问题中,我们经常需要根据已有数据来估计模型中的未知参数。
MATLAB提供了多种参数估计和拟合函数,如polyfit、lsqcurvefit等,可以帮助我们进行这些计算。
三、优化与最优化1. 单目标优化在数学建模中,我们常常需要优化某个目标函数。
MATLAB提供了多种优化函数,如fminsearch、fminunc等,可以帮助我们找到目标函数的最小值。
2. 多目标优化在某些情况下,我们可能需要优化多个目标函数。
MATLAB学习笔记

1. 有矩阵A 、矩阵B 和矩阵X 其关系为A*X=B,来求X ,在MA TLAB 中的语句为X=A\B2. 矩阵A 的分析求行列式 det(A) 求行列式的秩 rank(A) 求逆矩阵 inv(A) 求矩阵的转置A ’ 矩阵A 的特征向量和特征值[C,D]=eig(A) C 为特征向量 D 为特征值 3. 矩阵的数组运算元素之间的运算都叫阵列运算1》乘法(1) 矩阵运算A*B 矩阵的数组运算A.*B(元素与元素相乘)例如求y=sin(x^2) x=0:0.5:10,意思是要把x 每个元素平方后在求y 。
如果在MA TLAB 中运行的话会提示出错,因为x 是一个数组,而对数组每个元素进行运算的话要用数字运算,意思是要在想对应的运算符前加一点,写成y=sin(x.^2).4.函数cat 的使用 B=cat(dim,a1,a2…)意义:将多个同维a1,a2…构成一个高维数组B ,dim 是高维数组B 的维数,它必须等于大于a1,a2…的阶次。
5. 多项式以及表达式 假设y=Poly(A) 如果A 二维以上的数组,则y 表示由A 得特征根确定的多项式;如果A 为一维矩阵,则y 表示有A 的元素为多项式的跟确定的多项式。
即令y=0得到的值就是矩阵A 。
例如:A=[1 -2 3]则y=poly(A)=(x-1)(x+2)(x-3)的系数1 -2 -5 6. 4221-=A 二维向量,poly(A)为1 -5 8,即(x-1)(x-4)=-4的系数。
多项式函数的引用:polyval(1) y=polyval(px,x)(2) px 为多项式的系数,x 为多项式自变量取值,y 为对应多项式的函数值多项式的拟合方法:(1) 找出函数上的已知点系列(2) 有已知点系列确定多项式,即p=polyfit(x,y,n)式中,p 为模拟的多项式,x 和y 为已知点系列,n 是多项式的最高阶次。
第四章 符号运算(1) findsym(f,n)用来查找函数y 的变量次序,n 为查找变量的个数。
matlab学习笔记

>> [i,j,v]=find(A)
i =
1
2
1
2
3
j =
1
1
2
3
3
方法定义B{2}='hello'第二种方法比第一种方法更方便所以更常用。
这样B就有两个元素了,B(1)是{[1;2]},B(2)是{'hello'},
每个元素都是cell型的(注意和B{1}、B{2}的区别,B{1}是[1;2],B{2}是'hello')
cell函数是造元素为cell类型的矩阵
>> A = [1 0 4 -3 0 0 0 8 6];
>> X = find(A)
X =
1 3 4 8 9
find(A>5)返回矩阵A中大于5的元素所在位置
>> find(A>5)
ans =
8 9
[i,j,v]=find(A) 返回矩阵A中非零元素所在的行i,列j,和元素的值v(按所在位置先后顺序输出)
plot(x,z,'k-o','linewidth',2,'markersize',4);
legend 实验数据y 实验数据z %%%legend 设置相关线条表示的内容
box off %%%% box off表示去掉坐标框的上线和右线;
legend('boxoff')
ylabel('时间/s','fontname','标楷体','fontweight','bold','fontsize',12); %%ylabel和xlabel分别是设置X轴和Y轴的名称和单位;
MATLAB数学建模算法学习笔记

MATLAB数学建模算法学习笔记关于MATLAB的数学建模算法学习笔记目录线性规划中应用: (3)非线性规划: (3)指派问题;投资问题:(0-1问题) (3)1)应用fmincon命令语句 (3)2)应用指令函数:bintprog (5)重新整理矩阵类型 (6)1)应用reshape (6)2)应用命令:nonzeros (7)非线性的最小值得求法:含有一个变量时,应用命令:fminsearch(@fun,x0) (7)含有多个变量时用:fminunc() (7)求解非线性多变量等式应用命令fsolve (8)二次规划问题应用:quadprog (8)把有条件的问题转化成无条件问题。
罚函数法:fminunc (9)在Matlab中求解极值问题函数有: (9)1)fminbnd (9)1:在Matlab中求解距离的函数为:dist (9)最小生成树 (9)prim算法 (10)Find函数的应用 (10)关于图论的Matlab工具箱相关命令 (10)这些命令基本上都用到稀疏阵,产生稀疏阵用sparse命令 (10)查看网图用view (11)积分命令quadl (11)Matlab插值工具箱 (11)一维插值:interp1 (11)二维插值: (11)插值接点为网格节点:interp2 (11)插值节点为散乱节点:griddata (11)最小二乘法 (11)2)应用lsqlin命令语句 (12)三次样条差 (12)积分函数命令:quadl (13)同一组数据用不同插值方法效果比较线性插值、三次样条插值 (13) 参数估计 (14)1)非线性最小拟合 (14)命令:lsqcurvefit解决非线性拟合问题。
(14)2)线性最小二乘法 (15)解微分方程 (16)1)求解常微分、线性常微分、齐次与非齐次微分方程等问题 (16) 2)初值问题的matlab数值解 (16)3)高阶微分方程 (16)4)边值问题的Matlab数值解 (16)多目标规划问题 (18)解决方案: (18)1)加权系数法。
Matlab学习笔记(全)

Matlab学习笔记——《MATLAB与科学计算》王正盛国防工业出版社一.MATLAB入门 (4)who、whos和永久变量 (4)显示格式 (4)图形 (4)二.MATLAB数值计算 (5)1.常用命令: (5)2.矩阵的保存和获取 (5)3.矩阵的运算和数组的运算 (5)4.线性方程组 (5)5.多项式 (6)6.数值积分 (6)7.一般非线性方程组求解 (6)8.微分方程的数值求解 (7)三.MATLAB的符号计算 (7)1.符号变量和符号表达式 (7)2.微积分运算 (7)3.解方程 (8)4.化简和代换 (8)的符号表达式命令 (8)四.MATLAB的图形和可视化 (9)1.二维图形 (9)2图形标记 (9)3.特殊坐标和图形 (9)4.其他命令 (9)5.填充命令 (10)6.三维图形 (10)7.符号绘图 (10)8.其他 (10)五.MATLAB程序设计 (10)1.概述: (10)2.命令文件 (11)3.程序文件 (11)六.MATLAB图形用户界面(GUI)设计 (11)七.基于MATLAB的大规模矩阵计算 (11)1.稀疏矩阵 (11)八.基于MATLAB的最优化问题求解 (12)1.线性规划问题 (12)2.非线性问题 (12)3.二次规划问题 (12)九.基于MATLAB的数据插值和拟合 (12)1.一维数据插值 (12)2.二维数据插值 (13)3.曲线拟合 (13)十.基于MATLAB的图像处理初步 (13)1.图像分类 (13)2.图像的读取和显示 (13)一.MATLAB入门who、whos和永久变量who 变量名 %检查内存变量。
Whos %检查驻留变量的详细情况。
MATLAB自定义的永久变量:eps %计算机中的最小正数 inf %无穷大pi %圆周率 NaN %不定量flops %浮点运算次数 i,j%虚数单位显示格式MATLAB中以短格式(5个有效数字)显示计算结果,可以用format命令改变数字显示格式1.变量的存储和调用1)存储当前工作空间中的变量Save %将所有的变量存入文件中Save mydate %将所有变量存入指定文件Save mydate x y z %将指定的变量存入指定的文件中2)将数据文件的变量载入当前的工作空间将save换作load即可图形1.二维图形绘制命令Plot(x,y);2.三维图形绘制命令Mesh(z);2.用户目录的建立在命令窗口输入:cd c:\mydir二.MATLAB数值计算1.常用命令:Reshape命令X=1:1:6; %产生6个元素的行向量Reshape(x,2,3); %利用X行向量产生一个2*3的向量diag命令:ar=rand(4,4) %产生一个4*4的0-1均匀随机向量d=diag(ar) %用ar的主对角元形成向量dD=diag(d)%利用d构成对角矩阵DSize:获取矩阵的行数和列数2.矩阵的保存和获取1)利用m文件利用文件编辑器编辑矩阵AM=[1 2 3;4 5 6;7 8 9]——》保存为在自己的目录下名的——》在MATLAB命令窗口中只要输入matrix就可以调用AM矩阵2)通过mat文件Mat文件是MATLAB中保存数据的一种标准格式二进制文件,通过save和load执行,如前所述3)利用外部数据文件装入到指定矩阵中假如磁盘中已有名为c:\mydir\的二进制数据文件,利用load c:\mydir\命令可以在MATLAB工作空间中产生一个名为date的矩阵3.矩阵的运算和数组的运算矩阵运算是按矩阵的运算法则进行的;数组运算无论何种操作都是对元素逐个进行的,数组运算需要在运算符前加点号。
matlab笔记整理(部分代码含示例)【MATLAB入门必备】

matlab笔记整理(部分代码含例子)一元二次方程:方法一:p=[1,-3,1];x=roots(p)画图:x=-5:0.1:5;y1=x.*x-3*x+1;y2=zeros(size(x));plot(x,y1,x,y2);方法二:f=@(x)x*x-3*x+1;x1=fzero(f,0.5)x2=fzero(f,2.5)方法三:f=@(x)x*x-3*x+1;x1=fsolve(f,0.5,optimset('Display','off'))x2=fsolve(f,2.5,optimset('Display','off'))方法四:syms xx=solve(x^2-3*x+1)x=eval(x)求复数的实部:real求复数的虚部:imag命令输出格式:format(format long → format)(format rat 以有理数形式输出)求自然指数:exp三角函数以角度为单位的函数要再函数名后面加"d"abs函数可以求实数的绝对值、复数的模、字符串(要加引号)的ASCII码值取整:round(四舍五入)ceil(大于等于这个数的第一个整数)floor(小于等于这个数的第一个整数)fix(舍弃小数)取个位,十位,百位数字实例:(rem取余)m=345;m1=rem(m,10)m2=rem(fix(m/10),10)m3=fix(m/100)判断素数例子:(isprime(n),当n是素数时返回1,否则返回0)x=1:100;k=isprime(x);k1=find(k); //寻找k向量中非零元素的"序号"p=x(k1) //输出x中的全部素数开根号:sqrt()exp(pi/2):e的Π/2方预定义单位:i,j虚数单位NAN代表非数who命令和whos命令:who:工作区变量有哪些whos:变量的详细情况行向量的生成:1、冒号表达式2、linspace(a,b,n) n为元素总数结构矩阵:(格式:结构矩阵元素.成员名=表达式)a(1).x1=10;a(1).x2='liu';a(1).x3=[11,21;34,78];a(2).x1=12;a(2).x2='wang';a(2).x3=[34,191;27,578];a(3).x1=14;a(3).x2='cai';a(3).x3=[13,890;67,231];单元矩阵:(用大括号把元素括起来)b={10,'liu',[11,21;34,78];12,'wang',[34,191;27,578];...14,'cai',[13,890;67,231]}矩阵的引用:1、A(3,2):A矩阵第3行第2列元素2、通过序号来引用(矩阵元素先储存第一列元素,再储存第二列元素。
MATLAB学习笔记

Matlab学习笔记《第一章》矩阵及基本运算1、rand相关rand()随机矩阵,元素在(0,1)之间;randn()正态分布随机矩阵!元素大小是不限制的,方差为1randperm(n) 生成1到n之间n个随机数,相当于对n个数进行一个排列;2、blkdiag(a,b,c...)产生以a,b,c 为对角元素的对角矩阵;3、numel(A)计算矩阵A中元素的个数;4、compan 计算友矩阵,对于计算特征值特征向量很有帮助,eig为计算特征值;5、linspace(a,b ,n)将a,b等分为n等分,如果不输入n将视为默认1006、几个特殊矩阵:全一矩阵ones;单位矩阵eye;全零阵zeros7、logspace(a,b):产生在(10^a,10^b)之间的对数等分向量,同样可以在最后进行限制logspace(a,b,n),eg:logspace(1,2,6)结果为:ans =10.0000 15.8489 25.1189 39.8107 63.0957 100.0000,另外还有一个:y = logspace(a,pi),不太一样:logspace(1,pi,5) :ans =10.0000 7.4866 5.6050 4.1963 3.1416,这个主要应该是由于pi是Matlab内部定义的常数。
8、哈达玛(Hadamard)矩阵是由+1和-1元素构成的正交方阵;9、希尔伯特矩阵Hilbert:hilb(n),其元素为H(i,j)=1/(i+j-1)。
10、Pascal矩阵,magic魔方矩阵,Hankel方阵,托普利兹矩阵toeplitz,Wilkinson 特征值测试阵。
由于自己数学功底不是很强,这些矩阵还不是很理解,以后用到的时候再慢慢了解吧。
11、矩阵的乘法:A*B:两个矩阵相乘;A.*B:矩阵对应元素相乘;dot(A,B):矩阵的点成;cross(A,B):矩阵的叉乘;conv:矩阵的卷积;kron(A,B):矩阵的张量积,这个相当于用A中每个元素乘以矩阵B,所以这个矩阵还是蛮大的。
Matlab数学建模学习笔记——插值与拟合
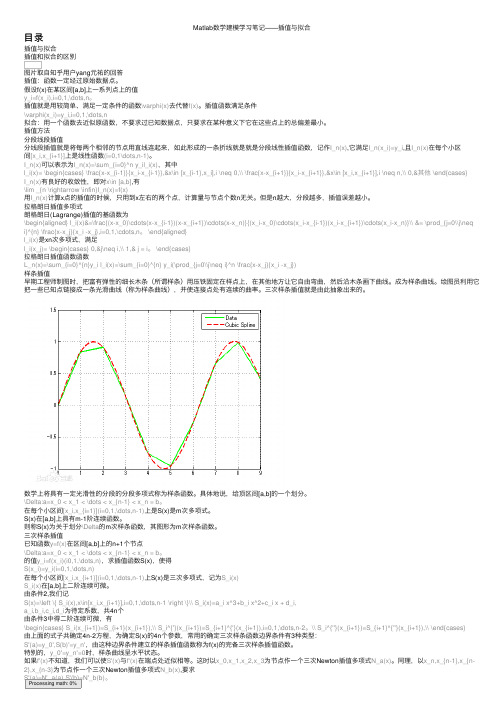
Matlab数学建模学习笔记——插值与拟合⽬录插值与拟合插值和拟合的区别图⽚取⾃知乎⽤户yang元祐的回答插值:函数⼀定经过原始数据点。
假设f(x)在某区间[a,b]上⼀系列点上的值y_i=f(x_i),i=0,1,\dots,n。
插值就是⽤较简单、满⾜⼀定条件的函数\varphi(x)去代替f(x)。
插值函数满⾜条件\varphi(x_i)=y_i,i=0,1,\dots,n拟合:⽤⼀个函数去近似原函数,不要求过已知数据点,只要求在某种意义下它在这些点上的总偏差最⼩。
插值⽅法分段线段插值分线段插值就是将每两个相邻的节点⽤直线连起来,如此形成的⼀条折线就是就是分段线性插值函数,记作I_n(x),它满⾜I_n(x_i)=y_i,且I_n(x)在每个⼩区间[x_i,x_{i+1}]上是线性函数(i=0,1\dots,n-1)。
I_n(x)可以表⽰为I_n(x)=\sum_{i=0}^n y_il_i(x),其中l_i(x)= \begin{cases} \frac{x-x_{i-1}}{x_i-x_{i-1}},&x\in [x_{i-1},x_i],i \neq 0,\\ \frac{x-x_{i+1}}{x_i-x_{i+1}},&x\in [x_i,x_{i+1}],i \neq n,\\ 0,&其他 \end{cases}I_n(x)有良好的收敛性,即对x\in [a,b],有\lim _{n \rightarrow \infin}I_n(x)=f(x)⽤I_n(x)计算x点的插值的时候,只⽤到x左右的两个点,计算量与节点个数n⽆关。
但是n越⼤,分段越多,插值误差越⼩。
拉格朗⽇插值多项式朗格朗⽇(Lagrange)插值的基函数为\begin{aligned} l_i(x)&=\frac{(x-x_0)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_n)}{(x_i-x_0)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i-x_n)}\\ &= \prod_{j=0\\j\neq i}^{n} \frac{x-x_j}{x_i -x_j},i=0,1,\cdots,n。
学习matlab笔记

matlab的仿真分析
在matlab 命令窗口中通过函数进行,格式:
[t,x,y]=sim(‘模型文件名’,[to tf],simser(‘参数1’,参数值1……)) simset定义仿真参数:
AbsTol:设定绝对误差范围。
Decimation:决定隔多少个点返回状态和参数会值。
Solver:解法器的选择。
MaxRows:默认值为0,表示不限制,若为大于0的值,则表示限制输出和输出状态的规模,使其最大行数等于该数值。
InitialStep:一个向量值,用于设定的初始状态。
FixedStep:用于正数表示步阶的大小,仅用于固定步长模式。
MaxStep:用于变步长模式,表示最大的步阶大小,默认值为“auto”. 如果知道模型的文件名称,可以用以下命令得到该模型的仿真参数:simger(‘模型文件名’)
求解方程组的方法(个人了解的):用solve函数求解,用矩阵求解:先求矩阵的逆,求乘,如:矩阵a,矩阵b;I=inv(a)*b;x=I(1) y=I(2) z=I(3)。
matlab在图像处理中的应用:
基本操作:
读取:A=imread(filename,fmt) fmt为图片格式如:A=imread(‘women’,’jpeg’)
写:imwrite(A,filename,fmt)
显示信息:imfinfo(filename,fmt) 显示:image(A)
处理中的常用函数:
imcrop 剪裁
imresize 放大
imrotate 旋转
medfilt2 滤波
imnoise 加入噪音。
MATLAB学习笔记整理

MATLAB笔记摘录:1、clc 命令清空命令窗口(The Command Windows)中的内容,可以用clf 清空当前图象窗口中的内容。
在工作空间窗口(The workspace browser)中变量可用clear命令清除。
2、能用diary 命令记录下在MATLAB 中运行过程中每个线程所做的事。
3、常见编程错误如果变量名与MATLAB 中的函数或命令重名,那么这个函数或命令将不能被访问。
4、常见编程错误不要创建和MATLAB 内建函数或命令同名的M 文件。
5、—which 命令,它能帮助我们找到正在执行的文件版本和它的路径。
6、命令窗口是最重要的窗口,因为所有的命令都得在此键入,所有的结果在此输出7、MATLAB 的变量名必须以字母开头,后面可以跟字母,数字和下划线(_).只有前31 个字符是有效的;如果超过了31 个字符,基余的字符将被忽略。
如果声明两个变量,两变量名只有第32 个字符不同,那么MATLAB 将它们当作同一变量对待8、像MATLAB 这样的叫做弱类型语言。
通过简单的赋值形式就可以创建变量,变量类型取决于创建时的类型。
9、。
有三种方式初始化MATLAB 中的变量:1.用赋值语句初始化变量2.用input 函数从键盘输入初始化变量3.从文件读取一个数据10、克隆运算符指定一系列的数值,它指定了这个系列数的第一值,步增和后一个值。
它的一般顺序始下first:incr:last11、捷径表达式可以联合转置运算符(’)来初始化行向量,或更加复杂的矩阵12、函数zeros 可以初始化任何大小的全为零的数组。
相似地,ones 函数产生的数组包含的元素全为1,eye 函数通常用来产生单位矩阵,只有对角线的元素为1.其他元素为0. 13、input 函数中有字符's'做为它的第二个参数,输入的数据就被当字符串. in2=input('enter data:','s') enter data:123 把字符串1.23 存储到in2 中.14、.数组,矩阵,向量有什么区别?答:矩阵是二维数组,向量是一维数组,矩阵和向量是数据的子集。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于MATLAB的数学建模算法学习笔记目录线性规划中应用: (3)非线性规划: (3)指派问题;投资问题:(0-1问题) (3)1)应用fmincon命令语句 (3)2)应用指令函数:bintprog (5)重新整理矩阵类型 (6)1)应用reshape (6)2)应用命令:nonzeros (7)非线性的最小值得求法:含有一个变量时,应用命令:fminsearch(@fun,x0) (7)含有多个变量时用:fminunc() (7)求解非线性多变量等式应用命令fsolve (8)二次规划问题应用:quadprog (8)把有条件的问题转化成无条件问题。
罚函数法:fminunc (9)在Matlab中求解极值问题函数有: (9)1)fminbnd (9)1:在Matlab中求解距离的函数为:dist (9)最小生成树 (9)prim算法 (10)Find函数的应用 (10)关于图论的Matlab工具箱相关命令 (10)这些命令基本上都用到稀疏阵,产生稀疏阵用sparse命令 (10)查看网图用view (11)积分命令quadl (11)Matlab插值工具箱 (11)一维插值:interp1 (11)二维插值: (11)插值接点为网格节点:interp2 (11)插值节点为散乱节点:griddata (11)最小二乘法 (11)2)应用lsqlin命令语句 (12)三次样条差 (12)积分函数命令:quadl (13)同一组数据用不同插值方法效果比较线性插值、三次样条插值 (13)参数估计 (14)1)非线性最小拟合 (14)命令:lsqcurvefit解决非线性拟合问题。
(14)2)线性最小二乘法 (15)解微分方程 (16)1)求解常微分、线性常微分、齐次与非齐次微分方程等问题 (16)2)初值问题的matlab数值解 (16)3)高阶微分方程 (16)4)边值问题的Matlab数值解 (16)多目标规划问题 (18)解决方案: (18)1)加权系数法。
(18)2)优先等级法。
(18)3)序贯算法 (18)4)应用多目标规划的MATLAB函数fgoalattain具体见《数学建模算法与应用》P131 (18)5)多目标规划可以归结为: (18)分类问题 (19)聚类分析:Q型和R型 (19)用于求元素之间距离的命令:mandist (19)去掉非零元命令:nonzeros (19)去掉重复的元素命令:union (19)Matlab聚类分析的相关命令 (19)知识点线性规划中应用:1)X=linprog(c,a,b,aeq,beq,zeros(x的个数,1) ) 用于在限制条件下的最小值;X=linprog(-c,a,b,aeq,beq,zeros(x的个数,1) ) 用于在限制条件下的最大值;非线性规划:1)X=fmincon(fun,X0,A,B,Aeq,Beq,LB,UB,NONLCON,OPTIONS)指派问题;投资问题:(0-1问题)1)应用fmincon命令语句Matlab 中非线性规划的数学模型写成以下形式其中 f ( x) 是标量函数,A, B, Aeq, Beq 是相应维数的矩阵和向量,C( x), Ceq( x) 是非线性向量函数。
Matlab 中的命令是X=FMINCON(FUN,X0,A,B,Aeq,Beq,LB,UB,NONLCON,OPTIONS) 它的返回值是向量x ,其中FUN 是用M 文件定义的函数 f ( x) ;X0 是x 的初始值;A,B,Aeq,Beq 定义了线性约束A * X B, Aeq * X Beq ,如果没有线性约束,则A=[],B=[],Aeq=[],Beq=[];LB 和UB 是变量x 的下界和上界,如果上界和下界没有约束,则LB=[],UB=[],如果x 无下界,则LB 的各分量都为-inf,如果x 无上界,则UB的各分量都为inf;NONLCON 是用M 文件定义的非线性向量函数C( x), Ceq( x) ;OPTIONS定义了优化参数,可以使用Matlab 缺省的参数设置。
例子:2)应用指令函数:bintprog重新整理矩阵类型1)应用reshape2)应用命令:nonzeros功能是将a=nonzeros(b)矩阵b按列逐次去值放在a中形成一个列向量。
非线性的最小值得求法:含有一个变量时,应用命令:fminsearch(@fun,x0)含有多个变量时用:fminunc()求解非线性多变量等式应用命令fsolve二次规划问题应用:quadprog把有条件的问题转化成无条件问题。
罚函数法:fminunc 其中:用法[X,Y]=fminunc(‘test3’,rand(1,2))与[X,Y]=fminunc(@test3,rand(1,2))相同。
缺点:精度不高。
在Matlab中求解极值问题函数有:1)fminbnd解决单变量非线性函数在区间上的极小值问题。
3)fseminf解决多变量、含有非线性约束的极小值问题。
3)fminimax解决多变量,满足在多个式子中极小——极大问题。
加一个负号就是解决多个式子中极大——极小值问题。
4)利用梯度求解约束优化问题。
1:在Matlab中求解距离的函数为:dist2:Sin()的反函数用asind()表示3:将数据生成txt文本:dlmwrite最小生成树prim算法Find函数的应用1)I=find(A)找出A内的非零元素位置,按列查找。
一次写在I 中。
2)[I,J,K]=find(A)找出A中非零元素的位置,将行标放入I中,将列表放入J中,将数值放入K中,按理寻找。
关于图论的Matlab工具箱相关命令这些命令基本上都用到稀疏阵,产生稀疏阵用sparse命令1)graphallshortestpaths 求图中所有顶点之间的最短距离2)graphconncomp 找无向图的连通分支,或有向图的强(弱)连通分支3)Graphisdag测试所有有向图是否含有圈,不含圈返回1,含圈返回04)Graphisomorphism确定连个图是否同构,同构返回1,否则返回05)Graphisspantree 确定一个图是否是生成树,是返回1,否则返回06) Graphmaxflow计算有向图的最大流7)Graphminspantree在图中找最小生成树8)Graphpred2path把前驱顶点的一对顶点间的最短距离和嘴短路径9)Graphtopoorder执行有向无圈图的拓扑排序10)Graphtraverse求从一顶点出发,所能遍历图中的顶点查看网图用view用法:view(biograph(ST,[],'ShowArrows','off','ShowWeights','on'))其中ST为树。
积分命令quadlMatlab插值工具箱一维插值:interp1二维插值:插值接点为网格节点:interp2插值节点为散乱节点:griddata最小二乘法1)2)应用lsqlin命令语句3)三次样条差积分函数命令:quadl同一组数据用不同插值方法效果比较线性插值、三次样条插值例子clc;clear;x0=[0 3 5 7 9 11 12 13 14 15];y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6]; x=0:0.1:15;y1=interp1(x0,y0,x);%%线性插值y2=interp1(x0,y0,x,'spline');%%%立方样条插值pp1=csape(x0,y0);y3=ppval(pp1,x);%%边界为一阶导插值pp2=csape(x0,y0,'second');y4=ppval(pp2,x);%%边界为二阶导插值[x',y1',y2',y3',y4'];subplot(1,3,1)plot(x0,y0,'+',x,y1)title('Piecewise linear')subplot(1,3,2)plot(x0,y0,'+',x,y2)title('Spline1')subplot(1,3,3)plot(x0,y0,'+',x,y3)title('Spline2')dx=diff(x);%%diff为一阶微分dy=diff(y3);dy_dx=dy./dx;dy_dx0=dy_dx(1)%% 求13<=x<=15内y的最小值ytemp=y3(131:151);ymin=min(ytemp);index=find(y3==ymin);%%xmin=x(index);[xmin,ymin]hold onplot(xmin,ymin,'ro')参数估计1)非线性最小拟合命令:lsqcurvefit解决非线性拟合问题。
人口数学模型的应用:例子:数学建模算法与应用的的6章人口预报模型clc, cleara=textread('data4.txt'); %把原始数据保存在纯文本文件data4.txt中x=a([2:2:6],:)'; %提出人口数据x=nonzeros(x); %去掉后面的零,并变成列向量t=[1790:10:2000]';t0=t(1); x0=x(1);fun=@(cs,td)cs(1)./(1+(cs(1)/x0-1)*exp(-cs(2)*(td-t0))); %cs(1)=x m,cs(2)=rcs=lsqcurvefit(fun,rand(2,1),t(2:end),x(2:end),zeros(2,1))%%拟合,满足使最小二乘最小的参数csxhat=fun(cs,[t;2010]) %预测已知年代和2010年的人口2)线性最小二乘法人口数学模型的应用,例子:1)利用后项查分clc, cleara=textread('data4.txt'); %把原始数据保存在纯文本文件data4.txt中x=a([2:2:6],:)';x=nonzeros(x);t=[1790:10:2000]';a=[ones(21,1), -x(2:end)];b=diff(x)./x(2:end)/10;%%时间间隔为10年cs=a\b;r=cs(1), xm=r/cs(2)2)利用前项查分clc, cleara=textread('data4.txt'); %把原始数据保存在纯文本文件data4.txt中x=a([2:2:6],:)'; x=nonzeros(x);t=[1790:10:2000]';a=[ones(21,1), -x(1:end-1)];b=diff(x)./x(1:end-1)/10;cs=a\b;r=cs(1), xm=r/cs(2)解微分方程1)求解常微分、线性常微分、齐次与非齐次微分方程等问题用命令:dsolve 数学建模算法与应用p112-P1142)初值问题的matlab数值解用:ode45 (采用四五阶龙哥库塔方简称RK方法)、ode23(采用二三阶RK方法)、ode113(采用多步法,效率一般比ode45高)用法:例如:[x,y]=ode45(fun,[a,d],y0) 其中fun为定义微分方程,[a,d]为定义区间,y0为初始值,x为在定义区间中采用四五阶龙哥库塔方法取a——d之间的值,y为其求解对应的值。
