CT图像三维重建(附源码)

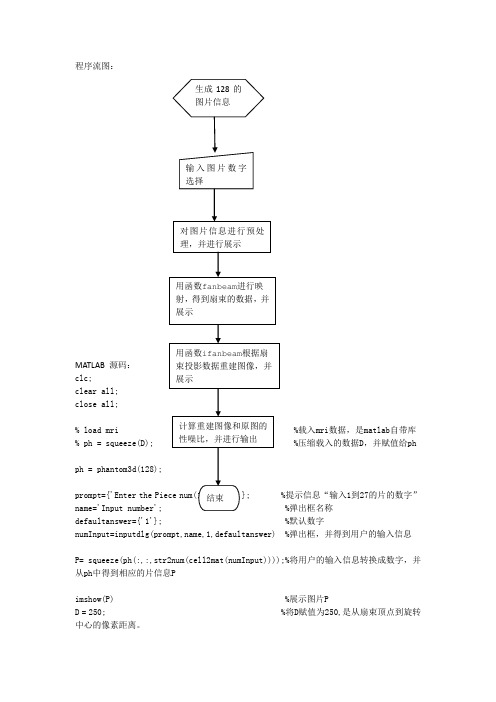
程序流图：MATLAB 源码：clc;clear all;close all;载入mri数据，是matlab自带库压缩载入的数据D，并赋值给ph ph = phantom3d(128);prompt={'Enter the 提示信息“输入1到27的片的数字”弹出框名称defaultanswer={'1'}; %默认数字numInput=inputdlg(prompt,name,1,defaultanswer) %弹出框，并得到用户的输入信息P= squeeze(ph(:,:,str2num(cell2mat(numInput))));%将用户的输入信息转换成数字，并从ph中得到相应的片信息Pimshow(P) %展示图片PD = 250; %将D赋值为250,是从扇束顶点到旋转中心的像素距离。

dsensor1 = 2; %正实数指定扇束传感器的间距2F1 = fanbeam(P,D,'FanSensorSpacing',dsensor1); %通过P，D等计算扇束的数据值dsensor2 = 1; %正实数指定扇束传感器的间距1F2 = fanbeam(P,D,'FanSensorSpacing',dsensor2); %通过P，D等计算扇束的数据值dsensor3 = 0.25 %正实数指定扇束传感器的间距0.25 [F3, sensor_pos3, fan_rot_angles3] = fanbeam(P,D,...'FanSensorSpacing',dsensor3); %通过P，D等计算扇束的数据值，并得到扇束传感器的位置sensor_pos3和旋转角度fan_rot_angles3figure, %创建窗口imagesc(fan_rot_angles3, sensor_pos3, F3) %根据计算出的位置和角度展示F3的图片colormap(hot); %设置色图为hotcolorbar; %显示色栏xlabel('Fan Rotation Angle (degrees)') %定义x坐标轴ylabel('Fan Sensor Position (degrees)') %定义y坐标轴output_size = max(size(P)); %得到P维数的最大值，并赋值给output_sizeIfan1 = ifanbeam(F1,D, ...'FanSensorSpacing',dsensor1,'OutputSize',output_size);%根据扇束投影数据F1及D等数据重建图像figure, imshow(Ifan1) %创建窗口，并展示图片Ifan1title('图一');disp('图一和原图的性噪比为：');result=psnr1(Ifan1,P);Ifan2 = ifanbeam(F2,D, ...'FanSensorSpacing',dsensor2,'OutputSize',output_size);%根据扇束投影数据F2及D等数据重建图像figure, imshow(Ifan2) %创建窗口，并展示图片Ifan2disp('图二和原图的性噪比为：');result=psnr1(Ifan2,P);title('图二');Ifan3 = ifanbeam(F3,D, ...'FanSensorSpacing',dsensor3,'OutputSize',output_size);%根据扇束投影数据F3及D等数据重建图像figure, imshow(Ifan3) %创建窗口，并展示图片Ifan3title('图三');disp('图三和原图的性噪比为：');result=psnr1(Ifan3,P);function [p,ellipse]=phantom3d(varargin)%PHANTOM3D Three-dimensional analogue of MATLAB Shepp-Logan phantom% P = PHANTOM3D(DEF,N) generates a 3D head phantom that can% be used to test 3-D reconstruction algorithms.%% DEF is a string that specifies the type of head phantom to generate.% Valid values are:%% 'Shepp-Logan' A test image used widely by researchers in% tomography% 'Modified Shepp-Logan' (default) A variant of the Shepp-Logan phantom % in which the contrast is improved for better % visual perception.%% N is a scalar that specifies the grid size of P.% If you omit the argument, N defaults to 64.%% P = PHANTOM3D(E,N) generates a user-defined phantom, where each row% of the matrix E specifies an ellipsoid in the image. E has ten columns,% with each column containing a different parameter for the ellipsoids:%% Column 1: A the additive intensity value of the ellipsoid% Column 2: a the length of the x semi-axis of the ellipsoid% Column 3: b the length of the y semi-axis of the ellipsoid% Column 4: c the length of the z semi-axis of the ellipsoid% Column 5: x0 the x-coordinate of the center of the ellipsoid% Column 6: y0 the y-coordinate of the center of the ellipsoid% Column 7: z0 the z-coordinate of the center of the ellipsoid% Column 8: phi phi Euler angle (in degrees) (rotation about z-axis)% Column 9: theta theta Euler angle (in degrees) (rotation about x-axis)% Column 10: psi psi Euler angle (in degrees) (rotation about z-axis)%% For purposes of generating the phantom, the domains for the x-, y-, and% z-axes span [-1,1]. Columns 2 through 7 must be specified in terms% of this range.%% [P,E] = PHANTOM3D(...) returns the matrix E used to generate the phantom.%% Class Support% -------------% All inputs must be of class double. All outputs are of class double.%% Remarks% -------% For any given voxel in the output image, the voxel's value is equal to the% sum of the additive intensity values of all ellipsoids that the voxel is a% part of. If a voxel is not part of any ellipsoid, its value is 0.%% The additive intensity value A for an ellipsoid can be positive or negative;% if it is negative, the ellipsoid will be darker than the surrounding pixels.% Note that, depending on the values of A, some voxels may have values outside % the range [0,1].%% Example% -------% ph = phantom3d(128);% figure, imshow(squeeze(ph(64,:,:)))%% Copyright2005MatthiasChristianSchabel(***************************) % University of Utah Department of Radiology% Utah Center for Advanced Imaging Research% 729 Arapeen Drive% Salt Lake City, UT 84108-1218%% This code is released under the Gnu Public License (GPL). For more information, % see : /copyleft/gpl.html%% Portions of this code are based on phantom.m, copyrighted by the Mathworks %[ellipse,n] = parse_inputs(varargin{:});p = zeros([n n n]);rng = ( (0:n-1)-(n-1)/2 ) / ((n-1)/2);[x,y,z] = meshgrid(rng,rng,rng);coord = [flatten(x); flatten(y); flatten(z)];p = flatten(p);for k = 1:size(ellipse,1)A = ellipse(k,1); % Amplitude change for this ellipsoidasq = ellipse(k,2)^2; % a^2bsq = ellipse(k,3)^2; % b^2csq = ellipse(k,4)^2; % c^2x0 = ellipse(k,5); % x offsety0 = ellipse(k,6); % y offsetz0 = ellipse(k,7); % z offsetphi = ellipse(k,8)*pi/180; % first Euler angle in radianstheta = ellipse(k,9)*pi/180; % second Euler angle in radianspsi = ellipse(k,10)*pi/180; % third Euler angle in radianscphi = cos(phi);sphi = sin(phi);ctheta = cos(theta);stheta = sin(theta);cpsi = cos(psi);spsi = sin(psi);% Euler rotation matrixalpha = [cpsi*cphi-ctheta*sphi*spsi cpsi*sphi+ctheta*cphi*spsi spsi*stheta;-spsi*cphi-ctheta*sphi*cpsi -spsi*sphi+ctheta*cphi*cpsi cpsi*stheta;stheta*sphi -stheta*cphi ctheta];% rotated ellipsoid coordinatescoordp = alpha*coord;idx = find((coordp(1,:)-x0).^2./asq + (coordp(2,:)-y0).^2./bsq + (coordp(3,:)-z0).^2./csq <= 1);p(idx) = p(idx) + A;endp = reshape(p,[n n n]);return;function out = flatten(in)out = reshape(in,[1 prod(size(in))]);return;function [e,n] = parse_inputs(varargin)% e is the m-by-10 array which defines ellipsoids% n is the size of the phantom brain imagen = 128; % The default sizee = [];defaults = {'shepp-logan', 'modified shepp-logan', 'yu-ye-wang'};for i=1:narginif ischar(varargin{i}) % Look for a default phantom def = lower(varargin{i});idx = strmatch(def, defaults);if isempty(idx)eid = sprintf('Images:%s:unknownPhantom',mfilename);msg = 'Unknown default phantom selected.';error(eid,'%s',msg);endswitch defaults{idx}case 'shepp-logan'e = shepp_logan;case 'modified shepp-logan'e = modified_shepp_logan;case 'yu-ye-wang'e = yu_ye_wang;endelseif numel(varargin{i})==1n = varargin{i}; % a scalar is the image size elseif ndims(varargin{i})==2 && size(varargin{i},2)==10e = varargin{i}; % user specified phantomelseeid = sprintf('Images:%s:invalidInputArgs',mfilename);msg = 'Invalid input arguments.';error(eid,'%s',msg);endend% ellipse is not yet definedif isempty(e)e = modified_shepp_logan;endreturn;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Default head phantoms: % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%function e = shepp_logane = modified_shepp_logan;e(:,1) = [1 -.98 -.02 -.02 .01 .01 .01 .01 .01 .01];return;function e = modified_shepp_logan%% This head phantom is the same as the Shepp-Logan except% the intensities are changed to yield higher contrast in% the image. Taken from Toft, 199-200.%% A a b c x0 y0 z0 phi theta psi% -----------------------------------------------------------------e = [ 1 .6900 .920 .810 0 0 0 0 0 0-.8 .6624 .874 .780 0 -.0184 0 0 0 0-.2 .1100 .310 .220 .22 0 0 -18 0 10-.2 .1600 .410 .280 -.22 0 0 18 0 10.1 .2100 .250 .410 0 .35 -.15 0 0 0.1 .0460 .046 .050 0 .1 .25 0 0 0.1 .0460 .046 .050 0 -.1 .25 0 0 0.1 .0460 .023 .050 -.08 -.605 0 0 0 0.1 .0230 .023 .020 0 -.606 0 0 0 0.1 .0230 .046 .020 .06 -.605 0 0 0 0 ]; return;function e = yu_ye_wang%% Yu H, Ye Y, Wang G, Katsevich-Type Algorithms for Variable Radius Spiral Cone-Beam CT%% A a b c x0 y0 z0 phi theta psi% -----------------------------------------------------------------e = [ 1 .6900 .920 .900 0 0 0 0 0 0-.8 .6624 .874 .880 0 0 0 0 0 0-.2 .4100 .160 .210 -.22 0 -.25 108 0 0-.2 .3100 .110 .220 .22 0 -.25 72 0 0.2 .2100 .250 .500 0 .35 -.25 0 0 0.2 .0460 .046 .046 0 .1 -.25 0 0 0.1 .0460 .023 .020 -.08 -.65 -.25 0 0 0.1 .0460 .023 .020 .06 -.65 -.25 90 0 0.2 .0560 .040 .100 .06 -.105 .625 90 0 0-.2 .0560 .056 .100 0 .100 .625 0 0 0 ];return;% func——计算两幅图像的psnr值function result=psnr1(in1,in2)z=mse(in1,in2);result=10*log10(255.^2/z)% plot(result)function z=mse(x,y)if ndims(x)==3x=rgb2gray(x);endif ndims(y)==3y=rgb2gray(y);endx=double(x);y=double(y);[m1,n1]=size(x);[m2,n2]=size(y);m=min(m1,m2);n=min(n1,n2);z=0;for i=1:mfor j=1:nz=z+(x(i,j)-y(i,j)).^2;endendz=z/(m*n);。