算法基本语句知识点及典型例题
常用算法举例

常用算法举例一、求面积、体积、方程的根,将公式的表达式用变量或常量表示出来,输出即可;二、累加、累乘(包括偶数和奇数的变换运算)三、典型算法举例:1、求两个数或三个数或多个数的最大值、最小值思路:用表判断的if语句就可完成,也可使用函数的调用;若是多个数,则采取从键盘上输入第一个数,并假定它是最大值存放在变量max中,以后每输入一个数便与max比较,若输入的数较大,则最大值是新的数值,存放到max中,数据输入完,最大值也就确定了。
main( ){int a,b,c,d;scanf(“%d,%d,%d”.&a,&b,&c);d=max(a,b,c);printf(“max=%d”,d);}int max(x,y,z)int x,y,z;{int p;p=x;if (p<y) p=y;if (p<z) p=z;return(p);}求10个数的最大值main( ){int I,k,max;scanf(“%d”,&max);for (I=2;I<11;I++){scanf(“%d”,&k);if (max<k) mzk=k;}printf(“max=%d\n”,max);}2、判断是否为闰年思路:闰年应满足条件之一:(a)能被4整除,但不能被100整除;(b)能被4整除又能被400整除main( ){int year,leap;scanf("%d",&year);if (year%4==0 ){ if (year%100==0){if (year%400==0)leap=1;else leap=0;}elseleap=1;}elseleap=0;if (leap)printf(“%d is “,year);elseprintf(“%d is not”,year);printf(“a leap year/n”);}此程序还可以简化用 (year%4==0 &&year%100!=0 || year%400==0)直接进行判断也可;此题还可求某范围内的闰年。
算法基本语句知识点及典型例题

基本算法语句一、输入、输出语句和赋值语句 (1)输入语句 ①输入语句的一般格式②输入语句的作用是实现算法的输入信息功能;③“提示内容”提示用户输入什么样的信息,变量是指程序在运行时其值是可以变化的量;④输入语句要求输入的值只能是具体的常数,不能是函数、变量或表达式; ⑤提示内容与变量之间用分号“;”隔开,若输入多个变量,变量与变量之间用逗号“,”隔开。
(2)输出语句 ①输出语句的一般格式②输出语句的作用是实现算法的输出结果功能;③ “提示内容”提示用户输入什么样的信息,表达式是指程序要输出的数据;④输出语句可以输出常量、变量或表达式的值以及字符。
(3)赋值语句 ①赋值语句的一般格式②赋值语句的作用是将表达式所代表的值赋给变量;③赋值语句中的“=”称作赋值号,与数学中的等号的意义是不同的。
赋值号的左右两边不能对换,它将赋值号右边的表达式的值赋给赋值号左边的变量; ④赋值语句左边只能是变量名字,而不是表达式,右边表达式可以是一个数据、常量或算式;⑤对于一个变量可以多次赋值。
注意:①赋值号左边只能是变量名字,而不能是表达式。
如:2=X 是错误的。
②赋值号左右不能对换。
如“A=B ”“B=A ”的含义运行结果是不同的。
③不能利用赋值语句进行代数式的演算。
(如化简、因式分解、解方程等) ④赋值号“=”与数学中的等号意义不同。
5:条件语句(1)条件语句的一般格式有两种:①IF—THEN—ELSE语句;②IF—THEN语句。
①IF—THEN—ELSE语句IF—THEN—ELSE语句的一般格式为图1,对应的程序框图为图2。
图1②IF—THEN语句IF—THEN语句的一般格式为图36:循环语句循环结构是由循环语句来实现的。
对应于程序框图中的两种循环结构,一般程序设计语言中也有当型(WHILE型)和直到型(UNTIL型)两种语句结构。
即WHILE语句和UNTIL语句。
(1)WHILE语句①WHILE语句的一般格式是②当计算机遇到WHILE语句时,先判断条件的真假,如果条件符合,就执行WHILE与WEND之间的循环体;然后再检查上述条件,如果条件仍符合,再次执行循环体,这个过程反复进行,直到某一次条件不符合为止。
专题50:算法初步知识点及典型例题(原卷版)

专题50:算法初步知识点及典型例题(原卷版)【知识梳理】知识点一、算法1.算法的概念(1)古代定义:指的是用阿拉伯数字进行算术运算的过程。
(2)现代定义:算法通常是指按照一定规则解决某一类问题的明确和有限的步骤。
(3)应用:算法通常可以编成计算机程序,让计算机执行并解决问题。
2.算法的特征:①指向性:能解决某一个或某一类问题;②精确性:每一步操作的内容和顺序必须是明确的;算法的每一步都应当做到准确无误,从开始的“第一步”直到“最后一步”之间做到环环相扣,分工明确.“前一步”是“后一步”的前提,“后一步”是“前一步”的继续.③有限性:必须在有限步内结束并返回一个结果;算法要有明确的开始和结束,当到达终止步骤时所要解决的问题必须有明确的结果,也就是说必须在有限步内完成任务,不能无限制的持续进行.④构造性:一个问题可以构造多个算法,算法有优劣之分。
3.算法的表示方法:(1) 用自然语言表示算法: 优点是使用日常用语, 通俗易懂;缺点是文字冗长, 容易出现歧义;(2) 用程序框图表示算法:用图框表示各种操作,优点是直观形象, 易于理解。
注:泛泛地谈算法是没有意义的,算法一定以问题为载体。
例1.下面给出一个问题的算法:S1输入x;S2若x≤2,则执行S3;否则,执行S4;S3输出-2x-1;S4输出x2-6x+3.问题:(1)这个算法解决的是什么问题?(2)当输入的x值为多大时,输出的数值最小?知识点二:流程图1. 流程图的概念:流程图,是由一些图框和流程线组成的,其中图框表示各种操作的类型,图框中的文字和符合表示操作的内容,流程线表示操作的先后次序。
2.流程图常用符号:图形符号名称含义开始/结束框用于表示算法的开始与结束输入/输出框用于表示数据的输入或结果的输出处理框描述基本的操作功能,如“赋值”操作、数学运算等判断框判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”流程线表示流程的路径和方向连接点用于连接另一页或另一部分的框图注释框框中内容是对某部分流程图做的解释说明3.画流程图的规则:(1)使用标准的框图的符号;(2)框图一般按从上到下、从左到右的方向画;(3)除判断框图外,大多数框图符号只有一个进入点和一个退出点。
基本算法语句与算法案例教案练习含答案

基本算法语句与算法案例教案练习含答案第一章:算法概述1.1 算法的定义与特性定义:算法是解决问题的一系列清晰、有序的步骤。
特性:可行性、确定性、有穷性、足够性。
1.2 算法的表示方法伪代码:使用简化的语言描述算法。
流程图:使用图形符号表示算法步骤。
第二章:基本算法语句2.1 输入输出语句输入:从用户或文件获取数据。
输出:向用户或文件输出数据。
2.2 赋值语句赋值:将一个值或表达式赋给变量。
2.3 条件语句如果:根据条件执行相应的操作。
否则:当条件不满足时执行的操作。
2.4 循环语句循环:重复执行一段代码直到条件不满足。
第三章:算法案例3.1 冒泡排序算法目的:对一组数据进行从小到大的排序。
步骤:比较相邻元素,交换不符合顺序的元素。
3.2 查找算法线性查找:从数组的一端开始,逐个比较元素。
二分查找:在有序数组中,通过比较中间元素确定位置。
3.3 插入排序算法目的:对一组数据进行从小到大的排序。
步骤:将未排序的元素插入到已排序的序列中。
第四章:算法分析4.1 时间复杂度分析定义:算法执行时间与输入规模的关系。
常见时间复杂度:O(1)、O(n)、O(n^2)、O(log n)。
4.2 空间复杂度分析定义:算法执行过程中所需内存与输入规模的关系。
常见空间复杂度:O(1)、O(n)。
第五章:算法设计与优化5.1 贪心算法特点:局部最优解构成全局最优解。
应用:最小树、最短路径等。
5.2 分治算法特点:将问题分解为子问题,递归解决。
应用:归并排序、快速傅里叶变换等。
5.3 动态规划算法特点:利用多阶段决策过程的最优解。
应用:背包问题、最长公共子序列等。
第六章:递归算法6.1 递归的基本概念定义:一个函数直接或间接地调用自身。
特点:自顶向下、分而治之。
6.2 递归算法的实现直接递归:函数直接调用自身。
间接递归:函数通过其他函数间接调用自身。
6.3 递归算法的应用计算阶乘、斐波那契数列等。
第七章:图算法7.1 图的基本概念顶点、边、无向图、有向图、权重等。
算法、程序框图与基本语句知识点及联系—精品文档
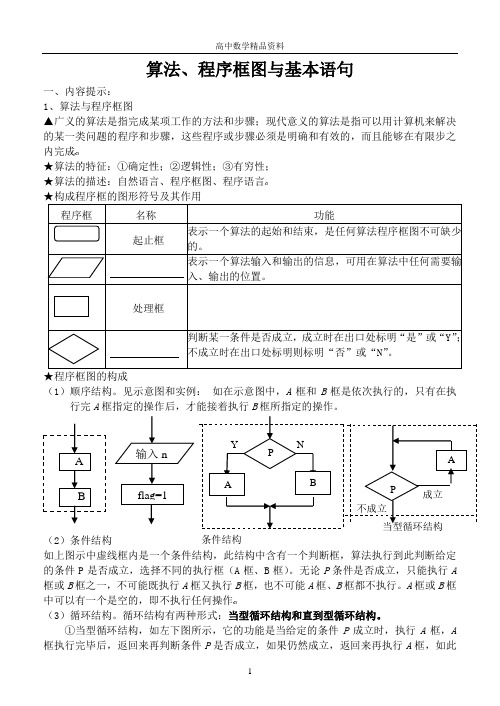
算法、程序框图与基本语句一、内容提示: 1、算法与程序框图▲广义的算法是指完成某项工作的方法和步骤;现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成★算法的特征:①确定性;②逻辑性;③有穷性; ★算法的描述:自然语言、程序框图、程序语言 ★构成程序框的图形符号及其作用程序框名称功能起止框表示一个算法的起始和结束,是任何算法程序框图不可缺少的。
表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置。
处理框判断某一条件是否成立,成立时在出口处标明“是”或“Y ”;不成立时在出口处标明则标明“否”或“N ”。
★程序框图的构成(1)顺序结构。
见示意图和实例: 如在示意图中,A 框和B 框是依次执行的,只有在执行完A 框指定的操作后,才能接着执行B 框所指定的操作。
(2)条件结构如上图示中虚线框内是一个条件结构,此结构中含有一个判断框,算法执行到此判断给定的条件P 是否成立,选择不同的执行框(A 框、B 框)。
无论P 条件是否成立,只能执行A 框或B 框之一,不可能既执行A 框又执行B 框,也不可能A 框、B 框都不执行。
A 框或B 框中可以有一个是空的,即不执行任何操作(3)循环结构。
循环结构有两种形式:当型循环结构和直到型循环结构。
①当型循环结构,如左下图所示,它的功能是当给定的条件P 成立时,执行A 框,A 框执行完毕后,返回来再判断条件P 是否成立,如果仍然成立,返回来再执行A 框,如此A B输入n flag=1 P A B YN A 成立 不成立 P 当型循环结构条件结构反复执行A 框,直到某一次返回来判断条件P 不成立时为止,此时不再执行A 框,离开循环结构。
继续执行下面的框图。
②直到型循环结构,如右下图所示,它的功能是先执行重复执行的A 框,然后判断给定的条件P 是否成立,如果P 仍然不成立,则返回来继续执行A 框,再判断条件P 是否成立。
基本算法语句(上课用)

【变式练习】
下列给出的赋值语句正确的是 ④ . ①3=B ②x+y=0 ③A=B=-2 ④T=T﹡T 【解析】根据赋值语句的格式可知,赋值号左侧为单 个变量,右侧为表达式(赋值语句有运算功能),故填 ④. 答案:④
1.了解算法的程序设计语言与算法的自然语言、程序框 图的差异. 2.正确理解输入语句、输出语句、赋值语句的结构. (重点) 3.能够准确应用输入、输出语句和赋值语句将程序框图 转化为算法语句.(难点)
微课1 例1.用描点法作函数y=x3+3x2-24x+30的图象时,需要 求出自变量和函数的一组对应值.编写程序,分别计算 当x= -5,-4,-3,-2,-1,0,1,2,3,4,5时的函数值.
INPUT “a,b,c=”;a,b,c
转化
在这个程序中,第3行中的PRINT语句称为输出 语句,其一般格式是:
PRINT “提示内容”;表达式
其中,“提示内容”一般是提示用户输出什么 样的信息,它通常是常量或变量的值;表达式一 般是表示输出信息所对应的字母或代数式.PRINT 语句可以在计算机的屏幕上输出运算结果和系统 信息.
多个变量,中间用 表达式之间用“,”隔 2.一个语句只能有
“,”隔开.
开.
一个“=”,并且
明
3.无计算功能,不能 输入表达式.
3.表达式可以是变量, 也可以是计算公式.
只能给一个变量赋 值.
4.输入多个数据时用 4.有计算功能,能直
“,”分隔
接输出计算公式的值
3.有计算功能,可 以把表达式的值赋 给一个变量
算法分析: 根据题意,对于每一个输入的自变量的值,都要
例谈基本算法语句
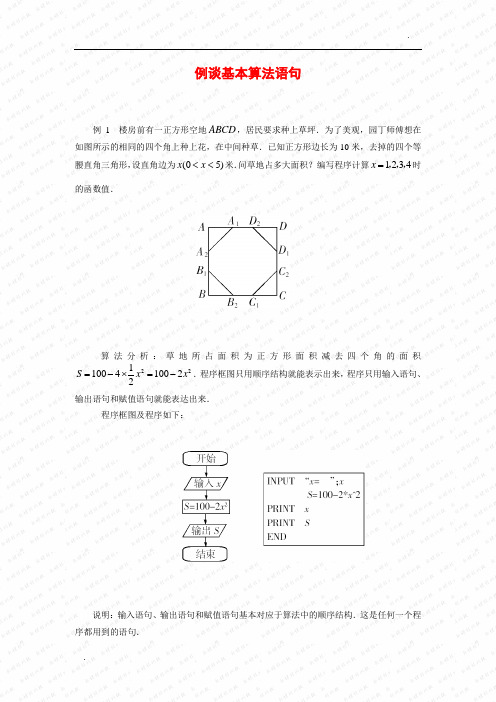
例谈基本算法语句例1楼房前有一正方形空地ABCD,居民要求种上草坪.为了美观,园丁师傅想在如图所示的相同的四个角上种上花,在中间种草.已知正方形边长为10米,去掉的四个等腰直角三角形,设直角边为(05)x x<<米.问草地占多大面积?编写程序计算1234x=,,,时的函数值.算法分析:草地所占面积为正方形面积减去四个角的面积221100410022S x x=-⨯=-.程序框图只用顺序结构就能表示出来,程序只用输入语句、输出语句和赋值语句就能表达出来.程序框图及程序如下:说明:输入语句、输出语句和赋值语句基本对应于算法中的顺序结构.这是任何一个程序都用到的语句.例2 邮局寄信不超过20克付邮资80分,超过20克不超过40克付邮资90分,超过40克不超过60克付邮资100分,现有一封信重x 克(060x <≤),问应付邮资多少分?算法分析:这是一个分段函数,80(020)()90(2040)100(4060)x f x x x ⎧<⎪=<⎨⎪<⎩≤ ≤ ≤,根据条件不同,结果不同,程序结构中需要用到条件结构,程序中用到条件语句.程序框图:说明:条件语句是表达算法中的条件结构,因为算法的流程根据条件是否成立有不同的流向,就需要对条件作出判断,所以程序中用到条件语句.例3 设计求2+4+6+…+2n 的值的算法,画出程序框图,编写程序.算法分析:只需一个累加变量和一个计数变量,将累加变量初始值设为0,计数变量是2~2n 之间的偶数.程序框图【当型(WHILE 型)】及程序如下:程序框图【直到型(UNTIL型)】及程序如下:说明:循环语句是用来实现循环结构的,对应程序框图中的两种循环结构,程序设计语言中也有当型和直到型两种语句,对于同一个题目可以分别用这两种语句表达.WHILE语句,先判断条件真假,如果条件符合就执行WHILE与WEND之间的循环体;然后检查上述条件反复进行,直到某一次条件不符合为止.因此,当型循环也称为“前测试型”循环,而直到型循环称为“后测试型”循环.。
基本算法语句与算法案例教案练习(含答案)

基本算法语句与算法案例教案练习(含答案)第一章:算法概述1.1 算法的定义介绍算法的概念和特点强调算法在解决问题中的重要性1.2 算法的特性讨论算法的输入、输出、有穷性和确定性举例说明算法的基本特性1.3 算法描述介绍算法描述的方法,如伪代码和流程图练习编写简单的算法描述第二章:基本算法语句2.1 输入输出语句学习输入输出语句的语法和使用方法练习编写输入输出语句2.2 赋值语句了解赋值语句的作用和格式练习使用赋值语句进行变量赋值2.3 条件语句掌握条件语句的语法和执行过程练习编写条件语句解决问题2.4 循环语句学习循环语句的种类和特点练习使用循环语句编写算法第三章:算法案例分析3.1 排序算法学习冒泡排序和选择排序的基本思想编写冒泡排序和选择排序的算法实现3.2 搜索算法了解二分查找和深度优先搜索的基本原理编写二分查找和深度优先搜索的算法实现3.3 递归算法理解递归算法的概念和应用编写递归算法的实例,如计算阶乘和Fibonacci 数列3.4 图算法学习图的基本概念和算法,如DFS 和BFS编写图算法的实例,如拓扑排序和最短路径第四章:算法设计与分析4.1 算法设计策略学习贪心算法、动态规划和分治算法的设计思想练习使用不同的算法设计策略解决问题4.2 算法分析方法了解时间复杂度和空间复杂度的概念分析常见算法的复杂度,并比较其优劣4.3 算法优化技巧学习常用的算法优化技巧,如缓存、预处理和分治练习使用算法优化技巧提高算法效率第五章:算法实践与测试5.1 算法编程基础学习编程语言的基本语法和数据结构练习使用编程语言实现算法5.2 算法测试与调试学习测试算法的方法和技巧练习使用调试工具和技巧解决算法问题5.3 算法竞赛与挑战了解算法竞赛和在线编程挑战的平台和规则参与算法竞赛和挑战,提高算法能力第六章:算法与数据结构6.1 数据结构基础介绍数据结构的概念和重要性学习线性表、栈、队列、链表等基本数据结构6.2 算法与数据结构的关联讨论算法和数据结构之间的关系学习如何选择合适的数据结构来优化算法6.3 常见数据结构算法掌握数组、链表、树、图等数据结构的操作算法练习使用不同数据结构解决实际问题第七章:算法伦理与算法文化7.1 算法伦理探讨算法伦理的重要性学习算法公平性、透明性和可解释性的概念7.2 算法在现实世界中的应用分析算法在各个领域中的应用和影响讨论算法如何影响社会和个人7.3 算法文化与历史了解算法的发展历程学习著名算法家和他们的贡献第八章:算法高级主题8.1 并行算法介绍并行算法的基本概念和原理学习并行算法的设计和分析方法8.2 分布式算法探讨分布式系统中的算法设计学习分布式算法的一致性和容错性8.3 量子算法简介量子计算和量子算法的基本原理了解量子算法与经典算法的关系和差异第九章:算法面试与职业发展9.1 算法面试准备学习算法面试的常见题型和准备策略练习解决算法面试中的典型问题9.2 算法面试技巧掌握算法面试的沟通和表达技巧学习如何在面试中展示自己的算法能力9.3 算法工程师的职业发展探讨算法工程师的职业路径和发展前景学习如何提升自己的算法技能和职业竞争力第十章:算法案例集锦10.1 经典算法案例收集和分析经典算法案例学习这些案例背后的算法思想和技巧10.2 创新算法案例探索新兴领域的算法应用学习创新算法如何解决现实问题10.3 算法案例解析分析算法案例的优缺点和适用场景学习如何从案例中汲取经验,提高自己的算法能力重点和难点解析重点一:算法的定义和特性算法的定义是计算机科学中的核心概念,理解算法的特性对于掌握算法至关重要。
基本算法语句与算法案例教案练习(含答案)

基本算法语句与算法案例教案练习(含答案)一、教学目标:1. 让学生掌握基本的算法语句,如输入、输出、赋值、条件判断、循环等。
2. 通过实例让学生了解算法在实际问题中的应用,提高解决问题的能力。
3. 培养学生动手实践和团队协作的能力。
二、教学内容:1. 算法语句概述:介绍基本算法语句的分类和作用。
2. 输入与输出:学习如何使用输入和输出语句进行数据的读取和显示。
3. 赋值语句:掌握赋值语句的用法,了解变量的概念。
4. 条件判断:学习条件语句的编写,了解逻辑运算符的使用。
5. 循环语句:掌握循环语句的原理和用法,包括for循环和while 循环。
三、教学方法:1. 讲授法:讲解算法语句的概念和用法。
2. 案例教学法:通过实例分析,让学生了解算法在实际问题中的应用。
3. 实践操作法:让学生动手编写代码,巩固所学知识。
4. 小组讨论法:鼓励学生分组讨论,培养团队协作能力。
四、教学准备:1. 教学课件:制作课件,展示算法语句的概念和用法。
2. 编程环境:为学生提供合适的编程环境,如在线编程平台或编程软件。
3. 实例素材:准备一些实际问题,用于讲解算法在实际中的应用。
五、教学过程:1. 导入新课:介绍本节课的学习目标和内容,激发学生的学习兴趣。
2. 讲解算法语句:讲解基本算法语句的概念和用法,如输入、输出、赋值、条件判断、循环等。
3. 案例分析:通过实例分析,让学生了解算法在实际问题中的应用。
4. 动手实践:让学生分组编写代码,实践所学知识。
5. 课堂总结:对本节课所学内容进行总结,回答学生的问题。
6. 课后作业:布置课后练习,巩固所学知识。
7. 课后辅导:为学生提供课后辅导,解答学生在练习过程中遇到的问题。
六、教学评估:1. 课堂互动:观察学生在课堂上的参与程度,了解他们对算法语句的理解程度。
2. 课后作业:检查学生的课后作业,评估他们对算法语句的掌握情况。
3. 小组讨论:评估学生在小组讨论中的表现,了解他们的团队协作和问题解决能力。
13.2 基本算法语句与算法案例

对甲、乙两程序和输出结果判断正确的是( B ) A.程序不同,结果不同 B.程序不同,结果相同 C.程序相同,结果不同 解析 D.程序相同,结果相同 从两个程序可知它们的程序语句不同,但其
算法都是求1+2+3+„+1 000,故结果相同.
题型分类 深度剖析
题型一 输入、输出、赋值语句的应用
【例1】 已知一个正三棱柱的底面边长为2,高 为3,用输入、输出语句和赋值语句表示出计算
(2)更相减损术的定义
任给两个正整数(若是偶数,先用2约数),以 较大的数减较小的数 ,接着把所得的差与较小的 数比较,并以大数减小数,直到所得的数 相等为止 , 则这个数(等数)(或这个数与约简的数的乘积)
就是所求的最大公约数.
(3)秦九韶算法 秦九韶算法是我国南宋数学家秦九韶在他的代表 作 《数书九章》中提出的一种用于计算 一元n次多 项式的值 的方法.
基础自测
1.下列关于赋值语句的说法中不正确的是( C ) A.赋值语句就是将表达式所代表的值赋给变量 B.赋值号左右不能互换 C.赋值号与数学中的等号有着完全相同的意义
D.执行赋值语句时,先计算“=”右边表达式
的值 解析 赋值语句中的“=”叫做赋值号,
它和数学中的等号不完全一样.
2.下列赋值语句正确的是( D ) A.a+b=5 B.5= a C.a=b=2 解析 D.a=a+1 赋值语句的一般格式是变量=表达式,赋
程序框图:
程序
题型二
条件语句的应用
【例2】 如图所示,在边长为4的正方形 ABCD的边上有一点P,沿着折线BCDA
由点B(起点)向点A(终点)运动.设 点P运动的路程为x,△APB的面积为y,
数学基础知识总复习第9章 第2节 基本算法语句

第二节基本算法语句理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.知识梳理一、各种程序设计语言中都包含下列基本的算法语句错误!二、基本算法语句1.输入语句.在程序中INPUT语句就是输入语句.这个语句的一般格式是:错误!其中,“提示内容”一般是提示用户输入什么样的信息.如每次运行程序时,依次输入-5,-4,-3,-2,-1,0,1,2,3,4,5,计算机每次都把新输入的值赋给变量“x",并按“x”新获得的值执行下面的语句.INPUT语句不但可以给单个变量赋值,还可以给多个变量赋值,INPUT “提示内容1,提示内容2,提示内容3,…”;变量1,变量2,变量3,…例如,输入一个学生数学,语文,英语三门课的成绩,可以写成:INPUT “数学,语文,英语”;a,b,c注:①“提示内容"与变量之间必须用分号“;”隔开.②各“提示内容”之间以及各变量之间必须用逗号“,”隔开.但最后的变量的后面不需要.2.输出语句.在程序中PRINT语句是输出语句.它的一般格式是:错误!同输入语句一样,表达式前也可以有“提示内容”.例如下面的语句可以输出斐波那契数列:The Fibonacci Progression is:1 1 2 3 5 8 13 21 34 55 …输出语句的用途:(1)输出常量,变量的值和系统信息.(2)输出数值计算的结果.3.赋值语句.用来表明赋给某一个变量一个具体的确定值的语句.除了输入语句,在程序中赋值语句也可以给变量提供初值.它的一般格式是:错误!赋值语句中的“="叫做赋值号.赋值语句的作用:先计算出赋值号右边表达式的值,然后把这个值赋给赋值号左边的变量,使该变量的值等于表达式的值.注意:①赋值号左边只能是变量名字,而不能是表达式.如2=X是错误的.②赋值号左右不能对换.如“A=B”和“B=A”的含义运行结果是不同的.③不能利用赋值语句进行代数式的演算(如化简、因式分解、解方程等).④赋值号“=”与数学中的等号意义不同.4.条件语句.算法中的条件结构是由条件语句来表达的,是处理条件分支逻辑结构的算法语句.它的一般格式是:IFTHENELSEEND IF格式,如左下图.IF条件THEN语句1ELSE语句2END IF首先对IF后的条件进行判断,如果条件符合,就执行THEN后的语句1,否则执行ELSE后的语句2(其对应的程序框图如右上图).在某些情况下,也可以只使用IFTHEN语句:IFTHENEND IF 格式,如左下图.IF条件THEN语句END IF,也是首先对IF后的条件进行判断,如果条件符合,就执行THEN后的语句,如果条件不符合,则直接结束该条件语句,转而执行其他语句(其对应的程序框图如右上图).条件语句的作用:在程序执行过程中,根据判断是否满足约定的条件而决定是否需要转换到何处去.需要计算机按条件进行分析、比较、判断,并按判断后的不同情况进行不同的处理.在某些较为复杂的算法中,有时需要对按条件要求执行的某一语句(特别是ELSE后的语句2)继续按照另一条件进行判断,这时可以再利用条件语句完成这一要求,其一般形式为:5.循环语句.算法中的循环结构是由循环语句来实现的.对应于程序框图中的两种循环结构,一般程序设计语言中也有当型(WHILE型)和直到型(UNTIL型)两种语句结构,即WHILE语句和UNTIL语句.(1)WHILE语句的一般格式是:WHILE条件循环体WENDWHILE后面的“条件”是用于控制计算机执行循环体或跳出循环体的.当计算机遇到WHILE语句时,先判断条件的真假,如果条件符合,就执行WHILE与WEND之间的循环体;然后再检查上述条件,如果条件仍符合,再次执行循环体,这个过程反复进行,直到某一次条件不符合为止.这时,计算机将不执行循环体,直接跳到WEND语句后,接着执行WEND之后的语句.因此,当型循环有时也称为“前测试型”循环.其对应的程序结构框图如右上页图.(2)UNTIL语句的一般格式是:DO循环体LOOP UNTIL条件基础自测1.下列赋值能使y的值为4的是()A.y-2=6 B.2*3-2=yC.4=y D.y=2*3-2解析:赋值时把“="右边的值赋给左边的变量.故选D。
常见的算法题

常见的算法题一、算法的基础知识算法是计算机科学的核心,它是一系列具体解决问题的步骤或指令。
一个算法应该具有明确性、可行性和效率。
常见的算法类型包括排序算法、搜索算法、图算法等。
二、常见的算法题目及解法1. 冒泡排序题目:对一个包含n个整数的数组进行排序。
解法:使用冒泡排序算法,比较相邻的两个数,如果顺序不对则交换它们。
重复执行此过程,直到所有数都排好序。
时间复杂度为O(n^2)。
2. 快速排序题目:对一个包含n个整数的数组进行排序。
解法:使用快速排序算法,选择一个基准元素,将数组分为两部分,小于基准的放在左边,大于等于基准的放在右边。
然后对左右两边的数组重复执行此过程。
时间复杂度为O(nlogn)。
3. 二分查找题目:在一个已排序的数组中查找一个元素。
解法:使用二分查找算法,将数组分为两部分,根据中间元素与目标元素的比较结果,不断缩小搜索范围,直到找到目标元素或确定元素不存在于数组中。
时间复杂度为O(logn)。
4. 深度优先搜索(DFS)题目:从一个节点开始,遍历一个图,找到所有的出边。
解法:使用深度优先搜索算法,从起点开始搜索,访问相邻的节点,直到遍历完所有的节点。
这种方法适用于有向图或无向图。
5. 广度优先搜索(BFS)题目:从一个节点开始,遍历一个图,找到从起点出发的所有路径。
解法:使用广度优先搜索算法,将起点加入队列中,依次取出队列中的节点,访问其相邻的节点,并将未访问过的相邻节点加入队列中。
这种方法适用于有向图或无向图。
6. 最短路径问题题目:在一个加权图中找到从起点到终点的最短路径。
解法:可以使用Dijkstra算法或Bellman-Ford算法来解决最短路径问题。
这两种算法都是通过迭代的方式逐步更新距离信息,最终找到最短路径。
Dijkstra算法适用于稀疏图,Bellman-Ford算法则适用于稠密图。
三、实战演练:编程实现常见算法1. Python实现冒泡排序以下是一个用Python实现冒泡排序的示例代码:```pythondef bubble_sort(arr):n = len(arr)for i in range(n):for j in range(0, n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j] # 交换位置return arr```这段代码可以对一个整数数组进行冒泡排序,并返回排序后的结果。
12基本算法语句lian

y=0 END IF IF X>0 THEN
y=x+1 END IF PRINT y END
巩固练习
右边给出的是用条件语 句编写的一个程序,根 据该程序回答:
2x(x 3)
y 0(x 3)
x2
1(
x
3)
(1)若输入5,则输出结果y {是
注意:⑶不能利用赋值语句进行代数的演算(如化简、 因式分解、解方程等)
例如:①x2+10x+16=0
(x+8)(x+2)=0 X=-8,x=-2
这是不能实现的
②y=x2-1=(x-1)(x+1)
问题3:我们知道a=a+1在数学中是不成立的, 但在赋值语句中成立吗?为什么?
答: 在赋值语句中是成立的,意思是将a的原值 加1在赋给a,即a的值增加1。如果多次给一个变量 赋值,则该变量的值取最后赋予的那个值。
b=c
c=a
d= 16
123
PRINT a,b,c 20 30 20
例如:编写一个程序,从键盘上输入一个整 数,若是正数就将其输出。
程序: INPUT “x=” ;x IF x>0 THEN PRINT x END IF END
例子、把下列语句的意义翻译成程序框图
(1)IF x>0 THEN (2)IF x<0 THEN
y=(-2)*x+1 ELSE
y=x+1 END IF PRINT y
END
变式:已知, 2x 1(x 0)
开始
编写程序, y= 0(x 0) 输输入出自相变 应量 的的 函值 数, 值。x 1(x 0) 是
基本算法语句与算法案例教案练习(含答案)

基本算法语句与算法案例教案练习(含答案)第一章:算法概述1.1 算法的定义与特性介绍算法的定义:解决特定问题的步骤序列讨论算法的特性:确定性、有穷性、可行性、输入和输出1.2 算法的表示方法介绍伪代码和流程图两种算法表示方法展示如何用伪代码和流程图表示简单的算法1.3 算法分析介绍时间复杂度和空间复杂度分析几种基本算法的时间和空间复杂度第二章:基本算法语句2.1 输入输出语句介绍输入输出语句的格式和用法练习编写使用输入输出语句的程序2.2 赋值语句解释赋值语句的作用和格式通过实例展示如何使用赋值语句2.3 条件语句讲解条件语句的语法和执行过程练习编写条件语句来控制程序流程2.4 循环语句介绍循环语句的种类(for、while)及其使用场合练习使用循环语句编写程序第三章:算法案例实践3.1 排序算法介绍冒泡排序、选择排序和插入排序的基本思想编写程序实现这三个排序算法3.2 搜索算法讲解线性搜索和二分搜索的原理练习编写线性搜索和二分搜索的程序3.3 递归算法解释递归的定义和特点实践编写递归计算斐波那契数列的程序3.4 模块化编程强调模块化编程的重要性通过实例展示如何将程序划分为模块并调用第四章:算法优化与调试4.1 算法优化原则讨论算法优化的目标和原则解释如何通过优化提高算法效率4.2 常见算法优化技巧介绍常用的算法优化技巧,如减少重复计算、贪心策略等4.3 算法调试介绍调试工具和调试方法指导如何找到并修复算法中的错误4.4 性能分析与改进展示如何对算法进行性能分析讲解如何根据分析结果改进算法第五章:算法应用与实践5.1 数学问题求解举例解决基本的数学问题,如求最大公约数、高斯求和等5.2 数据处理与分析使用算法处理和分析实际数据,如数据排序、查找重复值等5.3 图形处理算法实现一些基础的图形处理算法,如绘制线段、三角形等5.4 综合案例项目指导如何综合使用所学算法解决一个较大的问题鼓励学生自主选择项目进行实践第六章:算法设计与分析方法6.1 设计算法的方法介绍贪心法、动态规划、分治法等设计算法的方法分析各种方法的适用场景和特点6.2 算法分析的基本概念介绍时间复杂度和空间复杂度的概念学习如何评价和比较算法的好坏6.3 常用算法设计与分析技巧学习和实践常用的算法设计与分析技巧,如分治策略、递归技术、回溯法等第七章:图算法7.1 图的基本概念学习图的定义、顶点、边、图的类型等基本概念理解图的表示方法,如邻接矩阵和邻接表7.2 深度优先搜索(DFS)学习深度优先搜索算法的基本思想和实现方法完成深度优先搜索算法的编程实现7.3 广度优先搜索(BFS)学习广度优先搜索算法的基本思想和实现方法完成广度优先搜索算法的编程实现7.4 最小树和最短路径学习普里姆算法和克鲁斯卡尔算法求最小树学习迪杰斯特拉算法求单源最短路径第八章:高级算法主题8.1 动态规划基础介绍动态规划的基本思想和适用问题类型实践动态规划解决背包问题、最长公共子序列等经典问题8.2 回溯法与组合问题学习回溯法的原理和应用使用回溯法解决组合问题,如排列组合、棋盘问题等8.3 分治法进阶深入理解分治法,学习合并排序、快速排序等经典算法探讨分治法在多维数据结构上的应用8.4 启发式搜索与算法学习启发式搜索的基本概念实践启发式搜索算法解决旅行商问题(TSP)等优化问题第九章:算法与数据结构9.1 树结构及其算法学习二叉树、堆、平衡树(AVL)、红黑树等数据结构掌握在这些树结构上的基本算法,如插入、删除、查找等9.2 图形算法学习图形算法,如最短路径(Floyd-Warshall算法)、最小树(克鲁斯卡尔算法)实现这些算法的编程9.3 集合与字典数据结构学习集合和字典数据结构的基本操作使用集合和字典解决实际问题,如并查集、哈希表等9.4 算法与数据结构的优化学习如何根据数据结构的特点来优化算法实践不同的算法策略来提高程序的性能第十章:算法案例精讲与实战10.1 算法竞赛与问题建模介绍算法竞赛的基本规则和技巧学习如何从实际问题中提取关键信息,构建数学模型10.2 算法案例精讲深入讲解经典算法案例,如汉诺塔、八皇后问题等分析案例的解决思路和关键点10.3 实战模拟与题目解析模拟算法竞赛的环境,进行实战训练分析和解析真实竞赛题目,提供解题策略和思路10.4 项目实战与团队协作鼓励学生参与实际项目,将算法应用于解决实际问题强调团队协作在解决问题中的重要性,培养团队沟通与协作能力重点和难点解析1. 算法概述和算法的表示方法:理解算法的定义、特性和表示方法是学习算法的基础。
1.2.基本算法语句

【例题解析】 〖例2〗:编写程序,计算一个学生数学、语文、 英语三门课的平均成绩。
分析:先写出算法,画出程序框图,再进行编程。
程序框图
开始
输入a,b,c
y
a
b 3
c
输出y
程序:
INPUT “Maths,Chinese,English”;a,b,c y=(a+b+c)/3 PRINT “y=”;y END
满足条件? 否 是
语句1
语句2
IF 条件 THEN 语句体1
ELSE 语句体2
END IF
当计算机执行上述语句时,首先对IF后的 条件进行判断,如果条件符合,就执行THEN后 的语句体1,否则执行ELSE后的语句体2.
【例题解析】 1、编写一个程序,求任意实数的绝对值。
程序框图:开始
程序如下:
输入 x
i=1
i=1
S=10
SS==10
WHLIE i<=1n00
i=i+1
S=S+*i i
i≤i≤1n00?? 否
S=S+*i i 是
i=i+1 WEND PRINT S
输出S
当型循环 结构
END
变式训练(2): 编写程序求:1×3×5×7×……×101的值.
直到型 开始 如何修改? UNITL语句
i=1
INPUT “提示内容”;变量
输入x
INPUT “x=”; x
2. 常用格式:
输入a,b,c INPUT a,b,c
INPUT “提示内容”;变量 INPUT 变量 INPUT “提示内容”;变量1,变量2,变量3,·· INPUT 变量1,变量2,变量3,···
必修3算法初步知识点总结及本章测试题
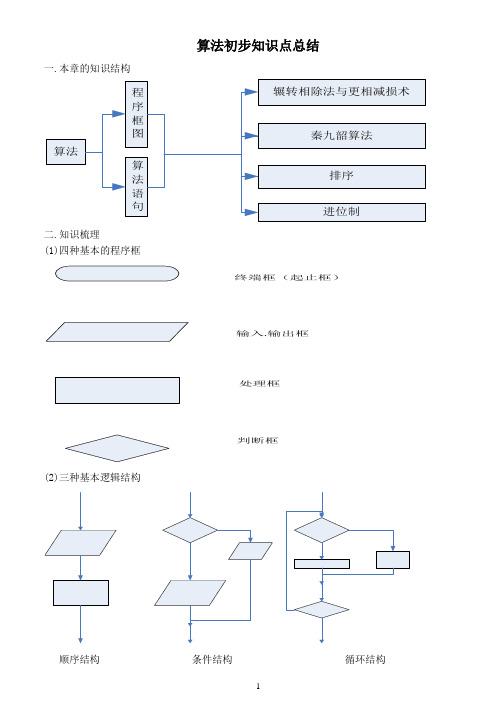
算法初步知识点总结一.本章的知识结构二.知识梳理(1)四种基本的程序框终端框(起止框)输入.输出框处理框判断框(2)三种基本逻辑结构顺序结构 条件结构 循环结构(3)基本算法语句 (一)输入语句(三)赋值语句(四)条件语句 IF -THEN -ELSE 格式当计算机执行上述语句时, 首先对IF 后的条件进行判断, 如果条件符合, 就执行THEN 后的语句1, 否则执行ELSE 后的语句2。
其对应的程序框图为: (如上右图)IF -THEN 格式计算机执行这种形式的条件语句时, 也是首先对IF 后的条件进行判断, 如果条件符合, 就执行THEN 后的语句, 如果条件不符合, 则直接结束该条件语句, 转而执行其他语句。
其对应的程序框图为: (如上右图) (五)循环语句(1)WHILE 语句IF 条件 THEN 语句 END IF其中循环体是由计算机反复执行的一组语句构成的。
WHLIE 后面的“条件”是用于控制计算机执行循环体或跳出循环体的。
当计算机遇到WHILE 语句时, 先判断条件的真假, 如果条件符合, 就执行WHILE 与WEND 之间的循环体;然后再检查上述条件, 如果条件仍符合, 再次执行循环体, 这个过程反复进行, 直到某一次条件不符合为止。
这时, 计算机将不执行循环体, 直接跳到WEND 语句后, 接着执行WEND 之后的语句。
因此, 当型循环有时也称为“前测试型”循环。
其对应的程序结构框图为: (如上右图)(2)UNTIL 语句其对应的程序结构框图为: (如上右图) (4)算法案例案例1 辗转相除法与更相减损术 案例2 秦九韶算法案例3 排序法: 直接插入排序法与冒泡排序法 案例4 进位制WHILE 条件循环体 WENDDO 循环体 LOOP UNTIL 条件算法初步综合检测一一、选择题1. 下列运算不属于我们所讨论算法范畴的是( )A. 已知圆的半径求圆的面积 B. 随意抽4张扑克牌算到二十四点的可能性 C. 已知坐标平面内两点求直线方程 D. 加减乘除法运算法则2. 早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个步骤、从下列选项中选最好的一种算法( )A. S1 洗脸刷牙、S2刷水壶、S3 烧水、S4 泡面、S5 吃饭、S6 听广播B. 刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5 听广播C. 刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭 同时 听广播D. 吃饭 同时 听广播、S2泡面、S3烧水同时洗脸刷牙、S4刷水壶3.以下关于排序的说法中, 正确的是( ) A. 排序就是将数按从小到大的顺序排序B. 排序只有两种方法, 即直接插入排序和冒泡排序C. 用冒泡排序把一列数从小到大排序时, 最小的数逐趟向上漂浮 D .用冒泡排序把一列数从小到大排序时, 最大的数逐趟向上漂浮4. 下列语句中:① ② ③ ④ ⑤2(1)22A B B =*+=*+ ⑥((73)5)1p x x x =+-+ 其中是赋值语句的个数为( )A. 6B. 5C. 4D. 35. 把“二进制”数 化为“五进制”数是( ) A. B. C. D.6. 840和1764的最大公约数是( ) A. 84 B. 12 C. 168 D. 2527. 下面为一个求20个数的平均数的程序,在横线上应填充的语句为 ( ) A. i>20 B. i<20 C. i>=20 D. i<=208.为了在运行下面的程序之后得到输出y =16, 键盘输入x 应该是( ) A. 或 B. C. 或 D. 或 二、填空题:9.已知有下面程序, 如果程序执行后输出的结果是11880, 那么在程序 UNTIL 后面的“条件”应为10. 给出下面的程序框图, 循环体执行的次数是11. 比较大小:12.用等值算法求294和84大公约数时, 需要做 次减法.13. 下列四个有关算法的说法中, 正确的........ ..要求只填写序.)⑴算法的某些步骤可以不明确或有歧义, 以便使算法能解决更多问题;⑵正确的算法执行后一定得到确定的结果;⑶解决某类问题的算法不一定是唯一的;⑷正确的算法一定能在有限步之内结束.15.读程序, 完成下面各题(1)输出结果... ..(2)输出结果... .三、解答题:16. 将十进制数30化为二进制.17.设计算法流程图, 要求输入自变量的值, 输出函数的值,并用复合IF语句描述算法.18. 设计程序框图求的值.19. 用循环语句描述1+ + + +…+ .20. 用秦九韶算法求多项式,x=-时的值.当0.2算法初步章末检测题二一、选择题1. 下列赋值语句正确的是A. B. C. D.2. 计算机执行下面左边的程序段后, 输出的结果是 A. , B. , C. , D. , 1a = 3b = a a b =+b a b =-PRINT , END第2题 第3题 3. 当 时, 上面右边的程序段输出的结果是 A. B. C. D.4.下边给出的各数, 不可能是七进制数的是 A . B . C . D . 5. 用“辗转相除法”求得和的最大公约数是A. B. C. D.6. 用秦九昭算法求 在 时的值, 的值为 A. B. C. D.7. 用冒泡法对 , , , , 从小到大排序, 需要排序的趟数为 A. B. C. D.IF 10a < THEN2y a =*ELSEy a a =*PRINT y8. 如下左边的程序框图, 若输出 的值为 , 则判断框内可填写的条件是 A. B. C. D. 9.如上右图,该程序框图的功能是A . 求 、 、 的最大数B . 求 、 、 的最小数C. 将 、 、 按从小到大排列D. 将 、 、 按从大到小排列10. 下面右边的程序的功能是: 判断任意输入的数 是否为正数, 若是, 输出它的平方值;否则输出它的相反数, 则应填入的条件是 A. B. C. D.INPUT xIF ______ THENy x =-ELSEy x x =*END IF PRINT y11.如上右图是计算 … 的值的一个程序框图, 其中判断框内应填入的条件是 A . B . C . D . 12.如上右边的程序,最后输出的结果为A. B. C. D. 二、填空题13. 将二进制 转化为十进制数结果是 . 14. 下面一段程序执行后的结果是 .A 2= A A 2=* A A 6=+PRINT A1WHILE 1001WEND 1j j j j j j j =*<=+=-INPUT “a =”;a INPUT “b =”;b IF a b > THEN第14题第15题15. 上面右边的程序输出的结果是.16.将下面的程序补充完整:输入两个数, 输出其中较大的数, 则①处应填.三、解答题17. 分别用辗转相除法和更相减损术求与的最大公约数.18. 用秦九昭算法计算函数当时的函数值.19. 设函数, 设计一个算法输入的值求函数值, 写出算法步骤并画出程序框图.20.设计一个算法求…, 作出程序框图并写出程序.21. 下列语句是求…的一个程序.(Ⅰ)程序中是否有错误?请改正;(Ⅱ)把程序改写成另一种循环语句.。
高考数学 15.2 基本算法语句与算法案例

15、算法初步15.2 基本算法语句与算法案例【知识网络】1.理解用伪代码表示的几种基本算法语句:赋值语句、输入语句、输出语句、条件语句、循环语句。
2.能用自然语言、流程图和伪代码表述算法,会用“While循环”和“For循环”语句或GoTo语句实施循环(注意:优先使用While和For语句,尽量少用GoTo语句)。
【典型例题】[例1](1)下列问题所描述出来的算法,其中不包含条件语句的为()A.读入三个表示三条边长的数,计算三角形的面积B.给出两点的坐标,计算直线的斜率C.给出一个数x,计算它的常用对数的值D.给出三棱锥的底面积与高,求其体积(2)设计一个计算1×3×5×7×9×11×13的算法.图中给出了程序的一部分,则在横线①上不能填入下面的那一个数?答:()A.13B.13.5C.14D.14.5(3)若mod(m,3)=1,则m的取值不可以是()A.2005 B.2006 C.2008 D.2020(4)下面的表述:①6←p;②t←3×5+2;③b+3←5;④p←((3x+2)-4)x+3;⑤a←a3;⑥x,y,z←5;⑦ab←3;⑧x ←y+2+x .其中正确表述的赋值语句有 . (注:要求把正确的表述全填上)(5)下面程序的运行结果为4[例2] 某百货公司为了促销,采用打折的优惠办法:每位顾客一次购物①在100元以上者(含100元,下同),按九五折优惠; ②在200元以上者,按九折优惠; ③在300元以上者,按八五折优惠; ④在500元以上者,按八折优惠. 试写出算法、画出流程图、伪代码,以求优惠价.[例3] 定义运算“!”为:n!=1×2×3×…×n ,其中n 为正整数,并且读作“n 的阶乘”,例如,5!=1×2×3×4×5=120,10!=9!×10= 3628800. 计算2007!写出算法分析与伪代码,并画出流程图。
基本算法语句与算法案例教案练习含答案

基本算法语句与算法案例教案练习含答案教案章节一:算法概述1. 教学目标:了解算法的定义和特点掌握算法的表示方法理解算法的作用和意义2. 教学内容:算法的定义和特点算法的表示方法算法的作用和意义3. 教学步骤:引入算法的概念,引导学生思考算法的作用和意义讲解算法的定义和特点,通过实例进行说明介绍算法的表示方法,如伪代码和流程图进行算法案例分析,让学生理解算法的作用和意义4. 练习题目:什么是算法?请举例说明。
算法的特点有哪些?请列举出来。
教案章节二:顺序结构1. 教学目标:掌握顺序结构的特点和应用学会使用顺序结构编写算法2. 教学内容:顺序结构的特点和应用顺序结构的表示方法顺序结构在算法中的应用3. 教学步骤:引入顺序结构的概念,引导学生理解顺序结构的特点和应用讲解顺序结构的表示方法,如顺序结构流程图通过实例讲解顺序结构在算法中的应用进行顺序结构练习,让学生掌握顺序结构的使用4. 练习题目:请描述顺序结构的特点和应用。
教案章节三:选择结构1. 教学目标:掌握选择结构的特点和应用学会使用选择结构编写算法2. 教学内容:选择结构的特点和应用选择结构的表示方法选择结构在算法中的应用3. 教学步骤:引入选择结构的概念,引导学生理解选择结构的特点和应用讲解选择结构的表示方法,如选择结构流程图通过实例讲解选择结构在算法中的应用进行选择结构练习,让学生掌握选择结构的使用4. 练习题目:请描述选择结构的特点和应用。
教案章节四:循环结构1. 教学目标:掌握循环结构的特点和应用学会使用循环结构编写算法2. 教学内容:循环结构的特点和应用循环结构的表示方法循环结构在算法中的应用3. 教学步骤:引入循环结构的概念,引导学生理解循环结构的特点和应用讲解循环结构的表示方法,如循环结构流程图通过实例讲解循环结构在算法中的应用进行循环结构练习,让学生掌握循环结构的使用4. 练习题目:请描述循环结构的特点和应用。
教案章节五:算法案例分析1. 教学目标:学会分析算法案例掌握算法案例的解题思路2. 教学内容:算法案例的分析方法算法案例的解题思路算法案例的实现3. 教学步骤:引入算法案例的概念,引导学生理解算法案例的分析方法和解题思路通过实例讲解算法案例的分析方法和解题思路进行算法案例练习,让学生掌握算法案例的解题思路和实现4. 练习题目:教案章节六:算法效率分析1. 教学目标:理解算法效率的概念学会分析算法的效率掌握算法优化的一般方法2. 教学内容:算法效率的定义和衡量指标算法时间复杂度和空间复杂度算法优化方法和策略3. 教学步骤:引入算法效率的概念,解释算法效率的重要性讲解算法效率的衡量指标,如时间复杂度和空间复杂度通过实例分析不同算法的效率,展示算法优化的效果引导学生思考如何对算法进行优化,介绍常见的优化方法和策略4. 练习题目:请解释算法效率的概念及其重要性。
基本算法语句与算法案例教案练习(含答案)

基本算法语句与算法案例教案练习(含答案)第一章:算法与程序设计概述1.1 算法的概念介绍算法的定义和特点解释算法在计算机科学中的重要性1.2 程序设计的基本概念解释程序和代码的区别介绍编程语言的分类和选择1.3 算法分析与评估介绍算法分析的目的和方法讲解算法效率的评估指标第二章:基本算法语句2.1 顺序结构介绍顺序结构的概念和作用示例顺序结构的算法案例2.2 选择结构介绍选择结构的概念和作用示例选择结构的算法案例2.3 循环结构介绍循环结构的概念和作用示例循环结构的算法案例第三章:算法案例实践3.1 求解线性方程介绍线性方程的求解方法示例求解线性方程的算法案例3.2 数列求和介绍数列求和的方法示例数列求和的算法案例3.3 字符串处理介绍字符串处理的基本方法示例字符串处理的算法案例第四章:算法优化与改进4.1 算法优化的目的与方法解释算法优化的意义和目的介绍算法优化的常见方法4.2 算法改进的策略讲解算法改进的策略和技巧示例算法改进的算法案例4.3 算法复杂度分析介绍算法复杂度的概念和计算方法示例算法复杂度分析的算法案例第五章:算法案例拓展5.1 排序算法介绍排序算法的概念和分类示例排序算法的算法案例5.2 图论算法介绍图论算法的基本概念示例图论算法的算法案例5.3 动态规划算法介绍动态规划算法的基本概念示例动态规划算法的算法案例第六章:算法与数据结构6.1 数据结构的基本概念介绍数据结构的概念和分类解释数据结构在算法设计中的重要性6.2 常见的数据结构介绍数组、链表、栈和队列等基本数据结构解释这些数据结构的特点和应用场景6.3 算法与数据结构的结合讲解如何选择合适的数据结构来优化算法示例结合数据结构的算法案例第七章:算法设计与分析方法7.1 贪心算法介绍贪心算法的概念和特点示例贪心算法的算法案例7.2 分治算法介绍分治算法的概念和特点示例分治算法的算法案例7.3 回溯算法介绍回溯算法的概念和特点示例回溯算法的算法案例第八章:高级算法主题8.1 并查集算法介绍并查集算法的基本概念和应用示例并查集算法的算法案例8.2 树状数组算法介绍树状数组算法的基本概念和应用示例树状数组算法的算法案例8.3 线段树算法介绍线段树算法的基本概念和应用示例线段树算法的算法案例第九章:算法与编程挑战9.1 算法竞赛的基本规则和技巧介绍算法竞赛的类型和规则讲解如何在算法竞赛中取得好成绩的技巧9.2 在线编程平台的应用介绍在线编程平台的使用方法和技巧示例在线编程的算法案例9.3 算法与编程挑战题解分析常见的算法挑战题目和解题思路示例算法挑战题目的算法案例第十章:算法与实际应用10.1 算法在中的应用介绍领域中常见的算法应用解释算法在中的关键作用10.2 算法在数据分析中的应用介绍数据分析领域中常见的算法应用解释算法在数据分析中的重要性和效果10.3 算法在其他领域的应用案例介绍算法在网络优化、密码学等领域的应用案例强调算法在解决实际问题中的重要性重点和难点解析重点环节一:算法的概念与特点重点关注算法的定义、特点及其在计算机科学中的重要性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本算法语句一、输入、输出语句和赋值语句 (1)输入语句 ①输入语句的一般格式②输入语句的作用是实现算法的输入信息功能;③“提示内容”提示用户输入什么样的信息,变量是指程序在运行时其值是可以变化的量;④输入语句要求输入的值只能是具体的常数,不能是函数、变量或表达式; ⑤提示内容与变量之间用分号“;”隔开,若输入多个变量,变量与变量之间用逗号“,”隔开。
(2)输出语句 ①输出语句的一般格式②输出语句的作用是实现算法的输出结果功能;③ “提示内容”提示用户输入什么样的信息,表达式是指程序要输出的数据;④输出语句可以输出常量、变量或表达式的值以及字符。
(3)赋值语句 ①赋值语句的一般格式②赋值语句的作用是将表达式所代表的值赋给变量;③赋值语句中的“=”称作赋值号,与数学中的等号的意义是不同的。
赋值号的左右两边不能对换,它将赋值号右边的表达式的值赋给赋值号左边的变量; ④赋值语句左边只能是变量名字,而不是表达式,右边表达式可以是一个数据、常量或算式;⑤对于一个变量可以多次赋值。
注意:①赋值号左边只能是变量名字,而不能是表达式。
如:2=X 是错误的。
②赋值号左右不能对换。
如“A=B ”“B=A ”的含义运行结果是不同的。
③不能利用赋值语句进行代数式的演算。
(如化简、因式分解、解方程等) ④赋值号“=”与数学中的等号意义不同。
5:条件语句(1)条件语句的一般格式有两种:①IF—THEN—ELSE语句;②IF—THEN语句。
①IF—THEN—ELSE语句IF—THEN—ELSE语句的一般格式为图1,对应的程序框图为图2。
图1②IF—THEN语句IF—THEN语句的一般格式为图36:循环语句循环结构是由循环语句来实现的。
对应于程序框图中的两种循环结构,一般程序设计语言中也有当型(WHILE型)和直到型(UNTIL型)两种语句结构。
即WHILE语句和UNTIL语句。
(1)WHILE语句①WHILE语句的一般格式是②当计算机遇到WHILE语句时,先判断条件的真假,如果条件符合,就执行WHILE与WEND之间的循环体;然后再检查上述条件,如果条件仍符合,再次执行循环体,这个过程反复进行,直到某一次条件不符合为止。
这时,计算机将不执行循环体,直接跳到WEND语句后,接着执行WEND之后的语句。
因此,当型循环有时也称为“前测试型”循环。
(2)UNTIL语句①UNTIL语句的一般格式是对应的程序框图是②直到型循环又称为“后测试型”循环,从UNTIL 型循环结构分析,计算机执行该语句时,先执行一次循环体,然后进行条件的判断,如果条件不满足,继续返回执行循环体,然后再进行条件的判断,这个过程反复进行,直到某一次条件满足时,不再执行循环体,跳到LOOP UNTIL 语句后执行其他语句,是先执行循环体后进行条件判断的循环语句。
分析:当型循环与直到型循环的区别:(1)当型循环先判断后执行,直到型循环先执行后判断; (2)在WHILE 语句中,是当条件满足时执行循环体,在UNTIL 语句中,是当条件不满足时执行循环. 7:辗转相除法与更相减损术(1)辗转相除法。
也叫欧几里德算法,用辗转相除法求最大公约数的步骤如下:①用较大的数m 除以较小的数n 得到一个商0S 和一个余数R ;②若R =0,则n 为m ,n 的最大公约数;若0R ≠0,则用除数n 除以余数R 得到一个商1S 和一个余数1R ;③若1R =0,则1R 为m ,n 的最大公约数;若1R ≠0,则用除数R 除以余数1R 得到一个商2S 和一个余数2R ;……依次计算直至n R =0,此时所得到的1n R 即为所求的最大公约数。
(2)更相减损术①任意给出两个正数;判断它们是否都是偶数。
若是,用2约简;若不是,执行第二步。
②以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数。
继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数。
(3)辗转相除法与更相减损术的区别:①都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
②从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到8:秦九韶算法与排序(1)秦九韶算法概念:f(x)=a n x n+a n-1x n-1+….+a1x+a0求值问题f(x)=a n x n+a n-1x n-1+….+a1x+a0=(a n x n-1+a n-1x n-2+….+a1)x+a0=(( a n x n-2+a n-1x n-3+….+a2)x+a1)x+a0 =......=(...( a n x+a n-1)x+a n-2)x+...+a1)x+a0求多项式的值时,首先计算最内层括号内依次多项式的值,即v1=a n x+a n-1然后由内向外逐层计算一次多项式的值,即v2=v1x+a n-2 v3=v2x+a n-3 ...... v n=v n-1x+a0这样,把n次多项式的求值问题转化成求n个一次多项式的值的问题。
(2)两种排序方法:直接插入排序和冒泡排序①直接插入排序基本思想:插入排序的思想就是读一个,排一个。
将第1个数放入数组的第1个元素中,以后读入的数与已存入数组的数进行比较,确定它在从大到小的排列中应处的位置.将该位置以及以后的元素向后推移一个位置,将读入的新数填入空出的位置中.(由于算法简单,可以举例说明)②冒泡排序基本思想:依次比较相邻的两个数,把大的放前面,小的放后面.即首先比较第1个数和第2个数,大数放前,小数放后.然后比较第2个数和第3个数......直到比较最后两个数.第一趟结束,最小的一定沉到最后.重复上过程,仍从第1个数开始,到最后第2个数...... 由于在排序过程中总是大数往前,小数往后,相当气泡上升,所以叫冒泡排序.9:进位制(1)概念:进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值。
可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n 进制。
现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数。
对于任何一个数,我们可以用不同的进位制来表示。
比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的。
一般地,若k 是一个大于一的整数,那么以k 为基数的k 进制可以表示为:110()110...(0,0,...,,)n n k n n a a a a a k a a a k --<<≤<,而表示各种进位制数一般在数字右下脚加注来表示,如111001(2)表示二进制数,34(5)表 典型例题例1.判断下列给出的输入语句、输出语句和赋值语句是否正确?为什么?(1)输入语句 INPUT a ;b ;c (2)输出语句 A =4 (3)赋值语句 3=B(4)赋值语句 A =B =-2解析:(1)错,变量之间应用“,”号隔开; (2)错,PRINT 语句不能用赋值号“=”; (3)错,赋值语句中“=”号左右不能互换; (4)错,一个赋值语句只能给一个变量赋值。
例2.请写出下面运算输出的结果。
(1) dd PRINT c c d b a c b a ;""2/)(35=*=+=== (2)cb ac b a PRINT bc a b b a c b a ,,;",,"21===-+=+===(3)cb ac b a PRINT ac c b b a c b a ,,;",,"302010=========解析:(1)16;语句2/)(b a c +=是将a ,b 和的一半赋值给变量c ,语句c c d *=是将c 的平方赋值给d ,最后输出d 的值。
(2)1,2,3;语句b a c +=是将a ,b 的和赋值给c ,语句b c a b -+=是将b c a -+的值赋值给了b 。
(3)20,30,20;经过语句b a =后a ,b ,c 的值是20,20,30。
经过语句c b =后a ,b ,c 的值是20,30,30。
经过语句a c =后a ,b ,c 的值是20,30,20。
练习:1.已知变量a ,b 已被赋值,要交换a 、b 的值,采用的算法是( )A .a =b ,b =aB .a =c ,b =a ,c =bC .a =c ,b =a ,c =aD .c =a ,a =b ,b =c 2.下列给出的赋值语句中正确的是( )A 4M =B M M =-C 3B A ==D 0x y +=例3.写出求三个数a ,b ,c 的方差的程序。
解析:方差是在初中统计内容中学习过的知识,计算所有数的方差首先计算所有数的平均数x ,通过公式nx x x x x x s n 222212)(........)()(-++-+-=来计算。
算法步骤:第一步:计算平均数3cb a x ++=; 第二步:计算方差3)()()(2222a x a x a x s -+-+-=;第三步:得到的结果即为所求。
程序如下: INPUT a ,b ,c y=(a+b+c)/3S=((a -y)2+ (b -y)2+ (c -y)2)/3 PRINT S END例4.编写一个程序,要求输入的两个正数a 和b 的值,输出a b 和b a 的值。
程序1:INPUT “a,b :”;a ,b A=a^b B=b^aPRINT “a b =”;A ,“b a =”;B END例5.编写程序,输出两个不相等的实数a 、b 的最大值。
解:算法:第一步:输入a , b 的数值;第二步:判断a ,b 的大小关系,若a >b ,则输出a 的值,否则输出b 的值。
程序如下:(“IF—THEN —ELSE”语句) IN PUT“a ,b”;a ,b IF a >b THEN PRINT a ELSEPRINT b END IF END例6.高等数学中经常用到符号函数,符号函数的定义为⎪⎩⎪⎨⎧<-=>=0,10,00,1x x x y ,试编写程序输入x 的值,输出y程序一:(嵌套结构) 程序框图:(右图) 程序语言: INPUT x IF x >0 THEN y =1 ELSEIF x =0 THEN y =0 ELSE y =-1 END IF END IF PRINT y END例7.设计一个计算1×3×5×7×…×99的算法,编写算法程序。
解析: 算法如下: 第一步:s =1; 第二步:i =3; 第三步:s =s×i; 第四步:i =i +2;第五步:如果i≤99,那么转到第三步; 第六步:输出s ; 程序如下:(“WHILE 型”循环语句) s =1 i =3WHILE i <=99 s =s*i i =i +2 WENDPRINT s END例8. 求三个数72,120,168的最大公约数. 解法1:用辗转相除法先求120,168的最大公约数,因为168120148,12048224,48242=⨯+=⨯+=⨯ 所以120,168的最大公约数是24. 再求72,24的最大公约数,因为72243=⨯,所以72,24的最大公约数为24, 即72,120,168的最大公约数为24.解法2:用更相减损术先求120,168的最大公约数,168-120=48,120-48=72,72-48=24,48-24=24 所以120,168的最大公约数为24. 再求72,24的最大公约数, 72-24=48,48-24=2472,24的最大公约数为24,即72,120,168的最大公约数为24.例9.用秦九韶算法求多项式5432()23456f x x x x x x =+++++在2x =时的值. 分析:先改写多项式,再由内向外计算.5432:()23456((((2)3)4)5)6f x x x x x x x x x x x =+++++=+++++解010*********,243114265576120v v v x v v x v v x v v x v v x ==+==+==+==+==+= 本题也可简写为下式:12345622822521144112657120例10.完成下列进制的转化(3)(10)(10)__________(8)(1)10202____(2)101==解: 420(3)(10)(1)10202132323101=⨯+⨯+⨯=(2)用8反复去除101,直到商为0止,所得的余数(从末位读起)就是十进制数101的8进制表示8101812581401余数 所以(10)(8)101145=一、选择题1 当2=x 时,下面的程序输出的结果是 ( )A 3B 7C 15D 17 2下边程序运行后输出的结果为( )A 50B 5C 25D 0二、填空题15()51a j WHILE j a a j MOD j j WENDPRINT aEND ==<==+=+10411i s WHILE i s s x i i WEND PRINT I s U xE T N NP D==<==*+=+1.下面程序运行后输出的结果为_______________解析: 22,-222 三个数324,243,135的最大公约数是_________________解析:324243181,13581154,8154127,54272=⨯+=⨯+=⨯+=⨯.填27 三、解答题用秦九韶算法求多项式5432()34157678f x x x x x x =+-+++在2x =-时的值.543201021324354:()34157678((((34)15)76)7)83,421511769871898386f x x x x x x x x x x x v v v x v v x v v x v v x v v x =+-+++=+-+++==+=-=-=-=+==+=-=+=9.解520033,x y IF x THEN x y ELSE y y END IF PRINT x y y xEND==-<=-=+--。
