静电场经典计算题

合集下载

静电场计算题

静电场计算题编者：王恒波AB θ静电场计算题1、如图所示，a、b、c、d为匀强电场中四个等势面，相邻等势面间距离为2cm，已知ac间电势差Uac=80V,求：（1）设B点的电势为零，求A点的电势。

（2）将q=2×10-10C的点电荷由B移到C，最后到D，电场力所做的功Wbcd2、如图所示光滑斜面倾角为370，一带有正电荷的小物块质量为m，电荷量为q，置于斜面顶端A点，在沿水平方向加如图所示的匀强电场时，带电小物块恰好静止在斜面上。

（1）计算此时电场强度的大小；（2）从某时刻开始电场强度变成原来的1/2时，求小物块沿斜面下滑的加速度；（3）已知斜面AB长为L，则小物块到达斜面底端B点时的速度是多少？3、在如图所示的匀强电场中，有A、B两点，且A、B两点间的距离为x=0.20 m，已知AB连线与电场线夹角为 =60°，今把一电荷量q=-2x10-8C的检验电荷放入该匀强电场中，其受到的电场力的大小为F=4.0X10-4N，方向水平向左。

求：（1）电场强度E的大小和方向；（2）若把该检验电荷从A点移到B点，电势能变化了多少；（3）若A点为零电势点，B点电势为多少。

4、如图所示，极板A、B间匀强电场的场强E=2X105V/m、a、b两点相距10cm，a距A极板2cm，b距B极板3cm。

求：（1）a、b两点哪点电势高？（2）外力把点电荷q=1x10-7C由b匀速移到a做多少功？如果选b为零电势点，q在a 点的电势能是多少？（3）UAB是多少？5、如图所示，用长为l的绝缘细线拴一个质量为m、带电量为 +q的小球（可视为质点）后悬挂于O点，整个装置处于水平向右的匀强电场中。

将小球拉至使悬线呈水平的位置A后，由静止开始将小球释放，小球从A点开始向下CBA摆动，当悬线转过60角到达位置B 时，速度恰好为零。

求：（1）B、A两点的电势差UBA；（2）电场强度E ；（3）小球到达B点时，悬线对小球的拉力（4）小球到达B点时的加速度大小6、在真空中存在空间范围足够大的、水平向右的匀强电场．若将一个质量为m、带正电、电荷量为q的小球在此电场中由静止释放，小球将沿与竖直方向夹角为53°的直线运动．现将该小球从电场中某点以初速度v0竖直向上抛出，求运动过程中(sin 53°＝0.8)(1)此电场的电场强度大小；(2)小球运动的抛出点至最高点之间的电势差U；(3)小球的最小动能．7、如图所示，在O点放置一个正电荷，在过O点的竖直平面内的A点，自由释放一个带正电的小球，小球的质量为m、电荷量为q。

高中物理静电场经典习题30道--带答案

高中物理静电场经典习题30道--带答案1.如图，在光滑绝缘水平面上，三个带电小球a、b和c 分别位于边长为l的正三角形的三个顶点上；a、b带正电，电荷量均为q，c带负电．整个系统置于方向水平的匀强电场中．已知静电力常量为k．若三个小球均处于静止状态，则匀强电场场强的大小为（）A．$\frac{kq}{l^2}$。

B．$\frac{\sqrt{3}kq}{l^2}$。

C．$\frac{2kq}{l^2}$。

D．$\frac{3kq}{l^2}$2.如图，一半径为R的圆盘上均匀分布着电荷量为Q的电荷，在垂直于圆盘且过圆心c的轴线上有a、b、d三个点，a和b、b和c、c和d间的距离均为R，在a点处有一电荷量为q（q＞）的固定点电荷．已知b点处的场强为零，则d点处场强的大小为（k为静电力常量）A．$\frac{kQ}{4R^2}$。

B．$\frac{\sqrt{2}kQ}{4R^2}$。

C．$\frac{kQ}{2R^2}$。

D．$\frac{\sqrt{2}kQ}{R^2}$3.如图所示，在光滑绝缘水平面上放置3个电荷量均为q （q＞）的相同小球，小球之间用劲度系数均为k的轻质弹簧绝缘连接．当3个小球处在静止状态时，每根弹簧长度为l．已知静电力常量为k，若不考虑弹簧的静电感应，则每根弹簧的原长为A．$l+\frac{2q^2}{kl}$。

B．$l-\frac{2q^2}{kl}$。

C．$l-\frac{q^2}{kl}$。

D．$l+\frac{q^2}{kl}$4.如图所示，在光滑的绝缘水平面上，由两个质量均为m 带电量分别为+q和﹣q的甲、乙两个小球，在力F的作用下匀加速直线运动，则甲、乙两球之间的距离r为A．$\frac{F}{2kq^2}$。

B．$\frac{F}{kq^2}$。

C．$\frac{F}{4kq^2}$。

D．$\frac{2F}{kq^2}$5.一带负电荷的质点，在电场力作用下沿曲线abc从a运动到c，已知质点的速率是递减的．关于b点电场强度E的方向，下列图示中可能正确的是（虚线是曲线在b点的切线）A．。

静电场习题汇总

1.已知一均匀带电球面，总带电量为q ，半径为 R ，2.已知一均匀带电球体，半径为 R ，带电量为q ，求1）整个空间的场强分布；2）整个空间的电势分布。

电荷均匀分布在球体内，求： 1）整个空间的场强分布； 2）整个空间的电势分布。

（整个空间介电常数按ε 计算）qR OrqR Or解：1）以O 为心，r 为半径建立球形高斯面K K v 1 ε0 ∑ ∫ φe = E ⋅dS = E ⋅4πr 2= q i 内解：1）以O 为心，r 为半径建立球形高斯面S iK K v ∫1 ∑ φe = E ⋅dS = E ⋅4πr 2= q i 内根据高斯定理ε0 S i当r < R 时， E ⋅4πr22= ε1 ⋅0 ∴E = 0根据高斯定理当r < R 时，4πr 3= ε1 ⋅q ∴E = q 当r > R 时， E ⋅4πr1 ⋅ 3 qr4πε R 04πε0r 2 E ⋅4πr 2 = q ∴E =ε 4 33 πR 30 2）当r < R 时，K K qq 4πε R = ε1 ⋅q ∴E =q 4πε0r 2∞ R ∞ ∫ ∫ ∫ U = E ⋅dl = 0dr + 4πε r dr = 当r > R 时， E ⋅4πr22r r R0 0当r > R 时， 2）当r < R 时，K K K K q q4πε0rqr4πε Rq4πε0r R∞ ∞ ∞R ∞∫ dr + ∫ ∫ ∫ ∫ U = E ⋅dl = 4πε0r dr = U = E ⋅dl = dr 2 3 2 r r r r q 8πε R 0q 3q + qr 2 = (R 2 −r 2)+ 4πε R = 8πε R 8πε R 3 3 0 0 0当r > R 时，K K q q 4πε0r∞ ∞ ∫ ∫ U = E ⋅dl = 4πε0r dr = 2 r r4．已知两同轴带电圆柱面，半径分别为a 和b ，内 3.已知两同心带电球面，半径分别为 R 、 R ，内 1 2 λ 电量为−λ，忽略边缘效应，求：圆柱面单位长度带电量为，外圆柱面单位长度带球面带电量为 q ,外球面带电量为−q ，求：-q b 求1）整个空间的场强分布； a q求1）整个空间的场强分布；2）两柱面之间的电势差U 。

静电场经典计算题.

静电场计算题1、如图所示，绝缘水平面上静止着两个质量均为m ，电量均为+Q 的物体A 和B （A 、B 均可视为质点），它们间的距离为r ，与平面间的动摩擦因数均为μ，求： ①图示A 、B 静止时A 受的摩擦力为多大？②如果将A 的电量增至+4Q ，两物体开始运动，当它们的加速度第一次为零时，A 、B 各运动了多远？2、质量为m 、带电量为+q 的小球从距地面高为h 处以一定的初速度水平抛出．在距抛出点水平距离为l 处，有一根管口比小球直径略大的上下都开口的竖直细管，管的上口距地面12h ．为使小球能无碰撞地从管子中通过，可在管子上方的整个区域里加一个电场强度方向水平向左的匀强电场，如图所示．求：小球的初速度v 0、电场强度E 的大小及小球落地时的动能E k ．3、如图所示，空间存在着强度E =2.5×102N/C 方向竖直向上的匀强电场，在电场内一长为L =0.5m 的绝缘细线，一端固定在O 点，一端拴着质量m =0.5kg 、电荷量q =4×10－2C的小球.现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.取g =10m/s 2.求：（1）小球的电性；（2）细线能承受的最大拉力；（3）当小球继续运动后与O 点水平方向距离为L 时，小球距O 点的高度.E O4、如图所示．半径为r 的绝缘光滑圆环固定在竖直平面内，环上套有质量为m 的带正电的珠子，空间存在水平向右的匀强电场，珠子所受静电力是其重力的3/4倍．将珠子从环上最低点A 静止释放，求珠子所能获得的最大动能E k .。

5、如图所示，水平地面上方分布着水平向右的匀强电场。

一“L”形的绝缘硬质管竖直固定在匀强电场中。

管的水平部分长为l 1=0.2m ，离水平面地面的距离为h=5.0m ，竖直部分长为l 2=0.1m 。

一带正电的小球从管的上端口A 由静止释放，小球与管间摩擦不计且小球通过管的弯曲部分（长度极短可不计）时没有能量损失，小球在电场中受到的电场力大小为重力的一半。

静电场计算题

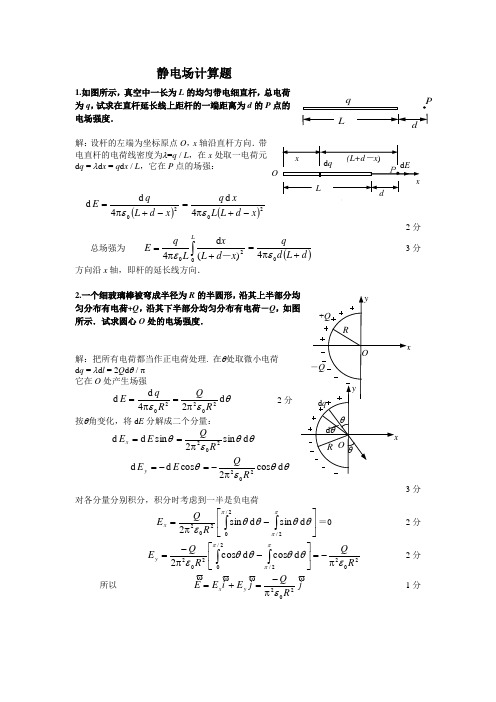
静电场计算题1.如图所示，真空中一长为L 的均匀带电细直杆，总电荷为q ，试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度．解：设杆的左端为坐标原点O ，x 轴沿直杆方向．带电直杆的电荷线密度为λ=q / L ，在x 处取一电荷元d q = λd x = q d x / L ，它在P 点的场强：()204d d x d L q E -+π=ε()204d x d L L xq -+π=ε 2分总场强为 ⎰+π=Lx d L x L q E 020)(d 4－ε()d L d q+π=04ε3分方向沿x 轴，即杆的延长线方向．2.一个细玻璃棒被弯成半径为R 的半圆形，匀分布有电荷+Q ，沿其下半部分均匀分布有电荷－Q ，所示．试求圆心O 处的电场强度．解：把所有电荷都当作正电荷处理. 在θ处取微小电荷 d q = λd l = 2Q d θ / π它在O 处产生场强 θεεd 24d d 20220R QR q E π=π= 2分按θ角变化，将d E 分解成二个分量：θθεθd sin 2sin d d 202RQ E E x π== θθεθd cos 2cos d d 202RQE E y π-=-= 3分对各分量分别积分，积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x ＝0 2分 2022/2/0202d cos d cos 2R QR Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 2分所以j RQ j E i E E y x202επ-=+= 1分LPd E O3.如图所示，一电荷面密度为σ的“无限大”平面，在距离平面a 处的一点的场强大小的一半是由平面上的一个半径为R 的圆面积范围内的电荷所产生的．试求该圆半径的大小．解：电荷面密度为σ的无限大均匀带电平面在任意点的场强大小为E =σ / (2ε0) 2分以图中O 点为圆心，取半径为r →r ＋d r 的环形面积，其电量为d q = σ2πr d r 2分它在距离平面为a 的一点处产生的场强()2/32202d ra a r d rE +=εσ 2分则半径为R 的圆面积内的电荷在该点的场强为()⎰+=R ra r r a E 02/3220d 2εσ⎪⎪⎭⎫⎝⎛+-=22012R a a εσ 2分由题意,令E =σ / (4ε0)，得到R ＝a 32分4.电荷线密度为λ的“无限长”均匀带电细线，弯成图示形状．若半圆弧AB 的半径为R ，试求圆心O 点的场强．解：以O 点作坐标原点，建立坐标如图所示．半无限长直线A ∞在O 点产生的场强1E ， ()j i R E --π=014ελ 2分半无限长直线B ∞在O 点产生的场强2E ， ()j i RE +-π=024ελ2分半圆弧线段在O 点产生的场强3E，i RE032ελπ= 2分由场强叠加原理，O 点合场强为0321=++=E E E E2分5. 将一“无限长”带电细线弯成图示形状，设电荷均匀分布，电荷线密度为λ，四分之一圆弧AB 的半径为R ，试求圆心O 点的场强．∞∞OBA∞∞解：在O 点建立坐标系如图所示．半无限长直线A ∞在O 点产生的场强：()j i R E -π=014ελ 2分半无限长直线B ∞在O 点产生的场强：()j i RE +-π=024ελ 2分四分之一圆弧段在O 点产生的场强： ()j i RE+π=034ελ 4分由场强叠加原理，O 点合场强为： ()j i RE E E E+π=++=03214ελ2分6.图中虚线所示为一立方形的高斯面，已知空间的场强分布为： E x ＝bx ， E y ＝0， E z ＝0．高斯面边长a ＝0.1 m ，常量b ＝1000 N/(C ·m)．试求该闭合面中包含的净电荷．(真空介电常数ε0＝8.85×10-12C 2·N -1·m -2 )解：设闭合面内包含净电荷为Q ．因场强只有x 分量不为零，故只是二个垂直于x 轴的平面上电场强度通量不为零．由高斯定理得：-E 1S 1+ E 2S 2=Q / ε0 ( S 1 = S 2 =S ) 3分则 Q = ε0S (E 2- E 1) = ε0Sb (x 2- x 1)= ε0ba 2(2a －a ) =ε0ba 3 = 8.85×10-12 C 2分7.真空中一立方体形的高斯面,边长a ＝0.1 m 置．已知空间的场强分布为： E x =bx , E y =0 , E z =0．常量b ＝1000 N/(C ·m)．试求通过该高斯面的电通量．解：通过x ＝a 处平面1的电场强度通量 Φ1 = -E 1 S 1= -b a 3 1分通过x = 2a 处平面2的电场强度通量Φ2 = E 2 S 2 = 2b a 3 1分其它平面的电场强度通量都为零．因而通过该高斯面的总电场强度通量为Φ = Φ1+ Φ2 = 2b a 3-b a 3 = b a 3 =1 N ·m 2/C 3分B A ∞x8. 图示一厚度为d 的“无限大”均匀带电平板，电荷体密度为ρ．试求板内外的场强分布，并画出场强随坐标x 变化的图线，即E —x 图线(设原点在带电平板的中央平面上，Ox 轴垂直于平板)．解：由电荷分布的对称性可知在中心平面两侧离中心平面相同距离处场强均沿x 轴，大小相等而方向相反．在板内作底面为S 的高斯柱面S 1（右图中厚度放大了）, 两底面距离中心平面均为⎢x ⎜, 由高斯定理得01/22ερS x S E ⋅=⋅则得 01/ερx E =即01/ερx E = ⎪⎭⎫ ⎝⎛≤≤-d x d 21214分在板外作底面为S 的高斯柱面S 2两底面距中心平面均为x ，由高斯定理得 02/2ερSd S E ⋅=⋅则得 ()022/ερd E ⋅= ⎪⎭⎫ ⎝⎛>d x 21即 ()022/ερd E ⋅= ⎪⎭⎫ ⎝⎛>d x 21，()022/ερd E ⋅-= ⎪⎭⎫ ⎝⎛-<d x 21 4分E ~ x 图线如图所示． 2分9.一半径为R 的带电球体，其电荷体密度分布为 ρ =Ar (r ≤R ) ， ρ =0 (r ＞R ) A 为一常量．试求球体内外的场强分布．解：在球内取半径为r 、厚为d r 的薄球壳，该壳内所包含的电荷为r r Ar V q d 4d d 2π⋅==ρ在半径为r 的球面内包含的总电荷为403d 4Ar r Ar dV q rVπ=π==⎰⎰ρ (r ≤R)以该球面为高斯面，按高斯定理有 0421/4εAr r E π=π⋅ 得到()0214/εAr E =， (r ≤R )方向沿径向，A >0时向外, A <0时向里． 3分在球体外作一半径为r 的同心高斯球面，按高斯定理有 0422/4εAR r E π=π⋅ 得到 ()20424/r AR E ε=， (r >R )方向沿径向，A >0时向外，A <0时向里． 2分2E 210.电荷面密度分别为+σ和－σ的两块“无限大”均匀带电平行平面，分别与x 轴垂直相交于x 1＝a ，x 2＝－a 两点．设坐标原点O 处电势为零，试求空间的电势分布表示式并画出其曲线．解：由高斯定理可得场强分布为：E =-σ / ε0 (－a ＜x ＜a )1分E = 0 (－∞＜x ＜－a，a ＜x ＜＋∞＝ 1分由此可求电势分布：在－∞＜x ≤－a 区间⎰⎰⎰---+==00/d d 0d aa xxx x x E U εσ0/εσa -= 2分在－a ≤x ≤a 区间000d d εσεσxx x E U xx=-==⎰⎰2分在a ≤x ＜∞区间000d d 0d εσεσax x x E U aaxx=-+==⎰⎰⎰2分图2分11.如图所示，两个点电荷＋q 和－3q ，相距为d . 试求：(1) 在它们的连线上电场强度0=E的点与电荷为＋q 的点电荷相距多远？ (2) 若选无穷远处电势为零，两点电荷之间电势U =0的点与电荷为＋q 的点电荷相距多远？解：设点电荷q 所在处为坐标原点O ，x 轴沿两点电荷的连线．(1) 设0=E的点的坐标为x '，则()04342020=-'π-'π=i d x q i x q E εε 3分可得 02222=-'+'d x d x解出 ()d x 3121+-=' 2分另有一解()d x 13212-=''不符合题意，舍去． (2) 设坐标x 处U ＝0，则 ()x d qx q U -π-π=00434εε ()0440=⎥⎦⎤⎢⎣⎡--π=x d x x d q ε 3分得 d - 4x = 0, x = d /4 2分12.图中所示为一沿x 轴放置的长度为l 的不均匀带电细棒，其电荷线密度为λ＝λ0 (x -a )，λ0为一常量．取无穷远处为电势零点，求坐标原点O 处的电势．x-a +aO xU+Ox解：在任意位置x 处取长度元d x ，其上带有电荷d q =λ0 (x －a )d x 1分它在O 点产生的电势 ()xxa x U 004d d ελπ-=2分O 点总电势⎥⎦⎤⎢⎣⎡-π==⎰⎰⎰++l a a la a x x a x dU U d d 400ελ⎥⎦⎤⎢⎣⎡+-π=a l a a l ln 400ελ 2分13. 图示一个均匀带电的球层，其电荷体密度为ρ，球层内表面半径为R 1，外表面半径为R 2．设无穷远处为电势零点，求球层中半径为r 处的电势．解：r 处的电势等于以r 为半径的球面以内的电荷在该处产生的电势U 1和球面以外的电荷产生的电势U 2之和，即 U = U 1 + U 2 ，其中U 1=q i/ (4πε0r )()()rR r 031343/4ερπ-π=⎪⎪⎭⎫ ⎝⎛-=r R r 31203ερ 4分为计算以r 为半径的球面外电荷产生的电势．在球面外取r '─→r '＋d r '的薄层．其电荷为 d q =ρ·4πr '2d r ' 它对该薄层内任一点产生的电势为()002/d 4/d d ερεr r r q U ''='π=则 ⎰⎰''==2d d 022R r r r U U ερ()2222r R -=ερ 4分于是全部电荷在半径为r 处产生的电势为()222031202123r R r R r U U U -+⎪⎪⎭⎫ ⎝⎛-=+=ερερ ⎪⎪⎭⎫ ⎝⎛--=r R r R 312220236ερ 2分若根据电势定义直接计算同样给分．14.电荷以相同的面密度σ 分布在半径为r 1＝10 cm 和r 2＝20 cm 的两个同心球面上．设无限远处电势为零，球心处的电势为U 0＝300 V ． (1) 求电荷面密度σ．(2) 若要使球心处的电势也为零，外球面上应放掉多少电荷？［ε0＝8.85×10-12 C 2 /(N ·m 2)］解：(1) 球心处的电势为两个同心带电球面各自在球心处产生的电势的叠加，即⎪⎪⎭⎫ ⎝⎛+π=22110041r q r q U ε⎪⎪⎭⎫ ⎝⎛π-ππ=22212104441r r r r σσε()210r r +=εσ3分 2100r r U +=εσ＝8.85×10-9 C / m 2 2分 (2) 设外球面上放电后电荷面密度为σ'，则应有O()2101r r U σσε'+='= 0即σσ21r r -=' 2分外球面上应变成带负电，共应放掉电荷()⎪⎪⎭⎫⎝⎛+π='-π='212222144r r r r q σσσ ()20021244r U r r r εσπ=+π=＝6.67×10-9 C 3分15.在强度的大小为E ，方向竖直向上的匀强电场中，有一半径为R 的半球形光滑绝缘槽放在光滑水平面上(如图所示)．槽的质量为M ，一质量为m 带有电荷＋q 的小球从槽的顶点A 处由静止释放．如果忽略空气阻力且质点受到的重力大于其所受电场力，求： (1) 小球由顶点A 滑至半球最低点Ｂ时相对地面的速度； (2) 小球通过B 点时，槽相对地面的速度；(3) 小球通过B 点后，能不能再上升到右端最高点C ？解：设小球滑到B 点时相对地的速度为v ，槽相对地的速度为V ．小球从A →B 过程中球、槽组成的系统水平方向动量守恒，m v ＋MV ＝0 ① 2分对该系统，由动能定理 mgR －EqR ＝21m v 2＋21MV 2 ②3分 ①、②两式联立解出 ()()m M m qE mg MR +-=2v 2分方向水平向右．()()m M M qE mg mR M m V +--=-=2v 1分方向水平向左． 1分小球通过B 点后，可以到达C 点． 1分16.两个带等量异号电荷的均匀带电同心球面，半径分别为R 1＝0.03 m 和R 2＝0.10 m ．已知两者的电势差为450 V ，求内球面上所带的电荷．解：设内球上所带电荷为Q ，则两球间的电场强度的大小为204rQE επ=(R 1＜r ＜R 2) 1分两球的电势差⎰⎰π==212120124d R R R R r drQ r E U ε⎪⎪⎭⎫ ⎝⎛-π=210114R R Q ε 2分 ∴ 12122104R R U R R Q -π=ε＝2.14×10-9 C 2分17.一均匀电场，场强大小为E ＝5×104 N/C ，方向竖直朝上，把一电荷为q＝ 2.5×10-8 C 的点电荷，置于此电场中的a 点，如图所示．求此点电荷在下列过程中电场力作的功．d(1) 沿半圆路径Ⅰ移到右方同高度的b 点，ab ＝45 cm ； (2) 沿直线路径Ⅱ向下移到c 点，ac ＝80 cm ；(3) 沿曲线路径Ⅲ朝右斜上方向移到d 点，ad ＝260 cm(与水平方向成45°角)．解：(1) 090cos d o1===⎰⋅ab qE S F A ba2分(2) o2180cos d ac qE S F A c a==⎰⋅ ＝－1×10-3 J 3分(3) o345sin d ad qE S F A d a==⎰⋅ ＝2.3×10-3 J 3分18.一带有电荷q ＝3×10-9 C 的粒子，位于均匀电场中，电场方向如图所示．当该粒子沿水平方向向右方运动5 cm 时，外力作功6×10-5 J ，粒子动能的增量为4.5×10-5 J ．求：(1) 粒子运动过程中电场力作功多少？(2) 该电场的场强多大？解：(1) 设外力作功为A F 电场力作功为A e ，由动能定理：A F + A F = ∆ E K则 A e ＝∆ E K －A F =－1.5×10-5 J 2分(2) qES S F S F A e e e -=-=⋅=()=-=qS A E e /105 N/C 3分19. 如图所示，一半径为R 的均匀带正电圆环，其电荷线密度为λ．在其轴线上有A 、B 两点，它们与环心的距离分别为R OA 3=，R OB 8= . 一质量为m 、电荷为q 的粒子从A 点运动到B 点．求在此过程中电场力所作的功．解：设无穷远处为电势零点，则A 、B 两点电势分别为220432ελελ=+=R R RU A 2分 0220682ελελ=+=R R R U B 1分 q 由A 点运动到B 点电场力作功()0001264ελελελq q U U q A B A =⎪⎪⎭⎫⎝⎛-=-= 2分注：也可以先求轴线上一点场强，用场强线积分计算．20.图示两个半径均为R 的非导体球壳，表面上均匀带电，电荷分别为＋Q 和－Q ，两球心相距为d (d>>2R )．求两球心间的电势差．解：均匀带电球面内的电势等于球面上的电势．球面外的电势相当于电荷集中在球心上的点电荷的电势．由此，按电势叠加原理球心O 1处的电势为： d QR Q U 00144εεπ-π= 2分球心O 2处的电势为： RQd Q U 00244εεπ-π= 2分 Eq则O 1、O 2间的电势差为： ()RdR d Q d R Q U 00122112εεπ-=⎪⎭⎫ ⎝⎛-π=1分21.一电子射入强度的大小为5000 N ·C -1的均匀电场中，电场的方向竖直向上．电子初速度为v 0＝107 m ·s -1，与水平方向成θ＝30°角，如图所示．求电子从射入位置上升的最大高度．(电子的质量m ＝9.1×10-31 kg ，电子电荷绝对值e ＝1.6×10 -19 C) 解：电子在电场中作斜抛运动，忽略重力，在竖直方向上有：a y ＝－eE / m 1分v y ＝v 0sin θ－eEt / m 1分2021sin eEt t y -=θv 1分电子上升至最高点的条件是v y ＝0，于是有： v 0sin θ－eEt 1 / m ＝0t 1 = m v 0sin θ / (eE ) 1分∴ ()22201042.12/sin -⨯==eE m y θv m 1分22.在真空中一长为l ＝10 cm 的细杆上均匀分布着电荷，其电荷线密度λ＝ 1.0×10-5C/m ．在杆的延长线上，距杆的一端距离d ＝10 cm 的一点上，有一点电荷q 0＝ 2.0×10-5 C ，如图所示．试求该点电荷所受的电场力．(真空介电常量ε0＝8.85×10-12 C 2·N -1·m -2 )解：选杆的左端为坐标原点，x 轴沿杆的方向．在x 处取一电荷元λd x ，它在点电荷所在处产生场强为：()204d d x d xE +π=ελ 3分整个杆上电荷在该点的场强为：()()l d d lx d x E l+π=+π=⎰00204d 4ελελ 2分点电荷q 0所受的电场力为：()l d d lq F +π=004ελ＝0.90 N 沿x 轴负向 3分23.如图所示，有一高为h 的直角形光滑斜面, 斜面倾角为α．在直角顶点A 处有一电荷为－q 的点电荷．另有一质量为m 、电荷＋q 的小球在斜面的顶点B 由静止下滑．设小球可看作质点，试求小球到达斜面底部C 点时的速率．解：因重力和电场力都是保守力，小球从顶点B 到达底部C 点过程中能量守恒．αεεctg 421402202h q m mgh h q π-=+π-v 3分 ∴ ()2/10221tg 2⎥⎦⎤⎢⎣⎡+-π=gh m h q αεv 2分O yθE 0vq24.一半径为R 的均匀带电细圆环，其电荷线密度为λ，水平放置．今有一质量为m 、电荷为q 的粒子沿圆环轴线自上而下向圆环的中心运动(如图)．已知该粒子在通过距环心高为h 的一点时的速率为v 1，试求该粒子到达环心时的速率．解：带电粒子处在h 高度时的静电势能为()2/122012R h qRW +=ελ 2分到达环心时的静电势能为 ()022/ελq W = 2分据能量守恒定律1212222121W mgh m W m ++=+v v 2分以上三式联立求解得到2/1220212112⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+--+=R h R m qR gh ελv v 2分25.如图所示，两个电荷分别为q 1＝20×10-9 C 和q 2＝－12×10-9 C 的点电荷，相距5 m ．在它们的连线上距q 2为1 m 处的A 点从静止释放一电子，则该电子沿连线运动到距q 1为1 m处的B 点时，其速度多大？(电子质量m e ＝9.11×10-31 kg ，基本电荷e ＝1.6×10-19 C ，41επ＝9×109 N ·m 2/C 2 ) 解：设无限远处为电势零点，则A 、B 两点的电势为： ⎪⎪⎭⎫ ⎝⎛+π=π+π=221102021014144r q r q r q r q U A εεε代入r 1=4 m ，r 2=1 m 得 U A ＝－63 V 2分⎪⎪⎭⎫ ⎝⎛'+'π='π+'π=221102021014144r q r q r q r q U B εεε代入1r '＝1 m ，2r '＝4 m 得 U B ＝153 V 2分电子在运动过程中，电势能减少，动能增加()B A e U U e m --=221v 2分 ()eB A m U U e --=2v ＝8.71×106 m/s 2分26.两个同心的导体球壳，半径分别为R 1＝0.145 m 和R 2＝0.207 m ，内球壳上带有负电荷q＝-6.0×10-8 C ．一电子以初速度为零自内球壳逸出．设两球壳之间的区域是真空，试计算电子撞到外球壳上时的速率．(电子电荷ｅ＝-1.6×10-19 C ，电子质量m e ＝9.1×10-31 kg ，ε0＝8.85×10-12 C 2 / N ·m 2）解：由高斯定理求得两球壳间的场强为()2120R4R r r q E <<π=ε 2分方向沿半径指向内球壳．电子在电场中受电场力的大小为q 2420r eqeE F επ== 2分方向沿半径指向外球壳．电子自内球壳到外球壳电场力作功为⎰⎰π==212120d 4d R R R R r r eqr F A ε()21012214114R R R R eq R R eqεεπ-=⎪⎪⎭⎫ ⎝⎛-π= 2分由动能定理()210122421R R R R eq m e επ-=v 2分得到 ()em R R R R eq 210122επ-=v ＝1.98×107 m/s 2分27. 电荷Q (Q ＞0)均匀分布在长为L 的细棒上，在细棒的延长线上距细棒中心O 距离为a 的P 点处放一电荷为q (q ＞0 )的点电荷，求带电细棒对该点电荷的静电力．解：沿棒方向取坐标Ox ，原点O 在棒中心处．求P 点场强：()()20204d 4d d x a xx a q E -π=-π=ελε 2分 ()⎰--π=2/2/204d L L x a xE ελ()2202/2/0414L a Qx a L L -π=-⋅π=-εελ 3分方向沿x 轴正向. 点电荷受力：==qE F ()2204πL a qQ-ε 方向沿x 轴正方向． 3分。

15《静电场》计算题专项训练典型问题分析(精品)

《静电场》计算题专项训练1．在光滑的绝缘水平面上，有一质量m ＝1.0 ⨯ 10－3 kg 、电量q ＝1.0 ⨯ 10－10 C 的带正电小球，静止在O 点，以O 点为原点，在该水平面内建立直角坐标系Oxy 。

现突然加一沿y 轴正方向、场强大小E 1＝6.0 ⨯ 106 V ／m 的匀强电场，使小球开始运动，经过1.0 s ，所加电场突然变为沿x 轴正方向、场强大小为E 2＝4.0 ⨯ 106 V ／m 的匀强电场，求再经过2.0 s 时小球的位置坐标。

1．【解析】a 1＝qE 1m ＝6⨯106⨯1⨯10－101⨯10－3m / s 2＝0.6 m / s 2v 1＝a 1t 1＝0.6⨯1 m / s ＝0.6 m / s ； y 1＝12 a 1t 12＝12 ⨯0.6⨯12 m ＝0.3 m ；a 2＝qE 2m ＝4⨯106⨯1⨯10－101⨯10－3m / s 2＝0.4 m / s 2y 2＝v 1t 2＝0.6⨯2 m ＝1.2 m ；y ＝y 1＋y 2＝（0.3＋1.2）m ＝1.5 m ； x ＝12 a 2t 22＝12⨯0.4⨯22m ＝0.8 m2．如图所示，固定于同一条竖直线上的A 、B 是两个带等量异种电荷的点电荷，电荷量均为Q ，其中A 带正电荷，B 带负电荷，D 、C 是它们连线的垂直平分线，A 、B 、C 三点构成一边长为d 的等边三角形。

另有一个带电小球E ，质量为m 、电荷量为＋q(可视为点电荷)，被长为L 的绝缘轻质细线悬挂于O 点，O 点在C 点的正上方。

现在把小球 E 拉起到M 点，使细线水平绷直且与A 、B 、C 处于同一竖直面内，并由静止开始释放，小球E 向下运动到最低点C 时，速度为v 。

已知静电力常量为k ，若取D 点的电势为零，试求： (1)在A 、B 所形成的电场中，M 的电势φM 。

(2)绝缘细线在C 点所受到的拉力T 。

2．【解析】(1)电荷E 从M 点运动到C 的过程中,电场力做正功,重力做正功．根据动能定理Uq+mgL=mv 2/2得M 、C 两点的电势差为 U MC ＝(mv 2-2mgL)/2q-------又,C 点与D 点为等势点,所以M 点的电势为U M ＝(mv 2-2mgL)/2q (2)在C 点时A 对E 的电场力F １与B 对E 的电场力F ２相等，且为 F １＝F ２＝kQq/d2又，A 、B 、C 为一等边三角形，所以F １、F ２的夹角为120０，故F 1、F 2的合力为 F 12= kQq/d 2, 且方向竖直向下。

静电场练习题及答案

静电场练习题一、电荷守恒定律、库仑定律练习题4．把两个完全一样的金属球A和B接触一下，再分开一段距离，发现两球之间相互排斥，则A、B两球原来的带电情况可能是 [ ]A．带有等量异种电荷B．带有等量同种电荷C．带有不等量异种电荷D．一个带电，另一个不带电8．真空中有两个固定的带正电的点电荷，其电量Q1＞Q2，点电荷q置于Q1、Q2连线上*点时，正好处于平衡，则 [ ]A．q一定是正电荷B．q一定是负电荷C．q离Q2比离Q1远D．q离Q2比离Q1近14．如图3所示，把质量为0.2克的带电小球A用丝线吊起，假设将带电量为4×10-8库的小球B靠近它，当两小球在同一高度相距3cm时，丝线与竖直夹角为45°，此时小球B受到的库仑力F＝______，小球A带的电量q A＝______．二、电场电场强度电场线练习题6．关于电场线的说法，正确的选项是 [ ]A．电场线的方向，就是电荷受力的方向B．正电荷只在电场力作用下一定沿电场线运动C．电场线越密的地方，同一电荷所受电场力越大D．静电场的电场线不可能是闭合的7．如图1所示，带箭头的直线是*一电场中的一条电场线，在这条线上有A、B两点，用E A、E B表示A、B两处的场强，则 [ ]A．A、B两处的场强方向一样B．因为A、B在一条电场上，且电场线是直线，所以E A＝E BC．电场线从A指向B，所以E A＞E BD．不知A、B附近电场线的分布情况，E A、E B的大小不能确定8．真空中两个等量异种点电荷电量的值均为q，相距r，两点电荷连线中点处的场强为 [ ]A．0 B．2kq／r2C．4kq／r2 D．8kq／r29．四种电场的电场线如图2所示．一正电荷q仅在电场力作用下由M点向N点作加速运动，且加速度越来越大．则该电荷所在的电场是图中的 [ ]11．如图4，真空中三个点电荷A、B、C，可以自由移动，依次排列在同一直线上，都处于平衡状态，假设三个电荷的带电量、电性及相互距离都未知，但AB＞BC，则根据平衡条件可断定 [ ]A．A、B、C分别带什么性质的电B．A、B、C中哪几个带同种电荷，哪几个带异种电荷C．A、B、C中哪个电量最大D．A、B、C中哪个电量最小二、填空题12．图5所示为*区域的电场线，把一个带负电的点电荷q放在点A或B时，在________点受的电场力大，方向为______．16．在*轴上有两个点电荷，一个带正电荷Q1，另一个带负电荷Q2，且Q1＝2Q2，用E1、E2表示这两个点电荷所产生的场强的大小，则在*轴上，E1＝E2的点共有____处，其中_______处的合场强为零，______处的合场强为2E2。

静电场经典题及答案

静电场习题一、不定项选择题(本题共12小题，每题4分，共48分．在每小题给出的四个选项中，有的小题只有一个选项符合题目要求，有些小题有多个选项符合题目要求)1．下列说法不正确的是A．电场中某点电势与零电势点的选取有关，而电场中某两点间的电势差与零电势点选取无关B．同一点电荷在电势高的地方电势能较大，在电势低的地方电势能较小C．同一点电荷，电场力做正功，其电势能一定减小；电场力做负功，其电势能一定增加D．同一点电荷在电场中任意两点间移动时，只要电场力做功相同，则两点间的电势差一定相同2．在静电场中A．电场强度处处为零的区域内，电势也一定处处为零B．电场强度处处相等的区域内，电势也一定处处相等C．电场强度的方向总是跟等势面垂直D．沿着电场线的方向电势是不断降低的3．一个电子在匀强电场中运动，且只受电场力作用，则在一段时间内A．电子的速率一定增大B．电子的动能可能减小C．电子的速率一定减小D．电子一定做匀变速运动4．两个相同的金属小球，分别带电后相距较远距离时的库仑力为F，将两球接触后放回原处，相互作用的库仑力大小仍为F，则两个小球原来所带的电荷A．可能为等量同种电荷B．可能为不等量的同种电荷C．可能为不等量的异种电荷D．不可能为异种电荷5．两个带电量均为Q的正电荷，固定于两点，它们连线的垂直平分线MN交其连线于O点，如图所示，现在MN上取a、b两点，且aO＝Ob，将电荷q从a移至b的过程中A．电场力一定先做正功后做负功B．电场力可能先做负功后做正功C．电场力一直做正功D．电场力一直做负功6．如图所示，在A点放有电量为Q的点电荷，在B点放有电量为－2Q的点电荷，在它们的连线上有M、N两点，且AM=BN，比较M、N两点的场强和电势高低，则A．E M >E NφM>φN B．E M >E NφM<φNC．E M<E NφM>φN D．E M <E NφM<φN7．如图所示，让平行板电容器带电后，静电计的指针偏转一定角度，若不改变A、B两极板带的电量而减小两极板间的距离，同时在两极板间插入电介质，那么静电计指针的偏转角度A．一定减小B．一定增大C．一定不变D．可能不变8．一平行板电容器通过开关和电源连接，如图所示，电源的电动势保持9V不变。

静电场典型计算题

(3 )根据匀强电场中的关系式有：旷二丙，由几何关系可知 "Mzsoog静电场典型计算题 1•将带电荷量为1X10「8C 的电荷，从无限远处移到电场中的 A 点，要克服静电力做功 1X10「J ，问:(1)电荷的电势能是增加还是减少？电荷在 A 点具有多少电势能？ (2) A 点的电势是多少? (3)若静电力可以把带电荷量为 2X10「8C 的电荷从无限远处移到电场中的 A 点，说明电荷带正电还是带负电？静电力做了多少功？(取无限远处为电势零点)答案：(1)增加1X10「J (2)100V (3) 带负电 2X10 "j 解析：(1)静电力做负功，电荷的电势能增加，因无限远处电势能为零，电荷在A 点具有的电势能为1X10「J. (2) A 吕A 1X10「6A=—=〜“—8V= 100V. q 1X10点的电势为： © (3)因静电力做正功，说明电荷受力方向与运动方向相同，说明电荷带负电，静电力做功为:W = 2W ^2X10「6J. 2 •一长为L 的细线，上端固定，下端拴一质量为 m 、带电荷量为q 的小球，处于如图所示的水平向右的匀强电场中，开始时，将线与小球拉成水平，然后释放小球由静止开始向下摆动，当细线转过60。

角时，小球到达B 点速度恰好为零.试求: (1)AB 两点的电势差U AB ; (2)匀强电场的场强大小; Veo*【解析】试题分析：(1)小球由A T B 过程中，由动能定理: 所以 • (2 )根据公式 _可得 3•如右图所示，板长L = 4 cm 的平行板电容器，板间距离d = 3 cm,板与水平线夹角a= 37°, 两板所加电压为 U= 100 V 。

有一带负电液滴，带电荷量为 q= 3X10- 10 C ，以V 0= 1 m/s 的水平速度自A 板边缘水平进入电场，在电场中仍沿水平方向并恰好从 B 板边缘水平飞出(取 g = 10 m/s 2， sin a= 0.6， cosa= 0.8)。

静电场习题及答案

静电场习题及答案静电场习题及答案静电场是物理学中的一个重要概念，它描述了由电荷引起的力的作用。

在学习静电场的过程中，我们常常会遇到一些习题来巩固所学的知识。

本文将介绍一些常见的静电场习题，并给出相应的答案和解析。

习题一：两个点电荷之间的力问题描述：两个点电荷Q1和Q2之间的距离为r，它们之间的电力为F，若将Q1的电荷加倍，Q2的电荷减半，它们之间的电力变为多少？答案与解析：根据库仑定律，两个点电荷之间的电力与它们的电荷量和距离的平方成反比。

设Q1的电荷为q1，Q2的电荷为q2，则有F = k * q1 * q2 / r^2，其中k为电磁力常数。

将Q1的电荷加倍，Q2的电荷减半后，新的电力为F' =k * (2q1) * (0.5q2) / r^2 = 2F。

所以，它们之间的电力变为原来的2倍。

习题二：电场强度的计算问题描述：一均匀带电球体的半径为R，总电荷量为Q，求球心处的电场强度E。

答案与解析：由于球体带电，所以球体上每一点都有电荷。

根据对称性，球心处的电场强度与球体上的电荷分布无关，只与总电荷量和球心距离有关。

根据库仑定律，球心处的电场强度E = k * Q / R^2，其中k为电磁力常数。

所以，球心处的电场强度与球体上的电荷分布无关，只与总电荷量和球心距离有关。

习题三：电势差的计算问题描述：在一个静电场中，一个带电粒子从A点移动到B点，A点的电势为V1，B点的电势为V2，求带电粒子在移动过程中所受的电势差ΔV。

答案与解析：电势差ΔV定义为电势的变化量，即ΔV = V2 - V1。

根据电势的定义，电势是单位正电荷所具有的势能，所以电势差表示单位正电荷从A点移动到B点所具有的势能变化量。

所以，带电粒子在移动过程中所受的电势差为ΔV = V2 - V1。

习题四：电场线的性质问题描述：在一个静电场中，电场线的性质有哪些？答案与解析：电场线是描述电场的一种图形表示方法。

电场线的性质包括以下几点：1. 电场线的方向与电场强度的方向相同，即电场线从正电荷指向负电荷。

高中物理第十章静电场中的能量典型例题(带答案)

高中物理第十章静电场中的能量典型例题单选题1、如图，a、b是正点电荷电场中的一条电场线上的二点，二点的电势和电场强度分别为φa、φb和E a、E b，则他们的大小关系是（）A．φa>φb，E a>E b B．φa>φb，E a<E bC．φa=φb，E a=E b D．φa<φb，E a>E b答案：AAB．假设电场线的方向向右，则正电荷在a的左侧，所以a点的电场强度大，即E a＞E b；沿电场线方向电势降低，可以比较电势高低，根据电场线方向可知φa>φb，选项A正确，B错误；C．沿着电场线电势会逐渐降低，a、b是正点电荷电场中的一条电场线上的二点，两点的场强和电势不可能相等，选项C错误；D．若电场线的方向向左，则正电荷在b的右侧，所以b点的电场强度大，即E b＞E a；沿电场线方向电势降低，可以比较电势高低，根据电场线方向可知φa<φb，选项D错误。

故选A。

2、静电纺纱是利用高压静电场使单纤维两端带异种电荷，在电场力作用下使纤维伸直、平行排列和凝聚的纺纱工艺。

如图所示为其电场分布简图，下列说法正确的是（）A．虚线可能是等势线B．电场强度EA＜EC＜EBC．负电荷在C点的电势能大于其在A点的电势能D．在C点静止释放一电子，它将在电场力作用下沿着虚线CD运动答案：CA．电极是等势体，其表面是等势面，根据电场线与等势面垂直可知虚线应是电场线，选项A错误；B．由电场线的疏密表示电场强度的大小可知EA＜EB＜EC选项B错误；C．电场线由高压电源的正极到负极，所以A点的电势高，C点的电势低，由E p=qφ可知，负电荷在C点的电势能大于其在A点的电势能，选项C正确；D．CD电场是曲线，在C点静止释放一电子，在电场力作用下不会沿着虚线CD运动，选项D错误。

故选C。

3、一平行板电容器充电后与电源断开，负极板接地。

两板间有一个正试探电荷固定在P点，如图所示，以C 表示电容器的电容，E表示两板间的电场强度，φ表示P点的电势，E p表示正电荷在P点的电势能。

静电场常见题型及答案

1. 如图所示,绝缘光滑水平轨道AB 的B 端与处于竖直平面内的四分之一圆弧形粗糙绝缘轨道BC 平滑连接,圆弧的半径R ＝0.40m.在轨道所在空间存在水平向右的匀强电场,电场强度E ＝1.0×104N/C.现有一质量m ＝0.10kg 的带电体(可视为质点)放在水平轨道上与B 端距离s ＝1.0m 的位置,由于受到电场力的作用带电体由静止开始运动,当运动到圆弧形轨道的C 端时,速度恰好为零.已知带电体所带电荷量q ＝8.0×10－5C,取g ＝10m/s 2,求: (1)带电体在水平轨道上运动的加速度大小及运动到B 端时的速度大小； (2)带电体运动到圆弧形轨道的B 端时对圆弧轨道的压力大小； (3)带电体沿圆弧形轨道从B 端运动到C 端的过程中,摩擦力做的功.2. 如图所示,水平放置的平行金属板的N 板接地,M 板电势为+U,两板间距离为d,d 比两板的尺寸小很多,在两板之间有一长为2L 的绝缘轻杆,可绕杆的水平固定轴O 在竖直面内无摩擦地转动,O 为杆的中点.杆的两端分别连着小球A 和B,它们的质量分别为2m 和m,它们的带电量分别为+q 和-q.当杆由图示水平位置从静止开始转过900到竖直位置时,已知重力加速度为g,求:(1)两球的电势能的变化； (2)两球的总动能； (3)杆对A 球的作用力.3. 如图所示,水平放置的平行板电容器,原来两板不带电,上极板接地,它的极板长L=0.1m,两板间距离d=0.4cm,有一束相同微粒组成的带电粒子流以相同的初速度从两板中央平行于极板射入,由于重力作用微粒能落到下板上,已知微粒质量m=2.0×10-6kg,电量q=1.0×10-8C,电容器电容C=1.0×10-6F,取g=10m/s 2.试求:(1)若第一个粒子刚好落到下板中点O 处,则带电粒子入射初速度的大小；(2)两板间电场强度为多大时,带电粒子能刚好落到下板右边缘B 点； (3)落到下极板上带电粒子总的个数.O4. 如图所示，质量为m、电荷量为+q的带电小球拴在一不可伸长的绝缘细线一端，绳的另一端固定于O点，绳长为l，O点有一电荷量为+Q（Q≥q）的点电荷，现加一个水平向右的匀强电场，小球静止于与竖直方向成θ=30°角的A点。

静电场测试题

静电场测试题静电场是物理学中重要的概念之一，广泛应用于各个领域。

为了帮助读者更好地理解和掌握静电场的相关知识，下面将提供一些静电场测试题，并附有详细的解答与解析。

题目一：一个点电荷在真空中产生的电场强度与离它的距离r的关系为E=k/r²，其中k为常数。

若电荷量q为3×10⁻⁶C，则在距该电荷5m处的电场强度大小为多少？解答一：由题意可知，点电荷在距离r处的电场强度E与距离r的关系为E=k/r²。

代入已知数据q=3×10⁻⁶C和r=5m，可求得k=q×r²=3×10⁻⁶C×(5m)²=7.5×10⁻⁵C·m²。

所以，在距离该电荷5m处的电场强度大小为E=k/r²=7.5×10⁻⁵C·m²/(5m)²=1.5×10⁻⁵N/C。

题目二：在电荷为q1的点电荷A周围，产生了一个电场E1；在电荷为q2的点电荷B周围，产生了一个电场E2。

若q1=2×10⁻⁶C，q2=5×10⁻⁶C，E1=4×10⁵N/C，E2=3×10⁵N/C，求两个电场的合成电场大小E。

解答二：根据电场的合成原理，两个电场的合成电场大小E为E=√(E1²+E2²)。

代入已知数据E1=4×10⁵N/C，E2=3×10⁵N/C，可求得E=√((4×10⁵N/C)²+(3×10⁵N/C)²)=√(16×10¹⁰N²/C²+9×10¹⁰N²/C²)=√(25×10¹⁰N²/C²)=5×10⁵N/C。

题目三：一个均匀带电球壳内部的电场强度为E0，球心处的电场强度为E。

物理静电场试题及答案

物理静电场试题及答案一、选择题1. 两个点电荷之间的距离为r，它们之间的库仑力大小为F，如果将它们之间的距离增加到2r，则它们之间的库仑力大小为：A. F/2B. F/4C. F/8D. 2F答案：B2. 电场强度的方向是：A. 正电荷所受电场力的方向B. 负电荷所受电场力的方向C. 正电荷所受电场力的反方向D. 与电场线的方向垂直答案：C3. 电容器的电容与下列哪个因素无关？A. 电容器两极板的面积B. 电容器两极板之间的距离C. 电容器两极板的材料D. 电容器两极板之间的电压答案：D二、填空题4. 一个电荷量为q的点电荷在电场中受到的电场力大小为F，则该点电荷所在位置的电场强度E等于______。

答案：F/q5. 两个相同大小的点电荷，分别带有+Q和-Q的电荷，它们之间的距离为r，若将它们之间的距离增加到原来的2倍，则它们之间的库仑力大小将变为原来的______。

答案：1/4三、计算题6. 一个半径为R的均匀带电球体，其电荷量为Q，求球体外距离球心r处的电场强度。

答案：若r > R，则电场强度E = kQ/r^2；若r < R，则电场强度E = 0。

7. 一个平行板电容器，其电容为C，两极板间的电压为U，求电容器所带的电荷量Q。

答案：Q = CU四、简答题8. 简述电场线的特点。

答案：电场线从正电荷出发，指向负电荷；电场线不相交；电场线越密集，电场强度越大。

9. 电容器在充电过程中，其电场能如何变化？答案：电容器在充电过程中，电场能逐渐增加，因为电容器存储了更多的电荷，两极板之间的电势差也随之增大。

静电场计算题

1．两个正点电荷Q 1=+Q 和Q 2=+4Q 分别固定在光滑绝缘水平面上的A 、B 两点，A 、B 两点相距L ，且A 、B 两点正好位于水平光滑绝缘半圆细管两个端点的出口处，如图所示．（1）在A 、B 连线上，由A 点到B 点，电势如何变化？（2）将一正检验电荷置于A 、B 连线上靠近A 处由静止释放，求它在A 、B 连线上运动的过程中能达到最大速度的位置离A 点的距离；（3）若把另一正检验电荷放于绝缘管内靠近A 点处由静止释放，试确定它在管内运动过程中速度为最大值时的位置P ，即求出图中PA 和AB 连线的夹角θ．2．如图所示，水平向左的匀强电场中，用长为l 的绝缘轻质细线悬挂一小球，小球质量为m ，带电量为q +，将小球拉至竖直方向最低位置A 点处无初速度释放，小球将向左摆动，细线向左偏离竖直方向的最大角度074θ=，（重力加速度为g ，0sin 0.637=，cos 0.837=）（1）求电场强度的大小E ；（2）求小球向左摆动的过程中，对细线拉力的最大值；（3）若从A 点处释放小球时，给小球一个水平向左的初速度0v ，则为保证小球能做完整的圆周运动，0v 的大小应满足什么条件？3．如图所示，在竖直平面内，光滑绝缘直杆AC 与半径为R 的圆周交于B 、C 两点，在圆心处有一固定的正点电荷，B 点为AC 的中点，C 点位于圆周的最低点。

现有一质量为m 、电荷量为q -，套在杆上的带负电小球（可视为质点）从A 点由静止开始沿杆下滑。

已知重力加速度为g ，A 点距过C 点的水平面的竖直高度为3R ，小球滑到B 点时的速度大小为（1）求小球滑至C 点时的速度大小；（2）求A 、B 两点间的电势差AB U ；（3）若以C 点为参考点（零电势点），试确定A 点的电势。

4．电视机的显像管中，电子束的偏转是用电偏转和磁偏转技术实现的．如图甲所示，电子枪发射出的电子经小孔S 1进入竖直放置的平行金属板M 、N 间，两板间所加电压为U 0；经电场加速后，电子由小孔S 2沿水平放置金属板P 和Q 的中心线射入，两板间距离和长度均为；距金属板P 和Q 右边缘处有一竖直放置的荧光屏；取屏上与S 1、S 2共线的O 点为原点，向上为正方向建立x 轴。

高中物理静电场必做经典例题(带答案)

高中物理阶段性测试(一)一、选择题（每题4分，共40分） 1．下列说法正确的是（） A ．元电荷就是质子 B ．点电荷是很小的带电体 C ．摩擦起电说明电荷可以创造D ．库仑定律适用于在真空中两个点电荷之间相互作用力的计算2．在电场中某点用+q 测得场强E ，当撤去+q 而放入－q/2时，则该点的场强 ( )A ．大小为E / 2，方向和E 相同B ．大小为E ／2，方向和E 相反C ．大小为E ，方向和E 相同D ．大小为E ，方向和E 相反3．绝缘细线的上端固定，下端悬挂一只轻质小球a ，a 表面镀有铝膜，在a 的近端有一绝缘金属球b ，开始时，a 、b 均不带电，如图所示．现使b 球带电，则（） A ．a 、b 之间不发生静电相互作用 B ．b 立即把a 排斥开C ．b 将吸引a ，吸住后不放开D ．b 将吸引a ，接触后又把a 排斥开4．关于点电荷，正确的说法是（） A ．只有体积很小带电体才能看作点电荷 B ．体积很大的带电体一定不能视为点电荷C ．当两个带电体的大小与形状对它们之间的相互静电力的影响可以忽略时，这两个带电体便可看作点电荷D ．一切带电体在任何情况下均可视为点电荷5．两只相同的金属小球（可视为点电荷）所带的电量大小之比为1:7，将它们相互接触后再放回到原来的位置，则它们之间库仑力的大小可能变为原来的（）A ．4/7B ．3/7C ．9/7D ．16/76．下列对公式 E =F/q 的理解正确的是（） A ．公式中的 q 是场源电荷的电荷量B ．电场中某点的电场强度 E 与电场力F 成正比，与电荷量q 成反比C ．电场中某点的电场强度 E 与q 无关D ．电场中某点的电场强度E 的方向与电荷在该点所受的电场力F 的方向一致7．下列关于电场线的说法正确的是（） A ．电场线是电荷运动的轨迹，因此两条电场线可能相交B ．电荷在电场线上会受到电场力，在两条电场线之间的某一点不受电场力C ．电场线是为了描述电场而假想的线，不是电场中真实存在的线D ．电场线不是假想的东西，而是电场中真实存在的物质8．关于把正电荷从静电场中电势较高的点移到电势较低的点，下列判断正确的是（）A ．电荷的电势能增加B ．电荷的电势能减少C ．电场力对电荷做正功D ．电荷克服电场力做功9．一个带负电的粒子只在静电力作用下从一个固定的点电荷附近飞过，运动轨迹如图中的实线所示，箭头表示粒子运动的方向。

静电场练习及答案

静电场练习题一、选择题1、设有一“无限大”均匀带正电荷的平面．取x 轴垂直带电平面，坐标原点在带电平面上，则其周围空间各点的电场强度E随距离平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负)：［］ 2、关于高斯定理的理解有下面几种说法，其中正确的是：［］ (A) 如果高斯面上E处处为零，则该面内必无电荷．(B) 如果高斯面内无电荷，则高斯面上E处处为零．(C) 如果高斯面上E处处不为零，则高斯面内必有电荷．(D)如果高斯面内有净电荷，则通过高斯面的电场强度通量必不为零．3、一个带正电荷的质点，在电场力作用下从A 点经C 点运动到B 点，其运动轨迹如图所示．已知质点运动的速率是递增的，下面关于C点场强方向的四个图示中正确的是：［］4、如图所示，两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电，沿轴线方向单位长度上所带电荷分别为λ1和λ2，则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小E为：［］ (A) r0212ελλπ+． (B) 20210122R R ελελπ+π(C) 1012R ελπ． (D) 0． 5、边长为a 的正方形的四个顶点各有一个电量为q 的点电荷，若将点电荷Q由远处移到正方形中心处，电场力的功是[ ]aQq A02πεaQq B 02πε-aQq C0πεaQq D 0πε-6、在X 轴上，点电荷Q 位于x =a 处，负的点电荷–Q 位于x = – a 处，点P 位于轴上x 处，当x»a 时，P 点的场强 E =[ ]xQq A04πε20x QaBπε30x Qa Cπε204xQ Dπε7、孤立导体球A 的半径为R ，带电量Q ，其电场能为W A ，孤立导体球B 的半径为R /2，带电量Q /2，xEAB C其电场能为W B ，则[]A W A =WB B W A =2W BC W A =W B /2D 以上都不对8、真空中一半径为R 的球面均匀带电Q ，在球心O 处有一带电为q 的点电荷。

选修3-1 静电场经典计算题

的匀强电场，电场线与轨道所在的平面平行，电场强度E=1.0×104N/C．现有
一电荷量q=+1.0×10-4C，质量m=0.10kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体恰好能通过半圆形轨道的最高点C，然后落至水平
轨道上的D点(图中没有标出) ．取g=10m/s2求：
（1）带电体在圆形轨道C点的速度大小．（2）PB间的距离XPB （3）D点到B点的距离XDB．
方向夹角为37° （取sin37°=0.6，cos37°。=0.8）。现将该小球从电场中某
点以初速度v0。竖直向上抛出。求运动过程中：（1）小球受到的电场力的大小及方向；
（2）小球从抛出点至最高点的电势能变化量；
（3）小球的最小速度的大小及方向。
9、如图，在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC，其下端（C端）距地面高度h=0.8m，有一质量为500g的带电小环套在
小滑块，（体积很小可视为质点），从C点由静止释放，滑到水平轨道上的A 点时速度减为零。若已知滑块与水平轨道间的动摩擦因数为μ=0.2，求：
（1）滑块通过B点时的速度大小；
（2）滑块通过B点时圆轨道B点受到的压力大小：（3）水平轨道上A.B两点之间的距离。
19、一个带正电的微粒，从A点射入水平方向的匀强电场中，微粒沿直线AB运动，如图所示．AB与电场线夹角θ＝30°，已知带电粒子的质量m＝1.0×10－7
直杆上，正以某一速度沿杆匀速下滑，小环离开杆后通过C端的正下方P点，求：
（1）小环离开直杆后运动的加速度大小和方向；（2）小环从C运动到P过程中的动能增量；
（3）小环在直杆上匀速运动速度的大小；
10、竖直放置的两块足够长的平行金属板间有匀强电场，其电场强度为E，在该匀强电场中，用丝线悬挂质量为m的带电小球，丝线跟竖直方向成θ角时小球