使用MATLAB曲线拟合工具箱做曲线拟合(2013)
[matlab曲线拟合]MATLAB的曲线拟合
![[matlab曲线拟合]MATLAB的曲线拟合](https://img.taocdn.com/s3/m/ddca46a8c67da26925c52cc58bd63186bceb9275.png)
[matlab 曲线拟合]MATLAB的曲线拟合篇一: MA TLAB的曲线拟合MA TLAB软件提供了基本的曲线拟合函数的命令。
曲线拟合就是计算出两组数据之间的一种函数关系,由此可描绘其变化曲线及估计非采集数据对应的变量信息。
1.线性拟合函数:regress调用格式:b =regress[b,bint,r,rint,stats]= regress[b,bint,r,rint,stats] =regressx=[ones …];y=x*[10;1]+normrnd;[b,bint]=regress结果得回归方程为:y=9.9213+1.0143xx=1:20;y=x+3*sin;p=polyfitxi=linspace;z=polyval;% 多项式求值函数plotlegendfunction yy=modela=beta0;b=beta0;yy=a+*exp);拟合程序:x=[8.00 8.00 10.00 10.00 10.00 10.00 12.00 12.00 12.00 14.00 14.0014.00...16.00 16.00 16.00 18.00 18.00 20.00 20.00 20.00 20.00 22.00 22.0024.00...24.00 24.00 26.00 26.00 26.00 28.00 28.00 30.00 30.00 30.00 32.0032.00...34.00 36.00 36.00 38.00 38.00 40.00 42.00]‟;y=[0.49 0.49 0.48 0.47 0.48 0.47 0.46 0.46 0.45 0.43 0.45 0.43 0.430.44 0.43...0.43 0.46 0.42 0.42 0.43 0.41 0.41 0.40 0.42 0.40 0.40 0.41 0.400.41 0.41...0.40 0.40 0.40 0.38 0.41 0.40 0.40 0.41 0.38 0.40 0.40 0.390.39]‟;beta0=[0.30 0.02];betafit = nlinfit结果:betafit =0.3896 0.1011即:a=0.3896 ,b=0.1011 拟合函数为:x1 =[1150,1000,900,850,700,625,550,475,3350,3500,5900,5800,5700,4600,4625,4725,11650,11200,11200 ]‟;x2 =[175,100,25,0,75,100,150,200,50,600,500,225,100,1225,1600,2000,1200,1000,1550 ]‟;x = [x1,x2];y=[1.44E-02,1.80E-02,6.08E-02,5.59E-02,3.42E-02,7.74E-03,1.17E-03,6.16E-03,1.91E-04,1.,resplot3)% 值的选取没有定法,与实际问题的模型有关。
用matlab的曲线拟合工具箱拟合曲线模型

用matlab的曲线拟合工具箱拟合曲线模型课题需要拟合一堆成本曲线,函数形式y=A*x*x+B*x,且A>0,B>0。
一帮人用eviews,spss都没搞定,只好要我编程,没想到matlab拟合工具箱帮了大忙,即形象,又方便。
不到一天工夫所有曲线估计完毕。
使用方法也很简单将x输入如x=[110.3323 148.7328 178.064 202.8258033 224.7105 244.5711 262.908280.0447 296.204 311.5475]输入y=[ 5 10 15 20 25 30 35 40 45 50]启动曲线拟合工具箱》cftool进行曲线拟合工具箱界面点data读入x,y,退出点fit点newfit点dataset进入数据集从type of fit中选custom equations,点new equation点general equation输入函数形式修改待估计参数的上下限,也就是把-inf,inf改成具体数据hko点ok点apply就可以得到函数,如下例:general model:f(x) = a*x*x+b*xCoefficients (with 95% confidence bounds):a = 0.009194 (0.009019, 0.00937)b = 1.78e-011 (fixed at bound)Goodness of fit:SSE: 6.146R-square: 0.997Adjusted R-square: 0.997RMSE: 0.8263analysis功能我就不介绍了曲线拟合工具箱拟合仅能拟合单变量曲线模型。
Matlab中的曲线拟合方法

Matlab中的曲线拟合方法引言在科学与工程领域,数据拟合是一个重要的技术,可用于分析实验数据、预测未知的对应关系,并量化观察到的现象。
其中,曲线拟合是一种常见的数据拟合方法,而Matlab作为一种功能强大的科学计算软件,提供了多种曲线拟合工具和函数,方便用户进行数据分析和模型建立。
本文将对Matlab中的曲线拟合方法进行详细介绍和讨论。
一、线性拟合线性拟合是最简单且常见的曲线拟合方法,其基本思想是通过一条直线拟合数据点,找到最佳拟合直线的参数。
在Matlab中,可以使用polyfit函数实现线性拟合。
该函数接受两个输入参数,第一个参数为数据点的x坐标,第二个参数为数据点的y坐标。
返回结果为一个一次多项式拟合模型的参数。
例如,我们有一组实验测量数据如下:x = [1, 2, 3, 4, 5];y = [3, 5, 7, 9, 11];通过polyfit函数进行线性拟合:coeff = polyfit(x, y, 1);其中,1表示要拟合的多项式的次数,这里我们选择了一次多项式(直线)。
coeff即为拟合得到的直线的参数,可以通过polyval函数将参数代入直线方程,得到对应x的y值。
y_fit = polyval(coeff, x);接下来,我们可以使用plot函数将原始数据点和拟合曲线都绘制在同一张图上:figure;plot(x, y, 'o', 'MarkerSize', 10); % 绘制原始数据点hold on;plot(x, y_fit); % 绘制拟合曲线xlabel('x');ylabel('y');legend('原始数据点', '拟合曲线');通过观察图像,我们可以初步判断拟合的效果如何。
如果数据点较为分散,直线拟合效果可能较差。
在此情况下,可以考虑使用更高次的多项式进行拟合。
二、多项式拟合多项式拟合是一种常见的曲线拟合方法,其基本思想是通过一个一定次数的多项式函数来拟合数据点。
matlab 自定义曲线数据拟合

在MATLAB中,您可以使用曲线拟合工具箱(Curve Fitting Toolbox)进行自定义曲线数据拟合。
以下是一个详细步骤:1. 打开MATLAB软件,点击主页选项卡下的“导入数据”按钮。
2. 在弹出的对话框中,选择包含x和y数据的文件,然后点击“导入所选内容”。
这将在工作区中生成两个列向量,分别为x和y数据。
3. 创建一个名为“cftool”的函数文件,以便在后续步骤中调用曲线拟合工具。
在函数文件中,编写以下代码:```MATLAB% 导入数据x = load('x_data.txt');y = load('y_data.txt');% 进行曲线拟合f = cftool('x', 'y', 'Custom');```4. 在上述代码中,'Custom'表示自定义函数。
接下来,我们需要编写自定义函数来描述拟合的曲线。
例如,如果您的数据符合二次多项式关系,可以编写以下自定义函数:```MATLABfunction y = custom_function(x)y = x^2 + 3*x + 2;end```5. 将自定义函数加载到cftool函数中:```MATLABerDefinedFunction = @(x) custom_function(x);```6. 拟合数据并查看结果:```MATLABf.FitTask.Options.Display = 'plot';f.FitTask.Options.PlotTitle = 'Custom Fit';f.FitTask.Options.XLabel = 'X';f.FitTask.Options.YLabel = 'Y';f.FitTask.Run();```7. 如果需要,您可以将拟合后的函数表达式保存到一个新的文件中。
曲线拟合法的Matlab实现

曲线拟合法的Matlab实现曲线拟合在许多科学和工程领域中都有广泛应用,包括机器学习,数据科学,信号处理,控制工程等。
在Matlab中实现曲线拟合的方法有多种,其中最常用的是使用fit()函数。
以下是一个基本的示例,演示如何在Matlab中使用fit()函数进行曲线拟合。
我们需要一些数据。
假设我们有一组x和y数据点,我们想要在这些点上拟合一条曲线。
y = 3*x.^2 + 2*x + 1 + randn(size(x));fitresult = fit(x, y, 'poly1');在这里,'poly1'表示我们想要拟合一个一次多项式。
你可以使用'poly2','poly3'等来拟合更高次的多项式。
同样,你也可以使用其他类型的模型,如指数、对数、自定义函数等。
然后,我们可以使用plot()函数将原始数据和拟合曲线一起绘制出来。
在这里,'hold on'命令用于保持当前图像,这样我们就可以在同一个图形上绘制多条线了。
我们可以使用fitresult来获取拟合曲线的参数和其他信息。
例如:以上就是在Matlab中进行曲线拟合的基本步骤。
需要注意的是,对于复杂的实际问题,可能需要进行更复杂的模型选择和参数优化。
也可以使用其他工具如curve fitting toolbox进行更详细的分析和拟合。
最小二乘曲线拟合是一种数学统计方法,用于根据给定数据点拟合出一条曲线或曲面,使得该曲线或曲面最小化每个数据点到拟合曲线或曲面的平方误差之和。
这种方法广泛应用于数据分析和科学计算等领域。
本文将介绍最小二乘曲线拟合的基本原理和在Matlab中的实现方法。
假设有一组数据点 (x_i, y_i),i=1,2,...,n,需要拟合出一条曲线y=f(x)。
最小二乘法要求曲线 f(x)最小化每个数据点到曲线的平方误差之和,即E = sum (f(x_i)-y_i)^2对曲线 f(x)进行求导,得到一元一次方程:f'(x)=sum(f(x)-y)*x-sum(f(x)-y)E = sum [(f'(x))^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * sum [f(x)^2]令 E对 f'(x)的导数为零,可得到最小二乘曲线拟合的方程:sum [f'(x)^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * n * f(x)^2 = 0在Matlab中,可以使用polyfit函数实现最小二乘曲线拟合。
曲线拟合的matlab程序

曲线拟合的matlab程序
曲线拟合是一种通过拟合曲线来获取数据规律的方法。
在matlab中,我们可以通过一些函数来实现曲线拟合。
本文将介绍使用matlab进行曲线拟合的方法以及对应程序。
1. 多项式拟合
多项式拟合是一种简单的曲线拟合方法。
在matlab中,我们可以使用polyfit函数进行多项式拟合。
例如,我们要对以下数据进行二次拟合:
x=[-2,-1,0,1,2];
y=[4,1,0,1,4];
p=polyfit(x,y,2);
x_new=-2:0.1:2;
y_new=polyval(p,x_new);
其中,polyfit函数用于拟合多项式曲线,x为自变量,y为因变量,2为多项式的次数。
polyval函数用于计算拟合后的数据点,x_new为计算的自变量范围,0.1为自变量的步长。
2. 最小二乘法拟合
我们可以使用以下程序进行对数曲线拟合:
fun=@(c,x)log(c(1)*x);
c0=[1];
c=lsqcurvefit(fun,c0,x,y);
x_new=1:0.1:5;
y_new=c(1)*x_new;
其中,fun为回归函数,c为回归系数,c0为回归系数的初值,lsqcurvefit函数使用最小二乘法进行拟合。
x_new和y_new同上。
3. 样条拟合
其中,spline函数用于进行样条拟合,x_new为计算的自变量范围,0.1为自变量的步长。
在一些实际应用中,数据可能受到一些约束条件的限制,例如非负性、线性等限制。
在matlab中,我们可以使用lsqnonlin函数进行最小二乘法带约束的拟合。
在Matlab中进行数据拟合和曲线拟合的方法

在Matlab中进行数据拟合和曲线拟合的方法在科学研究或工程应用中,数据拟合和曲线拟合是常见的计算任务之一。
Matlab作为一种强大的数值计算软件,提供了丰富的工具和函数,方便我们进行数据拟合和曲线拟合的操作。
本文将介绍在Matlab中进行数据拟合和曲线拟合的几种方法。
一、线性回归线性回归是最简单的数据拟合方法之一,常用于建立变量之间的线性关系模型。
在Matlab中,可以使用polyfit函数进行线性回归拟合。
该函数可以根据输入数据点的横纵坐标,拟合出一条直线,并返回直线的斜率和截距。
例如,以下代码演示了如何使用polyfit函数进行线性回归拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 3, 4, 5, 6];coefficients = polyfit(x, y, 1);slope = coefficients(1);intercept = coefficients(2);```在上述代码中,数组x和y分别表示数据点的横纵坐标。
polyfit函数的第三个参数1表示拟合的直线为一阶多项式。
函数返回的coefficients是一个包含斜率和截距的数组,可以通过coefficients(1)和coefficients(2)获取。
二、多项式拟合在实际应用中,线性模型并不适用于所有情况。
有时,数据点之间的关系可能更复杂,需要使用更高阶的多项式模型来拟合。
Matlab中的polyfit函数同样支持多项式拟合。
我们可以通过调整多项式的阶数来拟合不同次数的曲线。
以下代码展示了如何使用polyfit函数进行二次多项式拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 6, 10, 16, 24];coefficients = polyfit(x, y, 2);a = coefficients(1);b = coefficients(2);c = coefficients(3);```在上述代码中,polyfit的第三个参数2表示拟合的多项式为二阶。
如何使用MATLAB进行曲线拟合

如何使用MATLAB进行曲线拟合MATLAB是一种功能强大的数学软件,它提供了许多用于数据分析和曲线拟合的工具。
曲线拟合是一项常用的数学技术,它用于找到数据集中最符合实际情况的曲线。
在本文中,我们将探讨如何使用MATLAB进行曲线拟合,以及一些常见的曲线拟合方法。
在开始之前,让我们先了解一下曲线拟合的概念。
曲线拟合是通过将已知数据点拟合到合适的曲线上来预测未知数据点的技术。
它可以用于数据分析、模型建立、趋势预测等许多领域。
MATLAB提供了多种曲线拟合的方法,其中最常见的是最小二乘拟合。
最小二乘拟合是一种通过最小化观测数据的平方误差来确定参数的方法。
在MATLAB 中,可以使用"polyfit"函数进行最小二乘拟合。
该函数可以拟合多项式曲线和线性曲线。
例如,我们有一组数据点x和对应的y,我们想要拟合一个一次多项式曲线y= ax + b。
我们可以使用"polyfit"函数来找到最佳拟合,并返回系数a和b。
```matlabx = [1, 2, 3, 4, 5];y = [2, 3, 4, 5, 6];p = polyfit(x, y, 1);a = p(1);b = p(2);```在上面的代码中,"polyfit"函数的第一个参数是x值,第二个参数是y值,第三个参数是拟合多项式的阶数。
在这个例子中,我们使用一次多项式即阶数为1。
除了最小二乘拟合,MATLAB还提供了其他一些常用的曲线拟合方法,例如多项式拟合、指数拟合和对数拟合。
这些方法可以通过更改"polyfit"函数的第三个参数来使用。
另一个常用的曲线拟合方法是通过曲线拟合工具箱中的"fit"函数进行非线性拟合。
非线性拟合是指目标函数和参数之间是非线性关系的拟合。
与最小二乘拟合不同,非线性拟合能够拟合更复杂的曲线和模型。
例如,我们有一组数据点x和对应的y,我们想要拟合一个指数曲线y = ae^bx。
Excel、MATLAB拟合曲线方法

2017/3/31
软件版本Excel2013 MATLAB2014a
简单的用Excel拟合曲线,并显示公式
Ctrl+A选中数据——插入——散点图——选择平滑曲线
显示公式:
选中曲线——右键——添加趋势线——趋势线类型选择(拟合类型)-可以选择不同类型看哪个拟合效果最好——显示公式
2.MATLAB曲线拟合
将Excel中的数据导入MATLAB中拟合
导入数据——选择Excel文件——导入所选内容
应用程序——曲线拟合工具箱
选择X Y数据
Exponential:指数逼近,有2种类型,a*exp(b*x) 、a*exp(b*x) + c*exp(d*x)
Fourier:傅立叶逼近,有7种类型,基础型是a0 + a1*cos(x*w) + b1*sin(x*w) Gaussian:高斯逼近,有8种类型,基础型是a1*exp(-((x-b1)/c1)^2)
Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~ Power:幂逼近,有2种类型,a*x^b、a*x^b + c
Rational:有理数逼近。
matlab曲线拟合
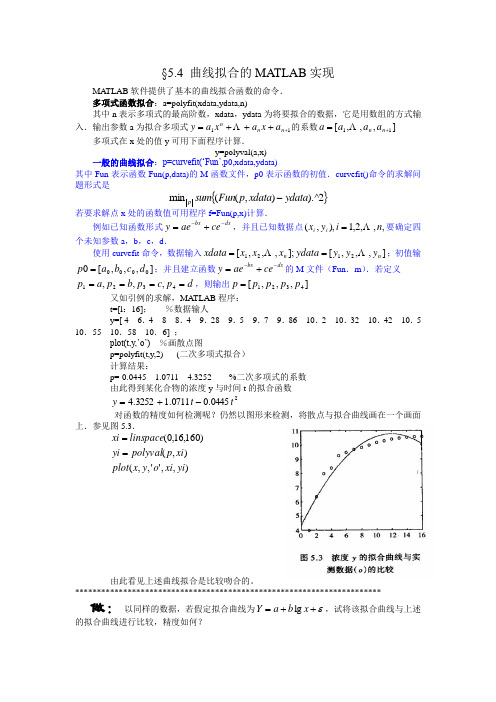
§5.4 曲线拟合的MATLAB 实现MATLAB 软件提供了基本的曲线拟合函数的命令.多项式函数拟合:a=polyfit(xdata,ydata,n)其中n 表示多项式的最高阶数,xdata ,ydata 为将要拟合的数据,它是用数组的方式输入.输出参数a 为拟合多项式11++++=n n n a x a x a y 的系数],,,[11+=n n a a a a 多项式在x 处的值y 可用下面程序计算.y=polyval(a,x)一般的曲线拟合:p=curvefit(‘Fun’,p 0,xdata,ydata)其中Fun 表示函数Fun(p,data)的M 函数文件,p0表示函数的初值.curvefit()命令的求解问题形式是{}2).^),((min ydata xdata p Fun sum p -若要求解点x 处的函数值可用程序f=Fun(p,x)计算.例如已知函数形式dx bx ce ae y --+=,并且已知数据点,,,2,1),,(n i y x i i =要确定四个未知参数a ,b ,c ,d .使用curvefit 命令,数据输入],,,[];,,,[2121n n y y y ydata x x x xdata ==;初值输],,,[00000d c b a p =;并且建立函数dx bx ce ae y --+=的M 文件(Fun .m ).若定义d p c p b p a p ====4321,,,,则输出],,,[4321p p p p p =又如引例的求解,MATLAB 程序:t=[l :16]; %数据输人y=[ 4 6.4 8 8.4 9.28 9.5 9.7 9.86 10.2 10.32 10.42 10.5 10.55 10.58 10.6] ;plot(t,y,’o’) %画散点图p=polyfit(t,y,2) (二次多项式拟合)计算结果:p=-0.0445 1.0711 4.3252 %二次多项式的系数由此得到某化合物的浓度y 与时间t 的拟合函数20445.00711.13252.4t t y -+=对函数的精度如何检测呢?仍然以图形来检测,将散点与拟合曲线画在一个画面上.参见图5.3.),,'',,(),()160,16,0(yi xi o y x plot xi p polyval yi linspace xi ==由此看见上述曲线拟合是比较吻合的。
使用MATLAB曲线拟合工具箱做曲线拟合

使用MATLAB曲线拟合工具箱做曲线拟合
胡庆婉
【期刊名称】《电脑知识与技术》
【年(卷),期】2010(006)021
【摘要】介绍了使用MATLAB曲线拟合工具箱(Curve Fitting Toolbox)对数据进行曲线拟合,给出数学建模中的实例用以介绍其具体使用方法,并且给出利用MATLAB曲线拟合工具箱改善拟合结果的方法.结果显示,用MATLAB曲线拟合工具箱能够很好的对数据进行曲线拟合的处理.
【总页数】2页(P5822-5823)
【作者】胡庆婉
【作者单位】曲靖师范学院数学与信息科学学院,云南,曲靖,655011
【正文语种】中文
【中图分类】O1-8
【相关文献】
1.基于Matlab曲线拟合工具箱的列表曲线拟合 [J], 史立新;聂信天;季明
2.Matlab曲线拟合工具箱在地基沉降预测模型中的应用 [J], 高艳平;王杰
3.基于MATLAB曲线拟合工具箱确定含水层参数 [J], 王杰;马秋娟;高艳平;李向辉
4.Matlab的CFtool工具箱在浮选尾矿灰分与图像灰度曲线拟合中的应用 [J], 高鹏
5.MATLAB曲线拟合工具箱在发电厂的运用 [J], 高文晔
因版权原因,仅展示原文概要,查看原文内容请购买。
matlab如何实现曲线拟合?matlab做曲线拟合的教程

matlab如何实现曲线拟合?matlab做曲线拟合的教程Matlab是⼀个很强⼤的数据处理软件,是⼈们进⾏数据分析的得⼒助⼿。
⼀般我们做社会调研或科学研究时,会得到很多实验
数据。
当需要研究两个变量之间的关系时,经常要⽤到曲线拟合。
曲线拟合不仅能给出拟合后的关系式,还能⽤图形直观的展现出变量之间的关系。
其实⽤matlab做曲线拟合很便捷,下⾯将以两个变量(y=f(x))为例详细介绍:
1、运⾏Matlab软件。
在⼯作空间中存⼊变量的实验数据。
具体如下:可以直接⽤矩阵来存放数据,直接在命令窗⼝输⼊
x=[数据x1,数据x2,...,数据xn];
y=[数据y1,数据y2,...,数据yn];
当数据较多时,可以从excel,txt等⽂件中导⼊。
2、把数据存⼊⼯作空间后,在命令窗⼝中输⼊cftool,回车运⾏。
3、在这个拟合⼯具窗⼝的左边,选择变量,即分别选择x,y。
4、选择拟合的曲线类型,⼀般是线性拟合,⾼斯曲线,平滑曲线等,根据需要选择。
选择完后会⾃动完成拟合,并且给出拟合函数表达式。
5、点击菜单栏中的“file”,选择“print to figure"进⾏画图。
6、在图形窗⼝中,可以对图形显⽰模式进⾏修改,如添加标题,坐标名称等。
7、最后得到⽐较完整的图形曲线。
点击”file"中的“save"进⾏保存。
注意事项:x和y的数据个数应该⼀致。
matlab指数函数曲线拟合

matlab指数函数曲线拟合在MATLAB中,可以使用曲线拟合工具箱(Curve Fitting Toolbox)来进行指数函数曲线的拟合。
以下是一个简单的示例,演示如何使用MATLAB进行指数函数曲线的拟合。
假设我们有一组数据点(x,y),其中y是关于x的指数函数,即y=aexp(bx)。
首先,需要安装和配置MATLAB的Curve Fitting Toolbox。
然后,可以按照以下步骤进行指数函数曲线的拟合:1、导入数据假设数据存储在一个名为data.txt的文本文件中,每行包含一对x和y值。
在MATLAB中,可以使用以下命令将数据导入到工作区:data = importdata('data.txt');x = data(:,1);y = data(:,2);2、定义拟合函数在MATLAB中,可以使用fit函数来拟合数据。
首先,需要定义一个拟合函数,该函数将接受一个x值并返回一个y值。
在本例中,我们将使用一个指数函数作为拟合函数:expfun = @(b,x)(b(1)*exp(b(2)*x));3、拟合数据使用fit函数来拟合数据。
在本例中,我们需要指定拟合函数、x值和y值,以及初始参数估计值。
这里假设初始参数估计值为[1, 0.5]。
b0 = [1, 0.5];expfit = fit(x', y', expfun, b0);4、显示拟合结果使用plot函数来显示原始数据点和拟合曲线。
plot(x, y, 'o', x', expfit(x'), '-');legend('Data', 'Exponential fit');以上是一个简单的示例,演示如何使用MATLAB进行指数函数曲线的拟合。
在实际应用中,可能需要根据具体的数据和问题来调整参数估计值和拟合函数。
用MATLAB作曲线拟合
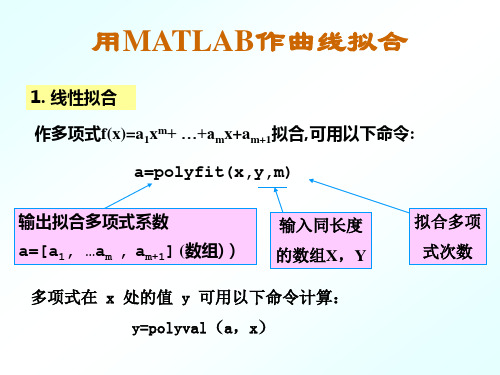
2. lsqnonlin 已知数据点: 已知数据点: xdata=(xdata1,xdata2,…,xdatan) ydata=(ydata1,ydata2,…,ydatan) lsqnonlin用以求含参量x(向量)的向量值函数 用以求含参量x 向量) 用以求含参量 f(x)=(f (x),…,f f(x)=(f1(x),f2(x), ,fn(x))T
T 2 2
中的参量x 中的参量x,使得
2
f ( x) f ( x) = f1 ( x) + f 2 ( x) + ⋯ + f n ( x)
最小。 最小。 其中 fi(x)=f(x,xdatai,ydatai) ) ( , =F(x,xdatai)-ydatai
输入格式为: 输入格式为: 1) x=lsqnonlin(‘fun’,x0); 2) x= lsqnonlin (‘fun’,x0,options); 3) x= lsqnonlin (‘fun’,x0,options,‘grad’); 4) [x,options]= lsqnonlin (‘fun’,x0,…); 5) [x,options,funval]= lsqnonlin (‘fun’, 说明:x= , , ); x0,…); lsqnonlin (‘fun’,x0,options); fun是一个事先建立的 是一个事先建立的 定义函数f(x)的M-文件, 文件, 定义函数 的 文件 自变量为x 自变量为 选项见无 迭代初值 约束优化
n 2 i i
∑ ( F ( x, xdata ) − ydata )
i =1
最小
输入格式为: 输入格式为: (1) x = lsqcurvefit (‘fun’,x0,xdata,ydata); (2) x =lsqcurvefit (‘fun’,x0,xdata,ydata,options); (3) x = lsqcurvefit (‘fun’,x0,xdata,ydata,options,’grad’); (4) [x, options] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); (5) [x, options,funval] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); (6) [x, options,funval, Jacob] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); 说明:x = lsqcurvefit (‘fun’,x0,xdata,ydata,options); fun是一个事先建立的 是一个事先建立的 定义函数F(x,xdata) 的 定义函数 M-文件 自变量为 和 文件 文件 自变量为x和 xdata 选项见无 迭代初值 已知数据点 约束优化
matlab拟合曲线并输出公式

matlab拟合曲线并输出公式在MATLAB中,可以使用curve fitting toolbox来拟合一个曲线并输出公式。
以下是使用多项式拟合的示例代码:```matlab% 输入数据x = [1, 2, 3, 4, 5];y = [2, 4, 5, 4, 2];% 多项式拟合degree = 3; % 多项式的阶数p = polyfit(x, y, degree); % 多项式系数% 输出拟合公式formula = 'y = ';for i = 1:degree+1if p(i) > 0formula = strcat(formula, ' + ');elseformula = strcat(formula, ' - ');endcoefficient = abs(p(i));formula = strcat(formula, num2str(coefficient));formula = strcat(formula, ' * x^');formula = strcat(formula, num2str(degree+1-i));end% 输出结果disp(formula);```以上代码假设要拟合的曲线为多项式,拟合阶数为3。
根据输入的x和y数据,使用`polyfit`函数进行多项式拟合,得到多项式系数。
然后根据系数构建拟合公式。
在这个示例中,将输出类似于`y =0.028571 * x^3 - 0.81429 * x^2 + 6.5714 * x^1 - 1.3143`的拟合公式。
请注意,对于其他类型的曲线,例如指数函数、对数函数等,可以使用不同的拟合方法和公式构建方式。
以上代码只适用于多项式拟合。
matlab2曲线拟合

第12页,共85页。
• 当选择Data sets列表框中的数据集时,单 • 击View按钮,打开View Data Set对话框
工作表方式
13
第13页,共85页。
2.数据的预处理
• 在曲线拟合工具箱中,数据的预处理主要包 • 括平滑法、排除法和区间排除法等。
• (1)平滑数据
• 打开拟合工具箱,单击Data按钮,打开 • Data对话框,选择Smooth选项卡
• .Data sets 选项以列表的形式显示所有拟合的
数据集。当选择一个数据集时,可以对它做 如下操作:
• .View 查看数据集,以图标形式和列表形式, 可以选择方法排除异常值;
• .Rename 重命名
• .Delete 删去数据组第8页,共85页。
8
例:输入数据,采用matlab自带的文件census
>> x=[1 3 4 5 6 7 8 9 10]; >> y=[10 5 4 2 1 1 2 3 4]; >> [p,s]=polyfit(x,y,4); >> y1=polyval(p,x); >> plot(x,y,'go',x,y1,'b--')
第35页,共85页。
10
9
8
7
6
5
4
3
2
1
1
• u1=mean(x),u2=std(x),通过这 • 样处理数据,使数据合理化。
30
第30页,共85页。
• [y,delta]=polyval(p,x,s) • [y,delta]=polyval(p,x,s,mu) • 产生置信区间y±delta。如果误差结果服从 • 标准正态分布,则实测数据落在y±delta区 • 间内的概率至少为50%。
使用Matlab进行曲线拟合

使用Matlab进行曲线拟合引言在科学研究和工程应用中,曲线拟合是一个非常常见和重要的问题。
通过拟合实验数据或者观测数据,我们可以找到一条曲线,以最佳地描述数据的趋势。
Matlab是一个功能强大的数值计算软件,提供了丰富的工具和函数,可以帮助我们对数据进行曲线拟合。
本文将介绍如何使用Matlab进行曲线拟合,并给出一些实际案例。
一、简单线性回归简单线性回归是曲线拟合中最基础的一种方法。
它假设数据可以用一条直线来表示。
在Matlab中,使用"polyfit"函数可以很方便地进行简单线性回归。
该函数可以从数据中拟合出一个多项式,我们可以选择线性多项式来进行简单线性回归。
下面是一个例子:```matlabx = [1, 2, 3, 4, 5];y = [2, 3, 4, 5, 6];p = polyfit(x, y, 1);f = polyval(p, x);plot(x, y, 'o'); % 绘制原始数据点hold on;plot(x, f, 'r-'); % 绘制拟合曲线```在这个例子中,我们有一个包含5个数据点的数据集,分别存储在向量"x"和"y"中。
通过polyfit函数,我们可以拟合出一个线性多项式的系数"p",然后使用polyval函数来计算拟合曲线上各个x点对应的y值。
最后,使用plot函数将原始数据点和拟合曲线绘制在同一张图上。
这样我们就可以直观地看到拟合效果。
二、非线性曲线拟合除了简单线性回归,Matlab还提供了许多其他方法来进行非线性曲线拟合。
这些方法通常需要指定一个函数形式,然后通过调整函数的参数来拟合数据。
其中最常用的方法之一是最小二乘法。
在Matlab中,可以使用lsqcurvefit函数来进行非线性曲线拟合。
下面是一个例子:```matlabx = [1, 2, 3, 4, 5];y = [5.1, 6.2, 7.1, 8.5, 9.9];f = @(c,x) c(1) * exp(-c(2)*x) + c(3); % 定义拟合函数c0 = [1, 1, 1]; % 初始参数猜测c = lsqcurvefit(f, c0, x, y); % 进行曲线拟合plot(x, y, 'o'); % 绘制原始数据点hold on;plot(x, f(c, x), 'r-'); % 绘制拟合曲线```在这个例子中,我们有一个包含5个数据点的数据集,存储在向量"x"和"y"中。
利用MATLAB进行曲线拟合
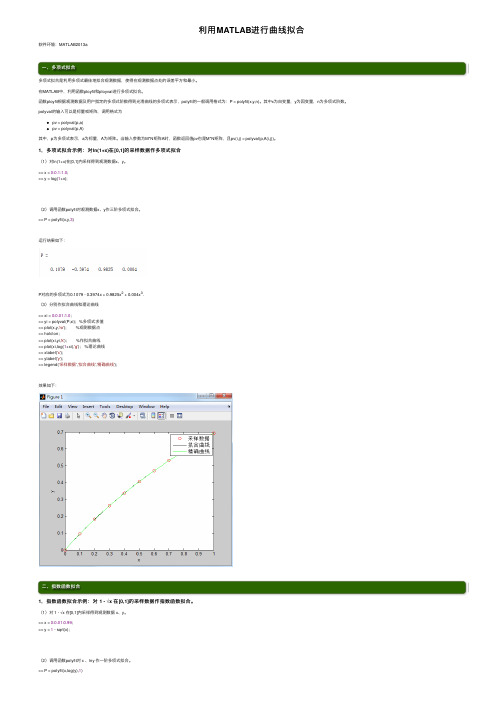
利⽤MATLAB进⾏曲线拟合软件环境:MATLAB2013a⼀、多项式拟合多项式拟合是利⽤多项式最佳地拟合观测数据,使得在观测数据点处的误差平⽅和最⼩。
在MATLAB中,利⽤函数ployfit和ployval进⾏多项式拟合。
函数ployfit根据观测数据及⽤户指定的多项式阶数得到光滑曲线的多项式表⽰,polyfit的⼀般调⽤格式为:P = polyfit(x,y,n)。
其中x为⾃变量,y为因变量,n为多项式阶数。
polyval的输⼊可以是标量或矩阵,调⽤格式为pv = polyval(p,a)pv = polyval(p,A)其中,p为多项式表⽰,a为标量,A为矩阵。
当输⼊参数为M*N矩阵A时,函数返回值pv也是M*N矩阵,且pv(i,j) = polyval(p,A(i,j))。
1,多项式拟合⽰例:对ln(1+x)在[0,1]的采样数据作多项式拟合(1)对ln(1+x)在[0,1]内采样得到观测数据x、y。
>> x = 0:0.1:1.0;>> y = log(1+x);(2)调⽤函数polyfit对观测数据x、y作三阶多项式拟合。
>> P = polyfit(x,y,3)运⾏结果如下:P对应的多项式为0.1079 - 0.3974x + 0.9825x2 + 0.004x3.(3)分别作拟合曲线和理论曲线>> xi = 0:0.01:1.0;>> yi = polyval(P,xi); %多项式求值>> plot(x,y,'ro'); %观测数据点>> hold on;>> plot(xi,yi,'k'); %作拟合曲线>> plot(xi,log(1+xi),'g'); %理论曲线>> xlabel('x');>> ylabel('y');>> legend('采样数据','拟合曲线','精确曲线');效果如下:⼆、指数函数拟合1,指数函数拟合⽰例:对 1 - √x 在[0,1]的采样数据作指数函数拟合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使用 MATLAB 曲线拟合工具箱做曲线拟合
在实际的工程应用领域和经济应用领域中,人们往往通过实验或者观测得到一些数据, 为了从这些数据中找到其内在的规律性, 也就是求得自变量和因变量之间的近似函数关系表 达式。
这类问题可以归结曲线拟合。
1.MATLAB 曲线拟合工具箱简介
MATLAB 做曲线拟合可以通过内建函数或者拟合工具箱(Curve Fitting Toolbox )。
这个 工具箱集成了用MATLAB 建立的图形用户界面(GUIs )和 M 文件函数。
利用这个工具箱 可以进行参数拟合(当想找出回归系数以及他们背后的物理意义的时候就可以采用参数拟 合),或者通过采用平滑样条或者其他各种插值方法进行参数拟合(当回归系数不具有物理 意义并且不在意他们的时候,就采用非参数拟合)。
利用这个界面,可以快速地在简单易用 的环境中实现许多基本的曲线拟合。
2.实际例子应用
数学模型书上关于汽车刹车距离模型,建立的模型如下:
2 1 d t v kv
=+ 其中v 是汽车速度, 1 t 是反应时间,按大多数人平均取 0.75 秒,d 是刹车距离。
交通部 门提供了一组刹车的距离实际数据如表1 所示(刹车距离括号内为最大值)。
表 1
车速(英尺 秒)
29.3 44 58.7 73.3 88 102.7 1173 刹车距离 (英尺) 42(44) 73.5(78) 116(124) 173(186) 248(268) 343(372) 464(506) 利用表 1 的数据,我们拟合
在 MATLAB 的 command window 里输入:
>>v=[29.3 44 58.7 73.3 88 102.7 117.3];
>>d1=[42 73.5 116 173 248 343 464];
>>cftool %cftool 是打开拟合工具箱的命令;
则跳出曲线拟合工具箱的界面如图 1 所示, 如果输入数据非常大, 并且每次输入有困难, 可以新建一个 M 文件,依次输入上述命令行,保存之后执行,同样可以进入曲线拟合工具 箱界面。
图1 拟合工具箱界面 图2 画散点图 点击“Data”按钮,则现如图 2 所示的 Data 窗口,我们选择 X data 为 v,Y Data为 d1, 则右侧会出现散点图。
我们还可以进行数据的加权拟合,权值可以是与数据相联系的一个权 向量。
在“Weight”的下拉菜单中可以选择。
点击“Create data set”,点击“Close”按钮 退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的散点图。
然后点击图 1 中“Fitting”按钮,出现“Fitting”窗口,点击“new fit”窗口如图 3 所
示。
然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:
Custom Equations (自定义函数)
Exponential (指数函数)
Fourier (傅里叶函数)
Gaussian (正态分布函数)
Interplant (内部插值)
Polynomial (多项式函数)
Power (幂函数)
等 11 种类型, 本例虽然是二次多项式, 但不是标准的二次多项式形式, 故我们选 Custom Equations ,点击“New equation”按钮,选择“General Equations”标签,出现如图 4 所示 窗口,输入自定义函数,设置初值以及参数的上下限,然后点击 OK。
类型设置完成后,点 击“Apply”按钮,就可以在“Fitting”窗口的 Results 框中得到拟合信息如表 2,同时,也 会在工具箱窗口中显示拟合曲线如图 5所示。
图4 设定拟合方程窗口 图5 拟合曲线
表 2
General model:
f(x) = 0.75*x+k*x^2
Coefficients (with 95% confidence bounds):
k = 0.02555 (0.02358, 0.02752) (注:给出参数 k 置信度为 95%的置信区间)
Goodness of fit:
SSE: 1576 (注:SSE 为误差平方和,越小越好)
Rsquare: 0.9888 (注:Rsquare为复相关系数,越接近 1越好)
Adjusted Rsquare: 0.9888 (注:Adjusted Rsquare为调整自由度复相关系数) RMSE: 16.2 (注:RMSE 为均方根误差)
3 利用 Curve Fitting Toolbox 改善拟合效果
很多因素会对曲线拟合产生影响,导致拟合效果有好有坏,我们仅从一些角度出发探讨 有可能改善拟合质量。
1)模型的选择: 这是最主要的一个因素, 试着用各种不同的模型对数据进行拟合比较;
2) 数据预处理: 在拟合钱对数据进行预处理也很有用, 这包括对相应数据进行变换以 及剔除 Infs ,NaNs ,以及有明显错误的点。
3) 合理的拟合应该具有处理出现奇异而使得预测趋于无穷大的时候的能力。
4) 知道越多的系数的估计信息,拟合越容易收敛。
5) 将数据分解为几个子集,对不同的子集采用不同的曲线拟合。
6) 复杂的问题最好通过进化的方式解决,即一个问题的少量独立变量先解决。
低阶问 题的解通常通过近似映射作为高阶问题解的起始点。
例如模型为 e sin()
cx y a b d kx =++ 那么最好每次拟合一个项,通常从最重要的项开始。
先拟合,然后利用拟合出的结果系 数作为上式中的a ,b ,c 的起始值进行完整的拟合。
4 结束语
MATLAB 曲线拟合工具箱使用方便、直观、快捷。
利用这个界面,可以快速地在简单 易用的环境中实现许多基本的曲线拟合。
