数学符号读法大全
常用数学符号读法大全

常用数学符号读法大全大写小写英文注音国际音标注音中文注音Αα alpha alfa阿耳法Ββ beta beta贝塔Γγ gamma gamma伽马Δδ deta delta德耳塔Εε epsilon epsilon艾普西隆Ζζ zeta zeta截塔Ηη eta eta艾塔Θθ theta θita西塔Ιι iotaiota 约塔Κκ kappa kappa卡帕∧λ lambda lambda兰姆达Μμ mumiu 缪Νν nuniu 纽Ξξ xiksi 可塞Οο omicron omikron奥密可戎∏π pipai 派Ρρ rho r ou 柔∑σ sigma sigma西格马Ττ tautau 套Υυ upsilon jupsilon 衣普西隆Φφ phifai 斐Χχ chi k hai 喜Ψψ psi psa i 普西Ωω omega omiga欧米伽1 Α α alpha a:lf 阿尔法角度;系数2 Β β beta bet 贝塔磁通系数;角度;系数3 Γ γ gamma ga:m 伽马电导系数(小写)4 Δ δ delta delt 德尔塔变动;密度;屈光度5 Ε ε epsilon ep`silon 伊普西龙对数之基数6 Ζ ζ zeta zat 截塔系数;方位角;阻抗;相对粘度;原子序数7 Η η eta eit 艾塔磁滞系数;效率(小写)8 Θ θ thet θit 西塔温度;相位角9 Ι ι iot aiot 约塔微小,一点儿10 Κ κ kappa kap 卡帕介质常数11 ∧ λ lambda lambd 兰布达波长(小写);体积12 Μ μ mu mju 缪磁导系数;微(千分之一);放大因数(小写)13 Ν ν nu nju 纽磁阻系数14 Ξ ξ xi ksi 克西15 Ο ο omicron omik`ron 奥密克戎16 ∏ π pi pai 派圆周率=圆周÷直径=3.141617 Ρ ρ rho rou 肉电阻系数(小写)18 ∑ σ sigma `sigma 西格马总和(大写),表面密度;跨导(小写)19 Τ τ tau tau 套时间常数20 Υ υ upsilon jup`silon 宇普西龙位移21 Φ φ phi fai 佛爱磁通;角22 Χ χ chi phai 西23 Ψ ψ psi psai 普西角速;介质电通量(静电力线);角24 Ω ω omega o`miga 欧米伽欧姆(大写);角速(小写);角小写大写读法α Α 阿尔法β Β 贝塔γ Γ ga马δ Δ 德尔塔ε Ε 伊普西龙ζ Ζ 截塔η Η 依塔θ Θ 西塔ι Ι 约塔κ Κ 卡帕λ ∧兰嘛达μ Μ 缪ν Ν 纽ξ Ξ 克赛ο Ο 奥密克戎π∏ 派ρ Ρ 肉σ ∑ 西格马τ Τ 套υ Υ 宇普西龙φ Φ Fai(四声)χ Χ 西ψ Ψ 普赛ω Ω 欧米伽。
各种数学符号及读法大全

各种数学符号及读法大全数学是一门充满符号的科学,这些符号就像一种特殊的语言,帮助我们更简洁、准确地表达数学概念和进行运算。
下面就为大家介绍一些常见的数学符号及其读法。
一、基本运算符号1、加号(+):读作“加”,例如“2 +3”读作“二加三”。
2、减号(-):读作“减”,比如“5 2”读作“五减二”。
3、乘号(×):读作“乘”,像“4 × 5”读作“四乘五”。
在数学中,有时也会用“·”表示乘号,例如“3·2”,同样读作“三乘二”。
4、除号(÷):读作“除以”,例如“6 ÷ 3”读作“六除以三”。
二、比较符号1、等于号(=):读作“等于”,比如“2 + 3 =5”读作“二加三等于五”。
2、大于号(>):读作“大于”,例如“5 >3”读作“五大于三”。
3、小于号(<):读作“小于”,像“2 <4”读作“二小于四”。
4、大于等于号(≥):读作“大于等于”,比如“x ≥ 5”读作“x 大于等于五”。
5、小于等于号(≤):读作“小于等于”,例如“y ≤ 8”读作“y 小于等于八”。
三、括号1、小括号():通常读作“括号”,例如“(2 + 3)× 4”读作“括号二加三括号乘四”。
2、中括号:读作“中括号”,像“ 5 (3 1)÷ 2”读作“中括号五减去括号三减一括号除以二”。
3、大括号{}:读作“大括号”,比如“{ 2, 4, 6, 8 }”读作“大括号二,四,六,八”。
四、分数符号1、分数线(—):例如“3/5”,读作“五分之三”。
分子在前,分母在后。
2、带分数:由整数部分和分数部分组成,例如“2 又1/3”,读作“二又三分之一”。
五、指数符号1、平方(²):例如“5²”,读作“五的平方”。
2、立方(³):像“2³”,读作“二的立方”。
3、多次方:比如“4 的 5 次方”写作“4^5”,读作“四的五次方”。
数学符号及读法大全

数学符号及读法大全一、基本符号及读法1. 加号(+):读作“加”或“正”。
例如,2 + 3 读作“二加三”或“二正三”。
2. 减号():读作“减”或“负”。
例如,5 2 读作“五减二”或“五负二”。
3. 乘号(×):读作“乘”。
例如,4 × 6 读作“四乘六”。
4. 除号(÷):读作“除以”。
例如,8 ÷ 2 读作“八除以二”。
5. 等号(=):读作“等于”。
例如,3 + 4 = 7 读作“三加四等于七”。
6. 不等号(≠):读作“不等于”。
例如,5 ≠ 6 读作“五不等于六”。
7. 大于号(>):读作“大于”。
例如,7 > 5 读作“七大于五”。
8. 小于号(<):读作“小于”。
例如,3 < 8 读作“三小于八”。
9. 大于等于号(≥):读作“大于等于”。
例如,x ≥ 5 读作“x大于等于五”。
10. 小于等于号(≤):读作“小于等于”。
例如,y ≤ 10 读作“y小于等于十”。
二、指数与对数符号及读法1. 指数符号(^):读作“的幂”。
例如,2^3 读作“二的三次幂”。
2. 对数符号(log):读作“以为底的对数”。
例如,log₂8 读作“以二为底八的对数”。
三、集合符号及读法1. 属于符号(∈):读作“属于”。
例如,3 ∈ {1, 2, 3} 读作“三属于集合{一、二、三}”。
2. 不属于符号(∉):读作“不属于”。
例如,4 ∉ {1, 2, 3} 读作“四不属于集合{一、二、三}”。
3. 空集符号(∅):读作“空集”。
例如,∅表示一个不包含任何元素的集合。
四、几何符号及读法1. 直线符号(→):读作“直线”。
例如,AB → 表示直线AB。
2. 射线符号(⇀):读作“射线”。
例如,AC ⇀表示射线AC。
3. 线段符号(|):读作“线段”。
例如,BC | 表示线段BC。
4. 角符号(∠):读作“角”。
例如,∠ABC 表示角ABC。
数学符号的读法

数学符号的读法α( 阿而法)β( 贝塔)γ(伽马)δ(德尔塔)ε(艾普西龙)ζ(截塔)η(艾塔)θ(西塔)ι约塔)κ(卡帕)λ(兰姆达)μ(米尤)ν(纽)ξ(可系)ο(奥密克戎)π (派)ρ (若)σ (西格马)τ (套)υ (英文或拉丁字母)φ(斐)χ(喜)ψ(普西))ω(欧米伽)α Α alpha 【'ælfə】β Β beta 【'bi:tə, 'beitə】γ Γ gamma 【'gæmə】δ Δ delta 【'deltə】ε Ε epsil on 【ep'sailən, 'epsilən】ζ Ζ zeta 【'zi:tə】η Η eta 【'i:tə】θ Θ theta 【'θi:tə】ι Ι iota 【ai'əutə】κ Κ kappa 【'kæpə】λ ∧lambda 【'læmdə】μ Μ mu 【mju:】ν Ν nu 【nju:】ξ Ξ xi 【ksai, ksi:】ο Ο omicron 【əu'maikrən】π ∏ pi 【pai】ρ Ρ rho 【rəu】σ ∑ sigma 【'sigmə】τ Τ tau 【tau】υ Υ upsilon 【ju:p'sailən】φ Φ phi 【fai】χ Χ chi 【kai, ki:】ψ Ψ psi 【psai】ω Ω omega 【'əumigə】更全面:1 Α α alpha a:lf 阿尔法角度;系数2 Β β beta bet 贝塔磁通系数;角度;系数3 Γ γ gamma ga:m 伽马电导系数(小写)4 Δ δ delta delt 德尔塔变动;密度;屈光度5 Ε ε epsilon ep`silon 伊普西龙对数之基数6 Ζ ζ zeta zat 截塔系数;方位角;阻抗;相对粘度;原子序数7 Η η eta eit 艾塔磁滞系数;效率(小写)8 Θ θ thet θit 西塔温度;相位角9 Ι ι iot aiot 约塔微小,一点儿10 Κ κ kappa kap 卡帕介质常数11 ∧λ lambda lambd 兰布达波长(小写);体积12 Μ μ mu mju 缪磁导系数;微(千分之一);放大因数(小写)13 Ν ν nu nju 纽磁阻系数14 Ξ ξ xi ksi 克西15 Ο ο omicron omik`ron 奥密克戎16 ∏ π pi pai 派圆周率=圆周÷直径=3.141617 Ρ ρ rho rou 肉电阻系数(小写)18 ∑ σ sigma `sigma 西格马总和(大写),表面密度;跨导(小写)19 Τ τ tau tau 套时间常数20 Υ υ upsilon jup`silon 宇普西龙位移21 Φ φ phi fai 佛爱磁通;角22 Χ χ chi phai 西23 Ψ ψ psi psai 普西角速;介质电通量(静电力线);角24 Ω ω omega o`miga 欧米伽欧姆(大写);角速(小写);角希腊字母读法Αα:阿尔法AlphaΒβ:贝塔BetaΓγ:伽玛GammaΔδ:德尔塔DelteΕε:艾普西龙Epsilonζ :捷塔ZetaΖη:依塔EtaΘθ:西塔ThetaΙι:艾欧塔IotaΚκ:喀帕Kappa∧λ:拉姆达LambdaΜμ:缪MuΝν:拗NuΞξ:克西XiΟο:欧麦克轮Omicron∏π:派PiΡρ:柔Rho∑σ:西格玛SigmaΤτ:套TauΥυ:宇普西龙UpsilonΦφ:fai PhiΧχ:器ChiΨψ:普赛PsiΩω:欧米伽Omega希腊字母怎么打打开Office文档之后,在你需要输入希腊字母的时候,先将输入法切换为英文状态,然后同时按下三个键Ctrl+Shift+Q ,工具栏上的“字体”就会发生变化此刻,你再对照下表输入a,b,c……即可得到您想要的希腊字母。
(完整版)数学符号及读法大全
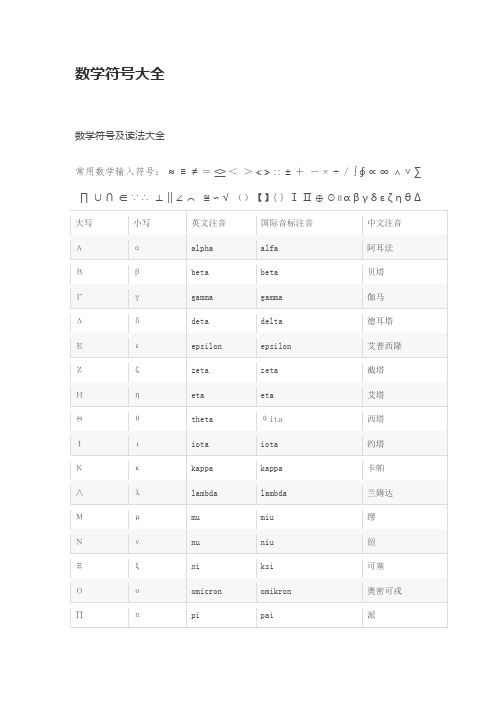
数学符号大全数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ公式输入符号≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒⊙≌∽√+:plus(positive正的)-:minus(negative负的)*:multiplied by÷:divided by=:be equal to≈:be approximately equal to():round brackets(parenthess)[]:square brackets{}:braces∵:because∴:therefore≤:less than or equal to≥:greater than or equal to∞:infinityLOGnX:logx to the base nxn:the nth power of xf(x):the function of xdx:diffrencial of xx+y:x plus y(a+b):bracket a plus b bracket closeda=b: a equals ba≠b: a isn't equal to ba>b : a is greater than ba>>b: a is much greater than ba≥b: a is greater than or equal to bx→∞:approches infinityx2:x squarex3:x cube√ ̄x:the square root of x3√ ̄x:the cube root of x3‰:three peimilln∑i=1xi:the summation of x where x goes from 1to nn∏i=1xi:the product of x sub i where igoes from 1to n ∫ab:integral betweens a and b数学符号(理科符号)——运算符号1.基本符号:+- × ÷(/)2.分数号:/3.正负号:±4.相似全等:∽≌5.因为所以:∵∴6.判断类:=≠<≮(不小于)>≯(不大于)7.集合类:∈(属于)∪(并集)∩(交集)8.求和符号:∑9.n次方符号:¹(一次方) ²(平方) ³(立方)⁴(4次方)ⁿ(n次方)10.下角标:₁₂₃₄(如:A₁B₂C₃D₄效果如何?)11.或与非的"非":¬12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:|21.弧:⌒22.圆:⊙11.或与非的"非":¬12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:|21.弧:⌒22.圆:⊙αβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯΔ。
数学符号读法大全(免费)
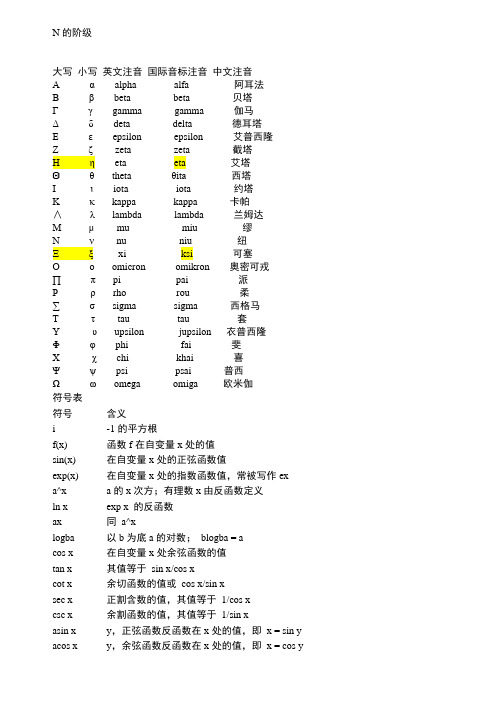
N的阶级大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Γδdeta delta 德耳塔Δεepsilon epsilon 艾普西隆Εδzeta zeta 截塔Ζεeta eta 艾塔Θζtheta ζita西塔Ηηiota iota 约塔Κθkappa kappa 卡帕∧ιlambda lambda 兰姆达Μκmu miu 缪Νλnu niu 纽Ξμxi ksi 可塞Ονomicron omikron 奥密可戎∏πpi pai 派Ρξrho rou 柔∑ζsigma sigma 西格马Τηtau tau 套Υυupsilon jupsilon 衣普西隆Φθphi fai 斐Φχchi khai 喜Χψpsi psai 普西Ψωomega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数;blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值,其值等于1/cos xcsc x 余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos yatan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yζ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z 用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
[Word]数学符号读法大全(免费)
![[Word]数学符号读法大全(免费)](https://img.taocdn.com/s3/m/6fb5790f11a6f524ccbff121dd36a32d7375c727.png)
N的阶级大写小写英文注音国际音标注音中文注音Αα alpha alfa 阿耳法Ββ beta beta 贝塔Γγ gamma gamma 伽马Γδ deta delta 德耳塔Δε epsilon epsilon 艾普西隆Εδ zeta zeta 截塔Ζε eta eta 艾塔Θζ theta ζita 西塔Ηη iota iota 约塔Κθ kappa kappa 卡帕∧ι lambda lambda 兰姆达Μκ mu miu 缪Νλ nu niu 纽Ξμ xi ksi 可塞Ον omicron omikron 奥密可戎∏π pi pai 派Ρξ rho rou 柔∑ζ sigma sigma 西格马Τη tau tau 套Υυ upsilon jupsilon 衣普西隆Φθ phi fai 斐Φχ chi khai 喜Χψ psi psai 普西Ψω omega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax 同 a^xlogba 以b为底a的对数; blogba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值,其值等于 1/cos xcsc x 余割函数的值,其值等于 1/sin xasin x y,正弦函数反函数在x处的值,即 x = sin yacos x y,余弦函数反函数在x处的值,即 x = cos y atan x y,正切函数反函数在x处的值,即 x = tan y acot x y,余切函数反函数在x处的值,即 x = cot y asec x y,正割函数反函数在x处的值,即 x = sec y acsc x y,余割函数反函数在x处的值,即 x = csc yζ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
常用数学符号读法大全

常用数学符号读法大全以下是常见的数学符号以及它们的读法:1. 加号 (+):读作 "加" 或 "加上"。
2. 减号 (-):读作 "减" 或 "减去"。
3. 乘号 (×):读作 "乘" 或 "乘以"。
4. 除号 (÷):读作 "除" 或 "除以"。
5. 等号 (=):读作 "等于" 或 "是"。
6. 大于号 (>):读作 "大于"。
7. 小于号 (<):读作 "小于"。
8. 大于等于号(≥):读作 "大于等于" 或 "不小于"。
9. 小于等于号(≤):读作 "小于等于" 或 "不大于"。
10. 不等号(≠):读作 "不等于" 或 "不是"。
11. 平方根(√):读作 "根号" 或 "平方根"。
12. 指数(ⁿ):读作 "的n次幂" 或 "的n次方"。
13. 求和符号(Σ):读作 "求和"。
14. 差集符号 (∖):读作 "差集"。
15. 交集符号(∩):读作 "交集"。
16. 并集符号 (∪):读作 "并集"。
17. 逻辑与符号 (∧):读作 "逻辑与"。
18. 逻辑或符号 (∨):读作 "逻辑或"。
19. 逻辑非符号 (¬):读作 "逻辑非"。
20. 有限集合符号(∑):读作 "有限集合"。
数学符号及读法大全

数学符号及读法大全第一部分:基本数学符号1. 加号 (+)读作:加2. 减号 ()读作:减3. 乘号(×)读作:乘4. 除号(÷)读作:除5. 等号 (=)读作:等于6. 不等号(≠)读作:不等于7. 大于号 (>)读作:大于8. 小于号 (<)读作:小于9. 大于等于号(≥)读作:大于等于10. 小于等于号(≤)读作:小于等于467. 静谧之海468. 翱翔天际469. 晨曦微光470. 暮色温柔471. 琴瑟和鸣472. 碧波荡漾473. 风轻云淡474. 星河滚烫475. 雨后初晴476. 月下独酌477. 寂静之声478. 花前月下479. 时光荏苒480. 笑忘书481. 梦开始的地方482. 时光旅行者483. 漫步星河484. 风起云涌485. 雨落花飞4. 月影斑驳487. 晨光熹微488. 暮色苍茫489. 静谧之夜490. 翱翔天际491. 晨曦微光492. 暮色温柔493. 琴瑟和鸣494. 碧波荡漾495. 风轻云淡496. 星河滚烫497. 雨后初晴498. 月下独酌499. 寂静之声500. 花前月下501. 时光荏苒502. 笑忘书503. 梦开始的地方504. 时光旅行者505. 漫步星河506. 风起云涌507. 雨落花飞508. 月影斑驳509. 晨光熹微510. 暮色苍茫511. 静谧之夜512. 翱翔天际513. 晨曦微光514. 暮色温柔515. 琴瑟和鸣516. 碧波荡漾517. 风轻云淡518. 星河滚烫519. 雨后初晴520. 月下独酌521. 寂静之声522. 花前月下523. 时光荏苒524. 笑忘书525. 梦开始的地方526. 时光旅行者527. 漫步星河528. 风起云涌529. 雨落花飞530. 月影斑驳531. 晨光熹微532. 暮色苍茫533. 静谧之夜534. 翱翔天际535. 晨曦微光536. 暮色温柔537. 琴瑟和鸣538. 碧波荡漾539. 风轻云淡540. 星河滚烫541. 雨后初晴542. 月下独酌543. 寂静之声544. 花前月下545. 时光荏苒546. 笑忘书547. 梦开始的地方548. 时光旅行者549. 漫步星河550. 风起云涌551. 雨落花飞552. 月影斑驳553. 晨光熹微554. 暮色苍茫555. 静谧之夜556. 翱翔天际557. 晨曦微光558. 暮色温柔559. 琴瑟和鸣560. 碧波荡漾561. 风轻云淡562. 星河滚烫563. 雨后初晴565. 寂静之声566. 花前月下567. 时光荏苒568. 笑忘书569. 梦开始的地方570. 时光旅行者571. 漫步星河572. 风起云涌573. 雨落花飞574. 月影斑驳575. 晨光熹微576. 暮色苍茫577. 静谧之夜578. 翱翔天际579. 晨曦微光580. 暮色温柔581. 琴瑟和鸣582. 碧波荡漾583. 风轻云淡584. 星河滚烫585. 雨后初晴5. 月下独酌587. 寂静之声589. 时光荏苒590. 笑忘书591. 梦开始的地方592. 时光旅行者593. 漫步星河594. 风起云涌595. 雨落花飞596. 月影斑驳597. 晨光熹微598. 暮色苍茫599. 静谧之夜600. 翱翔天际601. 晨曦微光602. 暮色温柔603. 琴瑟和鸣604. 碧波荡漾605. 风轻云淡606. 星河滚烫607. 雨后初晴608. 月下独酌609. 寂静之声610. 花前月下611. 时光荏苒612. 笑忘书613. 梦开始的地方614. 时光旅行者615. 漫步星河616. 风起云涌617. 雨落花飞618. 月影斑驳619. 晨光熹微620. 暮色苍茫621. 静谧之夜622. 翱翔天际623. 晨曦微光624. 暮色温柔625. 琴瑟和鸣626. 碧波荡漾627. 风轻云淡628. 星河滚烫629. 雨后初晴630. 月下独酌631. 寂静之声632. 花前月下633. 时光荏苒634. 笑忘书635. 梦开始的地方636. 时光旅行者637. 漫步星河638. 风起云涌639. 雨落花飞640. 月影斑驳641. 晨光熹微642. 暮色苍茫643. 静谧之夜644. 翱翔天际645. 晨曦微光646. 暮色温柔647. 琴瑟和鸣648. 碧波荡漾649. 风轻云淡650. 星河滚烫651. 雨后初晴652. 月下独酌653. 寂静之声654. 花前月下655. 时光荏苒656. 笑忘书657. 梦开始的地方658. 时光旅行者659. 漫步星河660. 风起云涌661. 雨落花飞662. 月影斑驳663. 晨光熹微664. 暮色苍茫665. 静谧之夜666. 翱翔天际667. 晨曦微光668. 暮色温柔669. 琴瑟和鸣670. 碧波荡漾671. 风轻云淡672. 星河滚烫673. 雨后初晴674. 月下独酌675. 寂静之声676. 花前月下677. 时光荏苒678. 笑忘书679. 梦开始的地方680. 时光旅行者681. 漫步星河682. 风起云涌683. 雨落花飞684. 月影斑驳685. 晨光熹微6. 暮色苍茫687. 静谧之夜688. 翱翔天际689. 晨曦微光690. 暮色温柔691. 琴瑟和鸣692. 碧波荡漾693. 风轻云淡694. 星河滚烫695. 雨后初晴696. 月下独酌697. 寂静之声698. 花前月下699. 时光荏苒700. 笑忘书701. 梦开始的地方702. 时光旅行者703. 漫步星河704. 风起云涌705. 雨落花飞706. 月影斑驳707. 晨光熹微708. 暮色苍茫709. 静谧之夜710. 翱翔天际711. 晨曦微光712. 暮色温柔713. 琴瑟和鸣714. 碧波荡漾715. 风轻云淡716. 星河滚烫717. 雨后初晴718. 月下独酌719. 寂静之声720. 花前月下721. 时光荏苒722. 笑忘书723. 梦开始的地方724. 时光旅行者725. 漫步星河726. 风起云涌727. 雨落花飞728. 月影斑驳729. 晨光熹微730. 暮色苍茫731. 静谧之夜732. 翱翔天际733. 晨曦微光734. 暮色温柔735. 琴瑟和鸣736. 碧波荡漾737. 风轻云淡738. 星河滚烫739. 雨后初晴740. 月下独酌741. 寂静之声742. 花前月下743. 时光荏苒744. 笑忘书745. 梦开始的地方746. 时光旅行者747. 漫步星河748. 风起云涌749. 雨落花飞750. 月影斑驳751. 晨光熹微752. 暮色苍茫753. 静谧之夜754. 翱翔天际755. 晨曦微光756. 暮色温柔757. 琴瑟和鸣758. 碧波荡漾759. 风轻云淡760. 星河滚烫761. 雨后初晴762. 月下独酌763. 寂静之声764. 花前月下765. 时光荏苒766. 笑忘书767. 梦开始的地方768. 时光旅行者769. 漫步星河770. 风起云涌771. 雨落花飞772. 月影斑驳773. 晨光熹微774. 暮色苍茫775. 静谧之夜776. 翱翔天际777. 晨曦微光778. 暮色温柔779. 琴瑟和鸣780. 碧波荡漾781. 风轻云淡782. 星河滚烫783. 雨后初晴784. 月下独酌785. 寂静之声7. 花前月下787. 时光荏苒788. 笑忘书789. 梦开始的地方790. 时光旅行者791. 漫步星河792. 风起云涌793. 雨落花飞794. 月影斑驳795. 晨光熹微796. 暮色苍茫797. 静谧之夜798. 翱翔天际799. 晨曦微光800. 暮色温柔801. 琴瑟和鸣802. 碧波荡漾803. 风轻云淡804. 星河滚烫805. 雨后初晴806. 月下独酌807. 寂静之声808. 花前月下809. 时光荏苒810. 笑忘书811. 梦开始的地方812. 时光旅行者813. 漫步星河814. 风起云涌815. 雨落花飞816. 月影斑驳817. 晨光熹微818. 暮色苍茫819. 静谧之夜820. 翱翔天际821. 晨曦微光822. 暮色温柔823. 琴瑟和鸣824. 碧波荡漾825. 风轻云淡826. 星河滚烫827. 雨后初晴829. 寂静之声830. 花前月下831. 时光荏苒832. 笑忘书833. 梦开始的地方834. 时光旅行者835. 漫步星河836. 风起云涌837. 雨落花飞838. 月影斑驳839. 晨光熹微840. 暮色苍茫841. 静谧之夜842. 翱翔天际843. 晨曦微光844. 暮色温柔845. 琴瑟和鸣846. 碧波荡漾847. 风轻云淡848. 星河滚烫849. 雨后初晴850. 月下独酌851. 寂静之声853. 时光荏苒854. 笑忘书855. 梦开始的地方856. 时光旅行者857. 漫步星河858. 风起云涌859. 雨落花飞0. 月影斑驳1. 晨光熹微2. 暮色苍茫3. 静谧之夜4. 翱翔天际5. 晨曦微光6. 暮色温柔7. 琴瑟和鸣8. 碧波荡漾9. 风轻云淡870. 星河滚烫871. 雨后初晴872. 月下独酌873. 寂静之声874. 花前月下875. 时光荏苒876. 笑忘书877. 梦开始的地方878. 时光旅行者879. 漫步星河880. 风起云涌881. 雨落花飞882. 月影斑驳883. 晨光熹微884. 暮色苍茫885. 静谧之夜8. 翱翔天际887. 晨曦微光888. 暮色温柔889. 琴瑟和鸣890. 碧波荡漾891. 风轻云淡892. 星河滚烫893. 雨后初晴894. 月下独酌895. 寂静之声896. 花前月下897. 时光荏苒898. 笑忘书899. 梦开始的地方900. 时光旅行者901. 漫步星河902. 风起云涌903. 雨落花飞904. 月影斑驳905. 晨光熹微906. 暮色苍茫907. 静谧之夜908. 翱翔天际909. 晨曦微光910. 暮色温柔911. 琴瑟和鸣912913. 紫藤花下914. 雪域之鹰915. 翠竹清风916. 风华正茂917. 水墨青花918. 晨曦暮雪919. 琴韵墨香920. 梦里江南921. 花影轻舞922. 时光流转923. 笑忘江湖924. 梦开始的地方925. 时光旅行者926. 漫步星河927. 风起云涌928. 雨落花飞929. 月影斑驳930. 晨光熹微931. 暮色苍茫932. 静谧之夜933. 翱翔天际934. 晨曦微光935. 暮色温柔936. 琴瑟和鸣937. 碧波荡漾938. 风轻云淡939. 星河滚烫940. 雨后初晴941. 月下独酌942. 寂静之声943. 花前月下944. 时光荏苒945. 笑忘书946. 梦开始的地方947. 时光旅行者948. 漫步星河949. 风起云涌950. 雨落花飞951. 月影斑驳952. 晨光熹微953. 暮色苍茫954. 静谧之夜955. 翱翔天际956. 晨曦微光957. 暮色温柔958. 琴瑟和鸣959. 碧波荡漾960. 风轻云淡961. 星河滚烫962. 雨后初晴963. 月下独酌964. 寂静之声965. 花前月下966. 时光荏苒967. 笑忘书968. 梦开始的地方969. 时光旅行者970. 漫步星河971. 风起云涌972. 雨落花飞973. 月影斑驳974. 晨光熹微975. 暮色苍茫976. 静谧之夜977. 翱翔天际978. 晨曦微光979. 暮色温柔980. 琴瑟和鸣981. 碧波荡漾982. 风轻云淡983. 星河滚烫984. 雨后初晴985. 月下独酌9. 寂静之声987. 花前月下988. 时光荏苒989. 笑忘书990. 梦开始的地方991. 时光旅行者992. 漫步星河993. 风起云涌994. 雨落花飞995. 月影斑驳996. 晨光熹微997. 暮色苍茫998. 静谧之夜999. 翱翔天际1000. 晨曦微光。
数学函数符号读法大全

数学函数符号读法大全1.函数名:-读作“函数f”:f(x)表示函数f的自变量为x。
-读作“函数g”:g(y)表示函数g的自变量为y。
-读作“函数h”:h(z)表示函数h的自变量为z。
2.自变量:-读作“x”:x表示函数的自变量。
-读作“y”:y表示函数的自变量。
-读作“z”:z表示函数的自变量。
3.箭头:-读作“映射到”:f:X→Y表示函数f将集合X中的元素映射到集合Y中的元素。
4.等号:-读作“等于”:f(x)=y表示函数f在自变量x的取值为y。
5.花括号:-读作“函数f的定义域是X”:f:X→Y表示函数f的定义域是集合X,即x的取值范围。
-读作“函数f的值域是Y”:f:X→Y表示函数f的值域是集合Y,即函数的输出值的范围。
6.圆括号:-读作“f的自变量为x”:f(x)表示函数f的自变量为x。
-读作“g的自变量为y”:g(y)表示函数g的自变量为y。
-读作“h的自变量为z”:h(z)表示函数h的自变量为z。
7.其他常见符号:-读作“f和g的复合函数”:(f∘g)(x)表示函数f和g的复合函数。
- 读作“f 在 x 处的极限是l”:lim(x→a) f(x) = l 表示函数 f 在 x 趋近于 a 时的极限是 l。
-读作“函数f的导数是f'”:f'(x)表示函数f的导数。
- 读作“函数 f 的积分是F”:∫ f(x) dx = F(x) 表示函数 f 的积分是 F。
- 读作“函数 f 在 x 处的微分是df”:df = f'(x) dx 表示函数f 在 x 处的微分是 df。
-读作“方程f(x)=0的解是x”:f(x)=0表示方程f(x)的解是x。
- 读作“函数 f 的最大值是M”:max f(x) = M 表示函数 f 的最大值是 M。
- 读作“函数 g 的最小值是m”:min g(x) = m 表示函数 g 的最小值是 m。
收集的数学符号读法大全

收集的数学符号读法大全
1、Α α alpha a:lf 阿尔法角度;系数
2 、Β β beta bet 贝塔磁通系数;角度;系数
3、Γ γ gamma ga:m 伽马电导系数(小写)
4、Γ δ delta delt 德尔塔变动;密度;屈光度
5、Δ ε epsilon ep`silon 伊普西龙对数之基数
6 、Ε δ zeta zat 截塔系数;方位角;阻抗;相对粘度;原子序数
7、Ζ ε eta eit 艾塔磁滞系数;效率(小写)
8 、Θ ζ thet ζit 西塔温度;相位角
9 、Η η iot aiot 约塔微小,一点儿
10、Κ θ kappa kap 卡帕介质常数
11、∧ι lambda lambd 兰布达波长(小写);体积
12、Μ κ mu mju 缪磁导系数;微(千分之一);放大因数(小写)
13、Ν λ nu nju 纽磁阻系数
14、Ξ μ xi ksi 克西
15、Ο ν omicron omik`ron 奥密克戎
16、∏ π pi pai 派圆周率=圆周÷直径=3.1416
17、Ρ ξ rho rou 肉电阻系数(小写)
18、∑ ζ sigma `sigma 西格马总和(大写),表面密度;跨导(小写)
19、Τ η tau tau 套时间常数
20 、Υ υ upsilon jup`silon 宇普西龙位移
21、Φ θ phi fai 佛爱磁通;角
22、Φ χ chi phai 西
23 、Χ ψ psi psai 普西角速;介质电通量(静电力线);角
24、Ψ ω omega o`miga 欧米伽欧姆(大写);角速(小写);角。
(完整版)数学符号及读法大全,推荐文档

数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>≮≯∷ ± +-× ÷ /∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ大写小写英文注音国际音标注音中文注音Ααalpha alfa阿耳法Ββbeta beta贝塔Γγgamma gamma伽马Δδdeta delta德耳塔Εεepsilon epsilon艾普西隆Ζζzeta zeta截塔Ηηeta eta艾塔Θθthetaθita西塔Ιιiota iota约塔Κκkappa kappa卡帕∧λlambda lambda兰姆达Μμmu miu缪Ννnu niu纽Ξξxi ksi可塞Οοomicron omikron奥密可戎∏πpi pai派Ρρrho rou柔∑σsigma sigma西格马Ττtau tau套Υυupsilon jupsilon衣普西隆Φφphi fai斐Χχchi khai喜Ψψpsi psai普西Ωωomega omiga欧米符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin yacos x y,余弦函数反函数在x处的值,即x = cos yatan x y,正切函数反函数在x处的值,即x = tan yacot x y,余切函数反函数在x处的值,即x = cot yasec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
常用数学符号读法大全

常用数学符号读法大全数学是一门重要的学科,无论是在学习、研究还是应用中,我们都离不开各种数学符号。
掌握这些符号的读法对于正确理解数学概念和计算方法至关重要。
本文将为您介绍一些常用数学符号的读法和用途。
数字和基本运算符号•0、1、2、3、4、5、6、7、8、9:分别读作零、一、二、三、四、五、六、七、八、九。
•加号+:读作加、加号。
•减号-:读作减、减号。
•乘号×:读作乘、乘号、乘以。
•除号÷:读作除、除号、除以。
•等号=:读作等于、等号。
基本代数符号•小于号<:读作小于、小于号。
•大于号>:读作大于、大于号。
•不等于号≠:读作不等于、不等号。
•小于等于号≤:读作小于等于、小于等于号。
•大于等于号≥:读作大于等于、大于等于号。
希腊字母希腊字母在数学、物理、工程等领域有广泛应用。
•α (Alpha):读作阿尔法。
•β (Beta):读作贝塔。
•γ (Gamma):读作伽马。
•δ (Delta):读作德尔塔。
•ε (Epsilon):读作伊普西隆。
•ζ (Zeta):读作泽塔。
•η (Eta):读作艾塔。
•θ (Theta):读作西塔。
•ι (Iota):读作约塔。
•κ (Kappa):读作卡帕。
•λ (Lambda):读作兰姆达。
•µ (Mu):读作缪。
•ν (Nu):读作纳。
•ξ (Xi):读作克西。
•π (Pi):读作派。
•ρ (Rho):读作柔。
•σ (Sigma):读作西格玛。
•τ (Tau):读作套。
•υ (Upsilon):读作宇普西隆。
•φ (Phi):读作费。
•χ (Chi):读作希。
•ψ (Psi):读作普赛。
•ω (Omega):读作欧米伽。
计量单位符号•° (Degree):读作度。
•% (Percent):读作百分之。
•‰ (Per mille):读作千分之。
•∞ (Infinity):读作无穷。
•π (Pi):读作派。
•e(Euler’s number):读作e。
(完整word版)数学符号及读法大全
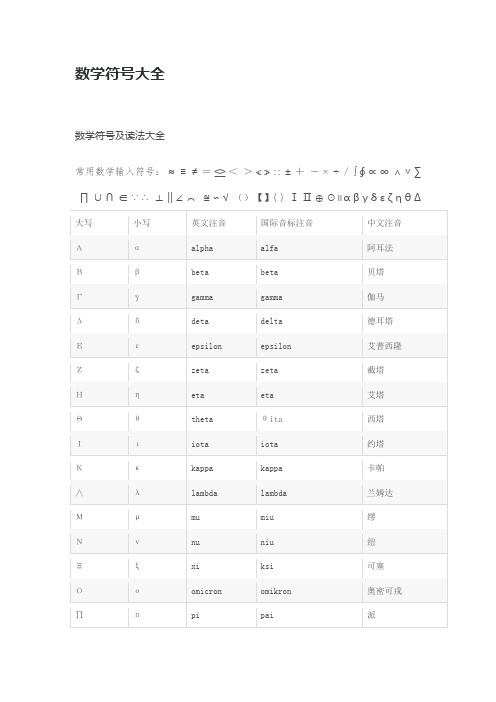
数学符号大全数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ公式输入符号≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒⊙≌∽√+:plus(positive正的)-:minus(negative负的)*:multiplied by÷:divided by=:be equal to≈:be approximately equal to():round brackets(parenthess)[]:square brackets{}:braces∵:because∴:therefore≤:less than or equal to≥:greater than or equal to∞:infinityLOGnX:logx to the base nxn:the nth power of xf(x):the function of xdx:diffrencial of xx+y:x plus y(a+b):bracket a plus b bracket closeda=b: a equals ba≠b: a isn't equal to ba>b : a is greater than ba>>b: a is much greater than ba≥b: a is greater than or equal to bx→∞:approches infinityx2:x squarex3:x cube√ ̄x:the square root of x3√ ̄x:the cube root of x3‰:three peimilln∑i=1xi:the summation of x where x goes from 1to nn∏i=1xi:the product of x sub i where igoes from 1to n ∫ab:integral betweens a and b数学符号(理科符号)——运算符号1.基本符号:+- × ÷(/)2.分数号:/3.正负号:±4.相似全等:∽≌5.因为所以:∵∴6.判断类:=≠<≮(不小于)>≯(不大于)7.集合类:∈(属于)∪(并集)∩(交集)8.求和符号:∑9.n次方符号:¹(一次方) ²(平方) ³(立方)⁴(4次方)ⁿ(n次方)10.下角标:₁₂₃₄(如:A₁B₂C₃D₄效果如何?)11.或与非的"非":¬12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:|21.弧:⌒22.圆:⊙11.或与非的"非":¬12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:|21.弧:⌒22.圆:⊙αβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯΔ。
常用数学符号的读法及其含义

常用数学符号的读法及其含义
1. 嘿,你知道“=”这个符号吧,它读作“等于”呀!比如说,
“1+1=2”,这就表示两边是相等的呀!这多简单明了,要是没有它,我们可怎么表达相等的概念呢?
2. 哇塞,“>”这个符号读作“大于”呢!就像 5>3,这不是很直白地告诉我们 5 比 3 要大嘛,它可太重要啦!
3. 哈哈,“<”就是“小于”呀!比如 2<4,一下子就能看出 2 是小于 4 的呀,没有它可不行哦!
4. “+”呀,读“加”!想想看,2+3=5,它就是把数字加在一起的意思呀,多神奇!
5. “-”呢,当然是“减”啦!像 5-3=2,它让我们能做减法运算呢,是不是很厉害?
6. “×”这个符号读作“乘”哟!比如3×4=12,乘法可少不了它呀!
7. “÷”就是“除”啦!像12÷3=4,没有它除法可就没法表示啦,对吧?
8. “π”呀,读“派”,它可是个很特别的符号呢!在计算圆的周长和面积时经常用到它呢,厉害吧!
9. “%”读作“百分之”,像 50%就是一半呀!在表示比例的时候经常出现呢,很实用呀!
10. 最后说说“!”,它读作“阶乘”哦!比如 5!就是
5×4×3×2×1,是不是很有意思呀!
我的观点结论就是:这些数学符号真的太重要啦,它们是数学世界的基石呀,没有它们数学可就没法玩啦!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009-08-14 22:20
学符号读法大全
写小写英文注音国际音标注音中文注音
α alpha alfa 阿耳法
β beta beta 贝塔
γ gamma gamma 伽马
δ deta delta 德耳塔
ε epsilon epsilon 艾普西隆
δ zeta zeta 截塔
ε eta eta 艾塔
ζ theta ζita 西塔η iota iota 约塔θ kappa kappa 卡帕
ι lambda lambda 兰姆达
κ mu miu 缪
λ nu niu 纽
μ xi ksi 可塞
ν omicron omikron 奥密可戎
π pi pai 派
ξ rho rou 柔
ζ sigma sigma 西格马
η tau tau 套
υ upsilon jupsilon 衣普西隆
θ phi fai 斐
χ chi khai 喜
ψ psi psai 普西
ω omega omiga 欧米伽
符号表
符号含义-1的平方根
(x) 函数f在自变量x处的值
in(x) 在自变量x处的正弦函数值
xp(x) 在自变量x处的指数函数值,常被写作e x
^x a的x次方;有理数x由反函数定义
n x exp x 的反函数
同 a^x
og
b a 以b为底a的对数; b log
b
a = a
os x 在自变量x处余弦函数的值
an x 其值等于 sin x/cos x
ot x 余切函数的值或 cos x/sin x
ec x 正割含数的值,其值等于 1/cos x
sc x 余割函数的值,其值等于 1/sin x
sin x y,正弦函数反函数在x处的值,即 x = sin y cos x y,余弦函数反函数在x处的值,即 x = cos y tan x y,正切函数反函数在x处的值,即 x = tan y cot x y,余切函数反函数在x处的值,即 x = cot y sec x y,正割函数反函数在x处的值,即 x = sec y
csc x y,余割函数反函数在x处的值,即 x = csc y
角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时
, j, k 分别表示x、y、z方向上的单位向量
a, b, c) 以a、b、c为元素的向量
a, b) 以a、b为元素的向量
a, b) a、b向量的点积
•b a、b向量的点积
a•b)a、b向量的点积
v| 向量v的模
x| 数x的绝对值
表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到100的和可以表示成:。
这表示 1 + 2 + … + n 表示一个矩阵或数列或其它
v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量
v| 被写成行或可被看成从1×k阶矩阵的向量
x 变量x的一个无穷小变化,dy, dz, dr等类似
s 长度的微小变化
变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离
变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离
M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积
|M|| 矩阵M的行列式的值,为一个面积、体积或超体积
et M M的行列式
1矩阵M的逆矩阵
×w向量v和w的向量积或叉积
vw
向量v和w之间的夹角
•B×C标量三重积,以A、B、C为列的矩阵的行列式
在向量w方向上的单位向量,即 w/|w|
f 函数f的微小变化,足够小以至适合于所有相关函数的线性近似
f/dx f关于x的导数,同时也是f的线性近似斜率
' 函数f关于相应自变量的导数,自变量通常为x
/∂x y、z固定时f关于x的偏导数。
通常f关于某变量q的偏导数为当其它几个变量固定时df与dq的比值。
任何可能导致变量混淆的地方都应明确地表述
f/∂x)|
r,z
保持r和z不变时,f关于x的偏导数
rad f 元素分别为f关于x、y、z偏导数 [(∂f/∂x), (∂f/∂y), (∂f/∂z)] 或 (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k; 的向量场,称为f的梯度
∇向量算子(∂/∂x)i + (∂/∂x)j + (∂/∂x)k, 读作 "del"
∇f f的梯度;它和 u
w
的点积为f在w方向上的方向导数
∇•w 向量场w的散度,为向量算子∇同向量 w的点积, 或 (∂w
x /∂x) + (∂w
y
/∂y) + (∂w
z
/∂z)
url w 向量算子∇同向量 w 的叉积
∇×w w的旋度,其元素为[(∂f
z /∂y) - (∂f
y
/∂z), (∂f
x
/∂z) - (∂f
z
/∂x), (∂f
y
/∂x) - (∂f
x
/∂y)]
∇•∇拉普拉斯微分算子: (∂2/∂x2) + (∂/∂y2) + (∂/∂z2) "(x) f关于x的二阶导数,f '(x)的导数
f/dx2f关于x的二阶导数
2)(x) 同样也是f关于x的二阶导数
k)(x) f关于x的第k阶导数,f(k-1) (x)的导数
曲线切线方向上的单位向量,如果曲线可以描述成 r(t), 则T = (dr/dt)/|dr/dt|
s 沿曲线方向距离的导数
曲线的曲率,单位切线向量相对曲线距离的导数的值:|dT/ds|
dT/ds投影方向单位向量,垂直于T
平面T和N的单位法向量,即曲率的平面
曲线的扭率: |dB/ds|
重力常数
力学中力的标准符号
弹簧的弹簧常数
第i个物体的动量
物理系统的哈密尔敦函数,即位置和动量表示的能量
Q, H} Q, H的泊松括号
以一个关于x的函数的形式表达的f(x)的积分
函数f 从a到b的定积分。
当f是正的且 a < b 时表示由x轴和直线y = a, y = b 及在这些直线之间的函数曲线所围起来图形的面积
(d) 相等子区间大小为d,每个子区间左端点的值为 f的黎曼和
(d) 相等子区间大小为d,每个子区间右端点的值为 f的黎曼和
(d) 相等子区间大小为d,每个子区间上的最大值为 f的黎曼和
(d) 相等子区间大小为d,每个子区间上的最小值为 f的黎曼和
plus(positive正的)。
