轴承故障特征倍频公式推导
滚动轴承频谱分析详解

滚动轴承频谱分析详解对于滚动轴承不能只依赖振动总量来精确评估滚动轴承的状态,也不能完全依赖超声频带测量:振动尖峰能量(Spike Energy)、高频加速度(High FrequencyAcceleration-HFD)、冲击脉冲(Shock Pules-SPM)。
只有将超声测量与振动特征信号分析结合使用才是最好的评定轴承的状态。
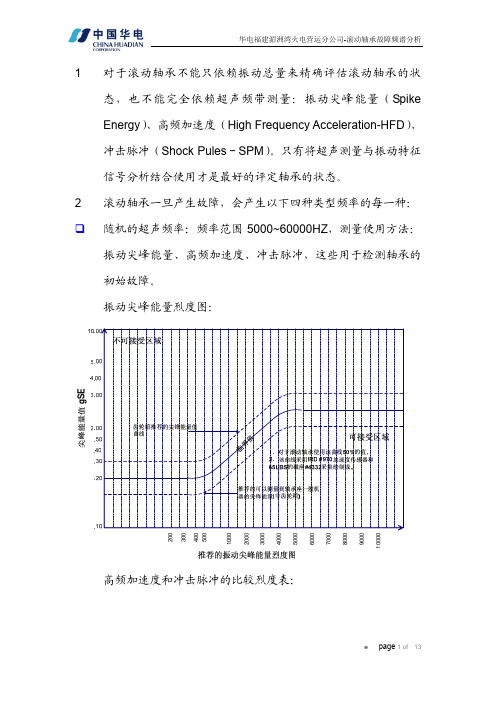
滚动轴承一旦产生故障,会产生以下四种类型频率的每一种:随机的超声频率:频率范围5000~60000HZ,测量使用方法:振动尖峰能量、高频加速度、冲击脉冲,这些用于检测轴承的初始故障。
振动尖峰能量烈度图:高频加速度和冲击脉冲的比较烈度表:轴承部件的自振频率:频率范围500~2000HZ,轴承零部件受到冲击时,以它们的自振频率“瞬时扰动”。
在滚动轴承中,滚动元件打击内外环跑道上的缺陷的间断的冲击激起它们的自振频率。
但故障扩展到微观大小时,它们开始激起这些轴承零部件的自振频率,成为“第二个检测症兆”。
故障恶化时,可引起更大的冲击,这些更大的冲击产生更大的自振频率尖峰响应。
磨损严重时,在这些共振附近出现更多频率分量,它们中许多是这些自振频率的1X转速的边带(往往,这些调制尖峰以轴承的故障频率为间隔,而不是1X转速频率的边带)。
轴承自振频率与转速无关,但它们的响应幅值与冲击速度成正比,意味着转速越高,响应幅值也越高。
旋转轴承的故障频率:轴承零部件故障频率与轴承的平均直径-Pa、滚动体直径-Ba、滚动体数目-Nb和接触角-ø有关。
FTF-保持架故障频率、BSF-滚动体故障频率、BPOR-内环故障率、BPIR-外环故障频率。
FTF、BSF、BPOR、BPIR简易计算公式(可参考平台内前期文章介绍)。
轴承故障频率都是转速频率的非整数倍(本人所遇确实如此,但曾看到过一篇文章说正好是转速频率整数倍)。
正常情况下滚动轴承故障频率不应存在,当存在轴承故障频率时,可以说明轴承至少发出初始故障信号。
滚动轴承内外圈都旋转的故障特征频率计算公式

滚动轴承是一种常见的旋转机械零部件,它承担着重要的转动功能。
在滚动轴承工作过程中,如果遇到内外圈都旋转的故障,就需要对其特征频率进行计算和分析。
本文将介绍滚动轴承内外圈都旋转的故障特征频率计算公式,希望能够为相关领域的研究和实践提供帮助。
一、滚动轴承内外圈都旋转的故障特征频率计算公式1. 滚动轴承内外圈都旋转的故障特征频率公式如下:f = (P/2) * (1 - (d/D)) * (n/60)其中,f为故障特征频率,P为滚动体的数量,d为滚动体直径,D为滚动道直径,n为转速。
2. 在计算滚动轴承内外圈都旋转的故障特征频率时,需要注意以下几点:(1) 滚动体的数量对故障特征频率有影响,一般来说,滚动体数量越多,故障特征频率越高。
(2) 滚动体直径和滚动道直径的比值(d/D)也会影响故障特征频率,当d/D接近1时,故障特征频率较低;当d/D远离1时,故障特征频率较高。
(3) 转速的变化会直接影响到故障特征频率的计算,转速越高,故障特征频率越高。
二、滚动轴承内外圈都旋转的故障特征频率计算实例分析以某型号滚动轴承为例,其内外圈都旋转的故障特征频率计算如下:1. 已知数据:滚动体数量P=14,滚动体直径d=6mm,滚动道直径D=20mm,转速n=1800rpm。
2. 按照公式进行计算:f = (14/2) * (1 - (6/20)) * (1800/60) = 7 * 0.7 * 30 = 1470Hz。
通过以上实例分析可知,滚动轴承内外圈都旋转的故障特征频率为1470Hz。
这个特征频率对于故障诊断和预防具有重要意义,需要在相关实际应用中加以重视。
三、滚动轴承内外圈都旋转的故障特征频率计算公式的应用意义滚动轴承内外圈都旋转的故障特征频率计算公式的应用意义主要体现在以下几个方面:1. 故障诊断和预防:通过计算故障特征频率,可以帮助实现滚动轴承内外圈都旋转故障的诊断和预防工作,及早发现并解决故障问题,提高设备的可靠性和稳定性。
基于阶次分析的变转速滚动轴承故障诊断

基于阶次分析的变转速滚动轴承故障诊断王贞云;刘永强;廖英英【摘要】变转速下机械设备的动态信号十分复杂,由于转速发生变化,轴承的特征谱线被转速调制,此时传统的共振解调方法已经失效.针对变转速工况下的滚动轴承,提出了基于阶比分析的共振解调方法.先将时域非平稳信号进行带通滤波,将滤波后的信号进行Hilbert包络后去除趋势项,对包络后时域的非稳态信号通过等角度采样转变成角域上的平稳信号,然后对角域信号进行包络解调.通过对仿真信号和试验信号的分析,从阶次谱上可以看出,该方法能够准确地找到轴承的故障类型,表明该方法能够有效地识别升速过程中滚动轴承的早期故障.【期刊名称】《汽车工程师》【年(卷),期】2016(000)007【总页数】5页(P46-50)【关键词】滚动轴承;阶次分析;共振解调;故障诊断【作者】王贞云;刘永强;廖英英【作者单位】石家庄铁道大学;石家庄铁道大学;石家庄铁道大学【正文语种】中文滚动轴承作为旋转机械设备中重要的部件之一,通常是机械设备中长期运行的易损坏部件[1]。
与此同时,滚动轴承作为机车轮对轴箱的重要组成部件,其运行的好坏直接关系到机车运行是否安全,因此研究机车轮对轴承的状态监测和早期故障识别方法就显得尤为重要。
文献[2]针对转速缓慢波变化的工况,采用等角度重采样和计算阶比跟踪技术对轴承振动信号进行处理,适用于传统的平方包络谱方法;文献[3]基于循环平稳信号处理方法对滚动轴承的早期微弱故障特征提取和故障诊断进行研究。
目前针对变转速轴承故障诊断的方法,要么只适用于转速缓慢波动的工况,要么过程太过繁琐。
机车加速过程中轴承的振动信号主要频率成分相差比较大,且与转速有着密切的关系,若直接使用FFT进行处理,则结果会出现严重的“频率模糊”现象[4-5]。
由此,文章提出了一种将阶次跟踪与共振解调相结合的轴承故障诊断方法。
1 理论基础1.1 阶次分析阶次分析可以克服传统的频谱分析方法从非平稳信号难以提取故障信息的问题,通过把采集的时域振动信号进行等角度采样转化为角域平稳信号,把传统的频谱分析转化为阶次谱分析,这样无论转频如何变化,对应要分析频率和转频的倍数是不会发生改变的,这个倍数就是要分析的阶比。
滚动轴承故障频谱分析
元件打击内外环跑道上的缺陷的间断的冲击激起它们的自振频
率。但故障扩展到微观大小时,它们开始激起这些轴承零部件
的自振频率,成为“第二个检测症兆”。故障恶化时,可引起更大
的冲击,这些更大的冲击产生更大的自振频率尖峰响应。磨损
严重时,在这些共振附近出现更多频率分量,它们中许多是这
些自振频率的 1X 转速的边带(往往,这些调制尖峰以轴承的故
华电福建湄洲湾火电营运分公司-滚动轴承故障频谱分析
频率、BSF-滚动体故障频率、BPOR-内环故障频率、BPIR外环故障频率。 FTF、BSF、BPOR、BPIR 简易计算公式。 轴承故障频率都是转速频率的非整数倍。 正常情况下滚动轴承故障频率不应存在,当存在轴承故障 频率时,可以说明轴承至少发出初始故障信号。然而,应 该明确一点:这些轴承故障频率的出现未必意味着轴承内 一定是轴承已损坏,由于轴承润滑不佳,发生金属对金属 的接触,轴承承受不适当的负载(过大的压配合-过盈配合 偏大,对不承受轴向推力的轴承施加了轴向推力,推力轴 承反向安装等等),也将出现轴承的故障频率。 内环故障频率+外环故障频率=滚动体通过频率(Nb×X)。 无论是内环还是外环故障,都有 1X 转速的边带,不转的 环边带要比转动的环边带多。如果内环两侧被 1X 转速边 带族环绕时,说明损坏的程度更严重。 解释内、外环故障往往伴有 1X 转速频率的边带? 内环、外环故障频率的相对幅值:外环故障频率的幅值高 于内环故障频率的幅值,只要是传感器靠近外环的原因。 轴承故障频率通常出现的次序:通常轴承故障的顺序轴承 内和外环→滚动体和保持架。此后,保持架故障频率以基 频或以其它频率的边带形式出现。滚动体故障频率有时以 边带形式出现在轴承内环/外环故障频率的左右侧。
滚动轴承故障诊断

滚动轴承故障诊断初步1、故障原因滚动轴承的早期故障是滚子和滚道剥落、凹痕、破裂、腐蚀和杂物嵌入。
即主要故障形式:疲劳剥落、磨损、塑性变形、锈蚀、断裂、胶合、保持架损坏。
产生主要原因包括搬运粗心、安装不当、不对中、轴承倾斜、轴承选用不正确、润滑不足或密封失效、负载不合适以及制造缺陷。
2、频谱和波形特征滚动轴承它是由内圈、外圈、滚动体和保持架四部分组成。
当滚动体和滚道接触处遇到一个局部缺陷时,就有一个冲击信号产生。
缺陷在不同的元件上,接触点经过缺陷的频率是不相同的,这个频率就称为滚动轴承的特征频率。
滚动轴承的故障特征频率的数值一般在几赫兹到几百赫兹之间,在频谱图中的1000Hz以内的低频区域轴承故障特征频率如下:1、滚动轴承故障特征频率(外圈静止)式中:Z——滚动体个数fr——转频(Hz)D——轴承节径(mm)d——滚动体直径(mm)α——接触角(1)滚动轴承内圈故障特征频率(2)滚动轴承外圈故障特征频率(3)滚动轴承滚动体特征频率(4)滚动轴承保持架特征频率2、滚动轴承故障特征频率的计算经验公式:二、滚动轴承故障诊断的要素滚动轴承由内圈、外圈、滚动体和保持架四部分组成,每个轴承部件对应一个轴承故障特征频率。
滚动轴承的故障频率分布有一个明显的特点,往往在低频和高频两个频段内都有表现。
所以在频率分析时,可以选择在这两个频段进行分析。
根据滚动轴承的故障形式在频域中的表现形式,将整个频域分为三个频段,既高频段、中频段和低频段。
l 高频阶段指频率范围处于2000-5000Hz 的频段,主要是轴承固有频率,在轴承故障的早期,高频段反映比较敏感;中频阶段指频率范围处于800-1600Hz 的频段,一般是由于轴承润滑不良而引起碰磨产生的频率范围;l 低频阶段指频率范围处于0-800Hz 的频段,基本覆盖轴承故障特征频率及谐波;在高频段和低频段中所体现的频率是否为轴承故障频率,还要通过其他方法进行印证加以确认。
根据滚动轴承的故障特征频率在频域和时域中的表现,可将滚动轴承的诊断方法总结为三个频段;八个确认,简称三八诊断法。
轴承信号分析基本理论

轴承信号分析基本理论1. 采样定理 定义:每秒钟采样的次数。
(例如每0.01秒采样一次,即在1秒钟内有100次等时距的采样,因此这次采样的采样频率为100Hz 。
)根据采样定律:采样频率必须不低于信号最高频率的两倍,否则会产生频混现象(频谱混叠效应)。
即f s >2f h2. 加窗定义:截断信号过长的时间历程,即将信号乘以时域的有限宽窗函数。
A 对周期信号进行整周期的截取,就无“泄漏”现象。
对周期信号进行非整周期的截取,会出现“泄漏”现象。
(在实际处理过程中,由于信号并不一定是周期信号,也并不一定是整周期截取,所以,加窗以后的信号在频谱图上除了有主要的频率以外,还出现了其他附加频率,从而造成能量不是集中于确定的主要频率上,而是部分泄漏到其他频率中。
这种由于时域上的截断所导致频域内附加一些成分,引起能量泄漏,称为泄漏误差,又叫做截断误差。
)B 为了减少泄漏误差,选择的窗函数应要求旁瓣高度与主瓣高度之比尽量要小,并且主瓣宽度要窄,旁瓣幅度要小。
因为窄的主瓣可以提高分辨率,小的旁瓣可以减小泄漏。
然而,事实上窗函数的选取往往是牺牲分辨率来换取泄漏的减少。
3. 平均 定义:在采集信号的过程中不可避免的会将噪声同时被采集入内,噪声是随机的,有时上升,有下降。
这些噪声在经过数量足够多的平均后,可以相互抵消。
4. 倒谱定义:这里轴承信号的分析,都采用实倒谱。
实倒频谱)(τx C 即功率谱对数谱的模,也就是说,在傅里叶正变换后,不考虑相位信息。
[])(log )()(1f S F C C x x -==ττ在所研究的信号中,其故障频率附近总是存在多族频率,习惯上把它们成为边频。
倒频谱能够分离和提取出密集边频信号中的周期成分,将原来频谱图上成簇的边频带谱线简化为单根谱线。
倒频谱在进行功率谱的对数转换时,给幅值较小的分量有较高的加权。
4. 细化谱4.1.1全频段细化过程一般的FFT 分析是一种基带的分析方法,在整个分析带宽内,频率是等分的,即T t N N f N f f s m 112=∆===∆ (4—1)式中: N ——采样点数;m f ——分析带宽的最高频率;s f ——采样频率,即为t∆1,依采样定理,取s f =2m f ;t ∆——采样间隔;T ——样本长度,即T=N t ∆。
SKF轴承异常振动频率的计算方法

SKF轴承异常振动频率的计算方法
我们在使用SKF轴承的时候,一定会遇到过轴承出现异常的时候,因为再好的轴承也不可能是无间断的正常运转,因为都会有个以外的情况发生,或者是因为设备问题,或者是因为SKF轴承本身,这些情况都是有可能发生的,所以我们只有事先准备好,有所了解,才能在故障发生的时候,能够应对自如,很好的解决出现的问题。
今天我们主要就是说一下SKF 轴承异常振动频率的计算方法,具体情况请看下面的公式和数据对应表:
SKF轴承外环故障频率:BPFOe≌N(0.5n-1.2)
轴承内环故障频率:BPFIe≌N(0.5n+1.2)
轴承滚动体故障频率:BSFe≌N(0.2n-1.2/n)
轴承保持架故障频率:FTFe≌N(0.5-1.2/n)
以上符号:
n=滚动体数目。
N=轴的转速。
注:1.滚动SKF轴承没有滑动;2.滚动轴承几何尺寸没有变化;3.轴承外环固定不旋转. SKF轴承外环故障频率:BPFOr≌0.4Nn
轴承内环故障频率:BPFIr≌0.6Nn
轴承保持架故障频率:FTFr≌0.4N
以上符号:
n=滚动体数目。
N=轴的转速。
注:1.滚动SKF轴承没有滑动;2.滚动轴承几何尺寸没有变化;3.轴承外环固定不旋转.。
滚动轴承的故障机理及诊断讲义

4.轴承故障分析 图2是一台三柱塞注水泵轴承的包络谱。泵转速335rpm,排出压力25MPa,流量16m3/h, 驱动电机功率132KW,电机转速985rpm,电机与泵通过皮带传动。泵轴承为双排球面滚子轴承,型号22330。 根据轴承尺寸计算的轴承故障频率如下: 内圈故障频率BPIR=49.6Hz 外圈故障频率BPOR=34.2Hz 滚动体BSF=14.7Hz 保持架FTF=2.3Hz 曲轴转频f0=335rpm/60s=5.58Hz
旋转设备约有30%的故障是因滚动轴承引起的,因滚动轴承抱轴、保持架散落造成转子严重损坏给设备造成的损失是巨大的。最初的轴承故障诊断是靠有经验的设备管理和维修人员利用听音棒来判断,只能发现处于晚期的故障,不能及时发现处于早、中期的轴承故障,从而造成设备故障的扩展,并延缓维修时间。随着设备监测诊断技术的发展,各种信号分析与处理技术被用于轴承的故障诊断。
⒌擦伤
由于轴承内外滚道和滚动体接触表面上的微观凸起或硬质颗粒使接触面受力不均,在润滑不良、高速重载工况下,因局部摩擦产生的热量造成接触面局部变形和摩擦焊合,严重时表面金属可能局部熔化,接触面上作用力将局部摩擦焊接点从基体上撕裂。
轴承失效通常划分为四个阶段: 第一阶段:在轴承失效的初始阶段,故障频率出现在超声频段。有多种信号处理手段能够检测到这些频率,如峰值能量gSE、应力波PeakVue、包络谱ESP、冲击脉冲SPM等。此时,轴承故障频率在加速度谱和速度频谱图上均无显示。
请各位专家给予批评指正!
9、静夜四无邻,荒居旧业贫。。10、雨中黄叶树,灯下白头人。。11、以我独沈久,愧君相见频。。12、故人江海别,几度隔山川。。13、乍见翻疑梦,相悲各问年。。14、他乡生白发,旧国见青山。。15、比不了得就不比,得不到的就不要。。。16、行动出成果,工作出财富。。17、做前,能够环视四周;做时,你只能或者最好沿着以脚为起点的射线向前。。9、没有失败,只有暂时停止成功!。10、很多事情努力了未必有结果,但是不努力却什么改变也没有。。11、成功就是日复一日那一点点小小努力的积累。。12、世间成事,不求其绝对圆满,留一份不足,可得无限完美。。13、不知香积寺,数里入云峰。。14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。15、楚塞三湘接,荆门九派通。。。16、少年十五二十时,步行夺得胡马骑。。17、空山新雨后,天气晚来秋。。9、杨柳散和风,青山澹吾虑。。10、阅读一切好书如同和过去最杰出的人谈话。11、越是没有本领的就越加自命不凡。12、越是无能的人,越喜欢挑剔别人的错儿。13、知人者智,自知者明。胜人者有力,自胜者强。14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。15、最具挑战性的挑战莫过于提升自我。。16、业余生活要有意义,不要越轨。17、一个人即使已登上顶峰,也仍要自强不息。
深沟球轴承系列特征频率计算分析

1 深 沟球轴承 的运动方程
深 沟 球 轴承 由 内圈 、 外圈 、 滚 珠 和 保 持架 组 成 , 如图1 所 示 。对轴承 做 如下假 设 : 1 )滚珠 一 方面 绕 轴承 轴 线做 公 转运 动 , 另 一方
频 率 与激 励 频 率相 同 或 者 接 近 时 轴 承 就 会 发 生 共
De e p Gr o o v e Ba l l Be a r i ng s
HU Li a n g.DONG Z h a o - y u.DAI Y u — l i n.C HE NG Z h i - x u e
( S c h o o l o f E n e r g y ,P o we r a n d Me c h ni a c a l E n g i n e e r i n g ,No r t h C h i n a E l e c t r i c P o we r U n i v e r s i t y ,
态 下 和 正常 状 态 下振 动 信 号 的特 征 , 为 轴 承 的 故 障 特 征分 析提 供指 导 。
2 深 沟 球 轴 承 系 列 固 有特 性 分 析
轴 承 的 固 有 特 性 指 的是 轴 承 的 固 有 频 率 和 振 型, 是轴 承 系 统 的基 本 动态 特 性 之一 。轴 承 的 固有
第3 5 卷 第3 期 2 0 1 5 年6 月
噪
NoI S E
声
与
振
动
控
制
CoNT ROL
V_ 0 l 3 5 NO . 3 J u n .2 01 5
AND
VI BR ATI oN
文 章编 号 : 1 0 0 6 — 1 3 5 5 ( 2 0 1 5 ) 0 3 . 0 1 — 0 4 + 1 9 4
滚动轴承故障诊断中精确转频的实用计算新方法

和公式 ( 7)可以得到时域上平均每周期的数据点数 N t
和频域上平均每周期的数据点数 N f 分别为:
Nt=
fs fr
( 8)
Nf=
fr = df
fr fs
@N FFT
如果 N t > Nf
即
f f
s
r
>
fr fs
@N FFT,
fr<
( 9)
f s 时在时域 N FFT
上求取转频误差会比较小。反之, 如果 f r > fs 时, N FFT
进行精确调节与选择的过程中, 择近原则是利用某一
66
振 动与 冲击
2007年第 26卷
加权函数对各转频点及其各阶倍频进行加权计算, 认 为计算后的结果就是该转频点处的能量值, 具有最大 能量总和的转频即为最佳转频。因此加权函数的选取 和参与加权计算的数据个数很重要, 可以根据实际情 况进行调节。
4 应用实例
p @ ( 2+
K@w ) 2 @ fs
@f r
@ v, 一般取
10 左右 的正 整数 。
5) 对于每一转频 f ri, 定义贴近度为
m
E R( f ri, S ) = R (f rij, S ) j= 1
( 14)
那么具有最大贴近度的转频 fri 即为最佳转频。这就是
择近原则的基本原理。
从上可以看出, 在对目标转 频前后若干个转频点
fr;
v为每个转频的倍频数, 一般
取 10左右的正整数。
2) 为提高频率分辨率, 对时标脉冲信号补 0 处
理, 进行频域分析, 求其功率谱 S
S = { sl }, l = 1, 2, ,, p
滚动轴承故障解释和频率计算

滚动轴承故障发展过程的四阶段中典型特征
第一阶段:1噪声正常;2.温度正常;3.可用超声,振动尖峰能量gSE声发 射测量出来,轴承外环有缺陷;4.振动总量较小,无离散的轴承故障频率尖 峰;5.轴承剩余寿命大于B-10规定的百分之十。
第二阶段:1.噪声略增大;2.温度正常;3.超声,声发射,振动尖峰能量 gSE明显增大,轴承外环有缺陷;4.振动总量略增大(振动加速度总量和振 动速度总量);5.在对数刻度的频谱上可清楚地看到轴承故障频率,而在线 性刻度的频谱上则很难看到;噪声地平明显提高;6.轴承剩余寿命大于B10规定的百分之五。
滚动轴承故障各阶段 振动频谱和解调频谱的特征
1X 2X 3X
B
常规振动频谱
dB 解调频谱
40
30
任意的基准电平
20
10
频率
频率
A. 正常状态
以上所示左图为常规振动频谱;右图为解调频 谱,此图中基准电平是任意选的平的噪声电平。
正常情况下滚动轴承的常规振动频谱和解调频 谱,如上图所示。
1X 2X 3X
第四种频率 :
和频与差频 --- 轴承的若干故障频率之间及与其它 振源频率之间相 加或相减
滚动轴承故障发展的四个阶 段
第 一 阶 段 :滚动轴承故障初始阶段 第 二 阶 段 :滚动轴承轻微故障阶段 第 三 阶 段 :滚动轴承宏观故障阶段 第 四 阶 段 :滚动轴承故障最后阶段
滚动轴承故障发展的第一阶 段
增大,轴承外环有缺陷 振动总量略增大(振动加速度总量和振
动速度总量) 在对数频谱上可清楚地看到轴承故障
频率,而在线性频谱上难以看到;噪 声地平明显提高 轴 承 剩 余 寿 命 小 于 B-10 规 定 的 百 分 之 五 ( 注)
轴承故障特征倍频公式推导

欢迎阅读滚动轴承可能由于润滑不良、载荷过大、材质不当、轴承内落入异物、锈蚀等原因,引起轴承工作表面上的剥落、裂纹、压痕、腐蚀凹坑和胶合等离散型缺陷或局部损伤。
当滚动轴承另一工作表面通过某个缺陷点时,就会产生一个微弱的冲击脉冲信号。
随着转轴的旋转,工作表面不断与缺陷点接触冲击,从而产生一个周期性的冲击振动信号[5]。
缺陷点处于不同的元件工作表面,冲击振动信号的周期间隔也即频率是不相同的,这个频率就称为冲击的间隔频率或滚动轴承的故障特征频率[4,6]。
可以根据轴承的几何参数和其转速计算轴承元件的故障特征频率[4,6,10]。
a.速度关系b.几何关系图4.1 滚动轴承中个元件的运动关系如图4.1所示,设外圈和内圈滚道上分别有一接触点A 和B ,假设为理想状态,径向游隙为零,则A 点和B 点的圆周速度分别为式中 令 式中 度]。
e m m 滚动体围绕轴承中心线的公转线速度乃是i v 和e v 的平均值,即滚动体的公转线速度也就是保持架中心圆的线速度。
保持架中心圆上某一点的线速度为 由上两式得保持架的转速为)]1()1([21γγ++-=e i m n n n (4-4) 内圈相对于保持架的转速为()()γ+-=-=121e i m i im n n n n n (4-5) 假设保持架上有z 个滚动体,内圈上某一点滚动体滚过频率为外圈相对于保持架的转速为()()γ--=-=121i e m e em n n n n n (4-6) 外圈上某一点滚动体滚过频率为滚动体的自转转速0n 可由接触点处两物体线速度相等的关系求得。
例如,滚动体与内圈接触的B 点相对于滚动体中心的线速度为式中 0n 为滚动体自转转速。
内圈滚道上与滚动体接触着的B 点相对于滚动体中心的线速度为根据纯滚动条件,滚动体上接触点B 和内圈滚道上相应的B 点速度相等,得到由此可得滚动体的自转转速为时,则有[6]外圈上某一点每分钟通过的滚动体数为z D d n z n N mem e cos 1(21α-== (4-9) 滚动体自转速度为)cos 1(2)1(222220αγmm m D d n d D n d D n -=-= (4-10) 假如内圈滚道、外圈滚道或滚动体上有一处缺陷(剥落或裂纹等局部缺陷),则两种金属体在缺陷处相接触就会发生冲击作用,冲击的间隔频率见表4-2。
转动机械常见故障的频率特征

随着齿轮故障发展,边频
越来越丰富,幅值增加。
下边频 2X
上边频
可用倒频谱作进一步分析。
可编辑ppt
13
确定报警值和危险值的方法
• 绝对法
根据相应的国际标准、国家标准、行业标准等, 如: ISO, GB, API 等。
• 相对法
以机器正常状态的振动值作为基数,自己和自己比。
出现0.5X,1.5X, 2.5X,3.5X...等 频率成分
可编辑ppt
8
滚动轴承故障的特征频率
外环故障频率
D
f z(1dcos)R
d
2D
内环故障频率
f z(1dcos)R
2D
滚珠故障频率
D — 节圆直径
f D d1(D d)2co2sR
保持架碰外环
d — 滚珠直径
— 接触角
f 1(1dcos)R
可编辑ppt
10
带滚动轴承的机械的频谱特点
Velocity in mm/s pk
3.5
不平衡 3.0
不对中 2.5
松动 2.0
1.5
滚动轴承故障频率
1.0
0.5
0
0 5 10 15 20 25 可30编辑3pp5t 40 45 50×R
11
Frequency in order
Displacement in m pk to pk
旋转机械 滑动轴承
1234 56 78
滚动轴承 齿轮
报警值 =(2~3) 正常值
危险值 =(4~6) 正常值
可编辑ppt
17
类比法确定振动限值
设备号
测点
ABCD
滚动轴承元件故障频率计算方法

滚动轴承元件故障频率计算方法滚动轴承元件故障特征频率计算方法方法1:保持架故障频率:FTF=(1/2){No[1+(d/D)Cos φ] +Ni [1-(d/D)Cos φ]} 滚动体旋转故障频率:BSF=(1/2)(D/d) |No-Ni|{ [1-(d/D)Cos φ]2}外环故障频率:BPFO=(1/2)n |No-Ni| [1-(d/D)Cosφ]内环故障频率:BPFI=(1/2)n |Ni- No| [1+(d/D)Cosφ]以上符号:d=滚动体直径;D=滚动轴承平均直径(滚动体中心处直径);φ=径向方向接触角;n-滚动体数目;No=轴承外环角速度;Ni=轴承内环角速度(=轴转速).注:1.滚动轴承没有滑动;2.滚动轴承几何尺寸没有变化;3.轴承外环和轴承内环都旋转.方法2:滚动轴承保持架故障频率:FTF=(N/2)[1-(d/D)Cos φ]滚动轴承滚动体旋转故障频率:BSF=(N/2)(D/d){1-[(d/D)Cos φ]2}滚动轴承外环故障频率:BPFO=(N/2)n[1-(d/D)Cosφ]滚动轴承内环故障频率:BPFI=(N/2)n[1+(d/D)Cosφ]以上符号:d=滚动体直径;D=滚动轴承平均直径(滚动体中心处直径);Φ= 径向方向接触角;n-滚动体数目;N=轴的转速。
注:适合1.滚动轴承没有滑动;2.滚动轴承几何尺寸没有变化;3.轴承外环固定不旋转.方法3:外环故障频率:BPFOr≌0.4Nn内环故障频率:BPFIr≌0.6Nn保持架故障频率:FTFr≌0.4N以上符号意义:n-滚动体数目;N=轴的转速。
注:1.滚动轴承没有滑动;2.滚动轴承几何尺寸没有变化;3.轴承外环固定不旋转.方法4:外环故障频率:BPFOe≌N(0.5n-1.2)内环故障频率:BPFIe≌N(0.5n+1.2)滚动体故障频率:BSFe≌N(0.2n-1.2/n)保持架故障频率:FTFe≌N(0.5-1.2/n)以上符号意义:n=滚动体数目;N=轴的转速。
频谱分析_滚动轴承_齿轮和电气故障

低压 (离心) 风机或送风机 – 通常不容易发生这类问题。 BPF(叶片通过频率) – 很少见的故障, 除非频率激发了下游管道系 统的共振频率。 通常是归类为噪声问题, 很少是结构问题。 它几乎不 能引起机械故障,如加速轴承或部件磨损。 紊流 – 能引起低频宽带振动 (低于或略高于 1x rpm)。
2) 回到 gSE 频谱,将振幅单位定为dB。 然后把这个故障频率峰值振幅 和附近的背景噪声比较 (周围的)。 如果差值为 12 - 18 dB, 说明发生了相 当明显的冲击。 如果差值为18+ dB, 说明有大量的冲击发生。 冲击等级 越高, 轴承破坏就越快。 注意 – 有两个主要原因: 如果你使用“过载” 或“幅度” (趋势) 值 而不分析包络频谱,你必须 意识到会有很多不同因素能引起冲击,而这些检测到的信号很多并不是 来自轴承故障。
紊流症状: (1)高频, 随机振动类似气穴。 (2)叶片或叶轮 (螺旋桨) 在通过频率 (指 ‘VPF’以下)振幅大。 (3)VPF谐波振幅大。
注意: 重要的是压缩机和送风机的 VPF是正常的机械振动。 过度依赖 初始读数而不知道正常的运行情况是十分危险的。 振幅也和负载有关, 应该不断地在同等的负载条件下采集读数。 如果压缩机负载或卸载读 数相同,就可采纳。
图 3典型的包络图说明轴承故障频率的影响
轴承特征信号提取

机械工程 郑佳文
滚动轴承的时域指标
滚动轴承故障信号大部分属于周期性函数,信号的简 谐性、周期性和瞬时脉冲性会比较明显,可以通过分 析故障信号的时域波形曲线从而了解轴承的性能。 通过反应信号波动曲线特征指标的特定参数实现评 估故障信号的变化。常用的时域指标参数有两类: 包括有量纲参数和无量纲参数。
希尔伯特变换
在信号分析处理过程中,希尔伯特变换是一种重要的算法工具, 它是把一个一维的、时域函数转换成唯一对应的一个二维时域 解析函数。这个解析函数的模代表了原函数的包络,相角代表 了原函数的相位特性,实现了对信号幅值及相位的解调。
一个因果系统,当T<0时,冲击响应 th等于 0,仅在t>0 情况下存在, 因此: h(t)的傅里叶变换也就是系统函数 H(ω)分解成实部 R(ω)和虚部 jx(ω) 之和 对式进行傅里叶变换得:
3.滚动轴承滚珠故障的特征提取
通过采集到的滚珠的故障信号的数据,对其进行希尔伯特解调。步骤 如上节类似,可以得到滚珠故障波形如图 3-10 所示。对其包络信号 做傅里叶变换得到滚珠故障的包络谱,如图 3-11 所示。
从图 3-11 可以看出,故障特征频率为 50H 左右,并同时伴有边频带, 其二倍频为100Hz 左右,从表 3-1 中可知,滚珠故障频率为 50.08Hz, 与解调信号频谱分析得出的频率接近。因此,提取的频率 50Hz 为 轴承滚珠故障的特征频率。
对其模拟轴承信号进行希尔伯特解调变换,提取的包络如图 3-4所示。提取包络之后再经过一次傅里叶变换就可以提取出合 成信号的包络谱,包络谱如图3-5所示。
从图 3-5 中可以得出故障频率为 100Hz 左右并且它的倍频 处存在峰值,与调制信号的调制频率是相近的,所以希尔 伯特解调法能够有效的提取出滚动轴承的故障特征。
轴承振动特征分析含轴承故障特征频率的特点及计算

FTFr≌0.4N
经验公式
n=滚动体数目; N=轴的转速。
注:1.滚动轴承没有滑动;2.滚动轴承几何尺寸没有变化; 3.轴承外环固定不旋转.
滚动轴承故障频率计算(4)
外环故障频率: BPFOe≌N(0.5n-1.2)
内环故障频率: BPFIe≌N(0.5n+1.2)
滚动体故障频率: BSFe≌N(0.2n-1.2/n)
滚动轴承故障频率计算(2)
保持架故障频率: FTF=(N/2)[1-(d/D)Cos φ ]
滚动体旋转故障频率: BSF=(N/2)(D/d){1-[(d/D)Cos φ ]²}
外环故障频率: BPFO=(N/2)n[1-(d/D)Cosφ ]
内环故障频率: BPFI=(N/2)n[1+(d/D)Cosφ ]
其它缩短滚动轴承寿命的因素
转子不只承受不平衡,还承受不对中、松动、气蚀或其它故障引起 的动载荷,轴承的实际寿命可能还要短。
其它因素:润滑不当,错误润滑剂,灰尘和其它污染物污染,储存 不当,潮气,运输或使用时嗑碰、刮伤,错用轴承型号,轴承安装 不当等。
最重要的对策是监测滚动轴承的状态,早期发现轴承故障,跟踪其 发展趋势,并知道何时需更换轴承;
由于安装不当对轴承施加了过大负荷。虽然,可能尚未发生实际损坏,但 是,如果检测不出这种故障问题并采取措施修正,则该轴承将在其预定寿命之 前很早就损坏。 15.轴承润滑不良产生的频率
特征是在900到1600Hz范围内,有3或4个尖峰,尖峰之间的差频在80到 130Hz。润滑良好的轴承可能也包括这些频率分量,然而,它们的幅值非常小, 约为1.27mm/s或更小。当润滑不良时,幅值增大到 2.54到5.08mm/s
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
滚动轴承可能由于润滑不良、载荷过大、材质不当、轴承内落入异物、锈蚀等原因,引起轴承工作表面上的剥落、裂纹、压痕、腐蚀凹坑和胶合等离散型缺陷或局部损伤。
当滚动轴承另一工作表面通过某个缺陷点时,就会产生一个微弱
的冲击脉冲信号。
随着转轴的旋转,工作表面不断与缺陷点接触冲击,从而产生一个周期性的冲击振动信号⑸。
缺陷点处于不同的元件工作表面,冲击振动信号的周期间隔
也即频率是不相同的,这个频率就称为冲击的间隔频率或滚动轴承的故障特征频率
[4,6]。
可以根据轴承的几何参数和其转速计算轴承元件的故障特征频率[4,6,1°]。
b.几何关系
图4.1滚动轴承中个元件的运动关系
如图4.1所示,设外圈和内圈滚道上分别有一接触点 A和B,假设为理想状态,径向游隙为零,贝U A点和B点的圆周速度分别为
_兀D e
(4-1)
V e _ 60 n e
兀
D i V i
=~60
n i
D i ——外圈、内圈滚道接触点处的直径,[mm ];
外圈上某一点滚动体滚过频率为
式中
V e
、 V i ――外圈、内圈滚道接触点处的圆周速度,[mm/s ]; n e
、
ni -- 外圈、内圈的转速, [r/mi n]。
d
Y =——cos a
D m
(4-3)
式中 d ---- 滚动体直径,[mm ]; D m ——滚动体中心圆直径,[mm ];
a ——接触角,指接触面中心与滚动体中心连线和轴承径向平面之 [弧度或角度]0
间的夹角, 由图4-1 (b)可见 D e =D m +dcosa = D m (1 +Y ) D i =D m -dco<s = D m (1-Y )
滚动体围绕轴承中心线的 公转线速度乃是V i 和V e 的平均值,即 V + V 八
V m===^D m [n i (1"n e (1F
滚动体的公转线速度也就是保持架中心圆的线速度。
保持架中心圆上某一点的线 速度为 沢D m Vm = —
n m
由上两式得保持架的转速为 (4-4) 内圈相对于保持架的转速为 F -nmni - ne [1 + Y ) 2 假设保持架上有z 个滚动体,内圈上某一点滚动体滚过频率为 N i =(n i -n m )z = 1
(n i - n e 11 + Y k 2 n m (4-5)
外圈相对于保持架的转速为 n em »n m
V n dO
(4-6)
(4-2)
D e 、
N e = (n e — n m)Z = 2 (H e —)(1 ―丫
滚动体的自转转速n o可由接触点处两物体线速度相等的关系求得。
例如, 滚动体与内圈接触的B点相对于滚动体中心的线速度为
2^0 d
V
OB=苛辽
保持架相对于外圈的转速
表4-1有局部缺陷引起的冲击振动间隔频率
缺陷位置
式中n o为滚动体自转转速。
内圈滚道上与滚动体接触着的 B点相对于滚动体中心的线速度为
60 2
根据纯滚动条件,滚动体上接触点B和内圈滚道上相应的B点速度相等, 得到
V oB ^V iB
由此可得滚动体的自转转速为
D i
n。
= (n i -n m)=
d D 2
D^g-n e)(1-Y2)
2d
(4-7)
假如内圈滚道、外圈滚道或滚动体上有一处缺陷(剥落或裂纹等局部缺陷),则两种金属体在缺陷处相接触就会发生冲击作用,冲击的间隔频率见表
绝大多数滚动轴承在实际应用中总是保持外圈静止,内圈与轴一起旋转,当轴的转速为n时,则有
4-1。
n i = n n e = 0 由上面式(4-5)可得内圈相对于保
持架的转速
1 「— 1 d cosa
因为保持架上有z个滚动体,所以内圈上某一点每分钟通过的滚动体数为
1 N i =nimz=1n(1+常)z
D m
(4-8)
"em
d COSG) =丄门(1 -Y )=- n(1-
2 2 D m
表有局部缺陷引起的冲击振动间隔频率⑹外圈上某一点每分钟通过的滚动体数为
1 N e=n em z=?n(1- d
cos。
)z
(4-
9)
滚动体缺陷位置
内圈
外圈
冲击单侧滚道
冲击两侧滚道
保持架与外圈摩擦保持架与内圈摩擦冲击振动发生的间隔频率[Hz]
n(1+竺竺)z
2X60 D m
2咒60(1—
d COSG
D m
)z
n D m(』cos2cQ
D
f0倍(1 dj)
D m
n 一dcosa、em2
石D
m
-^H + dcosa
2 咒60 f D
m
假如内圈滚道、外圈滚道或滚动体上有一处缺陷(剥落或裂纹等局部缺陷), 则两种
金属体在缺陷处相接触就会发生冲击作用,冲击的间隔频率见表
滚动体自转速度为 2
n
o 号心
航)
(4-10)
4-2。
