最小二乘法拟合原理及实例
最小二乘法拟合原理及实例

最小二乘法原理
若列表函数所有节点基本上呈现线性变化规律,用直线方程f (x) = a + b x描述
选取系数a, b,使偏差平方和e最小,就是最小二乘法的实质
最小二乘法处理的任务就是求直线方程中的待定系数a和b
最小二乘法步骤
①在坐标纸上标出列表函数各节点数据,并根据其趋势绘出大致
的曲线
②根据曲线确定近似的拟合函数类型,拟合函数可为代数多项式、
对数函数、指数函数…
③用最小二乘法原理确定函数中的待定系数
NEXT
莎图示*Z卄…
沪W Y(八兀・)-儿)2 = Y(a + bx.-儿)2
J=1 2=1 1=1
根据函数求极值性质,函数对自变量的偏导为零则令:
I da = 0
dtp /db = 0
求偏导数.得:
(XI TO
三2(p+bx i— J,) = 0 丫2
召@ +琳-开)=0 求得“=尹
_力0
—心厂刁
Z Xi (每-X)
NEXT
BACK 9例:疥中狀实昨为例’唉性方程 将表中数据代入前式得方程组: f5 a + 15Z? = 13
15cz+ 55b = 50
求解得:a=-0. 7 b=l. 1
贝 ij : f (x)二l.lx-o.7 • 1 Xi yt Xi 2 x iXi
1 1 0 1 0
2 2 2 4 4
3 3 2 9 6
4 4
5 1
6 20
5 5 4 25 20
s 15 13 55 50。
最小二乘法拟合曲线

m=6;n=3; A=zeros(n+1); for j=1:n+1 for i=1:n+1 for k=1:m+1 A(j,i)=A(j,i)+x(k)^(j+i-2) end end end;
B=B'; a=inv(A)*B; x=[-1.0:0.0001:2.0]; z=a(1)+a(2)*x+a(3)*x.^2+a(4)*x.^3; plot(x,z) legend('离散点','y=a(1)+a(2)*x+a(3)*x.^2+a(4)*x.^3') title('拟合图')
title('拟合图')
x=-1.0:0.5:2.0; y=[-4.447,-0.452,0.551,0.048,-0.447,0.549,4.552]; plot(x,y,'*') xlabel'x轴' ylabel'y轴' title'散点图' hold on
B=[0000]; for j=1:n+1 for i=1:m+1 B(j)=B(j)+y(i)*x(i)^(j-1) end end
的方法即为最小二乘法多项式拟合。
确定上述多项式的过程也就是确定
中的系数
的过程,根据最小二乘原则,则偏差平方和应该是这些系数的函数,即
为使上式取值最小,则其关于ak
的一阶导数应该为零,即有
将上面各等式写成方程组的形式可有
写成矩阵形式有
上述方程组可以通过克莱姆法则来计算,从而解出各系数
得到拟合方程。
最小二乘法拟合曲线01 来自景 04 算法目录CONTENTS
最小二乘法的原理及在建模中的应用分析

最小二乘法的原理及在建模中的应用分析最小二乘法(least squares method)是一种数学优化方法,用于解决线性回归和非线性回归问题,通过求取使得误差平方和最小化的参数估计值。
它的原理是寻找一条最佳拟合曲线或平面,使得观测值与拟合值之间的误差最小。
在线性回归问题中,最小二乘法可以用来估计回归模型的参数。
假设我们有n个样本点{(x1, y1), (x2, y2), ..., (xn, yn)},其中yi是对应的观测值,我们想要找到一个线性模型y = ax + b,使得拟合值与观测值之间的误差最小。
这个问题可以通过最小化误差平方和来求解。
误差平方和定义为E(a, b) = Σ(yi - (axi + b))^2,我们需要找到使得E(a, b)最小的a和b。
∂E/∂a = -2Σ(xi(yi - (axi + b))) = 0∂E/∂b = -2Σ(yi - (axi + b)) = 0将上述方程进行化简,可以得到如下的正规方程组:Σ(xi^2)a + Σ(xi)b = Σ(xi yi)Σ(xi)a + nb = Σ(yi)解这个方程组,可以得到最小二乘估计的参数值。
1.线性回归分析:最小二乘法可以用于估计线性回归模型的参数。
通过最小二乘估计,可以得到最佳拟合直线,并用这条直线来预测因变量。
2.时间序列分析:最小二乘法可以用于拟合时间序列模型。
通过寻找最佳拟合函数,可以识别出序列中的趋势和周期性变化。
3.统计数据处理:最小二乘法可以用于数据平滑和滤波处理。
通过拟合一个平滑曲线,可以去除数据中的噪声和不规则波动,从而提取出数据中的趋势信息。
4.多项式拟合:最小二乘法可以用于多项式拟合。
通过最小二乘估计,可以拟合出多项式函数,将其用于数据拟合和函数逼近。
5.曲线拟合:最小二乘法可以用于非线性曲线拟合。
通过选择合适的函数形式,并通过最小二乘估计求解参数,可以拟合出复杂的非线性曲线。
总之,最小二乘法是一种常用的参数估计方法,可以用于线性回归、非线性拟合、时间序列分析等多种建模问题。
最小二乘法曲线拟合_原理及matlab实现

曲线拟合(curve-fitting ):工程实践中,用测量到的一些离散的数据},...2,1,0),,{(m i y x i i =求一个近似的函数)(x ϕ来拟合这组数据,要求所得的拟合曲线能最好的反映数据的基本趋势(即使)(x ϕ最好地逼近()x f ,而不必满足插值原则。
因此没必要取)(i x ϕ=i y ,只要使i i i y x -=)(ϕδ尽可能地小)。
原理:给定数据点},...2,1,0),,{(m i y x i i =。
求近似曲线)(x ϕ。
并且使得近似曲线与()x f 的偏差最小。
近似曲线在该点处的偏差i i i y x -=)(ϕδ,i=1,2,...,m 。
常见的曲线拟合方法:1.使偏差绝对值之和最小2.使偏差绝对值最大的最小3.使偏差平方和最小最小二乘法:按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。
推导过程:1. 设拟合多项式为:kk x a x a a x +++=...)(10ϕ2. 各点到这条曲线的距离之和,即偏差平方和如下:3. 问题转化为求待定系数0a ...k a 对等式右边求i a 偏导数,因而我们得到了:.......4、 把这些等式化简并表示成矩阵的形式,就可以得到下面的矩阵:5. 将这个范德蒙得矩阵化简后可得到:6. 也就是说X*A=Y ,那么A = (X'*X)-1*X'*Y ,便得到了系数矩阵A ,同时,我们也就得到了拟合曲线。
MATLAB实现:MATLAB提供了polyfit()函数命令进行最小二乘曲线拟合。
调用格式:p=polyfit(x,y,n)[p,s]= polyfit(x,y,n)[p,s,mu]=polyfit(x,y,n)x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。
x 必须是单调的。
矩阵s包括R(对x进行QR分解的三角元素)、df(自由度)、normr(残差)用于生成预测值的误差估计。
最小二乘法曲线拟合-原理及matlab实现

曲线拟合(curve-fitting ):工程实践中,用测量到的一些离散的数据},...2,1,0),,{(m i y x i i =求一个近似的函数)(x ϕ来拟合这组数据,要求所得的拟合曲线能最好的反映数据的基本趋势(即使)(x ϕ最好地逼近()x f ,而不必满足插值原则。
因此没必要取)(i x ϕ=i y ,只要使i i i y x -=)(ϕδ尽可能地小)。
原理:给定数据点},...2,1,0),,{(m i y x i i =。
求近似曲线)(x ϕ。
并且使得近似曲线与()x f 的偏差最小。
近似曲线在该点处的偏差i i i y x -=)(ϕδ,i=1,2,...,m 。
常见的曲线拟合方法:1.使偏差绝对值之和最小2.使偏差绝对值最大的最小3.使偏差平方和最小最小二乘法:按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。
推导过程:1. 设拟合多项式为:kk x a x a a x +++=...)(10ϕ2. 各点到这条曲线的距离之和,即偏差平方和如下:3. 问题转化为求待定系数0a ...k a 对等式右边求i a 偏导数,因而我们得到了:.......4、 把这些等式化简并表示成矩阵的形式,就可以得到下面的矩阵:5. 将这个范德蒙得矩阵化简后可得到:6. 也就是说X*A=Y ,那么A = (X'*X)-1*X'*Y ,便得到了系数矩阵A ,同时,我们也就得到了拟合曲线。
MATLAB实现:MATLAB提供了polyfit()函数命令进行最小二乘曲线拟合。
调用格式:p=polyfit(x,y,n)[p,s]= polyfit(x,y,n)[p,s,mu]=polyfit(x,y,n)x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。
x 必须是单调的。
矩阵s包括R(对x进行QR分解的三角元素)、df(自由度)、normr(残差)用于生成预测值的误差估计。
excel最小二乘法拟合

excel最小二乘法拟合Excel是一款十分实用的电子表格软件,是办公室不可或缺的一种工具。
它提供了很多支持数据处理的功能,其中最小二乘法拟合就是其中之一。
在下面的文章中,我们将介绍Excel最小二乘法拟合的定义、原理、实现方法和应用场景。
一、最小二乘法拟合的定义最小二乘法拟合是一种利用直线、曲线等模型对数据进行拟合的统计技术,利用数学公式对实际数据进行回归分析,以求得最优解。
最小二乘法拟合的核心思想是:通过对数据进行拟合,得到一条最优的曲线,使该曲线与实际数据的偏差最小,从而找到最佳的拟合曲线。
这种方法在Excel中被广泛应用于数据趋势分析、曲线预测等实际应用领域中。
二、最小二乘法拟合的原理最小二乘法拟合的核心原理是:通过不断调整拟合曲线的参数,使得曲线与实际数据的差距最小,从而达到最优化的目的。
这一过程可以通过Excel中的线性回归操作来完成。
具体步骤如下:步骤1:打开Excel,将数据输入到表格中。
在数据的一侧,插入一个空白列。
在空白列中输入 1、2、3、4、5……,这一列是用于拟合曲线的自变量。
步骤2:选择“数据”->“数据分析”,在弹出的对话框中选择“回归”。
在“回归”窗口中,需要输入以下三个参数:i) 输入区域:选择要进行回归分析的数据区域。
ii) 输出区域:输入结果区域,可以选择开启图表输出。
iii) 统计方法:选择“阵列”。
步骤3:点击确定,Excel会返回一个包含回归方程及其系数的结果表格。
可以在该表格中查看算法使用的参数、标准误差、置信区间及偏差等信息。
步骤4:可以根据得到的拟合方程对数据进行预测,从而解决实际问题。
三、最小二乘法拟合的实现方法在Excel中,最小二乘法拟合的实现方法主要通过回归分析功能来完成。
以下是具体步骤:步骤1:将要分析的数据输入到Excel中。
步骤2:在Excel中打开“回归分析”功能。
选择“数据”->“数据分析”->“回归”。
步骤3:在“回归”窗口中,选择“阵列”方法。
第5章-1 曲线拟合(线性最小二乘法)讲解
求所需系数,得到方程: 29.139a+17.9b=29.7076 17.9a+11b=18.25
通过全选主元高斯消去求得:
a=0.912605
b=0.174034
所以线性拟合曲线函数为: y=0.912605x+0.174034
练习2
根据下列数据求拟合曲线函数: y=ax2+b
x 19 25 31 38 44 y 19.0 32.3 49.0 73.3 97.8
∑xi4 a + ∑xi2 b = ∑xi 2yi
∑xi2 a + n b = ∑yi
7277699a+5327b=369321.5 5327a+5b=271.4
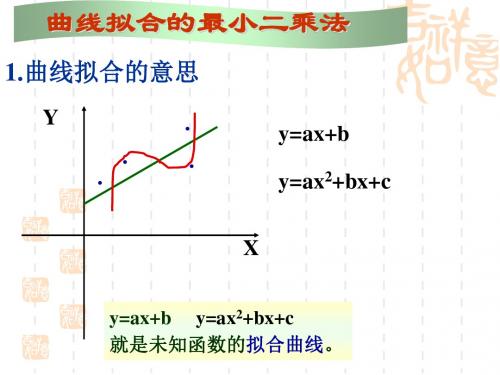
曲线拟合的最小二乘法
1.曲线拟合的意思
Y
.
.
.
.
y=ax+b y=ax2+bx+c
X
y=ax+b y=ax2+bx+c 就是未知函数的拟合曲线。
2最小二乘法原理
观测值与拟合曲线值误差的平方和为最小。
yi y0 y1 y2 y3 y4…… 观测值 y^i y^0 y^1 y^2 y^3 y^4…… 拟合曲线值
拟合曲线为: y=(-11x2-117x+56)/84
x
yHale Waihona Puke 1.61 1.641.63 1.66
1.6 1.63
1.67 1.7
1.64 1.67
1.63 1.66
1.61 1.64
1.66 1.69
1.59 1.62
(完整版)最小二乘法圆拟合

最小二乘法圆拟合1.最小二乘法圆拟合原理 1.1理论最小二乘法(Least Square Method )是一种数学优化技术。
它通过最小化误差的平方和找到一组数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
1.2最小二乘圆拟合模型公式推导在二维平面坐标系中,圆方程一般可表示为:()22020)(r y y x x =-+- (1) 对于最小二乘法的圆拟合,其误差平方的优化目标函数为:[]212020)()(∑=--+-=ni i i r y y x x S式中:()i i y x ,n i ,...,2,1=为圆弧上特征点坐标;n 为参与拟合的特征点数。
在保持这优化目标函数特征的前提上,我们需要对其用一种稍微不同的改进方法来定义误差平方,且其避免了平方根,同时可得到一个最小化问题的直接解,定义如下:[]2122020)()(∑=--+-=ni i i r y y x x E (2)则(2)式可改写为:()2122002200222∑=-+-++-=ni i ii iry y y y x x x x E (3)令,02y B -=,02x A -=22020r y x C -+= 即(3)式可表示为:()222∑=++++=ni i i i i C By Ax y x E由最小二乘法原理,参数A ,B ,C 应使E 取得极小值。
根据极小值的求法,A ,B 和C 应满足()02022=++++=∂∂∑=i ni i i i i x C By Ax y x A E(4) ()02022=++++=∂∂∑=i n i i i i i y C By Ax y x B E(5) ()02022=++++=∂∂∑=n i i i i i C By Ax y x C E(6) 求解方程组,先消去参数C ,则 式()()∑=*-*ni i x n 064得()002202030000002=+-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-∑∑∑∑∑∑∑∑∑∑==========ni i ni i i n i i i n i i n i n i i i n i i i n i n i i i n i i x y x y x n x n B y x y x n A x x x n (7)式()()∑=*-*ni i y n 065得()002202030002000=+-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-∑∑∑∑∑∑∑∑∑∑==========ni ini i i n i i i n i i n i n i i i n i i n i n i i i n i i i yy x y x n y n B y y y n A y x y x n (8) 令⎪⎭⎫⎝⎛-=∑∑∑===n i n i ni i i i x x x n M 000211(9)⎪⎭⎫⎝⎛-==∑∑∑===n i ni i i n i i i y x y x n M M 0002112(10)⎪⎭⎫⎝⎛-=∑∑∑===n i ni i i n i i y y y n M 000222(11)()∑∑∑∑====+-+=ni ini iin i ii n i ixyx y x n x n H 002202031(12)()∑∑∑∑====+-+=n i ini iini i ini iy yx y x n y n H 02202032(13)将(7),(8)式写成矩阵形式⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡2122211211H H B A M M M M (14) 根据式(14)和式(6)可得:21122211221122M M M M M H M H A --=22112112211112M M M M M H M H B --=()nBy Ax y xC ni ii i i∑=+++-=022从而求得最佳拟合圆心坐标()00,y x ,半径r 的拟合值:20A x -=,20B y -=,C B A r 42122-+= 2.仿真数据分析首先设置仿真圆心(x0,y0),半径R0,在根据实际数据任意选取一段圆弧,产生N 组随机数据。
已知半径 最小二乘法拟合圆公式推导及其实现

已知半径最小二乘法拟合圆公式推导及其实现一、引言在实际生活和工作中,我们经常会遇到需要拟合圆的问题,例如在图像处理、工程测量、地理信息系统等领域。
而已知圆的半径后,我们可以使用最小二乘法来拟合一个圆,从而得到圆心和半径的估计值。
本文将介绍已知圆的半径时,最小二乘法拟合圆的公式推导及其实现方法。
二、最小二乘法拟合圆公式推导1. 圆的一般方程设圆的方程可表示为:(x - a)² + (y - b)² = r²,其中(a, b)为圆心坐标,r为半径。
2. 圆的参数方程圆的参数方程可表示为:x = a + r * cos(θ),y = b + r * sin(θ),其中θ为参数。
3. 最小二乘法拟合圆原理已知若干个点(xi, yi),我们需要找到圆心(a, b)和半径r,使得所有点到圆的距离之和最小。
4. 使用最小二乘法拟合圆(1)定义误差函数设点(xi, yi)到圆的距离为di,误差函数可表示为:E = ∑(di - r)²。
(2)最小二乘法求解将参数方程带入误差函数,对E关于a、b和r求偏导数,并令偏导数为0,即可得到圆心(a, b)和半径r的估计值。
5. 拟合圆公式推导通过最小二乘法的求解过程,可以得到拟合圆的公式:a = (x¯ - r * cos(θ¯))b = (y¯ - r * sin(θ¯))r = sqrt((x¯ - a)² + (y¯ - b)²)其中(x¯, y¯)为所有点的平均坐标,θ¯为参数的平均值。
三、实现方法1. 数据预处理我们需要对已知的点坐标(xi, yi)进行数据预处理,计算出平均坐标(x¯, y¯),并求出参数的平均值θ¯。
2. 最小二乘法求解将已知的点坐标(xi, yi)带入拟合圆的公式中,使用最小二乘法求解圆心(a, b)和半径r。
最小二乘法的基本原理和多项式拟合matlab实现
最小二乘法的基本原理和多项式拟合一、最小二乘法的基本原理从整体上考虑近似函数)(x p 同所给数据点),(i i y x (i=0,1,…,m)误差i i i y x p r -=)((i=0,1,…,m)i i i y x p r -=)((i=0,1,…,m)绝对值的最大值im i r ≤≤0max ,即误差 向量T m r r r r ),,(10 =的∞—范数;二是误差绝对值的和∑=mi ir 0,即误差向量r 的1—范数;三是误差平方和∑=mi ir2的算术平方根,即误差向量r 的2—范数;前两种方法简单、自然,但不便于微分运算 ,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和∑=mi ir02来 度量误差i r (i=0,1,…,m)的整体大小。
数据拟合的具体作法是:对给定数据 ),(i i y x (i=0,1,…,m),在取定的函数类Φ中,求Φ∈)(x p ,使误差i i i y x p r -=)((i=0,1,…,m)的平方和最小,即∑=mi ir2[]∑==-mi iiy x p 02min)(从几何意义上讲,就是寻求与给定点),(i i y x (i=0,1,…,m)的距离平方和为最小的曲线)(x p y =(图6-1)。
函数)(x p 称为拟合函数或最小二乘解,求拟合函数p(x)的方法称为曲线拟合的最小二乘法。
合中,函数类Φ可有不同的选取方法.6—1二多项式拟合假设给定数据点),(i i y x (i=0,1,…,m),Φ为所有次数不超过)(m n n ≤的多项式构成的函数类,现求一Φ∈=∑=nk k k n x a x p 0)(,使得[]min )(00202=⎪⎭⎫⎝⎛-=-=∑∑∑===mi mi n k i k i k i i n y x a y x p I (1)当拟合函数为多项式时,称为多项式拟合,满足式(1)的)(x p n 称为最小二乘拟合多项式。
线性最小二乘法拟合

线性最小二乘法拟合
线性最小二乘法(Linear Least Squares,LLS)是一种用来对观测数据建立数学模型的最常见的统计学方法,它可以有效地从数据中恢复出一组最优参数值。
它可以用来拟合各种类型的多项式曲线,甚至可以应用到混合型曲线,并且具有良好的拟合效果。
一、线性最小二乘法的定义
线性最小二乘法是一种数学方法,记为$argmin \ \sum_{i=1}^{n} (Y_i - f(X_i))^2$,表明最小二乘法通过最小化残差(残差是指观测值与实际值的差异)的平方和,来估计参数模型的参数。
二、线性最小二乘法的原理
线性最小二乘法即最小误差平方和法,即参数估计问题关于误差平方和有最小值时参数向量,该参数向量即构成最小二乘解。
另外,在假定数据舍入误差符合高斯分布的情况下,最小二乘法可以被认为是可行统计方法的最优的一种。
三、线性最小二乘法的应用
(1)拟合函数式在数学及工程中,最小二乘法非常常见,主要用于拟合函数式,特别是二元一次函数式,如曲线或抛物线;
(2)计算未知参数线性最小二乘法可以用来解决只有已知数据,而求解未知参数的最小二乘问题,它除了可以拟合多项式表达式,还可以拟合非线性方程;
(3)建立数据模型经过数据分析处理,可以使用最小二乘法的方法建立数据模型,来求解某些复杂的问题。
四、线性最小二乘法的优缺点
(1)优点:算法简单,收敛速度快,适用于线性拟合;
(2)缺点:模型不一定适用所有数据,受输入噪声影响,不适用高次函数拟合。
线性最小二乘法是广泛用于统计学和工程领域的有效方法,它不仅可以提供良好的拟合效果,而且可以有效地恢复出参数模型的最优参数值,可以满足许多不同的场景的需求,也被广泛认可和使用。
最小二乘法计算例题

最小二乘法计算例题最小二乘法是数学统计学上十分常见的一种拟合方法,它可以用来在数据中拟合出一条曲线,使得一组数据集合最佳地拟合出一条曲线或多条曲线。
最小二乘法是统计方法中最常用的拟合方法,它的原理是根据给定的多个数据点,寻找最佳拟合的曲线,使得拟合曲线与所有已知数据点之间的距离最小。
最小二乘法最容易计算的曲线就是一元多项式曲线,它是任意数据点之间拟合出的参数曲线。
本文将介绍小二乘法的计算步骤和过程,以及一个示例,以帮助大家更加熟练地掌握这一知识点。
一、最小二乘法的概念最小二乘法是数学中一种常用的拟合方法,也叫参数估计法,它可以用来拟合给定的数据点,使得这个数据集合的距离最小。
最小二乘法的原理是尽可能最大地减少直线与数据点之间的距离,以期搜索到最佳拟合的曲线。
二、最小二乘法的计算步骤1.确定样本数据:首先要确定给定的样本数据,这些样本数据将用来计算最小二乘法获得最优拟合曲线。
2.计算最小二乘法残差:根据给定的数据点,可以计算出残差,残差就是拟合曲线与样本数据点之间的差值。
3.求解最小二乘公式:最小二乘法求解公式是用来获得拟合曲线中参数的最优值的公式。
4.使用极点最小二乘法:最小二乘法的极点求解法是求解最优拟合曲线的另一种方法,它的步骤与最小二乘法的求解步骤一样,但是使用了不同的数学方法。
三、最小二乘法计算例题下面我们来看一个具体的拟合曲线计算例题,此例题中要使用到最小二乘法,拟合给定的数据点。
所需数据: y=(3,2,1,0,-1)x=(1,2,3,4,5)要求:拟合出一条一元多项式曲线解法:1.计算残差:根据数据点求出残差,残差的计算公式为yi-ai-bxi,在此例题中,可以求出:3-a-b=12-a-2b=11-a-3b=20-a-4b=-1-1-a-5b=-32.求解最小二乘公式:根据求出的残差,可以求出最小二乘求解公式,公式为:b=(nΣxiyi-ΣxiΣyi) / (nΣx2i-(Σxi)2)a=(Σyi-bΣxi) / n在此例题中,可以求出:b= ( 5*6-15*-3) / (5*30-225) = 0.4a= (-3-0.4*15) / 5 = -2.23.使用极点最小二乘法:最后,我们可以使用极点最小二乘法,计算出最优的拟合曲线,其结果为:y=-2.2+0.4x因此,我们可以得出本例题的答案:y=-2.2+0.4x。
excel表格最小二乘法拟合

excel表格最小二乘法拟合一、最小二乘法拟合原理1. 基本概念- 在Excel表格中进行最小二乘法拟合,首先要理解最小二乘法的基本原理。
最小二乘法是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。
- 对于一组给定的数据点(x_i,y_i)(i = 1,2,·s,n),假设我们要拟合的函数为y = f(x),那么误差e_i=y_i - f(x_i)。
最小二乘法的目标就是使∑_{i = 1}^ne_{i}^2最小。
2. 线性拟合(以一元线性为例)- 对于一元线性函数y = ax + b,我们要根据给定的数据点(x_i,y_i)确定a和b 的值。
- 根据最小二乘法原理,a和b的计算公式为:- a=frac{n∑_{i = 1}^nx_iy_i-∑_{i = 1}^nx_i∑_{i = 1}^ny_i}{n∑_{i =1}^nx_{i}^2-(∑_{i = 1}^nx_i)^2}- b=frac{∑_{i = 1}^ny_i - a∑_{i = 1}^nx_i}{n}二、Excel中的操作步骤(以线性拟合为例)1. 准备数据- 在Excel中输入要拟合的数据,将自变量x的值放在一列(例如A列),因变量y的值放在另一列(例如B列)。
2. 绘制散点图- 选中数据(包括x和y的值),点击“插入”选项卡,选择“散点图”。
这一步可以直观地观察数据的分布情况。
3. 添加趋势线(进行拟合)- 在散点图上右键单击其中一个数据点,选择“添加趋势线”。
- 在弹出的“设置趋势线格式”对话框中:- 选择“线性”类型(如果是进行线性拟合)。
- 勾选“显示公式”和“显示R平方值”。
“显示公式”会给出拟合得到的线性方程y = ax + b的具体表达式,“显示R平方值”可以用来评估拟合的好坏,R^2的值越接近1,说明拟合效果越好。
三、实例演示假设我们有以下一组数据:x y1 23 44 55 61. 数据输入- 在Excel的A1 - A5单元格分别输入1、2、3、4、5,在B1 - B5单元格分别输入2、3、4、5、6。
最小二乘法拟合原理及代码的实现

上式是关于 (a0 , a1 ,...., an ) 的线性方程组,用矩阵表示为:
m 1 m xi i 0 m x n i i 0
xi
i 0 m
m
x
i 0
2 i
x
i 0
m
n 1 i
m n x y i i i 0 a0 i 0 m m xy a xin 1 i i 1 i 0 i 0 an m m n 2n x y xi i i i 0 i 0
最小二乘法拟合原理及代码实现
1. 最小二乘法定义 已知一组实验数据(xi, yi )(i = 0,1,2,….,m),且观测数据有误差 求自变量 x 与因变量 y 之间的函数关系 y = F(x),不要求 y = F(x)经过 所有点,而只要求在给定点的误差 δi = F(xi) – yi (i = 0,1,2,…,m) 按某种标准最小。 度量的标准不同,将导致不同的结果,常用的准则有如下三 种: a. 残差的最大绝对值为最小
解方程,得
a0
a1
x y x x y m x x m x y x y m x x
2 i i i i i 2 i 2 i i i i i 2 i 2 i
C#程序代码的实现:
} if(Math.Abs(fmX * fmX - fmXX * fn) < 0.000001) { return false; }
fk = (fmY * fmX - fmXY * fn)/(fmX * fmX - fmXX * fn); fb = (fmY - fmX * fk)/fn; return true; }
最小二乘法拟合二次方程

最小二乘法拟合二次方程一、概念与定义最小二乘法(Least Squares Method)是一种数学优化技术,它通过最小化误差的平方和来寻找数据的最佳函数匹配。
当处理的数据呈现某种趋势或模式时,如线性、二次或更高次的曲线,最小二乘法可以帮助我们找到最能代表这些数据的函数。
对于二次方程拟合,最小二乘法旨在找到一个形如(y = ax^2 + bx + c) 的二次函数,使得该函数与给定的数据点集之间的误差平方和最小。
这里的误差指的是每个数据点((x_i, y_i)) 到函数曲线上对应点((x_i, ax_i^2 + bx_i + c)) 的垂直距离。
二、性质最优性:最小二乘法得到的拟合曲线在误差平方和的意义下是最优的,即没有其他曲线能够使得误差平方和更小。
线性性:对于线性模型(包括二次模型),最小二乘法得到的解是线性的,即解可以通过数据的线性组合得到。
无偏性:在某些假设下(如误差项独立同分布,且期望为0),最小二乘法得到的估计量是无偏的,即估计量的期望等于真实参数值。
三、特点直观性:最小二乘法通过最小化误差平方和来寻找最佳拟合曲线,这一过程直观且易于理解。
计算简便:对于二次方程拟合,最小二乘法可以通过求解线性方程组来得到参数(a), (b), 和(c),计算过程相对简便。
适用性广:最小二乘法不仅适用于二次方程拟合,还可以扩展到更高次的多项式拟合以及其他类型的函数拟合。
四、规律在使用最小二乘法拟合二次方程时,我们通常会遵循以下步骤:收集数据:首先收集一组包含(x) 和(y) 值的数据点。
构建模型:根据数据点的分布趋势,构建一个形如(y = ax^2 + bx + c) 的二次模型。
计算误差平方和:对于给定的参数(a), (b), 和(c),计算每个数据点到模型曲线的垂直距离的平方和。
最小化误差平方和:通过调整参数(a), (b), 和(c) 的值,使得误差平方和达到最小。
这通常可以通过求解一个线性方程组来实现。
曲线拟合的最小二乘法原理及实现

曲线拟合的最小二乘法原理及实现
最小二乘法是一种用于拟合数据的常用方法,特别是在需要找到一条曲线或函数来最好地描述数据时。
它的基本思想是找到一条最适合数据的曲线,使得数据点与曲线之间的偏差最小。
具体来说,最小二乘法的原理是在给定一些数据点的情况下,通过最小化每个数据点到一条曲线或函数之间的垂直距离或水平距离来找到最适合这些数据的曲线或函数。
在实际应用中,可以使用最小二乘法来拟合各种类型的曲线,如线性、二次、三次、指数等。
下面是最小二乘法的基本步骤:
1.收集数据并确定要拟合的函数类型。
2.确定函数中的待定系数,例如线性函数中的截距和斜率,二次
函数中的二次项系数、一次项系数和截距等。
3.计算每个数据点到拟合曲线的垂直距离或水平距离。
4.通过最小化距离平方和来确定待定系数,例如线性函数中可以
使用公式(b-x)² + (c-y)² = 最小值,其中b和c是待定的截距和斜率。
5.求解方程组来确定待定系数,例如在线性函数中可以使用公式
b = ∑xiyi / ∑xi,
c = ∑xi² / ∑xi来计算截距和斜率。
6.使用确定的函数系数来绘制拟合曲线。
需要注意的是,最小二乘法可能不适用于所有类型的数据,并且可能需要使用其他曲线拟合方法来获得更好的结果。
在实际应用中,还需要考虑数据的准确性和可靠性,以及选择最适合数据类型的拟合方法。
最小二乘法的原理及应用

最小二乘法的原理及应用最小二乘法是一种统计学上的回归分析方法,它用于确定两个变量之间的线性关系。
最小二乘法可以用于处理一组数据,以得到数据中变量之间的关系。
在实际应用中,最小二乘法的应用非常广泛,如经济学、物理学、工程学等领域。
一、最小二乘法的原理最小二乘法的原理是通过最小化误差平方和来确定数据之间的线性关系。
在最小二乘法中,误差指的是预测值与实际值之间的差异。
最小二乘法的步骤如下:1. 收集数据,并绘制出散点图。
2. 绘制最佳拟合直线,使所有数据点到直线的距离之和最小。
3. 计算最佳拟合直线的方程式。
最小二乘法是通过最小化误差平方和的数学公式来计算最佳拟合直线的。
误差平方和等于每个数据点与最佳拟合直线之间的距离的平方和。
最小二乘法的目的就是要使这个误差平方和最小。
二、最小二乘法的应用最小二乘法的应用非常广泛,其中一些典型的应用包括:1. 经济学在经济学中,最小二乘法被用于研究价格、产量和需求之间的关系。
最小二乘法可以帮助经济学家确定供求曲线,并预测价格和数量的走向。
2. 物理学在物理学中,最小二乘法被用于研究物理系统中的不确定性。
物理学家可以使用最小二乘法来确定实验数据中的误差以及物理定律的适用性。
3. 工程学在工程学中,最小二乘法被用于研究不同变量之间的关系。
最小二乘法可以帮助工程师预测材料的性能、机器的寿命、以及其他相关的工程问题。
最小二乘法在各种学科中的应用范围是非常广泛的,它可以帮助研究人员发现不同变量之间的关系,从而预测未来的趋势。
因此,最小二乘法在科学研究和实践中具有重要地位。
最小二乘法多项式曲线拟合原理与实现

最小二乘法多项式曲线拟合原理与实现一、引言最小二乘法多项式曲线拟合是一种常用的数据拟合方法,它可以通过一组离散的数据点来拟合出一个多项式函数,从而达到对数据进行预测和分析的目的。
本文将详细介绍最小二乘法多项式曲线拟合的原理与实现。
二、最小二乘法最小二乘法是一种数学优化方法,它可以通过最小化误差平方和来求解未知参数。
在多项式曲线拟合中,我们需要求解多项式函数中各个系数的值,使得该函数与给定数据点之间的误差平方和最小。
三、多项式曲线拟合多项式曲线拟合是指通过一组离散的数据点来拟合出一个多项式函数,该函数能够较好地描述这些数据点之间的关系。
在实际应用中,我们通常使用低阶的多项式函数来进行拟合,例如一次、二次或三次多项式函数。
四、最小二乘法多项式曲线拟合原理假设我们有n个离散的数据点(x1,y1),(x2,y2),...,(xn,yn),其中xi表示自变量,yi表示因变量。
我们希望通过这些数据点来拟合出一个m次多项式函数y=f(x),其中m为多项式的阶数。
我们可以将多项式函数表示为如下形式:f(x)=a0+a1x+a2x^2+...+amxm其中a0,a1,...,am为待求解的系数。
我们需要通过最小二乘法来求解这些系数的值。
首先,我们需要定义误差平方和E(a0,a1,...,am):E(a0,a1,...,am)=∑i=1n(yi−f(xi))^2然后,我们需要求解使得误差平方和最小的系数值。
为了方便计算,我们可以将误差平方和展开:E(a0,a1,...,am)=∑i=1n(yi−a0−a1xi−a2xi^2−...−amxm)^2接下来,我们需要对误差平方和进行求导,并令导数等于零,从而得到使得误差平方和最小的系数值。
具体来说,我们需要分别对每个系数进行求导:∂E/∂a0=−2∑i=1n(yi−a0−a1xi−a2xi^2−...−amxm)∂E/∂a1=−2∑i=1n(xi(yi−a0−a1xi−a2xi^2−...−amxm))...∂E/∂am=−2∑i=1n(xmi(yi−a0−a1xi−a2xi^2−...−amxm))然后,我们将每个导数等于零,得到一个线性方程组:∑j=0maijaj=∑i=1nyi×xi^j其中aij表示第j个系数的第i次幂。
曲线拟合的最小二乘法原理及实现

曲线拟合的最小二乘法原理及实现任务名称简介在数据处理和统计分析中,曲线拟合是一种常见的技术,旨在通过数学函数找到最佳拟合曲线,以尽可能准确地描述给定数据集的变化趋势。
在曲线拟合的过程中,最小二乘法是一种常用的数学方法,用于选择最佳拟合曲线。
本文将详细介绍最小二乘法的原理和实现方法。
最小二乘法原理最小二乘法是一种通过最小化误差平方和来拟合数据的方法。
其基本原理是将数据集中的每个数据点与拟合曲线上对应点的差值进行平方,然后将所有差值的平方相加,得到误差平方和。
最小二乘法的目标是通过调整拟合曲线的参数,使得误差平方和达到最小值。
假设我们有一个包含n个数据点的数据集,每个数据点的横坐标为x,纵坐标为y。
我们希望找到一个拟合曲线,可以通过曲线上的点与数据点的差值来评估拟合效果。
拟合曲线的一般形式可以表示为:y = f(x, β)其中,β为拟合曲线的参数,f为拟合曲线的函数。
最小二乘法的基本思想是选择适当的参数β,使得误差平方和最小化。
误差平方和可以表示为:S(β) = Σ(y - f(x, β))^2其中,Σ表示求和操作,拟合曲线上的点的横坐标为x,纵坐标为f(x, β)。
为了找到误差平方和的最小值,我们需要对参数β进行求解。
最常用的方法是对参数β求导数,令导数为0,从而得到参数的估计值。
求解得到的参数估计值就是使得误差平方和最小化的参数。
最小二乘法实现步骤最小二乘法的实现可以分为以下几个步骤:1.确定拟合曲线的函数形式。
根据数据的特点和拟合的需求,选择合适的拟合曲线函数,例如线性函数、多项式函数等。
2.建立误差函数。
根据选择的拟合曲线函数,建立误差函数,即每个数据点与拟合曲线上对应点的差值的平方。
3.求解参数估计值。
对误差函数求导数,并令导数为0,求解得到参数的估计值。
4.进行拟合曲线的评估。
通过计算误差平方和等指标来评估拟合曲线的质量,可以使用残差平方和、R方值等指标。
5.优化拟合结果(可选)。
根据评估的结果,如有必要可以调整拟合曲线的参数或选择其他拟合曲线函数,以得到更好的拟合效果。
