《材料力学》第3章扭转习题解
材料力学 扭转答案

3—1 一传动轴作匀速转动,转速,轴上装有五个轮子,主动轮Ⅱ输入的功率为60kW,从动轮,Ⅰ,Ⅲ,Ⅳ,Ⅴ依次输出18kW,12kW,22kW和8kW。
试作轴的扭矩图。
解:kNkNkNkN返回3—2(3-3)圆轴的直径,转速为。
若该轴横截面上的最大切应力等于,试问所传递的功率为多大?解:故即又故返回3—3(3—5)实心圆轴的直径mm,长m,其两端所受外力偶矩,材料的切变模量。
试求:(1)最大切应力及两端截面间的相对扭转角;(2)图示截面上A,B,C三点处切应力的数值及方向;(3)C点处的切应变。
解:=返回3-4(3—6)图示一等直圆杆,已知,,,。
试求:(1)最大切应力;(2)截面A相对于截面C的扭转角。
解:(1)由已知得扭矩图(a)(2)返回3-5(3—12)长度相等的两根受扭圆轴,一为空心圆轴,一为实心圆轴,两者材料相同,受力情况也一样。
实心轴直径为d;空心轴外径为D,内径为,且。
试求当空心轴与实心轴的最大切应力均达到材料的许用切应力),扭矩T相等时的重量比和刚度比。
解:重量比=因为即故故刚度比==返回3—6(3-15)图示等直圆杆,已知外力偶矩,,许用切应力,许可单位长度扭转角,切变模量。
试确定该轴的直径d。
解:扭矩图如图(a)(1)考虑强度,最大扭矩在BC段,且(1)(2)考虑变形(2)比较式(1)、(2),取返回3-7(3—16) 阶梯形圆杆,AE段为空心,外径D=140mm,内径d=100mm;BC段为实心,直径d=100mm。
外力偶矩,,。
已知:,,。
试校核该轴的强度和刚度。
解:扭矩图如图(a)(1)强度=,BC段强度基本满足=故强度满足。
(2)刚度BC段:BC段刚度基本满足.AE段:AE段刚度满足,显然EB段刚度也满足.返回3—8(3-17)习题3—1中所示的轴,材料为钢,其许用切应力,切变模量,许可单位长度扭转角。
试按强度及刚度条件选择圆轴的直径。
解:由3—1题得:故选用.返回3-9(3-18)一直径为d的实心圆杆如图,在承受扭转力偶矩后,测得圆杆表面与纵向线成方向上的线应变为。
刘鸿文《材料力学》(第5版)笔记和课后习题(含考研真题)详解-扭转(圣才出品)

(1)一般矩形截面( h 10) b
分布特点:周边各点切应力与周边相切,没有垂直于周边的切应力分量,顶点处切应力 等于零,切应力变化情况如图 3-3(a)所示。
横截面上的最大切应力 max 发生在长边中点处
短边上切应力最大值发生在中点处
矩形截面扭转时,相对扭转角
7 / 44
;R 为弹簧圈平均半径, 。
6 / 44
圣才电子书 十万种考研考证电子书、题库视频学习平台
五、非圆截面杆扭转的概念 1.基本概念 (1)翘曲:扭转变形后杆的横截面不再保持为平面的现象。 (2)自由扭转:等直杆两端受扭转力偶作用,且翘曲不受任何限制的扭转。 变形和受力特点:各横截面的翘曲程度相同,纵向纤维的长度无变化;横截面上只有切 应力。 (3)约束扭转:等直杆两端受扭转力偶作用,且翘曲受到限制的扭转。 变形和受力特点:各横截面的翘曲程度不同,相邻两截面间纵向纤维的长度改变;横截 面上有切应力和正应力。
WP
=
D3 16
式中, = d 。 D
上述公式只适用于等直杆和线弹性范围。 (2)强度条件 对于等直杆
对于变截面杆件需综合考虑 T 和 Wt,以求得切应力的最大值。
强度条件的应用:
①强度校核
Tmax [ ] Wt
4 / 44
圣才电子书
②截面选择
十万种考研考证电子书、题库视频学习平台
G
=
E
2(1+
)
4.剪切应变能
在应力小于剪切比例极限的情况下,单位体积内的剪切应变能密度为
=
1 2
=
2 2G , v
= 1 2
上述公式主要用于线弹性范围内纯剪切应力状态下剪切应变能密度的计算。
材料力学_陈振中_习题第三章扭转
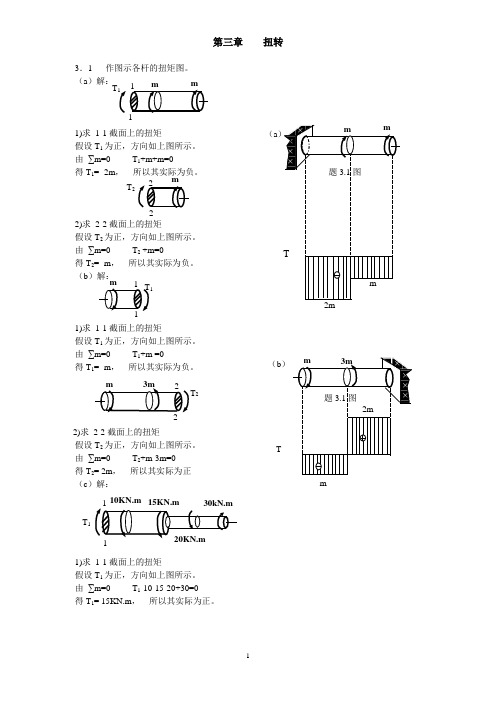
第三章 扭转3.1 作图示各杆的扭矩图。
(a )解:1)求 1-1截面上的扭矩假设T 1为正,方向如上图所示。
由 ∑m=0 T 1+m+m=0得T 1= -2m , 所以其实际为负。
2)求 2-2截面上的扭矩假设T 2为正,方向如上图所示。
由 ∑m=0 T 2 +m=0得T 2= -m , 所以其实际为负。
(b )解:1)求 1-1截面上的扭矩假设T 1为正,方向如上图所示。
由 ∑m=0 T 1+m =0得T 1= -m , 所以其实际为负。
2)求 2-2截面上的扭矩假设T 2为正,方向如上图所示。
由 ∑m=0 T 2+m-3m=0 得T 2= 2m , 所以其实际为正 (c )解:1)求 1-1截面上的扭矩假设T 1为正,方向如上图所示。
由 ∑m=0 T 1-10-15-20+30=0得T 1= 15KN.m , 所以其实际为正。
T 1T 2(a2(b )mTT 12)求 2-2截面上的扭矩假设T 2为正,方向如上图所示。
由 ∑m=0 T 2-15-20+30=0得T 2= 5KN.m , 所以其实际为正。
3)求 3-3截面上的扭矩 假设T 3为正,方向如上图所示。
由 ∑m=0 T 3-20+30=0得T 3= -10KN.m , 所以其实际为负。
4)求 4-4截面上的扭矩假设T 4为正,方向如上图所示。
由 ∑m=0 T 4 +30=0得T 4= -30KN.m , 所以其实际为负。
3.2 T 为圆杆横截面上的扭矩,试画出截面上与T 对应的剪应力分布图。
解:3.5 D=50mm 直径的圆轴,受到扭矩T=2.15KN .m 的作用。
试求在距离轴心10mm 处的剪应力,并求轴横截面上的最大剪应力。
T 230kN.m T 3T 4(题3.2图(a ) (b )解:求距离轴心10mm 处的剪应力, 由 I P =πD 4/32=π×0.054/32=6.13×10-7 m 4 W t = I P /R=6.13×10-7/0.025=2.454×10-5 m 3τρ=Tρ/ I P =2.15×103×10×10-3/(6.13 ×10-7 ) =35MPa求轴横截面上的最大剪应力τmax =T/ W t =2.15×103/(2.454 ×10-5 ) =87.6MPa3.8 阶梯形圆轴直径分别为d 1=40mm ,d 2=70mm ,轴上装有三个皮带轮,如图所示。
材料力学习题-第3章_扭转

第三章扭转一、是非判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
3.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
4.切应力互等定理仅适用于纯剪切情况。
5.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
6.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
7.受扭圆轴的最大切应力只出现在横截面上。
8.受扭圆轴内最大拉应力的值和最大切应力的值相等。
9.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距达到某一极限值时,圆杆将沿轴线方向出现裂纹。
答案:×,×,√,×,√,√,×,√,×二、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内边缘的切应力为()A τ;B ατ;C 零; D(1-4 )τ2.两根受扭圆轴的直径和长度均相同,但材料G不同,在扭矩相同的情况下,它们的最大切应力τ1、τ2和扭转角φ1、φ2之间的关系为( ) A 1τ=τ2, φ1=φ2 B 1τ=τ2, φ1≠φ2 C 1τ≠τ2, φ1=φ2 D 1τ≠τ2, φ1≠φ23.空心圆轴的外径为D ,内径为d, α=d /D,其抗扭截面系数为 ( ) A ()31 16p D W πα=- B ()321 16p DW πα=- C ()331 16p D W πα=- D ()341 16p D W πα=-4.对于受扭的圆轴,关于如下结论:①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是( )A ②③对B ①③对C ①②对D 全对5.单位长度扭转角θ与( )无关。
A 杆的长度;B 扭矩;C 材料性质;D 截面几何性质。
(完整版)扭转练习题
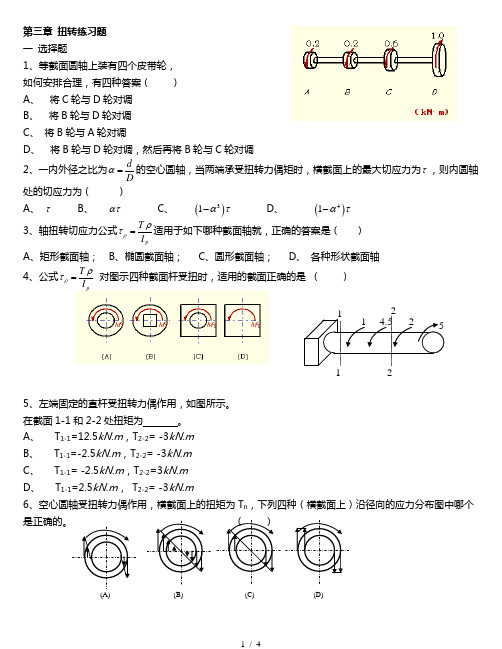
第三章 扭转练习题 一 选择题1、等截面圆轴上装有四个皮带轮, 如何安排合理,有四种答案( ) A 、 将C 轮与D 轮对调 B 、 将B 轮与D 轮对调 C 、 将B 轮与A 轮对调D 、 将B 轮与D 轮对调,然后再将B 轮与C 轮对调2、一内外径之比为dDα=的空心圆轴,当两端承受扭转力偶矩时,横截面上的最大切应力为τ,则内圆轴处的切应力为( )A 、 τB 、 ατC 、 ()31ατ-D 、 ()41ατ- 3、轴扭转切应力公式pT I ρρτ=适用于如下哪种截面轴就,正确的答案是( ) A 、矩形截面轴; B 、椭圆截面轴; C 、圆形截面轴; D 、 各种形状截面轴4、公式p T I ρρτ= 对图示四种截面杆受扭时,适用的截面正确的是 ( )5、左端固定的直杆受扭转力偶作用,如图所示。
在截面1-1和2-2处扭矩为 。
A 、 T 1-1=12.5kN.m ,T 2-2= -3kN.mB 、 T 1-1=-2.5kN.m ,T 2-2= -3kN.mC 、 T 1-1= -2.5kN.m ,T 2-2=3kN.mD 、 T 1-1=2.5kN.m , T 2-2= -3kN.m6、空心圆轴受扭转力偶作用,横截面上的扭矩为T n ,下列四种(横截面上)沿径向的应力分布图中哪个是正确的。
( )21 11 24.5 52(A)(B)(C)(D)7、图(1)、(2)所示两圆轴的材料、 长度均相同,扭转时两轴表面上 一点处的切应变相等γ1=γ2,则M e1与M e2的关系正确的是( )A 、 21e e M M =B 、 212e e M M =C 、 214e e M M =D 、 218e e M M = 8、一内、外直径分布为d 、D 的空心圆轴,其抗扭截面系数正确的是( )A 、 331616t D d W ππ=-; B 、333232t D d W ππ=- C 、 ()4416t W D d D π=- ; D 、 443232t D d W ππ=- 9、实心圆轴①和空心圆轴②,它们的横截面面积均相同,受相同扭矩作用,则其最大切应力正确的是( )A 、 max 2max1ττ>B 、 max 2max1ττ<C 、 max 2max1ττ=D 无法比较10 受扭圆轴,当横截面上的扭矩T 不变,而直径减小一半时,该横截面的最大切应力与原来的最大切应力之比正确的是( )A 、 2倍B 、 4倍C 、 6倍D 、 8倍 二、填空题1、当轴传递的功率一定时,轴的转速愈小,则轴受到的外力偶矩愈 ,当外力偶矩一定时,传递的功率愈大,则轴的转速愈 。
材料力学典型例题及解析 3.扭转典型习题解析

的切向内力所形成的力偶矩将由哪个力偶矩来平衡?
A M
B
A
M
B
C
z
D
A
(a)
C
dρ
ρ
R
(c)
D
题2图
BC Dx
(b)
θ dθ
(d)
解题分析:由切应力互等定理可知截面ABCD上的切向内力分布及其大小。该截面上切向内
力形成一个垂直向上的力偶矩。在图b中,左右两个横截面上的水平切向内力分量形成垂直
于截面ABCD的竖直向下的力偶矩,正好与截面ABCD上切向内力的合力偶矩平衡。
应力相等的条件下,试确定空心轴的外径,并比较实心轴和空心轴的重量。
解题分析:用空心轴代替实心轴,须保证二者强度相同。根据强度条件可求出D值,再用面
积比得出重量比。
解:1、根据两轴切应力相等的条件,确定空心轴外径
Tmax = Tmax = [τ ] WP实 WP空
πd 3 = πD3 (1 − α 4 ) 16 16
解得 D = 107.7 ×10−3 m = 107.7 mm
δ = D − d = 107.7mm −100mm = 3.85 mm
2
2
比较可知,两种设计的结果非常接近。
讨论: 当 δ ≤ R0 /10 时,即认为是薄壁圆管,可以直接使用薄壁管扭转公式。
2 图示受扭圆杆,沿平面ABCD截取下半部分为研究对象,如图b所示。试问截面ABCD上
4
即在强度相同条件下,空心轴可以节约近30%的材料。
讨论:在实际工程中常用空心圆轴代替实心圆轴,在保障安全运行的前提下,可以节约材料。
5 已知钻探机杆的外径D = 60 mm,内径d = 50 mm,功率P = 7.46 kW,转速n =180 r/min, 钻杆入土深度l = 40 m,G = 80 GPa,[τ]= 40 MPa。设土壤对钻杆的阻力是沿长度均匀分布 的,试求:(1) 单位长度上土壤对钻杆的阻力矩M;(2) 作钻杆的扭矩图,并进行强度校核; (3) 求A、B两截面相对扭转角。 解题分析:根据题意,为圆轴扭转问题。土壤对钻杆的阻力形成扭力矩作用在钻杆上,并沿
材料力学作业参考题解扭转

17.76MPa [ ]
(3)如图取坐标系,有:
T (x) m0 x
AB
l T (x) dx
m0
0 GI p
GI p
l
xdx
m0l 2
M 0l
0
2GI p 2GI p
32 389.9 40
0.064 [1
(5 /
6)4 ]
0.148弧度
8.48
3-16 如图所示,将空心圆杆(管)A套在实心圆杆B旳一端。两杆在同一横截面处有一直径 相同旳贯穿孔,但两孔旳中心线构成一β角,目前杆B上施加扭力偶使之扭转,将杆A和B旳 两孔对齐,装上销钉后卸去所施加旳扭力偶。试问两杆横截面上旳扭矩为多大?已知两杆旳 极惯性矩分别为 IpA和 IpB,且材料相同,切变模量为G。
620.7 16
0.043
49.4MPa [ ]
max 2
TDB W pDB
1432.4 16
0.073
21.3MPa [ ]
max
TAC GI pAC
180
80
32 620.7
109
180
0.044
1.77 / m [ ]
该轴满足强度与刚度要求
3-13 已知钻探机钻杆旳外径D=60mm,内径d=50mm,功率P=7.35kW,转速n=180r/min,钻 杆入土深度l=40m,材料旳G=80GPa,[ τ ]=40MPa。假设土壤对钻杆旳阻力沿长度均匀分布, 试求:(1)单位长度上土壤对钻杆旳阻力矩;(2)作钻杆旳扭矩图,并进行强度校核; (3)A、B两截面旳相对扭转角。
d 4
d 8
32 100 103
8 0.13
127MPa
材料力学第三章扭转复习题

第三章 扭转1.等截面圆轴上装有四个皮带轮,如何安排合理,现有四种答案:(A ) 将C 轮与D 轮对调; (B ) 将B 轮与D 轮对调; (C ) 将B 轮与C 轮对调;(D ) 将B 轮与D 轮对调;然后将B 轮与C 轮对调;正确答案是 a 。
2.薄壁圆管受扭转时的剪应力公式为 ()t R T 22/πτ= ,(R 为圆管的平均半径,t 为壁厚)。
关于下列叙述,(1) 该剪应力公式可根据平衡关系导出;(2) 该剪应力公式可根据平衡、几何、物理三方面条件导出; (3) 该剪应力公式符合“平面假设”;(4) 该剪应力公式仅适用于R t <<的圆管。
现有四种答案: (A ) (1)、(3)对; (B ) (1)、(4)对; (C ) (2)、(3)对; (D ) 全对;正确答案是 b 。
3.建立圆轴的扭转应力公式 p p I T /ρτ=时,“平面假设”起到的作用于有 下列四种答案:(A ) “平面假设”给出了横截面上内力与应力的关系⎰=AdA T τρ;(B ) “平面假设”给出了圆轴扭转时的变形规律;(C ) “平面假设”使物理方程得到简化;(D ) “平面假设”是建立剪应力互等定理的基础。
正确答案是 。
4.满足平衡条件,但剪应力超过比例极限时,有下述四种结论:(A ) (B ) (C ) (D ) 剪应力互等定理: 成立 不成立 不成立 成立 剪切虎克定律 : 成立 不成立 成立 不成立 正确答案是 。
D5.一内、外直径分别为d 、D 的空心圆轴,其抗扭截面系数有四种答案:(A )()()16/16/33d D W t ππ-=;(B )()()32/32/33d DW t ππ-=;(C )()[]()4416/d D D W t-=π; (D )()()32/32/44d D W tππ-=;正确答案是 c 。
6.一内外径之比为D d /=α的空心圆轴, 当两端受扭转力偶矩时,横截面的最大剪应为τ,则内圆周处的剪应力有四种答案: (A )τ; (B )ατ;(C ) ()τα31-; (D )()τα41-正确答案是 b 。
材料力学第3章扭转习题及答案

材料力学第3章扭转习题及答案第三章扭转一、判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(× ) 2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(× )3.圆杆扭转变形实质上是剪切变形。
(√ )4.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√ )5.材料相同的圆杆,它们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(× ) 6.切应力互等定理,仅适用于纯剪切情况。
(× ) 7.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √ ) 8.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√ ) 9.受扭圆轴的最大切应力只出现在横截面上。
(× ) 10.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭矩达到某一极限值时,圆杆将沿轴线方向出现裂纹。
(√ )二、填空题1.一级减速箱中的齿轮直径大小不等,在满足相同的强度条件下,高速齿轮轴的直径要比低速齿轮轴的直径(小)。
2.当实心圆轴的直径增加1培时,其抗扭强度增加到原来的( 8 )倍,抗扭刚度增加到原来的( 16 )倍。
3.直径D=50mm 的圆轴,受扭矩T=2.15kn.m ,该圆轴横截面上距离圆心10mm 处的剪应力τ=(35.0 MPa ),最大剪应力τmax=(87.6 MPa )。
4.一根空心轴的内外径分别为d ,D ,当D=2d 时,其抗扭截面模量为(33256153215D d ππ或)。
5.直径和长度均相等的两根轴,在相同的扭矩作用下,而材料不同,它们的τmax 是(相)同的,扭转角φ是(不)同的。
6.等截面圆轴扭转时的单位长度相对扭转角为θ,若圆轴直径增大一倍,则单位长度扭转角将变为(16θ)。
三、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ ,这时横截面上内边缘的切应力为( B )。
材料力学 第三章 扭转

为一很小的量,所以
tan 1.0103rad
G
(80 109 Pa)(1.0 103rad) 80 MPa
注意: 虽很小,但 G 很大,切应力 不小
例 3-3 一薄壁圆管,平均半径为R0,壁厚为,长度为l, 横截面上的扭矩为T,切变模量为G,试求扭转角。
解:
T
2πR02
G
T
2πGR02
塑性材料:[] =(0.5~0.6)[s] 脆性材料:[] = (0.8~1.0)[st]
例 3-1 已知 T=1.5 kN . m,[τ] = 50 MPa,试根据强度条 件设计实心圆轴与 a = 0.9 的空心圆轴,并进行比较。 解:1. 确定实心圆轴直径
max [ ]
max
T Wp
T πd 3
表示扭矩沿杆件轴线变化的图线(T-x曲线)-扭矩图
Tmax ml
[例3-1]已知:一传动轴, n =300r/min,主动轮输入 P1=500kW, 从动轮输出 P2=150kW,P3=150kW,P4=200kW,试绘制扭矩图。
解:1、计算外力偶矩
m2
m3
m1
m4
m1
9.55
P1 n
9.55
一、薄壁圆筒扭转时的应力
t
1、试验现象
壁厚
t
1 10
r0(r0:平均半径)
rO
各圆周线的形状不变,仅绕轴线作相对转动,距离不变。 当变形很小时,各纵向平行线仍然平行,倾斜一定的角度。
由于管壁薄,可近似认 为管内变形与管表面相 同,均仅存在切应变γ 。
2、应力公式 微小矩形单元体如图所示:
´
①无正应力
d T
dx GI p
刘鸿文《材料力学》(第6版)复习笔记和课后习题及考研真题详解-第3~4章【圣才出品】

2.切应力互等定理
2 / 166
圣才电子书 十万种考研考证电子书、题库视频学习平台
单元体相互垂直的两个平面上,切应力必然成对存在,且数值相等,都垂直于两个平面 的交线,方向则共同挃向或共同背离这一交线。
3.剪切胡克定律
(1)纯剪切
若单元体的各个侧面上只有切应力并无正应力,这种情况称为纯剪切。
4.剪切应变能
在应力小于剪切比例枀限的情况下,单位体积内的剪切应变能密度为
ν
1
2
2
2G
上述公式主要用于线弹性范围内纯剪切应力状态下剪切应变能密度的计算。
3 / 166
圣才电子书 十万种考研考证电子书、题库视频学习平台
三、囿轴扭转时的应力和变形 1.囿轴扭转时的应力 (1)应力计算公式 推导囿轴扭转时的应力计算公式,需同时考虑变形几何、物理和静力三方面的关系。 ①变形几何关系:囿轴扭转的平面假设; ②物理关系:剪切胡克定律; ③静力关系:横截面上的内力系对囿心的力矩合成为扭矩。 如图 3-1-2 所示,横截面上任一点的切应力为 τρ=Tρ/Ip 囿截面边缘的最大切应力 τmax=TR/Ip=T/Wt 式中,ρ 为应力点到囿心的距离;Ip 为横截面的枀惯性矩;Wt 为扭转截面系数。
4c 1 4c 4
0.615 c
8FD πd 3
k
8FD πd 3
式中,c 为弹簧挃数,c=D/d;k 为曲度系数
k 4c 1 0.615 4c 4 c
(3)强度条件
τmax≤[τ]
2.弹簧的变形计算
在作用点在弹簧圀中心的力 F 的作用下,沿力的作用方向的位秱
8FD3n 64FR3n F
图 3-1-2 对于直徂为 D 实心囿形截面 Ip=πD4/32,Wt=πD3/16 对于内徂为 d,外徂为 D 的空心囿截面
材料力学第三章答案

材料力学第三章答案【篇一:材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴,关于如下结论:①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是( a )a ②③对 b①③对 c①②对d 全对 7.扭转切应力公式?mnp?i?适用于( d)杆件。
pa 任意杆件;b 任意实心杆件;c 任意材料的圆截面;d 线弹性材料的圆截面。
9.若将受扭实心圆轴的直径增加一倍,则其刚度是原来的( d a 2倍; b 4倍; c 8倍; d 16倍。
三、计算题1.试用截面法求出图示圆轴各段内的扭矩t,并作扭矩图2.图示圆轴上作用有四个外力偶矩 me1 =1kn/m, me2 =0.6kn/m,)me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图;⑵若 me1与me2的作用位置互换,扭矩图有何变化?(1)(2)解: me1与me2的作用位置互换后,最大扭矩变小。
3.如图所示的空心圆轴,外径d=100㎜,内径d=80㎜,m=6kn/m,m=4kn/m.请绘出轴的扭矩图,并求出最大剪应力解:扭矩图如上,则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜,l=500tr4?103?50?103ip5.8?104.图示圆形截面轴的抗扭刚度为g ip,每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。
ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二:《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动,转速n?200r/min,轴上装有五个轮子,主动轮ii输入的功率为60kw,从动轮,i,iii,iv,v依次输出18kw,12kw,22kw和8kw。
材料力学第三章答案 景荣春

案
网
ww
w.
kh
da
w.
co
长度的变化) 皆为应力与应变成正比关系。 3 个弹性常量 E , G , μ 之间关系为 G =
课
3-5 圆轴扭转时如何确定危险截面、危险点及强度条件? 答 等截面圆轴扭转时的危险截面为扭矩最大的横截面,变截面圆轴扭转时的危险截面 在其扭矩与扭转截面系数比值最大的横截面;其危险点在该横截面的外边缘。强度条件为
τ max =
后
50 ⎛ ⎞ 8 × 1.5 × 10 3 × 50 × 10 −3 ⎜ 4 × + 2 ⎟ 8 FD(4c + 2) 8 ⎝ ⎠ = 458 MPa = 解 (1) τ max = 3 50 ( ) πd 4c − 3 ⎛ ⎞ π × 8 3 × 10 −9 × ⎜ 4 × − 3 ⎟ 8 ⎝ ⎠ τ max − [τ ] 8 = × 100% = 1.78% < 5% [τ ] 450
课
后
答
案
(1)求轴内的最大扭矩; (2)若将轮 A 与轮 C 的位置对调,试分析对轴的受力是否有利。
网
轮 B ,轮 C 与轮 D 为从动轮,输出功率分别为 PB = 10 kW, P C = P D = 30 kW。
解 (1) M B = 9549 ×
PB 10 = 9549 × = 191 N ⋅ m 500 n P 70 M A = 9549 × A = 9549 × = 1337 N ⋅ m 500 n
27
m
E 。 2(1 + μ )
思考题 3-6 解图
3-7 从强度方面考虑,空心圆轴为何比实心圆轴合理? 答 对于相同的横截面面积 (即用相同量材料) , 空心圆轴比实心圆轴的抗扭截面系数大, 从而强度高。 3-8 如何计算扭转变形?怎样建立刚度条件?什么样的构件需要进行刚度校核? 答 (1)写出扭矩方程或扭矩图;相距 l 的两截面间的扭转角
材料力学习题册答案-第3章 扭转(完整资料).doc

此文档下载后即可编辑第三章扭转一、是非判断题1.圆杆受扭时,杆内各点处于纯剪切状态。
(×)2.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(×)3.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(×)4.圆杆扭转变形实质上是剪切变形。
(×)5.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√)6.材料相同的圆杆,他们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(×)7.切应力互等定理仅适用于纯剪切情况。
(×)8.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
(√)9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√)10.受扭圆轴的最大切应力只出现在横截面上。
(×)11.受扭圆轴内最大拉应力的值和最大切应力的值相等。
(√ )12.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距达到某一极限值时,圆杆将沿轴线方向出现裂纹。
( × )二、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内边缘的切应力为 ( B )A τ;B ατ;C 零;D (1- 4α)τ 2.实心圆轴扭转时,不发生屈服的极限扭矩为T ,若将其横截面面积增加一倍,则极限扭矩为( C )A0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同,但材料C 不同,在扭矩相同的情况下,它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为( B )A 1τ=τ2, φ1=φ2B 1τ=τ2, φ1≠φ2C 1τ≠τ2, φ1=φ2D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在( D )A 扭矩最大的截面;B 直径最小的截面;C 单位长度扭转角最大的截面;D 不能确定。
《材料力学》第3章 扭转习题解

第三章 扭转 习题解[习题3-1] 一传动轴作匀速转动,转速min /200r n =,轴上装有五个轮子,主动轮II 输入的功率为60kW ,从动轮,I ,III ,IV ,V 依次输出18kW ,12kW ,22kW 和8kW 。
试作轴的扭图。
解:(1)计算各轮的力偶矩(外力偶矩)N T ke 55.9=(2) 作扭矩图[习题3-2] 一钻探机的功率为10kW ,转速min /180r n =。
钻杆钻入土层的深度m l 40=。
如土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度m ,并作钻杆的扭矩图。
解:(1)求分布力偶的集度m)(5305.018010549.9549.9m kN n N M k e ⋅=⨯== 设钻杆轴为x 轴,则:0=∑xMe M ml =)/(0133.0405305.0m kN l M m e ===(2)作钻杆的扭矩图x x lM mx x T e0133.0)(-=-=-=。
]40,0[∈x 0)0(=T ; )(5305.0)40(m kN M T e ⋅-== 扭矩图如图所示。
[习题3-3] 圆轴的直径mm d 50=,转速为120r/min 。
若该轴横截面上的最大切应力等于60MPa ,试问所传递的功率为多大? 解:(1)计算圆形截面的抗扭截面模量:)(245445014159.3161161333mm d W p =⨯⨯==π (2)计算扭矩2max /60mm N W Tp==τ )(473.1147264024544/6032m kN mm N mm mm N T ⋅=⋅=⨯=(3)计算所传递的功率 )(473.1549.9m kN nN M T ke ⋅=== )(5.18549.9/120473.1kW N k =⨯=[习题3-4] 空心钢轴的外径mm D 100=,内径mm d 50=。
已知间距为m l 7.2=的两横截面的相对扭转角o8.1=ϕ,材料的切变模量GPa G 80=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 扭转 习题解[习题3-1] 一传动轴作匀速转动,转速min /200r n =,轴上装有五个轮子,主动轮II 输入的功率为60kW ,从动轮,I ,III ,IV ,V 依次输出18kW ,12kW ,22kW 和8kW 。
试作轴的扭图。
解:(1)计算各轮的力偶矩(外力偶矩) nN T ke 55.9= 外力偶矩计算(kW 换算成kN.m)题目编号 轮子编号轮子作用 功率(kW) 转速r/minTe (kN.m ) 习题3-1I 从动轮 18 200 0.859 II 主动轮 60 200 2.865 III 从动轮 12 200 0.573 IV 从动轮 22 200 1.051 V从动轮82000.382(2) 作扭矩图[习题3-2] 一钻探机的功率为10kW ,转速min /180r n =。
钻杆钻入土层的深度m l 40=。
如土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度m ,并作钻杆的扭矩图。
解:(1)求分布力偶的集度m)(5305.018010549.9549.9m kN n N M k e ⋅=⨯== 设钻杆轴为x 轴,则:0=∑xMe M ml =)/(0133.0405305.0m kN l M m e ===(2)作钻杆的扭矩图T 图(kN.m)x x lM mx x T e0133.0)(-=-=-=。
]40,0[∈x 0)0(=T ; )(5305.0)40(m kN M T e ⋅-==扭矩图如图所示。
[习题3-3] 圆轴的直径mm d 50=,转速为120r/min 。
若该轴横截面上的最大切应力等于60MPa ,试问所传递的功率为多大? 解:(1)计算圆形截面的抗扭截面模量:)(245445014159.3161161333mm d W p =⨯⨯==π (2)计算扭矩2max /60mm N W Tp==τ )(473.1147264024544/6032m kN mm N mm mm N T ⋅=⋅=⨯=(3)计算所传递的功率 )(473.1549.9m kN nN M T ke ⋅=== )(5.18549.9/120473.1kW N k =⨯=[习题3-4] 空心钢轴的外径mm D 100=,内径mm d 50=。
已知间距为m l 7.2=的两横截面的相对扭转角o8.1=ϕ,材料的切变模量GPa G 80=。
试求: (1)轴内的最大切应力;(2)当轴以min /80r n =的速度旋转时,轴所传递的功率。
解;(1)计算轴内的最大切应力)(9203877)5.01(10014159.3321)1(32144444mm D I p =-⨯⨯⨯=-=απ。
)(184078)5.01(10014159.3161)1(16134343mm D W p =-⨯⨯⨯=-=απ式中,D d /=α。
pGI lT ⋅=ϕ, mmmm mm N lGI T p27009203877/80000180/14159.38.142⨯⨯⨯==ϕmm N ⋅=45.8563014)(563.8m kN ⋅=MPa mm mm N W T p 518.4618407845.85630143max =⋅==τ (2)当轴以min /80r n =的速度旋转时,轴所传递的功率 )(563.880549.9549.9m kN Nn N M T k k e ⋅=⨯=== )(74.71549.9/80563.8kW N k =⨯=[习题3-5] 实心圆轴的直径mm d 100=,长m l 1=,其两端所受外力偶矩m kN M e ⋅=14,材料的切变模量GPa G 80=。
试求:(1)最大切应力及两端面间的相对转角;(2)图示截面上A 、B 、C 三点处切应力的数值及方向; (3)C 点处的切应变。
解:(1)计算最大切应力及两端面间的相对转角 pe p W M W T==max τ。
式中,)(19634910014159.3161161333mm d W p =⨯⨯==π。
故:MPa mmmmN W M p e 302.71196349101436max=⋅⨯==τ pGI l T ⋅=ϕ 式中,)(981746910014159.3321321444mm d I p =⨯⨯==π。
故: o p rad mm N m m N GI l T 02.1)(0178254.010*******/108011400041229==⨯⨯⨯⨯⋅=⋅=-ϕ (2)求图示截面上A 、B 、C 三点处切应力的数值及方向 MPa B A 302.71max ===τττ 由横截面上切应力分布规律可知:MPa B C 66.35302.715.021=⨯==ττA 、B 、C 三点的切应力方向如图所示。
(3)计算C 点处的切应变 34310446.0104575.4108066.35--⨯≈⨯=⨯==MPaMPaGCC τγ[习题3-6] 图示一等直圆杆,已知mm d 40=,mm a 400=,GPa G 80=,oDB 1=ϕ。
试求:(1)最大切应力;(2)截面A 相对于截面C 的扭转角。
解:(1)计算最大切应力从AD 轴的外力偶分布情况可知:e CD AB M T T ==,0=BC T 。
p e p p e p CB CB p DC DC p i i DB GI aM GI a GI a M GI l T GI l T GI l T =⋅+⋅=⋅+⋅==∑0ϕ aGI M p e ϕ=式中,)(2513274014159.3321321444mm d I p =⨯⨯==π。
故: mm N mm mm mm N aGI M p e ⋅=⋅⨯==87729618014159.3400251327/8000042ϕpeW M =max τ 式中,)(125664014159.3161161333mm d W p =⨯⨯==π。
故: MPa mmmm N W M p e 815.69125668772963max =⋅==τ (2)计算截面A 相对于截面C 的扭转角o DB pe p p e p BC BC p AB AB p i i AC GI aM GI a GI a M GI l T GI l T GI l T 22202===⋅+⋅=⋅+⋅==∑ϕϕ [习题3-7] 某小型水电站的水轮机容量为50kW ,转速为300r/min ,钢轴直径为75mm ,若在正常运转下且只考虑扭矩作用,其许用切应力MPa 20][=τ。
试校核轴的强度。
解:(1)计算最大工作切应力 pp e W TW M ==max τ 式中,)(592.130050549.9549.9m kN n N M k e ⋅=⨯==; )(125667514159.3161161333mm d W p =⨯⨯==π。
故:MPa mmmmN W M p e 219.198283515920003max =⋅==τ (2)强度校核因为MPa 219.19max =τ,MPa 20][=τ,即][max ττ≤,所以轴的强度足够,不会发生破坏。
[习题3-8] 已知钻探机钻杆(参看题3-2图)的外径mm D 60=,内径mm d 50=,功率kW P 355.7=,转速min /180r n =,钻杆入土深度m l 40=,钻杆材料的GMPa G 80=,许用切应力MPa 40][=τ。
假设土壤对钻杆的阻力是沿长度均匀分布的,试求: (1)单位长度上土壤对钻杆的阻力矩集度m ;(2)作钻杆的扭矩图,并进行强度校核; (3)两端截面的相对扭转角。
解:(1)求单位长度上土壤对钻杆的阻力矩集度m)(390.0180355.7549.9549.9m kN n N M k e ⋅=⨯== 设钻杆轴为x 轴,则:0=∑xMe M ml =)/(00975.040390.0m kN l M m e ===(2)作钻杆的扭矩图,并进行强度校核①作钻杆扭矩图x x mx x T 00975.04039.0)(-=-=-=。
]40,0[∈x 0)0(=T ; )(390.0)40(m kN M T e ⋅-==扭矩图如图所示。
②强度校核peW M =max τ 式中,)(21958])6050(1[6014159.3161)1(16134343mm D W p =-⨯⨯⨯=-=απ MPa mmmm N W M p e 761.17219583900003max =⋅==τ 因为MPa 761.17max =τ,MPa 40][=τ,即][max ττ≤,所以轴的强度足够,不会发生破坏。
(3)计算两端截面的相对扭转角⎰=40)(pGI dxx T ϕ 式中,)(658752])6050(1[6014159.3321)1(32144444mm D I p =-⨯⨯⨯=-=απ 402404122640]2[10658752/108000975.000975.01|)(|x m m kN xdx GI GI dx x T pp ⎰⎰-⨯⨯⨯===ϕ 05.8)(148.0≈=rad[习题3-9] 图示绞车由两人同时操作,若每人在手柄上沿着旋转的切向作用力F 均为0.2kN ,已知轴材料的许用切应力MPa 40][=τ,试求: (1)AB 轴的直径;(2)绞车所能吊起的最大重量。
解:(1)计算AB 轴的直径AB 轴上带一个主动轮。
两个手柄所施加的外力偶 矩相等:)(08.04.02.0m kN M M e e ⋅=⨯==右左 )(16.02m kN M M e e ⋅==右主动轮 扭矩图如图所示。
由AB 轴的强度条件得: ][163max τπτ≤==dM W M e p e 右右 mm mm N mmN M d e 7.21/4014159.38000016][16323=⨯⋅⨯=≥τπ右(2)计算绞车所能吊起的最大重量主动轮与从动轮之间的啮合力相等:35.02.0从动轮主动轮e e M M =)(28.016.020.035.0m kN M e ⋅=⨯=从动轮 由卷扬机转筒的平衡条件得:从动轮e M P =⨯25.028.025.0=⨯P)(12.125.0/28.0kN P ==[习题3-10] 直径mm d 50=的等直圆杆,在自由端截面上承受外力偶m kN M e ⋅=6,而在圆杆表面上的A 点将移动到A 1点,如图所示。
已知mm AA s 31==∆⋂,圆杆材料的弹性模量GPa E 210=,试求泊松比ν(提示:各向同性材料的三个弹性常数E 、G 、ν间存在如下关系:)1(2ν+=EG 。
