--一半径为R的半圆细环上均匀地分布电荷--求环心处的
习题7─19 一细玻璃棒被弯成半径为R的半圆形

习题7─19 一细玻璃棒被弯成半径为R 的半圆形,沿其上半部分均匀分布有电量+Q ,沿其下半部分均匀分布有电量-Q ,如图所示,求圆心O 处的电场强度。
解:如图所示,在半圆形玻璃棒的上半部分取一线元θRd dl =,其位置处相应的半径与X 轴负向的夹角为θ,其带电量πθπλQd R dl Q dl dq 2)(2=⋅==,其在O 点产生的元场强的大小为2022024R Qd R dq dE επθπε==其方向如图所示。
由于各个线元产生的元场强方向不一致,因此需把E d分解2022s i n s i n R d Q dE dE y επθθθ-=-=由于电荷分布的对称性,最终O 点场强的X 分量0=xE 。
因此,圆心O 处的电场强度的Y 分量为2022202s i n 2R Qd R QdE E y y επθθεππ-=-==⎰⎰把O 处的电场强度写成矢量式为j R Qj E E y202επ-==习题7─20 在真空中有一长为l =10cm 的细杆,杆上均匀分布着电荷,已知其电荷线密度mC 10015/.-⨯=λ,在杆的延长线上,距杆的一端为d =10cm 的一点上,有一电量为C 100250-⨯=.q 的点电荷,如图所示,试求该点电荷所受的电场力。
解法Ⅰ:沿细杆方向建立X 轴方向向左,坐标原点就在q 0所在处,在细杆上x 处取线元dx ,其带电为dx dq λ=,线元在q 0所在处产生的元场大小为202044x dxx dq dE πελπε==整个细杆在q 0所在处产生的电场大小为)(4)11(440020l d d l ld d x dx dE E ld d+⋅=+-⋅===⎰⎰+πελπελπελ点电荷q 0所受的电场力为E dθ θdθRd dl =OdE x dE yX Y +Q –Q R习题7―19图x dxdlq 0XOλ习题7―20图N 99.820.010.01085.814.34100.210.0100.1)(41255000=⨯⨯⨯⨯⨯⨯⨯⨯⨯=+⋅⋅⋅==---l d d q l E q F πελ 习题7─22 如图所示为一沿X 轴放置的长度为l 的不均匀带电细棒,已知其电荷线密度为)(0a x -=λλ,式中0λ为常量,取0=∞U ,求坐标原点O 处的电势。
大学物理第7章 电场题库答案(含计算题答案)

9题图第七章 电场 填空题 (简单)1、两无限大平行平面的电荷面密度分别为σ+和σ+,则两无限大带电平面外的电场强度大小为σε ,方向为 垂直于两带电平面并背离它们 。
2、在静电场中,电场强度E 沿任意闭合路径的线积分为 0 ,这叫做静电场的 环路定理 。
3、静电场的环路定理的数学表达式为 0lE dl =⎰ ,该式可表述为 在静电场中,电场强度的环流恒等于零 。
4、只要有运动电荷,其周围就有 磁场 产生;5、一平行板电容器,若增大两极板的带电量,则其电容值会 不变 ;若在两极板间充入均 匀电介质,会使其两极板间的电势差 减少 。
(填“增大”,“减小”或“不变”)6、在静电场中,若将电量为q=2×108库仑的点电荷从电势V A =10伏的A 点移到电势V B = -2伏特的B 点,电场力对电荷所作的功A ab = 92.410⨯ 焦耳。
(一般)7、当导体处于静电平衡时,导体内部任一点的场强 为零 。
8、电荷在磁场中 不一定 (填一定或不一定)受磁场力的作用。
9、如图所示,在电场强度为E 的均匀磁场中,有一半径为R 的半球面,E 与半球面轴线的夹角为α。
则通过该半球面的电通量为 2cos B R πα-⋅ 。
10、真空中两带等量同号电荷的无限大平行平面的电荷面密度分别为σ+和σ+,则两无限大带电平面之间的电场强度大小为 0 ,两无限大带电平面外的电场强度大小为σε 。
11、在静电场中,电场力所做的功与 路径 无关,只与 起点 和 终点位置 有关。
12、由高斯定理可以证明,处于静电平衡态的导体其内部各处无 净电荷 ,电荷只能分布于 导体 外表面 。
因此,如果把任一物体放入空心导体的空腔内,该物体就不受任何外 电场的影响,这就是 静电屏蔽 的原理。
(一般)13、静电场的高斯定理表明静电场是 有源 场, (一般)14、带均匀正电荷的无限长直导线,电荷线密度为λ。
它在空间任意一点(距离直导线的垂直距离为x 处)的电场强度大小为02xλπε ,方向为 垂直于带电直导线并背离它 。
大学物理复习题(电磁学)

【课后习题】 第12章 一、填空题1、两个大小完全相同的带电金属小球,电量分别为2q 和-1q ,已知它们相距为r 时作用力为F ,则将它们放在相距3r 位置同时其电量均减半,相互作用力大小为____1/36________F 。
2、电场强度可以叙述为电场中某一点上单位正电荷所受的_____电场力___________;电场中某一点的电势可以叙述为:单位正电荷在该点所具有的__电势能_________。
3、真空环境中正电荷q 均匀地分布在半径为R 的细圆环上,在环环心O 处电场强度为____0________,环心的电势为__R q o πε4/_________。
4、高斯定理表明磁场是 无源 场,而静电场是有源场。
任意高斯面上的静电场强度通量积分结果仅仅取决于该高斯面内全部电荷的代数和。
现有图1-1所示的三个闭合曲面S 1、S 2、S 3,通过这些高斯面的电场强度通量计算结果分别为:⎰⎰⋅=Φ11S SE d ,⎰⎰⋅=Φ22S S E d ,⎰⎰⋅=Φ33S SE d ,则Φ1=___o q ε/_______;Φ2+Φ3=___o q ε/-_______。
5、静电场的场线只能相交于___电荷或无穷远________。
6、两个平行的无限大均匀带电平面,其电荷面密度分别如图所示,则A 、B 、C 三个区域的电场强度大小分别为:E A =_o εσ/4________;E B =_o εσ/________;E C =__o εσ/4_______。
7、由一根绝缘细线围成的边长为l的正方形线框,使它均匀带电,其电荷线密度为λ,则在正方形中心处的电场强度的大小E=____0____________.8、初速度为零的正电荷在电场力的作用下,总是从__高____电势处向_低____电势处运动。
9、静电场中场强环流为零,这表明静电力是__保守力_________。
10、如图所示,在电荷为q的点电荷的静电场中,将一电荷为q0的试验电荷从a点经任意路径移动到b点,外力所作的功W=___⎪⎪⎭⎫⎝⎛-12114rrQqπε___________.11、真空中有一半径为R的均匀带电半园环,带电量为Q,设无穷远处为电势零点,则圆心O处的电势为___RQ4πε_________;若将一带电量为q的点电荷从无穷远处移到O点,电场力所作的功为__RqQ4πε__________。
矿大《大学物理》习题解答(下)
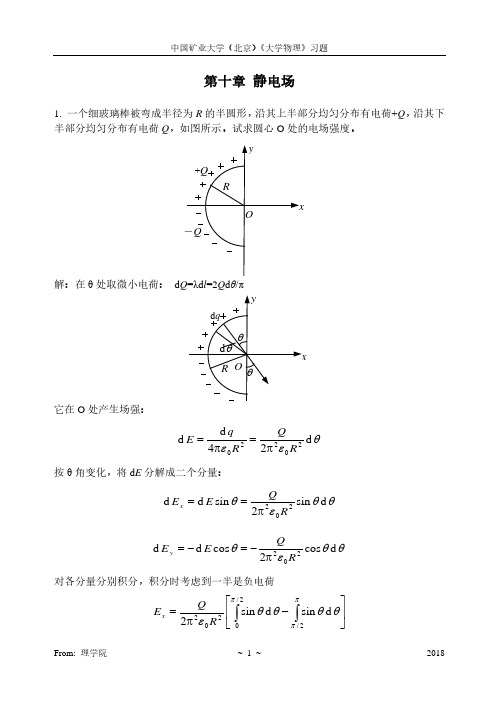
=
σ 2ε 0
1 −
a a2 +
R2
由题意,令 E=σ/(4ε0),得到
From: 理学院
~3~
2018
中国矿业大学(北京)《大学物理》习题
R= 3a
*4. 一半径为 R 的半球面,均匀地带有电荷,电荷面密度为 σ,求球心 O 处的电场强 度。
R dθ
θ
dE
O
x
解:选取坐标轴 Ox 沿半球面的对称轴,如图所示。把半球面分成许多微小宽度的环带, 每一环带之面积:
O 点处的总场强:
∫ σ
E= 2ε 0
π /2
sinθ
0
d(sinθ )
=
σ 2ε 0
sin 2 θ 2
|π0 / 2 =
σ 4ε 0
E = σ i 4ε 0
其中 i 为沿 x 轴正方向的单位矢量。
5. 半径为 R 的均匀带电球体内的电荷体密度为 ρ ,若在球内挖去一块半径为 r < R 的 小球体,如图所示.试求:两球心 O 与 O′ 点的场强,并证明小球空腔内的电场是均匀
E1
=
λ 4πε 0 R
(− i
−
j )
半无限长直线 B∞在 O 点产生的场强 E2 :
E2
=
λ 4πε 0 R
(− i
+
j学(北京)《大学物理》习题
半圆弧线段在 O 点产生的场强 E3 :
E3
=
λ 2πε 0 R
i
由场强叠加原理,O 点合场强为:
E = E1 + E2 + E3 = 0
From: 理学院
~4~
2018
的.
中国矿业大学(北京)《大学物理》习题
8-6-一半径为R的半圆细环上均匀地分布电荷--求环心处的

(力学部分)第一章重点:质点运动求导法和积分法,圆周运动角量和线量。
第二章重点:牛顿第二运动定律的应用(变形积分) 第三章重点:动量守恒定律和机械能守恒定律 第四章重点:刚体定轴转动定律和角动量守恒定律1.一质点沿半径为0.1=R m 的圆周作逆时针方向的圆周运动,质点在0~t 这段时间所经过的路程为422t tS ππ+=,式中S 以m 计,t 以s 计,则在t 时刻质点, (求导法)2.质点沿x 轴作直线运动,其加速度t a 4=m/s 2,在0=t 时刻,00=v ,100=x m ,则该质点的运动方程为=x (积分法)3.一质点从静止出发绕半径R 的圆周作匀变速圆周运动,角加速度为β,则该质点走完半周所经历的时间为。
(积分法)4.伽利略相对性原理表明对于不同的惯性系牛顿力学的规律都具有相同的形式。
5.一质量为kg m 2=的质点在力()()N t F x 32+=作用下由静止开始运动,若此力作用在质点上的时间为s 2,则该力在这s 2冲量的大小=I 10 NS ;质点在第s 2末的速度大小为 5 m/s 。
(动量定理和变力做功)6.一质点在平面运动, 其1c r =,2/c dt dv =;1c 、2c 为大于零的常数,则该质点作 匀加速圆周运动 。
7.一质点受力26x F -=的作用,式中x 以m 计,F 以N 计,则质点从0.1=x m沿X 轴运动到x=2.0 m 时,该力对质点所作的功A (变力做功)8.一滑冰者开始自转时其动能为20021ωJ ,当她将手臂收回, 其转动惯量减少为3J ,则她此时自转的角速度ω(角动量守恒定律)9.一质量为m 半径为R 的滑轮,如图所示,用细绳绕在其边缘,绳的另一端系一个质量也为m 的物体。
设绳的长度不变,绳与滑轮间无相对滑动,且不计滑轮与轴间的摩擦力矩,则滑轮的角加mg F =拉绳的一端,则滑轮的角加速(转动定律)10.一刚体绕定轴转动,初角速度80=ωrad/s ,现在大小为8(N ·m )的恒力矩作用下,刚体转动的角速度在2秒时间均匀减速到4=ωrad/s ,则刚体在此恒力矩的作用下的角加速度=α,刚体对此轴的转动惯量=J 4kg •m 2 。
大学物理II第10章静电场 作业题
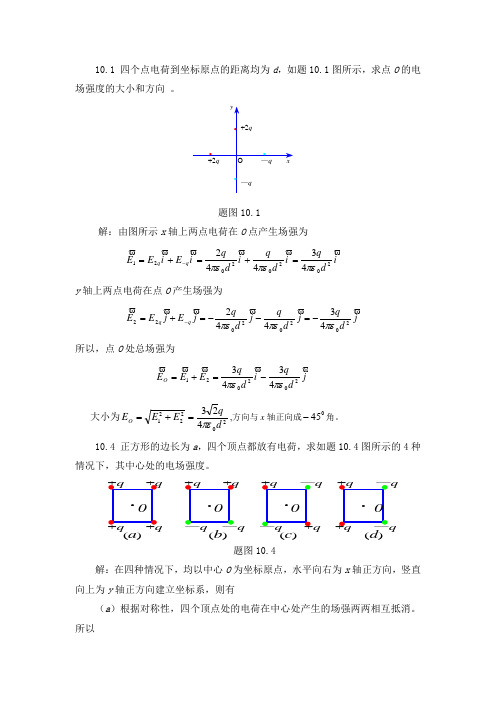
10.1 四个点电荷到坐标原点的距离均为d ,如题10.1图所示,求点O 的电场强度的大小和方向 。
题图10.1解:由图所示x 轴上两点电荷在O 点产生场强为i d q i d q i d q i E i E E q q2020*********πεπεπε=+=+=-y 轴上两点电荷在点O 产生场强为j dq j d q j d q j E j E E q q2020*********πεπεπε-=--=+=- 所以,点O 处总场强为j dq i d q E E E O2020214343πεπε-=+= 大小为202221423dq E E E O πε=+=,方向与x 轴正向成045-角。
10.4 正方形的边长为a ,四个顶点都放有电荷,求如题10.4图所示的4种情况下,其中心处的电场强度。
q qq q (a ) (b ) (c ) (d )题图10.4解:在四种情况下,均以中心O 为坐标原点,水平向右为x 轴正方向,竖直向上为y 轴正方向建立坐标系,则有(a )根据对称性,四个顶点处的电荷在中心处产生的场强两两相互抵消。
所以0=a E(b ) 根据对称性,电荷在中心处产生的场强在x 轴上抵消,只有y 轴上的分量,所以[]j aq j a a q j E E qy b20220245cos )2/()2/(444πεπε-=+-=-= (c ) 根据对称性,对角线上的电荷在中心处的场强可以相互抵消,所以0=c E(d ) 根据对称性,电荷在中心处产生的场强在y 轴上抵消,只有x 轴上的分量,所以[]i aq i a a q i E E qx d20220245sin )2/()2/(444πεπε=+== 10.5 一半径为R 的半圆细环上均匀地分布电荷+Q ,求环心处的电场强度。
题图10.5解:以环心O 为原心,取如图所示的坐标轴。
在环上取一线元dl ,其所带电量为RQdldq π=,它在环心O 处的电场强度E d 在y 轴上的分量为θππεsin 14120R R Qdl dE y =由于环对y 轴对称,电场强度在x 轴上的分量为零。
第7章 静电场习题

q 4πε 0 r 2
。由此可知,球外空间的场强与气球吹大过程无关。
(3)因为球表面的场强 E 表=
q 4πε 0 R 2
,在球吹大的过程中,R 变大,所以,
球表面的场强随气球的吹大而变小。 通过该立方体各面的 7-7 一个点电荷 q 位于一个边长为 a 的立方体的中心, 电通量是多少? 答:点电荷位于立方体中心时,通过该立方体各面的电通量都相等,并且等 于总通量的 1/6。由高斯定理可知总通量为
ε0
∑q
i
i
E2 4πr 2 =
由此可解得区域 II 的电场强度为
Q1
ε0
E2 =
4πε 0 r 2
Q1
在区域 III,做半径 r﹥R2 的球形高斯面。由于该高斯面内的电荷为 Q1+Q2, 由高斯定理可得
∫∫
S
r 1 r E 3 ⋅ dS =
ε0
∑q
i
i
E3 4πr 2 =
Q1 + Q2
ε0
E3 =
( 方向向上 )
7-5 如图 7-46 所示,长为 l 的细直线 OA 带电线密度为 λ ,求下面两种情 况下在线的延长线上距线的端点 O 点为 b 的 P 点的电场强度: (1) λ 为常量,且 λ >0;(2) λ =kx,k 为大于零的常量,(0≤x≤1)。
P O A x
b
54
第七章 静电场
合力的大小为
F = Fx = 2 F1cosθ = 2 ⋅
1 4πε 0
⋅
2e 2 d x2 + 2
2
⋅
2
x d x + 2
2
=
1
4πε 0 4 x 2 + d 2
大学物理B1复习题

一、选择题1.一质点作直线运动,其运动学方程为)(31232m t t x -+=,则在t=( A )秒时,质点的速度达到最大值。
(A )1 ;(B )3 ;(C )2 ;(D )4 。
2.一质量为m 的质点,从某高处无初速地下落,设所受阻力与其速率的一次方成正比,即υk f -=,则其收尾速度的大小为( B )。
(A )k m / ;(B )k mg /;(C )0 ;(D )∞。
3.一质量为4kg 的质点,在变力)(ˆsin 2N it F ππ=作用下由静止开始作直线运动,则此力持续作用2秒后质点的速率大小为( C )1-ms 。
(A )1 (B )2 (C )0 (D )44.均匀细杆OM 能绕O 轴在竖直平面内自由转动,如图1所示。
今使细杆OM 从水平位置开始摆下,在细杆摆动到竖直位置时,其角速度ω、角加速度α的值分别为( D )。
(A)0,0==αω;(B)0,0≠≠αω;(C)0,0≠=αω;(D) 0,0=≠αω。
5.一质点作直线运动,其运动学方程为2246,3t t y t t x ++=+=(长度以m 计,时间以s 计),则质点初速度的大小为( B )m/s 。
(A )3; (B )5 ; (C )4 ; (D )7。
6.一质量为m 的质点,作初速为0υ的直线运动,因受阻力作用速度逐渐变小。
设质点所受阻力的大小与质点速率的一次方成正比,方向与速度方向相反,即υmk f -=,则质点的速率从0υ减小到021υ,所需的时间为( C )s 。
(A )k /2ln 2;(B )2;(C )k /2ln ;(D )4。
7.一质点的质量为2kg ,受变力t F ππ2cos 12=(N )作用作初速为0的直线运动,则在t=0.25s 时质点速度的大小为( D )m/s 。
(A )0; (B )6; (C )4; (D )3。
8.如图1所示,在一质量为M 半径为R 的匀质薄圆盘的边缘放一质量为m 的物体,设二者一起以角速度ω绕中心轴以角速度ω匀速转动,则系统对中心轴的角动量的大小为( A )。
大学物理(2)期末复习试题库

大学物理(2)期末复习试题库第四篇 电磁学一、判断题1.关系H B μ=对所有各向同性线性介质都成立。
( )2.静电场中任何两条电力线不相交,说明静电场中每一点的场强是唯一的。
( )3.导体内部处处没有未被抵消的静电荷,静电荷只分布在导体的表面上。
( )4.电源电动势的方向是自正极经电源内部到负极的方向。
( )5.自感系数只依赖线圈本身的形状、大小及介质的磁导率而与电流无关。
( )6.恒定磁场中定理∑⎰=⋅I l d H 成立。
( )7.关系E D ε=对所有各向同性电介质都成立。
( )8. 0ε∑⎰⎰=⋅q s d E 对任意电场均成立。
( ) 9.可以把电子的自旋运动和宏观物体的自转运动相类比。
( )10.无论是在稳恒磁场还是非稳恒磁场中安培环路定理∑⎰=⋅i LI l d H 都成立。
( )11.导体静电平衡的条件是导体内部场强处处为零。
( )12.有人把⎰⎰=⋅0S B d 称为磁场高斯定理,它只对恒定磁场成立,在变化磁场中⎰⎰≠⋅0S B d 。
( )13.由电容计算公式ab U q C =,理解为当0=q 时电容0=C 。
( )14.洛伦兹力不能改变运动电荷速度的大小,只能改变速度的方向。
( )15.任何导体内部场强都处处为零。
( )16.由安培环路定理∑⎰=⋅I l d H 可知,H 仅与传导电流有关。
( )17. 自感系数为L 的载流线圈磁场能量的公式221LI W =只适用于无限长密绕螺线管。
( )18.当一个带电导体达到静电平衡时, 表面上电荷密度较大处电势较高。
( )19.高斯定理⎰⎰=⋅VS dV d ρS D ,只对静电场成立,对变化的电场不成立。
( ) 20.在电场中,电场强度为零的点,电势不一定为零。
( )21.稳恒电流磁场的磁场强度H 仅与传导电流有关 。
( )22.当一个带电导体达到静电平衡时, 导体内任一点与其表面上任一点的电势差等于零。
( )23.有人把0=⋅⎰Sd S B 称为磁高斯定理,它只对恒定磁场成立,在变化的磁场中该式不成立。
2010普物练习题

普通物理练习题一、 选择题1、如图所示,O 点是两个相同的点电荷所在连线的中点,P 点为中垂线上的一点,则O 、P 两点的电势和场强大小有如下关系[C ]。
(A ),0p U U >|0E |〉|p E |;(B )p U U <0,|0E |〈|p E |;(C ),0p U U >|0E |〈|p E |;(D )p U U <0,|0E |〉|p E |。
2.关于稳恒磁场的磁场强度H 的下列几种说法中哪个是正确的[D].(A) H 仅与传导电流有关; (B)以闭合曲线L 为边缘的任意曲面的H 通量均相等.(C)若闭合曲线内没有包围传导电流,则曲线上各点的H 必为零;(D)若闭合曲线上各点的H 均为零,则该曲线所包围传导电流的代数和为零;3、一电场强度为E 的均匀电场,E 的方向与X 轴正向平行,如图所示,则通过图中一半径为R 的半球面的电场强度通量为[D ]。
(A )E R 2π;(B )21E R 2π;(C )2E R 2π;(D )0。
4、如图所示,直线MN 长为2L ,弧OCD 是以N 点为中心,L 为半径的半圆弧,N 点有正点电荷+q ,M 点有负点电荷-q ,今将一实验电荷+0q 从O 点出发沿路经OCDP 移到无穷远处,设无穷远处的电势为零,则电场力的功为[ ]。
(A ) A 〈0且为有限常量;(B )A 〉0且为有限常量;(C )A=∞;(D )A=0。
5、一质量为m ,电量为q 的粒子,以与均匀磁场B 垂直的速度V 射入磁场内,则粒子运动轨道所包围的磁通量Φ与磁感应强度B 大小的关系曲线是[ ]。
(A ) (B ) (C ) (D ) (E )6、有两个长直密绕螺线管,长度及匝数均相同,半径分别为1r 和2r ,管内充满均匀介质,其磁导率分别为1μ和2μ。
设1:2:,2:1:2121==μμr r ,当两只螺线管串联在电路中,通电稳定后,其自感系数之比21:L L 与磁能之比21:W W 分别为[ ]。
真空中的静电场(含答案,大学物理作业,考研真题)

班级:
姓名:
学号:
第十章 真空中的静电场(3)
一 、选择题 1、静电场中某点电势的数值等于 (A)正试验电荷 q0 置于该点时具有的电势能; (B) 把正试验电荷 q0 从该点移到电势零点处电场力所作的功; (C) 把单位正电荷从该点移到电势零点处电场力所作的功
(D)把单位正电荷从该点移到电势零点处外力所作的功。
P(x,0) xx
[
]
3、(2010 年北京科技大学)两个带有等量同号电荷,形状相同的金属小球1和2,相互
作用力为 F,它们之间的距离远大于小球本身直径.现在用一个带有绝缘柄的原来不带电的相
同金属小球3去和小球1接触,再和小球2接触,然后移去.这样小球1和2之间的作用力变
为:
(A) F/2;
(B) F/4;
S1
S2
S3
3、(2012 年北京科技大学)两个平行的“无限大”均
+σ +2σ
匀带电平面,其电荷面密度分别为 和 2 ,如图所示,则 A、
B、C 三个区域的电场强度分别为:
EA
EB
A
B
C
EC
3
三 、计算题 1、两个无限长同轴圆柱面,半径分别为 R1 和 R2(R2>R1),带有等值异号电荷,每单位长 度的电量为λ(即电荷线密度)。试分别求(1)r < R1,(2)r > R2,(3)R1< r<R2 时,离轴线 为 r 处之电场强度。
若将 q 移至 B 点,则:
(A)、S 面上的总电通量改变,P 点的场强不变; (B)、S 面上的总电通量不变,P 点的场强改变;
P· S B·
q·
(C)、S 面上的总电通量和 P 点的场强都不变; (D)、S 面上的总电通量和 P 点的场强都改变。
2012-2013学年第一学期 期末考试 大学物理II 试卷B

ORλ上海第二工业大学 (试卷编号:B0609A )2012-2013学年第一学期大学物理 期末考试 试卷姓名: 学号: 班级: 成绩:(本试卷共4页,请先查看试卷有无缺页,然后答题,请将答案写在答题纸上,写在试卷上的无效。
考试时间90分钟;总分100分)一、选择题(共10小题,每小题3分,共30分)1.真空中的无限大均匀带电平面,其电荷密度为σ,则由对称性可知其两侧空间电场强度大小为( )。
A .0 B .02εσ C .0εσ D .023εσ2.一半径为R 的半圆细环上电荷均匀分布,电荷线密度为λ,则 环心处的电场强度大小0E 为( )。
A .R 04πελ B .04ελ C .08ελ D .R02πελ 3.半径为R 的均匀带电球面,带的电量为q ,若取无限远处为电势的零点,则球面外离球心r 处的电势r U 为( )。
A .0 B .Rq 04πε C .rq 04πε D .204rq πε4. 如图,电量为Q 的点电荷被曲面S 所包围,从无穷远处引另一电量为q 的点电荷至曲面外一点,则下列说法正确的是( )。
A .曲面S 的E 通量不变,曲面上各点场强不变 B .曲面S 的E 通量变化,曲面上各点场强不变 C .曲面S 的E 通量变化,曲面上各点场强变化 D .曲面S 的E 通量不变,曲面上各点场强变化5.下列物理量中,可以表述为:“在数值上等于将试探电荷0q 从电场中的某点移至零电势能处过程中电场力做功”的是( )。
A .电势B .电势差C .电势能D .电场强度S.Q.q∙I32π∙O o I ∙OI IO xo zy6.如图所示,一磁场的磁感应强度为k c j b i a B++=(SI ),则通过一半径为R ,开口向x 轴正方向的半球壳表面的磁通量大小为( )Wb 。
A .2R a πB .2R b πC .2R c πD . 07.恒定磁场安培环路定理表达式为:⎰=⋅ll d B( ),表明磁场是( )。
大学物理_上海交通大学-第四版答案

11静电场11-1.直角三角形ABC的A点上,有电荷C108.191-⨯=q,B点上有电荷C108.492-⨯-=q,试求C点的电场强度(设0.04mBC=,0.03mAC=)。
解:1q在C点产生的场强:1124ACqE irπε=,2q在C点产生的场强:2224BCqE jr=,∴C点的电场强度:44122.710 1.810E E E i j=+=⨯+⨯;C点的合场强:4123.2410VE m==⨯,方向如图:1.8arctan33.73342'2.7α===。
11-2.用细的塑料棒弯成半径为cm50的圆环,两端间空隙为cm2,电量为C1012.39-⨯和方向。
解:∵棒长为2 3.12l r d mπ=-=,∴电荷线密度:911.010q C mlλ--==⨯⋅可利用补偿法,若有一均匀带电闭合线圈,则圆心处的合场强为0,有一段空隙,则圆心处场强等于闭合线圈产生电场再减去md02.0=长的带电棒在该点产生的场强,即所求问题转化为求缺口处带负电荷的塑料棒在O点产生的场强。
解法1:利用微元积分:21cos4O xRddERλθθπε=⋅,∴2000cos2sin2444OdE dR R Rααλλλθθααπεπεπε-==⋅≈⋅=⎰10.72V m-=⋅;解法2:直接利用点电荷场强公式:由于d r<<,该小段可看成点电荷:112.010q d Cλ-'==⨯,则圆心处场强:1191222.0109.0100.724(0.5)OqE V mRπε--'⨯==⨯⨯=⋅。
方向由圆心指向缝隙处。
11-3.将一“无限长”带电细线弯成图示形状,设电荷均匀分布,电荷线密度为λ,四分之一圆弧AB的半径为R,试求圆ix心O 点的场强。
解:以O 为坐标原点建立xOy 坐标,如图所示。
①对于半无限长导线A ∞在O 点的场强:有:00(cos cos )42(sin sin )42Ax A y E R E R λπππελπππε=-=-⎧⎪⎪⎨⎪⎪⎩②对于半无限长导线B ∞在O 点的场强:有:00(sin sin )42(cos cos )42B x B y E R E R λπππελπππε=-=-⎧⎪⎪⎨⎪⎪⎩③对于AB 圆弧在O 点的场强:有:20002000cos (sin sin )442sin (cos cos )442AB x AB y E d R R E d R R ππλλπθθππεπελλπθθππεπε==-=⎧⎪⎪⎨⎪⎪=--⎩⎰⎰∴总场强:04O x E R λπε=,04O y E R λπε=,得:0()4O E i j R λπε=+。
物理答案

5-1 两个电量都是+q 的点电荷,相距2a ,连线的中点为O 。
今在它们连线的垂直平分线上放另一点电荷q ',q '与O 点相距r 。
(1)求q '所受的力;(2)q '放在哪一点时,所受的力最大?解:(1)()θπεsin 4'2220ar qq F += 22sin ar r +=θ ()232202'ar r qq F +=πε(2)()()()35222222522222'3()[2]22'[2]2qq F r a r r a r r qq a r a r πεπε---'=+-+⨯=+-令()0'=r F ,解得:a r r a 22222== 故q '放在离o 点a 22处时,所受的力最大。
5-3 一半径为R 的半细圆环,均匀地分布+Q 电荷。
求环心的电场强度大小和方向。
解:在圆周上任取电荷元dl RQdq .π=,它的场强大小为204RdqdE πε=由于电荷相对于y 轴对称,知合场强应沿y 方向,故⎰⎰⎰-=-===dl R QE d dE E E y y θεπθcos 4)cos (302因为θRd dl =,故22222002cos 42Q Q E d RRππθθπεπε---==⎰上式中“-”表明:当Q>0时,E 的方向与图中y 轴的正方向相反,而Q<0时,E 的方向同y 轴的正方向。
5-4 一半径为R 的半球面,均匀地带有电荷,电荷面密度为σ 。
求球心处电场强度的大小。
解:将半球面无限分割成小圆环,另设圆环所带的电荷为电荷元dqθθaa +q+qrFFθd θ()22sin 2sin dq R Rd R d σπθθπσθθ=⋅⋅=根据书本P132上带电圆环在轴线某点产生场强的公式2022042sin 4cos sin 2cos 4εθθσπεθθθσπθπεd R d R R dq dE === 002020048282cos 42sin εσεσεθσεθθσππ==-==⎰d E5-5 一无限大平面,开有一个半径为R 的圆洞,设平面均匀带电,电荷面密度为 σ ,求这洞的轴线上离洞心为r 处的场强。
8-6一半径为R的半圆细环上均匀地分布电荷,求环心处的电场强度

大学物理期末复习题(力学部分)第一章重点:质点运动求导法和积分法,圆周运动角量和线量。
第二章重点:三大守恒律---动量守恒定律、机械能守恒定律、角动量守恒定律 第三章重点:刚体定轴转动定律和角动量守恒定律1.一质点沿半径为0.1=R m 的圆周作逆时针方向的圆周运动,质点在0~t 这段时间内所经过的路程为422t t S ππ+=,式中S 以m 计,t 以s 计,则在t 时刻质点的角速度为 22t ππ+rad/s , 角加速度为 2/2s rad π。
(求导法)2.质点沿x 轴作直线运动,其加速度t a 4=m/s 2,在0=t 时刻,00=v ,100=x m ,则该质点的运动方程为=x 33210t x += 。
(积分法)3.一质点从静止出发绕半径R 的圆周作匀变速圆周运动,角加速度为β,则该质点走完半周所经历的时间为_____βπ2_ _____。
(积分法)4.一质点在平面内运动, 其1c r =,2/c dt dv =;1c 、2c 为大于零的常数,则该质点作 匀加速圆周运动 。
5.伽利略相对性原理表明对于不同的惯性系牛顿力学的规律都具有相同的形式。
6.一质量为kg m 2=的质点在力()()N t F x 32+=作用下由静止开始运动,若此力作用在质点上的时间为s 2,则该力在这s 2内冲量的大小=I 10 NS ;质点在第s 2末的速度大小为 5 m/s 。
(动量定理和变力做功)7.一质点受力26x F -=的作用,式中x 以m 计,F 以N 计,则质点从0.1=x m 沿X 轴运动到x=2.0 m 时,该力对质点所作的功=A J 14-。
(变力做功)8.一滑冰者开始自转时其动能为20021ωJ ,当她将手臂收回, 其转动惯量减少为3J ,则她此时自转的角速度=ω 03ω 。
(角动量守恒定律)9.一质量为m 半径为R 的滑轮,如图所示,用细绳绕在其边缘,绳的另一端系一个质量也为m 的物体。
《大学物理学》习题解答(第11章 静电场)

1
Q L
L
2 0 r 1 4r 2 L2
2 0 r
2
【11.5】一半径为 R 的半圆细环上均匀的分布电荷 Q,求环心处的电场强度。 解取坐标 Oxy ,电荷元 d q d l R d ,由点电荷场强公式
y
d
dl
dq dE eR 4 0 R 2
由于电荷对称分布,场强也对称,则: Ex dEx 0
13
以 1.0 10 C s 的变化率失去电荷,求两球彼此趋近的瞬时相对速率(即
9
1
T q F mg x
l q
dx )是多少? dt
解 (1)如图所示,小球平衡时,
T sin F , T cos mg , F
q
2
4 0 x 2
13
q 2l x , 很小时, tan sin ,因此 x 则 mg tan 2 mg 2l 4 0 x 2 0
E d S E d S ER 2 cos ER 2
S S
z
A F C E O D B
【11.11】边长为 a 的立方体如图所示,其表面分别平行于 xy , yz 和 zx 平 面,立方体的一个顶点为坐标原点。现将立方体置于电场强度
E ( E1 kx)i E2 j 的非均匀电场中, 求立方体各表面及整个立方体表面的
Q d x ,则 L
EP
Qdx Q 1 1 1 Q [ ] 2 2 L 2 4 L ( r x ) 4 0 L r L 2 r L 2 0 4r L2 0
L2
1
(2)若点 P 在棒的垂直平分线上,因对称性, E 沿 x 轴方向的分量叠加为零,因此, E 的方向沿 y 轴, 大小为
高中物理奥林匹克竞赛专题——静电场典型习题(有详解答案)

题7.1:1964年,盖尔曼等人提出基本粒子是由更基本的夸克构成,中子就是由一个带e 32的上夸克和两个带e 31-下夸克构成,若将夸克作为经典粒子处理(夸克线度约为10-20 m ),中子内的两个下夸克之间相距2.60⨯10-15 m 。
求它们之间的斥力。
题7.1解:由于夸克可视为经典点电荷,由库仑定律r r 220r 2210N 78.394141e e e F ===r e r q q πεπεF 与r e 方向相同表明它们之间为斥力。
题7.2:质量为m ,电荷为-e 的电子以圆轨道绕氢核旋转,其动能为E k 。
证明电子的旋转频率满足42k20232me E εν=其中是0ε真空电容率,电子的运动可视为遵守经典力学规律。
题7.2分析:根据题意将电子作为经典粒子处理。
电子、氢核的大小约为10-15 m ,轨道半径约为10-10 m ,故电子、氢核都可视作点电荷。
点电荷间的库仑引力是维持电子沿圆轨道运动的向心力,故有220241r e r v m πε= 由此出发命题可证。
证:由上述分析可得电子的动能为re mv E 202k 8121πε==电子旋转角速度为30224mr e πεω=由上述两式消去r ,得43k 20222324meE επων== 题7.3:在氯化铯晶体中,一价氯离于Cl -与其最邻近的八个一价格离子Cs +构成如图所示的立方晶格结构。
(1)求氯离子所受的库仑力;(2)假设图中箭头所指处缺少一个铯离子(称作品格缺陷),求此时氯离子所受的库仑力。
题7.3分析:铯离子和氯离子均可视作点电荷,可直接将晶格顶角铯离子与氯离子之间的库仑力进行矢量叠加。
为方便计算可以利用晶格的对称性求氯离子所受的合力。
解:(l )由对称性,每条对角线上的一对铯离子与氯离子间的作用合力为零,故01=F (2)除了有缺陷的那条对角线外,其它铯离子与氯离子的作用合力为零,所以氯离子所受的合力2F 的值为N 1092.134920220212-⨯===ae rq q F πεπε2F 方向如图所示。
大学物理习题及解答(电学)

1.一半径为R 的半圆细环上均匀分布电荷Q ,求环心处的电场强度。
2.两条无限长平行直导线相距为r 0,均匀带有等量异号电荷,电荷线密度为λ。
(1)求两导线构成的平面上任一点的电场强度(设该点到其中一线的垂直距离为x );(2)求每一根导线上单位长度导线受到另一根导线上电荷作用的电场力。
3.地球周围的大气犹如一部大电机,由于雷雨云和大气气流的作用,在晴天区域,大气电离层总是带有大量的正电荷,云层下地球表面必然带有负电荷。
晴天大气电场平均电场强度约为120 V ⋅m -1,方向指向地面。
试求地球表面单位面积所带的电荷。
(-1.06×10-9c/m 2)4.一无限大均匀带电薄平板,电荷面密度为σ,在平板中部有一半径为r 的小圆孔。
求圆孔中心轴线上与平板相距为x 的一点P 的电场强度。
(2202r x x+εσ)5.一无限长、半径为R 的圆柱体上电荷均匀分布。
圆柱体单位长度的电荷为λ,用高斯定理求圆柱体内距轴线距离为r 处的电场强度。
6.两个带有等量异号电荷的无限长同轴圆柱面,半径分别为R 1和R 2 (R 2 > R 1),单位长度上的电荷为λ。
求离轴线为r 处的电场强度:(1)r < R 1,(2)R 1 < r < R 2,(3)r > R 27.如图所示,有三个点电荷Q 1、Q 2、Q 3沿一条直线等间距分布,已知其中任一点电荷所受合力均为零,且Q 1 =Q 3=Q 。
求在固定Q 1、Q 3的情况下,将Q 2从点O 移到无穷远处外力所作的功。
解: :由题意Q 1所受的合力为零0244031021=+)d (Q Q d Q Q πεπε 解得Q Q Q 414132-=-= 在任一点电荷所受合力均为零时Q Q 412-=。
并由电势的叠加得Q 1、Q 3在点O 电势 d Qd Q d Q V o 00301244πεπεπε=+=将Q 2从点O 推到无穷远处的过程中,外力作功 d QV Q W o 0228πε=-=8.已知均匀带电长直线附近的电场强度近似为002r rE πελ= λ为电荷线密度。
大学物理B2习题修改版

大学物理B2习题一、电磁学部分1、如图所示,真空中一长为L 的均匀带电细直杆,总电荷为q ,试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度和电势.解:以直杆右端点为原点向左方向为x 轴正方向建立坐标系()204d d x d xE +π=ελ整个杆上电荷在该点的场强为:()()l d d lx d x E l +π=+π=⎰00204d 4ελελ沿x 轴负向 电荷元在O 点产生的电势)(4d d 0x d xV +π=ελO 点总电势()dld x d x V l +π=+π=⎰ln4d 4000ελελ2、一半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的电场强度和电势。
解: 如图在圆上取ϕRd dl =ϕλλd d d R l q ==,它在O 点产生场强大小为20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x ==ϕϕελϕπd cos π4)cos(d d 0RE E y -=-=R R E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=-=⎰ϕϕελπRE y∴ RE E x 0π2ελ==,方向沿x 轴正向.3、实验证明,地球表面上方电场不为0,晴天大气电场的平均场强约为120V/m ,方向向下,这意味着地球表面上有多少过剩电荷?试以每平方厘米的额外电子数表示。
(526.6410/cm ⨯个) 解:由高斯定理可知:所以单位面积带电量为=单位面积额外电子数为526.6410/cm ⨯个 4、地球表面上方电场方向向下,大小可能随高度变化,设在地面上方100m 高处场强为150N/C ,300m 高处场强为100N/C ,试由高斯定理求在这两个高度之间的平均体电荷密度,以多余的或缺少的电子数密度表示。
(缺少,721.3810/m ⨯个)5、如图所示,电量1q 均匀分布在半径为1R 的球面上,电量2q 均匀分布在同心的半径为2R 的球面上,2R >1R 。
北京航空航天大学大学物理上公式及例题大全

内容提要位矢:k t z j t y i t x t r r)()()()(++== 位移:k z j y i x t r t t r r ∆+∆+∆=-∆+=∆)()(一般情况,r r ∆≠∆速度:k z j y i x k dt dz j dtdy i dt dx dt r d t r t•••→∆++=++==∆∆=0lim υ 加速度:k z j y i x k dtz d j dt y d i dt x d dt r d dt d t a t ••••••→∆++=++===∆∆=222222220lim υυ圆周运动 角速度:•==θθωdtd 角加速度:••===θθωα22dtd dt d (或用β表示角加速度) 线加速度:t n a a a += 法向加速度:22ωυR R a n ==指向圆心 切向加速度:αυR dtd a t ==沿切线方向 线速率:ωυR =弧长:θR s = 解题参考大学物理是对中学物理的加深和拓展。
本章对质点运动的描述相对于中学时更强调其瞬时性、相对性和矢量性,特别是处理问题时微积分的引入,使问题的讨论在空间和时间上更具普遍性。
对于本章习题的解答应注意对基本概念和数学方法的掌握。
矢量的引入使得对物理量的表述更科学和简洁。
注意位矢、位移、速度和加速度定义式的矢量性,清楚圆周运动角位移、角速度和角加速度方向的规定。
微积分的应用是难点,应掌握运用微积分解题。
这种题型分为两大类,一种是从运动方程出发,通过微分求出质点在任意时刻的位矢、速度或加速度;另一种是已知加速度或速度与时间的关系及初始条件,通过积分求出任意时刻质点的速度、位矢或相互间的关系,注意式子变换过程中合理的运用已知公式进行变量的转换,掌握先分离变量后积分的数学方法。
内容提要动量:υm p = 冲量:⎰=21t t dt F I 动量定理:⎰=21t t dt F p d ⎰=-210t t dt F p p 动量守恒定律:若0==∑i i F F ,则常矢量==∑ii p p力矩:F r M ⨯=质点的角动量(动量矩):υ ⨯=⨯=r m p r L 角动量定理:dtL d M =外力 角动量守恒定律:若0==∑外力外力M M ,则常矢量==∑ii L L功:r d F dW •= ⎰•=B A AB r d F W 一般地 ⎰⎰⎰++=B A B A B A z z z y y y x x x AB dz F dy F dx F W 动能:221υm E k = 动能定理:质点, 222121A B AB m m W υυ-=质点系,0k k E E W W -=+内力外力保守力:做功与路程无关的力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
--一半径为R的半圆细环上均匀地分布电荷--求环心处的————————————————————————————————作者:————————————————————————————————日期:大学物理1期末复习题(力学部分)第一章重点:质点运动求导法和积分法,圆周运动角量和线量。
第二章重点:牛顿第二运动定律的应用(变形积分) 第三章重点:动量守恒定律和机械能守恒定律 第四章重点:刚体定轴转动定律和角动量守恒定律1.一质点沿半径为0.1=R m 的圆周作逆时针方向的圆周运动,质点在0~t 这段时间内所经过的路程为422t tS ππ+=,式中S 以m 计,t 以s 计,则在t 时刻质点的角速度为 22t ππ+rad/s , 角加速度为 2/2s rad π。
(求导法)2.质点沿x 轴作直线运动,其加速度t a 4=m/s 2,在0=t 时刻,00=v ,100=x m ,则该质点的运动方程为=x 33210t x += 。
(积分法)3.一质点从静止出发绕半径R 的圆周作匀变速圆周运动,角加速度为β,则该质点走完半周所经历的时间为_____βπ2_ _____。
(积分法)4.伽利略相对性原理表明对于不同的惯性系牛顿力学的规律都具有相同的形式。
5.一质量为kg m 2=的质点在力()()N t F x 32+=作用下由静止开始运动,若此力作用在质点上的时间为s 2,则该力在这s 2内冲量的大小=I 10 NS ;质点在第s 2末的速度大小为 5 m/s 。
(动量定理和变力做功)6.一质点在平面内运动, 其1c r =,2/c dt dv =;1c 、2c 为大于零的常数,则该质点作 匀加速圆周运动 。
7.一质点受力26x F -=的作用,式中x 以m 计,F 以N 计,则质点从0.1=x m 沿X 轴运动到x=2.0 m 时,该力对质点所作的功=A J 14-。
(变力做功)8.一滑冰者开始自转时其动能为20021ωJ ,当她将手臂收回, 其转动惯量减少为3J ,则她此时自转的角速度=ω 03ω 。
(角动量守恒定律)9.一质量为m 半径为R 的滑轮,如图所示,用细绳绕在其边缘,绳的另一端系一个质量也为m 的物体。
设绳的长度不变,绳与滑轮间无相对滑动,且不计滑轮与轴间的摩擦力矩,则滑轮的角加速度Rg32 ;若用力mg F =拉绳的一端,则滑轮的角加速度为 Rg2 。
(转动定律)10.一刚体绕定轴转动,初角速度80=ωrad/s ,现在大小为8(N ·m )的恒力矩作用下,刚体转动的角速度在2秒时间内均匀减速到4=ωrad/s ,则刚体在此恒力矩的作用下的角加速度=α____2/2s rad -__ _____,刚体对此轴的转动惯量=J 4kg •m 2 。
(转动定律) 11.一质点在平面内运动,其运动方程为 22 ,441x t y t t =⎧⎨=++⎩,式中x 、y 以m 计,t 以秒s 计,求:(1) 以t 为变量,写出质点位置矢量的表达式; (2) 轨迹方程;(3) 计算在1~2s 这段时间内质点的位移、平均速度; (4) t 时刻的速度表达式;(5) 计算在1~2s 这段时间内质点的平均加速度;在11=t s 时刻的瞬时加速度。
解:(1) ())m (14422j t t i t r+++=;(2)2)1(+=x y ;(3)(m)162Δj r+=i ; (m/s)162j+=i v ;(4))m/s ()48(2j t i dtrd ++==v ;(5) )(m/s 82j =a ;)(m/s 82j =1a (求导法)12.摩托快艇以速率0v 行驶,它受到的摩擦阻力与速度平方成正比,设比例系数为常数k ,即可表示为2kv F -=。
设快艇的质量为m ,当快艇发动机关闭后,(1)求速度随时间的变化规律;(2)求路程随时间的变化规律。
解:(1)2dvkv m dt-=mF0201vt v k dv dt v m =-⎰⎰ 00mv v m kv t =+ (2)0000xtmv dx dt m kv t =+⎰⎰0(1)kv t mx Ln k m =+(牛二定律变形积分)13.如图所示,两个带理想弹簧缓冲器的小车A和B ,质量分别为1m 和2m ,B 不动,A 以速度0v与B 碰撞,如已知两车的缓冲弹簧的倔强系数分别为1k 和2k ,在不计摩擦的情况下,求两车相对静止时,其间的作用力为多大?(弹簧质量忽略而不计)。
解:系统动量守恒: 1012()m v m m v =+系统机械能守恒: 2222101211221111()2222m v m m v k x k x =+++两车相对静止时弹力相等: 1122F k x k x ==F=02121212121][v k k kk m m m m +⋅+ (动量守恒和机械能守恒定律)14.有一质量为1m 长为l 的均匀细棒,静止平放在光滑的水平桌面上,它可绕通过其中点O 且与桌面垂直的固定光滑轴转动。
另有一水平运动的质量为2m 的子弹以速度v 射入杆端,其方向与杆及轴正交,求碰撞后棒端所获得的角速度。
解:系统角动量守恒: 2J 2lm v ω=总2212()122m l lJ m =+总 2126 (3)v m m m lω=+ (角动量守恒定律)电磁学部分第五章重点:点电荷系(矢量和)、均匀带电体(积分法)、对称性电场(高斯定理,分段积分)的电场强度E 和电势V 的计算。
第七章重点:简单形状载流导线(矢量和)、对称性磁场(安培环路定理)的磁感应强度BBA 1m2mv1k2k的计算,安培力F 的计算。
第八章重点:感生电动势(法拉第电磁感应定律)和动生电动势i ε的计算,磁通量m φ的计算。
1.一半径为R 的半圆细环上均匀地分布电荷Q ,求环心处的电场强度.[分析] 在求环心处的电场强度时,不能将带电半圆环视作点电荷.现将其抽象为带电半圆弧线。
在弧线上取线dl ,其电荷dl RQdq π=,此电荷元可视为点电荷,它在点O 的电场强度2041rdqdE πε=,因圆环上的电荷对y 轴呈对称性分布,电场分布也是轴对称的,则有0=⎰L xdE,点O 的合电场强度⎰=Ly dE E ,统一积分变量可求得E .解: (1)建立坐标系;(2)取电荷元dl RQdq π=(3)写2041rdq dE πε=(4)分解到对称轴方向θπεcos 4120rdqdE y =(5)积分:dl RQR E LO πθπε⋅⋅-=⎰20cos 41 由几何关系θRd dl =,统一积分变量后,有2022220202c o s 4R Q d R Q E επθθεπππ-=-=⎰-,方向沿y 轴负方向.(积分法五步走)2.两条无限长平行直导线相距为0r ,均匀带有等量异号电荷,电荷线密度为.λ(1)求两导线构成的平面上任一点的电场强度(设该点到其中一线的垂直距离为x ); (2)求每一根导线 上单位长度导线受到另一根导线上电荷作用的电场力.[分析]在两导线构成的平面上任一点的电场强度为两导线单独在此所激发的电场rE 02πελ=的叠加.解: 设点P 在导线构成的平面上,+E 、-E 分别表示正、负带电导线在P 点的电场强度,则有i x r x E E E⎪⎪⎭⎫ ⎝⎛-+=+=-+00112πελ()i x r x r -=0002πελ (矢量和)3.设均强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量.[分析] 方法1:由电场强度通量的定义,对半球面S 求积分,即⎰⋅=ΦSS S d E.方法2:作半径为R 的平面S '与半球面S 一起可构成闭合曲面,由于闭合面内无电荷,由高斯定理∑⎰==⋅01q dS E Sε 这表明穿过闭合曲面的净通量为零,穿入平面S '的电场强度通量在数值上等于穿出半球面S 的电场强度通量. 因而⎰⎰'⋅-=⋅=ΦSS S d E S d E解: 由于闭合曲面内无电荷分布,根据高斯定理,有 ⎰⎰'⋅-=⋅=ΦSS S d E S d E依照约定取闭合曲面的外法线方向为面元dS 的方向,E R R E 22cos πππ=⋅⋅-=Φ (高斯定理和电通量定义式)4.在电荷体密度为ρ的均匀带电球体中,存在一个球形空腔,若将带电体球心O 指向球形空腔球心O '的矢量用a 表示(图8-17).试证明球形空腔中任一点的电场强度为a E3ερ= [分析] 本题带电体的电荷分布不满足球对称,其电场分布也不是球对称分布,因此无法直接利用高斯定理求电场的分布,但可用补偿法求解.挖去球形空腔的带电球体在电学上等效于一个完整的、电荷体密度为ρ的均匀带电球和一个电荷体密度为ρ-、球心在O '的带电小球体(半径等于空腔球体的半径).大小球体在空腔内P 点产生的电场强度分别为1E 、2E ,则P 点的电场强度为两者矢量和。
. 证: 带电球体内部一点的电场强度为 r E 03ερ=所以 1013r E ερ=;2023r E ερ-=()210213r r E E E-=+=ερ 根据几何关系a r r=-21,上式可改写为a E 03ερ=(等效法和高斯定理) 5.一无限长、半径为R 的圆柱体上电荷均匀分布.圆柱体单位长度的电荷为λ,用高斯定理求圆柱体内距离为r 处的电场强度.[分析] 无限长圆柱体的电荷具有轴对称分布,电场强度也为轴对称分布,且沿径矢方向.取同轴柱面为高斯面,电场强度在圆柱侧面上大小相等,且与柱面正交.在圆柱的两个底面上,电场强度与底面平行,0=⋅dS E ,对电场强度通量的贡献为零.整个高斯面的电场强度通量为⎰⋅=⋅rL E dS E π2由于圆柱体电荷均匀分布,电荷体密度E,出于高斯面内的总电荷Lr q ∑⋅=2πρ由高斯定理⎰∑=⋅0εq dS E 可解得电场强度的分布.解: 取同轴柱面为高斯面,由上述分析得 L r RL r rL E 2202012ελπρεπ=⋅=⋅202RrE πελ=(高斯定理) 6.两个带有等量异号电荷的无限长同轴圆柱面,半径分别为1R 和()122R R R >,单位长度上的电荷为λ.求离轴线为r 处的电场强度:(1)1R r <,(2)21R r R <<,(3)2R r > [分析] 电荷分布在无限长同轴圆柱面上,电场强度也必定程轴对称分布,沿径向方向.去同轴圆柱为高斯面,只有侧面的电场强度通量不为零,且⎰⋅=⋅,2rL E dS E π求出不同半径高斯面内的电荷∑q .利用高斯定理可解得各区域电场的分布.解: 作同轴圆柱面为高斯面,根据高斯定理 ∑=⋅02επqrL E1R r <,∑=0q01=E21R r R <<,∑=L q λrE 022πελ=2R r >,∑=0q03=E在带电面附近,电场强度大小不连续,电场强度有一跃变 0022εσπλπελ===∆rL L r E (高斯定理) 7.如图所示,有三个点电荷 321Q Q Q 、、沿一条直线等间距分布,已知其中任一点电荷所受合力均为零,且Q Q Q ==21.求在固定1Q 、3Q 的情况下,将2Q 从点O 移到无穷远处外力所作的功.[分析] 由库仑力的定义,根据1Q 、3Q 所受合力为零可求得42QQ -=.外力作功W '应等于电场力作功W 的负值,即W W '-=.求电场力作功可根据功电场力作的功与电势能差的关系,有()0202V Q V V Q W =-=∞其中0V 是点电荷1Q 、3Q 在点O 产生的电势(取无穷远处为零电势).:解 在任一点电荷所受合力均为零时Q Q 412-=,并由电势的叠加1Q 、3Q 在O 的电势dQ dQ dQ V 003010244πεπεπε=+=将2Q 从点O 推到无穷远处的过程中,外力作功 dQ V Q W 02028πε=-=' (受力平衡、点电荷系电势、电场力做功)8.已知均匀带电长直线附近的电场强度近似为r e rE02πελ=λ为电荷线密度. (1)在求在1r r =和2r r =两点间的电势差;(2)在点电荷的电场中,我们曾取∞−→−r 处的电势为零,求均匀带电长直线附近的电势时,能否这样取?试说明.解 )(1由于电场力作功与路径无关,若取径矢为积分路径,则有12012ln 221r r r dr E U r r ⎰=⋅=∆επλ(电势差定义式)(2)不能. 严格地讲,电场强度 rE 02πελ=只适用于无限长的均匀带电直线,而此时电荷分布在无限空间,∞→r 处的电势应与直线上的电势相等.9.两个同心球面的半径分别为1R 和2R ,各自带有电荷1Q 和2Q .求:(1)各区域电势分布,并画出分布曲线;(2)两球面间的电势差为多少?[分析] 由于电荷均匀分布在球面上,电场分布也具有球对称性,因此,可根据电势与电场强度的积分关系求电势.取同心球面为高斯面,借助高斯定理可求得各区域的电场强度分布,再由⎰⎰∞∞⋅=⋅=rPP dr E l d E V 可求得电势分布.解: 由高斯定理可求得电场分布01=E 1R r < 20124r Q E πε=21R r R <<202134rQ Q E πε+= 2R r > 由电势 ⎰∞⋅=rdr E V 可求得区域的电势分布.当 1R r ≤时,有dr E dr E dr E V R R R R r⋅+⋅+⋅=⎰⎰⎰∞221132112021210141140R Q Q R R Q πεπε++⎪⎪⎭⎫ ⎝⎛-+= 20210144R Q R Q πεπε+=当21R r R ≤≤时,有dr E dr E V R R r⋅+⋅=⎰⎰∞22322202121014114R Q Q R r Q πεπε++⎪⎪⎭⎫ ⎝⎛-=2020144R Q rQ πεπε+=当1R r ≥ 时,有⎪⎪⎭⎫⎝⎛-=⋅=⎰∞210133114R R Q dr E V rπε(先用高斯定理求场强E,再用分段积分求电势V)10.两个很长的共轴圆柱面()m R m R 10.0,100.3221=⨯=,带有等量异号的电荷,两者的电势差为450V .求:(1)圆柱面单位长度上带有多少电荷?(2)两圆柱面之间的电场强度. 解 由8的结果,两圆柱面之间的电场 rE 02πελ= 根据电势差的定义有12012ln 221R R dr E U R R ⎰=⋅=∆πελ 解得 1812120101.2ln2--⋅⨯==m C R R U πελ V rr E 11074.3220⨯==πελ 两柱面间电场强度的大小与r 成反比. (电势差定义式)11.在Oxy 面上倒扣着半径为R 的半球面,半球面上电荷均匀分布,电荷密度为σ.A 点的坐标为()20R ,,B 点的坐标为()23R ,求电势差AB U . [分析] 电势的叠加是标量的叠加,根据对称性,带电半球面在Oxy 平面上各点产生的电势显然就等于带电球面在改点的电势的一半.据此,可先求出一个完整球面在B A 、间的电势差AB U ',再求出半球面时的电势差AB U .由于带电球面内等电势,球面内A 点的电势,故()B R ABAB V V U U '-'='=2121 其中R V '是带电球表面的电势,B V '是带电球面在B 点的电势. 解 假设将半球面扩展为带有相同电荷面密度σ的一个完整球面,此时在B A 、两点的电势分别为RAV RRQ V '==='004εσπε020324εσεσπεRr R r QV B ===' 则半球面在B A 、两点的电势差 ()0621εσR V V U B R AB ='-'==∆(点电荷电势式和电势差定义式)12.在半径为1R 的长直导线外,套有氯丁橡胶绝缘护套,护套外半径为2R ,相对电容率为r ε.设沿轴线单位长度上,导线的电荷密度为λ.试求介质层内的E D 、和P .[分析] 将长直导线视作无限长,自由电荷均匀分布在导线表面.在绝缘介质层的内、外表面分别出现极化电荷,这些电荷在内外表面呈均匀分布,所以电场是轴对称分布.取同轴柱面为高斯面,由介中的高斯定理可得电位移矢量D 的分布.在介质中E D r εε0=,E D P0ε-=,可进一步求得电场强度E 和电极化强度矢量P 的分布.解 由介质中的高斯定理,有⎰=⋅=⋅L rL D S d D λπ2得 rD πλ2= 在均匀各向同性介质中 rDE r rεπελεε002==r r e r E D P πλεε2110⎪⎪⎭⎫ ⎝⎛-=-= (有电介质时的高斯定理)13.设有两个薄导体同心球壳A 与B ,它们的半径分别为cm R 101=与cm R 203=,并分别带有电荷C C 78100.1100.4--⨯⨯-与.球壳间有两层介质,内层介质的0.2,0.421==r r εε外层介质的,其分界面的半径为.152cm R =球壳B 外为空气.求:(1)两球间的电势差AB U ;(2)离球心cm 30的电场强度;(3)2球A 的电势.[分析] 自由电荷和极化电荷均匀分布在球面上,电场呈球对称分布.取同心球面为高斯面,根据介质中的高斯定理可求得介质中的电场分布.由电势差和电场强度的积分关系可求得两导体球壳间的电势差,由于电荷分布在有限空间,通常取无穷远处为零电势⎰∞⋅=AA dl E V解 (1)由介质中的高斯定理,有124Q r D dS D =⋅=⋅⎰π 得 221214r e r Q D D π== r r e r D E 21011εε=R r R <<1r r r e rQ D E 220120224επεεε==32R r R <<两球壳间的电势差 ⎰⋅=31R R AB dl E Udl E dl E R R R R ⋅+⋅=⎰⎰322121⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=3220121101114114R R Q R R Q r r επεεπε V 2100.6⨯-= (2)同理由高斯定理可得 1320213100.64-⋅⨯=+=m V e e rQ Q E r r πε (3)取无穷远处电势为零,则 V R Q Q U dl E U V AB BAB A 330213101.24⨯=++=+=⎰∞πε(先由电介质中高斯定理求D 分布,再求E 分布,再分段积分求V 分布)14. 如图所示,几种载流导线在平面内分布,电流均为I ,它们在点O 的磁感应强度各为多少?[分析] 应用磁场叠加原理求解.将不同形状的载流导线分解成长直部分和圆弧部分,它们各自在点O 处所激发的磁感强度较容易求得,则总的磁感强度3210B B B B++=. 解 (a) 长直电流对点O 而言,它在延长线上点O 产生的磁场为零,则点O 处总的磁感强度为41圆弧电流所激发,故有: RIB 800μ=,方向垂直纸面向外Θ.(b) 将载流导线看作圆电流和长直电流,由叠加原理可得.RIRIB πμμ22000-= , 方向垂直纸面向里 ⊗(c) 将载流导线看作21圆电流和两段半无限长直电流,由叠加原理可得 RIR I R I R I R I B 42444000000μπμμπμπμ+=++=,方向垂直纸面向外. Θ (矢量和)15.载流长直导线的电流为I ,试求通过矩形线圈ABCD 的磁通量.[分析] 由于矩形平面上各点的磁感应强度不同,故磁通量BS ≠Φ.为此,可在矩形平面上取一矩形面元ldx dS =()[]b 1011-图,载流长直导线的磁场穿过该面元的磁通量为 ldx xIdS B d πμ20=⋅=Φ 矩形平面的总磁通量⎰Φ=Φd 解 由上述分析可得矩形平面的总磁通量 1200ln 2221d dIl ldx x I d d πμπμ==Φ⎰(积分法四步走) 16.有同轴电缆,其尺寸如图所示.两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑.试计算以下各处的磁感应强度:(1);1R r <(2)21R r R <<;(3)32R r R <<;(4)3R r >.画出r B -图线.[分析] 同轴电缆导体内的电流均匀分布,其磁场呈轴对称,取半径为r 的同心圆为积分路径,⎰⋅=⋅r B l d B π2 ,利用安培环路定理∑⎰=⋅I l d B 0μ,可解得各区域的磁感强度.解 由上述分析得1R r < 22112r R Ir B ππμπ=⋅ 21012R IrB πμ=21R r R << I r B 022μπ=⋅rIB πμ202=31R r R << ()()⎥⎦⎤⎢⎣⎡---=⋅I R R R r I r B 2223222032ππμπ2223223032R R r R r I B --=πμ 3R r > ()0204=-=⋅I I r B μπ04=B磁感强度()r B 的分布曲线略。
