matlab符号运算函数大全
MatLab常用函数大全

1、求组合数C,则输入:求knnchoosek(n,k)例:nchoosek(4,2) = 6.2、求阶乘求n!.则输入:Factorial(n).例:factorial(5) = 120.3、求全排列perms(x).例:求x = [1,2,3];Perms(x),输出结果为:ans =3 2 13 1 22 3 12 1 31 2 31 3 24、求指数求a^b:Power(a,b) ;例:求2^3 ;Ans = pow(2,3) ;5、求行列式求矩阵A的行列式:det(A);例:A=[1 2;3 4] ;则det(A) = -2 ;6、求矩阵的转置求矩阵A的转置矩阵:A’转置符号为单引号.7、求向量的指数求向量p=[1 2 3 4]'的三次方:p.^3 例:p=[1 2 3 4]'A=[p,p.^2,p.^3,p.^4]结果为:注意:在p与符号”^”之间的”.”不可少.8、求自然对数求ln(x):Log(x)例:log(2) = 0.69319、求矩阵的逆矩阵求矩阵A 的逆矩阵:inv(A)例:a= [1 2;3 4];则10、多项式的乘法运算函数conv(p1,p2)用于求多项式p1和p2的乘积。
这里,p1、p2是两个多项式系数向量。
例2-2 求多项式43810x x +-和223x x -+的乘积。
命令如下:p1=[1,8,0,0,-10];p2=[2,-1,3]; c=conv(p1,p2)11、多项式除法函数[q ,r]=deconv(p1,p2)用于多项式p1和p2作除法运算,其中q 返回多项式p1除以p2的商式,r 返回p1除以p2的余式。
这里,q 和r 仍是多项式系数向量。
例2-3 求多项式43810x x +-除以多项式223x x -+的结果。
命令如下:p1=[1,8,0,0,-10];p2=[2,-1,3]; [q,r]=deconv(p1,p2)12、求一个向量的最大值求一个向量x 的最大值的函数有两种调用格式,分别是:(1)max(x):返回向量x 的最大值,如果x 中包含复数元素,则按模取最大值。
Matlab符号函数

2
4
6
x
例17、 计算不定积分 eax sin(bx)dx
syms x
int('exp(a*x)*sin(b*x)')
g=simplify(ans)
g=
exp(a*x)*(-b*cos(b*x)+a*sin(b*x))/(a^2+b^2)
diff(g)
f=simplify(ans)
f=
exp(a*x)*sin(b*x)
eax
sin(bx)dx
a2
1
b2
eax[a sin(bx)
b cos(bx)]
例18、绘函数 f ( x) eax sinbx (a = 1, b = 3 )在[0,3.2]上的图形.
并计算 2 e x sin3xdx . 1
syms a b x f=exp(a*x)*sin(b*x) f1=subs(f,a,1),f1=subs(f1,b,3) ezplot(f1,0,3.22)
要将符号表达式中的某一个变量转换为一个数或者另 一个变量时,可用函数subs: subs(A, ‘old’, ‘new’) 用‘new’置换符号表达式A中的’old’ 得到新的符号表达式。
命令eval可计算符号表达式的值
例9. 求符号多项式的值。
>> syms a x >> f=a*x^2+3*x+4; >> subs(f1,x,5) >> f1=subs(f,a,2)
串分界符(‘),变量间用空格而不要用逗号分隔。
符号函数中只有一个符号变量时,默认其为自变量。
例1. 定义两个符号变量x,y,并绘制函数y=exp(-x^2)的图形。
MATLAB 中的符号运算

时函数的极限。
,求当 x 1, x 0 , x 0 , x
► syms x
%声明符号变量
► fx= 1/(1+exp(-1/x)); %建立符号函数fx
► limit(fx,x,1)
%求fx : x->1的极限
► limit(fx,x,0, 'right') %求fx : x->0的右极限
► limit(fx,x,0, 'left') %求fx : x->0的左极限
2、通过画图观察极限
lim
x0
cos
1 x
,
lim
x0
1 x
sin
1 x
,理解振荡间断点的
概念,无界量和无穷大量之间的关系。
3、设 y
3 e4t sin(4 2
3t
3
)
要求以
0.01秒为间隔,求出y的151个点,
并求出其导数的值和曲线.
fx=a*x^2+b*x+c %建立符号函数
solve(fx)
%求方程fx=0的符号解
ans = [ 1/2/a*(-b+(b^2-4*a*c)^(1/2))]
solve(fx, b )
%求方程fx=0关于变量b的符号解
ans = -(a*x^2+c)/x
上机练习题
1、已知函数 f (x) ex sin 4x, x [1,6] ,求出函数 f (x)的一阶导函数、 二阶导函数,并画出它们相应的曲线;研究函数性态,如单 调区间,极值点、拐点及凹凸区间。
或:
syms 符号变量1 符号变量2 …
f=表达式
例:符号多项式运算
MatLab常见函数和运算符号解读

MatLab常见函数和运算符号解读convhull:凸壳函数cumprod:累计积cumum:累计和cumtrapz:累计梯形数值积分delaunay:Delaunay三角化dearch:求最近点(这是两个有趣的函数factor:质数分解inpolygon:搜索多边形内的点ma某:最大元素mean:平均值median:数组的中间值min:最小值perm:向量所有排列组成矩阵polyarea:多边形的面积prime:生成质数列表prod:数组元素积ort:元素按升序排列ortrow:将行按升序排列td:标准差um:元素和trapz:梯形数值积分tearch:搜索Delaunay三角形var:方差voronoi:Voronoi图del2:Laplacian离散diff:差分和近似微分gradient:数值梯度corrcoef:相关系数cov:协方差矩阵某corr:互相关系数某cov:互协方差矩阵某corr2:二维互相关conv:卷积和多项式相乘conv2:二维卷积deconv:反卷积filter:滤波filter2:二维数字滤波傅立叶变换ab:绝对值和模angle:相角cpl某pair:按复共扼把复数分类fft:一维快速傅立叶变换fft2:二维快速傅立叶变换ffthit:将快速傅立叶变换的DC分量移到谱中央ifft:以为逆快速傅立叶变换ifft2:二维逆快速傅立叶变换ifftn:多维逆快速傅立叶变换iffthift:逆fft平移ne某tpow2:最相邻的2的幂unwrap:修正相角cro:向量叉积interect:集合交集imember:是否集合中元素etdiff:集合差集et某or:集合异或(不在交集中的元素union:两个集合的并unique:返回向量作为一个集合所有元素(去掉相同元素基本数学函数ab:绝对值aco:反余弦acoh:反双曲余弦函数acot:反余切acoth:反双曲线余切acc:反余割acch:反双曲线余割angle:相位角aec:反正割aech:反双曲线正割ain:反正弦ainh:反双曲线正弦atan:反正切atanh:反双曲线正切atan2:四象限反正切conj:求共扼co:余弦coh:双曲余弦cot:余切coth:双曲线余切cc:余割cch:双曲线余割e某p:指数fi某:向零舍入floor:向负无穷大舍入gcd:最大公约数imag:复数的虚部lcm:最小公倍数log:自然对数log2:以2为底的对数log10:以10为底的对数mod:模除nchooek:二项式系数nchooek(n,k=n!/{k!(n-k!}real:复数实部rem:余数round:四舍五入ec:正割ech:双曲线正割ign:符号函数in:正弦inh:双曲线正弦qrt:平方根tan:正切tanh:双曲线正切特殊函数airy:airy函数beelh:第三类贝塞尔函数;beelibeelk:改良型beelh函数beeljbeely:贝塞尔函数betabetaincbetaln:贝塔函数ellipj:雅克比椭圆函数ellipke:完全椭圆积分erferfcerfc某erfinv:误差函数e某pint:指数积分factorial:阶乘函数gammagammalngammainc:伽马函数legendre:勒让德函数pow2:2的幂次ratrat:有理逼近坐标变换cart2pol:笛卡儿坐标变换为极坐标或圆柱坐标cart2ph:笛卡儿坐标变换为球坐标pol2cart:极坐标变换为笛卡儿坐标ph2cart:球坐标变换为笛卡儿坐标矩阵和数组基础blkdiag:构造一个分块对角矩阵eye:创建单位矩阵flop:计算浮点操作次数,现已不再常用i:虚部单位inf:无穷大inputname:输入参数名j:虚部单位nan:非数值nargin:输入参数的数目nargout:输出参数的数目(用户定义函数pi:圆周率realma某:最大正浮点数realmin:最小正浮点数varargin,varargout:返回参数数目(matlab函数时间和日期calendar:返回日历clock:当前时间weekday:星期几矩阵操作cat:把矩阵按行或列连接起来diag:给定向量,构造对角矩阵fliplr:矩阵左右翻转flipud:矩阵上下翻转repmat:复制数组,repmat(A,m,n表示把A复制m行n列组成新数组rehape:按逐列来的方式重新整形数组rot:按逆时针方向旋转90度tril:返回一个矩阵的下三角矩阵triu:返回一个矩阵的上三角矩阵特殊函数矩阵gallery:测试矩阵,或者说大约50个矩阵模版hadamard:哈达马得矩阵hankel:汉克尔矩阵hilb:希尔波特矩阵invhilb:逆希尔波特矩阵magic:魔术方阵pacal:帕斯卡矩阵toeplitz:托普利茨矩阵wilkinon:维尔金森特征值测试矩阵算数运算符+:矩阵加-:减某:乘.某:数组乘^:矩阵乘方.^:数组乘方\\:矩阵左除/:矩阵右除.\\:数组左除./:数组右除kron:克罗内克张量积关系运算符&:逻辑与|:逻辑或~:逻辑非某or:逻辑异或∶:冒号,用于创建数组和下表[]:方括号,构成向量或矩阵(:圆括号,表示算术表达式优先级、放置函数参数、放置矩阵下标{}:单元数组(cellarray专用.:句点,小数点表示、数组运算符组成部分、字段(属性访问..:父目录,与cd一起使用...:连续三点,一行末尾表示续行,:逗号,格开参数;:分号,表示矩阵一行结束或者语句末尾使得执行结果不显示%:注释符':单引号,矩阵后表示转置或者成对出现括起字符串.':数组转置=:赋值逻辑函数all:向量中是否所有分量均非零any:是否有元素非零e某it:指定变量或文件是否存在find:返回矩阵中非零元素的索引和置i某:i系列,大部分根据名称可以知道功能icell(icelltr(iempty(:是否空数组iequal(:数组是否相等ifield(:是否结构数组中的字段ifinite(:数组中元素是否有限iglobal(:是否全局变量ihandle(:是否有效图形句柄ihold(:hold命令处于on状态与否iieee:是否使用IEEE算法iinf(:是否无穷大iletter(:数组元素是否是字母表中字母ilogical(:是否逻辑数组inan(:是否非数值数inumeric(:是否数值数组iobject(:是否对象iprime(:是否质数ireal(:是否实数ipace(:是否空字符ipare(:是否是按稀疏类别存储itruct(:是否结构类itudent:matlab版本是否学生版iuni某:是否uni某版本ia(:指定对象是否属于指定类logical(:把数值数组转变为逻辑数组A(B:A为数值数组,B为逻辑数组时,按B索引的非零元素返回A中相应位置元素milocked(:当前文件是否锁定仿真命令:im---仿真运行一个imulink模块ldebug---调试一个imulink模块imet---设置仿真参数imget---获取仿真参数线性化和整理命令:linmod---从连续时间系统中获取线性模型linmod2---也是获取线性模型,采用高级方法dinmod---从离散时间系统中获取线性模型trim---为一个仿真系统寻找稳定的状态参数构建模型命令:open_ytem--打开已有的模型cloe_ytem--关闭打开的模型或模块new_ytem--创建一个新的空模型窗口load_ytem--加载已有的模型并使模型不可见ave_ytem--保存一个打开的模型add_block--添加一个新的模块add_line--添加一条线(两个模块之间的连线)delete_block--删除一个模块delete_line--删除一根线find_ytem--查找一个模块hilite_ytem--使一个模块醒目显示replace_block--用一个新模块代替已有的模块et_param--为模型或模块设置参数get_param--获取模块或模型的参数add_param--为一个模型添加用户自定义的字符串参数delete_param--从一个模型中删除一个用户自定义的参数bdcloe--关闭一个imulink窗口bdroot--根层次下的模块名字gcb--获取当前模块的名字gcbh--获取当前模块的句柄gc--获取当前系统的名字getfullname--获取一个模块的完全路径名lupdate--将1.某的模块升级为3.某的模块addterm--为未连接的端口添加terminator模块booleanlhelp--将数值数组转化为布尔值--imulink挠没虻蓟蛘吣?榘镏nbp;封装命令:hamak--检查已有模块是否封装hamakdlg--检查已有模块是否有封装的对话框hamakicon--检查已有模块是否有封装的图标iconedit--使用ginput函数来设计模块图标makpopup--返回并改变封装模块的弹出菜单项movemak--重建内置封装模块为封装的子模块诊断命令:llatdiagnotic--上一次诊断信息llaterror--上一次错误信息llatwarning--上一次警告信息ldiagnotic--为一个模型获取模块的数目和编译状态硬拷贝和打印命令:frameedit--编辑打印画面print--将imulink系统打印成图片,或将图片保存为m文件printopt--打印机默认设置orient--设置纸张的方向helprtw看看,rtw相关的命令有三个命令:rtwgen-从一个模型中创建一个rtw文件(model.rtw,用此函数可以指定一些rtw的属性设置tlc-调用目标语言编译器rtwbuild-对一个模型调用rtw的build程序相关的命令好像还有make_rtw,rtw_c,tlc_c以上摘自:水木清华站。
matlab常用符号
返回值为f(g(y)) 返回值为f(g(z)) 返回值为f(g(z)) 返回值为f(g(z))
8 代数式展开
syms 表达式中包含的变量 expand(表达式) 9 合并同类项
syms 表达式中包含的变量
collect(表达式,指定的变量)
10 进行数学式化简
syms 表达式中包含的变量 simplify(表达式) 11 进行变量替换
conj(z)
求复数z的共轭复数
ceil(x) 求整函数与 截尾函数 floor(x)
表示大于或等于实数x的最小整 数 表示小于或等于实数x的最大整 数
round(x)
最接近x的整数
max([a,b,c 求最大数
最大、最小 ,...])
函数
min([a,b,c 求最小数
,..])
符号函数
sign(x)
5 自定义函数调用时:“[返回值列]=M文件名(参数列)”
function 返回变量=函数名(输入变量) 注释说明语句段(此部分可有可无) 函数体语句
6.进行函数的复合运算
compose(f,g) compose(f,g,z) compose(f,g,x,.z) compose(f,g,x,y,z) 7 因式分解 syms 表达式中包含的变量 factor(表达式)
ezplot('f(x)' ,[xmin,xmax]) ezplot('f(x)' ,[xmin,xmax,ymin,ymax])
17 求极限 (1) 极限:
syms x limit(f(x), x, a) (2)单侧极限: 左极限: syms x limit(f(x), x, a,’left’) 右极限: syms x limit(f(x), x, a,’right’)
(完整版)MATLAB常用函数总结,推荐文档

MATLAB 常用函数总结Matlab 的内部常数pi 圆周率exp(1)自然对数的底数ei 或j虚数单位Inf 或 inf无穷大Matlab 的常用内部数学函数指数函数exp(x)以e 为底数log(x)自然对数,即以e 为底数的对数log10(x)常用对数,即以10为底数的对数对数函数log2(x)以2为底数的x 的对数开方函数sqrt(x)表示x 的算术平方根绝对值函数abs(x)表示实数的绝对值以及复数的模sin(x)正弦函数cos(x)余弦函数tan(x)正切函数cot(x)余切函数sec(x)正割函数三角函数(自变量的单位为弧度)csc(x)余割函数反三角函数asin(x)反正弦函数acos(x)反余弦函数atan(x)反正切函数acot(x)反余切函数asec(x)反正割函数acsc(x)反余割函数sinh(x)双曲正弦函数cosh(x)双曲余弦函数tanh(x)双曲正切函数coth(x)双曲余切函数sech(x)双曲正割函数双曲函数csch(x)双曲余割函数asinh(x)反双曲正弦函数acosh(x)反双曲余弦函数atanh(x)反双曲正切函数acoth(x)反双曲余切函数asech(x)反双曲正割函数反双曲函数acsch(x)反双曲余割函数求角度函数atan2(y,x)以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度,范围为(,]gcd(a,b)两个整数的最大公约数数论函数lcm(a,b)两个整数的最小公倍数排列组合函数factorial(n)阶乘函数,表示n的阶乘real(z)实部函数imag(z)虚部函数复数函数abs(z)求复数z的模angle(z)求复数z 的辐角,其范围是( ,]conj(z)求复数z 的共轭复数ceil(x)表示大于或等于实数x 的最小整数floor(x)表示小于或等于实数x 的最大整数求整函数与截尾函数round(x)最接近x 的整数max([a ,b ,c ,...])求最大数最大、最小函数min([a ,b ,c ,..])求最小数符号函数sign(x)Matlab 中的数学运算符a+b 加法 a./b 数组右除a-b 减法 a.\b 数组左除a*b 矩阵乘法a^b 矩阵乘方a.*b 数组乘法 a.^b 数组乘方a/b 矩阵右除-a负号a\b矩阵左除' 共轭转置.'一般转置Matlab 的关系运算符 ==等于<小于>大于<=小于或等于>=大于或等于~=不等于如何用matlab求阶乘factorial(n) 求n的阶乘如何用matlab进行多项式运算(1)合并同类项 syms 表达式中包含的变量 collect(表达式,指定的变量)(2)因式分解 syms 表达式中包含的变量 factor(表达式)(3)展开syms 表达式中包含的变量 expand(表达式)(4)化简syms 表达式中包含的变量simplify(表达式) 如何用matlab进行复数运算 a+b*i 或 a +b*j表示复数a+bi 或 a+bjreal(z)求复数z的实部imag(z)求复数z的虚部abs(z)求复数z的模angle(z)求复数z的辐角,conj(z)求复数z的共轭复数exp(z)复数的指数函数,表示e^z如何用Matlab求集合的交集、并集、差集和补集 union(A,B)求集合A和B的并集intersect(A,B)求集合A和B的交集setdiff(A,B)求集合A和B的差集A-Bsetdiff(U,A)求集合A关于全集U的补集如何用matlab排序sort(v) 将向量v的元素从小到大排列(升序排列)sort(v,dim,’descend or ascend’)当dim=1时矩阵按列排序,descend or ascend用来控制升序还是降序当dim=2时矩阵按行排序,descend or ascend用来控制升序还是降序如何用Matlab求极限(1)极限:syms xlimit(f(x), x, a)求f(x)关于x趋于a时的极限(2)单侧极限:左极限:syms x limit(f(x), x, a,’left’)求f(x)关于x趋于a时的左极限右极限:syms x limit(f(x), x, a,’right’)求f(x)关于x趋于a时的右极限如何用Matlab求导数diff('f(x)') diff('f(x)','x') 求f(x)关于x的导数或者:syms x diff(f(x))syms x diff(f(x), x)如何用Matlab求高阶导数如何用Matlab求高阶导数diff('f(x)',n) diff('f(x)','x',n)求f(x)关于x的n阶导数syms x diff(f(x),n)syms x diff(f(x), x,n)如何用Matlab求不定积分int('f(x)') int ('f(x)','x')求f(x)关于x的积分syms x int(f(x))syms x int(f(x), x)如何用Matlab求定积分、广义积分int('f(x)',a,b) int ('f(x)','x',a,b)求f(x)关于x的积分,区间为a到b syms x int(f(x),a,b)syms x int(f(x), x,a,b)如何用Matlab展开级数syms x taylor(f(x), x, n,)a如何在Matlab中进行积分变换syms s tlaplace( f(t), t, s ) 拉普拉斯变换ilaplace( F(s), s, t ) 拉普拉斯变换的逆变换 syms t ωfourier( f(t), t, ω)傅立叶变换ifourier( F(ω), ω, t ) 傅立叶变换的逆变换 syms n zztrans( f(n), n, z) Z变换iztrans( F(z), z, n ) Z变换的逆变换 如何用Matlab解微分方程dsolve('微分方程','自变量')dsolve('微分方程','初始条件或边界条件','自变量') dsolve('D2x+2*x+x=sin(t)','x(0)=1','Dx(0)=1','t')如何用matlab求多变量函数的极限 以两个变量为例说明,多于两个变量的函数极限可以依次类推。
(完整版)MATLAB常用函数大全

(完整版)MATLAB常用函数大全一、MATLAB常用的基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):地板函数,即舍去正小数至最近整数ceil(x):天花板函数,即加入正小数至最近整数rat(x):将实数x化为分数表示rats(x):将实数x化为多项分数展开sign(x):符号函数(Signum function)。
当x<0时,sign(x)=-1;当x=0时,sign(x)=0;当x>0时,sign(x)=1。
rem(x,y):求x除以y的馀数gcd(x,y):整数x和y的最大公因数lcm(x,y):整数x和y的最小公倍数exp(x):自然指数pow2(x):2的指数log(x):以e为底的对数,即自然对数或log2(x):以2为底的对数log10(x):以10为底的对数二、MATLAB常用的三角函数sin(x):正弦函数cos(x):余弦函数tan(x):正切函数asin(x):反正弦函数acos(x):反馀弦函数atan(x):反正切函数atan2(x,y):四象限的反正切函数sinh(x):超越正弦函数cosh(x):超越馀弦函数tanh(x):超越正切函数asinh(x):反超越正弦函数acosh(x):反超越馀弦函数atanh(x):反超越正切函数三、适用於向量的常用函数有:min(x): 向量x的元素的最小值max(x): 向量x的元素的最大值mean(x): 向量x的元素的平均值median(x): 向量x的元素的中位数std(x): 向量x的元素的标准差diff(x): 向量x的相邻元素的差sort(x): 对向量x的元素进行排序(Sorting)length(x): 向量x的元素个数norm(x): 向量x的欧氏(Euclidean)长度sum(x): 向量x的元素总和prod(x): 向量x的元素总乘积cumsum(x): 向量x的累计元素总和cumprod(x): 向量x的累计元素总乘积dot(x, y): 向量x和y的内积cross(x, y): 向量x和y的外积四、MATLAB的永久常数i或j:基本虚数单位(即)eps:系统的浮点(Floating-point)精确度inf:无限大,例如1/0nan或NaN:非数值(Not a number),例如0/0 pi:圆周率p(= 3.1415926...)realmax:系统所能表示的最大数值realmin:系统所能表示的最小数值nargin: 函数的输入引数个数nargout: 函数的输出引数个数五、MATLAB基本绘图函数plot: x轴和y轴均为线性刻度(Linear scale)loglog: x轴和y轴均为对数刻度(Logarithmic scale)semilogx: x轴为对数刻度,y轴为线性刻度semilogy: x轴为线性刻度,y轴为对数刻度六、plot绘图函数的叁数字元颜色字元图线型态y 黄色 . 点k 黑色o 圆w 白色x xb 蓝色+ +g 绿色* *r 红色- 实线c 亮青色: 点线m 锰紫色-. 点虚线-- 虚线七、注解xlabel('Input Value'); % x轴注解ylabel('Function Value'); % y轴注解title('Two Trigonometric Functions'); % 图形标题legend('y = sin(x)','y = cos(x)'); % 图形注解grid on; % 显示格线八、二维绘图函数bar 长条图errorbar 图形加上误差范围fplot 较精确的函数图形polar 极座标图hist 累计图rose 极座标累计图stairs 阶梯图stem 针状图fill 实心图feather 羽毛图compass 罗盘图quiver 向量场图1、特殊变量与常数ans 计算结果的变量名computer 确定运行的计算机eps 浮点相对精度Inf 无穷大I 虚数单位inputname 输入参数名NaN 非数nargin 输入参数个数nargout 输出参数的数目pi 圆周率nargoutchk 有效的输出参数数目realmax 最大正浮点数realmin 最小正浮点数varargin 实际输入的参量varargout 实际返回的参量操作符与特殊字符+ 加- 减* 矩阵乘法 .* 数组乘(对应元素相乘)^ 矩阵幂 .^ 数组幂(各个元素求幂)\ 左除或反斜杠/ 右除或斜面杠./ 数组除(对应元素除)kron Kronecker张量积: 冒号() 圆括[] 方括 . 小数点.. 父目录 ... 继续, 逗号(分割多条命令); 分号(禁止结果显示)% 注释! 感叹号' 转置或引用= 赋值== 相等<> 不等于& 逻辑与| 逻辑或~ 逻辑非xor 逻辑异或2、基本数学函数abs 绝对值和复数模长acos,acodh 反余弦,反双曲余弦acot,acoth 反余切,反双曲余切acsc,acsch 反余割,反双曲余割angle 相角asec,asech 反正割,反双曲正割asin,asinh 反正弦,反双曲正弦atan,atanh 反正切,双曲正切tangent 正切atan2 四象限反正切ceil 向着无穷大舍入complex 建立一个复数conj 复数配对cos,cosh 余弦,双曲余弦csc,csch 余切,双曲余切cot,coth 余切,双曲余切exp 指数fix 朝0方向取整floor 朝负无穷取整gcd 最大公因数imag 复数值的虚部lcm 最小公倍数log 自然对数log2 以2为底的对数log10 常用对数mod 有符号的求余nchoosek 二项式系数和全部组合数real 复数的实部rem 相除后求余round 取整为最近的整数sec,sech 正割,双曲正割sign 符号数sin,sinh 正弦,双曲正弦tan,tanh 正切,双曲正切3、基本矩阵和矩阵操作blkding 从输入参量建立块对角矩阵eye 单位矩阵linespace 产生线性间隔的向量logspace 产生对数间隔的向量numel 元素个数ones 产生全为1的数组rand 均匀颁随机数和数组randn 正态分布随机数和数组zeros 建立一个全0矩阵colon) 等间隔向量cat 连接数组diag 对角矩阵和矩阵对角线fliplr 从左自右翻转矩阵flipud 从上到下翻转矩阵repmat 复制一个数组reshape 改造矩阵roy90 矩阵翻转90度tril 矩阵的下三角triu 矩阵的上三角dot 向量点集cross 向量叉集ismember 检测一个集合的元素intersect 向量的交集setxor 向量异或集setdiff 向是的差集union 向量的并集数值分析和傅立叶变换cumprod 累积cumsum 累加cumtrapz 累计梯形法计算数值微分factor 质因子inpolygon 删除多边形区域内的点max 最大值mean 数组的均值mediam 中值min 最小值perms 所有可能的转换polyarea 多边形区域primes 生成质数列表prod 数组元素的乘积rectint 矩形交集区域sort 按升序排列矩阵元素sortrows 按升序排列行std 标准偏差sum 求和trapz 梯形数值积分var 方差del2 离散拉普拉斯diff 差值和微分估计gradient 数值梯度cov 协方差矩阵corrcoef 相关系数conv2 二维卷积conv 卷积和多项式乘法filter IIR或FIR滤波器deconv 反卷积和多项式除法filter2 二维数字滤波器cplxpair 将复数值分类为共轭对fft 一维的快速傅立叶变换fft2 二维快速傅立叶变换fftshift 将FFT的DC分量移到频谱中心ifft 一维快速反傅立叶变换ifft2 二维傅立叶反变换ifftn 多维快速傅立叶变换ifftshift 反FFT偏移nextpow2 最靠近的2的幂次unwrap 校正相位角多项式与插值conv 卷积和多项式乘法roots 多项式的根poly 具有设定根的多项式polyder 多项式微分polyeig 多项式的特征根polyfit 多项式拟合polyint 解析多项式积分polyval 多项式求值polyvalm 矩阵变量多项式求值residue 部分分式展开interp1 一维插值interp2 二维插值interp3 三维插值interpft 使用FFT的一维插值interpn 多维插值meshgrid 为3维点生成x和y的网格ndgrid 生成多维函数和插值的数组pchip 分段3次Hermite插值多项式ppval 分段多项式的值spline 3次样条数据插值绘图函数bar 竖直条图barh 水平条图hist 直方图histc 直方图计数hold 保持当前图形loglog x,y对数坐标图pie 饼状图plot 绘二维图polar 极坐标图semilogy y轴对数坐标图semilogx x轴对数坐标subplot 绘制子图bar3 数值3D竖条图bar3h 水平3D条形图comet3 3D慧星图cylinder 圆柱体fill3 填充的3D多边形plot3 3维空间绘图quiver3 3D震动(速度)图slice 体积薄片图sphere 球stem3 绘制离散表面数据waterfall 绘制瀑布trisurf 三角表面clabel 增加轮廓标签到等高线图中datetick 数据格式标记grid 加网格线gtext 用鼠标将文本放在2D图中legend 图注plotyy 左右边都绘Y轴title 标题xlabel X轴标签ylabel Y轴标签zlabel Z轴标签contour 等高线图contourc 等高线计算contourf 填充的等高线图hidden 网格线消影meshc 连接网格/等高线mesh 具有参考轴的3D网格peaks 具有两个变量的采样函数surf 3D阴影表面图surface 建立表面低层对象surfc 海浪和等高线的结合surfl 具有光照的3D阴影表面trimesh 三角网格图Matlab函数大全信源函数randerr 产生比特误差样本randint 产生均匀分布的随机整数矩阵randsrc 根据给定的数字表产生随机矩阵wgn 产生高斯白噪声信号分析函数biterr 计算比特误差数和比特误差率eyediagram 绘制眼图scatterplot 绘制分布图symerr 计算符号误差数和符号误差率信源编码compand mu律/A律压缩/扩张dpcmdeco DPCM(差分脉冲编码调制)解码dpcmenco DPCM 编码dpcmopt 优化DPCM参数lloyds Lloyd法则优化量化器参数quantiz 给出量化后的级和输出值误差控制编码bchpoly 给出二进制BCH码的性能参数和产生多项式convenc 产生卷积码cyclgen 产生循环码的奇偶校验阵和生成矩阵cyclpoly 产生循环码的生成多项式decode 分组码解码器encode 分组码编码器gen2par 将奇偶校验阵和生成矩阵互相转换gfweight 计算线性分组码的最小距离hammgen 产生汉明码的奇偶校验阵和生成矩阵rsdecof 对Reed-Solomon编码的ASCII文件解码rsencof 用Reed-Solomon码对ASCII文件编码rspoly 给出Reed-Solomon码的生成多项式syndtable 产生伴随解码表vitdec 用Viterbi法则解卷积码(误差控制编码的低级函数)bchdeco BCH解码器bchenco BCH编码器rsdeco Reed-Solomon解码器rsdecode 用指数形式进行Reed-Solomon解码rsenco Reed-Solomon编码器rsencode 用指数形式进行Reed-Solomon编码调制与解调ademod 模拟通带解调器ademodce 模拟基带解调器amod 模拟通带调制器amodce 模拟基带调制器apkconst 绘制圆形的复合ASK-PSK星座图ddemod 数字通带解调器ddemodce 数字基带解调器demodmap 解调后的模拟信号星座图反映射到数字信号dmod 数字通带调制器dmodce 数字基带调制器modmap 把数字信号映射到模拟信号星座图(以供调制)qaskdeco 从方形的QASK星座图反映射到数字信号qaskenco 把数字信号映射到方形的QASK星座图专用滤波器hank2sys 把一个Hankel矩阵转换成一个线性系统模型hilbiir 设计一个希尔伯特变换IIR滤波器rcosflt 升余弦滤波器rcosine 设计一个升余弦滤波器(专用滤波器的低级函数)rcosfir 设计一个升余弦FIR滤波器rcosiir 设计一个升余弦IIR滤波器信道函数awgn 添加高斯白噪声伽罗域计算gfadd 伽罗域上的多项式加法gfconv 伽罗域上的多项式乘法gfcosets 生成伽罗域的分圆陪集gfdeconv 伽罗域上的多项式除法gfdiv 伽罗域上的元素除法gffilter 在质伽罗域上用多项式过滤数据gflineq 在至伽罗域上求Ax=b的一个特解gfminpol 求伽罗域上元素的最小多项式gfmul 伽罗域上的元素乘法gfplus GF(2^m)上的元素加法gfpretty 以通常方式显示多项式gfprimck 检测多项式是否是基本多项式gfprimdf 给出伽罗域的MATLAB默认的基本多项式gfprimfd 给出伽罗域的基本多项式gfrank 伽罗域上矩阵求秩gfrepcov GF(2)上多项式的表达方式转换gfroots 质伽罗域上的多项式求根gfsub 伽罗域上的多项式减法gftrunc 使多项式的表达最简化gftuple 简化或转换伽罗域上元素的形式工具函数bi2de 把二进制向量转换成十进制数de2bi 把十进制数转换成二进制向量erf 误差函数erfc 余误差函数istrellis 检测输入是否MATLAB的trellis结构(structure)marcumq 通用Marcum Q 函数oct2dec 八进制数转十进制数poly2trellis 把卷积码多项式转换成MATLAB的trellis描述vec2mat 把向量转换成矩阵——————————————————————————————————————————————————A aabs 绝对值、模、字符的ASCII码值acos 反余弦acosh 反双曲余弦acot 反余切acoth 反双曲余切acsc 反余割acsch 反双曲余割align 启动图形对象几何位置排列工具all 所有元素非零为真angle 相角ans 表达式计算结果的缺省变量名any 所有元素非全零为真area 面域图argnames 函数M文件宗量名asec 反正割asech 反双曲正割asin 反正弦asinh 反双曲正弦assignin 向变量赋值atan 反正切atan2四象限反正切atanh 反双曲正切autumn 红黄调秋色图阵axes 创建轴对象的低层指令axis 控制轴刻度和风格的高层指令B bbar 二维直方图bar3 三维直方图bar3h 三维水平直方图barh 二维水平直方图base2dec X进制转换为十进制bin2dec 二进制转换为十进制blanks 创建空格串bone 蓝色调黑白色图阵box 框状坐标轴break while 或for 环中断指令brighten 亮度控制C ccapture (3版以前)捕获当前图形cart2pol 直角坐标变为极或柱坐标cart2sph 直角坐标变为球坐标cat 串接成高维数组caxis 色标尺刻度cd 指定当前目录cdedit 启动用户菜单、控件回调函数设计工具cdf2rdf 复数特征值对角阵转为实数块对角阵ceil 向正无穷取整cell 创建元胞数组cell2struct 元胞数组转换为构架数组celldisp 显示元胞数组内容cellplot 元胞数组内部结构图示char 把数值、符号、内联类转换为字符对象chi2cdf 分布累计概率函数chi2inv 分布逆累计概率函数chi2pdf 分布概率密度函数chi2rnd 分布随机数发生器chol Cholesky分解clabel 等位线标识cla 清除当前轴class 获知对象类别或创建对象clc 清除指令窗clear 清除内存变量和函数clf 清除图对象clock 时钟colorcube 三浓淡多彩交叉色图矩阵colordef 设置色彩缺省值colormap 色图colspace 列空间的基close 关闭指定窗口colperm 列排序置换向量comet 彗星状轨迹图comet3 三维彗星轨迹图compass 射线图compose 求复合函数cond (逆)条件数condeig 计算特征值、特征向量同时给出条件数condest 范-1条件数估计conj 复数共轭contour 等位线contourf 填色等位线contour3 三维等位线contourslice 四维切片等位线图conv 多项式乘、卷积cool 青紫调冷色图copper 古铜调色图cos 余弦cosh 双曲余弦cot 余切coth 双曲余切cplxpair 复数共轭成对排列csc 余割csch 双曲余割cumsum 元素累计和cumtrapz 累计梯形积分cylinder 创建圆柱D ddblquad 二重数值积分deal 分配宗量deblank 删去串尾部的空格符dec2base 十进制转换为X进制dec2bin十进制转换为二进制dec2hex 十进制转换为十六进制deconv 多项式除、解卷delaunay Delaunay 三角剖分del2 离散Laplacian差分demo Matlab演示det 行列式diag 矩阵对角元素提取、创建对角阵diary Matlab指令窗文本内容记录diff 数值差分、符号微分digits 符号计算中设置符号数值的精度dir 目录列表disp 显示数组display 显示对象内容的重载函数dlinmod 离散系统的线性化模型dmperm 矩阵Dulmage-Mendelsohn 分解dos 执行DOS 指令并返回结果double 把其他类型对象转换为双精度数值drawnow 更新事件队列强迫Matlab刷新屏幕dsolve 符号计算解微分方程E eecho M文件被执行指令的显示edit 启动M文件编辑器eig 求特征值和特征向量eigs 求指定的几个特征值end 控制流FOR等结构体的结尾元素下标eps 浮点相对精度error 显示出错信息并中断执行errortrap 错误发生后程序是否继续执行的控制erf 误差函数erfc 误差补函数erfcx 刻度误差补函数erfinv 逆误差函数errorbar 带误差限的曲线图etreeplot 画消去树eval 串演算指令evalin 跨空间串演算指令exist 检查变量或函数是否已定义exit 退出Matlab环境exp 指数函数expand 符号计算中的展开操作expint 指数积分函数expm 常用矩阵指数函数expm1 Pade法求矩阵指数expm2 Taylor法求矩阵指数expm3 特征值分解法求矩阵指数eye 单位阵ezcontour 画等位线的简捷指令ezcontourf 画填色等位线的简捷指令ezgraph3 画表面图的通用简捷指令ezmesh 画网线图的简捷指令ezmeshc 画带等位线的网线图的简捷指令ezplot 画二维曲线的简捷指令ezplot3 画三维曲线的简捷指令ezpolar 画极坐标图的简捷指令ezsurf 画表面图的简捷指令ezsurfc 画带等位线的表面图的简捷指令F ffactor 符号计算的因式分解feather 羽毛图feedback 反馈连接feval 执行由串指定的函数fft 离散Fourier变换fft2 二维离散Fourier变换fftn 高维离散Fourier变换fftshift 直流分量对中的谱fieldnames 构架域名figure 创建图形窗fill3 三维多边形填色图find 寻找非零元素下标findobj 寻找具有指定属性的对象图柄findstr 寻找短串的起始字符下标findsym 机器确定内存中的符号变量finverse 符号计算中求反函数fix 向零取整flag 红白蓝黑交错色图阵fliplr 矩阵的左右翻转flipud 矩阵的上下翻转flipdim 矩阵沿指定维翻转floor 向负无穷取整flops 浮点运算次数flow Matlab提供的演示数据fmin 求单变量非线性函数极小值点(旧版)fminbnd 求单变量非线性函数极小值点fmins 单纯形法求多变量函数极小值点(旧版)。
MATLAB符号数学常用函数

第4章符号数学的基础sym(‘x’) 创建一个符号变量xSyms a b c …findsym对默认自变量进行查询。
findsym(f)factor(S)pretty(f) %将表达式按照类似书写习惯的方式显示。
expand(S) 因式展开符号表达式S。
collect(S,n) 将符号表达式S中自变量n的同次幂项的系数合并simplify(S) 化简函数,使用Maple的化简规则可用于化简各种表达式。
[r,how]=simple(S) 返回S的最简化形式[n,d]=numden(S) 将符号表达式S转换为分子和分母都是整系数的最佳多项式。
horner(S) 将符号表达式S转换为嵌套形式。
[Y,SIGMA]=subexpr(S,SIGMA) 此函数用变量SIGMA(字符或字符串)的值R=subs(S,old,new) 用新的符号变量new替换原来符号表达式S中的变量old。
limit(F,x,a) 计算符号表达式F在ax→条件下的极限limit(F,a) 计算符号表达式F中默认自变量趋向于a条件下的极限。
limit(F ) 计算符号表达式F在默认自变量趋向于0时的极限。
limit(F,x,a,‘right’) 计算符号表达式F在ax→条件下的右极限。
limit(F,x,a,’left’) 计算符号表达式F在ax→条件下的左极限。
diff(S) 求符号表达式S对于默认自变量的微分diff(S,v) 求符号表达式S对于自变量v的微分diff(S,n) 求符号表达式S对于默认自变量的n次微分int(S) 求符号表达式S对于默认自变量的不定积分int(S,v) 求符号表达式S对于自变量v的不定积分int(S,a,b) 求符号表达式S对于默认自变量从a到b的定积symsum(S) 求符号表达式S对于默认自变量的不定和。
symsum(S,v) 求符号表达式S对于自变量v的不定和。
symsum(S,a,b) 求符号表达式S对于默认自变量从a到b的有限和。
(完整)MatLab常用函数大全,推荐文档

13、求矩阵的最大值和最小值
求矩阵A的最大值的函数有三种调用格式,分别是:
(1)max(A):返回一个行向量,向量的i个元素是矩阵A的第i列的最大值。
(2)[y,u]=max(A):返回行向量y和u,y纪录A的每列的最大值,u纪录每列最大值的行号。
factor(s):对符号表达式s分解因式。
expand(s):对符号表达式s进行展开。
例如:
syms x y;
s1=x^3-6*x^2+11*x-6
s1 =
x^3-6*x^2+11*x-6
factor(s1)
ans =
(x-1)*(x-2)*(x-3)
s2=(x-y)*(x+y)
s2 =
(x-y)*(x+y)
findsym(s)
ans =
x, y
findsym(5*x+2)
ans =
x
findsym(a*x+b*y+c)%符号变量c不会出现在结果中
ans =
a, b, x, y
29、符号表达式四则运算
符号表达式的加、减、乘、除和幂运算可分别由函数symadd、symsub、symmul、symdiv和sympow来实现。例如
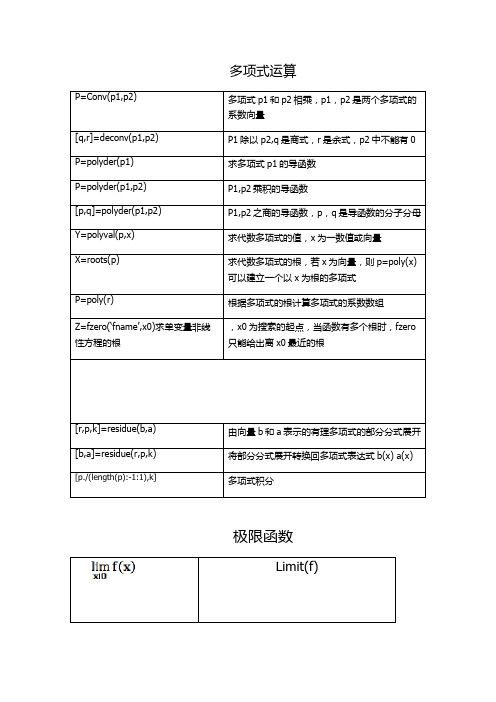
对多项式求导数的函数是:
p=polyder(p1):求多项式p1的导函数。
p=polyder(p1,p2):求多项式p1和p2乘积的导函数。
[p,q]=polyder(p1,p2):求多项式p1和p2之商的导函数,p、q是导函数的分子、分母。
例:求有理分式 的导函数。
命令如下:
p1=[1,-1];
Matlab运算符与常用函数

(2)数值计算方法求二重积分 先用 inline 函数建立求导的表达式,再用 dblquad 求二重积分
I =∫
1
−1 − 2
∫
2
e−x
2
/2
sin( x 2 + y )dxdy
f=inline('exp(-x.^2/2).*sin(x.^2+y)'); I=dblquad('f',-2,2,-1,1)
1 4x 2 + 2 = 1+ x+2 x −4 x−2
x=solve('1/(x+2)+4*x/(x^2-4)=1+2/(x-2)','x')
1 1 + 3 = 28 3 x y 1 1 + =4 x y
[x y]=solve('1/x^3+1/y^3=28','1/x+1/y=4','x,y')
(2)常用的产生通用特殊矩阵的函数有: zeros:产生全 0 矩阵(零矩阵)。 ones:产生全 1 矩阵(幺矩阵)。 eye:产生单位矩阵。 rand:产生 0~1 间均匀分布的随机矩阵。
在区间[20,50]内均匀分布的 5 阶随机矩阵:x=20+(50-20)*rand(5)
randn:产生均值为 0,方差为 1 的标准正态分布随机矩阵。
syms a x; f=(sqrt(x)-sqrt(a)-sqrt(x-a))/sqrt(x*x-a*a); limit(f,x,a,'right') %求极限(4)
matlab数值,符号运算指令
多项式运算极限函数微积分1.数值微分1.1数组差分dx=diff(x) 计算数据向量x的差分/差值当x为向量时,dx=x(2:n)-x(1:n-1);当x是矩阵时,dx=x(2:n,:)-x(1:n-1,:)。
Dx的长度比x的长度少一个元素Diff(x,n) 计算数据向量x的n阶差分/差值当f是向量时,df(1)=f(2)-f(1)(即:df(1)采用向前差值计算),df(end)=f(end)-f(end-1)(即:df(end)采用后向差值计算),df(2:end-1)=[f(3:end)-f(1:end-2)]/2(中心差值)。
Df的长度与f的相同Diff(y)./diff(x) 计算一元函数y=y(x)的数值微分1.2 梯度二元函数F=F(x,y)的梯度定义为▽F=三元函数F=F(x,y,z)的梯度▽F=+k[fx,fy]=gradient(F,hx,hy) 计算二元函数的梯度/差值,hx,hy为点间距[fx,fy,fz]= gradient(F,hx,hy,hz) 计算三元函数的梯度/差值,hx,hy,hz为点间距当f是矩阵时,fx fy 是与f同样大小的矩阵,fx的每行给出f相应元素间的差值,fy 的每列给出f相应列元素间的差值1.3Jacobi矩阵多元函数阵列的Jacobi 矩阵定义为Jacobian(F,v) 求解多元函数列阵F的Jacobi矩阵2.数值求和与近似数值积分Sx=sum(X) 沿列方向求和Scs=cusum 沿列方向求累积和St=trapz(x,y) 采用梯形法沿列方向求函数y关于自变量x的积分Sct=cumtrapz(x,y) 采用梯形法沿列方向求y关于x的累计积分S1=quad(fun,a,b,tol) 采用递推自适应辛普森(Simpson)法计算积分S1= quadl(fun,a,b,tol) 采用递推自适应洛巴托(Lobatto)法计算积分S2=dblquad(fun,xmin,xmax,ymin,ymax,tol) 二重(闭型)数值积分S3=triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol)三重(闭型)积分说明:1.若X是m×n数组,则sum(X)的结果Sx是一个1×n数组,全体元素之和。
Matlab符号数学函数

符号数学计算——基本函数介绍sym与syms函数功能介绍:符号对象的创建语法说明:✧variable=sym(A,flag)✧S=sym(‘A’,flag)✧syms a b c flag:用来创建多个符号变量【注】flag选项:d(最接近的十进制浮点精确表示)、e(带估计误差的有理表示)、f(十六进制浮点表示)、r(为默认设置时,最接近有理表示的形式);对于转换对象是字符串时:positive(先定A为整的实型符号变量)、real(限定A为实型符号变量)实例:>> r = sym(2/3)r =2/3>> f = sym(2/3, 'f')f =6004799503160661/9007199254740992>> d = sym(2/3, 'd')d =0.66666666666666662965923251249478>> e = sym(2/3, 'e')e =2/3 - eps/6>> syms a b c>> a, b, ca =ab =bc =c>> f = sym('a*x^4+b*x^3+c*x^2+d*x+e') f =a*x^4 + b*x^3 + c*x^2 + d*x + e>> syms a b c d e x>> f = a*x^4+b*x^3+c*x^2+d*x+ef =a*x^4 + b*x^3 + c*x^2 + d*x + e>> syms x y;>> m1 = [1, 2+x, 1; 2+x, 1, 3+y; 1, 3+y, 0 ] m1 =[ 1, x + 2, 1][ x + 2, 1, y + 3][ 1, y + 3, 0]>> m2 = sym('[1, 2+x, 1; 2+x, 1, 3+y; 1, 3+y, 0 ]')m2 =[ 1, x + 2, 1][ x + 2, 1, y + 3][ 1, y + 3, 0]findsym函数功能介绍:查找字符表达式中的符号变量语法说明:✧findsym(S):返回表达式S中的所有符号变量✧findsym(S,N):返回符号表达式中距离符号变量x或者X最接近的N个符号变量实例:>> syms x y z u v w>> f = sym('3*x^2+2*y+z+u^-1+v^-2+w^-3');>> findsym(f)ans =u,v,w,x,y,z>> findsym(f, 3)ans =x,y,wdigits函数功能介绍:设置近似解的精度语法说明:✧digits(d):修改当前数值计算精度为d位有效数字。
matlab符号函数

matlab符号函数
matlab符号函数是matlab中的一类函数,用于解决数学和科学的许多复杂问题。
它允许用户使用符号表达式,以帮助解决特定的问题,有效地优化计算过程,简化定义和数学运算。
常见的符号函数包括如下:
1)diff函数:用于计算一元函数的偏导函数。
2)int函数:用于求一元函数的积分。
3)poly函数:用于求多项式的系数。
4)solve函数:用于求解方程组的根。
5)determinant函数:用于求解矩阵的行列式。
6)simplify函数:用于简化表达式,即简化式中的各元素的计算。
7)factor函数:用来求代数多项式的相应因子。
8)sums函数:用于求数值序列的总和。
matlab符号函数在解决各种复杂问题中扮演了举足轻重的作用,能够更有效地求解出数据,节省计算时间。
matlab符号运算函数大全

3.1 算术符号操作命令+、-、*、.*、\、.\、/、./、^、.^、’、.’功能符号矩阵的算术操作用法如下:A+B、A-B 符号阵列的加法与减法。
若A与B为同型阵列时,A+B、A-B分别对对应分量进行加减;若A与B中至少有一个为标量,则把标量扩大为与另外一个同型的阵列,再按对应的分量进行加减。
A*B 符号矩阵乘法。
A*B为线性代数中定义的矩阵乘法。
按乘法定义要求必须有矩阵A的列数等于矩阵B的行数。
即:若A n*k*B k*m=(a ij)n*k.*(b ij)k*m=C n*m=(c ij)n*m,则,i=1,2,…,n;j=1,2,…,m。
或者至少有一个为标量时,方可进行乘法操作,否则将返回一出错信息。
A.*B 符号数组的乘法。
A.*B为按参量A与B对应的分量进行相乘。
A与B必须为同型阵列,或至少有一个为标量。
即:A n*m.*B n*m=(a ij)n*m.*(b ij)n*m=C n*m=(c ij)n*m,则c ij= a ij* b ij,i=1,2,…,n;j=1,2,…,m。
A\B 矩阵的左除法。
X=A\B为符号线性方程组A*X=B的解。
我们指出的是,A\B近似地等于inv(A)*B。
若X不存在或者不唯一,则产生一警告信息。
矩阵A可以是矩形矩阵(即非正方形矩阵),但此时要求方程组必须是相容的。
A.\B 数组的左除法。
A.\B为按对应的分量进行相除。
若A与B为同型阵列时,A n*m.\B n*m=(a ij)n*m.\(b ij)n*m=C n*m=(c ij)n*m,则c ij= a ij\ b ij,i=1,2,…,n;j=1,2,…,m。
若若A与B中至少有一个为标量,则把标量扩大为与另外一个同型的阵列,再按对应的分量进行操作。
A/B 矩阵的右除法。
X=B/A为符号线性方程组X*A=B的解。
我们指出的是,B/A粗略地等于B*inv(A)。
若X不存在或者不唯一,则产生一警告信息。
MATLAB常用函数总结

MATLAB常用函数总结MATLAB是一个功能强大的数值计算与科学数据可视化工具,具备丰富的函数库,可以用于各种数学计算、数据处理、统计分析和图形绘制等任务。
在下面的总结中,我们将介绍一些常用的MATLAB函数,以帮助您更好地使用这个软件。
一、数学计算函数1. abs(x):求x的绝对值。
2. sign(x):返回x的符号,正数返回1,负数返回-1,零返回0。
3. sqrt(x):求x的平方根。
4. exp(x):计算e的x次幂。
5. log(x):以e为底的对数。
6. log10(x):以10为底的对数。
7. sin(x):计算x的正弦值。
8. cos(x):计算x的余弦值。
9. tan(x):计算x的正切值。
10. asin(x):计算x的反正弦值。
11. acos(x):计算x的反余弦值。
12. atan(x):计算x的反正切值。
13. floor(x):返回不超过x的最大整数。
14. ceil(x):返回不小于x的最小整数。
15. round(x):将x四舍五入为最接近的整数。
二、数据处理函数1. size(A):返回矩阵A的大小。
2. length(A):返回矩阵A的最大维度。
3. sum(A):对矩阵A的元素求和。
4. mean(A):求矩阵A的平均值。
5. max(A):找到矩阵A的最大值。
6. min(A):找到矩阵A的最小值。
7. sort(A):对矩阵A进行排序。
8. reshape(A, m, n):将矩阵A重塑为m行n列的矩阵。
9. repmat(A, m, n):将矩阵A重复m行n列。
10. find(A):返回矩阵A中非零元素的索引。
三、统计分析函数1. mean(A):求矩阵A的平均值。
2. median(A):求矩阵A的中位数。
3. std(A):求矩阵A的标准差。
4. var(A):求矩阵A的方差。
5. corrcoef(A):计算矩阵A的相关系数矩阵。
6. cov(A):计算矩阵A的协方差矩阵。
matlab加减乘除运算

matlab加减乘除运算
Matlab是一款非常强大的数学软件,可以进行各种加减乘除运算。
在Matlab中进行加减乘除运算,我们需要使用不同的符号和函数。
下面是一些常见的Matlab运算符和函数:
1. 加法:使用“+”符号进行加法运算,例如:
a = 1 + 2;
2. 减法:使用“-”符号进行减法运算,例如:
b = 5 - 3;
3. 乘法:使用“*”符号进行乘法运算,例如:
c = 4 * 6;
4. 除法:使用“/”符号进行除法运算,例如:
d = 10 / 2;
5. 取余:使用“mod”函数进行取余运算,例如:
e = mod(10, 3);
6. 幂运算:使用“^”符号进行幂运算,例如:
f = 2^3;
除了这些基本的运算符和函数之外,Matlab还提供了许多高级的数学运算符和函数,例如三角函数、指数函数、对数函数等等。
通过熟练掌握这些运算符和函数,我们可以轻松进行各种复杂的数学运算。
- 1 -。
MATLAB的运算符号及函数

3.常用的函数及常量
常用的函数及常量如表7-2所示。
函数名 abc(x)
pi sin(x) asin(x) cos(x)
函数功能 绝对值函数 |x|
圆周率 正弦函数 sin(x) 反正弦函数 arcsin(x) 余弦函数 cos(x)
acos(x)
反余弦函数 arccos(x)
tan(x) cot(x)
经济数学
MATLAB的运算符号及函数
1.基本运算
MATLAB能识别常用的加(+)、减(-)、乘(*)、除(/)及 幂次运算符号(^)等绝大部分数学运算符号。因此,要在 MATLAB中进行基本数学运算,只需在命令窗口中的提示符(>>) 之后直接输入运算式并按Enter键即可。
例如:>>(2 * 3+3 * 4)/10
中(均用小括号),从最里层向最外层逐渐脱开。
2.常用快捷键 常用快捷键如表7-1所示。
快捷键 ↑(Ctrl+P) ↓(Ctrl+N) ←(Ctrl+B) →(Ctrl+F) Esc(Ctrl+U) Del(Ctrl+D)
表7-1
功能 调用上一行 调用下一行 光标左移一个字符 光标右移一个字符 清除当前输入行 删除光标处右侧字符
正切函数 tan(x) 余切函数 cot(x)
函数名 sum(x) sqrt(x)
inf exp(x) log(x)
log10(x)
log2(x) sign(x)
表7-2
函数功能 向量元素求和
平方根 无穷大 指数 ex 自然对数 lnx 以 10 为底的常用对数
lgx 以 2 为底的对数符号 Nhomakorabea数概率学与数理统计
matlab符号运算函数大全

3.1算术符号操作命令+、-、*、.*、\、.\、/、./、^、.^、’、.’功能符号矩阵的算术操作用法如下:A+B、A-B 符号阵列的加法与减法。
若A与B为同型阵列时,A+B、A-B分别对对应分量进行加减;若A与B中至少有一个为标量,则把标量扩大为与另外一个同型的阵列,再按对应的分量进行加减。
A*B 符号矩阵乘法。
A*B为线性代数中定义的矩阵乘法。
按乘法定义要求必须有矩阵A的列数等于矩阵B的行数。
即:若A n*k*B k*m=(a ij)n*k.*(b ij)k*m=C n*m=(c ij)n*m,则,i=1,2,…,n;j=1,2,…,m。
或者至少有一个为标量时,方可进行乘法操作,否则将返回一出错信息。
A.*B 符号数组的乘法。
A.*B为按参量A与B对应的分量进行相乘。
A与B必须为同型阵列,或至少有一个为标量。
即:A n*m.*B n*m=(a ij)n*m.*(b ij)n*m=C n*m=(c ij)n*m,则c ij= a ij* b ij,i=1,2,…,n;j=1,2,…,m。
A\B 矩阵的左除法。
X=A\B为符号线性方程组A*X=B的解。
我们指出的是,A\B近似地等于inv(A)*B。
若X不存在或者不唯一,则产生一警告信息。
矩阵A可以是矩形矩阵(即非正方形矩阵),但此时要求方程组必须是相容的。
A.\B 数组的左除法。
A.\B为按对应的分量进行相除。
若A与B为同型阵列时,A n*m.\B n*m=(a ij)n*m.\(b ij)n*m=C n*m=(c ij)n*m,则c ij= a ij\ b ij,i=1,2,…,n;j=1,2,…,m。
若若A与B中至少有一个为标量,则把标量扩大为与另外一个同型的阵列,再按对应的分量进行操作。
A/B 矩阵的右除法。
X=B/A为符号线性方程组X*A=B的解。
我们指出的是,B/A粗略地等于B*inv(A)。
若X不存在或者不唯一,则产生一警告信息。
MATLAB运算符和基本函数

MATLAB运算符和基本函数吉林农业大学·数学系·2013吉林农业大学·MATLAB运算符和基本函数-1-表1:MATLAB算术运算符序号运算符说明1A+B两矩阵相加或一个数和矩阵相加2A-B两矩阵相减或一个数和矩阵相减3-A矩阵的每个数取相反数4A*B两矩阵相乘或一个数和矩阵相乘5B/A方程XA=B的解6A“B方程AX=B的解7A^B A的B次幂,A—或B至少有一个是标量8 A.*B两数组逐元素对应相乘9 A./B数组A逐元素除以数组B10 A.“B数组B逐元素除以数组A11 A.^B数组A元素的对应数组B元素的次幂12A’矩阵的转置(数组的共轭转置)13 A.’数组的转置表2:MATLAB关系运算符序号运算符说明1A¡B小于,返回逻辑值,下同2A¡=B小于等于3A¿B大于4A¿=B大于等于5A==B等于6A˜=B不等于-2-吉林农业大学·MATLAB运算符和基本函数表3:MATLAB逻辑运算符序号运算符说明1A&&B短路逻辑与2A——B短路逻辑或3A&B逻辑与4A—B逻辑或5˜A逻辑非表4:MATLAB特殊符号序号运算符说明1=赋值2:冒号运算符3()输入参数,优先处理,下标4[]输出参数,构造数组5 3.14小数点6 A.B结构体A的成员B7 A.(B)结构体A的成员B8..父目录9...在下一行继续输入语句10,数组同行元素间,参数间,语句间的分隔符11;数组行间,语句间的分隔符12%注释13!执行系统命令14’s’字符串15@函数句柄16˜未使用的参数,逻辑非吉林农业大学·MATLAB运算符和基本函数-3-表5:MATLAB基本函数序号名字说明1abs计算绝对值或模2acos,acosd按弧度或度返回反余弦值3acot,acotd按弧度或度返回反余切值4acsc,acscd按弧度或度返回反余割值5all所有元素都为真才返回真6and逻辑与7angle计算复数的辐角8any某个元素为真就返回真9asec,asecd按弧度或度返回反正割值10asin,asind按弧度或度返回反正弦值11atan,atand按弧度或度返回反正切值12atan2atan的四象限版本13axis控制图形中轴的刻度和显示14box显示或隐藏图形的边界15break在for或while中退出循环16case定义switch中的一个块17cd改变当前工作目录18ceil向正无穷取整19cell产生元胞变量20char产生字符变量21clc清空命令窗口中所有的显示内容22clear从工作空间中删除变量23close关闭图形窗口24collect对符号表达式合并同类项25cond计算矩阵的条件数26conj计算复数的共轭27continue在for或while中退出本次循环28contour绘制等高线图29contourf绘制带填充的等高线图-4-吉林农业大学·MATLAB运算符和基本函数表5:(续表)30conv计算两个多项式的积31cos,cosd按弧度或度计算余弦32cot,cotd按弧度或度计算余切33cross计算两个三维向量的叉积34csc,cscd按弧度或度计算余割35cumprod计算累积积36cumsum计算累积和37deconv计算两个多项式的商和余式38det计算矩阵的行列式值39diag 返回矩阵的对角线元素,或者创建对角阵40diff 计算数值向量的差分,或计算符号变量的微分41dir显示目录及文件42disp在命令窗口中显示MATLAB变量43dot计算点积44double把给定的数转换成双精度数45eig求矩阵的特征值和特征向量46else if语句的一部分47elseif定义条件的语句,if语句的一部分48end 定义在if,switch,for或while的最后一行,表示语句的结束,或者用于数组下标中表示最大下标49eps浮点数的最小相对误差50error 脚本或函数异常终止,并可输出错误信息51eval执行字符串形式的表达式或命令52exist确定变量,文件,目录或类是否存在53exp指数函数54expand展开符号表达式55eye返回单位阵吉林农业大学·MATLAB运算符和基本函数-5-表5:(续表)56ezplot简易二维绘图57factor符号表达式的因式分解58false假59fclose关闭文件60feval使用函数句柄计算函数值61figure创建新图形窗口62fill绘制带填充颜色的多边形63find返回数组的非零值和相应的下标64findstr 返回一个字符串在另一个字符串中的位置65fix向零取整66fliplr左右翻转矩阵67flipud上下翻转矩阵68floor向负无穷取整69fminsearch计算函数的最小值70fopen打开文件,获得文件句柄71for指定循环次数的语句72format 改变命令窗口中数值的显示格式.尝试format long和format short73fplot函数二维绘图74fprintf把格式化数据写入文本文件75fread从文件中读二进制数据76fscanf从文本文件中读格式化数据77fsolve方程或方程组求解78full把稀疏矩阵转换成普通矩阵79function函数声明80fwrite把二进制数据写入文件81fzero计算函数的零点82global声明全局变量83help在命令窗口中显示函数的帮助信息-6-吉林农业大学·MATLAB运算符和基本函数表5:(续表)84hold 控制将要绘制的新图形是否覆盖原有图形85if定义条件的语句86image返回复数的虚部87ind2sub把单下标转换成多下标88inf无穷大的IEEE表示89inline产生内联函数90input在命令窗口输入数据91int计算符号表达式的积分92inv求矩阵的逆93isdir判断一个字符串是否为目录94isempty判断一个矩阵是否为空矩阵95isequal判断两个变量是否相等96isfinite判断一个数是否为有限的97isinf判断一个数是否为无限的98islogical判断一个变量是否为logical类型99isnan判断一个数是否为非数100isnumeric判断一个变量是否为数值类型101isreal判断变量是否为实数102isscalar判断一个变量是否为标量103legend在图形上加入图例104length返回数组的最长维的长度105light设置三维图形的灯光的位置106limit计算符号表达式的极限107linspace产生等间隔行向量108load从MAT文件中装载变量109log自然对数110log10常用对数111log2以2为底的对数112lower把字母转换为小写字母113lsqcurvefit最小二乘拟合吉林农业大学·MATLAB运算符和基本函数-7-表5:(续表)114max返回数组元素的最大值115mesh绘制三维网线图116meshgrid产生三维绘图使用的网格矩阵117min返回数组元素的最小值118mod,rem返回两数相除的余数119nan非数的IEEE表示120nargin返回函数输入参数的个数121nargout返回函数输出参数的个数122nnz返回矩阵非零元素的个数123not逻辑非124null计算矩阵行向量组的零空间的基125ones产生全1矩阵126or逻辑或127otherwise switch语句的一部分128pause执行暂停129pi圆周率π的16位近似值130pinv求矩阵的伪逆131plot二维曲线绘图函数132plot3三维曲线绘图函数133poly由根构造多项式134polyfit多项式拟合135polyval返回多项式的值136prod求积137pwd以字符串形式返回当前工作目录138rand产生[0,1]区间上均匀分布的随机数139randn产生标准正态分布的随机数140rank求矩阵的秩141real返回复数的实部142repmat复制并平铺矩阵143reshape改变矩阵的行列数144return从函数正常返回-8-吉林农业大学·MATLAB运算符和基本函数表5:(续表)145roots计算多项式的所有根146rot90如同图像一样把矩阵逆时针旋转90度147round向最近的整数取整,即四舍五入取整148save把变量存储到MAT文件149sec,secd按弧度或度计算正割150shading设置三维曲面图的色彩描绘模式151sign符号函数152simple化简符号表达式153sin,sind按弧度或度计算正弦154size返回数组各维的长度155sort数组元素排序156sortrows矩阵行向量排序157sparse生成稀疏矩阵158sphere绘制球体159sqrt算术平方根160std样本标准差161str2func,@生成函数句柄162strcmp比较字符串163strtok从一个字符串中提取子字符串164struct产生结构体变量165sub2ind把多下标转换成单下标166subplot子图函数167sum求和168surf绘制三维曲面图169surfc绘制带等高线的三维曲面图170switch使用表达式的多开关语句171sym,syms产生符号变量172symsum符号表达式求和173system执行操作系统命令174tan,tand按弧度或度计算正切175text在图形中的指定位置加入文本吉林农业大学·MATLAB运算符和基本函数-9-表5:(续表)176tic计时开始177title在图形上加入标题178toc 计时结束,并显示最近一次设置tic到此刻所经过的时间179trace求矩阵的迹180tril获取矩阵的下三角矩阵181triu获取矩阵的上三角矩阵182true真183upper把字母转换为大写字母184view设置三维图形的视点185vpa任意精度计算186which定位函数或文件187while不确定循环次数时的循环语句188whos 罗列工作空间中的所有变量的名字,数组大小,所占内存大小,所属类,属性等信息189xlabel为x轴加标记190xor逻辑异或191ylabel为y轴加标记192zeros产生全0矩阵193zlabel为z轴加标记。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1 算术符号操作命令+、-、*、.*、\、.\、/、./、^、.^、’、.’功能符号矩阵的算术操作用法如下:A+B、A-B 符号阵列的加法与减法。
若A与B为同型阵列时,A+B、A-B分别对对应分量进行加减;若A与B中至少有一个为标量,则把标量扩大为与另外一个同型的阵列,再按对应的分量进行加减。
A*B 符号矩阵乘法。
A*B为线性代数中定义的矩阵乘法。
按乘法定义要求必须有矩阵A的列数等于矩阵B的行数。
即:若A n*k*B k*m=(a ij)n*k.*(b ij)k*m=C n*m=(c ij)n*m,则,i=1,2,…,n;j=1,2,…,m。
或者至少有一个为标量时,方可进行乘法操作,否则将返回一出错信息。
A.*B 符号数组的乘法。
A.*B为按参量A与B对应的分量进行相乘。
A与B必须为同型阵列,或至少有一个为标量。
即:A n*m.*B n*m=(a ij)n*m.*(b ij)n*m=C n*m=(c ij)n*m,则c ij= a ij* b ij,i=1,2,…,n;j=1,2,…,m。
A\B 矩阵的左除法。
X=A\B为符号线性方程组A*X=B的解。
我们指出的是,A\B近似地等于inv(A)*B。
若X不存在或者不唯一,则产生一警告信息。
矩阵A可以是矩形矩阵(即非正方形矩阵),但此时要求方程组必须是相容的。
A.\B 数组的左除法。
A.\B为按对应的分量进行相除。
若A与B为同型阵列时,A n*m.\B n*m=(a ij)n*m.\(b ij)n*m=C n*m=(c ij)n*m,则c ij= a ij\ b ij,i=1,2,…,n;j=1,2,…,m。
若若A与B中至少有一个为标量,则把标量扩大为与另外一个同型的阵列,再按对应的分量进行操作。
A/B 矩阵的右除法。
X=B/A为符号线性方程组X*A=B的解。
我们指出的是,B/A粗略地等于B*inv(A)。
若X不存在或者不唯一,则产生一警告信息。
矩阵A可以是矩形矩阵(即非正方形矩阵),但此时要求方程组必须是相容的。
A./B 数组的右除法。
A./B为按对应的分量进行相除。
若A与B为同型阵列时,A n*m./B n*m=(a ij)n*m./(b ij)n*m=C n*m=(c ij)n*m,则c ij= a ij/b ij,i=1,2,…,n;j=1,2,…,m。
若A与B中至少有一个为标量,则把标量扩大为与另外一个同型的阵列,再按对应的分量进行操作。
A^B 矩阵的方幂。
计算矩阵A的整数B次方幂。
若A为标量而B为方阵,A^B用方阵B的特征值与特征向量计算数值。
若A与B同时为矩阵,则返回一错误信息。
A.^B 数组的方幂。
A.^B为按A与B对应的分量进行方幂计算。
若A与B为同型阵列时,A n*m..^B n*m=(a ij)n*m..^(b ij)n*m=C n*m=(c ij)n*m,则c ij= a ij^b ij,i=1,2,…,n;j=1,2,…,m。
若A与B中至少有一个为标量,则把标量扩大为与另外一个同型的阵列,再按对应的分量进行操作。
A' 矩阵的Hermition转置。
若A为复数矩阵,则A'为复数矩阵的共轭转置。
即,若A=(a ij)=(x ij+i*y ij),则。
A.' 数组转置。
A.'为真正的矩阵转置,其没有进行共轭转置。
例3-1>>syms a b c d e f g h;>>A = [a b; c d];>>B = [e f; g h];>>C1 = A.*B>>C2 = A.^B>>C3 = A*B/A>>C4 = A.*A-A^2>>syms a11 a12 a21 a22 b1 b2;>>A = [a11 a12; a21 a22];>>B = [b1 b2];>>X = B/A; % 求解符号线性方程组X*A=B的解>>x1 = X(1)>>x2 = X(2)计算结果为:C1 =[ a*e, b*f][ c*g, d*h]C2 =[ a^e, b^f][ c^g, d^h]C3 =[ -(a*c*f+c*b*h-a*e*d-b*d*g)/(a*d-b*c), (a*b*h-b^2*g+a^2*f-b*a*e)/(a*d-b*c)][ -(-c*e*d+c*d*h+c^2*f-d^2*g)/(a*d-b*c), (a*d*h+a*c*f-b*c*e-b*d*g)/(a*d-b*c)] C4 =[ -b*c, b^2-a*b-b*d][ c^2-a*c-d*c, -b*c]x1 =(-a22*b1+b2*a21)/(a12*a21-a11*a22)x2 =-(-a12*b1+a11*b2)/(a12*a21-a11*a22)3.2 基本运算命令1 合并同类项函数collect格式R = collect(S) %对于多项式S中的每一函数,collect(S)按缺省变量x的次数合并系数。
R = collect(S,v) %对指定的变量v计算,操作同上。
例3-2>>syms x y;>>R1 = collect((exp(x)+x)*(x+2))>>R2 = collect((x+y)*(x^2+y^2+1), y)>>R3 = collect([(x+1)*(y+1),x+y])计算结果为:R1 =x^2+(exp(x)+2)*x+2*exp(x)R2 =y^3+x*y^2+(x^2+1)*y+x*(x^2+1)R3 =[ (y+1)*x+y+1, x+y]命令2 列空间的基函数colspace格式 B = colspace(A) %返回矩阵B,其列向量形成由矩阵A的列向量形成的空间的坐标基,其中A可以是符号或数值矩阵。
而size(colspace(A),2)等于rank(A)。
即由A生成的空间维数等于A的秩。
例3-3>>syms a b c>>A = sym([1,a;2,b;3,c])>>B = colspace(A)计算结果为:A =[ 1, a][ 2, b][ 3, c]B =[ 1, 0][ 0, 1][ -(3*b-2*c)/(-b+2*a), (-c+3*a)/(-b+2*a)]命令3 复合函数计算函数compose格式compose(f,g) %返回复合函数f[g(y)],其中f=f(x),g=g(y)。
其中符号x为函数f中由命令findsym(f) 确定的符号变量,符号y为函数g中由命令findsym(g) 确定的符号变量。
compose(f,g,z) %返回复合函数f[g(z)],其中f=f(x),g=g(y),符号x、y为函数f、g中由命令findsym确定的符号变量。
compose(f,g,x,z) %返回复合函数f[g(z)],而令变量x为函数f中的自变量f=f(x)。
令x=g(z),再将x=g(z)代入函数f中。
compose(f,g,x,y,z) %返回复合函数f[g(z)]。
而令变量x为函数f中的自变量f=f(x),而令变量y为函数g中的自变量g=g(y)。
令x=g(y),再将x=g(y)代入函数f=f(x)中,得f[g(y)],最后用指定的变量z代替变量y,得f[g(z)]。
例3-4>>syms x y z t u v;>>f = 1/(1 + x^2*y); h = x^t; g = sin(y); p = sqrt(-y/u);>>C1 = compose(f,g) % 令x=g=sin(y),再替换f中的变量x=findsym(f)。
>>C2 = compose(f,g,t) % 令x=g=sin(t),再替换f中的变量x=findsym(f)。
>>C3 = compose(h,g,x,z) % 令x=g=sin(z),再替换h中的变量x。
>>C4 = compose(h,g,t,z) % 令t=g=sin(z),再替换h中的变量t。
>>C5 = compose(h,p,x,y,z) % 令x=p(y)=sqrt(-y/u),替换h中的变量x,再将y换成z。
>>C6 = compose(h,p,t,u,z) % 令t=p(u)=sqrt(-y/u),替换h中的变量t,再将u换成z。
计算结果为:C1 =1/(1+sin(y)^2*y)C2 =1/(1+sin(t)^2*y)C3 =sin(z)^tC4 =x^sin(z)C5 =((-z/u)^(1/2))^tC6 =x^((-y/z)^(1/2))命令4 符号复数的共轭函数conj格式conj(X) %返回符号复数X的共轭复数例3-5X=real(X) + i*imag(X),则conj(X)=real(X) - i*imag(X)命令5 符号复数的实数部分函数real格式real(Z) %返回符号复数z的实数部分命令6 符号复数的虚数部分函数imag格式imag(Z) %返回符号复数z的虚数部分命令7 余弦函数的整函数格式Y = cosint(X) %计算余弦函数在点X处的整函数值。
其中X可以是数值矩阵,或符号矩阵。
余弦函数的整函数定义为:,其中为Euler常数,=0.57721566490153286060651209…i=1,2,…,size(X)。
Euler常数可以通过命令vpa('eulergamma')获得。
例3-6>>cosint(7.2)>>cosint([0:0.1:1])>>syms x;>>f = cosint(x);>>diff(x)计算结果为:ans =0.0960ans =Columns 1 through 7Inf -1.7279 -1.0422 -0.6492 -0.3788 -0.1778 -0.0223Columns 8 through 110.1005 0.1983 0.2761 0.3374ans =1命令8 设置变量的精度函数digits格式digits(d) %设置当前的可变算术精度的位数为整数d位d = digits %返回当前的可变算术精度位数给ddigits %显示当前可变算术精度的位数说明设置有意义的十进制数值的、在Maple软件中用于做可变算术精度(命令为:vpa)计算的数字位数。
其缺省值为32位数字。
