多元统计分析——对应分析实验报告
多元统计分析 实验报告

多元统计分析实验报告1. 引言多元统计分析是一种用于研究多个变量之间关系的统计方法。
在实验中,我们使用了多元统计分析方法来探索一组数据中的变量之间的关系。
本报告将介绍我们的实验设计、数据收集和分析方法以及结果和讨论。
2. 实验设计为了进行多元统计分析,我们设计了一个实验,收集了一组相关变量的数据。
我们选择了X、Y和Z这三个变量作为我们的研究对象。
为了获得准确的结果,我们采用了以下实验设计:1.确定研究目的:我们的目标是探索X、Y和Z之间的关系,并确定它们之间是否存在任何相关性。
2.数据收集:我们通过调查问卷的方式收集了一组数据。
我们请参与者回答与X、Y和Z相关的问题,以获得关于这些变量的定量数据。
3.数据整理:在收集完数据后,我们将数据进行整理,将其转化为适合多元统计分析的格式。
我们使用Excel等工具进行数据整理和清洗。
4.数据验证:为了确保数据的准确性,我们对数据进行验证。
我们检查数据的有效性,比较数据之间的一致性,并排除任何异常值。
3. 数据分析在数据收集和整理完毕后,我们使用了一些常见的多元统计分析方法来分析我们的数据。
以下是我们使用的方法和步骤:1.描述统计分析:我们首先对数据进行了描述性统计分析。
我们计算了X、Y和Z的均值、标准差、最大值和最小值等。
这些统计量帮助我们了解数据的基本特征。
2.相关性分析:接下来,我们进行了相关性分析,以确定X、Y和Z之间是否存在相关关系。
我们计算了变量之间的相关系数,并绘制了相关系数矩阵。
这帮助我们确定变量之间的线性关系。
3.回归分析:为了更进一步地研究X、Y和Z之间的关系,我们进行了回归分析。
我们建立了一个多元回归模型,通过回归方程来预测因变量。
同时,我们还计算了回归系数和R方值,以评估模型的拟合度和预测能力。
4. 结果和讨论根据我们的实验设计和数据分析,我们得出了以下结果和讨论:1.描述统计分析结果显示,X的平均值为x,标准差为s;Y的平均值为y,标准差为s;Z的平均值为z,标准差为s。
多元统计实验报告

多元统计实验报告一、实验目的多元统计分析是统计学的一个重要分支,它能够处理多个变量之间的复杂关系。
本次实验的主要目的是通过实际操作和数据分析,深入理解多元统计分析的基本原理和方法,并掌握其在实际问题中的应用。
二、实验数据本次实验使用了一组来自某市场调研公司的数据集,包含了消费者的年龄、性别、收入、消费习惯等多个变量,共计_____个样本。
三、实验方法1、主成分分析(PCA)主成分分析是一种降维方法,它通过将多个相关变量转换为一组较少的不相关变量(即主成分),来简化数据结构并提取主要信息。
2、因子分析因子分析用于发现潜在的公共因子,这些因子能够解释多个观测变量之间的相关性。
3、聚类分析聚类分析将数据对象分组,使得同一组内的对象具有较高的相似性,而不同组之间的对象具有较大的差异性。
四、实验过程1、数据预处理首先,对原始数据进行了清洗和预处理,包括处理缺失值、异常值和数据标准化等操作,以确保数据的质量和可用性。
2、主成分分析使用统计软件进行主成分分析,计算出特征值、贡献率和累计贡献率。
根据特征值大于 1 的原则,确定了保留的主成分个数。
通过主成分载荷矩阵,解释了主成分的实际意义。
3、因子分析运用因子分析方法,提取公共因子,并通过旋转因子载荷矩阵,使得因子的解释更加清晰和具有实际意义。
计算因子得分,用于进一步的分析和应用。
4、聚类分析采用 KMeans 聚类算法,根据选定的变量对样本进行聚类。
通过不断调整聚类中心和重新分配样本,最终得到了较为合理的聚类结果。
五、实验结果与分析1、主成分分析结果提取了_____个主成分,它们累计解释了_____%的方差。
第一个主成分主要反映了_____,第二个主成分主要与_____相关,以此类推。
这为我们理解数据的主要结构提供了重要的线索。
2、因子分析结果成功提取了_____个公共因子,它们能够较好地解释原始变量之间的相关性。
每个因子所代表的潜在因素也得到了清晰的解释,有助于深入了解消费者的行为特征和市场结构。
多元统计实验报告

多元统计实验报告多元统计实验报告导言在现代科学研究中,多元统计方法被广泛应用于数据分析和模式识别等领域。
本次实验旨在通过多元统计方法探索变量之间的关系,并研究其对研究对象的影响。
实验设计我们选择了一个实验样本,包括100名大学生。
我们收集了他们的性别、年龄、身高、体重、学业成绩和运动习惯等多个变量。
通过对这些变量进行统计分析,我们希望能够了解它们之间的关系,并且进一步推断这些变量对大学生的影响。
数据预处理在进行多元统计分析之前,我们首先需要对数据进行预处理。
我们对缺失值进行了处理,使用均值填充了缺失的数据。
然后,我们进行了数据标准化,以消除不同变量之间的量纲差异。
主成分分析我们首先进行了主成分分析(PCA),以降低数据维度并寻找主要的变量。
通过PCA,我们得到了三个主成分,它们分别解释了总方差的70%、20%和10%。
这表明我们可以用这三个主成分来代表原始数据的大部分信息。
聚类分析接下来,我们进行了聚类分析,以研究样本之间的相似性和差异性。
我们使用了K-means算法,并将样本分为三个簇。
通过观察每个簇的特征,我们发现第一个簇主要包括男性、年龄较大、身高较高、体重较重、学业成绩较好和较少运动的大学生;第二个簇主要包括女性、年龄较小、身高较矮、体重较轻、学业成绩一般和较多运动的大学生;第三个簇则包括了男女性别各半、年龄、身高、体重、学业成绩和运动习惯都相对均衡的大学生。
相关分析为了研究变量之间的相关性,我们进行了相关分析。
我们发现学业成绩与年龄和身高之间存在较强的正相关关系,而与体重和运动习惯之间存在较弱的负相关关系。
这表明学业成绩可能受到年龄和身高的正向影响,而受到体重和运动习惯的负向影响。
回归分析最后,我们进行了回归分析,以探究变量对学业成绩的影响。
我们选择了年龄、身高、体重和运动习惯作为自变量,学业成绩作为因变量。
通过回归分析,我们得到了一个显著的回归模型,解释了学业成绩的40%的方差。
其中,年龄和身高对学业成绩有正向影响,而体重和运动习惯对学业成绩有负向影响。
多元统计课程实验报告

一、实验背景随着社会经济的发展和科学技术的进步,数据量日益庞大,如何从大量数据中提取有价值的信息,成为统计学研究的热点问题。
多元统计分析作为统计学的一个重要分支,通过对多个变量之间的关系进行分析,为决策者提供有力的数据支持。
本实验旨在通过实际操作,让学生熟练掌握多元统计分析方法,提高数据分析能力。
二、实验目的1. 掌握多元统计分析的基本概念和方法;2. 学会运用多元统计分析方法解决实际问题;3. 提高数据分析能力,为后续课程打下坚实基础。
三、实验内容本次实验以某城市居民消费数据为例,运用多元统计分析方法对其进行分析。
四、实验步骤1. 数据导入首先,将实验数据导入统计软件(如SPSS、R等)。
本实验采用SPSS软件,数据集包含以下变量:(1)收入(y):居民年收入;(2)教育程度(x1):居民最高学历;(3)年龄(x2):居民年龄;(4)家庭人口(x3):家庭人口数量;(5)住房面积(x4):家庭住房面积。
2. 描述性统计分析对数据集进行描述性统计分析,包括各变量的均值、标准差、最大值、最小值等。
3. 相关性分析运用皮尔逊相关系数、斯皮尔曼等级相关系数等方法,分析变量之间的相关关系。
4. 主成分分析运用主成分分析方法,提取主要成分,降低数据维度。
5. 聚类分析运用K-means聚类分析方法,将居民划分为不同的消费群体。
6. 随机森林回归分析运用随机森林回归分析方法,预测居民收入。
五、实验结果与分析1. 描述性统计分析根据描述性统计分析结果,可知居民年收入、教育程度、年龄、家庭人口、住房面积的平均值、标准差、最大值、最小值等。
2. 相关性分析通过相关性分析,发现收入与教育程度、年龄、家庭人口、住房面积之间存在显著的正相关关系。
3. 主成分分析根据主成分分析结果,提取出两个主成分,累计方差贡献率为84.95%,可以解释大部分的变量信息。
4. 聚类分析通过K-means聚类分析,将居民划分为3个消费群体。
应用多元统计分析实验报告

多元统计分析实验报告学院名称理学院专业班级应用统计学14-2学生姓名张艳雪学号201411081051工资、受教育年限、初始工资和工作经验资料如下表所示: 设职工总体的以上变量服从多元正态分布,根据样本资料利用 SPSS 软件求出均注 1:最大似然估计公式为: μˆ = X = ∑ ∑ (X i - X )(X i - X )' ; ˆ第一章 多元正态分布1.1 从某企业全部职工中随机抽取一容量为 6 的样本,该样本中个职工的目前值向量和协方差矩阵的最大似然估计。
1 n n i =1 X i , Σ = 1 nn i =1一.SPSS 操作步骤:第一步:利用 spss 建立数据集第二步:分析--描述统计--描述 计算样本均值向量 第三步:分析--相关--双变量计算样本协方差阵与样本相关系数二.输出结果:⎪ μ= 37125 ⎪ 152.50⎪ ⎛ 352068000 12500 -110677500 102000 ⎫= -110677500 - 86250 2192793750 691125 ⎪16695.1⎪⎭ ∑ X i,∑ (X i - X )(X i - X )'ˆ三.实验结果分析:样本均值为样本的协方差∑⎪⎪如此就可以按照极大似然估计方程:1 nΣ =n i =1得出均值向量与协方差向量的最大似然估计结果。
μ=X=1nn i=1ˆ第三章聚类分析3.1下表是15个上市公司2001年的一些主要财务指标,使用系统聚类法和K-均值法利用SPSS软件分别对这些公司进行聚类,并对结果进行比较分析。
公司编号净资产收益率每股净利润总资产周转率资产负债率流动负债比率每股净资产净利润增长率总资产增长率111.090.210.0596.9870.53 1.86-44.0481.99211.960.590.7451.7890.73 4.957.0216.11300.030.03181.99100-2.98103.3321.18411.580.130.1746.0792.18 1.14 6.55-56.325-6.19-0.090.0343.382.24 1.52-1713.5-3.366100.470.4868.486 4.7-11.560.85710.490.110.3582.9899.87 1.02100.2330.32811.12-1.690.12132.14100-0.66-4454.39-62.759 3.410.040.267.8698.51 1.25-11.25-11.4310 1.160.010.5443.7100 1.03-87.18-7.411130.220.160.487.3694.880.53729.41-9.97128.190.220.3830.31100 2.73-12.31-2.771395.79-5.20.5252.3499.34-5.42-9816.52-46.821416.550.350.9372.3184.05 2.14115.95123.4115-24.18-1.160.7956.2697.8 4.81-533.89-27.74一、实验原理:1.系统聚类的基本思想是:首先,每个样品(或变量)先聚成一类,然后,选择距离公式计算类与类之间的距离,把距离相近的样品(或变量)先聚成类,距离相远的后聚成类,该过程一直进行下去,每个样品(或变量)总能聚到合适的类中,最后,所有的样品(或变量)聚成一类。
多元统计分析实验4

3.88
实
验
结
果
分
析
Total Variance Explained
Component
Initial Eigenvalues
Extraction Sums of Squared Loadings
Rotation Sums of Squared Loadings
Total
% of Variance
因子4与蔬菜的相关系数较高,因子5与食油的相关系数较高。
所以,主成分分析结果为,我国2003年各地区农村居民家庭平均每人主要食品消费量是由家禽和水产品
粮食,酒,蔬菜,食油组成。
教师评语
成绩
教师签名
-.170
-.015
-.122
.054
蛋类及其制品
-.214
-.056
.399
.041
.212
水产品
.398
-.200
.190
-.163
.255
食糖
.155
.392
-.007
-.023
-.076
酒
.023
-.207
.881
.097
-.184
Undefined error #11401 - Cannot open text file "C:\PROGRA~1\IBM\SPSS\STATIS~1\19\lang\en\spss.err":
(2)第一主成分的表达式为___F1=_0.238x1+0.191x2+0.265x3+0.270x4+0.173x5+0.135X6-0.046x7___,该主成分包含了原始信息的66.219_%,第二主成分的表达式为__F2= -0.087x1+0.096x2-0.126x3-0.159 x4-0.628x5+0.167x6+0.477x7,该主成分的方差贡献率为_18.358%_。
SPSS多元统计分析实验报告

实 验 课名称:SPSS统计分析
实验项目名称:多元线性回归分析
专 业 名 称:统计学
班 级:
学 号:
学 生 姓 名:
教 师 姓 名:
2014年12月20日
组别同组同学
实验日期2014年12月20日 实验名称多元统计分析
一、实验名称:
多元统计分析
二、实验目的和要求:
通过运用SPSS软件的多元统计分析揭示主管性格与雇员对其整体满意度之间的关系掌握多元统计分析的原理及建模过程。
六、实验结果与分析
通过以上建模和检验过程,最后得到的符合实际且具有统计意义的方程为:Y=0.78X1,即雇员对主管的满意程度只与主管处理雇员的抱怨有关,且成正相关。
七、讨论和回答问题及体会:
1.通过学习,我掌握了多元线性回归的基本原理和步骤,并学会运用SPSS软件进行处理该类问题和比较熟练地分析结果。
设随机变量y与一般变量x1,x2……xk的线性回归模型为:
y=β0+β1*x1+β2*x2+……+βk*xk+ε
其中β0,β1,β2……+βk是k+1个未知参数,β0称为回归常数,β1,β2……+βk称为回归系数,y称为被解释变量;x1,x2……xk称为解释变量。通过最小二乘法估算出各系数,并测定方程的拟合程度、检验回归方程和回归系数的显著性,得到最后的方程。
3运用SPSS软件进行多元分析对模型进行整理,比较调整的R系数、方差分析表、回归分析结果(各系数机器t检验等)、共显性检验等统计方法,得出结果。
四、实验仪器与设备:
SPSS软件、兼容SPSS软件的电脑一台、老师给的数据素材。
五、实验原理:
多元线性回归模型是一元线性回归模型的扩展,其基本原理与一员线性回归模型类似,计算公式如下:
多元统计分析实验报告(精选多篇)

多元统计分析实验报告(精选多篇)第一篇:多元统计分析实验报告多元统计分析得实验报告院系:数学系班级:13级 B 班姓名:陈翔学号:20131611233 实验目得:比较三大行业得优劣性实验过程有如下得内容:(1)正态性检验;(2)主体间因子,多变量检验a;(3)主体间效应得检验;(4)对比结果(K 矩阵);(5)多变量检验结果;(6)单变量检验结果;(7)协方差矩阵等同性得Box 检验a,误差方差等同性得Levene 检验 a;(8)估计;(9)成对比较,多变量检验;(10)单变量检验。
实验结果:综上所述,我们对三个行业得运营能力进行了具体得比较分析,所得数据表明,从总体来瞧,信息技术业要稍好于电力、煤气及水得生产与供应业以及房地产业。
1。
正态性检验Kolmogorov-SmirnovaShapir o—Wilk 统计量 df Sig.统计量df Sig、净资产收益率。
113 35、200*。
978 35。
677 总资产报酬率。
121 35、200*。
964 35、298 资产负债率。
086 35。
200*.962 35、265 总资产周转率.180 35、006。
864 35。
000流动资产周转率、164 35、018.88535、002 已获利息倍数、28135.000。
55135、000 销售增长率.103 35、200*。
949 35、104 资本积累率。
251 35。
000、655 35。
000 *。
这就是真实显著水平得下限。
a。
Lilliefors显著水平修正此表给出了对每一个变量进行正态性检验得结果,因为该例中样本中n=35<2000,所以此处选用 Shapiro—W ilk 统计量。
由 Sig。
值可以瞧到,总资产周转率、流动资产周转率、已获利息倍数及资本积累率均明显不遵从正态分布,因此,在下面得分析中,我们只对净资产收益率、总资产报酬率、资产负债率及销售增长率这四个指标进行比较,并认为这四个变量组成得向量遵从正态分布(尽管事实上并非如此)。
多元统计分析 实验报告

多元统计分析实验报告多元统计分析实验报告一、引言多元统计分析是一种研究多个变量之间关系的统计方法,可以帮助我们更全面地了解数据集中的信息。
本实验旨在通过多元统计分析方法,探索不同变量之间的关系,并分析其对研究结果的影响。
二、数据收集与处理在本实验中,我们收集了一份关于学生学业成绩的数据集。
数据集包括学生的性别、年龄、家庭背景、学习时间、考试成绩等多个变量。
为了方便分析,我们对数据进行了清洗和预处理,包括删除缺失值、标准化处理等。
三、描述性统计分析在进行多元统计分析之前,我们首先对数据进行了描述性统计分析。
通过计算各变量的均值、标准差、最小值、最大值等统计量,我们对数据的整体情况有了初步的了解。
例如,我们发现男生和女生的平均成绩存在差异,家庭背景与学习时间之间存在一定的相关性等。
四、相关性分析为了探索不同变量之间的关系,我们进行了相关性分析。
通过计算各个变量之间的相关系数,我们可以了解它们之间的线性关系强弱。
通过绘制相关系数矩阵的热力图,我们可以直观地观察到各个变量之间的相关性。
例如,我们发现学习时间与考试成绩之间存在较强的正相关关系,而年龄与考试成绩之间的相关性较弱。
五、主成分分析主成分分析是一种常用的降维方法,可以将多个相关变量转化为少数几个无关的主成分。
在本实验中,我们应用主成分分析方法对数据进行了降维处理。
通过计算各个主成分的解释方差比例,我们可以确定保留的主成分个数。
通过绘制主成分得分图,我们可以观察到不同变量在主成分上的贡献程度。
例如,我们发现第一主成分主要与学习时间和考试成绩相关,而第二主成分主要与家庭背景和性别相关。
六、聚类分析聚类分析是一种将样本按照相似性进行分类的方法,可以帮助我们发现数据集中的潜在模式和群体。
在本实验中,我们应用聚类分析方法对学生进行了分类。
通过选择适当的聚类算法和距离度量,我们可以将学生分为不同的群体。
通过绘制聚类结果的散点图,我们可以观察到不同群体之间的差异。
多元统计分析实验报告

---------------------------------------------------------------最新资料推荐------------------------------------------------------多元统计分析实验报告实验一实验名称时间 2014-12-31 地点 S3-204对应分析一、实验目的及要求对应分析是你也降维的思想以达到减化数据结构的目的,凤的研究广泛用于定义属性变量构成的列联表利用对应分析方法分析问卷中教育程度与网上购物支付方式之间的相互关系。
二、实验环境 SPSS 19.0window 7 系统三、实验内容及实验步骤(实践内容、设计思想与实现步骤)实验题目:通过分析问卷数据,绘制如下的教育程度与网上购物支付方式的交叉表,运用对应分析方法研究教育程度与网上购物所选择的支付方式之间的相关性,及揭示不同人群网上购物的特征等问题。
设计思想:实现步骤:2 原假设:1 : 2 > [( ? 1)( ? 1)]1.在变量视窗中录入 3 个变量,用 edu 表示【教育程度】,用 fangshi 表示【在网上购物时采用什么样的支付方式】,用 pinshu 表示【频数】;如图所示:1/ 162.先对数据进行预处理。
执行【数据】→【加权个案】命令,弹出【加权个案】对话框。
选中【加权个案】按钮,把【频数】放入【频率变量】框中,点击【确定】按钮完成。
3.打开主窗口,选择菜单栏中的【分析】→【降维】→【对应分析】命令,弹出【对应分析】对话框。
4.将【教育程度】导入【行】,将【在网上购物时采用什么样的支付方式】导入【列】。
5. 单击【定义范围(D)】,打开【对应分析:定义行范围】对话框;定义行变量分类全距最小值为 1,最大值为 4,单击【更新】;点击【继续】,返回【对应分析】对话框;同方法打开【对应分析:定义列范围】对话框;定义列变量全距最小值为 1,最大值为 5,单击【更新】;6. 单击【统计量】打开【对应分析:统计量】对话框;选择【行轮廓表】,【列轮廓表】;单击【继续】,返回【对应分析】对话框,7.选择【绘制】→【对应分析:图】对话框,选择【散点图】中的【行点】、【列点】选择【线图】中的【已转换的行类别】、【已转换的列类别】,单击【继续】,返回【对应分析】对话框。
《多元统计分析分析》实验报告

《多元统计分析分析》实验报告2012 年月日学院经贸学院姓名学号实验实验成绩名称一、实验目的(一)利用SPSS对主成分回归进行计算机实现.(二)要求熟练软件操作步骤,重点掌握对软件处理结果的解释.二、实验内容以教材例题7.2为实验对象,应用软件对例题进行操作练习,以掌握多元统计分析方法的应用三、实验步骤(以文字列出软件操作过程并附上操作截图)1、数据文件的输入或建立:(文件名以学号或姓名命名)将表7.2数据输入spss:点击“文件”下“新建”——“数据”见图1:图1点击左下角“变量视图”首先定义变量名称及类型:见图2:图2:然后点击“数据视图”进行数据输入(图3):图3完成数据输入2、具体操作分析过程:(1)首先做因变量Y与自变量X1-X3的普通线性回归:在变量视图下点击“分析”菜单,选择“回归”-“线性”(图4):图4将因变量Y调入“因变量”栏,将x1-x3调入“自变量”栏(图5):然后选择相关要输出的结果:①点击右上角“统计量(s)”:“回归系数”下选择“估计”;“残差”下选择“D.W”;在右上角选择输出“模型拟合度”、“部分相关和偏相关”“共线性诊断”(后两项是做多重共线性检验)。
选完后点击“继续”(见图6)②如果需要对因变量与残差进行图形分析则需要在“绘制”下选择相关项目(图7),一般不需要则继续③如果需要将相关结果如因变量预测值、残差等保存则点击“保存”(图8),选择要保存的项目④如果是逐步回归法或者设置不带常数项的回归模型则点击“选项”(图9)其他选项按软件默认。
最后点击“确定”,运行线性回归,输出相关结果(见表1-3)图5 图6图7图8图9回归分析输出结果:的协差阵也就是相关阵进行分解做因子分析或主成分分析),如果不需要对变量做标准化处理就选“协方差矩阵”;“输出”中的两项都选,要求输出没有旋转的因子解(主成分分析必选项)和碎石图(用图形决定提取的主成分或因子的个数);“抽取“下,默认的是基于特征值(大于1表示提取的因子或主成分至少代表1个单位标准差的变量信息,因为标准化后的变量方差为1,因子或者主成分作为提取的综合变量应该至少代表1个变量的信息),也可以自选提取的因子个数(即第二项),本例中做主成分回归,选择提取全部可能的3个主成分,所以自选个数填3。
多元统计分析实验报告)

. . .数学与计算科学学院实验报告实验项目名称相应与典型相关分析所属课程名称多元统计分析实验实验类型验证型实验日期2016年6月13日星期一班级学号姓名成绩因素B 具有对等性。
通过变换。
得c '=ΣZ Z ,r '=ΣZZ 。
(3)对因素B 进行因子分析。
计算出c '=ΣZ Z 的特征向量 及其相应的特征向量计算出因素B 的因子)(4)对因素A 进行因子分析。
计算出r '=ΣZZ 的特征向量 及其相应的特征向量计算出因素A 的因子(5)选取因素B 的第一、第二公因子 选取因素A 的第一、第二公因子将B 因素的c 个水平,,A 因素的r 个水平同时反应到相同坐标轴的因子平面上上(6)根据因素A 和因素B 各个水平在平面图上的分布,描述两因素及各个水平之间的相关关系。
1.3 在进行相应分析时,应注意的问题要注意通过独立性检验判定是否有必要进行相应分析。
因此在进行相应分析前应做独立性检验。
独立性检验中,0H :因素A 和因素B 是独立的;1H :因素A 和因素B 不独立 由上面的假设所构造的统计量为2211ˆ[()]ˆ()rcij ij i j ijk E k E k χ==-=∑∑211()r c ij i j k z ===∑∑ 其中....(/)/ij ij i j i j z k k k k k k =-,拒绝区域为221[(1)(1)]r c αχχ->--()(1)()(1)i i P Pa X '++a X ()(2)()(2)i i q qb X '++b X(2))1=X 的条件下,使得()(2)()(2)i i q qb X '+b X(2))1=X 的条件下,使得(1)、(2)X 的第一对典型相关变量。
1,2,,)r()p⎦()p ⎥⎦pU⎥⎥⎦p V⎥⎥⎦*(1)*== A X V Bˆˆr() ++b bz【实验过程】(实验步骤、记录、数据、分析)一.问题1的求解步骤:1. 将数据输入在SPSS后,在窗口中选择数据→加权个案,调出加权个案主界面,并将变量人数移入加权个案中的频率变量框中。
多元统计分析——对应分析实验报告

多元统计分析实验报告表2-2 对应分析数据(老龄化数据)三、实验过程在spss16.0软件中,对表2-2数据做对应分析。
首先应对个案进行加权操作。
选择【Date】—【Weight Cases】,出现表3对话框。
选择frequency作为加权,如图3-1所示。
图3-1 加权个案对个案加权后,开始做对应分析。
选择【Analyze】—【Date Reduction】—【Corespondence Analysis】,会出现图3-2对话画框。
图3-2 对应分析对话框接下来对行变量和列变量进行设置。
将selfassess(自评健康状况)选入Row,作为行变量,并选择【Define Range】,填写范围后点击【Update】—【Continue】,如图3-3所示;按同样的步骤,将independence(生活自理能力)选入Column(列变量),并设置列变量,如图3-4所示;最终设置结果如图3-5所示。
图3-3 行变量设置图3-4 列变量设置图3-5 对应分析设置结果点击【OK】,便可得到对应分析结果。
四、实验过程表4-1为对应分析的版本信息。
图中显示为1.1版本。
表4-1 对应分析版本信息表4-2是列联表,列示了在各个水平下的人数。
表4-2 列联表表4-3为对应分析总述表。
表中显示了奇异值(Singular Value),第一个维度的奇异值为0.253,第二个维度的奇异值为0.125;惯量(Inertia)为特征根,就是奇异值的平方;Chi Square 值为212.593,是总样本数除以总的Inertia 觉原假设,认为两个随机变量不是相互独立的,本例中就是自评健康状况和生活自理能力不是相互独立的;贡献率(Accounted for)显示,第一个维度解释了总变异的80.4%,第二个维度解释了19.6%,两个维度解释了所有的变异;接下来依次为累计贡献率(Cumulative)、奇异值的方差(Standard Deviation)、奇异值的相关系数(Correlation)。
应用多元统计分析实验报告

应用多元统计分析实验报告一、引言多元统计分析是一种通过同时考虑多个自变量对因变量的影响来进行数据分析的方法。
它可以帮助研究人员了解不同自变量之间的关系,并预测因变量的表现。
本实验旨在应用多元统计分析方法,探索自变量对于因变量的影响。
二、实验设计在本次实验中,我们选择了一个具体的研究问题:探究学生的学习成绩在不同自变量下的表现。
我们收集了100名学生的数据,包括他们的性别(自变量1)、年龄(自变量2)、家庭背景(自变量3)以及他们的数学和语文成绩(因变量)。
三、数据收集与处理我们使用问卷调查的方式收集了学生的性别、年龄和家庭背景的数据,并从学校的成绩数据库中获取了他们的数学和语文成绩。
在处理数据之前,我们进行了数据清洗和缺失值处理。
四、数据分析步骤1.描述统计分析:首先,我们对数据进行了描述性统计分析,包括计算平均值、标准差、最小值、最大值等指标,以了解数据的基本情况。
2.相关性分析:接下来,我们进行了相关性分析,探索自变量与因变量之间的关系。
我们使用皮尔逊相关系数来衡量两个变量之间的线性相关性,并进行了显著性检验。
3.多元线性回归分析:为了探究多个自变量对因变量的综合影响,我们进行了多元线性回归分析。
我们选择了逐步回归的方法,逐步将自变量加入模型,并根据显著性检验的结果决定是否保留自变量。
4.方差分析:最后,我们进行了方差分析,检验不同自变量水平下因变量均值之间的差异是否显著。
我们使用了单因素方差分析和多重比较方法。
五、结果与讨论1.描述统计分析结果显示,学生平均年龄为18岁,数学平均成绩为80分,语文平均成绩为85分。
标准差较小,表明数据的波动较小。
2.相关性分析结果显示,学生的性别和家庭背景与他们的数学和语文成绩之间存在显著相关性(p < 0.05)。
而年龄与成绩之间的相关性不显著。
3.多元线性回归分析结果显示,性别和家庭背景对学生的成绩有显著影响(p < 0.05),而年龄的影响不显著。
对应分析实验报告

实验报告课程名称多元统计分析实验项目名称五、对应分析班级与班级代码实验室名称(或课室)专业任课教师学号:姓名:实验日期:姓名实验报告成绩评语:1.对对应分析问题的思路、理论和方法认识正确;2.SAS软件相应计算结果确认与应用正确;3.SAS软件相应过程命令正确。
注:“不正确”为有不正确之处,具体见后面批注。
指导教师(签名)说明:指导教师评分后,实验报告交院(系)办公室保存。
实验项目五对应分析实验目的:通过对应分析的实验,熟悉对应分析问题的提出、解决问题的思路、方法和技能,会调用SAS软件对应分析等有关过程命令,根据计算机计算的结果,分析和解决对应分析问题。
实验原理:解决对应分析问题的思路、理论和方法。
实验设备:计算机与SAS、SPSS软件。
实验数据:教科书p240例1数据。
实验步骤:1.指标的正向化和排序表1(单独计算,可在SPSS软件中计算);2. 调用因子分析过程命令输入正向化数据求得:前k个初始因子方差贡献解释,达到简单结构的初始因子载荷阵L0k(Factor Pattern)见表2,初始因子样品值矩阵F 0n×k,对L0k、L0k+1、…、L0p都进行方差最大化的正交旋转(穷举法),从中选出达到简单结构的旋转后因子载荷阵LГl(Rotated Factor Pattern)见表2, 前l个旋转后因子方差贡献i v(i v在SAS软件中Rotated Factor Pattern),旋转后因子样品值矩阵F Гn×l;3.设确定的正向化后因子载荷阵记为L*,正向化后因子记为 F *= (F1*,…,F m*)′,正向化后因子样品值矩阵为F *n×m,调用散点图过程命令输入变量点坐标L*、样品点坐标F *n×m的行数据给出因子坐标系F1*,…, F m*中的因子分析图1。
实验结果、实验分析、结论(有关表图要有序号、表的序号在左上方、图的序号在图的正下方、表的中英文名、表的上下线为粗线、表的内线为细线、表的左右边不封口,表图不能跨页、表图旁不能留空块, 引用结论要注明参考文献):因子双重信息图对应分析应用步骤如下:(1)给出原始数据阵正向化和排序表1,对该数据进行标准化;表1 数据阵正向化表XI X2 X3 X4 X5 X6 X7山西 1.712592694 0.11148 0.092473 0.050073 0.038193 0.018803 0.079946 内蒙古 1.720524829 0.081315 0.11238 0.042396 0.04328 0.040004 0.083339 辽宁 1.769798738 0.100121 0.12397 0.041121 0.043429 0.031328 0.078919 吉林 1.883530037 0.10536 0.116952 0.045064 0.043735 0.038508 0.095256 黑龙江 1.801149494 0.0965 0.143498 0.037566 0.052111 0.026267 0.072829 海南 1.526829447 0.047852 0.095238 0.047945 0.022134 0.018519 0.096844 四川 1.562470704 0.06168 0.116677 0.048471 0.033529 0.017439 0.072043 贵州 1.378855798 0.056362 0.073262 0.044388 0.016366 0.01572 0.057261 甘肃 1.473557019 0.058043 0.088316 0.0381 0.039794 0.015167 0.067999 青海 1.501697669 0.088508 0.096899 0.038191 0.039275 0.019243 0.033801其中X1进行正向化,100/X1为值,得到新的X1列,名为全部支出市食品支出的数倍。
多元统计分析实验报告
1.实验目的:(1)掌握均值向量及协方差阵的检验方法。
(2)能够用SPSS软件或R软件实现均值及协方差阵的检验,并正确理解输出结果。
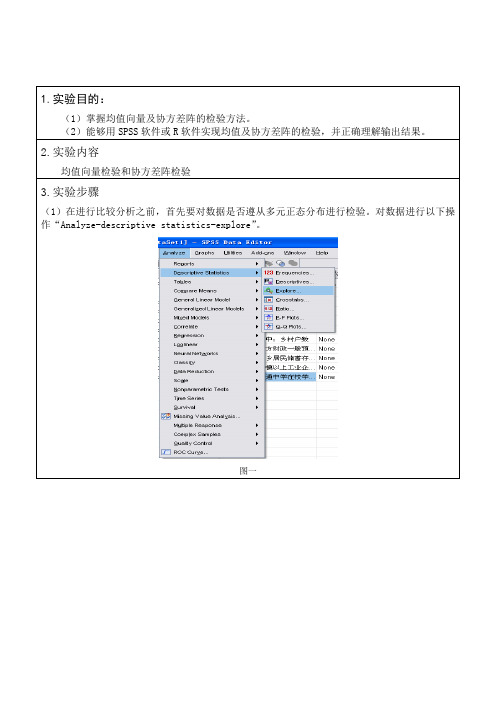
2.实验内容均值向量检验和协方差阵检验3.实验步骤(1)在进行比较分析之前,首先要对数据是否遵从多元正态分布进行检验。
对数据进行以下操作“Analyze-descriptive statistics-explore”。
图一图二单击plots,选择正态分布检验,单击continue,ok 得出结果。
图三(2)多元正态分布有关均值与方差的检验,单击“Analyze-general linear model-multivariate”,得到下图。
图4Options打开,将省份导入display means for中,如图5,continue继续,ok运行。
图54.实验结果(或心得体会)Tests of NormalityKolmogorov-Smirnov a Shapiro-WilkStatistic df Sig. Statistic df Sig.年末总户数(户).116 94 .003 .942 94 .000 年末总人口(万人).406 94 .000 .659 94 .000 地方财政一般预算收入(万元).174 94 .000 .842 94 .000 行政区域土地面积.177 94 .000 .837 94 .000 其中:乡村户数.141 94 .000 .924 94 .000 地方财政一般预算支出.258 94 .000 .777 94 .000 城乡居民储蓄存款余额.230 94 .000 .603 94 .000 规模以上工业企业个数.167 94 .000 .854 94 .000 普通中学在校学生数.336 94 .000 .588 94 .000。
多元统计分析实验报告

多元统计分析实验报告多元统计分析实验报告引言:多元统计分析是一种研究多个变量之间关系的方法,通过对多个变量进行综合分析,可以揭示出变量之间的相互作用和影响,帮助我们更好地理解数据背后的规律和现象。
本实验旨在通过对一组数据进行多元统计分析,探索变量之间的关系,并对实验结果进行解读。
实验设计:本实验选取了一组包含多个变量的数据集,其中包括性别、年龄、教育程度、收入水平、婚姻状况等变量。
通过对这些变量进行多元统计分析,我们希望了解这些变量之间是否存在相关性,并进一步探究各个变量对于整体数据集的影响。
数据收集与处理:首先,我们收集了一份包含上述变量的样本数据,共计1000个样本。
接下来,我们对数据进行了清洗和处理,包括去除异常值、缺失值的处理等。
经过处理后,我们得到了一份完整的数据集,可以进行后续的多元统计分析。
多元统计分析方法:在本实验中,我们使用了多元统计分析中的主成分分析和聚类分析两种方法。
主成分分析是一种通过将原始变量转化为一组新的综合变量,来降低数据维度并保留尽可能多的信息的方法。
聚类分析则是一种通过对样本进行分类,使得同一类别内的样本相似性较高,不同类别之间的差异性较大的方法。
实验结果与分析:经过主成分分析,我们得到了一组主成分,它们分别代表了原始变量的不同方面。
通过对主成分的解释,我们可以发现性别、年龄和教育程度等变量对于整体数据集的解释性较高,而收入水平和婚姻状况等变量的解释性较低。
这说明性别、年龄和教育程度等因素在整体数据中起着较为重要的作用。
接下来,我们进行了聚类分析,将样本分为若干个类别。
通过观察不同类别的样本特征,我们可以发现在同一类别内,样本的性别、年龄和教育程度等变量较为相似,而收入水平和婚姻状况等变量的差异较大。
这说明性别、年龄和教育程度等因素在样本分类中起到了重要的作用,而收入水平和婚姻状况等因素则对样本分类的影响较小。
结论与展望:通过本次实验的多元统计分析,我们可以得出以下结论:性别、年龄和教育程度等因素在整体数据集中起着较为重要的作用,并且对样本分类也具有一定的影响。
多元统计分析报告对应分析报告

学生实验报告学院:统计学院课程名称:多元统计分析专业班级:统计123班姓名:叶常青学号:0124253学生实验报告一、实验目的及要求:目的熟悉和掌握对应分析的原理和上机操作方法容及要求本次操作就父母与孩子的受教育程度的关系进行对应分析,分别对父亲与孩子和母亲与孩子的受教育程度做对应分析,最后再对输出结果进行详细的分析。
二、仪器用具:三、实验方法与步骤:打开GSS93 subset .sav数据,对变量Degree与变量padeg和madeg进行对应分析,依次选择分析→降维…进入对应分析对话框,进行进行如下设置,便可输出想要的数据的:四、实验结果与数据处理:按照上述方法和步骤得出以下输出结果.对父亲受教育程度与孩子受教育程度的关系进行分析如下:表1表21 .400 .160 .846 .846 .025 .2562 .164 .027 .142 .988 .0263.047 .002 .012 1.004.006 .000 .000 1.00总计. 228.193.000a 1.001.00a. 16 自由度,表3第二部分摘要给出了惯量,卡方值以及每一维度所解释的总惯量的百分比信息。
总惯量为0.,卡方值为228.193 ,有关系式228.193=0.*1205,由此可以清楚的看到总惯量和卡方的关系。
Sig.是假设卡方值为0成立的概率,它的值几乎为0说明列联表之间有较强的相关性。
表注表明的自由度为(5-1)*(5-1)=16。
惯量部分是四个公共因子分别解释总惯量的百分比。
表4表5LT High School .808 .487 .387 .218 .253 .467 High School .140 .392 .453 .383 .374 .353 Junior College .005 .017 .027 .039 .030 .Bachelor . .068 . .228 .182 .100 Graduate .016 . .040 .131 .162 .有效边际 1.000 1.000 1.000 1.000 1.000第三部分的结果是在对应分析中点击Statistics按钮,进入Statistics对话框,选中Row profiles和Column profiles 交友程序运行所得到的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多元统计分析——对应分析实验报告
————————————————————————————————作者: ————————————————————————————————日期:
ﻩ
多元统计分析实验报告
课程名称多元统计分析实验成绩
实验内容对应分析指导老师
姓名专业班级
一、实验目的
对应分析又称为相应分析,它研究的两组离散随机变量之间的关系,这些变量为定性变量。
本次实验目的为练习对应分析,熟练其操作步骤,并对结果进行说明。
二、实验数据
本文利用表2-1的数据进行分析。
其中,
表2-1北京老龄化数据
生活自理能力
完全自理部分自理不能自理合计
自评健康状况很好129 14 8 151 好931 146 96 1173 一般660 116 74 850 差251 104 81 436 很差11 7 23 41 没回答15 13 24 52 合计1997 400 306 2703
将表2-1数据保存为对应分析数据形式,如表2-2所示。
其中selfasses s(自评健康状况)的六个水平由1-6分别为“很好”“好”“一般”“差”“很差”“没回答”;independence(生活自理能力)的三个水平由1-3分别为“完全自理”“部分自理”“不能自理”;frenquency(频数)为各个水平下的人数,在接下来的分析中,会据其对变量进行加权再做分析。
表2-2 对应分析数据(北京老龄化数据)
三、实验过程
在spss16.0软件中,对表2-2数据做对应分析。
首先应对个案进行加权操作。
选择【Date】—【Weight Cases】,出现表3对话框。
选择frequency作为加权,如图3-1所示。
图3-1 加权个案
对个案加权后,开始做对应分析。
选择【Analyze】—【Date Redu ction】—【Corespondence Analysis】,会出现图3-2对话画框。
图3-2 对应分析对话框
接下来对行变量和列变量进行设置。
将selfassess(自评健康状况)选入Row,作为行变量,并选择【Define Range】,填写范围后点击【Update】—【Continue】,如图3-3所示;按同样的步骤,将independence(生活自理能力)选入Column(列变量),并设置列变量,如图3-4所示;最终设置结果如图3-5所示。
图3-3行变量设置
图3-4列变量设置
图3-5 对应分析设置结果
点击【OK】,便可得到对应分析结果。
四、实验过程
表4-1为对应分析的版本信息。
图中显示为1.1版本。
表4-1对应分析版本信息
表4-2是列联表,列示了在各个水平下的人数。
表4-2 列联表
表4-3为对应分析总述表。
表中显示了奇异值(Singular Value),第一个维度的奇异值为0.253,第二个维度的奇异值为0.125;惯量(Inertia)为特征根,就是奇异值的平方;Chi Square 值为212.593,是总样本数除以总的Inertia觉原假设,认为两个随机变量不是相互独立的,本例中就是自评健康状况和生活自理能力不是相互独立的;贡献率(Accounted for)显示,第一个维度解释了总变异的80.4%,第二个维度解释了19.6%,两个维度解释了所有的变异;接下来依次为累计贡献率(Cumulative)、奇异值的方差(Standard Deviation)、奇异值的相关系数(Correlation)。
表4-3 对应分析总述表
表4-4为行变量指标。
其中Mass就是自评健康状况各个水平的选择比例;Score in Dimension为自评健康状况在各维度上的得分,此得分就是行列得分图的坐标。
Inertia为总惯量在各类别的分配。
从惯量指标可以看出,“很差”、“差”这两类水平对总惯量的贡献最大,分别有0.035、0.025的惯量,总惯量仅有0.079;从组成(Contribution)中Of Point toInertiaof Dimension中可以看出,第一个维度主要反映了“很差”48.4%、“差”35.6%等类别,第二个维度主要反映了“没回答”54.5%、“很差”25.8%、“差”14.7%等类别,而从Of Dimensionto Inertia ofPoint可以看出,类别“很好”、“好”、“一般”、“差”、“很差”主要反映在第一维度上,反映在第一维度上的信息占其各自总反映信息的90%左右,类别“没回答”主要反映在第二维度上,反映在第二维度上的信息占其总反映信息的98%。
表4-4 行变量指标
表4-5为列变量指标。
其中Mass生活自理能力各个水平的选择比例;Score inDimension为生活自理能力在各维度上的得分,此得分就是行列得分图的坐标。
Inertia为总惯量在各类别的分配。
从惯量指标可以看出,“不能自理”这类水平对总惯量的贡献最大,惯量为0.046,总惯量为0.079,其解释了50%以上的总惯量;从组成(Contribution)中Of Point to Inertia o fDimension中可以看出,第一个维度主要反映了“完全自理”21.3%、“不能自理”66.6%等类别,第二个维度主要反映了“部分自理”73%、“不能自理”22.8%等类别,而从Of Dimension toInertia of Point可以看出,类别“完全自理”、“不能自理”、主要反映在第一维度上,反映在第一维度上的信息占其各自总反映信息的90%以上,类别“部分自理”主要反映在第二维度上,但是其反映在第二维度上的信息和第一维度的信息量差别不大,第二维度上反映
了59.7%的信息,第一维度上反映了40.3%的信息。
表4-5 列变量指标
图4-6为行列得分图,该图根据行列指标图中的各类别在各维度上的得分所绘制。
由图中可以看出,自评健康状况“很好”、“好”、“一般”,则生活自理能力越强,越接近“完全自理”;而自评状况“差”、则更接近于“部分自理”;自评状况为“很差”、“没回答”的会接近于“不能自理”。
图4-6 行列得分图
五、实验总结
通过对北京老龄化数据进行对应分析,可以看出,生活自理能力越强的老人,对自己的健康状况评价越高;生活自理能力越差,则自评健康状况越差。
这符合我们的基本认识。
另外我们还可以看到,没有回答自评状况的老人更接近与不能自理,反过来说,不能自理的老人更倾向于不回答健康状况的问题,这与老人的身体状况和心理状况是非常相关的。
对待老人,不仅要在身体上给与关心和照顾,也要在心理上给与安慰。
